Bijlage I

Effect van instroom en uitstroom op het prevalentiecijfer van een populatie

De analyse van het effect van de instroom en uitstroom op het prevalentiepercentage (decompositie-analyse) is uitgevoerd op de bevolking die aan het einde van het peiljaar (t1) 12 jaar of ouder was. Een deel van hen was in het begin van het jaar (t0) dus nog 11. En degenen die in het peiljaar zijn overleden zijn niet meegenomen.

Voor ieder jaar zijn er voor een regio dan drie stromen: instromers (I), uitstromers (U) en blijvers (B).

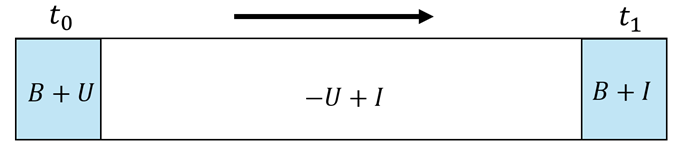
In het begin van het jaar bestaat de populatie uit blijvers en (toekomstige) uitstromers:

\begin{equation} N_{t0} = N_B + N_U \end{equation}

Aan het einde van het jaar zijn de uitstromers weg, en bestaat de populatie uit blijvers en instromers:

\begin{equation} N_{t1} = N_B + N_I \end{equation}

We zijn geïnteresseerd in een bepaald kenmerk X. Dit kenmerk verandert niet gedurende het hele jaar.

Het percentage met het bepaalde kenmerk X in het begin van het jaar is een gewogen gemiddelde van het percentage van de blijvers en (toekomstige) uitstromers:

\begin{equation} P_{BU; t0} = \frac{N_{B,X} + N_{U,X}}{N_{t0}} \end{equation}

Het percentage van het bepaalde kenmerk X aan het einde van het jaar is een gewogen gemiddelde van het percentage bij de blijvers en instromers:

\begin{equation} P_{BI; t1} = \frac{N_{B,X} + N_{I,X}}{N_{t1}} \end{equation}

Het effect van instroom + uitstroom samen is de verandering in percentage aan het eind t.o.v. het begin van het jaar:

\begin{equation} \Delta P = P_{BI; t1} - P_{BU; t0} \end{equation}

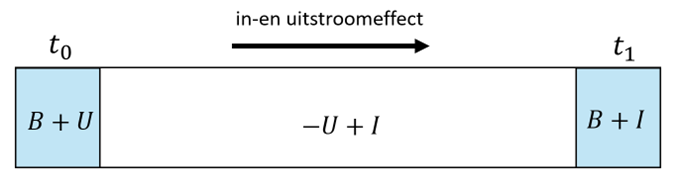
Om naar het effect van instroom en uitstroom apart te kijken, is uitgegaan van een decompositie gebaseerd op de methode van Shapley (Shorrocks, 2013), waarbij rekening wordt gehouden met de volgorde van instroom en uitstroom. Eerst worden de effecten berekend in het scenario waarbij de uitstroom vóór de instroom plaatsvindt. Daarna de effecten wanneer de instroom vóór de uitstroom plaatsvindt. Het uiteindelijke in- en uitstroomeffect is het gemiddelde van deze twee scenario’s.

Scenario 1: uitstroom vóór instroom

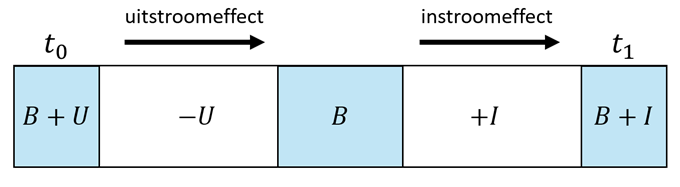
Uitstroomeffect

Als alle uitstroom vóór de instroom zou plaatsvinden, was het percentage met kenmerk X na uitstroom:

\begin{equation} P_B = \frac{N_{B,X}}{N_B} \end{equation}

Dus het effect van het verdwijnen van de uitstromers is:

\begin{equation} \Delta P_{U,scenario1} = P_{B} - P_{BU; t0} \end{equation}

Instroomeffect

In dit scenario vindt daarna de instroom plaats. Dus het effect van instroom is:

\begin{equation} \Delta P_{I,scenario1} = P_{BI;t1} - P_{B} \end{equation}

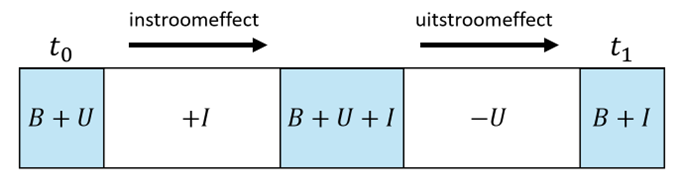
Scenario 2: instroom vóór uitstroom

Instroomeffect

Als alle instroom vóór de uitstroom plaats zou vinden was het percentage met kenmerk X na de instroom:

\begin{equation} P_{BUI} = \frac{N_{B,X} + N_{U,X} + N_{I,X}}{N_B+N_U+N_I} \end{equation}

Dus het effect van instroom is:

\begin{equation} \Delta P_{I, scenario2} = P_{BUI}-P_{BU;t0} \end{equation}

Uitstroomeffect

Daarna vindt de uitstroom plaats, dus het effect van het verdwijnen van de uitstromers is:

\begin{equation} \Delta P_{U, scenario2} = P_{BI;t1}-P_{BUI} \end{equation}

Totaal

Instroomeffect:

\begin{equation} \Delta P_I = (\Delta P_{I,scenario1} + \Delta P_{I,scenario2})/2 \end{equation}

Uitstroomeffect:

\begin{equation} \Delta P_U = (\Delta P_{U,scenario1} + \Delta P_{U,scenario2})/2 \end{equation}

Bij de berekening van het in-, en uitstroomeffect is gestratificeerd naar al dan niet emi- of immigranten.