Jaarlijkse Monitor Onderwijsachterstandenindicator, 2019-2023
Over deze publicatie
Voor het herziene onderwijsachterstandenbeleid maakt het ministerie van Onderwijs, Cultuur en Wetenschap (OCW) gebruik van de onderwijsachterstandenindicator die het Centraal Bureau voor de Statistiek eerder in opdracht van het ministerie heeft ontwikkeld. Om deze indicator actueel te kunnen houden, wil OCW de indicator jaarlijks evalueren. Daartoe hebben we verschillende analyses uitgevoerd voor de schooljaren 2019/’20 tot met 2022/’23. Als eindconclusie kunnen we stellen dat – op basis van de onderzochte schooljaren – het model van de onderwijsachterstandenindicator ieder jaar tot vergelijkbare uitkomsten leidt.
1. Inleiding
Het ministerie van Onderwijs, Cultuur en Wetenschap (OCW) heeft het onderwijsachterstandenbeleid voor het primair onderwijs en het gemeentelijke onderwijsachterstandenbeleid herzien. In het nieuwe beleid maakt zij gebruik van de risico-indicator onderwijsachterstanden die het Centraal Bureau voor de Statistiek (CBS) eerder in opdracht van het ministerie heeft ontwikkeld1). Met deze indicator wordt voor alle peuters van tweeëneenhalf tot vier jaar en alle basisschoolleerlingen een onderwijsscore berekend. Conform de Besluiten2) worden deze onderwijsscores geaggregeerd tot achterstandsscores per school en per gemeente. Zij drukken de verwachte onderwijsachterstandsproblematiek op scholen en in gemeenten uit, op basis waarvan OCW het onderwijsachterstandenbudget over de scholen en gemeenten verdeelt3). In 2019 was dit beleid voor het eerst van kracht.
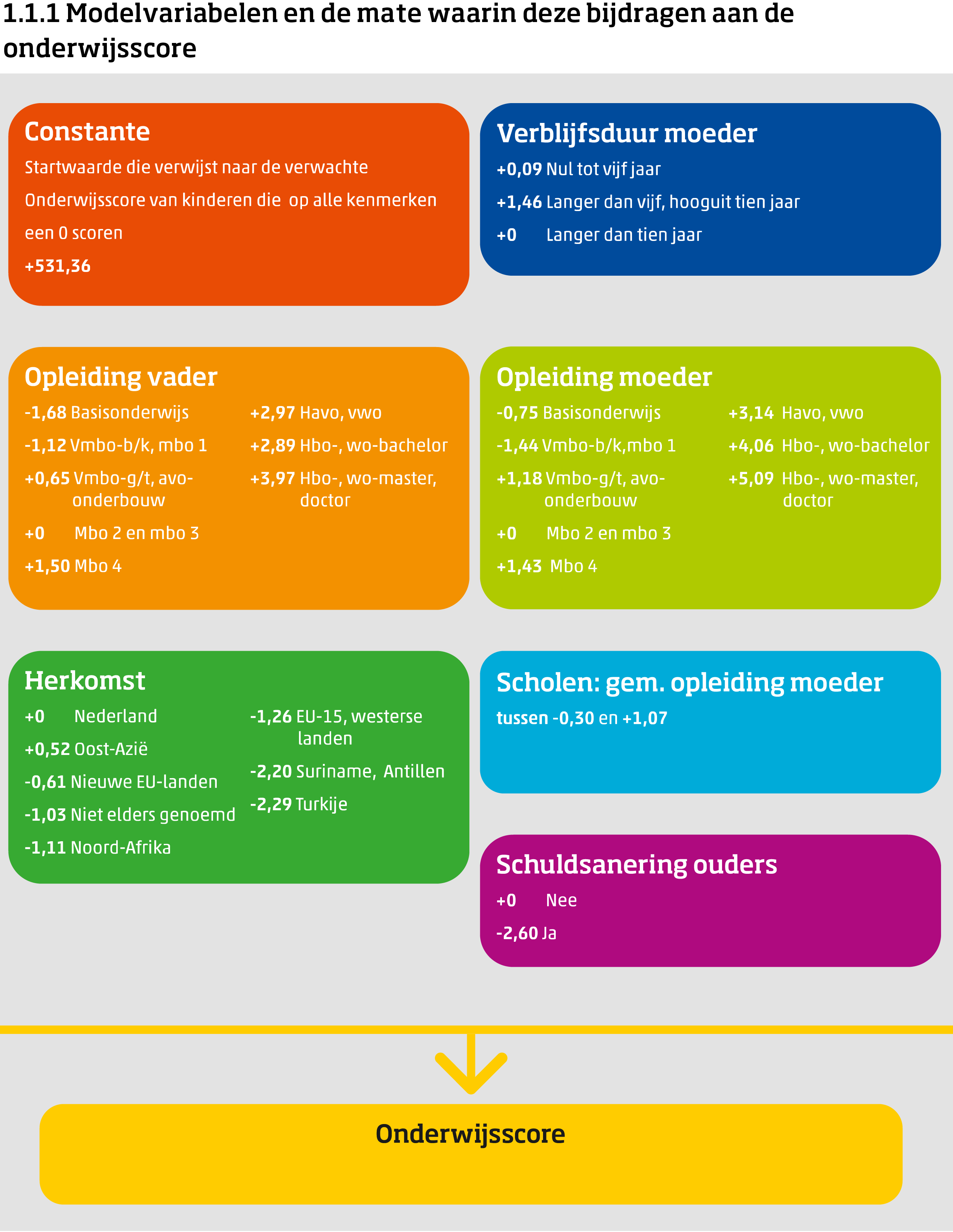
De hoogte van de onderwijsscore wordt bepaald door omgevingskenmerken van de peuters en leerlingen: het opleidingsniveau van de vader, opleidingsniveau van de moeder, verblijfsduur van de moeder in Nederland, land van herkomst van de ouders, of ouders in de Wet Schuldsanering Natuurlijke Personen (WSNP) zitten en het gemiddelde opleidingsniveau van moeders op school. Deze kenmerken zijn voor veel, maar niet voor alle leerlingen bekend. Afhankelijk van de informatie die wel bekend is, zijn de ontbrekende waardes op verschillende manieren geïmputeerd. Figuur 1.1.1 geeft een schematisch overzicht van de modelvariabelen van de onderwijsachterstandenindicator en hun bijdrage aan de onderwijsscore.
Bij de ontwikkeling van de indicator is gebruik gemaakt van twee typen toetsgegevens: de eindtoetsscores van de Centrale Eindtoets (CET; in het dagelijks taalgebruik wordt dit ook wel de Cito-toets genoemd) en de scores op de Niet Schoolse Cognitieve Capaciteiten Test (NSCCT) als maat voor intelligentie. De NSCCT-scores zijn verkregen uit het Cohort Onderzoek Onderwijs Loopbanen (COOL5-18). De meest recente gegevens die daarbij zijn gebruikt, hebben betrekking op het schooljaar 2013/’14. In dat jaar namen de leerlingen uit groep 5 uit het COOL-cohort van 2010/’11 deel aan de eindtoets van de basisschool. Verder zijn ook de NSCCT-scores uit het COOL-cohort van 2007/’08 gebruikt. De ontwikkeling en de toepassing van de indicator komt steeds verder uit elkaar te liggen. Als gevolg hiervan is het mogelijk dat de samenstelling van de populatie waarop de indicator wordt toegepast verandert, wat gevolgen kan hebben voor de werking van de indicator.
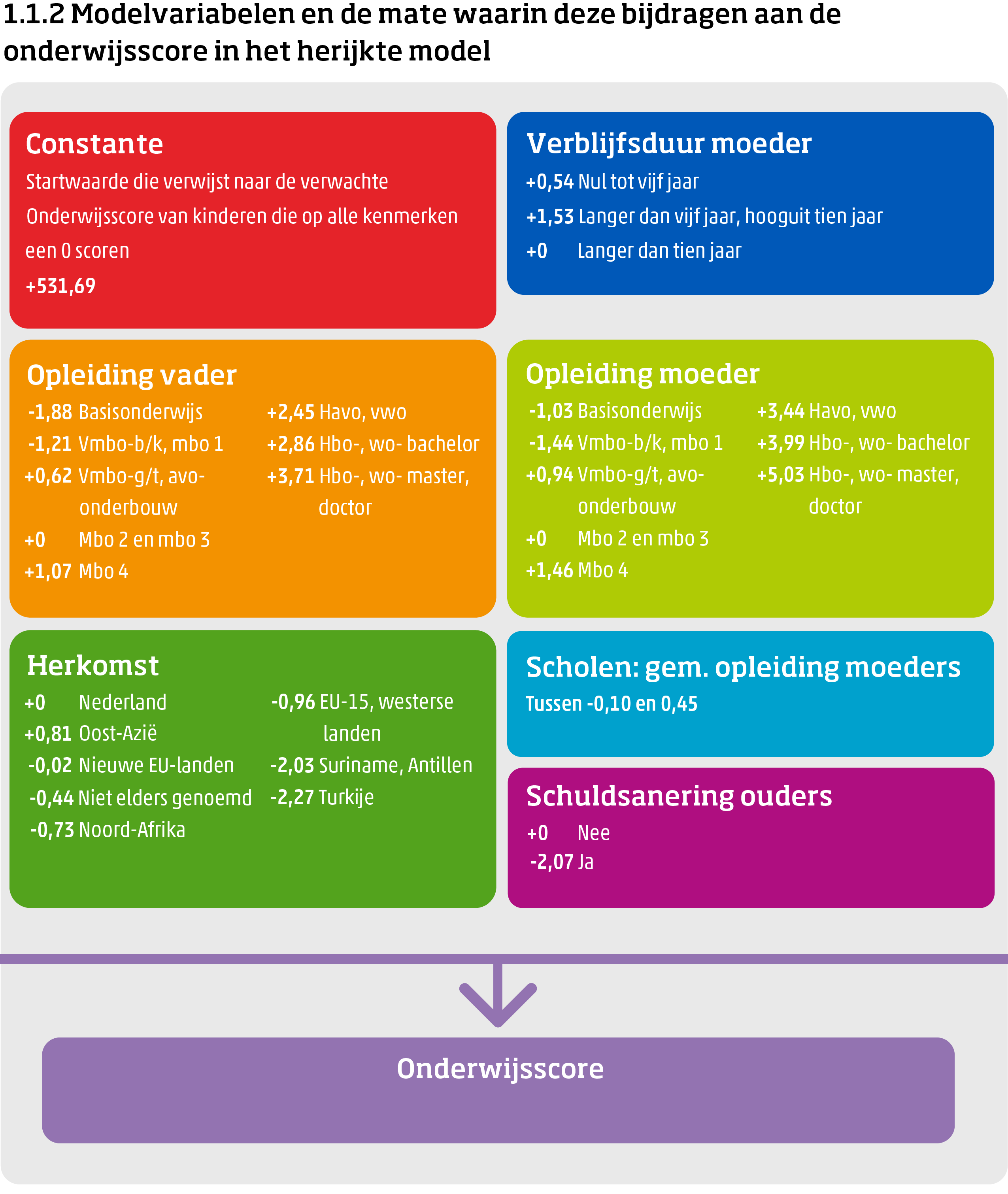
Om de onderwijsachterstandenindicator actueel te houden, wil het ministerie van Onderwijs, Cultuur en Wetenschap (OCW) de indicator periodiek evalueren. Hierdoor kunnen nieuwe ontwikkelingen mee worden genomen in de indicator. Als input voor deze periodieke evaluatie is het wenselijk om jaarlijks de werking van de indicator te monitoren. Daarnaast zijn de coëfficiënten en schaalwaarden die worden gebruikt om de onderwijsscores vast te stellen recent herijkt (zie: herijking onderwijsachterstandenindicator primair onderwijs 2021). Figuur 1.1.2 geeft schematisch overzicht van de modelvariabelen van de onderwijsachterstandindicator en hun bijdrage aan de onderwijsscore in het herijkte model. Op meetmoment februari 2022 is dit herijkte model voor het eerst gebruikt om onderwijsscores te berekenen. Daarom kijken we ook ditmaal naar het patroon van relaties tussen onderwijsscores en achtergrondkenmerken in vergelijking met voorgaande meetmomenten. Dit rapport is de vijfde jaarlijkse monitor die wordt gepubliceerd.4)
Dit rapport beschrijft de opzet en de uitkomsten van de vijfde jaarlijkse monitor. In hoofdstuk 2 worden de gebruikte data en methoden uiteengezet. Hoofdstuk 3 behandelt de resultaten van de frequentieanalyses en hoofdstuk 4 beschrijft de resultaten van de correlatie en regressieanalyses. Het rapport wordt in hoofdstuk 5 afgesloten met een samenvatting en conclusies.
2) Besluit van 27 augustus 2018 tot wijziging van het Besluit bekostiging WPO in verband met het aanpassen van de groeiregeling en van het onderwijsachterstandenbeleid in het primair onderwijs (Staatsblad 2018, 334), en Besluit van 27 augustus 2018, houdende regels met betrekking tot specifieke uitkeringen ten behoeve van het gemeentelijk onderwijsachterstandenbeleid (Besluit specifieke uitkeringen gemeentelijk onderwijsachterstandenbeleid) (Staatsblad 2018, 315).
3) De achterstandsscore wordt per school berekend, scholen worden bekostigd via hun schoolbestuur.
4) Eerder verschenen vier jaarlijkse monitoren. Het laatste rapport is hier te lezen.
2. Data en methoden
2.1 Selectie en afbakening onderzoeksdata
Voor het uitvoeren van deze jaarlijkse monitor is een onderzoeksbestand samengesteld met daarin de gegevens van de kinderen die in de schooljaren 2019/’20 tot en met 2022/’23 aan de eindtoets van de basisschool hebben deelgenomen (zie tabel 2.1.1 voor het aantal kinderen naar eindtoetsaanbieder en schooljaar).5) Voor de kinderen uit schooljaar 2021/’22 zijn zowel de onderwijsscores zoals berekend op de oude manier, als de onderwijsscores volgens het herijkte model gebruikt. Deze zijn respectievelijk terug te lezen in dit rapport als “2021/’22, okt” en “ 2021/’22 feb”. Van alle kinderen zijn de gegevens, zoals die in de analysebestanden van de onderwijsachterstandenindicator zijn opgeslagen, gekoppeld aan de eindtoetsgegevens uit het Stelsel van Sociaal-statistische Bestanden (SSB) van het CBS. De eindtoetsgegevens bestaan uit de eindtoetsscore, de aanbieder van de eindtoets en het uit de eindtoets voortvloeiende eindtoetsadvies. De keuze voor de eindtoetsscore is noodzakelijk omdat deze variabele is gebruikt als afhankelijke variabele bij de ontwikkeling van de indicator.
De onderwijsachterstandenindicator is oorspronkelijk ontwikkeld met behulp van de CET. Sinds de ontwikkeling van de onderwijsachterstandenindicator is het aandeel van deze eindtoets gedaald. Om die reden is de variabele waarin de aanbieder van de eindtoets is vastgelegd, meegenomen in het onderzoeksbestand. Hierdoor kan ook worden bekeken hoe goed de indicator werkt voor leerlingen van scholen die een andere eindtoets gebruiken dan degene waar de indicator mee is ontwikkeld.
Omdat we verwachten dat de eindtoets, ongeacht de aanbieder, tot een vergelijkbaar advies voor het te volgen voortgezet onderwijs komt, is ook het eindtoetsadvies opgenomen in het onderzoeksbestand. Hierdoor wordt het ook mogelijk om de uitkomsten van de eindtoets over de gehele onderzoekspopulatie te vergelijken; ongeacht aan welke eindtoets de basisschoolleerlingen hebben deelgenomen.
De kinderen in de onderzoekspopulatie die voorkomen in de registraties van het COA en de IND, zijn uitgesloten van de analyses. De reden hiervoor is dat deze kinderen – ongeacht hun achtergrondkenmerken – allen dezelfde onderwijsscore krijgen toegewezen6). Doordat er voor deze kinderen geen verband is tussen hun achtergrondkenmerken en hun onderwijsscore, zou het opnemen van deze kinderen tot vertekening leiden van de uitkomsten van de analyses.
| Eindtoetsaanbieder | 2020/'21 | 2021/'22, okt | 2021/'22, feb | 2022/'23 |
|---|---|---|---|---|
| AMN | 3 258 | 3 306 | 3 304 | 3 177 |
| CET | 80 284 | 76 704 | 76 701 | 74 564 |
| DIA | 6 517 | 7 067 | 7 068 | 7 545 |
| IEP | 57 050 | 59 095 | 59 081 | 62 082 |
| ROUTE 8 | 23 334 | 22 309 | 22 298 | 21 168 |
2.2 Gebruikte methoden
Om de werking van de onderwijsachterstandenindicator te kunnen monitoren, maken we gebruik van een drietal analyses: frequentieanalyses, correlatieanalyses en regressieanalyses.
Bij de frequentieanalyses bekijken we hoe vaak een bepaalde score voorkomt. Deze waarnemingen worden hiervoor opgedeeld in groepen. Dit wordt gedaan zodat we de grafieken inzichtelijker kunnen maken: kleine groepen kunnen dan worden samengevoegd en grote groepen juist weer opgesplitst zodat we meer detail kunnen zien. Het gevolg hiervan is dat sommige groepen meer waarnemingen behelzen dan andere groepen. Om de groepen toch vergelijkbaar te houden, worden de betreffende waardes gedeeld door de grootte van de categorie waar de waarde in valt.
Belangrijk in deze analyses is dat de zogenaamde frequentieverdelingen over de jaren heen dezelfde patronen laten zien. Hiertoe splitsen we de frequentieverdelingen uit naar doelvariabelen (eindtoetsadvies en aanbieder eindtoets), de modelvariabelen die worden gebruikt bij de berekening van onderwijsscores en de soort imputatie (imputatie opleidingsniveau ouders en directe imputatie onderwijsscore). Bij de uitsplitsing naar de doelvariabelen kijken we alleen naar de drie grootste aanbieders van de eindtoets: CET, IEP en ROUTE 8. Vanwege de lage aantallen deelnemers nemen we DIA en AMN niet mee in de analyses.
Om het verband tussen de onderwijsscore en de eindtoetsscore te onderzoeken, voeren we een correlatieanalyse uit. Om een beeld te krijgen van de samenhang tussen de onderwijsscore en de eindtoetsscore kijken we naar de correlatiecoëfficiënt (r). In aanvulling op de correlatieanalyse onderzoeken we met behulp van regressieanalyse welk deel van de variantie in de eindtoetsscore met de onderwijsscore kan worden verklaard. Hierbij kijken wij alleen naar de leerlingen die de CET als eindtoets hebben gemaakt omdat de onderwijsachterstandenindicator hiermee is ontwikkeld.
Bij de regressieanalyse maken we gebruik van een stapsgewijze aanpak. Vanuit een startmodel, met alleen de onderwijsscore als onafhankelijke variabele (ook wel voorspeller genoemd) en de eindtoetsscore als afhankelijke variabele, kijken we in hoeverre het toevoegen van variabelen met betrekking tot de beschikbaarheid van gegevens tot een beter model leidt. Daarvoor hebben we een drietal deelpopulatievariabelen gedefinieerd. Deelpopulatie 1 geeft aan in hoeverre het opleidingsniveau van de ouders bekend is. De verschillende categorieën voor deze variabele zijn weergegeven in tabel 2.2.1. Deelpopulatie 2 is een dichotome variabele die aangeeft of de onderwijsscore direct is berekend of is geïmputeerd. Deelpopulatie 3 is een combinatie van deelpopulatie 1 en deelpopulatie 2. De verschillende categorieën voor deze variabele zijn weergegeven in tabel 2.2.2.
| Deelpopulatie | Beschrijving |
|---|---|
| A | Het hoogste opleidingsniveau van beide ouders is niet bekend |
| B | Het hoogste opleidingsniveau is bekend voor de moeder maar niet voor de vader |
| C | Het hoogste opleidingsniveau is bekend voor de vader maar niet voor de moeder |
| D | Het hoogste opleidingsniveau van beide ouders is bekend |
| Deelpopulatie | Beschrijving |
|---|---|
| A1 | Het hoogste opleidingsniveau van beide ouders is niet bekend en de onderwijsscore is geïmputeerd |
| A0 | Het hoogste opleidingsniveau van beide ouders is niet bekend en de onderwijsscore is direct bepaald (niet geïmputeerd) |
| B1 | Het hoogste opleidingsniveau is bekend voor de moeder maar niet voor de vader en de onderwijsscore is geïmputeerd |
| B0 | Het hoogste opleidingsniveau is bekend voor de moeder maar niet voor de vader en de onderwijsscore is direct bepaald (niet geïmputeerd) |
| C1 | Het hoogste opleidingsniveau is bekend voor de vader maar niet voor de moeder en de onderwijsscore is geïmputeerd |
| C0 | Het hoogste opleidingsniveau is bekend voor de vader maar niet voor de moeder en de onderwijsscore is direct bepaald (niet geïmputeerd) |
| D0 | Het hoogste opleidingsniveau van beide ouders is bekend en de onderwijsscore is direct bepaald (niet geïmputeerd) |
Om te beoordelen of het toevoegen van een variabele tot een beter model leidt voor wat betreft de verklaarde variantie, kijken we naar de aangepaste R². Deze maat van verklaarde variantie corrigeert voor het aantal voorspellers dat gebruikt wordt in een regressiemodel. Daarnaast kijken we naar het Akaike Information Criterium (AIC) voor extra zekerheid. Deze maatstaf corrigeert ook voor het aantal parameters in een model, en is een uitdrukking van de hoeveelheid misfit tussen het model en de data. In andere woorden: AIC drukt uit in welke mate het model de data goed beschrijft. Een lagere AIC is beter.
6) Een uitgebreide uitleg hierover is te vinden in het vierde methoderapport.
3. Resultaten frequentieanalyses
In dit hoofdstuk bekijken we de frequentiedichtheid van de onderwijsscores uitgesplitst naar eindtoetsadvies en eindtoetsaanbieder en de verschillende modelvariabelen van de onderwijsachterstandenindicator. Daarnaast beoordelen we de frequentiedichtheid van de onderwijsscores naar de verschillende methoden van imputatie.
3.1 Onderwijsscores per schooljaar naar eindtoetsadvies en eindtoetsaanbieder
De figuren 3.1.1 tot en met 3.1.15 geven de frequentiedichtheid weer van de onderwijsscores per eindtoetsadvies en eindtoetsaanbieder uitgesplitst naar schooljaar. Elke eindtoets hanteert dezelfde indeling van mogelijke toetsadviezen met uitzondering van het vwo-advies betreft dit altijd gecombineerde adviezen.
De verwachting is dat kinderen met een lagere onderwijsscore gemiddeld een lager eindtoetsadvies hebben en dat kinderen met een hogere onderwijsscore gemiddeld een hoger eindtoetsadvies hebben. Daarnaast is de verwachting dat de verdeling stabiel is over de schooljaren en de verschillende type eindtoetsaanbieders heen. Er kan echter een klein verschil zijn na de herijking ten opzichte van voor de herijking.
De figuren 3.1.1 tot en met 3.1.15 laten zien dat over de verschillende jaren de frequentiedichtheid stabiel is met een klein verschil tussen de meetmomenten oktober 2021 en februari 2022. Dit is het gevolg van de herijking van het model. Dit is conform de verwachting. Wel lijkt er bij het vwo-toetsadvies over de jaren heen een steeds grotere dichtheid rond een onderwijsscore van 538 te vallen. Daarnaast kunnen we uit deze figuren aflezen dat de frequentiedichtheden voor de drie grootste toetsaanbieders vergelijkbaar zijn.
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 0,00045 | 0,00022 | 8e-05 | 5e-05 |
| 524,03718 | 0,00046 | 0,00022 | 8e-05 | 5e-05 |
| 524,07436 | 0,00048 | 0,00022 | 9e-05 | 5e-05 |
| 524,11155 | 0,00049 | 0,00021 | 1e-04 | 6e-05 |
| 524,14873 | 5e-04 | 0,00021 | 0,00011 | 6e-05 |
| 524,18591 | 0,00051 | 0,00021 | 0,00011 | 7e-05 |
| 524,22309 | 0,00052 | 2e-04 | 0,00012 | 7e-05 |
| 524,26027 | 0,00053 | 2e-04 | 0,00013 | 8e-05 |
| 524,29746 | 0,00054 | 0,00019 | 0,00014 | 8e-05 |
| 524,33464 | 0,00055 | 0,00019 | 0,00014 | 8e-05 |
| 524,37182 | 0,00056 | 0,00018 | 0,00015 | 9e-05 |
| 524,409 | 0,00056 | 0,00018 | 0,00016 | 9e-05 |
| 524,44618 | 0,00057 | 0,00018 | 0,00016 | 9e-05 |
| 524,48337 | 0,00058 | 0,00017 | 0,00017 | 9e-05 |
| 524,52055 | 0,00059 | 0,00017 | 0,00017 | 1e-04 |
| 524,55773 | 6e-04 | 0,00017 | 0,00017 | 1e-04 |
| 524,59491 | 0,00061 | 0,00017 | 0,00018 | 1e-04 |
| 524,63209 | 0,00063 | 0,00017 | 0,00018 | 1e-04 |
| 524,66928 | 0,00065 | 0,00017 | 0,00018 | 1e-04 |
| 524,70646 | 0,00066 | 0,00018 | 0,00019 | 1e-04 |
| 524,74364 | 0,00068 | 0,00018 | 0,00019 | 1e-04 |
| 524,78082 | 0,00071 | 0,00019 | 0,00019 | 0,00011 |
| 524,818 | 0,00074 | 2e-04 | 0,00019 | 0,00011 |
| 524,85519 | 0,00077 | 0,00022 | 2e-04 | 0,00012 |
| 524,89237 | 8e-04 | 0,00023 | 2e-04 | 0,00012 |
| 524,92955 | 0,00084 | 0,00025 | 0,00021 | 0,00013 |
| 524,96673 | 0,00088 | 0,00027 | 0,00022 | 0,00014 |
| 525,00391 | 0,00093 | 3e-04 | 0,00023 | 0,00015 |
| 525,0411 | 0,00098 | 0,00033 | 0,00024 | 0,00017 |
| 525,07828 | 0,00103 | 0,00036 | 0,00026 | 0,00019 |
| 525,11546 | 0,0011 | 4e-04 | 0,00028 | 0,00022 |
| 525,15264 | 0,00117 | 0,00045 | 0,00031 | 0,00025 |
| 525,18982 | 0,00124 | 5e-04 | 0,00034 | 0,00029 |
| 525,22701 | 0,00133 | 0,00056 | 0,00038 | 0,00033 |
| 525,26419 | 0,00142 | 0,00063 | 0,00043 | 0,00038 |
| 525,30137 | 0,00152 | 7e-04 | 0,00048 | 0,00044 |
| 525,33855 | 0,00163 | 0,00079 | 0,00055 | 0,00052 |
| 525,37573 | 0,00175 | 0,00088 | 0,00063 | 6e-04 |
| 525,41292 | 0,00189 | 0,00098 | 0,00072 | 0,00069 |
| 525,4501 | 0,00203 | 0,00109 | 0,00082 | 8e-04 |
| 525,48728 | 0,00219 | 0,00121 | 0,00094 | 0,00092 |
| 525,52446 | 0,00236 | 0,00135 | 0,00107 | 0,00105 |
| 525,56164 | 0,00255 | 0,00149 | 0,00122 | 0,00121 |
| 525,59883 | 0,00275 | 0,00165 | 0,00139 | 0,00137 |
| 525,63601 | 0,00297 | 0,00182 | 0,00158 | 0,00156 |
| 525,67319 | 0,00321 | 0,002 | 0,00178 | 0,00176 |
| 525,71037 | 0,00346 | 0,0022 | 0,00201 | 0,00199 |
| 525,74755 | 0,00372 | 0,00241 | 0,00225 | 0,00223 |
| 525,78474 | 0,00401 | 0,00264 | 0,00251 | 0,0025 |
| 525,82192 | 0,00432 | 0,00288 | 0,0028 | 0,00278 |
| 525,8591 | 0,00465 | 0,00314 | 0,00311 | 0,00308 |
| 525,89628 | 0,00499 | 0,00341 | 0,00343 | 0,00339 |
| 525,93346 | 0,00535 | 0,00369 | 0,00378 | 0,00373 |
| 525,97065 | 0,00574 | 0,00399 | 0,00414 | 0,00408 |
| 526,00783 | 0,00614 | 0,00431 | 0,00451 | 0,00444 |
| 526,04501 | 0,00656 | 0,00464 | 0,0049 | 0,00481 |
| 526,08219 | 0,007 | 0,00499 | 0,0053 | 0,00519 |
| 526,11937 | 0,00746 | 0,00535 | 0,00571 | 0,00557 |
| 526,15656 | 0,00794 | 0,00572 | 0,00612 | 0,00596 |
| 526,19374 | 0,00844 | 0,0061 | 0,00654 | 0,00635 |
| 526,23092 | 0,00895 | 0,0065 | 0,00696 | 0,00673 |
| 526,2681 | 0,00948 | 0,00692 | 0,00738 | 0,00711 |
| 526,30528 | 0,01002 | 0,00734 | 0,00779 | 0,00747 |
| 526,34247 | 0,01058 | 0,00777 | 0,00819 | 0,00783 |
| 526,37965 | 0,01114 | 0,0082 | 0,00858 | 0,00817 |
| 526,41683 | 0,01172 | 0,00865 | 0,00896 | 0,00849 |
| 526,45401 | 0,01231 | 0,0091 | 0,00932 | 0,0088 |
| 526,49119 | 0,0129 | 0,00955 | 0,00966 | 0,00908 |
| 526,52838 | 0,0135 | 0,01001 | 0,00998 | 0,00934 |
| 526,56556 | 0,0141 | 0,01047 | 0,01029 | 0,00958 |
| 526,60274 | 0,0147 | 0,01093 | 0,01057 | 0,0098 |
| 526,63992 | 0,01531 | 0,0114 | 0,01084 | 0,01 |
| 526,6771 | 0,01591 | 0,01186 | 0,01109 | 0,01018 |
| 526,71429 | 0,01652 | 0,01233 | 0,01131 | 0,01034 |
| 526,75147 | 0,01712 | 0,0128 | 0,01153 | 0,01049 |
| 526,78865 | 0,01771 | 0,01327 | 0,01173 | 0,01062 |
| 526,82583 | 0,01831 | 0,01375 | 0,01192 | 0,01075 |
| 526,86301 | 0,0189 | 0,01423 | 0,0121 | 0,01087 |
| 526,9002 | 0,01949 | 0,01472 | 0,01229 | 0,01099 |
| 526,93738 | 0,02008 | 0,01523 | 0,01247 | 0,01112 |
| 526,97456 | 0,02067 | 0,01574 | 0,01266 | 0,01125 |
| 527,01174 | 0,02126 | 0,01627 | 0,01287 | 0,0114 |
| 527,04892 | 0,02186 | 0,01682 | 0,01309 | 0,01156 |
| 527,08611 | 0,02246 | 0,01739 | 0,01334 | 0,01176 |
| 527,12329 | 0,02306 | 0,01798 | 0,01361 | 0,01198 |
| 527,16047 | 0,02368 | 0,01861 | 0,01391 | 0,01224 |
| 527,19765 | 0,02431 | 0,01927 | 0,01425 | 0,01253 |
| 527,23483 | 0,02495 | 0,01995 | 0,01464 | 0,01287 |
| 527,27202 | 0,02561 | 0,02067 | 0,01508 | 0,01325 |
| 527,3092 | 0,02628 | 0,02142 | 0,01556 | 0,01368 |
| 527,34638 | 0,02697 | 0,02222 | 0,0161 | 0,01417 |
| 527,38356 | 0,02769 | 0,02306 | 0,01669 | 0,01472 |
| 527,42074 | 0,02843 | 0,02393 | 0,01736 | 0,01533 |
| 527,45793 | 0,02919 | 0,02483 | 0,01809 | 0,016 |
| 527,49511 | 0,02997 | 0,02576 | 0,01888 | 0,01673 |
| 527,53229 | 0,03077 | 0,02673 | 0,01973 | 0,01754 |
| 527,56947 | 0,0316 | 0,02773 | 0,02065 | 0,01841 |
| 527,60665 | 0,03245 | 0,02875 | 0,02164 | 0,01935 |
| 527,64384 | 0,03331 | 0,0298 | 0,02269 | 0,02035 |
| 527,68102 | 0,0342 | 0,03086 | 0,02381 | 0,02141 |
| 527,7182 | 0,03509 | 0,03193 | 0,02498 | 0,02253 |
| 527,75538 | 0,036 | 0,033 | 0,02621 | 0,0237 |
| 527,79256 | 0,03692 | 0,03408 | 0,02748 | 0,02494 |
| 527,82975 | 0,03785 | 0,03516 | 0,02879 | 0,02623 |
| 527,86693 | 0,03879 | 0,03623 | 0,03014 | 0,02755 |
| 527,90411 | 0,03972 | 0,03729 | 0,03153 | 0,02891 |
| 527,94129 | 0,04065 | 0,03833 | 0,03293 | 0,0303 |
| 527,97847 | 0,04158 | 0,03935 | 0,03434 | 0,0317 |
| 528,01566 | 0,04251 | 0,04034 | 0,03575 | 0,03313 |
| 528,05284 | 0,04343 | 0,04132 | 0,03717 | 0,03456 |
| 528,09002 | 0,04434 | 0,04226 | 0,03857 | 0,03598 |
| 528,1272 | 0,04524 | 0,04318 | 0,03994 | 0,03739 |
| 528,16438 | 0,04613 | 0,04408 | 0,04129 | 0,03878 |
| 528,20157 | 0,04701 | 0,04494 | 0,0426 | 0,04015 |
| 528,23875 | 0,04789 | 0,04578 | 0,04388 | 0,04147 |
| 528,27593 | 0,04875 | 0,04659 | 0,0451 | 0,04275 |
| 528,31311 | 0,04961 | 0,04739 | 0,04627 | 0,04398 |
| 528,35029 | 0,05046 | 0,04816 | 0,04738 | 0,04516 |
| 528,38748 | 0,0513 | 0,04892 | 0,04843 | 0,04629 |
| 528,42466 | 0,05214 | 0,04966 | 0,04943 | 0,04736 |
| 528,46184 | 0,05298 | 0,0504 | 0,05036 | 0,04836 |
| 528,49902 | 0,05382 | 0,05112 | 0,05124 | 0,04929 |
| 528,5362 | 0,05466 | 0,05184 | 0,05206 | 0,05016 |
| 528,57339 | 0,05551 | 0,05256 | 0,05281 | 0,05097 |
| 528,61057 | 0,05635 | 0,05328 | 0,05352 | 0,05173 |
| 528,64775 | 0,0572 | 0,054 | 0,05418 | 0,05243 |
| 528,68493 | 0,05805 | 0,05472 | 0,0548 | 0,05308 |
| 528,72211 | 0,05891 | 0,05544 | 0,05538 | 0,05367 |
| 528,7593 | 0,05977 | 0,05617 | 0,05592 | 0,05422 |
| 528,79648 | 0,06063 | 0,0569 | 0,05642 | 0,05474 |
| 528,83366 | 0,0615 | 0,05763 | 0,05691 | 0,05522 |
| 528,87084 | 0,06236 | 0,05836 | 0,05737 | 0,05568 |
| 528,90802 | 0,06322 | 0,05909 | 0,05782 | 0,05611 |
| 528,94521 | 0,06408 | 0,05982 | 0,05826 | 0,05652 |
| 528,98239 | 0,06493 | 0,06054 | 0,05869 | 0,05692 |
| 529,01957 | 0,06577 | 0,06126 | 0,05911 | 0,05731 |
| 529,05675 | 0,06661 | 0,06197 | 0,05953 | 0,0577 |
| 529,09393 | 0,06743 | 0,06268 | 0,05996 | 0,05808 |
| 529,13112 | 0,06823 | 0,06338 | 0,06039 | 0,05847 |
| 529,1683 | 0,06902 | 0,06407 | 0,06084 | 0,05887 |
| 529,20548 | 0,0698 | 0,06476 | 0,0613 | 0,05929 |
| 529,24266 | 0,07055 | 0,06544 | 0,06177 | 0,05971 |
| 529,27984 | 0,07129 | 0,06612 | 0,06227 | 0,06016 |
| 529,31703 | 0,07202 | 0,06679 | 0,06279 | 0,06063 |
| 529,35421 | 0,07273 | 0,06748 | 0,06334 | 0,06112 |
| 529,39139 | 0,07342 | 0,06817 | 0,06392 | 0,06166 |
| 529,42857 | 0,0741 | 0,06887 | 0,06453 | 0,06222 |
| 529,46575 | 0,07477 | 0,06958 | 0,06519 | 0,06282 |
| 529,50294 | 0,07543 | 0,07031 | 0,06589 | 0,06346 |
| 529,54012 | 0,07608 | 0,07107 | 0,06663 | 0,06415 |
| 529,5773 | 0,07673 | 0,07185 | 0,06742 | 0,06488 |
| 529,61448 | 0,07738 | 0,07267 | 0,06826 | 0,06566 |
| 529,65166 | 0,07802 | 0,07351 | 0,06916 | 0,06649 |
| 529,68885 | 0,07866 | 0,07438 | 0,07011 | 0,06738 |
| 529,72603 | 0,07931 | 0,07528 | 0,07112 | 0,06831 |
| 529,76321 | 0,07995 | 0,07622 | 0,07219 | 0,0693 |
| 529,80039 | 0,0806 | 0,07718 | 0,0733 | 0,07033 |
| 529,83757 | 0,08124 | 0,07817 | 0,07446 | 0,07142 |
| 529,87476 | 0,08189 | 0,07919 | 0,07567 | 0,07255 |
| 529,91194 | 0,08253 | 0,08021 | 0,07692 | 0,07372 |
| 529,94912 | 0,08316 | 0,08125 | 0,07821 | 0,07493 |
| 529,9863 | 0,08378 | 0,08229 | 0,07953 | 0,07616 |
| 530,02348 | 0,08439 | 0,08332 | 0,08086 | 0,07742 |
| 530,06067 | 0,08498 | 0,08433 | 0,0822 | 0,07869 |
| 530,09785 | 0,08555 | 0,08531 | 0,08354 | 0,07997 |
| 530,13503 | 0,08609 | 0,08627 | 0,08487 | 0,08124 |
| 530,17221 | 0,0866 | 0,08718 | 0,08617 | 0,08249 |
| 530,20939 | 0,08707 | 0,08803 | 0,08743 | 0,08372 |
| 530,24658 | 0,08751 | 0,08882 | 0,08865 | 0,08492 |
| 530,28376 | 0,08791 | 0,08953 | 0,08981 | 0,08607 |
| 530,32094 | 0,08826 | 0,09018 | 0,09089 | 0,08716 |
| 530,35812 | 0,08856 | 0,09074 | 0,09189 | 0,08817 |
| 530,3953 | 0,08882 | 0,09123 | 0,09279 | 0,08911 |
| 530,43249 | 0,08903 | 0,09161 | 0,09359 | 0,08998 |
| 530,46967 | 0,0892 | 0,09191 | 0,09429 | 0,09075 |
| 530,50685 | 0,08933 | 0,09213 | 0,09489 | 0,09144 |
| 530,54403 | 0,08942 | 0,09227 | 0,09538 | 0,09202 |
| 530,58121 | 0,08947 | 0,09233 | 0,09575 | 0,0925 |
| 530,6184 | 0,0895 | 0,09233 | 0,09601 | 0,09289 |
| 530,65558 | 0,08951 | 0,09227 | 0,09618 | 0,09321 |
| 530,69276 | 0,08952 | 0,09215 | 0,09626 | 0,09344 |
| 530,72994 | 0,08952 | 0,09201 | 0,09626 | 0,09361 |
| 530,76712 | 0,08953 | 0,09184 | 0,09619 | 0,09372 |
| 530,80431 | 0,08956 | 0,09167 | 0,09606 | 0,09378 |
| 530,84149 | 0,08963 | 0,0915 | 0,0959 | 0,09382 |
| 530,87867 | 0,08973 | 0,09135 | 0,09572 | 0,09386 |
| 530,91585 | 0,08988 | 0,09124 | 0,09554 | 0,09389 |
| 530,95303 | 0,09009 | 0,09119 | 0,09537 | 0,09395 |
| 530,99022 | 0,09036 | 0,09119 | 0,09523 | 0,09406 |
| 531,0274 | 0,09072 | 0,09127 | 0,09514 | 0,09423 |
| 531,06458 | 0,09117 | 0,09143 | 0,09512 | 0,09447 |
| 531,10176 | 0,0917 | 0,09169 | 0,09517 | 0,09479 |
| 531,13894 | 0,09231 | 0,09205 | 0,09531 | 0,09521 |
| 531,17613 | 0,09301 | 0,09251 | 0,09554 | 0,09573 |
| 531,21331 | 0,0938 | 0,09306 | 0,09587 | 0,09636 |
| 531,25049 | 0,09468 | 0,09371 | 0,09632 | 0,09712 |
| 531,28767 | 0,09564 | 0,09445 | 0,09687 | 0,09798 |
| 531,32485 | 0,09667 | 0,09529 | 0,09753 | 0,09895 |
| 531,36204 | 0,09775 | 0,0962 | 0,09827 | 0,1 |
| 531,39922 | 0,09888 | 0,09717 | 0,0991 | 0,10114 |
| 531,4364 | 0,10004 | 0,09818 | 0,10001 | 0,10235 |
| 531,47358 | 0,10123 | 0,09923 | 0,10098 | 0,10362 |
| 531,51076 | 0,10242 | 0,10029 | 0,102 | 0,10492 |
| 531,54795 | 0,1036 | 0,10136 | 0,10305 | 0,10623 |
| 531,58513 | 0,10475 | 0,10239 | 0,10411 | 0,10753 |
| 531,62231 | 0,10586 | 0,10339 | 0,10516 | 0,1088 |
| 531,65949 | 0,10691 | 0,10434 | 0,1062 | 0,11002 |
| 531,69667 | 0,10789 | 0,10522 | 0,10719 | 0,11116 |
| 531,73386 | 0,10877 | 0,10603 | 0,10813 | 0,11221 |
| 531,77104 | 0,10956 | 0,10671 | 0,10899 | 0,11316 |
| 531,80822 | 0,11026 | 0,1073 | 0,10978 | 0,11399 |
| 531,8454 | 0,11084 | 0,10778 | 0,11049 | 0,11469 |
| 531,88258 | 0,11133 | 0,10816 | 0,1111 | 0,11527 |
| 531,91977 | 0,11169 | 0,10842 | 0,11162 | 0,11569 |
| 531,95695 | 0,11194 | 0,10857 | 0,11202 | 0,11597 |
| 531,99413 | 0,11208 | 0,1086 | 0,11233 | 0,11613 |
| 532,03131 | 0,11214 | 0,10854 | 0,11256 | 0,11617 |
| 532,06849 | 0,11212 | 0,10839 | 0,1127 | 0,11611 |
| 532,10568 | 0,11202 | 0,10818 | 0,11278 | 0,11595 |
| 532,14286 | 0,11186 | 0,10791 | 0,11281 | 0,11572 |
| 532,18004 | 0,11166 | 0,1076 | 0,11278 | 0,11542 |
| 532,21722 | 0,11144 | 0,10726 | 0,11272 | 0,1151 |
| 532,2544 | 0,1112 | 0,10693 | 0,11266 | 0,11477 |
| 532,29159 | 0,11098 | 0,10661 | 0,1126 | 0,11444 |
| 532,32877 | 0,11078 | 0,10632 | 0,11256 | 0,11414 |
| 532,36595 | 0,11061 | 0,10609 | 0,11254 | 0,11389 |
| 532,40313 | 0,11052 | 0,10591 | 0,11259 | 0,11371 |
| 532,44031 | 0,11049 | 0,10584 | 0,11268 | 0,11361 |
| 532,4775 | 0,11053 | 0,10586 | 0,11285 | 0,11361 |
| 532,51468 | 0,11067 | 0,10597 | 0,11308 | 0,1137 |
| 532,55186 | 0,11089 | 0,1062 | 0,11338 | 0,1139 |
| 532,58904 | 0,11121 | 0,10653 | 0,11376 | 0,11421 |
| 532,62622 | 0,11165 | 0,10699 | 0,11423 | 0,11464 |
| 532,66341 | 0,11219 | 0,10758 | 0,11477 | 0,11518 |
| 532,70059 | 0,11282 | 0,10827 | 0,11538 | 0,1158 |
| 532,73777 | 0,11353 | 0,10906 | 0,11603 | 0,11652 |
| 532,77495 | 0,11432 | 0,10993 | 0,11673 | 0,11731 |
| 532,81213 | 0,11518 | 0,11088 | 0,11747 | 0,11816 |
| 532,84932 | 0,1161 | 0,11189 | 0,11823 | 0,11907 |
| 532,8865 | 0,11705 | 0,11295 | 0,119 | 0,12 |
| 532,92368 | 0,11803 | 0,11403 | 0,11976 | 0,12094 |
| 532,96086 | 0,11901 | 0,1151 | 0,1205 | 0,12188 |
| 532,99804 | 0,11997 | 0,11616 | 0,12121 | 0,1228 |
| 533,03523 | 0,12092 | 0,11719 | 0,12188 | 0,12368 |
| 533,07241 | 0,1218 | 0,11815 | 0,12247 | 0,1245 |
| 533,10959 | 0,12262 | 0,11903 | 0,123 | 0,12524 |
| 533,14677 | 0,12336 | 0,11981 | 0,12345 | 0,12591 |
| 533,18395 | 0,12401 | 0,12048 | 0,12382 | 0,12649 |
| 533,22114 | 0,12456 | 0,12103 | 0,12411 | 0,12697 |
| 533,25832 | 0,125 | 0,12146 | 0,12431 | 0,12734 |
| 533,2955 | 0,12531 | 0,12174 | 0,12441 | 0,1276 |
| 533,33268 | 0,12548 | 0,12186 | 0,12442 | 0,12774 |
| 533,36986 | 0,12553 | 0,12183 | 0,12435 | 0,12777 |
| 533,40705 | 0,12546 | 0,12167 | 0,12421 | 0,1277 |
| 533,44423 | 0,12527 | 0,12138 | 0,124 | 0,12754 |
| 533,48141 | 0,12497 | 0,12096 | 0,12372 | 0,12728 |
| 533,51859 | 0,12454 | 0,12042 | 0,12339 | 0,12692 |
| 533,55577 | 0,12402 | 0,11976 | 0,12302 | 0,12649 |
| 533,59295 | 0,12341 | 0,11901 | 0,12262 | 0,12599 |
| 533,63014 | 0,12273 | 0,1182 | 0,12219 | 0,12545 |
| 533,66732 | 0,12199 | 0,11733 | 0,12175 | 0,12486 |
| 533,7045 | 0,12121 | 0,11642 | 0,12131 | 0,12423 |
| 533,74168 | 0,12039 | 0,11549 | 0,12086 | 0,12358 |
| 533,77886 | 0,11956 | 0,11455 | 0,12043 | 0,12292 |
| 533,81605 | 0,11872 | 0,11363 | 0,12 | 0,12225 |
| 533,85323 | 0,1179 | 0,11274 | 0,11959 | 0,12158 |
| 533,89041 | 0,1171 | 0,11189 | 0,11919 | 0,12091 |
| 533,92759 | 0,11632 | 0,11108 | 0,1188 | 0,12025 |
| 533,96477 | 0,11558 | 0,11035 | 0,11842 | 0,11959 |
| 534,00196 | 0,1149 | 0,10969 | 0,11804 | 0,11893 |
| 534,03914 | 0,11426 | 0,10909 | 0,11765 | 0,11827 |
| 534,07632 | 0,11367 | 0,10858 | 0,11725 | 0,1176 |
| 534,1135 | 0,11312 | 0,10813 | 0,11682 | 0,11692 |
| 534,15068 | 0,11261 | 0,10775 | 0,11635 | 0,11621 |
| 534,18787 | 0,11214 | 0,10744 | 0,11584 | 0,11547 |
| 534,22505 | 0,11171 | 0,10718 | 0,11525 | 0,11469 |
| 534,26223 | 0,1113 | 0,10697 | 0,1146 | 0,11384 |
| 534,29941 | 0,11089 | 0,10678 | 0,11386 | 0,11294 |
| 534,33659 | 0,11047 | 0,10662 | 0,11304 | 0,11197 |
| 534,37378 | 0,11004 | 0,10645 | 0,11212 | 0,11092 |
| 534,41096 | 0,10958 | 0,10627 | 0,11109 | 0,10978 |
| 534,44814 | 0,10907 | 0,10606 | 0,10994 | 0,10855 |
| 534,48532 | 0,10849 | 0,1058 | 0,10868 | 0,10722 |
| 534,5225 | 0,10784 | 0,10548 | 0,10731 | 0,1058 |
| 534,55969 | 0,10712 | 0,10509 | 0,10584 | 0,10429 |
| 534,59687 | 0,1063 | 0,10462 | 0,10428 | 0,10269 |
| 534,63405 | 0,10538 | 0,10404 | 0,10262 | 0,10102 |
| 534,67123 | 0,10434 | 0,10335 | 0,10086 | 0,09928 |
| 534,70841 | 0,10318 | 0,10256 | 0,09904 | 0,09747 |
| 534,7456 | 0,10192 | 0,10166 | 0,09718 | 0,09562 |
| 534,78278 | 0,10055 | 0,10065 | 0,09527 | 0,09374 |
| 534,81996 | 0,09909 | 0,09954 | 0,09335 | 0,09185 |
| 534,85714 | 0,09753 | 0,0983 | 0,09143 | 0,08996 |
| 534,89432 | 0,09588 | 0,09698 | 0,08953 | 0,08809 |
| 534,93151 | 0,09416 | 0,09558 | 0,08766 | 0,08626 |
| 534,96869 | 0,09239 | 0,09412 | 0,08586 | 0,08449 |
| 535,00587 | 0,09058 | 0,0926 | 0,08412 | 0,08279 |
| 535,04305 | 0,08876 | 0,09105 | 0,08248 | 0,08118 |
| 535,08023 | 0,08694 | 0,08948 | 0,08093 | 0,07967 |
| 535,11742 | 0,08515 | 0,08792 | 0,07952 | 0,07827 |
| 535,1546 | 0,0834 | 0,08638 | 0,07824 | 0,07703 |
| 535,19178 | 0,08171 | 0,08488 | 0,07709 | 0,07592 |
| 535,22896 | 0,08011 | 0,08343 | 0,07608 | 0,07494 |
| 535,26614 | 0,07859 | 0,08206 | 0,07522 | 0,07411 |
| 535,30333 | 0,07719 | 0,08079 | 0,0745 | 0,07343 |
| 535,34051 | 0,07591 | 0,07962 | 0,07394 | 0,0729 |
| 535,37769 | 0,07479 | 0,07856 | 0,07354 | 0,07254 |
| 535,41487 | 0,0738 | 0,07762 | 0,07327 | 0,07233 |
| 535,45205 | 0,07294 | 0,07679 | 0,07313 | 0,07225 |
| 535,48924 | 0,07223 | 0,07609 | 0,07311 | 0,07229 |
| 535,52642 | 0,07166 | 0,07554 | 0,07319 | 0,07245 |
| 535,5636 | 0,07123 | 0,07511 | 0,07339 | 0,07273 |
| 535,60078 | 0,07094 | 0,07479 | 0,07367 | 0,07311 |
| 535,63796 | 0,07077 | 0,07457 | 0,07403 | 0,07358 |
| 535,67515 | 0,0707 | 0,07444 | 0,07444 | 0,07411 |
| 535,71233 | 0,07072 | 0,0744 | 0,07489 | 0,07469 |
| 535,74951 | 0,07082 | 0,07444 | 0,07537 | 0,07532 |
| 535,78669 | 0,07098 | 0,07453 | 0,07586 | 0,07597 |
| 535,82387 | 0,07119 | 0,07466 | 0,07636 | 0,07663 |
| 535,86106 | 0,07143 | 0,07481 | 0,07685 | 0,07728 |
| 535,89824 | 0,07167 | 0,07496 | 0,07731 | 0,07792 |
| 535,93542 | 0,07191 | 0,07511 | 0,07775 | 0,07852 |
| 535,9726 | 0,07213 | 0,07523 | 0,07815 | 0,07909 |
| 536,00978 | 0,07232 | 0,07531 | 0,07849 | 0,07961 |
| 536,04697 | 0,07245 | 0,07534 | 0,07878 | 0,08006 |
| 536,08415 | 0,07253 | 0,07532 | 0,07902 | 0,08045 |
| 536,12133 | 0,07255 | 0,07524 | 0,07919 | 0,08076 |
| 536,15851 | 0,0725 | 0,07508 | 0,07931 | 0,08099 |
| 536,19569 | 0,07237 | 0,07484 | 0,07937 | 0,08116 |
| 536,23288 | 0,07217 | 0,07453 | 0,07937 | 0,08124 |
| 536,27006 | 0,07188 | 0,07414 | 0,07931 | 0,08124 |
| 536,30724 | 0,07151 | 0,07369 | 0,07919 | 0,08116 |
| 536,34442 | 0,07108 | 0,07317 | 0,07902 | 0,08099 |
| 536,3816 | 0,07058 | 0,0726 | 0,07881 | 0,08076 |
| 536,41879 | 0,07003 | 0,07196 | 0,07855 | 0,08046 |
| 536,45597 | 0,06942 | 0,07128 | 0,07825 | 0,08009 |
| 536,49315 | 0,06876 | 0,07058 | 0,0779 | 0,07966 |
| 536,53033 | 0,06807 | 0,06986 | 0,07751 | 0,07915 |
| 536,56751 | 0,06736 | 0,06912 | 0,07709 | 0,07858 |
| 536,6047 | 0,06663 | 0,06838 | 0,07663 | 0,07796 |
| 536,64188 | 0,0659 | 0,06766 | 0,07614 | 0,07728 |
| 536,67906 | 0,06517 | 0,06696 | 0,0756 | 0,07655 |
| 536,71624 | 0,06445 | 0,06628 | 0,07502 | 0,07576 |
| 536,75342 | 0,06375 | 0,06564 | 0,07439 | 0,07491 |
| 536,79061 | 0,06307 | 0,06503 | 0,07372 | 0,07401 |
| 536,82779 | 0,06242 | 0,06448 | 0,073 | 0,07306 |
| 536,86497 | 0,0618 | 0,06397 | 0,07223 | 0,07206 |
| 536,90215 | 0,06121 | 0,06351 | 0,0714 | 0,07101 |
| 536,93933 | 0,06066 | 0,06309 | 0,07051 | 0,06992 |
| 536,97652 | 0,06015 | 0,06272 | 0,06957 | 0,06877 |
| 537,0137 | 0,05966 | 0,06238 | 0,06857 | 0,06758 |
| 537,05088 | 0,0592 | 0,06208 | 0,06752 | 0,06636 |
| 537,08806 | 0,05875 | 0,0618 | 0,06642 | 0,06511 |
| 537,12524 | 0,05833 | 0,06154 | 0,06528 | 0,06384 |
| 537,16243 | 0,05792 | 0,0613 | 0,06409 | 0,06255 |
| 537,19961 | 0,05751 | 0,06105 | 0,06286 | 0,06126 |
| 537,23679 | 0,0571 | 0,0608 | 0,06162 | 0,05997 |
| 537,27397 | 0,05668 | 0,06054 | 0,06036 | 0,0587 |
| 537,31115 | 0,05624 | 0,06025 | 0,0591 | 0,05745 |
| 537,34834 | 0,05579 | 0,05993 | 0,05784 | 0,05624 |
| 537,38552 | 0,05531 | 0,05958 | 0,05661 | 0,05507 |
| 537,4227 | 0,0548 | 0,05919 | 0,05541 | 0,05396 |
| 537,45988 | 0,05426 | 0,05877 | 0,05425 | 0,05293 |
| 537,49706 | 0,05368 | 0,0583 | 0,05314 | 0,05198 |
| 537,53425 | 0,05308 | 0,05779 | 0,05209 | 0,0511 |
| 537,57143 | 0,05245 | 0,05724 | 0,05112 | 0,05031 |
| 537,60861 | 0,0518 | 0,05665 | 0,05024 | 0,04962 |
| 537,64579 | 0,05112 | 0,05604 | 0,04945 | 0,04902 |
| 537,68297 | 0,05042 | 0,05541 | 0,04876 | 0,04855 |
| 537,72016 | 0,04972 | 0,05476 | 0,04817 | 0,04818 |
| 537,75734 | 0,04902 | 0,0541 | 0,04768 | 0,0479 |
| 537,79452 | 0,04833 | 0,05345 | 0,04729 | 0,04773 |
| 537,8317 | 0,04766 | 0,05282 | 0,04703 | 0,04766 |
| 537,86888 | 0,04702 | 0,05221 | 0,04688 | 0,04768 |
| 537,90607 | 0,04641 | 0,05163 | 0,04683 | 0,04782 |
| 537,94325 | 0,04586 | 0,05111 | 0,04688 | 0,04804 |
| 537,98043 | 0,04535 | 0,05064 | 0,04702 | 0,04834 |
| 538,01761 | 0,0449 | 0,05024 | 0,04726 | 0,04872 |
| 538,05479 | 0,04452 | 0,04991 | 0,04759 | 0,04917 |
| 538,09198 | 0,04422 | 0,04965 | 0,048 | 0,04969 |
| 538,12916 | 0,044 | 0,04946 | 0,04847 | 0,05026 |
| 538,16634 | 0,04386 | 0,04937 | 0,04899 | 0,05088 |
| 538,20352 | 0,04378 | 0,04936 | 0,04956 | 0,05154 |
| 538,2407 | 0,04378 | 0,04943 | 0,05016 | 0,05221 |
| 538,27789 | 0,04384 | 0,04957 | 0,05077 | 0,05291 |
| 538,31507 | 0,04398 | 0,04977 | 0,05139 | 0,0536 |
| 538,35225 | 0,04417 | 0,05002 | 0,052 | 0,05428 |
| 538,38943 | 0,0444 | 0,05034 | 0,05258 | 0,05494 |
| 538,42661 | 0,04466 | 0,05068 | 0,05313 | 0,05555 |
| 538,4638 | 0,04494 | 0,05105 | 0,05362 | 0,05612 |
| 538,50098 | 0,04522 | 0,05142 | 0,05404 | 0,05662 |
| 538,53816 | 0,0455 | 0,05178 | 0,05438 | 0,05705 |
| 538,57534 | 0,04574 | 0,05212 | 0,05462 | 0,05738 |
| 538,61252 | 0,04595 | 0,05242 | 0,05477 | 0,0576 |
| 538,64971 | 0,0461 | 0,05266 | 0,05481 | 0,05772 |
| 538,68689 | 0,04618 | 0,05284 | 0,05474 | 0,05772 |
| 538,72407 | 0,04619 | 0,05294 | 0,05456 | 0,05761 |
| 538,76125 | 0,04611 | 0,05295 | 0,05424 | 0,05737 |
| 538,79843 | 0,04592 | 0,05288 | 0,0538 | 0,05701 |
| 538,83562 | 0,04562 | 0,05268 | 0,05326 | 0,0565 |
| 538,8728 | 0,04523 | 0,05237 | 0,05262 | 0,05588 |
| 538,90998 | 0,04473 | 0,05196 | 0,05188 | 0,05515 |
| 538,94716 | 0,04412 | 0,05144 | 0,05106 | 0,05432 |
| 538,98434 | 0,04341 | 0,05083 | 0,05014 | 0,0534 |
| 539,02153 | 0,0426 | 0,05012 | 0,04918 | 0,0524 |
| 539,05871 | 0,0417 | 0,0493 | 0,04816 | 0,05133 |
| 539,09589 | 0,04074 | 0,04841 | 0,04712 | 0,0502 |
| 539,13307 | 0,03972 | 0,04746 | 0,04605 | 0,04904 |
| 539,17025 | 0,03864 | 0,04645 | 0,04498 | 0,04785 |
| 539,20744 | 0,03754 | 0,0454 | 0,04391 | 0,04665 |
| 539,24462 | 0,03641 | 0,04432 | 0,04287 | 0,04545 |
| 539,2818 | 0,03528 | 0,04323 | 0,04184 | 0,04427 |
| 539,31898 | 0,03417 | 0,04213 | 0,04085 | 0,0431 |
| 539,35616 | 0,03307 | 0,04105 | 0,0399 | 0,04196 |
| 539,39335 | 0,03201 | 0,03999 | 0,03898 | 0,04085 |
| 539,43053 | 0,03099 | 0,03895 | 0,03811 | 0,03977 |
| 539,46771 | 0,03003 | 0,03796 | 0,03728 | 0,03873 |
| 539,50489 | 0,02912 | 0,03701 | 0,03649 | 0,03772 |
| 539,54207 | 0,02827 | 0,03612 | 0,03572 | 0,03675 |
| 539,57926 | 0,02749 | 0,03527 | 0,03498 | 0,0358 |
| 539,61644 | 0,02676 | 0,03447 | 0,03426 | 0,03487 |
| 539,65362 | 0,02608 | 0,03371 | 0,03355 | 0,03397 |
| 539,6908 | 0,02547 | 0,033 | 0,03284 | 0,03307 |
| 539,72798 | 0,0249 | 0,03234 | 0,03213 | 0,03218 |
| 539,76517 | 0,02437 | 0,03171 | 0,03141 | 0,0313 |
| 539,80235 | 0,02388 | 0,03111 | 0,03068 | 0,03042 |
| 539,83953 | 0,0234 | 0,03053 | 0,02993 | 0,02954 |
| 539,87671 | 0,02294 | 0,02996 | 0,02916 | 0,02866 |
| 539,91389 | 0,02249 | 0,0294 | 0,02837 | 0,02777 |
| 539,95108 | 0,02204 | 0,02884 | 0,02755 | 0,02688 |
| 539,98826 | 0,02158 | 0,02827 | 0,02672 | 0,02599 |
| 540,02544 | 0,02112 | 0,02769 | 0,02586 | 0,02511 |
| 540,06262 | 0,02063 | 0,02709 | 0,02499 | 0,02423 |
| 540,0998 | 0,02014 | 0,02648 | 0,02411 | 0,02336 |
| 540,13699 | 0,01962 | 0,02585 | 0,02323 | 0,02251 |
| 540,17417 | 0,01908 | 0,02519 | 0,02234 | 0,02168 |
| 540,21135 | 0,01853 | 0,02451 | 0,02146 | 0,02087 |
| 540,24853 | 0,01797 | 0,02381 | 0,02058 | 0,02009 |
| 540,28571 | 0,01739 | 0,02309 | 0,01972 | 0,01934 |
| 540,3229 | 0,01681 | 0,02235 | 0,01888 | 0,01862 |
| 540,36008 | 0,01623 | 0,02161 | 0,01806 | 0,01793 |
| 540,39726 | 0,01565 | 0,02085 | 0,01727 | 0,01727 |
| 540,43444 | 0,01508 | 0,02009 | 0,0165 | 0,01665 |
| 540,47162 | 0,01452 | 0,01934 | 0,01575 | 0,01606 |
| 540,50881 | 0,01399 | 0,01859 | 0,01504 | 0,0155 |
| 540,54599 | 0,01347 | 0,01784 | 0,01435 | 0,01496 |
| 540,58317 | 0,01299 | 0,01711 | 0,01368 | 0,01444 |
| 540,62035 | 0,01254 | 0,0164 | 0,01305 | 0,01394 |
| 540,65753 | 0,01211 | 0,01571 | 0,01243 | 0,01345 |
| 540,69472 | 0,01172 | 0,01504 | 0,01183 | 0,01298 |
| 540,7319 | 0,01136 | 0,0144 | 0,01125 | 0,0125 |
| 540,76908 | 0,01102 | 0,01377 | 0,01068 | 0,01203 |
| 540,80626 | 0,01072 | 0,01318 | 0,01013 | 0,01156 |
| 540,84344 | 0,01045 | 0,01261 | 0,0096 | 0,01108 |
| 540,88063 | 0,0102 | 0,01206 | 0,00907 | 0,0106 |
| 540,91781 | 0,00996 | 0,01153 | 0,00855 | 0,01011 |
| 540,95499 | 0,00974 | 0,01102 | 0,00804 | 0,00962 |
| 540,99217 | 0,00953 | 0,01054 | 0,00755 | 0,00912 |
| 541,02935 | 0,00933 | 0,01007 | 0,00706 | 0,00862 |
| 541,06654 | 0,00913 | 0,00961 | 0,00659 | 0,00812 |
| 541,10372 | 0,00892 | 0,00917 | 0,00612 | 0,00762 |
| 541,1409 | 0,00872 | 0,00874 | 0,00567 | 0,00712 |
| 541,17808 | 0,0085 | 0,00832 | 0,00523 | 0,00663 |
| 541,21526 | 0,00827 | 0,0079 | 0,00481 | 0,00614 |
| 541,25245 | 0,00803 | 0,0075 | 0,00441 | 0,00567 |
| 541,28963 | 0,00778 | 0,0071 | 0,00403 | 0,00521 |
| 541,32681 | 0,00751 | 0,0067 | 0,00366 | 0,00477 |
| 541,36399 | 0,00723 | 0,00631 | 0,00332 | 0,00435 |
| 541,40117 | 0,00693 | 0,00593 | 0,00299 | 0,00395 |
| 541,43836 | 0,00662 | 0,00555 | 0,00269 | 0,00357 |
| 541,47554 | 0,0063 | 0,00519 | 0,00241 | 0,00321 |
| 541,51272 | 0,00597 | 0,00483 | 0,00215 | 0,00288 |
| 541,5499 | 0,00564 | 0,00448 | 0,00192 | 0,00258 |
| 541,58708 | 0,0053 | 0,00414 | 0,0017 | 0,0023 |
| 541,62427 | 0,00496 | 0,00381 | 0,0015 | 0,00205 |
| 541,66145 | 0,00462 | 0,00349 | 0,00133 | 0,00182 |
| 541,69863 | 0,00428 | 0,00319 | 0,00117 | 0,00161 |
| 541,73581 | 0,00396 | 0,0029 | 0,00104 | 0,00143 |
| 541,77299 | 0,00364 | 0,00263 | 0,00092 | 0,00126 |
| 541,81018 | 0,00334 | 0,00237 | 0,00081 | 0,00112 |
| 541,84736 | 0,00304 | 0,00213 | 0,00072 | 0,00099 |
| 541,88454 | 0,00277 | 0,00191 | 0,00064 | 0,00089 |
| 541,92172 | 0,00251 | 0,0017 | 0,00057 | 0,00079 |
| 541,9589 | 0,00226 | 0,00152 | 0,00051 | 0,00071 |
| 541,99609 | 0,00204 | 0,00135 | 0,00046 | 0,00064 |
| 542,03327 | 0,00184 | 0,00119 | 0,00042 | 0,00058 |
| 542,07045 | 0,00165 | 0,00105 | 0,00038 | 0,00053 |
| 542,10763 | 0,00148 | 0,00093 | 0,00035 | 0,00049 |
| 542,14481 | 0,00133 | 0,00082 | 0,00033 | 0,00046 |
| 542,182 | 0,0012 | 0,00073 | 0,00031 | 0,00043 |
| 542,21918 | 0,00108 | 0,00064 | 0,00029 | 4e-04 |
| 542,25636 | 0,00098 | 0,00057 | 0,00027 | 0,00038 |
| 542,29354 | 0,00089 | 0,00051 | 0,00026 | 0,00036 |
| 542,33072 | 0,00081 | 0,00045 | 0,00025 | 0,00034 |
| 542,36791 | 0,00074 | 0,00041 | 0,00024 | 0,00033 |
| 542,40509 | 0,00069 | 0,00037 | 0,00023 | 0,00031 |
| 542,44227 | 0,00064 | 0,00034 | 0,00021 | 3e-04 |
| 542,47945 | 6e-04 | 0,00031 | 2e-04 | 0,00029 |
| 542,51663 | 0,00057 | 0,00029 | 0,00019 | 0,00027 |
| 542,55382 | 0,00054 | 0,00027 | 0,00018 | 0,00026 |
| 542,591 | 0,00052 | 0,00026 | 0,00017 | 0,00024 |
| 542,62818 | 5e-04 | 0,00024 | 0,00016 | 0,00023 |
| 542,66536 | 0,00048 | 0,00023 | 0,00015 | 0,00021 |
| 542,70254 | 0,00046 | 0,00022 | 0,00014 | 2e-04 |
| 542,73973 | 0,00044 | 0,00021 | 0,00013 | 0,00019 |
| 542,77691 | 0,00043 | 2e-04 | 0,00012 | 0,00017 |
| 542,81409 | 0,00041 | 0,00019 | 0,00011 | 0,00016 |
| 542,85127 | 4e-04 | 0,00019 | 1e-04 | 0,00014 |
| 542,88845 | 0,00038 | 0,00018 | 9e-05 | 0,00013 |
| 542,92564 | 0,00037 | 0,00017 | 9e-05 | 0,00012 |
| 542,96282 | 0,00035 | 0,00016 | 8e-05 | 0,00011 |
| 543 | 0,00033 | 0,00015 | 7e-05 | 9e-05 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 0 | 0,00015 | 0,00011 | 2e-04 |
| 524,03718 | 1e-05 | 0,00015 | 0,00011 | 0,00021 |
| 524,07436 | 1e-05 | 0,00015 | 0,00011 | 0,00021 |
| 524,11155 | 1e-05 | 0,00016 | 0,00011 | 0,00022 |
| 524,14873 | 1e-05 | 0,00017 | 0,00011 | 0,00022 |
| 524,18591 | 1e-05 | 0,00017 | 0,00011 | 0,00022 |
| 524,22309 | 1e-05 | 0,00018 | 0,00011 | 0,00023 |
| 524,26027 | 2e-05 | 0,00019 | 0,00011 | 0,00023 |
| 524,29746 | 2e-05 | 0,00019 | 0,00011 | 0,00023 |
| 524,33464 | 3e-05 | 2e-04 | 0,00011 | 0,00023 |
| 524,37182 | 3e-05 | 0,00021 | 1e-04 | 0,00022 |
| 524,409 | 4e-05 | 0,00022 | 1e-04 | 0,00022 |
| 524,44618 | 4e-05 | 0,00023 | 1e-04 | 0,00022 |
| 524,48337 | 5e-05 | 0,00024 | 9e-05 | 0,00022 |
| 524,52055 | 6e-05 | 0,00025 | 9e-05 | 0,00021 |
| 524,55773 | 7e-05 | 0,00027 | 9e-05 | 0,00021 |
| 524,59491 | 8e-05 | 0,00028 | 8e-05 | 0,00021 |
| 524,63209 | 1e-04 | 0,00029 | 8e-05 | 0,00021 |
| 524,66928 | 0,00011 | 3e-04 | 8e-05 | 2e-04 |
| 524,70646 | 0,00013 | 0,00031 | 8e-05 | 2e-04 |
| 524,74364 | 0,00015 | 0,00033 | 8e-05 | 2e-04 |
| 524,78082 | 0,00017 | 0,00034 | 8e-05 | 2e-04 |
| 524,818 | 0,00019 | 0,00035 | 9e-05 | 2e-04 |
| 524,85519 | 0,00022 | 0,00037 | 9e-05 | 2e-04 |
| 524,89237 | 0,00025 | 0,00038 | 1e-04 | 0,00021 |
| 524,92955 | 0,00028 | 4e-04 | 0,00011 | 0,00021 |
| 524,96673 | 0,00031 | 0,00042 | 0,00012 | 0,00022 |
| 525,00391 | 0,00035 | 0,00044 | 0,00014 | 0,00023 |
| 525,0411 | 0,00039 | 0,00047 | 0,00016 | 0,00024 |
| 525,07828 | 0,00044 | 0,00049 | 0,00018 | 0,00026 |
| 525,11546 | 0,00049 | 0,00053 | 0,00021 | 0,00027 |
| 525,15264 | 0,00055 | 0,00056 | 0,00024 | 3e-04 |
| 525,18982 | 0,00061 | 6e-04 | 0,00028 | 0,00032 |
| 525,22701 | 0,00067 | 0,00065 | 0,00033 | 0,00035 |
| 525,26419 | 0,00074 | 7e-04 | 0,00038 | 0,00039 |
| 525,30137 | 0,00082 | 0,00076 | 0,00043 | 0,00043 |
| 525,33855 | 0,00091 | 0,00083 | 5e-04 | 0,00048 |
| 525,37573 | 0,00101 | 0,00091 | 0,00057 | 0,00053 |
| 525,41292 | 0,00111 | 0,00099 | 0,00065 | 6e-04 |
| 525,4501 | 0,00122 | 0,00109 | 0,00074 | 0,00067 |
| 525,48728 | 0,00134 | 0,00119 | 0,00084 | 0,00075 |
| 525,52446 | 0,00147 | 0,0013 | 0,00095 | 0,00084 |
| 525,56164 | 0,00161 | 0,00143 | 0,00107 | 0,00094 |
| 525,59883 | 0,00176 | 0,00156 | 0,0012 | 0,00105 |
| 525,63601 | 0,00192 | 0,00171 | 0,00134 | 0,00117 |
| 525,67319 | 0,0021 | 0,00186 | 0,00149 | 0,0013 |
| 525,71037 | 0,00228 | 0,00203 | 0,00165 | 0,00144 |
| 525,74755 | 0,00248 | 0,0022 | 0,00182 | 0,0016 |
| 525,78474 | 0,00269 | 0,00239 | 0,002 | 0,00177 |
| 525,82192 | 0,00292 | 0,00259 | 0,00218 | 0,00194 |
| 525,8591 | 0,00316 | 0,0028 | 0,00238 | 0,00213 |
| 525,89628 | 0,00341 | 0,00302 | 0,00258 | 0,00233 |
| 525,93346 | 0,00367 | 0,00324 | 0,00279 | 0,00254 |
| 525,97065 | 0,00396 | 0,00347 | 0,003 | 0,00275 |
| 526,00783 | 0,00425 | 0,00372 | 0,00322 | 0,00298 |
| 526,04501 | 0,00456 | 0,00396 | 0,00344 | 0,00321 |
| 526,08219 | 0,00488 | 0,00422 | 0,00367 | 0,00345 |
| 526,11937 | 0,00521 | 0,00448 | 0,00389 | 0,00369 |
| 526,15656 | 0,00555 | 0,00474 | 0,00412 | 0,00393 |
| 526,19374 | 0,00591 | 0,00501 | 0,00434 | 0,00418 |
| 526,23092 | 0,00628 | 0,00528 | 0,00457 | 0,00443 |
| 526,2681 | 0,00666 | 0,00555 | 0,00479 | 0,00467 |
| 526,30528 | 0,00704 | 0,00583 | 0,005 | 0,00492 |
| 526,34247 | 0,00744 | 0,0061 | 0,00522 | 0,00516 |
| 526,37965 | 0,00784 | 0,00638 | 0,00543 | 0,0054 |
| 526,41683 | 0,00825 | 0,00665 | 0,00563 | 0,00563 |
| 526,45401 | 0,00867 | 0,00692 | 0,00583 | 0,00586 |
| 526,49119 | 0,00909 | 0,00719 | 0,00602 | 0,00608 |
| 526,52838 | 0,00952 | 0,00746 | 0,00621 | 0,00629 |
| 526,56556 | 0,00995 | 0,00773 | 0,00639 | 0,0065 |
| 526,60274 | 0,01039 | 0,008 | 0,00657 | 0,00671 |
| 526,63992 | 0,01083 | 0,00826 | 0,00675 | 0,0069 |
| 526,6771 | 0,01127 | 0,00853 | 0,00692 | 0,00709 |
| 526,71429 | 0,01172 | 0,00879 | 0,00709 | 0,00728 |
| 526,75147 | 0,01218 | 0,00906 | 0,00726 | 0,00746 |
| 526,78865 | 0,01263 | 0,00933 | 0,00743 | 0,00764 |
| 526,82583 | 0,0131 | 0,00961 | 0,0076 | 0,00782 |
| 526,86301 | 0,01357 | 0,00989 | 0,00778 | 0,008 |
| 526,9002 | 0,01405 | 0,01018 | 0,00796 | 0,00818 |
| 526,93738 | 0,01454 | 0,01048 | 0,00815 | 0,00837 |
| 526,97456 | 0,01504 | 0,0108 | 0,00835 | 0,00856 |
| 527,01174 | 0,01556 | 0,01113 | 0,00857 | 0,00876 |
| 527,04892 | 0,01608 | 0,01148 | 0,0088 | 0,00897 |
| 527,08611 | 0,01663 | 0,01185 | 0,00905 | 0,0092 |
| 527,12329 | 0,01719 | 0,01225 | 0,00932 | 0,00944 |
| 527,16047 | 0,01777 | 0,01268 | 0,00961 | 0,00971 |
| 527,19765 | 0,01837 | 0,01313 | 0,00994 | 0,01 |
| 527,23483 | 0,01899 | 0,01362 | 0,0103 | 0,01031 |
| 527,27202 | 0,01963 | 0,01414 | 0,0107 | 0,01065 |
| 527,3092 | 0,0203 | 0,0147 | 0,01113 | 0,01104 |
| 527,34638 | 0,02099 | 0,01531 | 0,0116 | 0,01145 |
| 527,38356 | 0,0217 | 0,01596 | 0,01213 | 0,01191 |
| 527,42074 | 0,02244 | 0,01664 | 0,01271 | 0,01242 |
| 527,45793 | 0,02319 | 0,01737 | 0,01334 | 0,01296 |
| 527,49511 | 0,02397 | 0,01813 | 0,01403 | 0,01356 |
| 527,53229 | 0,02478 | 0,01894 | 0,01477 | 0,01421 |
| 527,56947 | 0,0256 | 0,0198 | 0,01557 | 0,01492 |
| 527,60665 | 0,02644 | 0,0207 | 0,01645 | 0,01568 |
| 527,64384 | 0,0273 | 0,02163 | 0,01738 | 0,0165 |
| 527,68102 | 0,02818 | 0,02259 | 0,01837 | 0,01737 |
| 527,7182 | 0,02906 | 0,02359 | 0,01942 | 0,01829 |
| 527,75538 | 0,02997 | 0,02462 | 0,02053 | 0,01928 |
| 527,79256 | 0,03088 | 0,02568 | 0,02169 | 0,02032 |
| 527,82975 | 0,03179 | 0,02676 | 0,02291 | 0,02141 |
| 527,86693 | 0,03272 | 0,02786 | 0,02417 | 0,02255 |
| 527,90411 | 0,03364 | 0,02898 | 0,02548 | 0,02373 |
| 527,94129 | 0,03457 | 0,03011 | 0,02681 | 0,02495 |
| 527,97847 | 0,0355 | 0,03125 | 0,02818 | 0,0262 |
| 528,01566 | 0,03642 | 0,03239 | 0,02956 | 0,02748 |
| 528,05284 | 0,03734 | 0,03354 | 0,03096 | 0,02879 |
| 528,09002 | 0,03825 | 0,03468 | 0,03236 | 0,0301 |
| 528,1272 | 0,03915 | 0,03582 | 0,03376 | 0,03143 |
| 528,16438 | 0,04005 | 0,03695 | 0,03515 | 0,03275 |
| 528,20157 | 0,04094 | 0,03807 | 0,03652 | 0,03407 |
| 528,23875 | 0,04181 | 0,03918 | 0,03787 | 0,03538 |
| 528,27593 | 0,04267 | 0,04027 | 0,03918 | 0,03667 |
| 528,31311 | 0,04352 | 0,04135 | 0,04045 | 0,03793 |
| 528,35029 | 0,04436 | 0,04241 | 0,04168 | 0,03917 |
| 528,38748 | 0,04519 | 0,04346 | 0,04287 | 0,04037 |
| 528,42466 | 0,046 | 0,04448 | 0,04402 | 0,04154 |
| 528,46184 | 0,04679 | 0,04549 | 0,04512 | 0,04267 |
| 528,49902 | 0,04758 | 0,04647 | 0,04616 | 0,04375 |
| 528,5362 | 0,04835 | 0,04743 | 0,04715 | 0,04479 |
| 528,57339 | 0,0491 | 0,04838 | 0,04809 | 0,04579 |
| 528,61057 | 0,04984 | 0,0493 | 0,04898 | 0,04675 |
| 528,64775 | 0,05056 | 0,0502 | 0,04983 | 0,04766 |
| 528,68493 | 0,05126 | 0,05108 | 0,05064 | 0,04853 |
| 528,72211 | 0,05195 | 0,05194 | 0,0514 | 0,04935 |
| 528,7593 | 0,05263 | 0,05278 | 0,05213 | 0,05014 |
| 528,79648 | 0,05328 | 0,05359 | 0,05281 | 0,05088 |
| 528,83366 | 0,05392 | 0,05439 | 0,05347 | 0,05159 |
| 528,87084 | 0,05454 | 0,05516 | 0,05409 | 0,05227 |
| 528,90802 | 0,05514 | 0,05591 | 0,05469 | 0,05291 |
| 528,94521 | 0,05572 | 0,05664 | 0,05526 | 0,05352 |
| 528,98239 | 0,05629 | 0,05735 | 0,05581 | 0,0541 |
| 529,01957 | 0,05685 | 0,05805 | 0,05633 | 0,05465 |
| 529,05675 | 0,05739 | 0,05872 | 0,05684 | 0,05519 |
| 529,09393 | 0,05792 | 0,05938 | 0,05732 | 0,0557 |
| 529,13112 | 0,05844 | 0,06003 | 0,0578 | 0,0562 |
| 529,1683 | 0,05897 | 0,06067 | 0,05826 | 0,05669 |
| 529,20548 | 0,05949 | 0,0613 | 0,05871 | 0,05717 |
| 529,24266 | 0,06001 | 0,06192 | 0,05916 | 0,05765 |
| 529,27984 | 0,06054 | 0,06255 | 0,05961 | 0,05814 |
| 529,31703 | 0,0611 | 0,06318 | 0,06005 | 0,05865 |
| 529,35421 | 0,06167 | 0,06382 | 0,06051 | 0,05917 |
| 529,39139 | 0,06226 | 0,06448 | 0,06098 | 0,05972 |
| 529,42857 | 0,06289 | 0,06515 | 0,06147 | 0,06031 |
| 529,46575 | 0,06355 | 0,06585 | 0,06198 | 0,06094 |
| 529,50294 | 0,06426 | 0,06657 | 0,06253 | 0,06162 |
| 529,54012 | 0,06502 | 0,06733 | 0,06312 | 0,06236 |
| 529,5773 | 0,06582 | 0,06812 | 0,06375 | 0,06315 |
| 529,61448 | 0,06668 | 0,06896 | 0,06444 | 0,06403 |
| 529,65166 | 0,06759 | 0,06982 | 0,06519 | 0,06498 |
| 529,68885 | 0,06855 | 0,07073 | 0,06601 | 0,06601 |
| 529,72603 | 0,06957 | 0,07168 | 0,06689 | 0,06711 |
| 529,76321 | 0,07065 | 0,07267 | 0,06785 | 0,06829 |
| 529,80039 | 0,07177 | 0,07371 | 0,06888 | 0,06954 |
| 529,83757 | 0,07293 | 0,07477 | 0,06999 | 0,07088 |
| 529,87476 | 0,07413 | 0,07587 | 0,07119 | 0,07229 |
| 529,91194 | 0,07536 | 0,07699 | 0,07246 | 0,07376 |
| 529,94912 | 0,07662 | 0,07813 | 0,07381 | 0,07528 |
| 529,9863 | 0,07788 | 0,07929 | 0,07522 | 0,07684 |
| 530,02348 | 0,07915 | 0,08045 | 0,07669 | 0,07844 |
| 530,06067 | 0,08041 | 0,0816 | 0,0782 | 0,08006 |
| 530,09785 | 0,08165 | 0,08274 | 0,07976 | 0,08168 |
| 530,13503 | 0,08286 | 0,08387 | 0,08135 | 0,08329 |
| 530,17221 | 0,08404 | 0,08496 | 0,08295 | 0,08487 |
| 530,20939 | 0,08515 | 0,08601 | 0,08454 | 0,08641 |
| 530,24658 | 0,08621 | 0,08702 | 0,08612 | 0,08789 |
| 530,28376 | 0,0872 | 0,08797 | 0,08766 | 0,08931 |
| 530,32094 | 0,08812 | 0,08886 | 0,08916 | 0,09062 |
| 530,35812 | 0,08896 | 0,08969 | 0,09057 | 0,09183 |
| 530,3953 | 0,08971 | 0,09045 | 0,09191 | 0,09293 |
| 530,43249 | 0,09037 | 0,09112 | 0,09316 | 0,09391 |
| 530,46967 | 0,09094 | 0,09172 | 0,0943 | 0,09477 |
| 530,50685 | 0,09143 | 0,09225 | 0,09533 | 0,09551 |
| 530,54403 | 0,09185 | 0,09271 | 0,09624 | 0,09609 |
| 530,58121 | 0,09219 | 0,09311 | 0,097 | 0,09654 |
| 530,6184 | 0,09246 | 0,09344 | 0,09765 | 0,09688 |
| 530,65558 | 0,09266 | 0,09372 | 0,09817 | 0,09711 |
| 530,69276 | 0,09282 | 0,09395 | 0,09859 | 0,09725 |
| 530,72994 | 0,09295 | 0,09416 | 0,0989 | 0,0973 |
| 530,76712 | 0,09305 | 0,09435 | 0,09911 | 0,09727 |
| 530,80431 | 0,09314 | 0,09453 | 0,09923 | 0,0972 |
| 530,84149 | 0,09324 | 0,09471 | 0,0993 | 0,09711 |
| 530,87867 | 0,09336 | 0,09493 | 0,09933 | 0,09702 |
| 530,91585 | 0,09351 | 0,09518 | 0,09934 | 0,09694 |
| 530,95303 | 0,09371 | 0,09549 | 0,09936 | 0,09691 |
| 530,99022 | 0,09396 | 0,09586 | 0,0994 | 0,09696 |
| 531,0274 | 0,09428 | 0,0963 | 0,09949 | 0,0971 |
| 531,06458 | 0,09469 | 0,09682 | 0,09965 | 0,09734 |
| 531,10176 | 0,09519 | 0,09746 | 0,0999 | 0,09771 |
| 531,13894 | 0,09577 | 0,09819 | 0,10026 | 0,09821 |
| 531,17613 | 0,09645 | 0,09902 | 0,10072 | 0,09885 |
| 531,21331 | 0,09721 | 0,09995 | 0,10131 | 0,09965 |
| 531,25049 | 0,09806 | 0,10098 | 0,10205 | 0,10062 |
| 531,28767 | 0,09901 | 0,10209 | 0,10293 | 0,10174 |
| 531,32485 | 0,10003 | 0,1033 | 0,10393 | 0,10299 |
| 531,36204 | 0,10112 | 0,10458 | 0,10506 | 0,10437 |
| 531,39922 | 0,10226 | 0,10591 | 0,1063 | 0,10586 |
| 531,4364 | 0,10344 | 0,10727 | 0,10763 | 0,10745 |
| 531,47358 | 0,10465 | 0,10866 | 0,10907 | 0,10912 |
| 531,51076 | 0,10587 | 0,11004 | 0,11056 | 0,11083 |
| 531,54795 | 0,10708 | 0,1114 | 0,11209 | 0,11255 |
| 531,58513 | 0,10826 | 0,11271 | 0,11363 | 0,11427 |
| 531,62231 | 0,1094 | 0,11395 | 0,11516 | 0,11595 |
| 531,65949 | 0,11048 | 0,11511 | 0,11667 | 0,11757 |
| 531,69667 | 0,1115 | 0,11617 | 0,1181 | 0,11908 |
| 531,73386 | 0,11243 | 0,11712 | 0,11945 | 0,12047 |
| 531,77104 | 0,11326 | 0,1179 | 0,12069 | 0,12173 |
| 531,80822 | 0,11398 | 0,11855 | 0,12181 | 0,12284 |
| 531,8454 | 0,1146 | 0,11905 | 0,1228 | 0,12379 |
| 531,88258 | 0,11512 | 0,1194 | 0,12366 | 0,12456 |
| 531,91977 | 0,11552 | 0,11961 | 0,12435 | 0,12513 |
| 531,95695 | 0,11581 | 0,11966 | 0,12486 | 0,12551 |
| 531,99413 | 0,11598 | 0,11955 | 0,12523 | 0,12573 |
| 532,03131 | 0,11605 | 0,11931 | 0,12546 | 0,12578 |
| 532,06849 | 0,11605 | 0,11897 | 0,12556 | 0,12569 |
| 532,10568 | 0,11597 | 0,11852 | 0,12553 | 0,12547 |
| 532,14286 | 0,11583 | 0,118 | 0,12539 | 0,12511 |
| 532,18004 | 0,11564 | 0,11742 | 0,12515 | 0,12467 |
| 532,21722 | 0,11541 | 0,1168 | 0,12485 | 0,12416 |
| 532,2544 | 0,11517 | 0,11617 | 0,1245 | 0,12361 |
| 532,29159 | 0,11494 | 0,11555 | 0,12412 | 0,12305 |
| 532,32877 | 0,11472 | 0,11496 | 0,12374 | 0,12249 |
| 532,36595 | 0,11453 | 0,11442 | 0,12337 | 0,12196 |
| 532,40313 | 0,11438 | 0,11395 | 0,12304 | 0,12149 |
| 532,44031 | 0,1143 | 0,11359 | 0,12276 | 0,12109 |
| 532,4775 | 0,11429 | 0,11333 | 0,12255 | 0,12076 |
| 532,51468 | 0,11435 | 0,11318 | 0,1224 | 0,12053 |
| 532,55186 | 0,11449 | 0,11316 | 0,12233 | 0,1204 |
| 532,58904 | 0,11471 | 0,11326 | 0,12235 | 0,12037 |
| 532,62622 | 0,11502 | 0,11349 | 0,12248 | 0,12047 |
| 532,66341 | 0,11543 | 0,11387 | 0,12268 | 0,12065 |
| 532,70059 | 0,11591 | 0,11437 | 0,12297 | 0,12093 |
| 532,73777 | 0,11646 | 0,11497 | 0,12333 | 0,12129 |
| 532,77495 | 0,11707 | 0,11567 | 0,12376 | 0,12171 |
| 532,81213 | 0,11773 | 0,11646 | 0,12424 | 0,12219 |
| 532,84932 | 0,11844 | 0,11732 | 0,12478 | 0,12271 |
| 532,8865 | 0,11917 | 0,11822 | 0,12534 | 0,12325 |
| 532,92368 | 0,1199 | 0,11915 | 0,12591 | 0,12379 |
| 532,96086 | 0,12062 | 0,12008 | 0,12648 | 0,1243 |
| 532,99804 | 0,12132 | 0,12099 | 0,12704 | 0,12479 |
| 533,03523 | 0,12199 | 0,12186 | 0,12757 | 0,12523 |
| 533,07241 | 0,12259 | 0,12267 | 0,12805 | 0,12559 |
| 533,10959 | 0,12311 | 0,12338 | 0,12849 | 0,12587 |
| 533,14677 | 0,12356 | 0,124 | 0,12886 | 0,12606 |
| 533,18395 | 0,12391 | 0,1245 | 0,12916 | 0,12616 |
| 533,22114 | 0,12416 | 0,12489 | 0,1294 | 0,12616 |
| 533,25832 | 0,1243 | 0,12514 | 0,12956 | 0,12607 |
| 533,2955 | 0,12433 | 0,12525 | 0,12963 | 0,12586 |
| 533,33268 | 0,12423 | 0,1252 | 0,12962 | 0,12556 |
| 533,36986 | 0,12402 | 0,12501 | 0,12953 | 0,12517 |
| 533,40705 | 0,12371 | 0,12469 | 0,12938 | 0,12471 |
| 533,44423 | 0,1233 | 0,12425 | 0,12917 | 0,12417 |
| 533,48141 | 0,12281 | 0,1237 | 0,12889 | 0,12359 |
| 533,51859 | 0,12222 | 0,12304 | 0,12857 | 0,12296 |
| 533,55577 | 0,12157 | 0,12228 | 0,12819 | 0,1223 |
| 533,59295 | 0,12086 | 0,12146 | 0,12779 | 0,12164 |
| 533,63014 | 0,12011 | 0,12059 | 0,12736 | 0,12098 |
| 533,66732 | 0,11935 | 0,11969 | 0,12691 | 0,12034 |
| 533,7045 | 0,11857 | 0,11877 | 0,12645 | 0,11972 |
| 533,74168 | 0,1178 | 0,11786 | 0,12598 | 0,11915 |
| 533,77886 | 0,11705 | 0,11698 | 0,12552 | 0,11863 |
| 533,81605 | 0,11634 | 0,11614 | 0,12505 | 0,11817 |
| 533,85323 | 0,11567 | 0,11535 | 0,12458 | 0,11776 |
| 533,89041 | 0,11505 | 0,11462 | 0,1241 | 0,11741 |
| 533,92759 | 0,11449 | 0,11397 | 0,12363 | 0,11711 |
| 533,96477 | 0,11401 | 0,1134 | 0,12314 | 0,11686 |
| 534,00196 | 0,1136 | 0,11292 | 0,12264 | 0,11666 |
| 534,03914 | 0,11326 | 0,11252 | 0,1221 | 0,11648 |
| 534,07632 | 0,11298 | 0,1122 | 0,12154 | 0,11632 |
| 534,1135 | 0,11276 | 0,11196 | 0,12093 | 0,11615 |
| 534,15068 | 0,11259 | 0,11178 | 0,12027 | 0,11598 |
| 534,18787 | 0,11248 | 0,11167 | 0,11955 | 0,11577 |
| 534,22505 | 0,1124 | 0,1116 | 0,11874 | 0,11551 |
| 534,26223 | 0,11233 | 0,11156 | 0,11785 | 0,11517 |
| 534,29941 | 0,11227 | 0,11153 | 0,11687 | 0,11475 |
| 534,33659 | 0,11219 | 0,1115 | 0,11579 | 0,11423 |
| 534,37378 | 0,11209 | 0,11145 | 0,11461 | 0,1136 |
| 534,41096 | 0,11194 | 0,11136 | 0,11332 | 0,11286 |
| 534,44814 | 0,11172 | 0,11121 | 0,11191 | 0,11196 |
| 534,48532 | 0,11141 | 0,11098 | 0,11039 | 0,11091 |
| 534,5225 | 0,11102 | 0,11067 | 0,10878 | 0,10973 |
| 534,55969 | 0,11052 | 0,11027 | 0,10707 | 0,10841 |
| 534,59687 | 0,10991 | 0,10976 | 0,10527 | 0,10695 |
| 534,63405 | 0,10916 | 0,10911 | 0,1034 | 0,10537 |
| 534,67123 | 0,10826 | 0,10833 | 0,10145 | 0,10365 |
| 534,70841 | 0,10723 | 0,10742 | 0,09946 | 0,10182 |
| 534,7456 | 0,10608 | 0,1064 | 0,09743 | 0,09991 |
| 534,78278 | 0,1048 | 0,10525 | 0,09539 | 0,09792 |
| 534,81996 | 0,1034 | 0,10399 | 0,09335 | 0,09588 |
| 534,85714 | 0,10187 | 0,1026 | 0,09133 | 0,0938 |
| 534,89432 | 0,10024 | 0,10112 | 0,08935 | 0,09171 |
| 534,93151 | 0,09853 | 0,09957 | 0,08743 | 0,08964 |
| 534,96869 | 0,09676 | 0,09795 | 0,08559 | 0,0876 |
| 535,00587 | 0,09495 | 0,09629 | 0,08384 | 0,08561 |
| 535,04305 | 0,09311 | 0,0946 | 0,0822 | 0,0837 |
| 535,08023 | 0,09127 | 0,09291 | 0,08067 | 0,08189 |
| 535,11742 | 0,08946 | 0,09124 | 0,0793 | 0,08018 |
| 535,1546 | 0,08769 | 0,0896 | 0,07808 | 0,07863 |
| 535,19178 | 0,08599 | 0,08802 | 0,07701 | 0,07722 |
| 535,22896 | 0,08437 | 0,08651 | 0,07609 | 0,07597 |
| 535,26614 | 0,08285 | 0,08509 | 0,07534 | 0,07487 |
| 535,30333 | 0,08147 | 0,08378 | 0,07474 | 0,07393 |
| 535,34051 | 0,08022 | 0,0826 | 0,07432 | 0,07316 |
| 535,37769 | 0,07912 | 0,08153 | 0,07407 | 0,0726 |
| 535,41487 | 0,07817 | 0,08059 | 0,07397 | 0,0722 |
| 535,45205 | 0,07737 | 0,07977 | 0,074 | 0,07195 |
| 535,48924 | 0,07672 | 0,07908 | 0,07417 | 0,07185 |
| 535,52642 | 0,07624 | 0,07854 | 0,07445 | 0,07189 |
| 535,5636 | 0,07592 | 0,07812 | 0,07485 | 0,07206 |
| 535,60078 | 0,07574 | 0,0778 | 0,07534 | 0,07236 |
| 535,63796 | 0,07567 | 0,07757 | 0,07591 | 0,07276 |
| 535,67515 | 0,07573 | 0,07743 | 0,07653 | 0,07324 |
| 535,71233 | 0,07588 | 0,07737 | 0,07719 | 0,07378 |
| 535,74951 | 0,07613 | 0,07736 | 0,07788 | 0,07436 |
| 535,78669 | 0,07644 | 0,07739 | 0,07857 | 0,07498 |
| 535,82387 | 0,0768 | 0,07744 | 0,07925 | 0,07561 |
| 535,86106 | 0,07719 | 0,07749 | 0,0799 | 0,07624 |
| 535,89824 | 0,07758 | 0,07753 | 0,08052 | 0,07685 |
| 535,93542 | 0,07797 | 0,07755 | 0,08108 | 0,07743 |
| 535,9726 | 0,07833 | 0,07751 | 0,08159 | 0,07796 |
| 536,00978 | 0,07865 | 0,07743 | 0,08203 | 0,07845 |
| 536,04697 | 0,07891 | 0,07728 | 0,08237 | 0,07887 |
| 536,08415 | 0,0791 | 0,07707 | 0,08263 | 0,07922 |
| 536,12133 | 0,07922 | 0,07678 | 0,08281 | 0,0795 |
| 536,15851 | 0,07926 | 0,07642 | 0,08291 | 0,07971 |
| 536,19569 | 0,0792 | 0,07596 | 0,08292 | 0,07985 |
| 536,23288 | 0,07903 | 0,07542 | 0,08284 | 0,07992 |
| 536,27006 | 0,07877 | 0,07481 | 0,08267 | 0,07991 |
| 536,30724 | 0,07842 | 0,07414 | 0,08242 | 0,07983 |
| 536,34442 | 0,07798 | 0,07341 | 0,0821 | 0,07969 |
| 536,3816 | 0,07746 | 0,07262 | 0,08171 | 0,07949 |
| 536,41879 | 0,07685 | 0,07178 | 0,08126 | 0,07923 |
| 536,45597 | 0,07616 | 0,07092 | 0,08075 | 0,07893 |
| 536,49315 | 0,07541 | 0,07004 | 0,08018 | 0,07857 |
| 536,53033 | 0,07461 | 0,06915 | 0,07956 | 0,07816 |
| 536,56751 | 0,07377 | 0,06826 | 0,07889 | 0,07771 |
| 536,6047 | 0,0729 | 0,06739 | 0,07817 | 0,07721 |
| 536,64188 | 0,072 | 0,06654 | 0,07742 | 0,07667 |
| 536,67906 | 0,07109 | 0,06574 | 0,07662 | 0,07609 |
| 536,71624 | 0,07018 | 0,06497 | 0,07577 | 0,07546 |
| 536,75342 | 0,06928 | 0,06425 | 0,07488 | 0,07478 |
| 536,79061 | 0,06839 | 0,06358 | 0,07394 | 0,07405 |
| 536,82779 | 0,06751 | 0,06297 | 0,07296 | 0,07327 |
| 536,86497 | 0,06667 | 0,06242 | 0,07193 | 0,07244 |
| 536,90215 | 0,06585 | 0,06192 | 0,07086 | 0,07155 |
| 536,93933 | 0,06506 | 0,06147 | 0,06974 | 0,07061 |
| 536,97652 | 0,0643 | 0,06106 | 0,06856 | 0,06962 |
| 537,0137 | 0,06357 | 0,06069 | 0,06734 | 0,06857 |
| 537,05088 | 0,06287 | 0,06035 | 0,06609 | 0,06747 |
| 537,08806 | 0,06219 | 0,06004 | 0,06479 | 0,06634 |
| 537,12524 | 0,06153 | 0,05974 | 0,06347 | 0,06516 |
| 537,16243 | 0,06089 | 0,05944 | 0,06211 | 0,06396 |
| 537,19961 | 0,06026 | 0,05914 | 0,06074 | 0,06273 |
| 537,23679 | 0,05964 | 0,05882 | 0,05936 | 0,0615 |
| 537,27397 | 0,05901 | 0,05848 | 0,05798 | 0,06026 |
| 537,31115 | 0,05839 | 0,0581 | 0,05662 | 0,05904 |
| 537,34834 | 0,05775 | 0,05768 | 0,05528 | 0,05784 |
| 537,38552 | 0,05711 | 0,05723 | 0,05397 | 0,05668 |
| 537,4227 | 0,05646 | 0,05673 | 0,05271 | 0,05557 |
| 537,45988 | 0,05579 | 0,05618 | 0,05152 | 0,05452 |
| 537,49706 | 0,05511 | 0,05559 | 0,05039 | 0,05355 |
| 537,53425 | 0,05441 | 0,05495 | 0,04934 | 0,05266 |
| 537,57143 | 0,05371 | 0,05427 | 0,04837 | 0,05186 |
| 537,60861 | 0,053 | 0,05356 | 0,04749 | 0,05115 |
| 537,64579 | 0,05229 | 0,05283 | 0,04673 | 0,05054 |
| 537,68297 | 0,05159 | 0,05209 | 0,04608 | 0,05007 |
| 537,72016 | 0,0509 | 0,05134 | 0,04553 | 0,04971 |
| 537,75734 | 0,05023 | 0,05059 | 0,04509 | 0,04946 |
| 537,79452 | 0,04959 | 0,04988 | 0,04476 | 0,04932 |
| 537,8317 | 0,04899 | 0,04919 | 0,04454 | 0,04929 |
| 537,86888 | 0,04843 | 0,04854 | 0,04445 | 0,04938 |
| 537,90607 | 0,04793 | 0,04795 | 0,04447 | 0,04959 |
| 537,94325 | 0,04748 | 0,04743 | 0,04458 | 0,0499 |
| 537,98043 | 0,04711 | 0,04699 | 0,04478 | 0,0503 |
| 538,01761 | 0,04682 | 0,04664 | 0,04508 | 0,05079 |
| 538,05479 | 0,04661 | 0,04637 | 0,04545 | 0,05135 |
| 538,09198 | 0,04648 | 0,0462 | 0,0459 | 0,05199 |
| 538,12916 | 0,04642 | 0,04612 | 0,04641 | 0,05268 |
| 538,16634 | 0,04645 | 0,04614 | 0,04697 | 0,05342 |
| 538,20352 | 0,04656 | 0,04627 | 0,04756 | 0,05419 |
| 538,2407 | 0,04676 | 0,04649 | 0,04818 | 0,05497 |
| 538,27789 | 0,04701 | 0,04678 | 0,0488 | 0,05575 |
| 538,31507 | 0,04733 | 0,04715 | 0,04943 | 0,05651 |
| 538,35225 | 0,04768 | 0,04758 | 0,05003 | 0,05724 |
| 538,38943 | 0,04808 | 0,04806 | 0,0506 | 0,05792 |
| 538,42661 | 0,0485 | 0,04858 | 0,05113 | 0,05852 |
| 538,4638 | 0,04893 | 0,04911 | 0,0516 | 0,05905 |
| 538,50098 | 0,04935 | 0,04964 | 0,052 | 0,05948 |
| 538,53816 | 0,04974 | 0,05016 | 0,0523 | 0,0598 |
| 538,57534 | 0,05009 | 0,05065 | 0,05251 | 0,06 |
| 538,61252 | 0,05039 | 0,05109 | 0,05261 | 0,06004 |
| 538,64971 | 0,05062 | 0,05145 | 0,05261 | 0,05995 |
| 538,68689 | 0,05075 | 0,05174 | 0,05249 | 0,05971 |
| 538,72407 | 0,05079 | 0,05193 | 0,05226 | 0,05932 |
| 538,76125 | 0,05073 | 0,05203 | 0,05191 | 0,05879 |
| 538,79843 | 0,05057 | 0,05202 | 0,05142 | 0,05812 |
| 538,83562 | 0,05029 | 0,05189 | 0,05083 | 0,05727 |
| 538,8728 | 0,04988 | 0,05162 | 0,05014 | 0,0563 |
| 538,90998 | 0,04935 | 0,05124 | 0,04935 | 0,05522 |
| 538,94716 | 0,0487 | 0,05075 | 0,04848 | 0,05403 |
| 538,98434 | 0,04796 | 0,05014 | 0,04753 | 0,05276 |
| 539,02153 | 0,04711 | 0,04944 | 0,04652 | 0,05141 |
| 539,05871 | 0,04618 | 0,04862 | 0,04545 | 0,05 |
| 539,09589 | 0,04516 | 0,04772 | 0,04435 | 0,04855 |
| 539,13307 | 0,04408 | 0,04675 | 0,04324 | 0,04708 |
| 539,17025 | 0,04294 | 0,04572 | 0,04211 | 0,04561 |
| 539,20744 | 0,04178 | 0,04465 | 0,04097 | 0,04416 |
| 539,24462 | 0,04059 | 0,04355 | 0,03986 | 0,04273 |
| 539,2818 | 0,03939 | 0,04242 | 0,03876 | 0,04134 |
| 539,31898 | 0,0382 | 0,0413 | 0,03769 | 0,04 |
| 539,35616 | 0,03703 | 0,04018 | 0,03666 | 0,03872 |
| 539,39335 | 0,03589 | 0,03908 | 0,03565 | 0,03749 |
| 539,43053 | 0,03479 | 0,03801 | 0,03468 | 0,03632 |
| 539,46771 | 0,03373 | 0,03697 | 0,03375 | 0,03521 |
| 539,50489 | 0,03271 | 0,03597 | 0,03285 | 0,03417 |
| 539,54207 | 0,03176 | 0,03502 | 0,03198 | 0,03318 |
| 539,57926 | 0,03086 | 0,03412 | 0,03114 | 0,03224 |
| 539,61644 | 0,03001 | 0,03325 | 0,03031 | 0,03134 |
| 539,65362 | 0,02921 | 0,03243 | 0,0295 | 0,03047 |
| 539,6908 | 0,02846 | 0,03164 | 0,0287 | 0,02963 |
| 539,72798 | 0,02775 | 0,0309 | 0,0279 | 0,02881 |
| 539,76517 | 0,02708 | 0,03018 | 0,02711 | 0,028 |
| 539,80235 | 0,02644 | 0,02948 | 0,02631 | 0,0272 |
| 539,83953 | 0,02581 | 0,02879 | 0,0255 | 0,0264 |
| 539,87671 | 0,02521 | 0,02812 | 0,0247 | 0,02561 |
| 539,91389 | 0,02461 | 0,02744 | 0,02388 | 0,02481 |
| 539,95108 | 0,02402 | 0,02677 | 0,02305 | 0,02401 |
| 539,98826 | 0,02342 | 0,02608 | 0,02223 | 0,0232 |
| 540,02544 | 0,02282 | 0,02539 | 0,0214 | 0,0224 |
| 540,06262 | 0,02221 | 0,02468 | 0,02057 | 0,0216 |
| 540,0998 | 0,02159 | 0,02396 | 0,01975 | 0,0208 |
| 540,13699 | 0,02096 | 0,02322 | 0,01894 | 0,02002 |
| 540,17417 | 0,02031 | 0,02247 | 0,01815 | 0,01924 |
| 540,21135 | 0,01965 | 0,0217 | 0,01737 | 0,01849 |
| 540,24853 | 0,01899 | 0,02092 | 0,01662 | 0,01776 |
| 540,28571 | 0,01832 | 0,02014 | 0,01589 | 0,01705 |
| 540,3229 | 0,01765 | 0,01936 | 0,01518 | 0,01637 |
| 540,36008 | 0,01698 | 0,01858 | 0,01451 | 0,01572 |
| 540,39726 | 0,01632 | 0,0178 | 0,01388 | 0,01509 |
| 540,43444 | 0,01567 | 0,01704 | 0,01327 | 0,0145 |
| 540,47162 | 0,01504 | 0,0163 | 0,01269 | 0,01394 |
| 540,50881 | 0,01442 | 0,01557 | 0,01214 | 0,0134 |
| 540,54599 | 0,01383 | 0,01488 | 0,01161 | 0,01289 |
| 540,58317 | 0,01326 | 0,0142 | 0,01111 | 0,0124 |
| 540,62035 | 0,01272 | 0,01357 | 0,01064 | 0,01193 |
| 540,65753 | 0,01221 | 0,01296 | 0,01018 | 0,01147 |
| 540,69472 | 0,01173 | 0,01239 | 0,00974 | 0,01103 |
| 540,7319 | 0,01127 | 0,01185 | 0,00931 | 0,0106 |
| 540,76908 | 0,01085 | 0,01134 | 0,00889 | 0,01017 |
| 540,80626 | 0,01045 | 0,01086 | 0,00848 | 0,00975 |
| 540,84344 | 0,01008 | 0,01042 | 0,00808 | 0,00932 |
| 540,88063 | 0,00973 | 0,01 | 0,00768 | 0,0089 |
| 540,91781 | 0,0094 | 0,00961 | 0,00728 | 0,00848 |
| 540,95499 | 0,00909 | 0,00924 | 0,00688 | 0,00806 |
| 540,99217 | 0,00879 | 0,00888 | 0,00649 | 0,00763 |
| 541,02935 | 0,0085 | 0,00854 | 0,0061 | 0,00721 |
| 541,06654 | 0,00822 | 0,00822 | 0,00571 | 0,00678 |
| 541,10372 | 0,00794 | 0,0079 | 0,00533 | 0,00636 |
| 541,1409 | 0,00766 | 0,00758 | 0,00495 | 0,00595 |
| 541,17808 | 0,00739 | 0,00727 | 0,00458 | 0,00554 |
| 541,21526 | 0,00711 | 0,00697 | 0,00422 | 0,00513 |
| 541,25245 | 0,00682 | 0,00666 | 0,00388 | 0,00474 |
| 541,28963 | 0,00654 | 0,00635 | 0,00354 | 0,00436 |
| 541,32681 | 0,00624 | 0,00605 | 0,00322 | 0,004 |
| 541,36399 | 0,00594 | 0,00574 | 0,00292 | 0,00365 |
| 541,40117 | 0,00564 | 0,00543 | 0,00263 | 0,00332 |
| 541,43836 | 0,00534 | 0,00512 | 0,00236 | 0,003 |
| 541,47554 | 0,00503 | 0,00481 | 0,00211 | 0,00271 |
| 541,51272 | 0,00473 | 0,0045 | 0,00188 | 0,00243 |
| 541,5499 | 0,00442 | 0,0042 | 0,00167 | 0,00218 |
| 541,58708 | 0,00412 | 0,00391 | 0,00148 | 0,00194 |
| 541,62427 | 0,00382 | 0,00362 | 0,00131 | 0,00173 |
| 541,66145 | 0,00353 | 0,00333 | 0,00115 | 0,00153 |
| 541,69863 | 0,00325 | 0,00306 | 0,00102 | 0,00136 |
| 541,73581 | 0,00297 | 0,0028 | 9e-04 | 0,00119 |
| 541,77299 | 0,00271 | 0,00255 | 0,00079 | 0,00105 |
| 541,81018 | 0,00247 | 0,00232 | 7e-04 | 0,00092 |
| 541,84736 | 0,00223 | 0,00209 | 0,00062 | 0,00081 |
| 541,88454 | 0,00201 | 0,00188 | 0,00055 | 0,00071 |
| 541,92172 | 0,00181 | 0,00169 | 5e-04 | 0,00063 |
| 541,9589 | 0,00162 | 0,00152 | 0,00045 | 0,00055 |
| 541,99609 | 0,00145 | 0,00136 | 0,00041 | 0,00048 |
| 542,03327 | 0,00129 | 0,00121 | 0,00038 | 0,00042 |
| 542,07045 | 0,00115 | 0,00108 | 0,00035 | 0,00038 |
| 542,10763 | 0,00102 | 0,00096 | 0,00033 | 0,00033 |
| 542,14481 | 9e-04 | 0,00085 | 0,00031 | 3e-04 |
| 542,182 | 8e-04 | 0,00076 | 3e-04 | 0,00027 |
| 542,21918 | 0,00071 | 0,00068 | 0,00029 | 0,00024 |
| 542,25636 | 0,00063 | 0,00061 | 0,00028 | 0,00021 |
| 542,29354 | 0,00056 | 0,00055 | 0,00027 | 2e-04 |
| 542,33072 | 5e-04 | 0,00049 | 0,00026 | 0,00018 |
| 542,36791 | 0,00045 | 0,00045 | 0,00025 | 0,00016 |
| 542,40509 | 0,00041 | 0,00041 | 0,00025 | 0,00015 |
| 542,44227 | 0,00037 | 0,00038 | 0,00024 | 0,00014 |
| 542,47945 | 0,00034 | 0,00036 | 0,00023 | 0,00013 |
| 542,51663 | 0,00031 | 0,00033 | 0,00022 | 0,00012 |
| 542,55382 | 0,00029 | 0,00031 | 0,00021 | 0,00011 |
| 542,591 | 0,00027 | 3e-04 | 2e-04 | 1e-04 |
| 542,62818 | 0,00025 | 0,00028 | 0,00019 | 9e-05 |
| 542,66536 | 0,00023 | 0,00027 | 0,00018 | 8e-05 |
| 542,70254 | 0,00022 | 0,00026 | 0,00017 | 8e-05 |
| 542,73973 | 0,00021 | 0,00025 | 0,00016 | 7e-05 |
| 542,77691 | 2e-04 | 0,00024 | 0,00015 | 6e-05 |
| 542,81409 | 0,00018 | 0,00023 | 0,00013 | 6e-05 |
| 542,85127 | 0,00017 | 0,00022 | 0,00012 | 5e-05 |
| 542,88845 | 0,00017 | 0,00021 | 0,00011 | 5e-05 |
| 542,92564 | 0,00016 | 2e-04 | 1e-04 | 4e-05 |
| 542,96282 | 0,00015 | 0,00019 | 9e-05 | 4e-05 |
| 543 | 0,00014 | 0,00018 | 8e-05 | 3e-05 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 0,00012 | 8e-05 | 1e-05 | 0 |
| 524,03718 | 0,00013 | 9e-05 | 1e-05 | 0 |
| 524,07436 | 0,00015 | 0,00011 | 1e-05 | 0 |
| 524,11155 | 0,00017 | 0,00012 | 1e-05 | 0 |
| 524,14873 | 0,00019 | 0,00013 | 1e-05 | 0 |
| 524,18591 | 0,00021 | 0,00015 | 1e-05 | 0 |
| 524,22309 | 0,00023 | 0,00016 | 2e-05 | 0 |
| 524,26027 | 0,00025 | 0,00018 | 2e-05 | 0 |
| 524,29746 | 0,00028 | 0,00019 | 3e-05 | 0 |
| 524,33464 | 0,00031 | 0,00021 | 3e-05 | 0 |
| 524,37182 | 0,00033 | 0,00023 | 4e-05 | 1e-05 |
| 524,409 | 0,00036 | 0,00025 | 4e-05 | 1e-05 |
| 524,44618 | 0,00039 | 0,00026 | 5e-05 | 1e-05 |
| 524,48337 | 0,00043 | 0,00028 | 6e-05 | 1e-05 |
| 524,52055 | 0,00046 | 3e-04 | 7e-05 | 2e-05 |
| 524,55773 | 0,00049 | 0,00032 | 8e-05 | 2e-05 |
| 524,59491 | 0,00053 | 0,00034 | 1e-04 | 2e-05 |
| 524,63209 | 0,00056 | 0,00036 | 0,00011 | 3e-05 |
| 524,66928 | 6e-04 | 0,00038 | 0,00013 | 4e-05 |
| 524,70646 | 0,00064 | 4e-04 | 0,00015 | 4e-05 |
| 524,74364 | 0,00068 | 0,00043 | 0,00017 | 5e-05 |
| 524,78082 | 0,00072 | 0,00045 | 0,00019 | 7e-05 |
| 524,818 | 0,00076 | 0,00047 | 0,00022 | 8e-05 |
| 524,85519 | 8e-04 | 0,00049 | 0,00025 | 1e-04 |
| 524,89237 | 0,00084 | 0,00051 | 0,00028 | 0,00011 |
| 524,92955 | 0,00088 | 0,00053 | 0,00032 | 0,00014 |
| 524,96673 | 0,00092 | 0,00055 | 0,00036 | 0,00016 |
| 525,00391 | 0,00097 | 0,00057 | 0,00041 | 0,00019 |
| 525,0411 | 0,00101 | 0,00059 | 0,00046 | 0,00023 |
| 525,07828 | 0,00106 | 0,00062 | 0,00051 | 0,00026 |
| 525,11546 | 0,00111 | 0,00064 | 0,00057 | 0,00031 |
| 525,15264 | 0,00115 | 0,00067 | 0,00063 | 0,00036 |
| 525,18982 | 0,00121 | 7e-04 | 7e-04 | 0,00042 |
| 525,22701 | 0,00126 | 0,00073 | 0,00078 | 0,00048 |
| 525,26419 | 0,00131 | 0,00077 | 0,00086 | 0,00055 |
| 525,30137 | 0,00137 | 0,00081 | 0,00095 | 0,00063 |
| 525,33855 | 0,00143 | 0,00086 | 0,00105 | 0,00072 |
| 525,37573 | 0,0015 | 0,00091 | 0,00115 | 0,00081 |
| 525,41292 | 0,00156 | 0,00097 | 0,00126 | 0,00092 |
| 525,4501 | 0,00163 | 0,00103 | 0,00138 | 0,00103 |
| 525,48728 | 0,00171 | 0,0011 | 0,00151 | 0,00116 |
| 525,52446 | 0,00179 | 0,00118 | 0,00165 | 0,00129 |
| 525,56164 | 0,00187 | 0,00127 | 0,00179 | 0,00144 |
| 525,59883 | 0,00196 | 0,00137 | 0,00194 | 0,00159 |
| 525,63601 | 0,00206 | 0,00147 | 0,0021 | 0,00176 |
| 525,67319 | 0,00216 | 0,00159 | 0,00227 | 0,00193 |
| 525,71037 | 0,00227 | 0,00172 | 0,00245 | 0,00211 |
| 525,74755 | 0,00238 | 0,00187 | 0,00264 | 0,0023 |
| 525,78474 | 0,0025 | 0,00202 | 0,00283 | 0,00251 |
| 525,82192 | 0,00263 | 0,00219 | 0,00303 | 0,00271 |
| 525,8591 | 0,00276 | 0,00237 | 0,00324 | 0,00292 |
| 525,89628 | 0,0029 | 0,00256 | 0,00346 | 0,00314 |
| 525,93346 | 0,00305 | 0,00277 | 0,00368 | 0,00336 |
| 525,97065 | 0,0032 | 0,00299 | 0,00391 | 0,00359 |
| 526,00783 | 0,00336 | 0,00323 | 0,00415 | 0,00382 |
| 526,04501 | 0,00353 | 0,00348 | 0,00438 | 0,00404 |
| 526,08219 | 0,0037 | 0,00374 | 0,00463 | 0,00427 |
| 526,11937 | 0,00389 | 0,00401 | 0,00487 | 0,00449 |
| 526,15656 | 0,00408 | 0,0043 | 0,00511 | 0,00471 |
| 526,19374 | 0,00427 | 0,0046 | 0,00536 | 0,00492 |
| 526,23092 | 0,00448 | 0,00491 | 0,00561 | 0,00513 |
| 526,2681 | 0,00469 | 0,00524 | 0,00585 | 0,00533 |
| 526,30528 | 0,00491 | 0,00557 | 0,0061 | 0,00552 |
| 526,34247 | 0,00514 | 0,00591 | 0,00634 | 0,0057 |
| 526,37965 | 0,00538 | 0,00626 | 0,00658 | 0,00588 |
| 526,41683 | 0,00563 | 0,00662 | 0,00681 | 0,00604 |
| 526,45401 | 0,00588 | 0,00699 | 0,00705 | 0,00619 |
| 526,49119 | 0,00615 | 0,00737 | 0,00727 | 0,00634 |
| 526,52838 | 0,00642 | 0,00775 | 0,0075 | 0,00647 |
| 526,56556 | 0,0067 | 0,00813 | 0,00772 | 0,0066 |
| 526,60274 | 0,00699 | 0,00852 | 0,00794 | 0,00672 |
| 526,63992 | 0,0073 | 0,00892 | 0,00815 | 0,00683 |
| 526,6771 | 0,00761 | 0,00931 | 0,00836 | 0,00694 |
| 526,71429 | 0,00793 | 0,00972 | 0,00857 | 0,00705 |
| 526,75147 | 0,00827 | 0,01012 | 0,00879 | 0,00716 |
| 526,78865 | 0,00862 | 0,01053 | 0,009 | 0,00727 |
| 526,82583 | 0,00898 | 0,01094 | 0,00921 | 0,00739 |
| 526,86301 | 0,00936 | 0,01135 | 0,00943 | 0,00751 |
| 526,9002 | 0,00975 | 0,01177 | 0,00965 | 0,00765 |
| 526,93738 | 0,01016 | 0,01218 | 0,00988 | 0,0078 |
| 526,97456 | 0,01058 | 0,01261 | 0,01012 | 0,00797 |
| 527,01174 | 0,01103 | 0,01304 | 0,01037 | 0,00815 |
| 527,04892 | 0,01149 | 0,01347 | 0,01063 | 0,00837 |
| 527,08611 | 0,01197 | 0,01391 | 0,0109 | 0,0086 |
| 527,12329 | 0,01246 | 0,01435 | 0,01118 | 0,00887 |
| 527,16047 | 0,01299 | 0,0148 | 0,01149 | 0,00917 |
| 527,19765 | 0,01354 | 0,01526 | 0,01181 | 0,00951 |
| 527,23483 | 0,01411 | 0,01573 | 0,01215 | 0,00988 |
| 527,27202 | 0,0147 | 0,01621 | 0,01251 | 0,01029 |
| 527,3092 | 0,01532 | 0,0167 | 0,0129 | 0,01074 |
| 527,34638 | 0,01596 | 0,0172 | 0,0133 | 0,01124 |
| 527,38356 | 0,01663 | 0,01772 | 0,01373 | 0,01179 |
| 527,42074 | 0,01733 | 0,01825 | 0,0142 | 0,01238 |
| 527,45793 | 0,01806 | 0,01879 | 0,01468 | 0,01301 |
| 527,49511 | 0,01881 | 0,01934 | 0,01519 | 0,01369 |
| 527,53229 | 0,01958 | 0,01991 | 0,01573 | 0,01442 |
| 527,56947 | 0,02039 | 0,0205 | 0,0163 | 0,0152 |
| 527,60665 | 0,02123 | 0,02111 | 0,01689 | 0,01602 |
| 527,64384 | 0,02208 | 0,02173 | 0,01752 | 0,01689 |
| 527,68102 | 0,02296 | 0,02237 | 0,01817 | 0,01779 |
| 527,7182 | 0,02386 | 0,02302 | 0,01885 | 0,01873 |
| 527,75538 | 0,02479 | 0,02369 | 0,01956 | 0,01971 |
| 527,79256 | 0,02573 | 0,02438 | 0,02029 | 0,02073 |
| 527,82975 | 0,02669 | 0,02509 | 0,02105 | 0,02177 |
| 527,86693 | 0,02766 | 0,02581 | 0,02183 | 0,02284 |
| 527,90411 | 0,02864 | 0,02655 | 0,02264 | 0,02393 |
| 527,94129 | 0,02964 | 0,0273 | 0,02346 | 0,02504 |
| 527,97847 | 0,03064 | 0,02808 | 0,02431 | 0,02616 |
| 528,01566 | 0,03164 | 0,02886 | 0,02518 | 0,0273 |
| 528,05284 | 0,03264 | 0,02966 | 0,02606 | 0,02843 |
| 528,09002 | 0,03363 | 0,03047 | 0,02696 | 0,02957 |
| 528,1272 | 0,03462 | 0,0313 | 0,02787 | 0,03071 |
| 528,16438 | 0,03559 | 0,03213 | 0,02879 | 0,03183 |
| 528,20157 | 0,03655 | 0,03298 | 0,02972 | 0,03295 |
| 528,23875 | 0,03749 | 0,03383 | 0,03066 | 0,03405 |
| 528,27593 | 0,03841 | 0,03469 | 0,0316 | 0,03513 |
| 528,31311 | 0,03931 | 0,03556 | 0,03255 | 0,03619 |
| 528,35029 | 0,04017 | 0,03643 | 0,03349 | 0,03722 |
| 528,38748 | 0,041 | 0,03731 | 0,03444 | 0,03823 |
| 528,42466 | 0,0418 | 0,03818 | 0,03538 | 0,0392 |
| 528,46184 | 0,04257 | 0,03906 | 0,03631 | 0,04015 |
| 528,49902 | 0,0433 | 0,03993 | 0,03724 | 0,04107 |
| 528,5362 | 0,04399 | 0,0408 | 0,03816 | 0,04196 |
| 528,57339 | 0,04464 | 0,04167 | 0,03907 | 0,04281 |
| 528,61057 | 0,04525 | 0,04253 | 0,03996 | 0,04363 |
| 528,64775 | 0,04582 | 0,04338 | 0,04084 | 0,04442 |
| 528,68493 | 0,04636 | 0,04422 | 0,04171 | 0,04518 |
| 528,72211 | 0,04685 | 0,04504 | 0,04256 | 0,04592 |
| 528,7593 | 0,04731 | 0,04586 | 0,0434 | 0,04662 |
| 528,79648 | 0,04774 | 0,04666 | 0,04422 | 0,0473 |
| 528,83366 | 0,04814 | 0,04745 | 0,04502 | 0,04796 |
| 528,87084 | 0,04851 | 0,04823 | 0,04581 | 0,0486 |
| 528,90802 | 0,04885 | 0,049 | 0,04658 | 0,04923 |
| 528,94521 | 0,04918 | 0,04975 | 0,04733 | 0,04984 |
| 528,98239 | 0,04949 | 0,05049 | 0,04807 | 0,05044 |
| 529,01957 | 0,04979 | 0,05122 | 0,0488 | 0,05104 |
| 529,05675 | 0,05008 | 0,05195 | 0,04951 | 0,05164 |
| 529,09393 | 0,05038 | 0,05266 | 0,05022 | 0,05223 |
| 529,13112 | 0,05068 | 0,05337 | 0,05092 | 0,05284 |
| 529,1683 | 0,05098 | 0,05408 | 0,05161 | 0,05346 |
| 529,20548 | 0,05131 | 0,05479 | 0,05231 | 0,05409 |
| 529,24266 | 0,05165 | 0,0555 | 0,053 | 0,05474 |
| 529,27984 | 0,05202 | 0,05622 | 0,0537 | 0,05542 |
| 529,31703 | 0,05242 | 0,05695 | 0,05441 | 0,05612 |
| 529,35421 | 0,05285 | 0,0577 | 0,05514 | 0,05687 |
| 529,39139 | 0,05332 | 0,05845 | 0,05588 | 0,05765 |
| 529,42857 | 0,05383 | 0,05923 | 0,05664 | 0,05847 |
| 529,46575 | 0,05439 | 0,06003 | 0,05743 | 0,05933 |
| 529,50294 | 0,05501 | 0,06085 | 0,05825 | 0,06024 |
| 529,54012 | 0,05567 | 0,06169 | 0,05909 | 0,06121 |
| 529,5773 | 0,05638 | 0,06256 | 0,05998 | 0,06222 |
| 529,61448 | 0,05714 | 0,06346 | 0,06091 | 0,06329 |
| 529,65166 | 0,05796 | 0,06438 | 0,06187 | 0,06441 |
| 529,68885 | 0,05883 | 0,06534 | 0,06287 | 0,06558 |
| 529,72603 | 0,05976 | 0,06631 | 0,06391 | 0,0668 |
| 529,76321 | 0,06073 | 0,06731 | 0,065 | 0,06808 |
| 529,80039 | 0,06174 | 0,06833 | 0,06613 | 0,06939 |
| 529,83757 | 0,0628 | 0,06936 | 0,0673 | 0,07075 |
| 529,87476 | 0,06391 | 0,07041 | 0,06851 | 0,07213 |
| 529,91194 | 0,06504 | 0,07146 | 0,06974 | 0,07355 |
| 529,94912 | 0,0662 | 0,07252 | 0,071 | 0,07499 |
| 529,9863 | 0,06739 | 0,07358 | 0,07229 | 0,07645 |
| 530,02348 | 0,06859 | 0,07464 | 0,0736 | 0,07791 |
| 530,06067 | 0,06981 | 0,07568 | 0,07491 | 0,07936 |
| 530,09785 | 0,07102 | 0,0767 | 0,07623 | 0,08081 |
| 530,13503 | 0,07224 | 0,0777 | 0,07754 | 0,08223 |
| 530,17221 | 0,07345 | 0,07867 | 0,07884 | 0,08362 |
| 530,20939 | 0,07464 | 0,07962 | 0,08012 | 0,08498 |
| 530,24658 | 0,07582 | 0,08052 | 0,08137 | 0,08628 |
| 530,28376 | 0,07696 | 0,08139 | 0,08258 | 0,08754 |
| 530,32094 | 0,07808 | 0,08221 | 0,08376 | 0,08873 |
| 530,35812 | 0,07916 | 0,083 | 0,08488 | 0,08985 |
| 530,3953 | 0,08021 | 0,08374 | 0,08594 | 0,0909 |
| 530,43249 | 0,08122 | 0,08444 | 0,08695 | 0,09187 |
| 530,46967 | 0,08218 | 0,08509 | 0,0879 | 0,09278 |
| 530,50685 | 0,0831 | 0,08571 | 0,08879 | 0,09361 |
| 530,54403 | 0,08399 | 0,08629 | 0,08961 | 0,09436 |
| 530,58121 | 0,08483 | 0,08684 | 0,09035 | 0,09504 |
| 530,6184 | 0,08564 | 0,08736 | 0,09104 | 0,09565 |
| 530,65558 | 0,08641 | 0,08786 | 0,09166 | 0,09622 |
| 530,69276 | 0,08716 | 0,08834 | 0,09224 | 0,09673 |
| 530,72994 | 0,08788 | 0,08882 | 0,09276 | 0,09719 |
| 530,76712 | 0,08859 | 0,08929 | 0,09324 | 0,09762 |
| 530,80431 | 0,08928 | 0,08977 | 0,09368 | 0,09803 |
| 530,84149 | 0,08997 | 0,09027 | 0,0941 | 0,09843 |
| 530,87867 | 0,09067 | 0,09078 | 0,0945 | 0,09883 |
| 530,91585 | 0,09137 | 0,09133 | 0,09489 | 0,09924 |
| 530,95303 | 0,09209 | 0,0919 | 0,09529 | 0,09968 |
| 530,99022 | 0,09284 | 0,0925 | 0,09569 | 0,10015 |
| 531,0274 | 0,09361 | 0,09316 | 0,09612 | 0,10067 |
| 531,06458 | 0,09443 | 0,09386 | 0,09657 | 0,10123 |
| 531,10176 | 0,09527 | 0,09461 | 0,09706 | 0,10184 |
| 531,13894 | 0,09616 | 0,09539 | 0,09759 | 0,10253 |
| 531,17613 | 0,09709 | 0,09623 | 0,09818 | 0,10329 |
| 531,21331 | 0,09807 | 0,09711 | 0,09881 | 0,10411 |
| 531,25049 | 0,09909 | 0,09804 | 0,09949 | 0,10499 |
| 531,28767 | 0,10016 | 0,099 | 0,10023 | 0,10593 |
| 531,32485 | 0,10126 | 0,09999 | 0,10101 | 0,10694 |
| 531,36204 | 0,10239 | 0,10101 | 0,10186 | 0,108 |
| 531,39922 | 0,10356 | 0,10204 | 0,10275 | 0,10911 |
| 531,4364 | 0,10475 | 0,10308 | 0,10367 | 0,11025 |
| 531,47358 | 0,10595 | 0,10412 | 0,10463 | 0,11141 |
| 531,51076 | 0,10715 | 0,10515 | 0,10562 | 0,11259 |
| 531,54795 | 0,10836 | 0,10617 | 0,10662 | 0,11377 |
| 531,58513 | 0,10955 | 0,10715 | 0,10764 | 0,11493 |
| 531,62231 | 0,11072 | 0,10809 | 0,10865 | 0,11606 |
| 531,65949 | 0,11186 | 0,10899 | 0,10965 | 0,11717 |
| 531,69667 | 0,11296 | 0,10984 | 0,11064 | 0,11822 |
| 531,73386 | 0,11402 | 0,11064 | 0,1116 | 0,11921 |
| 531,77104 | 0,11502 | 0,11137 | 0,11251 | 0,12012 |
| 531,80822 | 0,11595 | 0,11202 | 0,11339 | 0,12096 |
| 531,8454 | 0,11682 | 0,1126 | 0,11422 | 0,12171 |
| 531,88258 | 0,11762 | 0,11312 | 0,11501 | 0,12239 |
| 531,91977 | 0,11836 | 0,11358 | 0,11574 | 0,12297 |
| 531,95695 | 0,11902 | 0,11397 | 0,11641 | 0,12344 |
| 531,99413 | 0,11959 | 0,11428 | 0,11702 | 0,12384 |
| 532,03131 | 0,1201 | 0,11454 | 0,11758 | 0,12415 |
| 532,06849 | 0,12054 | 0,11475 | 0,1181 | 0,12439 |
| 532,10568 | 0,12092 | 0,11492 | 0,11857 | 0,12455 |
| 532,14286 | 0,12124 | 0,11505 | 0,119 | 0,12463 |
| 532,18004 | 0,1215 | 0,11516 | 0,11939 | 0,12466 |
| 532,21722 | 0,12172 | 0,11526 | 0,11976 | 0,12465 |
| 532,2544 | 0,12191 | 0,11535 | 0,12011 | 0,12461 |
| 532,29159 | 0,12208 | 0,11545 | 0,12045 | 0,12454 |
| 532,32877 | 0,12222 | 0,11556 | 0,12078 | 0,12445 |
| 532,36595 | 0,12236 | 0,1157 | 0,12112 | 0,12436 |
| 532,40313 | 0,12249 | 0,11588 | 0,12148 | 0,12428 |
| 532,44031 | 0,12264 | 0,1161 | 0,12185 | 0,1242 |
| 532,4775 | 0,1228 | 0,11636 | 0,12225 | 0,12415 |
| 532,51468 | 0,12297 | 0,11668 | 0,12268 | 0,12412 |
| 532,55186 | 0,12318 | 0,11706 | 0,12314 | 0,12413 |
| 532,58904 | 0,12342 | 0,1175 | 0,12364 | 0,12417 |
| 532,62622 | 0,1237 | 0,118 | 0,12417 | 0,12424 |
| 532,66341 | 0,12401 | 0,11855 | 0,12474 | 0,12434 |
| 532,70059 | 0,12435 | 0,11915 | 0,12534 | 0,12448 |
| 532,73777 | 0,12473 | 0,11981 | 0,12598 | 0,12465 |
| 532,77495 | 0,12515 | 0,12052 | 0,12664 | 0,12484 |
| 532,81213 | 0,12559 | 0,12125 | 0,12732 | 0,12505 |
| 532,84932 | 0,12606 | 0,12202 | 0,12801 | 0,12527 |
| 532,8865 | 0,12654 | 0,12279 | 0,12872 | 0,12549 |
| 532,92368 | 0,12703 | 0,12358 | 0,12943 | 0,12572 |
| 532,96086 | 0,12752 | 0,12436 | 0,13013 | 0,12593 |
| 532,99804 | 0,12801 | 0,12512 | 0,13082 | 0,12613 |
| 533,03523 | 0,12848 | 0,12586 | 0,1315 | 0,12631 |
| 533,07241 | 0,12894 | 0,12655 | 0,13214 | 0,12646 |
| 533,10959 | 0,12936 | 0,12721 | 0,13276 | 0,12657 |
| 533,14677 | 0,12974 | 0,12779 | 0,13333 | 0,12664 |
| 533,18395 | 0,13007 | 0,12831 | 0,13386 | 0,12667 |
| 533,22114 | 0,13036 | 0,12875 | 0,13434 | 0,12665 |
| 533,25832 | 0,13058 | 0,12912 | 0,13478 | 0,12659 |
| 533,2955 | 0,13075 | 0,12941 | 0,13517 | 0,12648 |
| 533,33268 | 0,13085 | 0,1296 | 0,13549 | 0,12631 |
| 533,36986 | 0,13087 | 0,1297 | 0,13576 | 0,1261 |
| 533,40705 | 0,13082 | 0,12971 | 0,13597 | 0,12585 |
| 533,44423 | 0,13071 | 0,12964 | 0,13614 | 0,12556 |
| 533,48141 | 0,13053 | 0,1295 | 0,13626 | 0,12524 |
| 533,51859 | 0,13027 | 0,12927 | 0,13632 | 0,12488 |
| 533,55577 | 0,12995 | 0,12896 | 0,13632 | 0,12449 |
| 533,59295 | 0,12957 | 0,12858 | 0,13629 | 0,12408 |
| 533,63014 | 0,12913 | 0,12816 | 0,13621 | 0,12366 |
| 533,66732 | 0,12865 | 0,12769 | 0,13609 | 0,12322 |
| 533,7045 | 0,12812 | 0,12717 | 0,13593 | 0,12278 |
| 533,74168 | 0,12755 | 0,12662 | 0,13573 | 0,12233 |
| 533,77886 | 0,12695 | 0,12605 | 0,13549 | 0,12187 |
| 533,81605 | 0,12632 | 0,12546 | 0,13521 | 0,12142 |
| 533,85323 | 0,12568 | 0,12487 | 0,1349 | 0,12096 |
| 533,89041 | 0,12502 | 0,12427 | 0,13454 | 0,1205 |
| 533,92759 | 0,12434 | 0,12368 | 0,13413 | 0,12004 |
| 533,96477 | 0,12367 | 0,1231 | 0,13368 | 0,11958 |
| 534,00196 | 0,12299 | 0,12253 | 0,13317 | 0,1191 |
| 534,03914 | 0,12231 | 0,12197 | 0,13262 | 0,11861 |
| 534,07632 | 0,12164 | 0,12143 | 0,132 | 0,1181 |
| 534,1135 | 0,12097 | 0,12091 | 0,13132 | 0,11757 |
| 534,15068 | 0,1203 | 0,12039 | 0,13055 | 0,117 |
| 534,18787 | 0,11963 | 0,11989 | 0,12971 | 0,1164 |
| 534,22505 | 0,11895 | 0,11938 | 0,12879 | 0,11575 |
| 534,26223 | 0,11828 | 0,11888 | 0,12779 | 0,11505 |
| 534,29941 | 0,11759 | 0,11837 | 0,1267 | 0,1143 |
| 534,33659 | 0,11688 | 0,11785 | 0,1255 | 0,11348 |
| 534,37378 | 0,11616 | 0,1173 | 0,12421 | 0,11259 |
| 534,41096 | 0,11541 | 0,11672 | 0,12282 | 0,11163 |
| 534,44814 | 0,11464 | 0,11611 | 0,12135 | 0,11061 |
| 534,48532 | 0,11382 | 0,11546 | 0,11978 | 0,10951 |
| 534,5225 | 0,11297 | 0,11474 | 0,11811 | 0,10833 |
| 534,55969 | 0,11207 | 0,11398 | 0,11635 | 0,10707 |
| 534,59687 | 0,11112 | 0,11315 | 0,11452 | 0,10575 |
| 534,63405 | 0,11012 | 0,11227 | 0,11262 | 0,10436 |
| 534,67123 | 0,10907 | 0,11131 | 0,11066 | 0,10292 |
| 534,70841 | 0,10795 | 0,11027 | 0,10864 | 0,10142 |
| 534,7456 | 0,10678 | 0,10917 | 0,10659 | 0,09987 |
| 534,78278 | 0,10556 | 0,108 | 0,10451 | 0,0983 |
| 534,81996 | 0,1043 | 0,10677 | 0,10242 | 0,0967 |
| 534,85714 | 0,10298 | 0,10548 | 0,10033 | 0,09509 |
| 534,89432 | 0,10162 | 0,10413 | 0,09825 | 0,09348 |
| 534,93151 | 0,10022 | 0,10273 | 0,09621 | 0,09188 |
| 534,96869 | 0,0988 | 0,1013 | 0,09422 | 0,09031 |
| 535,00587 | 0,09736 | 0,09984 | 0,09228 | 0,08878 |
| 535,04305 | 0,0959 | 0,09837 | 0,09041 | 0,08729 |
| 535,08023 | 0,09444 | 0,09688 | 0,08862 | 0,08586 |
| 535,11742 | 0,093 | 0,0954 | 0,08694 | 0,0845 |
| 535,1546 | 0,09156 | 0,09394 | 0,08537 | 0,08324 |
| 535,19178 | 0,09016 | 0,0925 | 0,0839 | 0,08205 |
| 535,22896 | 0,08878 | 0,0911 | 0,08255 | 0,08096 |
| 535,26614 | 0,08746 | 0,08975 | 0,08132 | 0,07997 |
| 535,30333 | 0,08619 | 0,08846 | 0,08023 | 0,07907 |
| 535,34051 | 0,08497 | 0,08723 | 0,07928 | 0,07831 |
| 535,37769 | 0,08382 | 0,08607 | 0,07846 | 0,07764 |
| 535,41487 | 0,08273 | 0,08498 | 0,07775 | 0,07709 |
| 535,45205 | 0,08172 | 0,08398 | 0,07717 | 0,07663 |
| 535,48924 | 0,08079 | 0,08307 | 0,07671 | 0,07627 |
| 535,52642 | 0,07993 | 0,08224 | 0,07638 | 0,07602 |
| 535,5636 | 0,07914 | 0,08148 | 0,07616 | 0,07587 |
| 535,60078 | 0,07842 | 0,0808 | 0,07602 | 0,0758 |
| 535,63796 | 0,07777 | 0,0802 | 0,07597 | 0,07581 |
| 535,67515 | 0,0772 | 0,07968 | 0,076 | 0,07588 |
| 535,71233 | 0,07669 | 0,07922 | 0,07611 | 0,07603 |
| 535,74951 | 0,07623 | 0,07881 | 0,07627 | 0,07623 |
| 535,78669 | 0,07581 | 0,07845 | 0,07648 | 0,07648 |
| 535,82387 | 0,07544 | 0,07813 | 0,07671 | 0,07675 |
| 535,86106 | 0,07512 | 0,07785 | 0,07697 | 0,07706 |
| 535,89824 | 0,07481 | 0,07758 | 0,07725 | 0,07738 |
| 535,93542 | 0,07453 | 0,07733 | 0,07752 | 0,07772 |
| 535,9726 | 0,07427 | 0,07707 | 0,07779 | 0,07806 |
| 536,00978 | 0,07401 | 0,07682 | 0,07803 | 0,07839 |
| 536,04697 | 0,07377 | 0,07655 | 0,07825 | 0,07872 |
| 536,08415 | 0,07352 | 0,07626 | 0,07844 | 0,07903 |
| 536,12133 | 0,07326 | 0,07595 | 0,07857 | 0,07931 |
| 536,15851 | 0,073 | 0,0756 | 0,07866 | 0,07956 |
| 536,19569 | 0,07273 | 0,07523 | 0,0787 | 0,07979 |
| 536,23288 | 0,07245 | 0,07482 | 0,07869 | 0,07998 |
| 536,27006 | 0,07215 | 0,07437 | 0,07861 | 0,08014 |
| 536,30724 | 0,07185 | 0,07388 | 0,07845 | 0,08026 |
| 536,34442 | 0,07153 | 0,07336 | 0,07824 | 0,08032 |
| 536,3816 | 0,0712 | 0,07281 | 0,07795 | 0,08035 |
| 536,41879 | 0,07086 | 0,07222 | 0,0776 | 0,08034 |
| 536,45597 | 0,07052 | 0,0716 | 0,07719 | 0,08028 |
| 536,49315 | 0,07017 | 0,07096 | 0,07669 | 0,08018 |
| 536,53033 | 0,06982 | 0,07031 | 0,07613 | 0,08001 |
| 536,56751 | 0,06947 | 0,06964 | 0,0755 | 0,07981 |
| 536,6047 | 0,06912 | 0,06895 | 0,07482 | 0,07955 |
| 536,64188 | 0,06878 | 0,06827 | 0,07407 | 0,07924 |
| 536,67906 | 0,06845 | 0,06759 | 0,07326 | 0,07889 |
| 536,71624 | 0,06812 | 0,06691 | 0,0724 | 0,07848 |
| 536,75342 | 0,06781 | 0,06624 | 0,07148 | 0,07801 |
| 536,79061 | 0,06751 | 0,06558 | 0,07052 | 0,07749 |
| 536,82779 | 0,06722 | 0,06495 | 0,06952 | 0,07692 |
| 536,86497 | 0,06694 | 0,06433 | 0,06848 | 0,0763 |
| 536,90215 | 0,06667 | 0,06373 | 0,0674 | 0,07563 |
| 536,93933 | 0,06641 | 0,06315 | 0,0663 | 0,0749 |
| 536,97652 | 0,06616 | 0,06259 | 0,06517 | 0,07411 |
| 537,0137 | 0,06591 | 0,06205 | 0,06403 | 0,07329 |
| 537,05088 | 0,06567 | 0,06154 | 0,06287 | 0,07241 |
| 537,08806 | 0,06542 | 0,06105 | 0,06171 | 0,0715 |
| 537,12524 | 0,06518 | 0,06057 | 0,06055 | 0,07054 |
| 537,16243 | 0,06492 | 0,06011 | 0,0594 | 0,06955 |
| 537,19961 | 0,06466 | 0,05966 | 0,05827 | 0,06852 |
| 537,23679 | 0,06438 | 0,05923 | 0,05715 | 0,06748 |
| 537,27397 | 0,06409 | 0,05881 | 0,05606 | 0,06642 |
| 537,31115 | 0,06379 | 0,05839 | 0,05501 | 0,06535 |
| 537,34834 | 0,06347 | 0,05798 | 0,054 | 0,06427 |
| 537,38552 | 0,06312 | 0,05757 | 0,05304 | 0,06319 |
| 537,4227 | 0,06276 | 0,05717 | 0,05212 | 0,06213 |
| 537,45988 | 0,06238 | 0,05677 | 0,05127 | 0,06109 |
| 537,49706 | 0,06199 | 0,05638 | 0,05049 | 0,06007 |
| 537,53425 | 0,06158 | 0,05598 | 0,04977 | 0,05909 |
| 537,57143 | 0,06115 | 0,05559 | 0,04913 | 0,05815 |
| 537,60861 | 0,06071 | 0,05521 | 0,04855 | 0,05725 |
| 537,64579 | 0,06026 | 0,05483 | 0,04805 | 0,05641 |
| 537,68297 | 0,05981 | 0,05447 | 0,04766 | 0,05562 |
| 537,72016 | 0,05936 | 0,05411 | 0,04734 | 0,0549 |
| 537,75734 | 0,05891 | 0,05377 | 0,0471 | 0,05425 |
| 537,79452 | 0,05847 | 0,05345 | 0,04693 | 0,05367 |
| 537,8317 | 0,05804 | 0,05315 | 0,04685 | 0,05315 |
| 537,86888 | 0,05763 | 0,05288 | 0,04686 | 0,0527 |
| 537,90607 | 0,05723 | 0,05262 | 0,04694 | 0,05233 |
| 537,94325 | 0,05686 | 0,0524 | 0,0471 | 0,05203 |
| 537,98043 | 0,05652 | 0,05221 | 0,04731 | 0,0518 |
| 538,01761 | 0,05621 | 0,05205 | 0,04759 | 0,05163 |
| 538,05479 | 0,05592 | 0,05192 | 0,04792 | 0,05151 |
| 538,09198 | 0,05567 | 0,05181 | 0,04831 | 0,05145 |
| 538,12916 | 0,05544 | 0,05174 | 0,04874 | 0,05144 |
| 538,16634 | 0,05525 | 0,05171 | 0,04919 | 0,05147 |
| 538,20352 | 0,05509 | 0,05169 | 0,04966 | 0,05153 |
| 538,2407 | 0,05495 | 0,0517 | 0,05015 | 0,05161 |
| 538,27789 | 0,05483 | 0,05173 | 0,05063 | 0,05171 |
| 538,31507 | 0,05472 | 0,05176 | 0,05111 | 0,05181 |
| 538,35225 | 0,05463 | 0,05181 | 0,05157 | 0,05191 |
| 538,38943 | 0,05454 | 0,05186 | 0,052 | 0,05199 |
| 538,42661 | 0,05445 | 0,0519 | 0,0524 | 0,05206 |
| 538,4638 | 0,05436 | 0,05193 | 0,05274 | 0,05209 |
| 538,50098 | 0,05424 | 0,05195 | 0,05302 | 0,05209 |
| 538,53816 | 0,0541 | 0,05194 | 0,05324 | 0,05203 |
| 538,57534 | 0,05393 | 0,05189 | 0,0534 | 0,05193 |
| 538,61252 | 0,05372 | 0,0518 | 0,05348 | 0,05177 |
| 538,64971 | 0,05347 | 0,05167 | 0,05348 | 0,05155 |
| 538,68689 | 0,05317 | 0,0515 | 0,05339 | 0,05127 |
| 538,72407 | 0,05281 | 0,05127 | 0,05321 | 0,05091 |
| 538,76125 | 0,05239 | 0,05097 | 0,05295 | 0,05048 |
| 538,79843 | 0,05191 | 0,05062 | 0,05261 | 0,04998 |
| 538,83562 | 0,05136 | 0,05021 | 0,05219 | 0,04942 |
| 538,8728 | 0,05075 | 0,04974 | 0,05166 | 0,0488 |
| 538,90998 | 0,05007 | 0,04921 | 0,05106 | 0,04811 |
| 538,94716 | 0,04932 | 0,04862 | 0,0504 | 0,04736 |
| 538,98434 | 0,0485 | 0,04796 | 0,04966 | 0,04655 |
| 539,02153 | 0,04763 | 0,04726 | 0,04887 | 0,04571 |
| 539,05871 | 0,04671 | 0,04652 | 0,04802 | 0,04482 |
| 539,09589 | 0,04573 | 0,04573 | 0,04711 | 0,04389 |
| 539,13307 | 0,0447 | 0,04489 | 0,04617 | 0,04293 |
| 539,17025 | 0,04363 | 0,04403 | 0,0452 | 0,04195 |
| 539,20744 | 0,04253 | 0,04314 | 0,0442 | 0,04095 |
| 539,24462 | 0,04141 | 0,04223 | 0,04317 | 0,03994 |
| 539,2818 | 0,04027 | 0,04131 | 0,04214 | 0,03892 |
| 539,31898 | 0,03912 | 0,04038 | 0,04109 | 0,0379 |
| 539,35616 | 0,03796 | 0,03945 | 0,04005 | 0,03688 |
| 539,39335 | 0,03681 | 0,03852 | 0,039 | 0,03587 |
| 539,43053 | 0,03566 | 0,0376 | 0,03796 | 0,03486 |
| 539,46771 | 0,03453 | 0,03669 | 0,03693 | 0,03386 |
| 539,50489 | 0,03342 | 0,0358 | 0,03591 | 0,03288 |
| 539,54207 | 0,03233 | 0,03492 | 0,0349 | 0,03191 |
| 539,57926 | 0,03128 | 0,03406 | 0,0339 | 0,03095 |
| 539,61644 | 0,03025 | 0,03322 | 0,03292 | 0,03 |
| 539,65362 | 0,02925 | 0,03239 | 0,03195 | 0,02907 |
| 539,6908 | 0,02829 | 0,03159 | 0,031 | 0,02814 |
| 539,72798 | 0,02737 | 0,03081 | 0,03006 | 0,02723 |
| 539,76517 | 0,02648 | 0,03005 | 0,02913 | 0,02633 |
| 539,80235 | 0,02562 | 0,0293 | 0,02821 | 0,02544 |
| 539,83953 | 0,0248 | 0,02857 | 0,02731 | 0,02456 |
| 539,87671 | 0,02401 | 0,02785 | 0,02642 | 0,02368 |
| 539,91389 | 0,02325 | 0,02714 | 0,02554 | 0,02282 |
| 539,95108 | 0,02252 | 0,02644 | 0,02467 | 0,02196 |
| 539,98826 | 0,02182 | 0,02575 | 0,02382 | 0,02111 |
| 540,02544 | 0,02113 | 0,02506 | 0,02297 | 0,02027 |
| 540,06262 | 0,02048 | 0,02438 | 0,02214 | 0,01943 |
| 540,0998 | 0,01984 | 0,0237 | 0,02133 | 0,01861 |
| 540,13699 | 0,01922 | 0,02303 | 0,02052 | 0,01781 |
| 540,17417 | 0,01862 | 0,02236 | 0,01973 | 0,01701 |
| 540,21135 | 0,01803 | 0,02169 | 0,01896 | 0,01623 |
| 540,24853 | 0,01746 | 0,02102 | 0,01821 | 0,01547 |
| 540,28571 | 0,0169 | 0,02036 | 0,01747 | 0,01472 |
| 540,3229 | 0,01635 | 0,0197 | 0,01676 | 0,01399 |
| 540,36008 | 0,01582 | 0,01905 | 0,01606 | 0,01329 |
| 540,39726 | 0,01529 | 0,01841 | 0,01538 | 0,01261 |
| 540,43444 | 0,01477 | 0,01777 | 0,01473 | 0,01195 |
| 540,47162 | 0,01427 | 0,01715 | 0,01409 | 0,01131 |
| 540,50881 | 0,01377 | 0,01653 | 0,01348 | 0,0107 |
| 540,54599 | 0,01329 | 0,01593 | 0,01289 | 0,01012 |
| 540,58317 | 0,01281 | 0,01534 | 0,01232 | 0,00956 |
| 540,62035 | 0,01235 | 0,01476 | 0,01176 | 0,00903 |
| 540,65753 | 0,01189 | 0,0142 | 0,01124 | 0,00852 |
| 540,69472 | 0,01145 | 0,01366 | 0,01073 | 0,00804 |
| 540,7319 | 0,01101 | 0,01314 | 0,01023 | 0,00758 |
| 540,76908 | 0,01058 | 0,01263 | 0,00976 | 0,00715 |
| 540,80626 | 0,01017 | 0,01213 | 0,00929 | 0,00673 |
| 540,84344 | 0,00976 | 0,01166 | 0,00885 | 0,00634 |
| 540,88063 | 0,00936 | 0,0112 | 0,00842 | 0,00597 |
| 540,91781 | 0,00897 | 0,01076 | 0,00801 | 0,00562 |
| 540,95499 | 0,00859 | 0,01033 | 0,0076 | 0,00528 |
| 540,99217 | 0,00822 | 0,00992 | 0,00721 | 0,00497 |
| 541,02935 | 0,00786 | 0,00951 | 0,00683 | 0,00466 |
| 541,06654 | 0,0075 | 0,00913 | 0,00647 | 0,00438 |
| 541,10372 | 0,00715 | 0,00875 | 0,00611 | 0,0041 |
| 541,1409 | 0,00681 | 0,00838 | 0,00576 | 0,00385 |
| 541,17808 | 0,00648 | 0,00803 | 0,00543 | 0,0036 |
| 541,21526 | 0,00615 | 0,00768 | 0,0051 | 0,00336 |
| 541,25245 | 0,00583 | 0,00734 | 0,00479 | 0,00314 |
| 541,28963 | 0,00552 | 0,007 | 0,00448 | 0,00293 |
| 541,32681 | 0,00521 | 0,00668 | 0,00419 | 0,00272 |
| 541,36399 | 0,00492 | 0,00636 | 0,0039 | 0,00253 |
| 541,40117 | 0,00463 | 0,00604 | 0,00363 | 0,00235 |
| 541,43836 | 0,00435 | 0,00573 | 0,00337 | 0,00217 |
| 541,47554 | 0,00408 | 0,00543 | 0,00312 | 0,00201 |
| 541,51272 | 0,00381 | 0,00513 | 0,00288 | 0,00185 |
| 541,5499 | 0,00356 | 0,00484 | 0,00265 | 0,00171 |
| 541,58708 | 0,00332 | 0,00456 | 0,00243 | 0,00157 |
| 541,62427 | 0,00308 | 0,00428 | 0,00223 | 0,00144 |
| 541,66145 | 0,00286 | 0,00401 | 0,00204 | 0,00131 |
| 541,69863 | 0,00265 | 0,00375 | 0,00186 | 0,0012 |
| 541,73581 | 0,00245 | 0,00349 | 0,00169 | 0,00109 |
| 541,77299 | 0,00225 | 0,00325 | 0,00153 | 0,00099 |
| 541,81018 | 0,00207 | 0,00301 | 0,00138 | 0,00089 |
| 541,84736 | 0,00191 | 0,00278 | 0,00124 | 8e-04 |
| 541,88454 | 0,00175 | 0,00256 | 0,00112 | 0,00072 |
| 541,92172 | 0,0016 | 0,00235 | 0,001 | 0,00065 |
| 541,9589 | 0,00147 | 0,00216 | 0,00089 | 0,00058 |
| 541,99609 | 0,00134 | 0,00197 | 0,00079 | 0,00052 |
| 542,03327 | 0,00123 | 0,00179 | 7e-04 | 0,00046 |
| 542,07045 | 0,00112 | 0,00163 | 0,00062 | 0,00041 |
| 542,10763 | 0,00102 | 0,00147 | 0,00055 | 0,00036 |
| 542,14481 | 0,00093 | 0,00132 | 0,00048 | 0,00032 |
| 542,182 | 0,00085 | 0,00119 | 0,00042 | 0,00028 |
| 542,21918 | 0,00078 | 0,00106 | 0,00037 | 0,00024 |
| 542,25636 | 0,00072 | 0,00095 | 0,00032 | 0,00021 |
| 542,29354 | 0,00066 | 0,00085 | 0,00028 | 0,00019 |
| 542,33072 | 0,00061 | 0,00075 | 0,00024 | 0,00016 |
| 542,36791 | 0,00056 | 0,00066 | 0,00021 | 0,00014 |
| 542,40509 | 0,00052 | 0,00058 | 0,00018 | 0,00012 |
| 542,44227 | 0,00048 | 0,00051 | 0,00015 | 1e-04 |
| 542,47945 | 0,00045 | 0,00045 | 0,00013 | 9e-05 |
| 542,51663 | 0,00042 | 0,00039 | 0,00011 | 7e-05 |
| 542,55382 | 0,00039 | 0,00034 | 9e-05 | 6e-05 |
| 542,591 | 0,00036 | 0,00029 | 8e-05 | 5e-05 |
| 542,62818 | 0,00034 | 0,00025 | 7e-05 | 5e-05 |
| 542,66536 | 0,00032 | 0,00022 | 6e-05 | 4e-05 |
| 542,70254 | 3e-04 | 0,00018 | 5e-05 | 3e-05 |
| 542,73973 | 0,00028 | 0,00016 | 4e-05 | 3e-05 |
| 542,77691 | 0,00026 | 0,00013 | 3e-05 | 2e-05 |
| 542,81409 | 0,00025 | 0,00011 | 3e-05 | 2e-05 |
| 542,85127 | 0,00023 | 1e-04 | 2e-05 | 1e-05 |
| 542,88845 | 0,00022 | 8e-05 | 2e-05 | 1e-05 |
| 542,92564 | 2e-04 | 7e-05 | 1e-05 | 1e-05 |
| 542,96282 | 0,00019 | 6e-05 | 1e-05 | 1e-05 |
| 543 | 0,00017 | 5e-05 | 1e-05 | 1e-05 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 0,00029 | 0,00014 | 8e-05 | 0 |
| 524,03718 | 3e-04 | 0,00015 | 8e-05 | 0 |
| 524,07436 | 0,00031 | 0,00015 | 9e-05 | 0 |
| 524,11155 | 0,00032 | 0,00016 | 1e-04 | 0 |
| 524,14873 | 0,00033 | 0,00017 | 0,00011 | 1e-05 |
| 524,18591 | 0,00034 | 0,00017 | 0,00012 | 1e-05 |
| 524,22309 | 0,00034 | 0,00018 | 0,00013 | 1e-05 |
| 524,26027 | 0,00035 | 0,00019 | 0,00013 | 1e-05 |
| 524,29746 | 0,00036 | 2e-04 | 0,00014 | 1e-05 |
| 524,33464 | 0,00036 | 0,00021 | 0,00015 | 1e-05 |
| 524,37182 | 0,00037 | 0,00022 | 0,00016 | 2e-05 |
| 524,409 | 0,00037 | 0,00024 | 0,00017 | 2e-05 |
| 524,44618 | 0,00037 | 0,00025 | 0,00017 | 2e-05 |
| 524,48337 | 0,00038 | 0,00026 | 0,00018 | 2e-05 |
| 524,52055 | 0,00038 | 0,00028 | 0,00019 | 3e-05 |
| 524,55773 | 0,00038 | 0,00029 | 0,00019 | 3e-05 |
| 524,59491 | 0,00039 | 0,00031 | 2e-04 | 4e-05 |
| 524,63209 | 0,00039 | 0,00033 | 2e-04 | 4e-05 |
| 524,66928 | 0,00039 | 0,00035 | 0,00021 | 4e-05 |
| 524,70646 | 4e-04 | 0,00036 | 0,00021 | 5e-05 |
| 524,74364 | 0,00041 | 0,00038 | 0,00022 | 5e-05 |
| 524,78082 | 0,00042 | 4e-04 | 0,00022 | 6e-05 |
| 524,818 | 0,00043 | 0,00042 | 0,00023 | 7e-05 |
| 524,85519 | 0,00044 | 0,00044 | 0,00023 | 7e-05 |
| 524,89237 | 0,00045 | 0,00046 | 0,00024 | 8e-05 |
| 524,92955 | 0,00047 | 0,00048 | 0,00025 | 9e-05 |
| 524,96673 | 0,00048 | 5e-04 | 0,00026 | 1e-04 |
| 525,00391 | 5e-04 | 0,00052 | 0,00027 | 0,00011 |
| 525,0411 | 0,00053 | 0,00054 | 0,00028 | 0,00012 |
| 525,07828 | 0,00055 | 0,00056 | 0,00029 | 0,00013 |
| 525,11546 | 0,00058 | 0,00059 | 0,00031 | 0,00015 |
| 525,15264 | 0,00061 | 0,00061 | 0,00033 | 0,00016 |
| 525,18982 | 0,00064 | 0,00064 | 0,00035 | 0,00018 |
| 525,22701 | 0,00068 | 0,00067 | 0,00038 | 0,00021 |
| 525,26419 | 0,00071 | 7e-04 | 0,00041 | 0,00023 |
| 525,30137 | 0,00076 | 0,00073 | 0,00045 | 0,00026 |
| 525,33855 | 8e-04 | 0,00077 | 5e-04 | 3e-04 |
| 525,37573 | 0,00085 | 0,00081 | 0,00055 | 0,00034 |
| 525,41292 | 0,00091 | 0,00086 | 0,00061 | 0,00038 |
| 525,4501 | 0,00097 | 0,00091 | 0,00068 | 0,00043 |
| 525,48728 | 0,00103 | 0,00097 | 0,00076 | 0,00049 |
| 525,52446 | 0,0011 | 0,00104 | 0,00086 | 0,00056 |
| 525,56164 | 0,00118 | 0,00111 | 0,00096 | 0,00063 |
| 525,59883 | 0,00126 | 0,00119 | 0,00107 | 0,00072 |
| 525,63601 | 0,00134 | 0,00128 | 0,0012 | 0,00081 |
| 525,67319 | 0,00144 | 0,00138 | 0,00134 | 0,00091 |
| 525,71037 | 0,00154 | 0,00149 | 0,00149 | 0,00102 |
| 525,74755 | 0,00165 | 0,00161 | 0,00166 | 0,00114 |
| 525,78474 | 0,00177 | 0,00174 | 0,00184 | 0,00127 |
| 525,82192 | 0,00189 | 0,00187 | 0,00204 | 0,00141 |
| 525,8591 | 0,00202 | 0,00202 | 0,00224 | 0,00155 |
| 525,89628 | 0,00216 | 0,00218 | 0,00246 | 0,00171 |
| 525,93346 | 0,00232 | 0,00235 | 0,0027 | 0,00187 |
| 525,97065 | 0,00248 | 0,00253 | 0,00294 | 0,00204 |
| 526,00783 | 0,00265 | 0,00272 | 0,00319 | 0,00222 |
| 526,04501 | 0,00283 | 0,00292 | 0,00345 | 0,0024 |
| 526,08219 | 0,00302 | 0,00314 | 0,00372 | 0,00258 |
| 526,11937 | 0,00322 | 0,00336 | 0,00399 | 0,00276 |
| 526,15656 | 0,00343 | 0,0036 | 0,00425 | 0,00295 |
| 526,19374 | 0,00366 | 0,00384 | 0,00452 | 0,00313 |
| 526,23092 | 0,00389 | 0,00409 | 0,00478 | 0,00331 |
| 526,2681 | 0,00414 | 0,00436 | 0,00504 | 0,00348 |
| 526,30528 | 0,00439 | 0,00463 | 0,00529 | 0,00365 |
| 526,34247 | 0,00466 | 0,00491 | 0,00553 | 0,00382 |
| 526,37965 | 0,00494 | 0,0052 | 0,00576 | 0,00397 |
| 526,41683 | 0,00523 | 0,00549 | 0,00597 | 0,00412 |
| 526,45401 | 0,00553 | 0,00579 | 0,00617 | 0,00426 |
| 526,49119 | 0,00584 | 0,00609 | 0,00635 | 0,00439 |
| 526,52838 | 0,00615 | 0,0064 | 0,00651 | 0,00451 |
| 526,56556 | 0,00647 | 0,00671 | 0,00667 | 0,00462 |
| 526,60274 | 0,00681 | 0,00703 | 0,0068 | 0,00472 |
| 526,63992 | 0,00714 | 0,00735 | 0,00693 | 0,00482 |
| 526,6771 | 0,00749 | 0,00767 | 0,00704 | 0,00491 |
| 526,71429 | 0,00784 | 0,00799 | 0,00714 | 0,005 |
| 526,75147 | 0,00819 | 0,00832 | 0,00724 | 0,00508 |
| 526,78865 | 0,00855 | 0,00865 | 0,00733 | 0,00516 |
| 526,82583 | 0,00892 | 0,00898 | 0,00742 | 0,00525 |
| 526,86301 | 0,00929 | 0,00932 | 0,00752 | 0,00534 |
| 526,9002 | 0,00966 | 0,00966 | 0,00762 | 0,00543 |
| 526,93738 | 0,01005 | 0,01001 | 0,00774 | 0,00553 |
| 526,97456 | 0,01044 | 0,01037 | 0,00787 | 0,00565 |
| 527,01174 | 0,01084 | 0,01074 | 0,00802 | 0,00577 |
| 527,04892 | 0,01125 | 0,01113 | 0,00819 | 0,00592 |
| 527,08611 | 0,01168 | 0,01152 | 0,00838 | 0,00608 |
| 527,12329 | 0,01212 | 0,01194 | 0,00861 | 0,00626 |
| 527,16047 | 0,01257 | 0,01236 | 0,00887 | 0,00647 |
| 527,19765 | 0,01304 | 0,01281 | 0,00916 | 0,0067 |
| 527,23483 | 0,01353 | 0,01327 | 0,00949 | 0,00696 |
| 527,27202 | 0,01404 | 0,01375 | 0,00985 | 0,00725 |
| 527,3092 | 0,01457 | 0,01426 | 0,01025 | 0,00758 |
| 527,34638 | 0,01513 | 0,01478 | 0,01069 | 0,00794 |
| 527,38356 | 0,01571 | 0,01533 | 0,01118 | 0,00833 |
| 527,42074 | 0,01632 | 0,01589 | 0,01171 | 0,00876 |
| 527,45793 | 0,01694 | 0,01647 | 0,01227 | 0,00923 |
| 527,49511 | 0,01759 | 0,01706 | 0,01288 | 0,00975 |
| 527,53229 | 0,01826 | 0,01768 | 0,01352 | 0,01031 |
| 527,56947 | 0,01896 | 0,01831 | 0,0142 | 0,01091 |
| 527,60665 | 0,01967 | 0,01895 | 0,01492 | 0,01154 |
| 527,64384 | 0,02039 | 0,01959 | 0,01568 | 0,01222 |
| 527,68102 | 0,02113 | 0,02025 | 0,01647 | 0,01294 |
| 527,7182 | 0,02187 | 0,0209 | 0,01729 | 0,0137 |
| 527,75538 | 0,02262 | 0,02157 | 0,01813 | 0,0145 |
| 527,79256 | 0,02337 | 0,02223 | 0,01899 | 0,01534 |
| 527,82975 | 0,02411 | 0,02288 | 0,01988 | 0,0162 |
| 527,86693 | 0,02485 | 0,02354 | 0,02078 | 0,01709 |
| 527,90411 | 0,02557 | 0,02418 | 0,0217 | 0,018 |
| 527,94129 | 0,02628 | 0,02482 | 0,02261 | 0,01893 |
| 527,97847 | 0,02698 | 0,02545 | 0,02353 | 0,01988 |
| 528,01566 | 0,02765 | 0,02607 | 0,02445 | 0,02083 |
| 528,05284 | 0,0283 | 0,02669 | 0,02536 | 0,02177 |
| 528,09002 | 0,02892 | 0,02729 | 0,02625 | 0,02272 |
| 528,1272 | 0,02951 | 0,02788 | 0,02713 | 0,02365 |
| 528,16438 | 0,03008 | 0,02846 | 0,02798 | 0,02456 |
| 528,20157 | 0,03062 | 0,02903 | 0,02881 | 0,02546 |
| 528,23875 | 0,03114 | 0,02959 | 0,02961 | 0,02632 |
| 528,27593 | 0,03163 | 0,03014 | 0,03038 | 0,02714 |
| 528,31311 | 0,0321 | 0,03069 | 0,03111 | 0,02794 |
| 528,35029 | 0,03254 | 0,03123 | 0,0318 | 0,02869 |
| 528,38748 | 0,03296 | 0,03177 | 0,03246 | 0,02941 |
| 528,42466 | 0,03337 | 0,0323 | 0,03308 | 0,03009 |
| 528,46184 | 0,03376 | 0,03284 | 0,03367 | 0,03072 |
| 528,49902 | 0,03414 | 0,03337 | 0,03423 | 0,03132 |
| 528,5362 | 0,0345 | 0,0339 | 0,03475 | 0,03187 |
| 528,57339 | 0,03485 | 0,03443 | 0,03524 | 0,0324 |
| 528,61057 | 0,0352 | 0,03496 | 0,0357 | 0,0329 |
| 528,64775 | 0,03554 | 0,03549 | 0,03614 | 0,03336 |
| 528,68493 | 0,03588 | 0,03603 | 0,03655 | 0,03381 |
| 528,72211 | 0,03621 | 0,03656 | 0,03695 | 0,03423 |
| 528,7593 | 0,03653 | 0,0371 | 0,03733 | 0,03463 |
| 528,79648 | 0,03686 | 0,03764 | 0,0377 | 0,03503 |
| 528,83366 | 0,03718 | 0,03818 | 0,03805 | 0,03542 |
| 528,87084 | 0,03751 | 0,03873 | 0,03839 | 0,0358 |
| 528,90802 | 0,03783 | 0,03928 | 0,03873 | 0,03617 |
| 528,94521 | 0,03815 | 0,03982 | 0,03906 | 0,03655 |
| 528,98239 | 0,03847 | 0,04037 | 0,03938 | 0,03692 |
| 529,01957 | 0,03879 | 0,04092 | 0,0397 | 0,0373 |
| 529,05675 | 0,03912 | 0,04148 | 0,04001 | 0,03768 |
| 529,09393 | 0,03944 | 0,04203 | 0,04033 | 0,03806 |
| 529,13112 | 0,03977 | 0,04259 | 0,04064 | 0,03845 |
| 529,1683 | 0,04011 | 0,04316 | 0,04095 | 0,03884 |
| 529,20548 | 0,04045 | 0,04373 | 0,04126 | 0,03923 |
| 529,24266 | 0,04081 | 0,04431 | 0,04158 | 0,03964 |
| 529,27984 | 0,04118 | 0,04489 | 0,04191 | 0,04006 |
| 529,31703 | 0,04156 | 0,04548 | 0,04225 | 0,04048 |
| 529,35421 | 0,04197 | 0,04609 | 0,04261 | 0,04093 |
| 529,39139 | 0,0424 | 0,04671 | 0,04298 | 0,04139 |
| 529,42857 | 0,04286 | 0,04734 | 0,04338 | 0,04187 |
| 529,46575 | 0,04334 | 0,04799 | 0,0438 | 0,04238 |
| 529,50294 | 0,04387 | 0,04865 | 0,04426 | 0,04292 |
| 529,54012 | 0,04443 | 0,04933 | 0,04476 | 0,0435 |
| 529,5773 | 0,04503 | 0,05003 | 0,0453 | 0,04411 |
| 529,61448 | 0,04568 | 0,05075 | 0,04589 | 0,04477 |
| 529,65166 | 0,04636 | 0,05148 | 0,04652 | 0,04547 |
| 529,68885 | 0,04709 | 0,05224 | 0,04721 | 0,04622 |
| 529,72603 | 0,04786 | 0,053 | 0,04796 | 0,04703 |
| 529,76321 | 0,04868 | 0,05378 | 0,04877 | 0,04789 |
| 529,80039 | 0,04953 | 0,05458 | 0,04964 | 0,0488 |
| 529,83757 | 0,05042 | 0,05538 | 0,05057 | 0,04976 |
| 529,87476 | 0,05134 | 0,05619 | 0,05154 | 0,05077 |
| 529,91194 | 0,05229 | 0,05699 | 0,05257 | 0,05183 |
| 529,94912 | 0,05325 | 0,0578 | 0,05364 | 0,05294 |
| 529,9863 | 0,05423 | 0,05859 | 0,05477 | 0,05407 |
| 530,02348 | 0,05522 | 0,05938 | 0,05592 | 0,05523 |
| 530,06067 | 0,0562 | 0,06015 | 0,0571 | 0,05641 |
| 530,09785 | 0,05717 | 0,06089 | 0,05829 | 0,0576 |
| 530,13503 | 0,05812 | 0,0616 | 0,05949 | 0,05879 |
| 530,17221 | 0,05904 | 0,06229 | 0,06068 | 0,05996 |
| 530,20939 | 0,05993 | 0,06293 | 0,06185 | 0,0611 |
| 530,24658 | 0,06076 | 0,06354 | 0,06299 | 0,06221 |
| 530,28376 | 0,06155 | 0,0641 | 0,06409 | 0,06327 |
| 530,32094 | 0,06228 | 0,0646 | 0,06514 | 0,06427 |
| 530,35812 | 0,06295 | 0,06505 | 0,06613 | 0,0652 |
| 530,3953 | 0,06356 | 0,06546 | 0,06704 | 0,06604 |
| 530,43249 | 0,0641 | 0,06581 | 0,06788 | 0,0668 |
| 530,46967 | 0,06455 | 0,06611 | 0,06861 | 0,06746 |
| 530,50685 | 0,06495 | 0,06636 | 0,06925 | 0,06803 |
| 530,54403 | 0,06528 | 0,06655 | 0,06981 | 0,06851 |
| 530,58121 | 0,06554 | 0,0667 | 0,07027 | 0,06889 |
| 530,6184 | 0,06576 | 0,06681 | 0,07063 | 0,06918 |
| 530,65558 | 0,06592 | 0,06689 | 0,07091 | 0,06937 |
| 530,69276 | 0,06604 | 0,06694 | 0,07109 | 0,06948 |
| 530,72994 | 0,06613 | 0,06698 | 0,0712 | 0,06954 |
| 530,76712 | 0,0662 | 0,06701 | 0,07125 | 0,06954 |
| 530,80431 | 0,06627 | 0,06704 | 0,07126 | 0,06951 |
| 530,84149 | 0,06634 | 0,06708 | 0,07122 | 0,06945 |
| 530,87867 | 0,06644 | 0,06715 | 0,07116 | 0,06938 |
| 530,91585 | 0,06657 | 0,06725 | 0,0711 | 0,06933 |
| 530,95303 | 0,06675 | 0,06739 | 0,07105 | 0,06932 |
| 530,99022 | 0,06699 | 0,0676 | 0,07103 | 0,06934 |
| 531,0274 | 0,06731 | 0,06787 | 0,07106 | 0,06943 |
| 531,06458 | 0,0677 | 0,06822 | 0,07114 | 0,06959 |
| 531,10176 | 0,06818 | 0,06864 | 0,07129 | 0,06984 |
| 531,13894 | 0,06876 | 0,06914 | 0,07152 | 0,0702 |
| 531,17613 | 0,06945 | 0,06973 | 0,07187 | 0,07066 |
| 531,21331 | 0,07024 | 0,07041 | 0,0723 | 0,07124 |
| 531,25049 | 0,07112 | 0,07118 | 0,07284 | 0,07192 |
| 531,28767 | 0,0721 | 0,07204 | 0,07348 | 0,0727 |
| 531,32485 | 0,07316 | 0,07297 | 0,07422 | 0,07359 |
| 531,36204 | 0,0743 | 0,07397 | 0,07505 | 0,07459 |
| 531,39922 | 0,07551 | 0,07503 | 0,07599 | 0,07568 |
| 531,4364 | 0,07678 | 0,07614 | 0,07701 | 0,07683 |
| 531,47358 | 0,07807 | 0,0773 | 0,07809 | 0,07803 |
| 531,51076 | 0,07939 | 0,07847 | 0,07922 | 0,07926 |
| 531,54795 | 0,0807 | 0,07964 | 0,08039 | 0,08052 |
| 531,58513 | 0,082 | 0,08081 | 0,08158 | 0,08177 |
| 531,62231 | 0,08326 | 0,08195 | 0,08277 | 0,08299 |
| 531,65949 | 0,08447 | 0,08306 | 0,08395 | 0,08417 |
| 531,69667 | 0,08561 | 0,08411 | 0,08509 | 0,08528 |
| 531,73386 | 0,08668 | 0,08509 | 0,0862 | 0,08631 |
| 531,77104 | 0,08765 | 0,086 | 0,08724 | 0,08725 |
| 531,80822 | 0,08853 | 0,08682 | 0,08822 | 0,08809 |
| 531,8454 | 0,08931 | 0,08756 | 0,08912 | 0,08879 |
| 531,88258 | 0,08996 | 0,08821 | 0,08992 | 0,08937 |
| 531,91977 | 0,09051 | 0,08874 | 0,09063 | 0,08982 |
| 531,95695 | 0,09096 | 0,08919 | 0,09126 | 0,09016 |
| 531,99413 | 0,09132 | 0,08954 | 0,09181 | 0,09038 |
| 532,03131 | 0,09159 | 0,08982 | 0,09228 | 0,09049 |
| 532,06849 | 0,09179 | 0,09003 | 0,09267 | 0,09051 |
| 532,10568 | 0,09191 | 0,09017 | 0,093 | 0,09043 |
| 532,14286 | 0,092 | 0,09026 | 0,09328 | 0,0903 |
| 532,18004 | 0,09205 | 0,09031 | 0,09352 | 0,09014 |
| 532,21722 | 0,0921 | 0,09035 | 0,09375 | 0,08995 |
| 532,2544 | 0,09214 | 0,09039 | 0,09397 | 0,08977 |
| 532,29159 | 0,09221 | 0,09043 | 0,0942 | 0,08961 |
| 532,32877 | 0,09232 | 0,09051 | 0,09446 | 0,0895 |
| 532,36595 | 0,09248 | 0,09063 | 0,09476 | 0,08946 |
| 532,40313 | 0,09272 | 0,09082 | 0,09512 | 0,0895 |
| 532,44031 | 0,09304 | 0,09108 | 0,09553 | 0,08964 |
| 532,4775 | 0,09345 | 0,09141 | 0,09601 | 0,08988 |
| 532,51468 | 0,09395 | 0,09184 | 0,09657 | 0,09023 |
| 532,55186 | 0,09456 | 0,09236 | 0,0972 | 0,09072 |
| 532,58904 | 0,0953 | 0,09298 | 0,09793 | 0,09133 |
| 532,62622 | 0,09615 | 0,09372 | 0,09873 | 0,09207 |
| 532,66341 | 0,09711 | 0,09455 | 0,09961 | 0,09292 |
| 532,70059 | 0,09816 | 0,09547 | 0,10054 | 0,09387 |
| 532,73777 | 0,09931 | 0,09648 | 0,10154 | 0,09491 |
| 532,77495 | 0,10054 | 0,09756 | 0,10258 | 0,09603 |
| 532,81213 | 0,10185 | 0,0987 | 0,10366 | 0,09723 |
| 532,84932 | 0,10322 | 0,0999 | 0,10475 | 0,09846 |
| 532,8865 | 0,10462 | 0,10113 | 0,10585 | 0,09972 |
| 532,92368 | 0,10604 | 0,10236 | 0,10695 | 0,10098 |
| 532,96086 | 0,10747 | 0,10359 | 0,10802 | 0,10224 |
| 532,99804 | 0,10887 | 0,1048 | 0,10906 | 0,10346 |
| 533,03523 | 0,11023 | 0,10597 | 0,11004 | 0,10463 |
| 533,07241 | 0,11152 | 0,10706 | 0,11097 | 0,10573 |
| 533,10959 | 0,11273 | 0,10807 | 0,11182 | 0,10676 |
| 533,14677 | 0,11385 | 0,10898 | 0,11259 | 0,10769 |
| 533,18395 | 0,11485 | 0,10979 | 0,11329 | 0,10853 |
| 533,22114 | 0,11573 | 0,11047 | 0,1139 | 0,10927 |
| 533,25832 | 0,11647 | 0,11103 | 0,11443 | 0,10991 |
| 533,2955 | 0,11705 | 0,11142 | 0,11485 | 0,11042 |
| 533,33268 | 0,11748 | 0,11167 | 0,1152 | 0,11083 |
| 533,36986 | 0,11776 | 0,11179 | 0,11546 | 0,11114 |
| 533,40705 | 0,1179 | 0,11177 | 0,11566 | 0,11137 |
| 533,44423 | 0,1179 | 0,11162 | 0,11579 | 0,11152 |
| 533,48141 | 0,11777 | 0,11135 | 0,11587 | 0,11161 |
| 533,51859 | 0,11751 | 0,11096 | 0,11589 | 0,11163 |
| 533,55577 | 0,11713 | 0,11046 | 0,11588 | 0,11161 |
| 533,59295 | 0,11667 | 0,1099 | 0,11585 | 0,11157 |
| 533,63014 | 0,11614 | 0,10927 | 0,11581 | 0,11153 |
| 533,66732 | 0,11556 | 0,10861 | 0,11575 | 0,11148 |
| 533,7045 | 0,11494 | 0,10792 | 0,11571 | 0,11145 |
| 533,74168 | 0,1143 | 0,10722 | 0,11566 | 0,11144 |
| 533,77886 | 0,11367 | 0,10655 | 0,11564 | 0,11147 |
| 533,81605 | 0,11306 | 0,10591 | 0,11563 | 0,11154 |
| 533,85323 | 0,11249 | 0,10531 | 0,11564 | 0,11166 |
| 533,89041 | 0,11197 | 0,10478 | 0,11566 | 0,11181 |
| 533,92759 | 0,11152 | 0,10433 | 0,11569 | 0,11201 |
| 533,96477 | 0,11114 | 0,10395 | 0,11573 | 0,11224 |
| 534,00196 | 0,11085 | 0,10369 | 0,11576 | 0,1125 |
| 534,03914 | 0,11066 | 0,10352 | 0,11577 | 0,11278 |
| 534,07632 | 0,11055 | 0,10344 | 0,11576 | 0,11305 |
| 534,1135 | 0,11053 | 0,10345 | 0,1157 | 0,11331 |
| 534,15068 | 0,11059 | 0,10355 | 0,11559 | 0,11354 |
| 534,18787 | 0,11072 | 0,10373 | 0,11542 | 0,11372 |
| 534,22505 | 0,11092 | 0,10399 | 0,11516 | 0,11383 |
| 534,26223 | 0,11118 | 0,10431 | 0,11479 | 0,11383 |
| 534,29941 | 0,11147 | 0,10465 | 0,11431 | 0,11373 |
| 534,33659 | 0,11177 | 0,10501 | 0,11372 | 0,11351 |
| 534,37378 | 0,11208 | 0,10538 | 0,11299 | 0,11315 |
| 534,41096 | 0,11236 | 0,10572 | 0,11213 | 0,11264 |
| 534,44814 | 0,1126 | 0,10602 | 0,11114 | 0,11198 |
| 534,48532 | 0,11277 | 0,10625 | 0,10998 | 0,11114 |
| 534,5225 | 0,11285 | 0,10639 | 0,10867 | 0,11012 |
| 534,55969 | 0,11283 | 0,10643 | 0,10723 | 0,10894 |
| 534,59687 | 0,11269 | 0,10635 | 0,10567 | 0,10761 |
| 534,63405 | 0,11242 | 0,10615 | 0,10399 | 0,10613 |
| 534,67123 | 0,11201 | 0,10579 | 0,1022 | 0,10451 |
| 534,70841 | 0,11143 | 0,10526 | 0,10031 | 0,10277 |
| 534,7456 | 0,11067 | 0,10457 | 0,09834 | 0,10092 |
| 534,78278 | 0,10976 | 0,10373 | 0,09633 | 0,09899 |
| 534,81996 | 0,1087 | 0,10273 | 0,09428 | 0,09702 |
| 534,85714 | 0,1075 | 0,10159 | 0,09221 | 0,09502 |
| 534,89432 | 0,10615 | 0,1003 | 0,09016 | 0,09302 |
| 534,93151 | 0,10469 | 0,09888 | 0,08813 | 0,09105 |
| 534,96869 | 0,1031 | 0,09734 | 0,08617 | 0,08913 |
| 535,00587 | 0,10144 | 0,09573 | 0,08428 | 0,08731 |
| 535,04305 | 0,09973 | 0,09405 | 0,08249 | 0,0856 |
| 535,08023 | 0,098 | 0,09234 | 0,08081 | 0,08401 |
| 535,11742 | 0,09626 | 0,0906 | 0,07926 | 0,08257 |
| 535,1546 | 0,09454 | 0,08888 | 0,07785 | 0,0813 |
| 535,19178 | 0,09288 | 0,0872 | 0,07662 | 0,08021 |
| 535,22896 | 0,09131 | 0,08558 | 0,07557 | 0,07934 |
| 535,26614 | 0,08984 | 0,08404 | 0,07469 | 0,07868 |
| 535,30333 | 0,08849 | 0,08261 | 0,07399 | 0,07822 |
| 535,34051 | 0,08729 | 0,08129 | 0,07347 | 0,07797 |
| 535,37769 | 0,08623 | 0,08014 | 0,07313 | 0,07792 |
| 535,41487 | 0,08536 | 0,07915 | 0,07299 | 0,07806 |
| 535,45205 | 0,08469 | 0,07831 | 0,07304 | 0,07841 |
| 535,48924 | 0,08418 | 0,07764 | 0,07325 | 0,07896 |
| 535,52642 | 0,08386 | 0,07713 | 0,07362 | 0,07966 |
| 535,5636 | 0,0837 | 0,07679 | 0,07413 | 0,0805 |
| 535,60078 | 0,08369 | 0,07662 | 0,07477 | 0,08147 |
| 535,63796 | 0,08384 | 0,07661 | 0,07552 | 0,08254 |
| 535,67515 | 0,08414 | 0,07674 | 0,0764 | 0,0837 |
| 535,71233 | 0,08455 | 0,07699 | 0,07736 | 0,08494 |
| 535,74951 | 0,08504 | 0,07734 | 0,07838 | 0,0862 |
| 535,78669 | 0,0856 | 0,07778 | 0,07944 | 0,08749 |
| 535,82387 | 0,0862 | 0,0783 | 0,08054 | 0,08876 |
| 535,86106 | 0,08682 | 0,07887 | 0,08165 | 0,09002 |
| 535,89824 | 0,08744 | 0,07947 | 0,08276 | 0,09124 |
| 535,93542 | 0,08802 | 0,08007 | 0,08385 | 0,09239 |
| 535,9726 | 0,08855 | 0,08067 | 0,08491 | 0,09346 |
| 536,00978 | 0,089 | 0,08124 | 0,08593 | 0,09444 |
| 536,04697 | 0,08938 | 0,08176 | 0,0869 | 0,09534 |
| 536,08415 | 0,08965 | 0,08222 | 0,08781 | 0,09613 |
| 536,12133 | 0,08981 | 0,08261 | 0,08866 | 0,09682 |
| 536,15851 | 0,08983 | 0,08293 | 0,08942 | 0,09741 |
| 536,19569 | 0,08972 | 0,08317 | 0,09012 | 0,09787 |
| 536,23288 | 0,0895 | 0,08332 | 0,09075 | 0,09823 |
| 536,27006 | 0,08915 | 0,08339 | 0,09131 | 0,0985 |
| 536,30724 | 0,0887 | 0,08335 | 0,0918 | 0,09868 |
| 536,34442 | 0,08814 | 0,08324 | 0,09223 | 0,09878 |
| 536,3816 | 0,08747 | 0,08306 | 0,09258 | 0,0988 |
| 536,41879 | 0,08672 | 0,08282 | 0,09287 | 0,09875 |
| 536,45597 | 0,08592 | 0,08252 | 0,09311 | 0,09864 |
| 536,49315 | 0,08508 | 0,08218 | 0,09329 | 0,09847 |
| 536,53033 | 0,08421 | 0,0818 | 0,09341 | 0,09825 |
| 536,56751 | 0,08334 | 0,08141 | 0,09347 | 0,09799 |
| 536,6047 | 0,08247 | 0,08101 | 0,09347 | 0,09768 |
| 536,64188 | 0,08164 | 0,08061 | 0,09339 | 0,09733 |
| 536,67906 | 0,08086 | 0,08023 | 0,09325 | 0,09692 |
| 536,71624 | 0,08014 | 0,07988 | 0,09303 | 0,09645 |
| 536,75342 | 0,07948 | 0,07956 | 0,09274 | 0,09593 |
| 536,79061 | 0,07891 | 0,07928 | 0,09236 | 0,09534 |
| 536,82779 | 0,07841 | 0,07904 | 0,09188 | 0,09469 |
| 536,86497 | 0,07802 | 0,07884 | 0,09129 | 0,09395 |
| 536,90215 | 0,07772 | 0,07869 | 0,09059 | 0,09312 |
| 536,93933 | 0,0775 | 0,07859 | 0,08978 | 0,0922 |
| 536,97652 | 0,07735 | 0,07852 | 0,08887 | 0,09118 |
| 537,0137 | 0,07727 | 0,07849 | 0,08785 | 0,09007 |
| 537,05088 | 0,07725 | 0,07849 | 0,08673 | 0,08888 |
| 537,08806 | 0,07728 | 0,0785 | 0,0855 | 0,08759 |
| 537,12524 | 0,07733 | 0,07852 | 0,08417 | 0,08623 |
| 537,16243 | 0,0774 | 0,07854 | 0,08278 | 0,08478 |
| 537,19961 | 0,07747 | 0,07855 | 0,08132 | 0,08328 |
| 537,23679 | 0,07752 | 0,07854 | 0,07982 | 0,08174 |
| 537,27397 | 0,07754 | 0,07849 | 0,07829 | 0,08019 |
| 537,31115 | 0,07751 | 0,07841 | 0,07675 | 0,07863 |
| 537,34834 | 0,07742 | 0,07828 | 0,07523 | 0,07708 |
| 537,38552 | 0,07725 | 0,0781 | 0,07375 | 0,07558 |
| 537,4227 | 0,07701 | 0,07787 | 0,07233 | 0,07415 |
| 537,45988 | 0,07668 | 0,07757 | 0,07099 | 0,0728 |
| 537,49706 | 0,07628 | 0,07721 | 0,06975 | 0,07156 |
| 537,53425 | 0,07579 | 0,07679 | 0,06862 | 0,07043 |
| 537,57143 | 0,07521 | 0,07633 | 0,06766 | 0,06944 |
| 537,60861 | 0,07457 | 0,07583 | 0,06686 | 0,0686 |
| 537,64579 | 0,07386 | 0,07529 | 0,06621 | 0,06796 |
| 537,68297 | 0,07311 | 0,07472 | 0,06574 | 0,06749 |
| 537,72016 | 0,07232 | 0,07415 | 0,06545 | 0,0672 |
| 537,75734 | 0,07152 | 0,07358 | 0,06534 | 0,0671 |
| 537,79452 | 0,07072 | 0,07304 | 0,06545 | 0,06718 |
| 537,8317 | 0,06994 | 0,07254 | 0,06575 | 0,06745 |
| 537,86888 | 0,06922 | 0,07208 | 0,06624 | 0,06793 |
| 537,90607 | 0,06856 | 0,07171 | 0,06691 | 0,0686 |
| 537,94325 | 0,06798 | 0,07144 | 0,06776 | 0,06945 |
| 537,98043 | 0,0675 | 0,07127 | 0,06876 | 0,07046 |
| 538,01761 | 0,06713 | 0,07122 | 0,06993 | 0,07163 |
| 538,05479 | 0,06693 | 0,0713 | 0,07126 | 0,07294 |
| 538,09198 | 0,06687 | 0,07152 | 0,07271 | 0,07439 |
| 538,12916 | 0,06696 | 0,07189 | 0,07425 | 0,07598 |
| 538,16634 | 0,06721 | 0,07243 | 0,07589 | 0,07766 |
| 538,20352 | 0,06761 | 0,07311 | 0,07759 | 0,07942 |
| 538,2407 | 0,06817 | 0,07394 | 0,07933 | 0,08123 |
| 538,27789 | 0,06889 | 0,0749 | 0,0811 | 0,08308 |
| 538,31507 | 0,06976 | 0,07598 | 0,08284 | 0,08494 |
| 538,35225 | 0,07074 | 0,07717 | 0,08455 | 0,08677 |
| 538,38943 | 0,07181 | 0,07846 | 0,0862 | 0,08855 |
| 538,42661 | 0,07296 | 0,07981 | 0,08775 | 0,09025 |
| 538,4638 | 0,07415 | 0,08119 | 0,08919 | 0,09184 |
| 538,50098 | 0,07537 | 0,08258 | 0,09046 | 0,09329 |
| 538,53816 | 0,07657 | 0,08394 | 0,09155 | 0,09458 |
| 538,57534 | 0,07772 | 0,08526 | 0,09244 | 0,09567 |
| 538,61252 | 0,07879 | 0,08648 | 0,09312 | 0,09651 |
| 538,64971 | 0,07975 | 0,08757 | 0,09357 | 0,09711 |
| 538,68689 | 0,08058 | 0,08852 | 0,09379 | 0,09746 |
| 538,72407 | 0,08125 | 0,0893 | 0,09376 | 0,09756 |
| 538,76125 | 0,0817 | 0,08989 | 0,09344 | 0,09738 |
| 538,79843 | 0,08194 | 0,09028 | 0,09289 | 0,09695 |
| 538,83562 | 0,08196 | 0,0904 | 0,0921 | 0,09622 |
| 538,8728 | 0,08176 | 0,09028 | 0,09111 | 0,09523 |
| 538,90998 | 0,08134 | 0,08993 | 0,08991 | 0,09403 |
| 538,94716 | 0,0807 | 0,08935 | 0,08855 | 0,09263 |
| 538,98434 | 0,07982 | 0,08854 | 0,08701 | 0,09106 |
| 539,02153 | 0,07873 | 0,08752 | 0,08536 | 0,08936 |
| 539,05871 | 0,07748 | 0,08629 | 0,08363 | 0,08754 |
| 539,09589 | 0,07607 | 0,08486 | 0,08185 | 0,08565 |
| 539,13307 | 0,07455 | 0,0833 | 0,08004 | 0,08373 |
| 539,17025 | 0,07294 | 0,08163 | 0,07824 | 0,08181 |
| 539,20744 | 0,07126 | 0,07986 | 0,07646 | 0,07992 |
| 539,24462 | 0,06955 | 0,07804 | 0,07475 | 0,07808 |
| 539,2818 | 0,06785 | 0,07619 | 0,07311 | 0,07632 |
| 539,31898 | 0,06618 | 0,07434 | 0,07155 | 0,07466 |
| 539,35616 | 0,06458 | 0,07254 | 0,07008 | 0,0731 |
| 539,39335 | 0,06306 | 0,07079 | 0,0687 | 0,07165 |
| 539,43053 | 0,06163 | 0,06911 | 0,06741 | 0,07029 |
| 539,46771 | 0,06034 | 0,06753 | 0,06622 | 0,06902 |
| 539,50489 | 0,05917 | 0,06605 | 0,06509 | 0,06784 |
| 539,54207 | 0,05812 | 0,06471 | 0,06402 | 0,06672 |
| 539,57926 | 0,0572 | 0,06348 | 0,06299 | 0,06565 |
| 539,61644 | 0,05638 | 0,06236 | 0,06197 | 0,0646 |
| 539,65362 | 0,05566 | 0,06135 | 0,06097 | 0,06356 |
| 539,6908 | 0,05504 | 0,06043 | 0,05995 | 0,0625 |
| 539,72798 | 0,05448 | 0,05959 | 0,0589 | 0,06141 |
| 539,76517 | 0,05397 | 0,05882 | 0,05781 | 0,06027 |
| 539,80235 | 0,05347 | 0,0581 | 0,05667 | 0,05907 |
| 539,83953 | 0,05298 | 0,0574 | 0,05547 | 0,0578 |
| 539,87671 | 0,05246 | 0,0567 | 0,05422 | 0,05646 |
| 539,91389 | 0,0519 | 0,056 | 0,0529 | 0,05506 |
| 539,95108 | 0,05128 | 0,05526 | 0,05153 | 0,05359 |
| 539,98826 | 0,05057 | 0,05447 | 0,05011 | 0,05208 |
| 540,02544 | 0,04979 | 0,05361 | 0,04866 | 0,05052 |
| 540,06262 | 0,04891 | 0,05269 | 0,04718 | 0,04893 |
| 540,0998 | 0,04794 | 0,05169 | 0,0457 | 0,04734 |
| 540,13699 | 0,04688 | 0,05062 | 0,04421 | 0,04575 |
| 540,17417 | 0,04571 | 0,04947 | 0,04275 | 0,04418 |
| 540,21135 | 0,04447 | 0,04824 | 0,04132 | 0,04266 |
| 540,24853 | 0,04316 | 0,04694 | 0,03993 | 0,04118 |
| 540,28571 | 0,04179 | 0,04559 | 0,0386 | 0,03977 |
| 540,3229 | 0,04039 | 0,0442 | 0,03731 | 0,03844 |
| 540,36008 | 0,03896 | 0,04278 | 0,03609 | 0,03718 |
| 540,39726 | 0,03753 | 0,04135 | 0,03493 | 0,03599 |
| 540,43444 | 0,03611 | 0,03992 | 0,03384 | 0,03487 |
| 540,47162 | 0,03473 | 0,0385 | 0,0328 | 0,03383 |
| 540,50881 | 0,03339 | 0,03712 | 0,03181 | 0,03285 |
| 540,54599 | 0,0321 | 0,03577 | 0,03086 | 0,03192 |
| 540,58317 | 0,03088 | 0,03448 | 0,02994 | 0,03103 |
| 540,62035 | 0,02972 | 0,03325 | 0,02905 | 0,03016 |
| 540,65753 | 0,02866 | 0,03208 | 0,02817 | 0,02931 |
| 540,69472 | 0,02768 | 0,031 | 0,02728 | 0,02846 |
| 540,7319 | 0,02677 | 0,02998 | 0,02639 | 0,0276 |
| 540,76908 | 0,02594 | 0,02904 | 0,02548 | 0,02672 |
| 540,80626 | 0,02518 | 0,02815 | 0,02455 | 0,02581 |
| 540,84344 | 0,02447 | 0,02733 | 0,0236 | 0,02487 |
| 540,88063 | 0,02382 | 0,02656 | 0,02261 | 0,02388 |
| 540,91781 | 0,02322 | 0,02584 | 0,0216 | 0,02287 |
| 540,95499 | 0,02264 | 0,02516 | 0,02055 | 0,02181 |
| 540,99217 | 0,02209 | 0,02449 | 0,01948 | 0,02072 |
| 541,02935 | 0,02153 | 0,02384 | 0,0184 | 0,0196 |
| 541,06654 | 0,02098 | 0,0232 | 0,0173 | 0,01846 |
| 541,10372 | 0,02042 | 0,02255 | 0,01619 | 0,01731 |
| 541,1409 | 0,01983 | 0,02189 | 0,01509 | 0,01615 |
| 541,17808 | 0,01922 | 0,0212 | 0,01399 | 0,01501 |
| 541,21526 | 0,01858 | 0,0205 | 0,01292 | 0,01387 |
| 541,25245 | 0,01791 | 0,01976 | 0,01188 | 0,01277 |
| 541,28963 | 0,0172 | 0,019 | 0,01086 | 0,01171 |
| 541,32681 | 0,01647 | 0,01821 | 0,00989 | 0,01068 |
| 541,36399 | 0,0157 | 0,01739 | 0,00897 | 0,0097 |
| 541,40117 | 0,0149 | 0,01654 | 0,00811 | 0,00878 |
| 541,43836 | 0,01409 | 0,01568 | 0,0073 | 0,00791 |
| 541,47554 | 0,01326 | 0,0148 | 0,00654 | 0,0071 |
| 541,51272 | 0,01242 | 0,01391 | 0,00584 | 0,00637 |
| 541,5499 | 0,01158 | 0,01301 | 0,0052 | 0,00569 |
| 541,58708 | 0,01074 | 0,01212 | 0,00463 | 0,00508 |
| 541,62427 | 0,00992 | 0,01125 | 0,00411 | 0,00452 |
| 541,66145 | 0,00912 | 0,01039 | 0,00365 | 0,00402 |
| 541,69863 | 0,00834 | 0,00955 | 0,00323 | 0,00357 |
| 541,73581 | 0,00759 | 0,00875 | 0,00287 | 0,00317 |
| 541,77299 | 0,00688 | 0,00797 | 0,00255 | 0,00283 |
| 541,81018 | 0,0062 | 0,00724 | 0,00227 | 0,00252 |
| 541,84736 | 0,00557 | 0,00655 | 0,00203 | 0,00226 |
| 541,88454 | 0,00499 | 0,00591 | 0,00183 | 0,00202 |
| 541,92172 | 0,00444 | 0,00532 | 0,00166 | 0,00182 |
| 541,9589 | 0,00395 | 0,00477 | 0,00151 | 0,00164 |
| 541,99609 | 0,00349 | 0,00426 | 0,00138 | 0,00149 |
| 542,03327 | 0,00308 | 0,0038 | 0,00127 | 0,00136 |
| 542,07045 | 0,00271 | 0,0034 | 0,00119 | 0,00125 |
| 542,10763 | 0,00239 | 0,00304 | 0,00111 | 0,00114 |
| 542,14481 | 0,00211 | 0,00271 | 0,00105 | 0,00106 |
| 542,182 | 0,00185 | 0,00243 | 0,00099 | 0,00098 |
| 542,21918 | 0,00163 | 0,00218 | 0,00094 | 0,00091 |
| 542,25636 | 0,00144 | 0,00196 | 9e-04 | 0,00084 |
| 542,29354 | 0,00128 | 0,00177 | 0,00086 | 0,00078 |
| 542,33072 | 0,00114 | 0,00161 | 0,00082 | 0,00073 |
| 542,36791 | 0,00103 | 0,00147 | 0,00078 | 0,00068 |
| 542,40509 | 0,00093 | 0,00135 | 0,00075 | 0,00063 |
| 542,44227 | 0,00084 | 0,00125 | 0,00071 | 0,00058 |
| 542,47945 | 0,00077 | 0,00116 | 0,00068 | 0,00054 |
| 542,51663 | 0,00071 | 0,00108 | 0,00064 | 5e-04 |
| 542,55382 | 0,00066 | 0,00101 | 6e-04 | 0,00046 |
| 542,591 | 0,00062 | 0,00095 | 0,00057 | 0,00042 |
| 542,62818 | 0,00058 | 9e-04 | 0,00053 | 0,00038 |
| 542,66536 | 0,00055 | 0,00085 | 0,00049 | 0,00035 |
| 542,70254 | 0,00052 | 0,00081 | 0,00045 | 0,00031 |
| 542,73973 | 0,00049 | 0,00076 | 0,00042 | 0,00028 |
| 542,77691 | 0,00047 | 0,00072 | 0,00038 | 0,00025 |
| 542,81409 | 0,00044 | 0,00068 | 0,00035 | 0,00022 |
| 542,85127 | 0,00042 | 0,00064 | 0,00031 | 2e-04 |
| 542,88845 | 4e-04 | 6e-04 | 0,00028 | 0,00017 |
| 542,92564 | 0,00037 | 0,00057 | 0,00025 | 0,00015 |
| 542,96282 | 0,00035 | 0,00053 | 0,00022 | 0,00013 |
| 543 | 0,00033 | 0,00049 | 0,00019 | 0,00011 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 6e-05 | 9e-05 | 0 | 7e-05 |
| 524,03718 | 7e-05 | 9e-05 | 0 | 7e-05 |
| 524,07436 | 7e-05 | 1e-04 | 1e-05 | 8e-05 |
| 524,11155 | 7e-05 | 0,00011 | 1e-05 | 8e-05 |
| 524,14873 | 7e-05 | 0,00012 | 1e-05 | 9e-05 |
| 524,18591 | 7e-05 | 0,00013 | 1e-05 | 1e-04 |
| 524,22309 | 7e-05 | 0,00014 | 1e-05 | 1e-04 |
| 524,26027 | 7e-05 | 0,00015 | 2e-05 | 0,00011 |
| 524,29746 | 7e-05 | 0,00016 | 2e-05 | 0,00011 |
| 524,33464 | 7e-05 | 0,00017 | 2e-05 | 0,00011 |
| 524,37182 | 7e-05 | 0,00018 | 3e-05 | 0,00012 |
| 524,409 | 7e-05 | 0,00019 | 3e-05 | 0,00012 |
| 524,44618 | 7e-05 | 0,00021 | 4e-05 | 0,00012 |
| 524,48337 | 6e-05 | 0,00022 | 4e-05 | 0,00013 |
| 524,52055 | 6e-05 | 0,00023 | 5e-05 | 0,00013 |
| 524,55773 | 6e-05 | 0,00024 | 6e-05 | 0,00013 |
| 524,59491 | 6e-05 | 0,00025 | 6e-05 | 0,00013 |
| 524,63209 | 6e-05 | 0,00026 | 7e-05 | 0,00013 |
| 524,66928 | 5e-05 | 0,00027 | 8e-05 | 0,00012 |
| 524,70646 | 5e-05 | 0,00028 | 9e-05 | 0,00012 |
| 524,74364 | 5e-05 | 0,00029 | 1e-04 | 0,00012 |
| 524,78082 | 5e-05 | 3e-04 | 0,00011 | 0,00012 |
| 524,818 | 5e-05 | 0,00031 | 0,00012 | 0,00011 |
| 524,85519 | 5e-05 | 0,00032 | 0,00014 | 0,00011 |
| 524,89237 | 6e-05 | 0,00033 | 0,00015 | 0,00011 |
| 524,92955 | 6e-05 | 0,00034 | 0,00016 | 0,00011 |
| 524,96673 | 7e-05 | 0,00036 | 0,00018 | 0,00011 |
| 525,00391 | 7e-05 | 0,00037 | 0,00019 | 0,00011 |
| 525,0411 | 8e-05 | 0,00038 | 0,00021 | 0,00011 |
| 525,07828 | 9e-05 | 0,00039 | 0,00023 | 0,00012 |
| 525,11546 | 0,00011 | 0,00041 | 0,00024 | 0,00012 |
| 525,15264 | 0,00012 | 0,00042 | 0,00026 | 0,00013 |
| 525,18982 | 0,00014 | 0,00044 | 0,00028 | 0,00015 |
| 525,22701 | 0,00016 | 0,00046 | 3e-04 | 0,00016 |
| 525,26419 | 0,00018 | 0,00048 | 0,00032 | 0,00018 |
| 525,30137 | 2e-04 | 5e-04 | 0,00035 | 0,00021 |
| 525,33855 | 0,00023 | 0,00052 | 0,00038 | 0,00024 |
| 525,37573 | 0,00026 | 0,00055 | 0,00041 | 0,00027 |
| 525,41292 | 3e-04 | 0,00058 | 0,00044 | 0,00031 |
| 525,4501 | 0,00033 | 0,00061 | 0,00047 | 0,00036 |
| 525,48728 | 0,00038 | 0,00065 | 0,00052 | 0,00042 |
| 525,52446 | 0,00042 | 0,00069 | 0,00056 | 0,00048 |
| 525,56164 | 0,00048 | 0,00073 | 0,00061 | 0,00055 |
| 525,59883 | 0,00053 | 0,00078 | 0,00067 | 0,00062 |
| 525,63601 | 0,00059 | 0,00083 | 0,00073 | 0,00071 |
| 525,67319 | 0,00066 | 0,00088 | 8e-04 | 8e-04 |
| 525,71037 | 0,00073 | 0,00095 | 0,00088 | 9e-04 |
| 525,74755 | 0,00081 | 0,00101 | 0,00096 | 0,00101 |
| 525,78474 | 9e-04 | 0,00108 | 0,00105 | 0,00113 |
| 525,82192 | 0,00099 | 0,00116 | 0,00114 | 0,00126 |
| 525,8591 | 0,00109 | 0,00124 | 0,00125 | 0,00139 |
| 525,89628 | 0,0012 | 0,00133 | 0,00135 | 0,00153 |
| 525,93346 | 0,00131 | 0,00143 | 0,00147 | 0,00168 |
| 525,97065 | 0,00143 | 0,00153 | 0,00159 | 0,00183 |
| 526,00783 | 0,00157 | 0,00163 | 0,00172 | 0,00199 |
| 526,04501 | 0,00171 | 0,00174 | 0,00185 | 0,00216 |
| 526,08219 | 0,00186 | 0,00186 | 0,00198 | 0,00233 |
| 526,11937 | 0,00202 | 0,00199 | 0,00212 | 0,0025 |
| 526,15656 | 0,00219 | 0,00212 | 0,00226 | 0,00267 |
| 526,19374 | 0,00237 | 0,00226 | 0,0024 | 0,00284 |
| 526,23092 | 0,00256 | 0,0024 | 0,00255 | 0,00301 |
| 526,2681 | 0,00277 | 0,00256 | 0,00269 | 0,00319 |
| 526,30528 | 0,00298 | 0,00271 | 0,00283 | 0,00336 |
| 526,34247 | 0,00319 | 0,00288 | 0,00298 | 0,00352 |
| 526,37965 | 0,00342 | 0,00305 | 0,00312 | 0,00369 |
| 526,41683 | 0,00366 | 0,00323 | 0,00326 | 0,00385 |
| 526,45401 | 0,0039 | 0,00342 | 0,0034 | 0,00401 |
| 526,49119 | 0,00415 | 0,00362 | 0,00354 | 0,00416 |
| 526,52838 | 0,00441 | 0,00382 | 0,00368 | 0,00431 |
| 526,56556 | 0,00467 | 0,00403 | 0,00382 | 0,00446 |
| 526,60274 | 0,00493 | 0,00425 | 0,00397 | 0,0046 |
| 526,63992 | 0,0052 | 0,00449 | 0,00411 | 0,00473 |
| 526,6771 | 0,00547 | 0,00473 | 0,00427 | 0,00487 |
| 526,71429 | 0,00574 | 0,00498 | 0,00442 | 0,005 |
| 526,75147 | 0,00602 | 0,00525 | 0,00458 | 0,00513 |
| 526,78865 | 0,00629 | 0,00553 | 0,00475 | 0,00526 |
| 526,82583 | 0,00657 | 0,00582 | 0,00493 | 0,0054 |
| 526,86301 | 0,00684 | 0,00614 | 0,00511 | 0,00553 |
| 526,9002 | 0,00712 | 0,00647 | 0,00531 | 0,00567 |
| 526,93738 | 0,00741 | 0,00681 | 0,00552 | 0,00581 |
| 526,97456 | 0,00769 | 0,00718 | 0,00575 | 0,00596 |
| 527,01174 | 0,00799 | 0,00756 | 0,00598 | 0,00611 |
| 527,04892 | 0,00829 | 0,00797 | 0,00624 | 0,00627 |
| 527,08611 | 0,00859 | 0,00841 | 0,00651 | 0,00645 |
| 527,12329 | 0,00891 | 0,00887 | 0,00679 | 0,00664 |
| 527,16047 | 0,00924 | 0,00935 | 0,0071 | 0,00684 |
| 527,19765 | 0,00959 | 0,00986 | 0,00743 | 0,00706 |
| 527,23483 | 0,00996 | 0,0104 | 0,00778 | 0,00729 |
| 527,27202 | 0,01034 | 0,01096 | 0,00815 | 0,00755 |
| 527,3092 | 0,01075 | 0,01155 | 0,00855 | 0,00783 |
| 527,34638 | 0,01118 | 0,01217 | 0,00897 | 0,00814 |
| 527,38356 | 0,01163 | 0,01281 | 0,00942 | 0,00847 |
| 527,42074 | 0,01212 | 0,01348 | 0,0099 | 0,00884 |
| 527,45793 | 0,01262 | 0,01417 | 0,01041 | 0,00923 |
| 527,49511 | 0,01316 | 0,01488 | 0,01095 | 0,00966 |
| 527,53229 | 0,01372 | 0,01561 | 0,01152 | 0,01012 |
| 527,56947 | 0,0143 | 0,01635 | 0,01212 | 0,01063 |
| 527,60665 | 0,01491 | 0,01711 | 0,01277 | 0,01117 |
| 527,64384 | 0,01554 | 0,01788 | 0,01345 | 0,01174 |
| 527,68102 | 0,0162 | 0,01866 | 0,01416 | 0,01236 |
| 527,7182 | 0,01687 | 0,01944 | 0,01491 | 0,01301 |
| 527,75538 | 0,01755 | 0,02022 | 0,01568 | 0,01371 |
| 527,79256 | 0,01824 | 0,021 | 0,01649 | 0,01444 |
| 527,82975 | 0,01895 | 0,02177 | 0,01733 | 0,0152 |
| 527,86693 | 0,01966 | 0,02253 | 0,01819 | 0,016 |
| 527,90411 | 0,02037 | 0,02327 | 0,01907 | 0,01682 |
| 527,94129 | 0,02107 | 0,024 | 0,01997 | 0,01765 |
| 527,97847 | 0,02177 | 0,02471 | 0,02087 | 0,01851 |
| 528,01566 | 0,02247 | 0,02539 | 0,02178 | 0,01938 |
| 528,05284 | 0,02315 | 0,02605 | 0,0227 | 0,02025 |
| 528,09002 | 0,02382 | 0,02668 | 0,0236 | 0,02112 |
| 528,1272 | 0,02448 | 0,02729 | 0,02448 | 0,02198 |
| 528,16438 | 0,02512 | 0,02786 | 0,02535 | 0,02283 |
| 528,20157 | 0,02574 | 0,02841 | 0,02619 | 0,02366 |
| 528,23875 | 0,02635 | 0,02893 | 0,027 | 0,02446 |
| 528,27593 | 0,02694 | 0,02941 | 0,02777 | 0,02522 |
| 528,31311 | 0,02751 | 0,02988 | 0,0285 | 0,02595 |
| 528,35029 | 0,02807 | 0,03032 | 0,02918 | 0,02664 |
| 528,38748 | 0,02861 | 0,03074 | 0,02982 | 0,02729 |
| 528,42466 | 0,02914 | 0,03113 | 0,03041 | 0,02791 |
| 528,46184 | 0,02965 | 0,03151 | 0,03096 | 0,02847 |
| 528,49902 | 0,03016 | 0,03188 | 0,03146 | 0,02899 |
| 528,5362 | 0,03066 | 0,03223 | 0,03191 | 0,02947 |
| 528,57339 | 0,03115 | 0,03258 | 0,03233 | 0,02992 |
| 528,61057 | 0,03163 | 0,03293 | 0,03271 | 0,03034 |
| 528,64775 | 0,03211 | 0,03327 | 0,03306 | 0,03073 |
| 528,68493 | 0,03259 | 0,03361 | 0,03338 | 0,0311 |
| 528,72211 | 0,03307 | 0,03396 | 0,03369 | 0,03144 |
| 528,7593 | 0,03354 | 0,03431 | 0,03398 | 0,03178 |
| 528,79648 | 0,03402 | 0,03468 | 0,03427 | 0,03211 |
| 528,83366 | 0,0345 | 0,03505 | 0,03455 | 0,03244 |
| 528,87084 | 0,03498 | 0,03544 | 0,03484 | 0,03277 |
| 528,90802 | 0,03546 | 0,03584 | 0,03514 | 0,03311 |
| 528,94521 | 0,03596 | 0,03626 | 0,03545 | 0,03346 |
| 528,98239 | 0,03645 | 0,03669 | 0,03579 | 0,03383 |
| 529,01957 | 0,03695 | 0,03714 | 0,03614 | 0,03421 |
| 529,05675 | 0,03747 | 0,03761 | 0,03653 | 0,03461 |
| 529,09393 | 0,03799 | 0,03809 | 0,03694 | 0,03502 |
| 529,13112 | 0,03852 | 0,03859 | 0,03738 | 0,03546 |
| 529,1683 | 0,03907 | 0,03911 | 0,03785 | 0,03592 |
| 529,20548 | 0,03964 | 0,03966 | 0,03835 | 0,0364 |
| 529,24266 | 0,04022 | 0,04022 | 0,03889 | 0,0369 |
| 529,27984 | 0,04082 | 0,0408 | 0,03945 | 0,03742 |
| 529,31703 | 0,04144 | 0,0414 | 0,04005 | 0,03797 |
| 529,35421 | 0,0421 | 0,04203 | 0,04068 | 0,03853 |
| 529,39139 | 0,04278 | 0,04268 | 0,04133 | 0,03912 |
| 529,42857 | 0,04349 | 0,04336 | 0,04201 | 0,03974 |
| 529,46575 | 0,04423 | 0,04407 | 0,04272 | 0,04039 |
| 529,50294 | 0,045 | 0,0448 | 0,04346 | 0,04107 |
| 529,54012 | 0,04582 | 0,04556 | 0,04422 | 0,04178 |
| 529,5773 | 0,04667 | 0,04635 | 0,04502 | 0,04253 |
| 529,61448 | 0,04756 | 0,04717 | 0,04583 | 0,04331 |
| 529,65166 | 0,04848 | 0,04803 | 0,04667 | 0,04413 |
| 529,68885 | 0,04944 | 0,04891 | 0,04754 | 0,04501 |
| 529,72603 | 0,05043 | 0,04982 | 0,04844 | 0,04593 |
| 529,76321 | 0,05145 | 0,05076 | 0,04936 | 0,0469 |
| 529,80039 | 0,0525 | 0,05172 | 0,05031 | 0,04792 |
| 529,83757 | 0,05357 | 0,05271 | 0,05129 | 0,04899 |
| 529,87476 | 0,05465 | 0,05371 | 0,05229 | 0,0501 |
| 529,91194 | 0,05573 | 0,05473 | 0,05331 | 0,05127 |
| 529,94912 | 0,05682 | 0,05575 | 0,05436 | 0,05248 |
| 529,9863 | 0,0579 | 0,05677 | 0,05543 | 0,05373 |
| 530,02348 | 0,05896 | 0,05778 | 0,05651 | 0,05501 |
| 530,06067 | 0,06 | 0,05878 | 0,05761 | 0,05631 |
| 530,09785 | 0,061 | 0,05976 | 0,05871 | 0,05762 |
| 530,13503 | 0,06196 | 0,06071 | 0,05981 | 0,05894 |
| 530,17221 | 0,06288 | 0,06162 | 0,0609 | 0,06026 |
| 530,20939 | 0,06373 | 0,06249 | 0,06199 | 0,06155 |
| 530,24658 | 0,06451 | 0,06331 | 0,06304 | 0,0628 |
| 530,28376 | 0,06522 | 0,06407 | 0,06407 | 0,06402 |
| 530,32094 | 0,06586 | 0,06475 | 0,06505 | 0,06517 |
| 530,35812 | 0,06642 | 0,06537 | 0,06599 | 0,06626 |
| 530,3953 | 0,06691 | 0,06592 | 0,06688 | 0,06726 |
| 530,43249 | 0,06731 | 0,0664 | 0,0677 | 0,06816 |
| 530,46967 | 0,06763 | 0,06681 | 0,06844 | 0,06896 |
| 530,50685 | 0,06787 | 0,06715 | 0,06911 | 0,06967 |
| 530,54403 | 0,06805 | 0,06742 | 0,06971 | 0,07026 |
| 530,58121 | 0,06817 | 0,06763 | 0,07022 | 0,07076 |
| 530,6184 | 0,06823 | 0,06778 | 0,07067 | 0,07115 |
| 530,65558 | 0,06825 | 0,0679 | 0,07103 | 0,07142 |
| 530,69276 | 0,06824 | 0,06798 | 0,07132 | 0,07161 |
| 530,72994 | 0,0682 | 0,06805 | 0,07155 | 0,07173 |
| 530,76712 | 0,06817 | 0,0681 | 0,07174 | 0,07179 |
| 530,80431 | 0,06815 | 0,06817 | 0,07188 | 0,0718 |
| 530,84149 | 0,06815 | 0,06827 | 0,07201 | 0,07179 |
| 530,87867 | 0,06819 | 0,06841 | 0,07212 | 0,07177 |
| 530,91585 | 0,06828 | 0,06859 | 0,07224 | 0,07177 |
| 530,95303 | 0,06845 | 0,06885 | 0,07239 | 0,07181 |
| 530,99022 | 0,06871 | 0,0692 | 0,07258 | 0,07191 |
| 531,0274 | 0,06905 | 0,06965 | 0,07284 | 0,07208 |
| 531,06458 | 0,0695 | 0,07021 | 0,07316 | 0,07235 |
| 531,10176 | 0,07005 | 0,07088 | 0,07357 | 0,07273 |
| 531,13894 | 0,07071 | 0,07166 | 0,07408 | 0,07326 |
| 531,17613 | 0,07151 | 0,07255 | 0,07471 | 0,07392 |
| 531,21331 | 0,07243 | 0,07359 | 0,07546 | 0,07473 |
| 531,25049 | 0,07346 | 0,07474 | 0,07633 | 0,07567 |
| 531,28767 | 0,07459 | 0,076 | 0,07732 | 0,07676 |
| 531,32485 | 0,07582 | 0,07735 | 0,07841 | 0,07798 |
| 531,36204 | 0,07713 | 0,07878 | 0,07962 | 0,07934 |
| 531,39922 | 0,07852 | 0,08029 | 0,08095 | 0,08082 |
| 531,4364 | 0,07998 | 0,08184 | 0,08237 | 0,08239 |
| 531,47358 | 0,08146 | 0,08343 | 0,08385 | 0,08402 |
| 531,51076 | 0,08297 | 0,08502 | 0,08539 | 0,0857 |
| 531,54795 | 0,08447 | 0,0866 | 0,08696 | 0,08741 |
| 531,58513 | 0,08595 | 0,08815 | 0,08855 | 0,08911 |
| 531,62231 | 0,0874 | 0,08964 | 0,09013 | 0,09077 |
| 531,65949 | 0,08877 | 0,09105 | 0,09167 | 0,09236 |
| 531,69667 | 0,09007 | 0,09235 | 0,09317 | 0,09385 |
| 531,73386 | 0,09127 | 0,09353 | 0,09459 | 0,09524 |
| 531,77104 | 0,09237 | 0,09459 | 0,09593 | 0,09649 |
| 531,80822 | 0,09335 | 0,09552 | 0,09717 | 0,0976 |
| 531,8454 | 0,09422 | 0,0963 | 0,09829 | 0,0985 |
| 531,88258 | 0,09494 | 0,09693 | 0,09926 | 0,09922 |
| 531,91977 | 0,09552 | 0,09739 | 0,10011 | 0,09976 |
| 531,95695 | 0,09598 | 0,0977 | 0,10083 | 0,10013 |
| 531,99413 | 0,09632 | 0,09788 | 0,10143 | 0,10032 |
| 532,03131 | 0,09656 | 0,09793 | 0,1019 | 0,10034 |
| 532,06849 | 0,09669 | 0,09787 | 0,10227 | 0,10021 |
| 532,10568 | 0,09672 | 0,09771 | 0,10252 | 0,09993 |
| 532,14286 | 0,09669 | 0,09746 | 0,10269 | 0,09955 |
| 532,18004 | 0,0966 | 0,09715 | 0,1028 | 0,0991 |
| 532,21722 | 0,09649 | 0,09681 | 0,10286 | 0,0986 |
| 532,2544 | 0,09636 | 0,09646 | 0,1029 | 0,09807 |
| 532,29159 | 0,09624 | 0,09612 | 0,10294 | 0,09754 |
| 532,32877 | 0,09615 | 0,09582 | 0,10299 | 0,09705 |
| 532,36595 | 0,09612 | 0,09557 | 0,10309 | 0,09663 |
| 532,40313 | 0,09616 | 0,09542 | 0,10324 | 0,09629 |
| 532,44031 | 0,09629 | 0,09536 | 0,10347 | 0,09605 |
| 532,4775 | 0,09651 | 0,09541 | 0,10377 | 0,09594 |
| 532,51468 | 0,09684 | 0,09559 | 0,10417 | 0,09595 |
| 532,55186 | 0,09729 | 0,0959 | 0,10466 | 0,09611 |
| 532,58904 | 0,09789 | 0,09636 | 0,10527 | 0,09644 |
| 532,62622 | 0,09861 | 0,09698 | 0,10599 | 0,09691 |
| 532,66341 | 0,09946 | 0,09775 | 0,1068 | 0,09752 |
| 532,70059 | 0,10043 | 0,09865 | 0,1077 | 0,09826 |
| 532,73777 | 0,10152 | 0,09967 | 0,10868 | 0,09912 |
| 532,77495 | 0,1027 | 0,10081 | 0,10973 | 0,10009 |
| 532,81213 | 0,10398 | 0,10205 | 0,11084 | 0,10116 |
| 532,84932 | 0,10533 | 0,10337 | 0,11199 | 0,1023 |
| 532,8865 | 0,10673 | 0,10475 | 0,11316 | 0,10349 |
| 532,92368 | 0,10816 | 0,10616 | 0,11433 | 0,1047 |
| 532,96086 | 0,10959 | 0,10757 | 0,11549 | 0,10591 |
| 532,99804 | 0,111 | 0,10896 | 0,11662 | 0,10711 |
| 533,03523 | 0,11238 | 0,11031 | 0,1177 | 0,10828 |
| 533,07241 | 0,11368 | 0,11158 | 0,1187 | 0,10938 |
| 533,10959 | 0,11489 | 0,11275 | 0,11962 | 0,11041 |
| 533,14677 | 0,116 | 0,1138 | 0,12046 | 0,11136 |
| 533,18395 | 0,11698 | 0,11472 | 0,12119 | 0,11222 |
| 533,22114 | 0,11784 | 0,1155 | 0,12182 | 0,11298 |
| 533,25832 | 0,11856 | 0,11613 | 0,12234 | 0,11363 |
| 533,2955 | 0,1191 | 0,11657 | 0,12272 | 0,11414 |
| 533,33268 | 0,11948 | 0,11683 | 0,12299 | 0,11455 |
| 533,36986 | 0,11971 | 0,11693 | 0,12315 | 0,11486 |
| 533,40705 | 0,1198 | 0,11687 | 0,12321 | 0,11508 |
| 533,44423 | 0,11975 | 0,11667 | 0,12317 | 0,11521 |
| 533,48141 | 0,11958 | 0,11633 | 0,12305 | 0,11526 |
| 533,51859 | 0,11928 | 0,11586 | 0,12284 | 0,11525 |
| 533,55577 | 0,11887 | 0,11528 | 0,12257 | 0,11518 |
| 533,59295 | 0,1184 | 0,11462 | 0,12224 | 0,11509 |
| 533,63014 | 0,11787 | 0,1139 | 0,12189 | 0,11499 |
| 533,66732 | 0,11731 | 0,11315 | 0,1215 | 0,11488 |
| 533,7045 | 0,11673 | 0,11238 | 0,12111 | 0,11479 |
| 533,74168 | 0,11615 | 0,11162 | 0,12072 | 0,11472 |
| 533,77886 | 0,11561 | 0,1109 | 0,12033 | 0,11469 |
| 533,81605 | 0,11511 | 0,11023 | 0,11997 | 0,11471 |
| 533,85323 | 0,11467 | 0,10962 | 0,11962 | 0,11477 |
| 533,89041 | 0,11431 | 0,1091 | 0,11931 | 0,11488 |
| 533,92759 | 0,11402 | 0,10867 | 0,11901 | 0,11503 |
| 533,96477 | 0,11383 | 0,10834 | 0,11874 | 0,11522 |
| 534,00196 | 0,11375 | 0,10815 | 0,11849 | 0,11544 |
| 534,03914 | 0,11377 | 0,10807 | 0,11826 | 0,11568 |
| 534,07632 | 0,11389 | 0,1081 | 0,11802 | 0,11592 |
| 534,1135 | 0,11409 | 0,10823 | 0,11777 | 0,11614 |
| 534,15068 | 0,11437 | 0,10846 | 0,1175 | 0,11633 |
| 534,18787 | 0,11473 | 0,10877 | 0,11719 | 0,11646 |
| 534,22505 | 0,11514 | 0,10918 | 0,11682 | 0,11652 |
| 534,26223 | 0,11559 | 0,10964 | 0,11638 | 0,11646 |
| 534,29941 | 0,11606 | 0,11013 | 0,11585 | 0,11628 |
| 534,33659 | 0,11652 | 0,11063 | 0,11522 | 0,11596 |
| 534,37378 | 0,11696 | 0,11113 | 0,11449 | 0,11549 |
| 534,41096 | 0,11735 | 0,1116 | 0,11364 | 0,11486 |
| 534,44814 | 0,11768 | 0,112 | 0,11267 | 0,11406 |
| 534,48532 | 0,11789 | 0,11232 | 0,11153 | 0,11305 |
| 534,5225 | 0,11799 | 0,11254 | 0,11027 | 0,11185 |
| 534,55969 | 0,11796 | 0,11264 | 0,10888 | 0,11048 |
| 534,59687 | 0,11778 | 0,1126 | 0,10736 | 0,10894 |
| 534,63405 | 0,11745 | 0,11241 | 0,10573 | 0,10724 |
| 534,67123 | 0,11695 | 0,11204 | 0,10399 | 0,1054 |
| 534,70841 | 0,11624 | 0,11147 | 0,10215 | 0,10344 |
| 534,7456 | 0,11535 | 0,11073 | 0,10024 | 0,10136 |
| 534,78278 | 0,11429 | 0,10981 | 0,09827 | 0,09921 |
| 534,81996 | 0,11307 | 0,10873 | 0,09628 | 0,09702 |
| 534,85714 | 0,11169 | 0,10748 | 0,09427 | 0,09481 |
| 534,89432 | 0,11017 | 0,10608 | 0,09228 | 0,09262 |
| 534,93151 | 0,10851 | 0,10452 | 0,09032 | 0,09046 |
| 534,96869 | 0,10675 | 0,10286 | 0,08844 | 0,08839 |
| 535,00587 | 0,10493 | 0,10112 | 0,08665 | 0,08644 |
| 535,04305 | 0,10306 | 0,09932 | 0,08496 | 0,08461 |
| 535,08023 | 0,10117 | 0,09748 | 0,08339 | 0,08294 |
| 535,11742 | 0,0993 | 0,09564 | 0,08196 | 0,08144 |
| 535,1546 | 0,09747 | 0,09383 | 0,08069 | 0,08013 |
| 535,19178 | 0,09572 | 0,09208 | 0,07961 | 0,07903 |
| 535,22896 | 0,09408 | 0,09041 | 0,07872 | 0,07819 |
| 535,26614 | 0,09256 | 0,08885 | 0,07801 | 0,07756 |
| 535,30333 | 0,09119 | 0,08741 | 0,07748 | 0,07716 |
| 535,34051 | 0,08998 | 0,08612 | 0,07714 | 0,07698 |
| 535,37769 | 0,08895 | 0,08502 | 0,07698 | 0,07702 |
| 535,41487 | 0,08814 | 0,08409 | 0,07701 | 0,07727 |
| 535,45205 | 0,08753 | 0,08335 | 0,07723 | 0,07774 |
| 535,48924 | 0,08711 | 0,08278 | 0,07761 | 0,07841 |
| 535,52642 | 0,08689 | 0,08239 | 0,07812 | 0,07925 |
| 535,5636 | 0,08684 | 0,08218 | 0,07876 | 0,08022 |
| 535,60078 | 0,08697 | 0,08215 | 0,07952 | 0,08133 |
| 535,63796 | 0,08726 | 0,08228 | 0,08037 | 0,08253 |
| 535,67515 | 0,0877 | 0,08253 | 0,08131 | 0,08383 |
| 535,71233 | 0,08825 | 0,0829 | 0,08231 | 0,08518 |
| 535,74951 | 0,08888 | 0,08336 | 0,08335 | 0,08657 |
| 535,78669 | 0,08957 | 0,08389 | 0,0844 | 0,08796 |
| 535,82387 | 0,09029 | 0,08447 | 0,08546 | 0,08934 |
| 535,86106 | 0,09102 | 0,08507 | 0,08651 | 0,0907 |
| 535,89824 | 0,09172 | 0,08567 | 0,08754 | 0,092 |
| 535,93542 | 0,09237 | 0,08623 | 0,08851 | 0,09324 |
| 535,9726 | 0,09294 | 0,08676 | 0,08944 | 0,09439 |
| 536,00978 | 0,09343 | 0,08722 | 0,09031 | 0,09545 |
| 536,04697 | 0,0938 | 0,0876 | 0,09111 | 0,09641 |
| 536,08415 | 0,09406 | 0,08787 | 0,09185 | 0,09727 |
| 536,12133 | 0,09416 | 0,08804 | 0,0925 | 0,09804 |
| 536,15851 | 0,09412 | 0,0881 | 0,09308 | 0,09869 |
| 536,19569 | 0,09393 | 0,08804 | 0,09358 | 0,09923 |
| 536,23288 | 0,09361 | 0,08788 | 0,09402 | 0,09967 |
| 536,27006 | 0,09316 | 0,08761 | 0,09439 | 0,10003 |
| 536,30724 | 0,09258 | 0,08721 | 0,0947 | 0,1003 |
| 536,34442 | 0,09188 | 0,08672 | 0,09496 | 0,1005 |
| 536,3816 | 0,09107 | 0,08616 | 0,09515 | 0,10062 |
| 536,41879 | 0,09019 | 0,08553 | 0,09531 | 0,10067 |
| 536,45597 | 0,08926 | 0,08484 | 0,09541 | 0,10066 |
| 536,49315 | 0,08828 | 0,08413 | 0,09548 | 0,10059 |
| 536,53033 | 0,08729 | 0,08338 | 0,09551 | 0,10047 |
| 536,56751 | 0,08629 | 0,08265 | 0,0955 | 0,10029 |
| 536,6047 | 0,08532 | 0,08192 | 0,09544 | 0,10006 |
| 536,64188 | 0,08438 | 0,08123 | 0,09532 | 0,09976 |
| 536,67906 | 0,0835 | 0,08059 | 0,09515 | 0,09938 |
| 536,71624 | 0,08268 | 0,07999 | 0,09492 | 0,09893 |
| 536,75342 | 0,08194 | 0,07948 | 0,09461 | 0,0984 |
| 536,79061 | 0,08128 | 0,07904 | 0,09423 | 0,09777 |
| 536,82779 | 0,08071 | 0,07868 | 0,09376 | 0,09704 |
| 536,86497 | 0,08024 | 0,0784 | 0,09318 | 0,09621 |
| 536,90215 | 0,07984 | 0,0782 | 0,09249 | 0,09525 |
| 536,93933 | 0,07953 | 0,07807 | 0,09169 | 0,09417 |
| 536,97652 | 0,07928 | 0,07802 | 0,09079 | 0,09297 |
| 537,0137 | 0,0791 | 0,07804 | 0,08977 | 0,09166 |
| 537,05088 | 0,07897 | 0,0781 | 0,08863 | 0,09023 |
| 537,08806 | 0,07888 | 0,07819 | 0,08738 | 0,08871 |
| 537,12524 | 0,07881 | 0,07831 | 0,08602 | 0,08709 |
| 537,16243 | 0,07874 | 0,07844 | 0,08457 | 0,08539 |
| 537,19961 | 0,07866 | 0,07856 | 0,08305 | 0,08363 |
| 537,23679 | 0,07856 | 0,07866 | 0,08147 | 0,08184 |
| 537,27397 | 0,07843 | 0,07872 | 0,07985 | 0,08003 |
| 537,31115 | 0,07825 | 0,07873 | 0,0782 | 0,07823 |
| 537,34834 | 0,078 | 0,07868 | 0,07655 | 0,07646 |
| 537,38552 | 0,07769 | 0,07857 | 0,07492 | 0,07476 |
| 537,4227 | 0,07732 | 0,07839 | 0,07334 | 0,07314 |
| 537,45988 | 0,07687 | 0,07811 | 0,07182 | 0,07162 |
| 537,49706 | 0,07636 | 0,07775 | 0,07039 | 0,07023 |
| 537,53425 | 0,07577 | 0,07732 | 0,06905 | 0,06898 |
| 537,57143 | 0,07512 | 0,07681 | 0,06786 | 0,06788 |
| 537,60861 | 0,07442 | 0,07625 | 0,06681 | 0,06696 |
| 537,64579 | 0,07369 | 0,07562 | 0,0659 | 0,06625 |
| 537,68297 | 0,07293 | 0,07495 | 0,06516 | 0,06573 |
| 537,72016 | 0,07216 | 0,07426 | 0,06457 | 0,0654 |
| 537,75734 | 0,07139 | 0,07356 | 0,06416 | 0,06527 |
| 537,79452 | 0,07066 | 0,07286 | 0,06394 | 0,06534 |
| 537,8317 | 0,06996 | 0,07219 | 0,06391 | 0,0656 |
| 537,86888 | 0,06934 | 0,07156 | 0,06405 | 0,06609 |
| 537,90607 | 0,06878 | 0,07101 | 0,06436 | 0,06678 |
| 537,94325 | 0,06833 | 0,07054 | 0,06482 | 0,06763 |
| 537,98043 | 0,06798 | 0,07017 | 0,06544 | 0,06866 |
| 538,01761 | 0,06778 | 0,06991 | 0,06621 | 0,06984 |
| 538,05479 | 0,06771 | 0,06978 | 0,06712 | 0,07117 |
| 538,09198 | 0,06779 | 0,06977 | 0,06814 | 0,07265 |
| 538,12916 | 0,06801 | 0,06991 | 0,06926 | 0,07425 |
| 538,16634 | 0,06838 | 0,07022 | 0,07046 | 0,07593 |
| 538,20352 | 0,06889 | 0,07066 | 0,07172 | 0,07769 |
| 538,2407 | 0,06957 | 0,07123 | 0,07302 | 0,0795 |
| 538,27789 | 0,07037 | 0,07192 | 0,07435 | 0,08134 |
| 538,31507 | 0,07129 | 0,07273 | 0,07567 | 0,08318 |
| 538,35225 | 0,07229 | 0,07364 | 0,07697 | 0,08498 |
| 538,38943 | 0,07337 | 0,07464 | 0,07821 | 0,08672 |
| 538,42661 | 0,0745 | 0,07568 | 0,07938 | 0,08837 |
| 538,4638 | 0,07565 | 0,07675 | 0,08046 | 0,0899 |
| 538,50098 | 0,07679 | 0,07782 | 0,08141 | 0,09128 |
| 538,53816 | 0,07788 | 0,07887 | 0,0822 | 0,09248 |
| 538,57534 | 0,0789 | 0,07986 | 0,08284 | 0,09347 |
| 538,61252 | 0,07982 | 0,08075 | 0,0833 | 0,0942 |
| 538,64971 | 0,08062 | 0,08152 | 0,08358 | 0,09469 |
| 538,68689 | 0,08125 | 0,08215 | 0,08367 | 0,09493 |
| 538,72407 | 0,08168 | 0,08263 | 0,08356 | 0,0949 |
| 538,76125 | 0,0819 | 0,08293 | 0,08322 | 0,0946 |
| 538,79843 | 0,08192 | 0,08304 | 0,08268 | 0,09403 |
| 538,83562 | 0,08171 | 0,08292 | 0,08196 | 0,09315 |
| 538,8728 | 0,08128 | 0,08259 | 0,08107 | 0,09204 |
| 538,90998 | 0,08062 | 0,08205 | 0,08003 | 0,09071 |
| 538,94716 | 0,07971 | 0,08132 | 0,07885 | 0,08918 |
| 538,98434 | 0,07858 | 0,0804 | 0,07754 | 0,08748 |
| 539,02153 | 0,07726 | 0,07931 | 0,07614 | 0,08565 |
| 539,05871 | 0,07578 | 0,07804 | 0,07468 | 0,08369 |
| 539,09589 | 0,07416 | 0,07663 | 0,07318 | 0,08166 |
| 539,13307 | 0,07242 | 0,07512 | 0,07167 | 0,0796 |
| 539,17025 | 0,07058 | 0,07354 | 0,07016 | 0,07754 |
| 539,20744 | 0,06867 | 0,0719 | 0,06869 | 0,0755 |
| 539,24462 | 0,06675 | 0,07023 | 0,06726 | 0,0735 |
| 539,2818 | 0,06483 | 0,06857 | 0,06589 | 0,07156 |
| 539,31898 | 0,06294 | 0,06693 | 0,06458 | 0,06972 |
| 539,35616 | 0,06109 | 0,06535 | 0,06334 | 0,06796 |
| 539,39335 | 0,05932 | 0,06384 | 0,06216 | 0,0663 |
| 539,43053 | 0,05766 | 0,0624 | 0,06104 | 0,06473 |
| 539,46771 | 0,0561 | 0,06106 | 0,05999 | 0,06323 |
| 539,50489 | 0,05465 | 0,05981 | 0,05899 | 0,06182 |
| 539,54207 | 0,05331 | 0,05868 | 0,058 | 0,06047 |
| 539,57926 | 0,05208 | 0,05765 | 0,05704 | 0,05918 |
| 539,61644 | 0,05096 | 0,0567 | 0,05607 | 0,05791 |
| 539,65362 | 0,04995 | 0,05583 | 0,05509 | 0,05665 |
| 539,6908 | 0,04902 | 0,05502 | 0,05409 | 0,0554 |
| 539,72798 | 0,04816 | 0,05426 | 0,05304 | 0,05414 |
| 539,76517 | 0,04734 | 0,05354 | 0,05194 | 0,05285 |
| 539,80235 | 0,04656 | 0,05284 | 0,05079 | 0,05153 |
| 539,83953 | 0,0458 | 0,05212 | 0,04959 | 0,05018 |
| 539,87671 | 0,04505 | 0,05139 | 0,04833 | 0,0488 |
| 539,91389 | 0,04427 | 0,05062 | 0,04701 | 0,04738 |
| 539,95108 | 0,04346 | 0,04981 | 0,04565 | 0,04594 |
| 539,98826 | 0,04262 | 0,04893 | 0,04425 | 0,04448 |
| 540,02544 | 0,04173 | 0,04798 | 0,04282 | 0,04302 |
| 540,06262 | 0,04079 | 0,04695 | 0,04139 | 0,04156 |
| 540,0998 | 0,03979 | 0,04586 | 0,03996 | 0,04012 |
| 540,13699 | 0,03874 | 0,0447 | 0,03854 | 0,03872 |
| 540,17417 | 0,03763 | 0,04348 | 0,03715 | 0,03735 |
| 540,21135 | 0,03649 | 0,04219 | 0,0358 | 0,03604 |
| 540,24853 | 0,03531 | 0,04085 | 0,03451 | 0,03479 |
| 540,28571 | 0,03411 | 0,03948 | 0,03327 | 0,03362 |
| 540,3229 | 0,0329 | 0,03809 | 0,03209 | 0,03252 |
| 540,36008 | 0,0317 | 0,0367 | 0,03098 | 0,03149 |
| 540,39726 | 0,0305 | 0,03531 | 0,02994 | 0,03053 |
| 540,43444 | 0,02934 | 0,03395 | 0,02898 | 0,02963 |
| 540,47162 | 0,02821 | 0,03262 | 0,02807 | 0,02879 |
| 540,50881 | 0,02713 | 0,03135 | 0,02721 | 0,028 |
| 540,54599 | 0,0261 | 0,03013 | 0,0264 | 0,02725 |
| 540,58317 | 0,02513 | 0,02897 | 0,02563 | 0,02652 |
| 540,62035 | 0,02424 | 0,02789 | 0,02489 | 0,0258 |
| 540,65753 | 0,02341 | 0,02688 | 0,02416 | 0,02509 |
| 540,69472 | 0,02264 | 0,02596 | 0,02344 | 0,02436 |
| 540,7319 | 0,02194 | 0,02512 | 0,02272 | 0,02362 |
| 540,76908 | 0,02129 | 0,02435 | 0,02199 | 0,02285 |
| 540,80626 | 0,02069 | 0,02364 | 0,02124 | 0,02204 |
| 540,84344 | 0,02015 | 0,02299 | 0,02048 | 0,02119 |
| 540,88063 | 0,01964 | 0,02239 | 0,01968 | 0,02031 |
| 540,91781 | 0,01915 | 0,02184 | 0,01886 | 0,01939 |
| 540,95499 | 0,01868 | 0,02132 | 0,01802 | 0,01844 |
| 540,99217 | 0,01822 | 0,02083 | 0,01715 | 0,01745 |
| 541,02935 | 0,01776 | 0,02034 | 0,01627 | 0,01643 |
| 541,06654 | 0,01729 | 0,01986 | 0,01537 | 0,0154 |
| 541,10372 | 0,01681 | 0,01937 | 0,01446 | 0,01436 |
| 541,1409 | 0,0163 | 0,01887 | 0,01355 | 0,01333 |
| 541,17808 | 0,01577 | 0,01834 | 0,01264 | 0,0123 |
| 541,21526 | 0,01521 | 0,01779 | 0,01175 | 0,01128 |
| 541,25245 | 0,01463 | 0,01721 | 0,01087 | 0,0103 |
| 541,28963 | 0,01402 | 0,01661 | 0,01001 | 0,00936 |
| 541,32681 | 0,01337 | 0,01597 | 0,00918 | 0,00846 |
| 541,36399 | 0,01271 | 0,0153 | 0,00839 | 0,0076 |
| 541,40117 | 0,01203 | 0,0146 | 0,00764 | 0,00679 |
| 541,43836 | 0,01133 | 0,01388 | 0,00693 | 0,00604 |
| 541,47554 | 0,01062 | 0,01314 | 0,00626 | 0,00535 |
| 541,51272 | 0,00991 | 0,01239 | 0,00564 | 0,00473 |
| 541,5499 | 0,0092 | 0,01163 | 0,00506 | 0,00416 |
| 541,58708 | 0,0085 | 0,01086 | 0,00453 | 0,00364 |
| 541,62427 | 0,00782 | 0,0101 | 0,00405 | 0,00318 |
| 541,66145 | 0,00715 | 0,00935 | 0,00361 | 0,00277 |
| 541,69863 | 0,00651 | 0,00862 | 0,00321 | 0,00242 |
| 541,73581 | 0,00589 | 0,00791 | 0,00285 | 0,00211 |
| 541,77299 | 0,00531 | 0,00722 | 0,00252 | 0,00185 |
| 541,81018 | 0,00477 | 0,00656 | 0,00223 | 0,00163 |
| 541,84736 | 0,00426 | 0,00594 | 0,00198 | 0,00143 |
| 541,88454 | 0,00378 | 0,00535 | 0,00176 | 0,00127 |
| 541,92172 | 0,00335 | 0,00481 | 0,00156 | 0,00114 |
| 541,9589 | 0,00295 | 0,0043 | 0,00139 | 0,00103 |
| 541,99609 | 0,00259 | 0,00383 | 0,00124 | 0,00094 |
| 542,03327 | 0,00227 | 0,00339 | 0,00111 | 0,00087 |
| 542,07045 | 0,00199 | 0,00301 | 0,00099 | 0,00081 |
| 542,10763 | 0,00173 | 0,00266 | 9e-04 | 0,00077 |
| 542,14481 | 0,00151 | 0,00234 | 0,00081 | 0,00073 |
| 542,182 | 0,00131 | 0,00206 | 0,00074 | 7e-04 |
| 542,21918 | 0,00114 | 0,00181 | 0,00067 | 0,00067 |
| 542,25636 | 0,00099 | 0,00159 | 0,00061 | 0,00065 |
| 542,29354 | 0,00087 | 0,0014 | 0,00056 | 0,00063 |
| 542,33072 | 0,00076 | 0,00123 | 0,00052 | 0,00061 |
| 542,36791 | 0,00067 | 0,00109 | 0,00048 | 0,00059 |
| 542,40509 | 0,00059 | 0,00096 | 0,00044 | 0,00057 |
| 542,44227 | 0,00052 | 0,00086 | 0,00041 | 0,00054 |
| 542,47945 | 0,00046 | 0,00076 | 0,00038 | 0,00052 |
| 542,51663 | 0,00042 | 0,00068 | 0,00035 | 5e-04 |
| 542,55382 | 0,00037 | 0,00062 | 0,00033 | 0,00047 |
| 542,591 | 0,00034 | 0,00056 | 3e-04 | 0,00044 |
| 542,62818 | 0,00031 | 0,00051 | 0,00028 | 0,00042 |
| 542,66536 | 0,00028 | 0,00047 | 0,00026 | 0,00039 |
| 542,70254 | 0,00025 | 0,00043 | 0,00023 | 0,00036 |
| 542,73973 | 0,00023 | 0,00039 | 0,00021 | 0,00033 |
| 542,77691 | 0,00021 | 0,00036 | 0,00019 | 3e-04 |
| 542,81409 | 0,00019 | 0,00034 | 0,00018 | 0,00028 |
| 542,85127 | 0,00017 | 0,00031 | 0,00016 | 0,00025 |
| 542,88845 | 0,00016 | 0,00029 | 0,00014 | 0,00022 |
| 542,92564 | 0,00014 | 0,00027 | 0,00013 | 2e-04 |
| 542,96282 | 0,00013 | 0,00024 | 0,00011 | 0,00018 |
| 543 | 0,00012 | 0,00023 | 1e-04 | 0,00015 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 2e-05 | 2e-05 | 0 | 1e-05 |
| 524,03718 | 3e-05 | 2e-05 | 0 | 1e-05 |
| 524,07436 | 3e-05 | 3e-05 | 0 | 1e-05 |
| 524,11155 | 3e-05 | 3e-05 | 0 | 2e-05 |
| 524,14873 | 4e-05 | 4e-05 | 0 | 2e-05 |
| 524,18591 | 5e-05 | 4e-05 | 0 | 2e-05 |
| 524,22309 | 5e-05 | 5e-05 | 0 | 3e-05 |
| 524,26027 | 6e-05 | 6e-05 | 0 | 3e-05 |
| 524,29746 | 7e-05 | 7e-05 | 0 | 3e-05 |
| 524,33464 | 8e-05 | 8e-05 | 0 | 4e-05 |
| 524,37182 | 9e-05 | 9e-05 | 1e-05 | 4e-05 |
| 524,409 | 1e-04 | 1e-04 | 1e-05 | 5e-05 |
| 524,44618 | 0,00011 | 0,00012 | 1e-05 | 6e-05 |
| 524,48337 | 0,00012 | 0,00013 | 1e-05 | 6e-05 |
| 524,52055 | 0,00013 | 0,00015 | 1e-05 | 7e-05 |
| 524,55773 | 0,00014 | 0,00017 | 2e-05 | 8e-05 |
| 524,59491 | 0,00015 | 0,00019 | 2e-05 | 8e-05 |
| 524,63209 | 0,00017 | 0,00021 | 3e-05 | 9e-05 |
| 524,66928 | 0,00018 | 0,00023 | 3e-05 | 1e-04 |
| 524,70646 | 0,00019 | 0,00026 | 4e-05 | 0,00011 |
| 524,74364 | 2e-04 | 0,00029 | 5e-05 | 0,00012 |
| 524,78082 | 0,00022 | 0,00032 | 6e-05 | 0,00013 |
| 524,818 | 0,00023 | 0,00035 | 7e-05 | 0,00014 |
| 524,85519 | 0,00024 | 0,00039 | 8e-05 | 0,00015 |
| 524,89237 | 0,00025 | 0,00042 | 1e-04 | 0,00017 |
| 524,92955 | 0,00027 | 0,00046 | 0,00012 | 0,00018 |
| 524,96673 | 0,00028 | 5e-04 | 0,00014 | 0,00019 |
| 525,00391 | 0,00029 | 0,00055 | 0,00016 | 0,00021 |
| 525,0411 | 3e-04 | 0,00059 | 0,00019 | 0,00023 |
| 525,07828 | 0,00031 | 0,00064 | 0,00022 | 0,00024 |
| 525,11546 | 0,00032 | 0,00069 | 0,00026 | 0,00026 |
| 525,15264 | 0,00033 | 0,00075 | 3e-04 | 0,00029 |
| 525,18982 | 0,00034 | 8e-04 | 0,00035 | 0,00031 |
| 525,22701 | 0,00035 | 0,00086 | 4e-04 | 0,00034 |
| 525,26419 | 0,00036 | 0,00092 | 0,00045 | 0,00037 |
| 525,30137 | 0,00037 | 0,00099 | 0,00052 | 4e-04 |
| 525,33855 | 0,00038 | 0,00105 | 0,00059 | 0,00044 |
| 525,37573 | 4e-04 | 0,00112 | 0,00066 | 0,00048 |
| 525,41292 | 0,00041 | 0,00119 | 0,00075 | 0,00052 |
| 525,4501 | 0,00043 | 0,00126 | 0,00084 | 0,00058 |
| 525,48728 | 0,00045 | 0,00134 | 0,00094 | 0,00063 |
| 525,52446 | 0,00047 | 0,00142 | 0,00104 | 0,00069 |
| 525,56164 | 5e-04 | 0,0015 | 0,00116 | 0,00076 |
| 525,59883 | 0,00054 | 0,00158 | 0,00128 | 0,00084 |
| 525,63601 | 0,00057 | 0,00167 | 0,00141 | 0,00092 |
| 525,67319 | 0,00062 | 0,00176 | 0,00155 | 0,001 |
| 525,71037 | 0,00067 | 0,00185 | 0,00169 | 0,0011 |
| 525,74755 | 0,00072 | 0,00194 | 0,00184 | 0,0012 |
| 525,78474 | 0,00079 | 0,00204 | 0,002 | 0,00131 |
| 525,82192 | 0,00086 | 0,00214 | 0,00216 | 0,00143 |
| 525,8591 | 0,00094 | 0,00224 | 0,00233 | 0,00155 |
| 525,89628 | 0,00102 | 0,00235 | 0,0025 | 0,00168 |
| 525,93346 | 0,00112 | 0,00246 | 0,00268 | 0,00182 |
| 525,97065 | 0,00122 | 0,00257 | 0,00286 | 0,00196 |
| 526,00783 | 0,00134 | 0,00269 | 0,00304 | 0,00211 |
| 526,04501 | 0,00146 | 0,00281 | 0,00323 | 0,00227 |
| 526,08219 | 0,00159 | 0,00294 | 0,00341 | 0,00242 |
| 526,11937 | 0,00173 | 0,00306 | 0,00359 | 0,00259 |
| 526,15656 | 0,00188 | 0,0032 | 0,00377 | 0,00275 |
| 526,19374 | 0,00203 | 0,00333 | 0,00395 | 0,00292 |
| 526,23092 | 0,0022 | 0,00347 | 0,00413 | 0,00309 |
| 526,2681 | 0,00237 | 0,00362 | 0,0043 | 0,00326 |
| 526,30528 | 0,00256 | 0,00377 | 0,00447 | 0,00343 |
| 526,34247 | 0,00275 | 0,00392 | 0,00463 | 0,0036 |
| 526,37965 | 0,00294 | 0,00408 | 0,00478 | 0,00377 |
| 526,41683 | 0,00314 | 0,00424 | 0,00493 | 0,00394 |
| 526,45401 | 0,00336 | 0,00441 | 0,00508 | 0,0041 |
| 526,49119 | 0,00357 | 0,00459 | 0,00521 | 0,00427 |
| 526,52838 | 0,00379 | 0,00477 | 0,00534 | 0,00443 |
| 526,56556 | 0,00402 | 0,00495 | 0,00546 | 0,00459 |
| 526,60274 | 0,00425 | 0,00515 | 0,00558 | 0,00474 |
| 526,63992 | 0,00449 | 0,00534 | 0,00569 | 0,00489 |
| 526,6771 | 0,00473 | 0,00555 | 0,0058 | 0,00504 |
| 526,71429 | 0,00498 | 0,00576 | 0,00591 | 0,00519 |
| 526,75147 | 0,00523 | 0,00598 | 0,00601 | 0,00533 |
| 526,78865 | 0,00549 | 0,00621 | 0,00611 | 0,00548 |
| 526,82583 | 0,00575 | 0,00644 | 0,00621 | 0,00562 |
| 526,86301 | 0,00602 | 0,00669 | 0,00631 | 0,00576 |
| 526,9002 | 0,0063 | 0,00694 | 0,00642 | 0,00591 |
| 526,93738 | 0,00657 | 0,00721 | 0,00653 | 0,00605 |
| 526,97456 | 0,00686 | 0,00748 | 0,00664 | 0,00621 |
| 527,01174 | 0,00715 | 0,00776 | 0,00676 | 0,00636 |
| 527,04892 | 0,00744 | 0,00805 | 0,0069 | 0,00652 |
| 527,08611 | 0,00775 | 0,00836 | 0,00704 | 0,00669 |
| 527,12329 | 0,00806 | 0,00868 | 0,00719 | 0,00687 |
| 527,16047 | 0,00837 | 0,00901 | 0,00736 | 0,00706 |
| 527,19765 | 0,0087 | 0,00935 | 0,00755 | 0,00726 |
| 527,23483 | 0,00903 | 0,0097 | 0,00775 | 0,00748 |
| 527,27202 | 0,00937 | 0,01007 | 0,00796 | 0,00771 |
| 527,3092 | 0,00972 | 0,01045 | 0,0082 | 0,00796 |
| 527,34638 | 0,01008 | 0,01085 | 0,00846 | 0,00823 |
| 527,38356 | 0,01045 | 0,01125 | 0,00874 | 0,00853 |
| 527,42074 | 0,01082 | 0,01167 | 0,00904 | 0,00884 |
| 527,45793 | 0,01121 | 0,0121 | 0,00936 | 0,00918 |
| 527,49511 | 0,0116 | 0,01255 | 0,0097 | 0,00954 |
| 527,53229 | 0,012 | 0,01301 | 0,01007 | 0,00993 |
| 527,56947 | 0,01242 | 0,01348 | 0,01046 | 0,01035 |
| 527,60665 | 0,01284 | 0,01395 | 0,01088 | 0,0108 |
| 527,64384 | 0,01327 | 0,01444 | 0,01131 | 0,01128 |
| 527,68102 | 0,01371 | 0,01494 | 0,01177 | 0,01178 |
| 527,7182 | 0,01415 | 0,01545 | 0,01225 | 0,01231 |
| 527,75538 | 0,01461 | 0,01596 | 0,01275 | 0,01288 |
| 527,79256 | 0,01507 | 0,01649 | 0,01327 | 0,01347 |
| 527,82975 | 0,01553 | 0,01701 | 0,0138 | 0,01409 |
| 527,86693 | 0,016 | 0,01755 | 0,01435 | 0,01474 |
| 527,90411 | 0,01648 | 0,01808 | 0,01492 | 0,01541 |
| 527,94129 | 0,01696 | 0,01862 | 0,0155 | 0,0161 |
| 527,97847 | 0,01745 | 0,01917 | 0,0161 | 0,01681 |
| 528,01566 | 0,01794 | 0,01971 | 0,0167 | 0,01755 |
| 528,05284 | 0,01843 | 0,02026 | 0,01731 | 0,0183 |
| 528,09002 | 0,01892 | 0,0208 | 0,01793 | 0,01906 |
| 528,1272 | 0,01941 | 0,02135 | 0,01856 | 0,01983 |
| 528,16438 | 0,01991 | 0,0219 | 0,01919 | 0,02061 |
| 528,20157 | 0,0204 | 0,02245 | 0,01982 | 0,02139 |
| 528,23875 | 0,0209 | 0,02299 | 0,02045 | 0,02218 |
| 528,27593 | 0,02139 | 0,02354 | 0,02109 | 0,02297 |
| 528,31311 | 0,02188 | 0,02408 | 0,02172 | 0,02375 |
| 528,35029 | 0,02237 | 0,02463 | 0,02236 | 0,02452 |
| 528,38748 | 0,02286 | 0,02517 | 0,02299 | 0,02529 |
| 528,42466 | 0,02334 | 0,02572 | 0,02362 | 0,02604 |
| 528,46184 | 0,02383 | 0,02626 | 0,02424 | 0,02678 |
| 528,49902 | 0,02431 | 0,02681 | 0,02486 | 0,0275 |
| 528,5362 | 0,02479 | 0,02735 | 0,02548 | 0,02821 |
| 528,57339 | 0,02527 | 0,0279 | 0,0261 | 0,0289 |
| 528,61057 | 0,02575 | 0,02844 | 0,02672 | 0,02957 |
| 528,64775 | 0,02623 | 0,02899 | 0,02733 | 0,03021 |
| 528,68493 | 0,0267 | 0,02955 | 0,02794 | 0,03084 |
| 528,72211 | 0,02718 | 0,0301 | 0,02855 | 0,03144 |
| 528,7593 | 0,02766 | 0,03066 | 0,02916 | 0,03203 |
| 528,79648 | 0,02814 | 0,03122 | 0,02977 | 0,03259 |
| 528,83366 | 0,02863 | 0,03179 | 0,03039 | 0,03313 |
| 528,87084 | 0,02911 | 0,03237 | 0,031 | 0,03365 |
| 528,90802 | 0,02961 | 0,03295 | 0,03162 | 0,03415 |
| 528,94521 | 0,03011 | 0,03354 | 0,03224 | 0,03464 |
| 528,98239 | 0,03061 | 0,03414 | 0,03287 | 0,03511 |
| 529,01957 | 0,03113 | 0,03475 | 0,0335 | 0,03557 |
| 529,05675 | 0,03166 | 0,03537 | 0,03414 | 0,03602 |
| 529,09393 | 0,0322 | 0,03601 | 0,03478 | 0,03646 |
| 529,13112 | 0,03276 | 0,03666 | 0,03544 | 0,0369 |
| 529,1683 | 0,03334 | 0,03733 | 0,0361 | 0,03733 |
| 529,20548 | 0,03394 | 0,03801 | 0,03677 | 0,03777 |
| 529,24266 | 0,03456 | 0,03872 | 0,03745 | 0,03821 |
| 529,27984 | 0,03521 | 0,03945 | 0,03815 | 0,03866 |
| 529,31703 | 0,03588 | 0,0402 | 0,03885 | 0,03913 |
| 529,35421 | 0,03659 | 0,04098 | 0,03958 | 0,03961 |
| 529,39139 | 0,03733 | 0,04178 | 0,04031 | 0,04011 |
| 529,42857 | 0,0381 | 0,0426 | 0,04107 | 0,04064 |
| 529,46575 | 0,0389 | 0,04345 | 0,04184 | 0,0412 |
| 529,50294 | 0,03974 | 0,04434 | 0,04263 | 0,04179 |
| 529,54012 | 0,04062 | 0,04525 | 0,04344 | 0,0424 |
| 529,5773 | 0,04154 | 0,04618 | 0,04427 | 0,04305 |
| 529,61448 | 0,04248 | 0,04713 | 0,04512 | 0,04375 |
| 529,65166 | 0,04346 | 0,0481 | 0,04599 | 0,04448 |
| 529,68885 | 0,04447 | 0,0491 | 0,04688 | 0,04525 |
| 529,72603 | 0,0455 | 0,05011 | 0,04779 | 0,04605 |
| 529,76321 | 0,04655 | 0,05113 | 0,04872 | 0,04689 |
| 529,80039 | 0,04762 | 0,05216 | 0,04966 | 0,04776 |
| 529,83757 | 0,0487 | 0,05319 | 0,05062 | 0,04868 |
| 529,87476 | 0,04979 | 0,05422 | 0,0516 | 0,04961 |
| 529,91194 | 0,05087 | 0,05524 | 0,05258 | 0,05057 |
| 529,94912 | 0,05194 | 0,05625 | 0,05356 | 0,05155 |
| 529,9863 | 0,053 | 0,05724 | 0,05455 | 0,05254 |
| 530,02348 | 0,05403 | 0,0582 | 0,05554 | 0,05354 |
| 530,06067 | 0,05503 | 0,05914 | 0,05652 | 0,05454 |
| 530,09785 | 0,056 | 0,06004 | 0,05749 | 0,05554 |
| 530,13503 | 0,05693 | 0,06089 | 0,05844 | 0,05652 |
| 530,17221 | 0,0578 | 0,0617 | 0,05937 | 0,05748 |
| 530,20939 | 0,05862 | 0,06247 | 0,06028 | 0,05841 |
| 530,24658 | 0,05938 | 0,06318 | 0,06114 | 0,05931 |
| 530,28376 | 0,06008 | 0,06384 | 0,06197 | 0,06016 |
| 530,32094 | 0,06072 | 0,06443 | 0,06276 | 0,06098 |
| 530,35812 | 0,0613 | 0,06497 | 0,06351 | 0,06174 |
| 530,3953 | 0,06181 | 0,06545 | 0,06422 | 0,06245 |
| 530,43249 | 0,06226 | 0,06588 | 0,06487 | 0,0631 |
| 530,46967 | 0,06265 | 0,06626 | 0,06546 | 0,06369 |
| 530,50685 | 0,06299 | 0,06658 | 0,06601 | 0,06422 |
| 530,54403 | 0,06328 | 0,06685 | 0,06651 | 0,06469 |
| 530,58121 | 0,06353 | 0,06709 | 0,06697 | 0,06512 |
| 530,6184 | 0,06374 | 0,0673 | 0,06738 | 0,06549 |
| 530,65558 | 0,06393 | 0,06748 | 0,06775 | 0,0658 |
| 530,69276 | 0,0641 | 0,06763 | 0,06809 | 0,06608 |
| 530,72994 | 0,06427 | 0,06778 | 0,06841 | 0,06632 |
| 530,76712 | 0,06444 | 0,06792 | 0,0687 | 0,06654 |
| 530,80431 | 0,06462 | 0,06807 | 0,06899 | 0,06674 |
| 530,84149 | 0,06484 | 0,06824 | 0,06928 | 0,06693 |
| 530,87867 | 0,06509 | 0,06842 | 0,06958 | 0,06712 |
| 530,91585 | 0,06538 | 0,06865 | 0,06989 | 0,06733 |
| 530,95303 | 0,06572 | 0,06891 | 0,07023 | 0,06756 |
| 530,99022 | 0,06612 | 0,06921 | 0,07061 | 0,06781 |
| 531,0274 | 0,0666 | 0,06957 | 0,07103 | 0,0681 |
| 531,06458 | 0,06715 | 0,06998 | 0,07151 | 0,06845 |
| 531,10176 | 0,06778 | 0,07046 | 0,07204 | 0,06885 |
| 531,13894 | 0,06848 | 0,071 | 0,07264 | 0,06931 |
| 531,17613 | 0,06926 | 0,07161 | 0,0733 | 0,06982 |
| 531,21331 | 0,07013 | 0,07227 | 0,07403 | 0,07041 |
| 531,25049 | 0,07108 | 0,073 | 0,07483 | 0,07106 |
| 531,28767 | 0,0721 | 0,07379 | 0,07571 | 0,07179 |
| 531,32485 | 0,07318 | 0,07464 | 0,07664 | 0,07258 |
| 531,36204 | 0,07431 | 0,07553 | 0,07764 | 0,07342 |
| 531,39922 | 0,0755 | 0,07647 | 0,07868 | 0,07433 |
| 531,4364 | 0,07674 | 0,07743 | 0,07977 | 0,07527 |
| 531,47358 | 0,078 | 0,07842 | 0,08091 | 0,07627 |
| 531,51076 | 0,07929 | 0,07943 | 0,08207 | 0,0773 |
| 531,54795 | 0,08058 | 0,08045 | 0,08324 | 0,07835 |
| 531,58513 | 0,08186 | 0,08146 | 0,08442 | 0,0794 |
| 531,62231 | 0,08314 | 0,08245 | 0,0856 | 0,08047 |
| 531,65949 | 0,08439 | 0,08342 | 0,08676 | 0,08152 |
| 531,69667 | 0,0856 | 0,08436 | 0,08789 | 0,08255 |
| 531,73386 | 0,08677 | 0,08525 | 0,08899 | 0,08355 |
| 531,77104 | 0,08789 | 0,0861 | 0,09004 | 0,08452 |
| 531,80822 | 0,08895 | 0,08689 | 0,09104 | 0,08545 |
| 531,8454 | 0,08995 | 0,08763 | 0,09198 | 0,08633 |
| 531,88258 | 0,09087 | 0,08831 | 0,09286 | 0,08715 |
| 531,91977 | 0,09173 | 0,08892 | 0,09366 | 0,08792 |
| 531,95695 | 0,09252 | 0,08946 | 0,09441 | 0,08863 |
| 531,99413 | 0,09326 | 0,08995 | 0,09509 | 0,08929 |
| 532,03131 | 0,09393 | 0,09038 | 0,09571 | 0,0899 |
| 532,06849 | 0,09453 | 0,09077 | 0,09627 | 0,09046 |
| 532,10568 | 0,09508 | 0,0911 | 0,09677 | 0,09097 |
| 532,14286 | 0,09559 | 0,0914 | 0,09723 | 0,09145 |
| 532,18004 | 0,09607 | 0,09168 | 0,09765 | 0,09191 |
| 532,21722 | 0,09652 | 0,09193 | 0,09805 | 0,09234 |
| 532,2544 | 0,09695 | 0,09218 | 0,09843 | 0,09278 |
| 532,29159 | 0,09738 | 0,09243 | 0,09879 | 0,09321 |
| 532,32877 | 0,09781 | 0,0927 | 0,09917 | 0,09365 |
| 532,36595 | 0,09824 | 0,09299 | 0,09955 | 0,09412 |
| 532,40313 | 0,0987 | 0,09332 | 0,09995 | 0,09462 |
| 532,44031 | 0,09919 | 0,09369 | 0,10038 | 0,09515 |
| 532,4775 | 0,09971 | 0,0941 | 0,10085 | 0,09573 |
| 532,51468 | 0,10028 | 0,09458 | 0,10136 | 0,09637 |
| 532,55186 | 0,10089 | 0,09512 | 0,10192 | 0,09706 |
| 532,58904 | 0,10154 | 0,09573 | 0,10253 | 0,0978 |
| 532,62622 | 0,10224 | 0,09641 | 0,10318 | 0,0986 |
| 532,66341 | 0,10299 | 0,09714 | 0,10388 | 0,09946 |
| 532,70059 | 0,10379 | 0,09795 | 0,10464 | 0,10038 |
| 532,73777 | 0,10463 | 0,09883 | 0,10545 | 0,10136 |
| 532,77495 | 0,1055 | 0,09976 | 0,1063 | 0,10239 |
| 532,81213 | 0,1064 | 0,10074 | 0,10718 | 0,10345 |
| 532,84932 | 0,10732 | 0,10176 | 0,10809 | 0,10455 |
| 532,8865 | 0,10825 | 0,10282 | 0,10903 | 0,10568 |
| 532,92368 | 0,10918 | 0,1039 | 0,10998 | 0,10683 |
| 532,96086 | 0,11011 | 0,105 | 0,11095 | 0,10798 |
| 532,99804 | 0,11101 | 0,10609 | 0,11191 | 0,10914 |
| 533,03523 | 0,11188 | 0,10717 | 0,11287 | 0,11029 |
| 533,07241 | 0,11271 | 0,10824 | 0,11381 | 0,11143 |
| 533,10959 | 0,11348 | 0,10927 | 0,11473 | 0,11254 |
| 533,14677 | 0,11419 | 0,11024 | 0,11562 | 0,11361 |
| 533,18395 | 0,11484 | 0,11117 | 0,11647 | 0,11464 |
| 533,22114 | 0,11541 | 0,11203 | 0,11729 | 0,11564 |
| 533,25832 | 0,11591 | 0,11283 | 0,11807 | 0,11658 |
| 533,2955 | 0,11633 | 0,11356 | 0,1188 | 0,11747 |
| 533,33268 | 0,11666 | 0,1142 | 0,11948 | 0,11829 |
| 533,36986 | 0,11691 | 0,11475 | 0,12011 | 0,11905 |
| 533,40705 | 0,11709 | 0,11523 | 0,12069 | 0,11975 |
| 533,44423 | 0,1172 | 0,11563 | 0,12123 | 0,12039 |
| 533,48141 | 0,11724 | 0,11596 | 0,12172 | 0,12098 |
| 533,51859 | 0,11723 | 0,1162 | 0,12217 | 0,1215 |
| 533,55577 | 0,11717 | 0,11637 | 0,12256 | 0,12195 |
| 533,59295 | 0,11707 | 0,11649 | 0,12292 | 0,12235 |
| 533,63014 | 0,11695 | 0,11656 | 0,12324 | 0,1227 |
| 533,66732 | 0,11682 | 0,11659 | 0,12353 | 0,12299 |
| 533,7045 | 0,11669 | 0,11658 | 0,12378 | 0,12323 |
| 533,74168 | 0,11657 | 0,11654 | 0,12398 | 0,12341 |
| 533,77886 | 0,11647 | 0,11649 | 0,12416 | 0,12354 |
| 533,81605 | 0,11641 | 0,11643 | 0,1243 | 0,12363 |
| 533,85323 | 0,11639 | 0,11638 | 0,1244 | 0,12366 |
| 533,89041 | 0,11641 | 0,11633 | 0,12447 | 0,12364 |
| 533,92759 | 0,11649 | 0,1163 | 0,12449 | 0,12356 |
| 533,96477 | 0,11663 | 0,1163 | 0,12445 | 0,12342 |
| 534,00196 | 0,11683 | 0,11631 | 0,12437 | 0,12322 |
| 534,03914 | 0,11709 | 0,11636 | 0,12423 | 0,12296 |
| 534,07632 | 0,1174 | 0,11642 | 0,12404 | 0,12263 |
| 534,1135 | 0,11776 | 0,11652 | 0,12378 | 0,12223 |
| 534,15068 | 0,11817 | 0,11663 | 0,12343 | 0,12174 |
| 534,18787 | 0,11861 | 0,11676 | 0,123 | 0,12116 |
| 534,22505 | 0,11907 | 0,1169 | 0,12248 | 0,1205 |
| 534,26223 | 0,11953 | 0,11704 | 0,12188 | 0,11975 |
| 534,29941 | 0,11999 | 0,11718 | 0,12119 | 0,11892 |
| 534,33659 | 0,12043 | 0,11729 | 0,1204 | 0,11798 |
| 534,37378 | 0,12083 | 0,11738 | 0,1195 | 0,11693 |
| 534,41096 | 0,12117 | 0,11742 | 0,1185 | 0,1158 |
| 534,44814 | 0,12144 | 0,11742 | 0,11741 | 0,11457 |
| 534,48532 | 0,12163 | 0,11737 | 0,11623 | 0,11326 |
| 534,5225 | 0,12172 | 0,11724 | 0,11496 | 0,11187 |
| 534,55969 | 0,1217 | 0,11702 | 0,1136 | 0,11039 |
| 534,59687 | 0,12153 | 0,11672 | 0,11216 | 0,10884 |
| 534,63405 | 0,12124 | 0,11634 | 0,11066 | 0,10723 |
| 534,67123 | 0,12081 | 0,11586 | 0,10911 | 0,10558 |
| 534,70841 | 0,12025 | 0,11529 | 0,10752 | 0,1039 |
| 534,7456 | 0,11955 | 0,1146 | 0,1059 | 0,1022 |
| 534,78278 | 0,11869 | 0,11381 | 0,10427 | 0,10049 |
| 534,81996 | 0,11769 | 0,11294 | 0,10264 | 0,0988 |
| 534,85714 | 0,11657 | 0,11199 | 0,10104 | 0,09713 |
| 534,89432 | 0,11534 | 0,11097 | 0,09946 | 0,09551 |
| 534,93151 | 0,11401 | 0,10987 | 0,09793 | 0,09393 |
| 534,96869 | 0,11258 | 0,10871 | 0,09648 | 0,09244 |
| 535,00587 | 0,11108 | 0,10751 | 0,09511 | 0,09104 |
| 535,04305 | 0,10953 | 0,10629 | 0,09384 | 0,08974 |
| 535,08023 | 0,10795 | 0,10506 | 0,09266 | 0,08855 |
| 535,11742 | 0,10636 | 0,10383 | 0,0916 | 0,08747 |
| 535,1546 | 0,10478 | 0,10262 | 0,09066 | 0,08652 |
| 535,19178 | 0,10323 | 0,10145 | 0,08987 | 0,08573 |
| 535,22896 | 0,10173 | 0,10032 | 0,08923 | 0,08508 |
| 535,26614 | 0,1003 | 0,09926 | 0,08871 | 0,08457 |
| 535,30333 | 0,09895 | 0,09826 | 0,08834 | 0,08419 |
| 535,34051 | 0,09769 | 0,09736 | 0,0881 | 0,08396 |
| 535,37769 | 0,09653 | 0,09656 | 0,08802 | 0,08389 |
| 535,41487 | 0,09552 | 0,09586 | 0,08808 | 0,08396 |
| 535,45205 | 0,09463 | 0,09525 | 0,08826 | 0,08415 |
| 535,48924 | 0,09386 | 0,09475 | 0,08856 | 0,08446 |
| 535,52642 | 0,09322 | 0,09435 | 0,08897 | 0,08488 |
| 535,5636 | 0,09269 | 0,09407 | 0,08948 | 0,08541 |
| 535,60078 | 0,09229 | 0,09388 | 0,0901 | 0,08605 |
| 535,63796 | 0,09202 | 0,09378 | 0,09078 | 0,08677 |
| 535,67515 | 0,09185 | 0,09375 | 0,09152 | 0,08755 |
| 535,71233 | 0,09177 | 0,0938 | 0,09231 | 0,08838 |
| 535,74951 | 0,09177 | 0,09391 | 0,09314 | 0,08927 |
| 535,78669 | 0,09183 | 0,09407 | 0,09399 | 0,09019 |
| 535,82387 | 0,09195 | 0,09426 | 0,09484 | 0,09113 |
| 535,86106 | 0,0921 | 0,09447 | 0,09568 | 0,09208 |
| 535,89824 | 0,09227 | 0,09469 | 0,0965 | 0,09303 |
| 535,93542 | 0,09244 | 0,09491 | 0,0973 | 0,09398 |
| 535,9726 | 0,09261 | 0,0951 | 0,09805 | 0,09491 |
| 536,00978 | 0,09276 | 0,09526 | 0,09874 | 0,0958 |
| 536,04697 | 0,09287 | 0,09539 | 0,09938 | 0,09667 |
| 536,08415 | 0,09294 | 0,09547 | 0,09995 | 0,0975 |
| 536,12133 | 0,09296 | 0,0955 | 0,10044 | 0,09828 |
| 536,15851 | 0,09293 | 0,09546 | 0,10087 | 0,09902 |
| 536,19569 | 0,09283 | 0,09536 | 0,1012 | 0,0997 |
| 536,23288 | 0,09267 | 0,09519 | 0,10145 | 0,10032 |
| 536,27006 | 0,09245 | 0,09497 | 0,10161 | 0,10089 |
| 536,30724 | 0,09216 | 0,09469 | 0,10169 | 0,1014 |
| 536,34442 | 0,09183 | 0,09434 | 0,10169 | 0,10185 |
| 536,3816 | 0,09144 | 0,09394 | 0,10161 | 0,10225 |
| 536,41879 | 0,09102 | 0,09349 | 0,10143 | 0,10256 |
| 536,45597 | 0,09055 | 0,09301 | 0,10116 | 0,10281 |
| 536,49315 | 0,09005 | 0,09249 | 0,10083 | 0,103 |
| 536,53033 | 0,08954 | 0,09194 | 0,10042 | 0,10312 |
| 536,56751 | 0,08902 | 0,09137 | 0,09993 | 0,10317 |
| 536,6047 | 0,08849 | 0,0908 | 0,09937 | 0,10315 |
| 536,64188 | 0,08798 | 0,09022 | 0,09873 | 0,10304 |
| 536,67906 | 0,08748 | 0,08964 | 0,09802 | 0,10286 |
| 536,71624 | 0,08701 | 0,08907 | 0,09725 | 0,10261 |
| 536,75342 | 0,08656 | 0,08851 | 0,09641 | 0,10228 |
| 536,79061 | 0,08614 | 0,08798 | 0,09551 | 0,10188 |
| 536,82779 | 0,08576 | 0,08745 | 0,09454 | 0,10138 |
| 536,86497 | 0,08541 | 0,08695 | 0,09351 | 0,1008 |
| 536,90215 | 0,0851 | 0,08647 | 0,09243 | 0,10014 |
| 536,93933 | 0,08482 | 0,086 | 0,09131 | 0,09941 |
| 536,97652 | 0,08457 | 0,08556 | 0,09013 | 0,0986 |
| 537,0137 | 0,08434 | 0,08512 | 0,08891 | 0,09772 |
| 537,05088 | 0,08412 | 0,08469 | 0,08765 | 0,09676 |
| 537,08806 | 0,08392 | 0,08427 | 0,08636 | 0,09574 |
| 537,12524 | 0,08373 | 0,08384 | 0,08506 | 0,09467 |
| 537,16243 | 0,08352 | 0,08341 | 0,08374 | 0,09355 |
| 537,19961 | 0,08331 | 0,08297 | 0,08241 | 0,0924 |
| 537,23679 | 0,08308 | 0,08251 | 0,08109 | 0,09121 |
| 537,27397 | 0,08282 | 0,08203 | 0,07978 | 0,09001 |
| 537,31115 | 0,08252 | 0,08153 | 0,07851 | 0,0888 |
| 537,34834 | 0,08219 | 0,081 | 0,07726 | 0,08759 |
| 537,38552 | 0,08182 | 0,08044 | 0,07606 | 0,08641 |
| 537,4227 | 0,0814 | 0,07985 | 0,07493 | 0,08525 |
| 537,45988 | 0,08095 | 0,07923 | 0,07387 | 0,08414 |
| 537,49706 | 0,08045 | 0,07859 | 0,07288 | 0,08309 |
| 537,53425 | 0,07991 | 0,07794 | 0,07199 | 0,0821 |
| 537,57143 | 0,07935 | 0,07726 | 0,07118 | 0,08118 |
| 537,60861 | 0,07876 | 0,07657 | 0,07047 | 0,08034 |
| 537,64579 | 0,07815 | 0,07588 | 0,06989 | 0,0796 |
| 537,68297 | 0,07754 | 0,07519 | 0,06943 | 0,07897 |
| 537,72016 | 0,07693 | 0,07452 | 0,06908 | 0,07844 |
| 537,75734 | 0,07635 | 0,07387 | 0,06884 | 0,07801 |
| 537,79452 | 0,07579 | 0,07326 | 0,06872 | 0,07769 |
| 537,8317 | 0,07527 | 0,07269 | 0,06872 | 0,07748 |
| 537,86888 | 0,07481 | 0,07217 | 0,06885 | 0,0774 |
| 537,90607 | 0,07441 | 0,0717 | 0,06909 | 0,07742 |
| 537,94325 | 0,0741 | 0,0713 | 0,06942 | 0,07754 |
| 537,98043 | 0,07387 | 0,07099 | 0,06985 | 0,07776 |
| 538,01761 | 0,07373 | 0,07076 | 0,07036 | 0,07806 |
| 538,05479 | 0,07369 | 0,07061 | 0,07096 | 0,07846 |
| 538,09198 | 0,07374 | 0,07053 | 0,07162 | 0,07893 |
| 538,12916 | 0,07391 | 0,07054 | 0,07233 | 0,07946 |
| 538,16634 | 0,07418 | 0,07065 | 0,07308 | 0,08003 |
| 538,20352 | 0,07454 | 0,07083 | 0,07385 | 0,08064 |
| 538,2407 | 0,07498 | 0,07109 | 0,07464 | 0,08128 |
| 538,27789 | 0,07549 | 0,07141 | 0,07542 | 0,08192 |
| 538,31507 | 0,07607 | 0,07178 | 0,07618 | 0,08255 |
| 538,35225 | 0,0767 | 0,0722 | 0,0769 | 0,08315 |
| 538,38943 | 0,07735 | 0,07266 | 0,07759 | 0,08372 |
| 538,42661 | 0,07802 | 0,07314 | 0,07821 | 0,08424 |
| 538,4638 | 0,07868 | 0,07361 | 0,07875 | 0,08468 |
| 538,50098 | 0,07932 | 0,07408 | 0,0792 | 0,08503 |
| 538,53816 | 0,0799 | 0,07453 | 0,07956 | 0,0853 |
| 538,57534 | 0,08041 | 0,07494 | 0,07982 | 0,08545 |
| 538,61252 | 0,08083 | 0,07529 | 0,07998 | 0,08551 |
| 538,64971 | 0,08116 | 0,07557 | 0,08002 | 0,08544 |
| 538,68689 | 0,08137 | 0,07578 | 0,07993 | 0,08522 |
| 538,72407 | 0,08145 | 0,07591 | 0,07972 | 0,08487 |
| 538,76125 | 0,08137 | 0,07594 | 0,0794 | 0,08439 |
| 538,79843 | 0,08113 | 0,07585 | 0,07897 | 0,08379 |
| 538,83562 | 0,08075 | 0,07566 | 0,07844 | 0,08306 |
| 538,8728 | 0,08022 | 0,07537 | 0,07779 | 0,0822 |
| 538,90998 | 0,07954 | 0,07497 | 0,07703 | 0,08121 |
| 538,94716 | 0,0787 | 0,07447 | 0,0762 | 0,08012 |
| 538,98434 | 0,07771 | 0,07385 | 0,07529 | 0,07894 |
| 539,02153 | 0,07659 | 0,07313 | 0,07431 | 0,07767 |
| 539,05871 | 0,07536 | 0,07233 | 0,07327 | 0,07633 |
| 539,09589 | 0,07404 | 0,07145 | 0,07217 | 0,07491 |
| 539,13307 | 0,07263 | 0,0705 | 0,07104 | 0,07345 |
| 539,17025 | 0,07114 | 0,06949 | 0,06988 | 0,07195 |
| 539,20744 | 0,0696 | 0,06842 | 0,0687 | 0,07043 |
| 539,24462 | 0,06804 | 0,06731 | 0,0675 | 0,06888 |
| 539,2818 | 0,06646 | 0,06618 | 0,06629 | 0,06734 |
| 539,31898 | 0,06488 | 0,06503 | 0,06509 | 0,06579 |
| 539,35616 | 0,06331 | 0,06387 | 0,06388 | 0,06426 |
| 539,39335 | 0,06177 | 0,06271 | 0,06267 | 0,06274 |
| 539,43053 | 0,06027 | 0,06155 | 0,06146 | 0,06124 |
| 539,46771 | 0,05882 | 0,0604 | 0,06026 | 0,05975 |
| 539,50489 | 0,05741 | 0,05926 | 0,05906 | 0,0583 |
| 539,54207 | 0,05606 | 0,05814 | 0,05786 | 0,05687 |
| 539,57926 | 0,05477 | 0,05704 | 0,05666 | 0,05547 |
| 539,61644 | 0,05354 | 0,05595 | 0,05546 | 0,05408 |
| 539,65362 | 0,05236 | 0,05488 | 0,05424 | 0,05272 |
| 539,6908 | 0,05123 | 0,05382 | 0,05302 | 0,05137 |
| 539,72798 | 0,05014 | 0,05277 | 0,05178 | 0,05004 |
| 539,76517 | 0,04908 | 0,05173 | 0,05052 | 0,04872 |
| 539,80235 | 0,04806 | 0,05068 | 0,04925 | 0,04742 |
| 539,83953 | 0,04706 | 0,04963 | 0,04796 | 0,04612 |
| 539,87671 | 0,04607 | 0,04858 | 0,04666 | 0,04483 |
| 539,91389 | 0,04509 | 0,04752 | 0,04534 | 0,04355 |
| 539,95108 | 0,04411 | 0,04644 | 0,04401 | 0,04228 |
| 539,98826 | 0,04313 | 0,04534 | 0,04266 | 0,04102 |
| 540,02544 | 0,04213 | 0,04423 | 0,04131 | 0,03977 |
| 540,06262 | 0,04113 | 0,0431 | 0,03996 | 0,03853 |
| 540,0998 | 0,04011 | 0,04195 | 0,03861 | 0,0373 |
| 540,13699 | 0,03908 | 0,04079 | 0,03726 | 0,03609 |
| 540,17417 | 0,03803 | 0,03961 | 0,03593 | 0,0349 |
| 540,21135 | 0,03697 | 0,03841 | 0,03461 | 0,03373 |
| 540,24853 | 0,03591 | 0,03721 | 0,03331 | 0,03259 |
| 540,28571 | 0,03483 | 0,03601 | 0,03203 | 0,03146 |
| 540,3229 | 0,03376 | 0,0348 | 0,03078 | 0,03037 |
| 540,36008 | 0,0327 | 0,0336 | 0,02956 | 0,0293 |
| 540,39726 | 0,03164 | 0,03241 | 0,02837 | 0,02827 |
| 540,43444 | 0,0306 | 0,03123 | 0,02722 | 0,02725 |
| 540,47162 | 0,02958 | 0,03008 | 0,02609 | 0,02627 |
| 540,50881 | 0,02857 | 0,02894 | 0,025 | 0,02531 |
| 540,54599 | 0,0276 | 0,02783 | 0,02395 | 0,02438 |
| 540,58317 | 0,02665 | 0,02676 | 0,02293 | 0,02347 |
| 540,62035 | 0,02573 | 0,02572 | 0,02194 | 0,02258 |
| 540,65753 | 0,02485 | 0,02471 | 0,02097 | 0,02171 |
| 540,69472 | 0,024 | 0,02374 | 0,02003 | 0,02086 |
| 540,7319 | 0,02318 | 0,0228 | 0,01912 | 0,02002 |
| 540,76908 | 0,02239 | 0,02189 | 0,01823 | 0,0192 |
| 540,80626 | 0,02163 | 0,02103 | 0,01736 | 0,01839 |
| 540,84344 | 0,02089 | 0,0202 | 0,01651 | 0,01758 |
| 540,88063 | 0,02018 | 0,0194 | 0,01567 | 0,01678 |
| 540,91781 | 0,01949 | 0,01862 | 0,01486 | 0,01599 |
| 540,95499 | 0,01881 | 0,01787 | 0,01406 | 0,01521 |
| 540,99217 | 0,01814 | 0,01715 | 0,01327 | 0,01444 |
| 541,02935 | 0,01749 | 0,01645 | 0,0125 | 0,01368 |
| 541,06654 | 0,01684 | 0,01577 | 0,01175 | 0,01292 |
| 541,10372 | 0,0162 | 0,0151 | 0,01101 | 0,01218 |
| 541,1409 | 0,01555 | 0,01445 | 0,0103 | 0,01144 |
| 541,17808 | 0,01491 | 0,0138 | 0,0096 | 0,01073 |
| 541,21526 | 0,01427 | 0,01317 | 0,00893 | 0,01003 |
| 541,25245 | 0,01362 | 0,01255 | 0,00828 | 0,00935 |
| 541,28963 | 0,01298 | 0,01193 | 0,00765 | 0,00869 |
| 541,32681 | 0,01234 | 0,01132 | 0,00704 | 0,00805 |
| 541,36399 | 0,01169 | 0,01072 | 0,00647 | 0,00744 |
| 541,40117 | 0,01105 | 0,01013 | 0,00592 | 0,00685 |
| 541,43836 | 0,01042 | 0,00954 | 0,00541 | 0,0063 |
| 541,47554 | 0,00979 | 0,00897 | 0,00492 | 0,00577 |
| 541,51272 | 0,00917 | 0,0084 | 0,00446 | 0,00527 |
| 541,5499 | 0,00856 | 0,00785 | 0,00403 | 0,0048 |
| 541,58708 | 0,00797 | 0,00731 | 0,00364 | 0,00436 |
| 541,62427 | 0,00739 | 0,00678 | 0,00327 | 0,00396 |
| 541,66145 | 0,00683 | 0,00628 | 0,00293 | 0,00358 |
| 541,69863 | 0,0063 | 0,00579 | 0,00262 | 0,00324 |
| 541,73581 | 0,00578 | 0,00531 | 0,00234 | 0,00291 |
| 541,77299 | 0,0053 | 0,00486 | 0,00209 | 0,00263 |
| 541,81018 | 0,00483 | 0,00444 | 0,00186 | 0,00237 |
| 541,84736 | 0,00439 | 0,00403 | 0,00165 | 0,00213 |
| 541,88454 | 0,00398 | 0,00365 | 0,00146 | 0,00191 |
| 541,92172 | 0,0036 | 0,00329 | 0,00129 | 0,00172 |
| 541,9589 | 0,00325 | 0,00295 | 0,00114 | 0,00154 |
| 541,99609 | 0,00292 | 0,00264 | 0,00102 | 0,00139 |
| 542,03327 | 0,00262 | 0,00235 | 9e-04 | 0,00125 |
| 542,07045 | 0,00234 | 0,00209 | 8e-04 | 0,00113 |
| 542,10763 | 0,0021 | 0,00184 | 0,00071 | 0,00102 |
| 542,14481 | 0,00187 | 0,00162 | 0,00063 | 0,00092 |
| 542,182 | 0,00167 | 0,00142 | 0,00056 | 0,00084 |
| 542,21918 | 0,00148 | 0,00124 | 5e-04 | 0,00076 |
| 542,25636 | 0,00132 | 0,00108 | 0,00044 | 0,00069 |
| 542,29354 | 0,00117 | 0,00093 | 0,00039 | 0,00063 |
| 542,33072 | 0,00105 | 8e-04 | 0,00035 | 0,00058 |
| 542,36791 | 0,00093 | 0,00069 | 0,00032 | 0,00053 |
| 542,40509 | 0,00083 | 0,00059 | 0,00028 | 0,00048 |
| 542,44227 | 0,00074 | 5e-04 | 0,00025 | 0,00044 |
| 542,47945 | 0,00066 | 0,00042 | 0,00023 | 0,00041 |
| 542,51663 | 6e-04 | 0,00036 | 0,00021 | 0,00037 |
| 542,55382 | 0,00054 | 3e-04 | 0,00018 | 0,00034 |
| 542,591 | 0,00048 | 0,00025 | 0,00017 | 0,00031 |
| 542,62818 | 0,00044 | 0,00021 | 0,00015 | 0,00029 |
| 542,66536 | 4e-04 | 0,00017 | 0,00013 | 0,00026 |
| 542,70254 | 0,00036 | 0,00014 | 0,00012 | 0,00024 |
| 542,73973 | 0,00033 | 0,00012 | 0,00011 | 0,00022 |
| 542,77691 | 3e-04 | 9e-05 | 1e-04 | 2e-04 |
| 542,81409 | 0,00027 | 8e-05 | 8e-05 | 0,00018 |
| 542,85127 | 0,00025 | 6e-05 | 8e-05 | 0,00016 |
| 542,88845 | 0,00023 | 5e-05 | 7e-05 | 0,00015 |
| 542,92564 | 0,00021 | 4e-05 | 6e-05 | 0,00013 |
| 542,96282 | 0,00019 | 3e-05 | 5e-05 | 0,00012 |
| 543 | 0,00018 | 3e-05 | 5e-05 | 0,00011 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 0,00013 | 4e-05 | 0 | 2e-05 |
| 524,03718 | 0,00013 | 4e-05 | 0 | 3e-05 |
| 524,07436 | 0,00014 | 5e-05 | 0 | 3e-05 |
| 524,11155 | 0,00014 | 5e-05 | 0 | 3e-05 |
| 524,14873 | 0,00014 | 5e-05 | 1e-05 | 3e-05 |
| 524,18591 | 0,00015 | 5e-05 | 1e-05 | 4e-05 |
| 524,22309 | 0,00015 | 5e-05 | 1e-05 | 4e-05 |
| 524,26027 | 0,00015 | 5e-05 | 1e-05 | 4e-05 |
| 524,29746 | 0,00016 | 5e-05 | 1e-05 | 4e-05 |
| 524,33464 | 0,00016 | 5e-05 | 1e-05 | 4e-05 |
| 524,37182 | 0,00016 | 5e-05 | 1e-05 | 5e-05 |
| 524,409 | 0,00016 | 6e-05 | 2e-05 | 5e-05 |
| 524,44618 | 0,00016 | 6e-05 | 2e-05 | 5e-05 |
| 524,48337 | 0,00016 | 6e-05 | 2e-05 | 5e-05 |
| 524,52055 | 0,00016 | 6e-05 | 2e-05 | 5e-05 |
| 524,55773 | 0,00016 | 6e-05 | 3e-05 | 5e-05 |
| 524,59491 | 0,00016 | 6e-05 | 3e-05 | 5e-05 |
| 524,63209 | 0,00016 | 7e-05 | 3e-05 | 5e-05 |
| 524,66928 | 0,00016 | 7e-05 | 4e-05 | 4e-05 |
| 524,70646 | 0,00016 | 7e-05 | 4e-05 | 4e-05 |
| 524,74364 | 0,00016 | 8e-05 | 5e-05 | 4e-05 |
| 524,78082 | 0,00016 | 8e-05 | 5e-05 | 4e-05 |
| 524,818 | 0,00016 | 9e-05 | 5e-05 | 4e-05 |
| 524,85519 | 0,00016 | 9e-05 | 6e-05 | 4e-05 |
| 524,89237 | 0,00016 | 1e-04 | 6e-05 | 4e-05 |
| 524,92955 | 0,00016 | 1e-04 | 6e-05 | 3e-05 |
| 524,96673 | 0,00016 | 0,00011 | 7e-05 | 3e-05 |
| 525,00391 | 0,00016 | 0,00012 | 7e-05 | 3e-05 |
| 525,0411 | 0,00017 | 0,00012 | 8e-05 | 4e-05 |
| 525,07828 | 0,00017 | 0,00013 | 8e-05 | 4e-05 |
| 525,11546 | 0,00018 | 0,00014 | 9e-05 | 4e-05 |
| 525,15264 | 0,00019 | 0,00015 | 1e-04 | 5e-05 |
| 525,18982 | 2e-04 | 0,00016 | 1e-04 | 5e-05 |
| 525,22701 | 0,00021 | 0,00017 | 0,00011 | 6e-05 |
| 525,26419 | 0,00022 | 0,00019 | 0,00012 | 7e-05 |
| 525,30137 | 0,00024 | 2e-04 | 0,00014 | 9e-05 |
| 525,33855 | 0,00026 | 0,00022 | 0,00015 | 1e-04 |
| 525,37573 | 0,00028 | 0,00024 | 0,00017 | 0,00013 |
| 525,41292 | 0,00031 | 0,00026 | 0,00019 | 0,00015 |
| 525,4501 | 0,00034 | 0,00028 | 0,00022 | 0,00018 |
| 525,48728 | 0,00038 | 0,00031 | 0,00025 | 0,00022 |
| 525,52446 | 0,00042 | 0,00034 | 0,00029 | 0,00026 |
| 525,56164 | 0,00046 | 0,00037 | 0,00033 | 3e-04 |
| 525,59883 | 0,00051 | 0,00041 | 0,00038 | 0,00036 |
| 525,63601 | 0,00056 | 0,00045 | 0,00043 | 0,00042 |
| 525,67319 | 0,00062 | 0,00049 | 5e-04 | 0,00049 |
| 525,71037 | 0,00068 | 0,00055 | 0,00057 | 0,00056 |
| 525,74755 | 0,00075 | 6e-04 | 0,00065 | 0,00065 |
| 525,78474 | 0,00083 | 0,00066 | 0,00074 | 0,00074 |
| 525,82192 | 0,00091 | 0,00073 | 0,00084 | 0,00084 |
| 525,8591 | 0,001 | 0,00081 | 0,00094 | 0,00095 |
| 525,89628 | 0,0011 | 0,00089 | 0,00106 | 0,00107 |
| 525,93346 | 0,0012 | 0,00098 | 0,00118 | 0,00119 |
| 525,97065 | 0,00131 | 0,00107 | 0,00132 | 0,00132 |
| 526,00783 | 0,00143 | 0,00118 | 0,00145 | 0,00146 |
| 526,04501 | 0,00156 | 0,00129 | 0,0016 | 0,0016 |
| 526,08219 | 0,00169 | 0,00141 | 0,00175 | 0,00175 |
| 526,11937 | 0,00183 | 0,00153 | 0,0019 | 0,00189 |
| 526,15656 | 0,00197 | 0,00167 | 0,00206 | 0,00204 |
| 526,19374 | 0,00212 | 0,00181 | 0,00221 | 0,00219 |
| 526,23092 | 0,00228 | 0,00196 | 0,00237 | 0,00233 |
| 526,2681 | 0,00245 | 0,00211 | 0,00252 | 0,00247 |
| 526,30528 | 0,00261 | 0,00227 | 0,00267 | 0,0026 |
| 526,34247 | 0,00279 | 0,00244 | 0,00281 | 0,00272 |
| 526,37965 | 0,00297 | 0,00261 | 0,00294 | 0,00283 |
| 526,41683 | 0,00315 | 0,00278 | 0,00306 | 0,00293 |
| 526,45401 | 0,00333 | 0,00296 | 0,00318 | 0,00303 |
| 526,49119 | 0,00352 | 0,00314 | 0,00328 | 0,00311 |
| 526,52838 | 0,00371 | 0,00333 | 0,00337 | 0,00317 |
| 526,56556 | 0,0039 | 0,00351 | 0,00345 | 0,00322 |
| 526,60274 | 0,00409 | 0,0037 | 0,00352 | 0,00326 |
| 526,63992 | 0,00428 | 0,00388 | 0,00358 | 0,00329 |
| 526,6771 | 0,00448 | 0,00407 | 0,00363 | 0,00331 |
| 526,71429 | 0,00467 | 0,00425 | 0,00368 | 0,00333 |
| 526,75147 | 0,00486 | 0,00443 | 0,00372 | 0,00333 |
| 526,78865 | 0,00506 | 0,00462 | 0,00376 | 0,00333 |
| 526,82583 | 0,00525 | 0,0048 | 0,00379 | 0,00332 |
| 526,86301 | 0,00545 | 0,00499 | 0,00383 | 0,00332 |
| 526,9002 | 0,00565 | 0,00518 | 0,00388 | 0,00332 |
| 526,93738 | 0,00585 | 0,00537 | 0,00393 | 0,00332 |
| 526,97456 | 0,00606 | 0,00557 | 0,00399 | 0,00334 |
| 527,01174 | 0,00627 | 0,00578 | 0,00406 | 0,00336 |
| 527,04892 | 0,00649 | 0,006 | 0,00415 | 0,0034 |
| 527,08611 | 0,00672 | 0,00623 | 0,00425 | 0,00345 |
| 527,12329 | 0,00695 | 0,00647 | 0,00437 | 0,00352 |
| 527,16047 | 0,0072 | 0,00673 | 0,00452 | 0,00362 |
| 527,19765 | 0,00746 | 0,00701 | 0,00468 | 0,00373 |
| 527,23483 | 0,00773 | 0,00731 | 0,00487 | 0,00387 |
| 527,27202 | 0,00802 | 0,00764 | 0,00508 | 0,00404 |
| 527,3092 | 0,00832 | 0,00798 | 0,00532 | 0,00425 |
| 527,34638 | 0,00863 | 0,00835 | 0,00558 | 0,00448 |
| 527,38356 | 0,00897 | 0,00875 | 0,00587 | 0,00474 |
| 527,42074 | 0,00932 | 0,00917 | 0,0062 | 0,00504 |
| 527,45793 | 0,00969 | 0,00961 | 0,00655 | 0,00537 |
| 527,49511 | 0,01008 | 0,01008 | 0,00694 | 0,00574 |
| 527,53229 | 0,01048 | 0,01056 | 0,00735 | 0,00614 |
| 527,56947 | 0,0109 | 0,01107 | 0,00779 | 0,00658 |
| 527,60665 | 0,01133 | 0,0116 | 0,00826 | 0,00706 |
| 527,64384 | 0,01178 | 0,01213 | 0,00877 | 0,00757 |
| 527,68102 | 0,01223 | 0,01268 | 0,0093 | 0,0081 |
| 527,7182 | 0,0127 | 0,01323 | 0,00987 | 0,00867 |
| 527,75538 | 0,01317 | 0,01379 | 0,01045 | 0,00927 |
| 527,79256 | 0,01364 | 0,01435 | 0,01106 | 0,00989 |
| 527,82975 | 0,01412 | 0,01489 | 0,01169 | 0,01053 |
| 527,86693 | 0,01459 | 0,01543 | 0,01234 | 0,01118 |
| 527,90411 | 0,01506 | 0,01596 | 0,01299 | 0,01184 |
| 527,94129 | 0,01552 | 0,01647 | 0,01366 | 0,01251 |
| 527,97847 | 0,01597 | 0,01696 | 0,01433 | 0,01317 |
| 528,01566 | 0,01642 | 0,01743 | 0,01499 | 0,01384 |
| 528,05284 | 0,01684 | 0,01789 | 0,01565 | 0,01449 |
| 528,09002 | 0,01726 | 0,01831 | 0,0163 | 0,01512 |
| 528,1272 | 0,01766 | 0,01871 | 0,01693 | 0,01573 |
| 528,16438 | 0,01804 | 0,01908 | 0,01753 | 0,01632 |
| 528,20157 | 0,01841 | 0,01944 | 0,0181 | 0,01688 |
| 528,23875 | 0,01876 | 0,01977 | 0,01864 | 0,0174 |
| 528,27593 | 0,01909 | 0,02008 | 0,01914 | 0,01789 |
| 528,31311 | 0,01941 | 0,02037 | 0,01961 | 0,01834 |
| 528,35029 | 0,01972 | 0,02064 | 0,02003 | 0,01875 |
| 528,38748 | 0,02002 | 0,0209 | 0,02041 | 0,01913 |
| 528,42466 | 0,0203 | 0,02115 | 0,02074 | 0,01947 |
| 528,46184 | 0,02058 | 0,02139 | 0,02104 | 0,01979 |
| 528,49902 | 0,02084 | 0,02162 | 0,02129 | 0,02006 |
| 528,5362 | 0,02111 | 0,02184 | 0,02151 | 0,02031 |
| 528,57339 | 0,02136 | 0,02206 | 0,02169 | 0,02054 |
| 528,61057 | 0,02162 | 0,02227 | 0,02184 | 0,02074 |
| 528,64775 | 0,02187 | 0,02248 | 0,02197 | 0,02093 |
| 528,68493 | 0,02211 | 0,02269 | 0,02207 | 0,02111 |
| 528,72211 | 0,02236 | 0,0229 | 0,02216 | 0,02128 |
| 528,7593 | 0,02261 | 0,02311 | 0,02224 | 0,02145 |
| 528,79648 | 0,02286 | 0,02332 | 0,02232 | 0,02162 |
| 528,83366 | 0,02312 | 0,02353 | 0,0224 | 0,02179 |
| 528,87084 | 0,02337 | 0,02373 | 0,02247 | 0,02197 |
| 528,90802 | 0,02363 | 0,02394 | 0,02256 | 0,02215 |
| 528,94521 | 0,0239 | 0,02415 | 0,02266 | 0,02234 |
| 528,98239 | 0,02416 | 0,02435 | 0,02277 | 0,02253 |
| 529,01957 | 0,02443 | 0,02456 | 0,0229 | 0,02274 |
| 529,05675 | 0,02471 | 0,02476 | 0,02304 | 0,02296 |
| 529,09393 | 0,025 | 0,02497 | 0,0232 | 0,02318 |
| 529,13112 | 0,02529 | 0,02518 | 0,02338 | 0,02341 |
| 529,1683 | 0,02559 | 0,02539 | 0,02358 | 0,02365 |
| 529,20548 | 0,0259 | 0,02561 | 0,0238 | 0,0239 |
| 529,24266 | 0,02622 | 0,02583 | 0,02405 | 0,02416 |
| 529,27984 | 0,02654 | 0,02607 | 0,02431 | 0,02443 |
| 529,31703 | 0,02689 | 0,02632 | 0,0246 | 0,02472 |
| 529,35421 | 0,02724 | 0,02658 | 0,0249 | 0,02501 |
| 529,39139 | 0,02761 | 0,02685 | 0,02523 | 0,02532 |
| 529,42857 | 0,028 | 0,02715 | 0,02558 | 0,02564 |
| 529,46575 | 0,0284 | 0,02747 | 0,02596 | 0,02598 |
| 529,50294 | 0,02883 | 0,0278 | 0,02637 | 0,02635 |
| 529,54012 | 0,02927 | 0,02817 | 0,0268 | 0,02674 |
| 529,5773 | 0,02973 | 0,02856 | 0,02726 | 0,02716 |
| 529,61448 | 0,03022 | 0,02898 | 0,02774 | 0,0276 |
| 529,65166 | 0,03073 | 0,02943 | 0,02825 | 0,02808 |
| 529,68885 | 0,03126 | 0,0299 | 0,02878 | 0,0286 |
| 529,72603 | 0,03182 | 0,0304 | 0,02935 | 0,02915 |
| 529,76321 | 0,03239 | 0,03093 | 0,02995 | 0,02974 |
| 529,80039 | 0,03299 | 0,03149 | 0,03057 | 0,03037 |
| 529,83757 | 0,03362 | 0,03208 | 0,03121 | 0,03104 |
| 529,87476 | 0,03426 | 0,03268 | 0,03188 | 0,03174 |
| 529,91194 | 0,03491 | 0,03331 | 0,03256 | 0,03248 |
| 529,94912 | 0,03558 | 0,03395 | 0,03327 | 0,03325 |
| 529,9863 | 0,03626 | 0,0346 | 0,034 | 0,03404 |
| 530,02348 | 0,03695 | 0,03526 | 0,03474 | 0,03486 |
| 530,06067 | 0,03764 | 0,03593 | 0,03549 | 0,0357 |
| 530,09785 | 0,03832 | 0,0366 | 0,03625 | 0,03655 |
| 530,13503 | 0,039 | 0,03726 | 0,03701 | 0,0374 |
| 530,17221 | 0,03966 | 0,03792 | 0,03776 | 0,03824 |
| 530,20939 | 0,04029 | 0,03856 | 0,03851 | 0,03908 |
| 530,24658 | 0,04091 | 0,03918 | 0,03924 | 0,03989 |
| 530,28376 | 0,04149 | 0,03978 | 0,03996 | 0,04067 |
| 530,32094 | 0,04204 | 0,04035 | 0,04065 | 0,04141 |
| 530,35812 | 0,04253 | 0,04088 | 0,04131 | 0,04211 |
| 530,3953 | 0,04299 | 0,04138 | 0,04194 | 0,04275 |
| 530,43249 | 0,0434 | 0,04185 | 0,04253 | 0,04333 |
| 530,46967 | 0,04376 | 0,04227 | 0,04307 | 0,04386 |
| 530,50685 | 0,04407 | 0,04266 | 0,04357 | 0,04431 |
| 530,54403 | 0,04433 | 0,043 | 0,04402 | 0,04468 |
| 530,58121 | 0,04454 | 0,04329 | 0,04441 | 0,045 |
| 530,6184 | 0,0447 | 0,04355 | 0,04476 | 0,04524 |
| 530,65558 | 0,04483 | 0,04377 | 0,04507 | 0,04543 |
| 530,69276 | 0,04493 | 0,04396 | 0,04533 | 0,04556 |
| 530,72994 | 0,045 | 0,04412 | 0,04554 | 0,04565 |
| 530,76712 | 0,04506 | 0,04427 | 0,04573 | 0,0457 |
| 530,80431 | 0,04512 | 0,0444 | 0,04589 | 0,04572 |
| 530,84149 | 0,04518 | 0,04454 | 0,04603 | 0,04574 |
| 530,87867 | 0,04526 | 0,04468 | 0,04617 | 0,04575 |
| 530,91585 | 0,04536 | 0,04484 | 0,04632 | 0,04579 |
| 530,95303 | 0,04551 | 0,04503 | 0,04648 | 0,04585 |
| 530,99022 | 0,04571 | 0,04526 | 0,04667 | 0,04596 |
| 531,0274 | 0,04597 | 0,04553 | 0,0469 | 0,04613 |
| 531,06458 | 0,0463 | 0,04588 | 0,04718 | 0,04638 |
| 531,10176 | 0,04672 | 0,04629 | 0,04752 | 0,0467 |
| 531,13894 | 0,04722 | 0,04678 | 0,04793 | 0,04711 |
| 531,17613 | 0,0478 | 0,04735 | 0,04841 | 0,04761 |
| 531,21331 | 0,04847 | 0,048 | 0,04898 | 0,0482 |
| 531,25049 | 0,04923 | 0,04873 | 0,04963 | 0,0489 |
| 531,28767 | 0,05008 | 0,04956 | 0,05037 | 0,0497 |
| 531,32485 | 0,05102 | 0,05047 | 0,05119 | 0,05059 |
| 531,36204 | 0,05203 | 0,05146 | 0,05209 | 0,05156 |
| 531,39922 | 0,0531 | 0,05251 | 0,05305 | 0,05261 |
| 531,4364 | 0,05422 | 0,05362 | 0,05408 | 0,05371 |
| 531,47358 | 0,05538 | 0,05478 | 0,05517 | 0,05486 |
| 531,51076 | 0,05657 | 0,05597 | 0,05631 | 0,05605 |
| 531,54795 | 0,05777 | 0,05719 | 0,05746 | 0,05725 |
| 531,58513 | 0,05896 | 0,0584 | 0,05863 | 0,05845 |
| 531,62231 | 0,06012 | 0,05959 | 0,0598 | 0,05963 |
| 531,65949 | 0,06125 | 0,06075 | 0,06094 | 0,06077 |
| 531,69667 | 0,06233 | 0,06187 | 0,06206 | 0,06186 |
| 531,73386 | 0,06335 | 0,06293 | 0,06312 | 0,06289 |
| 531,77104 | 0,0643 | 0,06391 | 0,06411 | 0,06383 |
| 531,80822 | 0,06516 | 0,0648 | 0,06502 | 0,06467 |
| 531,8454 | 0,06593 | 0,06559 | 0,06585 | 0,06541 |
| 531,88258 | 0,06661 | 0,06628 | 0,06659 | 0,06605 |
| 531,91977 | 0,0672 | 0,06687 | 0,06723 | 0,06659 |
| 531,95695 | 0,0677 | 0,06735 | 0,06777 | 0,06702 |
| 531,99413 | 0,06811 | 0,06773 | 0,0682 | 0,06735 |
| 532,03131 | 0,06844 | 0,06801 | 0,06854 | 0,06758 |
| 532,06849 | 0,0687 | 0,06818 | 0,06879 | 0,06772 |
| 532,10568 | 0,06889 | 0,06827 | 0,06897 | 0,0678 |
| 532,14286 | 0,06905 | 0,0683 | 0,0691 | 0,06782 |
| 532,18004 | 0,06916 | 0,06827 | 0,06917 | 0,06781 |
| 532,21722 | 0,06926 | 0,06821 | 0,06921 | 0,06778 |
| 532,2544 | 0,06936 | 0,06811 | 0,06924 | 0,06774 |
| 532,29159 | 0,06946 | 0,06802 | 0,06927 | 0,06772 |
| 532,32877 | 0,0696 | 0,06793 | 0,06933 | 0,06775 |
| 532,36595 | 0,06978 | 0,06789 | 0,06944 | 0,06782 |
| 532,40313 | 0,07002 | 0,06789 | 0,0696 | 0,06796 |
| 532,44031 | 0,07032 | 0,06795 | 0,06982 | 0,06818 |
| 532,4775 | 0,0707 | 0,06809 | 0,07013 | 0,06848 |
| 532,51468 | 0,07116 | 0,06832 | 0,07055 | 0,06889 |
| 532,55186 | 0,07174 | 0,06867 | 0,07107 | 0,06942 |
| 532,58904 | 0,07241 | 0,06914 | 0,07168 | 0,07004 |
| 532,62622 | 0,07319 | 0,06971 | 0,07239 | 0,07077 |
| 532,66341 | 0,07406 | 0,0704 | 0,07321 | 0,0716 |
| 532,70059 | 0,07504 | 0,0712 | 0,07411 | 0,07252 |
| 532,73777 | 0,0761 | 0,07211 | 0,0751 | 0,07353 |
| 532,77495 | 0,07725 | 0,07314 | 0,07618 | 0,07462 |
| 532,81213 | 0,07849 | 0,07426 | 0,07732 | 0,07578 |
| 532,84932 | 0,07978 | 0,07545 | 0,0785 | 0,07698 |
| 532,8865 | 0,08111 | 0,07671 | 0,07972 | 0,07821 |
| 532,92368 | 0,08248 | 0,078 | 0,08095 | 0,07947 |
| 532,96086 | 0,08385 | 0,07932 | 0,0822 | 0,08072 |
| 532,99804 | 0,08522 | 0,08064 | 0,08343 | 0,08197 |
| 533,03523 | 0,08656 | 0,08194 | 0,08464 | 0,08319 |
| 533,07241 | 0,08786 | 0,0832 | 0,0858 | 0,08436 |
| 533,10959 | 0,08909 | 0,08439 | 0,08692 | 0,08548 |
| 533,14677 | 0,09025 | 0,08551 | 0,08799 | 0,08654 |
| 533,18395 | 0,09132 | 0,08654 | 0,08899 | 0,08753 |
| 533,22114 | 0,0923 | 0,08746 | 0,08992 | 0,08845 |
| 533,25832 | 0,09316 | 0,08826 | 0,09077 | 0,08928 |
| 533,2955 | 0,09388 | 0,08893 | 0,09154 | 0,09002 |
| 533,33268 | 0,09449 | 0,08946 | 0,09224 | 0,09067 |
| 533,36986 | 0,09497 | 0,08987 | 0,09288 | 0,09125 |
| 533,40705 | 0,09535 | 0,09017 | 0,09345 | 0,09175 |
| 533,44423 | 0,09561 | 0,09035 | 0,09397 | 0,09218 |
| 533,48141 | 0,09576 | 0,09042 | 0,09444 | 0,09255 |
| 533,51859 | 0,09582 | 0,0904 | 0,09487 | 0,09287 |
| 533,55577 | 0,09579 | 0,09029 | 0,09528 | 0,09315 |
| 533,59295 | 0,09569 | 0,09013 | 0,09567 | 0,09341 |
| 533,63014 | 0,09555 | 0,08993 | 0,09606 | 0,09366 |
| 533,66732 | 0,09537 | 0,0897 | 0,09646 | 0,0939 |
| 533,7045 | 0,09518 | 0,08947 | 0,09688 | 0,09416 |
| 533,74168 | 0,09499 | 0,08926 | 0,09731 | 0,09444 |
| 533,77886 | 0,09482 | 0,08908 | 0,09778 | 0,09476 |
| 533,81605 | 0,09468 | 0,08896 | 0,09829 | 0,09512 |
| 533,85323 | 0,0946 | 0,0889 | 0,09883 | 0,09551 |
| 533,89041 | 0,09457 | 0,08892 | 0,09941 | 0,09596 |
| 533,92759 | 0,09462 | 0,08903 | 0,10001 | 0,09645 |
| 533,96477 | 0,09475 | 0,08922 | 0,10063 | 0,09697 |
| 534,00196 | 0,09497 | 0,08953 | 0,10127 | 0,09753 |
| 534,03914 | 0,0953 | 0,08995 | 0,10191 | 0,09811 |
| 534,07632 | 0,09571 | 0,09048 | 0,10253 | 0,0987 |
| 534,1135 | 0,09622 | 0,0911 | 0,10312 | 0,09927 |
| 534,15068 | 0,09681 | 0,09181 | 0,10366 | 0,09982 |
| 534,18787 | 0,09748 | 0,0926 | 0,10413 | 0,10032 |
| 534,22505 | 0,09821 | 0,09346 | 0,10451 | 0,10076 |
| 534,26223 | 0,099 | 0,09438 | 0,1048 | 0,10111 |
| 534,29941 | 0,09982 | 0,09532 | 0,10494 | 0,10134 |
| 534,33659 | 0,10065 | 0,09628 | 0,10493 | 0,10144 |
| 534,37378 | 0,10147 | 0,09722 | 0,10477 | 0,1014 |
| 534,41096 | 0,10226 | 0,09813 | 0,10445 | 0,10119 |
| 534,44814 | 0,10299 | 0,09897 | 0,10395 | 0,10083 |
| 534,48532 | 0,10365 | 0,09973 | 0,10328 | 0,10028 |
| 534,5225 | 0,10418 | 0,10036 | 0,10242 | 0,09954 |
| 534,55969 | 0,10457 | 0,10085 | 0,10136 | 0,0986 |
| 534,59687 | 0,10482 | 0,10118 | 0,10012 | 0,09748 |
| 534,63405 | 0,1049 | 0,10134 | 0,09873 | 0,0962 |
| 534,67123 | 0,1048 | 0,10132 | 0,09719 | 0,09477 |
| 534,70841 | 0,10451 | 0,1011 | 0,09553 | 0,09321 |
| 534,7456 | 0,104 | 0,10067 | 0,09377 | 0,09152 |
| 534,78278 | 0,10327 | 0,1 | 0,09192 | 0,08973 |
| 534,81996 | 0,10235 | 0,09914 | 0,09001 | 0,08787 |
| 534,85714 | 0,10124 | 0,0981 | 0,08808 | 0,08598 |
| 534,89432 | 0,09996 | 0,09689 | 0,08617 | 0,08409 |
| 534,93151 | 0,09852 | 0,09552 | 0,08428 | 0,08223 |
| 534,96869 | 0,09695 | 0,09402 | 0,08247 | 0,08041 |
| 535,00587 | 0,09527 | 0,09241 | 0,08074 | 0,07867 |
| 535,04305 | 0,09351 | 0,09073 | 0,07913 | 0,07707 |
| 535,08023 | 0,09172 | 0,08903 | 0,07769 | 0,07561 |
| 535,11742 | 0,08994 | 0,08732 | 0,07642 | 0,07432 |
| 535,1546 | 0,08818 | 0,08565 | 0,07534 | 0,07321 |
| 535,19178 | 0,08649 | 0,08404 | 0,07446 | 0,0723 |
| 535,22896 | 0,0849 | 0,08254 | 0,07378 | 0,07159 |
| 535,26614 | 0,08347 | 0,08119 | 0,07333 | 0,07113 |
| 535,30333 | 0,0822 | 0,08 | 0,07313 | 0,07093 |
| 535,34051 | 0,08113 | 0,07901 | 0,07318 | 0,07096 |
| 535,37769 | 0,08026 | 0,07822 | 0,07346 | 0,07122 |
| 535,41487 | 0,07963 | 0,07765 | 0,07397 | 0,07171 |
| 535,45205 | 0,07922 | 0,0773 | 0,07468 | 0,07241 |
| 535,48924 | 0,07908 | 0,0772 | 0,0756 | 0,07332 |
| 535,52642 | 0,07922 | 0,07737 | 0,07671 | 0,07443 |
| 535,5636 | 0,07958 | 0,07776 | 0,07801 | 0,07574 |
| 535,60078 | 0,08018 | 0,07836 | 0,07947 | 0,07718 |
| 535,63796 | 0,08098 | 0,07916 | 0,08106 | 0,07876 |
| 535,67515 | 0,08197 | 0,08013 | 0,08276 | 0,08043 |
| 535,71233 | 0,08313 | 0,08126 | 0,08454 | 0,08219 |
| 535,74951 | 0,08446 | 0,08253 | 0,08638 | 0,084 |
| 535,78669 | 0,08589 | 0,0839 | 0,08827 | 0,08585 |
| 535,82387 | 0,08739 | 0,08533 | 0,09016 | 0,08769 |
| 535,86106 | 0,08894 | 0,08678 | 0,09203 | 0,08951 |
| 535,89824 | 0,09049 | 0,08823 | 0,09386 | 0,0913 |
| 535,93542 | 0,09202 | 0,08965 | 0,09563 | 0,09302 |
| 535,9726 | 0,09349 | 0,09101 | 0,09731 | 0,09466 |
| 536,00978 | 0,09485 | 0,09226 | 0,0989 | 0,09622 |
| 536,04697 | 0,0961 | 0,09339 | 0,10037 | 0,09765 |
| 536,08415 | 0,09721 | 0,09438 | 0,1017 | 0,09898 |
| 536,12133 | 0,09815 | 0,09521 | 0,10289 | 0,10019 |
| 536,15851 | 0,09893 | 0,09587 | 0,10393 | 0,10128 |
| 536,19569 | 0,09952 | 0,09637 | 0,10484 | 0,10226 |
| 536,23288 | 0,0999 | 0,09667 | 0,1056 | 0,10313 |
| 536,27006 | 0,10007 | 0,09677 | 0,10623 | 0,1039 |
| 536,30724 | 0,10006 | 0,09671 | 0,10673 | 0,10455 |
| 536,34442 | 0,09987 | 0,09649 | 0,10709 | 0,10513 |
| 536,3816 | 0,09952 | 0,09612 | 0,10734 | 0,10562 |
| 536,41879 | 0,09902 | 0,09563 | 0,10749 | 0,10605 |
| 536,45597 | 0,0984 | 0,09504 | 0,10756 | 0,10642 |
| 536,49315 | 0,09765 | 0,09435 | 0,10755 | 0,10673 |
| 536,53033 | 0,09683 | 0,0936 | 0,10747 | 0,10699 |
| 536,56751 | 0,09597 | 0,09283 | 0,10733 | 0,1072 |
| 536,6047 | 0,09508 | 0,09204 | 0,10713 | 0,10735 |
| 536,64188 | 0,09419 | 0,09128 | 0,10687 | 0,10745 |
| 536,67906 | 0,09332 | 0,09054 | 0,10655 | 0,10748 |
| 536,71624 | 0,0925 | 0,08987 | 0,10617 | 0,10745 |
| 536,75342 | 0,09176 | 0,08928 | 0,10573 | 0,10733 |
| 536,79061 | 0,09111 | 0,08878 | 0,10521 | 0,1071 |
| 536,82779 | 0,09056 | 0,08838 | 0,1046 | 0,10675 |
| 536,86497 | 0,09011 | 0,08808 | 0,10388 | 0,10628 |
| 536,90215 | 0,08977 | 0,08788 | 0,10305 | 0,10568 |
| 536,93933 | 0,08953 | 0,08779 | 0,10211 | 0,10494 |
| 536,97652 | 0,08943 | 0,0878 | 0,10104 | 0,10405 |
| 537,0137 | 0,08942 | 0,0879 | 0,09985 | 0,10302 |
| 537,05088 | 0,08949 | 0,08808 | 0,09854 | 0,10181 |
| 537,08806 | 0,08964 | 0,08831 | 0,0971 | 0,10047 |
| 537,12524 | 0,08984 | 0,08858 | 0,09553 | 0,099 |
| 537,16243 | 0,09007 | 0,08888 | 0,09387 | 0,09743 |
| 537,19961 | 0,09033 | 0,08917 | 0,09214 | 0,09578 |
| 537,23679 | 0,09057 | 0,08945 | 0,09035 | 0,09406 |
| 537,27397 | 0,09078 | 0,08967 | 0,08853 | 0,0923 |
| 537,31115 | 0,09095 | 0,08984 | 0,0867 | 0,09054 |
| 537,34834 | 0,09105 | 0,08994 | 0,0849 | 0,08881 |
| 537,38552 | 0,09108 | 0,08995 | 0,08316 | 0,08714 |
| 537,4227 | 0,09102 | 0,08986 | 0,08152 | 0,08557 |
| 537,45988 | 0,09084 | 0,08968 | 0,08 | 0,0841 |
| 537,49706 | 0,09056 | 0,08937 | 0,07862 | 0,08278 |
| 537,53425 | 0,09018 | 0,08895 | 0,07741 | 0,08165 |
| 537,57143 | 0,0897 | 0,08845 | 0,0764 | 0,08072 |
| 537,60861 | 0,08914 | 0,08786 | 0,07562 | 0,08001 |
| 537,64579 | 0,0885 | 0,08721 | 0,07509 | 0,07951 |
| 537,68297 | 0,08781 | 0,08651 | 0,07481 | 0,07925 |
| 537,72016 | 0,08708 | 0,08578 | 0,07478 | 0,07922 |
| 537,75734 | 0,08634 | 0,08505 | 0,07502 | 0,07944 |
| 537,79452 | 0,08563 | 0,08436 | 0,07551 | 0,07995 |
| 537,8317 | 0,08497 | 0,08373 | 0,07627 | 0,08071 |
| 537,86888 | 0,0844 | 0,0832 | 0,07733 | 0,08171 |
| 537,90607 | 0,08393 | 0,08279 | 0,07866 | 0,08296 |
| 537,94325 | 0,08361 | 0,08253 | 0,08024 | 0,08443 |
| 537,98043 | 0,0835 | 0,08248 | 0,08206 | 0,08614 |
| 538,01761 | 0,08359 | 0,08266 | 0,08411 | 0,08807 |
| 538,05479 | 0,08391 | 0,08308 | 0,08637 | 0,09025 |
| 538,09198 | 0,08447 | 0,08377 | 0,08885 | 0,09262 |
| 538,12916 | 0,0853 | 0,08472 | 0,09154 | 0,09517 |
| 538,16634 | 0,0864 | 0,08596 | 0,09439 | 0,09788 |
| 538,20352 | 0,08781 | 0,08748 | 0,09738 | 0,10074 |
| 538,2407 | 0,08951 | 0,08934 | 0,10047 | 0,1037 |
| 538,27789 | 0,09146 | 0,09147 | 0,10364 | 0,10676 |
| 538,31507 | 0,09364 | 0,09384 | 0,10685 | 0,10988 |
| 538,35225 | 0,09604 | 0,09644 | 0,11007 | 0,113 |
| 538,38943 | 0,09861 | 0,09922 | 0,11324 | 0,11608 |
| 538,42661 | 0,10132 | 0,10216 | 0,11631 | 0,11909 |
| 538,4638 | 0,10413 | 0,10521 | 0,11923 | 0,12197 |
| 538,50098 | 0,10695 | 0,1083 | 0,12196 | 0,12469 |
| 538,53816 | 0,10974 | 0,11138 | 0,12445 | 0,12718 |
| 538,57534 | 0,11244 | 0,11437 | 0,12667 | 0,12937 |
| 538,61252 | 0,11499 | 0,11722 | 0,12857 | 0,13125 |
| 538,64971 | 0,11735 | 0,11989 | 0,13003 | 0,13279 |
| 538,68689 | 0,11942 | 0,1223 | 0,1311 | 0,13397 |
| 538,72407 | 0,12113 | 0,12437 | 0,13176 | 0,13476 |
| 538,76125 | 0,12247 | 0,12605 | 0,13201 | 0,13516 |
| 538,79843 | 0,12343 | 0,12733 | 0,13185 | 0,13511 |
| 538,83562 | 0,12396 | 0,12819 | 0,13129 | 0,13466 |
| 538,8728 | 0,12406 | 0,12861 | 0,13033 | 0,13387 |
| 538,90998 | 0,12373 | 0,12858 | 0,12899 | 0,13275 |
| 538,94716 | 0,12289 | 0,12811 | 0,12737 | 0,13137 |
| 538,98434 | 0,12164 | 0,12712 | 0,12553 | 0,12975 |
| 539,02153 | 0,12001 | 0,12574 | 0,12352 | 0,12796 |
| 539,05871 | 0,11805 | 0,12402 | 0,12139 | 0,12603 |
| 539,09589 | 0,11581 | 0,12199 | 0,11922 | 0,12406 |
| 539,13307 | 0,11333 | 0,11972 | 0,11707 | 0,1221 |
| 539,17025 | 0,11068 | 0,11725 | 0,11501 | 0,1202 |
| 539,20744 | 0,10791 | 0,11465 | 0,11309 | 0,1184 |
| 539,24462 | 0,10511 | 0,112 | 0,11134 | 0,11673 |
| 539,2818 | 0,10235 | 0,10938 | 0,10979 | 0,11523 |
| 539,31898 | 0,09969 | 0,10685 | 0,10846 | 0,11393 |
| 539,35616 | 0,09716 | 0,10446 | 0,10734 | 0,1128 |
| 539,39335 | 0,09481 | 0,10225 | 0,10645 | 0,11184 |
| 539,43053 | 0,09271 | 0,10026 | 0,10576 | 0,11103 |
| 539,46771 | 0,0909 | 0,09857 | 0,10523 | 0,11033 |
| 539,50489 | 0,08935 | 0,09717 | 0,10479 | 0,10971 |
| 539,54207 | 0,08807 | 0,09605 | 0,10443 | 0,10914 |
| 539,57926 | 0,08705 | 0,0952 | 0,10408 | 0,10855 |
| 539,61644 | 0,08628 | 0,09461 | 0,10369 | 0,1079 |
| 539,65362 | 0,08574 | 0,09424 | 0,10321 | 0,10715 |
| 539,6908 | 0,08542 | 0,09406 | 0,10258 | 0,10626 |
| 539,72798 | 0,08524 | 0,09405 | 0,10178 | 0,10521 |
| 539,76517 | 0,08516 | 0,09413 | 0,10078 | 0,10397 |
| 539,80235 | 0,08512 | 0,09424 | 0,09956 | 0,10249 |
| 539,83953 | 0,08509 | 0,09433 | 0,09813 | 0,1008 |
| 539,87671 | 0,08502 | 0,09436 | 0,09647 | 0,09891 |
| 539,91389 | 0,08487 | 0,09427 | 0,09459 | 0,09684 |
| 539,95108 | 0,08457 | 0,09402 | 0,09253 | 0,09461 |
| 539,98826 | 0,08411 | 0,09355 | 0,09034 | 0,09226 |
| 540,02544 | 0,08346 | 0,09285 | 0,08807 | 0,08982 |
| 540,06262 | 0,08262 | 0,09191 | 0,08574 | 0,08734 |
| 540,0998 | 0,08158 | 0,09074 | 0,08341 | 0,08487 |
| 540,13699 | 0,08034 | 0,08932 | 0,08112 | 0,08245 |
| 540,17417 | 0,07888 | 0,08767 | 0,07895 | 0,08012 |
| 540,21135 | 0,07723 | 0,08578 | 0,07691 | 0,07792 |
| 540,24853 | 0,07545 | 0,08372 | 0,07503 | 0,07586 |
| 540,28571 | 0,07355 | 0,08152 | 0,07333 | 0,07398 |
| 540,3229 | 0,07158 | 0,07923 | 0,07182 | 0,07231 |
| 540,36008 | 0,06956 | 0,07689 | 0,0705 | 0,07081 |
| 540,39726 | 0,06752 | 0,07454 | 0,06936 | 0,06949 |
| 540,43444 | 0,06553 | 0,07222 | 0,06841 | 0,06831 |
| 540,47162 | 0,06362 | 0,07 | 0,06759 | 0,06727 |
| 540,50881 | 0,06181 | 0,06791 | 0,06686 | 0,06632 |
| 540,54599 | 0,06013 | 0,06598 | 0,06617 | 0,06544 |
| 540,58317 | 0,05859 | 0,06422 | 0,06549 | 0,06457 |
| 540,62035 | 0,05721 | 0,06266 | 0,06478 | 0,06367 |
| 540,65753 | 0,05601 | 0,0613 | 0,06399 | 0,06271 |
| 540,69472 | 0,055 | 0,06015 | 0,06305 | 0,06165 |
| 540,7319 | 0,05414 | 0,05923 | 0,06196 | 0,06046 |
| 540,76908 | 0,05343 | 0,05848 | 0,06067 | 0,05912 |
| 540,80626 | 0,05283 | 0,05788 | 0,05919 | 0,05758 |
| 540,84344 | 0,05234 | 0,05741 | 0,05749 | 0,05584 |
| 540,88063 | 0,05191 | 0,05703 | 0,05558 | 0,05392 |
| 540,91781 | 0,05153 | 0,05671 | 0,05345 | 0,05183 |
| 540,95499 | 0,05114 | 0,05641 | 0,05109 | 0,04956 |
| 540,99217 | 0,05072 | 0,05608 | 0,04857 | 0,04714 |
| 541,02935 | 0,05023 | 0,05569 | 0,04592 | 0,04459 |
| 541,06654 | 0,04966 | 0,0552 | 0,04315 | 0,04193 |
| 541,10372 | 0,04898 | 0,05458 | 0,0403 | 0,03921 |
| 541,1409 | 0,04815 | 0,05382 | 0,03742 | 0,03646 |
| 541,17808 | 0,04715 | 0,05288 | 0,03452 | 0,03371 |
| 541,21526 | 0,04599 | 0,05172 | 0,03167 | 0,03099 |
| 541,25245 | 0,04467 | 0,05037 | 0,02888 | 0,02833 |
| 541,28963 | 0,04319 | 0,04883 | 0,02619 | 0,02576 |
| 541,32681 | 0,04155 | 0,04711 | 0,02362 | 0,02332 |
| 541,36399 | 0,03977 | 0,04521 | 0,02119 | 0,021 |
| 541,40117 | 0,03785 | 0,04315 | 0,0189 | 0,01884 |
| 541,43836 | 0,03582 | 0,04095 | 0,01679 | 0,01682 |
| 541,47554 | 0,03372 | 0,03863 | 0,01487 | 0,01497 |
| 541,51272 | 0,03155 | 0,03624 | 0,01312 | 0,01327 |
| 541,5499 | 0,02936 | 0,03379 | 0,01153 | 0,01176 |
| 541,58708 | 0,02715 | 0,03133 | 0,01011 | 0,01041 |
| 541,62427 | 0,02496 | 0,02887 | 0,00885 | 0,00922 |
| 541,66145 | 0,02282 | 0,02643 | 0,00774 | 0,00817 |
| 541,69863 | 0,02075 | 0,02407 | 0,00678 | 0,00725 |
| 541,73581 | 0,01876 | 0,0218 | 0,00596 | 0,00645 |
| 541,77299 | 0,01687 | 0,01963 | 0,00524 | 0,00577 |
| 541,81018 | 0,01508 | 0,01758 | 0,00463 | 0,0052 |
| 541,84736 | 0,01342 | 0,01565 | 0,00412 | 0,00473 |
| 541,88454 | 0,01188 | 0,01387 | 0,00368 | 0,00433 |
| 541,92172 | 0,0105 | 0,01222 | 0,00331 | 0,004 |
| 541,9589 | 0,00924 | 0,01075 | 0,00301 | 0,00373 |
| 541,99609 | 0,00811 | 0,00943 | 0,00276 | 0,0035 |
| 542,03327 | 0,0071 | 0,00824 | 0,00256 | 0,00332 |
| 542,07045 | 0,00621 | 0,00718 | 0,00239 | 0,00318 |
| 542,10763 | 0,00544 | 0,00626 | 0,00224 | 0,00306 |
| 542,14481 | 0,00478 | 0,00545 | 0,00212 | 0,00296 |
| 542,182 | 0,00422 | 0,00476 | 0,00202 | 0,00287 |
| 542,21918 | 0,00374 | 0,00417 | 0,00193 | 0,00279 |
| 542,25636 | 0,00335 | 0,00368 | 0,00185 | 0,00272 |
| 542,29354 | 0,00301 | 0,00326 | 0,00177 | 0,00265 |
| 542,33072 | 0,00274 | 0,00291 | 0,0017 | 0,00257 |
| 542,36791 | 0,00251 | 0,00261 | 0,00162 | 0,00249 |
| 542,40509 | 0,00234 | 0,00237 | 0,00155 | 0,00241 |
| 542,44227 | 0,0022 | 0,00217 | 0,00148 | 0,00232 |
| 542,47945 | 0,00208 | 0,00201 | 0,0014 | 0,00222 |
| 542,51663 | 0,00199 | 0,00187 | 0,00133 | 0,00212 |
| 542,55382 | 0,00191 | 0,00175 | 0,00125 | 0,00201 |
| 542,591 | 0,00184 | 0,00165 | 0,00117 | 0,0019 |
| 542,62818 | 0,00178 | 0,00157 | 0,00108 | 0,00178 |
| 542,66536 | 0,00172 | 0,00149 | 0,001 | 0,00166 |
| 542,70254 | 0,00166 | 0,00142 | 0,00092 | 0,00154 |
| 542,73973 | 0,0016 | 0,00135 | 0,00084 | 0,00141 |
| 542,77691 | 0,00155 | 0,00128 | 0,00077 | 0,00129 |
| 542,81409 | 0,00148 | 0,00121 | 0,00069 | 0,00118 |
| 542,85127 | 0,00142 | 0,00115 | 0,00062 | 0,00106 |
| 542,88845 | 0,00135 | 0,00108 | 0,00055 | 0,00096 |
| 542,92564 | 0,00128 | 0,00102 | 0,00049 | 0,00085 |
| 542,96282 | 0,0012 | 0,00095 | 0,00043 | 0,00076 |
| 543 | 0,00113 | 0,00089 | 0,00038 | 0,00067 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 5e-05 | 5e-05 | 1e-05 | 0 |
| 524,03718 | 5e-05 | 6e-05 | 1e-05 | 0 |
| 524,07436 | 5e-05 | 7e-05 | 1e-05 | 0 |
| 524,11155 | 5e-05 | 8e-05 | 1e-05 | 0 |
| 524,14873 | 5e-05 | 9e-05 | 2e-05 | 0 |
| 524,18591 | 5e-05 | 1e-04 | 2e-05 | 0 |
| 524,22309 | 5e-05 | 0,00011 | 3e-05 | 0 |
| 524,26027 | 5e-05 | 0,00012 | 3e-05 | 0 |
| 524,29746 | 5e-05 | 0,00014 | 3e-05 | 0 |
| 524,33464 | 5e-05 | 0,00015 | 4e-05 | 0 |
| 524,37182 | 5e-05 | 0,00016 | 5e-05 | 0 |
| 524,409 | 5e-05 | 0,00017 | 5e-05 | 0 |
| 524,44618 | 5e-05 | 0,00018 | 6e-05 | 0 |
| 524,48337 | 6e-05 | 0,00019 | 7e-05 | 0 |
| 524,52055 | 6e-05 | 0,00021 | 7e-05 | 0 |
| 524,55773 | 7e-05 | 0,00022 | 8e-05 | 0 |
| 524,59491 | 7e-05 | 0,00023 | 9e-05 | 0 |
| 524,63209 | 8e-05 | 0,00024 | 1e-04 | 0 |
| 524,66928 | 9e-05 | 0,00025 | 0,00011 | 0 |
| 524,70646 | 9e-05 | 0,00025 | 0,00012 | 0 |
| 524,74364 | 1e-04 | 0,00026 | 0,00013 | 0 |
| 524,78082 | 0,00011 | 0,00027 | 0,00014 | 0 |
| 524,818 | 0,00012 | 0,00028 | 0,00015 | 0 |
| 524,85519 | 0,00013 | 0,00029 | 0,00016 | 0 |
| 524,89237 | 0,00014 | 0,00029 | 0,00017 | 0 |
| 524,92955 | 0,00015 | 3e-04 | 0,00018 | 1e-05 |
| 524,96673 | 0,00016 | 0,00031 | 0,00018 | 1e-05 |
| 525,00391 | 0,00018 | 0,00032 | 0,00019 | 1e-05 |
| 525,0411 | 0,00019 | 0,00033 | 2e-04 | 1e-05 |
| 525,07828 | 2e-04 | 0,00035 | 0,00021 | 2e-05 |
| 525,11546 | 0,00022 | 0,00036 | 0,00022 | 2e-05 |
| 525,15264 | 0,00023 | 0,00038 | 0,00024 | 2e-05 |
| 525,18982 | 0,00025 | 4e-04 | 0,00025 | 3e-05 |
| 525,22701 | 0,00026 | 0,00043 | 0,00026 | 4e-05 |
| 525,26419 | 0,00028 | 0,00045 | 0,00028 | 5e-05 |
| 525,30137 | 3e-04 | 0,00048 | 3e-04 | 6e-05 |
| 525,33855 | 0,00032 | 0,00052 | 0,00032 | 7e-05 |
| 525,37573 | 0,00035 | 0,00056 | 0,00035 | 8e-05 |
| 525,41292 | 0,00037 | 6e-04 | 0,00038 | 1e-04 |
| 525,4501 | 4e-04 | 0,00064 | 0,00041 | 0,00012 |
| 525,48728 | 0,00043 | 0,00069 | 0,00045 | 0,00015 |
| 525,52446 | 0,00047 | 0,00075 | 0,00049 | 0,00017 |
| 525,56164 | 0,00051 | 8e-04 | 0,00054 | 2e-04 |
| 525,59883 | 0,00055 | 0,00086 | 6e-04 | 0,00024 |
| 525,63601 | 6e-04 | 0,00093 | 0,00066 | 0,00028 |
| 525,67319 | 0,00065 | 0,001 | 0,00073 | 0,00032 |
| 525,71037 | 7e-04 | 0,00107 | 0,00081 | 0,00037 |
| 525,74755 | 0,00076 | 0,00114 | 0,00089 | 0,00043 |
| 525,78474 | 0,00082 | 0,00122 | 0,00098 | 0,00049 |
| 525,82192 | 0,00089 | 0,0013 | 0,00107 | 0,00055 |
| 525,8591 | 0,00096 | 0,00139 | 0,00118 | 0,00062 |
| 525,89628 | 0,00104 | 0,00147 | 0,00128 | 7e-04 |
| 525,93346 | 0,00112 | 0,00156 | 0,00139 | 0,00078 |
| 525,97065 | 0,00121 | 0,00165 | 0,00151 | 0,00087 |
| 526,00783 | 0,0013 | 0,00174 | 0,00163 | 0,00097 |
| 526,04501 | 0,0014 | 0,00184 | 0,00175 | 0,00106 |
| 526,08219 | 0,0015 | 0,00193 | 0,00188 | 0,00117 |
| 526,11937 | 0,00161 | 0,00203 | 0,002 | 0,00127 |
| 526,15656 | 0,00172 | 0,00213 | 0,00213 | 0,00138 |
| 526,19374 | 0,00183 | 0,00223 | 0,00225 | 0,00149 |
| 526,23092 | 0,00196 | 0,00233 | 0,00237 | 0,00161 |
| 526,2681 | 0,00208 | 0,00243 | 0,00249 | 0,00172 |
| 526,30528 | 0,00221 | 0,00253 | 0,0026 | 0,00184 |
| 526,34247 | 0,00235 | 0,00264 | 0,00271 | 0,00195 |
| 526,37965 | 0,00249 | 0,00274 | 0,00282 | 0,00207 |
| 526,41683 | 0,00264 | 0,00285 | 0,00292 | 0,00218 |
| 526,45401 | 0,00279 | 0,00295 | 0,00301 | 0,00229 |
| 526,49119 | 0,00295 | 0,00306 | 0,0031 | 0,0024 |
| 526,52838 | 0,00311 | 0,00317 | 0,00318 | 0,0025 |
| 526,56556 | 0,00327 | 0,00328 | 0,00325 | 0,0026 |
| 526,60274 | 0,00344 | 0,00339 | 0,00332 | 0,0027 |
| 526,63992 | 0,00361 | 0,0035 | 0,00338 | 0,0028 |
| 526,6771 | 0,00379 | 0,00361 | 0,00343 | 0,00289 |
| 526,71429 | 0,00397 | 0,00372 | 0,00348 | 0,00299 |
| 526,75147 | 0,00415 | 0,00384 | 0,00353 | 0,00308 |
| 526,78865 | 0,00433 | 0,00395 | 0,00358 | 0,00316 |
| 526,82583 | 0,00452 | 0,00408 | 0,00362 | 0,00325 |
| 526,86301 | 0,00471 | 0,0042 | 0,00367 | 0,00334 |
| 526,9002 | 0,0049 | 0,00433 | 0,00371 | 0,00344 |
| 526,93738 | 0,00509 | 0,00447 | 0,00376 | 0,00353 |
| 526,97456 | 0,00529 | 0,00462 | 0,00381 | 0,00363 |
| 527,01174 | 0,00549 | 0,00478 | 0,00387 | 0,00374 |
| 527,04892 | 0,00569 | 0,00495 | 0,00394 | 0,00385 |
| 527,08611 | 0,0059 | 0,00514 | 0,00401 | 0,00397 |
| 527,12329 | 0,00611 | 0,00534 | 0,0041 | 0,0041 |
| 527,16047 | 0,00633 | 0,00556 | 0,0042 | 0,00425 |
| 527,19765 | 0,00656 | 0,0058 | 0,00431 | 0,0044 |
| 527,23483 | 0,00679 | 0,00606 | 0,00444 | 0,00457 |
| 527,27202 | 0,00704 | 0,00634 | 0,00459 | 0,00475 |
| 527,3092 | 0,00729 | 0,00666 | 0,00476 | 0,00495 |
| 527,34638 | 0,00755 | 0,00699 | 0,00495 | 0,00517 |
| 527,38356 | 0,00783 | 0,00735 | 0,00517 | 0,00541 |
| 527,42074 | 0,00812 | 0,00774 | 0,00541 | 0,00567 |
| 527,45793 | 0,00842 | 0,00815 | 0,00568 | 0,00594 |
| 527,49511 | 0,00874 | 0,0086 | 0,00597 | 0,00624 |
| 527,53229 | 0,00907 | 0,00906 | 0,0063 | 0,00657 |
| 527,56947 | 0,00941 | 0,00955 | 0,00666 | 0,00691 |
| 527,60665 | 0,00977 | 0,01006 | 0,00706 | 0,00728 |
| 527,64384 | 0,01014 | 0,01058 | 0,00748 | 0,00768 |
| 527,68102 | 0,01052 | 0,01111 | 0,00794 | 0,0081 |
| 527,7182 | 0,01092 | 0,01166 | 0,00844 | 0,00854 |
| 527,75538 | 0,01132 | 0,01222 | 0,00896 | 0,00901 |
| 527,79256 | 0,01174 | 0,01277 | 0,00951 | 0,00951 |
| 527,82975 | 0,01216 | 0,01333 | 0,01009 | 0,01002 |
| 527,86693 | 0,01259 | 0,01388 | 0,0107 | 0,01056 |
| 527,90411 | 0,01302 | 0,01443 | 0,01133 | 0,01111 |
| 527,94129 | 0,01345 | 0,01496 | 0,01198 | 0,01169 |
| 527,97847 | 0,01389 | 0,01548 | 0,01264 | 0,01227 |
| 528,01566 | 0,01433 | 0,01597 | 0,01331 | 0,01287 |
| 528,05284 | 0,01476 | 0,01645 | 0,01398 | 0,01347 |
| 528,09002 | 0,01519 | 0,01692 | 0,01466 | 0,01408 |
| 528,1272 | 0,01561 | 0,01736 | 0,01533 | 0,01469 |
| 528,16438 | 0,01603 | 0,01778 | 0,01598 | 0,0153 |
| 528,20157 | 0,01644 | 0,01817 | 0,01662 | 0,0159 |
| 528,23875 | 0,01684 | 0,01855 | 0,01725 | 0,01648 |
| 528,27593 | 0,01724 | 0,01891 | 0,01785 | 0,01706 |
| 528,31311 | 0,01762 | 0,01925 | 0,01842 | 0,01761 |
| 528,35029 | 0,018 | 0,01957 | 0,01896 | 0,01815 |
| 528,38748 | 0,01837 | 0,01988 | 0,01946 | 0,01866 |
| 528,42466 | 0,01873 | 0,02018 | 0,01994 | 0,01915 |
| 528,46184 | 0,01908 | 0,02047 | 0,02038 | 0,01961 |
| 528,49902 | 0,01943 | 0,02076 | 0,02079 | 0,02005 |
| 528,5362 | 0,01976 | 0,02103 | 0,02117 | 0,02046 |
| 528,57339 | 0,02009 | 0,02131 | 0,02151 | 0,02085 |
| 528,61057 | 0,02042 | 0,02159 | 0,02183 | 0,02121 |
| 528,64775 | 0,02074 | 0,02186 | 0,02212 | 0,02154 |
| 528,68493 | 0,02105 | 0,02214 | 0,02239 | 0,02185 |
| 528,72211 | 0,02136 | 0,02241 | 0,02264 | 0,02215 |
| 528,7593 | 0,02166 | 0,02269 | 0,02287 | 0,02243 |
| 528,79648 | 0,02196 | 0,02298 | 0,0231 | 0,02269 |
| 528,83366 | 0,02226 | 0,02326 | 0,02331 | 0,02294 |
| 528,87084 | 0,02255 | 0,02355 | 0,02351 | 0,02318 |
| 528,90802 | 0,02284 | 0,02384 | 0,02371 | 0,0234 |
| 528,94521 | 0,02313 | 0,02413 | 0,02391 | 0,02363 |
| 528,98239 | 0,02342 | 0,02443 | 0,02411 | 0,02384 |
| 529,01957 | 0,0237 | 0,02472 | 0,02432 | 0,02406 |
| 529,05675 | 0,02399 | 0,02502 | 0,02452 | 0,02427 |
| 529,09393 | 0,02428 | 0,02533 | 0,02474 | 0,02449 |
| 529,13112 | 0,02457 | 0,02563 | 0,02496 | 0,02471 |
| 529,1683 | 0,02487 | 0,02594 | 0,02519 | 0,02494 |
| 529,20548 | 0,02517 | 0,02626 | 0,02544 | 0,02517 |
| 529,24266 | 0,02549 | 0,02659 | 0,0257 | 0,02542 |
| 529,27984 | 0,02582 | 0,02692 | 0,02597 | 0,02567 |
| 529,31703 | 0,02616 | 0,02727 | 0,02626 | 0,02594 |
| 529,35421 | 0,02652 | 0,02763 | 0,02657 | 0,02624 |
| 529,39139 | 0,0269 | 0,028 | 0,02691 | 0,02655 |
| 529,42857 | 0,02731 | 0,0284 | 0,02726 | 0,02689 |
| 529,46575 | 0,02774 | 0,02883 | 0,02765 | 0,02725 |
| 529,50294 | 0,02821 | 0,02927 | 0,02806 | 0,02764 |
| 529,54012 | 0,0287 | 0,02975 | 0,02851 | 0,02807 |
| 529,5773 | 0,02923 | 0,03025 | 0,02899 | 0,02852 |
| 529,61448 | 0,02979 | 0,03078 | 0,02951 | 0,02902 |
| 529,65166 | 0,03038 | 0,03134 | 0,03006 | 0,02956 |
| 529,68885 | 0,03101 | 0,03194 | 0,03065 | 0,03014 |
| 529,72603 | 0,03168 | 0,03257 | 0,03128 | 0,03075 |
| 529,76321 | 0,03238 | 0,03323 | 0,03194 | 0,0314 |
| 529,80039 | 0,03311 | 0,03391 | 0,03265 | 0,03209 |
| 529,83757 | 0,03386 | 0,03462 | 0,03339 | 0,03282 |
| 529,87476 | 0,03464 | 0,03536 | 0,03417 | 0,03358 |
| 529,91194 | 0,03543 | 0,03611 | 0,03497 | 0,03437 |
| 529,94912 | 0,03624 | 0,03688 | 0,0358 | 0,03519 |
| 529,9863 | 0,03705 | 0,03765 | 0,03666 | 0,03603 |
| 530,02348 | 0,03787 | 0,03843 | 0,03753 | 0,03689 |
| 530,06067 | 0,03867 | 0,0392 | 0,03841 | 0,03775 |
| 530,09785 | 0,03947 | 0,03996 | 0,0393 | 0,03862 |
| 530,13503 | 0,04024 | 0,04071 | 0,04018 | 0,03949 |
| 530,17221 | 0,04099 | 0,04143 | 0,04105 | 0,04034 |
| 530,20939 | 0,0417 | 0,04213 | 0,04191 | 0,04117 |
| 530,24658 | 0,04237 | 0,04278 | 0,04274 | 0,04198 |
| 530,28376 | 0,043 | 0,0434 | 0,04354 | 0,04276 |
| 530,32094 | 0,04358 | 0,04398 | 0,04429 | 0,0435 |
| 530,35812 | 0,0441 | 0,04451 | 0,04499 | 0,04419 |
| 530,3953 | 0,04457 | 0,04497 | 0,04564 | 0,04482 |
| 530,43249 | 0,04498 | 0,04539 | 0,04623 | 0,0454 |
| 530,46967 | 0,04533 | 0,04575 | 0,04676 | 0,04593 |
| 530,50685 | 0,04562 | 0,04606 | 0,04723 | 0,0464 |
| 530,54403 | 0,04587 | 0,04632 | 0,04762 | 0,04681 |
| 530,58121 | 0,04606 | 0,04654 | 0,04795 | 0,04716 |
| 530,6184 | 0,04622 | 0,04671 | 0,04821 | 0,04746 |
| 530,65558 | 0,04633 | 0,04685 | 0,04841 | 0,04771 |
| 530,69276 | 0,04641 | 0,04696 | 0,04856 | 0,04792 |
| 530,72994 | 0,04647 | 0,04705 | 0,04867 | 0,0481 |
| 530,76712 | 0,04652 | 0,04714 | 0,04875 | 0,04826 |
| 530,80431 | 0,04657 | 0,04723 | 0,0488 | 0,0484 |
| 530,84149 | 0,04663 | 0,04733 | 0,04883 | 0,04854 |
| 530,87867 | 0,04671 | 0,04746 | 0,04888 | 0,0487 |
| 530,91585 | 0,04683 | 0,04764 | 0,04893 | 0,04888 |
| 530,95303 | 0,04699 | 0,04786 | 0,04902 | 0,04909 |
| 530,99022 | 0,0472 | 0,04814 | 0,04915 | 0,04935 |
| 531,0274 | 0,04748 | 0,04849 | 0,04933 | 0,04967 |
| 531,06458 | 0,04781 | 0,04892 | 0,0496 | 0,05005 |
| 531,10176 | 0,04823 | 0,04943 | 0,04994 | 0,05053 |
| 531,13894 | 0,04873 | 0,05003 | 0,05037 | 0,05108 |
| 531,17613 | 0,04932 | 0,05073 | 0,0509 | 0,05172 |
| 531,21331 | 0,04999 | 0,0515 | 0,05152 | 0,05245 |
| 531,25049 | 0,05074 | 0,05237 | 0,05224 | 0,05327 |
| 531,28767 | 0,05156 | 0,05331 | 0,05307 | 0,05418 |
| 531,32485 | 0,05246 | 0,05432 | 0,05401 | 0,0552 |
| 531,36204 | 0,05343 | 0,05541 | 0,05504 | 0,05629 |
| 531,39922 | 0,05447 | 0,05655 | 0,05614 | 0,05745 |
| 531,4364 | 0,05555 | 0,05772 | 0,05732 | 0,05866 |
| 531,47358 | 0,05666 | 0,05891 | 0,05856 | 0,05993 |
| 531,51076 | 0,05779 | 0,06012 | 0,05983 | 0,06123 |
| 531,54795 | 0,05894 | 0,06131 | 0,06114 | 0,06256 |
| 531,58513 | 0,06008 | 0,06249 | 0,06245 | 0,06389 |
| 531,62231 | 0,0612 | 0,06361 | 0,06375 | 0,0652 |
| 531,65949 | 0,06228 | 0,06469 | 0,06502 | 0,06648 |
| 531,69667 | 0,06333 | 0,0657 | 0,06625 | 0,06771 |
| 531,73386 | 0,06432 | 0,06663 | 0,06742 | 0,06889 |
| 531,77104 | 0,06525 | 0,06748 | 0,06851 | 0,07 |
| 531,80822 | 0,06611 | 0,06824 | 0,0695 | 0,07101 |
| 531,8454 | 0,06689 | 0,06888 | 0,0704 | 0,07191 |
| 531,88258 | 0,06758 | 0,06943 | 0,0712 | 0,07272 |
| 531,91977 | 0,0682 | 0,06988 | 0,07189 | 0,07342 |
| 531,95695 | 0,06873 | 0,07024 | 0,07249 | 0,07402 |
| 531,99413 | 0,0692 | 0,07051 | 0,07298 | 0,07452 |
| 532,03131 | 0,06959 | 0,07071 | 0,07338 | 0,07491 |
| 532,06849 | 0,06992 | 0,07084 | 0,07369 | 0,07519 |
| 532,10568 | 0,0702 | 0,07091 | 0,07394 | 0,0754 |
| 532,14286 | 0,07043 | 0,07095 | 0,07414 | 0,07554 |
| 532,18004 | 0,07064 | 0,07097 | 0,07431 | 0,07563 |
| 532,21722 | 0,07083 | 0,07098 | 0,07445 | 0,07569 |
| 532,2544 | 0,07102 | 0,071 | 0,0746 | 0,07572 |
| 532,29159 | 0,07123 | 0,07105 | 0,07477 | 0,07575 |
| 532,32877 | 0,07146 | 0,07116 | 0,07498 | 0,07579 |
| 532,36595 | 0,07174 | 0,07133 | 0,07525 | 0,07587 |
| 532,40313 | 0,07208 | 0,07157 | 0,07558 | 0,076 |
| 532,44031 | 0,07249 | 0,0719 | 0,07599 | 0,07619 |
| 532,4775 | 0,07297 | 0,07234 | 0,07649 | 0,07644 |
| 532,51468 | 0,07354 | 0,07288 | 0,07708 | 0,07678 |
| 532,55186 | 0,0742 | 0,07354 | 0,07779 | 0,07721 |
| 532,58904 | 0,07498 | 0,07434 | 0,0786 | 0,07773 |
| 532,62622 | 0,07586 | 0,07525 | 0,0795 | 0,07834 |
| 532,66341 | 0,07684 | 0,07628 | 0,0805 | 0,07904 |
| 532,70059 | 0,07791 | 0,07743 | 0,08158 | 0,07982 |
| 532,73777 | 0,07907 | 0,07867 | 0,08274 | 0,08067 |
| 532,77495 | 0,08032 | 0,08001 | 0,08398 | 0,08159 |
| 532,81213 | 0,08165 | 0,08145 | 0,08526 | 0,08256 |
| 532,84932 | 0,08304 | 0,08294 | 0,08659 | 0,08357 |
| 532,8865 | 0,08448 | 0,08447 | 0,08794 | 0,08461 |
| 532,92368 | 0,08593 | 0,08602 | 0,08929 | 0,08565 |
| 532,96086 | 0,0874 | 0,08758 | 0,09064 | 0,08669 |
| 532,99804 | 0,08886 | 0,08911 | 0,09197 | 0,08771 |
| 533,03523 | 0,09028 | 0,09059 | 0,09326 | 0,0887 |
| 533,07241 | 0,09166 | 0,092 | 0,09449 | 0,08963 |
| 533,10959 | 0,09297 | 0,09332 | 0,09567 | 0,0905 |
| 533,14677 | 0,09419 | 0,09454 | 0,09678 | 0,09131 |
| 533,18395 | 0,09533 | 0,09563 | 0,09781 | 0,09205 |
| 533,22114 | 0,09635 | 0,09658 | 0,09876 | 0,09271 |
| 533,25832 | 0,09727 | 0,09739 | 0,09962 | 0,09328 |
| 533,2955 | 0,09804 | 0,09802 | 0,10038 | 0,09377 |
| 533,33268 | 0,09868 | 0,09849 | 0,10106 | 0,09418 |
| 533,36986 | 0,09921 | 0,0988 | 0,10166 | 0,09452 |
| 533,40705 | 0,09961 | 0,09897 | 0,10219 | 0,0948 |
| 533,44423 | 0,0999 | 0,099 | 0,10265 | 0,09503 |
| 533,48141 | 0,10009 | 0,0989 | 0,10306 | 0,09522 |
| 533,51859 | 0,10018 | 0,09867 | 0,1034 | 0,09538 |
| 533,55577 | 0,10019 | 0,09834 | 0,10372 | 0,09553 |
| 533,59295 | 0,10013 | 0,09794 | 0,104 | 0,09568 |
| 533,63014 | 0,10004 | 0,09748 | 0,10428 | 0,09586 |
| 533,66732 | 0,09992 | 0,09699 | 0,10455 | 0,09606 |
| 533,7045 | 0,09979 | 0,0965 | 0,10483 | 0,09631 |
| 533,74168 | 0,09967 | 0,09601 | 0,10512 | 0,09661 |
| 533,77886 | 0,09958 | 0,09556 | 0,10543 | 0,09698 |
| 533,81605 | 0,09954 | 0,09517 | 0,10576 | 0,09742 |
| 533,85323 | 0,09956 | 0,09486 | 0,10611 | 0,09793 |
| 533,89041 | 0,09965 | 0,09463 | 0,10648 | 0,09851 |
| 533,92759 | 0,09981 | 0,09451 | 0,10687 | 0,09915 |
| 533,96477 | 0,10006 | 0,09449 | 0,10726 | 0,09984 |
| 534,00196 | 0,10041 | 0,0946 | 0,10765 | 0,10058 |
| 534,03914 | 0,10086 | 0,09485 | 0,10801 | 0,10135 |
| 534,07632 | 0,10139 | 0,09521 | 0,10834 | 0,10212 |
| 534,1135 | 0,10201 | 0,09569 | 0,10862 | 0,10288 |
| 534,15068 | 0,10269 | 0,09628 | 0,10884 | 0,10359 |
| 534,18787 | 0,10344 | 0,09696 | 0,10897 | 0,10425 |
| 534,22505 | 0,10424 | 0,09772 | 0,109 | 0,10483 |
| 534,26223 | 0,10507 | 0,09856 | 0,1089 | 0,10528 |
| 534,29941 | 0,10591 | 0,09944 | 0,10865 | 0,10559 |
| 534,33659 | 0,10673 | 0,10033 | 0,10825 | 0,10575 |
| 534,37378 | 0,10751 | 0,10122 | 0,10769 | 0,10573 |
| 534,41096 | 0,10823 | 0,10208 | 0,10697 | 0,10553 |
| 534,44814 | 0,10887 | 0,10288 | 0,10608 | 0,10513 |
| 534,48532 | 0,10938 | 0,10358 | 0,10502 | 0,10452 |
| 534,5225 | 0,10975 | 0,10416 | 0,10376 | 0,10366 |
| 534,55969 | 0,10997 | 0,10461 | 0,10235 | 0,1026 |
| 534,59687 | 0,11002 | 0,1049 | 0,10079 | 0,10134 |
| 534,63405 | 0,10988 | 0,10502 | 0,09911 | 0,09989 |
| 534,67123 | 0,10955 | 0,10496 | 0,09731 | 0,09828 |
| 534,70841 | 0,10901 | 0,1047 | 0,09542 | 0,09652 |
| 534,7456 | 0,10824 | 0,10419 | 0,09347 | 0,09462 |
| 534,78278 | 0,10728 | 0,10349 | 0,09147 | 0,09261 |
| 534,81996 | 0,10613 | 0,10259 | 0,08947 | 0,09055 |
| 534,85714 | 0,10481 | 0,10152 | 0,08749 | 0,08845 |
| 534,89432 | 0,10334 | 0,10027 | 0,08556 | 0,08636 |
| 534,93151 | 0,10173 | 0,09888 | 0,0837 | 0,08429 |
| 534,96869 | 0,1 | 0,09734 | 0,08194 | 0,08229 |
| 535,00587 | 0,09821 | 0,09571 | 0,08032 | 0,0804 |
| 535,04305 | 0,09638 | 0,09402 | 0,07888 | 0,07865 |
| 535,08023 | 0,09454 | 0,09231 | 0,0776 | 0,07705 |
| 535,11742 | 0,09274 | 0,0906 | 0,07651 | 0,07564 |
| 535,1546 | 0,09099 | 0,08893 | 0,07562 | 0,07442 |
| 535,19178 | 0,08935 | 0,08733 | 0,07494 | 0,07343 |
| 535,22896 | 0,08785 | 0,08586 | 0,07448 | 0,07267 |
| 535,26614 | 0,08651 | 0,08453 | 0,07428 | 0,0722 |
| 535,30333 | 0,08536 | 0,08337 | 0,07431 | 0,07197 |
| 535,34051 | 0,08439 | 0,0824 | 0,07455 | 0,07199 |
| 535,37769 | 0,08364 | 0,08163 | 0,07501 | 0,07225 |
| 535,41487 | 0,08312 | 0,08108 | 0,07567 | 0,07275 |
| 535,45205 | 0,08287 | 0,08078 | 0,07652 | 0,07347 |
| 535,48924 | 0,08284 | 0,08074 | 0,07756 | 0,07445 |
| 535,52642 | 0,08304 | 0,08091 | 0,07879 | 0,07562 |
| 535,5636 | 0,08344 | 0,08131 | 0,08016 | 0,07697 |
| 535,60078 | 0,08404 | 0,0819 | 0,08164 | 0,07848 |
| 535,63796 | 0,08482 | 0,08269 | 0,08323 | 0,08011 |
| 535,67515 | 0,08577 | 0,08364 | 0,0849 | 0,08184 |
| 535,71233 | 0,08685 | 0,08476 | 0,08663 | 0,08366 |
| 535,74951 | 0,08803 | 0,08598 | 0,0884 | 0,08554 |
| 535,78669 | 0,08927 | 0,08727 | 0,09018 | 0,08744 |
| 535,82387 | 0,09055 | 0,08861 | 0,09195 | 0,08934 |
| 535,86106 | 0,09184 | 0,08997 | 0,09369 | 0,09122 |
| 535,89824 | 0,09311 | 0,09131 | 0,09539 | 0,09305 |
| 535,93542 | 0,09432 | 0,09261 | 0,09702 | 0,09482 |
| 535,9726 | 0,09545 | 0,09382 | 0,09858 | 0,09651 |
| 536,00978 | 0,09648 | 0,09493 | 0,10003 | 0,09808 |
| 536,04697 | 0,09739 | 0,09591 | 0,10138 | 0,09955 |
| 536,08415 | 0,09817 | 0,09676 | 0,10262 | 0,10091 |
| 536,12133 | 0,09881 | 0,09746 | 0,10375 | 0,10215 |
| 536,15851 | 0,09928 | 0,09799 | 0,10476 | 0,10327 |
| 536,19569 | 0,09957 | 0,09833 | 0,10566 | 0,10427 |
| 536,23288 | 0,09972 | 0,0985 | 0,10645 | 0,10513 |
| 536,27006 | 0,09972 | 0,09852 | 0,10711 | 0,10589 |
| 536,30724 | 0,09959 | 0,09838 | 0,10768 | 0,10654 |
| 536,34442 | 0,09933 | 0,09811 | 0,10816 | 0,10709 |
| 536,3816 | 0,09895 | 0,09771 | 0,10855 | 0,10756 |
| 536,41879 | 0,09847 | 0,09719 | 0,10887 | 0,10795 |
| 536,45597 | 0,09792 | 0,09659 | 0,10911 | 0,10826 |
| 536,49315 | 0,09733 | 0,09593 | 0,10929 | 0,10849 |
| 536,53033 | 0,09671 | 0,09523 | 0,10939 | 0,10865 |
| 536,56751 | 0,09609 | 0,09453 | 0,10944 | 0,10875 |
| 536,6047 | 0,09549 | 0,09383 | 0,10943 | 0,10878 |
| 536,64188 | 0,09493 | 0,09316 | 0,10935 | 0,10873 |
| 536,67906 | 0,09443 | 0,09256 | 0,1092 | 0,10861 |
| 536,71624 | 0,09401 | 0,09202 | 0,10898 | 0,10839 |
| 536,75342 | 0,09367 | 0,09157 | 0,10866 | 0,10807 |
| 536,79061 | 0,09341 | 0,09121 | 0,10824 | 0,10764 |
| 536,82779 | 0,09326 | 0,09095 | 0,10771 | 0,10709 |
| 536,86497 | 0,09321 | 0,0908 | 0,10707 | 0,10642 |
| 536,90215 | 0,09327 | 0,09076 | 0,10631 | 0,10561 |
| 536,93933 | 0,09342 | 0,09083 | 0,10543 | 0,10467 |
| 536,97652 | 0,09364 | 0,09099 | 0,10441 | 0,10355 |
| 537,0137 | 0,09393 | 0,09122 | 0,10324 | 0,1023 |
| 537,05088 | 0,09427 | 0,09151 | 0,10194 | 0,10091 |
| 537,08806 | 0,09464 | 0,09186 | 0,10053 | 0,0994 |
| 537,12524 | 0,09503 | 0,09224 | 0,09902 | 0,09777 |
| 537,16243 | 0,09541 | 0,09262 | 0,09741 | 0,09605 |
| 537,19961 | 0,09576 | 0,09299 | 0,09573 | 0,09425 |
| 537,23679 | 0,09606 | 0,09333 | 0,09399 | 0,0924 |
| 537,27397 | 0,09629 | 0,09361 | 0,09224 | 0,09053 |
| 537,31115 | 0,09645 | 0,09383 | 0,09049 | 0,08868 |
| 537,34834 | 0,0965 | 0,09397 | 0,08877 | 0,08686 |
| 537,38552 | 0,09644 | 0,094 | 0,08711 | 0,08512 |
| 537,4227 | 0,09626 | 0,09392 | 0,08554 | 0,08348 |
| 537,45988 | 0,09597 | 0,09373 | 0,08408 | 0,08199 |
| 537,49706 | 0,09558 | 0,09343 | 0,08279 | 0,08067 |
| 537,53425 | 0,09507 | 0,09304 | 0,08167 | 0,07954 |
| 537,57143 | 0,09447 | 0,09254 | 0,08073 | 0,07862 |
| 537,60861 | 0,09377 | 0,09197 | 0,07999 | 0,07792 |
| 537,64579 | 0,09302 | 0,09131 | 0,07946 | 0,07747 |
| 537,68297 | 0,09223 | 0,09062 | 0,07916 | 0,07728 |
| 537,72016 | 0,09142 | 0,08991 | 0,07911 | 0,07739 |
| 537,75734 | 0,09062 | 0,08921 | 0,07932 | 0,07777 |
| 537,79452 | 0,08987 | 0,08854 | 0,07978 | 0,07841 |
| 537,8317 | 0,08919 | 0,08793 | 0,08047 | 0,07932 |
| 537,86888 | 0,08862 | 0,08743 | 0,08139 | 0,08049 |
| 537,90607 | 0,08818 | 0,08707 | 0,08254 | 0,08192 |
| 537,94325 | 0,08791 | 0,08687 | 0,08391 | 0,08363 |
| 537,98043 | 0,08781 | 0,08684 | 0,08551 | 0,08558 |
| 538,01761 | 0,08791 | 0,08702 | 0,08732 | 0,08774 |
| 538,05479 | 0,08825 | 0,08742 | 0,08931 | 0,0901 |
| 538,09198 | 0,08885 | 0,08807 | 0,09146 | 0,09264 |
| 538,12916 | 0,0897 | 0,08901 | 0,09375 | 0,09533 |
| 538,16634 | 0,09079 | 0,09019 | 0,09616 | 0,09816 |
| 538,20352 | 0,09211 | 0,09162 | 0,09866 | 0,10111 |
| 538,2407 | 0,09365 | 0,09328 | 0,10124 | 0,10411 |
| 538,27789 | 0,09541 | 0,09516 | 0,10385 | 0,10715 |
| 538,31507 | 0,09737 | 0,09724 | 0,10645 | 0,11017 |
| 538,35225 | 0,09948 | 0,0995 | 0,10902 | 0,11316 |
| 538,38943 | 0,10169 | 0,10189 | 0,1115 | 0,11606 |
| 538,42661 | 0,10397 | 0,10435 | 0,11388 | 0,11881 |
| 538,4638 | 0,10627 | 0,10683 | 0,11609 | 0,12137 |
| 538,50098 | 0,10854 | 0,10931 | 0,11808 | 0,12371 |
| 538,53816 | 0,11073 | 0,11171 | 0,11983 | 0,12578 |
| 538,57534 | 0,11276 | 0,11399 | 0,12131 | 0,12757 |
| 538,61252 | 0,1146 | 0,11606 | 0,12249 | 0,12903 |
| 538,64971 | 0,11621 | 0,11789 | 0,12334 | 0,13014 |
| 538,68689 | 0,11756 | 0,11944 | 0,12386 | 0,13081 |
| 538,72407 | 0,11859 | 0,12069 | 0,12399 | 0,1311 |
| 538,76125 | 0,1193 | 0,12159 | 0,12373 | 0,13101 |
| 538,79843 | 0,11957 | 0,12213 | 0,12313 | 0,13055 |
| 538,83562 | 0,11947 | 0,12222 | 0,12221 | 0,12974 |
| 538,8728 | 0,119 | 0,12191 | 0,12098 | 0,1286 |
| 538,90998 | 0,11816 | 0,12121 | 0,11949 | 0,12714 |
| 538,94716 | 0,11698 | 0,12015 | 0,11775 | 0,1254 |
| 538,98434 | 0,11547 | 0,11875 | 0,1158 | 0,12347 |
| 539,02153 | 0,11364 | 0,11703 | 0,11372 | 0,12139 |
| 539,05871 | 0,11154 | 0,11503 | 0,11156 | 0,11922 |
| 539,09589 | 0,10924 | 0,11277 | 0,10938 | 0,117 |
| 539,13307 | 0,10679 | 0,11035 | 0,10721 | 0,11478 |
| 539,17025 | 0,10425 | 0,10783 | 0,10509 | 0,11261 |
| 539,20744 | 0,10165 | 0,10524 | 0,10308 | 0,11056 |
| 539,24462 | 0,09905 | 0,10265 | 0,10122 | 0,10863 |
| 539,2818 | 0,09652 | 0,1001 | 0,09951 | 0,10684 |
| 539,31898 | 0,09409 | 0,09765 | 0,09797 | 0,10522 |
| 539,35616 | 0,09181 | 0,09535 | 0,09659 | 0,10376 |
| 539,39335 | 0,08969 | 0,09322 | 0,09538 | 0,10247 |
| 539,43053 | 0,08776 | 0,09129 | 0,09431 | 0,10135 |
| 539,46771 | 0,08603 | 0,08956 | 0,09338 | 0,10035 |
| 539,50489 | 0,08455 | 0,08804 | 0,09255 | 0,09943 |
| 539,54207 | 0,08329 | 0,08675 | 0,09178 | 0,09858 |
| 539,57926 | 0,08223 | 0,0857 | 0,09103 | 0,09775 |
| 539,61644 | 0,08135 | 0,08483 | 0,09027 | 0,09691 |
| 539,65362 | 0,08062 | 0,08411 | 0,08947 | 0,09602 |
| 539,6908 | 0,08003 | 0,08352 | 0,08859 | 0,09504 |
| 539,72798 | 0,07953 | 0,08302 | 0,0876 | 0,09394 |
| 539,76517 | 0,07911 | 0,08258 | 0,08648 | 0,09272 |
| 539,80235 | 0,07869 | 0,08217 | 0,08523 | 0,09134 |
| 539,83953 | 0,07827 | 0,08172 | 0,08384 | 0,08982 |
| 539,87671 | 0,07779 | 0,08122 | 0,08231 | 0,08815 |
| 539,91389 | 0,07724 | 0,08062 | 0,08066 | 0,08631 |
| 539,95108 | 0,07659 | 0,07991 | 0,07889 | 0,08434 |
| 539,98826 | 0,07579 | 0,07907 | 0,07703 | 0,08228 |
| 540,02544 | 0,07485 | 0,07806 | 0,07511 | 0,08014 |
| 540,06262 | 0,07377 | 0,07688 | 0,07317 | 0,07796 |
| 540,0998 | 0,07255 | 0,07553 | 0,07122 | 0,07576 |
| 540,13699 | 0,07118 | 0,07403 | 0,06931 | 0,07358 |
| 540,17417 | 0,06969 | 0,07239 | 0,06745 | 0,07146 |
| 540,21135 | 0,06807 | 0,07063 | 0,06569 | 0,06942 |
| 540,24853 | 0,06636 | 0,06876 | 0,06403 | 0,06747 |
| 540,28571 | 0,06458 | 0,06681 | 0,06249 | 0,06564 |
| 540,3229 | 0,06276 | 0,06482 | 0,06107 | 0,06393 |
| 540,36008 | 0,06093 | 0,06282 | 0,05977 | 0,06234 |
| 540,39726 | 0,05912 | 0,06084 | 0,05858 | 0,0609 |
| 540,43444 | 0,05734 | 0,05891 | 0,05749 | 0,05958 |
| 540,47162 | 0,05565 | 0,05705 | 0,0565 | 0,05836 |
| 540,50881 | 0,05404 | 0,0553 | 0,05556 | 0,05721 |
| 540,54599 | 0,05254 | 0,05368 | 0,05464 | 0,05611 |
| 540,58317 | 0,05115 | 0,0522 | 0,05373 | 0,05504 |
| 540,62035 | 0,04988 | 0,05086 | 0,05279 | 0,05398 |
| 540,65753 | 0,04874 | 0,04967 | 0,0518 | 0,05288 |
| 540,69472 | 0,04773 | 0,04862 | 0,05073 | 0,05173 |
| 540,7319 | 0,04684 | 0,0477 | 0,04955 | 0,0505 |
| 540,76908 | 0,04606 | 0,04693 | 0,04825 | 0,04919 |
| 540,80626 | 0,04535 | 0,04627 | 0,04682 | 0,04776 |
| 540,84344 | 0,04472 | 0,04569 | 0,04526 | 0,04623 |
| 540,88063 | 0,04413 | 0,04516 | 0,04357 | 0,04456 |
| 540,91781 | 0,04356 | 0,04468 | 0,04175 | 0,04276 |
| 540,95499 | 0,043 | 0,0442 | 0,03979 | 0,04086 |
| 540,99217 | 0,04241 | 0,04372 | 0,03773 | 0,03887 |
| 541,02935 | 0,04178 | 0,04318 | 0,03559 | 0,0368 |
| 541,06654 | 0,04109 | 0,04258 | 0,03339 | 0,03466 |
| 541,10372 | 0,04032 | 0,0419 | 0,03116 | 0,03248 |
| 541,1409 | 0,03947 | 0,04111 | 0,0289 | 0,03027 |
| 541,17808 | 0,0385 | 0,04022 | 0,02666 | 0,02808 |
| 541,21526 | 0,03742 | 0,03922 | 0,02446 | 0,02591 |
| 541,25245 | 0,03623 | 0,03806 | 0,02232 | 0,02378 |
| 541,28963 | 0,03494 | 0,03679 | 0,02025 | 0,02172 |
| 541,32681 | 0,03355 | 0,0354 | 0,01828 | 0,01975 |
| 541,36399 | 0,03207 | 0,0339 | 0,01642 | 0,01787 |
| 541,40117 | 0,0305 | 0,03231 | 0,01467 | 0,01611 |
| 541,43836 | 0,02887 | 0,03063 | 0,01306 | 0,01447 |
| 541,47554 | 0,02718 | 0,02889 | 0,01159 | 0,01295 |
| 541,51272 | 0,02546 | 0,0271 | 0,01025 | 0,01155 |
| 541,5499 | 0,02373 | 0,02528 | 0,00904 | 0,01028 |
| 541,58708 | 0,022 | 0,02346 | 0,00796 | 0,00913 |
| 541,62427 | 0,02029 | 0,02165 | 0,007 | 0,00811 |
| 541,66145 | 0,01861 | 0,01987 | 0,00616 | 0,00721 |
| 541,69863 | 0,01699 | 0,01814 | 0,00544 | 0,00641 |
| 541,73581 | 0,01543 | 0,01648 | 0,00482 | 0,00572 |
| 541,77299 | 0,01394 | 0,01489 | 0,00429 | 0,00511 |
| 541,81018 | 0,01254 | 0,0134 | 0,00384 | 0,00458 |
| 541,84736 | 0,01122 | 0,012 | 0,00346 | 0,00414 |
| 541,88454 | 0,01 | 0,01069 | 0,00314 | 0,00377 |
| 541,92172 | 0,00889 | 0,00949 | 0,00288 | 0,00345 |
| 541,9589 | 0,00788 | 0,00841 | 0,00268 | 0,00319 |
| 541,99609 | 0,00696 | 0,00744 | 0,00251 | 0,00297 |
| 542,03327 | 0,00614 | 0,00657 | 0,00237 | 0,00278 |
| 542,07045 | 0,00541 | 0,0058 | 0,00226 | 0,00263 |
| 542,10763 | 0,00476 | 0,00512 | 0,00216 | 0,0025 |
| 542,14481 | 0,00421 | 0,00452 | 0,00208 | 0,00239 |
| 542,182 | 0,00374 | 0,00401 | 0,00202 | 0,0023 |
| 542,21918 | 0,00333 | 0,00358 | 0,00196 | 0,00222 |
| 542,25636 | 0,00299 | 0,00322 | 0,0019 | 0,00214 |
| 542,29354 | 0,0027 | 0,00292 | 0,00184 | 0,00207 |
| 542,33072 | 0,00245 | 0,00267 | 0,00178 | 0,002 |
| 542,36791 | 0,00225 | 0,00246 | 0,00172 | 0,00193 |
| 542,40509 | 0,00209 | 0,00228 | 0,00166 | 0,00186 |
| 542,44227 | 0,00196 | 0,00214 | 0,00159 | 0,00178 |
| 542,47945 | 0,00185 | 0,00203 | 0,00151 | 0,0017 |
| 542,51663 | 0,00176 | 0,00193 | 0,00143 | 0,00162 |
| 542,55382 | 0,00169 | 0,00185 | 0,00135 | 0,00154 |
| 542,591 | 0,00163 | 0,00178 | 0,00127 | 0,00145 |
| 542,62818 | 0,00157 | 0,00172 | 0,00118 | 0,00136 |
| 542,66536 | 0,00152 | 0,00166 | 0,0011 | 0,00127 |
| 542,70254 | 0,00147 | 0,0016 | 0,00101 | 0,00118 |
| 542,73973 | 0,00142 | 0,00154 | 0,00092 | 0,00109 |
| 542,77691 | 0,00137 | 0,00148 | 0,00084 | 0,001 |
| 542,81409 | 0,00132 | 0,00142 | 0,00075 | 0,00091 |
| 542,85127 | 0,00126 | 0,00136 | 0,00067 | 0,00082 |
| 542,88845 | 0,0012 | 0,00129 | 6e-04 | 0,00074 |
| 542,92564 | 0,00114 | 0,00122 | 0,00053 | 0,00066 |
| 542,96282 | 0,00108 | 0,00115 | 0,00046 | 0,00059 |
| 543 | 0,00102 | 0,00108 | 4e-04 | 0,00052 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 |
| 524,29746 | 1e-05 | 0 | 0 | 0 |
| 524,33464 | 1e-05 | 0 | 0 | 0 |
| 524,37182 | 1e-05 | 0 | 0 | 0 |
| 524,409 | 1e-05 | 0 | 0 | 0 |
| 524,44618 | 1e-05 | 0 | 0 | 0 |
| 524,48337 | 1e-05 | 0 | 0 | 0 |
| 524,52055 | 2e-05 | 0 | 0 | 0 |
| 524,55773 | 2e-05 | 1e-05 | 0 | 0 |
| 524,59491 | 2e-05 | 1e-05 | 0 | 0 |
| 524,63209 | 3e-05 | 1e-05 | 0 | 0 |
| 524,66928 | 3e-05 | 1e-05 | 1e-05 | 0 |
| 524,70646 | 4e-05 | 1e-05 | 1e-05 | 0 |
| 524,74364 | 4e-05 | 2e-05 | 1e-05 | 0 |
| 524,78082 | 5e-05 | 2e-05 | 1e-05 | 1e-05 |
| 524,818 | 6e-05 | 2e-05 | 1e-05 | 1e-05 |
| 524,85519 | 7e-05 | 3e-05 | 2e-05 | 1e-05 |
| 524,89237 | 8e-05 | 3e-05 | 2e-05 | 1e-05 |
| 524,92955 | 9e-05 | 4e-05 | 2e-05 | 1e-05 |
| 524,96673 | 1e-04 | 5e-05 | 3e-05 | 2e-05 |
| 525,00391 | 0,00011 | 6e-05 | 3e-05 | 2e-05 |
| 525,0411 | 0,00012 | 7e-05 | 4e-05 | 3e-05 |
| 525,07828 | 0,00014 | 8e-05 | 5e-05 | 3e-05 |
| 525,11546 | 0,00015 | 9e-05 | 6e-05 | 4e-05 |
| 525,15264 | 0,00017 | 0,00011 | 7e-05 | 5e-05 |
| 525,18982 | 0,00019 | 0,00012 | 8e-05 | 5e-05 |
| 525,22701 | 0,00021 | 0,00014 | 9e-05 | 6e-05 |
| 525,26419 | 0,00023 | 0,00016 | 0,00011 | 8e-05 |
| 525,30137 | 0,00026 | 0,00019 | 0,00012 | 9e-05 |
| 525,33855 | 0,00028 | 0,00021 | 0,00014 | 1e-04 |
| 525,37573 | 0,00031 | 0,00024 | 0,00016 | 0,00012 |
| 525,41292 | 0,00033 | 0,00027 | 0,00019 | 0,00014 |
| 525,4501 | 0,00036 | 3e-04 | 0,00021 | 0,00017 |
| 525,48728 | 0,00039 | 0,00034 | 0,00024 | 0,00019 |
| 525,52446 | 0,00043 | 0,00037 | 0,00027 | 0,00022 |
| 525,56164 | 0,00046 | 0,00041 | 0,00031 | 0,00025 |
| 525,59883 | 5e-04 | 0,00046 | 0,00034 | 0,00028 |
| 525,63601 | 0,00054 | 5e-04 | 0,00038 | 0,00032 |
| 525,67319 | 0,00057 | 0,00055 | 0,00042 | 0,00036 |
| 525,71037 | 0,00062 | 6e-04 | 0,00047 | 0,00041 |
| 525,74755 | 0,00066 | 0,00065 | 0,00052 | 0,00046 |
| 525,78474 | 7e-04 | 0,00071 | 0,00057 | 0,00051 |
| 525,82192 | 0,00075 | 0,00077 | 0,00062 | 0,00057 |
| 525,8591 | 8e-04 | 0,00083 | 0,00068 | 0,00063 |
| 525,89628 | 0,00085 | 0,00089 | 0,00073 | 0,00069 |
| 525,93346 | 9e-04 | 0,00095 | 8e-04 | 0,00075 |
| 525,97065 | 0,00095 | 0,00102 | 0,00086 | 0,00082 |
| 526,00783 | 0,00101 | 0,00109 | 0,00093 | 0,00089 |
| 526,04501 | 0,00106 | 0,00116 | 0,00099 | 0,00097 |
| 526,08219 | 0,00112 | 0,00123 | 0,00107 | 0,00104 |
| 526,11937 | 0,00118 | 0,00131 | 0,00114 | 0,00112 |
| 526,15656 | 0,00125 | 0,00138 | 0,00121 | 0,00119 |
| 526,19374 | 0,00131 | 0,00146 | 0,00129 | 0,00127 |
| 526,23092 | 0,00138 | 0,00154 | 0,00137 | 0,00135 |
| 526,2681 | 0,00145 | 0,00162 | 0,00145 | 0,00142 |
| 526,30528 | 0,00153 | 0,00171 | 0,00153 | 0,0015 |
| 526,34247 | 0,00161 | 0,0018 | 0,00161 | 0,00157 |
| 526,37965 | 0,00169 | 0,00189 | 0,0017 | 0,00164 |
| 526,41683 | 0,00177 | 0,00198 | 0,00178 | 0,00171 |
| 526,45401 | 0,00186 | 0,00208 | 0,00186 | 0,00178 |
| 526,49119 | 0,00195 | 0,00218 | 0,00195 | 0,00185 |
| 526,52838 | 0,00205 | 0,00228 | 0,00204 | 0,00191 |
| 526,56556 | 0,00215 | 0,00239 | 0,00212 | 0,00197 |
| 526,60274 | 0,00225 | 0,0025 | 0,00221 | 0,00202 |
| 526,63992 | 0,00236 | 0,00262 | 0,0023 | 0,00208 |
| 526,6771 | 0,00247 | 0,00274 | 0,00238 | 0,00213 |
| 526,71429 | 0,00259 | 0,00287 | 0,00247 | 0,00218 |
| 526,75147 | 0,00272 | 0,003 | 0,00256 | 0,00222 |
| 526,78865 | 0,00285 | 0,00314 | 0,00265 | 0,00227 |
| 526,82583 | 0,00299 | 0,00328 | 0,00274 | 0,00232 |
| 526,86301 | 0,00313 | 0,00343 | 0,00283 | 0,00236 |
| 526,9002 | 0,00328 | 0,00359 | 0,00293 | 0,00241 |
| 526,93738 | 0,00344 | 0,00375 | 0,00302 | 0,00246 |
| 526,97456 | 0,0036 | 0,00393 | 0,00312 | 0,00251 |
| 527,01174 | 0,00378 | 0,00411 | 0,00323 | 0,00257 |
| 527,04892 | 0,00396 | 0,00429 | 0,00334 | 0,00263 |
| 527,08611 | 0,00416 | 0,00449 | 0,00345 | 0,0027 |
| 527,12329 | 0,00436 | 0,00469 | 0,00357 | 0,00277 |
| 527,16047 | 0,00457 | 0,0049 | 0,0037 | 0,00286 |
| 527,19765 | 0,0048 | 0,00513 | 0,00384 | 0,00295 |
| 527,23483 | 0,00504 | 0,00536 | 0,00398 | 0,00306 |
| 527,27202 | 0,00528 | 0,0056 | 0,00414 | 0,00317 |
| 527,3092 | 0,00554 | 0,00585 | 0,0043 | 0,0033 |
| 527,34638 | 0,00582 | 0,00611 | 0,00448 | 0,00344 |
| 527,38356 | 0,0061 | 0,00638 | 0,00467 | 0,0036 |
| 527,42074 | 0,0064 | 0,00666 | 0,00487 | 0,00377 |
| 527,45793 | 0,00671 | 0,00695 | 0,00509 | 0,00396 |
| 527,49511 | 0,00704 | 0,00725 | 0,00531 | 0,00417 |
| 527,53229 | 0,00737 | 0,00755 | 0,00556 | 0,00439 |
| 527,56947 | 0,00772 | 0,00787 | 0,00581 | 0,00464 |
| 527,60665 | 0,00808 | 0,00819 | 0,00608 | 0,0049 |
| 527,64384 | 0,00845 | 0,00852 | 0,00636 | 0,00518 |
| 527,68102 | 0,00883 | 0,00886 | 0,00666 | 0,00548 |
| 527,7182 | 0,00922 | 0,00921 | 0,00697 | 0,0058 |
| 527,75538 | 0,00962 | 0,00956 | 0,00729 | 0,00613 |
| 527,79256 | 0,01002 | 0,00991 | 0,00762 | 0,00649 |
| 527,82975 | 0,01043 | 0,01027 | 0,00796 | 0,00686 |
| 527,86693 | 0,01085 | 0,01064 | 0,00831 | 0,00724 |
| 527,90411 | 0,01128 | 0,011 | 0,00867 | 0,00764 |
| 527,94129 | 0,0117 | 0,01136 | 0,00904 | 0,00805 |
| 527,97847 | 0,01213 | 0,01173 | 0,00941 | 0,00848 |
| 528,01566 | 0,01256 | 0,01209 | 0,00979 | 0,00891 |
| 528,05284 | 0,01298 | 0,01245 | 0,01017 | 0,00936 |
| 528,09002 | 0,01341 | 0,01281 | 0,01055 | 0,0098 |
| 528,1272 | 0,01383 | 0,01316 | 0,01094 | 0,01026 |
| 528,16438 | 0,01425 | 0,01351 | 0,01133 | 0,01071 |
| 528,20157 | 0,01466 | 0,01386 | 0,01172 | 0,01116 |
| 528,23875 | 0,01507 | 0,0142 | 0,0121 | 0,01162 |
| 528,27593 | 0,01547 | 0,01454 | 0,01249 | 0,01207 |
| 528,31311 | 0,01586 | 0,01487 | 0,01288 | 0,01251 |
| 528,35029 | 0,01624 | 0,01519 | 0,01326 | 0,01295 |
| 528,38748 | 0,01662 | 0,01551 | 0,01365 | 0,01338 |
| 528,42466 | 0,01699 | 0,01582 | 0,01403 | 0,01381 |
| 528,46184 | 0,01734 | 0,01613 | 0,01441 | 0,01422 |
| 528,49902 | 0,01769 | 0,01643 | 0,0148 | 0,01462 |
| 528,5362 | 0,01802 | 0,01673 | 0,01518 | 0,01501 |
| 528,57339 | 0,01835 | 0,01703 | 0,01557 | 0,01539 |
| 528,61057 | 0,01867 | 0,01732 | 0,01596 | 0,01576 |
| 528,64775 | 0,01899 | 0,01762 | 0,01635 | 0,01611 |
| 528,68493 | 0,01929 | 0,0179 | 0,01674 | 0,01646 |
| 528,72211 | 0,01959 | 0,01819 | 0,01714 | 0,01679 |
| 528,7593 | 0,01988 | 0,01848 | 0,01754 | 0,01711 |
| 528,79648 | 0,02017 | 0,01877 | 0,01795 | 0,01743 |
| 528,83366 | 0,02045 | 0,01906 | 0,01836 | 0,01773 |
| 528,87084 | 0,02073 | 0,01936 | 0,01878 | 0,01803 |
| 528,90802 | 0,02101 | 0,01966 | 0,01921 | 0,01832 |
| 528,94521 | 0,02129 | 0,01996 | 0,01964 | 0,01861 |
| 528,98239 | 0,02158 | 0,02027 | 0,02009 | 0,01889 |
| 529,01957 | 0,02186 | 0,02059 | 0,02053 | 0,01917 |
| 529,05675 | 0,02215 | 0,02092 | 0,02099 | 0,01945 |
| 529,09393 | 0,02245 | 0,02126 | 0,02145 | 0,01973 |
| 529,13112 | 0,02276 | 0,02161 | 0,02192 | 0,02002 |
| 529,1683 | 0,02308 | 0,02197 | 0,0224 | 0,02031 |
| 529,20548 | 0,02341 | 0,02235 | 0,02289 | 0,0206 |
| 529,24266 | 0,02375 | 0,02274 | 0,02338 | 0,02091 |
| 529,27984 | 0,02411 | 0,02315 | 0,02389 | 0,02123 |
| 529,31703 | 0,02449 | 0,02359 | 0,0244 | 0,02156 |
| 529,35421 | 0,02489 | 0,02404 | 0,02492 | 0,02191 |
| 529,39139 | 0,02531 | 0,02451 | 0,02546 | 0,02228 |
| 529,42857 | 0,02576 | 0,02501 | 0,02601 | 0,02267 |
| 529,46575 | 0,02623 | 0,02552 | 0,02657 | 0,02308 |
| 529,50294 | 0,02672 | 0,02607 | 0,02714 | 0,02352 |
| 529,54012 | 0,02725 | 0,02664 | 0,02773 | 0,02398 |
| 529,5773 | 0,0278 | 0,02723 | 0,02833 | 0,02447 |
| 529,61448 | 0,02837 | 0,02785 | 0,02896 | 0,02499 |
| 529,65166 | 0,02897 | 0,02848 | 0,02959 | 0,02554 |
| 529,68885 | 0,0296 | 0,02914 | 0,03025 | 0,02612 |
| 529,72603 | 0,03025 | 0,02982 | 0,03092 | 0,02674 |
| 529,76321 | 0,03093 | 0,03052 | 0,0316 | 0,02739 |
| 529,80039 | 0,03162 | 0,03124 | 0,03231 | 0,02806 |
| 529,83757 | 0,03233 | 0,03196 | 0,03302 | 0,02877 |
| 529,87476 | 0,03305 | 0,0327 | 0,03375 | 0,0295 |
| 529,91194 | 0,03378 | 0,03345 | 0,0345 | 0,03027 |
| 529,94912 | 0,03452 | 0,0342 | 0,03525 | 0,03106 |
| 529,9863 | 0,03526 | 0,03495 | 0,036 | 0,03186 |
| 530,02348 | 0,03599 | 0,0357 | 0,03676 | 0,03269 |
| 530,06067 | 0,03672 | 0,03644 | 0,03752 | 0,03352 |
| 530,09785 | 0,03743 | 0,03718 | 0,03827 | 0,03437 |
| 530,13503 | 0,03812 | 0,0379 | 0,03901 | 0,03521 |
| 530,17221 | 0,03879 | 0,0386 | 0,03973 | 0,03606 |
| 530,20939 | 0,03943 | 0,03928 | 0,04044 | 0,0369 |
| 530,24658 | 0,04004 | 0,03994 | 0,04113 | 0,03772 |
| 530,28376 | 0,04061 | 0,04058 | 0,04179 | 0,03853 |
| 530,32094 | 0,04115 | 0,04119 | 0,04242 | 0,03932 |
| 530,35812 | 0,04165 | 0,04177 | 0,04301 | 0,04008 |
| 530,3953 | 0,0421 | 0,04232 | 0,04357 | 0,04081 |
| 530,43249 | 0,04251 | 0,04285 | 0,04409 | 0,04151 |
| 530,46967 | 0,04288 | 0,04335 | 0,04458 | 0,04217 |
| 530,50685 | 0,04321 | 0,04383 | 0,04501 | 0,04281 |
| 530,54403 | 0,0435 | 0,04429 | 0,04541 | 0,0434 |
| 530,58121 | 0,04376 | 0,04473 | 0,04578 | 0,04396 |
| 530,6184 | 0,04398 | 0,04516 | 0,04611 | 0,04448 |
| 530,65558 | 0,04418 | 0,04558 | 0,04642 | 0,04498 |
| 530,69276 | 0,04437 | 0,04599 | 0,0467 | 0,04546 |
| 530,72994 | 0,04454 | 0,04642 | 0,04696 | 0,04592 |
| 530,76712 | 0,04471 | 0,04685 | 0,04721 | 0,04637 |
| 530,80431 | 0,04488 | 0,0473 | 0,04746 | 0,04682 |
| 530,84149 | 0,04507 | 0,04777 | 0,04772 | 0,04727 |
| 530,87867 | 0,04527 | 0,04828 | 0,04799 | 0,04774 |
| 530,91585 | 0,04551 | 0,04881 | 0,04829 | 0,04823 |
| 530,95303 | 0,04577 | 0,04939 | 0,04863 | 0,04874 |
| 530,99022 | 0,04609 | 0,05002 | 0,04901 | 0,04931 |
| 531,0274 | 0,04647 | 0,05071 | 0,04944 | 0,04992 |
| 531,06458 | 0,0469 | 0,05144 | 0,04993 | 0,05058 |
| 531,10176 | 0,04739 | 0,05223 | 0,05048 | 0,05129 |
| 531,13894 | 0,04794 | 0,05306 | 0,0511 | 0,05207 |
| 531,17613 | 0,04857 | 0,05396 | 0,05181 | 0,05292 |
| 531,21331 | 0,04928 | 0,05491 | 0,05258 | 0,05385 |
| 531,25049 | 0,05006 | 0,05591 | 0,05342 | 0,05483 |
| 531,28767 | 0,05091 | 0,05694 | 0,05433 | 0,05588 |
| 531,32485 | 0,05182 | 0,05801 | 0,05531 | 0,05699 |
| 531,36204 | 0,05279 | 0,0591 | 0,05635 | 0,05815 |
| 531,39922 | 0,05383 | 0,06021 | 0,05745 | 0,05936 |
| 531,4364 | 0,05492 | 0,06133 | 0,05859 | 0,06061 |
| 531,47358 | 0,05605 | 0,06244 | 0,05976 | 0,06188 |
| 531,51076 | 0,05721 | 0,06353 | 0,06096 | 0,06316 |
| 531,54795 | 0,05839 | 0,0646 | 0,06216 | 0,06445 |
| 531,58513 | 0,05959 | 0,06563 | 0,06336 | 0,06572 |
| 531,62231 | 0,06079 | 0,0666 | 0,06455 | 0,06697 |
| 531,65949 | 0,06198 | 0,06751 | 0,0657 | 0,06818 |
| 531,69667 | 0,06315 | 0,06835 | 0,06681 | 0,06933 |
| 531,73386 | 0,0643 | 0,06912 | 0,06787 | 0,07043 |
| 531,77104 | 0,06541 | 0,06981 | 0,06887 | 0,07146 |
| 531,80822 | 0,06648 | 0,07041 | 0,06979 | 0,07241 |
| 531,8454 | 0,0675 | 0,07091 | 0,07063 | 0,07327 |
| 531,88258 | 0,06845 | 0,07132 | 0,07139 | 0,07403 |
| 531,91977 | 0,06936 | 0,07165 | 0,07207 | 0,07472 |
| 531,95695 | 0,0702 | 0,0719 | 0,07266 | 0,07531 |
| 531,99413 | 0,07099 | 0,07207 | 0,07317 | 0,07582 |
| 532,03131 | 0,07172 | 0,07216 | 0,07359 | 0,07624 |
| 532,06849 | 0,07239 | 0,07219 | 0,07393 | 0,07658 |
| 532,10568 | 0,07301 | 0,07217 | 0,07422 | 0,07686 |
| 532,14286 | 0,07358 | 0,07212 | 0,07445 | 0,07708 |
| 532,18004 | 0,07412 | 0,07204 | 0,07463 | 0,07727 |
| 532,21722 | 0,07463 | 0,07195 | 0,07478 | 0,07742 |
| 532,2544 | 0,07512 | 0,07186 | 0,07491 | 0,07755 |
| 532,29159 | 0,07559 | 0,07179 | 0,07503 | 0,07769 |
| 532,32877 | 0,07607 | 0,07175 | 0,07516 | 0,07784 |
| 532,36595 | 0,07655 | 0,07175 | 0,07531 | 0,07801 |
| 532,40313 | 0,07706 | 0,07181 | 0,07548 | 0,07822 |
| 532,44031 | 0,07758 | 0,07192 | 0,0757 | 0,07848 |
| 532,4775 | 0,07815 | 0,07213 | 0,07598 | 0,0788 |
| 532,51468 | 0,07876 | 0,07242 | 0,07631 | 0,0792 |
| 532,55186 | 0,07941 | 0,07279 | 0,07671 | 0,07967 |
| 532,58904 | 0,08012 | 0,07324 | 0,07717 | 0,08021 |
| 532,62622 | 0,08088 | 0,07379 | 0,0777 | 0,08083 |
| 532,66341 | 0,08169 | 0,07442 | 0,07833 | 0,08154 |
| 532,70059 | 0,08258 | 0,07516 | 0,07902 | 0,08234 |
| 532,73777 | 0,08351 | 0,07597 | 0,07979 | 0,0832 |
| 532,77495 | 0,08449 | 0,07685 | 0,08062 | 0,08414 |
| 532,81213 | 0,08551 | 0,07779 | 0,08151 | 0,08514 |
| 532,84932 | 0,08657 | 0,07878 | 0,08246 | 0,08619 |
| 532,8865 | 0,08766 | 0,07982 | 0,08346 | 0,0873 |
| 532,92368 | 0,08878 | 0,08088 | 0,0845 | 0,08845 |
| 532,96086 | 0,0899 | 0,08196 | 0,08557 | 0,08962 |
| 532,99804 | 0,09102 | 0,08304 | 0,08665 | 0,0908 |
| 533,03523 | 0,09214 | 0,08411 | 0,08776 | 0,09199 |
| 533,07241 | 0,09324 | 0,08516 | 0,08886 | 0,09319 |
| 533,10959 | 0,0943 | 0,08617 | 0,08997 | 0,09436 |
| 533,14677 | 0,09532 | 0,08713 | 0,09106 | 0,09552 |
| 533,18395 | 0,09629 | 0,08803 | 0,09213 | 0,09664 |
| 533,22114 | 0,09721 | 0,08887 | 0,09319 | 0,09774 |
| 533,25832 | 0,09807 | 0,08965 | 0,09421 | 0,0988 |
| 533,2955 | 0,09886 | 0,09035 | 0,09521 | 0,09982 |
| 533,33268 | 0,09956 | 0,09097 | 0,09617 | 0,10079 |
| 533,36986 | 0,1002 | 0,09152 | 0,0971 | 0,10171 |
| 533,40705 | 0,10076 | 0,092 | 0,09799 | 0,10259 |
| 533,44423 | 0,10125 | 0,09241 | 0,09886 | 0,10343 |
| 533,48141 | 0,10167 | 0,09276 | 0,0997 | 0,10423 |
| 533,51859 | 0,10202 | 0,09306 | 0,1005 | 0,10499 |
| 533,55577 | 0,1023 | 0,09331 | 0,10128 | 0,10571 |
| 533,59295 | 0,10253 | 0,09353 | 0,10204 | 0,10639 |
| 533,63014 | 0,10271 | 0,09372 | 0,10277 | 0,10704 |
| 533,66732 | 0,10285 | 0,09391 | 0,10349 | 0,10766 |
| 533,7045 | 0,10296 | 0,09409 | 0,10419 | 0,10826 |
| 533,74168 | 0,10303 | 0,09429 | 0,10488 | 0,10882 |
| 533,77886 | 0,10309 | 0,09452 | 0,10555 | 0,10935 |
| 533,81605 | 0,10314 | 0,09478 | 0,1062 | 0,10985 |
| 533,85323 | 0,10318 | 0,09507 | 0,10683 | 0,11033 |
| 533,89041 | 0,10322 | 0,09542 | 0,10745 | 0,11077 |
| 533,92759 | 0,10326 | 0,09582 | 0,10803 | 0,11117 |
| 533,96477 | 0,10331 | 0,09629 | 0,10859 | 0,11152 |
| 534,00196 | 0,10336 | 0,09681 | 0,1091 | 0,11182 |
| 534,03914 | 0,10343 | 0,0974 | 0,10957 | 0,11206 |
| 534,07632 | 0,1035 | 0,09804 | 0,10998 | 0,11223 |
| 534,1135 | 0,10357 | 0,09873 | 0,11033 | 0,11234 |
| 534,15068 | 0,10365 | 0,09946 | 0,11062 | 0,11236 |
| 534,18787 | 0,10372 | 0,10024 | 0,11081 | 0,11227 |
| 534,22505 | 0,10377 | 0,10103 | 0,1109 | 0,11209 |
| 534,26223 | 0,10381 | 0,10184 | 0,1109 | 0,11181 |
| 534,29941 | 0,10383 | 0,10264 | 0,11079 | 0,11142 |
| 534,33659 | 0,10381 | 0,10342 | 0,11057 | 0,11092 |
| 534,37378 | 0,10374 | 0,10416 | 0,11023 | 0,1103 |
| 534,41096 | 0,10362 | 0,10485 | 0,10974 | 0,10954 |
| 534,44814 | 0,10344 | 0,10546 | 0,10913 | 0,10867 |
| 534,48532 | 0,1032 | 0,106 | 0,10839 | 0,1077 |
| 534,5225 | 0,10289 | 0,10643 | 0,10753 | 0,10662 |
| 534,55969 | 0,10251 | 0,10677 | 0,10655 | 0,10544 |
| 534,59687 | 0,10203 | 0,10695 | 0,10545 | 0,10415 |
| 534,63405 | 0,10147 | 0,10699 | 0,10423 | 0,10279 |
| 534,67123 | 0,10084 | 0,1069 | 0,10292 | 0,10136 |
| 534,70841 | 0,10014 | 0,10668 | 0,10153 | 0,09989 |
| 534,7456 | 0,09937 | 0,10631 | 0,10007 | 0,09838 |
| 534,78278 | 0,09853 | 0,10579 | 0,09857 | 0,09685 |
| 534,81996 | 0,09762 | 0,10512 | 0,09702 | 0,09532 |
| 534,85714 | 0,09668 | 0,10432 | 0,09546 | 0,09382 |
| 534,89432 | 0,0957 | 0,10341 | 0,09391 | 0,09236 |
| 534,93151 | 0,09471 | 0,1024 | 0,09238 | 0,09096 |
| 534,96869 | 0,0937 | 0,10131 | 0,0909 | 0,08962 |
| 535,00587 | 0,09272 | 0,10015 | 0,08949 | 0,08839 |
| 535,04305 | 0,09176 | 0,09894 | 0,08817 | 0,08729 |
| 535,08023 | 0,09085 | 0,09772 | 0,08696 | 0,0863 |
| 535,11742 | 0,09 | 0,09649 | 0,08587 | 0,08546 |
| 535,1546 | 0,08922 | 0,0953 | 0,08492 | 0,08475 |
| 535,19178 | 0,08853 | 0,09414 | 0,08412 | 0,0842 |
| 535,22896 | 0,08796 | 0,09308 | 0,08348 | 0,08383 |
| 535,26614 | 0,08751 | 0,09211 | 0,08303 | 0,08364 |
| 535,30333 | 0,08718 | 0,09125 | 0,08278 | 0,08361 |
| 535,34051 | 0,08698 | 0,09052 | 0,0827 | 0,08374 |
| 535,37769 | 0,08691 | 0,08993 | 0,0828 | 0,08403 |
| 535,41487 | 0,08698 | 0,08949 | 0,08308 | 0,08447 |
| 535,45205 | 0,08722 | 0,08925 | 0,08354 | 0,08508 |
| 535,48924 | 0,08758 | 0,08916 | 0,08421 | 0,08584 |
| 535,52642 | 0,08806 | 0,08924 | 0,08504 | 0,08671 |
| 535,5636 | 0,08866 | 0,08948 | 0,08603 | 0,08768 |
| 535,60078 | 0,08937 | 0,08987 | 0,08715 | 0,08875 |
| 535,63796 | 0,09019 | 0,09042 | 0,0884 | 0,08991 |
| 535,67515 | 0,0911 | 0,09112 | 0,08977 | 0,09113 |
| 535,71233 | 0,09206 | 0,09193 | 0,09125 | 0,0924 |
| 535,74951 | 0,09307 | 0,09284 | 0,0928 | 0,09369 |
| 535,78669 | 0,09412 | 0,09383 | 0,09442 | 0,09499 |
| 535,82387 | 0,09517 | 0,09488 | 0,09607 | 0,09629 |
| 535,86106 | 0,09623 | 0,09598 | 0,09774 | 0,09757 |
| 535,89824 | 0,09725 | 0,09708 | 0,09943 | 0,09881 |
| 535,93542 | 0,09824 | 0,09818 | 0,10109 | 0,1 |
| 535,9726 | 0,09918 | 0,09925 | 0,10272 | 0,10114 |
| 536,00978 | 0,10005 | 0,10027 | 0,10431 | 0,10221 |
| 536,04697 | 0,10084 | 0,10124 | 0,10584 | 0,10322 |
| 536,08415 | 0,10153 | 0,1021 | 0,1073 | 0,10413 |
| 536,12133 | 0,10213 | 0,10286 | 0,10867 | 0,10496 |
| 536,15851 | 0,10263 | 0,10353 | 0,10993 | 0,1057 |
| 536,19569 | 0,10303 | 0,10408 | 0,11108 | 0,10636 |
| 536,23288 | 0,10333 | 0,10451 | 0,11213 | 0,10694 |
| 536,27006 | 0,10351 | 0,10481 | 0,11307 | 0,10743 |
| 536,30724 | 0,10359 | 0,10497 | 0,11389 | 0,10782 |
| 536,34442 | 0,10358 | 0,10502 | 0,11457 | 0,10812 |
| 536,3816 | 0,1035 | 0,10496 | 0,11511 | 0,10835 |
| 536,41879 | 0,10334 | 0,1048 | 0,11553 | 0,10851 |
| 536,45597 | 0,10312 | 0,10455 | 0,11583 | 0,10859 |
| 536,49315 | 0,10283 | 0,1042 | 0,11601 | 0,1086 |
| 536,53033 | 0,1025 | 0,10377 | 0,11606 | 0,10852 |
| 536,56751 | 0,10215 | 0,1033 | 0,11596 | 0,10838 |
| 536,6047 | 0,10178 | 0,10279 | 0,11573 | 0,10816 |
| 536,64188 | 0,10139 | 0,10225 | 0,11539 | 0,10788 |
| 536,67906 | 0,101 | 0,1017 | 0,11493 | 0,10753 |
| 536,71624 | 0,10063 | 0,10114 | 0,11436 | 0,1071 |
| 536,75342 | 0,10026 | 0,1006 | 0,11367 | 0,10659 |
| 536,79061 | 0,09992 | 0,10008 | 0,11284 | 0,10601 |
| 536,82779 | 0,09959 | 0,09959 | 0,11191 | 0,10535 |
| 536,86497 | 0,09929 | 0,09913 | 0,11088 | 0,10463 |
| 536,90215 | 0,09901 | 0,09872 | 0,10975 | 0,10383 |
| 536,93933 | 0,09876 | 0,09835 | 0,10854 | 0,10295 |
| 536,97652 | 0,09853 | 0,09803 | 0,10723 | 0,102 |
| 537,0137 | 0,09831 | 0,09775 | 0,10584 | 0,10099 |
| 537,05088 | 0,0981 | 0,0975 | 0,10439 | 0,09992 |
| 537,08806 | 0,09789 | 0,0973 | 0,10289 | 0,09881 |
| 537,12524 | 0,09768 | 0,09712 | 0,10136 | 0,09766 |
| 537,16243 | 0,09746 | 0,09697 | 0,09979 | 0,09647 |
| 537,19961 | 0,09723 | 0,09683 | 0,09822 | 0,09528 |
| 537,23679 | 0,09697 | 0,0967 | 0,09666 | 0,09409 |
| 537,27397 | 0,09669 | 0,09657 | 0,09513 | 0,09291 |
| 537,31115 | 0,09638 | 0,09643 | 0,09365 | 0,09177 |
| 537,34834 | 0,09603 | 0,09629 | 0,09222 | 0,09067 |
| 537,38552 | 0,09565 | 0,09613 | 0,09088 | 0,08966 |
| 537,4227 | 0,09524 | 0,09595 | 0,08964 | 0,08874 |
| 537,45988 | 0,09481 | 0,09575 | 0,08853 | 0,08792 |
| 537,49706 | 0,09436 | 0,09554 | 0,08756 | 0,08721 |
| 537,53425 | 0,09389 | 0,09532 | 0,08673 | 0,08664 |
| 537,57143 | 0,09341 | 0,09509 | 0,08606 | 0,08622 |
| 537,60861 | 0,09295 | 0,09486 | 0,08555 | 0,08599 |
| 537,64579 | 0,09251 | 0,09463 | 0,08526 | 0,08593 |
| 537,68297 | 0,0921 | 0,09443 | 0,08517 | 0,08605 |
| 537,72016 | 0,09173 | 0,09426 | 0,08528 | 0,08635 |
| 537,75734 | 0,09145 | 0,09414 | 0,08558 | 0,08683 |
| 537,79452 | 0,09125 | 0,09408 | 0,08608 | 0,08754 |
| 537,8317 | 0,09114 | 0,0941 | 0,08678 | 0,08845 |
| 537,86888 | 0,09114 | 0,0942 | 0,08772 | 0,08954 |
| 537,90607 | 0,09125 | 0,0944 | 0,08885 | 0,09081 |
| 537,94325 | 0,09151 | 0,09471 | 0,09015 | 0,09224 |
| 537,98043 | 0,09194 | 0,09517 | 0,09163 | 0,09383 |
| 538,01761 | 0,09251 | 0,09576 | 0,09325 | 0,0956 |
| 538,05479 | 0,09323 | 0,09648 | 0,09502 | 0,09749 |
| 538,09198 | 0,09409 | 0,09734 | 0,09694 | 0,09948 |
| 538,12916 | 0,09511 | 0,09833 | 0,09896 | 0,10156 |
| 538,16634 | 0,09629 | 0,09946 | 0,10105 | 0,1037 |
| 538,20352 | 0,09761 | 0,10073 | 0,10318 | 0,10589 |
| 538,2407 | 0,09904 | 0,10212 | 0,10535 | 0,10808 |
| 538,27789 | 0,10057 | 0,10359 | 0,10752 | 0,11026 |
| 538,31507 | 0,10217 | 0,10514 | 0,10966 | 0,1124 |
| 538,35225 | 0,10383 | 0,10674 | 0,11172 | 0,11446 |
| 538,38943 | 0,10552 | 0,10838 | 0,1137 | 0,11643 |
| 538,42661 | 0,1072 | 0,11002 | 0,11557 | 0,11827 |
| 538,4638 | 0,10885 | 0,11162 | 0,11729 | 0,11994 |
| 538,50098 | 0,11043 | 0,11316 | 0,11883 | 0,12143 |
| 538,53816 | 0,11193 | 0,11462 | 0,12015 | 0,12273 |
| 538,57534 | 0,1133 | 0,11597 | 0,12126 | 0,12383 |
| 538,61252 | 0,11449 | 0,11715 | 0,12214 | 0,1247 |
| 538,64971 | 0,11551 | 0,11814 | 0,12278 | 0,12529 |
| 538,68689 | 0,11634 | 0,11894 | 0,12318 | 0,12563 |
| 538,72407 | 0,11696 | 0,11953 | 0,12329 | 0,12572 |
| 538,76125 | 0,11735 | 0,1199 | 0,12313 | 0,12557 |
| 538,79843 | 0,11747 | 0,12003 | 0,12272 | 0,12517 |
| 538,83562 | 0,11733 | 0,11986 | 0,12207 | 0,12455 |
| 538,8728 | 0,11696 | 0,11944 | 0,12121 | 0,12364 |
| 538,90998 | 0,11635 | 0,11879 | 0,12015 | 0,12254 |
| 538,94716 | 0,11553 | 0,11791 | 0,11886 | 0,12126 |
| 538,98434 | 0,11449 | 0,11681 | 0,11742 | 0,11982 |
| 539,02153 | 0,11322 | 0,11549 | 0,11585 | 0,11823 |
| 539,05871 | 0,11179 | 0,11397 | 0,11417 | 0,1165 |
| 539,09589 | 0,11021 | 0,1123 | 0,11241 | 0,11467 |
| 539,13307 | 0,10853 | 0,11051 | 0,11059 | 0,11277 |
| 539,17025 | 0,10675 | 0,10862 | 0,10873 | 0,11082 |
| 539,20744 | 0,10491 | 0,10665 | 0,10687 | 0,10884 |
| 539,24462 | 0,10302 | 0,10464 | 0,10502 | 0,10684 |
| 539,2818 | 0,10114 | 0,1026 | 0,10319 | 0,10484 |
| 539,31898 | 0,09927 | 0,10058 | 0,10139 | 0,10287 |
| 539,35616 | 0,09743 | 0,09859 | 0,09964 | 0,10092 |
| 539,39335 | 0,09565 | 0,09664 | 0,09795 | 0,099 |
| 539,43053 | 0,09394 | 0,09475 | 0,0963 | 0,09711 |
| 539,46771 | 0,09231 | 0,09296 | 0,0947 | 0,09526 |
| 539,50489 | 0,09077 | 0,09124 | 0,09314 | 0,09346 |
| 539,54207 | 0,08931 | 0,08961 | 0,09162 | 0,09169 |
| 539,57926 | 0,08793 | 0,08805 | 0,09012 | 0,08994 |
| 539,61644 | 0,08662 | 0,08658 | 0,08863 | 0,08822 |
| 539,65362 | 0,0854 | 0,08518 | 0,08714 | 0,08652 |
| 539,6908 | 0,08423 | 0,08385 | 0,08565 | 0,08482 |
| 539,72798 | 0,0831 | 0,08256 | 0,08414 | 0,08314 |
| 539,76517 | 0,082 | 0,0813 | 0,08261 | 0,08145 |
| 539,80235 | 0,08091 | 0,08007 | 0,08104 | 0,07976 |
| 539,83953 | 0,07983 | 0,07884 | 0,07943 | 0,07807 |
| 539,87671 | 0,07872 | 0,07761 | 0,07779 | 0,07637 |
| 539,91389 | 0,07759 | 0,07636 | 0,07611 | 0,07467 |
| 539,95108 | 0,07641 | 0,07507 | 0,07439 | 0,07297 |
| 539,98826 | 0,07519 | 0,07375 | 0,07265 | 0,07126 |
| 540,02544 | 0,07392 | 0,07239 | 0,07088 | 0,06957 |
| 540,06262 | 0,07257 | 0,07098 | 0,0691 | 0,06788 |
| 540,0998 | 0,07117 | 0,06951 | 0,06731 | 0,06621 |
| 540,13699 | 0,06971 | 0,068 | 0,06552 | 0,06457 |
| 540,17417 | 0,06819 | 0,06645 | 0,06374 | 0,06296 |
| 540,21135 | 0,06663 | 0,06487 | 0,06198 | 0,06137 |
| 540,24853 | 0,06502 | 0,06326 | 0,06024 | 0,05983 |
| 540,28571 | 0,06338 | 0,06163 | 0,05854 | 0,05832 |
| 540,3229 | 0,06172 | 0,06 | 0,05687 | 0,05684 |
| 540,36008 | 0,06005 | 0,05838 | 0,05524 | 0,05542 |
| 540,39726 | 0,05839 | 0,05677 | 0,05364 | 0,05402 |
| 540,43444 | 0,05673 | 0,05519 | 0,05208 | 0,05266 |
| 540,47162 | 0,0551 | 0,05364 | 0,05055 | 0,05132 |
| 540,50881 | 0,0535 | 0,05214 | 0,04906 | 0,05001 |
| 540,54599 | 0,05195 | 0,05069 | 0,04759 | 0,0487 |
| 540,58317 | 0,05043 | 0,04931 | 0,04613 | 0,0474 |
| 540,62035 | 0,04897 | 0,04797 | 0,04469 | 0,0461 |
| 540,65753 | 0,04755 | 0,0467 | 0,04325 | 0,04479 |
| 540,69472 | 0,04619 | 0,04548 | 0,04181 | 0,04346 |
| 540,7319 | 0,04488 | 0,04433 | 0,04036 | 0,04211 |
| 540,76908 | 0,04361 | 0,04322 | 0,0389 | 0,04073 |
| 540,80626 | 0,04238 | 0,04216 | 0,03742 | 0,03931 |
| 540,84344 | 0,04119 | 0,04113 | 0,03592 | 0,03786 |
| 540,88063 | 0,04003 | 0,04013 | 0,03441 | 0,03638 |
| 540,91781 | 0,03889 | 0,03915 | 0,03287 | 0,03486 |
| 540,95499 | 0,03776 | 0,03818 | 0,03132 | 0,03331 |
| 540,99217 | 0,03664 | 0,03721 | 0,02975 | 0,03173 |
| 541,02935 | 0,03553 | 0,03624 | 0,02818 | 0,03013 |
| 541,06654 | 0,0344 | 0,03525 | 0,02661 | 0,02851 |
| 541,10372 | 0,03327 | 0,03423 | 0,02504 | 0,02689 |
| 541,1409 | 0,03211 | 0,0332 | 0,02348 | 0,02526 |
| 541,17808 | 0,03094 | 0,03212 | 0,02194 | 0,02365 |
| 541,21526 | 0,02975 | 0,03102 | 0,02044 | 0,02206 |
| 541,25245 | 0,02854 | 0,02988 | 0,01896 | 0,02049 |
| 541,28963 | 0,02731 | 0,02871 | 0,01753 | 0,01897 |
| 541,32681 | 0,02606 | 0,0275 | 0,01615 | 0,01749 |
| 541,36399 | 0,0248 | 0,02627 | 0,01483 | 0,01605 |
| 541,40117 | 0,02353 | 0,02501 | 0,01358 | 0,01468 |
| 541,43836 | 0,02226 | 0,02373 | 0,01238 | 0,01338 |
| 541,47554 | 0,02098 | 0,02245 | 0,01125 | 0,01216 |
| 541,51272 | 0,01972 | 0,02115 | 0,01019 | 0,011 |
| 541,5499 | 0,01847 | 0,01986 | 0,00921 | 0,00991 |
| 541,58708 | 0,01725 | 0,01858 | 0,0083 | 0,0089 |
| 541,62427 | 0,01605 | 0,01731 | 0,00746 | 0,00797 |
| 541,66145 | 0,01488 | 0,01607 | 0,00669 | 0,00712 |
| 541,69863 | 0,01376 | 0,01487 | 0,00598 | 0,00635 |
| 541,73581 | 0,01268 | 0,01369 | 0,00534 | 0,00564 |
| 541,77299 | 0,01165 | 0,01256 | 0,00477 | 0,005 |
| 541,81018 | 0,01068 | 0,01148 | 0,00425 | 0,00442 |
| 541,84736 | 0,00976 | 0,01046 | 0,00379 | 0,00392 |
| 541,88454 | 0,0089 | 0,00949 | 0,00337 | 0,00347 |
| 541,92172 | 0,00809 | 0,00857 | 0,003 | 0,00307 |
| 541,9589 | 0,00735 | 0,00771 | 0,00267 | 0,00272 |
| 541,99609 | 0,00668 | 0,00692 | 0,00239 | 0,00241 |
| 542,03327 | 0,00605 | 0,00619 | 0,00213 | 0,00214 |
| 542,07045 | 0,00549 | 0,00552 | 0,00191 | 0,00191 |
| 542,10763 | 0,00497 | 0,0049 | 0,00171 | 0,0017 |
| 542,14481 | 0,0045 | 0,00434 | 0,00154 | 0,00153 |
| 542,182 | 0,00409 | 0,00383 | 0,00138 | 0,00138 |
| 542,21918 | 0,00373 | 0,00338 | 0,00125 | 0,00124 |
| 542,25636 | 0,0034 | 0,00297 | 0,00113 | 0,00113 |
| 542,29354 | 0,00311 | 0,00262 | 0,00103 | 0,00103 |
| 542,33072 | 0,00286 | 0,0023 | 0,00094 | 0,00094 |
| 542,36791 | 0,00263 | 0,00201 | 0,00086 | 0,00087 |
| 542,40509 | 0,00244 | 0,00177 | 0,00078 | 8e-04 |
| 542,44227 | 0,00226 | 0,00155 | 0,00072 | 0,00073 |
| 542,47945 | 0,00211 | 0,00137 | 0,00066 | 0,00068 |
| 542,51663 | 0,00197 | 0,00121 | 0,00061 | 0,00063 |
| 542,55382 | 0,00185 | 0,00107 | 0,00057 | 0,00058 |
| 542,591 | 0,00174 | 0,00095 | 0,00053 | 0,00054 |
| 542,62818 | 0,00164 | 0,00085 | 0,00049 | 5e-04 |
| 542,66536 | 0,00155 | 0,00076 | 0,00045 | 0,00046 |
| 542,70254 | 0,00146 | 0,00069 | 0,00042 | 0,00042 |
| 542,73973 | 0,00138 | 0,00063 | 4e-04 | 0,00039 |
| 542,77691 | 0,00131 | 0,00057 | 0,00037 | 0,00036 |
| 542,81409 | 0,00124 | 0,00052 | 0,00035 | 0,00032 |
| 542,85127 | 0,00117 | 0,00048 | 0,00032 | 0,00029 |
| 542,88845 | 0,0011 | 0,00045 | 3e-04 | 0,00027 |
| 542,92564 | 0,00103 | 0,00041 | 0,00029 | 0,00024 |
| 542,96282 | 0,00097 | 0,00039 | 0,00027 | 0,00022 |
| 543 | 9e-04 | 0,00036 | 0,00025 | 0,00019 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 2e-05 | 5e-05 | 0 | 0 |
| 524,03718 | 2e-05 | 6e-05 | 0 | 0 |
| 524,07436 | 2e-05 | 6e-05 | 1e-05 | 0 |
| 524,11155 | 3e-05 | 6e-05 | 1e-05 | 0 |
| 524,14873 | 3e-05 | 6e-05 | 1e-05 | 0 |
| 524,18591 | 4e-05 | 6e-05 | 1e-05 | 0 |
| 524,22309 | 4e-05 | 6e-05 | 1e-05 | 0 |
| 524,26027 | 5e-05 | 6e-05 | 1e-05 | 0 |
| 524,29746 | 5e-05 | 6e-05 | 1e-05 | 0 |
| 524,33464 | 6e-05 | 6e-05 | 2e-05 | 0 |
| 524,37182 | 7e-05 | 6e-05 | 2e-05 | 0 |
| 524,409 | 8e-05 | 6e-05 | 2e-05 | 0 |
| 524,44618 | 8e-05 | 6e-05 | 2e-05 | 0 |
| 524,48337 | 9e-05 | 6e-05 | 3e-05 | 0 |
| 524,52055 | 1e-04 | 6e-05 | 3e-05 | 1e-05 |
| 524,55773 | 0,00011 | 6e-05 | 3e-05 | 1e-05 |
| 524,59491 | 0,00012 | 6e-05 | 4e-05 | 1e-05 |
| 524,63209 | 0,00013 | 6e-05 | 4e-05 | 1e-05 |
| 524,66928 | 0,00014 | 6e-05 | 4e-05 | 1e-05 |
| 524,70646 | 0,00014 | 6e-05 | 5e-05 | 1e-05 |
| 524,74364 | 0,00015 | 6e-05 | 5e-05 | 2e-05 |
| 524,78082 | 0,00016 | 7e-05 | 5e-05 | 2e-05 |
| 524,818 | 0,00017 | 7e-05 | 6e-05 | 3e-05 |
| 524,85519 | 0,00018 | 7e-05 | 6e-05 | 3e-05 |
| 524,89237 | 0,00019 | 8e-05 | 6e-05 | 4e-05 |
| 524,92955 | 2e-04 | 8e-05 | 7e-05 | 4e-05 |
| 524,96673 | 2e-04 | 9e-05 | 7e-05 | 5e-05 |
| 525,00391 | 0,00021 | 1e-04 | 7e-05 | 6e-05 |
| 525,0411 | 0,00022 | 1e-04 | 8e-05 | 6e-05 |
| 525,07828 | 0,00022 | 0,00011 | 8e-05 | 7e-05 |
| 525,11546 | 0,00023 | 0,00012 | 8e-05 | 8e-05 |
| 525,15264 | 0,00024 | 0,00013 | 9e-05 | 9e-05 |
| 525,18982 | 0,00024 | 0,00014 | 9e-05 | 0,00011 |
| 525,22701 | 0,00025 | 0,00015 | 1e-04 | 0,00012 |
| 525,26419 | 0,00026 | 0,00017 | 0,00011 | 0,00014 |
| 525,30137 | 0,00026 | 0,00018 | 0,00012 | 0,00015 |
| 525,33855 | 0,00027 | 0,00019 | 0,00013 | 0,00017 |
| 525,37573 | 0,00028 | 0,00021 | 0,00014 | 0,00019 |
| 525,41292 | 0,00029 | 0,00022 | 0,00015 | 0,00021 |
| 525,4501 | 0,00029 | 0,00024 | 0,00017 | 0,00024 |
| 525,48728 | 3e-04 | 0,00026 | 0,00019 | 0,00026 |
| 525,52446 | 0,00031 | 0,00027 | 0,00022 | 0,00029 |
| 525,56164 | 0,00032 | 0,00029 | 0,00025 | 0,00033 |
| 525,59883 | 0,00034 | 0,00031 | 0,00028 | 0,00036 |
| 525,63601 | 0,00035 | 0,00033 | 0,00031 | 4e-04 |
| 525,67319 | 0,00037 | 0,00036 | 0,00035 | 0,00044 |
| 525,71037 | 0,00038 | 0,00038 | 0,00039 | 0,00049 |
| 525,74755 | 4e-04 | 0,00041 | 0,00044 | 0,00054 |
| 525,78474 | 0,00042 | 0,00044 | 0,00049 | 0,00059 |
| 525,82192 | 0,00045 | 0,00047 | 0,00054 | 0,00065 |
| 525,8591 | 0,00048 | 5e-04 | 6e-04 | 0,00071 |
| 525,89628 | 0,00051 | 0,00053 | 0,00066 | 0,00078 |
| 525,93346 | 0,00054 | 0,00057 | 0,00072 | 0,00085 |
| 525,97065 | 0,00058 | 0,00061 | 0,00079 | 0,00092 |
| 526,00783 | 0,00062 | 0,00065 | 0,00085 | 0,00099 |
| 526,04501 | 0,00066 | 0,00069 | 0,00092 | 0,00107 |
| 526,08219 | 0,00071 | 0,00074 | 0,00099 | 0,00115 |
| 526,11937 | 0,00077 | 0,00079 | 0,00105 | 0,00123 |
| 526,15656 | 0,00082 | 0,00084 | 0,00112 | 0,00132 |
| 526,19374 | 0,00089 | 0,00089 | 0,00119 | 0,0014 |
| 526,23092 | 0,00095 | 0,00095 | 0,00125 | 0,00148 |
| 526,2681 | 0,00102 | 0,00101 | 0,00131 | 0,00156 |
| 526,30528 | 0,0011 | 0,00107 | 0,00137 | 0,00164 |
| 526,34247 | 0,00118 | 0,00114 | 0,00142 | 0,00172 |
| 526,37965 | 0,00126 | 0,0012 | 0,00147 | 0,00179 |
| 526,41683 | 0,00135 | 0,00128 | 0,00152 | 0,00185 |
| 526,45401 | 0,00144 | 0,00135 | 0,00156 | 0,00191 |
| 526,49119 | 0,00153 | 0,00143 | 0,0016 | 0,00197 |
| 526,52838 | 0,00162 | 0,00151 | 0,00163 | 0,00202 |
| 526,56556 | 0,00172 | 0,00159 | 0,00167 | 0,00207 |
| 526,60274 | 0,00183 | 0,00168 | 0,0017 | 0,00211 |
| 526,63992 | 0,00193 | 0,00178 | 0,00173 | 0,00214 |
| 526,6771 | 0,00204 | 0,00187 | 0,00175 | 0,00217 |
| 526,71429 | 0,00215 | 0,00198 | 0,00178 | 0,00219 |
| 526,75147 | 0,00226 | 0,00209 | 0,00181 | 0,00221 |
| 526,78865 | 0,00237 | 0,0022 | 0,00184 | 0,00223 |
| 526,82583 | 0,00249 | 0,00233 | 0,00187 | 0,00224 |
| 526,86301 | 0,00262 | 0,00246 | 0,00191 | 0,00226 |
| 526,9002 | 0,00275 | 0,00259 | 0,00195 | 0,00227 |
| 526,93738 | 0,00288 | 0,00274 | 0,00199 | 0,00228 |
| 526,97456 | 0,00302 | 0,0029 | 0,00205 | 0,0023 |
| 527,01174 | 0,00317 | 0,00307 | 0,00211 | 0,00232 |
| 527,04892 | 0,00333 | 0,00324 | 0,00218 | 0,00235 |
| 527,08611 | 0,00349 | 0,00343 | 0,00226 | 0,00238 |
| 527,12329 | 0,00367 | 0,00363 | 0,00235 | 0,00242 |
| 527,16047 | 0,00386 | 0,00384 | 0,00246 | 0,00248 |
| 527,19765 | 0,00406 | 0,00407 | 0,00258 | 0,00254 |
| 527,23483 | 0,00427 | 0,0043 | 0,00271 | 0,00262 |
| 527,27202 | 0,0045 | 0,00455 | 0,00285 | 0,0027 |
| 527,3092 | 0,00475 | 0,00481 | 0,00302 | 0,00281 |
| 527,34638 | 0,00501 | 0,00508 | 0,00319 | 0,00293 |
| 527,38356 | 0,00528 | 0,00537 | 0,00339 | 0,00307 |
| 527,42074 | 0,00558 | 0,00567 | 0,0036 | 0,00322 |
| 527,45793 | 0,00588 | 0,00597 | 0,00383 | 0,00339 |
| 527,49511 | 0,0062 | 0,00629 | 0,00408 | 0,00359 |
| 527,53229 | 0,00653 | 0,00662 | 0,00434 | 0,0038 |
| 527,56947 | 0,00688 | 0,00695 | 0,00462 | 0,00403 |
| 527,60665 | 0,00724 | 0,0073 | 0,00492 | 0,00428 |
| 527,64384 | 0,0076 | 0,00764 | 0,00524 | 0,00455 |
| 527,68102 | 0,00797 | 0,008 | 0,00557 | 0,00484 |
| 527,7182 | 0,00834 | 0,00835 | 0,00591 | 0,00515 |
| 527,75538 | 0,00871 | 0,00871 | 0,00627 | 0,00547 |
| 527,79256 | 0,00908 | 0,00906 | 0,00664 | 0,00581 |
| 527,82975 | 0,00944 | 0,00942 | 0,00702 | 0,00617 |
| 527,86693 | 0,00979 | 0,00977 | 0,00741 | 0,00654 |
| 527,90411 | 0,01014 | 0,01011 | 0,0078 | 0,00691 |
| 527,94129 | 0,01047 | 0,01045 | 0,0082 | 0,0073 |
| 527,97847 | 0,01079 | 0,01079 | 0,00859 | 0,00769 |
| 528,01566 | 0,01108 | 0,01111 | 0,00899 | 0,00808 |
| 528,05284 | 0,01137 | 0,01143 | 0,00938 | 0,00847 |
| 528,09002 | 0,01163 | 0,01173 | 0,00976 | 0,00886 |
| 528,1272 | 0,01188 | 0,01202 | 0,01014 | 0,00924 |
| 528,16438 | 0,01211 | 0,01231 | 0,01051 | 0,00962 |
| 528,20157 | 0,01232 | 0,01258 | 0,01087 | 0,00998 |
| 528,23875 | 0,01252 | 0,01283 | 0,01121 | 0,01033 |
| 528,27593 | 0,0127 | 0,01308 | 0,01154 | 0,01067 |
| 528,31311 | 0,01287 | 0,01331 | 0,01186 | 0,011 |
| 528,35029 | 0,01304 | 0,01354 | 0,01217 | 0,0113 |
| 528,38748 | 0,01319 | 0,01375 | 0,01246 | 0,01159 |
| 528,42466 | 0,01335 | 0,01395 | 0,01274 | 0,01187 |
| 528,46184 | 0,0135 | 0,01414 | 0,013 | 0,01213 |
| 528,49902 | 0,01365 | 0,01432 | 0,01326 | 0,01237 |
| 528,5362 | 0,01381 | 0,01449 | 0,0135 | 0,0126 |
| 528,57339 | 0,01398 | 0,01465 | 0,01374 | 0,01282 |
| 528,61057 | 0,01415 | 0,01481 | 0,01397 | 0,01303 |
| 528,64775 | 0,01434 | 0,01496 | 0,01419 | 0,01323 |
| 528,68493 | 0,01454 | 0,0151 | 0,01441 | 0,01342 |
| 528,72211 | 0,01475 | 0,01524 | 0,01462 | 0,01361 |
| 528,7593 | 0,01498 | 0,01538 | 0,01483 | 0,01379 |
| 528,79648 | 0,01522 | 0,01551 | 0,01504 | 0,01397 |
| 528,83366 | 0,01547 | 0,01564 | 0,01524 | 0,01415 |
| 528,87084 | 0,01574 | 0,01578 | 0,01545 | 0,01433 |
| 528,90802 | 0,01602 | 0,01591 | 0,01565 | 0,01451 |
| 528,94521 | 0,01631 | 0,01604 | 0,01585 | 0,01469 |
| 528,98239 | 0,01661 | 0,01617 | 0,01605 | 0,01486 |
| 529,01957 | 0,01692 | 0,01631 | 0,01625 | 0,01504 |
| 529,05675 | 0,01724 | 0,01645 | 0,01644 | 0,01522 |
| 529,09393 | 0,01756 | 0,0166 | 0,01664 | 0,0154 |
| 529,13112 | 0,01788 | 0,01675 | 0,01683 | 0,01557 |
| 529,1683 | 0,01821 | 0,01691 | 0,01702 | 0,01575 |
| 529,20548 | 0,01854 | 0,01707 | 0,01722 | 0,01592 |
| 529,24266 | 0,01887 | 0,01725 | 0,01741 | 0,01609 |
| 529,27984 | 0,01919 | 0,01743 | 0,0176 | 0,01625 |
| 529,31703 | 0,01951 | 0,01762 | 0,01779 | 0,01642 |
| 529,35421 | 0,01984 | 0,01782 | 0,01799 | 0,01658 |
| 529,39139 | 0,02016 | 0,01804 | 0,01819 | 0,01674 |
| 529,42857 | 0,02047 | 0,01826 | 0,0184 | 0,0169 |
| 529,46575 | 0,02079 | 0,01849 | 0,01861 | 0,01707 |
| 529,50294 | 0,02111 | 0,01874 | 0,01884 | 0,01723 |
| 529,54012 | 0,02142 | 0,019 | 0,01907 | 0,0174 |
| 529,5773 | 0,02174 | 0,01928 | 0,01931 | 0,01759 |
| 529,61448 | 0,02207 | 0,01956 | 0,01957 | 0,01778 |
| 529,65166 | 0,0224 | 0,01986 | 0,01984 | 0,01798 |
| 529,68885 | 0,02273 | 0,02017 | 0,02013 | 0,0182 |
| 529,72603 | 0,02307 | 0,0205 | 0,02043 | 0,01843 |
| 529,76321 | 0,02343 | 0,02083 | 0,02074 | 0,01869 |
| 529,80039 | 0,02379 | 0,02118 | 0,02107 | 0,01896 |
| 529,83757 | 0,02416 | 0,02154 | 0,02141 | 0,01926 |
| 529,87476 | 0,02453 | 0,0219 | 0,02176 | 0,01959 |
| 529,91194 | 0,02492 | 0,02227 | 0,02213 | 0,01994 |
| 529,94912 | 0,02532 | 0,02265 | 0,02251 | 0,02031 |
| 529,9863 | 0,02572 | 0,02303 | 0,02289 | 0,02071 |
| 530,02348 | 0,02612 | 0,02341 | 0,02328 | 0,02114 |
| 530,06067 | 0,02653 | 0,02378 | 0,02367 | 0,02159 |
| 530,09785 | 0,02694 | 0,02416 | 0,02406 | 0,02206 |
| 530,13503 | 0,02734 | 0,02452 | 0,02444 | 0,02255 |
| 530,17221 | 0,02774 | 0,02488 | 0,02482 | 0,02306 |
| 530,20939 | 0,02813 | 0,02522 | 0,02519 | 0,02357 |
| 530,24658 | 0,0285 | 0,02554 | 0,02555 | 0,02409 |
| 530,28376 | 0,02886 | 0,02585 | 0,02589 | 0,02462 |
| 530,32094 | 0,0292 | 0,02614 | 0,02621 | 0,02514 |
| 530,35812 | 0,02952 | 0,0264 | 0,02651 | 0,02565 |
| 530,3953 | 0,02982 | 0,02665 | 0,02679 | 0,02615 |
| 530,43249 | 0,03009 | 0,02687 | 0,02704 | 0,02663 |
| 530,46967 | 0,03034 | 0,02707 | 0,02727 | 0,02708 |
| 530,50685 | 0,03056 | 0,02724 | 0,02748 | 0,02751 |
| 530,54403 | 0,03076 | 0,0274 | 0,02766 | 0,02791 |
| 530,58121 | 0,03093 | 0,02753 | 0,02781 | 0,02827 |
| 530,6184 | 0,03108 | 0,02765 | 0,02794 | 0,0286 |
| 530,65558 | 0,03121 | 0,02775 | 0,02806 | 0,02889 |
| 530,69276 | 0,03132 | 0,02784 | 0,02816 | 0,02915 |
| 530,72994 | 0,03142 | 0,02793 | 0,02825 | 0,02937 |
| 530,76712 | 0,03151 | 0,02801 | 0,02833 | 0,02956 |
| 530,80431 | 0,0316 | 0,0281 | 0,02842 | 0,02973 |
| 530,84149 | 0,03169 | 0,02819 | 0,02851 | 0,02987 |
| 530,87867 | 0,03179 | 0,0283 | 0,02861 | 0,02999 |
| 530,91585 | 0,0319 | 0,02842 | 0,02873 | 0,0301 |
| 530,95303 | 0,03204 | 0,02857 | 0,02888 | 0,03022 |
| 530,99022 | 0,0322 | 0,02876 | 0,02906 | 0,03033 |
| 531,0274 | 0,03239 | 0,02897 | 0,02928 | 0,03045 |
| 531,06458 | 0,03262 | 0,02922 | 0,02954 | 0,0306 |
| 531,10176 | 0,03288 | 0,02952 | 0,02986 | 0,03077 |
| 531,13894 | 0,03321 | 0,02986 | 0,03023 | 0,03098 |
| 531,17613 | 0,03357 | 0,03025 | 0,03066 | 0,03121 |
| 531,21331 | 0,03399 | 0,03069 | 0,03114 | 0,03149 |
| 531,25049 | 0,03446 | 0,03117 | 0,03169 | 0,03182 |
| 531,28767 | 0,03498 | 0,03171 | 0,03229 | 0,03219 |
| 531,32485 | 0,03555 | 0,03228 | 0,03297 | 0,03261 |
| 531,36204 | 0,03616 | 0,0329 | 0,0337 | 0,03308 |
| 531,39922 | 0,03682 | 0,03357 | 0,03449 | 0,03359 |
| 531,4364 | 0,03752 | 0,03427 | 0,03532 | 0,03413 |
| 531,47358 | 0,03825 | 0,03499 | 0,03619 | 0,03471 |
| 531,51076 | 0,039 | 0,03574 | 0,0371 | 0,03532 |
| 531,54795 | 0,03977 | 0,0365 | 0,03803 | 0,03596 |
| 531,58513 | 0,04054 | 0,03727 | 0,03898 | 0,0366 |
| 531,62231 | 0,04132 | 0,03805 | 0,03994 | 0,03724 |
| 531,65949 | 0,04208 | 0,03881 | 0,04089 | 0,03788 |
| 531,69667 | 0,04283 | 0,03957 | 0,04183 | 0,03851 |
| 531,73386 | 0,04355 | 0,04031 | 0,04274 | 0,03911 |
| 531,77104 | 0,04424 | 0,04102 | 0,04363 | 0,03968 |
| 531,80822 | 0,0449 | 0,04171 | 0,04447 | 0,04021 |
| 531,8454 | 0,04551 | 0,04237 | 0,04526 | 0,0407 |
| 531,88258 | 0,04607 | 0,04298 | 0,046 | 0,04115 |
| 531,91977 | 0,04658 | 0,04356 | 0,04669 | 0,04155 |
| 531,95695 | 0,04704 | 0,0441 | 0,04732 | 0,0419 |
| 531,99413 | 0,04746 | 0,0446 | 0,04789 | 0,04222 |
| 532,03131 | 0,04783 | 0,04507 | 0,04841 | 0,04249 |
| 532,06849 | 0,04816 | 0,0455 | 0,04887 | 0,04272 |
| 532,10568 | 0,04844 | 0,0459 | 0,04929 | 0,04294 |
| 532,14286 | 0,04869 | 0,04628 | 0,04967 | 0,04314 |
| 532,18004 | 0,04892 | 0,04665 | 0,05003 | 0,04333 |
| 532,21722 | 0,04913 | 0,04701 | 0,05036 | 0,04353 |
| 532,2544 | 0,04934 | 0,04737 | 0,05069 | 0,04374 |
| 532,29159 | 0,04954 | 0,04773 | 0,05102 | 0,04399 |
| 532,32877 | 0,04976 | 0,04812 | 0,05136 | 0,04428 |
| 532,36595 | 0,05001 | 0,04853 | 0,05172 | 0,04462 |
| 532,40313 | 0,05028 | 0,04899 | 0,05212 | 0,04502 |
| 532,44031 | 0,05059 | 0,04948 | 0,05256 | 0,04549 |
| 532,4775 | 0,05096 | 0,05004 | 0,05304 | 0,04603 |
| 532,51468 | 0,05137 | 0,05064 | 0,05358 | 0,04664 |
| 532,55186 | 0,05185 | 0,05132 | 0,05418 | 0,04735 |
| 532,58904 | 0,05241 | 0,05208 | 0,05483 | 0,04815 |
| 532,62622 | 0,05304 | 0,0529 | 0,05555 | 0,04902 |
| 532,66341 | 0,05374 | 0,0538 | 0,05632 | 0,04997 |
| 532,70059 | 0,0545 | 0,05477 | 0,05714 | 0,05098 |
| 532,73777 | 0,05534 | 0,0558 | 0,05801 | 0,05206 |
| 532,77495 | 0,05625 | 0,0569 | 0,05892 | 0,05321 |
| 532,81213 | 0,05722 | 0,05805 | 0,05987 | 0,0544 |
| 532,84932 | 0,05825 | 0,05925 | 0,06083 | 0,05562 |
| 532,8865 | 0,05932 | 0,06048 | 0,0618 | 0,05687 |
| 532,92368 | 0,06043 | 0,06172 | 0,06278 | 0,05812 |
| 532,96086 | 0,06156 | 0,06296 | 0,06375 | 0,05937 |
| 532,99804 | 0,0627 | 0,0642 | 0,0647 | 0,06061 |
| 533,03523 | 0,06385 | 0,06541 | 0,06562 | 0,06182 |
| 533,07241 | 0,06497 | 0,06656 | 0,0665 | 0,06298 |
| 533,10959 | 0,06608 | 0,06766 | 0,06733 | 0,0641 |
| 533,14677 | 0,06714 | 0,06869 | 0,06812 | 0,06516 |
| 533,18395 | 0,06815 | 0,06964 | 0,06885 | 0,06616 |
| 533,22114 | 0,06911 | 0,07049 | 0,06952 | 0,06709 |
| 533,25832 | 0,07001 | 0,07124 | 0,07013 | 0,06794 |
| 533,2955 | 0,07081 | 0,07187 | 0,07067 | 0,06871 |
| 533,33268 | 0,07154 | 0,07238 | 0,07116 | 0,06941 |
| 533,36986 | 0,07219 | 0,07277 | 0,0716 | 0,07004 |
| 533,40705 | 0,07275 | 0,07307 | 0,07199 | 0,07062 |
| 533,44423 | 0,07323 | 0,07325 | 0,07235 | 0,07113 |
| 533,48141 | 0,07364 | 0,07334 | 0,07267 | 0,0716 |
| 533,51859 | 0,07397 | 0,07332 | 0,07297 | 0,07203 |
| 533,55577 | 0,07422 | 0,07322 | 0,07326 | 0,07243 |
| 533,59295 | 0,07442 | 0,07306 | 0,07355 | 0,07283 |
| 533,63014 | 0,07457 | 0,07285 | 0,07384 | 0,07322 |
| 533,66732 | 0,07469 | 0,0726 | 0,07416 | 0,07361 |
| 533,7045 | 0,07478 | 0,07233 | 0,07449 | 0,07403 |
| 533,74168 | 0,07485 | 0,07205 | 0,07486 | 0,07448 |
| 533,77886 | 0,07493 | 0,07179 | 0,07527 | 0,07496 |
| 533,81605 | 0,07501 | 0,07155 | 0,07572 | 0,07549 |
| 533,85323 | 0,07513 | 0,07136 | 0,07621 | 0,07606 |
| 533,89041 | 0,07527 | 0,07121 | 0,07674 | 0,07667 |
| 533,92759 | 0,07546 | 0,07113 | 0,07731 | 0,07732 |
| 533,96477 | 0,07569 | 0,07111 | 0,0779 | 0,07801 |
| 534,00196 | 0,07599 | 0,07119 | 0,07851 | 0,07872 |
| 534,03914 | 0,07636 | 0,07135 | 0,07914 | 0,07946 |
| 534,07632 | 0,07679 | 0,0716 | 0,07976 | 0,0802 |
| 534,1135 | 0,07729 | 0,07192 | 0,08036 | 0,08092 |
| 534,15068 | 0,07785 | 0,07233 | 0,08093 | 0,08162 |
| 534,18787 | 0,07846 | 0,07281 | 0,08146 | 0,08227 |
| 534,22505 | 0,07913 | 0,07336 | 0,08193 | 0,08286 |
| 534,26223 | 0,07984 | 0,07398 | 0,08231 | 0,08336 |
| 534,29941 | 0,08058 | 0,07463 | 0,08259 | 0,08376 |
| 534,33659 | 0,08134 | 0,07531 | 0,08276 | 0,08404 |
| 534,37378 | 0,08209 | 0,076 | 0,08282 | 0,0842 |
| 534,41096 | 0,08283 | 0,07669 | 0,08275 | 0,08422 |
| 534,44814 | 0,08353 | 0,07736 | 0,08256 | 0,08409 |
| 534,48532 | 0,08418 | 0,07799 | 0,08222 | 0,08381 |
| 534,5225 | 0,08475 | 0,07855 | 0,08172 | 0,08334 |
| 534,55969 | 0,08524 | 0,07904 | 0,08108 | 0,08272 |
| 534,59687 | 0,08563 | 0,07945 | 0,08032 | 0,08195 |
| 534,63405 | 0,08592 | 0,07976 | 0,07944 | 0,08104 |
| 534,67123 | 0,08608 | 0,07996 | 0,07846 | 0,07999 |
| 534,70841 | 0,08612 | 0,08003 | 0,07738 | 0,07883 |
| 534,7456 | 0,086 | 0,07996 | 0,07621 | 0,07757 |
| 534,78278 | 0,08575 | 0,07978 | 0,07499 | 0,07622 |
| 534,81996 | 0,08538 | 0,07948 | 0,07374 | 0,07482 |
| 534,85714 | 0,0849 | 0,07907 | 0,07249 | 0,07339 |
| 534,89432 | 0,0843 | 0,07855 | 0,07124 | 0,07195 |
| 534,93151 | 0,08362 | 0,07794 | 0,07004 | 0,07054 |
| 534,96869 | 0,08284 | 0,07724 | 0,06889 | 0,06917 |
| 535,00587 | 0,08202 | 0,07649 | 0,06785 | 0,06788 |
| 535,04305 | 0,08117 | 0,0757 | 0,06692 | 0,0667 |
| 535,08023 | 0,08031 | 0,0749 | 0,06612 | 0,06565 |
| 535,11742 | 0,07947 | 0,07411 | 0,06547 | 0,06473 |
| 535,1546 | 0,07866 | 0,07334 | 0,06497 | 0,06397 |
| 535,19178 | 0,07793 | 0,07264 | 0,06465 | 0,06339 |
| 535,22896 | 0,0773 | 0,07203 | 0,06453 | 0,06299 |
| 535,26614 | 0,07679 | 0,07151 | 0,06462 | 0,06283 |
| 535,30333 | 0,0764 | 0,0711 | 0,06491 | 0,06288 |
| 535,34051 | 0,07616 | 0,07083 | 0,06538 | 0,06313 |
| 535,37769 | 0,07607 | 0,0707 | 0,06605 | 0,06359 |
| 535,41487 | 0,07614 | 0,07073 | 0,06689 | 0,06425 |
| 535,45205 | 0,07641 | 0,07094 | 0,06791 | 0,06511 |
| 535,48924 | 0,07685 | 0,07131 | 0,06911 | 0,06616 |
| 535,52642 | 0,07745 | 0,07183 | 0,07046 | 0,06742 |
| 535,5636 | 0,07819 | 0,0725 | 0,07193 | 0,06882 |
| 535,60078 | 0,07908 | 0,0733 | 0,0735 | 0,07037 |
| 535,63796 | 0,08009 | 0,07423 | 0,07516 | 0,07203 |
| 535,67515 | 0,08121 | 0,0753 | 0,07689 | 0,0738 |
| 535,71233 | 0,08243 | 0,07644 | 0,07866 | 0,07564 |
| 535,74951 | 0,08369 | 0,07765 | 0,08045 | 0,07755 |
| 535,78669 | 0,08498 | 0,07891 | 0,08224 | 0,07948 |
| 535,82387 | 0,08628 | 0,08018 | 0,084 | 0,08142 |
| 535,86106 | 0,08756 | 0,08146 | 0,08573 | 0,08334 |
| 535,89824 | 0,0888 | 0,0827 | 0,08739 | 0,08523 |
| 535,93542 | 0,08996 | 0,08389 | 0,08898 | 0,08706 |
| 535,9726 | 0,09102 | 0,08501 | 0,09048 | 0,08883 |
| 536,00978 | 0,09197 | 0,08604 | 0,09187 | 0,0905 |
| 536,04697 | 0,09279 | 0,08697 | 0,09316 | 0,09206 |
| 536,08415 | 0,09348 | 0,08778 | 0,09434 | 0,09352 |
| 536,12133 | 0,09402 | 0,08847 | 0,09542 | 0,09488 |
| 536,15851 | 0,0944 | 0,089 | 0,09638 | 0,09612 |
| 536,19569 | 0,0946 | 0,08939 | 0,09724 | 0,09726 |
| 536,23288 | 0,09467 | 0,08966 | 0,09799 | 0,09828 |
| 536,27006 | 0,09459 | 0,0898 | 0,09864 | 0,09919 |
| 536,30724 | 0,09438 | 0,08982 | 0,09922 | 0,10001 |
| 536,34442 | 0,09406 | 0,08973 | 0,09972 | 0,10074 |
| 536,3816 | 0,09364 | 0,08953 | 0,10016 | 0,1014 |
| 536,41879 | 0,09312 | 0,08925 | 0,10055 | 0,10199 |
| 536,45597 | 0,09255 | 0,08891 | 0,10088 | 0,10252 |
| 536,49315 | 0,09195 | 0,08852 | 0,10116 | 0,10299 |
| 536,53033 | 0,09134 | 0,08812 | 0,10141 | 0,10341 |
| 536,56751 | 0,09074 | 0,0877 | 0,10163 | 0,10379 |
| 536,6047 | 0,09017 | 0,0873 | 0,10182 | 0,10412 |
| 536,64188 | 0,08966 | 0,08693 | 0,10196 | 0,1044 |
| 536,67906 | 0,08923 | 0,08661 | 0,10207 | 0,10463 |
| 536,71624 | 0,08889 | 0,08635 | 0,10212 | 0,1048 |
| 536,75342 | 0,08865 | 0,08617 | 0,1021 | 0,10488 |
| 536,79061 | 0,08852 | 0,08606 | 0,10202 | 0,10487 |
| 536,82779 | 0,0885 | 0,08604 | 0,10187 | 0,10477 |
| 536,86497 | 0,08861 | 0,08612 | 0,10162 | 0,10456 |
| 536,90215 | 0,08886 | 0,08629 | 0,10128 | 0,10424 |
| 536,93933 | 0,08921 | 0,08655 | 0,10083 | 0,10379 |
| 536,97652 | 0,08967 | 0,08688 | 0,10026 | 0,1032 |
| 537,0137 | 0,09022 | 0,08729 | 0,09957 | 0,10246 |
| 537,05088 | 0,09085 | 0,08775 | 0,09878 | 0,10159 |
| 537,08806 | 0,09154 | 0,08827 | 0,09788 | 0,1006 |
| 537,12524 | 0,09228 | 0,08882 | 0,09689 | 0,09949 |
| 537,16243 | 0,09304 | 0,08938 | 0,0958 | 0,09827 |
| 537,19961 | 0,0938 | 0,08993 | 0,09464 | 0,09697 |
| 537,23679 | 0,09454 | 0,09048 | 0,09343 | 0,0956 |
| 537,27397 | 0,09524 | 0,09099 | 0,0922 | 0,09419 |
| 537,31115 | 0,09589 | 0,09145 | 0,09096 | 0,09278 |
| 537,34834 | 0,09646 | 0,09185 | 0,08975 | 0,0914 |
| 537,38552 | 0,09693 | 0,09218 | 0,08859 | 0,09007 |
| 537,4227 | 0,09732 | 0,09244 | 0,0875 | 0,08881 |
| 537,45988 | 0,0976 | 0,09263 | 0,08654 | 0,08767 |
| 537,49706 | 0,09778 | 0,09273 | 0,08571 | 0,0867 |
| 537,53425 | 0,09786 | 0,09277 | 0,08505 | 0,0859 |
| 537,57143 | 0,09784 | 0,09273 | 0,08456 | 0,0853 |
| 537,60861 | 0,09772 | 0,09264 | 0,08426 | 0,08492 |
| 537,64579 | 0,09753 | 0,09252 | 0,08418 | 0,08476 |
| 537,68297 | 0,09728 | 0,09238 | 0,08436 | 0,08485 |
| 537,72016 | 0,09701 | 0,09225 | 0,0848 | 0,08522 |
| 537,75734 | 0,09673 | 0,09215 | 0,0855 | 0,08589 |
| 537,79452 | 0,09646 | 0,09211 | 0,08645 | 0,08683 |
| 537,8317 | 0,09624 | 0,09216 | 0,08766 | 0,08805 |
| 537,86888 | 0,0961 | 0,09234 | 0,08914 | 0,08954 |
| 537,90607 | 0,09608 | 0,09266 | 0,09088 | 0,0913 |
| 537,94325 | 0,09619 | 0,09315 | 0,09293 | 0,09332 |
| 537,98043 | 0,09646 | 0,09384 | 0,09523 | 0,09564 |
| 538,01761 | 0,09692 | 0,09475 | 0,09777 | 0,09822 |
| 538,05479 | 0,09759 | 0,09595 | 0,10054 | 0,10103 |
| 538,09198 | 0,09854 | 0,09741 | 0,10353 | 0,10405 |
| 538,12916 | 0,09973 | 0,09913 | 0,10671 | 0,10726 |
| 538,16634 | 0,10118 | 0,10112 | 0,11008 | 0,11064 |
| 538,20352 | 0,10287 | 0,10337 | 0,11361 | 0,11417 |
| 538,2407 | 0,10482 | 0,10589 | 0,11725 | 0,11783 |
| 538,27789 | 0,107 | 0,10869 | 0,12096 | 0,12155 |
| 538,31507 | 0,10943 | 0,1117 | 0,12471 | 0,1253 |
| 538,35225 | 0,11207 | 0,11489 | 0,12846 | 0,12903 |
| 538,38943 | 0,11485 | 0,11822 | 0,13216 | 0,13272 |
| 538,42661 | 0,11775 | 0,12164 | 0,13576 | 0,1363 |
| 538,4638 | 0,12072 | 0,12513 | 0,13919 | 0,13972 |
| 538,50098 | 0,12372 | 0,12861 | 0,14243 | 0,1429 |
| 538,53816 | 0,12669 | 0,13201 | 0,14543 | 0,14584 |
| 538,57534 | 0,12955 | 0,13528 | 0,14815 | 0,14847 |
| 538,61252 | 0,13225 | 0,13837 | 0,15057 | 0,15078 |
| 538,64971 | 0,13475 | 0,14122 | 0,15262 | 0,15274 |
| 538,68689 | 0,13699 | 0,14379 | 0,15424 | 0,15431 |
| 538,72407 | 0,13894 | 0,14603 | 0,15548 | 0,15543 |
| 538,76125 | 0,14057 | 0,14783 | 0,15634 | 0,15613 |
| 538,79843 | 0,14176 | 0,14922 | 0,15684 | 0,15644 |
| 538,83562 | 0,14254 | 0,15019 | 0,15697 | 0,1564 |
| 538,8728 | 0,14292 | 0,15073 | 0,15678 | 0,15602 |
| 538,90998 | 0,1429 | 0,15086 | 0,15626 | 0,15534 |
| 538,94716 | 0,14249 | 0,15057 | 0,15548 | 0,15441 |
| 538,98434 | 0,14171 | 0,14983 | 0,15453 | 0,15326 |
| 539,02153 | 0,14057 | 0,14873 | 0,15344 | 0,152 |
| 539,05871 | 0,13909 | 0,14733 | 0,15228 | 0,15068 |
| 539,09589 | 0,13738 | 0,14569 | 0,15109 | 0,14936 |
| 539,13307 | 0,13548 | 0,14385 | 0,14993 | 0,1481 |
| 539,17025 | 0,13347 | 0,14188 | 0,14886 | 0,14694 |
| 539,20744 | 0,13138 | 0,13983 | 0,14791 | 0,14595 |
| 539,24462 | 0,12929 | 0,1378 | 0,1471 | 0,14516 |
| 539,2818 | 0,12727 | 0,13584 | 0,14645 | 0,14458 |
| 539,31898 | 0,12537 | 0,134 | 0,14596 | 0,14421 |
| 539,35616 | 0,12365 | 0,13234 | 0,14562 | 0,14404 |
| 539,39335 | 0,12213 | 0,13088 | 0,14544 | 0,14405 |
| 539,43053 | 0,12085 | 0,12966 | 0,14537 | 0,14422 |
| 539,46771 | 0,11982 | 0,12876 | 0,14537 | 0,14452 |
| 539,50489 | 0,11909 | 0,12814 | 0,14538 | 0,14488 |
| 539,54207 | 0,11865 | 0,12778 | 0,14538 | 0,14524 |
| 539,57926 | 0,11845 | 0,12767 | 0,14531 | 0,14555 |
| 539,61644 | 0,11847 | 0,12778 | 0,14513 | 0,14576 |
| 539,65362 | 0,11869 | 0,12808 | 0,14476 | 0,14583 |
| 539,6908 | 0,11905 | 0,12856 | 0,14419 | 0,1457 |
| 539,72798 | 0,11951 | 0,12912 | 0,14339 | 0,14531 |
| 539,76517 | 0,12003 | 0,12972 | 0,14237 | 0,14467 |
| 539,80235 | 0,12053 | 0,1303 | 0,1411 | 0,14378 |
| 539,83953 | 0,12097 | 0,1308 | 0,13961 | 0,14264 |
| 539,87671 | 0,12128 | 0,13119 | 0,13788 | 0,14127 |
| 539,91389 | 0,12144 | 0,13141 | 0,13594 | 0,13969 |
| 539,95108 | 0,12141 | 0,13137 | 0,13387 | 0,13793 |
| 539,98826 | 0,12113 | 0,13109 | 0,13171 | 0,13606 |
| 540,02544 | 0,12056 | 0,13054 | 0,1295 | 0,13413 |
| 540,06262 | 0,11973 | 0,12973 | 0,12729 | 0,13221 |
| 540,0998 | 0,11864 | 0,12864 | 0,12513 | 0,13034 |
| 540,13699 | 0,1173 | 0,12728 | 0,1231 | 0,12858 |
| 540,17417 | 0,11573 | 0,12564 | 0,12123 | 0,12697 |
| 540,21135 | 0,11395 | 0,12378 | 0,11955 | 0,12558 |
| 540,24853 | 0,11197 | 0,12176 | 0,11807 | 0,12442 |
| 540,28571 | 0,10988 | 0,11961 | 0,1168 | 0,12349 |
| 540,3229 | 0,10772 | 0,11739 | 0,11575 | 0,12278 |
| 540,36008 | 0,10553 | 0,11514 | 0,11491 | 0,12228 |
| 540,39726 | 0,10337 | 0,11291 | 0,11427 | 0,12195 |
| 540,43444 | 0,10128 | 0,11077 | 0,11375 | 0,12177 |
| 540,47162 | 0,09932 | 0,10875 | 0,11331 | 0,12168 |
| 540,50881 | 0,09754 | 0,1069 | 0,1129 | 0,12158 |
| 540,54599 | 0,09594 | 0,10524 | 0,11245 | 0,12141 |
| 540,58317 | 0,09455 | 0,10379 | 0,11192 | 0,12112 |
| 540,62035 | 0,09338 | 0,10257 | 0,11121 | 0,12062 |
| 540,65753 | 0,09243 | 0,10162 | 0,11026 | 0,11987 |
| 540,69472 | 0,09171 | 0,10089 | 0,10903 | 0,11876 |
| 540,7319 | 0,09122 | 0,10035 | 0,10748 | 0,11722 |
| 540,76908 | 0,0909 | 0,09998 | 0,10558 | 0,11527 |
| 540,80626 | 0,0907 | 0,09974 | 0,10332 | 0,11287 |
| 540,84344 | 0,0906 | 0,09961 | 0,10067 | 0,11003 |
| 540,88063 | 0,09055 | 0,09952 | 0,09756 | 0,10674 |
| 540,91781 | 0,0905 | 0,09941 | 0,09408 | 0,10302 |
| 540,95499 | 0,09039 | 0,09923 | 0,09027 | 0,09884 |
| 540,99217 | 0,09017 | 0,09893 | 0,08616 | 0,0943 |
| 541,02935 | 0,08978 | 0,09846 | 0,08179 | 0,08947 |
| 541,06654 | 0,08919 | 0,09778 | 0,07721 | 0,0844 |
| 541,10372 | 0,08837 | 0,09684 | 0,07246 | 0,07916 |
| 541,1409 | 0,08729 | 0,09556 | 0,06761 | 0,07381 |
| 541,17808 | 0,0859 | 0,09397 | 0,06273 | 0,0684 |
| 541,21526 | 0,08416 | 0,09205 | 0,05788 | 0,06303 |
| 541,25245 | 0,0821 | 0,08981 | 0,05311 | 0,05776 |
| 541,28963 | 0,07973 | 0,08723 | 0,04846 | 0,05263 |
| 541,32681 | 0,07707 | 0,08434 | 0,04397 | 0,04769 |
| 541,36399 | 0,07413 | 0,0811 | 0,03972 | 0,04298 |
| 541,40117 | 0,07094 | 0,0776 | 0,03572 | 0,03853 |
| 541,43836 | 0,06749 | 0,07387 | 0,03198 | 0,0344 |
| 541,47554 | 0,06386 | 0,06996 | 0,02851 | 0,0306 |
| 541,51272 | 0,0601 | 0,0659 | 0,02532 | 0,02712 |
| 541,5499 | 0,05625 | 0,06174 | 0,02241 | 0,02394 |
| 541,58708 | 0,05235 | 0,05752 | 0,01979 | 0,02108 |
| 541,62427 | 0,04844 | 0,05331 | 0,01749 | 0,01851 |
| 541,66145 | 0,04457 | 0,04914 | 0,01545 | 0,01624 |
| 541,69863 | 0,04078 | 0,04505 | 0,01365 | 0,01428 |
| 541,73581 | 0,03712 | 0,04109 | 0,01208 | 0,01257 |
| 541,77299 | 0,0336 | 0,03727 | 0,01072 | 0,01109 |
| 541,81018 | 0,03024 | 0,03363 | 0,00955 | 0,00982 |
| 541,84736 | 0,02707 | 0,03024 | 0,00858 | 0,00874 |
| 541,88454 | 0,02411 | 0,02707 | 0,00776 | 0,00782 |
| 541,92172 | 0,02141 | 0,02413 | 0,00708 | 0,00706 |
| 541,9589 | 0,01893 | 0,02142 | 0,0065 | 0,00644 |
| 541,99609 | 0,01668 | 0,01896 | 0,00603 | 0,00592 |
| 542,03327 | 0,01464 | 0,01673 | 0,00563 | 0,00549 |
| 542,07045 | 0,01282 | 0,01476 | 0,00531 | 0,00514 |
| 542,10763 | 0,01121 | 0,01303 | 0,00505 | 0,00484 |
| 542,14481 | 0,00981 | 0,0115 | 0,00482 | 0,0046 |
| 542,182 | 0,00861 | 0,01017 | 0,00463 | 0,00439 |
| 542,21918 | 0,00757 | 0,00901 | 0,00446 | 0,00421 |
| 542,25636 | 0,00668 | 0,00801 | 0,0043 | 0,00405 |
| 542,29354 | 0,00593 | 0,00717 | 0,00415 | 0,0039 |
| 542,33072 | 0,00529 | 0,00647 | 0,00401 | 0,00376 |
| 542,36791 | 0,00476 | 0,00588 | 0,00386 | 0,00361 |
| 542,40509 | 0,00434 | 0,00539 | 0,00371 | 0,00347 |
| 542,44227 | 0,00399 | 0,00497 | 0,00356 | 0,00332 |
| 542,47945 | 0,0037 | 0,00463 | 0,00339 | 0,00316 |
| 542,51663 | 0,00347 | 0,00434 | 0,00322 | 0,003 |
| 542,55382 | 0,00327 | 0,0041 | 0,00305 | 0,00283 |
| 542,591 | 0,00311 | 0,00389 | 0,00287 | 0,00266 |
| 542,62818 | 0,00297 | 0,00371 | 0,00268 | 0,00248 |
| 542,66536 | 0,00286 | 0,00354 | 0,0025 | 0,00231 |
| 542,70254 | 0,00275 | 0,00339 | 0,00231 | 0,00212 |
| 542,73973 | 0,00265 | 0,00325 | 0,00212 | 0,00195 |
| 542,77691 | 0,00255 | 0,00311 | 0,00194 | 0,00177 |
| 542,81409 | 0,00246 | 0,00297 | 0,00176 | 0,0016 |
| 542,85127 | 0,00236 | 0,00283 | 0,00159 | 0,00143 |
| 542,88845 | 0,00226 | 0,00268 | 0,00143 | 0,00128 |
| 542,92564 | 0,00216 | 0,00254 | 0,00127 | 0,00113 |
| 542,96282 | 0,00205 | 0,00239 | 0,00113 | 0,00099 |
| 543 | 0,00194 | 0,00224 | 0,00099 | 0,00086 |
| "Onderwijsscore" | "2019/'20" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|---|
| 524 | 8e-04 | 0,00051 | 0,00033 | 0 | 0 |
| 524,03718 | 0,00086 | 0,00053 | 0,00036 | 0 | 0 |
| 524,07436 | 0,00092 | 0,00055 | 0,00039 | 1e-05 | 0 |
| 524,11155 | 0,00097 | 0,00056 | 0,00042 | 1e-05 | 0 |
| 524,14873 | 0,00101 | 0,00057 | 0,00045 | 1e-05 | 0 |
| 524,18591 | 0,00104 | 0,00057 | 0,00048 | 2e-05 | 0 |
| 524,22309 | 0,00106 | 0,00056 | 5e-04 | 3e-05 | 1e-05 |
| 524,26027 | 0,00108 | 0,00055 | 0,00052 | 4e-05 | 1e-05 |
| 524,29746 | 0,00108 | 0,00053 | 0,00054 | 5e-05 | 1e-05 |
| 524,33464 | 0,00108 | 0,00051 | 0,00057 | 6e-05 | 2e-05 |
| 524,37182 | 0,00107 | 0,00049 | 0,00059 | 8e-05 | 2e-05 |
| 524,409 | 0,00105 | 0,00047 | 0,00061 | 0,00011 | 3e-05 |
| 524,44618 | 0,00102 | 0,00044 | 0,00064 | 0,00014 | 4e-05 |
| 524,48337 | 0,001 | 0,00042 | 0,00067 | 0,00018 | 5e-05 |
| 524,52055 | 0,00097 | 4e-04 | 7e-04 | 0,00022 | 6e-05 |
| 524,55773 | 0,00094 | 0,00039 | 0,00073 | 0,00027 | 8e-05 |
| 524,59491 | 0,00091 | 0,00037 | 0,00076 | 0,00032 | 1e-04 |
| 524,63209 | 0,00088 | 0,00037 | 0,00079 | 0,00038 | 0,00013 |
| 524,66928 | 0,00085 | 0,00037 | 0,00082 | 0,00045 | 0,00015 |
| 524,70646 | 0,00083 | 0,00037 | 0,00084 | 0,00052 | 0,00018 |
| 524,74364 | 0,00081 | 0,00039 | 0,00087 | 0,00059 | 0,00021 |
| 524,78082 | 8e-04 | 4e-04 | 0,00089 | 0,00066 | 0,00024 |
| 524,818 | 0,00079 | 0,00043 | 9e-04 | 0,00074 | 0,00028 |
| 524,85519 | 0,00079 | 0,00046 | 0,00091 | 0,00081 | 0,00031 |
| 524,89237 | 0,00079 | 0,00049 | 0,00092 | 0,00087 | 0,00035 |
| 524,92955 | 8e-04 | 0,00053 | 0,00092 | 0,00093 | 0,00038 |
| 524,96673 | 0,00082 | 0,00057 | 0,00092 | 0,00098 | 0,00041 |
| 525,00391 | 0,00084 | 0,00061 | 0,00092 | 0,00102 | 0,00043 |
| 525,0411 | 0,00087 | 0,00065 | 0,00092 | 0,00105 | 0,00045 |
| 525,07828 | 9e-04 | 0,00069 | 0,00091 | 0,00106 | 0,00046 |
| 525,11546 | 0,00094 | 0,00073 | 0,00091 | 0,00107 | 0,00047 |
| 525,15264 | 0,00098 | 0,00076 | 0,00091 | 0,00106 | 0,00047 |
| 525,18982 | 0,00102 | 0,00079 | 0,00091 | 0,00104 | 0,00046 |
| 525,22701 | 0,00107 | 0,00082 | 0,00091 | 0,001 | 0,00045 |
| 525,26419 | 0,00113 | 0,00084 | 0,00092 | 0,00096 | 0,00043 |
| 525,30137 | 0,00118 | 0,00085 | 0,00093 | 0,00091 | 4e-04 |
| 525,33855 | 0,00124 | 0,00086 | 0,00095 | 0,00086 | 0,00037 |
| 525,37573 | 0,0013 | 0,00087 | 0,00098 | 8e-04 | 0,00034 |
| 525,41292 | 0,00136 | 0,00087 | 0,00101 | 0,00074 | 0,00031 |
| 525,4501 | 0,00143 | 0,00087 | 0,00105 | 0,00068 | 0,00028 |
| 525,48728 | 0,0015 | 0,00087 | 0,0011 | 0,00063 | 0,00024 |
| 525,52446 | 0,00157 | 0,00087 | 0,00115 | 0,00057 | 0,00021 |
| 525,56164 | 0,00165 | 0,00088 | 0,00122 | 0,00052 | 0,00019 |
| 525,59883 | 0,00173 | 0,00089 | 0,00128 | 0,00048 | 0,00017 |
| 525,63601 | 0,00182 | 9e-04 | 0,00136 | 0,00044 | 0,00015 |
| 525,67319 | 0,00192 | 0,00092 | 0,00144 | 0,00041 | 0,00014 |
| 525,71037 | 0,00203 | 0,00096 | 0,00154 | 0,00039 | 0,00013 |
| 525,74755 | 0,00216 | 0,00101 | 0,00163 | 0,00038 | 0,00013 |
| 525,78474 | 0,0023 | 0,00107 | 0,00174 | 0,00037 | 0,00014 |
| 525,82192 | 0,00247 | 0,00117 | 0,00186 | 0,00037 | 0,00016 |
| 525,8591 | 0,00268 | 0,00129 | 0,00199 | 0,00038 | 2e-04 |
| 525,89628 | 0,00291 | 0,00144 | 0,00214 | 0,00041 | 0,00024 |
| 525,93346 | 0,00319 | 0,00164 | 0,00232 | 0,00044 | 3e-04 |
| 525,97065 | 0,00351 | 0,00188 | 0,00251 | 5e-04 | 0,00037 |
| 526,00783 | 0,00389 | 0,00216 | 0,00274 | 0,00057 | 0,00046 |
| 526,04501 | 0,00433 | 0,00251 | 0,00301 | 0,00065 | 0,00057 |
| 526,08219 | 0,00483 | 0,00291 | 0,00331 | 0,00076 | 0,00071 |
| 526,11937 | 0,0054 | 0,00338 | 0,00367 | 9e-04 | 0,00087 |
| 526,15656 | 0,00606 | 0,00391 | 0,00408 | 0,00106 | 0,00107 |
| 526,19374 | 0,00679 | 0,00452 | 0,00455 | 0,00126 | 0,00131 |
| 526,23092 | 0,0076 | 0,00519 | 0,00508 | 0,0015 | 0,00159 |
| 526,2681 | 0,00848 | 0,00592 | 0,00567 | 0,00179 | 0,00192 |
| 526,30528 | 0,00943 | 0,0067 | 0,00633 | 0,00213 | 0,00232 |
| 526,34247 | 0,01043 | 0,00753 | 0,00703 | 0,00253 | 0,00278 |
| 526,37965 | 0,01148 | 0,00839 | 0,00779 | 0,003 | 0,00331 |
| 526,41683 | 0,01255 | 0,00927 | 0,00858 | 0,00355 | 0,00393 |
| 526,45401 | 0,01365 | 0,01017 | 0,00941 | 0,00418 | 0,00464 |
| 526,49119 | 0,01475 | 0,01106 | 0,01024 | 0,00491 | 0,00545 |
| 526,52838 | 0,01582 | 0,01194 | 0,01108 | 0,00574 | 0,00638 |
| 526,56556 | 0,01687 | 0,01279 | 0,01191 | 0,00669 | 0,00741 |
| 526,60274 | 0,01788 | 0,0136 | 0,01272 | 0,00778 | 0,00856 |
| 526,63992 | 0,01884 | 0,01438 | 0,01349 | 0,00899 | 0,00982 |
| 526,6771 | 0,01974 | 0,01511 | 0,01421 | 0,01033 | 0,0112 |
| 526,71429 | 0,0206 | 0,01581 | 0,0149 | 0,01179 | 0,01267 |
| 526,75147 | 0,0214 | 0,01648 | 0,01555 | 0,01338 | 0,01423 |
| 526,78865 | 0,02217 | 0,01713 | 0,01616 | 0,01508 | 0,01586 |
| 526,82583 | 0,02291 | 0,01776 | 0,01674 | 0,01687 | 0,01756 |
| 526,86301 | 0,02364 | 0,01841 | 0,01731 | 0,01873 | 0,01928 |
| 526,9002 | 0,02437 | 0,01908 | 0,01788 | 0,02064 | 0,021 |
| 526,93738 | 0,02512 | 0,01978 | 0,01847 | 0,02256 | 0,02267 |
| 526,97456 | 0,0259 | 0,02053 | 0,01909 | 0,02444 | 0,02428 |
| 527,01174 | 0,02672 | 0,02132 | 0,01975 | 0,02624 | 0,02578 |
| 527,04892 | 0,02757 | 0,02216 | 0,02046 | 0,02792 | 0,02714 |
| 527,08611 | 0,02847 | 0,02305 | 0,02123 | 0,02943 | 0,02832 |
| 527,12329 | 0,02941 | 0,02397 | 0,02204 | 0,03073 | 0,0293 |
| 527,16047 | 0,03038 | 0,02493 | 0,0229 | 0,03179 | 0,03002 |
| 527,19765 | 0,03136 | 0,0259 | 0,02379 | 0,03257 | 0,03048 |
| 527,23483 | 0,03234 | 0,02687 | 0,02471 | 0,03306 | 0,03067 |
| 527,27202 | 0,03332 | 0,02782 | 0,02564 | 0,03322 | 0,03059 |
| 527,3092 | 0,03427 | 0,02875 | 0,02656 | 0,03306 | 0,03026 |
| 527,34638 | 0,03519 | 0,02965 | 0,02745 | 0,03261 | 0,02968 |
| 527,38356 | 0,03608 | 0,03051 | 0,02832 | 0,0319 | 0,02889 |
| 527,42074 | 0,03693 | 0,03133 | 0,02916 | 0,03097 | 0,02792 |
| 527,45793 | 0,03775 | 0,03213 | 0,02996 | 0,02986 | 0,02681 |
| 527,49511 | 0,03854 | 0,03292 | 0,03074 | 0,02862 | 0,02559 |
| 527,53229 | 0,03932 | 0,0337 | 0,0315 | 0,0273 | 0,02432 |
| 527,56947 | 0,0401 | 0,03452 | 0,03225 | 0,02595 | 0,02307 |
| 527,60665 | 0,0409 | 0,03537 | 0,03302 | 0,02464 | 0,02188 |
| 527,64384 | 0,04173 | 0,03629 | 0,03382 | 0,02342 | 0,02078 |
| 527,68102 | 0,04261 | 0,03728 | 0,03467 | 0,02234 | 0,01984 |
| 527,7182 | 0,04355 | 0,03837 | 0,03558 | 0,02145 | 0,01908 |
| 527,75538 | 0,04457 | 0,03957 | 0,03658 | 0,02077 | 0,01853 |
| 527,79256 | 0,04567 | 0,04089 | 0,03768 | 0,02035 | 0,01824 |
| 527,82975 | 0,04686 | 0,04234 | 0,03887 | 0,0202 | 0,01824 |
| 527,86693 | 0,04817 | 0,04392 | 0,04017 | 0,02036 | 0,01856 |
| 527,90411 | 0,04957 | 0,04563 | 0,04159 | 0,02084 | 0,01918 |
| 527,94129 | 0,05109 | 0,04746 | 0,04313 | 0,02165 | 0,02011 |
| 527,97847 | 0,05271 | 0,0494 | 0,0448 | 0,02284 | 0,02136 |
| 528,01566 | 0,05444 | 0,05146 | 0,04659 | 0,02437 | 0,02292 |
| 528,05284 | 0,05627 | 0,05363 | 0,0485 | 0,02623 | 0,02478 |
| 528,09002 | 0,05822 | 0,05589 | 0,05053 | 0,0284 | 0,02692 |
| 528,1272 | 0,06027 | 0,05825 | 0,05267 | 0,03086 | 0,02932 |
| 528,16438 | 0,06243 | 0,06069 | 0,05493 | 0,03358 | 0,03199 |
| 528,20157 | 0,06468 | 0,06322 | 0,05731 | 0,03654 | 0,03488 |
| 528,23875 | 0,06702 | 0,0658 | 0,05979 | 0,03971 | 0,03796 |
| 528,27593 | 0,06944 | 0,06845 | 0,06237 | 0,04304 | 0,0412 |
| 528,31311 | 0,07193 | 0,07113 | 0,06506 | 0,04653 | 0,04459 |
| 528,35029 | 0,07449 | 0,07386 | 0,06784 | 0,05014 | 0,04812 |
| 528,38748 | 0,07711 | 0,07662 | 0,07071 | 0,05384 | 0,05177 |
| 528,42466 | 0,07979 | 0,07941 | 0,07366 | 0,05763 | 0,05555 |
| 528,46184 | 0,08254 | 0,08224 | 0,0767 | 0,06151 | 0,05948 |
| 528,49902 | 0,08536 | 0,08511 | 0,07983 | 0,06551 | 0,06359 |
| 528,5362 | 0,08829 | 0,08803 | 0,08306 | 0,06964 | 0,06791 |
| 528,57339 | 0,09132 | 0,09103 | 0,0864 | 0,07394 | 0,07247 |
| 528,61057 | 0,09448 | 0,09412 | 0,08988 | 0,07845 | 0,07732 |
| 528,64775 | 0,09779 | 0,09732 | 0,09352 | 0,08322 | 0,08249 |
| 528,68493 | 0,10124 | 0,10063 | 0,09734 | 0,08832 | 0,08801 |
| 528,72211 | 0,10486 | 0,10408 | 0,10134 | 0,09376 | 0,09391 |
| 528,7593 | 0,10864 | 0,10765 | 0,10552 | 0,09953 | 0,10017 |
| 528,79648 | 0,11256 | 0,11135 | 0,10985 | 0,10564 | 0,1068 |
| 528,83366 | 0,1166 | 0,11515 | 0,11432 | 0,11204 | 0,11375 |
| 528,87084 | 0,1207 | 0,11902 | 0,11887 | 0,11867 | 0,12093 |
| 528,90802 | 0,12479 | 0,12288 | 0,12345 | 0,12544 | 0,12821 |
| 528,94521 | 0,12881 | 0,12668 | 0,12796 | 0,13223 | 0,13545 |
| 528,98239 | 0,13268 | 0,13034 | 0,13232 | 0,13889 | 0,14251 |
| 529,01957 | 0,13632 | 0,1338 | 0,13638 | 0,14522 | 0,1492 |
| 529,05675 | 0,13965 | 0,13697 | 0,14007 | 0,15104 | 0,15538 |
| 529,09393 | 0,14261 | 0,1398 | 0,1433 | 0,15621 | 0,16087 |
| 529,13112 | 0,14514 | 0,14223 | 0,14599 | 0,1606 | 0,16554 |
| 529,1683 | 0,14715 | 0,14416 | 0,1481 | 0,16411 | 0,16919 |
| 529,20548 | 0,14862 | 0,14558 | 0,14958 | 0,16666 | 0,17173 |
| 529,24266 | 0,1496 | 0,14653 | 0,15045 | 0,16823 | 0,17321 |
| 529,27984 | 0,1501 | 0,14702 | 0,15071 | 0,16883 | 0,17363 |
| 529,31703 | 0,15016 | 0,14709 | 0,15042 | 0,16851 | 0,17307 |
| 529,35421 | 0,14983 | 0,14677 | 0,14962 | 0,16733 | 0,1716 |
| 529,39139 | 0,14917 | 0,14614 | 0,14842 | 0,16543 | 0,16936 |
| 529,42857 | 0,14826 | 0,14526 | 0,14695 | 0,16301 | 0,16647 |
| 529,46575 | 0,14715 | 0,14419 | 0,14532 | 0,1602 | 0,1631 |
| 529,50294 | 0,14592 | 0,143 | 0,1436 | 0,15716 | 0,15938 |
| 529,54012 | 0,14465 | 0,14177 | 0,14189 | 0,154 | 0,1555 |
| 529,5773 | 0,1434 | 0,14055 | 0,14027 | 0,15083 | 0,15161 |
| 529,61448 | 0,1422 | 0,13939 | 0,13878 | 0,14775 | 0,14783 |
| 529,65166 | 0,14111 | 0,13833 | 0,13748 | 0,14482 | 0,14424 |
| 529,68885 | 0,14013 | 0,1374 | 0,13641 | 0,1421 | 0,14093 |
| 529,72603 | 0,13932 | 0,13663 | 0,13561 | 0,13965 | 0,13795 |
| 529,76321 | 0,13869 | 0,13605 | 0,13508 | 0,13749 | 0,13536 |
| 529,80039 | 0,13827 | 0,13569 | 0,13485 | 0,13564 | 0,1332 |
| 529,83757 | 0,13812 | 0,13561 | 0,13494 | 0,13415 | 0,13155 |
| 529,87476 | 0,1383 | 0,13587 | 0,13539 | 0,13304 | 0,13045 |
| 529,91194 | 0,13883 | 0,13649 | 0,13626 | 0,13238 | 0,12993 |
| 529,94912 | 0,13979 | 0,13755 | 0,13759 | 0,13224 | 0,13004 |
| 529,9863 | 0,14122 | 0,1391 | 0,13946 | 0,1327 | 0,13087 |
| 530,02348 | 0,14318 | 0,14121 | 0,14195 | 0,13385 | 0,13247 |
| 530,06067 | 0,14575 | 0,14393 | 0,14521 | 0,13589 | 0,13493 |
| 530,09785 | 0,14895 | 0,14733 | 0,14925 | 0,13885 | 0,13831 |
| 530,13503 | 0,15281 | 0,15142 | 0,15408 | 0,1428 | 0,14266 |
| 530,17221 | 0,15739 | 0,15627 | 0,15971 | 0,14778 | 0,14811 |
| 530,20939 | 0,16264 | 0,16184 | 0,16613 | 0,15382 | 0,15462 |
| 530,24658 | 0,16844 | 0,16801 | 0,17326 | 0,16087 | 0,16207 |
| 530,28376 | 0,17469 | 0,17468 | 0,18099 | 0,16887 | 0,17035 |
| 530,32094 | 0,18124 | 0,18171 | 0,18918 | 0,17766 | 0,17927 |
| 530,35812 | 0,18792 | 0,18892 | 0,19761 | 0,18704 | 0,18863 |
| 530,3953 | 0,19456 | 0,19611 | 0,20604 | 0,19676 | 0,19814 |
| 530,43249 | 0,20093 | 0,20308 | 0,21414 | 0,2064 | 0,20751 |
| 530,46967 | 0,20683 | 0,20958 | 0,22161 | 0,21558 | 0,21637 |
| 530,50685 | 0,21197 | 0,21532 | 0,22819 | 0,22391 | 0,2243 |
| 530,54403 | 0,21611 | 0,22004 | 0,2336 | 0,23105 | 0,23088 |
| 530,58121 | 0,21915 | 0,22362 | 0,23763 | 0,23664 | 0,23588 |
| 530,6184 | 0,22097 | 0,22591 | 0,2401 | 0,24044 | 0,23908 |
| 530,65558 | 0,22148 | 0,22682 | 0,24087 | 0,24222 | 0,24031 |
| 530,69276 | 0,22066 | 0,22632 | 0,23989 | 0,2419 | 0,23953 |
| 530,72994 | 0,21852 | 0,22441 | 0,23709 | 0,23941 | 0,23676 |
| 530,76712 | 0,21513 | 0,22116 | 0,2325 | 0,23472 | 0,2321 |
| 530,80431 | 0,21059 | 0,21668 | 0,22645 | 0,2283 | 0,22576 |
| 530,84149 | 0,20499 | 0,21106 | 0,21917 | 0,22047 | 0,21793 |
| 530,87867 | 0,19858 | 0,20456 | 0,21091 | 0,21159 | 0,20906 |
| 530,91585 | 0,19164 | 0,19747 | 0,20197 | 0,20208 | 0,1996 |
| 530,95303 | 0,18438 | 0,19003 | 0,19263 | 0,19232 | 0,18993 |
| 530,99022 | 0,17702 | 0,18247 | 0,18319 | 0,18272 | 0,18041 |
| 531,0274 | 0,16975 | 0,175 | 0,17394 | 0,17362 | 0,17136 |
| 531,06458 | 0,16279 | 0,16783 | 0,16513 | 0,16533 | 0,16306 |
| 531,10176 | 0,15629 | 0,16114 | 0,15709 | 0,15823 | 0,15572 |
| 531,13894 | 0,15042 | 0,15508 | 0,14996 | 0,15242 | 0,14951 |
| 531,17613 | 0,14536 | 0,14986 | 0,14386 | 0,14791 | 0,14461 |
| 531,21331 | 0,1412 | 0,14557 | 0,13887 | 0,14473 | 0,14105 |
| 531,25049 | 0,13797 | 0,14221 | 0,13506 | 0,14281 | 0,13871 |
| 531,28767 | 0,13569 | 0,13983 | 0,13246 | 0,14207 | 0,13751 |
| 531,32485 | 0,13438 | 0,13844 | 0,13106 | 0,14239 | 0,13736 |
| 531,36204 | 0,13403 | 0,13804 | 0,13087 | 0,14364 | 0,13816 |
| 531,39922 | 0,13462 | 0,13861 | 0,13184 | 0,14567 | 0,1398 |
| 531,4364 | 0,13612 | 0,14013 | 0,13403 | 0,14838 | 0,14217 |
| 531,47358 | 0,13848 | 0,14255 | 0,13733 | 0,15165 | 0,14519 |
| 531,51076 | 0,14169 | 0,14588 | 0,14161 | 0,15534 | 0,14881 |
| 531,54795 | 0,14564 | 0,15 | 0,14679 | 0,15941 | 0,15298 |
| 531,58513 | 0,15019 | 0,15479 | 0,15278 | 0,16381 | 0,15762 |
| 531,62231 | 0,15524 | 0,16013 | 0,15946 | 0,16855 | 0,1627 |
| 531,65949 | 0,16066 | 0,1659 | 0,16671 | 0,17361 | 0,16819 |
| 531,69667 | 0,16633 | 0,17197 | 0,17437 | 0,17899 | 0,17407 |
| 531,73386 | 0,17211 | 0,17816 | 0,18227 | 0,18468 | 0,18026 |
| 531,77104 | 0,17785 | 0,18433 | 0,19021 | 0,19064 | 0,1867 |
| 531,80822 | 0,18338 | 0,19028 | 0,19792 | 0,19681 | 0,19328 |
| 531,8454 | 0,1885 | 0,1958 | 0,20516 | 0,203 | 0,19983 |
| 531,88258 | 0,19302 | 0,20065 | 0,2117 | 0,20906 | 0,20612 |
| 531,91977 | 0,19681 | 0,2047 | 0,21731 | 0,21476 | 0,21193 |
| 531,95695 | 0,19975 | 0,20779 | 0,22178 | 0,21986 | 0,217 |
| 531,99413 | 0,20172 | 0,20979 | 0,22492 | 0,22409 | 0,22111 |
| 532,03131 | 0,20264 | 0,21061 | 0,22659 | 0,2272 | 0,22401 |
| 532,06849 | 0,20245 | 0,21019 | 0,22668 | 0,22895 | 0,2255 |
| 532,10568 | 0,20114 | 0,2085 | 0,22513 | 0,22913 | 0,2254 |
| 532,14286 | 0,19872 | 0,20555 | 0,22175 | 0,22739 | 0,22361 |
| 532,18004 | 0,19517 | 0,20131 | 0,21681 | 0,22382 | 0,21993 |
| 532,21722 | 0,19061 | 0,19592 | 0,21046 | 0,21851 | 0,21442 |
| 532,2544 | 0,18524 | 0,1896 | 0,20288 | 0,21157 | 0,20733 |
| 532,29159 | 0,17919 | 0,18252 | 0,19429 | 0,20319 | 0,19885 |
| 532,32877 | 0,17263 | 0,17484 | 0,18492 | 0,19362 | 0,18922 |
| 532,36595 | 0,16572 | 0,16675 | 0,17501 | 0,18315 | 0,17871 |
| 532,40313 | 0,15861 | 0,15845 | 0,16482 | 0,1721 | 0,16761 |
| 532,44031 | 0,15145 | 0,1501 | 0,15459 | 0,16078 | 0,15622 |
| 532,4775 | 0,14438 | 0,14188 | 0,14456 | 0,14954 | 0,14485 |
| 532,51468 | 0,13755 | 0,13396 | 0,13496 | 0,13872 | 0,1338 |
| 532,55186 | 0,13107 | 0,1265 | 0,12591 | 0,12852 | 0,12336 |
| 532,58904 | 0,125 | 0,11955 | 0,11753 | 0,1191 | 0,11367 |
| 532,62622 | 0,11939 | 0,11319 | 0,10989 | 0,1106 | 0,10486 |
| 532,66341 | 0,11425 | 0,10744 | 0,10302 | 0,10306 | 0,09699 |
| 532,70059 | 0,1096 | 0,10234 | 0,09693 | 0,09651 | 0,09012 |
| 532,73777 | 0,10545 | 0,09787 | 0,09163 | 0,09093 | 0,08422 |
| 532,77495 | 0,10176 | 0,09402 | 0,08707 | 0,08626 | 0,07928 |
| 532,81213 | 0,09854 | 0,09077 | 0,08322 | 0,08246 | 0,07522 |
| 532,84932 | 0,09576 | 0,08811 | 0,08009 | 0,07946 | 0,07203 |
| 532,8865 | 0,0934 | 0,08598 | 0,07752 | 0,07708 | 0,06959 |
| 532,92368 | 0,09139 | 0,08429 | 0,07547 | 0,07522 | 0,06775 |
| 532,96086 | 0,0897 | 0,08301 | 0,07387 | 0,07377 | 0,06641 |
| 532,99804 | 0,08831 | 0,08208 | 0,07267 | 0,07266 | 0,0655 |
| 533,03523 | 0,08718 | 0,08146 | 0,07183 | 0,07179 | 0,06492 |
| 533,07241 | 0,08629 | 0,08112 | 0,07131 | 0,0711 | 0,0646 |
| 533,10959 | 0,08561 | 0,081 | 0,07105 | 0,07053 | 0,06448 |
| 533,14677 | 0,08513 | 0,08109 | 0,07104 | 0,07003 | 0,0645 |
| 533,18395 | 0,08482 | 0,08134 | 0,07125 | 0,06956 | 0,06463 |
| 533,22114 | 0,08466 | 0,08173 | 0,07163 | 0,0691 | 0,06481 |
| 533,25832 | 0,08461 | 0,08222 | 0,07216 | 0,06863 | 0,06503 |
| 533,2955 | 0,08464 | 0,08276 | 0,07281 | 0,06815 | 0,06526 |
| 533,33268 | 0,08474 | 0,08332 | 0,07355 | 0,06766 | 0,06551 |
| 533,36986 | 0,08486 | 0,08389 | 0,07435 | 0,06719 | 0,06578 |
| 533,40705 | 0,08498 | 0,08441 | 0,07518 | 0,06674 | 0,06607 |
| 533,44423 | 0,08507 | 0,08486 | 0,07601 | 0,06634 | 0,06641 |
| 533,48141 | 0,08509 | 0,08521 | 0,07681 | 0,06602 | 0,0668 |
| 533,51859 | 0,08501 | 0,08541 | 0,07751 | 0,06582 | 0,06727 |
| 533,55577 | 0,08478 | 0,08542 | 0,07809 | 0,06576 | 0,06785 |
| 533,59295 | 0,08438 | 0,08523 | 0,07849 | 0,06587 | 0,06853 |
| 533,63014 | 0,08379 | 0,08481 | 0,07868 | 0,06615 | 0,06934 |
| 533,66732 | 0,083 | 0,08415 | 0,07864 | 0,06661 | 0,07027 |
| 533,7045 | 0,08199 | 0,08324 | 0,07833 | 0,06727 | 0,07132 |
| 533,74168 | 0,08076 | 0,08209 | 0,07774 | 0,0681 | 0,07248 |
| 533,77886 | 0,07933 | 0,08069 | 0,07687 | 0,0691 | 0,07374 |
| 533,81605 | 0,07771 | 0,07908 | 0,07572 | 0,07024 | 0,07509 |
| 533,85323 | 0,07592 | 0,07727 | 0,07433 | 0,07149 | 0,07651 |
| 533,89041 | 0,07402 | 0,07532 | 0,07272 | 0,07284 | 0,07798 |
| 533,92759 | 0,07207 | 0,0733 | 0,071 | 0,07424 | 0,07947 |
| 533,96477 | 0,07013 | 0,07128 | 0,06923 | 0,07568 | 0,081 |
| 534,00196 | 0,06828 | 0,06932 | 0,06752 | 0,07714 | 0,08257 |
| 534,03914 | 0,06659 | 0,06751 | 0,06596 | 0,07863 | 0,08419 |
| 534,07632 | 0,06512 | 0,06593 | 0,06464 | 0,08018 | 0,0859 |
| 534,1135 | 0,06394 | 0,06466 | 0,06368 | 0,08181 | 0,08773 |
| 534,15068 | 0,06313 | 0,06376 | 0,06316 | 0,08358 | 0,08973 |
| 534,18787 | 0,06275 | 0,06335 | 0,06318 | 0,08553 | 0,09198 |
| 534,22505 | 0,06287 | 0,06348 | 0,06386 | 0,08775 | 0,09452 |
| 534,26223 | 0,06347 | 0,06416 | 0,06521 | 0,09027 | 0,09736 |
| 534,29941 | 0,06454 | 0,06539 | 0,06722 | 0,09309 | 0,1005 |
| 534,33659 | 0,06606 | 0,06716 | 0,06985 | 0,09622 | 0,10392 |
| 534,37378 | 0,06799 | 0,06942 | 0,07305 | 0,09959 | 0,10755 |
| 534,41096 | 0,07027 | 0,07211 | 0,07675 | 0,10312 | 0,11131 |
| 534,44814 | 0,07281 | 0,07515 | 0,0808 | 0,1067 | 0,11506 |
| 534,48532 | 0,07551 | 0,07842 | 0,08508 | 0,11017 | 0,11866 |
| 534,5225 | 0,07824 | 0,08181 | 0,08941 | 0,11334 | 0,12189 |
| 534,55969 | 0,08087 | 0,08512 | 0,09359 | 0,11598 | 0,12451 |
| 534,59687 | 0,08325 | 0,08821 | 0,09738 | 0,11784 | 0,12637 |
| 534,63405 | 0,08526 | 0,09093 | 0,10061 | 0,11878 | 0,1273 |
| 534,67123 | 0,08682 | 0,09316 | 0,10313 | 0,11867 | 0,12719 |
| 534,70841 | 0,08781 | 0,09476 | 0,10479 | 0,11742 | 0,12595 |
| 534,7456 | 0,08818 | 0,09566 | 0,1055 | 0,115 | 0,12354 |
| 534,78278 | 0,08788 | 0,09578 | 0,10519 | 0,11143 | 0,11998 |
| 534,81996 | 0,0869 | 0,09509 | 0,10384 | 0,1068 | 0,11535 |
| 534,85714 | 0,0852 | 0,09353 | 0,10148 | 0,10124 | 0,10972 |
| 534,89432 | 0,08283 | 0,09115 | 0,09815 | 0,09491 | 0,10329 |
| 534,93151 | 0,07992 | 0,08808 | 0,0939 | 0,08802 | 0,09634 |
| 534,96869 | 0,07656 | 0,08442 | 0,08898 | 0,08089 | 0,08911 |
| 535,00587 | 0,07284 | 0,08028 | 0,08358 | 0,07375 | 0,08181 |
| 535,04305 | 0,0689 | 0,0758 | 0,07785 | 0,0668 | 0,07465 |
| 535,08023 | 0,06482 | 0,07112 | 0,07197 | 0,06024 | 0,06783 |
| 535,11742 | 0,06074 | 0,06636 | 0,06612 | 0,05422 | 0,06152 |
| 535,1546 | 0,05674 | 0,06165 | 0,06045 | 0,04886 | 0,05584 |
| 535,19178 | 0,05294 | 0,05714 | 0,05509 | 0,04424 | 0,05095 |
| 535,22896 | 0,04943 | 0,05294 | 0,05015 | 0,04042 | 0,04693 |
| 535,26614 | 0,04625 | 0,04913 | 0,04578 | 0,03748 | 0,04371 |
| 535,30333 | 0,04344 | 0,04573 | 0,04201 | 0,03533 | 0,04127 |
| 535,34051 | 0,04101 | 0,0428 | 0,03883 | 0,03388 | 0,03957 |
| 535,37769 | 0,03896 | 0,04033 | 0,03625 | 0,03306 | 0,03852 |
| 535,41487 | 0,03728 | 0,03833 | 0,03423 | 0,03279 | 0,03804 |
| 535,45205 | 0,03595 | 0,03677 | 0,03274 | 0,03296 | 0,03802 |
| 535,48924 | 0,03492 | 0,0356 | 0,03172 | 0,03348 | 0,03836 |
| 535,52642 | 0,03418 | 0,03481 | 0,03111 | 0,03423 | 0,03894 |
| 535,5636 | 0,03367 | 0,03432 | 0,03084 | 0,03511 | 0,03963 |
| 535,60078 | 0,0333 | 0,03404 | 0,03084 | 0,03602 | 0,04032 |
| 535,63796 | 0,03304 | 0,03391 | 0,03101 | 0,03684 | 0,04092 |
| 535,67515 | 0,03283 | 0,03387 | 0,03128 | 0,03751 | 0,04134 |
| 535,71233 | 0,03263 | 0,03386 | 0,03155 | 0,03796 | 0,04154 |
| 535,74951 | 0,03241 | 0,03383 | 0,03179 | 0,03816 | 0,04146 |
| 535,78669 | 0,03213 | 0,03373 | 0,03192 | 0,03806 | 0,04108 |
| 535,82387 | 0,03176 | 0,03353 | 0,03193 | 0,03765 | 0,04039 |
| 535,86106 | 0,03128 | 0,03319 | 0,03177 | 0,03695 | 0,03938 |
| 535,89824 | 0,03067 | 0,03269 | 0,03142 | 0,03597 | 0,03807 |
| 535,93542 | 0,02994 | 0,03204 | 0,03088 | 0,03473 | 0,03653 |
| 535,9726 | 0,0291 | 0,03125 | 0,03013 | 0,03326 | 0,0348 |
| 536,00978 | 0,02816 | 0,03031 | 0,0292 | 0,03163 | 0,03293 |
| 536,04697 | 0,02713 | 0,02926 | 0,02814 | 0,0299 | 0,03097 |
| 536,08415 | 0,02603 | 0,0281 | 0,02695 | 0,02811 | 0,02896 |
| 536,12133 | 0,02487 | 0,02687 | 0,02568 | 0,02631 | 0,02696 |
| 536,15851 | 0,02369 | 0,02559 | 0,02435 | 0,02452 | 0,025 |
| 536,19569 | 0,02249 | 0,02427 | 0,023 | 0,0228 | 0,02313 |
| 536,23288 | 0,0213 | 0,02296 | 0,02165 | 0,02115 | 0,02136 |
| 536,27006 | 0,02013 | 0,02167 | 0,02034 | 0,0196 | 0,01971 |
| 536,30724 | 0,01901 | 0,02042 | 0,01909 | 0,01816 | 0,01819 |
| 536,34442 | 0,01793 | 0,01923 | 0,01793 | 0,01685 | 0,0168 |
| 536,3816 | 0,01691 | 0,0181 | 0,01685 | 0,01565 | 0,01553 |
| 536,41879 | 0,01596 | 0,01703 | 0,01586 | 0,01455 | 0,01438 |
| 536,45597 | 0,01506 | 0,01605 | 0,01497 | 0,01356 | 0,01334 |
| 536,49315 | 0,01423 | 0,01514 | 0,01417 | 0,01266 | 0,0124 |
| 536,53033 | 0,01347 | 0,01432 | 0,01346 | 0,01184 | 0,01155 |
| 536,56751 | 0,01277 | 0,01358 | 0,01283 | 0,0111 | 0,01078 |
| 536,6047 | 0,01212 | 0,0129 | 0,01227 | 0,01044 | 0,01008 |
| 536,64188 | 0,01152 | 0,01229 | 0,01177 | 0,00984 | 0,00943 |
| 536,67906 | 0,01097 | 0,01174 | 0,01132 | 0,0093 | 0,00884 |
| 536,71624 | 0,01045 | 0,01124 | 0,01091 | 0,00881 | 0,00829 |
| 536,75342 | 0,00998 | 0,01078 | 0,01052 | 0,00837 | 0,00778 |
| 536,79061 | 0,00954 | 0,01036 | 0,01014 | 0,00797 | 0,00731 |
| 536,82779 | 0,00912 | 0,00996 | 0,00978 | 0,00761 | 0,00688 |
| 536,86497 | 0,00874 | 0,00959 | 0,00942 | 0,00729 | 0,00647 |
| 536,90215 | 0,00839 | 0,00924 | 0,00906 | 0,00699 | 0,00611 |
| 536,93933 | 0,00805 | 0,0089 | 0,00869 | 0,00673 | 0,00576 |
| 536,97652 | 0,00774 | 0,00857 | 0,00832 | 0,00648 | 0,00545 |
| 537,0137 | 0,00744 | 0,00825 | 0,00795 | 0,00625 | 0,00516 |
| 537,05088 | 0,00716 | 0,00793 | 0,00757 | 0,00603 | 0,00489 |
| 537,08806 | 0,00689 | 0,00761 | 0,0072 | 0,00583 | 0,00464 |
| 537,12524 | 0,00662 | 0,0073 | 0,00682 | 0,00563 | 0,00441 |
| 537,16243 | 0,00637 | 0,00699 | 0,00645 | 0,00544 | 0,00419 |
| 537,19961 | 0,00612 | 0,00668 | 0,00609 | 0,00525 | 0,00399 |
| 537,23679 | 0,00587 | 0,00637 | 0,00574 | 0,00507 | 0,00381 |
| 537,27397 | 0,00563 | 0,00608 | 0,0054 | 0,00489 | 0,00363 |
| 537,31115 | 0,00538 | 0,00579 | 0,00507 | 0,00472 | 0,00347 |
| 537,34834 | 0,00515 | 0,00551 | 0,00476 | 0,00456 | 0,00332 |
| 537,38552 | 0,00491 | 0,00524 | 0,00447 | 0,0044 | 0,00317 |
| 537,4227 | 0,00468 | 0,00499 | 0,00419 | 0,00425 | 0,00303 |
| 537,45988 | 0,00445 | 0,00474 | 0,00393 | 0,0041 | 0,0029 |
| 537,49706 | 0,00423 | 0,00451 | 0,00369 | 0,00395 | 0,00277 |
| 537,53425 | 0,00401 | 0,00429 | 0,00346 | 0,00381 | 0,00265 |
| 537,57143 | 0,0038 | 0,00408 | 0,00325 | 0,00367 | 0,00253 |
| 537,60861 | 0,00359 | 0,00387 | 0,00305 | 0,00353 | 0,00241 |
| 537,64579 | 0,00339 | 0,00368 | 0,00287 | 0,00338 | 0,0023 |
| 537,68297 | 0,00319 | 0,0035 | 0,0027 | 0,00323 | 0,0022 |
| 537,72016 | 0,003 | 0,00332 | 0,00255 | 0,00307 | 0,00209 |
| 537,75734 | 0,00281 | 0,00314 | 0,00241 | 0,0029 | 0,00199 |
| 537,79452 | 0,00263 | 0,00297 | 0,00229 | 0,00273 | 0,00189 |
| 537,8317 | 0,00245 | 0,0028 | 0,00217 | 0,00255 | 0,0018 |
| 537,86888 | 0,00228 | 0,00264 | 0,00206 | 0,00237 | 0,0017 |
| 537,90607 | 0,00211 | 0,00248 | 0,00197 | 0,00218 | 0,00161 |
| 537,94325 | 0,00195 | 0,00232 | 0,00188 | 0,002 | 0,00152 |
| 537,98043 | 0,00179 | 0,00217 | 0,00181 | 0,00182 | 0,00144 |
| 538,01761 | 0,00164 | 0,00202 | 0,00174 | 0,00164 | 0,00136 |
| 538,05479 | 0,0015 | 0,00187 | 0,00167 | 0,00148 | 0,00128 |
| 538,09198 | 0,00136 | 0,00174 | 0,00161 | 0,00132 | 0,00121 |
| 538,12916 | 0,00124 | 0,00161 | 0,00156 | 0,00118 | 0,00113 |
| 538,16634 | 0,00113 | 0,00148 | 0,00151 | 0,00104 | 0,00107 |
| 538,20352 | 0,00103 | 0,00137 | 0,00146 | 0,00092 | 0,001 |
| 538,2407 | 0,00094 | 0,00127 | 0,00142 | 0,00081 | 0,00094 |
| 538,27789 | 0,00086 | 0,00117 | 0,00138 | 0,00071 | 0,00088 |
| 538,31507 | 0,00079 | 0,00109 | 0,00134 | 0,00062 | 0,00083 |
| 538,35225 | 0,00073 | 0,00101 | 0,0013 | 0,00055 | 0,00077 |
| 538,38943 | 0,00068 | 0,00094 | 0,00126 | 0,00048 | 0,00072 |
| 538,42661 | 0,00064 | 0,00087 | 0,00123 | 0,00042 | 0,00067 |
| 538,4638 | 6e-04 | 0,00081 | 0,00119 | 0,00036 | 0,00063 |
| 538,50098 | 0,00057 | 0,00076 | 0,00115 | 0,00031 | 0,00058 |
| 538,53816 | 0,00054 | 0,00071 | 0,00111 | 0,00027 | 0,00054 |
| 538,57534 | 0,00051 | 0,00066 | 0,00107 | 0,00023 | 5e-04 |
| 538,61252 | 0,00049 | 0,00062 | 0,00103 | 0,00019 | 0,00046 |
| 538,64971 | 0,00047 | 0,00058 | 0,00098 | 0,00016 | 0,00042 |
| 538,68689 | 0,00044 | 0,00053 | 0,00093 | 0,00013 | 0,00038 |
| 538,72407 | 0,00042 | 0,00049 | 0,00088 | 0,00011 | 0,00035 |
| 538,76125 | 4e-04 | 0,00045 | 0,00082 | 9e-05 | 0,00032 |
| 538,79843 | 0,00038 | 0,00041 | 0,00076 | 7e-05 | 0,00029 |
| 538,83562 | 0,00035 | 0,00038 | 7e-04 | 6e-05 | 0,00027 |
| 538,8728 | 0,00033 | 0,00034 | 0,00064 | 4e-05 | 0,00025 |
| 538,90998 | 3e-04 | 3e-04 | 0,00058 | 3e-05 | 0,00023 |
| 538,94716 | 0,00028 | 0,00027 | 0,00052 | 3e-05 | 0,00022 |
| 538,98434 | 0,00026 | 0,00024 | 0,00045 | 2e-05 | 2e-04 |
| 539,02153 | 0,00023 | 0,00021 | 4e-04 | 1e-05 | 0,00019 |
| 539,05871 | 0,00021 | 0,00018 | 0,00034 | 1e-05 | 0,00019 |
| 539,09589 | 0,00019 | 0,00015 | 0,00029 | 1e-05 | 0,00018 |
| 539,13307 | 0,00017 | 0,00013 | 0,00024 | 0 | 0,00017 |
| 539,17025 | 0,00015 | 0,00011 | 2e-04 | 0 | 0,00017 |
| 539,20744 | 0,00013 | 9e-05 | 0,00016 | 0 | 0,00017 |
| 539,24462 | 0,00011 | 8e-05 | 0,00013 | 0 | 0,00016 |
| 539,2818 | 1e-04 | 7e-05 | 0,00011 | 0 | 0,00016 |
| 539,31898 | 8e-05 | 6e-05 | 8e-05 | 0 | 0,00016 |
| 539,35616 | 7e-05 | 5e-05 | 6e-05 | 0 | 0,00016 |
| 539,39335 | 6e-05 | 5e-05 | 5e-05 | 0 | 0,00017 |
| 539,43053 | 5e-05 | 5e-05 | 4e-05 | 0 | 0,00017 |
| 539,46771 | 4e-05 | 5e-05 | 3e-05 | 0 | 0,00018 |
| 539,50489 | 3e-05 | 5e-05 | 2e-05 | 0 | 0,00018 |
| 539,54207 | 3e-05 | 6e-05 | 1e-05 | 0 | 0,00019 |
| 539,57926 | 2e-05 | 6e-05 | 1e-05 | 0 | 2e-04 |
| 539,61644 | 2e-05 | 7e-05 | 1e-05 | 0 | 0,00021 |
| 539,65362 | 1e-05 | 7e-05 | 0 | 0 | 0,00022 |
| 539,6908 | 1e-05 | 8e-05 | 0 | 0 | 0,00023 |
| 539,72798 | 1e-05 | 9e-05 | 0 | 0 | 0,00024 |
| 539,76517 | 0 | 1e-04 | 0 | 0 | 0,00024 |
| 539,80235 | 0 | 1e-04 | 0 | 0 | 0,00025 |
| 539,83953 | 0 | 0,00011 | 0 | 1e-05 | 0,00025 |
| 539,87671 | 0 | 0,00011 | 0 | 1e-05 | 0,00024 |
| 539,91389 | 0 | 0,00011 | 0 | 1e-05 | 0,00024 |
| 539,95108 | 0 | 0,00011 | 0 | 2e-05 | 0,00023 |
| 539,98826 | 0 | 0,00011 | 0 | 3e-05 | 0,00022 |
| 540,02544 | 0 | 0,00011 | 0 | 4e-05 | 0,00021 |
| 540,06262 | 0 | 1e-04 | 0 | 5e-05 | 0,00019 |
| 540,0998 | 0 | 1e-04 | 0 | 6e-05 | 0,00018 |
| 540,13699 | 0 | 9e-05 | 0 | 8e-05 | 0,00016 |
| 540,17417 | 0 | 8e-05 | 0 | 1e-04 | 0,00014 |
| 540,21135 | 0 | 8e-05 | 0 | 0,00012 | 0,00012 |
| 540,24853 | 0 | 7e-05 | 0 | 0,00014 | 0,00011 |
| 540,28571 | 0 | 6e-05 | 0 | 0,00017 | 9e-05 |
| 540,3229 | 0 | 5e-05 | 0 | 2e-04 | 7e-05 |
| 540,36008 | 0 | 4e-05 | 0 | 0,00023 | 6e-05 |
| 540,39726 | 0 | 4e-05 | 0 | 0,00026 | 5e-05 |
| 540,43444 | 0 | 3e-05 | 0 | 0,00028 | 4e-05 |
| 540,47162 | 0 | 2e-05 | 1e-05 | 0,00031 | 3e-05 |
| 540,50881 | 0 | 2e-05 | 1e-05 | 0,00033 | 2e-05 |
| 540,54599 | 0 | 1e-05 | 1e-05 | 0,00035 | 2e-05 |
| 540,58317 | 0 | 1e-05 | 1e-05 | 0,00037 | 1e-05 |
| 540,62035 | 0 | 1e-05 | 2e-05 | 0,00037 | 1e-05 |
| 540,65753 | 0 | 1e-05 | 2e-05 | 0,00038 | 1e-05 |
| 540,69472 | 0 | 0 | 3e-05 | 0,00037 | 1e-05 |
| 540,7319 | 0 | 0 | 3e-05 | 0,00036 | 0 |
| 540,76908 | 0 | 0 | 4e-05 | 0,00034 | 0 |
| 540,80626 | 0 | 0 | 5e-05 | 0,00032 | 0 |
| 540,84344 | 0 | 0 | 6e-05 | 3e-04 | 0 |
| 540,88063 | 0 | 0 | 7e-05 | 0,00027 | 0 |
| 540,91781 | 0 | 0 | 8e-05 | 0,00024 | 0 |
| 540,95499 | 0 | 0 | 9e-05 | 0,00021 | 0 |
| 540,99217 | 0 | 0 | 1e-04 | 0,00018 | 0 |
| 541,02935 | 0 | 0 | 0,00011 | 0,00016 | 0 |
| 541,06654 | 0 | 0 | 0,00012 | 0,00013 | 0 |
| 541,10372 | 0 | 0 | 0,00012 | 0,00011 | 0 |
| 541,1409 | 0 | 0 | 0,00013 | 9e-05 | 0 |
| 541,17808 | 0 | 0 | 0,00013 | 7e-05 | 0 |
| 541,21526 | 0 | 0 | 0,00013 | 5e-05 | 0 |
| 541,25245 | 0 | 0 | 0,00012 | 4e-05 | 0 |
| 541,28963 | 0 | 0 | 0,00012 | 3e-05 | 0 |
| 541,32681 | 0 | 0 | 0,00011 | 2e-05 | 0 |
| 541,36399 | 0 | 0 | 0,00011 | 2e-05 | 0 |
| 541,40117 | 0 | 0 | 1e-04 | 1e-05 | 0 |
| 541,43836 | 0 | 0 | 9e-05 | 1e-05 | 0 |
| 541,47554 | 0 | 0 | 8e-05 | 1e-05 | 0 |
| 541,51272 | 0 | 0 | 7e-05 | 0 | 0 |
| 541,5499 | 0 | 0 | 6e-05 | 0 | 0 |
| 541,58708 | 0 | 0 | 5e-05 | 0 | 0 |
| 541,62427 | 0 | 0 | 4e-05 | 0 | 0 |
| 541,66145 | 0 | 0 | 3e-05 | 0 | 0 |
| 541,69863 | 0 | 0 | 3e-05 | 0 | 0 |
| 541,73581 | 0 | 0 | 2e-05 | 0 | 0 |
| 541,77299 | 0 | 0 | 2e-05 | 0 | 0 |
| 541,81018 | 0 | 0 | 1e-05 | 0 | 0 |
| 541,84736 | 0 | 0 | 1e-05 | 0 | 0 |
| 541,88454 | 0 | 0 | 1e-05 | 0 | 0 |
| 541,92172 | 0 | 0 | 0 | 0 | 0 |
| 541,9589 | 0 | 0 | 0 | 0 | 0 |
| 541,99609 | 0 | 0 | 0 | 0 | 0 |
| 542,03327 | 0 | 0 | 0 | 0 | 0 |
| 542,07045 | 0 | 0 | 0 | 0 | 0 |
| 542,10763 | 0 | 0 | 0 | 0 | 0 |
| 542,14481 | 0 | 0 | 0 | 0 | 0 |
| 542,182 | 0 | 0 | 0 | 0 | 0 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 1e-05 |
| 524,70646 | 0 | 0 | 0 | 1e-05 |
| 524,74364 | 0 | 0 | 0 | 1e-05 |
| 524,78082 | 0 | 0 | 0 | 1e-05 |
| 524,818 | 0 | 0 | 0 | 1e-05 |
| 524,85519 | 0 | 0 | 1e-05 | 2e-05 |
| 524,89237 | 0 | 0 | 1e-05 | 2e-05 |
| 524,92955 | 0 | 1e-05 | 1e-05 | 2e-05 |
| 524,96673 | 0 | 1e-05 | 1e-05 | 3e-05 |
| 525,00391 | 0 | 1e-05 | 1e-05 | 3e-05 |
| 525,0411 | 0 | 1e-05 | 2e-05 | 4e-05 |
| 525,07828 | 0 | 1e-05 | 2e-05 | 4e-05 |
| 525,11546 | 0 | 2e-05 | 2e-05 | 5e-05 |
| 525,15264 | 0 | 2e-05 | 3e-05 | 6e-05 |
| 525,18982 | 0 | 2e-05 | 4e-05 | 7e-05 |
| 525,22701 | 0 | 3e-05 | 4e-05 | 8e-05 |
| 525,26419 | 0 | 3e-05 | 5e-05 | 9e-05 |
| 525,30137 | 0 | 4e-05 | 6e-05 | 1e-04 |
| 525,33855 | 1e-05 | 5e-05 | 7e-05 | 0,00011 |
| 525,37573 | 1e-05 | 6e-05 | 8e-05 | 0,00013 |
| 525,41292 | 1e-05 | 7e-05 | 1e-04 | 0,00015 |
| 525,4501 | 1e-05 | 8e-05 | 0,00011 | 0,00016 |
| 525,48728 | 1e-05 | 9e-05 | 0,00013 | 0,00018 |
| 525,52446 | 2e-05 | 0,00011 | 0,00015 | 2e-04 |
| 525,56164 | 2e-05 | 0,00012 | 0,00017 | 0,00022 |
| 525,59883 | 2e-05 | 0,00014 | 2e-04 | 0,00025 |
| 525,63601 | 3e-05 | 0,00016 | 0,00022 | 0,00027 |
| 525,67319 | 3e-05 | 0,00019 | 0,00025 | 0,00029 |
| 525,71037 | 4e-05 | 0,00021 | 0,00029 | 0,00032 |
| 525,74755 | 4e-05 | 0,00024 | 0,00032 | 0,00035 |
| 525,78474 | 5e-05 | 0,00027 | 0,00036 | 0,00037 |
| 525,82192 | 6e-05 | 0,00031 | 4e-04 | 4e-04 |
| 525,8591 | 7e-05 | 0,00034 | 0,00045 | 0,00043 |
| 525,89628 | 8e-05 | 0,00038 | 0,00049 | 0,00046 |
| 525,93346 | 9e-05 | 0,00043 | 0,00055 | 0,00048 |
| 525,97065 | 0,00011 | 0,00047 | 6e-04 | 0,00051 |
| 526,00783 | 0,00012 | 0,00052 | 0,00065 | 0,00054 |
| 526,04501 | 0,00014 | 0,00057 | 0,00071 | 0,00057 |
| 526,08219 | 0,00016 | 0,00063 | 0,00077 | 6e-04 |
| 526,11937 | 0,00018 | 0,00068 | 0,00083 | 0,00062 |
| 526,15656 | 0,00021 | 0,00074 | 9e-04 | 0,00065 |
| 526,19374 | 0,00023 | 8e-04 | 0,00096 | 0,00067 |
| 526,23092 | 0,00026 | 0,00087 | 0,00103 | 7e-04 |
| 526,2681 | 0,00029 | 0,00093 | 0,00109 | 0,00073 |
| 526,30528 | 0,00033 | 0,001 | 0,00116 | 0,00075 |
| 526,34247 | 0,00037 | 0,00107 | 0,00122 | 0,00077 |
| 526,37965 | 0,00041 | 0,00114 | 0,00129 | 8e-04 |
| 526,41683 | 0,00046 | 0,00121 | 0,00136 | 0,00082 |
| 526,45401 | 0,00051 | 0,00128 | 0,00142 | 0,00085 |
| 526,49119 | 0,00057 | 0,00135 | 0,00148 | 0,00087 |
| 526,52838 | 0,00063 | 0,00143 | 0,00154 | 9e-04 |
| 526,56556 | 7e-04 | 0,0015 | 0,0016 | 0,00093 |
| 526,60274 | 0,00077 | 0,00158 | 0,00166 | 0,00096 |
| 526,63992 | 0,00085 | 0,00166 | 0,00172 | 0,00099 |
| 526,6771 | 0,00094 | 0,00173 | 0,00177 | 0,00102 |
| 526,71429 | 0,00103 | 0,00181 | 0,00182 | 0,00105 |
| 526,75147 | 0,00113 | 0,0019 | 0,00188 | 0,00109 |
| 526,78865 | 0,00124 | 0,00198 | 0,00192 | 0,00112 |
| 526,82583 | 0,00136 | 0,00206 | 0,00197 | 0,00117 |
| 526,86301 | 0,00148 | 0,00215 | 0,00202 | 0,00121 |
| 526,9002 | 0,00162 | 0,00224 | 0,00206 | 0,00126 |
| 526,93738 | 0,00177 | 0,00234 | 0,00211 | 0,00131 |
| 526,97456 | 0,00192 | 0,00244 | 0,00215 | 0,00137 |
| 527,01174 | 0,00209 | 0,00254 | 0,0022 | 0,00143 |
| 527,04892 | 0,00227 | 0,00265 | 0,00224 | 0,00149 |
| 527,08611 | 0,00246 | 0,00277 | 0,00229 | 0,00156 |
| 527,12329 | 0,00267 | 0,00289 | 0,00234 | 0,00164 |
| 527,16047 | 0,00288 | 0,00302 | 0,00239 | 0,00172 |
| 527,19765 | 0,00311 | 0,00315 | 0,00245 | 0,00181 |
| 527,23483 | 0,00335 | 0,0033 | 0,00251 | 0,00191 |
| 527,27202 | 0,0036 | 0,00345 | 0,00258 | 0,00201 |
| 527,3092 | 0,00387 | 0,00361 | 0,00266 | 0,00213 |
| 527,34638 | 0,00415 | 0,00378 | 0,00274 | 0,00225 |
| 527,38356 | 0,00444 | 0,00396 | 0,00283 | 0,00238 |
| 527,42074 | 0,00474 | 0,00415 | 0,00293 | 0,00252 |
| 527,45793 | 0,00505 | 0,00434 | 0,00304 | 0,00267 |
| 527,49511 | 0,00537 | 0,00455 | 0,00315 | 0,00283 |
| 527,53229 | 0,0057 | 0,00476 | 0,00328 | 0,00301 |
| 527,56947 | 0,00604 | 0,00499 | 0,00342 | 0,00319 |
| 527,60665 | 0,00639 | 0,00522 | 0,00357 | 0,00339 |
| 527,64384 | 0,00674 | 0,00546 | 0,00374 | 0,00361 |
| 527,68102 | 0,0071 | 0,00571 | 0,00391 | 0,00383 |
| 527,7182 | 0,00747 | 0,00596 | 0,00409 | 0,00407 |
| 527,75538 | 0,00783 | 0,00623 | 0,00429 | 0,00433 |
| 527,79256 | 0,00819 | 0,0065 | 0,0045 | 0,00459 |
| 527,82975 | 0,00856 | 0,00677 | 0,00472 | 0,00487 |
| 527,86693 | 0,00892 | 0,00705 | 0,00495 | 0,00517 |
| 527,90411 | 0,00928 | 0,00733 | 0,00519 | 0,00548 |
| 527,94129 | 0,00963 | 0,00762 | 0,00544 | 0,00579 |
| 527,97847 | 0,00998 | 0,00791 | 0,0057 | 0,00612 |
| 528,01566 | 0,01031 | 0,0082 | 0,00597 | 0,00646 |
| 528,05284 | 0,01064 | 0,00849 | 0,00624 | 0,00681 |
| 528,09002 | 0,01095 | 0,00879 | 0,00652 | 0,00717 |
| 528,1272 | 0,01126 | 0,00908 | 0,0068 | 0,00753 |
| 528,16438 | 0,01155 | 0,00938 | 0,00709 | 0,0079 |
| 528,20157 | 0,01182 | 0,00967 | 0,00738 | 0,00827 |
| 528,23875 | 0,01208 | 0,00996 | 0,00767 | 0,00865 |
| 528,27593 | 0,01233 | 0,01025 | 0,00797 | 0,00903 |
| 528,31311 | 0,01255 | 0,01054 | 0,00827 | 0,00941 |
| 528,35029 | 0,01276 | 0,01082 | 0,00857 | 0,00978 |
| 528,38748 | 0,01295 | 0,0111 | 0,00886 | 0,01016 |
| 528,42466 | 0,01313 | 0,01138 | 0,00916 | 0,01053 |
| 528,46184 | 0,01329 | 0,01165 | 0,00946 | 0,0109 |
| 528,49902 | 0,01343 | 0,01192 | 0,00975 | 0,01126 |
| 528,5362 | 0,01356 | 0,01219 | 0,01005 | 0,01162 |
| 528,57339 | 0,01367 | 0,01245 | 0,01034 | 0,01197 |
| 528,61057 | 0,01377 | 0,0127 | 0,01064 | 0,01231 |
| 528,64775 | 0,01385 | 0,01295 | 0,01093 | 0,01265 |
| 528,68493 | 0,01392 | 0,0132 | 0,01122 | 0,01298 |
| 528,72211 | 0,01399 | 0,01345 | 0,01151 | 0,01331 |
| 528,7593 | 0,01404 | 0,01368 | 0,0118 | 0,01363 |
| 528,79648 | 0,01408 | 0,01392 | 0,01209 | 0,01394 |
| 528,83366 | 0,01412 | 0,01415 | 0,01239 | 0,01425 |
| 528,87084 | 0,01416 | 0,01438 | 0,01268 | 0,01455 |
| 528,90802 | 0,01419 | 0,01461 | 0,01297 | 0,01484 |
| 528,94521 | 0,01423 | 0,01484 | 0,01327 | 0,01513 |
| 528,98239 | 0,01427 | 0,01506 | 0,01357 | 0,01542 |
| 529,01957 | 0,0143 | 0,01529 | 0,01387 | 0,01571 |
| 529,05675 | 0,01435 | 0,01552 | 0,01418 | 0,01599 |
| 529,09393 | 0,0144 | 0,01575 | 0,01449 | 0,01627 |
| 529,13112 | 0,01447 | 0,01598 | 0,01481 | 0,01655 |
| 529,1683 | 0,01454 | 0,01622 | 0,01513 | 0,01683 |
| 529,20548 | 0,01463 | 0,01646 | 0,01546 | 0,01711 |
| 529,24266 | 0,01473 | 0,01672 | 0,0158 | 0,01739 |
| 529,27984 | 0,01485 | 0,01697 | 0,01615 | 0,01768 |
| 529,31703 | 0,01499 | 0,01724 | 0,0165 | 0,01796 |
| 529,35421 | 0,01514 | 0,01752 | 0,01687 | 0,01826 |
| 529,39139 | 0,01532 | 0,01781 | 0,01724 | 0,01855 |
| 529,42857 | 0,01551 | 0,01812 | 0,01763 | 0,01886 |
| 529,46575 | 0,01573 | 0,01843 | 0,01802 | 0,01917 |
| 529,50294 | 0,01597 | 0,01876 | 0,01843 | 0,01949 |
| 529,54012 | 0,01623 | 0,0191 | 0,01885 | 0,01982 |
| 529,5773 | 0,01651 | 0,01945 | 0,01928 | 0,02016 |
| 529,61448 | 0,01682 | 0,01982 | 0,01972 | 0,0205 |
| 529,65166 | 0,01714 | 0,0202 | 0,02018 | 0,02087 |
| 529,68885 | 0,01749 | 0,02058 | 0,02064 | 0,02124 |
| 529,72603 | 0,01786 | 0,02098 | 0,02112 | 0,02163 |
| 529,76321 | 0,01824 | 0,02139 | 0,0216 | 0,02203 |
| 529,80039 | 0,01864 | 0,0218 | 0,02209 | 0,02244 |
| 529,83757 | 0,01906 | 0,02222 | 0,02259 | 0,02286 |
| 529,87476 | 0,01949 | 0,02264 | 0,02309 | 0,0233 |
| 529,91194 | 0,01993 | 0,02306 | 0,0236 | 0,02375 |
| 529,94912 | 0,02038 | 0,02348 | 0,0241 | 0,0242 |
| 529,9863 | 0,02084 | 0,0239 | 0,02461 | 0,02467 |
| 530,02348 | 0,0213 | 0,02431 | 0,02511 | 0,02514 |
| 530,06067 | 0,02176 | 0,02471 | 0,0256 | 0,02562 |
| 530,09785 | 0,02223 | 0,02511 | 0,02608 | 0,0261 |
| 530,13503 | 0,0227 | 0,02549 | 0,02656 | 0,02658 |
| 530,17221 | 0,02316 | 0,02585 | 0,02702 | 0,02705 |
| 530,20939 | 0,02361 | 0,02621 | 0,02747 | 0,02752 |
| 530,24658 | 0,02406 | 0,02654 | 0,0279 | 0,02799 |
| 530,28376 | 0,0245 | 0,02687 | 0,02831 | 0,02844 |
| 530,32094 | 0,02493 | 0,02717 | 0,0287 | 0,02888 |
| 530,35812 | 0,02535 | 0,02745 | 0,02907 | 0,0293 |
| 530,3953 | 0,02576 | 0,02772 | 0,02942 | 0,02971 |
| 530,43249 | 0,02615 | 0,02798 | 0,02975 | 0,0301 |
| 530,46967 | 0,02654 | 0,02822 | 0,03005 | 0,03047 |
| 530,50685 | 0,02691 | 0,02845 | 0,03034 | 0,03082 |
| 530,54403 | 0,02727 | 0,02867 | 0,0306 | 0,03114 |
| 530,58121 | 0,02762 | 0,02889 | 0,03085 | 0,03145 |
| 530,6184 | 0,02796 | 0,0291 | 0,03109 | 0,03173 |
| 530,65558 | 0,0283 | 0,0293 | 0,03131 | 0,032 |
| 530,69276 | 0,02863 | 0,02952 | 0,03151 | 0,03225 |
| 530,72994 | 0,02896 | 0,02973 | 0,03172 | 0,03249 |
| 530,76712 | 0,02929 | 0,02996 | 0,03191 | 0,03271 |
| 530,80431 | 0,02962 | 0,03021 | 0,03211 | 0,03294 |
| 530,84149 | 0,02996 | 0,03047 | 0,03231 | 0,03315 |
| 530,87867 | 0,03031 | 0,03075 | 0,03252 | 0,03337 |
| 530,91585 | 0,03067 | 0,03106 | 0,03274 | 0,0336 |
| 530,95303 | 0,03104 | 0,0314 | 0,03298 | 0,03383 |
| 530,99022 | 0,03143 | 0,03177 | 0,03323 | 0,03408 |
| 531,0274 | 0,03184 | 0,03218 | 0,0335 | 0,03435 |
| 531,06458 | 0,03226 | 0,03261 | 0,03381 | 0,03464 |
| 531,10176 | 0,03272 | 0,03309 | 0,03413 | 0,03495 |
| 531,13894 | 0,0332 | 0,03361 | 0,03449 | 0,0353 |
| 531,17613 | 0,0337 | 0,03416 | 0,03487 | 0,03568 |
| 531,21331 | 0,03423 | 0,03475 | 0,03528 | 0,03609 |
| 531,25049 | 0,03478 | 0,03537 | 0,03572 | 0,03653 |
| 531,28767 | 0,03536 | 0,03602 | 0,0362 | 0,03701 |
| 531,32485 | 0,03596 | 0,03671 | 0,03671 | 0,03752 |
| 531,36204 | 0,03659 | 0,03742 | 0,03724 | 0,03806 |
| 531,39922 | 0,03724 | 0,03816 | 0,0378 | 0,03863 |
| 531,4364 | 0,03791 | 0,03891 | 0,03838 | 0,03923 |
| 531,47358 | 0,0386 | 0,03968 | 0,03899 | 0,03985 |
| 531,51076 | 0,03931 | 0,04046 | 0,03962 | 0,04049 |
| 531,54795 | 0,04003 | 0,04124 | 0,04026 | 0,04115 |
| 531,58513 | 0,04076 | 0,04202 | 0,04091 | 0,04181 |
| 531,62231 | 0,04149 | 0,04279 | 0,04157 | 0,04248 |
| 531,65949 | 0,04224 | 0,04356 | 0,04224 | 0,04314 |
| 531,69667 | 0,04298 | 0,04431 | 0,04292 | 0,0438 |
| 531,73386 | 0,04372 | 0,04504 | 0,04359 | 0,04445 |
| 531,77104 | 0,04447 | 0,04575 | 0,04426 | 0,04509 |
| 531,80822 | 0,0452 | 0,04644 | 0,04492 | 0,0457 |
| 531,8454 | 0,04593 | 0,0471 | 0,04559 | 0,0463 |
| 531,88258 | 0,04666 | 0,04774 | 0,04624 | 0,04687 |
| 531,91977 | 0,04737 | 0,04835 | 0,04688 | 0,04741 |
| 531,95695 | 0,04808 | 0,04893 | 0,04752 | 0,04793 |
| 531,99413 | 0,04877 | 0,04949 | 0,04816 | 0,04843 |
| 532,03131 | 0,04946 | 0,05003 | 0,04878 | 0,0489 |
| 532,06849 | 0,05015 | 0,05055 | 0,0494 | 0,04935 |
| 532,10568 | 0,05082 | 0,05106 | 0,05002 | 0,04978 |
| 532,14286 | 0,0515 | 0,05155 | 0,05063 | 0,05019 |
| 532,18004 | 0,05217 | 0,05204 | 0,05125 | 0,05059 |
| 532,21722 | 0,05285 | 0,05253 | 0,05187 | 0,05099 |
| 532,2544 | 0,05353 | 0,05302 | 0,0525 | 0,05139 |
| 532,29159 | 0,05422 | 0,05352 | 0,05314 | 0,05179 |
| 532,32877 | 0,05491 | 0,05403 | 0,05379 | 0,0522 |
| 532,36595 | 0,05563 | 0,05456 | 0,05445 | 0,05263 |
| 532,40313 | 0,05635 | 0,05511 | 0,05513 | 0,05308 |
| 532,44031 | 0,0571 | 0,05569 | 0,05583 | 0,05355 |
| 532,4775 | 0,05786 | 0,05629 | 0,05655 | 0,05405 |
| 532,51468 | 0,05865 | 0,05692 | 0,05729 | 0,05459 |
| 532,55186 | 0,05947 | 0,05759 | 0,05805 | 0,05517 |
| 532,58904 | 0,0603 | 0,05829 | 0,05884 | 0,05578 |
| 532,62622 | 0,06117 | 0,05901 | 0,05964 | 0,05643 |
| 532,66341 | 0,06205 | 0,05977 | 0,06047 | 0,05712 |
| 532,70059 | 0,06296 | 0,06055 | 0,06132 | 0,05785 |
| 532,73777 | 0,06389 | 0,06136 | 0,06218 | 0,05862 |
| 532,77495 | 0,06483 | 0,06219 | 0,06307 | 0,05942 |
| 532,81213 | 0,0658 | 0,06304 | 0,06396 | 0,06025 |
| 532,84932 | 0,06677 | 0,0639 | 0,06487 | 0,06111 |
| 532,8865 | 0,06775 | 0,06476 | 0,06579 | 0,06199 |
| 532,92368 | 0,06874 | 0,06563 | 0,06671 | 0,06289 |
| 532,96086 | 0,06972 | 0,06649 | 0,06764 | 0,0638 |
| 532,99804 | 0,0707 | 0,06734 | 0,06856 | 0,06473 |
| 533,03523 | 0,07167 | 0,06817 | 0,06949 | 0,06565 |
| 533,07241 | 0,07262 | 0,06899 | 0,07041 | 0,06658 |
| 533,10959 | 0,07356 | 0,06978 | 0,07133 | 0,0675 |
| 533,14677 | 0,07446 | 0,07053 | 0,07223 | 0,06842 |
| 533,18395 | 0,07534 | 0,07125 | 0,07313 | 0,06933 |
| 533,22114 | 0,07619 | 0,07194 | 0,07402 | 0,07022 |
| 533,25832 | 0,07701 | 0,07258 | 0,07491 | 0,0711 |
| 533,2955 | 0,07779 | 0,07319 | 0,07578 | 0,07196 |
| 533,33268 | 0,07853 | 0,07375 | 0,07664 | 0,07281 |
| 533,36986 | 0,07923 | 0,07426 | 0,07749 | 0,07364 |
| 533,40705 | 0,0799 | 0,07474 | 0,07833 | 0,07446 |
| 533,44423 | 0,08053 | 0,07519 | 0,07917 | 0,07527 |
| 533,48141 | 0,08113 | 0,0756 | 0,08 | 0,07606 |
| 533,51859 | 0,0817 | 0,07597 | 0,08083 | 0,07685 |
| 533,55577 | 0,08224 | 0,07632 | 0,08165 | 0,07763 |
| 533,59295 | 0,08276 | 0,07665 | 0,08246 | 0,0784 |
| 533,63014 | 0,08326 | 0,07696 | 0,08328 | 0,07917 |
| 533,66732 | 0,08374 | 0,07727 | 0,08409 | 0,07995 |
| 533,7045 | 0,08421 | 0,07756 | 0,08489 | 0,08072 |
| 533,74168 | 0,08468 | 0,07786 | 0,08569 | 0,08149 |
| 533,77886 | 0,08514 | 0,07817 | 0,08648 | 0,08226 |
| 533,81605 | 0,08561 | 0,07849 | 0,08725 | 0,08303 |
| 533,85323 | 0,08608 | 0,07882 | 0,08801 | 0,08379 |
| 533,89041 | 0,08655 | 0,07917 | 0,08875 | 0,08455 |
| 533,92759 | 0,08703 | 0,07955 | 0,08946 | 0,0853 |
| 533,96477 | 0,08753 | 0,07996 | 0,09013 | 0,08603 |
| 534,00196 | 0,08803 | 0,0804 | 0,09076 | 0,08675 |
| 534,03914 | 0,08853 | 0,08086 | 0,09135 | 0,08743 |
| 534,07632 | 0,08905 | 0,08135 | 0,09189 | 0,08809 |
| 534,1135 | 0,08956 | 0,08186 | 0,09236 | 0,0887 |
| 534,15068 | 0,09007 | 0,08241 | 0,09276 | 0,08926 |
| 534,18787 | 0,09057 | 0,08297 | 0,09307 | 0,08975 |
| 534,22505 | 0,09105 | 0,08355 | 0,09331 | 0,09019 |
| 534,26223 | 0,09151 | 0,08413 | 0,09346 | 0,09055 |
| 534,29941 | 0,09195 | 0,08472 | 0,09352 | 0,09084 |
| 534,33659 | 0,09235 | 0,08531 | 0,09348 | 0,09103 |
| 534,37378 | 0,09269 | 0,08588 | 0,09332 | 0,09112 |
| 534,41096 | 0,09299 | 0,08644 | 0,09307 | 0,09112 |
| 534,44814 | 0,09323 | 0,08697 | 0,09273 | 0,09102 |
| 534,48532 | 0,09341 | 0,08746 | 0,09228 | 0,09083 |
| 534,5225 | 0,09351 | 0,08792 | 0,09175 | 0,09054 |
| 534,55969 | 0,09353 | 0,08831 | 0,09111 | 0,09013 |
| 534,59687 | 0,09347 | 0,08866 | 0,09039 | 0,08964 |
| 534,63405 | 0,09334 | 0,08894 | 0,08961 | 0,08906 |
| 534,67123 | 0,09313 | 0,08917 | 0,08876 | 0,0884 |
| 534,70841 | 0,09285 | 0,08933 | 0,08786 | 0,08768 |
| 534,7456 | 0,09247 | 0,08941 | 0,08693 | 0,08689 |
| 534,78278 | 0,09203 | 0,08942 | 0,08596 | 0,08605 |
| 534,81996 | 0,09153 | 0,08937 | 0,085 | 0,08519 |
| 534,85714 | 0,09098 | 0,08927 | 0,08404 | 0,08431 |
| 534,89432 | 0,09038 | 0,0891 | 0,0831 | 0,08343 |
| 534,93151 | 0,08976 | 0,08888 | 0,08219 | 0,08257 |
| 534,96869 | 0,08911 | 0,08862 | 0,08135 | 0,08174 |
| 535,00587 | 0,08847 | 0,08832 | 0,08058 | 0,08097 |
| 535,04305 | 0,08784 | 0,08801 | 0,07988 | 0,08027 |
| 535,08023 | 0,08723 | 0,08767 | 0,07928 | 0,07964 |
| 535,11742 | 0,08667 | 0,08734 | 0,07878 | 0,07911 |
| 535,1546 | 0,08617 | 0,08702 | 0,07841 | 0,0787 |
| 535,19178 | 0,08575 | 0,08672 | 0,07817 | 0,07843 |
| 535,22896 | 0,08541 | 0,08645 | 0,07807 | 0,07828 |
| 535,26614 | 0,08516 | 0,08622 | 0,0781 | 0,07826 |
| 535,30333 | 0,08501 | 0,08604 | 0,07827 | 0,07838 |
| 535,34051 | 0,08499 | 0,08593 | 0,07858 | 0,07866 |
| 535,37769 | 0,08509 | 0,08589 | 0,07905 | 0,07911 |
| 535,41487 | 0,08532 | 0,08592 | 0,07967 | 0,0797 |
| 535,45205 | 0,08567 | 0,08603 | 0,08042 | 0,08043 |
| 535,48924 | 0,08613 | 0,08621 | 0,0813 | 0,08129 |
| 535,52642 | 0,08671 | 0,08649 | 0,0823 | 0,08228 |
| 535,5636 | 0,08743 | 0,08686 | 0,08342 | 0,08341 |
| 535,60078 | 0,08824 | 0,08729 | 0,08466 | 0,08465 |
| 535,63796 | 0,08915 | 0,0878 | 0,086 | 0,08599 |
| 535,67515 | 0,09012 | 0,08837 | 0,08741 | 0,0874 |
| 535,71233 | 0,09117 | 0,08901 | 0,08889 | 0,08887 |
| 535,74951 | 0,09227 | 0,08971 | 0,09043 | 0,09041 |
| 535,78669 | 0,09341 | 0,09045 | 0,09202 | 0,09198 |
| 535,82387 | 0,09456 | 0,09123 | 0,09364 | 0,09358 |
| 535,86106 | 0,09571 | 0,09202 | 0,09527 | 0,09518 |
| 535,89824 | 0,09684 | 0,09283 | 0,0969 | 0,09677 |
| 535,93542 | 0,09794 | 0,09365 | 0,09853 | 0,09835 |
| 535,9726 | 0,09899 | 0,09446 | 0,10013 | 0,09988 |
| 536,00978 | 0,09997 | 0,09525 | 0,10169 | 0,10136 |
| 536,04697 | 0,10088 | 0,09602 | 0,10321 | 0,10279 |
| 536,08415 | 0,10171 | 0,09676 | 0,10468 | 0,10416 |
| 536,12133 | 0,10245 | 0,09746 | 0,10608 | 0,10545 |
| 536,15851 | 0,10307 | 0,09812 | 0,10742 | 0,10666 |
| 536,19569 | 0,10359 | 0,09873 | 0,10867 | 0,10777 |
| 536,23288 | 0,10401 | 0,09929 | 0,10983 | 0,10879 |
| 536,27006 | 0,10433 | 0,0998 | 0,11091 | 0,10972 |
| 536,30724 | 0,10455 | 0,10026 | 0,11189 | 0,11056 |
| 536,34442 | 0,10467 | 0,10067 | 0,11278 | 0,1113 |
| 536,3816 | 0,10468 | 0,10103 | 0,11358 | 0,11192 |
| 536,41879 | 0,10462 | 0,10135 | 0,11425 | 0,11244 |
| 536,45597 | 0,10449 | 0,10164 | 0,11482 | 0,11286 |
| 536,49315 | 0,10429 | 0,10189 | 0,11529 | 0,11318 |
| 536,53033 | 0,10405 | 0,10211 | 0,11566 | 0,11341 |
| 536,56751 | 0,10376 | 0,1023 | 0,11592 | 0,11352 |
| 536,6047 | 0,10344 | 0,10248 | 0,11607 | 0,11353 |
| 536,64188 | 0,10311 | 0,10265 | 0,1161 | 0,11344 |
| 536,67906 | 0,10276 | 0,10281 | 0,11604 | 0,11325 |
| 536,71624 | 0,10242 | 0,10296 | 0,11587 | 0,11298 |
| 536,75342 | 0,10209 | 0,10312 | 0,1156 | 0,11261 |
| 536,79061 | 0,10178 | 0,10327 | 0,11524 | 0,11212 |
| 536,82779 | 0,1015 | 0,10343 | 0,11476 | 0,11155 |
| 536,86497 | 0,10124 | 0,10359 | 0,11419 | 0,1109 |
| 536,90215 | 0,10101 | 0,10376 | 0,11354 | 0,11017 |
| 536,93933 | 0,10081 | 0,10393 | 0,11282 | 0,10937 |
| 536,97652 | 0,10065 | 0,1041 | 0,11202 | 0,10849 |
| 537,0137 | 0,10052 | 0,10426 | 0,11115 | 0,10755 |
| 537,05088 | 0,10041 | 0,10442 | 0,11022 | 0,10657 |
| 537,08806 | 0,10033 | 0,10457 | 0,10925 | 0,10555 |
| 537,12524 | 0,10027 | 0,1047 | 0,10826 | 0,10451 |
| 537,16243 | 0,10023 | 0,10482 | 0,10724 | 0,10346 |
| 537,19961 | 0,1002 | 0,10491 | 0,10622 | 0,10242 |
| 537,23679 | 0,10017 | 0,10498 | 0,10522 | 0,1014 |
| 537,27397 | 0,10015 | 0,10503 | 0,10424 | 0,10042 |
| 537,31115 | 0,10013 | 0,10505 | 0,10331 | 0,0995 |
| 537,34834 | 0,10011 | 0,10504 | 0,10244 | 0,09865 |
| 537,38552 | 0,10009 | 0,105 | 0,10164 | 0,09791 |
| 537,4227 | 0,10007 | 0,10494 | 0,10094 | 0,09729 |
| 537,45988 | 0,10005 | 0,10487 | 0,10037 | 0,0968 |
| 537,49706 | 0,10003 | 0,10478 | 0,09992 | 0,09645 |
| 537,53425 | 0,10002 | 0,10469 | 0,0996 | 0,09626 |
| 537,57143 | 0,10004 | 0,10461 | 0,09943 | 0,09625 |
| 537,60861 | 0,10008 | 0,10454 | 0,09941 | 0,09647 |
| 537,64579 | 0,10016 | 0,1045 | 0,0996 | 0,09688 |
| 537,68297 | 0,10029 | 0,10449 | 0,09998 | 0,0975 |
| 537,72016 | 0,10047 | 0,10455 | 0,10053 | 0,09833 |
| 537,75734 | 0,10072 | 0,10468 | 0,10126 | 0,09936 |
| 537,79452 | 0,10108 | 0,10489 | 0,10218 | 0,10066 |
| 537,8317 | 0,10153 | 0,10519 | 0,1033 | 0,10218 |
| 537,86888 | 0,10208 | 0,10559 | 0,10463 | 0,1039 |
| 537,90607 | 0,10274 | 0,1061 | 0,10613 | 0,10583 |
| 537,94325 | 0,10352 | 0,10677 | 0,1078 | 0,10794 |
| 537,98043 | 0,10447 | 0,10757 | 0,10961 | 0,11024 |
| 538,01761 | 0,10554 | 0,10851 | 0,11157 | 0,11274 |
| 538,05479 | 0,10675 | 0,10958 | 0,11369 | 0,11537 |
| 538,09198 | 0,10809 | 0,11078 | 0,11591 | 0,11811 |
| 538,12916 | 0,10955 | 0,11215 | 0,11821 | 0,12095 |
| 538,16634 | 0,11115 | 0,11365 | 0,12058 | 0,12387 |
| 538,20352 | 0,11287 | 0,11526 | 0,123 | 0,12684 |
| 538,2407 | 0,11467 | 0,11698 | 0,12543 | 0,12983 |
| 538,27789 | 0,11655 | 0,11879 | 0,12786 | 0,13279 |
| 538,31507 | 0,11849 | 0,12067 | 0,13026 | 0,13572 |
| 538,35225 | 0,12046 | 0,12262 | 0,13259 | 0,13857 |
| 538,38943 | 0,12244 | 0,12458 | 0,13485 | 0,14132 |
| 538,42661 | 0,1244 | 0,12655 | 0,13701 | 0,14391 |
| 538,4638 | 0,12631 | 0,1285 | 0,13901 | 0,14635 |
| 538,50098 | 0,12815 | 0,13041 | 0,14086 | 0,1486 |
| 538,53816 | 0,12991 | 0,13222 | 0,14254 | 0,15066 |
| 538,57534 | 0,13152 | 0,13393 | 0,14404 | 0,1525 |
| 538,61252 | 0,13298 | 0,13553 | 0,14535 | 0,15406 |
| 538,64971 | 0,13427 | 0,13698 | 0,14644 | 0,15535 |
| 538,68689 | 0,13539 | 0,13828 | 0,14729 | 0,15639 |
| 538,72407 | 0,13632 | 0,13937 | 0,14792 | 0,15717 |
| 538,76125 | 0,13703 | 0,14025 | 0,14835 | 0,1577 |
| 538,79843 | 0,13749 | 0,14094 | 0,14857 | 0,15795 |
| 538,83562 | 0,13774 | 0,14143 | 0,14859 | 0,1579 |
| 538,8728 | 0,13778 | 0,14172 | 0,14838 | 0,15762 |
| 538,90998 | 0,13763 | 0,1418 | 0,14798 | 0,15712 |
| 538,94716 | 0,13728 | 0,14164 | 0,14743 | 0,15642 |
| 538,98434 | 0,13672 | 0,1413 | 0,14673 | 0,15552 |
| 539,02153 | 0,136 | 0,14079 | 0,14591 | 0,15441 |
| 539,05871 | 0,13514 | 0,14013 | 0,14496 | 0,15316 |
| 539,09589 | 0,13416 | 0,13933 | 0,1439 | 0,15178 |
| 539,13307 | 0,13308 | 0,13837 | 0,14277 | 0,1503 |
| 539,17025 | 0,13192 | 0,13732 | 0,14157 | 0,14872 |
| 539,20744 | 0,1307 | 0,13619 | 0,14033 | 0,14707 |
| 539,24462 | 0,12946 | 0,135 | 0,13905 | 0,14536 |
| 539,2818 | 0,12821 | 0,13376 | 0,13773 | 0,14362 |
| 539,31898 | 0,12696 | 0,13249 | 0,13639 | 0,14184 |
| 539,35616 | 0,12573 | 0,1312 | 0,13503 | 0,14006 |
| 539,39335 | 0,12455 | 0,12992 | 0,13367 | 0,13826 |
| 539,43053 | 0,1234 | 0,12865 | 0,13228 | 0,13645 |
| 539,46771 | 0,12231 | 0,1274 | 0,13088 | 0,13464 |
| 539,50489 | 0,12126 | 0,12616 | 0,12946 | 0,13283 |
| 539,54207 | 0,12026 | 0,12495 | 0,12801 | 0,13101 |
| 539,57926 | 0,11931 | 0,12376 | 0,12653 | 0,12918 |
| 539,61644 | 0,1184 | 0,12258 | 0,12502 | 0,12734 |
| 539,65362 | 0,11751 | 0,12142 | 0,12347 | 0,12549 |
| 539,6908 | 0,11663 | 0,12025 | 0,12186 | 0,12362 |
| 539,72798 | 0,11576 | 0,11908 | 0,1202 | 0,12172 |
| 539,76517 | 0,11487 | 0,11788 | 0,1185 | 0,1198 |
| 539,80235 | 0,11395 | 0,11666 | 0,11674 | 0,11786 |
| 539,83953 | 0,11299 | 0,1154 | 0,11493 | 0,11587 |
| 539,87671 | 0,11198 | 0,1141 | 0,11307 | 0,11386 |
| 539,91389 | 0,11091 | 0,11273 | 0,11116 | 0,11183 |
| 539,95108 | 0,10977 | 0,1113 | 0,10921 | 0,10977 |
| 539,98826 | 0,10855 | 0,1098 | 0,10722 | 0,10769 |
| 540,02544 | 0,10724 | 0,10824 | 0,10521 | 0,10559 |
| 540,06262 | 0,10585 | 0,10661 | 0,10318 | 0,10348 |
| 540,0998 | 0,10439 | 0,10492 | 0,10113 | 0,10137 |
| 540,13699 | 0,10286 | 0,10315 | 0,09908 | 0,09925 |
| 540,17417 | 0,10125 | 0,10133 | 0,09703 | 0,09714 |
| 540,21135 | 0,09958 | 0,09946 | 0,09499 | 0,09504 |
| 540,24853 | 0,09785 | 0,09756 | 0,09296 | 0,09294 |
| 540,28571 | 0,09609 | 0,09563 | 0,09095 | 0,09087 |
| 540,3229 | 0,0943 | 0,09367 | 0,08896 | 0,0888 |
| 540,36008 | 0,09249 | 0,09172 | 0,08698 | 0,08675 |
| 540,39726 | 0,09068 | 0,08976 | 0,08502 | 0,08471 |
| 540,43444 | 0,08887 | 0,08783 | 0,08307 | 0,08269 |
| 540,47162 | 0,08707 | 0,08591 | 0,08112 | 0,08066 |
| 540,50881 | 0,08529 | 0,08402 | 0,07918 | 0,07864 |
| 540,54599 | 0,08353 | 0,08218 | 0,07723 | 0,07661 |
| 540,58317 | 0,08181 | 0,08038 | 0,07526 | 0,07457 |
| 540,62035 | 0,08012 | 0,07862 | 0,07327 | 0,07251 |
| 540,65753 | 0,07846 | 0,0769 | 0,07126 | 0,07042 |
| 540,69472 | 0,07682 | 0,07522 | 0,06921 | 0,0683 |
| 540,7319 | 0,07521 | 0,07358 | 0,06711 | 0,06615 |
| 540,76908 | 0,07362 | 0,07198 | 0,06497 | 0,06397 |
| 540,80626 | 0,07204 | 0,0704 | 0,06278 | 0,06174 |
| 540,84344 | 0,07046 | 0,06884 | 0,06055 | 0,05947 |
| 540,88063 | 0,06888 | 0,06729 | 0,05827 | 0,05716 |
| 540,91781 | 0,06728 | 0,06574 | 0,05593 | 0,05482 |
| 540,95499 | 0,06565 | 0,06418 | 0,05356 | 0,05244 |
| 540,99217 | 0,064 | 0,0626 | 0,05115 | 0,05004 |
| 541,02935 | 0,06229 | 0,06099 | 0,04871 | 0,04761 |
| 541,06654 | 0,06055 | 0,05936 | 0,04626 | 0,04517 |
| 541,10372 | 0,05875 | 0,05769 | 0,0438 | 0,04274 |
| 541,1409 | 0,0569 | 0,05596 | 0,04134 | 0,04031 |
| 541,17808 | 0,055 | 0,05419 | 0,0389 | 0,0379 |
| 541,21526 | 0,05302 | 0,05237 | 0,03649 | 0,03553 |
| 541,25245 | 0,051 | 0,0505 | 0,03411 | 0,03319 |
| 541,28963 | 0,04893 | 0,04859 | 0,03178 | 0,03092 |
| 541,32681 | 0,04682 | 0,04662 | 0,02952 | 0,02871 |
| 541,36399 | 0,04467 | 0,04462 | 0,02734 | 0,02657 |
| 541,40117 | 0,04249 | 0,04259 | 0,02524 | 0,0245 |
| 541,43836 | 0,04029 | 0,04053 | 0,02322 | 0,02253 |
| 541,47554 | 0,03809 | 0,03846 | 0,02129 | 0,02067 |
| 541,51272 | 0,03589 | 0,03638 | 0,01946 | 0,0189 |
| 541,5499 | 0,03371 | 0,03431 | 0,01776 | 0,01723 |
| 541,58708 | 0,03154 | 0,03226 | 0,01616 | 0,01567 |
| 541,62427 | 0,02943 | 0,03023 | 0,01467 | 0,0142 |
| 541,66145 | 0,02736 | 0,02823 | 0,01327 | 0,01287 |
| 541,69863 | 0,02535 | 0,02627 | 0,01198 | 0,01164 |
| 541,73581 | 0,0234 | 0,02438 | 0,0108 | 0,0105 |
| 541,77299 | 0,02153 | 0,02256 | 0,00974 | 0,00946 |
| 541,81018 | 0,01975 | 0,0208 | 0,00876 | 0,00851 |
| 541,84736 | 0,01806 | 0,01911 | 0,00787 | 0,00766 |
| 541,88454 | 0,01646 | 0,0175 | 0,00707 | 0,00691 |
| 541,92172 | 0,01495 | 0,01598 | 0,00634 | 0,00622 |
| 541,9589 | 0,01354 | 0,01457 | 0,0057 | 0,00561 |
| 541,99609 | 0,01223 | 0,01323 | 0,00513 | 0,00506 |
| 542,03327 | 0,01103 | 0,01199 | 0,00462 | 0,00458 |
| 542,07045 | 0,00992 | 0,01083 | 0,00416 | 0,00415 |
| 542,10763 | 0,00891 | 0,00976 | 0,00375 | 0,00378 |
| 542,14481 | 0,00798 | 0,00879 | 0,00339 | 0,00345 |
| 542,182 | 0,00713 | 0,00791 | 0,00307 | 0,00315 |
| 542,21918 | 0,00638 | 0,0071 | 0,00279 | 0,00289 |
| 542,25636 | 0,00571 | 0,00636 | 0,00254 | 0,00265 |
| 542,29354 | 0,00511 | 0,00569 | 0,00231 | 0,00245 |
| 542,33072 | 0,00456 | 0,0051 | 0,00211 | 0,00227 |
| 542,36791 | 0,00408 | 0,00458 | 0,00194 | 0,0021 |
| 542,40509 | 0,00366 | 0,0041 | 0,00178 | 0,00195 |
| 542,44227 | 0,00329 | 0,00368 | 0,00163 | 0,00181 |
| 542,47945 | 0,00297 | 0,0033 | 0,0015 | 0,00169 |
| 542,51663 | 0,00268 | 0,00297 | 0,00137 | 0,00157 |
| 542,55382 | 0,00242 | 0,00268 | 0,00126 | 0,00146 |
| 542,591 | 0,0022 | 0,00243 | 0,00116 | 0,00136 |
| 542,62818 | 0,00201 | 0,0022 | 0,00107 | 0,00127 |
| 542,66536 | 0,00184 | 0,00199 | 0,00098 | 0,00117 |
| 542,70254 | 0,00169 | 0,00181 | 0,00089 | 0,00109 |
| 542,73973 | 0,00155 | 0,00165 | 0,00082 | 0,00101 |
| 542,77691 | 0,00143 | 0,00151 | 0,00074 | 0,00093 |
| 542,81409 | 0,00132 | 0,00138 | 0,00068 | 0,00085 |
| 542,85127 | 0,00122 | 0,00127 | 0,00061 | 0,00078 |
| 542,88845 | 0,00113 | 0,00116 | 0,00055 | 0,00072 |
| 542,92564 | 0,00105 | 0,00106 | 5e-04 | 0,00065 |
| 542,96282 | 0,00097 | 0,00098 | 0,00045 | 0,00059 |
| 543 | 9e-04 | 9e-04 | 4e-04 | 0,00054 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 0 | 0 |
| 524,74364 | 0 | 0 | 0 | 0 |
| 524,78082 | 0 | 0 | 0 | 0 |
| 524,818 | 0 | 0 | 0 | 0 |
| 524,85519 | 0 | 0 | 0 | 0 |
| 524,89237 | 0 | 0 | 0 | 0 |
| 524,92955 | 1e-05 | 1e-05 | 0 | 0 |
| 524,96673 | 1e-05 | 1e-05 | 0 | 0 |
| 525,00391 | 1e-05 | 1e-05 | 0 | 0 |
| 525,0411 | 1e-05 | 1e-05 | 1e-05 | 0 |
| 525,07828 | 1e-05 | 2e-05 | 1e-05 | 0 |
| 525,11546 | 1e-05 | 2e-05 | 1e-05 | 1e-05 |
| 525,15264 | 2e-05 | 2e-05 | 1e-05 | 1e-05 |
| 525,18982 | 2e-05 | 3e-05 | 1e-05 | 1e-05 |
| 525,22701 | 2e-05 | 4e-05 | 2e-05 | 1e-05 |
| 525,26419 | 3e-05 | 4e-05 | 2e-05 | 2e-05 |
| 525,30137 | 3e-05 | 5e-05 | 3e-05 | 2e-05 |
| 525,33855 | 4e-05 | 6e-05 | 4e-05 | 3e-05 |
| 525,37573 | 4e-05 | 7e-05 | 5e-05 | 3e-05 |
| 525,41292 | 5e-05 | 8e-05 | 6e-05 | 4e-05 |
| 525,4501 | 6e-05 | 1e-04 | 7e-05 | 5e-05 |
| 525,48728 | 7e-05 | 0,00011 | 8e-05 | 6e-05 |
| 525,52446 | 7e-05 | 0,00013 | 1e-04 | 7e-05 |
| 525,56164 | 8e-05 | 0,00015 | 0,00012 | 8e-05 |
| 525,59883 | 1e-04 | 0,00017 | 0,00014 | 1e-04 |
| 525,63601 | 0,00011 | 0,00019 | 0,00016 | 0,00011 |
| 525,67319 | 0,00012 | 0,00021 | 0,00019 | 0,00013 |
| 525,71037 | 0,00013 | 0,00024 | 0,00022 | 0,00015 |
| 525,74755 | 0,00015 | 0,00026 | 0,00025 | 0,00018 |
| 525,78474 | 0,00017 | 0,00029 | 0,00028 | 2e-04 |
| 525,82192 | 0,00019 | 0,00032 | 0,00032 | 0,00023 |
| 525,8591 | 0,00021 | 0,00035 | 0,00036 | 0,00026 |
| 525,89628 | 0,00023 | 0,00038 | 0,00041 | 0,00029 |
| 525,93346 | 0,00025 | 0,00041 | 0,00045 | 0,00033 |
| 525,97065 | 0,00028 | 0,00044 | 5e-04 | 0,00036 |
| 526,00783 | 0,00031 | 0,00047 | 0,00055 | 4e-04 |
| 526,04501 | 0,00034 | 0,00051 | 0,00061 | 0,00044 |
| 526,08219 | 0,00038 | 0,00054 | 0,00066 | 0,00048 |
| 526,11937 | 0,00041 | 0,00058 | 0,00071 | 0,00052 |
| 526,15656 | 0,00045 | 0,00061 | 0,00077 | 0,00056 |
| 526,19374 | 5e-04 | 0,00065 | 0,00082 | 6e-04 |
| 526,23092 | 0,00054 | 0,00069 | 0,00088 | 0,00064 |
| 526,2681 | 0,00059 | 0,00074 | 0,00093 | 0,00068 |
| 526,30528 | 0,00064 | 0,00078 | 0,00098 | 0,00072 |
| 526,34247 | 7e-04 | 0,00083 | 0,00103 | 0,00076 |
| 526,37965 | 0,00075 | 0,00088 | 0,00108 | 8e-04 |
| 526,41683 | 0,00081 | 0,00093 | 0,00112 | 0,00083 |
| 526,45401 | 0,00087 | 0,00099 | 0,00116 | 0,00087 |
| 526,49119 | 0,00093 | 0,00105 | 0,0012 | 9e-04 |
| 526,52838 | 0,001 | 0,00111 | 0,00123 | 0,00093 |
| 526,56556 | 0,00106 | 0,00118 | 0,00126 | 0,00095 |
| 526,60274 | 0,00113 | 0,00125 | 0,00129 | 0,00098 |
| 526,63992 | 0,00119 | 0,00132 | 0,00131 | 0,001 |
| 526,6771 | 0,00126 | 0,0014 | 0,00133 | 0,00102 |
| 526,71429 | 0,00132 | 0,00148 | 0,00136 | 0,00103 |
| 526,75147 | 0,00139 | 0,00156 | 0,00137 | 0,00104 |
| 526,78865 | 0,00146 | 0,00164 | 0,00139 | 0,00105 |
| 526,82583 | 0,00153 | 0,00173 | 0,00141 | 0,00106 |
| 526,86301 | 0,00159 | 0,00182 | 0,00143 | 0,00107 |
| 526,9002 | 0,00167 | 0,00192 | 0,00146 | 0,00108 |
| 526,93738 | 0,00174 | 0,00201 | 0,00148 | 0,00108 |
| 526,97456 | 0,00181 | 0,00211 | 0,00151 | 0,00109 |
| 527,01174 | 0,00189 | 0,00221 | 0,00155 | 0,0011 |
| 527,04892 | 0,00198 | 0,00232 | 0,00159 | 0,00111 |
| 527,08611 | 0,00207 | 0,00243 | 0,00163 | 0,00113 |
| 527,12329 | 0,00216 | 0,00254 | 0,00169 | 0,00115 |
| 527,16047 | 0,00226 | 0,00266 | 0,00175 | 0,00118 |
| 527,19765 | 0,00237 | 0,00279 | 0,00182 | 0,00121 |
| 527,23483 | 0,00249 | 0,00291 | 0,00189 | 0,00125 |
| 527,27202 | 0,00262 | 0,00305 | 0,00198 | 0,0013 |
| 527,3092 | 0,00275 | 0,00319 | 0,00208 | 0,00136 |
| 527,34638 | 0,0029 | 0,00334 | 0,00218 | 0,00143 |
| 527,38356 | 0,00306 | 0,0035 | 0,0023 | 0,00152 |
| 527,42074 | 0,00323 | 0,00366 | 0,00242 | 0,00161 |
| 527,45793 | 0,00341 | 0,00383 | 0,00256 | 0,00172 |
| 527,49511 | 0,0036 | 0,00401 | 0,0027 | 0,00184 |
| 527,53229 | 0,00379 | 0,0042 | 0,00285 | 0,00197 |
| 527,56947 | 0,004 | 0,00439 | 0,00302 | 0,00212 |
| 527,60665 | 0,00421 | 0,00459 | 0,00319 | 0,00227 |
| 527,64384 | 0,00443 | 0,0048 | 0,00337 | 0,00244 |
| 527,68102 | 0,00466 | 0,00501 | 0,00356 | 0,00262 |
| 527,7182 | 0,00489 | 0,00522 | 0,00376 | 0,0028 |
| 527,75538 | 0,00512 | 0,00543 | 0,00397 | 0,003 |
| 527,79256 | 0,00535 | 0,00565 | 0,00419 | 0,0032 |
| 527,82975 | 0,00557 | 0,00586 | 0,00442 | 0,00341 |
| 527,86693 | 0,0058 | 0,00607 | 0,00465 | 0,00362 |
| 527,90411 | 0,00602 | 0,00628 | 0,00488 | 0,00384 |
| 527,94129 | 0,00624 | 0,00648 | 0,00512 | 0,00405 |
| 527,97847 | 0,00644 | 0,00667 | 0,00537 | 0,00426 |
| 528,01566 | 0,00664 | 0,00686 | 0,00561 | 0,00447 |
| 528,05284 | 0,00684 | 0,00703 | 0,00585 | 0,00468 |
| 528,09002 | 0,00702 | 0,00719 | 0,00609 | 0,00487 |
| 528,1272 | 0,00719 | 0,00734 | 0,00632 | 0,00506 |
| 528,16438 | 0,00736 | 0,00747 | 0,00655 | 0,00524 |
| 528,20157 | 0,00751 | 0,0076 | 0,00676 | 0,00541 |
| 528,23875 | 0,00766 | 0,00771 | 0,00696 | 0,00557 |
| 528,27593 | 0,00779 | 0,00781 | 0,00716 | 0,00572 |
| 528,31311 | 0,00792 | 0,0079 | 0,00733 | 0,00585 |
| 528,35029 | 0,00805 | 0,00797 | 0,00749 | 0,00597 |
| 528,38748 | 0,00817 | 0,00804 | 0,00763 | 0,00608 |
| 528,42466 | 0,00828 | 0,0081 | 0,00775 | 0,00618 |
| 528,46184 | 0,00839 | 0,00814 | 0,00786 | 0,00627 |
| 528,49902 | 0,00849 | 0,00818 | 0,00795 | 0,00636 |
| 528,5362 | 0,00859 | 0,00822 | 0,00803 | 0,00643 |
| 528,57339 | 0,0087 | 0,00824 | 0,00809 | 0,0065 |
| 528,61057 | 0,0088 | 0,00827 | 0,00814 | 0,00657 |
| 528,64775 | 0,0089 | 0,00829 | 0,00818 | 0,00664 |
| 528,68493 | 0,009 | 0,00831 | 0,00821 | 0,00671 |
| 528,72211 | 0,0091 | 0,00832 | 0,00823 | 0,00678 |
| 528,7593 | 0,0092 | 0,00834 | 0,00826 | 0,00685 |
| 528,79648 | 0,0093 | 0,00836 | 0,00828 | 0,00693 |
| 528,83366 | 0,00941 | 0,00838 | 0,0083 | 0,00701 |
| 528,87084 | 0,00952 | 0,00841 | 0,00832 | 0,0071 |
| 528,90802 | 0,00962 | 0,00844 | 0,00835 | 0,0072 |
| 528,94521 | 0,00973 | 0,00848 | 0,00838 | 0,0073 |
| 528,98239 | 0,00984 | 0,00852 | 0,00842 | 0,00741 |
| 529,01957 | 0,00996 | 0,00857 | 0,00846 | 0,00753 |
| 529,05675 | 0,01007 | 0,00863 | 0,00852 | 0,00765 |
| 529,09393 | 0,01018 | 0,0087 | 0,00858 | 0,00778 |
| 529,13112 | 0,0103 | 0,00878 | 0,00865 | 0,00791 |
| 529,1683 | 0,01042 | 0,00886 | 0,00873 | 0,00805 |
| 529,20548 | 0,01054 | 0,00896 | 0,00882 | 0,0082 |
| 529,24266 | 0,01066 | 0,00906 | 0,00892 | 0,00835 |
| 529,27984 | 0,01079 | 0,00918 | 0,00902 | 0,0085 |
| 529,31703 | 0,01092 | 0,00931 | 0,00913 | 0,00866 |
| 529,35421 | 0,01106 | 0,00944 | 0,00925 | 0,00882 |
| 529,39139 | 0,0112 | 0,00959 | 0,00938 | 0,00899 |
| 529,42857 | 0,01135 | 0,00974 | 0,00951 | 0,00917 |
| 529,46575 | 0,0115 | 0,00991 | 0,00965 | 0,00935 |
| 529,50294 | 0,01167 | 0,01008 | 0,00979 | 0,00953 |
| 529,54012 | 0,01184 | 0,01027 | 0,00994 | 0,00972 |
| 529,5773 | 0,01202 | 0,01046 | 0,0101 | 0,00992 |
| 529,61448 | 0,01222 | 0,01066 | 0,01027 | 0,01012 |
| 529,65166 | 0,01242 | 0,01087 | 0,01044 | 0,01033 |
| 529,68885 | 0,01263 | 0,01108 | 0,01063 | 0,01055 |
| 529,72603 | 0,01285 | 0,01131 | 0,01082 | 0,01077 |
| 529,76321 | 0,01309 | 0,01154 | 0,01102 | 0,01099 |
| 529,80039 | 0,01333 | 0,01178 | 0,01123 | 0,01123 |
| 529,83757 | 0,01358 | 0,01202 | 0,01145 | 0,01146 |
| 529,87476 | 0,01383 | 0,01227 | 0,01168 | 0,0117 |
| 529,91194 | 0,0141 | 0,01253 | 0,01193 | 0,01195 |
| 529,94912 | 0,01436 | 0,01278 | 0,01219 | 0,01221 |
| 529,9863 | 0,01463 | 0,01304 | 0,01245 | 0,01247 |
| 530,02348 | 0,01491 | 0,01331 | 0,01273 | 0,01274 |
| 530,06067 | 0,01518 | 0,01357 | 0,01302 | 0,01301 |
| 530,09785 | 0,01544 | 0,01383 | 0,01332 | 0,0133 |
| 530,13503 | 0,01571 | 0,01409 | 0,01362 | 0,01359 |
| 530,17221 | 0,01597 | 0,01435 | 0,01393 | 0,01388 |
| 530,20939 | 0,01622 | 0,0146 | 0,01425 | 0,01419 |
| 530,24658 | 0,01646 | 0,01485 | 0,01456 | 0,01449 |
| 530,28376 | 0,0167 | 0,01508 | 0,01488 | 0,0148 |
| 530,32094 | 0,01692 | 0,01531 | 0,01518 | 0,01511 |
| 530,35812 | 0,01712 | 0,01553 | 0,01549 | 0,01542 |
| 530,3953 | 0,01732 | 0,01574 | 0,01578 | 0,01573 |
| 530,43249 | 0,0175 | 0,01594 | 0,01605 | 0,01603 |
| 530,46967 | 0,01767 | 0,01613 | 0,01631 | 0,01632 |
| 530,50685 | 0,01782 | 0,0163 | 0,01656 | 0,0166 |
| 530,54403 | 0,01795 | 0,01646 | 0,01678 | 0,01686 |
| 530,58121 | 0,01808 | 0,01661 | 0,01699 | 0,01711 |
| 530,6184 | 0,01819 | 0,01675 | 0,01717 | 0,01733 |
| 530,65558 | 0,01829 | 0,01689 | 0,01733 | 0,01754 |
| 530,69276 | 0,01839 | 0,01701 | 0,01747 | 0,01772 |
| 530,72994 | 0,01847 | 0,01713 | 0,01759 | 0,01789 |
| 530,76712 | 0,01856 | 0,01725 | 0,0177 | 0,01803 |
| 530,80431 | 0,01864 | 0,01737 | 0,01779 | 0,01816 |
| 530,84149 | 0,01873 | 0,01749 | 0,01788 | 0,01828 |
| 530,87867 | 0,01882 | 0,01761 | 0,01797 | 0,0184 |
| 530,91585 | 0,01892 | 0,01775 | 0,01805 | 0,01851 |
| 530,95303 | 0,01904 | 0,01789 | 0,01814 | 0,01862 |
| 530,99022 | 0,01918 | 0,01806 | 0,01825 | 0,01874 |
| 531,0274 | 0,01934 | 0,01824 | 0,01838 | 0,01888 |
| 531,06458 | 0,01953 | 0,01845 | 0,01853 | 0,01904 |
| 531,10176 | 0,01975 | 0,01868 | 0,0187 | 0,01923 |
| 531,13894 | 0,01999 | 0,01893 | 0,01891 | 0,01945 |
| 531,17613 | 0,02027 | 0,01922 | 0,01916 | 0,01971 |
| 531,21331 | 0,02059 | 0,01953 | 0,01945 | 0,02001 |
| 531,25049 | 0,02094 | 0,01986 | 0,01978 | 0,02036 |
| 531,28767 | 0,02133 | 0,02023 | 0,02015 | 0,02075 |
| 531,32485 | 0,02176 | 0,02062 | 0,02056 | 0,02118 |
| 531,36204 | 0,02221 | 0,02103 | 0,02101 | 0,02165 |
| 531,39922 | 0,0227 | 0,02146 | 0,02149 | 0,02216 |
| 531,4364 | 0,02321 | 0,02191 | 0,022 | 0,0227 |
| 531,47358 | 0,02374 | 0,02236 | 0,02253 | 0,02328 |
| 531,51076 | 0,02429 | 0,02282 | 0,02308 | 0,02387 |
| 531,54795 | 0,02486 | 0,02328 | 0,02364 | 0,02447 |
| 531,58513 | 0,02543 | 0,02373 | 0,02421 | 0,02507 |
| 531,62231 | 0,02599 | 0,02416 | 0,02476 | 0,02567 |
| 531,65949 | 0,02656 | 0,02459 | 0,02531 | 0,02625 |
| 531,69667 | 0,02711 | 0,02499 | 0,02584 | 0,02681 |
| 531,73386 | 0,02764 | 0,02537 | 0,02634 | 0,02733 |
| 531,77104 | 0,02814 | 0,02571 | 0,0268 | 0,02781 |
| 531,80822 | 0,02862 | 0,02603 | 0,02723 | 0,02824 |
| 531,8454 | 0,02907 | 0,02631 | 0,02763 | 0,02862 |
| 531,88258 | 0,02949 | 0,02656 | 0,02798 | 0,02895 |
| 531,91977 | 0,02987 | 0,02678 | 0,02829 | 0,02922 |
| 531,95695 | 0,03021 | 0,02698 | 0,02857 | 0,02942 |
| 531,99413 | 0,03052 | 0,02714 | 0,0288 | 0,02957 |
| 532,03131 | 0,03079 | 0,02728 | 0,029 | 0,02967 |
| 532,06849 | 0,03103 | 0,02741 | 0,02917 | 0,02972 |
| 532,10568 | 0,03125 | 0,02752 | 0,02933 | 0,02974 |
| 532,14286 | 0,03144 | 0,02763 | 0,02947 | 0,02973 |
| 532,18004 | 0,03162 | 0,02774 | 0,02961 | 0,02969 |
| 532,21722 | 0,03179 | 0,02786 | 0,02975 | 0,02964 |
| 532,2544 | 0,03195 | 0,02799 | 0,0299 | 0,02959 |
| 532,29159 | 0,03212 | 0,02815 | 0,03008 | 0,02956 |
| 532,32877 | 0,0323 | 0,02833 | 0,03028 | 0,02954 |
| 532,36595 | 0,03251 | 0,02856 | 0,03052 | 0,02956 |
| 532,40313 | 0,03274 | 0,02883 | 0,03079 | 0,02962 |
| 532,44031 | 0,033 | 0,02914 | 0,03111 | 0,02972 |
| 532,4775 | 0,03331 | 0,02951 | 0,03149 | 0,02989 |
| 532,51468 | 0,03368 | 0,02994 | 0,03192 | 0,03012 |
| 532,55186 | 0,0341 | 0,03043 | 0,0324 | 0,03041 |
| 532,58904 | 0,03458 | 0,03099 | 0,03293 | 0,03077 |
| 532,62622 | 0,03513 | 0,03161 | 0,03351 | 0,03119 |
| 532,66341 | 0,03574 | 0,03229 | 0,03414 | 0,03167 |
| 532,70059 | 0,03642 | 0,03302 | 0,03482 | 0,03222 |
| 532,73777 | 0,03716 | 0,03381 | 0,03554 | 0,03283 |
| 532,77495 | 0,03797 | 0,03465 | 0,03629 | 0,03349 |
| 532,81213 | 0,03885 | 0,03554 | 0,03707 | 0,03419 |
| 532,84932 | 0,03978 | 0,03645 | 0,03787 | 0,03493 |
| 532,8865 | 0,04075 | 0,03739 | 0,03869 | 0,03569 |
| 532,92368 | 0,04176 | 0,03834 | 0,03951 | 0,03647 |
| 532,96086 | 0,0428 | 0,03929 | 0,04034 | 0,03727 |
| 532,99804 | 0,04387 | 0,04024 | 0,04116 | 0,03806 |
| 533,03523 | 0,04493 | 0,04116 | 0,04196 | 0,03885 |
| 533,07241 | 0,046 | 0,04205 | 0,04275 | 0,03962 |
| 533,10959 | 0,04704 | 0,0429 | 0,04352 | 0,04036 |
| 533,14677 | 0,04806 | 0,0437 | 0,04425 | 0,04109 |
| 533,18395 | 0,04903 | 0,04444 | 0,04496 | 0,04177 |
| 533,22114 | 0,04996 | 0,04513 | 0,04563 | 0,04243 |
| 533,25832 | 0,05083 | 0,04574 | 0,04627 | 0,04304 |
| 533,2955 | 0,05163 | 0,04628 | 0,04687 | 0,04362 |
| 533,33268 | 0,05235 | 0,04676 | 0,04743 | 0,04416 |
| 533,36986 | 0,053 | 0,04716 | 0,04796 | 0,04466 |
| 533,40705 | 0,05357 | 0,04751 | 0,04847 | 0,04514 |
| 533,44423 | 0,05406 | 0,04781 | 0,04894 | 0,0456 |
| 533,48141 | 0,05448 | 0,04805 | 0,0494 | 0,04603 |
| 533,51859 | 0,05482 | 0,04826 | 0,04984 | 0,04646 |
| 533,55577 | 0,05509 | 0,04843 | 0,05027 | 0,04688 |
| 533,59295 | 0,0553 | 0,04859 | 0,0507 | 0,04731 |
| 533,63014 | 0,05546 | 0,04874 | 0,05113 | 0,04775 |
| 533,66732 | 0,05558 | 0,04889 | 0,05158 | 0,04821 |
| 533,7045 | 0,05567 | 0,04906 | 0,05204 | 0,0487 |
| 533,74168 | 0,05573 | 0,04924 | 0,05252 | 0,04923 |
| 533,77886 | 0,05579 | 0,04947 | 0,05304 | 0,04979 |
| 533,81605 | 0,05585 | 0,04974 | 0,05359 | 0,0504 |
| 533,85323 | 0,05593 | 0,05007 | 0,05417 | 0,05105 |
| 533,89041 | 0,05603 | 0,05045 | 0,05478 | 0,05175 |
| 533,92759 | 0,05616 | 0,05088 | 0,05543 | 0,05248 |
| 533,96477 | 0,05634 | 0,05138 | 0,0561 | 0,05324 |
| 534,00196 | 0,05657 | 0,05194 | 0,05679 | 0,05403 |
| 534,03914 | 0,05686 | 0,05258 | 0,0575 | 0,05484 |
| 534,07632 | 0,05721 | 0,05327 | 0,05822 | 0,05565 |
| 534,1135 | 0,05763 | 0,05401 | 0,05893 | 0,05646 |
| 534,15068 | 0,0581 | 0,0548 | 0,05962 | 0,05724 |
| 534,18787 | 0,05863 | 0,05563 | 0,06028 | 0,05799 |
| 534,22505 | 0,05921 | 0,05649 | 0,0609 | 0,05869 |
| 534,26223 | 0,05983 | 0,05736 | 0,06146 | 0,05932 |
| 534,29941 | 0,0605 | 0,05823 | 0,06195 | 0,05987 |
| 534,33659 | 0,06118 | 0,05908 | 0,06234 | 0,06031 |
| 534,37378 | 0,06187 | 0,05991 | 0,06264 | 0,06064 |
| 534,41096 | 0,06256 | 0,06068 | 0,06282 | 0,06086 |
| 534,44814 | 0,06322 | 0,06139 | 0,0629 | 0,06096 |
| 534,48532 | 0,06384 | 0,06203 | 0,06285 | 0,06093 |
| 534,5225 | 0,06441 | 0,06256 | 0,06269 | 0,06077 |
| 534,55969 | 0,0649 | 0,06297 | 0,06238 | 0,06047 |
| 534,59687 | 0,0653 | 0,06327 | 0,06195 | 0,06004 |
| 534,63405 | 0,06561 | 0,06343 | 0,0614 | 0,05949 |
| 534,67123 | 0,06581 | 0,06346 | 0,06074 | 0,05883 |
| 534,70841 | 0,0659 | 0,06335 | 0,05999 | 0,05809 |
| 534,7456 | 0,06587 | 0,06311 | 0,05916 | 0,05726 |
| 534,78278 | 0,06572 | 0,06271 | 0,05826 | 0,05638 |
| 534,81996 | 0,06544 | 0,06218 | 0,05731 | 0,05545 |
| 534,85714 | 0,06506 | 0,06153 | 0,05634 | 0,0545 |
| 534,89432 | 0,06459 | 0,06079 | 0,05536 | 0,05355 |
| 534,93151 | 0,06405 | 0,05996 | 0,0544 | 0,05263 |
| 534,96869 | 0,06344 | 0,05908 | 0,05348 | 0,05176 |
| 535,00587 | 0,06279 | 0,05814 | 0,05262 | 0,05095 |
| 535,04305 | 0,06213 | 0,05719 | 0,05184 | 0,05022 |
| 535,08023 | 0,06147 | 0,05626 | 0,05117 | 0,0496 |
| 535,11742 | 0,06084 | 0,05536 | 0,05063 | 0,04913 |
| 535,1546 | 0,06027 | 0,05453 | 0,05022 | 0,04879 |
| 535,19178 | 0,05979 | 0,05378 | 0,04997 | 0,04861 |
| 535,22896 | 0,0594 | 0,05314 | 0,04987 | 0,04858 |
| 535,26614 | 0,05913 | 0,05264 | 0,04994 | 0,04873 |
| 535,30333 | 0,05902 | 0,0523 | 0,05018 | 0,04905 |
| 535,34051 | 0,05907 | 0,05213 | 0,0506 | 0,04956 |
| 535,37769 | 0,05929 | 0,05214 | 0,05122 | 0,05027 |
| 535,41487 | 0,05968 | 0,05232 | 0,05201 | 0,05115 |
| 535,45205 | 0,06025 | 0,05269 | 0,05296 | 0,0522 |
| 535,48924 | 0,06099 | 0,05324 | 0,05406 | 0,0534 |
| 535,52642 | 0,06189 | 0,054 | 0,0553 | 0,05475 |
| 535,5636 | 0,06299 | 0,05493 | 0,05666 | 0,05623 |
| 535,60078 | 0,06423 | 0,05603 | 0,05815 | 0,05783 |
| 535,63796 | 0,06559 | 0,05726 | 0,05974 | 0,05954 |
| 535,67515 | 0,06706 | 0,05861 | 0,0614 | 0,06131 |
| 535,71233 | 0,06861 | 0,06006 | 0,0631 | 0,06314 |
| 535,74951 | 0,07022 | 0,0616 | 0,06484 | 0,06501 |
| 535,78669 | 0,07187 | 0,06319 | 0,06659 | 0,06688 |
| 535,82387 | 0,07353 | 0,0648 | 0,06834 | 0,06874 |
| 535,86106 | 0,07515 | 0,0664 | 0,07006 | 0,07057 |
| 535,89824 | 0,07672 | 0,06798 | 0,07172 | 0,07235 |
| 535,93542 | 0,07821 | 0,06949 | 0,07333 | 0,07405 |
| 535,9726 | 0,0796 | 0,07093 | 0,07485 | 0,07568 |
| 536,00978 | 0,08087 | 0,07227 | 0,0763 | 0,07721 |
| 536,04697 | 0,08199 | 0,07346 | 0,07764 | 0,07864 |
| 536,08415 | 0,08293 | 0,07452 | 0,07889 | 0,07998 |
| 536,12133 | 0,0837 | 0,07543 | 0,08003 | 0,0812 |
| 536,15851 | 0,0843 | 0,07618 | 0,08106 | 0,0823 |
| 536,19569 | 0,08473 | 0,07678 | 0,08199 | 0,08331 |
| 536,23288 | 0,08498 | 0,07723 | 0,08282 | 0,08423 |
| 536,27006 | 0,08508 | 0,07751 | 0,08357 | 0,08507 |
| 536,30724 | 0,085 | 0,07763 | 0,08425 | 0,08585 |
| 536,34442 | 0,08477 | 0,07762 | 0,08486 | 0,08658 |
| 536,3816 | 0,08444 | 0,07751 | 0,08541 | 0,08726 |
| 536,41879 | 0,08401 | 0,0773 | 0,08591 | 0,08792 |
| 536,45597 | 0,08351 | 0,07702 | 0,08638 | 0,08856 |
| 536,49315 | 0,08296 | 0,07669 | 0,08682 | 0,08921 |
| 536,53033 | 0,08239 | 0,07633 | 0,08724 | 0,08985 |
| 536,56751 | 0,08183 | 0,07596 | 0,08764 | 0,0905 |
| 536,6047 | 0,0813 | 0,07562 | 0,08802 | 0,09115 |
| 536,64188 | 0,08083 | 0,07532 | 0,08838 | 0,09179 |
| 536,67906 | 0,08044 | 0,07507 | 0,0887 | 0,09242 |
| 536,71624 | 0,08013 | 0,0749 | 0,08898 | 0,09301 |
| 536,75342 | 0,07993 | 0,07482 | 0,0892 | 0,09355 |
| 536,79061 | 0,07984 | 0,07485 | 0,08936 | 0,09402 |
| 536,82779 | 0,07989 | 0,07499 | 0,08944 | 0,0944 |
| 536,86497 | 0,08006 | 0,07523 | 0,08941 | 0,09467 |
| 536,90215 | 0,08035 | 0,07558 | 0,08928 | 0,09481 |
| 536,93933 | 0,08074 | 0,07602 | 0,08901 | 0,09477 |
| 536,97652 | 0,08124 | 0,07656 | 0,0886 | 0,09456 |
| 537,0137 | 0,08182 | 0,07718 | 0,08807 | 0,09418 |
| 537,05088 | 0,08247 | 0,07787 | 0,08741 | 0,09363 |
| 537,08806 | 0,08319 | 0,0786 | 0,08663 | 0,0929 |
| 537,12524 | 0,08393 | 0,07936 | 0,08573 | 0,09201 |
| 537,16243 | 0,08467 | 0,08013 | 0,08473 | 0,09096 |
| 537,19961 | 0,08541 | 0,0809 | 0,08365 | 0,08976 |
| 537,23679 | 0,08612 | 0,08164 | 0,08253 | 0,08846 |
| 537,27397 | 0,08678 | 0,08233 | 0,08139 | 0,08709 |
| 537,31115 | 0,08738 | 0,08295 | 0,08027 | 0,0857 |
| 537,34834 | 0,08788 | 0,08351 | 0,07919 | 0,0843 |
| 537,38552 | 0,0883 | 0,08398 | 0,07819 | 0,08293 |
| 537,4227 | 0,08863 | 0,08437 | 0,07731 | 0,08164 |
| 537,45988 | 0,08886 | 0,08467 | 0,0766 | 0,08049 |
| 537,49706 | 0,089 | 0,08488 | 0,07607 | 0,07949 |
| 537,53425 | 0,08906 | 0,08501 | 0,07576 | 0,07868 |
| 537,57143 | 0,08902 | 0,08507 | 0,07567 | 0,07808 |
| 537,60861 | 0,08893 | 0,08509 | 0,07583 | 0,07772 |
| 537,64579 | 0,08879 | 0,08507 | 0,07625 | 0,07763 |
| 537,68297 | 0,08863 | 0,08506 | 0,07697 | 0,07781 |
| 537,72016 | 0,08848 | 0,08507 | 0,07803 | 0,07834 |
| 537,75734 | 0,08837 | 0,08512 | 0,0794 | 0,07919 |
| 537,79452 | 0,08832 | 0,08529 | 0,08107 | 0,08036 |
| 537,8317 | 0,08837 | 0,0856 | 0,08305 | 0,08186 |
| 537,86888 | 0,08859 | 0,08607 | 0,08533 | 0,08368 |
| 537,90607 | 0,08898 | 0,08674 | 0,08793 | 0,08584 |
| 537,94325 | 0,08958 | 0,08765 | 0,09085 | 0,08833 |
| 537,98043 | 0,09042 | 0,08883 | 0,09411 | 0,09121 |
| 538,01761 | 0,09154 | 0,09033 | 0,09766 | 0,09441 |
| 538,05479 | 0,09295 | 0,09221 | 0,10149 | 0,09793 |
| 538,09198 | 0,09475 | 0,09444 | 0,10559 | 0,10174 |
| 538,12916 | 0,09692 | 0,09704 | 0,10994 | 0,10584 |
| 538,16634 | 0,09944 | 0,10001 | 0,11452 | 0,11019 |
| 538,20352 | 0,10232 | 0,10335 | 0,11932 | 0,11478 |
| 538,2407 | 0,10556 | 0,10705 | 0,1243 | 0,1196 |
| 538,27789 | 0,10914 | 0,11114 | 0,12941 | 0,12456 |
| 538,31507 | 0,11304 | 0,11555 | 0,13459 | 0,12961 |
| 538,35225 | 0,11726 | 0,12021 | 0,13979 | 0,13471 |
| 538,38943 | 0,12171 | 0,12507 | 0,14497 | 0,13979 |
| 538,42661 | 0,12632 | 0,13008 | 0,15006 | 0,14479 |
| 538,4638 | 0,13103 | 0,13516 | 0,15499 | 0,14964 |
| 538,50098 | 0,13576 | 0,14025 | 0,15965 | 0,15423 |
| 538,53816 | 0,14046 | 0,14524 | 0,16401 | 0,15851 |
| 538,57534 | 0,14502 | 0,15004 | 0,16799 | 0,16241 |
| 538,61252 | 0,14932 | 0,15458 | 0,17156 | 0,1659 |
| 538,64971 | 0,1533 | 0,15878 | 0,17466 | 0,16892 |
| 538,68689 | 0,15689 | 0,16257 | 0,17726 | 0,17144 |
| 538,72407 | 0,16002 | 0,16589 | 0,17931 | 0,17345 |
| 538,76125 | 0,16266 | 0,16867 | 0,18075 | 0,17485 |
| 538,79843 | 0,16474 | 0,17078 | 0,18167 | 0,17572 |
| 538,83562 | 0,1662 | 0,17229 | 0,18211 | 0,17612 |
| 538,8728 | 0,16697 | 0,17319 | 0,18211 | 0,17611 |
| 538,90998 | 0,16715 | 0,17351 | 0,18173 | 0,17575 |
| 538,94716 | 0,16677 | 0,17326 | 0,18104 | 0,17511 |
| 538,98434 | 0,16586 | 0,17249 | 0,18011 | 0,17427 |
| 539,02153 | 0,16447 | 0,1712 | 0,17906 | 0,17334 |
| 539,05871 | 0,16268 | 0,1695 | 0,178 | 0,17244 |
| 539,09589 | 0,16055 | 0,16751 | 0,17702 | 0,17167 |
| 539,13307 | 0,15818 | 0,16534 | 0,1762 | 0,1711 |
| 539,17025 | 0,15572 | 0,16306 | 0,17561 | 0,17079 |
| 539,20744 | 0,15325 | 0,16078 | 0,17531 | 0,17081 |
| 539,24462 | 0,15088 | 0,15859 | 0,17535 | 0,1712 |
| 539,2818 | 0,14869 | 0,15663 | 0,1758 | 0,17201 |
| 539,31898 | 0,14677 | 0,15497 | 0,17659 | 0,17322 |
| 539,35616 | 0,14524 | 0,15368 | 0,17769 | 0,17476 |
| 539,39335 | 0,14416 | 0,1528 | 0,17906 | 0,17657 |
| 539,43053 | 0,14354 | 0,15236 | 0,18064 | 0,17859 |
| 539,46771 | 0,14338 | 0,15239 | 0,18234 | 0,18074 |
| 539,50489 | 0,14369 | 0,15288 | 0,18408 | 0,18292 |
| 539,54207 | 0,14446 | 0,15391 | 0,18573 | 0,18502 |
| 539,57926 | 0,14565 | 0,15533 | 0,1872 | 0,18691 |
| 539,61644 | 0,14726 | 0,15709 | 0,18839 | 0,1885 |
| 539,65362 | 0,14916 | 0,15912 | 0,18925 | 0,18973 |
| 539,6908 | 0,15124 | 0,16133 | 0,18971 | 0,19054 |
| 539,72798 | 0,15343 | 0,16365 | 0,18972 | 0,19088 |
| 539,76517 | 0,15564 | 0,16598 | 0,18926 | 0,19073 |
| 539,80235 | 0,15777 | 0,16819 | 0,18826 | 0,19003 |
| 539,83953 | 0,15974 | 0,17019 | 0,18684 | 0,18886 |
| 539,87671 | 0,16138 | 0,17191 | 0,18506 | 0,18731 |
| 539,91389 | 0,16268 | 0,17327 | 0,18301 | 0,18547 |
| 539,95108 | 0,16357 | 0,17424 | 0,18076 | 0,18344 |
| 539,98826 | 0,16401 | 0,17475 | 0,17843 | 0,18131 |
| 540,02544 | 0,164 | 0,17475 | 0,17612 | 0,17922 |
| 540,06262 | 0,1635 | 0,17421 | 0,17402 | 0,17731 |
| 540,0998 | 0,16253 | 0,17323 | 0,17222 | 0,17574 |
| 540,13699 | 0,16107 | 0,17183 | 0,17082 | 0,17459 |
| 540,17417 | 0,15926 | 0,17007 | 0,16988 | 0,17394 |
| 540,21135 | 0,15715 | 0,16802 | 0,16948 | 0,17384 |
| 540,24853 | 0,15483 | 0,16574 | 0,16964 | 0,17434 |
| 540,28571 | 0,15238 | 0,16333 | 0,17038 | 0,17544 |
| 540,3229 | 0,14989 | 0,16091 | 0,17177 | 0,17717 |
| 540,36008 | 0,14747 | 0,15859 | 0,17362 | 0,17944 |
| 540,39726 | 0,14524 | 0,15645 | 0,17584 | 0,18209 |
| 540,43444 | 0,14329 | 0,15458 | 0,17832 | 0,18501 |
| 540,47162 | 0,14167 | 0,15305 | 0,18093 | 0,18805 |
| 540,50881 | 0,14045 | 0,15192 | 0,18351 | 0,19105 |
| 540,54599 | 0,13967 | 0,15134 | 0,18592 | 0,19385 |
| 540,58317 | 0,13936 | 0,15123 | 0,18789 | 0,19623 |
| 540,62035 | 0,13958 | 0,1516 | 0,18931 | 0,19796 |
| 540,65753 | 0,1403 | 0,15243 | 0,19003 | 0,19893 |
| 540,69472 | 0,14143 | 0,15368 | 0,18994 | 0,19902 |
| 540,7319 | 0,14293 | 0,15529 | 0,18894 | 0,19813 |
| 540,76908 | 0,14471 | 0,15721 | 0,18697 | 0,19619 |
| 540,80626 | 0,1467 | 0,15934 | 0,18397 | 0,19314 |
| 540,84344 | 0,14879 | 0,16152 | 0,17973 | 0,18888 |
| 540,88063 | 0,15087 | 0,16366 | 0,17451 | 0,18343 |
| 540,91781 | 0,15279 | 0,16564 | 0,16834 | 0,17697 |
| 540,95499 | 0,15444 | 0,16734 | 0,16133 | 0,16959 |
| 540,99217 | 0,15572 | 0,16867 | 0,15357 | 0,16141 |
| 541,02935 | 0,15654 | 0,16945 | 0,14517 | 0,15256 |
| 541,06654 | 0,1568 | 0,16957 | 0,13628 | 0,14318 |
| 541,10372 | 0,15644 | 0,16901 | 0,127 | 0,13339 |
| 541,1409 | 0,15523 | 0,16772 | 0,11757 | 0,12341 |
| 541,17808 | 0,15328 | 0,16566 | 0,10812 | 0,11341 |
| 541,21526 | 0,15057 | 0,16281 | 0,09878 | 0,10353 |
| 541,25245 | 0,14711 | 0,15918 | 0,08967 | 0,09389 |
| 541,28963 | 0,14292 | 0,15464 | 0,08087 | 0,08459 |
| 541,32681 | 0,13805 | 0,14938 | 0,07249 | 0,07574 |
| 541,36399 | 0,13252 | 0,14347 | 0,0647 | 0,06745 |
| 541,40117 | 0,12634 | 0,13699 | 0,05746 | 0,05982 |
| 541,43836 | 0,11972 | 0,13002 | 0,0508 | 0,05281 |
| 541,47554 | 0,11274 | 0,12264 | 0,04473 | 0,04643 |
| 541,51272 | 0,1055 | 0,11496 | 0,03925 | 0,04068 |
| 541,5499 | 0,09809 | 0,10707 | 0,03435 | 0,03555 |
| 541,58708 | 0,09061 | 0,09912 | 0,03001 | 0,03102 |
| 541,62427 | 0,08316 | 0,09121 | 0,0263 | 0,0271 |
| 541,66145 | 0,07587 | 0,08341 | 0,02307 | 0,02376 |
| 541,69863 | 0,06879 | 0,07582 | 0,02029 | 0,0209 |
| 541,73581 | 0,06201 | 0,0685 | 0,01791 | 0,01847 |
| 541,77299 | 0,05556 | 0,06155 | 0,01589 | 0,01643 |
| 541,81018 | 0,0495 | 0,05505 | 0,0142 | 0,01474 |
| 541,84736 | 0,04385 | 0,04898 | 0,0128 | 0,01334 |
| 541,88454 | 0,0387 | 0,04338 | 0,01168 | 0,01222 |
| 541,92172 | 0,03405 | 0,03824 | 0,01076 | 0,01135 |
| 541,9589 | 0,02986 | 0,03359 | 0,01001 | 0,01065 |
| 541,99609 | 0,02611 | 0,0294 | 0,0094 | 0,01009 |
| 542,03327 | 0,0228 | 0,02575 | 0,0089 | 0,00965 |
| 542,07045 | 0,0199 | 0,02255 | 0,0085 | 0,0093 |
| 542,10763 | 0,01739 | 0,01976 | 0,00816 | 0,00902 |
| 542,14481 | 0,01527 | 0,01734 | 0,00788 | 0,00879 |
| 542,182 | 0,0135 | 0,01527 | 0,00764 | 0,00859 |
| 542,21918 | 0,01201 | 0,01352 | 0,00741 | 0,0084 |
| 542,25636 | 0,01077 | 0,01204 | 0,00718 | 0,0082 |
| 542,29354 | 0,00974 | 0,01086 | 0,00696 | 0,008 |
| 542,33072 | 0,00891 | 0,00988 | 0,00673 | 0,00778 |
| 542,36791 | 0,00823 | 0,00907 | 0,00648 | 0,00754 |
| 542,40509 | 0,0077 | 0,00841 | 0,00622 | 0,00726 |
| 542,44227 | 0,00728 | 0,00787 | 0,00593 | 0,00696 |
| 542,47945 | 0,00693 | 0,00742 | 0,00563 | 0,00663 |
| 542,51663 | 0,00664 | 0,00705 | 0,00532 | 0,00628 |
| 542,55382 | 0,0064 | 0,00674 | 0,00499 | 0,00591 |
| 542,591 | 0,00618 | 0,00647 | 0,00465 | 0,00552 |
| 542,62818 | 0,00598 | 0,00622 | 0,0043 | 0,00512 |
| 542,66536 | 0,00579 | 0,00599 | 0,00395 | 0,00471 |
| 542,70254 | 0,00559 | 0,00576 | 0,0036 | 0,0043 |
| 542,73973 | 0,00539 | 0,00553 | 0,00326 | 0,00389 |
| 542,77691 | 0,00518 | 0,0053 | 0,00293 | 0,0035 |
| 542,81409 | 0,00496 | 0,00506 | 0,00261 | 0,00312 |
| 542,85127 | 0,00472 | 0,0048 | 0,00231 | 0,00276 |
| 542,88845 | 0,00448 | 0,00454 | 0,00203 | 0,00242 |
| 542,92564 | 0,00422 | 0,00427 | 0,00177 | 0,0021 |
| 542,96282 | 0,00395 | 0,004 | 0,00153 | 0,00182 |
| 543 | 0,00367 | 0,00372 | 0,00131 | 0,00156 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 |
| 524,33464 | 1e-05 | 0 | 0 | 0 |
| 524,37182 | 1e-05 | 0 | 0 | 0 |
| 524,409 | 1e-05 | 1e-05 | 0 | 0 |
| 524,44618 | 1e-05 | 1e-05 | 0 | 0 |
| 524,48337 | 1e-05 | 1e-05 | 0 | 0 |
| 524,52055 | 1e-05 | 1e-05 | 0 | 0 |
| 524,55773 | 2e-05 | 1e-05 | 0 | 0 |
| 524,59491 | 2e-05 | 2e-05 | 0 | 0 |
| 524,63209 | 2e-05 | 2e-05 | 0 | 0 |
| 524,66928 | 2e-05 | 2e-05 | 0 | 0 |
| 524,70646 | 3e-05 | 3e-05 | 0 | 0 |
| 524,74364 | 3e-05 | 3e-05 | 0 | 0 |
| 524,78082 | 4e-05 | 4e-05 | 0 | 0 |
| 524,818 | 4e-05 | 5e-05 | 0 | 0 |
| 524,85519 | 5e-05 | 6e-05 | 0 | 0 |
| 524,89237 | 5e-05 | 7e-05 | 1e-05 | 0 |
| 524,92955 | 6e-05 | 8e-05 | 1e-05 | 0 |
| 524,96673 | 6e-05 | 9e-05 | 1e-05 | 0 |
| 525,00391 | 7e-05 | 1e-04 | 1e-05 | 0 |
| 525,0411 | 7e-05 | 0,00012 | 1e-05 | 0 |
| 525,07828 | 8e-05 | 0,00014 | 2e-05 | 0 |
| 525,11546 | 9e-05 | 0,00015 | 2e-05 | 0 |
| 525,15264 | 9e-05 | 0,00017 | 3e-05 | 0 |
| 525,18982 | 1e-04 | 0,00019 | 3e-05 | 1e-05 |
| 525,22701 | 0,00011 | 0,00022 | 4e-05 | 1e-05 |
| 525,26419 | 0,00012 | 0,00024 | 5e-05 | 1e-05 |
| 525,30137 | 0,00013 | 0,00026 | 6e-05 | 1e-05 |
| 525,33855 | 0,00014 | 0,00029 | 7e-05 | 1e-05 |
| 525,37573 | 0,00014 | 0,00032 | 8e-05 | 2e-05 |
| 525,41292 | 0,00015 | 0,00034 | 1e-04 | 2e-05 |
| 525,4501 | 0,00017 | 0,00037 | 0,00011 | 3e-05 |
| 525,48728 | 0,00018 | 4e-04 | 0,00013 | 3e-05 |
| 525,52446 | 0,00019 | 0,00043 | 0,00015 | 4e-05 |
| 525,56164 | 2e-04 | 0,00046 | 0,00018 | 4e-05 |
| 525,59883 | 0,00022 | 0,00049 | 2e-04 | 5e-05 |
| 525,63601 | 0,00023 | 0,00052 | 0,00023 | 6e-05 |
| 525,67319 | 0,00025 | 0,00055 | 0,00026 | 7e-05 |
| 525,71037 | 0,00027 | 0,00058 | 0,00029 | 9e-05 |
| 525,74755 | 0,00029 | 0,00061 | 0,00032 | 1e-04 |
| 525,78474 | 0,00031 | 0,00063 | 0,00036 | 0,00012 |
| 525,82192 | 0,00033 | 0,00066 | 0,00039 | 0,00013 |
| 525,8591 | 0,00035 | 0,00068 | 0,00043 | 0,00015 |
| 525,89628 | 0,00038 | 0,00071 | 0,00047 | 0,00017 |
| 525,93346 | 4e-04 | 0,00073 | 0,00051 | 2e-04 |
| 525,97065 | 0,00043 | 0,00075 | 0,00055 | 0,00022 |
| 526,00783 | 0,00045 | 0,00076 | 6e-04 | 0,00025 |
| 526,04501 | 0,00048 | 0,00078 | 0,00064 | 0,00027 |
| 526,08219 | 0,00051 | 8e-04 | 0,00068 | 3e-04 |
| 526,11937 | 0,00053 | 0,00081 | 0,00072 | 0,00033 |
| 526,15656 | 0,00056 | 0,00082 | 0,00076 | 0,00036 |
| 526,19374 | 0,00059 | 0,00084 | 8e-04 | 4e-04 |
| 526,23092 | 0,00061 | 0,00085 | 0,00084 | 0,00043 |
| 526,2681 | 0,00064 | 0,00086 | 0,00087 | 0,00046 |
| 526,30528 | 0,00066 | 0,00087 | 0,00091 | 5e-04 |
| 526,34247 | 0,00069 | 0,00088 | 0,00094 | 0,00053 |
| 526,37965 | 0,00072 | 9e-04 | 0,00097 | 0,00056 |
| 526,41683 | 0,00075 | 0,00091 | 0,001 | 6e-04 |
| 526,45401 | 0,00077 | 0,00093 | 0,00103 | 0,00063 |
| 526,49119 | 8e-04 | 0,00095 | 0,00105 | 0,00067 |
| 526,52838 | 0,00083 | 0,00097 | 0,00107 | 7e-04 |
| 526,56556 | 0,00086 | 0,00099 | 0,00109 | 0,00073 |
| 526,60274 | 9e-04 | 0,00102 | 0,0011 | 0,00077 |
| 526,63992 | 0,00094 | 0,00105 | 0,00112 | 8e-04 |
| 526,6771 | 0,00098 | 0,00109 | 0,00113 | 0,00083 |
| 526,71429 | 0,00102 | 0,00113 | 0,00114 | 0,00087 |
| 526,75147 | 0,00107 | 0,00117 | 0,00115 | 0,00091 |
| 526,78865 | 0,00113 | 0,00122 | 0,00115 | 0,00095 |
| 526,82583 | 0,00119 | 0,00128 | 0,00116 | 0,00099 |
| 526,86301 | 0,00125 | 0,00134 | 0,00117 | 0,00103 |
| 526,9002 | 0,00133 | 0,0014 | 0,00117 | 0,00108 |
| 526,93738 | 0,00141 | 0,00147 | 0,00118 | 0,00114 |
| 526,97456 | 0,0015 | 0,00155 | 0,00119 | 0,0012 |
| 527,01174 | 0,0016 | 0,00163 | 0,0012 | 0,00126 |
| 527,04892 | 0,00171 | 0,00172 | 0,00121 | 0,00134 |
| 527,08611 | 0,00182 | 0,00181 | 0,00123 | 0,00141 |
| 527,12329 | 0,00195 | 0,00191 | 0,00125 | 0,0015 |
| 527,16047 | 0,00208 | 0,00202 | 0,00128 | 0,0016 |
| 527,19765 | 0,00222 | 0,00213 | 0,00132 | 0,0017 |
| 527,23483 | 0,00238 | 0,00225 | 0,00136 | 0,00181 |
| 527,27202 | 0,00254 | 0,00238 | 0,00141 | 0,00193 |
| 527,3092 | 0,00271 | 0,00252 | 0,00147 | 0,00206 |
| 527,34638 | 0,00289 | 0,00266 | 0,00154 | 0,0022 |
| 527,38356 | 0,00308 | 0,00281 | 0,00163 | 0,00234 |
| 527,42074 | 0,00327 | 0,00297 | 0,00172 | 0,0025 |
| 527,45793 | 0,00347 | 0,00313 | 0,00183 | 0,00266 |
| 527,49511 | 0,00368 | 0,00331 | 0,00195 | 0,00283 |
| 527,53229 | 0,00389 | 0,0035 | 0,00208 | 0,003 |
| 527,56947 | 0,00411 | 0,00369 | 0,00223 | 0,00318 |
| 527,60665 | 0,00433 | 0,00389 | 0,0024 | 0,00337 |
| 527,64384 | 0,00455 | 0,0041 | 0,00258 | 0,00356 |
| 527,68102 | 0,00478 | 0,00431 | 0,00277 | 0,00376 |
| 527,7182 | 0,005 | 0,00454 | 0,00298 | 0,00396 |
| 527,75538 | 0,00523 | 0,00477 | 0,0032 | 0,00416 |
| 527,79256 | 0,00545 | 0,00501 | 0,00343 | 0,00437 |
| 527,82975 | 0,00566 | 0,00526 | 0,00368 | 0,00458 |
| 527,86693 | 0,00588 | 0,00551 | 0,00393 | 0,00479 |
| 527,90411 | 0,00608 | 0,00576 | 0,0042 | 0,005 |
| 527,94129 | 0,00628 | 0,00602 | 0,00447 | 0,00521 |
| 527,97847 | 0,00648 | 0,00628 | 0,00475 | 0,00541 |
| 528,01566 | 0,00666 | 0,00654 | 0,00504 | 0,00562 |
| 528,05284 | 0,00683 | 0,0068 | 0,00533 | 0,00582 |
| 528,09002 | 0,007 | 0,00707 | 0,00562 | 0,00602 |
| 528,1272 | 0,00715 | 0,00733 | 0,00591 | 0,00622 |
| 528,16438 | 0,0073 | 0,00759 | 0,00621 | 0,00641 |
| 528,20157 | 0,00743 | 0,00784 | 0,0065 | 0,0066 |
| 528,23875 | 0,00756 | 0,0081 | 0,0068 | 0,00677 |
| 528,27593 | 0,00767 | 0,00834 | 0,00709 | 0,00695 |
| 528,31311 | 0,00778 | 0,00859 | 0,00737 | 0,00711 |
| 528,35029 | 0,00789 | 0,00882 | 0,00766 | 0,00728 |
| 528,38748 | 0,00799 | 0,00905 | 0,00794 | 0,00743 |
| 528,42466 | 0,00808 | 0,00927 | 0,00821 | 0,00758 |
| 528,46184 | 0,00818 | 0,00949 | 0,00849 | 0,00772 |
| 528,49902 | 0,00827 | 0,0097 | 0,00875 | 0,00786 |
| 528,5362 | 0,00836 | 0,0099 | 0,00901 | 0,008 |
| 528,57339 | 0,00846 | 0,01009 | 0,00927 | 0,00814 |
| 528,61057 | 0,00856 | 0,01027 | 0,00952 | 0,00828 |
| 528,64775 | 0,00867 | 0,01045 | 0,00977 | 0,00841 |
| 528,68493 | 0,00878 | 0,01061 | 0,01001 | 0,00856 |
| 528,72211 | 0,0089 | 0,01077 | 0,01024 | 0,0087 |
| 528,7593 | 0,00904 | 0,01092 | 0,01046 | 0,00885 |
| 528,79648 | 0,00918 | 0,01107 | 0,01068 | 0,009 |
| 528,83366 | 0,00933 | 0,0112 | 0,01089 | 0,00916 |
| 528,87084 | 0,0095 | 0,01134 | 0,01109 | 0,00933 |
| 528,90802 | 0,00968 | 0,01146 | 0,01128 | 0,00951 |
| 528,94521 | 0,00987 | 0,01158 | 0,01146 | 0,00969 |
| 528,98239 | 0,01007 | 0,0117 | 0,01163 | 0,00988 |
| 529,01957 | 0,01028 | 0,01182 | 0,01178 | 0,01007 |
| 529,05675 | 0,01051 | 0,01193 | 0,01193 | 0,01027 |
| 529,09393 | 0,01075 | 0,01204 | 0,01206 | 0,01047 |
| 529,13112 | 0,01101 | 0,01216 | 0,01218 | 0,01068 |
| 529,1683 | 0,01127 | 0,01228 | 0,0123 | 0,01088 |
| 529,20548 | 0,01154 | 0,01239 | 0,0124 | 0,01109 |
| 529,24266 | 0,01183 | 0,01252 | 0,01249 | 0,01129 |
| 529,27984 | 0,01212 | 0,01265 | 0,01257 | 0,01149 |
| 529,31703 | 0,01242 | 0,01278 | 0,01266 | 0,01169 |
| 529,35421 | 0,01273 | 0,01292 | 0,01273 | 0,01188 |
| 529,39139 | 0,01305 | 0,01307 | 0,01281 | 0,01206 |
| 529,42857 | 0,01338 | 0,01323 | 0,01289 | 0,01224 |
| 529,46575 | 0,01371 | 0,01339 | 0,01298 | 0,01241 |
| 529,50294 | 0,01404 | 0,01357 | 0,01308 | 0,01257 |
| 529,54012 | 0,01438 | 0,01376 | 0,01318 | 0,01272 |
| 529,5773 | 0,01472 | 0,01395 | 0,0133 | 0,01287 |
| 529,61448 | 0,01506 | 0,01416 | 0,01344 | 0,01301 |
| 529,65166 | 0,01541 | 0,01438 | 0,0136 | 0,01315 |
| 529,68885 | 0,01575 | 0,01461 | 0,01377 | 0,01328 |
| 529,72603 | 0,0161 | 0,01485 | 0,01397 | 0,01341 |
| 529,76321 | 0,01644 | 0,01509 | 0,0142 | 0,01353 |
| 529,80039 | 0,01678 | 0,01535 | 0,01445 | 0,01366 |
| 529,83757 | 0,01711 | 0,01562 | 0,01472 | 0,01379 |
| 529,87476 | 0,01744 | 0,01589 | 0,01502 | 0,01392 |
| 529,91194 | 0,01776 | 0,01618 | 0,01534 | 0,01406 |
| 529,94912 | 0,01808 | 0,01646 | 0,01569 | 0,0142 |
| 529,9863 | 0,01838 | 0,01675 | 0,01606 | 0,01434 |
| 530,02348 | 0,01868 | 0,01705 | 0,01644 | 0,01449 |
| 530,06067 | 0,01896 | 0,01734 | 0,01685 | 0,01465 |
| 530,09785 | 0,01923 | 0,01763 | 0,01726 | 0,01481 |
| 530,13503 | 0,01948 | 0,01792 | 0,01769 | 0,01498 |
| 530,17221 | 0,01973 | 0,01821 | 0,01812 | 0,01516 |
| 530,20939 | 0,01995 | 0,01848 | 0,01855 | 0,01534 |
| 530,24658 | 0,02016 | 0,01875 | 0,01898 | 0,01552 |
| 530,28376 | 0,02035 | 0,019 | 0,0194 | 0,01571 |
| 530,32094 | 0,02052 | 0,01924 | 0,01982 | 0,01589 |
| 530,35812 | 0,02067 | 0,01946 | 0,02022 | 0,01608 |
| 530,3953 | 0,02081 | 0,01967 | 0,0206 | 0,01626 |
| 530,43249 | 0,02093 | 0,01986 | 0,02095 | 0,01643 |
| 530,46967 | 0,02103 | 0,02003 | 0,02128 | 0,0166 |
| 530,50685 | 0,02112 | 0,02017 | 0,02159 | 0,01677 |
| 530,54403 | 0,02119 | 0,0203 | 0,02187 | 0,01693 |
| 530,58121 | 0,02125 | 0,02041 | 0,02212 | 0,01708 |
| 530,6184 | 0,0213 | 0,0205 | 0,02234 | 0,01723 |
| 530,65558 | 0,02135 | 0,02058 | 0,02253 | 0,01738 |
| 530,69276 | 0,0214 | 0,02065 | 0,0227 | 0,01752 |
| 530,72994 | 0,02145 | 0,0207 | 0,02285 | 0,01766 |
| 530,76712 | 0,02151 | 0,02075 | 0,02298 | 0,0178 |
| 530,80431 | 0,02159 | 0,0208 | 0,0231 | 0,01795 |
| 530,84149 | 0,02168 | 0,02085 | 0,0232 | 0,01811 |
| 530,87867 | 0,0218 | 0,02091 | 0,0233 | 0,01829 |
| 530,91585 | 0,02194 | 0,02098 | 0,0234 | 0,01848 |
| 530,95303 | 0,02212 | 0,02107 | 0,02351 | 0,0187 |
| 530,99022 | 0,02234 | 0,02119 | 0,02362 | 0,01894 |
| 531,0274 | 0,02261 | 0,02134 | 0,02376 | 0,01921 |
| 531,06458 | 0,02292 | 0,02153 | 0,02391 | 0,01951 |
| 531,10176 | 0,02328 | 0,02175 | 0,02408 | 0,01985 |
| 531,13894 | 0,0237 | 0,02201 | 0,02428 | 0,02023 |
| 531,17613 | 0,02417 | 0,02231 | 0,02452 | 0,02065 |
| 531,21331 | 0,0247 | 0,02266 | 0,02479 | 0,02112 |
| 531,25049 | 0,02528 | 0,02307 | 0,02509 | 0,02161 |
| 531,28767 | 0,02591 | 0,02351 | 0,02542 | 0,02215 |
| 531,32485 | 0,02658 | 0,024 | 0,02578 | 0,02273 |
| 531,36204 | 0,0273 | 0,02453 | 0,02618 | 0,02334 |
| 531,39922 | 0,02806 | 0,0251 | 0,02661 | 0,02398 |
| 531,4364 | 0,02885 | 0,0257 | 0,02707 | 0,02464 |
| 531,47358 | 0,02967 | 0,02633 | 0,02754 | 0,02532 |
| 531,51076 | 0,03051 | 0,02698 | 0,02803 | 0,02601 |
| 531,54795 | 0,03135 | 0,02765 | 0,02854 | 0,02671 |
| 531,58513 | 0,0322 | 0,02832 | 0,02906 | 0,02741 |
| 531,62231 | 0,03304 | 0,02899 | 0,02958 | 0,0281 |
| 531,65949 | 0,03386 | 0,02965 | 0,0301 | 0,02877 |
| 531,69667 | 0,03467 | 0,0303 | 0,03061 | 0,02942 |
| 531,73386 | 0,03545 | 0,03092 | 0,03111 | 0,03005 |
| 531,77104 | 0,0362 | 0,03151 | 0,03159 | 0,03065 |
| 531,80822 | 0,03691 | 0,03208 | 0,03206 | 0,03121 |
| 531,8454 | 0,03758 | 0,0326 | 0,03251 | 0,03174 |
| 531,88258 | 0,03821 | 0,03308 | 0,03294 | 0,03222 |
| 531,91977 | 0,03879 | 0,03352 | 0,03334 | 0,03267 |
| 531,95695 | 0,03933 | 0,03391 | 0,03373 | 0,03308 |
| 531,99413 | 0,03982 | 0,03426 | 0,03409 | 0,03346 |
| 532,03131 | 0,04028 | 0,03458 | 0,03444 | 0,03381 |
| 532,06849 | 0,04071 | 0,03486 | 0,03477 | 0,03413 |
| 532,10568 | 0,0411 | 0,0351 | 0,03509 | 0,03442 |
| 532,14286 | 0,04147 | 0,03532 | 0,03541 | 0,03471 |
| 532,18004 | 0,04182 | 0,03552 | 0,03573 | 0,03499 |
| 532,21722 | 0,04216 | 0,03571 | 0,03605 | 0,03526 |
| 532,2544 | 0,0425 | 0,0359 | 0,03639 | 0,03555 |
| 532,29159 | 0,04284 | 0,03609 | 0,03674 | 0,03585 |
| 532,32877 | 0,0432 | 0,03629 | 0,03711 | 0,03617 |
| 532,36595 | 0,04357 | 0,03652 | 0,03752 | 0,03652 |
| 532,40313 | 0,04398 | 0,03678 | 0,03796 | 0,03691 |
| 532,44031 | 0,04442 | 0,03707 | 0,03843 | 0,03733 |
| 532,4775 | 0,04489 | 0,03741 | 0,03895 | 0,03778 |
| 532,51468 | 0,04541 | 0,0378 | 0,0395 | 0,03828 |
| 532,55186 | 0,04596 | 0,03823 | 0,0401 | 0,03882 |
| 532,58904 | 0,04658 | 0,03873 | 0,04075 | 0,03941 |
| 532,62622 | 0,04724 | 0,03929 | 0,04143 | 0,04003 |
| 532,66341 | 0,04794 | 0,03991 | 0,04216 | 0,04068 |
| 532,70059 | 0,04869 | 0,04058 | 0,04292 | 0,04135 |
| 532,73777 | 0,04947 | 0,0413 | 0,04371 | 0,04206 |
| 532,77495 | 0,05029 | 0,04208 | 0,04454 | 0,04277 |
| 532,81213 | 0,05114 | 0,0429 | 0,04538 | 0,0435 |
| 532,84932 | 0,052 | 0,04376 | 0,04625 | 0,04422 |
| 532,8865 | 0,05287 | 0,04465 | 0,04712 | 0,04494 |
| 532,92368 | 0,05375 | 0,04557 | 0,04799 | 0,04565 |
| 532,96086 | 0,05461 | 0,0465 | 0,04887 | 0,04633 |
| 532,99804 | 0,05545 | 0,04744 | 0,04974 | 0,04699 |
| 533,03523 | 0,05626 | 0,04837 | 0,0506 | 0,04761 |
| 533,07241 | 0,05703 | 0,04929 | 0,05144 | 0,0482 |
| 533,10959 | 0,05775 | 0,05018 | 0,05225 | 0,04875 |
| 533,14677 | 0,05842 | 0,05105 | 0,05305 | 0,04925 |
| 533,18395 | 0,05902 | 0,05187 | 0,05382 | 0,04972 |
| 533,22114 | 0,05956 | 0,05266 | 0,05456 | 0,05016 |
| 533,25832 | 0,06004 | 0,0534 | 0,05528 | 0,05056 |
| 533,2955 | 0,06043 | 0,05408 | 0,05596 | 0,05092 |
| 533,33268 | 0,06075 | 0,0547 | 0,05662 | 0,05126 |
| 533,36986 | 0,06101 | 0,05527 | 0,05727 | 0,05159 |
| 533,40705 | 0,06121 | 0,05579 | 0,05789 | 0,05191 |
| 533,44423 | 0,06135 | 0,05625 | 0,0585 | 0,05223 |
| 533,48141 | 0,06144 | 0,05666 | 0,0591 | 0,05256 |
| 533,51859 | 0,06149 | 0,05703 | 0,05969 | 0,05291 |
| 533,55577 | 0,06151 | 0,05736 | 0,06029 | 0,0533 |
| 533,59295 | 0,06151 | 0,05765 | 0,06089 | 0,05373 |
| 533,63014 | 0,0615 | 0,05793 | 0,06151 | 0,0542 |
| 533,66732 | 0,0615 | 0,05819 | 0,06214 | 0,05472 |
| 533,7045 | 0,06152 | 0,05845 | 0,06278 | 0,05531 |
| 533,74168 | 0,06156 | 0,05871 | 0,06345 | 0,05595 |
| 533,77886 | 0,06164 | 0,05898 | 0,06414 | 0,05667 |
| 533,81605 | 0,06178 | 0,05928 | 0,06485 | 0,05744 |
| 533,85323 | 0,06197 | 0,05962 | 0,06558 | 0,05828 |
| 533,89041 | 0,06222 | 0,05999 | 0,06633 | 0,05916 |
| 533,92759 | 0,06255 | 0,0604 | 0,06708 | 0,06009 |
| 533,96477 | 0,06294 | 0,06087 | 0,06785 | 0,06105 |
| 534,00196 | 0,06342 | 0,06139 | 0,06861 | 0,06204 |
| 534,03914 | 0,06398 | 0,06198 | 0,06936 | 0,06303 |
| 534,07632 | 0,06461 | 0,06262 | 0,07008 | 0,06401 |
| 534,1135 | 0,0653 | 0,06331 | 0,07077 | 0,06496 |
| 534,15068 | 0,06606 | 0,06405 | 0,07141 | 0,06587 |
| 534,18787 | 0,06686 | 0,06483 | 0,072 | 0,06672 |
| 534,22505 | 0,06771 | 0,06565 | 0,07252 | 0,06749 |
| 534,26223 | 0,06859 | 0,06649 | 0,07294 | 0,06815 |
| 534,29941 | 0,06948 | 0,06734 | 0,07327 | 0,06869 |
| 534,33659 | 0,07037 | 0,06818 | 0,07349 | 0,06912 |
| 534,37378 | 0,07124 | 0,06901 | 0,0736 | 0,06941 |
| 534,41096 | 0,07207 | 0,06981 | 0,0736 | 0,06956 |
| 534,44814 | 0,07286 | 0,07055 | 0,07347 | 0,06956 |
| 534,48532 | 0,07357 | 0,07122 | 0,0732 | 0,06941 |
| 534,5225 | 0,07419 | 0,0718 | 0,07279 | 0,06909 |
| 534,55969 | 0,07472 | 0,07229 | 0,07227 | 0,06863 |
| 534,59687 | 0,07514 | 0,07267 | 0,07164 | 0,06804 |
| 534,63405 | 0,07545 | 0,07294 | 0,0709 | 0,06733 |
| 534,67123 | 0,07564 | 0,07307 | 0,07007 | 0,06651 |
| 534,70841 | 0,07568 | 0,07306 | 0,06915 | 0,0656 |
| 534,7456 | 0,0756 | 0,07292 | 0,06816 | 0,0646 |
| 534,78278 | 0,0754 | 0,07265 | 0,06713 | 0,06356 |
| 534,81996 | 0,07508 | 0,07226 | 0,06607 | 0,0625 |
| 534,85714 | 0,07465 | 0,07175 | 0,06502 | 0,06144 |
| 534,89432 | 0,07414 | 0,07115 | 0,06397 | 0,0604 |
| 534,93151 | 0,07353 | 0,07045 | 0,06297 | 0,0594 |
| 534,96869 | 0,07286 | 0,06968 | 0,06203 | 0,05848 |
| 535,00587 | 0,07215 | 0,06887 | 0,06118 | 0,05766 |
| 535,04305 | 0,07143 | 0,06805 | 0,06044 | 0,05697 |
| 535,08023 | 0,07071 | 0,06723 | 0,05981 | 0,05641 |
| 535,11742 | 0,07001 | 0,06643 | 0,05932 | 0,056 |
| 535,1546 | 0,06937 | 0,06569 | 0,05897 | 0,05575 |
| 535,19178 | 0,06881 | 0,06504 | 0,0588 | 0,05568 |
| 535,22896 | 0,06833 | 0,0645 | 0,05882 | 0,05582 |
| 535,26614 | 0,06797 | 0,06408 | 0,05902 | 0,05616 |
| 535,30333 | 0,06774 | 0,06379 | 0,0594 | 0,0567 |
| 535,34051 | 0,06764 | 0,06366 | 0,05996 | 0,05742 |
| 535,37769 | 0,06769 | 0,06372 | 0,0607 | 0,05833 |
| 535,41487 | 0,06792 | 0,06397 | 0,06162 | 0,05942 |
| 535,45205 | 0,06832 | 0,06441 | 0,06273 | 0,06069 |
| 535,48924 | 0,06887 | 0,06502 | 0,06401 | 0,06214 |
| 535,52642 | 0,06957 | 0,0658 | 0,06542 | 0,06373 |
| 535,5636 | 0,07042 | 0,06676 | 0,06697 | 0,06544 |
| 535,60078 | 0,07141 | 0,06788 | 0,06864 | 0,06724 |
| 535,63796 | 0,07255 | 0,06916 | 0,0704 | 0,06914 |
| 535,67515 | 0,07379 | 0,07056 | 0,07226 | 0,07109 |
| 535,71233 | 0,07511 | 0,07205 | 0,07418 | 0,07309 |
| 535,74951 | 0,0765 | 0,07362 | 0,07614 | 0,07511 |
| 535,78669 | 0,07793 | 0,07524 | 0,07813 | 0,07712 |
| 535,82387 | 0,07939 | 0,07689 | 0,08012 | 0,0791 |
| 535,86106 | 0,08085 | 0,07854 | 0,0821 | 0,08105 |
| 535,89824 | 0,08228 | 0,08015 | 0,08405 | 0,08293 |
| 535,93542 | 0,08366 | 0,08171 | 0,08595 | 0,08474 |
| 535,9726 | 0,08497 | 0,08319 | 0,08779 | 0,08644 |
| 536,00978 | 0,0862 | 0,08457 | 0,08956 | 0,08805 |
| 536,04697 | 0,08734 | 0,08585 | 0,09124 | 0,08955 |
| 536,08415 | 0,08835 | 0,08697 | 0,09285 | 0,09095 |
| 536,12133 | 0,08921 | 0,08795 | 0,09435 | 0,09224 |
| 536,15851 | 0,08995 | 0,08878 | 0,09575 | 0,09343 |
| 536,19569 | 0,09056 | 0,08946 | 0,09705 | 0,0945 |
| 536,23288 | 0,09103 | 0,08999 | 0,09825 | 0,09547 |
| 536,27006 | 0,09138 | 0,09039 | 0,09935 | 0,09636 |
| 536,30724 | 0,0916 | 0,09063 | 0,10037 | 0,09717 |
| 536,34442 | 0,09169 | 0,09073 | 0,1013 | 0,09791 |
| 536,3816 | 0,09169 | 0,09074 | 0,10213 | 0,09859 |
| 536,41879 | 0,09161 | 0,09065 | 0,10288 | 0,09922 |
| 536,45597 | 0,09147 | 0,0905 | 0,10355 | 0,09979 |
| 536,49315 | 0,09129 | 0,09029 | 0,10415 | 0,10033 |
| 536,53033 | 0,09108 | 0,09004 | 0,10467 | 0,10083 |
| 536,56751 | 0,09087 | 0,08979 | 0,10512 | 0,10129 |
| 536,6047 | 0,09068 | 0,08955 | 0,1055 | 0,10171 |
| 536,64188 | 0,09052 | 0,08934 | 0,10578 | 0,10209 |
| 536,67906 | 0,09042 | 0,08917 | 0,10597 | 0,1024 |
| 536,71624 | 0,09038 | 0,08906 | 0,10608 | 0,10265 |
| 536,75342 | 0,09042 | 0,08902 | 0,10608 | 0,10282 |
| 536,79061 | 0,09055 | 0,08908 | 0,10598 | 0,1029 |
| 536,82779 | 0,09078 | 0,08922 | 0,10577 | 0,10288 |
| 536,86497 | 0,09111 | 0,08944 | 0,10542 | 0,10275 |
| 536,90215 | 0,09152 | 0,08975 | 0,10494 | 0,1025 |
| 536,93933 | 0,09201 | 0,09013 | 0,10432 | 0,1021 |
| 536,97652 | 0,09258 | 0,09058 | 0,10358 | 0,10156 |
| 537,0137 | 0,09322 | 0,0911 | 0,10271 | 0,10089 |
| 537,05088 | 0,09392 | 0,09167 | 0,10172 | 0,10009 |
| 537,08806 | 0,09465 | 0,09226 | 0,10061 | 0,09917 |
| 537,12524 | 0,09539 | 0,09287 | 0,09939 | 0,09814 |
| 537,16243 | 0,09612 | 0,09347 | 0,09808 | 0,09701 |
| 537,19961 | 0,09684 | 0,09406 | 0,09672 | 0,0958 |
| 537,23679 | 0,09753 | 0,09461 | 0,09533 | 0,09455 |
| 537,27397 | 0,09815 | 0,09511 | 0,09392 | 0,09329 |
| 537,31115 | 0,0987 | 0,09554 | 0,09253 | 0,09204 |
| 537,34834 | 0,09917 | 0,09591 | 0,09119 | 0,09083 |
| 537,38552 | 0,09956 | 0,0962 | 0,08995 | 0,08971 |
| 537,4227 | 0,09985 | 0,09642 | 0,08883 | 0,08871 |
| 537,45988 | 0,10007 | 0,09655 | 0,08785 | 0,08787 |
| 537,49706 | 0,10018 | 0,09661 | 0,08704 | 0,08721 |
| 537,53425 | 0,10022 | 0,0966 | 0,08644 | 0,08675 |
| 537,57143 | 0,1002 | 0,09655 | 0,08606 | 0,08652 |
| 537,60861 | 0,10013 | 0,09647 | 0,08599 | 0,08654 |
| 537,64579 | 0,10005 | 0,09638 | 0,08618 | 0,08684 |
| 537,68297 | 0,09997 | 0,0963 | 0,08667 | 0,08747 |
| 537,72016 | 0,09992 | 0,09628 | 0,08745 | 0,08841 |
| 537,75734 | 0,09995 | 0,09634 | 0,08854 | 0,08964 |
| 537,79452 | 0,10007 | 0,09651 | 0,08994 | 0,09119 |
| 537,8317 | 0,10033 | 0,09681 | 0,09171 | 0,09305 |
| 537,86888 | 0,10074 | 0,09728 | 0,09381 | 0,09522 |
| 537,90607 | 0,10135 | 0,09795 | 0,09621 | 0,09776 |
| 537,94325 | 0,10217 | 0,09889 | 0,09891 | 0,1006 |
| 537,98043 | 0,10329 | 0,1001 | 0,1019 | 0,10372 |
| 538,01761 | 0,10468 | 0,10158 | 0,10515 | 0,10712 |
| 538,05479 | 0,10635 | 0,10336 | 0,10866 | 0,11077 |
| 538,09198 | 0,10831 | 0,10543 | 0,11242 | 0,11465 |
| 538,12916 | 0,11057 | 0,10781 | 0,11636 | 0,11876 |
| 538,16634 | 0,11311 | 0,11052 | 0,12046 | 0,12306 |
| 538,20352 | 0,11598 | 0,11356 | 0,12468 | 0,12751 |
| 538,2407 | 0,11911 | 0,11685 | 0,12897 | 0,13204 |
| 538,27789 | 0,12247 | 0,12039 | 0,1333 | 0,13664 |
| 538,31507 | 0,126 | 0,12412 | 0,13762 | 0,14125 |
| 538,35225 | 0,12969 | 0,12802 | 0,14186 | 0,14584 |
| 538,38943 | 0,13347 | 0,13204 | 0,14598 | 0,15032 |
| 538,42661 | 0,1373 | 0,13612 | 0,14993 | 0,15464 |
| 538,4638 | 0,1411 | 0,14018 | 0,15367 | 0,15876 |
| 538,50098 | 0,14481 | 0,14416 | 0,15716 | 0,16263 |
| 538,53816 | 0,14836 | 0,148 | 0,16031 | 0,16621 |
| 538,57534 | 0,15171 | 0,15165 | 0,16307 | 0,16946 |
| 538,61252 | 0,15479 | 0,15504 | 0,16546 | 0,17232 |
| 538,64971 | 0,15755 | 0,15804 | 0,16745 | 0,17471 |
| 538,68689 | 0,15986 | 0,16066 | 0,16903 | 0,17668 |
| 538,72407 | 0,16176 | 0,16287 | 0,1702 | 0,17823 |
| 538,76125 | 0,16323 | 0,16463 | 0,17097 | 0,17936 |
| 538,79843 | 0,16424 | 0,16593 | 0,17126 | 0,18009 |
| 538,83562 | 0,16479 | 0,16676 | 0,1712 | 0,18044 |
| 538,8728 | 0,16489 | 0,16702 | 0,17082 | 0,18041 |
| 538,90998 | 0,16447 | 0,16682 | 0,17017 | 0,18009 |
| 538,94716 | 0,16363 | 0,16619 | 0,16929 | 0,17954 |
| 538,98434 | 0,16243 | 0,16517 | 0,16825 | 0,17884 |
| 539,02153 | 0,16092 | 0,16382 | 0,16707 | 0,17803 |
| 539,05871 | 0,15915 | 0,16217 | 0,16586 | 0,17719 |
| 539,09589 | 0,15717 | 0,16027 | 0,16466 | 0,17635 |
| 539,13307 | 0,15504 | 0,15821 | 0,16352 | 0,17562 |
| 539,17025 | 0,15285 | 0,15608 | 0,16248 | 0,17501 |
| 539,20744 | 0,15067 | 0,15395 | 0,16158 | 0,17457 |
| 539,24462 | 0,14855 | 0,15187 | 0,16084 | 0,17431 |
| 539,2818 | 0,14656 | 0,1499 | 0,16032 | 0,17424 |
| 539,31898 | 0,14472 | 0,14811 | 0,15997 | 0,17435 |
| 539,35616 | 0,14311 | 0,14657 | 0,15978 | 0,17465 |
| 539,39335 | 0,14177 | 0,14529 | 0,15974 | 0,1751 |
| 539,43053 | 0,14069 | 0,14427 | 0,15982 | 0,17563 |
| 539,46771 | 0,13987 | 0,14354 | 0,15998 | 0,1762 |
| 539,50489 | 0,1393 | 0,14308 | 0,16018 | 0,17675 |
| 539,54207 | 0,13897 | 0,1429 | 0,16037 | 0,17723 |
| 539,57926 | 0,13885 | 0,143 | 0,16049 | 0,17759 |
| 539,61644 | 0,13894 | 0,1433 | 0,16051 | 0,17772 |
| 539,65362 | 0,13915 | 0,14375 | 0,16039 | 0,1776 |
| 539,6908 | 0,13943 | 0,14432 | 0,16011 | 0,17721 |
| 539,72798 | 0,13974 | 0,14494 | 0,15962 | 0,17651 |
| 539,76517 | 0,14003 | 0,14557 | 0,1589 | 0,17551 |
| 539,80235 | 0,14025 | 0,14613 | 0,15798 | 0,1742 |
| 539,83953 | 0,14034 | 0,14658 | 0,15686 | 0,17256 |
| 539,87671 | 0,14024 | 0,14686 | 0,15557 | 0,17063 |
| 539,91389 | 0,13995 | 0,14696 | 0,15414 | 0,16848 |
| 539,95108 | 0,13943 | 0,14684 | 0,1526 | 0,16618 |
| 539,98826 | 0,13869 | 0,14647 | 0,15099 | 0,16376 |
| 540,02544 | 0,1377 | 0,14582 | 0,14937 | 0,1613 |
| 540,06262 | 0,13645 | 0,14489 | 0,1478 | 0,15885 |
| 540,0998 | 0,13496 | 0,14372 | 0,1463 | 0,1565 |
| 540,13699 | 0,13327 | 0,14233 | 0,14493 | 0,1543 |
| 540,17417 | 0,13143 | 0,14075 | 0,14371 | 0,1523 |
| 540,21135 | 0,12946 | 0,13902 | 0,14268 | 0,15052 |
| 540,24853 | 0,12741 | 0,13716 | 0,14188 | 0,14899 |
| 540,28571 | 0,12531 | 0,13524 | 0,14126 | 0,14771 |
| 540,3229 | 0,12324 | 0,13331 | 0,14081 | 0,14669 |
| 540,36008 | 0,12123 | 0,13144 | 0,14052 | 0,14592 |
| 540,39726 | 0,11933 | 0,12965 | 0,14035 | 0,14532 |
| 540,43444 | 0,11757 | 0,12798 | 0,14025 | 0,14484 |
| 540,47162 | 0,11598 | 0,12649 | 0,14016 | 0,14442 |
| 540,50881 | 0,11459 | 0,12523 | 0,14 | 0,144 |
| 540,54599 | 0,11345 | 0,12419 | 0,13971 | 0,1435 |
| 540,58317 | 0,11254 | 0,12338 | 0,13923 | 0,1428 |
| 540,62035 | 0,11184 | 0,1228 | 0,1385 | 0,14185 |
| 540,65753 | 0,11134 | 0,12242 | 0,13746 | 0,14057 |
| 540,69472 | 0,11102 | 0,12224 | 0,13601 | 0,13893 |
| 540,7319 | 0,11085 | 0,12225 | 0,1341 | 0,13687 |
| 540,76908 | 0,1108 | 0,12238 | 0,13174 | 0,13436 |
| 540,80626 | 0,1108 | 0,12257 | 0,12893 | 0,13134 |
| 540,84344 | 0,11081 | 0,12277 | 0,12564 | 0,12776 |
| 540,88063 | 0,11078 | 0,12293 | 0,12191 | 0,12371 |
| 540,91781 | 0,11065 | 0,12301 | 0,11772 | 0,11921 |
| 540,95499 | 0,11037 | 0,12291 | 0,11305 | 0,1143 |
| 540,99217 | 0,1099 | 0,12257 | 0,10803 | 0,10903 |
| 541,02935 | 0,10913 | 0,12196 | 0,10272 | 0,10345 |
| 541,06654 | 0,10809 | 0,12104 | 0,09716 | 0,09758 |
| 541,10372 | 0,10673 | 0,11978 | 0,09143 | 0,09155 |
| 541,1409 | 0,10504 | 0,11815 | 0,08557 | 0,08544 |
| 541,17808 | 0,10301 | 0,1161 | 0,07967 | 0,07931 |
| 541,21526 | 0,10062 | 0,11359 | 0,07379 | 0,07322 |
| 541,25245 | 0,09781 | 0,11068 | 0,06801 | 0,06724 |
| 541,28963 | 0,09467 | 0,10738 | 0,06237 | 0,06143 |
| 541,32681 | 0,09123 | 0,10372 | 0,05692 | 0,05588 |
| 541,36399 | 0,0875 | 0,09972 | 0,05169 | 0,05061 |
| 541,40117 | 0,08352 | 0,09541 | 0,04674 | 0,04563 |
| 541,43836 | 0,07933 | 0,09079 | 0,04214 | 0,04097 |
| 541,47554 | 0,07496 | 0,08598 | 0,03786 | 0,03665 |
| 541,51272 | 0,07046 | 0,08101 | 0,0339 | 0,03268 |
| 541,5499 | 0,06591 | 0,07595 | 0,03026 | 0,0291 |
| 541,58708 | 0,06134 | 0,07084 | 0,02696 | 0,02589 |
| 541,62427 | 0,0568 | 0,06572 | 0,02397 | 0,02301 |
| 541,66145 | 0,05232 | 0,06067 | 0,02135 | 0,02044 |
| 541,69863 | 0,04796 | 0,05573 | 0,01902 | 0,01817 |
| 541,73581 | 0,04377 | 0,05095 | 0,01698 | 0,01617 |
| 541,77299 | 0,03976 | 0,04634 | 0,01518 | 0,01444 |
| 541,81018 | 0,03595 | 0,04195 | 0,01362 | 0,01298 |
| 541,84736 | 0,03236 | 0,03779 | 0,01227 | 0,01172 |
| 541,88454 | 0,02901 | 0,03392 | 0,01112 | 0,01064 |
| 541,92172 | 0,02591 | 0,03036 | 0,01017 | 0,00972 |
| 541,9589 | 0,02311 | 0,02707 | 0,00936 | 0,00894 |
| 541,99609 | 0,02055 | 0,02406 | 0,00867 | 0,00827 |
| 542,03327 | 0,01824 | 0,02133 | 0,00808 | 0,00772 |
| 542,07045 | 0,01617 | 0,01887 | 0,00759 | 0,00725 |
| 542,10763 | 0,01432 | 0,01669 | 0,00717 | 0,00685 |
| 542,14481 | 0,01268 | 0,01479 | 0,00682 | 0,0065 |
| 542,182 | 0,01128 | 0,01313 | 0,00652 | 0,00618 |
| 542,21918 | 0,01006 | 0,01167 | 0,00625 | 0,0059 |
| 542,25636 | 0,009 | 0,01041 | 0,006 | 0,00564 |
| 542,29354 | 0,00809 | 0,00933 | 0,00577 | 0,0054 |
| 542,33072 | 0,0073 | 0,00841 | 0,00555 | 0,00516 |
| 542,36791 | 0,00663 | 0,00765 | 0,00533 | 0,00492 |
| 542,40509 | 0,00607 | 0,00701 | 0,00512 | 0,00469 |
| 542,44227 | 0,00559 | 0,00647 | 0,0049 | 0,00445 |
| 542,47945 | 0,00519 | 0,00601 | 0,00467 | 0,00421 |
| 542,51663 | 0,00483 | 0,00563 | 0,00444 | 0,00397 |
| 542,55382 | 0,00453 | 0,0053 | 0,0042 | 0,00372 |
| 542,591 | 0,00426 | 0,00502 | 0,00396 | 0,00347 |
| 542,62818 | 0,00402 | 0,00478 | 0,00371 | 0,00322 |
| 542,66536 | 0,0038 | 0,00457 | 0,00346 | 0,00297 |
| 542,70254 | 0,0036 | 0,00437 | 0,00321 | 0,00273 |
| 542,73973 | 0,00341 | 0,00418 | 0,00297 | 0,00249 |
| 542,77691 | 0,00322 | 0,004 | 0,00272 | 0,00225 |
| 542,81409 | 0,00305 | 0,00382 | 0,00248 | 0,00203 |
| 542,85127 | 0,00287 | 0,00365 | 0,00225 | 0,00182 |
| 542,88845 | 0,0027 | 0,00347 | 0,00203 | 0,00162 |
| 542,92564 | 0,00253 | 0,00329 | 0,00182 | 0,00143 |
| 542,96282 | 0,00236 | 0,00311 | 0,00162 | 0,00125 |
| 543 | 0,00219 | 0,00292 | 0,00144 | 0,00109 |
| "Onderwijsscore" | "2020/'21" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 0 | 0 |
| 524,74364 | 0 | 0 | 0 | 0 |
| 524,78082 | 0 | 0 | 0 | 0 |
| 524,818 | 0 | 0 | 0 | 0 |
| 524,85519 | 0 | 0 | 0 | 0 |
| 524,89237 | 0 | 0 | 0 | 0 |
| 524,92955 | 0 | 0 | 0 | 0 |
| 524,96673 | 0 | 0 | 0 | 1e-05 |
| 525,00391 | 0 | 0 | 1e-05 | 1e-05 |
| 525,0411 | 0 | 0 | 1e-05 | 1e-05 |
| 525,07828 | 0 | 0 | 1e-05 | 1e-05 |
| 525,11546 | 0 | 0 | 1e-05 | 1e-05 |
| 525,15264 | 1e-05 | 1e-05 | 1e-05 | 2e-05 |
| 525,18982 | 1e-05 | 1e-05 | 2e-05 | 2e-05 |
| 525,22701 | 1e-05 | 1e-05 | 2e-05 | 3e-05 |
| 525,26419 | 1e-05 | 1e-05 | 2e-05 | 3e-05 |
| 525,30137 | 1e-05 | 1e-05 | 3e-05 | 4e-05 |
| 525,33855 | 2e-05 | 2e-05 | 3e-05 | 5e-05 |
| 525,37573 | 2e-05 | 2e-05 | 4e-05 | 6e-05 |
| 525,41292 | 2e-05 | 2e-05 | 5e-05 | 7e-05 |
| 525,4501 | 3e-05 | 3e-05 | 6e-05 | 8e-05 |
| 525,48728 | 3e-05 | 4e-05 | 7e-05 | 9e-05 |
| 525,52446 | 4e-05 | 4e-05 | 8e-05 | 0,00011 |
| 525,56164 | 5e-05 | 5e-05 | 9e-05 | 0,00012 |
| 525,59883 | 5e-05 | 6e-05 | 0,00011 | 0,00014 |
| 525,63601 | 6e-05 | 7e-05 | 0,00012 | 0,00016 |
| 525,67319 | 7e-05 | 8e-05 | 0,00014 | 0,00018 |
| 525,71037 | 9e-05 | 1e-04 | 0,00016 | 0,00021 |
| 525,74755 | 1e-04 | 0,00011 | 0,00018 | 0,00024 |
| 525,78474 | 0,00012 | 0,00013 | 0,00021 | 0,00027 |
| 525,82192 | 0,00013 | 0,00015 | 0,00023 | 3e-04 |
| 525,8591 | 0,00015 | 0,00017 | 0,00026 | 0,00033 |
| 525,89628 | 0,00017 | 2e-04 | 0,00029 | 0,00037 |
| 525,93346 | 2e-04 | 0,00022 | 0,00033 | 0,00041 |
| 525,97065 | 0,00022 | 0,00025 | 0,00036 | 0,00045 |
| 526,00783 | 0,00025 | 0,00028 | 4e-04 | 0,00049 |
| 526,04501 | 0,00028 | 0,00032 | 0,00043 | 0,00053 |
| 526,08219 | 0,00031 | 0,00035 | 0,00047 | 0,00058 |
| 526,11937 | 0,00034 | 0,00039 | 0,00051 | 0,00062 |
| 526,15656 | 0,00038 | 0,00043 | 0,00055 | 0,00067 |
| 526,19374 | 0,00042 | 0,00048 | 0,00059 | 0,00072 |
| 526,23092 | 0,00046 | 0,00052 | 0,00063 | 0,00077 |
| 526,2681 | 5e-04 | 0,00057 | 0,00067 | 0,00081 |
| 526,30528 | 0,00054 | 0,00062 | 0,00071 | 0,00086 |
| 526,34247 | 0,00059 | 0,00067 | 0,00075 | 9e-04 |
| 526,37965 | 0,00064 | 0,00073 | 0,00079 | 0,00095 |
| 526,41683 | 0,00069 | 0,00078 | 0,00083 | 0,00099 |
| 526,45401 | 0,00074 | 0,00084 | 0,00086 | 0,00103 |
| 526,49119 | 0,00079 | 9e-04 | 9e-04 | 0,00107 |
| 526,52838 | 0,00085 | 0,00096 | 0,00093 | 0,00111 |
| 526,56556 | 9e-04 | 0,00102 | 0,00096 | 0,00115 |
| 526,60274 | 0,00096 | 0,00108 | 0,00099 | 0,00119 |
| 526,63992 | 0,00102 | 0,00114 | 0,00101 | 0,00122 |
| 526,6771 | 0,00108 | 0,0012 | 0,00103 | 0,00126 |
| 526,71429 | 0,00114 | 0,00127 | 0,00105 | 0,00129 |
| 526,75147 | 0,0012 | 0,00133 | 0,00107 | 0,00132 |
| 526,78865 | 0,00126 | 0,00139 | 0,00109 | 0,00136 |
| 526,82583 | 0,00133 | 0,00146 | 0,00111 | 0,00139 |
| 526,86301 | 0,00139 | 0,00152 | 0,00112 | 0,00142 |
| 526,9002 | 0,00146 | 0,00159 | 0,00114 | 0,00146 |
| 526,93738 | 0,00153 | 0,00166 | 0,00116 | 0,00149 |
| 526,97456 | 0,0016 | 0,00173 | 0,00118 | 0,00153 |
| 527,01174 | 0,00168 | 0,0018 | 0,0012 | 0,00157 |
| 527,04892 | 0,00175 | 0,00187 | 0,00122 | 0,00161 |
| 527,08611 | 0,00183 | 0,00194 | 0,00124 | 0,00166 |
| 527,12329 | 0,00191 | 0,00202 | 0,00127 | 0,0017 |
| 527,16047 | 0,002 | 0,0021 | 0,00131 | 0,00175 |
| 527,19765 | 0,00209 | 0,00218 | 0,00135 | 0,00181 |
| 527,23483 | 0,00218 | 0,00227 | 0,00139 | 0,00186 |
| 527,27202 | 0,00228 | 0,00236 | 0,00145 | 0,00192 |
| 527,3092 | 0,00238 | 0,00246 | 0,00151 | 0,00199 |
| 527,34638 | 0,00249 | 0,00256 | 0,00158 | 0,00205 |
| 527,38356 | 0,0026 | 0,00266 | 0,00166 | 0,00212 |
| 527,42074 | 0,00271 | 0,00277 | 0,00175 | 0,00219 |
| 527,45793 | 0,00283 | 0,00288 | 0,00185 | 0,00227 |
| 527,49511 | 0,00295 | 0,003 | 0,00196 | 0,00235 |
| 527,53229 | 0,00308 | 0,00313 | 0,00208 | 0,00243 |
| 527,56947 | 0,00321 | 0,00325 | 0,00221 | 0,00251 |
| 527,60665 | 0,00335 | 0,00339 | 0,00235 | 0,0026 |
| 527,64384 | 0,00349 | 0,00352 | 0,00251 | 0,00269 |
| 527,68102 | 0,00363 | 0,00366 | 0,00267 | 0,00278 |
| 527,7182 | 0,00378 | 0,00381 | 0,00284 | 0,00287 |
| 527,75538 | 0,00393 | 0,00395 | 0,00302 | 0,00296 |
| 527,79256 | 0,00408 | 0,0041 | 0,00322 | 0,00306 |
| 527,82975 | 0,00423 | 0,00425 | 0,00342 | 0,00316 |
| 527,86693 | 0,00439 | 0,0044 | 0,00362 | 0,00326 |
| 527,90411 | 0,00455 | 0,00456 | 0,00383 | 0,00336 |
| 527,94129 | 0,00471 | 0,00471 | 0,00405 | 0,00346 |
| 527,97847 | 0,00487 | 0,00486 | 0,00427 | 0,00357 |
| 528,01566 | 0,00503 | 0,00501 | 0,00449 | 0,00367 |
| 528,05284 | 0,00519 | 0,00516 | 0,00471 | 0,00378 |
| 528,09002 | 0,00536 | 0,00531 | 0,00493 | 0,00388 |
| 528,1272 | 0,00552 | 0,00546 | 0,00515 | 0,00399 |
| 528,16438 | 0,00568 | 0,0056 | 0,00536 | 0,0041 |
| 528,20157 | 0,00585 | 0,00574 | 0,00557 | 0,00421 |
| 528,23875 | 0,00601 | 0,00587 | 0,00577 | 0,00432 |
| 528,27593 | 0,00618 | 0,006 | 0,00596 | 0,00442 |
| 528,31311 | 0,00634 | 0,00613 | 0,00614 | 0,00453 |
| 528,35029 | 0,00651 | 0,00626 | 0,00631 | 0,00464 |
| 528,38748 | 0,00668 | 0,00638 | 0,00647 | 0,00475 |
| 528,42466 | 0,00684 | 0,00649 | 0,00662 | 0,00486 |
| 528,46184 | 0,00701 | 0,0066 | 0,00676 | 0,00497 |
| 528,49902 | 0,00718 | 0,00671 | 0,00688 | 0,00508 |
| 528,5362 | 0,00735 | 0,00681 | 0,00699 | 0,0052 |
| 528,57339 | 0,00752 | 0,00691 | 0,00708 | 0,00531 |
| 528,61057 | 0,00769 | 0,00701 | 0,00717 | 0,00542 |
| 528,64775 | 0,00786 | 0,0071 | 0,00724 | 0,00553 |
| 528,68493 | 0,00804 | 0,0072 | 0,0073 | 0,00565 |
| 528,72211 | 0,00821 | 0,00729 | 0,00735 | 0,00577 |
| 528,7593 | 0,00839 | 0,00738 | 0,00739 | 0,00589 |
| 528,79648 | 0,00856 | 0,00747 | 0,00743 | 0,00601 |
| 528,83366 | 0,00874 | 0,00756 | 0,00745 | 0,00613 |
| 528,87084 | 0,00892 | 0,00765 | 0,00748 | 0,00626 |
| 528,90802 | 0,0091 | 0,00775 | 0,00749 | 0,00638 |
| 528,94521 | 0,00928 | 0,00784 | 0,00751 | 0,00651 |
| 528,98239 | 0,00946 | 0,00794 | 0,00752 | 0,00664 |
| 529,01957 | 0,00965 | 0,00805 | 0,00754 | 0,00678 |
| 529,05675 | 0,00983 | 0,00816 | 0,00755 | 0,00692 |
| 529,09393 | 0,01002 | 0,00828 | 0,00758 | 0,00705 |
| 529,13112 | 0,01021 | 0,00841 | 0,00761 | 0,0072 |
| 529,1683 | 0,01041 | 0,00854 | 0,00764 | 0,00734 |
| 529,20548 | 0,0106 | 0,00867 | 0,00768 | 0,00749 |
| 529,24266 | 0,0108 | 0,00882 | 0,00774 | 0,00763 |
| 529,27984 | 0,011 | 0,00898 | 0,0078 | 0,00779 |
| 529,31703 | 0,0112 | 0,00914 | 0,00788 | 0,00794 |
| 529,35421 | 0,01141 | 0,00931 | 0,00798 | 0,0081 |
| 529,39139 | 0,01162 | 0,00948 | 0,00809 | 0,00826 |
| 529,42857 | 0,01183 | 0,00967 | 0,00821 | 0,00842 |
| 529,46575 | 0,01205 | 0,00986 | 0,00836 | 0,00859 |
| 529,50294 | 0,01227 | 0,01005 | 0,00852 | 0,00876 |
| 529,54012 | 0,0125 | 0,01025 | 0,0087 | 0,00894 |
| 529,5773 | 0,01273 | 0,01046 | 0,0089 | 0,00912 |
| 529,61448 | 0,01296 | 0,01066 | 0,00912 | 0,0093 |
| 529,65166 | 0,0132 | 0,01087 | 0,00936 | 0,0095 |
| 529,68885 | 0,01344 | 0,01108 | 0,00962 | 0,0097 |
| 529,72603 | 0,01369 | 0,0113 | 0,0099 | 0,0099 |
| 529,76321 | 0,01394 | 0,01151 | 0,01019 | 0,01011 |
| 529,80039 | 0,01419 | 0,01172 | 0,01051 | 0,01033 |
| 529,83757 | 0,01444 | 0,01193 | 0,01083 | 0,01056 |
| 529,87476 | 0,01469 | 0,01213 | 0,01118 | 0,01079 |
| 529,91194 | 0,01495 | 0,01233 | 0,01153 | 0,01103 |
| 529,94912 | 0,0152 | 0,01253 | 0,0119 | 0,01128 |
| 529,9863 | 0,01545 | 0,01273 | 0,01227 | 0,01153 |
| 530,02348 | 0,0157 | 0,01292 | 0,01265 | 0,01179 |
| 530,06067 | 0,01595 | 0,01311 | 0,01303 | 0,01205 |
| 530,09785 | 0,01619 | 0,01329 | 0,01341 | 0,01231 |
| 530,13503 | 0,01643 | 0,01347 | 0,01379 | 0,01258 |
| 530,17221 | 0,01666 | 0,01365 | 0,01416 | 0,01284 |
| 530,20939 | 0,01689 | 0,01382 | 0,01452 | 0,01311 |
| 530,24658 | 0,01711 | 0,014 | 0,01487 | 0,01337 |
| 530,28376 | 0,01732 | 0,01416 | 0,01521 | 0,01363 |
| 530,32094 | 0,01753 | 0,01433 | 0,01554 | 0,01388 |
| 530,35812 | 0,01773 | 0,0145 | 0,01584 | 0,01413 |
| 530,3953 | 0,01792 | 0,01467 | 0,01612 | 0,01437 |
| 530,43249 | 0,01811 | 0,01484 | 0,01639 | 0,01461 |
| 530,46967 | 0,01829 | 0,01501 | 0,01663 | 0,01483 |
| 530,50685 | 0,01846 | 0,01518 | 0,01685 | 0,01505 |
| 530,54403 | 0,01864 | 0,01535 | 0,01705 | 0,01526 |
| 530,58121 | 0,01881 | 0,01553 | 0,01722 | 0,01546 |
| 530,6184 | 0,01898 | 0,01571 | 0,01738 | 0,01566 |
| 530,65558 | 0,01915 | 0,01589 | 0,01752 | 0,01585 |
| 530,69276 | 0,01932 | 0,01608 | 0,01764 | 0,01603 |
| 530,72994 | 0,01951 | 0,01628 | 0,01775 | 0,01621 |
| 530,76712 | 0,0197 | 0,01648 | 0,01784 | 0,01639 |
| 530,80431 | 0,0199 | 0,01669 | 0,01793 | 0,01657 |
| 530,84149 | 0,02011 | 0,01691 | 0,01801 | 0,01675 |
| 530,87867 | 0,02034 | 0,01713 | 0,01809 | 0,01694 |
| 530,91585 | 0,02058 | 0,01736 | 0,01817 | 0,01714 |
| 530,95303 | 0,02085 | 0,0176 | 0,01826 | 0,01735 |
| 530,99022 | 0,02113 | 0,01785 | 0,01836 | 0,01757 |
| 531,0274 | 0,02144 | 0,01811 | 0,01847 | 0,0178 |
| 531,06458 | 0,02177 | 0,01838 | 0,0186 | 0,01806 |
| 531,10176 | 0,02212 | 0,01866 | 0,01874 | 0,01833 |
| 531,13894 | 0,0225 | 0,01895 | 0,01891 | 0,01862 |
| 531,17613 | 0,0229 | 0,01925 | 0,0191 | 0,01894 |
| 531,21331 | 0,02332 | 0,01956 | 0,01931 | 0,01927 |
| 531,25049 | 0,02377 | 0,01988 | 0,01956 | 0,01963 |
| 531,28767 | 0,02423 | 0,02021 | 0,01983 | 0,02002 |
| 531,32485 | 0,02472 | 0,02055 | 0,02012 | 0,02042 |
| 531,36204 | 0,02522 | 0,0209 | 0,02044 | 0,02083 |
| 531,39922 | 0,02574 | 0,02126 | 0,02079 | 0,02127 |
| 531,4364 | 0,02627 | 0,02162 | 0,02116 | 0,02172 |
| 531,47358 | 0,0268 | 0,022 | 0,02156 | 0,02219 |
| 531,51076 | 0,02735 | 0,02238 | 0,02197 | 0,02266 |
| 531,54795 | 0,02789 | 0,02277 | 0,02241 | 0,02314 |
| 531,58513 | 0,02843 | 0,02316 | 0,02286 | 0,02363 |
| 531,62231 | 0,02897 | 0,02355 | 0,02332 | 0,02411 |
| 531,65949 | 0,0295 | 0,02395 | 0,0238 | 0,02459 |
| 531,69667 | 0,03002 | 0,02436 | 0,02429 | 0,02506 |
| 531,73386 | 0,03053 | 0,02476 | 0,02479 | 0,02552 |
| 531,77104 | 0,03102 | 0,02517 | 0,02529 | 0,02598 |
| 531,80822 | 0,0315 | 0,02559 | 0,0258 | 0,02642 |
| 531,8454 | 0,03196 | 0,026 | 0,02631 | 0,02684 |
| 531,88258 | 0,03241 | 0,02642 | 0,02682 | 0,02725 |
| 531,91977 | 0,03284 | 0,02685 | 0,02734 | 0,02765 |
| 531,95695 | 0,03325 | 0,02728 | 0,02786 | 0,02803 |
| 531,99413 | 0,03364 | 0,02772 | 0,02838 | 0,0284 |
| 532,03131 | 0,03403 | 0,02816 | 0,02891 | 0,02876 |
| 532,06849 | 0,0344 | 0,02862 | 0,02945 | 0,02911 |
| 532,10568 | 0,03477 | 0,0291 | 0,02999 | 0,02946 |
| 532,14286 | 0,03513 | 0,02959 | 0,03055 | 0,02981 |
| 532,18004 | 0,03549 | 0,0301 | 0,03111 | 0,03016 |
| 532,21722 | 0,03585 | 0,03062 | 0,03169 | 0,03051 |
| 532,2544 | 0,03623 | 0,03118 | 0,03229 | 0,03088 |
| 532,29159 | 0,03661 | 0,03176 | 0,0329 | 0,03127 |
| 532,32877 | 0,03702 | 0,03237 | 0,03354 | 0,03168 |
| 532,36595 | 0,03744 | 0,03302 | 0,0342 | 0,03211 |
| 532,40313 | 0,03789 | 0,03369 | 0,03488 | 0,03257 |
| 532,44031 | 0,03837 | 0,0344 | 0,03558 | 0,03306 |
| 532,4775 | 0,03888 | 0,03515 | 0,03632 | 0,03359 |
| 532,51468 | 0,03942 | 0,03594 | 0,03708 | 0,03416 |
| 532,55186 | 0,04 | 0,03676 | 0,03787 | 0,03476 |
| 532,58904 | 0,04062 | 0,03762 | 0,03867 | 0,03539 |
| 532,62622 | 0,04128 | 0,03851 | 0,0395 | 0,03606 |
| 532,66341 | 0,04197 | 0,03944 | 0,04036 | 0,03677 |
| 532,70059 | 0,0427 | 0,04039 | 0,04123 | 0,03751 |
| 532,73777 | 0,04347 | 0,04137 | 0,04213 | 0,03829 |
| 532,77495 | 0,04427 | 0,04238 | 0,04303 | 0,03909 |
| 532,81213 | 0,04509 | 0,0434 | 0,04395 | 0,03992 |
| 532,84932 | 0,04594 | 0,04443 | 0,04488 | 0,04077 |
| 532,8865 | 0,04681 | 0,04547 | 0,04581 | 0,04164 |
| 532,92368 | 0,04771 | 0,04651 | 0,04675 | 0,04252 |
| 532,96086 | 0,04861 | 0,04754 | 0,04769 | 0,04341 |
| 532,99804 | 0,04951 | 0,04856 | 0,04862 | 0,04431 |
| 533,03523 | 0,05041 | 0,04957 | 0,04955 | 0,04521 |
| 533,07241 | 0,05131 | 0,05056 | 0,05048 | 0,04611 |
| 533,10959 | 0,0522 | 0,05151 | 0,0514 | 0,04701 |
| 533,14677 | 0,05307 | 0,05244 | 0,05231 | 0,0479 |
| 533,18395 | 0,05392 | 0,05333 | 0,0532 | 0,04878 |
| 533,22114 | 0,05475 | 0,05418 | 0,05409 | 0,04966 |
| 533,25832 | 0,05554 | 0,055 | 0,05498 | 0,05052 |
| 533,2955 | 0,05631 | 0,05577 | 0,05585 | 0,05138 |
| 533,33268 | 0,05704 | 0,0565 | 0,05671 | 0,05223 |
| 533,36986 | 0,05773 | 0,05719 | 0,05756 | 0,05308 |
| 533,40705 | 0,05838 | 0,05783 | 0,0584 | 0,05391 |
| 533,44423 | 0,059 | 0,05845 | 0,05924 | 0,05474 |
| 533,48141 | 0,05958 | 0,05903 | 0,06008 | 0,05557 |
| 533,51859 | 0,06013 | 0,05957 | 0,06091 | 0,0564 |
| 533,55577 | 0,06063 | 0,06009 | 0,06174 | 0,05722 |
| 533,59295 | 0,06111 | 0,06058 | 0,06256 | 0,05805 |
| 533,63014 | 0,06156 | 0,06106 | 0,06338 | 0,05888 |
| 533,66732 | 0,06199 | 0,06153 | 0,0642 | 0,0597 |
| 533,7045 | 0,06239 | 0,06199 | 0,06502 | 0,06053 |
| 533,74168 | 0,06277 | 0,06245 | 0,06583 | 0,06135 |
| 533,77886 | 0,06314 | 0,0629 | 0,06663 | 0,06217 |
| 533,81605 | 0,06349 | 0,06337 | 0,06742 | 0,06298 |
| 533,85323 | 0,06384 | 0,06384 | 0,0682 | 0,06378 |
| 533,89041 | 0,06418 | 0,06432 | 0,06896 | 0,06457 |
| 533,92759 | 0,06451 | 0,06482 | 0,06969 | 0,06533 |
| 533,96477 | 0,06484 | 0,06533 | 0,0704 | 0,06606 |
| 534,00196 | 0,06518 | 0,06585 | 0,07107 | 0,06676 |
| 534,03914 | 0,06551 | 0,06638 | 0,07169 | 0,06742 |
| 534,07632 | 0,06583 | 0,06692 | 0,07228 | 0,06802 |
| 534,1135 | 0,06616 | 0,06747 | 0,07281 | 0,06858 |
| 534,15068 | 0,06648 | 0,06802 | 0,07328 | 0,06906 |
| 534,18787 | 0,0668 | 0,06856 | 0,07367 | 0,06946 |
| 534,22505 | 0,0671 | 0,06909 | 0,07399 | 0,06979 |
| 534,26223 | 0,0674 | 0,06961 | 0,07424 | 0,07004 |
| 534,29941 | 0,06767 | 0,0701 | 0,07441 | 0,07019 |
| 534,33659 | 0,06793 | 0,07057 | 0,07449 | 0,07026 |
| 534,37378 | 0,06815 | 0,07099 | 0,07447 | 0,07022 |
| 534,41096 | 0,06835 | 0,07136 | 0,07436 | 0,07007 |
| 534,44814 | 0,06852 | 0,07169 | 0,07416 | 0,06984 |
| 534,48532 | 0,06865 | 0,07196 | 0,07388 | 0,06951 |
| 534,5225 | 0,06874 | 0,07218 | 0,07352 | 0,06909 |
| 534,55969 | 0,06879 | 0,07231 | 0,07308 | 0,06859 |
| 534,59687 | 0,0688 | 0,07238 | 0,07255 | 0,068 |
| 534,63405 | 0,06876 | 0,07237 | 0,07195 | 0,06734 |
| 534,67123 | 0,06869 | 0,0723 | 0,07131 | 0,06662 |
| 534,70841 | 0,06858 | 0,07216 | 0,07062 | 0,06586 |
| 534,7456 | 0,06843 | 0,07196 | 0,06989 | 0,06506 |
| 534,78278 | 0,06825 | 0,07168 | 0,06914 | 0,06424 |
| 534,81996 | 0,06804 | 0,07135 | 0,06839 | 0,06342 |
| 534,85714 | 0,06783 | 0,07098 | 0,06764 | 0,06261 |
| 534,89432 | 0,0676 | 0,07057 | 0,06691 | 0,06183 |
| 534,93151 | 0,06738 | 0,07014 | 0,06622 | 0,06108 |
| 534,96869 | 0,06717 | 0,06968 | 0,06557 | 0,06039 |
| 535,00587 | 0,06699 | 0,06923 | 0,06499 | 0,05979 |
| 535,04305 | 0,06684 | 0,06878 | 0,06449 | 0,05927 |
| 535,08023 | 0,06673 | 0,06836 | 0,06408 | 0,05886 |
| 535,11742 | 0,06668 | 0,06797 | 0,06376 | 0,05855 |
| 535,1546 | 0,0667 | 0,06763 | 0,06355 | 0,05835 |
| 535,19178 | 0,06681 | 0,06736 | 0,06344 | 0,0583 |
| 535,22896 | 0,067 | 0,06717 | 0,06349 | 0,0584 |
| 535,26614 | 0,06727 | 0,06705 | 0,06366 | 0,05865 |
| 535,30333 | 0,06764 | 0,06701 | 0,06395 | 0,05903 |
| 535,34051 | 0,06813 | 0,06707 | 0,06437 | 0,05956 |
| 535,37769 | 0,06873 | 0,06725 | 0,06492 | 0,06024 |
| 535,41487 | 0,06943 | 0,06753 | 0,06559 | 0,06108 |
| 535,45205 | 0,07023 | 0,06792 | 0,06641 | 0,06207 |
| 535,48924 | 0,07112 | 0,06841 | 0,06733 | 0,06318 |
| 535,52642 | 0,07211 | 0,069 | 0,06836 | 0,06442 |
| 535,5636 | 0,0732 | 0,06968 | 0,06948 | 0,06578 |
| 535,60078 | 0,07437 | 0,07047 | 0,0707 | 0,06723 |
| 535,63796 | 0,07559 | 0,07134 | 0,072 | 0,0688 |
| 535,67515 | 0,07687 | 0,07228 | 0,07338 | 0,07045 |
| 535,71233 | 0,07819 | 0,07328 | 0,07481 | 0,07215 |
| 535,74951 | 0,07954 | 0,07433 | 0,07629 | 0,07391 |
| 535,78669 | 0,08089 | 0,07542 | 0,07779 | 0,0757 |
| 535,82387 | 0,08224 | 0,07653 | 0,07933 | 0,07751 |
| 535,86106 | 0,08358 | 0,07765 | 0,08088 | 0,07933 |
| 535,89824 | 0,08488 | 0,07878 | 0,08244 | 0,08113 |
| 535,93542 | 0,08613 | 0,07989 | 0,08398 | 0,08292 |
| 535,9726 | 0,08732 | 0,08097 | 0,08552 | 0,08467 |
| 536,00978 | 0,08843 | 0,08201 | 0,08704 | 0,08637 |
| 536,04697 | 0,08947 | 0,08301 | 0,08853 | 0,08801 |
| 536,08415 | 0,09042 | 0,08396 | 0,08999 | 0,08957 |
| 536,12133 | 0,09128 | 0,08485 | 0,0914 | 0,09106 |
| 536,15851 | 0,09203 | 0,08567 | 0,09279 | 0,09246 |
| 536,19569 | 0,09268 | 0,08643 | 0,09413 | 0,09377 |
| 536,23288 | 0,09322 | 0,08711 | 0,09542 | 0,095 |
| 536,27006 | 0,09368 | 0,08772 | 0,09666 | 0,0961 |
| 536,30724 | 0,09404 | 0,08827 | 0,09785 | 0,0971 |
| 536,34442 | 0,09431 | 0,08876 | 0,09899 | 0,09799 |
| 536,3816 | 0,09448 | 0,0892 | 0,10007 | 0,09879 |
| 536,41879 | 0,09458 | 0,08957 | 0,1011 | 0,09948 |
| 536,45597 | 0,09462 | 0,0899 | 0,10206 | 0,10006 |
| 536,49315 | 0,09461 | 0,09019 | 0,10295 | 0,10052 |
| 536,53033 | 0,09454 | 0,09045 | 0,10377 | 0,10088 |
| 536,56751 | 0,09444 | 0,0907 | 0,10451 | 0,10114 |
| 536,6047 | 0,09432 | 0,09092 | 0,10517 | 0,10131 |
| 536,64188 | 0,09418 | 0,09113 | 0,10575 | 0,10138 |
| 536,67906 | 0,09403 | 0,09135 | 0,10623 | 0,10135 |
| 536,71624 | 0,09389 | 0,09157 | 0,1066 | 0,10121 |
| 536,75342 | 0,09376 | 0,0918 | 0,10686 | 0,101 |
| 536,79061 | 0,09365 | 0,09203 | 0,10702 | 0,1007 |
| 536,82779 | 0,09356 | 0,09229 | 0,10707 | 0,10033 |
| 536,86497 | 0,0935 | 0,09256 | 0,107 | 0,09989 |
| 536,90215 | 0,09347 | 0,09285 | 0,1068 | 0,09936 |
| 536,93933 | 0,09347 | 0,09315 | 0,10647 | 0,09879 |
| 536,97652 | 0,09351 | 0,09346 | 0,10603 | 0,09816 |
| 537,0137 | 0,09358 | 0,09378 | 0,10548 | 0,0975 |
| 537,05088 | 0,09368 | 0,09411 | 0,10484 | 0,09681 |
| 537,08806 | 0,09381 | 0,09444 | 0,1041 | 0,09611 |
| 537,12524 | 0,09396 | 0,09476 | 0,10326 | 0,0954 |
| 537,16243 | 0,09415 | 0,09508 | 0,10237 | 0,0947 |
| 537,19961 | 0,09436 | 0,09538 | 0,10142 | 0,09403 |
| 537,23679 | 0,09459 | 0,09567 | 0,10045 | 0,09341 |
| 537,27397 | 0,09483 | 0,09594 | 0,09947 | 0,09284 |
| 537,31115 | 0,0951 | 0,0962 | 0,09851 | 0,09235 |
| 537,34834 | 0,09538 | 0,09644 | 0,09759 | 0,09197 |
| 537,38552 | 0,09568 | 0,09667 | 0,09673 | 0,0917 |
| 537,4227 | 0,09601 | 0,09689 | 0,09597 | 0,09155 |
| 537,45988 | 0,09636 | 0,09711 | 0,09531 | 0,09154 |
| 537,49706 | 0,09674 | 0,09735 | 0,09479 | 0,09167 |
| 537,53425 | 0,09715 | 0,0976 | 0,09445 | 0,09202 |
| 537,57143 | 0,09761 | 0,09789 | 0,09431 | 0,09255 |
| 537,60861 | 0,09814 | 0,09823 | 0,09437 | 0,09328 |
| 537,64579 | 0,09873 | 0,09864 | 0,09465 | 0,0942 |
| 537,68297 | 0,09939 | 0,09914 | 0,09517 | 0,09533 |
| 537,72016 | 0,10013 | 0,09974 | 0,09592 | 0,09668 |
| 537,75734 | 0,10097 | 0,10046 | 0,09699 | 0,09829 |
| 537,79452 | 0,10195 | 0,10131 | 0,09834 | 0,10012 |
| 537,8317 | 0,10305 | 0,10232 | 0,09995 | 0,10216 |
| 537,86888 | 0,10427 | 0,10353 | 0,10182 | 0,10442 |
| 537,90607 | 0,10563 | 0,10493 | 0,10396 | 0,10688 |
| 537,94325 | 0,10712 | 0,10652 | 0,10636 | 0,10957 |
| 537,98043 | 0,1088 | 0,1083 | 0,10906 | 0,11246 |
| 538,01761 | 0,11063 | 0,11029 | 0,11198 | 0,11553 |
| 538,05479 | 0,11261 | 0,11253 | 0,11512 | 0,11874 |
| 538,09198 | 0,11474 | 0,11498 | 0,11844 | 0,1221 |
| 538,12916 | 0,117 | 0,11763 | 0,12193 | 0,12557 |
| 538,16634 | 0,1194 | 0,12045 | 0,12558 | 0,12915 |
| 538,20352 | 0,12193 | 0,12344 | 0,12934 | 0,1328 |
| 538,2407 | 0,12456 | 0,12658 | 0,13318 | 0,13648 |
| 538,27789 | 0,12726 | 0,12986 | 0,13705 | 0,14018 |
| 538,31507 | 0,13001 | 0,13322 | 0,14092 | 0,14386 |
| 538,35225 | 0,1328 | 0,13663 | 0,14478 | 0,14749 |
| 538,38943 | 0,1356 | 0,14007 | 0,14855 | 0,15103 |
| 538,42661 | 0,13836 | 0,14349 | 0,15221 | 0,15446 |
| 538,4638 | 0,14106 | 0,14685 | 0,15573 | 0,15775 |
| 538,50098 | 0,14369 | 0,1501 | 0,15909 | 0,16089 |
| 538,53816 | 0,14621 | 0,15322 | 0,16225 | 0,16386 |
| 538,57534 | 0,14858 | 0,15617 | 0,1652 | 0,1666 |
| 538,61252 | 0,15077 | 0,15893 | 0,16785 | 0,1691 |
| 538,64971 | 0,15277 | 0,16146 | 0,17024 | 0,17138 |
| 538,68689 | 0,15458 | 0,16367 | 0,17236 | 0,17342 |
| 538,72407 | 0,15617 | 0,16561 | 0,17422 | 0,17524 |
| 538,76125 | 0,15755 | 0,16727 | 0,1758 | 0,17682 |
| 538,79843 | 0,15865 | 0,16864 | 0,17709 | 0,17812 |
| 538,83562 | 0,15951 | 0,16971 | 0,17807 | 0,17921 |
| 538,8728 | 0,16015 | 0,17044 | 0,17882 | 0,18009 |
| 538,90998 | 0,16059 | 0,17087 | 0,17933 | 0,18079 |
| 538,94716 | 0,16081 | 0,17104 | 0,17963 | 0,18133 |
| 538,98434 | 0,16084 | 0,17097 | 0,17975 | 0,1817 |
| 539,02153 | 0,16067 | 0,17068 | 0,17966 | 0,18193 |
| 539,05871 | 0,16036 | 0,17019 | 0,17943 | 0,18206 |
| 539,09589 | 0,15993 | 0,1695 | 0,17908 | 0,18211 |
| 539,13307 | 0,1594 | 0,1687 | 0,17864 | 0,1821 |
| 539,17025 | 0,1588 | 0,16781 | 0,17812 | 0,18204 |
| 539,20744 | 0,15814 | 0,16686 | 0,17754 | 0,18194 |
| 539,24462 | 0,15746 | 0,16587 | 0,17691 | 0,18181 |
| 539,2818 | 0,15677 | 0,16488 | 0,17625 | 0,18167 |
| 539,31898 | 0,1561 | 0,16392 | 0,17557 | 0,18152 |
| 539,35616 | 0,15545 | 0,163 | 0,17486 | 0,18135 |
| 539,39335 | 0,15484 | 0,16214 | 0,17414 | 0,18117 |
| 539,43053 | 0,15429 | 0,16134 | 0,1734 | 0,18096 |
| 539,46771 | 0,15377 | 0,16062 | 0,17263 | 0,18071 |
| 539,50489 | 0,1533 | 0,15999 | 0,17182 | 0,18042 |
| 539,54207 | 0,15288 | 0,15943 | 0,17098 | 0,18007 |
| 539,57926 | 0,15248 | 0,15892 | 0,17009 | 0,17966 |
| 539,61644 | 0,15211 | 0,15846 | 0,16915 | 0,17917 |
| 539,65362 | 0,15175 | 0,15802 | 0,16813 | 0,17857 |
| 539,6908 | 0,15138 | 0,15761 | 0,16705 | 0,17789 |
| 539,72798 | 0,15099 | 0,15717 | 0,1659 | 0,1771 |
| 539,76517 | 0,15057 | 0,15671 | 0,16468 | 0,17622 |
| 539,80235 | 0,15008 | 0,1562 | 0,1634 | 0,17524 |
| 539,83953 | 0,14952 | 0,15562 | 0,16205 | 0,17415 |
| 539,87671 | 0,14889 | 0,15497 | 0,16063 | 0,17296 |
| 539,91389 | 0,14817 | 0,15419 | 0,15916 | 0,17169 |
| 539,95108 | 0,14736 | 0,15331 | 0,15766 | 0,17036 |
| 539,98826 | 0,14645 | 0,15232 | 0,15614 | 0,16897 |
| 540,02544 | 0,14543 | 0,15122 | 0,1546 | 0,16753 |
| 540,06262 | 0,14431 | 0,15002 | 0,15305 | 0,16605 |
| 540,0998 | 0,14312 | 0,14869 | 0,15151 | 0,16455 |
| 540,13699 | 0,14184 | 0,14727 | 0,14998 | 0,16304 |
| 540,17417 | 0,14051 | 0,14577 | 0,14846 | 0,16152 |
| 540,21135 | 0,13911 | 0,1442 | 0,14697 | 0,15999 |
| 540,24853 | 0,13767 | 0,14259 | 0,14548 | 0,15846 |
| 540,28571 | 0,13621 | 0,14094 | 0,14401 | 0,15691 |
| 540,3229 | 0,13474 | 0,13928 | 0,14254 | 0,15534 |
| 540,36008 | 0,13327 | 0,13763 | 0,14105 | 0,15373 |
| 540,39726 | 0,13181 | 0,13599 | 0,13952 | 0,15208 |
| 540,43444 | 0,13039 | 0,13438 | 0,13795 | 0,15036 |
| 540,47162 | 0,129 | 0,13282 | 0,13631 | 0,14854 |
| 540,50881 | 0,12764 | 0,1313 | 0,13454 | 0,1466 |
| 540,54599 | 0,12632 | 0,12984 | 0,13266 | 0,14451 |
| 540,58317 | 0,12503 | 0,12842 | 0,13062 | 0,14227 |
| 540,62035 | 0,12378 | 0,12705 | 0,12843 | 0,13986 |
| 540,65753 | 0,12254 | 0,1257 | 0,12606 | 0,13725 |
| 540,69472 | 0,1213 | 0,12438 | 0,12347 | 0,13437 |
| 540,7319 | 0,12006 | 0,12306 | 0,12064 | 0,13127 |
| 540,76908 | 0,11879 | 0,12171 | 0,11759 | 0,12794 |
| 540,80626 | 0,11747 | 0,12033 | 0,11432 | 0,12438 |
| 540,84344 | 0,11607 | 0,11889 | 0,11083 | 0,12059 |
| 540,88063 | 0,11458 | 0,11737 | 0,10713 | 0,11655 |
| 540,91781 | 0,11299 | 0,11574 | 0,10321 | 0,11228 |
| 540,95499 | 0,11128 | 0,11397 | 0,09909 | 0,10782 |
| 540,99217 | 0,10943 | 0,11205 | 0,09482 | 0,10319 |
| 541,02935 | 0,1074 | 0,10997 | 0,09041 | 0,09843 |
| 541,06654 | 0,10519 | 0,10773 | 0,08591 | 0,09356 |
| 541,10372 | 0,10282 | 0,10531 | 0,08132 | 0,08858 |
| 541,1409 | 0,10027 | 0,10267 | 0,07669 | 0,08357 |
| 541,17808 | 0,09754 | 0,09983 | 0,07206 | 0,07855 |
| 541,21526 | 0,09463 | 0,09681 | 0,06745 | 0,07356 |
| 541,25245 | 0,09152 | 0,09362 | 0,06291 | 0,06862 |
| 541,28963 | 0,08826 | 0,09026 | 0,05845 | 0,06376 |
| 541,32681 | 0,08487 | 0,08675 | 0,05411 | 0,05905 |
| 541,36399 | 0,08135 | 0,08308 | 0,04994 | 0,05449 |
| 541,40117 | 0,07772 | 0,07931 | 0,04594 | 0,0501 |
| 541,43836 | 0,07399 | 0,07546 | 0,04213 | 0,04589 |
| 541,47554 | 0,07021 | 0,07154 | 0,03851 | 0,04188 |
| 541,51272 | 0,06639 | 0,06758 | 0,03509 | 0,0381 |
| 541,5499 | 0,06257 | 0,06362 | 0,03192 | 0,03458 |
| 541,58708 | 0,05876 | 0,05968 | 0,029 | 0,03129 |
| 541,62427 | 0,05498 | 0,05578 | 0,0263 | 0,02822 |
| 541,66145 | 0,05129 | 0,05195 | 0,02382 | 0,02538 |
| 541,69863 | 0,04767 | 0,04821 | 0,02155 | 0,02277 |
| 541,73581 | 0,04417 | 0,04458 | 0,01949 | 0,0204 |
| 541,77299 | 0,04077 | 0,04111 | 0,01766 | 0,01827 |
| 541,81018 | 0,03752 | 0,03778 | 0,01603 | 0,01632 |
| 541,84736 | 0,03445 | 0,03462 | 0,01457 | 0,01457 |
| 541,88454 | 0,03154 | 0,03161 | 0,01327 | 0,01298 |
| 541,92172 | 0,02879 | 0,02878 | 0,01211 | 0,01156 |
| 541,9589 | 0,02622 | 0,02616 | 0,0111 | 0,01033 |
| 541,99609 | 0,02381 | 0,02373 | 0,01023 | 0,00923 |
| 542,03327 | 0,02161 | 0,02149 | 0,00946 | 0,00826 |
| 542,07045 | 0,0196 | 0,01942 | 0,00878 | 0,00739 |
| 542,10763 | 0,01775 | 0,01752 | 0,00818 | 0,00663 |
| 542,14481 | 0,01605 | 0,0158 | 0,00766 | 0,00596 |
| 542,182 | 0,01452 | 0,01427 | 0,00719 | 0,00538 |
| 542,21918 | 0,01314 | 0,01289 | 0,00678 | 0,00488 |
| 542,25636 | 0,01192 | 0,01165 | 0,00641 | 0,00443 |
| 542,29354 | 0,01083 | 0,01053 | 0,00607 | 0,00403 |
| 542,33072 | 0,00985 | 0,00954 | 0,00575 | 0,00368 |
| 542,36791 | 0,00898 | 0,00868 | 0,00546 | 0,00337 |
| 542,40509 | 0,0082 | 0,00792 | 0,00518 | 0,0031 |
| 542,44227 | 0,00753 | 0,00725 | 0,00492 | 0,00286 |
| 542,47945 | 0,00694 | 0,00666 | 0,00466 | 0,00264 |
| 542,51663 | 0,00642 | 0,00613 | 0,00441 | 0,00244 |
| 542,55382 | 0,00595 | 0,00567 | 0,00417 | 0,00226 |
| 542,591 | 0,00553 | 0,00527 | 0,00393 | 0,0021 |
| 542,62818 | 0,00516 | 0,00492 | 0,00369 | 0,00196 |
| 542,66536 | 0,00484 | 0,0046 | 0,00346 | 0,00182 |
| 542,70254 | 0,00454 | 0,00431 | 0,00323 | 0,00169 |
| 542,73973 | 0,00426 | 0,00404 | 0,00301 | 0,00157 |
| 542,77691 | 0,00401 | 0,00381 | 0,00279 | 0,00146 |
| 542,81409 | 0,00377 | 0,00359 | 0,00257 | 0,00136 |
| 542,85127 | 0,00355 | 0,00338 | 0,00237 | 0,00126 |
| 542,88845 | 0,00334 | 0,00319 | 0,00217 | 0,00117 |
| 542,92564 | 0,00314 | 0,003 | 0,00197 | 0,00109 |
| 542,96282 | 0,00295 | 0,00282 | 0,00179 | 0,001 |
| 543 | 0,00276 | 0,00265 | 0,00162 | 0,00093 |
3.2 Onderwijsscores per schooljaar naar modelvariabelen
In deze sectie kijken we naar de frequentiedichtheid van de onderwijsscores per schooljaar uitgesplitst naar de verschillende modelvariabelen. Er zijn zes modelvariabelen:
- het opleidingsniveau van de moeder van het kind
- het opleidingsniveau van de vader van het kind
- de verblijfsduur van de moeder van het kind
- het land van herkomst van het kind
- één of beide ouders vallen onder de wet schuldsanering natuurlijke personen
- het gemiddelde opleidingsniveau van de moeders op de school van het kind
Een schematisch overzicht van de modelvariabelen van de onderwijsachterstandenindicator en hun invloed op de onderwijsscore is in de inleiding in figuren 1.1.1 en 1.1.2 weergegeven.
Opleidingsniveau van de vader en moeder
De figuren 3.2.1 tot en met 3.2.18 tonen de frequentiedichtheid van de onderwijsscores per opleidingsniveau van de vader en de moeder van het kind uitgesplitst naar schooljaar. De verwachting is dat kinderen met ouders met een lager opleidingsniveau een lagere onderwijsscore hebben en dat kinderen met ouders met een hoger opleidingsniveau een hogere onderwijsscore hebben.
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00068 | 0,00084 | 0,00017 | 3e-05 | 5e-05 |
| 524,03718 | 0,00072 | 0,00091 | 0,00019 | 4e-05 | 6e-05 |
| 524,07436 | 0,00075 | 0,00098 | 0,00022 | 5e-05 | 8e-05 |
| 524,11155 | 0,00078 | 0,00104 | 0,00026 | 6e-05 | 1e-04 |
| 524,14873 | 8e-04 | 0,00109 | 0,00029 | 7e-05 | 0,00012 |
| 524,18591 | 0,00082 | 0,00113 | 0,00033 | 8e-05 | 0,00014 |
| 524,22309 | 0,00083 | 0,00116 | 0,00038 | 1e-04 | 0,00017 |
| 524,26027 | 0,00083 | 0,00117 | 0,00042 | 0,00011 | 0,00019 |
| 524,29746 | 0,00084 | 0,00117 | 0,00047 | 0,00013 | 0,00022 |
| 524,33464 | 0,00084 | 0,00115 | 0,00053 | 0,00015 | 0,00026 |
| 524,37182 | 0,00084 | 0,00113 | 0,00059 | 0,00017 | 0,00029 |
| 524,409 | 0,00085 | 0,00109 | 0,00065 | 0,00019 | 0,00032 |
| 524,44618 | 0,00085 | 0,00104 | 0,00071 | 0,00022 | 0,00035 |
| 524,48337 | 0,00086 | 0,00099 | 0,00077 | 0,00025 | 0,00038 |
| 524,52055 | 0,00087 | 0,00094 | 0,00084 | 0,00027 | 0,00041 |
| 524,55773 | 0,00089 | 0,00088 | 9e-04 | 0,00031 | 0,00044 |
| 524,59491 | 0,00091 | 0,00083 | 0,00096 | 0,00034 | 0,00046 |
| 524,63209 | 0,00093 | 0,00079 | 0,00101 | 0,00038 | 0,00048 |
| 524,66928 | 0,00095 | 0,00075 | 0,00107 | 0,00043 | 5e-04 |
| 524,70646 | 0,00098 | 0,00073 | 0,00111 | 0,00047 | 0,00052 |
| 524,74364 | 0,00101 | 0,00072 | 0,00116 | 0,00053 | 0,00053 |
| 524,78082 | 0,00105 | 0,00072 | 0,00119 | 0,00059 | 0,00054 |
| 524,818 | 0,00108 | 0,00073 | 0,00122 | 0,00065 | 0,00055 |
| 524,85519 | 0,00112 | 0,00076 | 0,00125 | 0,00071 | 0,00056 |
| 524,89237 | 0,00116 | 0,00081 | 0,00127 | 0,00078 | 0,00057 |
| 524,92955 | 0,0012 | 0,00086 | 0,00129 | 0,00084 | 0,00058 |
| 524,96673 | 0,00124 | 0,00093 | 0,0013 | 9e-04 | 0,00059 |
| 525,00391 | 0,00128 | 0,00101 | 0,00131 | 0,00096 | 6e-04 |
| 525,0411 | 0,00133 | 0,0011 | 0,00132 | 0,00102 | 6e-04 |
| 525,07828 | 0,00138 | 0,00119 | 0,00133 | 0,00106 | 0,00061 |
| 525,11546 | 0,00143 | 0,00129 | 0,00134 | 0,0011 | 0,00061 |
| 525,15264 | 0,00148 | 0,00139 | 0,00136 | 0,00113 | 0,00061 |
| 525,18982 | 0,00153 | 0,00148 | 0,00137 | 0,00114 | 0,00061 |
| 525,22701 | 0,00159 | 0,00157 | 0,0014 | 0,00115 | 6e-04 |
| 525,26419 | 0,00164 | 0,00165 | 0,00142 | 0,00115 | 0,00059 |
| 525,30137 | 0,0017 | 0,00173 | 0,00146 | 0,00114 | 0,00059 |
| 525,33855 | 0,00177 | 0,00179 | 0,0015 | 0,00112 | 0,00058 |
| 525,37573 | 0,00183 | 0,00183 | 0,00155 | 0,00111 | 0,00057 |
| 525,41292 | 0,00191 | 0,00186 | 0,0016 | 0,00109 | 0,00056 |
| 525,4501 | 0,00198 | 0,00188 | 0,00167 | 0,00108 | 0,00056 |
| 525,48728 | 0,00207 | 0,00189 | 0,00175 | 0,00107 | 0,00056 |
| 525,52446 | 0,00216 | 0,00189 | 0,00184 | 0,00108 | 0,00058 |
| 525,56164 | 0,00225 | 0,00188 | 0,00195 | 0,0011 | 0,00061 |
| 525,59883 | 0,00236 | 0,00187 | 0,00207 | 0,00115 | 0,00066 |
| 525,63601 | 0,00247 | 0,00186 | 0,00221 | 0,00123 | 0,00074 |
| 525,67319 | 0,00259 | 0,00186 | 0,00237 | 0,00135 | 0,00085 |
| 525,71037 | 0,00272 | 0,00187 | 0,00254 | 0,00151 | 0,00102 |
| 525,74755 | 0,00286 | 0,0019 | 0,00274 | 0,00174 | 0,00124 |
| 525,78474 | 0,00303 | 0,00196 | 0,00297 | 0,00205 | 0,00154 |
| 525,82192 | 0,00321 | 0,00206 | 0,00322 | 0,00246 | 0,00194 |
| 525,8591 | 0,00342 | 0,00221 | 0,00352 | 0,00301 | 0,00245 |
| 525,89628 | 0,00368 | 0,00241 | 0,00386 | 0,00372 | 0,0031 |
| 525,93346 | 0,00398 | 0,00269 | 0,00426 | 0,00462 | 0,00391 |
| 525,97065 | 0,00436 | 0,00305 | 0,00472 | 0,00574 | 0,00491 |
| 526,00783 | 0,00483 | 0,00351 | 0,00526 | 0,00711 | 0,00612 |
| 526,04501 | 0,00542 | 0,00411 | 0,00589 | 0,00877 | 0,0076 |
| 526,08219 | 0,00616 | 0,00486 | 0,00664 | 0,01073 | 0,00934 |
| 526,11937 | 0,00708 | 0,00577 | 0,00752 | 0,01302 | 0,01135 |
| 526,15656 | 0,0082 | 0,00686 | 0,00858 | 0,01562 | 0,01362 |
| 526,19374 | 0,00955 | 0,00815 | 0,00982 | 0,01855 | 0,01614 |
| 526,23092 | 0,01115 | 0,00966 | 0,01125 | 0,0218 | 0,01888 |
| 526,2681 | 0,01301 | 0,01141 | 0,01288 | 0,02527 | 0,02179 |
| 526,30528 | 0,01515 | 0,0134 | 0,01472 | 0,0289 | 0,02483 |
| 526,34247 | 0,01756 | 0,01564 | 0,01678 | 0,03259 | 0,02792 |
| 526,37965 | 0,02024 | 0,01815 | 0,01905 | 0,03626 | 0,03098 |
| 526,41683 | 0,02319 | 0,02086 | 0,02151 | 0,03979 | 0,03389 |
| 526,45401 | 0,02632 | 0,02377 | 0,02415 | 0,04307 | 0,03658 |
| 526,49119 | 0,02958 | 0,02682 | 0,02693 | 0,04601 | 0,03896 |
| 526,52838 | 0,03292 | 0,02998 | 0,02979 | 0,04851 | 0,04096 |
| 526,56556 | 0,03627 | 0,0332 | 0,03267 | 0,05045 | 0,04254 |
| 526,60274 | 0,03957 | 0,03641 | 0,03554 | 0,05179 | 0,04365 |
| 526,63992 | 0,04273 | 0,03955 | 0,03832 | 0,05256 | 0,04429 |
| 526,6771 | 0,0457 | 0,04256 | 0,04097 | 0,05277 | 0,04446 |
| 526,71429 | 0,04842 | 0,04537 | 0,04343 | 0,05247 | 0,04419 |
| 526,75147 | 0,05081 | 0,04793 | 0,04567 | 0,05173 | 0,04353 |
| 526,78865 | 0,05287 | 0,05023 | 0,0476 | 0,05065 | 0,0426 |
| 526,82583 | 0,0546 | 0,05223 | 0,04923 | 0,04931 | 0,04149 |
| 526,86301 | 0,05602 | 0,05393 | 0,05056 | 0,04783 | 0,04027 |
| 526,9002 | 0,05714 | 0,05532 | 0,0516 | 0,04632 | 0,03904 |
| 526,93738 | 0,058 | 0,05642 | 0,05237 | 0,04487 | 0,03786 |
| 526,97456 | 0,05865 | 0,05726 | 0,05291 | 0,04358 | 0,03681 |
| 527,01174 | 0,05914 | 0,05785 | 0,05324 | 0,04248 | 0,03591 |
| 527,04892 | 0,05953 | 0,05826 | 0,05344 | 0,0416 | 0,03521 |
| 527,08611 | 0,05987 | 0,05857 | 0,05354 | 0,04094 | 0,03474 |
| 527,12329 | 0,06025 | 0,05881 | 0,05364 | 0,0405 | 0,03445 |
| 527,16047 | 0,06072 | 0,05906 | 0,05382 | 0,04025 | 0,03434 |
| 527,19765 | 0,06135 | 0,05938 | 0,05414 | 0,04016 | 0,03437 |
| 527,23483 | 0,06217 | 0,05984 | 0,05468 | 0,0402 | 0,03453 |
| 527,27202 | 0,06327 | 0,0605 | 0,05552 | 0,04035 | 0,0348 |
| 527,3092 | 0,06469 | 0,06145 | 0,05673 | 0,04058 | 0,03517 |
| 527,34638 | 0,06651 | 0,0628 | 0,05839 | 0,04089 | 0,03565 |
| 527,38356 | 0,06878 | 0,06461 | 0,06055 | 0,04132 | 0,03626 |
| 527,42074 | 0,07163 | 0,06693 | 0,06336 | 0,04191 | 0,03708 |
| 527,45793 | 0,07509 | 0,06985 | 0,06685 | 0,04273 | 0,03816 |
| 527,49511 | 0,0792 | 0,07341 | 0,07105 | 0,04385 | 0,03958 |
| 527,53229 | 0,08399 | 0,07765 | 0,07598 | 0,04539 | 0,04144 |
| 527,56947 | 0,08948 | 0,08261 | 0,08164 | 0,04745 | 0,04384 |
| 527,60665 | 0,09565 | 0,0883 | 0,08804 | 0,05021 | 0,04688 |
| 527,64384 | 0,10248 | 0,09472 | 0,09514 | 0,05379 | 0,05066 |
| 527,68102 | 0,10991 | 0,10187 | 0,10289 | 0,05825 | 0,05525 |
| 527,7182 | 0,11785 | 0,10958 | 0,11122 | 0,06367 | 0,06075 |
| 527,75538 | 0,12622 | 0,11776 | 0,12006 | 0,07008 | 0,06732 |
| 527,79256 | 0,13484 | 0,12628 | 0,12922 | 0,07751 | 0,07483 |
| 527,82975 | 0,14352 | 0,135 | 0,13853 | 0,08594 | 0,08325 |
| 527,86693 | 0,15212 | 0,14377 | 0,14785 | 0,0953 | 0,09253 |
| 527,90411 | 0,16048 | 0,15245 | 0,15702 | 0,10549 | 0,10256 |
| 527,94129 | 0,16848 | 0,16088 | 0,1659 | 0,11641 | 0,11321 |
| 527,97847 | 0,17599 | 0,16889 | 0,17433 | 0,12786 | 0,12433 |
| 528,01566 | 0,18291 | 0,17634 | 0,1822 | 0,13958 | 0,13573 |
| 528,05284 | 0,18917 | 0,18316 | 0,18935 | 0,15134 | 0,14723 |
| 528,09002 | 0,19465 | 0,18928 | 0,19564 | 0,16293 | 0,15857 |
| 528,1272 | 0,19936 | 0,19467 | 0,20109 | 0,17411 | 0,16953 |
| 528,16438 | 0,20334 | 0,19929 | 0,20567 | 0,1847 | 0,17994 |
| 528,20157 | 0,2066 | 0,20316 | 0,20937 | 0,1945 | 0,18961 |
| 528,23875 | 0,20917 | 0,20627 | 0,21222 | 0,20337 | 0,19841 |
| 528,27593 | 0,21108 | 0,20865 | 0,21422 | 0,21118 | 0,20622 |
| 528,31311 | 0,21236 | 0,21026 | 0,21543 | 0,2177 | 0,21296 |
| 528,35029 | 0,21304 | 0,2112 | 0,2159 | 0,22304 | 0,21858 |
| 528,38748 | 0,21314 | 0,21154 | 0,2156 | 0,22722 | 0,22306 |
| 528,42466 | 0,21267 | 0,21131 | 0,21465 | 0,2303 | 0,22633 |
| 528,46184 | 0,21164 | 0,21055 | 0,21315 | 0,23234 | 0,22851 |
| 528,49902 | 0,21014 | 0,20931 | 0,21116 | 0,23347 | 0,22974 |
| 528,5362 | 0,2082 | 0,20762 | 0,20874 | 0,23377 | 0,2301 |
| 528,57339 | 0,20588 | 0,20554 | 0,20596 | 0,23337 | 0,22971 |
| 528,61057 | 0,20325 | 0,20311 | 0,20288 | 0,23238 | 0,22866 |
| 528,64775 | 0,20036 | 0,20036 | 0,19958 | 0,23086 | 0,22706 |
| 528,68493 | 0,1973 | 0,1974 | 0,19613 | 0,22894 | 0,22499 |
| 528,72211 | 0,19416 | 0,1943 | 0,1926 | 0,22668 | 0,22253 |
| 528,7593 | 0,19103 | 0,19114 | 0,1891 | 0,22413 | 0,21973 |
| 528,79648 | 0,18805 | 0,18799 | 0,18569 | 0,22132 | 0,21665 |
| 528,83366 | 0,18528 | 0,18493 | 0,18245 | 0,21824 | 0,21334 |
| 528,87084 | 0,18283 | 0,18204 | 0,17943 | 0,21492 | 0,20983 |
| 528,90802 | 0,18076 | 0,17938 | 0,17671 | 0,21138 | 0,20616 |
| 528,94521 | 0,17913 | 0,17705 | 0,17434 | 0,20762 | 0,20236 |
| 528,98239 | 0,17801 | 0,17515 | 0,17235 | 0,2037 | 0,1985 |
| 529,01957 | 0,17742 | 0,17369 | 0,17083 | 0,19969 | 0,19463 |
| 529,05675 | 0,1774 | 0,17271 | 0,16981 | 0,19568 | 0,19082 |
| 529,09393 | 0,17797 | 0,17225 | 0,16928 | 0,19179 | 0,1872 |
| 529,13112 | 0,17918 | 0,17231 | 0,16924 | 0,18813 | 0,18388 |
| 529,1683 | 0,18094 | 0,17291 | 0,1697 | 0,18481 | 0,18094 |
| 529,20548 | 0,18322 | 0,17405 | 0,17064 | 0,18195 | 0,17848 |
| 529,24266 | 0,18597 | 0,17571 | 0,17204 | 0,17961 | 0,17656 |
| 529,27984 | 0,18913 | 0,17788 | 0,17388 | 0,17788 | 0,17521 |
| 529,31703 | 0,19263 | 0,18053 | 0,17611 | 0,17678 | 0,17447 |
| 529,35421 | 0,19638 | 0,18353 | 0,17873 | 0,17637 | 0,17431 |
| 529,39139 | 0,20029 | 0,18684 | 0,18164 | 0,17654 | 0,17469 |
| 529,42857 | 0,20425 | 0,19035 | 0,18475 | 0,17718 | 0,17555 |
| 529,46575 | 0,20814 | 0,19399 | 0,18797 | 0,17817 | 0,17678 |
| 529,50294 | 0,21183 | 0,19764 | 0,19123 | 0,1794 | 0,17822 |
| 529,54012 | 0,2152 | 0,20122 | 0,19444 | 0,18074 | 0,17974 |
| 529,5773 | 0,21817 | 0,2046 | 0,19748 | 0,18204 | 0,18122 |
| 529,61448 | 0,22063 | 0,20765 | 0,20029 | 0,1832 | 0,18256 |
| 529,65166 | 0,22249 | 0,21026 | 0,20274 | 0,18411 | 0,18366 |
| 529,68885 | 0,22371 | 0,21236 | 0,20469 | 0,18469 | 0,18446 |
| 529,72603 | 0,22421 | 0,21388 | 0,20611 | 0,18488 | 0,18492 |
| 529,76321 | 0,22397 | 0,21477 | 0,20694 | 0,18471 | 0,18501 |
| 529,80039 | 0,22289 | 0,21498 | 0,20714 | 0,1842 | 0,1847 |
| 529,83757 | 0,22107 | 0,2145 | 0,20669 | 0,18338 | 0,18409 |
| 529,87476 | 0,21856 | 0,21332 | 0,20557 | 0,18232 | 0,18322 |
| 529,91194 | 0,2154 | 0,21147 | 0,20382 | 0,18107 | 0,18215 |
| 529,94912 | 0,21169 | 0,20889 | 0,20144 | 0,17972 | 0,18094 |
| 529,9863 | 0,20748 | 0,20575 | 0,19847 | 0,17832 | 0,17967 |
| 530,02348 | 0,20289 | 0,20212 | 0,19499 | 0,17696 | 0,1784 |
| 530,06067 | 0,198 | 0,19809 | 0,19113 | 0,17572 | 0,1772 |
| 530,09785 | 0,19293 | 0,19377 | 0,187 | 0,17466 | 0,17613 |
| 530,13503 | 0,18778 | 0,18925 | 0,18269 | 0,17383 | 0,17529 |
| 530,17221 | 0,18268 | 0,18464 | 0,17832 | 0,17329 | 0,17472 |
| 530,20939 | 0,17773 | 0,18004 | 0,17399 | 0,17309 | 0,17445 |
| 530,24658 | 0,17302 | 0,17555 | 0,16981 | 0,17327 | 0,17454 |
| 530,28376 | 0,16862 | 0,17133 | 0,16587 | 0,17385 | 0,17502 |
| 530,32094 | 0,1646 | 0,16741 | 0,1623 | 0,17489 | 0,17592 |
| 530,35812 | 0,16101 | 0,16389 | 0,15917 | 0,17638 | 0,17724 |
| 530,3953 | 0,15791 | 0,16081 | 0,1565 | 0,17837 | 0,17898 |
| 530,43249 | 0,1553 | 0,15821 | 0,15432 | 0,18081 | 0,18113 |
| 530,46967 | 0,15327 | 0,15611 | 0,15266 | 0,18362 | 0,18367 |
| 530,50685 | 0,15177 | 0,15452 | 0,15151 | 0,18674 | 0,18649 |
| 530,54403 | 0,15076 | 0,15344 | 0,15085 | 0,19006 | 0,18948 |
| 530,58121 | 0,15021 | 0,15286 | 0,15064 | 0,19346 | 0,19253 |
| 530,6184 | 0,15007 | 0,15274 | 0,15086 | 0,19679 | 0,19551 |
| 530,65558 | 0,15029 | 0,15299 | 0,15146 | 0,19992 | 0,19828 |
| 530,69276 | 0,1508 | 0,15352 | 0,15231 | 0,20268 | 0,20072 |
| 530,72994 | 0,15155 | 0,15428 | 0,15336 | 0,20488 | 0,20267 |
| 530,76712 | 0,15245 | 0,15517 | 0,15452 | 0,20634 | 0,20403 |
| 530,80431 | 0,15344 | 0,15612 | 0,15573 | 0,20698 | 0,20462 |
| 530,84149 | 0,15443 | 0,15705 | 0,1569 | 0,20674 | 0,20439 |
| 530,87867 | 0,15534 | 0,15788 | 0,15797 | 0,20557 | 0,20336 |
| 530,91585 | 0,1561 | 0,15851 | 0,15889 | 0,20349 | 0,20154 |
| 530,95303 | 0,15668 | 0,15889 | 0,15958 | 0,20051 | 0,19895 |
| 530,99022 | 0,15701 | 0,15897 | 0,15999 | 0,19673 | 0,19566 |
| 531,0274 | 0,15705 | 0,15872 | 0,1601 | 0,19223 | 0,19177 |
| 531,06458 | 0,15679 | 0,15813 | 0,15989 | 0,18715 | 0,18738 |
| 531,10176 | 0,15618 | 0,15717 | 0,15934 | 0,18158 | 0,18259 |
| 531,13894 | 0,1552 | 0,15584 | 0,15845 | 0,17577 | 0,17753 |
| 531,17613 | 0,15383 | 0,15416 | 0,15722 | 0,16984 | 0,17234 |
| 531,21331 | 0,15209 | 0,15213 | 0,15564 | 0,16393 | 0,16713 |
| 531,25049 | 0,14999 | 0,14975 | 0,15374 | 0,15815 | 0,162 |
| 531,28767 | 0,14755 | 0,14707 | 0,15147 | 0,15259 | 0,15703 |
| 531,32485 | 0,14477 | 0,14413 | 0,1489 | 0,14732 | 0,15229 |
| 531,36204 | 0,14169 | 0,14097 | 0,14605 | 0,1424 | 0,14782 |
| 531,39922 | 0,13831 | 0,13761 | 0,14295 | 0,13786 | 0,14366 |
| 531,4364 | 0,13468 | 0,13409 | 0,13961 | 0,13375 | 0,13983 |
| 531,47358 | 0,13081 | 0,13044 | 0,13607 | 0,13005 | 0,13638 |
| 531,51076 | 0,12674 | 0,12669 | 0,13235 | 0,12671 | 0,1333 |
| 531,54795 | 0,12254 | 0,12288 | 0,12848 | 0,12372 | 0,13054 |
| 531,58513 | 0,11825 | 0,11903 | 0,1245 | 0,12103 | 0,12808 |
| 531,62231 | 0,11393 | 0,11521 | 0,12044 | 0,11859 | 0,12587 |
| 531,65949 | 0,10963 | 0,11143 | 0,11636 | 0,11636 | 0,12386 |
| 531,69667 | 0,10541 | 0,10775 | 0,11231 | 0,11428 | 0,12199 |
| 531,73386 | 0,10132 | 0,10421 | 0,10833 | 0,11228 | 0,12019 |
| 531,77104 | 0,09743 | 0,10084 | 0,10448 | 0,11032 | 0,11839 |
| 531,80822 | 0,09379 | 0,09768 | 0,10081 | 0,10831 | 0,11651 |
| 531,8454 | 0,0905 | 0,09479 | 0,09736 | 0,10621 | 0,11447 |
| 531,88258 | 0,08757 | 0,09222 | 0,0942 | 0,10397 | 0,11222 |
| 531,91977 | 0,08505 | 0,09001 | 0,0914 | 0,10158 | 0,10975 |
| 531,95695 | 0,08297 | 0,08819 | 0,08899 | 0,09901 | 0,10703 |
| 531,99413 | 0,08135 | 0,08675 | 0,087 | 0,09628 | 0,10408 |
| 532,03131 | 0,08019 | 0,08571 | 0,08543 | 0,09339 | 0,10092 |
| 532,06849 | 0,07951 | 0,08508 | 0,0843 | 0,09038 | 0,0976 |
| 532,10568 | 0,07927 | 0,08483 | 0,0836 | 0,0873 | 0,09417 |
| 532,14286 | 0,07946 | 0,08495 | 0,08331 | 0,08419 | 0,0907 |
| 532,18004 | 0,08006 | 0,0854 | 0,0834 | 0,08112 | 0,08728 |
| 532,21722 | 0,08096 | 0,08615 | 0,08384 | 0,07817 | 0,08399 |
| 532,2544 | 0,08208 | 0,08711 | 0,08458 | 0,07536 | 0,0809 |
| 532,29159 | 0,08333 | 0,0882 | 0,08552 | 0,07276 | 0,07806 |
| 532,32877 | 0,08462 | 0,08934 | 0,08657 | 0,0704 | 0,0755 |
| 532,36595 | 0,08586 | 0,09045 | 0,08766 | 0,06829 | 0,07326 |
| 532,40313 | 0,08696 | 0,09145 | 0,08871 | 0,06646 | 0,07134 |
| 532,44031 | 0,08784 | 0,09227 | 0,08963 | 0,06491 | 0,06974 |
| 532,4775 | 0,08841 | 0,09283 | 0,09036 | 0,06366 | 0,06844 |
| 532,51468 | 0,08857 | 0,09307 | 0,09083 | 0,06266 | 0,06746 |
| 532,55186 | 0,0883 | 0,09291 | 0,09096 | 0,06189 | 0,06671 |
| 532,58904 | 0,08758 | 0,09233 | 0,09069 | 0,06131 | 0,06615 |
| 532,62622 | 0,08642 | 0,09134 | 0,09003 | 0,0609 | 0,06574 |
| 532,66341 | 0,08484 | 0,08994 | 0,08898 | 0,06061 | 0,06545 |
| 532,70059 | 0,08285 | 0,08815 | 0,08753 | 0,06043 | 0,06523 |
| 532,73777 | 0,08051 | 0,08599 | 0,08571 | 0,06032 | 0,06507 |
| 532,77495 | 0,07788 | 0,08352 | 0,08356 | 0,06026 | 0,06493 |
| 532,81213 | 0,075 | 0,08077 | 0,08111 | 0,06023 | 0,06481 |
| 532,84932 | 0,07194 | 0,0778 | 0,07841 | 0,06021 | 0,06468 |
| 532,8865 | 0,0688 | 0,07467 | 0,0755 | 0,06019 | 0,06456 |
| 532,92368 | 0,06563 | 0,07145 | 0,07248 | 0,06017 | 0,06443 |
| 532,96086 | 0,0625 | 0,06822 | 0,0694 | 0,06013 | 0,06431 |
| 532,99804 | 0,05946 | 0,06501 | 0,06633 | 0,06009 | 0,06419 |
| 533,03523 | 0,05655 | 0,06189 | 0,06333 | 0,06004 | 0,0641 |
| 533,07241 | 0,05382 | 0,0589 | 0,06045 | 0,06 | 0,06404 |
| 533,10959 | 0,05129 | 0,05609 | 0,05773 | 0,05997 | 0,06401 |
| 533,14677 | 0,04899 | 0,05348 | 0,05523 | 0,05996 | 0,06403 |
| 533,18395 | 0,04698 | 0,05112 | 0,05297 | 0,05999 | 0,0641 |
| 533,22114 | 0,04526 | 0,04907 | 0,05104 | 0,06006 | 0,06423 |
| 533,25832 | 0,04383 | 0,0473 | 0,04941 | 0,0602 | 0,06441 |
| 533,2955 | 0,0427 | 0,04584 | 0,04811 | 0,06039 | 0,06465 |
| 533,33268 | 0,04188 | 0,04469 | 0,04713 | 0,06064 | 0,06493 |
| 533,36986 | 0,04136 | 0,04386 | 0,04649 | 0,06095 | 0,06524 |
| 533,40705 | 0,04114 | 0,04333 | 0,04617 | 0,06129 | 0,06558 |
| 533,44423 | 0,04121 | 0,0431 | 0,04615 | 0,06166 | 0,06591 |
| 533,48141 | 0,04156 | 0,04315 | 0,04643 | 0,06202 | 0,06621 |
| 533,51859 | 0,04216 | 0,04348 | 0,04698 | 0,06232 | 0,06645 |
| 533,55577 | 0,04299 | 0,04403 | 0,04777 | 0,06252 | 0,06657 |
| 533,59295 | 0,04399 | 0,04476 | 0,04872 | 0,06257 | 0,06655 |
| 533,63014 | 0,0451 | 0,04563 | 0,04979 | 0,06243 | 0,06634 |
| 533,66732 | 0,04627 | 0,04658 | 0,05093 | 0,06204 | 0,06591 |
| 533,7045 | 0,04745 | 0,04757 | 0,05208 | 0,06139 | 0,06523 |
| 533,74168 | 0,04859 | 0,04855 | 0,05318 | 0,06045 | 0,06428 |
| 533,77886 | 0,04962 | 0,04947 | 0,05418 | 0,0592 | 0,06305 |
| 533,81605 | 0,05049 | 0,0503 | 0,05503 | 0,05767 | 0,06154 |
| 533,85323 | 0,05115 | 0,05096 | 0,05564 | 0,05586 | 0,05977 |
| 533,89041 | 0,05152 | 0,05142 | 0,05599 | 0,0538 | 0,05774 |
| 533,92759 | 0,05161 | 0,05167 | 0,05605 | 0,05158 | 0,05554 |
| 533,96477 | 0,05139 | 0,05168 | 0,05581 | 0,04926 | 0,05321 |
| 534,00196 | 0,05085 | 0,05144 | 0,05526 | 0,0469 | 0,05081 |
| 534,03914 | 0,05001 | 0,05095 | 0,05439 | 0,04457 | 0,04839 |
| 534,07632 | 0,04887 | 0,05021 | 0,05321 | 0,04232 | 0,04601 |
| 534,1135 | 0,04746 | 0,04924 | 0,05176 | 0,04022 | 0,04372 |
| 534,15068 | 0,04581 | 0,04805 | 0,05006 | 0,0383 | 0,04157 |
| 534,18787 | 0,04396 | 0,04664 | 0,04813 | 0,03659 | 0,03959 |
| 534,22505 | 0,04196 | 0,04509 | 0,04605 | 0,03514 | 0,03783 |
| 534,26223 | 0,03986 | 0,04342 | 0,04387 | 0,03392 | 0,03627 |
| 534,29941 | 0,03773 | 0,04167 | 0,04164 | 0,03292 | 0,03492 |
| 534,33659 | 0,0356 | 0,03988 | 0,03941 | 0,03211 | 0,03377 |
| 534,37378 | 0,03351 | 0,03807 | 0,03722 | 0,03146 | 0,03279 |
| 534,41096 | 0,0315 | 0,03629 | 0,03511 | 0,03093 | 0,03195 |
| 534,44814 | 0,02959 | 0,03455 | 0,03313 | 0,03047 | 0,03122 |
| 534,48532 | 0,02781 | 0,0329 | 0,03131 | 0,03005 | 0,03058 |
| 534,5225 | 0,02617 | 0,03135 | 0,02967 | 0,02963 | 0,02999 |
| 534,55969 | 0,0247 | 0,02992 | 0,02822 | 0,02916 | 0,02941 |
| 534,59687 | 0,02338 | 0,0286 | 0,02697 | 0,02861 | 0,02881 |
| 534,63405 | 0,02221 | 0,02741 | 0,0259 | 0,02797 | 0,02817 |
| 534,67123 | 0,02118 | 0,02634 | 0,025 | 0,02723 | 0,02749 |
| 534,70841 | 0,02028 | 0,02539 | 0,02427 | 0,02638 | 0,02676 |
| 534,7456 | 0,01949 | 0,02454 | 0,02369 | 0,02543 | 0,02597 |
| 534,78278 | 0,0188 | 0,0238 | 0,02323 | 0,0244 | 0,02513 |
| 534,81996 | 0,0182 | 0,02314 | 0,02289 | 0,0233 | 0,02425 |
| 534,85714 | 0,01767 | 0,02256 | 0,02261 | 0,02216 | 0,02334 |
| 534,89432 | 0,01719 | 0,02203 | 0,02237 | 0,021 | 0,02243 |
| 534,93151 | 0,01675 | 0,02155 | 0,02216 | 0,01985 | 0,02153 |
| 534,96869 | 0,01633 | 0,02108 | 0,02194 | 0,01873 | 0,02065 |
| 535,00587 | 0,01591 | 0,02063 | 0,02171 | 0,01768 | 0,0198 |
| 535,04305 | 0,01549 | 0,02018 | 0,02144 | 0,0167 | 0,019 |
| 535,08023 | 0,01506 | 0,01972 | 0,02112 | 0,0158 | 0,01824 |
| 535,11742 | 0,01461 | 0,01924 | 0,02074 | 0,015 | 0,01754 |
| 535,1546 | 0,01415 | 0,01873 | 0,0203 | 0,01429 | 0,01688 |
| 535,19178 | 0,01366 | 0,01819 | 0,0198 | 0,01368 | 0,01626 |
| 535,22896 | 0,01314 | 0,01762 | 0,01923 | 0,01316 | 0,01569 |
| 535,26614 | 0,01261 | 0,01701 | 0,01862 | 0,01274 | 0,01516 |
| 535,30333 | 0,01207 | 0,01638 | 0,01796 | 0,01238 | 0,01465 |
| 535,34051 | 0,01153 | 0,01572 | 0,01726 | 0,01208 | 0,01417 |
| 535,37769 | 0,01098 | 0,01503 | 0,01653 | 0,01182 | 0,0137 |
| 535,41487 | 0,01044 | 0,01434 | 0,01579 | 0,0116 | 0,01325 |
| 535,45205 | 0,00991 | 0,01363 | 0,01505 | 0,01139 | 0,01282 |
| 535,48924 | 0,0094 | 0,01293 | 0,01431 | 0,01119 | 0,0124 |
| 535,52642 | 0,00892 | 0,01224 | 0,01359 | 0,011 | 0,01201 |
| 535,5636 | 0,00847 | 0,01157 | 0,01289 | 0,0108 | 0,01163 |
| 535,60078 | 0,00805 | 0,01092 | 0,01222 | 0,01059 | 0,01128 |
| 535,63796 | 0,00767 | 0,01031 | 0,01159 | 0,01036 | 0,01096 |
| 535,67515 | 0,00733 | 0,00975 | 0,011 | 0,01012 | 0,01068 |
| 535,71233 | 0,00703 | 0,00922 | 0,01045 | 0,00988 | 0,01042 |
| 535,74951 | 0,00676 | 0,00875 | 0,00994 | 0,00962 | 0,0102 |
| 535,78669 | 0,00653 | 0,00833 | 0,00948 | 0,00936 | 0,01002 |
| 535,82387 | 0,00633 | 0,00797 | 0,00907 | 0,00911 | 0,00987 |
| 535,86106 | 0,00618 | 0,00766 | 0,0087 | 0,00885 | 0,00975 |
| 535,89824 | 0,00605 | 0,0074 | 0,00837 | 0,00861 | 0,00965 |
| 535,93542 | 0,00596 | 0,00719 | 0,00808 | 0,00837 | 0,00957 |
| 535,9726 | 0,00589 | 0,00702 | 0,00783 | 0,00815 | 0,00951 |
| 536,00978 | 0,00585 | 0,00689 | 0,00762 | 0,00794 | 0,00944 |
| 536,04697 | 0,00583 | 0,00681 | 0,00745 | 0,00775 | 0,00937 |
| 536,08415 | 0,00582 | 0,00675 | 0,0073 | 0,00757 | 0,0093 |
| 536,12133 | 0,00583 | 0,00673 | 0,00719 | 0,00739 | 0,00921 |
| 536,15851 | 0,00584 | 0,00673 | 0,0071 | 0,00723 | 0,0091 |
| 536,19569 | 0,00586 | 0,00675 | 0,00703 | 0,00707 | 0,00897 |
| 536,23288 | 0,00587 | 0,00678 | 0,00698 | 0,00692 | 0,00882 |
| 536,27006 | 0,00588 | 0,00681 | 0,00693 | 0,00677 | 0,00865 |
| 536,30724 | 0,00588 | 0,00685 | 0,00689 | 0,00663 | 0,00847 |
| 536,34442 | 0,00587 | 0,00688 | 0,00685 | 0,0065 | 0,00827 |
| 536,3816 | 0,00584 | 0,00691 | 0,00681 | 0,00637 | 0,00807 |
| 536,41879 | 0,0058 | 0,00691 | 0,00675 | 0,00625 | 0,00787 |
| 536,45597 | 0,00573 | 0,0069 | 0,00667 | 0,00615 | 0,00767 |
| 536,49315 | 0,00564 | 0,00687 | 0,00658 | 0,00605 | 0,00747 |
| 536,53033 | 0,00553 | 0,00681 | 0,00647 | 0,00597 | 0,00729 |
| 536,56751 | 0,0054 | 0,00672 | 0,00633 | 0,00591 | 0,00712 |
| 536,6047 | 0,00525 | 0,00661 | 0,00618 | 0,00585 | 0,00695 |
| 536,64188 | 0,00508 | 0,00647 | 0,006 | 0,00581 | 0,0068 |
| 536,67906 | 0,00489 | 0,00631 | 0,00581 | 0,00578 | 0,00666 |
| 536,71624 | 0,00469 | 0,00613 | 0,00561 | 0,00575 | 0,00652 |
| 536,75342 | 0,00449 | 0,00594 | 0,00539 | 0,00572 | 0,00638 |
| 536,79061 | 0,00427 | 0,00573 | 0,00518 | 0,00569 | 0,00624 |
| 536,82779 | 0,00406 | 0,00551 | 0,00496 | 0,00564 | 0,0061 |
| 536,86497 | 0,00384 | 0,00529 | 0,00476 | 0,00559 | 0,00595 |
| 536,90215 | 0,00363 | 0,00507 | 0,00456 | 0,00552 | 0,00579 |
| 536,93933 | 0,00343 | 0,00486 | 0,00437 | 0,00543 | 0,00562 |
| 536,97652 | 0,00325 | 0,00466 | 0,00421 | 0,00533 | 0,00544 |
| 537,0137 | 0,00308 | 0,00446 | 0,00406 | 0,00521 | 0,00526 |
| 537,05088 | 0,00293 | 0,00428 | 0,00393 | 0,00507 | 0,00507 |
| 537,08806 | 0,0028 | 0,00411 | 0,00383 | 0,00492 | 0,00488 |
| 537,12524 | 0,00269 | 0,00396 | 0,00374 | 0,00476 | 0,00469 |
| 537,16243 | 0,00261 | 0,00383 | 0,00367 | 0,0046 | 0,00451 |
| 537,19961 | 0,00255 | 0,00371 | 0,00362 | 0,00444 | 0,00433 |
| 537,23679 | 0,00251 | 0,0036 | 0,00358 | 0,00429 | 0,00416 |
| 537,27397 | 0,0025 | 0,0035 | 0,00355 | 0,00414 | 0,00401 |
| 537,31115 | 0,00251 | 0,00342 | 0,00353 | 0,004 | 0,00386 |
| 537,34834 | 0,00254 | 0,00335 | 0,00352 | 0,00389 | 0,00372 |
| 537,38552 | 0,00257 | 0,00329 | 0,00351 | 0,00379 | 0,0036 |
| 537,4227 | 0,00262 | 0,00324 | 0,00349 | 0,00371 | 0,00348 |
| 537,45988 | 0,00267 | 0,00319 | 0,00348 | 0,00364 | 0,00337 |
| 537,49706 | 0,00272 | 0,00315 | 0,00346 | 0,0036 | 0,00327 |
| 537,53425 | 0,00277 | 0,00311 | 0,00343 | 0,00357 | 0,00318 |
| 537,57143 | 0,00282 | 0,00308 | 0,0034 | 0,00356 | 0,00309 |
| 537,60861 | 0,00285 | 0,00304 | 0,00336 | 0,00356 | 0,003 |
| 537,64579 | 0,00288 | 0,00301 | 0,00331 | 0,00356 | 0,00292 |
| 537,68297 | 0,00289 | 0,00298 | 0,00325 | 0,00358 | 0,00284 |
| 537,72016 | 0,00289 | 0,00294 | 0,00319 | 0,00359 | 0,00276 |
| 537,75734 | 0,00287 | 0,0029 | 0,00312 | 0,00361 | 0,00269 |
| 537,79452 | 0,00285 | 0,00285 | 0,00305 | 0,00363 | 0,00262 |
| 537,8317 | 0,00281 | 0,0028 | 0,00298 | 0,00364 | 0,00256 |
| 537,86888 | 0,00277 | 0,00274 | 0,0029 | 0,00365 | 0,0025 |
| 537,90607 | 0,00271 | 0,00267 | 0,00282 | 0,00365 | 0,00245 |
| 537,94325 | 0,00265 | 0,0026 | 0,00275 | 0,00365 | 0,0024 |
| 537,98043 | 0,00259 | 0,00252 | 0,00268 | 0,00364 | 0,00235 |
| 538,01761 | 0,00252 | 0,00244 | 0,00261 | 0,00363 | 0,00231 |
| 538,05479 | 0,00245 | 0,00236 | 0,00255 | 0,00361 | 0,00227 |
| 538,09198 | 0,00238 | 0,00227 | 0,0025 | 0,00358 | 0,00224 |
| 538,12916 | 0,00231 | 0,00218 | 0,00245 | 0,00355 | 0,00221 |
| 538,16634 | 0,00225 | 0,0021 | 0,00241 | 0,00351 | 0,00218 |
| 538,20352 | 0,00219 | 0,00202 | 0,00238 | 0,00347 | 0,00215 |
| 538,2407 | 0,00213 | 0,00194 | 0,00236 | 0,00342 | 0,00213 |
| 538,27789 | 0,00209 | 0,00187 | 0,00235 | 0,00338 | 0,00212 |
| 538,31507 | 0,00204 | 0,00182 | 0,00235 | 0,00333 | 0,00211 |
| 538,35225 | 0,00201 | 0,00177 | 0,00236 | 0,00329 | 0,0021 |
| 538,38943 | 0,00199 | 0,00174 | 0,00238 | 0,00325 | 0,0021 |
| 538,42661 | 0,00197 | 0,00172 | 0,00241 | 0,00322 | 0,0021 |
| 538,4638 | 0,00197 | 0,00171 | 0,00244 | 0,00319 | 0,00211 |
| 538,50098 | 0,00197 | 0,00171 | 0,00249 | 0,00316 | 0,00212 |
| 538,53816 | 0,00198 | 0,00172 | 0,00253 | 0,00313 | 0,00213 |
| 538,57534 | 0,002 | 0,00174 | 0,00258 | 0,00311 | 0,00214 |
| 538,61252 | 0,00203 | 0,00176 | 0,00263 | 0,00308 | 0,00215 |
| 538,64971 | 0,00207 | 0,00178 | 0,00268 | 0,00306 | 0,00215 |
| 538,68689 | 0,0021 | 0,00181 | 0,00272 | 0,00302 | 0,00214 |
| 538,72407 | 0,00214 | 0,00182 | 0,00276 | 0,00298 | 0,00213 |
| 538,76125 | 0,00217 | 0,00183 | 0,00278 | 0,00293 | 0,0021 |
| 538,79843 | 0,0022 | 0,00183 | 0,00279 | 0,00286 | 0,00206 |
| 538,83562 | 0,00222 | 0,00181 | 0,00278 | 0,00279 | 0,00201 |
| 538,8728 | 0,00223 | 0,00179 | 0,00276 | 0,00269 | 0,00195 |
| 538,90998 | 0,00222 | 0,00175 | 0,00272 | 0,00259 | 0,00188 |
| 538,94716 | 0,0022 | 0,0017 | 0,00267 | 0,00248 | 0,0018 |
| 538,98434 | 0,00217 | 0,00164 | 0,0026 | 0,00236 | 0,00171 |
| 539,02153 | 0,00211 | 0,00158 | 0,00252 | 0,00223 | 0,00161 |
| 539,05871 | 0,00205 | 0,0015 | 0,00242 | 0,0021 | 0,00152 |
| 539,09589 | 0,00197 | 0,00142 | 0,00232 | 0,00198 | 0,00143 |
| 539,13307 | 0,00187 | 0,00134 | 0,00221 | 0,00186 | 0,00134 |
| 539,17025 | 0,00177 | 0,00126 | 0,0021 | 0,00176 | 0,00126 |
| 539,20744 | 0,00166 | 0,00118 | 0,00199 | 0,00167 | 0,00119 |
| 539,24462 | 0,00155 | 0,0011 | 0,00188 | 0,00159 | 0,00112 |
| 539,2818 | 0,00144 | 0,00103 | 0,00178 | 0,00153 | 0,00107 |
| 539,31898 | 0,00134 | 0,00096 | 0,00169 | 0,00149 | 0,00103 |
| 539,35616 | 0,00124 | 9e-04 | 0,00161 | 0,00147 | 0,00101 |
| 539,39335 | 0,00115 | 0,00085 | 0,00155 | 0,00146 | 0,00099 |
| 539,43053 | 0,00107 | 0,00081 | 0,0015 | 0,00146 | 0,00098 |
| 539,46771 | 0,001 | 0,00077 | 0,00145 | 0,00147 | 0,00098 |
| 539,50489 | 0,00094 | 0,00074 | 0,00142 | 0,0015 | 0,00099 |
| 539,54207 | 9e-04 | 0,00072 | 0,00141 | 0,00152 | 0,001 |
| 539,57926 | 0,00087 | 7e-04 | 0,0014 | 0,00154 | 0,00101 |
| 539,61644 | 0,00085 | 0,00068 | 0,00139 | 0,00156 | 0,00102 |
| 539,65362 | 0,00085 | 0,00068 | 0,00139 | 0,00157 | 0,00103 |
| 539,6908 | 0,00086 | 0,00067 | 0,0014 | 0,00158 | 0,00104 |
| 539,72798 | 0,00088 | 0,00067 | 0,0014 | 0,00157 | 0,00104 |
| 539,76517 | 9e-04 | 0,00067 | 0,0014 | 0,00155 | 0,00103 |
| 539,80235 | 0,00094 | 0,00067 | 0,0014 | 0,00152 | 0,00102 |
| 539,83953 | 0,00097 | 0,00067 | 0,00139 | 0,00148 | 0,001 |
| 539,87671 | 0,00102 | 0,00066 | 0,00138 | 0,00143 | 0,00098 |
| 539,91389 | 0,00106 | 0,00066 | 0,00135 | 0,00138 | 0,00094 |
| 539,95108 | 0,0011 | 0,00065 | 0,00132 | 0,00132 | 0,00091 |
| 539,98826 | 0,00114 | 0,00064 | 0,00128 | 0,00125 | 0,00087 |
| 540,02544 | 0,00117 | 0,00063 | 0,00123 | 0,00118 | 0,00082 |
| 540,06262 | 0,0012 | 0,00062 | 0,00118 | 0,00112 | 0,00078 |
| 540,0998 | 0,00121 | 6e-04 | 0,00111 | 0,00106 | 0,00073 |
| 540,13699 | 0,00122 | 0,00058 | 0,00105 | 0,001 | 0,00069 |
| 540,17417 | 0,00121 | 0,00056 | 0,00098 | 0,00095 | 0,00064 |
| 540,21135 | 0,00119 | 0,00055 | 9e-04 | 0,00091 | 0,00061 |
| 540,24853 | 0,00116 | 0,00053 | 0,00083 | 0,00088 | 0,00057 |
| 540,28571 | 0,00111 | 0,00051 | 0,00076 | 0,00086 | 0,00054 |
| 540,3229 | 0,00105 | 5e-04 | 0,00069 | 0,00084 | 0,00052 |
| 540,36008 | 0,00099 | 0,00048 | 0,00062 | 0,00083 | 5e-04 |
| 540,39726 | 0,00091 | 0,00047 | 0,00056 | 0,00083 | 0,00049 |
| 540,43444 | 0,00083 | 0,00047 | 0,00051 | 0,00084 | 0,00048 |
| 540,47162 | 0,00075 | 0,00046 | 0,00046 | 0,00084 | 0,00047 |
| 540,50881 | 0,00067 | 0,00046 | 0,00042 | 0,00085 | 0,00047 |
| 540,54599 | 0,00058 | 0,00047 | 0,00039 | 0,00086 | 0,00047 |
| 540,58317 | 5e-04 | 0,00047 | 0,00037 | 0,00087 | 0,00047 |
| 540,62035 | 0,00043 | 0,00048 | 0,00035 | 0,00088 | 0,00046 |
| 540,65753 | 0,00036 | 0,00048 | 0,00034 | 0,00088 | 0,00046 |
| 540,69472 | 3e-04 | 0,00049 | 0,00034 | 0,00087 | 0,00045 |
| 540,7319 | 0,00024 | 0,00049 | 0,00034 | 0,00085 | 0,00044 |
| 540,76908 | 2e-04 | 5e-04 | 0,00035 | 0,00083 | 0,00042 |
| 540,80626 | 0,00016 | 0,00049 | 0,00036 | 8e-04 | 0,00041 |
| 540,84344 | 0,00013 | 0,00049 | 0,00037 | 0,00076 | 0,00038 |
| 540,88063 | 1e-04 | 0,00048 | 0,00039 | 0,00072 | 0,00036 |
| 540,91781 | 8e-05 | 0,00047 | 4e-04 | 0,00067 | 0,00033 |
| 540,95499 | 7e-05 | 0,00045 | 0,00042 | 0,00061 | 3e-04 |
| 540,99217 | 6e-05 | 0,00043 | 0,00043 | 0,00055 | 0,00027 |
| 541,02935 | 6e-05 | 4e-04 | 0,00044 | 0,00049 | 0,00024 |
| 541,06654 | 6e-05 | 0,00037 | 0,00045 | 0,00043 | 0,00021 |
| 541,10372 | 6e-05 | 0,00034 | 0,00046 | 0,00038 | 0,00018 |
| 541,1409 | 7e-05 | 0,00031 | 0,00046 | 0,00032 | 0,00015 |
| 541,17808 | 7e-05 | 0,00028 | 0,00046 | 0,00027 | 0,00013 |
| 541,21526 | 8e-05 | 0,00024 | 0,00045 | 0,00022 | 1e-04 |
| 541,25245 | 9e-05 | 0,00021 | 0,00044 | 0,00018 | 8e-05 |
| 541,28963 | 1e-04 | 0,00018 | 0,00042 | 0,00015 | 7e-05 |
| 541,32681 | 0,00011 | 0,00015 | 4e-04 | 0,00012 | 5e-05 |
| 541,36399 | 0,00011 | 0,00013 | 0,00038 | 9e-05 | 4e-05 |
| 541,40117 | 0,00012 | 0,00011 | 0,00035 | 7e-05 | 3e-05 |
| 541,43836 | 0,00012 | 9e-05 | 0,00033 | 5e-05 | 2e-05 |
| 541,47554 | 0,00013 | 7e-05 | 3e-04 | 4e-05 | 2e-05 |
| 541,51272 | 0,00013 | 5e-05 | 0,00027 | 3e-05 | 1e-05 |
| 541,5499 | 0,00013 | 4e-05 | 0,00024 | 2e-05 | 1e-05 |
| 541,58708 | 0,00012 | 3e-05 | 0,00021 | 1e-05 | 1e-05 |
| 541,62427 | 0,00012 | 2e-05 | 0,00018 | 1e-05 | 0 |
| 541,66145 | 0,00011 | 2e-05 | 0,00016 | 1e-05 | 0 |
| 541,69863 | 0,00011 | 1e-05 | 0,00013 | 0 | 0 |
| 541,73581 | 1e-04 | 1e-05 | 0,00011 | 0 | 0 |
| 541,77299 | 9e-05 | 1e-05 | 9e-05 | 0 | 0 |
| 541,81018 | 8e-05 | 0 | 7e-05 | 0 | 0 |
| 541,84736 | 7e-05 | 0 | 6e-05 | 0 | 0 |
| 541,88454 | 6e-05 | 0 | 5e-05 | 0 | 0 |
| 541,92172 | 5e-05 | 0 | 4e-05 | 0 | 0 |
| 541,9589 | 4e-05 | 0 | 3e-05 | 0 | 0 |
| 541,99609 | 3e-05 | 0 | 2e-05 | 0 | 0 |
| 542,03327 | 3e-05 | 0 | 2e-05 | 0 | 0 |
| 542,07045 | 2e-05 | 0 | 1e-05 | 0 | 0 |
| 542,10763 | 2e-05 | 0 | 1e-05 | 0 | 0 |
| 542,14481 | 1e-05 | 0 | 1e-05 | 0 | 0 |
| 542,182 | 1e-05 | 0 | 0 | 0 | 0 |
| 542,21918 | 1e-05 | 0 | 0 | 0 | 0 |
| 542,25636 | 1e-05 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00109 | 0,00098 | 0,00072 | 0,00021 | 2e-04 |
| 524,03718 | 0,00116 | 0,00097 | 0,00072 | 0,00024 | 0,00022 |
| 524,07436 | 0,00122 | 0,00096 | 0,00071 | 0,00027 | 0,00025 |
| 524,11155 | 0,00127 | 0,00094 | 7e-04 | 0,00031 | 0,00027 |
| 524,14873 | 0,00132 | 0,00092 | 0,00069 | 0,00034 | 0,00029 |
| 524,18591 | 0,00135 | 9e-04 | 0,00067 | 0,00037 | 3e-04 |
| 524,22309 | 0,00138 | 0,00088 | 0,00066 | 4e-04 | 0,00031 |
| 524,26027 | 0,00139 | 0,00086 | 0,00065 | 0,00043 | 0,00031 |
| 524,29746 | 0,0014 | 0,00084 | 0,00063 | 0,00046 | 0,00031 |
| 524,33464 | 0,00139 | 0,00083 | 0,00062 | 0,00048 | 0,00031 |
| 524,37182 | 0,00138 | 0,00083 | 0,00062 | 5e-04 | 3e-04 |
| 524,409 | 0,00137 | 0,00084 | 0,00062 | 0,00051 | 0,00029 |
| 524,44618 | 0,00135 | 0,00085 | 0,00063 | 0,00053 | 0,00027 |
| 524,48337 | 0,00134 | 0,00088 | 0,00065 | 0,00054 | 0,00026 |
| 524,52055 | 0,00133 | 0,00093 | 0,00067 | 0,00055 | 0,00025 |
| 524,55773 | 0,00133 | 0,00098 | 0,00071 | 0,00057 | 0,00025 |
| 524,59491 | 0,00133 | 0,00104 | 0,00075 | 0,00059 | 0,00024 |
| 524,63209 | 0,00134 | 0,00111 | 0,00079 | 0,00061 | 0,00025 |
| 524,66928 | 0,00137 | 0,00119 | 0,00085 | 0,00064 | 0,00026 |
| 524,70646 | 0,0014 | 0,00127 | 9e-04 | 0,00067 | 0,00028 |
| 524,74364 | 0,00144 | 0,00135 | 0,00096 | 7e-04 | 0,00031 |
| 524,78082 | 0,00148 | 0,00144 | 0,00103 | 0,00074 | 0,00034 |
| 524,818 | 0,00154 | 0,00153 | 0,00109 | 0,00077 | 0,00038 |
| 524,85519 | 0,0016 | 0,00162 | 0,00115 | 0,00081 | 0,00041 |
| 524,89237 | 0,00167 | 0,0017 | 0,00121 | 0,00083 | 0,00045 |
| 524,92955 | 0,00174 | 0,00178 | 0,00127 | 0,00085 | 0,00048 |
| 524,96673 | 0,00181 | 0,00186 | 0,00133 | 0,00085 | 5e-04 |
| 525,00391 | 0,00189 | 0,00194 | 0,00139 | 0,00084 | 0,00052 |
| 525,0411 | 0,00196 | 0,00201 | 0,00144 | 0,00082 | 0,00053 |
| 525,07828 | 0,00203 | 0,00208 | 0,0015 | 0,00079 | 0,00052 |
| 525,11546 | 0,00211 | 0,00215 | 0,00155 | 0,00076 | 0,00051 |
| 525,15264 | 0,00218 | 0,00221 | 0,00161 | 0,00071 | 0,00049 |
| 525,18982 | 0,00226 | 0,00227 | 0,00166 | 0,00067 | 0,00047 |
| 525,22701 | 0,00235 | 0,00233 | 0,00172 | 0,00063 | 0,00044 |
| 525,26419 | 0,00246 | 0,00239 | 0,00179 | 0,00059 | 0,00041 |
| 525,30137 | 0,00259 | 0,00247 | 0,00186 | 0,00057 | 0,00039 |
| 525,33855 | 0,00275 | 0,00255 | 0,00196 | 0,00057 | 0,00038 |
| 525,37573 | 0,00297 | 0,00266 | 0,00209 | 0,00058 | 0,00038 |
| 525,41292 | 0,00324 | 0,0028 | 0,00225 | 0,00063 | 4e-04 |
| 525,4501 | 0,00359 | 0,00298 | 0,00246 | 0,00071 | 0,00045 |
| 525,48728 | 0,00404 | 0,00322 | 0,00274 | 0,00083 | 0,00054 |
| 525,52446 | 0,00461 | 0,00353 | 0,00308 | 0,00101 | 0,00067 |
| 525,56164 | 0,00532 | 0,00393 | 0,00353 | 0,00125 | 0,00088 |
| 525,59883 | 0,00616 | 0,00443 | 0,00408 | 0,00158 | 0,00116 |
| 525,63601 | 0,00716 | 0,00505 | 0,00476 | 0,002 | 0,00155 |
| 525,67319 | 0,00831 | 0,00578 | 0,00556 | 0,00255 | 0,00206 |
| 525,71037 | 0,0096 | 0,00662 | 0,00648 | 0,00324 | 0,00272 |
| 525,74755 | 0,01103 | 0,00759 | 0,00754 | 0,00408 | 0,00354 |
| 525,78474 | 0,01258 | 0,00867 | 0,00871 | 0,00511 | 0,00456 |
| 525,82192 | 0,01421 | 0,00985 | 0,00999 | 0,00633 | 0,00578 |
| 525,8591 | 0,0159 | 0,01111 | 0,01135 | 0,00775 | 0,00723 |
| 525,89628 | 0,0176 | 0,01243 | 0,01277 | 0,00933 | 0,00887 |
| 525,93346 | 0,01927 | 0,01379 | 0,01422 | 0,01104 | 0,01067 |
| 525,97065 | 0,02086 | 0,01515 | 0,01567 | 0,01284 | 0,0126 |
| 526,00783 | 0,02234 | 0,01648 | 0,01707 | 0,01467 | 0,0146 |
| 526,04501 | 0,02369 | 0,01776 | 0,01839 | 0,01646 | 0,01659 |
| 526,08219 | 0,02489 | 0,01897 | 0,01962 | 0,01813 | 0,01852 |
| 526,11937 | 0,02591 | 0,0201 | 0,02073 | 0,01963 | 0,0203 |
| 526,15656 | 0,02677 | 0,02113 | 0,0217 | 0,02087 | 0,02185 |
| 526,19374 | 0,02747 | 0,02207 | 0,02254 | 0,02182 | 0,02313 |
| 526,23092 | 0,02803 | 0,02291 | 0,02323 | 0,02241 | 0,02407 |
| 526,2681 | 0,02847 | 0,02366 | 0,02381 | 0,02264 | 0,02462 |
| 526,30528 | 0,02883 | 0,02433 | 0,02426 | 0,02254 | 0,02481 |
| 526,34247 | 0,02914 | 0,02494 | 0,02462 | 0,02216 | 0,02469 |
| 526,37965 | 0,02943 | 0,02551 | 0,02491 | 0,02155 | 0,0243 |
| 526,41683 | 0,02972 | 0,02605 | 0,02517 | 0,02077 | 0,0237 |
| 526,45401 | 0,03003 | 0,02657 | 0,02539 | 0,0199 | 0,02298 |
| 526,49119 | 0,03036 | 0,02708 | 0,02561 | 0,01903 | 0,02222 |
| 526,52838 | 0,03071 | 0,02759 | 0,02583 | 0,01822 | 0,02149 |
| 526,56556 | 0,03109 | 0,0281 | 0,02606 | 0,01755 | 0,02087 |
| 526,60274 | 0,0315 | 0,02863 | 0,02632 | 0,01707 | 0,02042 |
| 526,63992 | 0,03193 | 0,02919 | 0,0266 | 0,01684 | 0,02019 |
| 526,6771 | 0,03239 | 0,02979 | 0,02692 | 0,01687 | 0,02021 |
| 526,71429 | 0,03289 | 0,03045 | 0,02728 | 0,01715 | 0,02046 |
| 526,75147 | 0,03343 | 0,03119 | 0,0277 | 0,01767 | 0,02092 |
| 526,78865 | 0,03404 | 0,03203 | 0,02819 | 0,01839 | 0,02154 |
| 526,82583 | 0,03475 | 0,03299 | 0,02877 | 0,01927 | 0,02228 |
| 526,86301 | 0,03558 | 0,0341 | 0,02946 | 0,02025 | 0,02309 |
| 526,9002 | 0,03657 | 0,03537 | 0,03028 | 0,02128 | 0,02389 |
| 526,93738 | 0,03773 | 0,0368 | 0,03124 | 0,02229 | 0,02465 |
| 526,97456 | 0,03911 | 0,03841 | 0,03237 | 0,02324 | 0,02531 |
| 527,01174 | 0,0407 | 0,04021 | 0,03368 | 0,02409 | 0,02584 |
| 527,04892 | 0,0425 | 0,04215 | 0,03519 | 0,02478 | 0,02621 |
| 527,08611 | 0,04448 | 0,04421 | 0,03686 | 0,02534 | 0,02642 |
| 527,12329 | 0,04663 | 0,04636 | 0,0387 | 0,02578 | 0,02649 |
| 527,16047 | 0,0489 | 0,04856 | 0,04067 | 0,02613 | 0,02647 |
| 527,19765 | 0,05125 | 0,05077 | 0,04276 | 0,02646 | 0,02642 |
| 527,23483 | 0,05364 | 0,05295 | 0,04495 | 0,02682 | 0,02641 |
| 527,27202 | 0,05604 | 0,05508 | 0,0472 | 0,02729 | 0,0265 |
| 527,3092 | 0,05839 | 0,05712 | 0,0495 | 0,02795 | 0,02679 |
| 527,34638 | 0,06066 | 0,05907 | 0,05182 | 0,02886 | 0,02733 |
| 527,38356 | 0,06283 | 0,06091 | 0,05414 | 0,03008 | 0,0282 |
| 527,42074 | 0,06488 | 0,06263 | 0,05645 | 0,03166 | 0,02944 |
| 527,45793 | 0,06681 | 0,06426 | 0,05873 | 0,03363 | 0,03109 |
| 527,49511 | 0,0686 | 0,06581 | 0,06096 | 0,03593 | 0,03314 |
| 527,53229 | 0,07025 | 0,06726 | 0,06313 | 0,03852 | 0,03555 |
| 527,56947 | 0,07176 | 0,06864 | 0,06523 | 0,04132 | 0,03824 |
| 527,60665 | 0,07312 | 0,06994 | 0,06722 | 0,04426 | 0,04114 |
| 527,64384 | 0,07432 | 0,07115 | 0,0691 | 0,04725 | 0,04419 |
| 527,68102 | 0,07536 | 0,07227 | 0,07083 | 0,05022 | 0,04729 |
| 527,7182 | 0,07622 | 0,07328 | 0,07239 | 0,05311 | 0,05039 |
| 527,75538 | 0,0769 | 0,07414 | 0,07374 | 0,05586 | 0,05342 |
| 527,79256 | 0,07741 | 0,07487 | 0,07489 | 0,05848 | 0,05636 |
| 527,82975 | 0,07776 | 0,07545 | 0,07583 | 0,06098 | 0,05921 |
| 527,86693 | 0,07799 | 0,07589 | 0,07657 | 0,0634 | 0,06198 |
| 527,90411 | 0,07811 | 0,0762 | 0,07715 | 0,06584 | 0,06474 |
| 527,94129 | 0,07818 | 0,07641 | 0,0776 | 0,06841 | 0,06758 |
| 527,97847 | 0,07824 | 0,07655 | 0,07796 | 0,0712 | 0,07059 |
| 528,01566 | 0,07836 | 0,07668 | 0,07831 | 0,07432 | 0,07385 |
| 528,05284 | 0,0786 | 0,07683 | 0,07869 | 0,07784 | 0,07746 |
| 528,09002 | 0,07904 | 0,07708 | 0,07917 | 0,08182 | 0,08146 |
| 528,1272 | 0,07972 | 0,07749 | 0,07985 | 0,08628 | 0,0859 |
| 528,16438 | 0,08067 | 0,07811 | 0,08075 | 0,09118 | 0,09076 |
| 528,20157 | 0,08194 | 0,07897 | 0,08192 | 0,09644 | 0,09597 |
| 528,23875 | 0,08353 | 0,08011 | 0,08337 | 0,10192 | 0,10143 |
| 528,27593 | 0,08544 | 0,08155 | 0,08512 | 0,10739 | 0,10694 |
| 528,31311 | 0,08766 | 0,0833 | 0,08717 | 0,11261 | 0,11227 |
| 528,35029 | 0,09019 | 0,08535 | 0,0895 | 0,1173 | 0,11717 |
| 528,38748 | 0,09299 | 0,08771 | 0,09212 | 0,12123 | 0,12141 |
| 528,42466 | 0,09606 | 0,09036 | 0,095 | 0,12419 | 0,12479 |
| 528,46184 | 0,09936 | 0,09333 | 0,09814 | 0,12604 | 0,12716 |
| 528,49902 | 0,10288 | 0,09657 | 0,10155 | 0,12671 | 0,12847 |
| 528,5362 | 0,1066 | 0,10009 | 0,1052 | 0,12625 | 0,12873 |
| 528,57339 | 0,11052 | 0,10388 | 0,10912 | 0,12479 | 0,1281 |
| 528,61057 | 0,11465 | 0,10795 | 0,1133 | 0,12259 | 0,1268 |
| 528,64775 | 0,11899 | 0,11228 | 0,11777 | 0,11998 | 0,12518 |
| 528,68493 | 0,12355 | 0,11689 | 0,12252 | 0,11745 | 0,12372 |
| 528,72211 | 0,12832 | 0,12176 | 0,12757 | 0,11549 | 0,1229 |
| 528,7593 | 0,13328 | 0,12686 | 0,13288 | 0,11453 | 0,12317 |
| 528,79648 | 0,1384 | 0,13216 | 0,13841 | 0,11491 | 0,12489 |
| 528,83366 | 0,14359 | 0,13759 | 0,14409 | 0,11691 | 0,12832 |
| 528,87084 | 0,14875 | 0,14303 | 0,14981 | 0,12064 | 0,13357 |
| 528,90802 | 0,15376 | 0,14836 | 0,15541 | 0,1261 | 0,14061 |
| 528,94521 | 0,15848 | 0,15345 | 0,16075 | 0,13309 | 0,14922 |
| 528,98239 | 0,16277 | 0,15816 | 0,16565 | 0,14129 | 0,15903 |
| 529,01957 | 0,16648 | 0,16234 | 0,16997 | 0,15024 | 0,16952 |
| 529,05675 | 0,16947 | 0,16585 | 0,17354 | 0,15937 | 0,18007 |
| 529,09393 | 0,17161 | 0,16856 | 0,17622 | 0,16795 | 0,18982 |
| 529,13112 | 0,17282 | 0,17038 | 0,17791 | 0,1754 | 0,19813 |
| 529,1683 | 0,17292 | 0,17121 | 0,17852 | 0,18123 | 0,20444 |
| 529,20548 | 0,17201 | 0,17096 | 0,17793 | 0,18509 | 0,20834 |
| 529,24266 | 0,17018 | 0,16978 | 0,17632 | 0,18677 | 0,20959 |
| 529,27984 | 0,16754 | 0,16775 | 0,1738 | 0,18625 | 0,20816 |
| 529,31703 | 0,16424 | 0,16501 | 0,17055 | 0,18364 | 0,20418 |
| 529,35421 | 0,16049 | 0,16171 | 0,16676 | 0,17922 | 0,19799 |
| 529,39139 | 0,15651 | 0,15807 | 0,16268 | 0,17338 | 0,19003 |
| 529,42857 | 0,15255 | 0,15431 | 0,15858 | 0,16659 | 0,18085 |
| 529,46575 | 0,14889 | 0,15066 | 0,15473 | 0,15934 | 0,17104 |
| 529,50294 | 0,1458 | 0,14738 | 0,15142 | 0,15221 | 0,16129 |
| 529,54012 | 0,14365 | 0,14477 | 0,14898 | 0,14565 | 0,15215 |
| 529,5773 | 0,14261 | 0,1431 | 0,14774 | 0,14 | 0,14407 |
| 529,61448 | 0,14288 | 0,14255 | 0,14785 | 0,13555 | 0,1374 |
| 529,65166 | 0,14459 | 0,1433 | 0,14947 | 0,13251 | 0,13237 |
| 529,68885 | 0,14787 | 0,1455 | 0,15273 | 0,13102 | 0,12919 |
| 529,72603 | 0,15277 | 0,14925 | 0,15772 | 0,13122 | 0,12799 |
| 529,76321 | 0,1593 | 0,15464 | 0,16444 | 0,13318 | 0,12885 |
| 529,80039 | 0,16742 | 0,16168 | 0,17286 | 0,13702 | 0,13187 |
| 529,83757 | 0,17703 | 0,17033 | 0,1829 | 0,14282 | 0,13713 |
| 529,87476 | 0,18803 | 0,1805 | 0,19441 | 0,15083 | 0,1448 |
| 529,91194 | 0,20021 | 0,19217 | 0,20725 | 0,16115 | 0,1551 |
| 529,94912 | 0,21316 | 0,20495 | 0,22105 | 0,17373 | 0,16793 |
| 529,9863 | 0,22659 | 0,2185 | 0,23542 | 0,18862 | 0,1833 |
| 530,02348 | 0,24015 | 0,2325 | 0,24998 | 0,20574 | 0,20118 |
| 530,06067 | 0,25347 | 0,24655 | 0,26434 | 0,2249 | 0,22137 |
| 530,09785 | 0,26619 | 0,26027 | 0,27808 | 0,24579 | 0,24357 |
| 530,13503 | 0,27795 | 0,27324 | 0,29083 | 0,26791 | 0,26728 |
| 530,17221 | 0,28841 | 0,28507 | 0,30219 | 0,29062 | 0,29184 |
| 530,20939 | 0,29727 | 0,2954 | 0,31182 | 0,31316 | 0,31644 |
| 530,24658 | 0,30414 | 0,30389 | 0,31945 | 0,33463 | 0,3401 |
| 530,28376 | 0,30885 | 0,31004 | 0,32457 | 0,35386 | 0,36164 |
| 530,32094 | 0,31144 | 0,31394 | 0,32729 | 0,36989 | 0,37981 |
| 530,35812 | 0,31191 | 0,31554 | 0,32764 | 0,38203 | 0,39385 |
| 530,3953 | 0,31033 | 0,31488 | 0,32567 | 0,38974 | 0,40305 |
| 530,43249 | 0,30686 | 0,31207 | 0,32154 | 0,39269 | 0,40699 |
| 530,46967 | 0,30167 | 0,30731 | 0,31545 | 0,39084 | 0,40555 |
| 530,50685 | 0,29501 | 0,30083 | 0,30766 | 0,38443 | 0,3989 |
| 530,54403 | 0,28715 | 0,2929 | 0,29845 | 0,37393 | 0,38751 |
| 530,58121 | 0,27835 | 0,28382 | 0,28813 | 0,36003 | 0,37209 |
| 530,6184 | 0,26885 | 0,27387 | 0,277 | 0,34354 | 0,35355 |
| 530,65558 | 0,25899 | 0,26336 | 0,26536 | 0,32538 | 0,33289 |
| 530,69276 | 0,24898 | 0,25262 | 0,25354 | 0,30643 | 0,31115 |
| 530,72994 | 0,239 | 0,24185 | 0,24175 | 0,28766 | 0,28947 |
| 530,76712 | 0,22919 | 0,23123 | 0,23018 | 0,26971 | 0,26869 |
| 530,80431 | 0,21964 | 0,22087 | 0,21894 | 0,25306 | 0,24942 |
| 530,84149 | 0,21041 | 0,21088 | 0,20813 | 0,23802 | 0,23211 |
| 530,87867 | 0,20157 | 0,20132 | 0,19784 | 0,22478 | 0,21703 |
| 530,91585 | 0,19313 | 0,19224 | 0,18809 | 0,21341 | 0,20431 |
| 530,95303 | 0,18511 | 0,18366 | 0,17894 | 0,2039 | 0,19395 |
| 530,99022 | 0,1776 | 0,17566 | 0,17044 | 0,19618 | 0,18589 |
| 531,0274 | 0,17055 | 0,16825 | 0,16263 | 0,19019 | 0,18 |
| 531,06458 | 0,16401 | 0,16144 | 0,15551 | 0,18582 | 0,17612 |
| 531,10176 | 0,15801 | 0,15529 | 0,14912 | 0,18312 | 0,17422 |
| 531,13894 | 0,15261 | 0,14984 | 0,14351 | 0,18186 | 0,17397 |
| 531,17613 | 0,14786 | 0,14517 | 0,13873 | 0,18187 | 0,17509 |
| 531,21331 | 0,14383 | 0,14134 | 0,13484 | 0,18298 | 0,17732 |
| 531,25049 | 0,14056 | 0,13842 | 0,13189 | 0,18495 | 0,18034 |
| 531,28767 | 0,13812 | 0,13646 | 0,12993 | 0,18747 | 0,1838 |
| 531,32485 | 0,13655 | 0,13552 | 0,12897 | 0,19018 | 0,18728 |
| 531,36204 | 0,13592 | 0,1357 | 0,12911 | 0,19267 | 0,19037 |
| 531,39922 | 0,13612 | 0,13688 | 0,13024 | 0,19451 | 0,19262 |
| 531,4364 | 0,13709 | 0,13896 | 0,13224 | 0,19528 | 0,19364 |
| 531,47358 | 0,13872 | 0,14184 | 0,135 | 0,19463 | 0,19308 |
| 531,51076 | 0,14088 | 0,14535 | 0,13837 | 0,19208 | 0,19051 |
| 531,54795 | 0,14341 | 0,1493 | 0,14215 | 0,18768 | 0,18596 |
| 531,58513 | 0,14611 | 0,15348 | 0,14614 | 0,18147 | 0,17953 |
| 531,62231 | 0,14879 | 0,15763 | 0,15012 | 0,17363 | 0,17141 |
| 531,65949 | 0,15123 | 0,16152 | 0,15382 | 0,16443 | 0,1619 |
| 531,69667 | 0,15317 | 0,16486 | 0,15703 | 0,15424 | 0,15138 |
| 531,73386 | 0,15439 | 0,16731 | 0,15938 | 0,14347 | 0,14026 |
| 531,77104 | 0,15475 | 0,16875 | 0,16077 | 0,13251 | 0,12895 |
| 531,80822 | 0,15414 | 0,16901 | 0,16105 | 0,12176 | 0,11786 |
| 531,8454 | 0,1525 | 0,16802 | 0,16013 | 0,11155 | 0,10731 |
| 531,88258 | 0,1498 | 0,16573 | 0,15798 | 0,10214 | 0,09756 |
| 531,91977 | 0,14608 | 0,16216 | 0,1546 | 0,09381 | 0,0889 |
| 531,95695 | 0,14142 | 0,15739 | 0,15007 | 0,08654 | 0,08132 |
| 531,99413 | 0,13591 | 0,15154 | 0,1445 | 0,08031 | 0,0748 |
| 532,03131 | 0,12973 | 0,14477 | 0,13804 | 0,07509 | 0,0693 |
| 532,06849 | 0,123 | 0,13726 | 0,13086 | 0,07076 | 0,06473 |
| 532,10568 | 0,11599 | 0,12926 | 0,12318 | 0,06724 | 0,061 |
| 532,14286 | 0,10888 | 0,12103 | 0,11527 | 0,06441 | 0,058 |
| 532,18004 | 0,10185 | 0,11278 | 0,10733 | 0,06217 | 0,05564 |
| 532,21722 | 0,09505 | 0,10472 | 0,09953 | 0,06043 | 0,05383 |
| 532,2544 | 0,08862 | 0,09698 | 0,09204 | 0,05912 | 0,05251 |
| 532,29159 | 0,08265 | 0,08973 | 0,08499 | 0,0582 | 0,05162 |
| 532,32877 | 0,07724 | 0,08306 | 0,07847 | 0,05767 | 0,05117 |
| 532,36595 | 0,07244 | 0,07706 | 0,07258 | 0,0575 | 0,05109 |
| 532,40313 | 0,06829 | 0,07178 | 0,06737 | 0,05769 | 0,05136 |
| 532,44031 | 0,06489 | 0,06734 | 0,06294 | 0,05825 | 0,05199 |
| 532,4775 | 0,0622 | 0,06372 | 0,05929 | 0,05921 | 0,05296 |
| 532,51468 | 0,06019 | 0,06091 | 0,0564 | 0,06057 | 0,05427 |
| 532,55186 | 0,05887 | 0,0589 | 0,05428 | 0,06234 | 0,05591 |
| 532,58904 | 0,05825 | 0,0577 | 0,05294 | 0,06448 | 0,05786 |
| 532,62622 | 0,0583 | 0,0573 | 0,05238 | 0,06699 | 0,06011 |
| 532,66341 | 0,05904 | 0,05772 | 0,05261 | 0,0698 | 0,06262 |
| 532,70059 | 0,06046 | 0,05895 | 0,05363 | 0,07287 | 0,06537 |
| 532,73777 | 0,06253 | 0,06096 | 0,05543 | 0,07614 | 0,06833 |
| 532,77495 | 0,06525 | 0,06374 | 0,058 | 0,07951 | 0,07144 |
| 532,81213 | 0,06862 | 0,06732 | 0,06139 | 0,08295 | 0,07469 |
| 532,84932 | 0,07252 | 0,07156 | 0,06545 | 0,08642 | 0,07807 |
| 532,8865 | 0,07686 | 0,07635 | 0,07009 | 0,08989 | 0,08156 |
| 532,92368 | 0,08153 | 0,08157 | 0,07521 | 0,09336 | 0,08517 |
| 532,96086 | 0,08641 | 0,08709 | 0,08067 | 0,09682 | 0,08889 |
| 532,99804 | 0,09136 | 0,09273 | 0,08632 | 0,10026 | 0,09269 |
| 533,03523 | 0,0962 | 0,09832 | 0,09197 | 0,10366 | 0,09655 |
| 533,07241 | 0,10077 | 0,10367 | 0,09744 | 0,10696 | 0,10037 |
| 533,10959 | 0,1049 | 0,10856 | 0,10253 | 0,11005 | 0,10404 |
| 533,14677 | 0,10839 | 0,11277 | 0,10702 | 0,11275 | 0,10734 |
| 533,18395 | 0,11101 | 0,11605 | 0,11064 | 0,11491 | 0,11009 |
| 533,22114 | 0,1127 | 0,1183 | 0,11329 | 0,11633 | 0,11208 |
| 533,25832 | 0,11339 | 0,11943 | 0,11486 | 0,11682 | 0,11309 |
| 533,2955 | 0,11302 | 0,11937 | 0,11527 | 0,11622 | 0,11297 |
| 533,33268 | 0,1116 | 0,1181 | 0,1145 | 0,11441 | 0,11159 |
| 533,36986 | 0,10915 | 0,11565 | 0,11255 | 0,11136 | 0,10891 |
| 533,40705 | 0,10575 | 0,1121 | 0,1095 | 0,10709 | 0,10495 |
| 533,44423 | 0,10152 | 0,10757 | 0,10544 | 0,10172 | 0,09983 |
| 533,48141 | 0,09658 | 0,10221 | 0,10051 | 0,09542 | 0,09373 |
| 533,51859 | 0,09108 | 0,09615 | 0,09484 | 0,08843 | 0,08688 |
| 533,55577 | 0,08521 | 0,08966 | 0,08868 | 0,08107 | 0,07962 |
| 533,59295 | 0,07918 | 0,08296 | 0,08225 | 0,0737 | 0,07229 |
| 533,63014 | 0,07314 | 0,07624 | 0,07574 | 0,06657 | 0,06517 |
| 533,66732 | 0,06724 | 0,06967 | 0,06933 | 0,05993 | 0,05849 |
| 533,7045 | 0,06159 | 0,06341 | 0,06316 | 0,05398 | 0,05245 |
| 533,74168 | 0,05629 | 0,05757 | 0,05736 | 0,04883 | 0,04718 |
| 533,77886 | 0,05143 | 0,05225 | 0,05203 | 0,04457 | 0,04275 |
| 533,81605 | 0,04705 | 0,04751 | 0,04724 | 0,04121 | 0,03917 |
| 533,85323 | 0,04319 | 0,04339 | 0,04303 | 0,03871 | 0,03642 |
| 533,89041 | 0,03991 | 0,03995 | 0,03949 | 0,037 | 0,03441 |
| 533,92759 | 0,03716 | 0,03713 | 0,03655 | 0,03599 | 0,03309 |
| 533,96477 | 0,03491 | 0,03487 | 0,03417 | 0,0355 | 0,03227 |
| 534,00196 | 0,03312 | 0,03311 | 0,03229 | 0,03536 | 0,0318 |
| 534,03914 | 0,03173 | 0,03179 | 0,03085 | 0,0354 | 0,03153 |
| 534,07632 | 0,0307 | 0,03084 | 0,0298 | 0,0355 | 0,03134 |
| 534,1135 | 0,02998 | 0,0302 | 0,02906 | 0,03554 | 0,03111 |
| 534,15068 | 0,0295 | 0,02978 | 0,02856 | 0,0354 | 0,03076 |
| 534,18787 | 0,02922 | 0,02953 | 0,02824 | 0,03502 | 0,03023 |
| 534,22505 | 0,02906 | 0,02939 | 0,02802 | 0,03437 | 0,02946 |
| 534,26223 | 0,02898 | 0,02929 | 0,02785 | 0,03342 | 0,02845 |
| 534,29941 | 0,02891 | 0,02918 | 0,02767 | 0,03219 | 0,02721 |
| 534,33659 | 0,02882 | 0,02902 | 0,02744 | 0,0307 | 0,02577 |
| 534,37378 | 0,02867 | 0,0288 | 0,02713 | 0,02904 | 0,0242 |
| 534,41096 | 0,02844 | 0,02848 | 0,02672 | 0,02729 | 0,02256 |
| 534,44814 | 0,0281 | 0,02807 | 0,0262 | 0,02551 | 0,02092 |
| 534,48532 | 0,02765 | 0,02756 | 0,02557 | 0,02376 | 0,01934 |
| 534,5225 | 0,02709 | 0,02695 | 0,02483 | 0,02211 | 0,01786 |
| 534,55969 | 0,02641 | 0,02624 | 0,02399 | 0,02059 | 0,01653 |
| 534,59687 | 0,02562 | 0,02545 | 0,02306 | 0,01923 | 0,01535 |
| 534,63405 | 0,02473 | 0,02458 | 0,02207 | 0,01804 | 0,01436 |
| 534,67123 | 0,02377 | 0,02366 | 0,02104 | 0,01703 | 0,01353 |
| 534,70841 | 0,02275 | 0,02271 | 0,01998 | 0,01617 | 0,01286 |
| 534,7456 | 0,0217 | 0,02172 | 0,01891 | 0,01548 | 0,01234 |
| 534,78278 | 0,02063 | 0,02073 | 0,01785 | 0,0149 | 0,01193 |
| 534,81996 | 0,01955 | 0,01973 | 0,01681 | 0,01442 | 0,01159 |
| 534,85714 | 0,0185 | 0,01874 | 0,01581 | 0,014 | 0,01132 |
| 534,89432 | 0,01747 | 0,01778 | 0,01486 | 0,01365 | 0,01108 |
| 534,93151 | 0,01649 | 0,01684 | 0,01395 | 0,01333 | 0,01086 |
| 534,96869 | 0,01556 | 0,01594 | 0,01311 | 0,01303 | 0,01064 |
| 535,00587 | 0,01471 | 0,01509 | 0,01234 | 0,01275 | 0,01042 |
| 535,04305 | 0,01392 | 0,01429 | 0,01163 | 0,01247 | 0,01019 |
| 535,08023 | 0,0132 | 0,01353 | 0,01099 | 0,01219 | 0,00996 |
| 535,11742 | 0,01255 | 0,01283 | 0,01042 | 0,01191 | 0,00971 |
| 535,1546 | 0,01197 | 0,01218 | 0,0099 | 0,01161 | 0,00946 |
| 535,19178 | 0,01146 | 0,01158 | 0,00945 | 0,0113 | 0,00921 |
| 535,22896 | 0,011 | 0,01103 | 0,00906 | 0,01098 | 0,00895 |
| 535,26614 | 0,01061 | 0,01053 | 0,00872 | 0,01065 | 0,00871 |
| 535,30333 | 0,01026 | 0,01008 | 0,00843 | 0,01031 | 0,00847 |
| 535,34051 | 0,00997 | 0,00967 | 0,0082 | 0,00997 | 0,00825 |
| 535,37769 | 0,00972 | 0,00931 | 0,00802 | 0,00962 | 0,00804 |
| 535,41487 | 0,00951 | 0,009 | 0,00787 | 0,00928 | 0,00786 |
| 535,45205 | 0,00933 | 0,00871 | 0,00777 | 0,00894 | 0,0077 |
| 535,48924 | 0,00918 | 0,00847 | 0,00771 | 0,00862 | 0,00757 |
| 535,52642 | 0,00906 | 0,00826 | 0,00768 | 0,00831 | 0,00746 |
| 535,5636 | 0,00896 | 0,00809 | 0,00768 | 0,00801 | 0,00739 |
| 535,60078 | 0,00888 | 0,00795 | 0,00771 | 0,00774 | 0,00734 |
| 535,63796 | 0,00882 | 0,00784 | 0,00777 | 0,00748 | 0,00733 |
| 535,67515 | 0,00878 | 0,00775 | 0,00786 | 0,00726 | 0,00735 |
| 535,71233 | 0,00874 | 0,0077 | 0,00797 | 0,00706 | 0,00739 |
| 535,74951 | 0,00871 | 0,00766 | 0,00809 | 0,00689 | 0,00746 |
| 535,78669 | 0,00867 | 0,00763 | 0,00824 | 0,00676 | 0,00755 |
| 535,82387 | 0,00863 | 0,00762 | 0,00839 | 0,00666 | 0,00766 |
| 535,86106 | 0,00857 | 0,0076 | 0,00855 | 0,00661 | 0,00778 |
| 535,89824 | 0,0085 | 0,00759 | 0,00872 | 0,0066 | 0,0079 |
| 535,93542 | 0,0084 | 0,00756 | 0,00888 | 0,00664 | 0,00803 |
| 535,9726 | 0,00827 | 0,00753 | 0,00905 | 0,00671 | 0,00814 |
| 536,00978 | 0,00811 | 0,00747 | 0,0092 | 0,00683 | 0,00823 |
| 536,04697 | 0,00792 | 0,0074 | 0,00935 | 0,00697 | 0,0083 |
| 536,08415 | 0,00769 | 0,00731 | 0,00947 | 0,00713 | 0,00833 |
| 536,12133 | 0,00743 | 0,00719 | 0,00957 | 0,0073 | 0,00832 |
| 536,15851 | 0,00714 | 0,00706 | 0,00963 | 0,00746 | 0,00827 |
| 536,19569 | 0,00682 | 0,0069 | 0,00967 | 0,0076 | 0,00818 |
| 536,23288 | 0,00648 | 0,00673 | 0,00966 | 0,0077 | 0,00804 |
| 536,27006 | 0,00613 | 0,00655 | 0,00962 | 0,00776 | 0,00786 |
| 536,30724 | 0,00576 | 0,00635 | 0,00952 | 0,00777 | 0,00764 |
| 536,34442 | 0,0054 | 0,00615 | 0,00939 | 0,0077 | 0,00739 |
| 536,3816 | 0,00505 | 0,00594 | 0,0092 | 0,00757 | 0,00713 |
| 536,41879 | 0,0047 | 0,00573 | 0,00897 | 0,00736 | 0,00685 |
| 536,45597 | 0,00438 | 0,00552 | 0,00869 | 0,0071 | 0,00657 |
| 536,49315 | 0,00408 | 0,00532 | 0,00838 | 0,00678 | 0,00629 |
| 536,53033 | 0,0038 | 0,00511 | 0,00805 | 0,00642 | 0,00603 |
| 536,56751 | 0,00356 | 0,00491 | 0,00769 | 0,00603 | 0,00579 |
| 536,6047 | 0,00335 | 0,00472 | 0,00731 | 0,00562 | 0,00556 |
| 536,64188 | 0,00317 | 0,00453 | 0,00692 | 0,0052 | 0,00536 |
| 536,67906 | 0,00302 | 0,00435 | 0,00653 | 0,00479 | 0,00517 |
| 536,71624 | 0,0029 | 0,00417 | 0,00615 | 0,0044 | 0,00499 |
| 536,75342 | 0,00281 | 0,004 | 0,00577 | 0,00403 | 0,00483 |
| 536,79061 | 0,00274 | 0,00384 | 0,00542 | 0,0037 | 0,00468 |
| 536,82779 | 0,00271 | 0,0037 | 0,00508 | 0,00342 | 0,00453 |
| 536,86497 | 0,00269 | 0,00356 | 0,00478 | 0,00317 | 0,00439 |
| 536,90215 | 0,00269 | 0,00344 | 0,0045 | 0,00296 | 0,00425 |
| 536,93933 | 0,0027 | 0,00334 | 0,00425 | 0,00279 | 0,00411 |
| 536,97652 | 0,00273 | 0,00325 | 0,00405 | 0,00265 | 0,00397 |
| 537,0137 | 0,00277 | 0,00319 | 0,00388 | 0,00254 | 0,00384 |
| 537,05088 | 0,00282 | 0,00315 | 0,00375 | 0,00246 | 0,00371 |
| 537,08806 | 0,00288 | 0,00314 | 0,00365 | 0,00241 | 0,0036 |
| 537,12524 | 0,00295 | 0,00314 | 0,0036 | 0,00237 | 0,0035 |
| 537,16243 | 0,00303 | 0,00318 | 0,00359 | 0,00235 | 0,00342 |
| 537,19961 | 0,00312 | 0,00323 | 0,0036 | 0,00235 | 0,00335 |
| 537,23679 | 0,00322 | 0,00329 | 0,00365 | 0,00236 | 0,00329 |
| 537,27397 | 0,00333 | 0,00337 | 0,00372 | 0,00238 | 0,00323 |
| 537,31115 | 0,00344 | 0,00346 | 0,0038 | 0,0024 | 0,00318 |
| 537,34834 | 0,00356 | 0,00356 | 0,0039 | 0,00244 | 0,00312 |
| 537,38552 | 0,00367 | 0,00365 | 0,004 | 0,00247 | 0,00306 |
| 537,4227 | 0,00378 | 0,00374 | 0,00411 | 0,00251 | 0,00299 |
| 537,45988 | 0,00388 | 0,00383 | 0,00421 | 0,00256 | 0,00292 |
| 537,49706 | 0,00397 | 0,0039 | 0,0043 | 0,00259 | 0,00284 |
| 537,53425 | 0,00404 | 0,00397 | 0,00437 | 0,00263 | 0,00276 |
| 537,57143 | 0,00408 | 0,00401 | 0,00443 | 0,00266 | 0,00269 |
| 537,60861 | 0,0041 | 0,00405 | 0,00447 | 0,00268 | 0,00262 |
| 537,64579 | 0,00409 | 0,00406 | 0,0045 | 0,0027 | 0,00258 |
| 537,68297 | 0,00406 | 0,00405 | 0,0045 | 0,00271 | 0,00256 |
| 537,72016 | 0,00399 | 0,00403 | 0,00449 | 0,00272 | 0,00257 |
| 537,75734 | 0,00389 | 0,00399 | 0,00445 | 0,00273 | 0,00261 |
| 537,79452 | 0,00377 | 0,00392 | 0,0044 | 0,00274 | 0,00267 |
| 537,8317 | 0,00362 | 0,00384 | 0,00433 | 0,00275 | 0,00275 |
| 537,86888 | 0,00346 | 0,00374 | 0,00424 | 0,00278 | 0,00285 |
| 537,90607 | 0,00328 | 0,00363 | 0,00413 | 0,00282 | 0,00296 |
| 537,94325 | 0,00309 | 0,0035 | 0,004 | 0,00288 | 0,00307 |
| 537,98043 | 0,0029 | 0,00337 | 0,00386 | 0,00296 | 0,00318 |
| 538,01761 | 0,00272 | 0,00322 | 0,00372 | 0,00306 | 0,00327 |
| 538,05479 | 0,00254 | 0,00308 | 0,00356 | 0,00317 | 0,00336 |
| 538,09198 | 0,00237 | 0,00294 | 0,00341 | 0,0033 | 0,00343 |
| 538,12916 | 0,00223 | 0,00281 | 0,00325 | 0,00342 | 0,00348 |
| 538,16634 | 0,0021 | 0,00268 | 0,00311 | 0,00355 | 0,00353 |
| 538,20352 | 0,002 | 0,00257 | 0,00298 | 0,00367 | 0,00356 |
| 538,2407 | 0,00192 | 0,00248 | 0,00287 | 0,00378 | 0,00359 |
| 538,27789 | 0,00187 | 0,0024 | 0,00279 | 0,00386 | 0,00362 |
| 538,31507 | 0,00185 | 0,00235 | 0,00274 | 0,00392 | 0,00364 |
| 538,35225 | 0,00185 | 0,00231 | 0,00272 | 0,00396 | 0,00367 |
| 538,38943 | 0,00188 | 0,00229 | 0,00273 | 0,00397 | 0,00369 |
| 538,42661 | 0,00194 | 0,00229 | 0,00278 | 0,00396 | 0,00372 |
| 538,4638 | 0,00201 | 0,0023 | 0,00286 | 0,00393 | 0,00375 |
| 538,50098 | 0,0021 | 0,00233 | 0,00296 | 0,00388 | 0,00378 |
| 538,53816 | 0,00221 | 0,00237 | 0,00309 | 0,00383 | 0,00381 |
| 538,57534 | 0,00233 | 0,00241 | 0,00322 | 0,00377 | 0,00384 |
| 538,61252 | 0,00244 | 0,00246 | 0,00336 | 0,00371 | 0,00386 |
| 538,64971 | 0,00255 | 0,00251 | 0,0035 | 0,00364 | 0,00387 |
| 538,68689 | 0,00266 | 0,00255 | 0,00361 | 0,00357 | 0,00387 |
| 538,72407 | 0,00274 | 0,00259 | 0,00371 | 0,0035 | 0,00386 |
| 538,76125 | 0,00281 | 0,00262 | 0,00377 | 0,00342 | 0,00383 |
| 538,79843 | 0,00285 | 0,00264 | 0,00379 | 0,00334 | 0,00378 |
| 538,83562 | 0,00287 | 0,00264 | 0,00378 | 0,00324 | 0,00371 |
| 538,8728 | 0,00286 | 0,00264 | 0,00372 | 0,00312 | 0,00361 |
| 538,90998 | 0,00281 | 0,00262 | 0,00362 | 0,00299 | 0,00351 |
| 538,94716 | 0,00274 | 0,00259 | 0,00348 | 0,00285 | 0,00338 |
| 538,98434 | 0,00265 | 0,00254 | 0,00331 | 0,0027 | 0,00325 |
| 539,02153 | 0,00253 | 0,00248 | 0,00311 | 0,00254 | 0,00311 |
| 539,05871 | 0,00239 | 0,00241 | 0,00289 | 0,00237 | 0,00296 |
| 539,09589 | 0,00225 | 0,00233 | 0,00266 | 0,0022 | 0,00282 |
| 539,13307 | 0,00209 | 0,00224 | 0,00243 | 0,00203 | 0,00268 |
| 539,17025 | 0,00194 | 0,00214 | 0,0022 | 0,00187 | 0,00255 |
| 539,20744 | 0,00179 | 0,00203 | 0,00199 | 0,00173 | 0,00243 |
| 539,24462 | 0,00165 | 0,00192 | 0,00179 | 0,0016 | 0,00232 |
| 539,2818 | 0,00152 | 0,00181 | 0,00162 | 0,0015 | 0,00223 |
| 539,31898 | 0,0014 | 0,0017 | 0,00148 | 0,00141 | 0,00214 |
| 539,35616 | 0,00131 | 0,00158 | 0,00138 | 0,00136 | 0,00207 |
| 539,39335 | 0,00123 | 0,00148 | 0,0013 | 0,00132 | 0,002 |
| 539,43053 | 0,00118 | 0,00137 | 0,00126 | 0,00131 | 0,00195 |
| 539,46771 | 0,00114 | 0,00128 | 0,00125 | 0,00132 | 0,0019 |
| 539,50489 | 0,00112 | 0,0012 | 0,00126 | 0,00133 | 0,00185 |
| 539,54207 | 0,00112 | 0,00113 | 0,0013 | 0,00136 | 0,0018 |
| 539,57926 | 0,00113 | 0,00107 | 0,00136 | 0,00139 | 0,00175 |
| 539,61644 | 0,00115 | 0,00102 | 0,00143 | 0,00141 | 0,0017 |
| 539,65362 | 0,00118 | 0,00098 | 0,00152 | 0,00143 | 0,00164 |
| 539,6908 | 0,00121 | 0,00096 | 0,00161 | 0,00143 | 0,00158 |
| 539,72798 | 0,00124 | 0,00095 | 0,00171 | 0,00141 | 0,00152 |
| 539,76517 | 0,00127 | 0,00095 | 0,00181 | 0,00138 | 0,00145 |
| 539,80235 | 0,0013 | 0,00095 | 0,0019 | 0,00132 | 0,00137 |
| 539,83953 | 0,00132 | 0,00097 | 0,00198 | 0,00125 | 0,00129 |
| 539,87671 | 0,00133 | 0,00098 | 0,00205 | 0,00117 | 0,00121 |
| 539,91389 | 0,00133 | 0,001 | 0,0021 | 0,00107 | 0,00112 |
| 539,95108 | 0,00132 | 0,00101 | 0,00214 | 0,00096 | 0,00104 |
| 539,98826 | 0,0013 | 0,00102 | 0,00216 | 0,00085 | 0,00095 |
| 540,02544 | 0,00127 | 0,00102 | 0,00216 | 0,00075 | 0,00086 |
| 540,06262 | 0,00122 | 0,00101 | 0,00214 | 0,00065 | 0,00078 |
| 540,0998 | 0,00117 | 0,00099 | 0,0021 | 0,00056 | 7e-04 |
| 540,13699 | 0,0011 | 0,00096 | 0,00204 | 0,00048 | 0,00063 |
| 540,17417 | 0,00103 | 0,00092 | 0,00197 | 0,00042 | 0,00057 |
| 540,21135 | 0,00096 | 0,00087 | 0,00188 | 0,00038 | 0,00051 |
| 540,24853 | 0,00088 | 0,00082 | 0,00177 | 0,00035 | 0,00047 |
| 540,28571 | 8e-04 | 0,00075 | 0,00166 | 0,00034 | 0,00045 |
| 540,3229 | 0,00073 | 0,00068 | 0,00154 | 0,00035 | 0,00043 |
| 540,36008 | 0,00065 | 0,00061 | 0,00142 | 0,00036 | 0,00043 |
| 540,39726 | 0,00058 | 0,00054 | 0,0013 | 0,00038 | 0,00045 |
| 540,43444 | 0,00052 | 0,00048 | 0,00118 | 0,00041 | 0,00048 |
| 540,47162 | 0,00046 | 0,00042 | 0,00107 | 0,00044 | 0,00052 |
| 540,50881 | 4e-04 | 0,00037 | 0,00096 | 0,00047 | 0,00056 |
| 540,54599 | 0,00035 | 0,00032 | 0,00086 | 5e-04 | 0,00062 |
| 540,58317 | 0,00031 | 0,00028 | 0,00077 | 0,00051 | 0,00067 |
| 540,62035 | 0,00027 | 0,00026 | 7e-04 | 0,00052 | 0,00072 |
| 540,65753 | 0,00023 | 0,00024 | 0,00063 | 0,00051 | 0,00077 |
| 540,69472 | 2e-04 | 0,00022 | 0,00057 | 5e-04 | 8e-04 |
| 540,7319 | 0,00017 | 0,00022 | 0,00051 | 0,00047 | 0,00083 |
| 540,76908 | 0,00014 | 0,00022 | 0,00047 | 0,00044 | 0,00084 |
| 540,80626 | 0,00012 | 0,00022 | 0,00043 | 4e-04 | 0,00084 |
| 540,84344 | 1e-04 | 0,00023 | 0,00039 | 0,00035 | 0,00083 |
| 540,88063 | 8e-05 | 0,00024 | 0,00035 | 3e-04 | 8e-04 |
| 540,91781 | 6e-05 | 0,00025 | 0,00032 | 0,00026 | 0,00076 |
| 540,95499 | 5e-05 | 0,00025 | 0,00029 | 0,00021 | 0,00072 |
| 540,99217 | 4e-05 | 0,00026 | 0,00026 | 0,00017 | 0,00068 |
| 541,02935 | 3e-05 | 0,00026 | 0,00023 | 0,00014 | 0,00063 |
| 541,06654 | 2e-05 | 0,00026 | 2e-04 | 0,00011 | 0,00059 |
| 541,10372 | 2e-05 | 0,00025 | 0,00017 | 8e-05 | 0,00055 |
| 541,1409 | 1e-05 | 0,00025 | 0,00015 | 6e-05 | 0,00052 |
| 541,17808 | 1e-05 | 0,00024 | 0,00012 | 4e-05 | 5e-04 |
| 541,21526 | 1e-05 | 0,00022 | 1e-04 | 3e-05 | 0,00047 |
| 541,25245 | 0 | 0,00021 | 8e-05 | 2e-05 | 0,00045 |
| 541,28963 | 0 | 0,00019 | 7e-05 | 1e-05 | 0,00044 |
| 541,32681 | 0 | 0,00017 | 5e-05 | 1e-05 | 0,00042 |
| 541,36399 | 0 | 0,00015 | 4e-05 | 1e-05 | 4e-04 |
| 541,40117 | 0 | 0,00013 | 3e-05 | 0 | 0,00037 |
| 541,43836 | 0 | 0,00011 | 2e-05 | 0 | 0,00034 |
| 541,47554 | 0 | 9e-05 | 2e-05 | 0 | 0,00031 |
| 541,51272 | 0 | 8e-05 | 1e-05 | 0 | 0,00028 |
| 541,5499 | 0 | 6e-05 | 1e-05 | 0 | 0,00025 |
| 541,58708 | 0 | 5e-05 | 1e-05 | 0 | 0,00021 |
| 541,62427 | 0 | 4e-05 | 0 | 0 | 0,00018 |
| 541,66145 | 0 | 3e-05 | 0 | 0 | 0,00015 |
| 541,69863 | 0 | 2e-05 | 0 | 0 | 0,00012 |
| 541,73581 | 0 | 2e-05 | 0 | 0 | 9e-05 |
| 541,77299 | 0 | 1e-05 | 0 | 0 | 7e-05 |
| 541,81018 | 0 | 1e-05 | 0 | 0 | 5e-05 |
| 541,84736 | 0 | 1e-05 | 0 | 0 | 4e-05 |
| 541,88454 | 0 | 0 | 0 | 0 | 3e-05 |
| 541,92172 | 0 | 0 | 0 | 0 | 2e-05 |
| 541,9589 | 0 | 0 | 0 | 0 | 1e-05 |
| 541,99609 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,03327 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,07045 | 0 | 0 | 0 | 0 | 0 |
| 542,10763 | 0 | 0 | 0 | 0 | 0 |
| 542,14481 | 0 | 0 | 0 | 0 | 0 |
| 542,182 | 0 | 0 | 0 | 0 | 0 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 3e-05 | 0 | 0 |
| 524,03718 | 0 | 0 | 4e-05 | 0 | 0 |
| 524,07436 | 0 | 0 | 5e-05 | 0 | 0 |
| 524,11155 | 0 | 0 | 6e-05 | 0 | 0 |
| 524,14873 | 0 | 0 | 7e-05 | 0 | 0 |
| 524,18591 | 0 | 0 | 8e-05 | 0 | 0 |
| 524,22309 | 0 | 0 | 1e-04 | 0 | 0 |
| 524,26027 | 0 | 0 | 0,00012 | 0 | 0 |
| 524,29746 | 0 | 0 | 0,00013 | 0 | 0 |
| 524,33464 | 0 | 0 | 0,00015 | 0 | 0 |
| 524,37182 | 0 | 0 | 0,00017 | 0 | 0 |
| 524,409 | 0 | 0 | 0,00019 | 0 | 0 |
| 524,44618 | 0 | 0 | 0,00021 | 0 | 0 |
| 524,48337 | 0 | 0 | 0,00023 | 0 | 0 |
| 524,52055 | 0 | 0 | 0,00024 | 0 | 0 |
| 524,55773 | 0 | 0 | 0,00026 | 0 | 0 |
| 524,59491 | 0 | 0 | 0,00027 | 0 | 0 |
| 524,63209 | 0 | 0 | 0,00028 | 0 | 0 |
| 524,66928 | 0 | 0 | 0,00028 | 0 | 0 |
| 524,70646 | 0 | 0 | 0,00029 | 0 | 0 |
| 524,74364 | 0 | 0 | 0,00029 | 0 | 0 |
| 524,78082 | 0 | 0 | 0,00028 | 0 | 0 |
| 524,818 | 0 | 0 | 0,00028 | 0 | 0 |
| 524,85519 | 0 | 0 | 0,00027 | 0 | 0 |
| 524,89237 | 0 | 0 | 0,00026 | 0 | 0 |
| 524,92955 | 0 | 0 | 0,00025 | 0 | 0 |
| 524,96673 | 0 | 0 | 0,00023 | 0 | 0 |
| 525,00391 | 0 | 0 | 0,00022 | 0 | 0 |
| 525,0411 | 0 | 1e-05 | 0,00021 | 0 | 0 |
| 525,07828 | 0 | 1e-05 | 2e-04 | 0 | 0 |
| 525,11546 | 1e-05 | 1e-05 | 0,00019 | 1e-05 | 0 |
| 525,15264 | 1e-05 | 1e-05 | 0,00019 | 1e-05 | 0 |
| 525,18982 | 1e-05 | 2e-05 | 0,00019 | 1e-05 | 0 |
| 525,22701 | 2e-05 | 3e-05 | 0,00019 | 2e-05 | 0 |
| 525,26419 | 2e-05 | 3e-05 | 2e-04 | 3e-05 | 1e-05 |
| 525,30137 | 3e-05 | 4e-05 | 0,00021 | 4e-05 | 1e-05 |
| 525,33855 | 4e-05 | 5e-05 | 0,00023 | 5e-05 | 1e-05 |
| 525,37573 | 5e-05 | 7e-05 | 0,00026 | 6e-05 | 1e-05 |
| 525,41292 | 7e-05 | 9e-05 | 0,00029 | 9e-05 | 2e-05 |
| 525,4501 | 9e-05 | 0,00011 | 0,00033 | 0,00011 | 3e-05 |
| 525,48728 | 0,00012 | 0,00013 | 0,00037 | 0,00015 | 4e-05 |
| 525,52446 | 0,00015 | 0,00016 | 0,00042 | 0,00019 | 5e-05 |
| 525,56164 | 0,00019 | 0,00019 | 0,00048 | 0,00024 | 6e-05 |
| 525,59883 | 0,00024 | 0,00022 | 0,00053 | 3e-04 | 7e-05 |
| 525,63601 | 0,00029 | 0,00026 | 6e-04 | 0,00037 | 9e-05 |
| 525,67319 | 0,00036 | 3e-04 | 0,00066 | 0,00044 | 0,00011 |
| 525,71037 | 0,00043 | 0,00034 | 0,00073 | 0,00053 | 0,00013 |
| 525,74755 | 0,00052 | 0,00039 | 0,00079 | 0,00063 | 0,00016 |
| 525,78474 | 0,00061 | 0,00044 | 0,00086 | 0,00074 | 0,00019 |
| 525,82192 | 0,00072 | 0,00049 | 0,00093 | 0,00086 | 0,00021 |
| 525,8591 | 0,00084 | 0,00054 | 0,00099 | 0,00099 | 0,00024 |
| 525,89628 | 0,00097 | 0,00059 | 0,00105 | 0,00112 | 0,00027 |
| 525,93346 | 0,00111 | 0,00063 | 0,00111 | 0,00126 | 3e-04 |
| 525,97065 | 0,00126 | 0,00068 | 0,00116 | 0,00141 | 0,00032 |
| 526,00783 | 0,00142 | 0,00072 | 0,00121 | 0,00155 | 0,00035 |
| 526,04501 | 0,00158 | 0,00076 | 0,00125 | 0,0017 | 0,00037 |
| 526,08219 | 0,00175 | 0,00079 | 0,00129 | 0,00185 | 0,00039 |
| 526,11937 | 0,00191 | 0,00082 | 0,00133 | 0,002 | 4e-04 |
| 526,15656 | 0,00208 | 0,00085 | 0,00137 | 0,00214 | 0,00042 |
| 526,19374 | 0,00224 | 0,00086 | 0,0014 | 0,00228 | 0,00043 |
| 526,23092 | 0,0024 | 0,00088 | 0,00143 | 0,0024 | 0,00043 |
| 526,2681 | 0,00255 | 0,00089 | 0,00146 | 0,00252 | 0,00044 |
| 526,30528 | 0,00269 | 9e-04 | 0,00149 | 0,00262 | 0,00045 |
| 526,34247 | 0,00281 | 9e-04 | 0,00153 | 0,0027 | 0,00045 |
| 526,37965 | 0,00292 | 9e-04 | 0,00156 | 0,00277 | 0,00046 |
| 526,41683 | 0,00301 | 9e-04 | 0,0016 | 0,00281 | 0,00047 |
| 526,45401 | 0,00309 | 9e-04 | 0,00164 | 0,00284 | 0,00048 |
| 526,49119 | 0,00314 | 9e-04 | 0,00168 | 0,00284 | 5e-04 |
| 526,52838 | 0,00317 | 0,00091 | 0,00172 | 0,00283 | 0,00052 |
| 526,56556 | 0,00319 | 0,00091 | 0,00176 | 0,0028 | 0,00054 |
| 526,60274 | 0,00318 | 0,00091 | 0,00179 | 0,00275 | 0,00057 |
| 526,63992 | 0,00315 | 0,00092 | 0,00183 | 0,0027 | 6e-04 |
| 526,6771 | 0,00311 | 0,00093 | 0,00187 | 0,00263 | 0,00064 |
| 526,71429 | 0,00306 | 0,00094 | 0,0019 | 0,00256 | 0,00067 |
| 526,75147 | 0,00299 | 0,00095 | 0,00193 | 0,00249 | 0,00072 |
| 526,78865 | 0,00292 | 0,00097 | 0,00195 | 0,00242 | 0,00077 |
| 526,82583 | 0,00284 | 0,00099 | 0,00197 | 0,00236 | 0,00082 |
| 526,86301 | 0,00276 | 0,00102 | 0,00199 | 0,00231 | 0,00088 |
| 526,9002 | 0,00269 | 0,00104 | 0,00201 | 0,00227 | 0,00094 |
| 526,93738 | 0,00263 | 0,00108 | 0,00203 | 0,00224 | 0,00101 |
| 526,97456 | 0,00257 | 0,00111 | 0,00206 | 0,00222 | 0,00109 |
| 527,01174 | 0,00254 | 0,00115 | 0,00209 | 0,00222 | 0,00118 |
| 527,04892 | 0,00252 | 0,0012 | 0,00212 | 0,00223 | 0,00128 |
| 527,08611 | 0,00251 | 0,00126 | 0,00216 | 0,00226 | 0,00138 |
| 527,12329 | 0,00253 | 0,00132 | 0,00221 | 0,0023 | 0,0015 |
| 527,16047 | 0,00258 | 0,00139 | 0,00228 | 0,00236 | 0,00164 |
| 527,19765 | 0,00264 | 0,00148 | 0,00235 | 0,00243 | 0,00179 |
| 527,23483 | 0,00273 | 0,00157 | 0,00244 | 0,00252 | 0,00196 |
| 527,27202 | 0,00285 | 0,00167 | 0,00254 | 0,00262 | 0,00215 |
| 527,3092 | 0,00298 | 0,00179 | 0,00266 | 0,00274 | 0,00236 |
| 527,34638 | 0,00314 | 0,00192 | 0,00279 | 0,00287 | 0,00259 |
| 527,38356 | 0,00332 | 0,00206 | 0,00293 | 0,00302 | 0,00285 |
| 527,42074 | 0,00352 | 0,00222 | 0,00308 | 0,00319 | 0,00313 |
| 527,45793 | 0,00374 | 0,00239 | 0,00323 | 0,00338 | 0,00344 |
| 527,49511 | 0,00397 | 0,00258 | 0,0034 | 0,00359 | 0,00379 |
| 527,53229 | 0,00423 | 0,00279 | 0,00358 | 0,00381 | 0,00416 |
| 527,56947 | 0,00451 | 0,00301 | 0,00376 | 0,00404 | 0,00456 |
| 527,60665 | 0,00481 | 0,00325 | 0,00394 | 0,00429 | 0,00498 |
| 527,64384 | 0,00513 | 0,00351 | 0,00414 | 0,00455 | 0,00544 |
| 527,68102 | 0,00547 | 0,00379 | 0,00434 | 0,00482 | 0,00592 |
| 527,7182 | 0,00583 | 0,00409 | 0,00455 | 0,00511 | 0,00644 |
| 527,75538 | 0,00622 | 0,00442 | 0,00477 | 0,00542 | 0,00699 |
| 527,79256 | 0,00664 | 0,00476 | 0,005 | 0,00576 | 0,00757 |
| 527,82975 | 0,0071 | 0,00513 | 0,00526 | 0,00612 | 0,0082 |
| 527,86693 | 0,00758 | 0,00553 | 0,00553 | 0,00652 | 0,00887 |
| 527,90411 | 0,00811 | 0,00595 | 0,00583 | 0,00697 | 0,0096 |
| 527,94129 | 0,00867 | 0,00639 | 0,00617 | 0,00747 | 0,01039 |
| 527,97847 | 0,00928 | 0,00686 | 0,00654 | 0,00804 | 0,01125 |
| 528,01566 | 0,00993 | 0,00736 | 0,00696 | 0,0087 | 0,01218 |
| 528,05284 | 0,01062 | 0,00788 | 0,00743 | 0,00944 | 0,01319 |
| 528,09002 | 0,01137 | 0,00842 | 0,00795 | 0,01029 | 0,01427 |
| 528,1272 | 0,01217 | 0,00899 | 0,00854 | 0,01125 | 0,01544 |
| 528,16438 | 0,01302 | 0,00957 | 0,0092 | 0,01232 | 0,0167 |
| 528,20157 | 0,01392 | 0,01018 | 0,00993 | 0,01348 | 0,01801 |
| 528,23875 | 0,01486 | 0,01081 | 0,01073 | 0,01473 | 0,01938 |
| 528,27593 | 0,01585 | 0,01145 | 0,0116 | 0,01605 | 0,02077 |
| 528,31311 | 0,01688 | 0,01212 | 0,01255 | 0,01742 | 0,02217 |
| 528,35029 | 0,01795 | 0,01279 | 0,01356 | 0,0188 | 0,02354 |
| 528,38748 | 0,01904 | 0,01349 | 0,01464 | 0,02017 | 0,02486 |
| 528,42466 | 0,02015 | 0,01419 | 0,01578 | 0,0215 | 0,02609 |
| 528,46184 | 0,02127 | 0,0149 | 0,01698 | 0,02273 | 0,0272 |
| 528,49902 | 0,02238 | 0,01563 | 0,01821 | 0,02384 | 0,02814 |
| 528,5362 | 0,02348 | 0,01636 | 0,01948 | 0,02481 | 0,02891 |
| 528,57339 | 0,02456 | 0,0171 | 0,02075 | 0,02563 | 0,0295 |
| 528,61057 | 0,02561 | 0,01784 | 0,02203 | 0,02628 | 0,02989 |
| 528,64775 | 0,02661 | 0,01859 | 0,02331 | 0,02676 | 0,03009 |
| 528,68493 | 0,02756 | 0,01934 | 0,02456 | 0,02709 | 0,03011 |
| 528,72211 | 0,02844 | 0,02008 | 0,02578 | 0,02729 | 0,02996 |
| 528,7593 | 0,02924 | 0,02083 | 0,02695 | 0,02737 | 0,02968 |
| 528,79648 | 0,02998 | 0,02158 | 0,02807 | 0,02738 | 0,02928 |
| 528,83366 | 0,03064 | 0,02233 | 0,02912 | 0,02735 | 0,02881 |
| 528,87084 | 0,03122 | 0,02307 | 0,03012 | 0,02733 | 0,0283 |
| 528,90802 | 0,03173 | 0,02381 | 0,03104 | 0,02734 | 0,02779 |
| 528,94521 | 0,03217 | 0,02455 | 0,0319 | 0,02741 | 0,02732 |
| 528,98239 | 0,03255 | 0,02529 | 0,03269 | 0,02757 | 0,0269 |
| 529,01957 | 0,03286 | 0,02603 | 0,03341 | 0,02781 | 0,02657 |
| 529,05675 | 0,03311 | 0,02677 | 0,03406 | 0,02816 | 0,02632 |
| 529,09393 | 0,03333 | 0,02752 | 0,03465 | 0,0286 | 0,02617 |
| 529,13112 | 0,03351 | 0,02828 | 0,03519 | 0,02914 | 0,02611 |
| 529,1683 | 0,03368 | 0,02905 | 0,03569 | 0,02974 | 0,02617 |
| 529,20548 | 0,03384 | 0,02984 | 0,03614 | 0,03037 | 0,02631 |
| 529,24266 | 0,034 | 0,03066 | 0,03656 | 0,03102 | 0,02651 |
| 529,27984 | 0,03419 | 0,03151 | 0,03696 | 0,03166 | 0,02678 |
| 529,31703 | 0,03441 | 0,0324 | 0,03735 | 0,03227 | 0,02708 |
| 529,35421 | 0,03468 | 0,03334 | 0,03773 | 0,03282 | 0,02741 |
| 529,39139 | 0,03501 | 0,03434 | 0,03811 | 0,03332 | 0,02777 |
| 529,42857 | 0,03542 | 0,03542 | 0,03852 | 0,03375 | 0,02814 |
| 529,46575 | 0,03592 | 0,03657 | 0,03895 | 0,0341 | 0,02853 |
| 529,50294 | 0,03651 | 0,0378 | 0,03943 | 0,03439 | 0,02895 |
| 529,54012 | 0,03721 | 0,03912 | 0,03995 | 0,03465 | 0,0294 |
| 529,5773 | 0,03802 | 0,04053 | 0,04053 | 0,0349 | 0,0299 |
| 529,61448 | 0,03896 | 0,04203 | 0,04118 | 0,03516 | 0,03046 |
| 529,65166 | 0,04002 | 0,04362 | 0,04193 | 0,03547 | 0,03111 |
| 529,68885 | 0,04121 | 0,04531 | 0,04277 | 0,03585 | 0,03186 |
| 529,72603 | 0,0425 | 0,04709 | 0,0437 | 0,03634 | 0,03274 |
| 529,76321 | 0,0439 | 0,04894 | 0,04474 | 0,03696 | 0,03375 |
| 529,80039 | 0,04541 | 0,05086 | 0,04588 | 0,03776 | 0,03492 |
| 529,83757 | 0,047 | 0,05283 | 0,04713 | 0,03874 | 0,03627 |
| 529,87476 | 0,04868 | 0,05484 | 0,04849 | 0,03992 | 0,03778 |
| 529,91194 | 0,05044 | 0,05688 | 0,04995 | 0,04129 | 0,03947 |
| 529,94912 | 0,05227 | 0,05894 | 0,05153 | 0,04285 | 0,04132 |
| 529,9863 | 0,05415 | 0,061 | 0,0532 | 0,04461 | 0,04332 |
| 530,02348 | 0,05607 | 0,06305 | 0,05496 | 0,04656 | 0,04549 |
| 530,06067 | 0,05802 | 0,06507 | 0,05679 | 0,04869 | 0,04781 |
| 530,09785 | 0,06001 | 0,06706 | 0,05868 | 0,051 | 0,05028 |
| 530,13503 | 0,06201 | 0,069 | 0,06061 | 0,0535 | 0,05291 |
| 530,17221 | 0,06403 | 0,07089 | 0,06259 | 0,05618 | 0,05573 |
| 530,20939 | 0,06606 | 0,07272 | 0,06457 | 0,05905 | 0,05874 |
| 530,24658 | 0,06809 | 0,07448 | 0,06656 | 0,0621 | 0,06194 |
| 530,28376 | 0,07013 | 0,07615 | 0,06854 | 0,06537 | 0,06535 |
| 530,32094 | 0,07215 | 0,07775 | 0,07048 | 0,06884 | 0,06899 |
| 530,35812 | 0,07417 | 0,07926 | 0,07239 | 0,07253 | 0,07287 |
| 530,3953 | 0,07618 | 0,08068 | 0,07425 | 0,07644 | 0,07699 |
| 530,43249 | 0,07818 | 0,08203 | 0,07606 | 0,08056 | 0,08135 |
| 530,46967 | 0,08017 | 0,08331 | 0,07783 | 0,0849 | 0,08592 |
| 530,50685 | 0,08214 | 0,08451 | 0,07954 | 0,08939 | 0,09069 |
| 530,54403 | 0,0841 | 0,08566 | 0,08122 | 0,09398 | 0,09558 |
| 530,58121 | 0,08605 | 0,08675 | 0,08288 | 0,0986 | 0,10049 |
| 530,6184 | 0,088 | 0,08782 | 0,08453 | 0,10318 | 0,10536 |
| 530,65558 | 0,08994 | 0,08888 | 0,08619 | 0,10763 | 0,11008 |
| 530,69276 | 0,09187 | 0,08995 | 0,08788 | 0,11186 | 0,11455 |
| 530,72994 | 0,09381 | 0,09106 | 0,08962 | 0,11579 | 0,11866 |
| 530,76712 | 0,09576 | 0,09223 | 0,09142 | 0,11932 | 0,12233 |
| 530,80431 | 0,09771 | 0,09348 | 0,09329 | 0,12236 | 0,12547 |
| 530,84149 | 0,09968 | 0,09484 | 0,09528 | 0,12487 | 0,12797 |
| 530,87867 | 0,10167 | 0,09635 | 0,09738 | 0,12686 | 0,12985 |
| 530,91585 | 0,10368 | 0,09803 | 0,0996 | 0,12835 | 0,13115 |
| 530,95303 | 0,10572 | 0,09988 | 0,10195 | 0,12942 | 0,13195 |
| 530,99022 | 0,1078 | 0,10192 | 0,10442 | 0,13013 | 0,13233 |
| 531,0274 | 0,10992 | 0,10416 | 0,10704 | 0,13061 | 0,13242 |
| 531,06458 | 0,11208 | 0,1066 | 0,10979 | 0,13097 | 0,13235 |
| 531,10176 | 0,1143 | 0,10924 | 0,11268 | 0,13134 | 0,1323 |
| 531,13894 | 0,1166 | 0,11208 | 0,11573 | 0,13189 | 0,13241 |
| 531,17613 | 0,11896 | 0,11511 | 0,11892 | 0,13275 | 0,13287 |
| 531,21331 | 0,1214 | 0,11831 | 0,12222 | 0,134 | 0,13381 |
| 531,25049 | 0,12391 | 0,12161 | 0,12564 | 0,13567 | 0,13526 |
| 531,28767 | 0,12648 | 0,125 | 0,12914 | 0,13777 | 0,13724 |
| 531,32485 | 0,12911 | 0,12842 | 0,13272 | 0,14024 | 0,13973 |
| 531,36204 | 0,13178 | 0,13183 | 0,13634 | 0,143 | 0,14263 |
| 531,39922 | 0,13446 | 0,13517 | 0,13997 | 0,14593 | 0,14584 |
| 531,4364 | 0,13711 | 0,13839 | 0,14354 | 0,14886 | 0,14917 |
| 531,47358 | 0,13968 | 0,14139 | 0,14701 | 0,15162 | 0,15246 |
| 531,51076 | 0,14215 | 0,14413 | 0,15031 | 0,15394 | 0,15544 |
| 531,54795 | 0,14444 | 0,14655 | 0,15339 | 0,15569 | 0,15789 |
| 531,58513 | 0,14652 | 0,1486 | 0,15619 | 0,15672 | 0,15967 |
| 531,62231 | 0,14833 | 0,15024 | 0,15863 | 0,15694 | 0,16063 |
| 531,65949 | 0,14983 | 0,15145 | 0,16067 | 0,15628 | 0,16069 |
| 531,69667 | 0,15099 | 0,15219 | 0,16225 | 0,15474 | 0,15979 |
| 531,73386 | 0,15169 | 0,15246 | 0,16326 | 0,15235 | 0,15794 |
| 531,77104 | 0,15199 | 0,15219 | 0,16371 | 0,14921 | 0,1552 |
| 531,80822 | 0,15189 | 0,15148 | 0,16361 | 0,14543 | 0,15168 |
| 531,8454 | 0,15142 | 0,15038 | 0,16298 | 0,14117 | 0,14747 |
| 531,88258 | 0,1506 | 0,14895 | 0,16184 | 0,13671 | 0,14284 |
| 531,91977 | 0,14949 | 0,14725 | 0,16025 | 0,13228 | 0,13803 |
| 531,95695 | 0,14816 | 0,14538 | 0,15826 | 0,1281 | 0,13327 |
| 531,99413 | 0,14669 | 0,14342 | 0,15596 | 0,12438 | 0,1288 |
| 532,03131 | 0,14519 | 0,14149 | 0,15345 | 0,12134 | 0,12484 |
| 532,06849 | 0,14381 | 0,13972 | 0,15089 | 0,11917 | 0,12164 |
| 532,10568 | 0,14264 | 0,13824 | 0,14842 | 0,11807 | 0,1194 |
| 532,14286 | 0,14181 | 0,13715 | 0,14617 | 0,1182 | 0,11833 |
| 532,18004 | 0,14143 | 0,13654 | 0,14426 | 0,1199 | 0,11877 |
| 532,21722 | 0,1416 | 0,13652 | 0,14283 | 0,12311 | 0,12082 |
| 532,2544 | 0,1424 | 0,13716 | 0,142 | 0,1279 | 0,12453 |
| 532,29159 | 0,14392 | 0,13853 | 0,14187 | 0,1343 | 0,12997 |
| 532,32877 | 0,14632 | 0,14069 | 0,14264 | 0,14228 | 0,13716 |
| 532,36595 | 0,14955 | 0,14378 | 0,14432 | 0,15181 | 0,14606 |
| 532,40313 | 0,15358 | 0,14768 | 0,14691 | 0,16276 | 0,15657 |
| 532,44031 | 0,15839 | 0,15235 | 0,1504 | 0,17497 | 0,16853 |
| 532,4775 | 0,16391 | 0,15775 | 0,15477 | 0,18822 | 0,18172 |
| 532,51468 | 0,17007 | 0,1638 | 0,15995 | 0,20226 | 0,1959 |
| 532,55186 | 0,17677 | 0,17041 | 0,16588 | 0,21662 | 0,2106 |
| 532,58904 | 0,18388 | 0,17748 | 0,17243 | 0,23088 | 0,22535 |
| 532,62622 | 0,19128 | 0,18487 | 0,17951 | 0,24466 | 0,23973 |
| 532,66341 | 0,19876 | 0,19242 | 0,18689 | 0,25755 | 0,2533 |
| 532,70059 | 0,20614 | 0,19995 | 0,19438 | 0,26917 | 0,26567 |
| 532,73777 | 0,21328 | 0,2073 | 0,2018 | 0,27919 | 0,27647 |
| 532,77495 | 0,22001 | 0,21432 | 0,20898 | 0,28734 | 0,28538 |
| 532,81213 | 0,22622 | 0,22087 | 0,21575 | 0,2934 | 0,29219 |
| 532,84932 | 0,23177 | 0,22683 | 0,22196 | 0,29703 | 0,29657 |
| 532,8865 | 0,23656 | 0,23207 | 0,22748 | 0,29842 | 0,29856 |
| 532,92368 | 0,24042 | 0,23647 | 0,2321 | 0,29776 | 0,2984 |
| 532,96086 | 0,24332 | 0,23987 | 0,23575 | 0,29526 | 0,29629 |
| 532,99804 | 0,24532 | 0,24234 | 0,23844 | 0,29121 | 0,29249 |
| 533,03523 | 0,2464 | 0,24386 | 0,24017 | 0,28592 | 0,28732 |
| 533,07241 | 0,24661 | 0,24445 | 0,24095 | 0,27975 | 0,28114 |
| 533,10959 | 0,24598 | 0,24413 | 0,24083 | 0,27306 | 0,27431 |
| 533,14677 | 0,2446 | 0,24295 | 0,23986 | 0,26621 | 0,26719 |
| 533,18395 | 0,24252 | 0,24098 | 0,23812 | 0,25956 | 0,26017 |
| 533,22114 | 0,23979 | 0,23825 | 0,23567 | 0,25345 | 0,25359 |
| 533,25832 | 0,23653 | 0,23485 | 0,23263 | 0,24807 | 0,24767 |
| 533,2955 | 0,23287 | 0,23095 | 0,22917 | 0,24356 | 0,24259 |
| 533,33268 | 0,22889 | 0,22664 | 0,22539 | 0,24002 | 0,23846 |
| 533,36986 | 0,22468 | 0,22202 | 0,22137 | 0,23749 | 0,23533 |
| 533,40705 | 0,2203 | 0,21717 | 0,2172 | 0,23595 | 0,23319 |
| 533,44423 | 0,21581 | 0,21218 | 0,21297 | 0,23536 | 0,23202 |
| 533,48141 | 0,21129 | 0,20713 | 0,20873 | 0,2356 | 0,2317 |
| 533,51859 | 0,20678 | 0,2021 | 0,20455 | 0,23659 | 0,23214 |
| 533,55577 | 0,20236 | 0,19719 | 0,2005 | 0,2381 | 0,23313 |
| 533,59295 | 0,19806 | 0,19244 | 0,19661 | 0,23989 | 0,2344 |
| 533,63014 | 0,19394 | 0,18793 | 0,19291 | 0,24172 | 0,23571 |
| 533,66732 | 0,19003 | 0,1837 | 0,18945 | 0,24336 | 0,23684 |
| 533,7045 | 0,1864 | 0,17981 | 0,18625 | 0,24457 | 0,23752 |
| 533,74168 | 0,18307 | 0,17629 | 0,18335 | 0,24512 | 0,23754 |
| 533,77886 | 0,1801 | 0,1732 | 0,18079 | 0,24478 | 0,23667 |
| 533,81605 | 0,17757 | 0,17062 | 0,17864 | 0,24335 | 0,23472 |
| 533,85323 | 0,17553 | 0,16857 | 0,17693 | 0,24061 | 0,23146 |
| 533,89041 | 0,17397 | 0,16703 | 0,17566 | 0,23639 | 0,22676 |
| 533,92759 | 0,1729 | 0,166 | 0,17486 | 0,23077 | 0,22071 |
| 533,96477 | 0,17234 | 0,16547 | 0,17452 | 0,22379 | 0,21335 |
| 534,00196 | 0,17225 | 0,16541 | 0,17464 | 0,21555 | 0,20478 |
| 534,03914 | 0,17263 | 0,16578 | 0,1752 | 0,20619 | 0,19517 |
| 534,07632 | 0,17341 | 0,16653 | 0,17616 | 0,19592 | 0,1847 |
| 534,1135 | 0,17454 | 0,1676 | 0,17748 | 0,18496 | 0,17361 |
| 534,15068 | 0,17591 | 0,16887 | 0,17908 | 0,17356 | 0,16214 |
| 534,18787 | 0,17739 | 0,17021 | 0,18083 | 0,16198 | 0,15056 |
| 534,22505 | 0,17885 | 0,17151 | 0,1826 | 0,15055 | 0,13917 |
| 534,26223 | 0,18016 | 0,17266 | 0,18429 | 0,13948 | 0,1282 |
| 534,29941 | 0,18119 | 0,17355 | 0,18576 | 0,12898 | 0,11781 |
| 534,33659 | 0,18182 | 0,17405 | 0,1869 | 0,11918 | 0,10815 |
| 534,37378 | 0,18193 | 0,17409 | 0,18758 | 0,11019 | 0,09933 |
| 534,41096 | 0,18136 | 0,17347 | 0,18764 | 0,10207 | 0,0914 |
| 534,44814 | 0,17998 | 0,17216 | 0,18693 | 0,09486 | 0,0844 |
| 534,48532 | 0,17778 | 0,17015 | 0,18545 | 0,08856 | 0,07833 |
| 534,5225 | 0,17476 | 0,1674 | 0,18315 | 0,08314 | 0,0732 |
| 534,55969 | 0,1709 | 0,16394 | 0,18001 | 0,07865 | 0,06899 |
| 534,59687 | 0,16623 | 0,15976 | 0,17603 | 0,07492 | 0,06555 |
| 534,63405 | 0,1608 | 0,15492 | 0,17124 | 0,07188 | 0,06284 |
| 534,67123 | 0,15468 | 0,14947 | 0,16568 | 0,06948 | 0,06079 |
| 534,70841 | 0,14795 | 0,14344 | 0,15942 | 0,06767 | 0,05936 |
| 534,7456 | 0,14071 | 0,13701 | 0,15252 | 0,06641 | 0,05849 |
| 534,78278 | 0,13316 | 0,13029 | 0,1452 | 0,06566 | 0,05815 |
| 534,81996 | 0,12546 | 0,1234 | 0,13757 | 0,0654 | 0,05831 |
| 534,85714 | 0,11772 | 0,11646 | 0,12977 | 0,06561 | 0,05898 |
| 534,89432 | 0,11011 | 0,10959 | 0,12193 | 0,06634 | 0,06015 |
| 534,93151 | 0,10274 | 0,10289 | 0,11419 | 0,06751 | 0,06176 |
| 534,96869 | 0,09575 | 0,09649 | 0,10667 | 0,06911 | 0,0638 |
| 535,00587 | 0,08926 | 0,09058 | 0,09953 | 0,07112 | 0,06626 |
| 535,04305 | 0,08347 | 0,0852 | 0,09294 | 0,07352 | 0,06912 |
| 535,08023 | 0,0784 | 0,08045 | 0,08696 | 0,07629 | 0,07235 |
| 535,11742 | 0,07411 | 0,07638 | 0,08167 | 0,07941 | 0,07594 |
| 535,1546 | 0,07065 | 0,07306 | 0,07714 | 0,08282 | 0,07984 |
| 535,19178 | 0,06806 | 0,07054 | 0,07342 | 0,0865 | 0,08404 |
| 535,22896 | 0,06634 | 0,06886 | 0,07057 | 0,09041 | 0,08847 |
| 535,26614 | 0,06551 | 0,06803 | 0,06861 | 0,09445 | 0,09306 |
| 535,30333 | 0,06556 | 0,0682 | 0,06757 | 0,09855 | 0,09773 |
| 535,34051 | 0,06656 | 0,06921 | 0,06753 | 0,10263 | 0,1024 |
| 535,37769 | 0,06831 | 0,07101 | 0,06835 | 0,1066 | 0,10699 |
| 535,41487 | 0,07076 | 0,07356 | 0,06996 | 0,11034 | 0,11137 |
| 535,45205 | 0,07381 | 0,07676 | 0,07229 | 0,11376 | 0,11545 |
| 535,48924 | 0,07735 | 0,08055 | 0,07527 | 0,11674 | 0,1191 |
| 535,52642 | 0,08128 | 0,08481 | 0,07878 | 0,11914 | 0,12217 |
| 535,5636 | 0,08546 | 0,08943 | 0,08272 | 0,12078 | 0,12446 |
| 535,60078 | 0,08978 | 0,09426 | 0,08696 | 0,12156 | 0,12592 |
| 535,63796 | 0,09405 | 0,09913 | 0,09133 | 0,12143 | 0,12647 |
| 535,67515 | 0,09813 | 0,10387 | 0,09566 | 0,12032 | 0,12603 |
| 535,71233 | 0,10187 | 0,10834 | 0,09979 | 0,11823 | 0,12457 |
| 535,74951 | 0,10516 | 0,11242 | 0,10358 | 0,11515 | 0,12209 |
| 535,78669 | 0,10789 | 0,11597 | 0,1069 | 0,11114 | 0,11864 |
| 535,82387 | 0,10995 | 0,11888 | 0,10964 | 0,10628 | 0,11428 |
| 535,86106 | 0,11128 | 0,12104 | 0,11169 | 0,10071 | 0,10912 |
| 535,89824 | 0,11182 | 0,12225 | 0,11295 | 0,09455 | 0,1033 |
| 535,93542 | 0,11142 | 0,1226 | 0,11324 | 0,08804 | 0,09706 |
| 535,9726 | 0,11018 | 0,12207 | 0,11267 | 0,0814 | 0,09062 |
| 536,00978 | 0,10816 | 0,12068 | 0,11125 | 0,07481 | 0,08416 |
| 536,04697 | 0,1054 | 0,11847 | 0,109 | 0,06846 | 0,07785 |
| 536,08415 | 0,10198 | 0,11549 | 0,10599 | 0,06249 | 0,07186 |
| 536,12133 | 0,09798 | 0,11182 | 0,10228 | 0,05704 | 0,06633 |
| 536,15851 | 0,09351 | 0,10754 | 0,09798 | 0,05219 | 0,06136 |
| 536,19569 | 0,08868 | 0,10274 | 0,09318 | 0,04799 | 0,05704 |
| 536,23288 | 0,08357 | 0,09762 | 0,08796 | 0,04452 | 0,05345 |
| 536,27006 | 0,07837 | 0,09229 | 0,08254 | 0,04174 | 0,05051 |
| 536,30724 | 0,07319 | 0,08687 | 0,07702 | 0,03954 | 0,04817 |
| 536,34442 | 0,06812 | 0,08146 | 0,07152 | 0,03784 | 0,04635 |
| 536,3816 | 0,06324 | 0,07617 | 0,06613 | 0,03654 | 0,04496 |
| 536,41879 | 0,05864 | 0,07108 | 0,06095 | 0,03553 | 0,04391 |
| 536,45597 | 0,05437 | 0,06629 | 0,05605 | 0,03471 | 0,04308 |
| 536,49315 | 0,05047 | 0,06188 | 0,05149 | 0,03398 | 0,04236 |
| 536,53033 | 0,04703 | 0,05786 | 0,04738 | 0,03325 | 0,04167 |
| 536,56751 | 0,04402 | 0,05425 | 0,04369 | 0,03243 | 0,0409 |
| 536,6047 | 0,04141 | 0,05104 | 0,04043 | 0,03145 | 0,03997 |
| 536,64188 | 0,03918 | 0,04824 | 0,03758 | 0,03029 | 0,03885 |
| 536,67906 | 0,03731 | 0,04583 | 0,03513 | 0,02894 | 0,03752 |
| 536,71624 | 0,03576 | 0,04378 | 0,03305 | 0,02742 | 0,03596 |
| 536,75342 | 0,03449 | 0,04207 | 0,03131 | 0,02574 | 0,0342 |
| 536,79061 | 0,03345 | 0,04067 | 0,02985 | 0,02394 | 0,03225 |
| 536,82779 | 0,0326 | 0,03949 | 0,02868 | 0,02206 | 0,03015 |
| 536,86497 | 0,03188 | 0,03848 | 0,02769 | 0,02016 | 0,02795 |
| 536,90215 | 0,03124 | 0,03761 | 0,02684 | 0,01827 | 0,0257 |
| 536,93933 | 0,03063 | 0,03684 | 0,0261 | 0,01646 | 0,02345 |
| 536,97652 | 0,03003 | 0,03612 | 0,02541 | 0,01477 | 0,02126 |
| 537,0137 | 0,0294 | 0,03542 | 0,02475 | 0,01321 | 0,01916 |
| 537,05088 | 0,02871 | 0,0347 | 0,02408 | 0,01182 | 0,01719 |
| 537,08806 | 0,02796 | 0,03395 | 0,0234 | 0,0106 | 0,01537 |
| 537,12524 | 0,02712 | 0,03314 | 0,02267 | 0,00955 | 0,01371 |
| 537,16243 | 0,02619 | 0,03226 | 0,02189 | 0,00867 | 0,01223 |
| 537,19961 | 0,02518 | 0,03131 | 0,02106 | 0,00795 | 0,01092 |
| 537,23679 | 0,02409 | 0,03029 | 0,02018 | 0,00737 | 0,00982 |
| 537,27397 | 0,02293 | 0,0292 | 0,01926 | 0,00693 | 0,00887 |
| 537,31115 | 0,02171 | 0,02805 | 0,01831 | 0,00658 | 0,00807 |
| 537,34834 | 0,02045 | 0,02684 | 0,01733 | 0,00631 | 0,0074 |
| 537,38552 | 0,01916 | 0,02559 | 0,01634 | 0,0061 | 0,00684 |
| 537,4227 | 0,01785 | 0,02431 | 0,01535 | 0,00592 | 0,00639 |
| 537,45988 | 0,01655 | 0,02302 | 0,01437 | 0,00576 | 0,00602 |
| 537,49706 | 0,01528 | 0,02173 | 0,01342 | 0,00562 | 0,00572 |
| 537,53425 | 0,01403 | 0,02045 | 0,0125 | 0,00548 | 0,00548 |
| 537,57143 | 0,01283 | 0,0192 | 0,01161 | 0,00533 | 0,00529 |
| 537,60861 | 0,01169 | 0,01797 | 0,01077 | 0,00517 | 0,00514 |
| 537,64579 | 0,0106 | 0,0168 | 0,00997 | 0,005 | 0,00502 |
| 537,68297 | 0,00959 | 0,01568 | 0,00921 | 0,00482 | 0,00493 |
| 537,72016 | 0,00865 | 0,01461 | 0,00851 | 0,00463 | 0,00486 |
| 537,75734 | 0,00779 | 0,01361 | 0,00785 | 0,00443 | 0,0048 |
| 537,79452 | 0,00702 | 0,01267 | 0,00723 | 0,00424 | 0,00475 |
| 537,8317 | 0,00632 | 0,01178 | 0,00665 | 0,00404 | 0,00472 |
| 537,86888 | 0,00569 | 0,01097 | 0,00612 | 0,00385 | 0,00469 |
| 537,90607 | 0,00514 | 0,01021 | 0,00562 | 0,00367 | 0,00467 |
| 537,94325 | 0,00466 | 0,00952 | 0,00515 | 0,00351 | 0,00465 |
| 537,98043 | 0,00425 | 0,00889 | 0,00472 | 0,00336 | 0,00463 |
| 538,01761 | 0,0039 | 0,00832 | 0,00433 | 0,00323 | 0,00461 |
| 538,05479 | 0,00362 | 0,0078 | 0,00397 | 0,00311 | 0,00458 |
| 538,09198 | 0,00338 | 0,00733 | 0,00365 | 0,00302 | 0,00454 |
| 538,12916 | 0,0032 | 0,00691 | 0,00335 | 0,00295 | 0,0045 |
| 538,16634 | 0,00306 | 0,00654 | 0,00309 | 0,00291 | 0,00444 |
| 538,20352 | 0,00295 | 0,00621 | 0,00286 | 0,00288 | 0,00438 |
| 538,2407 | 0,00288 | 0,00592 | 0,00267 | 0,00288 | 0,0043 |
| 538,27789 | 0,00284 | 0,00568 | 0,0025 | 0,0029 | 0,00422 |
| 538,31507 | 0,00282 | 0,00547 | 0,00236 | 0,00294 | 0,00413 |
| 538,35225 | 0,00283 | 0,0053 | 0,00226 | 0,00299 | 0,00404 |
| 538,38943 | 0,00285 | 0,00515 | 0,00218 | 0,00306 | 0,00394 |
| 538,42661 | 0,00289 | 0,00504 | 0,00212 | 0,00313 | 0,00386 |
| 538,4638 | 0,00293 | 0,00494 | 0,00209 | 0,00321 | 0,00377 |
| 538,50098 | 0,00298 | 0,00486 | 0,00207 | 0,00328 | 0,0037 |
| 538,53816 | 0,00302 | 0,0048 | 0,00206 | 0,00334 | 0,00363 |
| 538,57534 | 0,00307 | 0,00475 | 0,00207 | 0,00339 | 0,00357 |
| 538,61252 | 0,00312 | 0,0047 | 0,00208 | 0,00341 | 0,00352 |
| 538,64971 | 0,00315 | 0,00464 | 0,0021 | 0,00342 | 0,00347 |
| 538,68689 | 0,00318 | 0,00458 | 0,00211 | 0,00339 | 0,00343 |
| 538,72407 | 0,00319 | 0,00451 | 0,00212 | 0,00333 | 0,00338 |
| 538,76125 | 0,0032 | 0,00443 | 0,00212 | 0,00325 | 0,00333 |
| 538,79843 | 0,00318 | 0,00433 | 0,00212 | 0,00313 | 0,00327 |
| 538,83562 | 0,00316 | 0,0042 | 0,0021 | 0,00299 | 0,00321 |
| 538,8728 | 0,00312 | 0,00406 | 0,00207 | 0,00283 | 0,00313 |
| 538,90998 | 0,00306 | 0,0039 | 0,00203 | 0,00265 | 0,00304 |
| 538,94716 | 0,00298 | 0,00372 | 0,00197 | 0,00245 | 0,00294 |
| 538,98434 | 0,0029 | 0,00353 | 0,0019 | 0,00225 | 0,00283 |
| 539,02153 | 0,0028 | 0,00332 | 0,00183 | 0,00205 | 0,00272 |
| 539,05871 | 0,00269 | 0,0031 | 0,00174 | 0,00186 | 0,0026 |
| 539,09589 | 0,00257 | 0,00288 | 0,00165 | 0,00168 | 0,00247 |
| 539,13307 | 0,00244 | 0,00265 | 0,00156 | 0,00152 | 0,00236 |
| 539,17025 | 0,00231 | 0,00242 | 0,00148 | 0,00137 | 0,00224 |
| 539,20744 | 0,00218 | 0,0022 | 0,00139 | 0,00125 | 0,00214 |
| 539,24462 | 0,00205 | 0,00198 | 0,00131 | 0,00115 | 0,00204 |
| 539,2818 | 0,00192 | 0,00178 | 0,00125 | 0,00108 | 0,00196 |
| 539,31898 | 0,0018 | 0,00159 | 0,00119 | 0,00103 | 0,00189 |
| 539,35616 | 0,00169 | 0,00142 | 0,00115 | 0,00101 | 0,00183 |
| 539,39335 | 0,00159 | 0,00126 | 0,00112 | 0,001 | 0,00178 |
| 539,43053 | 0,0015 | 0,00113 | 0,00111 | 0,001 | 0,00175 |
| 539,46771 | 0,00142 | 0,00102 | 0,00111 | 0,00102 | 0,00172 |
| 539,50489 | 0,00135 | 0,00092 | 0,00113 | 0,00105 | 0,00169 |
| 539,54207 | 0,0013 | 0,00084 | 0,00115 | 0,00108 | 0,00167 |
| 539,57926 | 0,00126 | 0,00078 | 0,00119 | 0,00112 | 0,00165 |
| 539,61644 | 0,00124 | 0,00073 | 0,00124 | 0,00115 | 0,00164 |
| 539,65362 | 0,00123 | 7e-04 | 0,00129 | 0,00118 | 0,00162 |
| 539,6908 | 0,00122 | 0,00068 | 0,00134 | 0,00121 | 0,0016 |
| 539,72798 | 0,00123 | 0,00067 | 0,0014 | 0,00122 | 0,00158 |
| 539,76517 | 0,00124 | 0,00067 | 0,00146 | 0,00123 | 0,00155 |
| 539,80235 | 0,00126 | 0,00067 | 0,00151 | 0,00123 | 0,00152 |
| 539,83953 | 0,00128 | 0,00068 | 0,00155 | 0,00122 | 0,00148 |
| 539,87671 | 0,00131 | 0,00069 | 0,00159 | 0,00121 | 0,00144 |
| 539,91389 | 0,00133 | 7e-04 | 0,00162 | 0,00118 | 0,00138 |
| 539,95108 | 0,00135 | 0,00071 | 0,00164 | 0,00115 | 0,00133 |
| 539,98826 | 0,00136 | 0,00072 | 0,00164 | 0,00111 | 0,00126 |
| 540,02544 | 0,00137 | 0,00072 | 0,00164 | 0,00107 | 0,0012 |
| 540,06262 | 0,00137 | 0,00073 | 0,00163 | 0,00102 | 0,00113 |
| 540,0998 | 0,00137 | 0,00072 | 0,0016 | 0,00097 | 0,00106 |
| 540,13699 | 0,00135 | 0,00072 | 0,00157 | 0,00092 | 0,00099 |
| 540,17417 | 0,00132 | 0,00071 | 0,00152 | 0,00087 | 0,00093 |
| 540,21135 | 0,00129 | 0,00069 | 0,00147 | 0,00082 | 0,00088 |
| 540,24853 | 0,00124 | 0,00067 | 0,0014 | 0,00077 | 0,00083 |
| 540,28571 | 0,00119 | 0,00065 | 0,00133 | 0,00073 | 0,00079 |
| 540,3229 | 0,00113 | 0,00062 | 0,00126 | 0,00068 | 0,00077 |
| 540,36008 | 0,00107 | 0,00059 | 0,00118 | 0,00065 | 0,00076 |
| 540,39726 | 0,001 | 0,00056 | 0,0011 | 0,00061 | 0,00076 |
| 540,43444 | 0,00093 | 0,00052 | 0,00101 | 0,00058 | 0,00078 |
| 540,47162 | 0,00085 | 0,00049 | 0,00092 | 0,00055 | 8e-04 |
| 540,50881 | 0,00077 | 0,00046 | 0,00084 | 0,00053 | 0,00084 |
| 540,54599 | 7e-04 | 0,00043 | 0,00075 | 0,00051 | 0,00088 |
| 540,58317 | 0,00062 | 4e-04 | 0,00067 | 0,00049 | 0,00092 |
| 540,62035 | 0,00055 | 0,00037 | 0,00059 | 0,00047 | 0,00096 |
| 540,65753 | 0,00049 | 0,00035 | 0,00052 | 0,00046 | 0,001 |
| 540,69472 | 0,00042 | 0,00033 | 0,00045 | 0,00044 | 0,00103 |
| 540,7319 | 0,00036 | 0,00031 | 0,00038 | 0,00042 | 0,00105 |
| 540,76908 | 0,00031 | 3e-04 | 0,00033 | 0,00041 | 0,00106 |
| 540,80626 | 0,00026 | 0,00029 | 0,00027 | 0,00039 | 0,00105 |
| 540,84344 | 0,00022 | 0,00028 | 0,00023 | 0,00037 | 0,00104 |
| 540,88063 | 0,00018 | 0,00028 | 0,00019 | 0,00034 | 0,001 |
| 540,91781 | 0,00015 | 0,00028 | 0,00015 | 0,00032 | 0,00096 |
| 540,95499 | 0,00012 | 0,00028 | 0,00012 | 0,00029 | 9e-04 |
| 540,99217 | 1e-04 | 0,00029 | 1e-04 | 0,00026 | 0,00083 |
| 541,02935 | 8e-05 | 0,00029 | 8e-05 | 0,00023 | 0,00076 |
| 541,06654 | 6e-05 | 0,00029 | 6e-05 | 0,00021 | 0,00068 |
| 541,10372 | 5e-05 | 0,00029 | 5e-05 | 0,00018 | 6e-04 |
| 541,1409 | 4e-05 | 0,00029 | 4e-05 | 0,00015 | 0,00052 |
| 541,17808 | 3e-05 | 0,00029 | 3e-05 | 0,00013 | 0,00045 |
| 541,21526 | 2e-05 | 0,00029 | 2e-05 | 0,00011 | 0,00038 |
| 541,25245 | 2e-05 | 0,00028 | 1e-05 | 9e-05 | 0,00032 |
| 541,28963 | 1e-05 | 0,00027 | 1e-05 | 7e-05 | 0,00026 |
| 541,32681 | 1e-05 | 0,00026 | 1e-05 | 6e-05 | 0,00021 |
| 541,36399 | 1e-05 | 0,00025 | 1e-05 | 4e-05 | 0,00017 |
| 541,40117 | 0 | 0,00023 | 0 | 3e-05 | 0,00013 |
| 541,43836 | 0 | 0,00022 | 0 | 3e-05 | 1e-04 |
| 541,47554 | 0 | 2e-04 | 0 | 2e-05 | 8e-05 |
| 541,51272 | 0 | 0,00018 | 0 | 1e-05 | 6e-05 |
| 541,5499 | 0 | 0,00016 | 0 | 1e-05 | 4e-05 |
| 541,58708 | 0 | 0,00015 | 0 | 1e-05 | 3e-05 |
| 541,62427 | 0 | 0,00013 | 0 | 0 | 2e-05 |
| 541,66145 | 0 | 0,00011 | 0 | 0 | 1e-05 |
| 541,69863 | 0 | 1e-04 | 0 | 0 | 1e-05 |
| 541,73581 | 0 | 8e-05 | 0 | 0 | 1e-05 |
| 541,77299 | 0 | 7e-05 | 0 | 0 | 0 |
| 541,81018 | 0 | 6e-05 | 0 | 0 | 0 |
| 541,84736 | 0 | 5e-05 | 0 | 0 | 0 |
| 541,88454 | 0 | 4e-05 | 0 | 0 | 0 |
| 541,92172 | 0 | 3e-05 | 0 | 0 | 0 |
| 541,9589 | 0 | 2e-05 | 0 | 0 | 0 |
| 541,99609 | 0 | 2e-05 | 0 | 0 | 0 |
| 542,03327 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,07045 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,10763 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,14481 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,182 | 0 | 0 | 0 | 0 | 0 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 6e-05 |
| 524,03718 | 0 | 0 | 0 | 0 | 8e-05 |
| 524,07436 | 0 | 0 | 0 | 0 | 1e-04 |
| 524,11155 | 0 | 0 | 0 | 0 | 0,00011 |
| 524,14873 | 0 | 0 | 0 | 0 | 0,00012 |
| 524,18591 | 0 | 0 | 0 | 0 | 0,00012 |
| 524,22309 | 0 | 0 | 0 | 0 | 0,00012 |
| 524,26027 | 0 | 0 | 0 | 0 | 0,00012 |
| 524,29746 | 0 | 0 | 0 | 0 | 0,00011 |
| 524,33464 | 0 | 0 | 0 | 0 | 0,00011 |
| 524,37182 | 0 | 0 | 0 | 0 | 0,00011 |
| 524,409 | 0 | 0 | 0 | 0 | 0,00011 |
| 524,44618 | 1e-05 | 0 | 0 | 0 | 0,00012 |
| 524,48337 | 1e-05 | 1e-05 | 0 | 0 | 0,00012 |
| 524,52055 | 1e-05 | 1e-05 | 1e-05 | 0 | 0,00012 |
| 524,55773 | 2e-05 | 2e-05 | 1e-05 | 0 | 0,00012 |
| 524,59491 | 3e-05 | 3e-05 | 1e-05 | 0 | 0,00011 |
| 524,63209 | 4e-05 | 4e-05 | 2e-05 | 0 | 9e-05 |
| 524,66928 | 6e-05 | 5e-05 | 3e-05 | 0 | 7e-05 |
| 524,70646 | 8e-05 | 7e-05 | 5e-05 | 0 | 6e-05 |
| 524,74364 | 1e-04 | 9e-05 | 7e-05 | 0 | 4e-05 |
| 524,78082 | 0,00012 | 0,00011 | 1e-04 | 0 | 3e-05 |
| 524,818 | 0,00015 | 0,00013 | 0,00013 | 0 | 2e-05 |
| 524,85519 | 0,00017 | 0,00015 | 0,00017 | 0 | 1e-05 |
| 524,89237 | 0,00019 | 0,00016 | 0,00021 | 0 | 1e-05 |
| 524,92955 | 0,00021 | 0,00018 | 0,00026 | 0 | 0 |
| 524,96673 | 0,00023 | 0,00019 | 0,00031 | 0 | 0 |
| 525,00391 | 0,00024 | 0,00019 | 0,00036 | 0 | 0 |
| 525,0411 | 0,00024 | 0,00019 | 4e-04 | 0 | 0 |
| 525,07828 | 0,00025 | 0,00019 | 0,00043 | 0 | 0 |
| 525,11546 | 0,00025 | 0,00018 | 0,00045 | 0 | 1e-05 |
| 525,15264 | 0,00025 | 0,00018 | 0,00046 | 0 | 1e-05 |
| 525,18982 | 0,00025 | 0,00018 | 0,00046 | 0 | 3e-05 |
| 525,22701 | 0,00026 | 0,00018 | 0,00045 | 1e-05 | 4e-05 |
| 525,26419 | 0,00027 | 0,00018 | 0,00043 | 2e-05 | 7e-05 |
| 525,30137 | 0,00029 | 0,00019 | 0,00042 | 3e-05 | 1e-04 |
| 525,33855 | 0,00032 | 2e-04 | 0,00041 | 4e-05 | 0,00015 |
| 525,37573 | 0,00036 | 0,00022 | 0,00041 | 7e-05 | 2e-04 |
| 525,41292 | 0,00041 | 0,00024 | 0,00041 | 1e-04 | 0,00026 |
| 525,4501 | 0,00047 | 0,00026 | 0,00043 | 0,00014 | 0,00032 |
| 525,48728 | 0,00054 | 0,00028 | 0,00046 | 0,00019 | 0,00038 |
| 525,52446 | 0,00061 | 0,00031 | 0,00049 | 0,00024 | 0,00043 |
| 525,56164 | 0,00068 | 0,00034 | 0,00052 | 3e-04 | 0,00046 |
| 525,59883 | 0,00076 | 0,00037 | 0,00055 | 0,00035 | 0,00048 |
| 525,63601 | 0,00083 | 4e-04 | 0,00058 | 0,00039 | 0,00049 |
| 525,67319 | 0,00091 | 0,00044 | 6e-04 | 0,00043 | 0,00048 |
| 525,71037 | 0,00098 | 0,00049 | 0,00061 | 0,00045 | 0,00045 |
| 525,74755 | 0,00105 | 0,00055 | 0,00062 | 0,00045 | 0,00042 |
| 525,78474 | 0,00111 | 0,00061 | 0,00062 | 0,00044 | 0,00038 |
| 525,82192 | 0,00118 | 0,00068 | 0,00061 | 0,00043 | 0,00035 |
| 525,8591 | 0,00124 | 0,00076 | 0,00061 | 0,00041 | 0,00033 |
| 525,89628 | 0,00129 | 0,00084 | 0,00059 | 0,00039 | 0,00033 |
| 525,93346 | 0,00135 | 0,00093 | 0,00058 | 0,00037 | 0,00034 |
| 525,97065 | 0,00139 | 0,00101 | 0,00056 | 0,00038 | 0,00037 |
| 526,00783 | 0,00143 | 0,00109 | 0,00054 | 4e-04 | 4e-04 |
| 526,04501 | 0,00146 | 0,00116 | 0,00053 | 0,00044 | 0,00045 |
| 526,08219 | 0,00148 | 0,00122 | 0,00053 | 5e-04 | 5e-04 |
| 526,11937 | 0,00149 | 0,00127 | 0,00054 | 0,00058 | 0,00056 |
| 526,15656 | 0,00149 | 0,0013 | 0,00056 | 0,00067 | 0,00063 |
| 526,19374 | 0,00149 | 0,00131 | 6e-04 | 0,00078 | 7e-04 |
| 526,23092 | 0,00148 | 0,00132 | 0,00065 | 9e-04 | 0,00079 |
| 526,2681 | 0,00149 | 0,00131 | 0,00072 | 0,00101 | 0,00091 |
| 526,30528 | 0,00151 | 0,00131 | 0,00081 | 0,00114 | 0,00104 |
| 526,34247 | 0,00155 | 0,00131 | 9e-04 | 0,00126 | 0,00118 |
| 526,37965 | 0,00161 | 0,00132 | 0,00101 | 0,00138 | 0,00133 |
| 526,41683 | 0,00171 | 0,00135 | 0,00112 | 0,00149 | 0,00146 |
| 526,45401 | 0,00183 | 0,0014 | 0,00124 | 0,00158 | 0,00156 |
| 526,49119 | 0,00199 | 0,00147 | 0,00135 | 0,00164 | 0,00162 |
| 526,52838 | 0,00217 | 0,00156 | 0,00147 | 0,00167 | 0,00163 |
| 526,56556 | 0,00237 | 0,00167 | 0,00158 | 0,00165 | 0,00159 |
| 526,60274 | 0,00256 | 0,00179 | 0,00169 | 0,00159 | 0,00152 |
| 526,63992 | 0,00275 | 0,00192 | 0,00179 | 0,00149 | 0,00144 |
| 526,6771 | 0,00291 | 0,00206 | 0,00189 | 0,00138 | 0,00136 |
| 526,71429 | 0,00304 | 0,00219 | 0,00199 | 0,00126 | 0,00131 |
| 526,75147 | 0,00314 | 0,0023 | 0,00208 | 0,00116 | 0,00128 |
| 526,78865 | 0,00321 | 0,00241 | 0,00217 | 0,00108 | 0,00128 |
| 526,82583 | 0,00325 | 0,00249 | 0,00225 | 0,00104 | 0,0013 |
| 526,86301 | 0,00327 | 0,00256 | 0,00232 | 0,00103 | 0,00134 |
| 526,9002 | 0,0033 | 0,00261 | 0,00238 | 0,00106 | 0,00139 |
| 526,93738 | 0,00335 | 0,00265 | 0,00244 | 0,00111 | 0,00144 |
| 526,97456 | 0,00344 | 0,00268 | 0,00251 | 0,00118 | 0,00147 |
| 527,01174 | 0,00358 | 0,00273 | 0,00259 | 0,00126 | 0,0015 |
| 527,04892 | 0,0038 | 0,0028 | 0,0027 | 0,00134 | 0,00151 |
| 527,08611 | 0,00412 | 0,00291 | 0,00287 | 0,00142 | 0,0015 |
| 527,12329 | 0,00455 | 0,00309 | 0,00311 | 0,00151 | 0,00148 |
| 527,16047 | 0,00509 | 0,00336 | 0,00345 | 0,00163 | 0,00147 |
| 527,19765 | 0,00575 | 0,00375 | 0,00391 | 0,0018 | 0,0015 |
| 527,23483 | 0,00652 | 0,00428 | 0,0045 | 0,00207 | 0,0016 |
| 527,27202 | 0,00739 | 0,00497 | 0,00524 | 0,00247 | 0,00182 |
| 527,3092 | 0,00835 | 0,00581 | 0,00612 | 0,00304 | 0,00222 |
| 527,34638 | 0,00936 | 0,00678 | 0,00714 | 0,00384 | 0,00284 |
| 527,38356 | 0,01038 | 0,00786 | 0,00827 | 0,00487 | 0,00373 |
| 527,42074 | 0,01137 | 0,009 | 0,00946 | 0,00614 | 0,00488 |
| 527,45793 | 0,01229 | 0,01016 | 0,01067 | 0,00761 | 0,00627 |
| 527,49511 | 0,01311 | 0,01127 | 0,01184 | 0,00922 | 0,0078 |
| 527,53229 | 0,0138 | 0,01229 | 0,01291 | 0,01087 | 0,00938 |
| 527,56947 | 0,01434 | 0,01319 | 0,01383 | 0,01244 | 0,01086 |
| 527,60665 | 0,01475 | 0,01395 | 0,01456 | 0,01382 | 0,0121 |
| 527,64384 | 0,01505 | 0,01457 | 0,01508 | 0,01491 | 0,01301 |
| 527,68102 | 0,01528 | 0,01506 | 0,01541 | 0,01565 | 0,01351 |
| 527,7182 | 0,01548 | 0,01545 | 0,01559 | 0,01604 | 0,0136 |
| 527,75538 | 0,01567 | 0,01577 | 0,01567 | 0,01607 | 0,01331 |
| 527,79256 | 0,01588 | 0,01606 | 0,0157 | 0,01578 | 0,01269 |
| 527,82975 | 0,01612 | 0,01636 | 0,01576 | 0,01522 | 0,01184 |
| 527,86693 | 0,01641 | 0,01669 | 0,01587 | 0,01446 | 0,01087 |
| 527,90411 | 0,01673 | 0,01708 | 0,01608 | 0,01358 | 0,00989 |
| 527,94129 | 0,01707 | 0,0175 | 0,0164 | 0,01267 | 0,009 |
| 527,97847 | 0,0174 | 0,01796 | 0,01681 | 0,01182 | 0,0083 |
| 528,01566 | 0,01769 | 0,01843 | 0,01729 | 0,01114 | 0,00787 |
| 528,05284 | 0,01793 | 0,01888 | 0,01778 | 0,0107 | 0,00778 |
| 528,09002 | 0,01809 | 0,01927 | 0,01824 | 0,01059 | 0,00808 |
| 528,1272 | 0,01818 | 0,01958 | 0,01861 | 0,01085 | 0,00876 |
| 528,16438 | 0,0182 | 0,01979 | 0,01888 | 0,01149 | 0,00979 |
| 528,20157 | 0,01817 | 0,0199 | 0,01902 | 0,01245 | 0,01112 |
| 528,23875 | 0,01813 | 0,01992 | 0,01908 | 0,01367 | 0,01265 |
| 528,27593 | 0,01812 | 0,01987 | 0,01909 | 0,01505 | 0,01431 |
| 528,31311 | 0,01817 | 0,0198 | 0,01911 | 0,01649 | 0,016 |
| 528,35029 | 0,01834 | 0,01978 | 0,0192 | 0,01788 | 0,01765 |
| 528,38748 | 0,01865 | 0,01985 | 0,01942 | 0,01912 | 0,01919 |
| 528,42466 | 0,01913 | 0,02006 | 0,01982 | 0,02011 | 0,02054 |
| 528,46184 | 0,01981 | 0,02045 | 0,02045 | 0,02078 | 0,0216 |
| 528,49902 | 0,02067 | 0,02105 | 0,02131 | 0,02106 | 0,02231 |
| 528,5362 | 0,02169 | 0,02184 | 0,02242 | 0,02093 | 0,02258 |
| 528,57339 | 0,02285 | 0,02282 | 0,02374 | 0,02039 | 0,02237 |
| 528,61057 | 0,02409 | 0,02393 | 0,02523 | 0,01951 | 0,02169 |
| 528,64775 | 0,02536 | 0,02512 | 0,02682 | 0,01838 | 0,0206 |
| 528,68493 | 0,02663 | 0,02634 | 0,02846 | 0,01713 | 0,01923 |
| 528,72211 | 0,02788 | 0,02753 | 0,03005 | 0,01592 | 0,01772 |
| 528,7593 | 0,02909 | 0,02867 | 0,03155 | 0,01494 | 0,01626 |
| 528,79648 | 0,03028 | 0,02972 | 0,03292 | 0,01433 | 0,01504 |
| 528,83366 | 0,03147 | 0,03072 | 0,03415 | 0,01424 | 0,01422 |
| 528,87084 | 0,03271 | 0,0317 | 0,03527 | 0,01475 | 0,01394 |
| 528,90802 | 0,03401 | 0,03272 | 0,03633 | 0,01591 | 0,01431 |
| 528,94521 | 0,03542 | 0,03384 | 0,03738 | 0,01771 | 0,01537 |
| 528,98239 | 0,03693 | 0,03509 | 0,03849 | 0,02004 | 0,0171 |
| 529,01957 | 0,03855 | 0,03649 | 0,03971 | 0,02276 | 0,01942 |
| 529,05675 | 0,04023 | 0,03805 | 0,04105 | 0,02565 | 0,02215 |
| 529,09393 | 0,04193 | 0,03971 | 0,04251 | 0,02849 | 0,02507 |
| 529,13112 | 0,04356 | 0,0414 | 0,04404 | 0,03105 | 0,02793 |
| 529,1683 | 0,04507 | 0,04304 | 0,04555 | 0,03319 | 0,03053 |
| 529,20548 | 0,04638 | 0,04453 | 0,04696 | 0,03486 | 0,03281 |
| 529,24266 | 0,04744 | 0,04576 | 0,04814 | 0,03609 | 0,03476 |
| 529,27984 | 0,04823 | 0,04666 | 0,04902 | 0,03702 | 0,03647 |
| 529,31703 | 0,04874 | 0,04719 | 0,04958 | 0,03781 | 0,03809 |
| 529,35421 | 0,04899 | 0,04733 | 0,04982 | 0,03867 | 0,03973 |
| 529,39139 | 0,04901 | 0,04715 | 0,04978 | 0,03973 | 0,04147 |
| 529,42857 | 0,04887 | 0,04674 | 0,04955 | 0,04107 | 0,04334 |
| 529,46575 | 0,04862 | 0,04622 | 0,04922 | 0,04276 | 0,04534 |
| 529,50294 | 0,04835 | 0,04569 | 0,04891 | 0,0448 | 0,04746 |
| 529,54012 | 0,04812 | 0,04526 | 0,04872 | 0,04725 | 0,04971 |
| 529,5773 | 0,04801 | 0,04502 | 0,04872 | 0,05014 | 0,0522 |
| 529,61448 | 0,04807 | 0,04504 | 0,04899 | 0,05353 | 0,05506 |
| 529,65166 | 0,04833 | 0,04538 | 0,04956 | 0,05742 | 0,05848 |
| 529,68885 | 0,04882 | 0,04607 | 0,05043 | 0,06181 | 0,06259 |
| 529,72603 | 0,04954 | 0,0471 | 0,0516 | 0,06658 | 0,06754 |
| 529,76321 | 0,05049 | 0,04846 | 0,05303 | 0,07154 | 0,07317 |
| 529,80039 | 0,05164 | 0,05013 | 0,05466 | 0,07642 | 0,0792 |
| 529,83757 | 0,05296 | 0,05206 | 0,05642 | 0,08087 | 0,08519 |
| 529,87476 | 0,05442 | 0,0542 | 0,05825 | 0,08452 | 0,09054 |
| 529,91194 | 0,05599 | 0,05647 | 0,06009 | 0,08699 | 0,09464 |
| 529,94912 | 0,05764 | 0,05883 | 0,06191 | 0,08789 | 0,09693 |
| 529,9863 | 0,05938 | 0,06122 | 0,0637 | 0,08715 | 0,09703 |
| 530,02348 | 0,06121 | 0,06363 | 0,06549 | 0,0848 | 0,09479 |
| 530,06067 | 0,0632 | 0,0661 | 0,06736 | 0,08108 | 0,0904 |
| 530,09785 | 0,06543 | 0,06869 | 0,06942 | 0,07638 | 0,08433 |
| 530,13503 | 0,06799 | 0,07151 | 0,07183 | 0,07124 | 0,07731 |
| 530,17221 | 0,07098 | 0,0747 | 0,07477 | 0,06631 | 0,07021 |
| 530,20939 | 0,07451 | 0,07841 | 0,07842 | 0,06228 | 0,06397 |
| 530,24658 | 0,07864 | 0,08277 | 0,08293 | 0,05985 | 0,05954 |
| 530,28376 | 0,08339 | 0,08789 | 0,08842 | 0,05965 | 0,05776 |
| 530,32094 | 0,08875 | 0,09379 | 0,09495 | 0,06224 | 0,05937 |
| 530,35812 | 0,09462 | 0,10039 | 0,10235 | 0,06802 | 0,06518 |
| 530,3953 | 0,10085 | 0,10756 | 0,11038 | 0,07714 | 0,07529 |
| 530,43249 | 0,10721 | 0,11494 | 0,11872 | 0,08941 | 0,08949 |
| 530,46967 | 0,11343 | 0,12216 | 0,12698 | 0,10424 | 0,10707 |
| 530,50685 | 0,11919 | 0,1288 | 0,13467 | 0,12059 | 0,1267 |
| 530,54403 | 0,12411 | 0,13445 | 0,14135 | 0,13692 | 0,14653 |
| 530,58121 | 0,12784 | 0,13872 | 0,14656 | 0,15139 | 0,16437 |
| 530,6184 | 0,13017 | 0,1413 | 0,14992 | 0,1624 | 0,17807 |
| 530,65558 | 0,13094 | 0,14198 | 0,15118 | 0,16868 | 0,1859 |
| 530,69276 | 0,1301 | 0,14069 | 0,1502 | 0,16959 | 0,1869 |
| 530,72994 | 0,12769 | 0,13749 | 0,14702 | 0,16518 | 0,18111 |
| 530,76712 | 0,12388 | 0,13257 | 0,14181 | 0,15618 | 0,1695 |
| 530,80431 | 0,11891 | 0,12625 | 0,13491 | 0,14382 | 0,15378 |
| 530,84149 | 0,11308 | 0,11892 | 0,1267 | 0,1296 | 0,136 |
| 530,87867 | 0,10676 | 0,11103 | 0,11776 | 0,11501 | 0,11814 |
| 530,91585 | 0,10028 | 0,10307 | 0,10861 | 0,10127 | 0,10179 |
| 530,95303 | 0,094 | 0,09548 | 0,09972 | 0,08925 | 0,08797 |
| 530,99022 | 0,0882 | 0,08863 | 0,09146 | 0,07939 | 0,07724 |
| 531,0274 | 0,08318 | 0,08278 | 0,08416 | 0,07176 | 0,0694 |
| 531,06458 | 0,07924 | 0,07817 | 0,0781 | 0,06618 | 0,06404 |
| 531,10176 | 0,0765 | 0,07496 | 0,07354 | 0,06235 | 0,06071 |
| 531,13894 | 0,07515 | 0,07334 | 0,07073 | 0,05997 | 0,05901 |
| 531,17613 | 0,07535 | 0,07346 | 0,06991 | 0,05868 | 0,05859 |
| 531,21331 | 0,07728 | 0,0755 | 0,0714 | 0,05827 | 0,05918 |
| 531,25049 | 0,08108 | 0,07969 | 0,07549 | 0,05864 | 0,0606 |
| 531,28767 | 0,08689 | 0,08623 | 0,08248 | 0,05984 | 0,06276 |
| 531,32485 | 0,09481 | 0,09531 | 0,09263 | 0,06202 | 0,06568 |
| 531,36204 | 0,10487 | 0,10709 | 0,10616 | 0,06553 | 0,06958 |
| 531,39922 | 0,11703 | 0,1216 | 0,12323 | 0,0709 | 0,07493 |
| 531,4364 | 0,1311 | 0,13889 | 0,1434 | 0,07887 | 0,08252 |
| 531,47358 | 0,14682 | 0,15852 | 0,16621 | 0,0904 | 0,0935 |
| 531,51076 | 0,16375 | 0,17987 | 0,19097 | 0,10652 | 0,10931 |
| 531,54795 | 0,18133 | 0,20223 | 0,21676 | 0,12827 | 0,13152 |
| 531,58513 | 0,19879 | 0,2247 | 0,2425 | 0,15637 | 0,16152 |
| 531,62231 | 0,21541 | 0,24629 | 0,26699 | 0,191 | 0,20045 |
| 531,65949 | 0,23047 | 0,26601 | 0,28907 | 0,23146 | 0,24751 |
| 531,69667 | 0,24335 | 0,2829 | 0,30762 | 0,276 | 0,30034 |
| 531,73386 | 0,25355 | 0,2962 | 0,32177 | 0,32164 | 0,35516 |
| 531,77104 | 0,26077 | 0,30537 | 0,33091 | 0,36422 | 0,40702 |
| 531,80822 | 0,26492 | 0,31017 | 0,33482 | 0,3998 | 0,45052 |
| 531,8454 | 0,26612 | 0,3107 | 0,33367 | 0,42501 | 0,48086 |
| 531,88258 | 0,26473 | 0,30738 | 0,328 | 0,43769 | 0,49479 |
| 531,91977 | 0,26126 | 0,30091 | 0,31855 | 0,43732 | 0,49132 |
| 531,95695 | 0,25632 | 0,29212 | 0,30667 | 0,42503 | 0,4719 |
| 531,99413 | 0,2506 | 0,28216 | 0,29359 | 0,40339 | 0,44009 |
| 532,03131 | 0,24475 | 0,27201 | 0,28036 | 0,37581 | 0,40072 |
| 532,06849 | 0,23937 | 0,26242 | 0,26785 | 0,34592 | 0,35894 |
| 532,10568 | 0,23484 | 0,25396 | 0,25668 | 0,31695 | 0,31927 |
| 532,14286 | 0,23134 | 0,24693 | 0,24721 | 0,29133 | 0,28498 |
| 532,18004 | 0,22891 | 0,24142 | 0,23952 | 0,27051 | 0,25779 |
| 532,21722 | 0,22743 | 0,23733 | 0,23351 | 0,25496 | 0,23808 |
| 532,2544 | 0,22669 | 0,23442 | 0,22891 | 0,24439 | 0,22538 |
| 532,29159 | 0,22642 | 0,23234 | 0,22536 | 0,23802 | 0,21813 |
| 532,32877 | 0,22629 | 0,23073 | 0,22248 | 0,23487 | 0,21465 |
| 532,36595 | 0,22601 | 0,22923 | 0,21987 | 0,23365 | 0,21348 |
| 532,40313 | 0,22534 | 0,22752 | 0,21721 | 0,23334 | 0,21342 |
| 532,44031 | 0,22409 | 0,22534 | 0,21421 | 0,23322 | 0,21358 |
| 532,4775 | 0,22216 | 0,22249 | 0,21068 | 0,23291 | 0,21346 |
| 532,51468 | 0,21954 | 0,21891 | 0,20657 | 0,23248 | 0,21308 |
| 532,55186 | 0,21628 | 0,21465 | 0,20194 | 0,23243 | 0,21299 |
| 532,58904 | 0,21261 | 0,20983 | 0,19692 | 0,2336 | 0,21419 |
| 532,62622 | 0,20873 | 0,20466 | 0,19173 | 0,2371 | 0,21805 |
| 532,66341 | 0,20493 | 0,19942 | 0,18665 | 0,24395 | 0,22597 |
| 532,70059 | 0,20148 | 0,19446 | 0,18202 | 0,25485 | 0,23903 |
| 532,73777 | 0,19868 | 0,19014 | 0,17824 | 0,26986 | 0,25758 |
| 532,77495 | 0,19683 | 0,18686 | 0,17568 | 0,28814 | 0,28091 |
| 532,81213 | 0,19621 | 0,18501 | 0,17474 | 0,30797 | 0,30703 |
| 532,84932 | 0,19705 | 0,18491 | 0,17576 | 0,32683 | 0,33283 |
| 532,8865 | 0,19951 | 0,18683 | 0,17899 | 0,34185 | 0,35419 |
| 532,92368 | 0,20366 | 0,19092 | 0,18461 | 0,34995 | 0,36709 |
| 532,96086 | 0,20948 | 0,19717 | 0,19261 | 0,34912 | 0,36908 |
| 532,99804 | 0,21677 | 0,20549 | 0,20294 | 0,33908 | 0,35921 |
| 533,03523 | 0,22525 | 0,21544 | 0,21499 | 0,32063 | 0,33842 |
| 533,07241 | 0,23431 | 0,22635 | 0,22809 | 0,29571 | 0,3092 |
| 533,10959 | 0,24332 | 0,23748 | 0,24141 | 0,26695 | 0,27502 |
| 533,14677 | 0,2516 | 0,24799 | 0,25397 | 0,23713 | 0,23955 |
| 533,18395 | 0,25846 | 0,25703 | 0,26476 | 0,20871 | 0,206 |
| 533,22114 | 0,2633 | 0,26379 | 0,27284 | 0,18353 | 0,1766 |
| 533,25832 | 0,26562 | 0,26761 | 0,27739 | 0,16259 | 0,15249 |
| 533,2955 | 0,26511 | 0,26807 | 0,27785 | 0,14617 | 0,13381 |
| 533,33268 | 0,26167 | 0,26497 | 0,274 | 0,13393 | 0,11999 |
| 533,36986 | 0,25543 | 0,25843 | 0,26594 | 0,12517 | 0,11009 |
| 533,40705 | 0,24669 | 0,24881 | 0,25412 | 0,11907 | 0,10311 |
| 533,44423 | 0,23593 | 0,23667 | 0,23927 | 0,1148 | 0,09817 |
| 533,48141 | 0,22373 | 0,22274 | 0,22231 | 0,11171 | 0,09464 |
| 533,51859 | 0,2107 | 0,20776 | 0,20425 | 0,10933 | 0,09209 |
| 533,55577 | 0,1975 | 0,19255 | 0,18615 | 0,10735 | 0,09024 |
| 533,59295 | 0,18464 | 0,17775 | 0,16885 | 0,10561 | 0,08888 |
| 533,63014 | 0,1725 | 0,16381 | 0,1529 | 0,10404 | 0,08791 |
| 533,66732 | 0,16132 | 0,15105 | 0,13867 | 0,10262 | 0,0872 |
| 533,7045 | 0,15124 | 0,13963 | 0,1263 | 0,10132 | 0,08666 |
| 533,74168 | 0,1423 | 0,1296 | 0,11577 | 0,10009 | 0,08618 |
| 533,77886 | 0,13447 | 0,12092 | 0,10695 | 0,09887 | 0,08568 |
| 533,81605 | 0,12765 | 0,11347 | 0,09965 | 0,09762 | 0,08509 |
| 533,85323 | 0,12172 | 0,10712 | 0,09364 | 0,09631 | 0,08436 |
| 533,89041 | 0,11656 | 0,10171 | 0,0887 | 0,09497 | 0,0835 |
| 533,92759 | 0,11204 | 0,09709 | 0,08465 | 0,0937 | 0,08263 |
| 533,96477 | 0,10808 | 0,09316 | 0,08135 | 0,09269 | 0,08192 |
| 534,00196 | 0,10462 | 0,08981 | 0,0787 | 0,09216 | 0,08166 |
| 534,03914 | 0,10171 | 0,08704 | 0,07665 | 0,09234 | 0,08217 |
| 534,07632 | 0,09938 | 0,08487 | 0,07526 | 0,09343 | 0,08377 |
| 534,1135 | 0,09772 | 0,08338 | 0,07455 | 0,09553 | 0,08666 |
| 534,15068 | 0,09688 | 0,0827 | 0,07466 | 0,09856 | 0,09083 |
| 534,18787 | 0,09701 | 0,083 | 0,07574 | 0,10221 | 0,09598 |
| 534,22505 | 0,09826 | 0,08448 | 0,07798 | 0,10605 | 0,10145 |
| 534,26223 | 0,10076 | 0,08731 | 0,08157 | 0,10968 | 0,10653 |
| 534,29941 | 0,10459 | 0,09166 | 0,0867 | 0,11277 | 0,1106 |
| 534,33659 | 0,10976 | 0,09761 | 0,09346 | 0,11522 | 0,1133 |
| 534,37378 | 0,11621 | 0,10517 | 0,10188 | 0,11723 | 0,11474 |
| 534,41096 | 0,12379 | 0,11423 | 0,11185 | 0,11932 | 0,11559 |
| 534,44814 | 0,13223 | 0,12454 | 0,12312 | 0,12224 | 0,11692 |
| 534,48532 | 0,14118 | 0,1357 | 0,13525 | 0,12678 | 0,12006 |
| 534,5225 | 0,15013 | 0,14718 | 0,14768 | 0,13354 | 0,12614 |
| 534,55969 | 0,15851 | 0,15828 | 0,1597 | 0,14269 | 0,13578 |
| 534,59687 | 0,16575 | 0,16817 | 0,17041 | 0,15379 | 0,14872 |
| 534,63405 | 0,17134 | 0,17616 | 0,17899 | 0,16573 | 0,16371 |
| 534,67123 | 0,17483 | 0,18163 | 0,1848 | 0,17685 | 0,17867 |
| 534,70841 | 0,17591 | 0,18412 | 0,18734 | 0,18511 | 0,19098 |
| 534,7456 | 0,1744 | 0,18339 | 0,18639 | 0,18851 | 0,19813 |
| 534,78278 | 0,17032 | 0,17943 | 0,18195 | 0,18613 | 0,1981 |
| 534,81996 | 0,16385 | 0,17245 | 0,17429 | 0,17777 | 0,19011 |
| 534,85714 | 0,15534 | 0,16286 | 0,16392 | 0,16412 | 0,1753 |
| 534,89432 | 0,14524 | 0,15125 | 0,1515 | 0,14659 | 0,15551 |
| 534,93151 | 0,13408 | 0,13826 | 0,13777 | 0,12698 | 0,13313 |
| 534,96869 | 0,12243 | 0,12458 | 0,12348 | 0,10713 | 0,11052 |
| 535,00587 | 0,11082 | 0,11083 | 0,10931 | 0,0886 | 0,08963 |
| 535,04305 | 0,09975 | 0,09758 | 0,09582 | 0,0725 | 0,07174 |
| 535,08023 | 0,08954 | 0,0853 | 0,08342 | 0,05942 | 0,05743 |
| 535,11742 | 0,08039 | 0,07436 | 0,07242 | 0,04945 | 0,04669 |
| 535,1546 | 0,07243 | 0,06486 | 0,063 | 0,04235 | 0,03915 |
| 535,19178 | 0,06567 | 0,05687 | 0,05507 | 0,03768 | 0,03427 |
| 535,22896 | 0,0601 | 0,05037 | 0,04856 | 0,03494 | 0,03151 |
| 535,26614 | 0,05563 | 0,04529 | 0,04337 | 0,03372 | 0,03045 |
| 535,30333 | 0,05219 | 0,04152 | 0,03938 | 0,0337 | 0,03076 |
| 535,34051 | 0,04968 | 0,03892 | 0,03647 | 0,03469 | 0,03226 |
| 535,37769 | 0,04799 | 0,03736 | 0,03451 | 0,03648 | 0,03478 |
| 535,41487 | 0,04704 | 0,0367 | 0,0334 | 0,03895 | 0,03815 |
| 535,45205 | 0,04672 | 0,03679 | 0,03304 | 0,04191 | 0,04209 |
| 535,48924 | 0,04695 | 0,03751 | 0,03333 | 0,0451 | 0,0462 |
| 535,52642 | 0,04762 | 0,03872 | 0,03416 | 0,04819 | 0,05001 |
| 535,5636 | 0,04858 | 0,04029 | 0,03544 | 0,05084 | 0,05306 |
| 535,60078 | 0,0497 | 0,0421 | 0,03703 | 0,05272 | 0,05493 |
| 535,63796 | 0,05085 | 0,04399 | 0,03882 | 0,05357 | 0,05535 |
| 535,67515 | 0,05192 | 0,04581 | 0,04065 | 0,05329 | 0,05423 |
| 535,71233 | 0,05279 | 0,04743 | 0,04236 | 0,05189 | 0,05169 |
| 535,74951 | 0,05338 | 0,04875 | 0,0438 | 0,04955 | 0,048 |
| 535,78669 | 0,05363 | 0,04966 | 0,04486 | 0,04654 | 0,04357 |
| 535,82387 | 0,0535 | 0,0501 | 0,04546 | 0,04316 | 0,03883 |
| 535,86106 | 0,05299 | 0,05006 | 0,04552 | 0,03973 | 0,03419 |
| 535,89824 | 0,05211 | 0,04952 | 0,04505 | 0,03649 | 0,02996 |
| 535,93542 | 0,05092 | 0,04854 | 0,04407 | 0,03363 | 0,02634 |
| 535,9726 | 0,04945 | 0,04715 | 0,04265 | 0,0312 | 0,02345 |
| 536,00978 | 0,04776 | 0,04545 | 0,04088 | 0,02921 | 0,02128 |
| 536,04697 | 0,04594 | 0,0435 | 0,03887 | 0,02762 | 0,01981 |
| 536,08415 | 0,04404 | 0,0414 | 0,03671 | 0,02635 | 0,01892 |
| 536,12133 | 0,04212 | 0,03921 | 0,03452 | 0,02534 | 0,01846 |
| 536,15851 | 0,04023 | 0,03702 | 0,03236 | 0,0245 | 0,01829 |
| 536,19569 | 0,0384 | 0,03487 | 0,03032 | 0,02376 | 0,01824 |
| 536,23288 | 0,03667 | 0,0328 | 0,02843 | 0,02307 | 0,0182 |
| 536,27006 | 0,03503 | 0,03085 | 0,0267 | 0,02236 | 0,01806 |
| 536,30724 | 0,0335 | 0,02901 | 0,02513 | 0,02158 | 0,01775 |
| 536,34442 | 0,03208 | 0,0273 | 0,02371 | 0,02071 | 0,01727 |
| 536,3816 | 0,03074 | 0,0257 | 0,02241 | 0,01974 | 0,01663 |
| 536,41879 | 0,02947 | 0,0242 | 0,02123 | 0,01869 | 0,01589 |
| 536,45597 | 0,02824 | 0,02281 | 0,02013 | 0,01758 | 0,01511 |
| 536,49315 | 0,02705 | 0,02152 | 0,01911 | 0,01647 | 0,01434 |
| 536,53033 | 0,02587 | 0,02031 | 0,01815 | 0,0154 | 0,01362 |
| 536,56751 | 0,0247 | 0,01918 | 0,01725 | 0,01444 | 0,01297 |
| 536,6047 | 0,02353 | 0,01814 | 0,01639 | 0,0136 | 0,01239 |
| 536,64188 | 0,02236 | 0,01716 | 0,01557 | 0,01291 | 0,01186 |
| 536,67906 | 0,0212 | 0,01625 | 0,01478 | 0,01236 | 0,01136 |
| 536,71624 | 0,02005 | 0,01539 | 0,01401 | 0,01194 | 0,01089 |
| 536,75342 | 0,01893 | 0,01455 | 0,01325 | 0,01162 | 0,01044 |
| 536,79061 | 0,01784 | 0,01374 | 0,0125 | 0,01137 | 0,01002 |
| 536,82779 | 0,01678 | 0,01294 | 0,01175 | 0,01116 | 0,00963 |
| 536,86497 | 0,01576 | 0,01216 | 0,011 | 0,01097 | 0,00927 |
| 536,90215 | 0,01478 | 0,01139 | 0,01027 | 0,01077 | 0,00894 |
| 536,93933 | 0,01385 | 0,01065 | 0,00956 | 0,01054 | 0,00862 |
| 536,97652 | 0,01297 | 0,00995 | 0,00889 | 0,01027 | 0,0083 |
| 537,0137 | 0,01216 | 0,00931 | 0,00825 | 0,00996 | 0,00796 |
| 537,05088 | 0,01142 | 0,00875 | 0,00767 | 0,00961 | 0,00758 |
| 537,08806 | 0,01076 | 0,00827 | 0,00715 | 0,00922 | 0,00716 |
| 537,12524 | 0,0102 | 0,00788 | 0,0067 | 0,0088 | 0,0067 |
| 537,16243 | 0,00973 | 0,00758 | 0,00632 | 0,00834 | 0,00622 |
| 537,19961 | 0,00936 | 0,00737 | 0,00602 | 0,00787 | 0,00573 |
| 537,23679 | 0,00908 | 0,00723 | 0,00579 | 0,00739 | 0,00525 |
| 537,27397 | 0,00889 | 0,00713 | 0,00564 | 0,0069 | 0,0048 |
| 537,31115 | 0,00877 | 0,00707 | 0,00554 | 0,00641 | 0,00439 |
| 537,34834 | 0,00869 | 0,00702 | 0,00548 | 0,00592 | 0,00403 |
| 537,38552 | 0,00863 | 0,00697 | 0,00544 | 0,00546 | 0,00372 |
| 537,4227 | 0,00857 | 0,00692 | 0,00541 | 0,00502 | 0,00347 |
| 537,45988 | 0,00849 | 0,00686 | 0,00538 | 0,00464 | 0,00327 |
| 537,49706 | 0,00835 | 0,00677 | 0,00534 | 0,00431 | 0,00313 |
| 537,53425 | 0,00817 | 0,00667 | 0,00528 | 0,00406 | 0,00306 |
| 537,57143 | 0,00793 | 0,00653 | 0,00521 | 0,00389 | 0,00305 |
| 537,60861 | 0,00764 | 0,00637 | 0,00513 | 0,00379 | 0,00309 |
| 537,64579 | 0,00731 | 0,00619 | 0,00505 | 0,00375 | 0,00318 |
| 537,68297 | 0,00695 | 0,00597 | 0,00498 | 0,00376 | 0,0033 |
| 537,72016 | 0,00656 | 0,00573 | 0,00492 | 0,00379 | 0,00343 |
| 537,75734 | 0,00617 | 0,00547 | 0,00487 | 0,00382 | 0,00358 |
| 537,79452 | 0,00579 | 0,0052 | 0,00485 | 0,00382 | 0,00374 |
| 537,8317 | 0,00542 | 0,00492 | 0,00483 | 0,00379 | 0,0039 |
| 537,86888 | 0,00507 | 0,00465 | 0,00482 | 0,00373 | 0,00407 |
| 537,90607 | 0,00475 | 0,00438 | 0,00479 | 0,00363 | 0,00423 |
| 537,94325 | 0,00446 | 0,00411 | 0,00474 | 0,00352 | 0,00437 |
| 537,98043 | 0,00422 | 0,00386 | 0,00464 | 0,00341 | 0,00447 |
| 538,01761 | 0,00401 | 0,00361 | 0,0045 | 0,00332 | 0,00453 |
| 538,05479 | 0,00383 | 0,00338 | 0,00431 | 0,00325 | 0,00454 |
| 538,09198 | 0,00368 | 0,00315 | 0,00408 | 0,00321 | 0,0045 |
| 538,12916 | 0,00356 | 0,00294 | 0,00382 | 0,00322 | 0,00443 |
| 538,16634 | 0,00345 | 0,00274 | 0,00355 | 0,00326 | 0,00435 |
| 538,20352 | 0,00335 | 0,00256 | 0,00329 | 0,00332 | 0,00427 |
| 538,2407 | 0,00326 | 0,00242 | 0,00305 | 0,0034 | 0,0042 |
| 538,27789 | 0,00318 | 0,0023 | 0,00286 | 0,00347 | 0,00412 |
| 538,31507 | 0,0031 | 0,00222 | 0,00272 | 0,00351 | 0,00404 |
| 538,35225 | 0,00302 | 0,00217 | 0,00264 | 0,00351 | 0,00393 |
| 538,38943 | 0,00295 | 0,00215 | 0,00261 | 0,00347 | 0,00379 |
| 538,42661 | 0,00288 | 0,00215 | 0,00262 | 0,00337 | 0,00361 |
| 538,4638 | 0,00283 | 0,00217 | 0,00266 | 0,00324 | 0,00342 |
| 538,50098 | 0,00279 | 0,00221 | 0,00272 | 0,00309 | 0,00323 |
| 538,53816 | 0,00277 | 0,00226 | 0,00279 | 0,00293 | 0,00308 |
| 538,57534 | 0,00276 | 0,00231 | 0,00285 | 0,00279 | 0,00301 |
| 538,61252 | 0,00277 | 0,00237 | 0,00289 | 0,00267 | 0,00304 |
| 538,64971 | 0,0028 | 0,00243 | 0,0029 | 0,00259 | 0,00317 |
| 538,68689 | 0,00283 | 0,0025 | 0,0029 | 0,00255 | 0,00336 |
| 538,72407 | 0,00287 | 0,00256 | 0,00286 | 0,00253 | 0,00358 |
| 538,76125 | 0,00292 | 0,00261 | 0,0028 | 0,00252 | 0,00376 |
| 538,79843 | 0,00295 | 0,00266 | 0,00271 | 0,00252 | 0,00387 |
| 538,83562 | 0,00297 | 0,0027 | 0,00261 | 0,0025 | 0,00386 |
| 538,8728 | 0,00298 | 0,00272 | 0,0025 | 0,00246 | 0,00372 |
| 538,90998 | 0,00296 | 0,00271 | 0,00239 | 0,00239 | 0,00346 |
| 538,94716 | 0,00291 | 0,00268 | 0,00227 | 0,00229 | 0,0031 |
| 538,98434 | 0,00283 | 0,0026 | 0,00216 | 0,00218 | 0,0027 |
| 539,02153 | 0,00272 | 0,00249 | 0,00205 | 0,00206 | 0,00227 |
| 539,05871 | 0,00258 | 0,00234 | 0,00194 | 0,00193 | 0,00187 |
| 539,09589 | 0,00243 | 0,00216 | 0,00183 | 0,0018 | 0,00152 |
| 539,13307 | 0,00226 | 0,00195 | 0,00173 | 0,00168 | 0,00124 |
| 539,17025 | 0,00209 | 0,00173 | 0,00163 | 0,00157 | 0,00103 |
| 539,20744 | 0,00191 | 0,00152 | 0,00153 | 0,00147 | 9e-04 |
| 539,24462 | 0,00173 | 0,00131 | 0,00144 | 0,00139 | 0,00085 |
| 539,2818 | 0,00156 | 0,00111 | 0,00136 | 0,00132 | 0,00086 |
| 539,31898 | 0,0014 | 0,00095 | 0,00129 | 0,00128 | 0,00091 |
| 539,35616 | 0,00126 | 0,00081 | 0,00124 | 0,00126 | 0,00101 |
| 539,39335 | 0,00113 | 7e-04 | 0,00122 | 0,00127 | 0,00112 |
| 539,43053 | 0,00103 | 0,00062 | 0,00123 | 0,00131 | 0,00125 |
| 539,46771 | 0,00096 | 0,00056 | 0,00126 | 0,00137 | 0,00138 |
| 539,50489 | 9e-04 | 0,00053 | 0,00131 | 0,00146 | 0,0015 |
| 539,54207 | 0,00088 | 0,00051 | 0,00139 | 0,00156 | 0,00161 |
| 539,57926 | 0,00087 | 0,00052 | 0,00147 | 0,00167 | 0,00172 |
| 539,61644 | 0,00088 | 0,00054 | 0,00157 | 0,00177 | 0,00181 |
| 539,65362 | 0,00091 | 0,00058 | 0,00165 | 0,00186 | 0,0019 |
| 539,6908 | 0,00096 | 0,00064 | 0,00174 | 0,00192 | 0,00197 |
| 539,72798 | 0,00102 | 0,00071 | 0,00181 | 0,00194 | 0,00201 |
| 539,76517 | 0,00109 | 8e-04 | 0,00186 | 0,00191 | 0,002 |
| 539,80235 | 0,00116 | 0,00091 | 0,00191 | 0,00183 | 0,00195 |
| 539,83953 | 0,00122 | 0,00101 | 0,00193 | 0,00171 | 0,00185 |
| 539,87671 | 0,00129 | 0,00112 | 0,00195 | 0,00155 | 0,00169 |
| 539,91389 | 0,00134 | 0,00121 | 0,00194 | 0,00136 | 0,00149 |
| 539,95108 | 0,00137 | 0,00129 | 0,00193 | 0,00117 | 0,00127 |
| 539,98826 | 0,00137 | 0,00135 | 0,0019 | 0,00098 | 0,00104 |
| 540,02544 | 0,00135 | 0,00139 | 0,00185 | 8e-04 | 0,00083 |
| 540,06262 | 0,00131 | 0,00139 | 0,00179 | 0,00064 | 0,00064 |
| 540,0998 | 0,00124 | 0,00137 | 0,00171 | 0,00051 | 0,00048 |
| 540,13699 | 0,00116 | 0,00132 | 0,00161 | 4e-04 | 0,00037 |
| 540,17417 | 0,00105 | 0,00125 | 0,00151 | 0,00031 | 0,00028 |
| 540,21135 | 0,00094 | 0,00115 | 0,00138 | 0,00023 | 0,00023 |
| 540,24853 | 0,00083 | 0,00104 | 0,00126 | 0,00018 | 0,00021 |
| 540,28571 | 0,00071 | 0,00091 | 0,00113 | 0,00013 | 2e-04 |
| 540,3229 | 6e-04 | 0,00078 | 0,001 | 1e-04 | 0,00021 |
| 540,36008 | 0,00049 | 0,00066 | 0,00088 | 9e-05 | 0,00023 |
| 540,39726 | 4e-04 | 0,00055 | 0,00077 | 9e-05 | 0,00027 |
| 540,43444 | 0,00031 | 0,00046 | 0,00067 | 1e-04 | 0,00031 |
| 540,47162 | 0,00025 | 0,00039 | 0,00059 | 0,00012 | 0,00037 |
| 540,50881 | 0,00019 | 0,00035 | 0,00053 | 0,00016 | 0,00043 |
| 540,54599 | 0,00015 | 0,00033 | 0,00049 | 2e-04 | 5e-04 |
| 540,58317 | 0,00012 | 0,00033 | 0,00047 | 0,00025 | 0,00057 |
| 540,62035 | 1e-04 | 0,00034 | 0,00046 | 3e-04 | 0,00063 |
| 540,65753 | 9e-05 | 0,00038 | 0,00047 | 0,00035 | 0,00068 |
| 540,69472 | 9e-05 | 0,00042 | 0,00049 | 0,00038 | 0,00071 |
| 540,7319 | 1e-04 | 0,00046 | 0,00052 | 4e-04 | 0,00072 |
| 540,76908 | 0,00011 | 5e-04 | 0,00055 | 4e-04 | 7e-04 |
| 540,80626 | 0,00012 | 0,00055 | 0,00059 | 0,00038 | 0,00066 |
| 540,84344 | 0,00015 | 0,00058 | 0,00061 | 0,00034 | 0,00061 |
| 540,88063 | 0,00017 | 6e-04 | 0,00063 | 3e-04 | 0,00054 |
| 540,91781 | 2e-04 | 0,00061 | 0,00065 | 0,00025 | 0,00046 |
| 540,95499 | 0,00023 | 0,00062 | 0,00065 | 2e-04 | 0,00038 |
| 540,99217 | 0,00026 | 6e-04 | 0,00064 | 0,00015 | 0,00031 |
| 541,02935 | 3e-04 | 0,00058 | 0,00063 | 0,00011 | 0,00026 |
| 541,06654 | 0,00033 | 0,00056 | 0,00061 | 7e-05 | 0,00022 |
| 541,10372 | 0,00037 | 0,00052 | 0,00059 | 5e-05 | 2e-04 |
| 541,1409 | 4e-04 | 0,00048 | 0,00057 | 3e-05 | 2e-04 |
| 541,17808 | 0,00042 | 0,00044 | 0,00054 | 2e-05 | 2e-04 |
| 541,21526 | 0,00044 | 4e-04 | 0,00051 | 1e-05 | 0,00021 |
| 541,25245 | 0,00044 | 0,00036 | 0,00048 | 0 | 0,00022 |
| 541,28963 | 0,00044 | 0,00031 | 0,00043 | 0 | 0,00022 |
| 541,32681 | 0,00042 | 0,00027 | 0,00039 | 0 | 0,00021 |
| 541,36399 | 4e-04 | 0,00023 | 0,00034 | 0 | 0,00019 |
| 541,40117 | 0,00036 | 0,00019 | 0,00028 | 0 | 0,00017 |
| 541,43836 | 0,00032 | 0,00015 | 0,00023 | 0 | 0,00014 |
| 541,47554 | 0,00028 | 0,00012 | 0,00018 | 0 | 0,00011 |
| 541,51272 | 0,00023 | 9e-05 | 0,00014 | 0 | 9e-05 |
| 541,5499 | 0,00019 | 7e-05 | 1e-04 | 0 | 6e-05 |
| 541,58708 | 0,00015 | 5e-05 | 7e-05 | 0 | 4e-05 |
| 541,62427 | 0,00011 | 3e-05 | 5e-05 | 0 | 3e-05 |
| 541,66145 | 8e-05 | 2e-05 | 3e-05 | 0 | 2e-05 |
| 541,69863 | 6e-05 | 1e-05 | 2e-05 | 0 | 1e-05 |
| 541,73581 | 4e-05 | 1e-05 | 1e-05 | 0 | 0 |
| 541,77299 | 3e-05 | 1e-05 | 1e-05 | 0 | 0 |
| 541,81018 | 2e-05 | 0 | 0 | 0 | 0 |
| 541,84736 | 1e-05 | 0 | 0 | 0 | 0 |
| 541,88454 | 1e-05 | 0 | 0 | 0 | 0 |
| 541,92172 | 0 | 0 | 0 | 0 | 0 |
| 541,9589 | 0 | 0 | 0 | 0 | 0 |
| 541,99609 | 0 | 0 | 0 | 0 | 0 |
| 542,03327 | 0 | 0 | 0 | 0 | 0 |
| 542,07045 | 0 | 0 | 0 | 0 | 0 |
| 542,10763 | 0 | 0 | 0 | 0 | 0 |
| 542,14481 | 0 | 0 | 0 | 0 | 0 |
| 542,182 | 0 | 0 | 0 | 0 | 0 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 1e-05 | 0 | 0 |
| 524,03718 | 0 | 0 | 2e-05 | 0 | 0 |
| 524,07436 | 0 | 0 | 2e-05 | 0 | 0 |
| 524,11155 | 0 | 0 | 3e-05 | 0 | 0 |
| 524,14873 | 0 | 0 | 4e-05 | 0 | 0 |
| 524,18591 | 0 | 0 | 4e-05 | 0 | 0 |
| 524,22309 | 0 | 0 | 5e-05 | 0 | 0 |
| 524,26027 | 0 | 0 | 5e-05 | 0 | 0 |
| 524,29746 | 0 | 0 | 6e-05 | 0 | 0 |
| 524,33464 | 0 | 0 | 6e-05 | 0 | 0 |
| 524,37182 | 0 | 0 | 6e-05 | 0 | 0 |
| 524,409 | 0 | 0 | 5e-05 | 0 | 0 |
| 524,44618 | 0 | 0 | 5e-05 | 0 | 0 |
| 524,48337 | 0 | 0 | 5e-05 | 0 | 0 |
| 524,52055 | 0 | 0 | 4e-05 | 0 | 0 |
| 524,55773 | 0 | 0 | 3e-05 | 0 | 0 |
| 524,59491 | 0 | 0 | 3e-05 | 0 | 0 |
| 524,63209 | 0 | 0 | 2e-05 | 0 | 0 |
| 524,66928 | 0 | 0 | 2e-05 | 0 | 0 |
| 524,70646 | 0 | 0 | 1e-05 | 0 | 0 |
| 524,74364 | 0 | 0 | 1e-05 | 0 | 0 |
| 524,78082 | 0 | 0 | 1e-05 | 0 | 0 |
| 524,818 | 0 | 0 | 1e-05 | 0 | 0 |
| 524,85519 | 1e-05 | 1e-05 | 1e-05 | 0 | 0 |
| 524,89237 | 1e-05 | 1e-05 | 2e-05 | 0 | 0 |
| 524,92955 | 1e-05 | 1e-05 | 2e-05 | 0 | 0 |
| 524,96673 | 2e-05 | 2e-05 | 3e-05 | 0 | 0 |
| 525,00391 | 2e-05 | 2e-05 | 4e-05 | 0 | 0 |
| 525,0411 | 3e-05 | 3e-05 | 4e-05 | 0 | 0 |
| 525,07828 | 4e-05 | 4e-05 | 5e-05 | 0 | 0 |
| 525,11546 | 4e-05 | 4e-05 | 6e-05 | 0 | 0 |
| 525,15264 | 5e-05 | 5e-05 | 7e-05 | 0 | 0 |
| 525,18982 | 5e-05 | 5e-05 | 9e-05 | 0 | 0 |
| 525,22701 | 6e-05 | 6e-05 | 1e-04 | 0 | 0 |
| 525,26419 | 6e-05 | 6e-05 | 0,00011 | 0 | 0 |
| 525,30137 | 6e-05 | 6e-05 | 0,00012 | 0 | 0 |
| 525,33855 | 6e-05 | 5e-05 | 0,00014 | 0 | 0 |
| 525,37573 | 5e-05 | 5e-05 | 0,00015 | 0 | 0 |
| 525,41292 | 5e-05 | 4e-05 | 0,00016 | 0 | 0 |
| 525,4501 | 5e-05 | 4e-05 | 0,00018 | 0 | 0 |
| 525,48728 | 5e-05 | 3e-05 | 0,00019 | 0 | 0 |
| 525,52446 | 5e-05 | 3e-05 | 2e-04 | 0 | 0 |
| 525,56164 | 5e-05 | 3e-05 | 2e-04 | 0 | 0 |
| 525,59883 | 5e-05 | 3e-05 | 0,00021 | 0 | 0 |
| 525,63601 | 5e-05 | 3e-05 | 0,00021 | 0 | 0 |
| 525,67319 | 6e-05 | 4e-05 | 2e-04 | 1e-05 | 0 |
| 525,71037 | 6e-05 | 4e-05 | 2e-04 | 1e-05 | 0 |
| 525,74755 | 6e-05 | 6e-05 | 0,00019 | 2e-05 | 0 |
| 525,78474 | 6e-05 | 7e-05 | 0,00018 | 2e-05 | 0 |
| 525,82192 | 5e-05 | 9e-05 | 0,00017 | 4e-05 | 1e-05 |
| 525,8591 | 5e-05 | 0,00011 | 0,00016 | 5e-05 | 1e-05 |
| 525,89628 | 5e-05 | 0,00012 | 0,00015 | 7e-05 | 2e-05 |
| 525,93346 | 5e-05 | 0,00015 | 0,00015 | 1e-04 | 2e-05 |
| 525,97065 | 5e-05 | 0,00017 | 0,00015 | 0,00013 | 3e-05 |
| 526,00783 | 5e-05 | 0,00019 | 0,00016 | 0,00017 | 5e-05 |
| 526,04501 | 6e-05 | 0,00021 | 0,00017 | 0,00021 | 6e-05 |
| 526,08219 | 7e-05 | 0,00023 | 0,00018 | 0,00025 | 8e-05 |
| 526,11937 | 8e-05 | 0,00026 | 2e-04 | 0,00029 | 9e-05 |
| 526,15656 | 1e-04 | 0,00028 | 0,00022 | 0,00034 | 0,00011 |
| 526,19374 | 0,00013 | 0,00031 | 0,00024 | 0,00038 | 0,00013 |
| 526,23092 | 0,00015 | 0,00034 | 0,00025 | 0,00041 | 0,00014 |
| 526,2681 | 0,00019 | 0,00037 | 0,00027 | 0,00044 | 0,00015 |
| 526,30528 | 0,00022 | 0,00041 | 0,00029 | 0,00045 | 0,00017 |
| 526,34247 | 0,00026 | 0,00044 | 0,00031 | 0,00046 | 0,00018 |
| 526,37965 | 3e-04 | 0,00048 | 0,00033 | 0,00046 | 0,00019 |
| 526,41683 | 0,00035 | 0,00052 | 0,00035 | 0,00045 | 0,00019 |
| 526,45401 | 0,00039 | 0,00056 | 0,00037 | 0,00044 | 2e-04 |
| 526,49119 | 0,00044 | 6e-04 | 4e-04 | 0,00041 | 0,00022 |
| 526,52838 | 0,00048 | 0,00065 | 0,00043 | 0,00039 | 0,00023 |
| 526,56556 | 0,00052 | 0,00069 | 0,00046 | 0,00036 | 0,00024 |
| 526,60274 | 0,00055 | 0,00073 | 0,00049 | 0,00034 | 0,00025 |
| 526,63992 | 0,00057 | 0,00078 | 0,00053 | 0,00032 | 0,00026 |
| 526,6771 | 0,00059 | 0,00082 | 0,00056 | 0,00031 | 0,00027 |
| 526,71429 | 6e-04 | 0,00085 | 0,00059 | 3e-04 | 0,00028 |
| 526,75147 | 6e-04 | 0,00089 | 0,00062 | 3e-04 | 0,00028 |
| 526,78865 | 0,00059 | 0,00091 | 0,00065 | 0,00031 | 0,00028 |
| 526,82583 | 0,00057 | 0,00093 | 0,00068 | 0,00033 | 0,00028 |
| 526,86301 | 0,00056 | 0,00094 | 7e-04 | 0,00035 | 0,00029 |
| 526,9002 | 0,00054 | 0,00095 | 0,00072 | 0,00038 | 0,00029 |
| 526,93738 | 0,00053 | 0,00095 | 0,00074 | 0,00042 | 3e-04 |
| 526,97456 | 0,00052 | 0,00095 | 0,00075 | 0,00046 | 0,00032 |
| 527,01174 | 0,00052 | 0,00096 | 0,00075 | 0,00049 | 0,00035 |
| 527,04892 | 0,00053 | 0,00096 | 0,00075 | 0,00053 | 0,00039 |
| 527,08611 | 0,00054 | 0,00097 | 0,00075 | 0,00056 | 0,00044 |
| 527,12329 | 0,00057 | 0,00099 | 0,00074 | 0,00058 | 0,00049 |
| 527,16047 | 6e-04 | 0,00101 | 0,00074 | 6e-04 | 0,00054 |
| 527,19765 | 0,00065 | 0,00104 | 0,00074 | 0,00062 | 6e-04 |
| 527,23483 | 7e-04 | 0,00108 | 0,00074 | 0,00064 | 0,00064 |
| 527,27202 | 0,00076 | 0,00111 | 0,00074 | 0,00066 | 0,00068 |
| 527,3092 | 0,00084 | 0,00114 | 0,00076 | 0,00068 | 7e-04 |
| 527,34638 | 0,00092 | 0,00117 | 0,00077 | 7e-04 | 0,00072 |
| 527,38356 | 0,00101 | 0,0012 | 8e-04 | 0,00072 | 0,00072 |
| 527,42074 | 0,00111 | 0,00122 | 0,00083 | 0,00075 | 0,00072 |
| 527,45793 | 0,00121 | 0,00123 | 0,00087 | 0,00079 | 0,00071 |
| 527,49511 | 0,00131 | 0,00125 | 0,00091 | 0,00083 | 0,00071 |
| 527,53229 | 0,00141 | 0,00127 | 0,00097 | 0,00087 | 0,00072 |
| 527,56947 | 0,00151 | 0,0013 | 0,00102 | 0,00092 | 0,00075 |
| 527,60665 | 0,00159 | 0,00134 | 0,00109 | 0,00097 | 0,00079 |
| 527,64384 | 0,00168 | 0,00138 | 0,00116 | 0,00103 | 0,00084 |
| 527,68102 | 0,00175 | 0,00144 | 0,00124 | 0,00108 | 9e-04 |
| 527,7182 | 0,00182 | 0,00151 | 0,00133 | 0,00113 | 0,00097 |
| 527,75538 | 0,00189 | 0,0016 | 0,00142 | 0,00118 | 0,00105 |
| 527,79256 | 0,00195 | 0,0017 | 0,00153 | 0,00123 | 0,00112 |
| 527,82975 | 0,00203 | 0,00181 | 0,00164 | 0,00128 | 0,00118 |
| 527,86693 | 0,0021 | 0,00195 | 0,00175 | 0,00132 | 0,00124 |
| 527,90411 | 0,00219 | 0,0021 | 0,00187 | 0,00137 | 0,00128 |
| 527,94129 | 0,00228 | 0,00226 | 0,002 | 0,00142 | 0,00132 |
| 527,97847 | 0,00238 | 0,00244 | 0,00212 | 0,00147 | 0,00135 |
| 528,01566 | 0,00248 | 0,00262 | 0,00225 | 0,00154 | 0,00139 |
| 528,05284 | 0,00259 | 0,00282 | 0,00237 | 0,00162 | 0,00144 |
| 528,09002 | 0,0027 | 0,00301 | 0,00249 | 0,00171 | 0,00151 |
| 528,1272 | 0,00281 | 0,00319 | 0,00261 | 0,00182 | 0,00161 |
| 528,16438 | 0,00292 | 0,00337 | 0,00272 | 0,00194 | 0,00175 |
| 528,20157 | 0,00303 | 0,00353 | 0,00283 | 0,00208 | 0,00191 |
| 528,23875 | 0,00314 | 0,00367 | 0,00294 | 0,00222 | 0,0021 |
| 528,27593 | 0,00325 | 0,00379 | 0,00305 | 0,00235 | 0,00232 |
| 528,31311 | 0,00337 | 0,00389 | 0,00316 | 0,00248 | 0,00255 |
| 528,35029 | 0,00348 | 0,00397 | 0,00327 | 0,0026 | 0,00277 |
| 528,38748 | 0,0036 | 0,00403 | 0,00337 | 0,00269 | 0,00298 |
| 528,42466 | 0,00373 | 0,00408 | 0,00348 | 0,00276 | 0,00316 |
| 528,46184 | 0,00386 | 0,00413 | 0,0036 | 0,00281 | 0,0033 |
| 528,49902 | 0,00402 | 0,00417 | 0,00373 | 0,00284 | 0,00339 |
| 528,5362 | 0,0042 | 0,00421 | 0,00387 | 0,00286 | 0,00344 |
| 528,57339 | 0,00442 | 0,00428 | 0,00403 | 0,00289 | 0,00346 |
| 528,61057 | 0,00469 | 0,00438 | 0,00422 | 0,00293 | 0,00347 |
| 528,64775 | 0,00501 | 0,00452 | 0,00445 | 0,003 | 0,0035 |
| 528,68493 | 0,00539 | 0,00471 | 0,00473 | 0,00313 | 0,00357 |
| 528,72211 | 0,00583 | 0,00495 | 0,00505 | 0,00333 | 0,00373 |
| 528,7593 | 0,00632 | 0,00525 | 0,00542 | 0,00362 | 0,00399 |
| 528,79648 | 0,00685 | 0,0056 | 0,00584 | 0,00401 | 0,00437 |
| 528,83366 | 0,0074 | 0,00599 | 0,00629 | 0,00451 | 0,0049 |
| 528,87084 | 0,00795 | 0,00641 | 0,00676 | 0,00511 | 0,00557 |
| 528,90802 | 0,00847 | 0,00684 | 0,00724 | 0,00581 | 0,00635 |
| 528,94521 | 0,00895 | 0,00727 | 0,00772 | 0,00659 | 0,00723 |
| 528,98239 | 0,00936 | 0,00768 | 0,00818 | 0,00739 | 0,00815 |
| 529,01957 | 0,00969 | 0,00805 | 0,00861 | 0,00819 | 0,00906 |
| 529,05675 | 0,00994 | 0,00838 | 0,009 | 0,00894 | 0,0099 |
| 529,09393 | 0,01013 | 0,00867 | 0,00934 | 0,0096 | 0,01063 |
| 529,13112 | 0,01025 | 0,00892 | 0,00963 | 0,01013 | 0,0112 |
| 529,1683 | 0,01035 | 0,00915 | 0,00988 | 0,01052 | 0,01158 |
| 529,20548 | 0,01042 | 0,00936 | 0,0101 | 0,01074 | 0,01178 |
| 529,24266 | 0,0105 | 0,00957 | 0,01029 | 0,0108 | 0,01178 |
| 529,27984 | 0,01059 | 0,00979 | 0,01046 | 0,0107 | 0,01162 |
| 529,31703 | 0,01071 | 0,01002 | 0,01063 | 0,01048 | 0,01132 |
| 529,35421 | 0,01085 | 0,01027 | 0,01078 | 0,01016 | 0,01093 |
| 529,39139 | 0,01102 | 0,01053 | 0,01094 | 0,00979 | 0,0105 |
| 529,42857 | 0,01121 | 0,0108 | 0,0111 | 0,0094 | 0,01006 |
| 529,46575 | 0,0114 | 0,01108 | 0,01126 | 0,00905 | 0,00967 |
| 529,50294 | 0,01159 | 0,01136 | 0,01142 | 0,00877 | 0,00937 |
| 529,54012 | 0,01175 | 0,01163 | 0,01158 | 0,0086 | 0,0092 |
| 529,5773 | 0,01188 | 0,01189 | 0,01174 | 0,00857 | 0,00916 |
| 529,61448 | 0,01199 | 0,01212 | 0,0119 | 0,00868 | 0,00928 |
| 529,65166 | 0,01208 | 0,01232 | 0,01207 | 0,00893 | 0,00954 |
| 529,68885 | 0,01216 | 0,0125 | 0,01224 | 0,00931 | 0,00994 |
| 529,72603 | 0,01224 | 0,01266 | 0,01243 | 0,00981 | 0,01043 |
| 529,76321 | 0,01234 | 0,01282 | 0,01265 | 0,01038 | 0,011 |
| 529,80039 | 0,01247 | 0,01297 | 0,0129 | 0,01101 | 0,0116 |
| 529,83757 | 0,01266 | 0,01314 | 0,01319 | 0,01164 | 0,0122 |
| 529,87476 | 0,0129 | 0,01333 | 0,01354 | 0,01223 | 0,01274 |
| 529,91194 | 0,01322 | 0,01356 | 0,01394 | 0,01275 | 0,01319 |
| 529,94912 | 0,01361 | 0,01382 | 0,01439 | 0,01315 | 0,01352 |
| 529,9863 | 0,01407 | 0,01411 | 0,01489 | 0,01341 | 0,0137 |
| 530,02348 | 0,01459 | 0,01444 | 0,01544 | 0,01352 | 0,01373 |
| 530,06067 | 0,01516 | 0,01478 | 0,01601 | 0,01348 | 0,01363 |
| 530,09785 | 0,01576 | 0,01512 | 0,01661 | 0,01332 | 0,01343 |
| 530,13503 | 0,01636 | 0,01546 | 0,01721 | 0,01308 | 0,01317 |
| 530,17221 | 0,01697 | 0,01579 | 0,0178 | 0,0128 | 0,01291 |
| 530,20939 | 0,01757 | 0,01612 | 0,01838 | 0,01255 | 0,01271 |
| 530,24658 | 0,01817 | 0,01646 | 0,01896 | 0,01239 | 0,01262 |
| 530,28376 | 0,01877 | 0,01683 | 0,01955 | 0,01238 | 0,01271 |
| 530,32094 | 0,01939 | 0,01727 | 0,02018 | 0,01257 | 0,013 |
| 530,35812 | 0,02006 | 0,01779 | 0,02087 | 0,01299 | 0,01351 |
| 530,3953 | 0,0208 | 0,01843 | 0,02165 | 0,01365 | 0,01424 |
| 530,43249 | 0,02163 | 0,01921 | 0,02253 | 0,01454 | 0,01517 |
| 530,46967 | 0,02255 | 0,02012 | 0,02355 | 0,01563 | 0,01625 |
| 530,50685 | 0,02359 | 0,02118 | 0,02468 | 0,01686 | 0,01743 |
| 530,54403 | 0,02471 | 0,02235 | 0,02593 | 0,01815 | 0,01864 |
| 530,58121 | 0,0259 | 0,0236 | 0,02727 | 0,01945 | 0,01983 |
| 530,6184 | 0,02711 | 0,02488 | 0,02865 | 0,02068 | 0,02096 |
| 530,65558 | 0,0283 | 0,02613 | 0,03001 | 0,02182 | 0,02203 |
| 530,69276 | 0,02942 | 0,02731 | 0,0313 | 0,02284 | 0,02303 |
| 530,72994 | 0,03043 | 0,02838 | 0,03247 | 0,02374 | 0,024 |
| 530,76712 | 0,0313 | 0,0293 | 0,03348 | 0,02456 | 0,02498 |
| 530,80431 | 0,03199 | 0,03007 | 0,03429 | 0,02535 | 0,02602 |
| 530,84149 | 0,03251 | 0,03068 | 0,0349 | 0,02616 | 0,02716 |
| 530,87867 | 0,03284 | 0,03115 | 0,0353 | 0,02706 | 0,02845 |
| 530,91585 | 0,03303 | 0,03152 | 0,03551 | 0,02812 | 0,02993 |
| 530,95303 | 0,03309 | 0,03181 | 0,03557 | 0,02941 | 0,03162 |
| 530,99022 | 0,03307 | 0,03207 | 0,03551 | 0,03098 | 0,03357 |
| 531,0274 | 0,03304 | 0,03233 | 0,03538 | 0,03286 | 0,03577 |
| 531,06458 | 0,03303 | 0,03264 | 0,03526 | 0,03504 | 0,03821 |
| 531,10176 | 0,03311 | 0,03304 | 0,03518 | 0,0375 | 0,04085 |
| 531,13894 | 0,0333 | 0,03353 | 0,03521 | 0,04017 | 0,04364 |
| 531,17613 | 0,03365 | 0,03414 | 0,03538 | 0,04299 | 0,04649 |
| 531,21331 | 0,03416 | 0,03488 | 0,03571 | 0,04583 | 0,0493 |
| 531,25049 | 0,03484 | 0,03575 | 0,03622 | 0,04857 | 0,05194 |
| 531,28767 | 0,0357 | 0,03673 | 0,0369 | 0,05107 | 0,05425 |
| 531,32485 | 0,03671 | 0,03782 | 0,03774 | 0,05317 | 0,05608 |
| 531,36204 | 0,03784 | 0,03899 | 0,03873 | 0,05475 | 0,05732 |
| 531,39922 | 0,03907 | 0,04024 | 0,03984 | 0,05571 | 0,05786 |
| 531,4364 | 0,04037 | 0,04156 | 0,04105 | 0,05599 | 0,05765 |
| 531,47358 | 0,0417 | 0,04293 | 0,04237 | 0,05558 | 0,05672 |
| 531,51076 | 0,04308 | 0,04439 | 0,04379 | 0,05454 | 0,05513 |
| 531,54795 | 0,04451 | 0,04597 | 0,04534 | 0,05307 | 0,05312 |
| 531,58513 | 0,04604 | 0,04772 | 0,04709 | 0,05138 | 0,05095 |
| 531,62231 | 0,04773 | 0,04971 | 0,0491 | 0,04973 | 0,04892 |
| 531,65949 | 0,04966 | 0,05201 | 0,05143 | 0,04841 | 0,04735 |
| 531,69667 | 0,05192 | 0,05467 | 0,05417 | 0,0477 | 0,04656 |
| 531,73386 | 0,05456 | 0,05773 | 0,05735 | 0,04789 | 0,04684 |
| 531,77104 | 0,05763 | 0,06121 | 0,06101 | 0,04921 | 0,04843 |
| 531,80822 | 0,06113 | 0,06505 | 0,06511 | 0,05181 | 0,05148 |
| 531,8454 | 0,06501 | 0,06917 | 0,06959 | 0,05576 | 0,05603 |
| 531,88258 | 0,06917 | 0,07345 | 0,07432 | 0,06099 | 0,06198 |
| 531,91977 | 0,07347 | 0,0777 | 0,07912 | 0,06731 | 0,06908 |
| 531,95695 | 0,07772 | 0,08174 | 0,08377 | 0,07438 | 0,07694 |
| 531,99413 | 0,08169 | 0,08535 | 0,08805 | 0,0817 | 0,08503 |
| 532,03131 | 0,08514 | 0,0883 | 0,09171 | 0,08866 | 0,09266 |
| 532,06849 | 0,08789 | 0,09041 | 0,09446 | 0,0947 | 0,0992 |
| 532,10568 | 0,08983 | 0,09162 | 0,09621 | 0,09933 | 0,10416 |
| 532,14286 | 0,09089 | 0,0919 | 0,0969 | 0,10222 | 0,10716 |
| 532,18004 | 0,0911 | 0,09131 | 0,09652 | 0,10319 | 0,10803 |
| 532,21722 | 0,09052 | 0,08995 | 0,09517 | 0,1023 | 0,10683 |
| 532,2544 | 0,08932 | 0,08801 | 0,09299 | 0,09976 | 0,10378 |
| 532,29159 | 0,08769 | 0,08568 | 0,09018 | 0,09592 | 0,09928 |
| 532,32877 | 0,08583 | 0,08317 | 0,08696 | 0,09125 | 0,0938 |
| 532,36595 | 0,08397 | 0,0807 | 0,08359 | 0,0862 | 0,08785 |
| 532,40313 | 0,08232 | 0,07844 | 0,08027 | 0,08122 | 0,08188 |
| 532,44031 | 0,08104 | 0,07655 | 0,07724 | 0,07667 | 0,07628 |
| 532,4775 | 0,08028 | 0,07514 | 0,07467 | 0,07278 | 0,07134 |
| 532,51468 | 0,08019 | 0,07433 | 0,07273 | 0,06978 | 0,06726 |
| 532,55186 | 0,08083 | 0,07424 | 0,07163 | 0,06767 | 0,06411 |
| 532,58904 | 0,08225 | 0,07489 | 0,07149 | 0,06641 | 0,06185 |
| 532,62622 | 0,08451 | 0,07638 | 0,07242 | 0,06595 | 0,06045 |
| 532,66341 | 0,0877 | 0,07881 | 0,07455 | 0,06627 | 0,05988 |
| 532,70059 | 0,09189 | 0,08232 | 0,07803 | 0,06732 | 0,06015 |
| 532,73777 | 0,09719 | 0,08702 | 0,083 | 0,06913 | 0,06127 |
| 532,77495 | 0,10368 | 0,09303 | 0,08956 | 0,07177 | 0,06334 |
| 532,81213 | 0,11142 | 0,10046 | 0,09782 | 0,0754 | 0,06653 |
| 532,84932 | 0,12044 | 0,10934 | 0,1078 | 0,08022 | 0,07109 |
| 532,8865 | 0,13069 | 0,11965 | 0,11946 | 0,08652 | 0,07732 |
| 532,92368 | 0,14204 | 0,13126 | 0,13263 | 0,09465 | 0,0856 |
| 532,96086 | 0,15428 | 0,14395 | 0,14706 | 0,10498 | 0,0963 |
| 532,99804 | 0,16707 | 0,1574 | 0,16234 | 0,11787 | 0,10979 |
| 533,03523 | 0,17996 | 0,17114 | 0,17795 | 0,1337 | 0,12647 |
| 533,07241 | 0,19244 | 0,18459 | 0,19317 | 0,15223 | 0,14605 |
| 533,10959 | 0,20403 | 0,19721 | 0,20734 | 0,17312 | 0,16813 |
| 533,14677 | 0,21427 | 0,20846 | 0,21982 | 0,19568 | 0,19195 |
| 533,18395 | 0,22282 | 0,21792 | 0,23008 | 0,2189 | 0,21647 |
| 533,22114 | 0,22945 | 0,22527 | 0,23772 | 0,24156 | 0,24035 |
| 533,25832 | 0,23408 | 0,23037 | 0,24253 | 0,26229 | 0,26219 |
| 533,2955 | 0,2368 | 0,23326 | 0,24453 | 0,27981 | 0,28063 |
| 533,33268 | 0,23782 | 0,23415 | 0,24395 | 0,29304 | 0,29456 |
| 533,36986 | 0,23747 | 0,2334 | 0,24118 | 0,30132 | 0,30328 |
| 533,40705 | 0,23617 | 0,23148 | 0,23677 | 0,30447 | 0,30658 |
| 533,44423 | 0,23435 | 0,22888 | 0,23136 | 0,30286 | 0,30481 |
| 533,48141 | 0,2324 | 0,22612 | 0,22557 | 0,29729 | 0,2988 |
| 533,51859 | 0,2307 | 0,22365 | 0,22005 | 0,28889 | 0,28966 |
| 533,55577 | 0,22951 | 0,22181 | 0,21532 | 0,27916 | 0,27894 |
| 533,59295 | 0,22894 | 0,22075 | 0,21167 | 0,26947 | 0,26806 |
| 533,63014 | 0,22901 | 0,2205 | 0,20925 | 0,26083 | 0,25807 |
| 533,66732 | 0,22965 | 0,221 | 0,20807 | 0,25391 | 0,24971 |
| 533,7045 | 0,23074 | 0,2221 | 0,20801 | 0,24906 | 0,24337 |
| 533,74168 | 0,23212 | 0,22362 | 0,20886 | 0,24631 | 0,23916 |
| 533,77886 | 0,23361 | 0,22536 | 0,21037 | 0,24545 | 0,23691 |
| 533,81605 | 0,23504 | 0,22715 | 0,21225 | 0,24614 | 0,23634 |
| 533,85323 | 0,23626 | 0,22879 | 0,21422 | 0,24799 | 0,23712 |
| 533,89041 | 0,23716 | 0,23017 | 0,21603 | 0,25065 | 0,23897 |
| 533,92759 | 0,23769 | 0,23118 | 0,21751 | 0,25394 | 0,24175 |
| 533,96477 | 0,23782 | 0,23178 | 0,21853 | 0,2578 | 0,24548 |
| 534,00196 | 0,23761 | 0,23193 | 0,21904 | 0,26239 | 0,25035 |
| 534,03914 | 0,23712 | 0,23169 | 0,21909 | 0,26809 | 0,25688 |
| 534,07632 | 0,23653 | 0,23117 | 0,21884 | 0,27528 | 0,2654 |
| 534,1135 | 0,23601 | 0,23053 | 0,21849 | 0,28426 | 0,27626 |
| 534,15068 | 0,23573 | 0,22998 | 0,21829 | 0,29513 | 0,28954 |
| 534,18787 | 0,2359 | 0,22977 | 0,21851 | 0,30774 | 0,30504 |
| 534,22505 | 0,23672 | 0,23015 | 0,21944 | 0,32155 | 0,3221 |
| 534,26223 | 0,23836 | 0,2314 | 0,22138 | 0,33565 | 0,33966 |
| 534,29941 | 0,241 | 0,23379 | 0,22458 | 0,34881 | 0,35633 |
| 534,33659 | 0,24477 | 0,23751 | 0,22927 | 0,35964 | 0,37046 |
| 534,37378 | 0,24972 | 0,2427 | 0,23555 | 0,36673 | 0,38044 |
| 534,41096 | 0,25585 | 0,24937 | 0,24345 | 0,36888 | 0,38487 |
| 534,44814 | 0,26303 | 0,25738 | 0,25283 | 0,36533 | 0,38278 |
| 534,48532 | 0,27098 | 0,26646 | 0,26342 | 0,3558 | 0,37383 |
| 534,5225 | 0,27931 | 0,27615 | 0,2747 | 0,34062 | 0,35819 |
| 534,55969 | 0,28738 | 0,28574 | 0,28593 | 0,32054 | 0,33689 |
| 534,59687 | 0,29449 | 0,29452 | 0,29636 | 0,29738 | 0,31185 |
| 534,63405 | 0,29993 | 0,30174 | 0,3052 | 0,27269 | 0,28484 |
| 534,67123 | 0,30305 | 0,30671 | 0,31168 | 0,24794 | 0,25755 |
| 534,70841 | 0,30329 | 0,30886 | 0,31517 | 0,22438 | 0,23144 |
| 534,7456 | 0,30031 | 0,30778 | 0,31519 | 0,2029 | 0,20759 |
| 534,78278 | 0,29397 | 0,30328 | 0,31152 | 0,18405 | 0,18668 |
| 534,81996 | 0,28442 | 0,29541 | 0,30416 | 0,16802 | 0,16895 |
| 534,85714 | 0,27203 | 0,28445 | 0,2934 | 0,15471 | 0,15433 |
| 534,89432 | 0,25736 | 0,27088 | 0,27972 | 0,14384 | 0,1425 |
| 534,93151 | 0,24112 | 0,25532 | 0,26377 | 0,13501 | 0,13301 |
| 534,96869 | 0,22406 | 0,23849 | 0,24631 | 0,12781 | 0,12536 |
| 535,00587 | 0,20691 | 0,2211 | 0,22811 | 0,12184 | 0,11909 |
| 535,04305 | 0,19036 | 0,2039 | 0,20998 | 0,11681 | 0,11387 |
| 535,08023 | 0,17492 | 0,18744 | 0,19248 | 0,11246 | 0,10937 |
| 535,11742 | 0,16084 | 0,17209 | 0,17602 | 0,10858 | 0,10539 |
| 535,1546 | 0,14826 | 0,15811 | 0,16086 | 0,10508 | 0,10183 |
| 535,19178 | 0,1372 | 0,14561 | 0,14717 | 0,1019 | 0,09863 |
| 535,22896 | 0,12759 | 0,1346 | 0,13498 | 0,09904 | 0,09578 |
| 535,26614 | 0,11931 | 0,12503 | 0,12425 | 0,09648 | 0,09328 |
| 535,30333 | 0,11223 | 0,1168 | 0,1149 | 0,09427 | 0,09116 |
| 535,34051 | 0,10622 | 0,1098 | 0,10683 | 0,09245 | 0,08946 |
| 535,37769 | 0,10117 | 0,10392 | 0,09993 | 0,0911 | 0,08827 |
| 535,41487 | 0,09702 | 0,09907 | 0,09413 | 0,09033 | 0,08768 |
| 535,45205 | 0,09372 | 0,09519 | 0,08938 | 0,09023 | 0,0878 |
| 535,48924 | 0,0913 | 0,09228 | 0,08575 | 0,09091 | 0,08874 |
| 535,52642 | 0,08982 | 0,09045 | 0,08323 | 0,09246 | 0,0906 |
| 535,5636 | 0,08947 | 0,08973 | 0,08193 | 0,09497 | 0,09345 |
| 535,60078 | 0,09033 | 0,09027 | 0,082 | 0,09838 | 0,0972 |
| 535,63796 | 0,09259 | 0,09226 | 0,08367 | 0,10256 | 0,10173 |
| 535,67515 | 0,09646 | 0,09591 | 0,08715 | 0,10738 | 0,1069 |
| 535,71233 | 0,10214 | 0,10146 | 0,09271 | 0,11271 | 0,11259 |
| 535,74951 | 0,10979 | 0,10908 | 0,10054 | 0,11849 | 0,11875 |
| 535,78669 | 0,11951 | 0,11893 | 0,11079 | 0,12477 | 0,12544 |
| 535,82387 | 0,13128 | 0,13102 | 0,12351 | 0,13174 | 0,13286 |
| 535,86106 | 0,14495 | 0,14525 | 0,13857 | 0,13973 | 0,14135 |
| 535,89824 | 0,16018 | 0,1613 | 0,15569 | 0,14915 | 0,15132 |
| 535,93542 | 0,17647 | 0,17869 | 0,17434 | 0,16039 | 0,16316 |
| 535,9726 | 0,19311 | 0,19672 | 0,19379 | 0,17366 | 0,1771 |
| 536,00978 | 0,20926 | 0,21442 | 0,21296 | 0,18893 | 0,19307 |
| 536,04697 | 0,22389 | 0,2307 | 0,23078 | 0,20573 | 0,21061 |
| 536,08415 | 0,23595 | 0,24455 | 0,24617 | 0,22303 | 0,22856 |
| 536,12133 | 0,2447 | 0,25505 | 0,25816 | 0,23928 | 0,2454 |
| 536,15851 | 0,24956 | 0,26149 | 0,26597 | 0,25288 | 0,25949 |
| 536,19569 | 0,2502 | 0,26341 | 0,26905 | 0,26225 | 0,26925 |
| 536,23288 | 0,24662 | 0,26066 | 0,26723 | 0,26616 | 0,27336 |
| 536,27006 | 0,23906 | 0,25344 | 0,26062 | 0,26387 | 0,27104 |
| 536,30724 | 0,22805 | 0,24222 | 0,24967 | 0,25529 | 0,26215 |
| 536,34442 | 0,21429 | 0,22772 | 0,23512 | 0,24096 | 0,24721 |
| 536,3816 | 0,1986 | 0,21084 | 0,21786 | 0,22201 | 0,22735 |
| 536,41879 | 0,1818 | 0,19252 | 0,19888 | 0,19996 | 0,20409 |
| 536,45597 | 0,16468 | 0,1737 | 0,17921 | 0,17648 | 0,17918 |
| 536,49315 | 0,14793 | 0,15523 | 0,15985 | 0,15319 | 0,15432 |
| 536,53033 | 0,13209 | 0,13789 | 0,14152 | 0,13148 | 0,131 |
| 536,56751 | 0,11767 | 0,12208 | 0,12473 | 0,11246 | 0,11063 |
| 536,6047 | 0,10484 | 0,10807 | 0,10982 | 0,09686 | 0,09367 |
| 536,64188 | 0,09367 | 0,09598 | 0,09695 | 0,08468 | 0,08034 |
| 536,67906 | 0,08418 | 0,08578 | 0,08613 | 0,07579 | 0,07058 |
| 536,71624 | 0,0763 | 0,07741 | 0,07731 | 0,06994 | 0,06414 |
| 536,75342 | 0,06996 | 0,07073 | 0,07034 | 0,06674 | 0,06065 |
| 536,79061 | 0,06503 | 0,06559 | 0,06505 | 0,06578 | 0,05968 |
| 536,82779 | 0,06139 | 0,06182 | 0,06125 | 0,06663 | 0,06076 |
| 536,86497 | 0,0589 | 0,05926 | 0,05877 | 0,06886 | 0,06342 |
| 536,90215 | 0,05744 | 0,05777 | 0,05741 | 0,07201 | 0,06715 |
| 536,93933 | 0,05686 | 0,0572 | 0,05704 | 0,0756 | 0,07141 |
| 536,97652 | 0,05702 | 0,05739 | 0,05746 | 0,07913 | 0,07565 |
| 537,0137 | 0,05775 | 0,05822 | 0,05844 | 0,08211 | 0,07933 |
| 537,05088 | 0,05888 | 0,05945 | 0,05981 | 0,08408 | 0,0819 |
| 537,08806 | 0,06022 | 0,06086 | 0,06135 | 0,08457 | 0,0829 |
| 537,12524 | 0,06154 | 0,06228 | 0,06287 | 0,08337 | 0,08217 |
| 537,16243 | 0,06263 | 0,06349 | 0,06417 | 0,08048 | 0,07966 |
| 537,19961 | 0,06332 | 0,06431 | 0,06508 | 0,07604 | 0,07553 |
| 537,23679 | 0,06345 | 0,06461 | 0,06544 | 0,07032 | 0,07005 |
| 537,27397 | 0,06291 | 0,06425 | 0,06515 | 0,06372 | 0,06361 |
| 537,31115 | 0,06163 | 0,06319 | 0,06414 | 0,05665 | 0,05666 |
| 537,34834 | 0,0596 | 0,06141 | 0,0624 | 0,04953 | 0,04961 |
| 537,38552 | 0,05689 | 0,05896 | 0,05996 | 0,04275 | 0,04287 |
| 537,4227 | 0,05359 | 0,05591 | 0,05688 | 0,03657 | 0,0367 |
| 537,45988 | 0,04984 | 0,05238 | 0,05329 | 0,03119 | 0,03131 |
| 537,49706 | 0,0458 | 0,04849 | 0,04933 | 0,02669 | 0,02678 |
| 537,53425 | 0,04163 | 0,04441 | 0,04517 | 0,02304 | 0,0231 |
| 537,57143 | 0,0375 | 0,04028 | 0,04092 | 0,02019 | 0,02025 |
| 537,60861 | 0,03353 | 0,03621 | 0,03672 | 0,01806 | 0,01807 |
| 537,64579 | 0,02984 | 0,03231 | 0,03266 | 0,01645 | 0,0164 |
| 537,68297 | 0,02646 | 0,02866 | 0,02882 | 0,01524 | 0,01513 |
| 537,72016 | 0,02345 | 0,0253 | 0,02527 | 0,0143 | 0,01412 |
| 537,75734 | 0,02081 | 0,02228 | 0,02205 | 0,01355 | 0,01329 |
| 537,79452 | 0,01852 | 0,01962 | 0,01919 | 0,01292 | 0,01258 |
| 537,8317 | 0,01657 | 0,01732 | 0,0167 | 0,01234 | 0,01192 |
| 537,86888 | 0,01493 | 0,01537 | 0,01456 | 0,01179 | 0,01128 |
| 537,90607 | 0,01355 | 0,01373 | 0,01276 | 0,01125 | 0,01066 |
| 537,94325 | 0,01239 | 0,01237 | 0,01129 | 0,0107 | 0,01004 |
| 537,98043 | 0,01142 | 0,01125 | 0,0101 | 0,01015 | 0,00943 |
| 538,01761 | 0,01059 | 0,01032 | 0,00914 | 0,00961 | 0,00884 |
| 538,05479 | 0,00989 | 0,00954 | 0,00838 | 0,00909 | 0,00827 |
| 538,09198 | 0,00928 | 0,00885 | 0,00777 | 0,00859 | 0,00774 |
| 538,12916 | 0,00873 | 0,00824 | 0,0073 | 0,00812 | 0,00725 |
| 538,16634 | 0,00824 | 0,00769 | 0,00692 | 0,0077 | 0,0068 |
| 538,20352 | 0,00778 | 0,00718 | 0,00662 | 0,0073 | 0,00641 |
| 538,2407 | 0,00735 | 0,00671 | 0,00638 | 0,00694 | 0,00607 |
| 538,27789 | 0,00695 | 0,00629 | 0,00619 | 0,0066 | 0,00579 |
| 538,31507 | 0,00657 | 0,00592 | 0,00602 | 0,00628 | 0,00557 |
| 538,35225 | 0,00621 | 0,0056 | 0,00589 | 0,00598 | 0,0054 |
| 538,38943 | 0,00588 | 0,00534 | 0,00577 | 0,0057 | 0,00529 |
| 538,42661 | 0,00556 | 0,00513 | 0,00566 | 0,00545 | 0,00523 |
| 538,4638 | 0,00528 | 0,00496 | 0,00557 | 0,00522 | 0,0052 |
| 538,50098 | 0,00501 | 0,00484 | 0,00549 | 0,00502 | 0,0052 |
| 538,53816 | 0,00477 | 0,00475 | 0,00542 | 0,00486 | 0,00522 |
| 538,57534 | 0,00456 | 0,00467 | 0,00535 | 0,00472 | 0,00523 |
| 538,61252 | 0,00436 | 0,0046 | 0,00529 | 0,00461 | 0,00522 |
| 538,64971 | 0,00418 | 0,00452 | 0,00522 | 0,00451 | 0,00518 |
| 538,68689 | 0,00401 | 0,00443 | 0,00514 | 0,0044 | 0,0051 |
| 538,72407 | 0,00384 | 0,00433 | 0,00505 | 0,00427 | 0,00496 |
| 538,76125 | 0,00368 | 0,00421 | 0,00494 | 0,00411 | 0,00476 |
| 538,79843 | 0,00351 | 0,00407 | 0,00481 | 0,00391 | 0,00451 |
| 538,83562 | 0,00334 | 0,00392 | 0,00465 | 0,00367 | 0,00421 |
| 538,8728 | 0,00315 | 0,00375 | 0,00446 | 0,00339 | 0,00387 |
| 538,90998 | 0,00296 | 0,00358 | 0,00424 | 0,00309 | 0,0035 |
| 538,94716 | 0,00277 | 0,00339 | 0,00401 | 0,00278 | 0,00312 |
| 538,98434 | 0,00257 | 0,00321 | 0,00375 | 0,00247 | 0,00275 |
| 539,02153 | 0,00237 | 0,00301 | 0,00348 | 0,00217 | 0,0024 |
| 539,05871 | 0,00217 | 0,00282 | 0,00321 | 0,0019 | 0,00208 |
| 539,09589 | 0,00199 | 0,00262 | 0,00293 | 0,00166 | 0,00181 |
| 539,13307 | 0,00182 | 0,00242 | 0,00264 | 0,00145 | 0,00158 |
| 539,17025 | 0,00165 | 0,00222 | 0,00236 | 0,00127 | 0,0014 |
| 539,20744 | 0,0015 | 0,00202 | 0,00208 | 0,00112 | 0,00126 |
| 539,24462 | 0,00135 | 0,00183 | 0,00182 | 0,001 | 0,00116 |
| 539,2818 | 0,00122 | 0,00164 | 0,00156 | 0,00089 | 0,00108 |
| 539,31898 | 0,00109 | 0,00148 | 0,00133 | 8e-04 | 0,00102 |
| 539,35616 | 0,00097 | 0,00133 | 0,00112 | 0,00072 | 0,00098 |
| 539,39335 | 0,00085 | 0,0012 | 0,00094 | 0,00066 | 0,00094 |
| 539,43053 | 0,00075 | 0,00109 | 0,00079 | 0,00061 | 0,00091 |
| 539,46771 | 0,00067 | 0,001 | 0,00068 | 0,00057 | 0,00089 |
| 539,50489 | 6e-04 | 0,00094 | 0,00059 | 0,00055 | 0,00086 |
| 539,54207 | 0,00055 | 0,00089 | 0,00055 | 0,00054 | 0,00085 |
| 539,57926 | 0,00052 | 0,00085 | 0,00053 | 0,00053 | 0,00084 |
| 539,61644 | 0,00051 | 0,00083 | 0,00054 | 0,00054 | 0,00083 |
| 539,65362 | 0,00052 | 0,00082 | 0,00057 | 0,00055 | 0,00082 |
| 539,6908 | 0,00054 | 0,00081 | 0,00061 | 0,00057 | 0,00082 |
| 539,72798 | 0,00058 | 0,00081 | 0,00067 | 0,00058 | 8e-04 |
| 539,76517 | 0,00062 | 0,00081 | 0,00073 | 6e-04 | 0,00078 |
| 539,80235 | 0,00067 | 0,00081 | 8e-04 | 0,00062 | 0,00075 |
| 539,83953 | 0,00072 | 0,00081 | 0,00085 | 0,00062 | 7e-04 |
| 539,87671 | 0,00076 | 0,00081 | 9e-04 | 0,00063 | 0,00065 |
| 539,91389 | 0,00079 | 0,00081 | 0,00093 | 0,00062 | 0,00058 |
| 539,95108 | 0,00081 | 8e-04 | 0,00095 | 6e-04 | 0,00051 |
| 539,98826 | 0,00082 | 8e-04 | 0,00094 | 0,00058 | 0,00044 |
| 540,02544 | 0,00082 | 0,00078 | 0,00092 | 0,00055 | 0,00036 |
| 540,06262 | 8e-04 | 0,00076 | 0,00089 | 0,00052 | 0,00029 |
| 540,0998 | 0,00077 | 0,00073 | 0,00084 | 0,00049 | 0,00024 |
| 540,13699 | 0,00072 | 7e-04 | 0,00078 | 0,00046 | 0,00019 |
| 540,17417 | 0,00067 | 0,00065 | 0,00072 | 0,00043 | 0,00015 |
| 540,21135 | 0,00061 | 6e-04 | 0,00066 | 0,00041 | 0,00013 |
| 540,24853 | 0,00055 | 0,00055 | 0,00059 | 0,00039 | 0,00011 |
| 540,28571 | 0,00048 | 0,00049 | 0,00053 | 0,00038 | 1e-04 |
| 540,3229 | 0,00042 | 0,00043 | 0,00047 | 0,00037 | 9e-05 |
| 540,36008 | 0,00036 | 0,00038 | 0,00042 | 0,00036 | 9e-05 |
| 540,39726 | 3e-04 | 0,00032 | 0,00037 | 0,00036 | 9e-05 |
| 540,43444 | 0,00025 | 0,00027 | 0,00033 | 0,00035 | 9e-05 |
| 540,47162 | 0,00021 | 0,00022 | 3e-04 | 0,00035 | 9e-05 |
| 540,50881 | 0,00018 | 0,00018 | 0,00026 | 0,00034 | 1e-04 |
| 540,54599 | 0,00017 | 0,00015 | 0,00024 | 0,00034 | 1e-04 |
| 540,58317 | 0,00016 | 0,00012 | 0,00021 | 0,00033 | 0,00011 |
| 540,62035 | 0,00016 | 1e-04 | 0,00019 | 0,00033 | 0,00011 |
| 540,65753 | 0,00017 | 9e-05 | 0,00017 | 0,00032 | 0,00012 |
| 540,69472 | 0,00019 | 8e-05 | 0,00016 | 0,00032 | 0,00012 |
| 540,7319 | 0,00021 | 8e-05 | 0,00015 | 0,00031 | 0,00012 |
| 540,76908 | 0,00024 | 9e-05 | 0,00014 | 3e-04 | 0,00012 |
| 540,80626 | 0,00027 | 0,00011 | 0,00013 | 0,00028 | 0,00012 |
| 540,84344 | 3e-04 | 0,00013 | 0,00013 | 0,00026 | 0,00011 |
| 540,88063 | 0,00033 | 0,00015 | 0,00012 | 0,00023 | 1e-04 |
| 540,91781 | 0,00035 | 0,00017 | 0,00012 | 2e-04 | 9e-05 |
| 540,95499 | 0,00038 | 2e-04 | 0,00012 | 0,00017 | 8e-05 |
| 540,99217 | 4e-04 | 0,00022 | 0,00012 | 0,00014 | 7e-05 |
| 541,02935 | 0,00042 | 0,00024 | 0,00012 | 0,00011 | 5e-05 |
| 541,06654 | 0,00043 | 0,00025 | 0,00012 | 9e-05 | 4e-05 |
| 541,10372 | 0,00044 | 0,00025 | 0,00012 | 6e-05 | 3e-05 |
| 541,1409 | 0,00045 | 0,00025 | 0,00013 | 5e-05 | 2e-05 |
| 541,17808 | 0,00044 | 0,00024 | 0,00013 | 3e-05 | 2e-05 |
| 541,21526 | 0,00043 | 0,00023 | 0,00013 | 2e-05 | 1e-05 |
| 541,25245 | 0,00041 | 0,00021 | 0,00012 | 1e-05 | 1e-05 |
| 541,28963 | 0,00038 | 0,00018 | 0,00011 | 1e-05 | 1e-05 |
| 541,32681 | 0,00035 | 0,00016 | 0,00011 | 1e-05 | 1e-05 |
| 541,36399 | 0,00031 | 0,00013 | 9e-05 | 0 | 1e-05 |
| 541,40117 | 0,00027 | 1e-04 | 8e-05 | 0 | 1e-05 |
| 541,43836 | 0,00023 | 8e-05 | 7e-05 | 0 | 1e-05 |
| 541,47554 | 0,00019 | 6e-05 | 6e-05 | 0 | 2e-05 |
| 541,51272 | 0,00015 | 5e-05 | 5e-05 | 0 | 2e-05 |
| 541,5499 | 0,00011 | 3e-05 | 3e-05 | 0 | 3e-05 |
| 541,58708 | 8e-05 | 2e-05 | 3e-05 | 0 | 4e-05 |
| 541,62427 | 6e-05 | 2e-05 | 2e-05 | 0 | 4e-05 |
| 541,66145 | 4e-05 | 1e-05 | 1e-05 | 0 | 5e-05 |
| 541,69863 | 3e-05 | 1e-05 | 1e-05 | 0 | 6e-05 |
| 541,73581 | 2e-05 | 0 | 1e-05 | 0 | 6e-05 |
| 541,77299 | 1e-05 | 0 | 0 | 0 | 6e-05 |
| 541,81018 | 1e-05 | 0 | 0 | 0 | 6e-05 |
| 541,84736 | 0 | 0 | 0 | 0 | 6e-05 |
| 541,88454 | 0 | 0 | 0 | 0 | 5e-05 |
| 541,92172 | 0 | 0 | 0 | 0 | 5e-05 |
| 541,9589 | 0 | 0 | 0 | 0 | 4e-05 |
| 541,99609 | 0 | 0 | 0 | 0 | 3e-05 |
| 542,03327 | 0 | 0 | 0 | 0 | 3e-05 |
| 542,07045 | 0 | 0 | 0 | 0 | 2e-05 |
| 542,10763 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,14481 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,182 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0,00014 | 0 | 0 | 0 |
| 524,03718 | 0 | 0,00015 | 0 | 0 | 0 |
| 524,07436 | 0 | 0,00015 | 0 | 0 | 0 |
| 524,11155 | 0 | 0,00014 | 0 | 0 | 0 |
| 524,14873 | 0 | 0,00014 | 0 | 0 | 0 |
| 524,18591 | 0 | 0,00013 | 0 | 0 | 0 |
| 524,22309 | 0 | 0,00013 | 0 | 0 | 0 |
| 524,26027 | 0 | 0,00012 | 0 | 0 | 0 |
| 524,29746 | 0 | 0,00011 | 0 | 0 | 0 |
| 524,33464 | 0 | 1e-04 | 0 | 0 | 0 |
| 524,37182 | 0 | 9e-05 | 0 | 0 | 0 |
| 524,409 | 0 | 8e-05 | 0 | 0 | 0 |
| 524,44618 | 0 | 7e-05 | 0 | 0 | 0 |
| 524,48337 | 0 | 6e-05 | 0 | 0 | 0 |
| 524,52055 | 0 | 5e-05 | 0 | 0 | 0 |
| 524,55773 | 0 | 4e-05 | 0 | 0 | 0 |
| 524,59491 | 0 | 3e-05 | 0 | 0 | 0 |
| 524,63209 | 0 | 3e-05 | 0 | 0 | 0 |
| 524,66928 | 0 | 2e-05 | 0 | 0 | 0 |
| 524,70646 | 0 | 2e-05 | 0 | 0 | 0 |
| 524,74364 | 0 | 1e-05 | 0 | 0 | 0 |
| 524,78082 | 0 | 1e-05 | 0 | 0 | 0 |
| 524,818 | 0 | 1e-05 | 0 | 0 | 0 |
| 524,85519 | 0 | 1e-05 | 0 | 0 | 0 |
| 524,89237 | 0 | 0 | 0 | 0 | 0 |
| 524,92955 | 0 | 0 | 0 | 0 | 0 |
| 524,96673 | 0 | 0 | 0 | 0 | 0 |
| 525,00391 | 0 | 0 | 0 | 0 | 0 |
| 525,0411 | 0 | 1e-05 | 0 | 0 | 0 |
| 525,07828 | 0 | 1e-05 | 0 | 0 | 0 |
| 525,11546 | 0 | 1e-05 | 0 | 0 | 0 |
| 525,15264 | 0 | 1e-05 | 0 | 0 | 0 |
| 525,18982 | 0 | 1e-05 | 0 | 0 | 0 |
| 525,22701 | 0 | 2e-05 | 0 | 0 | 0 |
| 525,26419 | 0 | 2e-05 | 0 | 1e-05 | 0 |
| 525,30137 | 0 | 3e-05 | 0 | 1e-05 | 0 |
| 525,33855 | 0 | 4e-05 | 0 | 1e-05 | 0 |
| 525,37573 | 0 | 5e-05 | 0 | 1e-05 | 0 |
| 525,41292 | 1e-05 | 6e-05 | 0 | 2e-05 | 0 |
| 525,4501 | 1e-05 | 7e-05 | 0 | 3e-05 | 0 |
| 525,48728 | 1e-05 | 9e-05 | 0 | 3e-05 | 0 |
| 525,52446 | 1e-05 | 1e-04 | 0 | 4e-05 | 0 |
| 525,56164 | 2e-05 | 0,00012 | 0 | 6e-05 | 0 |
| 525,59883 | 2e-05 | 0,00014 | 0 | 7e-05 | 0 |
| 525,63601 | 3e-05 | 0,00016 | 0 | 8e-05 | 0 |
| 525,67319 | 4e-05 | 0,00017 | 1e-05 | 1e-04 | 0 |
| 525,71037 | 4e-05 | 0,00019 | 1e-05 | 0,00012 | 0 |
| 525,74755 | 5e-05 | 0,00021 | 1e-05 | 0,00015 | 0 |
| 525,78474 | 6e-05 | 0,00023 | 1e-05 | 0,00017 | 0 |
| 525,82192 | 7e-05 | 0,00024 | 2e-05 | 2e-04 | 0 |
| 525,8591 | 9e-05 | 0,00026 | 2e-05 | 0,00022 | 0 |
| 525,89628 | 1e-04 | 0,00027 | 3e-05 | 0,00025 | 0 |
| 525,93346 | 0,00011 | 0,00028 | 4e-05 | 0,00027 | 0 |
| 525,97065 | 0,00012 | 0,00028 | 4e-05 | 3e-04 | 0 |
| 526,00783 | 0,00014 | 0,00028 | 5e-05 | 0,00032 | 1e-05 |
| 526,04501 | 0,00015 | 0,00028 | 6e-05 | 0,00035 | 1e-05 |
| 526,08219 | 0,00016 | 0,00028 | 8e-05 | 0,00037 | 1e-05 |
| 526,11937 | 0,00018 | 0,00028 | 9e-05 | 0,00039 | 2e-05 |
| 526,15656 | 0,00019 | 0,00028 | 1e-04 | 4e-04 | 3e-05 |
| 526,19374 | 2e-04 | 0,00027 | 0,00012 | 0,00042 | 4e-05 |
| 526,23092 | 0,00022 | 0,00027 | 0,00013 | 0,00043 | 5e-05 |
| 526,2681 | 0,00023 | 0,00026 | 0,00015 | 0,00044 | 6e-05 |
| 526,30528 | 0,00025 | 0,00026 | 0,00016 | 0,00045 | 8e-05 |
| 526,34247 | 0,00026 | 0,00026 | 0,00018 | 0,00046 | 1e-04 |
| 526,37965 | 0,00028 | 0,00026 | 0,00019 | 0,00047 | 0,00013 |
| 526,41683 | 3e-04 | 0,00027 | 0,00021 | 0,00048 | 0,00016 |
| 526,45401 | 0,00032 | 0,00028 | 0,00022 | 0,00049 | 0,00019 |
| 526,49119 | 0,00034 | 0,00029 | 0,00024 | 5e-04 | 0,00023 |
| 526,52838 | 0,00036 | 0,00031 | 0,00025 | 0,00051 | 0,00027 |
| 526,56556 | 0,00038 | 0,00033 | 0,00027 | 0,00052 | 0,00032 |
| 526,60274 | 4e-04 | 0,00035 | 0,00028 | 0,00053 | 0,00037 |
| 526,63992 | 0,00042 | 0,00037 | 3e-04 | 0,00053 | 0,00042 |
| 526,6771 | 0,00044 | 4e-04 | 0,00032 | 0,00054 | 0,00047 |
| 526,71429 | 0,00045 | 0,00043 | 0,00034 | 0,00054 | 0,00053 |
| 526,75147 | 0,00047 | 0,00046 | 0,00036 | 0,00055 | 0,00058 |
| 526,78865 | 0,00048 | 0,00049 | 0,00039 | 0,00055 | 0,00063 |
| 526,82583 | 0,00048 | 0,00053 | 0,00041 | 0,00055 | 0,00067 |
| 526,86301 | 0,00049 | 0,00056 | 0,00044 | 0,00055 | 0,00071 |
| 526,9002 | 0,00049 | 0,00059 | 0,00047 | 0,00054 | 0,00074 |
| 526,93738 | 5e-04 | 0,00063 | 0,00051 | 0,00054 | 0,00076 |
| 526,97456 | 5e-04 | 0,00066 | 0,00055 | 0,00054 | 0,00077 |
| 527,01174 | 5e-04 | 0,00069 | 0,00059 | 0,00053 | 0,00077 |
| 527,04892 | 0,00051 | 0,00071 | 0,00064 | 0,00053 | 0,00076 |
| 527,08611 | 0,00052 | 0,00074 | 7e-04 | 0,00053 | 0,00074 |
| 527,12329 | 0,00053 | 0,00076 | 0,00076 | 0,00054 | 0,00072 |
| 527,16047 | 0,00054 | 0,00079 | 0,00082 | 0,00055 | 0,00068 |
| 527,19765 | 0,00057 | 8e-04 | 9e-04 | 0,00057 | 0,00064 |
| 527,23483 | 6e-04 | 0,00082 | 0,00098 | 0,00059 | 6e-04 |
| 527,27202 | 0,00063 | 0,00084 | 0,00106 | 0,00062 | 0,00055 |
| 527,3092 | 0,00068 | 0,00086 | 0,00116 | 0,00066 | 5e-04 |
| 527,34638 | 0,00073 | 0,00088 | 0,00125 | 0,00071 | 0,00046 |
| 527,38356 | 0,00078 | 0,00091 | 0,00136 | 0,00076 | 0,00041 |
| 527,42074 | 0,00085 | 0,00095 | 0,00146 | 0,00082 | 0,00038 |
| 527,45793 | 0,00092 | 0,00099 | 0,00157 | 0,00089 | 0,00035 |
| 527,49511 | 0,00099 | 0,00104 | 0,00169 | 0,00097 | 0,00033 |
| 527,53229 | 0,00107 | 0,00111 | 0,0018 | 0,00104 | 0,00032 |
| 527,56947 | 0,00115 | 0,00119 | 0,00191 | 0,00112 | 0,00032 |
| 527,60665 | 0,00124 | 0,00128 | 0,00202 | 0,00121 | 0,00034 |
| 527,64384 | 0,00132 | 0,00139 | 0,00212 | 0,00129 | 0,00037 |
| 527,68102 | 0,00142 | 0,00151 | 0,00222 | 0,00138 | 0,00042 |
| 527,7182 | 0,00151 | 0,00165 | 0,00231 | 0,00147 | 0,00048 |
| 527,75538 | 0,00161 | 0,0018 | 0,0024 | 0,00155 | 0,00056 |
| 527,79256 | 0,00171 | 0,00196 | 0,00247 | 0,00164 | 0,00066 |
| 527,82975 | 0,00182 | 0,00213 | 0,00254 | 0,00173 | 0,00077 |
| 527,86693 | 0,00193 | 0,0023 | 0,0026 | 0,00182 | 9e-04 |
| 527,90411 | 0,00204 | 0,00248 | 0,00265 | 0,00192 | 0,00105 |
| 527,94129 | 0,00216 | 0,00265 | 0,00269 | 0,00202 | 0,00121 |
| 527,97847 | 0,00229 | 0,00281 | 0,00272 | 0,00212 | 0,00139 |
| 528,01566 | 0,00242 | 0,00297 | 0,00275 | 0,00224 | 0,00158 |
| 528,05284 | 0,00256 | 0,00312 | 0,00277 | 0,00236 | 0,00178 |
| 528,09002 | 0,0027 | 0,00326 | 0,00279 | 0,00249 | 0,00199 |
| 528,1272 | 0,00285 | 0,00338 | 0,0028 | 0,00263 | 0,0022 |
| 528,16438 | 0,00299 | 0,00349 | 0,00281 | 0,00277 | 0,00241 |
| 528,20157 | 0,00314 | 0,00358 | 0,00282 | 0,00292 | 0,00262 |
| 528,23875 | 0,00329 | 0,00366 | 0,00283 | 0,00308 | 0,00282 |
| 528,27593 | 0,00343 | 0,00372 | 0,00284 | 0,00323 | 0,00302 |
| 528,31311 | 0,00357 | 0,00376 | 0,00285 | 0,00339 | 0,0032 |
| 528,35029 | 0,00371 | 0,00378 | 0,00285 | 0,00354 | 0,00337 |
| 528,38748 | 0,00383 | 0,0038 | 0,00286 | 0,00367 | 0,00353 |
| 528,42466 | 0,00395 | 0,0038 | 0,00286 | 0,0038 | 0,00366 |
| 528,46184 | 0,00406 | 0,00379 | 0,00287 | 0,0039 | 0,00379 |
| 528,49902 | 0,00417 | 0,00377 | 0,00287 | 0,00399 | 0,00389 |
| 528,5362 | 0,00426 | 0,00374 | 0,00287 | 0,00406 | 0,00398 |
| 528,57339 | 0,00435 | 0,00371 | 0,00287 | 0,00411 | 0,00404 |
| 528,61057 | 0,00443 | 0,00368 | 0,00287 | 0,00412 | 0,0041 |
| 528,64775 | 0,0045 | 0,00365 | 0,00288 | 0,00412 | 0,00413 |
| 528,68493 | 0,00456 | 0,00362 | 0,00289 | 0,00409 | 0,00416 |
| 528,72211 | 0,00462 | 0,0036 | 0,00291 | 0,00405 | 0,00417 |
| 528,7593 | 0,00468 | 0,00358 | 0,00293 | 0,00399 | 0,00418 |
| 528,79648 | 0,00474 | 0,00358 | 0,00297 | 0,00391 | 0,00417 |
| 528,83366 | 0,0048 | 0,00358 | 0,00302 | 0,00383 | 0,00416 |
| 528,87084 | 0,00486 | 0,0036 | 0,00308 | 0,00375 | 0,00414 |
| 528,90802 | 0,00493 | 0,00363 | 0,00315 | 0,00366 | 0,00412 |
| 528,94521 | 0,005 | 0,00367 | 0,00324 | 0,00358 | 0,00409 |
| 528,98239 | 0,00509 | 0,00373 | 0,00335 | 0,00351 | 0,00405 |
| 529,01957 | 0,00518 | 0,00381 | 0,00347 | 0,00345 | 0,00402 |
| 529,05675 | 0,00529 | 0,0039 | 0,0036 | 0,00341 | 0,00398 |
| 529,09393 | 0,00542 | 0,00401 | 0,00373 | 0,00338 | 0,00395 |
| 529,13112 | 0,00555 | 0,00413 | 0,00388 | 0,00337 | 0,00392 |
| 529,1683 | 0,0057 | 0,00426 | 0,00403 | 0,00337 | 0,0039 |
| 529,20548 | 0,00586 | 0,0044 | 0,00418 | 0,0034 | 0,00389 |
| 529,24266 | 0,00603 | 0,00456 | 0,00432 | 0,00344 | 0,00389 |
| 529,27984 | 0,0062 | 0,00472 | 0,00447 | 0,00351 | 0,0039 |
| 529,31703 | 0,00638 | 0,00489 | 0,0046 | 0,00359 | 0,00394 |
| 529,35421 | 0,00656 | 0,00506 | 0,00473 | 0,00369 | 0,00399 |
| 529,39139 | 0,00673 | 0,00524 | 0,00485 | 0,00381 | 0,00407 |
| 529,42857 | 0,00689 | 0,00542 | 0,00496 | 0,00394 | 0,00416 |
| 529,46575 | 0,00704 | 0,00559 | 0,00506 | 0,0041 | 0,00427 |
| 529,50294 | 0,00718 | 0,00576 | 0,00516 | 0,00426 | 0,00441 |
| 529,54012 | 0,0073 | 0,00593 | 0,00524 | 0,00445 | 0,00455 |
| 529,5773 | 0,00742 | 0,00609 | 0,00533 | 0,00464 | 0,00472 |
| 529,61448 | 0,00751 | 0,00625 | 0,0054 | 0,00485 | 0,00489 |
| 529,65166 | 0,00759 | 0,0064 | 0,00548 | 0,00507 | 0,00507 |
| 529,68885 | 0,00766 | 0,00654 | 0,00556 | 0,0053 | 0,00525 |
| 529,72603 | 0,00772 | 0,00668 | 0,00564 | 0,00553 | 0,00543 |
| 529,76321 | 0,00777 | 0,00682 | 0,00573 | 0,00576 | 0,0056 |
| 529,80039 | 0,00782 | 0,00695 | 0,00583 | 0,006 | 0,00576 |
| 529,83757 | 0,00787 | 0,00707 | 0,00594 | 0,00623 | 0,00591 |
| 529,87476 | 0,00793 | 0,0072 | 0,00606 | 0,00646 | 0,00605 |
| 529,91194 | 0,008 | 0,00732 | 0,00621 | 0,00668 | 0,00618 |
| 529,94912 | 0,00809 | 0,00745 | 0,00637 | 0,00689 | 0,00629 |
| 529,9863 | 0,0082 | 0,00758 | 0,00656 | 0,0071 | 0,00639 |
| 530,02348 | 0,00834 | 0,00772 | 0,00678 | 0,0073 | 0,00648 |
| 530,06067 | 0,00851 | 0,00787 | 0,00703 | 0,00749 | 0,00657 |
| 530,09785 | 0,00872 | 0,00803 | 0,00731 | 0,00769 | 0,00666 |
| 530,13503 | 0,00896 | 0,00821 | 0,00761 | 0,00788 | 0,00675 |
| 530,17221 | 0,00925 | 0,00841 | 0,00795 | 0,00807 | 0,00684 |
| 530,20939 | 0,00958 | 0,00863 | 0,00832 | 0,00826 | 0,00695 |
| 530,24658 | 0,00995 | 0,00888 | 0,00871 | 0,00847 | 0,00707 |
| 530,28376 | 0,01036 | 0,00915 | 0,00913 | 0,00868 | 0,00721 |
| 530,32094 | 0,01082 | 0,00946 | 0,00957 | 0,00891 | 0,00736 |
| 530,35812 | 0,01131 | 0,00979 | 0,01003 | 0,00915 | 0,00754 |
| 530,3953 | 0,01182 | 0,01015 | 0,0105 | 0,00941 | 0,00774 |
| 530,43249 | 0,01236 | 0,01054 | 0,01098 | 0,00969 | 0,00796 |
| 530,46967 | 0,01291 | 0,01096 | 0,01145 | 0,00998 | 0,00821 |
| 530,50685 | 0,01347 | 0,01139 | 0,01193 | 0,0103 | 0,00847 |
| 530,54403 | 0,01403 | 0,01184 | 0,01239 | 0,01063 | 0,00876 |
| 530,58121 | 0,01457 | 0,0123 | 0,01284 | 0,01098 | 0,00908 |
| 530,6184 | 0,0151 | 0,01277 | 0,01327 | 0,01134 | 0,00941 |
| 530,65558 | 0,0156 | 0,01324 | 0,01368 | 0,01171 | 0,00977 |
| 530,69276 | 0,01607 | 0,0137 | 0,01406 | 0,01208 | 0,01015 |
| 530,72994 | 0,0165 | 0,01415 | 0,01442 | 0,01246 | 0,01054 |
| 530,76712 | 0,01689 | 0,01458 | 0,01475 | 0,01283 | 0,01096 |
| 530,80431 | 0,01725 | 0,015 | 0,01505 | 0,01318 | 0,01138 |
| 530,84149 | 0,01756 | 0,0154 | 0,01533 | 0,01352 | 0,01182 |
| 530,87867 | 0,01783 | 0,01578 | 0,0156 | 0,01383 | 0,01226 |
| 530,91585 | 0,01807 | 0,01614 | 0,01585 | 0,01411 | 0,0127 |
| 530,95303 | 0,01827 | 0,01646 | 0,01608 | 0,01435 | 0,01314 |
| 530,99022 | 0,01844 | 0,01677 | 0,01632 | 0,01455 | 0,01356 |
| 531,0274 | 0,01859 | 0,01704 | 0,01655 | 0,01471 | 0,01397 |
| 531,06458 | 0,01872 | 0,01729 | 0,01679 | 0,01483 | 0,01436 |
| 531,10176 | 0,01884 | 0,01751 | 0,01704 | 0,01491 | 0,01473 |
| 531,13894 | 0,01896 | 0,0177 | 0,01731 | 0,01496 | 0,01507 |
| 531,17613 | 0,01908 | 0,01786 | 0,0176 | 0,01498 | 0,01538 |
| 531,21331 | 0,01921 | 0,01799 | 0,01791 | 0,01499 | 0,01566 |
| 531,25049 | 0,01935 | 0,01809 | 0,01826 | 0,01499 | 0,01592 |
| 531,28767 | 0,01952 | 0,01817 | 0,01863 | 0,015 | 0,01615 |
| 531,32485 | 0,01971 | 0,01822 | 0,01904 | 0,01504 | 0,01637 |
| 531,36204 | 0,01993 | 0,01826 | 0,01949 | 0,0151 | 0,01659 |
| 531,39922 | 0,02019 | 0,01829 | 0,01997 | 0,01521 | 0,01679 |
| 531,4364 | 0,0205 | 0,01832 | 0,02048 | 0,01535 | 0,017 |
| 531,47358 | 0,02084 | 0,01836 | 0,02102 | 0,01555 | 0,01722 |
| 531,51076 | 0,02123 | 0,01842 | 0,0216 | 0,0158 | 0,01745 |
| 531,54795 | 0,02167 | 0,01851 | 0,02221 | 0,0161 | 0,01768 |
| 531,58513 | 0,02217 | 0,01865 | 0,02285 | 0,01645 | 0,01793 |
| 531,62231 | 0,02271 | 0,01883 | 0,02351 | 0,01682 | 0,01819 |
| 531,65949 | 0,0233 | 0,01907 | 0,02419 | 0,01722 | 0,01846 |
| 531,69667 | 0,02394 | 0,01939 | 0,0249 | 0,01762 | 0,01872 |
| 531,73386 | 0,02462 | 0,01977 | 0,02562 | 0,01802 | 0,01898 |
| 531,77104 | 0,02534 | 0,02023 | 0,02636 | 0,0184 | 0,01924 |
| 531,80822 | 0,0261 | 0,02078 | 0,02712 | 0,01876 | 0,01947 |
| 531,8454 | 0,0269 | 0,02141 | 0,02789 | 0,01908 | 0,01969 |
| 531,88258 | 0,02772 | 0,02214 | 0,02867 | 0,01935 | 0,01989 |
| 531,91977 | 0,02858 | 0,02295 | 0,02947 | 0,01959 | 0,02006 |
| 531,95695 | 0,02947 | 0,02385 | 0,03029 | 0,01978 | 0,02022 |
| 531,99413 | 0,03037 | 0,02481 | 0,03111 | 0,01993 | 0,02037 |
| 532,03131 | 0,03129 | 0,02585 | 0,03195 | 0,02005 | 0,02052 |
| 532,06849 | 0,03221 | 0,02694 | 0,03279 | 0,02016 | 0,02067 |
| 532,10568 | 0,03314 | 0,02808 | 0,03364 | 0,02027 | 0,02084 |
| 532,14286 | 0,03406 | 0,02924 | 0,03448 | 0,02039 | 0,02104 |
| 532,18004 | 0,03497 | 0,03043 | 0,0353 | 0,02054 | 0,02128 |
| 532,21722 | 0,03584 | 0,0316 | 0,03611 | 0,02074 | 0,02157 |
| 532,2544 | 0,03667 | 0,03276 | 0,03688 | 0,02102 | 0,02193 |
| 532,29159 | 0,03744 | 0,03387 | 0,0376 | 0,02137 | 0,02235 |
| 532,32877 | 0,03814 | 0,03493 | 0,03828 | 0,02182 | 0,02284 |
| 532,36595 | 0,03876 | 0,03592 | 0,0389 | 0,02238 | 0,02341 |
| 532,40313 | 0,0393 | 0,03682 | 0,03945 | 0,02305 | 0,02405 |
| 532,44031 | 0,03976 | 0,03764 | 0,03994 | 0,02383 | 0,02476 |
| 532,4775 | 0,04013 | 0,03837 | 0,04037 | 0,02473 | 0,02555 |
| 532,51468 | 0,04042 | 0,03901 | 0,04075 | 0,02575 | 0,0264 |
| 532,55186 | 0,04063 | 0,03956 | 0,04107 | 0,02689 | 0,02732 |
| 532,58904 | 0,04078 | 0,04004 | 0,04136 | 0,02814 | 0,02831 |
| 532,62622 | 0,0409 | 0,04046 | 0,04163 | 0,02947 | 0,02936 |
| 532,66341 | 0,041 | 0,04086 | 0,0419 | 0,03088 | 0,03048 |
| 532,70059 | 0,0411 | 0,04124 | 0,0422 | 0,03236 | 0,03166 |
| 532,73777 | 0,04124 | 0,04162 | 0,04254 | 0,0339 | 0,03292 |
| 532,77495 | 0,04143 | 0,04204 | 0,04294 | 0,03548 | 0,03426 |
| 532,81213 | 0,0417 | 0,04251 | 0,04343 | 0,0371 | 0,03568 |
| 532,84932 | 0,04208 | 0,04305 | 0,04401 | 0,03875 | 0,0372 |
| 532,8865 | 0,04259 | 0,04369 | 0,04473 | 0,04041 | 0,03881 |
| 532,92368 | 0,04325 | 0,04443 | 0,04559 | 0,04208 | 0,04052 |
| 532,96086 | 0,04406 | 0,0453 | 0,04658 | 0,04374 | 0,04231 |
| 532,99804 | 0,04504 | 0,04629 | 0,04772 | 0,0454 | 0,04416 |
| 533,03523 | 0,04619 | 0,04741 | 0,049 | 0,04703 | 0,04607 |
| 533,07241 | 0,04752 | 0,04867 | 0,05044 | 0,04862 | 0,048 |
| 533,10959 | 0,04902 | 0,05007 | 0,05202 | 0,05016 | 0,04994 |
| 533,14677 | 0,05069 | 0,05161 | 0,05374 | 0,05163 | 0,05185 |
| 533,18395 | 0,05253 | 0,05328 | 0,0556 | 0,05302 | 0,0537 |
| 533,22114 | 0,05453 | 0,0551 | 0,0576 | 0,0543 | 0,05544 |
| 533,25832 | 0,05666 | 0,05704 | 0,05971 | 0,05546 | 0,05706 |
| 533,2955 | 0,05889 | 0,05909 | 0,06192 | 0,05652 | 0,05853 |
| 533,33268 | 0,0612 | 0,06123 | 0,06419 | 0,05745 | 0,05984 |
| 533,36986 | 0,06356 | 0,06344 | 0,06652 | 0,05828 | 0,061 |
| 533,40705 | 0,06593 | 0,06571 | 0,06888 | 0,05902 | 0,06201 |
| 533,44423 | 0,06828 | 0,068 | 0,07123 | 0,05968 | 0,0629 |
| 533,48141 | 0,07058 | 0,07029 | 0,07354 | 0,06032 | 0,0637 |
| 533,51859 | 0,07276 | 0,07252 | 0,07578 | 0,06096 | 0,06444 |
| 533,55577 | 0,07479 | 0,07465 | 0,07787 | 0,06166 | 0,0652 |
| 533,59295 | 0,07663 | 0,07664 | 0,07981 | 0,06248 | 0,06603 |
| 533,63014 | 0,07824 | 0,07844 | 0,08153 | 0,06344 | 0,06698 |
| 533,66732 | 0,0796 | 0,08002 | 0,08301 | 0,06459 | 0,06808 |
| 533,7045 | 0,08068 | 0,08133 | 0,08422 | 0,06594 | 0,06936 |
| 533,74168 | 0,08146 | 0,08235 | 0,08511 | 0,06751 | 0,07085 |
| 533,77886 | 0,08195 | 0,08304 | 0,08569 | 0,06929 | 0,07252 |
| 533,81605 | 0,08213 | 0,0834 | 0,08593 | 0,07125 | 0,07437 |
| 533,85323 | 0,08198 | 0,08339 | 0,08579 | 0,07336 | 0,07635 |
| 533,89041 | 0,08157 | 0,08303 | 0,08532 | 0,07553 | 0,07837 |
| 533,92759 | 0,08094 | 0,08239 | 0,08457 | 0,07768 | 0,08035 |
| 533,96477 | 0,08012 | 0,08149 | 0,08358 | 0,07973 | 0,0822 |
| 534,00196 | 0,07917 | 0,0804 | 0,08238 | 0,08158 | 0,08382 |
| 534,03914 | 0,07816 | 0,07917 | 0,08106 | 0,08316 | 0,08512 |
| 534,07632 | 0,07715 | 0,0779 | 0,07968 | 0,08439 | 0,08604 |
| 534,1135 | 0,07621 | 0,07665 | 0,07831 | 0,08521 | 0,0865 |
| 534,15068 | 0,07541 | 0,07552 | 0,07706 | 0,08558 | 0,08647 |
| 534,18787 | 0,07486 | 0,07465 | 0,07603 | 0,08541 | 0,08585 |
| 534,22505 | 0,07463 | 0,07411 | 0,07532 | 0,08477 | 0,08472 |
| 534,26223 | 0,07477 | 0,07401 | 0,07498 | 0,08369 | 0,08314 |
| 534,29941 | 0,07535 | 0,0744 | 0,07511 | 0,08223 | 0,08118 |
| 534,33659 | 0,0764 | 0,07536 | 0,07575 | 0,08046 | 0,07892 |
| 534,37378 | 0,07797 | 0,07695 | 0,07697 | 0,07847 | 0,07647 |
| 534,41096 | 0,08007 | 0,07919 | 0,07878 | 0,07637 | 0,07394 |
| 534,44814 | 0,08272 | 0,08213 | 0,08122 | 0,07425 | 0,07146 |
| 534,48532 | 0,08592 | 0,08576 | 0,08433 | 0,07224 | 0,06916 |
| 534,5225 | 0,08966 | 0,09012 | 0,08806 | 0,07049 | 0,06721 |
| 534,55969 | 0,09384 | 0,09507 | 0,09232 | 0,0691 | 0,06573 |
| 534,59687 | 0,09839 | 0,10054 | 0,09704 | 0,06818 | 0,06481 |
| 534,63405 | 0,10321 | 0,10642 | 0,10214 | 0,06782 | 0,06454 |
| 534,67123 | 0,10823 | 0,11261 | 0,1075 | 0,0681 | 0,06502 |
| 534,70841 | 0,11333 | 0,11897 | 0,11303 | 0,06911 | 0,06631 |
| 534,7456 | 0,11841 | 0,12539 | 0,11861 | 0,0709 | 0,06847 |
| 534,78278 | 0,12339 | 0,13172 | 0,12412 | 0,07352 | 0,07152 |
| 534,81996 | 0,12812 | 0,13783 | 0,12939 | 0,077 | 0,07551 |
| 534,85714 | 0,13252 | 0,14354 | 0,13433 | 0,08144 | 0,08049 |
| 534,89432 | 0,13653 | 0,14879 | 0,13886 | 0,08668 | 0,08632 |
| 534,93151 | 0,14012 | 0,1535 | 0,14291 | 0,09267 | 0,09292 |
| 534,96869 | 0,14325 | 0,15761 | 0,14643 | 0,09931 | 0,10019 |
| 535,00587 | 0,14592 | 0,16111 | 0,14938 | 0,1065 | 0,108 |
| 535,04305 | 0,14814 | 0,16399 | 0,15177 | 0,11408 | 0,11621 |
| 535,08023 | 0,14994 | 0,16627 | 0,1536 | 0,12191 | 0,12464 |
| 535,11742 | 0,15135 | 0,16799 | 0,1549 | 0,1298 | 0,13312 |
| 535,1546 | 0,1524 | 0,16918 | 0,15568 | 0,13757 | 0,14143 |
| 535,19178 | 0,15319 | 0,16992 | 0,15607 | 0,14496 | 0,14932 |
| 535,22896 | 0,15379 | 0,17034 | 0,15614 | 0,15185 | 0,15663 |
| 535,26614 | 0,15426 | 0,17051 | 0,15598 | 0,15809 | 0,16323 |
| 535,30333 | 0,15465 | 0,1705 | 0,15564 | 0,16358 | 0,16899 |
| 535,34051 | 0,15502 | 0,17038 | 0,1552 | 0,16825 | 0,17385 |
| 535,37769 | 0,15539 | 0,17021 | 0,15473 | 0,17209 | 0,17777 |
| 535,41487 | 0,15581 | 0,17003 | 0,15427 | 0,1751 | 0,18076 |
| 535,45205 | 0,1563 | 0,16989 | 0,1539 | 0,17735 | 0,18286 |
| 535,48924 | 0,15689 | 0,16982 | 0,15365 | 0,17889 | 0,18413 |
| 535,52642 | 0,1576 | 0,16984 | 0,15356 | 0,1799 | 0,18477 |
| 535,5636 | 0,15843 | 0,16996 | 0,15365 | 0,18058 | 0,18498 |
| 535,60078 | 0,1594 | 0,17021 | 0,15395 | 0,18112 | 0,18495 |
| 535,63796 | 0,16054 | 0,1706 | 0,15449 | 0,18168 | 0,18486 |
| 535,67515 | 0,16186 | 0,17116 | 0,15529 | 0,18243 | 0,18491 |
| 535,71233 | 0,1634 | 0,17191 | 0,15638 | 0,18352 | 0,18526 |
| 535,74951 | 0,1652 | 0,17289 | 0,1578 | 0,18508 | 0,18608 |
| 535,78669 | 0,1673 | 0,17414 | 0,15963 | 0,18723 | 0,18748 |
| 535,82387 | 0,16978 | 0,17573 | 0,16187 | 0,19012 | 0,18969 |
| 535,86106 | 0,17263 | 0,17769 | 0,16454 | 0,19375 | 0,19269 |
| 535,89824 | 0,17589 | 0,18004 | 0,16766 | 0,1981 | 0,19648 |
| 535,93542 | 0,17957 | 0,1828 | 0,17125 | 0,20311 | 0,20105 |
| 535,9726 | 0,18368 | 0,18599 | 0,1753 | 0,20871 | 0,20634 |
| 536,00978 | 0,18819 | 0,18959 | 0,1798 | 0,2148 | 0,21225 |
| 536,04697 | 0,19307 | 0,19358 | 0,18468 | 0,22123 | 0,21865 |
| 536,08415 | 0,19824 | 0,19791 | 0,18991 | 0,22783 | 0,22537 |
| 536,12133 | 0,20363 | 0,2025 | 0,19538 | 0,23441 | 0,2322 |
| 536,15851 | 0,20908 | 0,20723 | 0,20091 | 0,24067 | 0,23887 |
| 536,19569 | 0,21444 | 0,21194 | 0,20636 | 0,24637 | 0,24511 |
| 536,23288 | 0,21953 | 0,21647 | 0,21157 | 0,25127 | 0,25065 |
| 536,27006 | 0,2242 | 0,22065 | 0,21637 | 0,25514 | 0,25525 |
| 536,30724 | 0,22828 | 0,22431 | 0,22058 | 0,2578 | 0,25868 |
| 536,34442 | 0,23159 | 0,22727 | 0,22404 | 0,25906 | 0,26075 |
| 536,3816 | 0,23399 | 0,22937 | 0,2266 | 0,25881 | 0,2613 |
| 536,41879 | 0,23535 | 0,23047 | 0,228 | 0,25696 | 0,26023 |
| 536,45597 | 0,23538 | 0,23037 | 0,22818 | 0,25349 | 0,25743 |
| 536,49315 | 0,23418 | 0,22894 | 0,22714 | 0,24824 | 0,25279 |
| 536,53033 | 0,23173 | 0,22624 | 0,22487 | 0,24155 | 0,24662 |
| 536,56751 | 0,22808 | 0,22228 | 0,22139 | 0,23362 | 0,23906 |
| 536,6047 | 0,22327 | 0,21713 | 0,21677 | 0,22464 | 0,23033 |
| 536,64188 | 0,2174 | 0,21086 | 0,2111 | 0,21488 | 0,22066 |
| 536,67906 | 0,2106 | 0,20359 | 0,2045 | 0,20457 | 0,21029 |
| 536,71624 | 0,20302 | 0,19549 | 0,19713 | 0,19399 | 0,19951 |
| 536,75342 | 0,1948 | 0,18673 | 0,18911 | 0,18339 | 0,18856 |
| 536,79061 | 0,18616 | 0,17749 | 0,18074 | 0,17301 | 0,17772 |
| 536,82779 | 0,17734 | 0,16804 | 0,17222 | 0,16316 | 0,16727 |
| 536,86497 | 0,16854 | 0,1586 | 0,16372 | 0,15394 | 0,15735 |
| 536,90215 | 0,15994 | 0,14939 | 0,15543 | 0,14549 | 0,14813 |
| 536,93933 | 0,15171 | 0,1406 | 0,14753 | 0,13787 | 0,13968 |
| 536,97652 | 0,14403 | 0,13241 | 0,14018 | 0,13115 | 0,13209 |
| 537,0137 | 0,13705 | 0,12499 | 0,13354 | 0,12533 | 0,12539 |
| 537,05088 | 0,13093 | 0,1185 | 0,12781 | 0,12042 | 0,1196 |
| 537,08806 | 0,1259 | 0,11309 | 0,12318 | 0,1164 | 0,11474 |
| 537,12524 | 0,1221 | 0,10905 | 0,11969 | 0,11328 | 0,11086 |
| 537,16243 | 0,11959 | 0,1064 | 0,11744 | 0,11106 | 0,10793 |
| 537,19961 | 0,11846 | 0,10522 | 0,11653 | 0,10965 | 0,10588 |
| 537,23679 | 0,11881 | 0,10559 | 0,11704 | 0,10902 | 0,10473 |
| 537,27397 | 0,1207 | 0,10758 | 0,11903 | 0,10917 | 0,10445 |
| 537,31115 | 0,12418 | 0,11122 | 0,12255 | 0,1101 | 0,10507 |
| 537,34834 | 0,12927 | 0,11656 | 0,12761 | 0,11183 | 0,10659 |
| 537,38552 | 0,13596 | 0,12357 | 0,13439 | 0,11437 | 0,10903 |
| 537,4227 | 0,14437 | 0,13221 | 0,1427 | 0,11774 | 0,11239 |
| 537,45988 | 0,15419 | 0,14258 | 0,15238 | 0,12204 | 0,1168 |
| 537,49706 | 0,16522 | 0,15429 | 0,16328 | 0,12728 | 0,12218 |
| 537,53425 | 0,17722 | 0,16712 | 0,17521 | 0,1334 | 0,12848 |
| 537,57143 | 0,18991 | 0,1808 | 0,18794 | 0,1404 | 0,13568 |
| 537,60861 | 0,20298 | 0,19501 | 0,20117 | 0,14825 | 0,14373 |
| 537,64579 | 0,21607 | 0,2094 | 0,21459 | 0,15691 | 0,15256 |
| 537,68297 | 0,2288 | 0,2236 | 0,22784 | 0,16633 | 0,16211 |
| 537,72016 | 0,24075 | 0,23719 | 0,2404 | 0,1764 | 0,17227 |
| 537,75734 | 0,25133 | 0,24972 | 0,25192 | 0,18703 | 0,18292 |
| 537,79452 | 0,26027 | 0,26057 | 0,26203 | 0,1981 | 0,19393 |
| 537,8317 | 0,26727 | 0,26953 | 0,27041 | 0,20936 | 0,20504 |
| 537,86888 | 0,27207 | 0,27629 | 0,27676 | 0,22058 | 0,21605 |
| 537,90607 | 0,27449 | 0,28062 | 0,28086 | 0,23151 | 0,22672 |
| 537,94325 | 0,27442 | 0,28237 | 0,28253 | 0,2419 | 0,23679 |
| 537,98043 | 0,27182 | 0,28146 | 0,2817 | 0,25145 | 0,246 |
| 538,01761 | 0,26677 | 0,27791 | 0,27818 | 0,25987 | 0,25407 |
| 538,05479 | 0,25925 | 0,27181 | 0,27205 | 0,26687 | 0,26073 |
| 538,09198 | 0,2495 | 0,26321 | 0,26371 | 0,27216 | 0,26568 |
| 538,12916 | 0,23804 | 0,25241 | 0,25342 | 0,27521 | 0,26846 |
| 538,16634 | 0,2252 | 0,23993 | 0,24148 | 0,27602 | 0,26911 |
| 538,20352 | 0,21137 | 0,22616 | 0,22825 | 0,27452 | 0,26753 |
| 538,2407 | 0,19693 | 0,2115 | 0,21409 | 0,27069 | 0,26373 |
| 538,27789 | 0,18226 | 0,19635 | 0,19941 | 0,26459 | 0,25775 |
| 538,31507 | 0,16775 | 0,18111 | 0,18458 | 0,25636 | 0,24974 |
| 538,35225 | 0,15373 | 0,16615 | 0,17007 | 0,24624 | 0,23993 |
| 538,38943 | 0,14064 | 0,15183 | 0,15623 | 0,23453 | 0,2286 |
| 538,42661 | 0,12873 | 0,13855 | 0,14335 | 0,22161 | 0,2161 |
| 538,4638 | 0,11815 | 0,12658 | 0,13165 | 0,20788 | 0,20289 |
| 538,50098 | 0,10902 | 0,11602 | 0,12128 | 0,19396 | 0,18951 |
| 538,53816 | 0,1014 | 0,10697 | 0,11238 | 0,18028 | 0,17639 |
| 538,57534 | 0,09533 | 0,09949 | 0,10498 | 0,16726 | 0,16392 |
| 538,61252 | 0,09076 | 0,09356 | 0,0991 | 0,15525 | 0,15244 |
| 538,64971 | 0,08761 | 0,08914 | 0,0947 | 0,14451 | 0,14223 |
| 538,68689 | 0,08576 | 0,08612 | 0,09181 | 0,13527 | 0,13349 |
| 538,72407 | 0,08519 | 0,08435 | 0,09008 | 0,12763 | 0,12633 |
| 538,76125 | 0,08551 | 0,08378 | 0,08932 | 0,12167 | 0,12091 |
| 538,79843 | 0,08651 | 0,08404 | 0,08934 | 0,11744 | 0,11712 |
| 538,83562 | 0,08799 | 0,08489 | 0,08993 | 0,11457 | 0,11467 |
| 538,8728 | 0,08971 | 0,08613 | 0,09087 | 0,11283 | 0,11334 |
| 538,90998 | 0,09148 | 0,08753 | 0,09196 | 0,11193 | 0,11286 |
| 538,94716 | 0,09311 | 0,0889 | 0,09301 | 0,11159 | 0,11293 |
| 538,98434 | 0,09442 | 0,09005 | 0,09379 | 0,11152 | 0,11325 |
| 539,02153 | 0,09524 | 0,09083 | 0,09414 | 0,1114 | 0,11352 |
| 539,05871 | 0,0954 | 0,09109 | 0,09396 | 0,111 | 0,11348 |
| 539,09589 | 0,09486 | 0,09064 | 0,09317 | 0,11002 | 0,11281 |
| 539,13307 | 0,09359 | 0,08951 | 0,09172 | 0,10826 | 0,11134 |
| 539,17025 | 0,09158 | 0,08768 | 0,08961 | 0,10568 | 0,10899 |
| 539,20744 | 0,08886 | 0,08517 | 0,08684 | 0,10225 | 0,10573 |
| 539,24462 | 0,08546 | 0,082 | 0,08346 | 0,09799 | 0,10158 |
| 539,2818 | 0,08145 | 0,07825 | 0,07951 | 0,09298 | 0,09661 |
| 539,31898 | 0,07692 | 0,07399 | 0,07504 | 0,08733 | 0,09092 |
| 539,35616 | 0,07194 | 0,06932 | 0,07021 | 0,08119 | 0,08466 |
| 539,39335 | 0,06666 | 0,06434 | 0,06513 | 0,07471 | 0,078 |
| 539,43053 | 0,06122 | 0,05918 | 0,05991 | 0,06806 | 0,07111 |
| 539,46771 | 0,05573 | 0,05396 | 0,05464 | 0,06145 | 0,06422 |
| 539,50489 | 0,05028 | 0,04879 | 0,04942 | 0,05503 | 0,05748 |
| 539,54207 | 0,04496 | 0,04376 | 0,04432 | 0,04892 | 0,05104 |
| 539,57926 | 0,03986 | 0,03893 | 0,03944 | 0,0432 | 0,04499 |
| 539,61644 | 0,03505 | 0,03438 | 0,03482 | 0,03794 | 0,03941 |
| 539,65362 | 0,03056 | 0,03014 | 0,03057 | 0,03318 | 0,03435 |
| 539,6908 | 0,02649 | 0,02626 | 0,02667 | 0,02893 | 0,02984 |
| 539,72798 | 0,02282 | 0,02277 | 0,02313 | 0,02518 | 0,02588 |
| 539,76517 | 0,01955 | 0,01967 | 0,01996 | 0,02195 | 0,02251 |
| 539,80235 | 0,01666 | 0,01695 | 0,01715 | 0,01917 | 0,01961 |
| 539,83953 | 0,01414 | 0,01456 | 0,0147 | 0,01677 | 0,01713 |
| 539,87671 | 0,01198 | 0,0125 | 0,01257 | 0,01471 | 0,01503 |
| 539,91389 | 0,01013 | 0,01074 | 0,01075 | 0,01293 | 0,01325 |
| 539,95108 | 0,00858 | 0,00925 | 0,00924 | 0,01139 | 0,01174 |
| 539,98826 | 0,00729 | 0,00799 | 0,00798 | 0,01006 | 0,01045 |
| 540,02544 | 0,00626 | 0,00695 | 0,00693 | 0,00891 | 0,00936 |
| 540,06262 | 0,00542 | 0,00611 | 0,00608 | 0,00791 | 0,00843 |
| 540,0998 | 0,00474 | 0,00543 | 0,00538 | 0,00705 | 0,00765 |
| 540,13699 | 0,00421 | 0,00488 | 0,00481 | 0,00631 | 0,00698 |
| 540,17417 | 0,00379 | 0,00443 | 0,00437 | 0,00568 | 0,0064 |
| 540,21135 | 0,00347 | 0,00408 | 0,00401 | 0,00514 | 0,00592 |
| 540,24853 | 0,00323 | 0,0038 | 0,00374 | 0,00469 | 0,00552 |
| 540,28571 | 0,00306 | 0,00359 | 0,00354 | 0,00433 | 0,00519 |
| 540,3229 | 0,00295 | 0,00342 | 0,00338 | 0,00404 | 0,00493 |
| 540,36008 | 0,00288 | 0,00329 | 0,00327 | 0,00383 | 0,00474 |
| 540,39726 | 0,00284 | 0,00319 | 0,00318 | 0,00368 | 0,00461 |
| 540,43444 | 0,00282 | 0,00311 | 0,00312 | 0,0036 | 0,00452 |
| 540,47162 | 0,00282 | 0,00304 | 0,00308 | 0,00355 | 0,00447 |
| 540,50881 | 0,00283 | 0,00298 | 0,00305 | 0,00354 | 0,00444 |
| 540,54599 | 0,00285 | 0,00292 | 0,00302 | 0,00354 | 0,00442 |
| 540,58317 | 0,00286 | 0,00286 | 0,00299 | 0,00355 | 0,0044 |
| 540,62035 | 0,00287 | 0,00279 | 0,00296 | 0,00356 | 0,00437 |
| 540,65753 | 0,00286 | 0,00271 | 0,00293 | 0,00356 | 0,00433 |
| 540,69472 | 0,00285 | 0,00263 | 0,00288 | 0,00354 | 0,00427 |
| 540,7319 | 0,00282 | 0,00253 | 0,00282 | 0,00349 | 0,00417 |
| 540,76908 | 0,00277 | 0,00243 | 0,00275 | 0,00341 | 0,00404 |
| 540,80626 | 0,0027 | 0,00232 | 0,00266 | 0,00329 | 0,00388 |
| 540,84344 | 0,00262 | 0,00221 | 0,00256 | 0,00315 | 0,00369 |
| 540,88063 | 0,00253 | 0,00209 | 0,00244 | 0,00297 | 0,00348 |
| 540,91781 | 0,00241 | 0,00196 | 0,00231 | 0,00277 | 0,00324 |
| 540,95499 | 0,00229 | 0,00184 | 0,00216 | 0,00256 | 0,003 |
| 540,99217 | 0,00216 | 0,00172 | 0,00201 | 0,00233 | 0,00275 |
| 541,02935 | 0,00202 | 0,00159 | 0,00185 | 0,00209 | 0,0025 |
| 541,06654 | 0,00188 | 0,00148 | 0,00169 | 0,00185 | 0,00226 |
| 541,10372 | 0,00173 | 0,00137 | 0,00152 | 0,00162 | 0,00203 |
| 541,1409 | 0,00159 | 0,00126 | 0,00136 | 0,00139 | 0,00181 |
| 541,17808 | 0,00144 | 0,00117 | 0,0012 | 0,00119 | 0,00162 |
| 541,21526 | 0,00131 | 0,00108 | 0,00105 | 0,001 | 0,00144 |
| 541,25245 | 0,00118 | 0,001 | 0,00091 | 0,00082 | 0,00128 |
| 541,28963 | 0,00105 | 0,00092 | 0,00078 | 0,00067 | 0,00114 |
| 541,32681 | 0,00093 | 0,00085 | 0,00066 | 0,00054 | 0,00102 |
| 541,36399 | 0,00082 | 0,00079 | 0,00056 | 0,00043 | 0,00091 |
| 541,40117 | 0,00072 | 0,00074 | 0,00046 | 0,00034 | 0,00082 |
| 541,43836 | 0,00063 | 0,00069 | 0,00038 | 0,00026 | 0,00073 |
| 541,47554 | 0,00054 | 0,00064 | 0,00031 | 2e-04 | 0,00066 |
| 541,51272 | 0,00047 | 6e-04 | 0,00025 | 0,00015 | 0,00059 |
| 541,5499 | 4e-04 | 0,00056 | 2e-04 | 0,00011 | 0,00053 |
| 541,58708 | 0,00033 | 0,00052 | 0,00016 | 8e-05 | 0,00047 |
| 541,62427 | 0,00028 | 0,00048 | 0,00012 | 6e-05 | 0,00042 |
| 541,66145 | 0,00023 | 0,00045 | 9e-05 | 4e-05 | 0,00037 |
| 541,69863 | 0,00019 | 0,00042 | 7e-05 | 3e-05 | 0,00032 |
| 541,73581 | 0,00015 | 0,00039 | 5e-05 | 2e-05 | 0,00028 |
| 541,77299 | 0,00012 | 0,00036 | 4e-05 | 1e-05 | 0,00024 |
| 541,81018 | 1e-04 | 0,00033 | 3e-05 | 1e-05 | 2e-04 |
| 541,84736 | 8e-05 | 0,00031 | 2e-05 | 1e-05 | 0,00017 |
| 541,88454 | 6e-05 | 0,00028 | 2e-05 | 0 | 0,00014 |
| 541,92172 | 4e-05 | 0,00026 | 1e-05 | 0 | 0,00011 |
| 541,9589 | 3e-05 | 0,00024 | 1e-05 | 0 | 9e-05 |
| 541,99609 | 3e-05 | 0,00021 | 1e-05 | 0 | 7e-05 |
| 542,03327 | 2e-05 | 0,00019 | 0 | 0 | 6e-05 |
| 542,07045 | 1e-05 | 0,00017 | 0 | 0 | 4e-05 |
| 542,10763 | 1e-05 | 0,00016 | 0 | 0 | 3e-05 |
| 542,14481 | 1e-05 | 0,00014 | 0 | 0 | 3e-05 |
| 542,182 | 0 | 0,00012 | 0 | 0 | 2e-05 |
| 542,21918 | 0 | 0,00011 | 0 | 0 | 1e-05 |
| 542,25636 | 0 | 9e-05 | 0 | 0 | 1e-05 |
| 542,29354 | 0 | 8e-05 | 0 | 0 | 1e-05 |
| 542,33072 | 0 | 6e-05 | 0 | 0 | 0 |
| 542,36791 | 0 | 5e-05 | 0 | 0 | 0 |
| 542,40509 | 0 | 4e-05 | 0 | 0 | 0 |
| 542,44227 | 0 | 4e-05 | 0 | 0 | 0 |
| 542,47945 | 0 | 3e-05 | 0 | 0 | 0 |
| 542,51663 | 0 | 2e-05 | 0 | 0 | 0 |
| 542,55382 | 0 | 2e-05 | 0 | 0 | 0 |
| 542,591 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,62818 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,66536 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,70254 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 0 | 0 | 0 |
| 524,74364 | 0 | 0 | 0 | 0 | 0 |
| 524,78082 | 0 | 0 | 0 | 0 | 0 |
| 524,818 | 0 | 0 | 0 | 0 | 0 |
| 524,85519 | 0 | 0 | 0 | 0 | 0 |
| 524,89237 | 0 | 0 | 0 | 0 | 0 |
| 524,92955 | 0 | 0 | 0 | 0 | 0 |
| 524,96673 | 0 | 0 | 0 | 0 | 0 |
| 525,00391 | 0 | 0 | 0 | 0 | 0 |
| 525,0411 | 0 | 1e-05 | 0 | 0 | 0 |
| 525,07828 | 0 | 1e-05 | 0 | 0 | 0 |
| 525,11546 | 0 | 2e-05 | 0 | 0 | 0 |
| 525,15264 | 0 | 2e-05 | 0 | 0 | 0 |
| 525,18982 | 0 | 3e-05 | 0 | 0 | 0 |
| 525,22701 | 0 | 3e-05 | 0 | 0 | 0 |
| 525,26419 | 0 | 4e-05 | 0 | 0 | 0 |
| 525,30137 | 0 | 5e-05 | 0 | 0 | 0 |
| 525,33855 | 0 | 5e-05 | 0 | 0 | 0 |
| 525,37573 | 0 | 5e-05 | 0 | 0 | 0 |
| 525,41292 | 0 | 5e-05 | 0 | 0 | 0 |
| 525,4501 | 0 | 4e-05 | 0 | 0 | 0 |
| 525,48728 | 0 | 4e-05 | 0 | 0 | 0 |
| 525,52446 | 0 | 3e-05 | 0 | 0 | 0 |
| 525,56164 | 0 | 2e-05 | 0 | 0 | 0 |
| 525,59883 | 0 | 2e-05 | 0 | 0 | 0 |
| 525,63601 | 0 | 1e-05 | 1e-05 | 0 | 0 |
| 525,67319 | 0 | 1e-05 | 1e-05 | 0 | 0 |
| 525,71037 | 0 | 1e-05 | 1e-05 | 0 | 0 |
| 525,74755 | 0 | 1e-05 | 2e-05 | 0 | 0 |
| 525,78474 | 0 | 1e-05 | 2e-05 | 0 | 0 |
| 525,82192 | 0 | 2e-05 | 3e-05 | 0 | 0 |
| 525,8591 | 0 | 2e-05 | 4e-05 | 0 | 0 |
| 525,89628 | 0 | 3e-05 | 4e-05 | 0 | 0 |
| 525,93346 | 0 | 4e-05 | 5e-05 | 0 | 0 |
| 525,97065 | 0 | 5e-05 | 5e-05 | 0 | 0 |
| 526,00783 | 0 | 7e-05 | 5e-05 | 0 | 1e-05 |
| 526,04501 | 0 | 8e-05 | 5e-05 | 0 | 1e-05 |
| 526,08219 | 1e-05 | 9e-05 | 4e-05 | 0 | 2e-05 |
| 526,11937 | 1e-05 | 1e-04 | 4e-05 | 1e-05 | 2e-05 |
| 526,15656 | 2e-05 | 1e-04 | 3e-05 | 1e-05 | 3e-05 |
| 526,19374 | 3e-05 | 1e-04 | 3e-05 | 2e-05 | 5e-05 |
| 526,23092 | 5e-05 | 9e-05 | 3e-05 | 3e-05 | 6e-05 |
| 526,2681 | 7e-05 | 8e-05 | 3e-05 | 4e-05 | 8e-05 |
| 526,30528 | 1e-04 | 7e-05 | 4e-05 | 5e-05 | 9e-05 |
| 526,34247 | 0,00013 | 6e-05 | 5e-05 | 7e-05 | 0,00011 |
| 526,37965 | 0,00016 | 5e-05 | 7e-05 | 9e-05 | 0,00013 |
| 526,41683 | 2e-04 | 5e-05 | 9e-05 | 0,00011 | 0,00015 |
| 526,45401 | 0,00023 | 5e-05 | 0,00012 | 0,00012 | 0,00017 |
| 526,49119 | 0,00026 | 5e-05 | 0,00014 | 0,00014 | 0,00018 |
| 526,52838 | 0,00028 | 6e-05 | 0,00017 | 0,00014 | 0,00019 |
| 526,56556 | 0,00029 | 7e-05 | 0,00019 | 0,00014 | 2e-04 |
| 526,60274 | 0,00029 | 9e-05 | 0,00021 | 0,00014 | 2e-04 |
| 526,63992 | 0,00028 | 0,00011 | 0,00023 | 0,00013 | 0,00019 |
| 526,6771 | 0,00026 | 0,00013 | 0,00023 | 0,00011 | 0,00018 |
| 526,71429 | 0,00024 | 0,00016 | 0,00023 | 1e-04 | 0,00017 |
| 526,75147 | 0,00022 | 0,00017 | 0,00022 | 9e-05 | 0,00015 |
| 526,78865 | 0,00019 | 0,00019 | 0,00021 | 8e-05 | 0,00014 |
| 526,82583 | 0,00017 | 2e-04 | 0,00019 | 7e-05 | 0,00012 |
| 526,86301 | 0,00014 | 0,00021 | 0,00017 | 8e-05 | 0,00011 |
| 526,9002 | 0,00012 | 0,00021 | 0,00015 | 9e-05 | 9e-05 |
| 526,93738 | 1e-04 | 0,00022 | 0,00012 | 1e-04 | 8e-05 |
| 526,97456 | 8e-05 | 0,00022 | 1e-04 | 0,00011 | 7e-05 |
| 527,01174 | 7e-05 | 0,00022 | 8e-05 | 0,00013 | 6e-05 |
| 527,04892 | 6e-05 | 0,00023 | 7e-05 | 0,00014 | 5e-05 |
| 527,08611 | 5e-05 | 0,00023 | 5e-05 | 0,00014 | 4e-05 |
| 527,12329 | 5e-05 | 0,00024 | 4e-05 | 0,00014 | 4e-05 |
| 527,16047 | 5e-05 | 0,00025 | 4e-05 | 0,00014 | 3e-05 |
| 527,19765 | 7e-05 | 0,00026 | 3e-05 | 0,00013 | 3e-05 |
| 527,23483 | 9e-05 | 0,00026 | 3e-05 | 0,00011 | 4e-05 |
| 527,27202 | 0,00012 | 0,00027 | 3e-05 | 1e-04 | 4e-05 |
| 527,3092 | 0,00015 | 0,00028 | 4e-05 | 9e-05 | 5e-05 |
| 527,34638 | 2e-04 | 3e-04 | 5e-05 | 8e-05 | 6e-05 |
| 527,38356 | 0,00024 | 0,00031 | 6e-05 | 7e-05 | 6e-05 |
| 527,42074 | 0,00029 | 0,00033 | 7e-05 | 7e-05 | 7e-05 |
| 527,45793 | 0,00034 | 0,00036 | 8e-05 | 8e-05 | 8e-05 |
| 527,49511 | 0,00038 | 0,00038 | 1e-04 | 1e-04 | 9e-05 |
| 527,53229 | 0,00042 | 4e-04 | 0,00013 | 0,00012 | 1e-04 |
| 527,56947 | 0,00045 | 0,00043 | 0,00016 | 0,00014 | 0,00011 |
| 527,60665 | 0,00048 | 0,00045 | 2e-04 | 0,00017 | 0,00012 |
| 527,64384 | 5e-04 | 0,00047 | 0,00025 | 0,00021 | 0,00013 |
| 527,68102 | 0,00052 | 0,00048 | 0,00031 | 0,00024 | 0,00013 |
| 527,7182 | 0,00053 | 0,00049 | 0,00038 | 0,00027 | 0,00014 |
| 527,75538 | 0,00054 | 0,00049 | 0,00046 | 0,00029 | 0,00016 |
| 527,79256 | 0,00055 | 5e-04 | 0,00055 | 0,00032 | 0,00017 |
| 527,82975 | 0,00057 | 5e-04 | 0,00064 | 0,00034 | 2e-04 |
| 527,86693 | 0,00057 | 0,00051 | 0,00073 | 0,00036 | 0,00023 |
| 527,90411 | 0,00058 | 0,00052 | 0,00081 | 0,00038 | 0,00027 |
| 527,94129 | 0,00059 | 0,00053 | 0,00089 | 4e-04 | 0,00031 |
| 527,97847 | 0,00059 | 0,00056 | 0,00095 | 0,00042 | 0,00035 |
| 528,01566 | 6e-04 | 0,00058 | 0,00099 | 0,00045 | 0,00039 |
| 528,05284 | 6e-04 | 0,00061 | 0,00102 | 0,00048 | 0,00043 |
| 528,09002 | 0,00061 | 0,00065 | 0,00103 | 0,00051 | 0,00046 |
| 528,1272 | 0,00063 | 0,00069 | 0,00103 | 0,00055 | 0,00048 |
| 528,16438 | 0,00065 | 0,00073 | 0,00102 | 0,00059 | 0,00049 |
| 528,20157 | 0,00067 | 0,00077 | 0,00101 | 0,00062 | 5e-04 |
| 528,23875 | 7e-04 | 0,00082 | 0,00099 | 0,00065 | 0,00051 |
| 528,27593 | 0,00073 | 0,00086 | 0,00098 | 0,00068 | 0,00052 |
| 528,31311 | 0,00076 | 0,00091 | 0,00097 | 7e-04 | 0,00053 |
| 528,35029 | 8e-04 | 0,00096 | 0,00096 | 0,00072 | 0,00056 |
| 528,38748 | 0,00084 | 0,00101 | 0,00096 | 0,00073 | 0,00058 |
| 528,42466 | 0,00088 | 0,00104 | 0,00097 | 0,00074 | 0,00061 |
| 528,46184 | 0,00094 | 0,00107 | 0,00098 | 0,00075 | 0,00064 |
| 528,49902 | 0,001 | 0,00108 | 0,00099 | 0,00075 | 0,00066 |
| 528,5362 | 0,00107 | 0,00108 | 0,001 | 0,00074 | 0,00068 |
| 528,57339 | 0,00114 | 0,00107 | 0,00101 | 0,00073 | 0,00069 |
| 528,61057 | 0,00121 | 0,00105 | 0,00102 | 0,00071 | 0,00068 |
| 528,64775 | 0,00127 | 0,00103 | 0,00103 | 0,00069 | 0,00066 |
| 528,68493 | 0,00132 | 0,00101 | 0,00105 | 0,00067 | 0,00064 |
| 528,72211 | 0,00135 | 0,00099 | 0,00107 | 0,00064 | 0,00061 |
| 528,7593 | 0,00136 | 0,00098 | 0,00109 | 0,00062 | 0,00058 |
| 528,79648 | 0,00136 | 0,00098 | 0,00113 | 0,00061 | 0,00055 |
| 528,83366 | 0,00134 | 0,00099 | 0,00116 | 0,00061 | 0,00053 |
| 528,87084 | 0,00131 | 0,00103 | 0,0012 | 0,00062 | 0,00052 |
| 528,90802 | 0,00127 | 0,00108 | 0,00124 | 0,00066 | 0,00053 |
| 528,94521 | 0,00124 | 0,00114 | 0,00128 | 0,00072 | 0,00055 |
| 528,98239 | 0,00121 | 0,00121 | 0,00133 | 8e-04 | 0,00058 |
| 529,01957 | 0,00119 | 0,0013 | 0,00137 | 9e-04 | 0,00063 |
| 529,05675 | 0,00118 | 0,00138 | 0,00142 | 0,00101 | 0,00069 |
| 529,09393 | 0,00118 | 0,00145 | 0,00147 | 0,00113 | 0,00075 |
| 529,13112 | 0,00118 | 0,00152 | 0,00152 | 0,00124 | 8e-04 |
| 529,1683 | 0,00118 | 0,00157 | 0,00156 | 0,00133 | 0,00086 |
| 529,20548 | 0,00118 | 0,00161 | 0,0016 | 0,0014 | 9e-04 |
| 529,24266 | 0,00118 | 0,00164 | 0,00161 | 0,00143 | 0,00093 |
| 529,27984 | 0,00119 | 0,00165 | 0,00162 | 0,00144 | 0,00095 |
| 529,31703 | 0,0012 | 0,00165 | 0,00161 | 0,00142 | 0,00095 |
| 529,35421 | 0,00121 | 0,00165 | 0,0016 | 0,00139 | 0,00095 |
| 529,39139 | 0,00123 | 0,00165 | 0,00158 | 0,00135 | 0,00094 |
| 529,42857 | 0,00125 | 0,00164 | 0,00157 | 0,00132 | 0,00093 |
| 529,46575 | 0,00128 | 0,00164 | 0,00157 | 0,00131 | 0,00092 |
| 529,50294 | 0,0013 | 0,00163 | 0,00157 | 0,00133 | 0,00092 |
| 529,54012 | 0,00132 | 0,00162 | 0,00159 | 0,00137 | 0,00093 |
| 529,5773 | 0,00134 | 0,00162 | 0,00162 | 0,00143 | 0,00095 |
| 529,61448 | 0,00136 | 0,00161 | 0,00165 | 0,00151 | 0,00097 |
| 529,65166 | 0,00138 | 0,0016 | 0,00168 | 0,00161 | 0,001 |
| 529,68885 | 0,00141 | 0,0016 | 0,0017 | 0,00171 | 0,00103 |
| 529,72603 | 0,00144 | 0,00161 | 0,00172 | 0,00182 | 0,00107 |
| 529,76321 | 0,00148 | 0,00163 | 0,00173 | 0,00191 | 0,0011 |
| 529,80039 | 0,00153 | 0,00167 | 0,00174 | 0,002 | 0,00115 |
| 529,83757 | 0,00158 | 0,00173 | 0,00176 | 0,00207 | 0,0012 |
| 529,87476 | 0,00164 | 0,0018 | 0,00178 | 0,00212 | 0,00127 |
| 529,91194 | 0,00171 | 0,0019 | 0,00183 | 0,00216 | 0,00134 |
| 529,94912 | 0,00179 | 0,00201 | 0,00189 | 0,00217 | 0,00142 |
| 529,9863 | 0,00187 | 0,00214 | 0,00197 | 0,00217 | 0,00151 |
| 530,02348 | 0,00196 | 0,00228 | 0,00207 | 0,00216 | 0,0016 |
| 530,06067 | 0,00206 | 0,00242 | 0,00218 | 0,00213 | 0,00169 |
| 530,09785 | 0,00216 | 0,00256 | 0,0023 | 0,0021 | 0,00178 |
| 530,13503 | 0,00226 | 0,0027 | 0,00241 | 0,00207 | 0,00188 |
| 530,17221 | 0,00237 | 0,00284 | 0,0025 | 0,00206 | 0,00197 |
| 530,20939 | 0,00247 | 0,00296 | 0,00258 | 0,00206 | 0,00206 |
| 530,24658 | 0,00258 | 0,00307 | 0,00264 | 0,00208 | 0,00216 |
| 530,28376 | 0,00269 | 0,00317 | 0,00268 | 0,00213 | 0,00225 |
| 530,32094 | 0,0028 | 0,00324 | 0,00272 | 0,00221 | 0,00234 |
| 530,35812 | 0,0029 | 0,00331 | 0,00275 | 0,0023 | 0,00243 |
| 530,3953 | 0,00299 | 0,00335 | 0,00279 | 0,00241 | 0,00252 |
| 530,43249 | 0,00308 | 0,00338 | 0,00284 | 0,00251 | 0,0026 |
| 530,46967 | 0,00316 | 0,00339 | 0,00289 | 0,00261 | 0,00267 |
| 530,50685 | 0,00323 | 0,00338 | 0,00295 | 0,0027 | 0,00274 |
| 530,54403 | 0,0033 | 0,00336 | 0,00301 | 0,00276 | 0,00279 |
| 530,58121 | 0,00337 | 0,00332 | 0,00307 | 0,00281 | 0,00284 |
| 530,6184 | 0,00344 | 0,00328 | 0,00313 | 0,00283 | 0,00287 |
| 530,65558 | 0,00351 | 0,00323 | 0,00319 | 0,00284 | 0,00289 |
| 530,69276 | 0,00357 | 0,0032 | 0,00324 | 0,00283 | 0,0029 |
| 530,72994 | 0,00362 | 0,00319 | 0,0033 | 0,00281 | 0,00289 |
| 530,76712 | 0,00365 | 0,00322 | 0,00335 | 0,00279 | 0,00289 |
| 530,80431 | 0,00365 | 0,00328 | 0,0034 | 0,00277 | 0,00288 |
| 530,84149 | 0,00364 | 0,00338 | 0,00345 | 0,00275 | 0,00288 |
| 530,87867 | 0,0036 | 0,00351 | 0,00349 | 0,00274 | 0,00288 |
| 530,91585 | 0,00354 | 0,00367 | 0,00352 | 0,00274 | 0,0029 |
| 530,95303 | 0,00347 | 0,00382 | 0,00353 | 0,00275 | 0,00291 |
| 530,99022 | 0,00339 | 0,00397 | 0,00353 | 0,00277 | 0,00293 |
| 531,0274 | 0,00331 | 0,00409 | 0,00351 | 0,0028 | 0,00296 |
| 531,06458 | 0,00323 | 0,00418 | 0,00349 | 0,00282 | 0,00298 |
| 531,10176 | 0,00315 | 0,00425 | 0,00348 | 0,00285 | 0,00301 |
| 531,13894 | 0,00309 | 0,0043 | 0,00348 | 0,00288 | 0,00305 |
| 531,17613 | 0,00304 | 0,00435 | 0,00351 | 0,00292 | 0,00311 |
| 531,21331 | 0,00302 | 0,0044 | 0,00359 | 0,00298 | 0,00321 |
| 531,25049 | 0,00303 | 0,00448 | 0,00373 | 0,00307 | 0,00334 |
| 531,28767 | 0,00307 | 0,00459 | 0,00392 | 0,0032 | 0,00351 |
| 531,32485 | 0,00316 | 0,00473 | 0,00415 | 0,00337 | 0,00371 |
| 531,36204 | 0,00329 | 0,00491 | 0,00442 | 0,00357 | 0,00394 |
| 531,39922 | 0,00348 | 0,00511 | 0,00472 | 0,00381 | 0,00419 |
| 531,4364 | 0,00371 | 0,00533 | 0,00504 | 0,00409 | 0,00444 |
| 531,47358 | 0,00399 | 0,00556 | 0,00535 | 0,00439 | 0,0047 |
| 531,51076 | 0,00431 | 0,00579 | 0,00566 | 0,00473 | 0,00494 |
| 531,54795 | 0,00465 | 0,00601 | 0,00595 | 0,00508 | 0,00517 |
| 531,58513 | 0,00502 | 0,00622 | 0,00623 | 0,00546 | 0,00537 |
| 531,62231 | 0,00538 | 0,00642 | 0,00649 | 0,00586 | 0,00555 |
| 531,65949 | 0,00573 | 0,0066 | 0,00672 | 0,00628 | 0,00571 |
| 531,69667 | 0,00607 | 0,00677 | 0,00693 | 0,00671 | 0,00586 |
| 531,73386 | 0,00637 | 0,00693 | 0,0071 | 0,00715 | 0,006 |
| 531,77104 | 0,00665 | 0,00707 | 0,00725 | 0,00757 | 0,00614 |
| 531,80822 | 0,0069 | 0,00721 | 0,00737 | 0,00794 | 0,00628 |
| 531,8454 | 0,00714 | 0,00733 | 0,00745 | 0,00825 | 0,00641 |
| 531,88258 | 0,00737 | 0,00745 | 0,00752 | 0,00846 | 0,00653 |
| 531,91977 | 0,00759 | 0,00757 | 0,00756 | 0,00857 | 0,00663 |
| 531,95695 | 0,0078 | 0,00771 | 0,00759 | 0,00858 | 0,0067 |
| 531,99413 | 0,008 | 0,00787 | 0,00761 | 0,00848 | 0,00674 |
| 532,03131 | 0,00818 | 0,00806 | 0,00762 | 0,00831 | 0,00675 |
| 532,06849 | 0,00833 | 0,00829 | 0,00762 | 0,0081 | 0,00673 |
| 532,10568 | 0,00844 | 0,00854 | 0,00763 | 0,00788 | 0,00669 |
| 532,14286 | 0,00852 | 0,00881 | 0,00764 | 0,00768 | 0,00664 |
| 532,18004 | 0,00856 | 0,00908 | 0,00767 | 0,00754 | 0,00659 |
| 532,21722 | 0,00857 | 0,00932 | 0,00772 | 0,00746 | 0,00657 |
| 532,2544 | 0,00857 | 0,00952 | 0,00779 | 0,00747 | 0,0066 |
| 532,29159 | 0,00855 | 0,00965 | 0,00789 | 0,00755 | 0,00667 |
| 532,32877 | 0,00854 | 0,00971 | 0,00802 | 0,00769 | 0,00682 |
| 532,36595 | 0,00853 | 0,00969 | 0,00818 | 0,00789 | 0,00704 |
| 532,40313 | 0,00852 | 0,00961 | 0,00837 | 0,0081 | 0,00732 |
| 532,44031 | 0,00852 | 0,00949 | 0,00856 | 0,00831 | 0,00764 |
| 532,4775 | 0,00851 | 0,00936 | 0,00875 | 0,00848 | 0,00799 |
| 532,51468 | 0,0085 | 0,00927 | 0,00894 | 0,00861 | 0,00833 |
| 532,55186 | 0,00848 | 0,00922 | 0,00912 | 0,00868 | 0,00865 |
| 532,58904 | 0,00848 | 0,00924 | 0,00929 | 0,0087 | 0,00893 |
| 532,62622 | 0,00848 | 0,00935 | 0,00945 | 0,00868 | 0,00915 |
| 532,66341 | 0,00851 | 0,00955 | 0,00961 | 0,00864 | 0,00931 |
| 532,70059 | 0,00856 | 0,00983 | 0,00975 | 0,00861 | 0,00942 |
| 532,73777 | 0,00863 | 0,01017 | 0,00988 | 0,00862 | 0,00949 |
| 532,77495 | 0,00874 | 0,01056 | 0,01 | 0,00868 | 0,00952 |
| 532,81213 | 0,00888 | 0,01097 | 0,0101 | 0,00882 | 0,00953 |
| 532,84932 | 0,00906 | 0,01139 | 0,0102 | 0,00902 | 0,00954 |
| 532,8865 | 0,00929 | 0,01178 | 0,01031 | 0,00929 | 0,00957 |
| 532,92368 | 0,00956 | 0,01215 | 0,01047 | 0,00962 | 0,00963 |
| 532,96086 | 0,0099 | 0,01248 | 0,01071 | 0,00999 | 0,00973 |
| 532,99804 | 0,01029 | 0,01278 | 0,01107 | 0,01038 | 0,00991 |
| 533,03523 | 0,01076 | 0,01307 | 0,01156 | 0,01078 | 0,01016 |
| 533,07241 | 0,01129 | 0,01335 | 0,01221 | 0,01119 | 0,0105 |
| 533,10959 | 0,01189 | 0,01366 | 0,01302 | 0,0116 | 0,01091 |
| 533,14677 | 0,01255 | 0,01402 | 0,01397 | 0,01199 | 0,0114 |
| 533,18395 | 0,01326 | 0,01443 | 0,01503 | 0,01238 | 0,01195 |
| 533,22114 | 0,014 | 0,01493 | 0,01614 | 0,01275 | 0,01254 |
| 533,25832 | 0,01475 | 0,01551 | 0,01724 | 0,01313 | 0,01317 |
| 533,2955 | 0,01551 | 0,01617 | 0,01827 | 0,0135 | 0,01382 |
| 533,33268 | 0,01625 | 0,01689 | 0,01918 | 0,01387 | 0,01448 |
| 533,36986 | 0,01694 | 0,01766 | 0,01991 | 0,01425 | 0,01515 |
| 533,40705 | 0,01758 | 0,01844 | 0,02046 | 0,01466 | 0,01583 |
| 533,44423 | 0,01815 | 0,01919 | 0,0208 | 0,01511 | 0,01653 |
| 533,48141 | 0,01863 | 0,01988 | 0,02097 | 0,01565 | 0,01727 |
| 533,51859 | 0,01901 | 0,02048 | 0,02099 | 0,01632 | 0,01807 |
| 533,55577 | 0,01933 | 0,02096 | 0,02092 | 0,01719 | 0,01897 |
| 533,59295 | 0,01959 | 0,02132 | 0,02081 | 0,01829 | 0,02 |
| 533,63014 | 0,01984 | 0,02158 | 0,02073 | 0,01965 | 0,02118 |
| 533,66732 | 0,02013 | 0,02176 | 0,0207 | 0,02128 | 0,02255 |
| 533,7045 | 0,02048 | 0,0219 | 0,02078 | 0,02314 | 0,02411 |
| 533,74168 | 0,02094 | 0,02206 | 0,02098 | 0,02518 | 0,02586 |
| 533,77886 | 0,02152 | 0,02228 | 0,0213 | 0,02729 | 0,02773 |
| 533,81605 | 0,02225 | 0,02262 | 0,02177 | 0,02937 | 0,02965 |
| 533,85323 | 0,02311 | 0,0231 | 0,02235 | 0,03128 | 0,03152 |
| 533,89041 | 0,02411 | 0,02376 | 0,02306 | 0,03292 | 0,0332 |
| 533,92759 | 0,02521 | 0,0246 | 0,02386 | 0,03418 | 0,03457 |
| 533,96477 | 0,02639 | 0,02564 | 0,02475 | 0,03501 | 0,03554 |
| 534,00196 | 0,02763 | 0,02683 | 0,02572 | 0,03537 | 0,03603 |
| 534,03914 | 0,0289 | 0,02817 | 0,02674 | 0,03529 | 0,03605 |
| 534,07632 | 0,03018 | 0,02962 | 0,02783 | 0,03484 | 0,03565 |
| 534,1135 | 0,03143 | 0,03112 | 0,02895 | 0,03411 | 0,03494 |
| 534,15068 | 0,03265 | 0,03265 | 0,03012 | 0,03328 | 0,03413 |
| 534,18787 | 0,03384 | 0,03416 | 0,03132 | 0,03254 | 0,0334 |
| 534,22505 | 0,03499 | 0,03564 | 0,03258 | 0,03207 | 0,03296 |
| 534,26223 | 0,03616 | 0,0371 | 0,0339 | 0,03206 | 0,03299 |
| 534,29941 | 0,03739 | 0,03857 | 0,03532 | 0,03269 | 0,03366 |
| 534,33659 | 0,03874 | 0,0401 | 0,03688 | 0,0341 | 0,03513 |
| 534,37378 | 0,04029 | 0,04174 | 0,03863 | 0,03638 | 0,03748 |
| 534,41096 | 0,04211 | 0,04356 | 0,04062 | 0,03957 | 0,04078 |
| 534,44814 | 0,04423 | 0,04562 | 0,04289 | 0,04361 | 0,04498 |
| 534,48532 | 0,04666 | 0,04793 | 0,04544 | 0,04834 | 0,04994 |
| 534,5225 | 0,04936 | 0,0505 | 0,04827 | 0,05349 | 0,05539 |
| 534,55969 | 0,05224 | 0,05327 | 0,05131 | 0,05869 | 0,06096 |
| 534,59687 | 0,05519 | 0,05612 | 0,05443 | 0,06351 | 0,06616 |
| 534,63405 | 0,05803 | 0,0589 | 0,05749 | 0,06751 | 0,07052 |
| 534,67123 | 0,06058 | 0,06139 | 0,06027 | 0,07029 | 0,07357 |
| 534,70841 | 0,06262 | 0,06341 | 0,06254 | 0,0715 | 0,07492 |
| 534,7456 | 0,06403 | 0,06481 | 0,06416 | 0,07119 | 0,0746 |
| 534,78278 | 0,06472 | 0,06547 | 0,065 | 0,06949 | 0,07277 |
| 534,81996 | 0,06468 | 0,06536 | 0,06501 | 0,06669 | 0,06974 |
| 534,85714 | 0,06394 | 0,06452 | 0,06423 | 0,06317 | 0,06593 |
| 534,89432 | 0,0626 | 0,06303 | 0,06277 | 0,05932 | 0,06179 |
| 534,93151 | 0,0608 | 0,06103 | 0,06077 | 0,05549 | 0,0577 |
| 534,96869 | 0,05871 | 0,05869 | 0,05842 | 0,05195 | 0,05394 |
| 535,00587 | 0,05648 | 0,05618 | 0,0559 | 0,04888 | 0,05068 |
| 535,04305 | 0,05426 | 0,05366 | 0,05337 | 0,04635 | 0,04799 |
| 535,08023 | 0,05215 | 0,05125 | 0,05097 | 0,04438 | 0,04585 |
| 535,11742 | 0,05025 | 0,04905 | 0,04877 | 0,0429 | 0,0442 |
| 535,1546 | 0,04858 | 0,04714 | 0,04684 | 0,04187 | 0,04295 |
| 535,19178 | 0,0472 | 0,04557 | 0,04521 | 0,0412 | 0,04204 |
| 535,22896 | 0,04613 | 0,04437 | 0,04392 | 0,04083 | 0,0414 |
| 535,26614 | 0,04539 | 0,04359 | 0,04304 | 0,04074 | 0,04099 |
| 535,30333 | 0,04503 | 0,04324 | 0,04261 | 0,04092 | 0,04083 |
| 535,34051 | 0,04512 | 0,04338 | 0,04271 | 0,04139 | 0,04092 |
| 535,37769 | 0,04572 | 0,04409 | 0,04348 | 0,04225 | 0,04135 |
| 535,41487 | 0,04697 | 0,04547 | 0,04501 | 0,04363 | 0,04228 |
| 535,45205 | 0,04897 | 0,04764 | 0,04744 | 0,04573 | 0,04392 |
| 535,48924 | 0,05185 | 0,05071 | 0,05088 | 0,04881 | 0,04656 |
| 535,52642 | 0,05571 | 0,05479 | 0,05541 | 0,05316 | 0,05056 |
| 535,5636 | 0,0606 | 0,05994 | 0,06104 | 0,05909 | 0,05628 |
| 535,60078 | 0,06647 | 0,06614 | 0,06775 | 0,06682 | 0,06403 |
| 535,63796 | 0,07318 | 0,0733 | 0,0754 | 0,07643 | 0,07396 |
| 535,67515 | 0,08047 | 0,08121 | 0,08375 | 0,08779 | 0,08598 |
| 535,71233 | 0,088 | 0,08954 | 0,09248 | 0,10044 | 0,09968 |
| 535,74951 | 0,09531 | 0,09789 | 0,10115 | 0,11364 | 0,11429 |
| 535,78669 | 0,10192 | 0,10575 | 0,10925 | 0,12637 | 0,12871 |
| 535,82387 | 0,10738 | 0,11253 | 0,11617 | 0,13748 | 0,14164 |
| 535,86106 | 0,11122 | 0,11784 | 0,12146 | 0,14564 | 0,15152 |
| 535,89824 | 0,11328 | 0,12137 | 0,12481 | 0,15015 | 0,15746 |
| 535,93542 | 0,11359 | 0,12302 | 0,12609 | 0,15076 | 0,159 |
| 535,9726 | 0,11236 | 0,12284 | 0,12537 | 0,14775 | 0,15628 |
| 536,00978 | 0,10994 | 0,12111 | 0,12291 | 0,14184 | 0,14997 |
| 536,04697 | 0,10679 | 0,11822 | 0,11915 | 0,13409 | 0,14116 |
| 536,08415 | 0,10341 | 0,11467 | 0,1146 | 0,12568 | 0,13114 |
| 536,12133 | 0,10025 | 0,11097 | 0,10983 | 0,11771 | 0,12121 |
| 536,15851 | 0,09769 | 0,10757 | 0,10536 | 0,11108 | 0,11246 |
| 536,19569 | 0,096 | 0,10483 | 0,1016 | 0,10634 | 0,10565 |
| 536,23288 | 0,09531 | 0,10299 | 0,09884 | 0,10375 | 0,1012 |
| 536,27006 | 0,09563 | 0,10213 | 0,09725 | 0,10322 | 0,09918 |
| 536,30724 | 0,0969 | 0,10221 | 0,09684 | 0,10449 | 0,0994 |
| 536,34442 | 0,09894 | 0,10309 | 0,09751 | 0,10712 | 0,10147 |
| 536,3816 | 0,10156 | 0,10459 | 0,0991 | 0,11069 | 0,10494 |
| 536,41879 | 0,10452 | 0,10644 | 0,1014 | 0,11479 | 0,10938 |
| 536,45597 | 0,10759 | 0,10842 | 0,10412 | 0,11919 | 0,11446 |
| 536,49315 | 0,11053 | 0,11037 | 0,10704 | 0,12383 | 0,11998 |
| 536,53033 | 0,11321 | 0,11214 | 0,10994 | 0,12896 | 0,12606 |
| 536,56751 | 0,11555 | 0,11368 | 0,11266 | 0,13502 | 0,13307 |
| 536,6047 | 0,11751 | 0,11494 | 0,11508 | 0,14268 | 0,14158 |
| 536,64188 | 0,11915 | 0,11593 | 0,11711 | 0,15268 | 0,15232 |
| 536,67906 | 0,12053 | 0,11672 | 0,11871 | 0,16569 | 0,16599 |
| 536,71624 | 0,12179 | 0,11737 | 0,11991 | 0,18212 | 0,18306 |
| 536,75342 | 0,12308 | 0,11803 | 0,1208 | 0,20193 | 0,20356 |
| 536,79061 | 0,12457 | 0,11886 | 0,1215 | 0,22443 | 0,22687 |
| 536,82779 | 0,12648 | 0,12008 | 0,12226 | 0,24829 | 0,25165 |
| 536,86497 | 0,12904 | 0,12193 | 0,12334 | 0,27154 | 0,2759 |
| 536,90215 | 0,13251 | 0,1247 | 0,12509 | 0,29185 | 0,29718 |
| 536,93933 | 0,1372 | 0,12878 | 0,12791 | 0,30689 | 0,31299 |
| 536,97652 | 0,14341 | 0,1345 | 0,13233 | 0,31473 | 0,32125 |
| 537,0137 | 0,1515 | 0,14213 | 0,13868 | 0,31398 | 0,32033 |
| 537,05088 | 0,16177 | 0,15185 | 0,14725 | 0,30465 | 0,31039 |
| 537,08806 | 0,17421 | 0,16376 | 0,15818 | 0,28832 | 0,29299 |
| 537,12524 | 0,18869 | 0,17773 | 0,17145 | 0,26699 | 0,27023 |
| 537,16243 | 0,20481 | 0,19342 | 0,18674 | 0,24299 | 0,24466 |
| 537,19961 | 0,22191 | 0,21023 | 0,2035 | 0,21858 | 0,21874 |
| 537,23679 | 0,23902 | 0,22734 | 0,22089 | 0,19563 | 0,19455 |
| 537,27397 | 0,25501 | 0,24372 | 0,23788 | 0,1754 | 0,17349 |
| 537,31115 | 0,26864 | 0,25825 | 0,25328 | 0,15853 | 0,15626 |
| 537,34834 | 0,27879 | 0,26987 | 0,26593 | 0,1451 | 0,14293 |
| 537,38552 | 0,28455 | 0,27765 | 0,27479 | 0,1348 | 0,13308 |
| 537,4227 | 0,2854 | 0,28096 | 0,27911 | 0,12709 | 0,12604 |
| 537,45988 | 0,28128 | 0,27955 | 0,27851 | 0,12139 | 0,12108 |
| 537,49706 | 0,27258 | 0,27349 | 0,27305 | 0,11715 | 0,11751 |
| 537,53425 | 0,2601 | 0,26327 | 0,26311 | 0,11394 | 0,11482 |
| 537,57143 | 0,24489 | 0,25002 | 0,24959 | 0,11142 | 0,11266 |
| 537,60861 | 0,22806 | 0,23473 | 0,23374 | 0,1094 | 0,11086 |
| 537,64579 | 0,21082 | 0,21841 | 0,21666 | 0,1077 | 0,10932 |
| 537,68297 | 0,19407 | 0,20194 | 0,19936 | 0,10623 | 0,108 |
| 537,72016 | 0,17838 | 0,18603 | 0,18265 | 0,10492 | 0,10689 |
| 537,75734 | 0,16414 | 0,1712 | 0,16716 | 0,10376 | 0,10594 |
| 537,79452 | 0,1515 | 0,15773 | 0,15325 | 0,10274 | 0,10513 |
| 537,8317 | 0,14049 | 0,14576 | 0,14109 | 0,10189 | 0,10442 |
| 537,86888 | 0,13105 | 0,13526 | 0,13069 | 0,10131 | 0,10383 |
| 537,90607 | 0,12305 | 0,12616 | 0,12192 | 0,10114 | 0,10348 |
| 537,94325 | 0,11635 | 0,11831 | 0,1146 | 0,10162 | 0,10354 |
| 537,98043 | 0,11081 | 0,11158 | 0,10852 | 0,10303 | 0,1043 |
| 538,01761 | 0,10628 | 0,10585 | 0,10346 | 0,10572 | 0,10612 |
| 538,05479 | 0,10265 | 0,10104 | 0,09927 | 0,11002 | 0,10939 |
| 538,09198 | 0,09984 | 0,09718 | 0,09585 | 0,11621 | 0,11444 |
| 538,12916 | 0,09783 | 0,09424 | 0,09324 | 0,12439 | 0,1215 |
| 538,16634 | 0,0967 | 0,09236 | 0,0915 | 0,13448 | 0,13058 |
| 538,20352 | 0,09677 | 0,09174 | 0,09086 | 0,14618 | 0,14146 |
| 538,2407 | 0,09839 | 0,09274 | 0,0917 | 0,15882 | 0,15358 |
| 538,27789 | 0,10213 | 0,09587 | 0,09455 | 0,1719 | 0,16644 |
| 538,31507 | 0,10877 | 0,10178 | 0,10011 | 0,18517 | 0,17979 |
| 538,35225 | 0,11924 | 0,11127 | 0,10919 | 0,19892 | 0,19386 |
| 538,38943 | 0,13455 | 0,12526 | 0,12273 | 0,2141 | 0,20952 |
| 538,42661 | 0,15569 | 0,14466 | 0,14163 | 0,23237 | 0,2283 |
| 538,4638 | 0,1835 | 0,17028 | 0,16671 | 0,25586 | 0,25225 |
| 538,50098 | 0,21841 | 0,20263 | 0,1985 | 0,28671 | 0,28344 |
| 538,53816 | 0,26031 | 0,24175 | 0,2371 | 0,32643 | 0,32339 |
| 538,57534 | 0,30836 | 0,28703 | 0,28196 | 0,37523 | 0,37235 |
| 538,61252 | 0,36083 | 0,33709 | 0,33182 | 0,43145 | 0,42873 |
| 538,64971 | 0,4152 | 0,38973 | 0,38464 | 0,49132 | 0,48887 |
| 538,68689 | 0,46822 | 0,44165 | 0,43751 | 0,54917 | 0,54718 |
| 538,72407 | 0,51623 | 0,48938 | 0,48674 | 0,59822 | 0,59688 |
| 538,76125 | 0,55535 | 0,52958 | 0,52894 | 0,63097 | 0,63015 |
| 538,79843 | 0,58178 | 0,55933 | 0,56107 | 0,64147 | 0,64154 |
| 538,83562 | 0,59399 | 0,57648 | 0,58082 | 0,62814 | 0,62913 |
| 538,8728 | 0,59122 | 0,57992 | 0,58687 | 0,59192 | 0,59374 |
| 538,90998 | 0,57403 | 0,56963 | 0,57901 | 0,5366 | 0,53907 |
| 538,94716 | 0,54408 | 0,54666 | 0,55811 | 0,46804 | 0,47091 |
| 538,98434 | 0,50389 | 0,51293 | 0,52592 | 0,39304 | 0,39605 |
| 539,02153 | 0,45645 | 0,47089 | 0,48485 | 0,31818 | 0,32113 |
| 539,05871 | 0,40483 | 0,42329 | 0,4376 | 0,24893 | 0,25167 |
| 539,09589 | 0,3519 | 0,37285 | 0,38693 | 0,18913 | 0,19158 |
| 539,13307 | 0,30009 | 0,32202 | 0,33538 | 0,14086 | 0,14299 |
| 539,17025 | 0,2513 | 0,2729 | 0,28514 | 0,10468 | 0,10648 |
| 539,20744 | 0,20686 | 0,22722 | 0,23798 | 0,08013 | 0,08158 |
| 539,24462 | 0,16763 | 0,18639 | 0,19522 | 0,06616 | 0,06722 |
| 539,2818 | 0,13406 | 0,15091 | 0,15809 | 0,06165 | 0,06222 |
| 539,31898 | 0,10628 | 0,12113 | 0,12671 | 0,06561 | 0,06556 |
| 539,35616 | 0,08447 | 0,09714 | 0,10122 | 0,07763 | 0,07691 |
| 539,39335 | 0,06831 | 0,07884 | 0,08153 | 0,09662 | 0,09497 |
| 539,43053 | 0,05736 | 0,06599 | 0,06743 | 0,12144 | 0,1188 |
| 539,46771 | 0,05133 | 0,0583 | 0,05858 | 0,15061 | 0,14696 |
| 539,50489 | 0,04992 | 0,0554 | 0,05465 | 0,18199 | 0,17744 |
| 539,54207 | 0,05285 | 0,05693 | 0,05526 | 0,21288 | 0,20762 |
| 539,57926 | 0,05984 | 0,06251 | 0,06004 | 0,24026 | 0,23455 |
| 539,61644 | 0,07051 | 0,0717 | 0,0686 | 0,26116 | 0,25528 |
| 539,65362 | 0,0844 | 0,08401 | 0,08048 | 0,27312 | 0,26738 |
| 539,6908 | 0,10087 | 0,09883 | 0,09512 | 0,27463 | 0,26928 |
| 539,72798 | 0,1191 | 0,11541 | 0,11184 | 0,26539 | 0,26064 |
| 539,76517 | 0,13809 | 0,13288 | 0,12978 | 0,24638 | 0,24235 |
| 539,80235 | 0,1567 | 0,15017 | 0,14798 | 0,21968 | 0,21643 |
| 539,83953 | 0,17377 | 0,16617 | 0,16529 | 0,1881 | 0,18561 |
| 539,87671 | 0,18821 | 0,17993 | 0,18056 | 0,1547 | 0,15291 |
| 539,91389 | 0,19909 | 0,19064 | 0,19292 | 0,12233 | 0,1212 |
| 539,95108 | 0,20548 | 0,1977 | 0,20165 | 0,09354 | 0,0929 |
| 539,98826 | 0,20731 | 0,20075 | 0,20628 | 0,06946 | 0,06916 |
| 540,02544 | 0,2047 | 0,19971 | 0,20662 | 0,05049 | 0,05039 |
| 540,06262 | 0,19796 | 0,19471 | 0,20272 | 0,03642 | 0,03641 |
| 540,0998 | 0,18763 | 0,1861 | 0,19486 | 0,02659 | 0,02658 |
| 540,13699 | 0,17433 | 0,17437 | 0,18348 | 0,02017 | 0,0201 |
| 540,17417 | 0,15877 | 0,16013 | 0,16918 | 0,01625 | 0,01608 |
| 540,21135 | 0,14169 | 0,14405 | 0,15267 | 0,01404 | 0,01376 |
| 540,24853 | 0,12379 | 0,12686 | 0,13471 | 0,01287 | 0,01248 |
| 540,28571 | 0,1058 | 0,1093 | 0,11613 | 0,01224 | 0,01176 |
| 540,3229 | 0,08834 | 0,09205 | 0,09771 | 0,0118 | 0,01127 |
| 540,36008 | 0,07201 | 0,07582 | 0,08019 | 0,01134 | 0,01081 |
| 540,39726 | 0,05727 | 0,06115 | 0,06422 | 0,01075 | 0,01027 |
| 540,43444 | 0,04443 | 0,04834 | 0,05035 | 0,01 | 0,00962 |
| 540,47162 | 0,03367 | 0,03754 | 0,03867 | 0,00909 | 0,00886 |
| 540,50881 | 0,02501 | 0,02875 | 0,0292 | 0,00809 | 0,00803 |
| 540,54599 | 0,01836 | 0,02182 | 0,0218 | 0,00704 | 0,00718 |
| 540,58317 | 0,01335 | 0,01652 | 0,01618 | 0,00602 | 0,00634 |
| 540,62035 | 0,00968 | 0,01257 | 0,01205 | 0,00508 | 0,00555 |
| 540,65753 | 0,00707 | 0,00968 | 0,00907 | 0,00424 | 0,00482 |
| 540,69472 | 0,00523 | 0,00757 | 0,00694 | 0,00353 | 0,00419 |
| 540,7319 | 0,00395 | 0,00602 | 0,00542 | 0,00297 | 0,00365 |
| 540,76908 | 0,00307 | 0,00487 | 0,00432 | 0,00257 | 0,00321 |
| 540,80626 | 0,00246 | 0,00398 | 0,00349 | 0,00232 | 0,00289 |
| 540,84344 | 0,00203 | 0,00329 | 0,00287 | 0,00222 | 0,00268 |
| 540,88063 | 0,00174 | 0,00273 | 0,0024 | 0,00229 | 0,0026 |
| 540,91781 | 0,00154 | 0,0023 | 0,00205 | 0,00251 | 0,00266 |
| 540,95499 | 0,00143 | 0,00196 | 0,00181 | 0,00288 | 0,00287 |
| 540,99217 | 0,0014 | 0,00172 | 0,00169 | 0,00338 | 0,00321 |
| 541,02935 | 0,00143 | 0,00157 | 0,00167 | 0,00398 | 0,00367 |
| 541,06654 | 0,00153 | 0,00149 | 0,00174 | 0,00465 | 0,00421 |
| 541,10372 | 0,00171 | 0,0015 | 0,0019 | 0,0053 | 0,00478 |
| 541,1409 | 0,00194 | 0,00157 | 0,00213 | 0,00587 | 0,0053 |
| 541,17808 | 0,00224 | 0,00169 | 0,00242 | 0,0063 | 0,00572 |
| 541,21526 | 0,00257 | 0,00186 | 0,00273 | 0,00651 | 0,00596 |
| 541,25245 | 0,00292 | 0,00205 | 0,00306 | 0,00649 | 0,00599 |
| 541,28963 | 0,00328 | 0,00224 | 0,00339 | 0,00623 | 0,0058 |
| 541,32681 | 0,00362 | 0,00243 | 0,00368 | 0,00575 | 0,00541 |
| 541,36399 | 0,00393 | 0,00258 | 0,00394 | 0,0051 | 0,00486 |
| 541,40117 | 0,00419 | 0,00271 | 0,00414 | 0,00434 | 0,0042 |
| 541,43836 | 0,00439 | 0,0028 | 0,0043 | 0,00356 | 0,00349 |
| 541,47554 | 0,00452 | 0,00284 | 0,0044 | 0,00279 | 0,0028 |
| 541,51272 | 0,00457 | 0,00285 | 0,00444 | 0,0021 | 0,00216 |
| 541,5499 | 0,00454 | 0,00283 | 0,00442 | 0,00152 | 0,00162 |
| 541,58708 | 0,00443 | 0,00277 | 0,00433 | 0,00106 | 0,00117 |
| 541,62427 | 0,00424 | 0,00268 | 0,00416 | 0,00071 | 0,00083 |
| 541,66145 | 0,00398 | 0,00255 | 0,00392 | 0,00046 | 0,00058 |
| 541,69863 | 0,00364 | 0,00238 | 0,0036 | 0,00029 | 4e-04 |
| 541,73581 | 0,00325 | 0,00218 | 0,00322 | 0,00018 | 0,00028 |
| 541,77299 | 0,00282 | 0,00194 | 0,00279 | 0,00011 | 0,00019 |
| 541,81018 | 0,00237 | 0,00168 | 0,00235 | 7e-05 | 0,00014 |
| 541,84736 | 0,00193 | 0,00141 | 0,00191 | 4e-05 | 9e-05 |
| 541,88454 | 0,00152 | 0,00115 | 0,00149 | 2e-05 | 6e-05 |
| 541,92172 | 0,00115 | 9e-04 | 0,00113 | 1e-05 | 4e-05 |
| 541,9589 | 0,00084 | 0,00068 | 0,00082 | 1e-05 | 3e-05 |
| 541,99609 | 0,00058 | 5e-04 | 0,00057 | 0 | 2e-05 |
| 542,03327 | 0,00039 | 0,00035 | 0,00038 | 0 | 1e-05 |
| 542,07045 | 0,00025 | 0,00025 | 0,00024 | 0 | 1e-05 |
| 542,10763 | 0,00015 | 0,00018 | 0,00015 | 0 | 1e-05 |
| 542,14481 | 9e-05 | 0,00013 | 9e-05 | 0 | 1e-05 |
| 542,182 | 5e-05 | 1e-04 | 5e-05 | 0 | 1e-05 |
| 542,21918 | 3e-05 | 8e-05 | 3e-05 | 0 | 1e-05 |
| 542,25636 | 1e-05 | 6e-05 | 1e-05 | 0 | 1e-05 |
| 542,29354 | 1e-05 | 5e-05 | 1e-05 | 0 | 2e-05 |
| 542,33072 | 0 | 5e-05 | 0 | 0 | 3e-05 |
| 542,36791 | 0 | 4e-05 | 0 | 0 | 3e-05 |
| 542,40509 | 0 | 3e-05 | 0 | 0 | 4e-05 |
| 542,44227 | 0 | 2e-05 | 0 | 0 | 4e-05 |
| 542,47945 | 0 | 2e-05 | 0 | 0 | 5e-05 |
| 542,51663 | 0 | 1e-05 | 0 | 0 | 5e-05 |
| 542,55382 | 0 | 1e-05 | 0 | 0 | 5e-05 |
| 542,591 | 0 | 1e-05 | 0 | 0 | 4e-05 |
| 542,62818 | 0 | 0 | 0 | 0 | 4e-05 |
| 542,66536 | 0 | 0 | 0 | 0 | 3e-05 |
| 542,70254 | 0 | 0 | 0 | 0 | 2e-05 |
| 542,73973 | 0 | 0 | 0 | 0 | 2e-05 |
| 542,77691 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,81409 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,85127 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 0 | 0 | 0 |
| 524,74364 | 0 | 0 | 0 | 0 | 0 |
| 524,78082 | 0 | 0 | 0 | 0 | 0 |
| 524,818 | 0 | 0 | 0 | 0 | 0 |
| 524,85519 | 0 | 0 | 0 | 0 | 0 |
| 524,89237 | 0 | 0 | 0 | 0 | 0 |
| 524,92955 | 0 | 0 | 0 | 0 | 0 |
| 524,96673 | 0 | 0 | 0 | 0 | 0 |
| 525,00391 | 0 | 0 | 0 | 0 | 0 |
| 525,0411 | 0 | 0 | 0 | 0 | 0 |
| 525,07828 | 0 | 0 | 0 | 0 | 0 |
| 525,11546 | 0 | 0 | 0 | 0 | 0 |
| 525,15264 | 0 | 0 | 0 | 0 | 0 |
| 525,18982 | 0 | 0 | 0 | 0 | 0 |
| 525,22701 | 0 | 0 | 0 | 0 | 0 |
| 525,26419 | 0 | 0 | 0 | 0 | 0 |
| 525,30137 | 0 | 0 | 0 | 0 | 0 |
| 525,33855 | 0 | 0 | 0 | 0 | 0 |
| 525,37573 | 0 | 0 | 0 | 0 | 0 |
| 525,41292 | 0 | 0 | 0 | 0 | 0 |
| 525,4501 | 0 | 0 | 0 | 0 | 0 |
| 525,48728 | 0 | 1e-05 | 0 | 0 | 0 |
| 525,52446 | 0 | 1e-05 | 0 | 0 | 0 |
| 525,56164 | 0 | 1e-05 | 0 | 0 | 0 |
| 525,59883 | 0 | 2e-05 | 0 | 0 | 0 |
| 525,63601 | 0 | 2e-05 | 0 | 0 | 0 |
| 525,67319 | 0 | 3e-05 | 0 | 0 | 0 |
| 525,71037 | 1e-05 | 4e-05 | 0 | 0 | 0 |
| 525,74755 | 1e-05 | 4e-05 | 0 | 0 | 0 |
| 525,78474 | 1e-05 | 5e-05 | 0 | 0 | 0 |
| 525,82192 | 2e-05 | 6e-05 | 0 | 0 | 0 |
| 525,8591 | 3e-05 | 7e-05 | 0 | 0 | 0 |
| 525,89628 | 3e-05 | 7e-05 | 0 | 0 | 0 |
| 525,93346 | 4e-05 | 7e-05 | 0 | 0 | 0 |
| 525,97065 | 5e-05 | 7e-05 | 0 | 0 | 0 |
| 526,00783 | 6e-05 | 7e-05 | 0 | 0 | 0 |
| 526,04501 | 6e-05 | 6e-05 | 0 | 0 | 0 |
| 526,08219 | 7e-05 | 6e-05 | 0 | 0 | 0 |
| 526,11937 | 7e-05 | 5e-05 | 0 | 0 | 0 |
| 526,15656 | 7e-05 | 5e-05 | 0 | 0 | 0 |
| 526,19374 | 7e-05 | 4e-05 | 0 | 0 | 0 |
| 526,23092 | 7e-05 | 4e-05 | 0 | 0 | 0 |
| 526,2681 | 6e-05 | 4e-05 | 0 | 0 | 0 |
| 526,30528 | 5e-05 | 5e-05 | 0 | 0 | 0 |
| 526,34247 | 5e-05 | 6e-05 | 0 | 0 | 0 |
| 526,37965 | 4e-05 | 7e-05 | 0 | 0 | 0 |
| 526,41683 | 3e-05 | 8e-05 | 0 | 0 | 0 |
| 526,45401 | 2e-05 | 9e-05 | 0 | 0 | 0 |
| 526,49119 | 2e-05 | 0,00011 | 1e-05 | 0 | 0 |
| 526,52838 | 1e-05 | 0,00012 | 1e-05 | 0 | 0 |
| 526,56556 | 1e-05 | 0,00013 | 2e-05 | 0 | 0 |
| 526,60274 | 1e-05 | 0,00015 | 2e-05 | 0 | 1e-05 |
| 526,63992 | 1e-05 | 0,00015 | 3e-05 | 0 | 1e-05 |
| 526,6771 | 1e-05 | 0,00016 | 4e-05 | 0 | 1e-05 |
| 526,71429 | 2e-05 | 0,00016 | 5e-05 | 0 | 2e-05 |
| 526,75147 | 2e-05 | 0,00016 | 6e-05 | 0 | 3e-05 |
| 526,78865 | 3e-05 | 0,00016 | 7e-05 | 0 | 4e-05 |
| 526,82583 | 4e-05 | 0,00015 | 7e-05 | 0 | 5e-05 |
| 526,86301 | 6e-05 | 0,00015 | 8e-05 | 0 | 6e-05 |
| 526,9002 | 7e-05 | 0,00014 | 9e-05 | 1e-05 | 7e-05 |
| 526,93738 | 9e-05 | 0,00013 | 9e-05 | 1e-05 | 7e-05 |
| 526,97456 | 1e-04 | 0,00012 | 1e-04 | 1e-05 | 8e-05 |
| 527,01174 | 0,00012 | 1e-04 | 1e-04 | 2e-05 | 8e-05 |
| 527,04892 | 0,00014 | 9e-05 | 0,00011 | 3e-05 | 8e-05 |
| 527,08611 | 0,00016 | 8e-05 | 0,00012 | 4e-05 | 7e-05 |
| 527,12329 | 0,00017 | 7e-05 | 0,00013 | 5e-05 | 6e-05 |
| 527,16047 | 0,00018 | 6e-05 | 0,00014 | 6e-05 | 5e-05 |
| 527,19765 | 0,00019 | 6e-05 | 0,00015 | 7e-05 | 4e-05 |
| 527,23483 | 2e-04 | 5e-05 | 0,00016 | 8e-05 | 3e-05 |
| 527,27202 | 2e-04 | 6e-05 | 0,00017 | 8e-05 | 2e-05 |
| 527,3092 | 0,00021 | 6e-05 | 0,00018 | 8e-05 | 2e-05 |
| 527,34638 | 0,00021 | 7e-05 | 0,00019 | 8e-05 | 1e-05 |
| 527,38356 | 0,00021 | 8e-05 | 2e-04 | 7e-05 | 1e-05 |
| 527,42074 | 0,00021 | 1e-04 | 0,00021 | 6e-05 | 1e-05 |
| 527,45793 | 0,00022 | 0,00012 | 0,00022 | 5e-05 | 1e-05 |
| 527,49511 | 0,00024 | 0,00014 | 0,00023 | 4e-05 | 1e-05 |
| 527,53229 | 0,00026 | 0,00017 | 0,00024 | 3e-05 | 2e-05 |
| 527,56947 | 3e-04 | 0,00019 | 0,00025 | 2e-05 | 3e-05 |
| 527,60665 | 0,00034 | 0,00022 | 0,00027 | 2e-05 | 4e-05 |
| 527,64384 | 0,00039 | 0,00025 | 0,00028 | 1e-05 | 5e-05 |
| 527,68102 | 0,00045 | 0,00028 | 3e-04 | 1e-05 | 7e-05 |
| 527,7182 | 0,00051 | 3e-04 | 0,00031 | 1e-05 | 9e-05 |
| 527,75538 | 0,00058 | 0,00034 | 0,00033 | 2e-05 | 0,00012 |
| 527,79256 | 0,00064 | 0,00037 | 0,00035 | 3e-05 | 0,00014 |
| 527,82975 | 0,00069 | 4e-04 | 0,00036 | 4e-05 | 0,00018 |
| 527,86693 | 0,00074 | 0,00044 | 0,00037 | 6e-05 | 0,00021 |
| 527,90411 | 0,00078 | 0,00047 | 0,00039 | 9e-05 | 0,00025 |
| 527,94129 | 0,00081 | 0,00051 | 0,00039 | 0,00012 | 3e-04 |
| 527,97847 | 0,00083 | 0,00055 | 4e-04 | 0,00016 | 0,00034 |
| 528,01566 | 0,00085 | 0,00058 | 4e-04 | 2e-04 | 0,00039 |
| 528,05284 | 0,00087 | 0,00062 | 4e-04 | 0,00024 | 0,00044 |
| 528,09002 | 0,00088 | 0,00066 | 4e-04 | 0,00028 | 0,00049 |
| 528,1272 | 0,00089 | 0,00069 | 4e-04 | 0,00032 | 0,00053 |
| 528,16438 | 9e-04 | 0,00073 | 0,00039 | 0,00036 | 0,00056 |
| 528,20157 | 0,00091 | 0,00076 | 0,00039 | 0,00041 | 0,00059 |
| 528,23875 | 0,00093 | 0,00079 | 4e-04 | 0,00046 | 0,00061 |
| 528,27593 | 0,00094 | 0,00081 | 0,00041 | 0,00053 | 0,00061 |
| 528,31311 | 0,00096 | 0,00084 | 0,00043 | 6e-04 | 0,00061 |
| 528,35029 | 0,00097 | 0,00086 | 0,00045 | 0,00069 | 0,00061 |
| 528,38748 | 0,00099 | 0,00087 | 0,00047 | 0,00079 | 6e-04 |
| 528,42466 | 0,001 | 0,00088 | 5e-04 | 0,00088 | 0,00059 |
| 528,46184 | 0,00101 | 0,00089 | 0,00052 | 0,00097 | 0,00057 |
| 528,49902 | 0,00101 | 9e-04 | 0,00055 | 0,00104 | 0,00056 |
| 528,5362 | 0,00101 | 0,00091 | 0,00057 | 0,00109 | 0,00055 |
| 528,57339 | 0,001 | 0,00091 | 0,00058 | 0,00112 | 0,00055 |
| 528,61057 | 0,00098 | 0,00092 | 6e-04 | 0,00112 | 0,00055 |
| 528,64775 | 0,00096 | 0,00092 | 0,00061 | 0,0011 | 0,00057 |
| 528,68493 | 0,00094 | 0,00093 | 0,00063 | 0,00106 | 0,00059 |
| 528,72211 | 0,00091 | 0,00093 | 0,00065 | 0,00101 | 0,00062 |
| 528,7593 | 0,00089 | 0,00094 | 0,00067 | 0,00096 | 0,00067 |
| 528,79648 | 0,00087 | 0,00094 | 0,00069 | 0,00092 | 0,00072 |
| 528,83366 | 0,00086 | 0,00095 | 0,00073 | 0,00087 | 0,00078 |
| 528,87084 | 0,00086 | 0,00095 | 0,00076 | 0,00084 | 0,00083 |
| 528,90802 | 0,00086 | 0,00095 | 8e-04 | 0,00082 | 0,00087 |
| 528,94521 | 0,00088 | 0,00096 | 0,00083 | 0,00082 | 9e-04 |
| 528,98239 | 0,00091 | 0,00097 | 0,00087 | 0,00083 | 0,00091 |
| 529,01957 | 0,00095 | 0,00099 | 0,00091 | 0,00085 | 0,00089 |
| 529,05675 | 0,001 | 0,00101 | 0,00095 | 0,00088 | 0,00086 |
| 529,09393 | 0,00105 | 0,00103 | 0,00099 | 0,00092 | 0,00081 |
| 529,13112 | 0,0011 | 0,00107 | 0,00103 | 0,00096 | 0,00075 |
| 529,1683 | 0,00115 | 0,0011 | 0,00107 | 0,001 | 0,00069 |
| 529,20548 | 0,00119 | 0,00113 | 0,00111 | 0,00104 | 0,00064 |
| 529,24266 | 0,00122 | 0,00117 | 0,00115 | 0,00108 | 0,00059 |
| 529,27984 | 0,00124 | 0,0012 | 0,00117 | 0,0011 | 0,00055 |
| 529,31703 | 0,00125 | 0,00122 | 0,0012 | 0,00113 | 0,00052 |
| 529,35421 | 0,00125 | 0,00124 | 0,00121 | 0,00115 | 5e-04 |
| 529,39139 | 0,00125 | 0,00125 | 0,00123 | 0,00117 | 0,00049 |
| 529,42857 | 0,00125 | 0,00125 | 0,00123 | 0,00119 | 0,00048 |
| 529,46575 | 0,00124 | 0,00125 | 0,00124 | 0,00122 | 0,00048 |
| 529,50294 | 0,00124 | 0,00124 | 0,00126 | 0,00124 | 0,00049 |
| 529,54012 | 0,00124 | 0,00122 | 0,00128 | 0,00127 | 5e-04 |
| 529,5773 | 0,00125 | 0,00121 | 0,00131 | 0,00129 | 0,00052 |
| 529,61448 | 0,00126 | 0,0012 | 0,00134 | 0,00132 | 0,00055 |
| 529,65166 | 0,00128 | 0,0012 | 0,00139 | 0,00134 | 0,00058 |
| 529,68885 | 0,00129 | 0,00122 | 0,00145 | 0,00136 | 0,00063 |
| 529,72603 | 0,00132 | 0,00125 | 0,00151 | 0,00139 | 0,00068 |
| 529,76321 | 0,00134 | 0,00129 | 0,00157 | 0,00142 | 0,00074 |
| 529,80039 | 0,00136 | 0,00135 | 0,00162 | 0,00144 | 0,00081 |
| 529,83757 | 0,00138 | 0,00143 | 0,00168 | 0,00147 | 0,00089 |
| 529,87476 | 0,0014 | 0,00152 | 0,00172 | 0,00149 | 0,00097 |
| 529,91194 | 0,00142 | 0,00162 | 0,00176 | 0,0015 | 0,00105 |
| 529,94912 | 0,00143 | 0,00172 | 0,00179 | 0,0015 | 0,00113 |
| 529,9863 | 0,00145 | 0,00182 | 0,00182 | 0,00149 | 0,00122 |
| 530,02348 | 0,00147 | 0,00192 | 0,00184 | 0,00146 | 0,0013 |
| 530,06067 | 0,0015 | 0,002 | 0,00186 | 0,00142 | 0,00139 |
| 530,09785 | 0,00152 | 0,00208 | 0,00187 | 0,00137 | 0,00147 |
| 530,13503 | 0,00155 | 0,00214 | 0,00188 | 0,00132 | 0,00155 |
| 530,17221 | 0,00158 | 0,00218 | 0,00189 | 0,00129 | 0,00163 |
| 530,20939 | 0,00162 | 0,0022 | 0,0019 | 0,00128 | 0,00171 |
| 530,24658 | 0,00165 | 0,00222 | 0,00191 | 0,0013 | 0,00179 |
| 530,28376 | 0,00169 | 0,00222 | 0,00193 | 0,00134 | 0,00187 |
| 530,32094 | 0,00173 | 0,00221 | 0,00195 | 0,00142 | 0,00195 |
| 530,35812 | 0,00176 | 0,0022 | 0,00198 | 0,00153 | 0,00203 |
| 530,3953 | 0,0018 | 0,0022 | 0,00203 | 0,00167 | 0,00212 |
| 530,43249 | 0,00184 | 0,0022 | 0,00208 | 0,00182 | 0,00222 |
| 530,46967 | 0,00188 | 0,00222 | 0,00215 | 0,00198 | 0,00232 |
| 530,50685 | 0,00192 | 0,00224 | 0,00222 | 0,00214 | 0,00241 |
| 530,54403 | 0,00195 | 0,00227 | 0,0023 | 0,00229 | 0,00251 |
| 530,58121 | 0,00198 | 0,00232 | 0,00238 | 0,00242 | 0,00258 |
| 530,6184 | 0,002 | 0,00236 | 0,00245 | 0,00253 | 0,00264 |
| 530,65558 | 0,00202 | 0,00241 | 0,00251 | 0,0026 | 0,00268 |
| 530,69276 | 0,00202 | 0,00245 | 0,00255 | 0,00264 | 0,00269 |
| 530,72994 | 0,00202 | 0,00248 | 0,00257 | 0,00264 | 0,00267 |
| 530,76712 | 0,00201 | 0,00249 | 0,00257 | 0,00263 | 0,00262 |
| 530,80431 | 0,002 | 0,00249 | 0,00255 | 0,00259 | 0,00256 |
| 530,84149 | 0,00199 | 0,00248 | 0,00251 | 0,00253 | 0,00248 |
| 530,87867 | 0,00198 | 0,00246 | 0,00246 | 0,00246 | 0,0024 |
| 530,91585 | 0,00197 | 0,00243 | 0,0024 | 0,00237 | 0,00231 |
| 530,95303 | 0,00198 | 0,0024 | 0,00234 | 0,00228 | 0,00221 |
| 530,99022 | 0,00201 | 0,00236 | 0,00228 | 0,00218 | 0,00212 |
| 531,0274 | 0,00205 | 0,00233 | 0,00224 | 0,00208 | 0,00203 |
| 531,06458 | 0,00211 | 0,0023 | 0,0022 | 0,00197 | 0,00194 |
| 531,10176 | 0,00218 | 0,00228 | 0,00218 | 0,00187 | 0,00185 |
| 531,13894 | 0,00226 | 0,00227 | 0,00218 | 0,00178 | 0,00177 |
| 531,17613 | 0,00234 | 0,00227 | 0,00218 | 0,00169 | 0,00169 |
| 531,21331 | 0,00243 | 0,00228 | 0,0022 | 0,00162 | 0,00161 |
| 531,25049 | 0,00252 | 0,0023 | 0,00223 | 0,00157 | 0,00154 |
| 531,28767 | 0,00259 | 0,00234 | 0,00227 | 0,00153 | 0,00148 |
| 531,32485 | 0,00266 | 0,00239 | 0,00233 | 0,00151 | 0,00143 |
| 531,36204 | 0,00271 | 0,00245 | 0,00239 | 0,00152 | 0,0014 |
| 531,39922 | 0,00274 | 0,00254 | 0,00247 | 0,00154 | 0,00138 |
| 531,4364 | 0,00277 | 0,00264 | 0,00257 | 0,00158 | 0,0014 |
| 531,47358 | 0,00278 | 0,00275 | 0,00269 | 0,00165 | 0,00146 |
| 531,51076 | 0,00279 | 0,00288 | 0,00283 | 0,00175 | 0,00155 |
| 531,54795 | 0,0028 | 0,00302 | 0,00299 | 0,00187 | 0,00167 |
| 531,58513 | 0,00281 | 0,00317 | 0,00317 | 0,00202 | 0,00184 |
| 531,62231 | 0,00282 | 0,00331 | 0,00335 | 0,00219 | 0,00203 |
| 531,65949 | 0,00285 | 0,00345 | 0,00352 | 0,00238 | 0,00224 |
| 531,69667 | 0,00289 | 0,00356 | 0,00369 | 0,00258 | 0,00244 |
| 531,73386 | 0,00294 | 0,00364 | 0,00383 | 0,00277 | 0,00263 |
| 531,77104 | 0,00301 | 0,00368 | 0,00393 | 0,00295 | 0,0028 |
| 531,80822 | 0,00308 | 0,00369 | 0,00401 | 0,0031 | 0,00291 |
| 531,8454 | 0,00316 | 0,00365 | 0,00404 | 0,0032 | 0,00298 |
| 531,88258 | 0,00325 | 0,00358 | 0,00404 | 0,00325 | 0,00299 |
| 531,91977 | 0,00334 | 0,00347 | 0,00401 | 0,00324 | 0,00296 |
| 531,95695 | 0,00344 | 0,00334 | 0,00395 | 0,00319 | 0,00289 |
| 531,99413 | 0,00353 | 0,0032 | 0,00387 | 0,00311 | 0,0028 |
| 532,03131 | 0,00362 | 0,00305 | 0,00377 | 0,003 | 0,0027 |
| 532,06849 | 0,0037 | 0,00291 | 0,00368 | 0,00289 | 0,00261 |
| 532,10568 | 0,00377 | 0,00279 | 0,00358 | 0,00279 | 0,00254 |
| 532,14286 | 0,00382 | 0,00268 | 0,00349 | 0,00271 | 0,00249 |
| 532,18004 | 0,00387 | 0,00261 | 0,0034 | 0,00265 | 0,00246 |
| 532,21722 | 0,0039 | 0,00256 | 0,00333 | 0,00261 | 0,00245 |
| 532,2544 | 0,00392 | 0,00253 | 0,00325 | 0,00259 | 0,00246 |
| 532,29159 | 0,00394 | 0,00253 | 0,00318 | 0,00258 | 0,00248 |
| 532,32877 | 0,00395 | 0,00256 | 0,00312 | 0,00256 | 0,00252 |
| 532,36595 | 0,00398 | 0,00261 | 0,00305 | 0,00254 | 0,00258 |
| 532,40313 | 0,00401 | 0,00268 | 0,00299 | 0,0025 | 0,00265 |
| 532,44031 | 0,00405 | 0,00276 | 0,00292 | 0,00246 | 0,00274 |
| 532,4775 | 0,0041 | 0,00286 | 0,00286 | 0,00242 | 0,00286 |
| 532,51468 | 0,00417 | 0,00298 | 0,00281 | 0,00239 | 0,00299 |
| 532,55186 | 0,00424 | 0,0031 | 0,00276 | 0,00237 | 0,00314 |
| 532,58904 | 0,00432 | 0,00324 | 0,00271 | 0,00237 | 0,0033 |
| 532,62622 | 0,0044 | 0,00338 | 0,00268 | 0,0024 | 0,00348 |
| 532,66341 | 0,00448 | 0,00353 | 0,00267 | 0,00246 | 0,00366 |
| 532,70059 | 0,00455 | 0,00369 | 0,00267 | 0,00255 | 0,00385 |
| 532,73777 | 0,00462 | 0,00385 | 0,00269 | 0,00266 | 0,00404 |
| 532,77495 | 0,00469 | 0,00402 | 0,00274 | 0,00277 | 0,00424 |
| 532,81213 | 0,00475 | 0,00418 | 0,00281 | 0,00289 | 0,00444 |
| 532,84932 | 0,00481 | 0,00436 | 0,00291 | 0,003 | 0,00464 |
| 532,8865 | 0,00488 | 0,00454 | 0,00304 | 0,0031 | 0,00485 |
| 532,92368 | 0,00495 | 0,00473 | 0,0032 | 0,00318 | 0,00506 |
| 532,96086 | 0,00503 | 0,00492 | 0,00338 | 0,00325 | 0,00528 |
| 532,99804 | 0,00511 | 0,00513 | 0,00358 | 0,00332 | 0,0055 |
| 533,03523 | 0,0052 | 0,00534 | 0,00381 | 0,00339 | 0,0057 |
| 533,07241 | 0,0053 | 0,00557 | 0,00404 | 0,00348 | 0,00589 |
| 533,10959 | 0,00542 | 0,00579 | 0,00429 | 0,00359 | 0,00606 |
| 533,14677 | 0,00555 | 0,00601 | 0,00454 | 0,00373 | 0,0062 |
| 533,18395 | 0,00569 | 0,00622 | 0,00478 | 0,00389 | 0,00631 |
| 533,22114 | 0,00585 | 0,00641 | 0,00501 | 0,00407 | 0,00639 |
| 533,25832 | 0,00602 | 0,00659 | 0,00522 | 0,00427 | 0,00642 |
| 533,2955 | 0,00621 | 0,00674 | 0,0054 | 0,00446 | 0,00642 |
| 533,33268 | 0,00641 | 0,00687 | 0,00555 | 0,00464 | 0,00637 |
| 533,36986 | 0,00662 | 0,00696 | 0,00566 | 0,00481 | 0,00629 |
| 533,40705 | 0,00685 | 0,00702 | 0,00575 | 0,00495 | 0,00619 |
| 533,44423 | 0,00708 | 0,00706 | 0,00582 | 0,00507 | 0,00606 |
| 533,48141 | 0,00731 | 0,00706 | 0,00588 | 0,00517 | 0,00593 |
| 533,51859 | 0,00754 | 0,00705 | 0,00595 | 0,00525 | 0,00582 |
| 533,55577 | 0,00778 | 0,00703 | 0,00603 | 0,00532 | 0,00574 |
| 533,59295 | 0,00801 | 0,00702 | 0,00613 | 0,00538 | 0,0057 |
| 533,63014 | 0,00824 | 0,00701 | 0,00627 | 0,00542 | 0,00571 |
| 533,66732 | 0,00846 | 0,00703 | 0,00644 | 0,00546 | 0,00576 |
| 533,7045 | 0,00868 | 0,00707 | 0,00665 | 0,00549 | 0,00586 |
| 533,74168 | 0,00889 | 0,00715 | 0,00687 | 0,00553 | 0,006 |
| 533,77886 | 0,0091 | 0,00725 | 0,0071 | 0,00559 | 0,00617 |
| 533,81605 | 0,0093 | 0,00737 | 0,00733 | 0,00567 | 0,00637 |
| 533,85323 | 0,0095 | 0,00751 | 0,00754 | 0,00578 | 0,00658 |
| 533,89041 | 0,00969 | 0,00767 | 0,00772 | 0,00595 | 0,00681 |
| 533,92759 | 0,0099 | 0,00783 | 0,00787 | 0,00616 | 0,00705 |
| 533,96477 | 0,01012 | 0,00799 | 0,00798 | 0,00643 | 0,00729 |
| 534,00196 | 0,01037 | 0,00815 | 0,00807 | 0,00674 | 0,00754 |
| 534,03914 | 0,01065 | 0,00832 | 0,00814 | 0,00709 | 0,0078 |
| 534,07632 | 0,01098 | 0,00851 | 0,00822 | 0,00746 | 0,00805 |
| 534,1135 | 0,01136 | 0,00871 | 0,00831 | 0,00782 | 0,0083 |
| 534,15068 | 0,01179 | 0,00894 | 0,00845 | 0,00815 | 0,00854 |
| 534,18787 | 0,01226 | 0,00921 | 0,00864 | 0,00845 | 0,00878 |
| 534,22505 | 0,01278 | 0,00951 | 0,0089 | 0,0087 | 0,009 |
| 534,26223 | 0,01332 | 0,00985 | 0,00922 | 0,00892 | 0,00922 |
| 534,29941 | 0,01387 | 0,01024 | 0,0096 | 0,0091 | 0,00944 |
| 534,33659 | 0,01442 | 0,01065 | 0,01003 | 0,00927 | 0,00966 |
| 534,37378 | 0,01497 | 0,01109 | 0,01049 | 0,00944 | 0,00988 |
| 534,41096 | 0,01549 | 0,01153 | 0,01096 | 0,00962 | 0,01011 |
| 534,44814 | 0,01599 | 0,01198 | 0,01142 | 0,00982 | 0,01036 |
| 534,48532 | 0,01647 | 0,01241 | 0,01183 | 0,01005 | 0,01061 |
| 534,5225 | 0,01693 | 0,01281 | 0,0122 | 0,01032 | 0,01089 |
| 534,55969 | 0,01738 | 0,01318 | 0,01252 | 0,01062 | 0,01119 |
| 534,59687 | 0,01782 | 0,01352 | 0,01278 | 0,01098 | 0,01152 |
| 534,63405 | 0,01826 | 0,01383 | 0,01302 | 0,0114 | 0,01191 |
| 534,67123 | 0,0187 | 0,0141 | 0,01324 | 0,0119 | 0,01237 |
| 534,70841 | 0,01914 | 0,01435 | 0,01347 | 0,01249 | 0,01291 |
| 534,7456 | 0,01959 | 0,01459 | 0,01371 | 0,01317 | 0,01353 |
| 534,78278 | 0,02004 | 0,01483 | 0,01399 | 0,01394 | 0,01423 |
| 534,81996 | 0,0205 | 0,01509 | 0,0143 | 0,01478 | 0,01498 |
| 534,85714 | 0,02095 | 0,01537 | 0,01465 | 0,01568 | 0,01576 |
| 534,89432 | 0,0214 | 0,01569 | 0,01504 | 0,0166 | 0,01652 |
| 534,93151 | 0,02184 | 0,01605 | 0,01544 | 0,0175 | 0,01723 |
| 534,96869 | 0,02226 | 0,01647 | 0,01587 | 0,01834 | 0,01784 |
| 535,00587 | 0,02268 | 0,01694 | 0,01631 | 0,01909 | 0,01831 |
| 535,04305 | 0,02309 | 0,01746 | 0,01675 | 0,01971 | 0,01861 |
| 535,08023 | 0,02349 | 0,01802 | 0,01721 | 0,02018 | 0,01875 |
| 535,11742 | 0,0239 | 0,0186 | 0,01767 | 0,02049 | 0,01871 |
| 535,1546 | 0,02432 | 0,0192 | 0,01813 | 0,02067 | 0,01855 |
| 535,19178 | 0,02478 | 0,01982 | 0,01859 | 0,02074 | 0,01829 |
| 535,22896 | 0,02527 | 0,02045 | 0,01907 | 0,02076 | 0,01802 |
| 535,26614 | 0,02583 | 0,02111 | 0,01955 | 0,0208 | 0,01781 |
| 535,30333 | 0,02647 | 0,02179 | 0,02005 | 0,02093 | 0,01776 |
| 535,34051 | 0,02718 | 0,02252 | 0,02059 | 0,02122 | 0,01795 |
| 535,37769 | 0,028 | 0,02332 | 0,02118 | 0,02171 | 0,01844 |
| 535,41487 | 0,02891 | 0,02421 | 0,02184 | 0,02248 | 0,0193 |
| 535,45205 | 0,02991 | 0,0252 | 0,02259 | 0,02353 | 0,02054 |
| 535,48924 | 0,03099 | 0,0263 | 0,02344 | 0,02487 | 0,02215 |
| 535,52642 | 0,03212 | 0,0275 | 0,02441 | 0,02647 | 0,02408 |
| 535,5636 | 0,03329 | 0,02878 | 0,02548 | 0,02828 | 0,02623 |
| 535,60078 | 0,03445 | 0,03011 | 0,02664 | 0,0302 | 0,02848 |
| 535,63796 | 0,03559 | 0,03146 | 0,02783 | 0,03209 | 0,03065 |
| 535,67515 | 0,03666 | 0,03279 | 0,02902 | 0,03382 | 0,03261 |
| 535,71233 | 0,03763 | 0,03404 | 0,03016 | 0,03526 | 0,0342 |
| 535,74951 | 0,03849 | 0,03517 | 0,03118 | 0,0363 | 0,03532 |
| 535,78669 | 0,0392 | 0,03615 | 0,03204 | 0,03685 | 0,03591 |
| 535,82387 | 0,03976 | 0,03694 | 0,0327 | 0,03694 | 0,03602 |
| 535,86106 | 0,04016 | 0,03753 | 0,03313 | 0,03665 | 0,03572 |
| 535,89824 | 0,0404 | 0,03791 | 0,03334 | 0,03608 | 0,03511 |
| 535,93542 | 0,04048 | 0,03809 | 0,03332 | 0,03533 | 0,03431 |
| 535,9726 | 0,04043 | 0,03809 | 0,03312 | 0,03453 | 0,03343 |
| 536,00978 | 0,04029 | 0,03795 | 0,03277 | 0,03377 | 0,03256 |
| 536,04697 | 0,04006 | 0,03772 | 0,03234 | 0,03311 | 0,03176 |
| 536,08415 | 0,03979 | 0,03744 | 0,03186 | 0,0326 | 0,03106 |
| 536,12133 | 0,0395 | 0,03715 | 0,0314 | 0,03223 | 0,03049 |
| 536,15851 | 0,03922 | 0,03686 | 0,03098 | 0,03201 | 0,03002 |
| 536,19569 | 0,03898 | 0,03662 | 0,03063 | 0,03191 | 0,02967 |
| 536,23288 | 0,0388 | 0,03643 | 0,03037 | 0,03192 | 0,02942 |
| 536,27006 | 0,0387 | 0,0363 | 0,03022 | 0,03202 | 0,02928 |
| 536,30724 | 0,03871 | 0,03626 | 0,03019 | 0,03219 | 0,02924 |
| 536,34442 | 0,03884 | 0,03632 | 0,03031 | 0,03245 | 0,02932 |
| 536,3816 | 0,03915 | 0,0365 | 0,03061 | 0,03282 | 0,02956 |
| 536,41879 | 0,03963 | 0,03684 | 0,03113 | 0,03333 | 0,02997 |
| 536,45597 | 0,04032 | 0,03737 | 0,03191 | 0,03404 | 0,03062 |
| 536,49315 | 0,04124 | 0,03814 | 0,03299 | 0,03502 | 0,03158 |
| 536,53033 | 0,04238 | 0,03916 | 0,0344 | 0,03635 | 0,03294 |
| 536,56751 | 0,04376 | 0,04046 | 0,03618 | 0,03813 | 0,0348 |
| 536,6047 | 0,04535 | 0,04204 | 0,03832 | 0,04042 | 0,03727 |
| 536,64188 | 0,04713 | 0,0439 | 0,04076 | 0,04329 | 0,04043 |
| 536,67906 | 0,04906 | 0,04599 | 0,04343 | 0,04675 | 0,04431 |
| 536,71624 | 0,05106 | 0,04824 | 0,04622 | 0,05074 | 0,04887 |
| 536,75342 | 0,05307 | 0,05058 | 0,04903 | 0,05514 | 0,05395 |
| 536,79061 | 0,05499 | 0,05289 | 0,0517 | 0,0597 | 0,05928 |
| 536,82779 | 0,05674 | 0,05507 | 0,0541 | 0,06413 | 0,06451 |
| 536,86497 | 0,05821 | 0,05702 | 0,05609 | 0,06806 | 0,06916 |
| 536,90215 | 0,05935 | 0,05862 | 0,05759 | 0,07108 | 0,07272 |
| 536,93933 | 0,06013 | 0,05978 | 0,05852 | 0,07288 | 0,0749 |
| 536,97652 | 0,06054 | 0,06048 | 0,05885 | 0,07335 | 0,07549 |
| 537,0137 | 0,06058 | 0,06074 | 0,05862 | 0,07251 | 0,07453 |
| 537,05088 | 0,06031 | 0,06059 | 0,05789 | 0,07052 | 0,07219 |
| 537,08806 | 0,05976 | 0,06011 | 0,05675 | 0,0677 | 0,06884 |
| 537,12524 | 0,05903 | 0,05937 | 0,05537 | 0,0644 | 0,06491 |
| 537,16243 | 0,05817 | 0,05848 | 0,05389 | 0,06103 | 0,06086 |
| 537,19961 | 0,05727 | 0,05755 | 0,05245 | 0,05795 | 0,05712 |
| 537,23679 | 0,05639 | 0,05666 | 0,05117 | 0,05543 | 0,05401 |
| 537,27397 | 0,05559 | 0,05589 | 0,05014 | 0,05366 | 0,05174 |
| 537,31115 | 0,05491 | 0,05531 | 0,04943 | 0,0527 | 0,05039 |
| 537,34834 | 0,05439 | 0,05494 | 0,04906 | 0,05254 | 0,04995 |
| 537,38552 | 0,05402 | 0,05479 | 0,04904 | 0,05308 | 0,05029 |
| 537,4227 | 0,05381 | 0,05486 | 0,04935 | 0,05419 | 0,0513 |
| 537,45988 | 0,05373 | 0,05509 | 0,04994 | 0,05573 | 0,05284 |
| 537,49706 | 0,05378 | 0,05546 | 0,05076 | 0,05758 | 0,05477 |
| 537,53425 | 0,05394 | 0,0559 | 0,05173 | 0,05968 | 0,05708 |
| 537,57143 | 0,05417 | 0,0564 | 0,05281 | 0,06206 | 0,05981 |
| 537,60861 | 0,05448 | 0,05693 | 0,05392 | 0,06487 | 0,06312 |
| 537,64579 | 0,05485 | 0,05747 | 0,05502 | 0,06833 | 0,06725 |
| 537,68297 | 0,05528 | 0,05803 | 0,05608 | 0,07272 | 0,07246 |
| 537,72016 | 0,05579 | 0,05862 | 0,05709 | 0,0783 | 0,07902 |
| 537,75734 | 0,05639 | 0,05927 | 0,05808 | 0,08526 | 0,0871 |
| 537,79452 | 0,05716 | 0,06002 | 0,05908 | 0,09362 | 0,09672 |
| 537,8317 | 0,05815 | 0,06091 | 0,06014 | 0,10318 | 0,10765 |
| 537,86888 | 0,05943 | 0,062 | 0,06134 | 0,11349 | 0,11939 |
| 537,90607 | 0,06108 | 0,06341 | 0,06277 | 0,12384 | 0,13117 |
| 537,94325 | 0,06319 | 0,0652 | 0,06452 | 0,13339 | 0,142 |
| 537,98043 | 0,06584 | 0,06747 | 0,0667 | 0,14122 | 0,15083 |
| 538,01761 | 0,0691 | 0,07033 | 0,06941 | 0,14647 | 0,15646 |
| 538,05479 | 0,07301 | 0,07386 | 0,07276 | 0,14845 | 0,15847 |
| 538,09198 | 0,07759 | 0,07812 | 0,07682 | 0,1472 | 0,15672 |
| 538,12916 | 0,0828 | 0,08315 | 0,08166 | 0,14298 | 0,15151 |
| 538,16634 | 0,08856 | 0,08889 | 0,0872 | 0,13636 | 0,14356 |
| 538,20352 | 0,09474 | 0,09527 | 0,09338 | 0,12812 | 0,13383 |
| 538,2407 | 0,10116 | 0,10211 | 0,10004 | 0,11911 | 0,12334 |
| 538,27789 | 0,10756 | 0,10919 | 0,10698 | 0,11011 | 0,11308 |
| 538,31507 | 0,11365 | 0,11621 | 0,11395 | 0,10175 | 0,1038 |
| 538,35225 | 0,11918 | 0,12287 | 0,12065 | 0,09447 | 0,09601 |
| 538,38943 | 0,12389 | 0,12875 | 0,1268 | 0,0885 | 0,08991 |
| 538,42661 | 0,12759 | 0,13358 | 0,1321 | 0,0839 | 0,08547 |
| 538,4638 | 0,13015 | 0,13714 | 0,13633 | 0,08061 | 0,08247 |
| 538,50098 | 0,13149 | 0,1393 | 0,13932 | 0,07849 | 0,0806 |
| 538,53816 | 0,13161 | 0,13999 | 0,14095 | 0,07735 | 0,07953 |
| 538,57534 | 0,13058 | 0,13925 | 0,14123 | 0,07702 | 0,079 |
| 538,61252 | 0,12852 | 0,1372 | 0,14012 | 0,07732 | 0,07873 |
| 538,64971 | 0,12561 | 0,13402 | 0,13783 | 0,07803 | 0,0786 |
| 538,68689 | 0,12203 | 0,12992 | 0,13456 | 0,07901 | 0,07855 |
| 538,72407 | 0,11797 | 0,12513 | 0,13052 | 0,08012 | 0,07856 |
| 538,76125 | 0,11362 | 0,1199 | 0,12589 | 0,08123 | 0,07862 |
| 538,79843 | 0,10916 | 0,11443 | 0,12089 | 0,08227 | 0,07875 |
| 538,83562 | 0,10474 | 0,10892 | 0,11569 | 0,08319 | 0,07895 |
| 538,8728 | 0,10044 | 0,10353 | 0,11046 | 0,08398 | 0,07927 |
| 538,90998 | 0,09635 | 0,09838 | 0,10533 | 0,0847 | 0,07973 |
| 538,94716 | 0,09252 | 0,09355 | 0,10044 | 0,08549 | 0,08042 |
| 538,98434 | 0,089 | 0,08911 | 0,09587 | 0,08653 | 0,08149 |
| 539,02153 | 0,08585 | 0,08511 | 0,09171 | 0,08809 | 0,08315 |
| 539,05871 | 0,08312 | 0,08161 | 0,08804 | 0,09051 | 0,08567 |
| 539,09589 | 0,08089 | 0,07868 | 0,08492 | 0,09412 | 0,08936 |
| 539,13307 | 0,07925 | 0,07642 | 0,08248 | 0,09927 | 0,09468 |
| 539,17025 | 0,07835 | 0,07495 | 0,08079 | 0,10633 | 0,10177 |
| 539,20744 | 0,07843 | 0,07443 | 0,07999 | 0,11528 | 0,1107 |
| 539,24462 | 0,07976 | 0,07508 | 0,08028 | 0,12598 | 0,1214 |
| 539,2818 | 0,08262 | 0,07714 | 0,08189 | 0,13817 | 0,13364 |
| 539,31898 | 0,08735 | 0,08092 | 0,08516 | 0,1515 | 0,14712 |
| 539,35616 | 0,09432 | 0,08696 | 0,09045 | 0,16567 | 0,16158 |
| 539,39335 | 0,10394 | 0,09556 | 0,0982 | 0,18059 | 0,17692 |
| 539,43053 | 0,11655 | 0,10704 | 0,10883 | 0,19651 | 0,1934 |
| 539,46771 | 0,13245 | 0,12175 | 0,12278 | 0,2141 | 0,21164 |
| 539,50489 | 0,1518 | 0,13992 | 0,1404 | 0,23439 | 0,23264 |
| 539,54207 | 0,17459 | 0,16163 | 0,16189 | 0,25856 | 0,25754 |
| 539,57926 | 0,20059 | 0,18676 | 0,18728 | 0,28765 | 0,28738 |
| 539,61644 | 0,22931 | 0,21498 | 0,21639 | 0,32213 | 0,32262 |
| 539,65362 | 0,26002 | 0,24568 | 0,2486 | 0,36147 | 0,36276 |
| 539,6908 | 0,29167 | 0,27798 | 0,28271 | 0,4039 | 0,40602 |
| 539,72798 | 0,32284 | 0,31077 | 0,31745 | 0,44605 | 0,44866 |
| 539,76517 | 0,35214 | 0,34276 | 0,35134 | 0,48338 | 0,48649 |
| 539,80235 | 0,37823 | 0,37257 | 0,38281 | 0,5115 | 0,51509 |
| 539,83953 | 0,39987 | 0,39843 | 0,41032 | 0,52659 | 0,53065 |
| 539,87671 | 0,41606 | 0,41915 | 0,43251 | 0,5262 | 0,53065 |
| 539,91389 | 0,42604 | 0,43382 | 0,44827 | 0,50964 | 0,51433 |
| 539,95108 | 0,4294 | 0,44177 | 0,45685 | 0,47815 | 0,48288 |
| 539,98826 | 0,42607 | 0,44268 | 0,45789 | 0,43466 | 0,43917 |
| 540,02544 | 0,41633 | 0,43661 | 0,45144 | 0,38329 | 0,38733 |
| 540,06262 | 0,40073 | 0,42394 | 0,4379 | 0,32864 | 0,33203 |
| 540,0998 | 0,38009 | 0,40535 | 0,418 | 0,27519 | 0,27782 |
| 540,13699 | 0,35541 | 0,38178 | 0,39248 | 0,22676 | 0,22861 |
| 540,17417 | 0,32768 | 0,35435 | 0,3629 | 0,18621 | 0,18732 |
| 540,21135 | 0,29846 | 0,32432 | 0,33071 | 0,15544 | 0,15589 |
| 540,24853 | 0,26897 | 0,29299 | 0,2973 | 0,13556 | 0,13626 |
| 540,28571 | 0,24034 | 0,2617 | 0,26405 | 0,12781 | 0,12841 |
| 540,3229 | 0,21366 | 0,23189 | 0,23226 | 0,1325 | 0,13277 |
| 540,36008 | 0,18989 | 0,20481 | 0,20315 | 0,1499 | 0,14988 |
| 540,39726 | 0,1699 | 0,18145 | 0,17778 | 0,18057 | 0,18028 |
| 540,43444 | 0,15441 | 0,16264 | 0,15703 | 0,22477 | 0,22421 |
| 540,47162 | 0,14399 | 0,14908 | 0,1416 | 0,28203 | 0,28116 |
| 540,50881 | 0,13909 | 0,14125 | 0,13202 | 0,35066 | 0,34947 |
| 540,54599 | 0,13999 | 0,13952 | 0,12864 | 0,42743 | 0,42596 |
| 540,58317 | 0,14684 | 0,14403 | 0,13166 | 0,50747 | 0,5058 |
| 540,62035 | 0,15972 | 0,15479 | 0,14119 | 0,58447 | 0,58273 |
| 540,65753 | 0,17871 | 0,17162 | 0,1576 | 0,6513 | 0,64969 |
| 540,69472 | 0,20294 | 0,19415 | 0,1801 | 0,70098 | 0,69966 |
| 540,7319 | 0,23176 | 0,22182 | 0,20821 | 0,72766 | 0,72679 |
| 540,76908 | 0,26434 | 0,25386 | 0,24123 | 0,72772 | 0,72737 |
| 540,80626 | 0,29964 | 0,28942 | 0,27823 | 0,70046 | 0,69904 |
| 540,84344 | 0,33645 | 0,32704 | 0,31804 | 0,64761 | 0,6464 |
| 540,88063 | 0,37341 | 0,36522 | 0,35927 | 0,57534 | 0,57536 |
| 540,91781 | 0,40907 | 0,40248 | 0,40032 | 0,49195 | 0,49308 |
| 540,95499 | 0,44194 | 0,43725 | 0,43949 | 0,40511 | 0,40708 |
| 540,99217 | 0,47054 | 0,46797 | 0,47498 | 0,32167 | 0,3241 |
| 541,02935 | 0,49348 | 0,49316 | 0,50502 | 0,24688 | 0,24939 |
| 541,06654 | 0,50953 | 0,51147 | 0,52794 | 0,18398 | 0,18626 |
| 541,10372 | 0,51732 | 0,52178 | 0,54226 | 0,13422 | 0,13604 |
| 541,1409 | 0,51601 | 0,52325 | 0,54648 | 0,09718 | 0,09843 |
| 541,17808 | 0,50582 | 0,51546 | 0,53963 | 0,07128 | 0,07195 |
| 541,21526 | 0,48698 | 0,49841 | 0,52223 | 0,0543 | 0,05447 |
| 541,25245 | 0,46018 | 0,47261 | 0,49487 | 0,04389 | 0,04366 |
| 541,28963 | 0,42654 | 0,43871 | 0,4588 | 0,03786 | 0,03738 |
| 541,32681 | 0,38752 | 0,39863 | 0,41578 | 0,03446 | 0,03383 |
| 541,36399 | 0,34487 | 0,35451 | 0,36801 | 0,03235 | 0,03173 |
| 541,40117 | 0,30044 | 0,30842 | 0,3179 | 0,03067 | 0,03007 |
| 541,43836 | 0,2561 | 0,26235 | 0,26784 | 0,02892 | 0,02838 |
| 541,47554 | 0,21352 | 0,21814 | 0,22002 | 0,02689 | 0,02646 |
| 541,51272 | 0,17412 | 0,17729 | 0,17623 | 0,0246 | 0,02427 |
| 541,5499 | 0,13893 | 0,14087 | 0,1377 | 0,0221 | 0,02186 |
| 541,58708 | 0,10887 | 0,10952 | 0,10511 | 0,01951 | 0,01935 |
| 541,62427 | 0,08395 | 0,08342 | 0,07858 | 0,01694 | 0,01683 |
| 541,66145 | 0,06379 | 0,0624 | 0,05808 | 0,01451 | 0,01443 |
| 541,69863 | 0,04793 | 0,04601 | 0,04265 | 0,01229 | 0,01223 |
| 541,73581 | 0,03577 | 0,03362 | 0,03128 | 0,01036 | 0,01032 |
| 541,77299 | 0,02667 | 0,02464 | 0,02312 | 0,00877 | 0,00875 |
| 541,81018 | 0,02 | 0,01826 | 0,01737 | 0,00758 | 0,00756 |
| 541,84736 | 0,01519 | 0,01376 | 0,01338 | 0,00683 | 0,00681 |
| 541,88454 | 0,01177 | 0,01065 | 0,01063 | 0,00654 | 0,00653 |
| 541,92172 | 0,00938 | 0,00856 | 0,00873 | 0,00674 | 0,00677 |
| 541,9589 | 0,00772 | 0,0072 | 0,00741 | 0,00747 | 0,00753 |
| 541,99609 | 0,0066 | 0,00638 | 0,00652 | 0,00873 | 0,00881 |
| 542,03327 | 0,0059 | 0,00595 | 0,00596 | 0,01046 | 0,01055 |
| 542,07045 | 0,00554 | 0,00582 | 0,00566 | 0,01259 | 0,01268 |
| 542,10763 | 0,00545 | 0,00593 | 0,00561 | 0,01499 | 0,01508 |
| 542,14481 | 0,00559 | 0,00624 | 0,00578 | 0,01749 | 0,01758 |
| 542,182 | 0,00594 | 0,00671 | 0,0062 | 0,01987 | 0,01996 |
| 542,21918 | 0,00646 | 0,00733 | 0,00682 | 0,02188 | 0,02199 |
| 542,25636 | 0,00714 | 0,00809 | 0,00763 | 0,02331 | 0,02344 |
| 542,29354 | 0,00795 | 0,00897 | 0,00859 | 0,02396 | 0,02415 |
| 542,33072 | 0,00885 | 0,00995 | 0,00969 | 0,02374 | 0,02399 |
| 542,36791 | 0,00981 | 0,01101 | 0,01088 | 0,02263 | 0,02296 |
| 542,40509 | 0,01079 | 0,01212 | 0,01212 | 0,02074 | 0,02114 |
| 542,44227 | 0,01175 | 0,01325 | 0,01336 | 0,01825 | 0,0187 |
| 542,47945 | 0,01263 | 0,01435 | 0,01454 | 0,01541 | 0,01588 |
| 542,51663 | 0,0134 | 0,01536 | 0,01561 | 0,01247 | 0,01296 |
| 542,55382 | 0,01398 | 0,01622 | 0,01649 | 0,00969 | 0,01017 |
| 542,591 | 0,01436 | 0,01686 | 0,01714 | 0,00724 | 0,00768 |
| 542,62818 | 0,01449 | 0,01724 | 0,01749 | 0,00521 | 0,00559 |
| 542,66536 | 0,01435 | 0,0173 | 0,01748 | 0,00362 | 0,00394 |
| 542,70254 | 0,01394 | 0,017 | 0,01708 | 0,00243 | 0,00269 |
| 542,73973 | 0,01328 | 0,01634 | 0,01631 | 0,0016 | 0,00181 |
| 542,77691 | 0,01238 | 0,01533 | 0,0152 | 0,00106 | 0,00121 |
| 542,81409 | 0,01129 | 0,01404 | 0,01382 | 0,00072 | 0,00083 |
| 542,85127 | 0,01006 | 0,01255 | 0,01223 | 0,00053 | 0,00059 |
| 542,88845 | 0,00876 | 0,01093 | 0,01054 | 0,00044 | 0,00046 |
| 542,92564 | 0,00745 | 0,00928 | 0,00884 | 0,00041 | 0,00038 |
| 542,96282 | 0,00619 | 0,00767 | 0,0072 | 0,00041 | 0,00033 |
| 543 | 0,00502 | 0,00618 | 0,00571 | 0,00043 | 0,00029 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00034 | 3e-05 | 0,00013 | 5e-05 | 2e-05 |
| 524,03718 | 0,00038 | 4e-05 | 0,00015 | 6e-05 | 3e-05 |
| 524,07436 | 0,00042 | 4e-05 | 0,00017 | 6e-05 | 3e-05 |
| 524,11155 | 0,00047 | 5e-05 | 0,00019 | 7e-05 | 3e-05 |
| 524,14873 | 0,00053 | 5e-05 | 0,00021 | 8e-05 | 4e-05 |
| 524,18591 | 0,00058 | 6e-05 | 0,00023 | 9e-05 | 4e-05 |
| 524,22309 | 0,00064 | 7e-05 | 0,00026 | 0,00011 | 5e-05 |
| 524,26027 | 0,00071 | 8e-05 | 0,00029 | 0,00012 | 6e-05 |
| 524,29746 | 0,00079 | 9e-05 | 0,00032 | 0,00014 | 6e-05 |
| 524,33464 | 0,00087 | 0,00011 | 0,00036 | 0,00015 | 7e-05 |
| 524,37182 | 0,00095 | 0,00012 | 4e-04 | 0,00017 | 8e-05 |
| 524,409 | 0,00105 | 0,00014 | 0,00044 | 0,00019 | 9e-05 |
| 524,44618 | 0,00115 | 0,00016 | 0,00048 | 0,00022 | 1e-04 |
| 524,48337 | 0,00125 | 0,00018 | 0,00053 | 0,00024 | 0,00012 |
| 524,52055 | 0,00137 | 2e-04 | 0,00059 | 0,00027 | 0,00013 |
| 524,55773 | 0,00149 | 0,00023 | 0,00064 | 3e-04 | 0,00015 |
| 524,59491 | 0,00163 | 0,00026 | 0,00071 | 0,00034 | 0,00017 |
| 524,63209 | 0,00177 | 0,00029 | 0,00077 | 0,00037 | 0,00018 |
| 524,66928 | 0,00192 | 0,00033 | 0,00085 | 0,00041 | 0,00021 |
| 524,70646 | 0,00208 | 0,00037 | 0,00092 | 0,00046 | 0,00023 |
| 524,74364 | 0,00225 | 0,00041 | 0,00101 | 5e-04 | 0,00026 |
| 524,78082 | 0,00243 | 0,00046 | 0,0011 | 0,00055 | 0,00028 |
| 524,818 | 0,00262 | 0,00051 | 0,00119 | 0,00061 | 0,00032 |
| 524,85519 | 0,00282 | 0,00057 | 0,00129 | 0,00067 | 0,00035 |
| 524,89237 | 0,00303 | 0,00063 | 0,0014 | 0,00073 | 0,00039 |
| 524,92955 | 0,00326 | 0,00071 | 0,00152 | 8e-04 | 0,00043 |
| 524,96673 | 0,00349 | 0,00078 | 0,00164 | 0,00087 | 0,00047 |
| 525,00391 | 0,00374 | 0,00087 | 0,00177 | 0,00095 | 0,00052 |
| 525,0411 | 0,00399 | 0,00096 | 0,00191 | 0,00103 | 0,00057 |
| 525,07828 | 0,00426 | 0,00106 | 0,00206 | 0,00112 | 0,00063 |
| 525,11546 | 0,00454 | 0,00117 | 0,00222 | 0,00121 | 0,00069 |
| 525,15264 | 0,00484 | 0,00129 | 0,00238 | 0,00131 | 0,00076 |
| 525,18982 | 0,00514 | 0,00141 | 0,00256 | 0,00141 | 0,00083 |
| 525,22701 | 0,00546 | 0,00155 | 0,00274 | 0,00152 | 0,00091 |
| 525,26419 | 0,00579 | 0,0017 | 0,00293 | 0,00164 | 0,001 |
| 525,30137 | 0,00613 | 0,00186 | 0,00314 | 0,00176 | 0,00109 |
| 525,33855 | 0,00648 | 0,00203 | 0,00335 | 0,00189 | 0,00119 |
| 525,37573 | 0,00684 | 0,00222 | 0,00358 | 0,00202 | 0,00129 |
| 525,41292 | 0,00722 | 0,00242 | 0,00381 | 0,00216 | 0,0014 |
| 525,4501 | 0,0076 | 0,00263 | 0,00406 | 0,0023 | 0,00152 |
| 525,48728 | 0,008 | 0,00286 | 0,00431 | 0,00245 | 0,00165 |
| 525,52446 | 0,00841 | 0,0031 | 0,00458 | 0,00261 | 0,00179 |
| 525,56164 | 0,00883 | 0,00336 | 0,00486 | 0,00277 | 0,00194 |
| 525,59883 | 0,00926 | 0,00364 | 0,00516 | 0,00294 | 0,0021 |
| 525,63601 | 0,00971 | 0,00393 | 0,00546 | 0,00312 | 0,00226 |
| 525,67319 | 0,01016 | 0,00425 | 0,00578 | 0,0033 | 0,00244 |
| 525,71037 | 0,01063 | 0,00457 | 0,00611 | 0,00348 | 0,00263 |
| 525,74755 | 0,0111 | 0,00492 | 0,00645 | 0,00368 | 0,00283 |
| 525,78474 | 0,01159 | 0,00529 | 0,00681 | 0,00387 | 0,00305 |
| 525,82192 | 0,01209 | 0,00568 | 0,00718 | 0,00408 | 0,00327 |
| 525,8591 | 0,0126 | 0,00609 | 0,00757 | 0,00429 | 0,00351 |
| 525,89628 | 0,01312 | 0,00652 | 0,00797 | 0,00451 | 0,00377 |
| 525,93346 | 0,01365 | 0,00697 | 0,00838 | 0,00473 | 0,00404 |
| 525,97065 | 0,0142 | 0,00745 | 0,00881 | 0,00496 | 0,00432 |
| 526,00783 | 0,01475 | 0,00794 | 0,00926 | 0,00519 | 0,00461 |
| 526,04501 | 0,01532 | 0,00847 | 0,00972 | 0,00544 | 0,00493 |
| 526,08219 | 0,0159 | 0,00901 | 0,0102 | 0,00569 | 0,00526 |
| 526,11937 | 0,0165 | 0,00958 | 0,01069 | 0,00594 | 0,00561 |
| 526,15656 | 0,01711 | 0,01017 | 0,01121 | 0,00621 | 0,00597 |
| 526,19374 | 0,01773 | 0,01079 | 0,01174 | 0,00648 | 0,00636 |
| 526,23092 | 0,01836 | 0,01143 | 0,01228 | 0,00676 | 0,00676 |
| 526,2681 | 0,01902 | 0,0121 | 0,01285 | 0,00706 | 0,00718 |
| 526,30528 | 0,01968 | 0,01278 | 0,01344 | 0,00736 | 0,00762 |
| 526,34247 | 0,02037 | 0,01351 | 0,01404 | 0,00768 | 0,00808 |
| 526,37965 | 0,02106 | 0,01425 | 0,01467 | 0,008 | 0,00856 |
| 526,41683 | 0,02178 | 0,01501 | 0,01531 | 0,00834 | 0,00906 |
| 526,45401 | 0,02252 | 0,0158 | 0,01598 | 0,00869 | 0,00958 |
| 526,49119 | 0,02328 | 0,01662 | 0,01667 | 0,00906 | 0,01013 |
| 526,52838 | 0,02405 | 0,01747 | 0,01737 | 0,00944 | 0,0107 |
| 526,56556 | 0,02484 | 0,01833 | 0,01811 | 0,00984 | 0,01129 |
| 526,60274 | 0,02566 | 0,01922 | 0,01886 | 0,01026 | 0,0119 |
| 526,63992 | 0,0265 | 0,02014 | 0,01963 | 0,01069 | 0,01254 |
| 526,6771 | 0,02736 | 0,02108 | 0,02043 | 0,01114 | 0,0132 |
| 526,71429 | 0,02824 | 0,02205 | 0,02125 | 0,01163 | 0,01389 |
| 526,75147 | 0,02915 | 0,02304 | 0,0221 | 0,01213 | 0,0146 |
| 526,78865 | 0,03009 | 0,02405 | 0,02296 | 0,01265 | 0,01534 |
| 526,82583 | 0,03104 | 0,02508 | 0,02385 | 0,0132 | 0,0161 |
| 526,86301 | 0,03203 | 0,02614 | 0,02477 | 0,01378 | 0,01688 |
| 526,9002 | 0,03304 | 0,02722 | 0,0257 | 0,01439 | 0,0177 |
| 526,93738 | 0,03407 | 0,02832 | 0,02666 | 0,01502 | 0,01853 |
| 526,97456 | 0,03513 | 0,02944 | 0,02764 | 0,01569 | 0,01939 |
| 527,01174 | 0,03622 | 0,03058 | 0,02865 | 0,01639 | 0,02028 |
| 527,04892 | 0,03733 | 0,03174 | 0,02967 | 0,01712 | 0,0212 |
| 527,08611 | 0,03847 | 0,03292 | 0,03072 | 0,01788 | 0,02214 |
| 527,12329 | 0,03964 | 0,03411 | 0,03179 | 0,01868 | 0,0231 |
| 527,16047 | 0,04084 | 0,03532 | 0,03288 | 0,01952 | 0,02409 |
| 527,19765 | 0,04206 | 0,03655 | 0,03398 | 0,02039 | 0,0251 |
| 527,23483 | 0,0433 | 0,0378 | 0,03511 | 0,02129 | 0,02614 |
| 527,27202 | 0,04457 | 0,03905 | 0,03625 | 0,02223 | 0,0272 |
| 527,3092 | 0,04586 | 0,04033 | 0,03741 | 0,02321 | 0,02828 |
| 527,34638 | 0,04718 | 0,04161 | 0,03859 | 0,02423 | 0,02939 |
| 527,38356 | 0,04852 | 0,04291 | 0,03978 | 0,02528 | 0,03052 |
| 527,42074 | 0,04988 | 0,04421 | 0,04098 | 0,02637 | 0,03166 |
| 527,45793 | 0,05126 | 0,04553 | 0,0422 | 0,02749 | 0,03283 |
| 527,49511 | 0,05266 | 0,04685 | 0,04342 | 0,02865 | 0,03402 |
| 527,53229 | 0,05408 | 0,04818 | 0,04466 | 0,02984 | 0,03523 |
| 527,56947 | 0,05551 | 0,04951 | 0,0459 | 0,03107 | 0,03645 |
| 527,60665 | 0,05697 | 0,05086 | 0,04715 | 0,03233 | 0,03769 |
| 527,64384 | 0,05843 | 0,0522 | 0,04841 | 0,03362 | 0,03894 |
| 527,68102 | 0,0599 | 0,05355 | 0,04967 | 0,03493 | 0,0402 |
| 527,7182 | 0,06139 | 0,0549 | 0,05093 | 0,03628 | 0,04148 |
| 527,75538 | 0,06289 | 0,05625 | 0,05219 | 0,03765 | 0,04277 |
| 527,79256 | 0,06439 | 0,0576 | 0,05345 | 0,03905 | 0,04406 |
| 527,82975 | 0,06589 | 0,05895 | 0,0547 | 0,04046 | 0,04536 |
| 527,86693 | 0,06741 | 0,0603 | 0,05595 | 0,0419 | 0,04667 |
| 527,90411 | 0,06892 | 0,06165 | 0,0572 | 0,04336 | 0,04799 |
| 527,94129 | 0,07043 | 0,06299 | 0,05844 | 0,04483 | 0,0493 |
| 527,97847 | 0,07194 | 0,06433 | 0,05967 | 0,04631 | 0,05062 |
| 528,01566 | 0,07345 | 0,06566 | 0,0609 | 0,0478 | 0,05193 |
| 528,05284 | 0,07495 | 0,06699 | 0,06211 | 0,0493 | 0,05325 |
| 528,09002 | 0,07645 | 0,06831 | 0,06331 | 0,05081 | 0,05456 |
| 528,1272 | 0,07794 | 0,06962 | 0,0645 | 0,05232 | 0,05586 |
| 528,16438 | 0,07941 | 0,07093 | 0,06567 | 0,05383 | 0,05716 |
| 528,20157 | 0,08088 | 0,07222 | 0,06683 | 0,05535 | 0,05845 |
| 528,23875 | 0,08233 | 0,07351 | 0,06798 | 0,05685 | 0,05973 |
| 528,27593 | 0,08377 | 0,07479 | 0,0691 | 0,05836 | 0,061 |
| 528,31311 | 0,0852 | 0,07605 | 0,07022 | 0,05985 | 0,06227 |
| 528,35029 | 0,0866 | 0,0773 | 0,07131 | 0,06133 | 0,06351 |
| 528,38748 | 0,08799 | 0,07855 | 0,07239 | 0,0628 | 0,06475 |
| 528,42466 | 0,08936 | 0,07978 | 0,07345 | 0,06426 | 0,06597 |
| 528,46184 | 0,09071 | 0,081 | 0,07449 | 0,0657 | 0,06718 |
| 528,49902 | 0,09203 | 0,08221 | 0,07551 | 0,06712 | 0,06837 |
| 528,5362 | 0,09334 | 0,0834 | 0,07651 | 0,06853 | 0,06954 |
| 528,57339 | 0,09463 | 0,08458 | 0,0775 | 0,06992 | 0,0707 |
| 528,61057 | 0,09588 | 0,08575 | 0,07847 | 0,07128 | 0,07185 |
| 528,64775 | 0,09711 | 0,0869 | 0,07942 | 0,07262 | 0,07297 |
| 528,68493 | 0,09832 | 0,08804 | 0,08034 | 0,07394 | 0,07408 |
| 528,72211 | 0,09951 | 0,08916 | 0,08126 | 0,07523 | 0,07518 |
| 528,7593 | 0,10066 | 0,09027 | 0,08215 | 0,0765 | 0,07626 |
| 528,79648 | 0,10179 | 0,09136 | 0,08303 | 0,07774 | 0,07732 |
| 528,83366 | 0,10289 | 0,09243 | 0,08388 | 0,07896 | 0,07837 |
| 528,87084 | 0,10397 | 0,09349 | 0,08473 | 0,08015 | 0,0794 |
| 528,90802 | 0,10501 | 0,09453 | 0,08555 | 0,08131 | 0,08042 |
| 528,94521 | 0,10602 | 0,09555 | 0,08635 | 0,08245 | 0,08142 |
| 528,98239 | 0,10701 | 0,09656 | 0,08714 | 0,08356 | 0,08241 |
| 529,01957 | 0,10796 | 0,09754 | 0,08792 | 0,08464 | 0,0834 |
| 529,05675 | 0,10888 | 0,0985 | 0,08867 | 0,08569 | 0,08436 |
| 529,09393 | 0,10977 | 0,09944 | 0,08941 | 0,08672 | 0,08532 |
| 529,13112 | 0,11063 | 0,10037 | 0,09014 | 0,08773 | 0,08627 |
| 529,1683 | 0,11146 | 0,10127 | 0,09085 | 0,08871 | 0,08721 |
| 529,20548 | 0,11225 | 0,10214 | 0,09154 | 0,08966 | 0,08814 |
| 529,24266 | 0,11301 | 0,103 | 0,09221 | 0,09059 | 0,08906 |
| 529,27984 | 0,11374 | 0,10383 | 0,09287 | 0,0915 | 0,08998 |
| 529,31703 | 0,11443 | 0,10464 | 0,09352 | 0,09237 | 0,09089 |
| 529,35421 | 0,11508 | 0,10542 | 0,09415 | 0,09323 | 0,09179 |
| 529,39139 | 0,1157 | 0,10618 | 0,09476 | 0,09406 | 0,09269 |
| 529,42857 | 0,11628 | 0,10691 | 0,09535 | 0,09488 | 0,09358 |
| 529,46575 | 0,11682 | 0,10761 | 0,09593 | 0,09567 | 0,09447 |
| 529,50294 | 0,11733 | 0,10828 | 0,09649 | 0,09644 | 0,09536 |
| 529,54012 | 0,11779 | 0,10893 | 0,09703 | 0,09719 | 0,09624 |
| 529,5773 | 0,11823 | 0,10955 | 0,09756 | 0,09792 | 0,09711 |
| 529,61448 | 0,11861 | 0,11014 | 0,09807 | 0,09863 | 0,09798 |
| 529,65166 | 0,11896 | 0,1107 | 0,09855 | 0,09932 | 0,09884 |
| 529,68885 | 0,11926 | 0,11124 | 0,09902 | 0,1 | 0,0997 |
| 529,72603 | 0,11954 | 0,11174 | 0,09947 | 0,10066 | 0,10056 |
| 529,76321 | 0,11976 | 0,11221 | 0,0999 | 0,1013 | 0,1014 |
| 529,80039 | 0,11994 | 0,11266 | 0,10031 | 0,10192 | 0,10224 |
| 529,83757 | 0,12009 | 0,11308 | 0,1007 | 0,10253 | 0,10307 |
| 529,87476 | 0,1202 | 0,11346 | 0,10107 | 0,10313 | 0,10388 |
| 529,91194 | 0,12025 | 0,11381 | 0,10141 | 0,1037 | 0,10469 |
| 529,94912 | 0,12027 | 0,11414 | 0,10174 | 0,10427 | 0,10548 |
| 529,9863 | 0,12026 | 0,11444 | 0,10204 | 0,10482 | 0,10626 |
| 530,02348 | 0,12021 | 0,1147 | 0,10232 | 0,10535 | 0,10703 |
| 530,06067 | 0,12011 | 0,11494 | 0,10258 | 0,10587 | 0,10777 |
| 530,09785 | 0,11997 | 0,11515 | 0,10281 | 0,10638 | 0,1085 |
| 530,13503 | 0,1198 | 0,11533 | 0,10302 | 0,10687 | 0,10921 |
| 530,17221 | 0,1196 | 0,11548 | 0,10321 | 0,10735 | 0,10989 |
| 530,20939 | 0,11936 | 0,11561 | 0,10338 | 0,10781 | 0,11055 |
| 530,24658 | 0,11909 | 0,11572 | 0,10352 | 0,10827 | 0,11118 |
| 530,28376 | 0,11878 | 0,11579 | 0,10364 | 0,10871 | 0,11179 |
| 530,32094 | 0,11845 | 0,11583 | 0,10374 | 0,10913 | 0,11238 |
| 530,35812 | 0,11809 | 0,11586 | 0,10381 | 0,10955 | 0,11292 |
| 530,3953 | 0,1177 | 0,11586 | 0,10386 | 0,10995 | 0,11343 |
| 530,43249 | 0,11729 | 0,11583 | 0,1039 | 0,11033 | 0,11391 |
| 530,46967 | 0,11685 | 0,11578 | 0,1039 | 0,11071 | 0,11436 |
| 530,50685 | 0,11639 | 0,11571 | 0,10389 | 0,11106 | 0,11476 |
| 530,54403 | 0,11592 | 0,11562 | 0,10386 | 0,11141 | 0,11513 |
| 530,58121 | 0,11543 | 0,1155 | 0,10381 | 0,11174 | 0,11546 |
| 530,6184 | 0,11492 | 0,11536 | 0,10374 | 0,11205 | 0,11576 |
| 530,65558 | 0,1144 | 0,1152 | 0,10365 | 0,11235 | 0,116 |
| 530,69276 | 0,11387 | 0,11502 | 0,10354 | 0,11264 | 0,11621 |
| 530,72994 | 0,11333 | 0,11482 | 0,10342 | 0,11291 | 0,11638 |
| 530,76712 | 0,11278 | 0,11459 | 0,10328 | 0,11316 | 0,11651 |
| 530,80431 | 0,11223 | 0,11435 | 0,10313 | 0,1134 | 0,11659 |
| 530,84149 | 0,11168 | 0,11409 | 0,10296 | 0,11362 | 0,11663 |
| 530,87867 | 0,11112 | 0,1138 | 0,10278 | 0,11382 | 0,11663 |
| 530,91585 | 0,11057 | 0,1135 | 0,10259 | 0,114 | 0,1166 |
| 530,95303 | 0,11001 | 0,11319 | 0,10239 | 0,11417 | 0,11651 |
| 530,99022 | 0,10946 | 0,11284 | 0,10218 | 0,11431 | 0,11639 |
| 531,0274 | 0,10892 | 0,11248 | 0,10195 | 0,11444 | 0,11624 |
| 531,06458 | 0,10838 | 0,1121 | 0,10172 | 0,11455 | 0,11605 |
| 531,10176 | 0,10785 | 0,11171 | 0,10148 | 0,11463 | 0,11582 |
| 531,13894 | 0,10733 | 0,11129 | 0,10124 | 0,11469 | 0,11555 |
| 531,17613 | 0,10681 | 0,11086 | 0,10098 | 0,11474 | 0,11526 |
| 531,21331 | 0,10631 | 0,11041 | 0,10072 | 0,11476 | 0,11494 |
| 531,25049 | 0,10582 | 0,10994 | 0,10046 | 0,11475 | 0,11458 |
| 531,28767 | 0,10533 | 0,10945 | 0,1002 | 0,11472 | 0,1142 |
| 531,32485 | 0,10486 | 0,10895 | 0,09992 | 0,11468 | 0,1138 |
| 531,36204 | 0,1044 | 0,10843 | 0,09965 | 0,1146 | 0,11337 |
| 531,39922 | 0,10396 | 0,10789 | 0,09937 | 0,1145 | 0,11292 |
| 531,4364 | 0,10352 | 0,10734 | 0,0991 | 0,11437 | 0,11245 |
| 531,47358 | 0,1031 | 0,10677 | 0,09881 | 0,11423 | 0,11197 |
| 531,51076 | 0,10269 | 0,10619 | 0,09853 | 0,11405 | 0,11147 |
| 531,54795 | 0,10229 | 0,10559 | 0,09825 | 0,11385 | 0,11097 |
| 531,58513 | 0,1019 | 0,10498 | 0,09796 | 0,11362 | 0,11045 |
| 531,62231 | 0,10152 | 0,10436 | 0,09768 | 0,11338 | 0,10992 |
| 531,65949 | 0,10115 | 0,10373 | 0,09739 | 0,1131 | 0,10939 |
| 531,69667 | 0,1008 | 0,10308 | 0,0971 | 0,1128 | 0,10886 |
| 531,73386 | 0,10045 | 0,10243 | 0,09681 | 0,11247 | 0,10832 |
| 531,77104 | 0,10011 | 0,10176 | 0,09651 | 0,11213 | 0,10779 |
| 531,80822 | 0,09979 | 0,1011 | 0,09622 | 0,11175 | 0,10725 |
| 531,8454 | 0,09947 | 0,10042 | 0,09592 | 0,11136 | 0,10672 |
| 531,88258 | 0,09915 | 0,09974 | 0,09562 | 0,11094 | 0,10619 |
| 531,91977 | 0,09885 | 0,09905 | 0,09532 | 0,1105 | 0,10567 |
| 531,95695 | 0,09855 | 0,09837 | 0,09502 | 0,11004 | 0,10516 |
| 531,99413 | 0,09826 | 0,09768 | 0,09472 | 0,10957 | 0,10465 |
| 532,03131 | 0,09798 | 0,09699 | 0,09441 | 0,10907 | 0,10415 |
| 532,06849 | 0,0977 | 0,0963 | 0,0941 | 0,10856 | 0,10366 |
| 532,10568 | 0,09742 | 0,09562 | 0,09378 | 0,10802 | 0,10319 |
| 532,14286 | 0,09716 | 0,09494 | 0,09347 | 0,10748 | 0,10272 |
| 532,18004 | 0,09689 | 0,09427 | 0,09314 | 0,10692 | 0,10227 |
| 532,21722 | 0,09663 | 0,09361 | 0,09282 | 0,10635 | 0,10182 |
| 532,2544 | 0,09638 | 0,09295 | 0,09249 | 0,10576 | 0,10139 |
| 532,29159 | 0,09613 | 0,0923 | 0,09216 | 0,10517 | 0,10097 |
| 532,32877 | 0,09588 | 0,09167 | 0,09182 | 0,10457 | 0,10056 |
| 532,36595 | 0,09564 | 0,09104 | 0,09148 | 0,10396 | 0,10017 |
| 532,40313 | 0,0954 | 0,09043 | 0,09114 | 0,10334 | 0,09978 |
| 532,44031 | 0,09516 | 0,08984 | 0,09079 | 0,10272 | 0,09941 |
| 532,4775 | 0,09493 | 0,08926 | 0,09043 | 0,1021 | 0,09905 |
| 532,51468 | 0,0947 | 0,08869 | 0,09008 | 0,10148 | 0,0987 |
| 532,55186 | 0,09447 | 0,08815 | 0,08972 | 0,10085 | 0,09836 |
| 532,58904 | 0,09424 | 0,08762 | 0,08935 | 0,10023 | 0,09802 |
| 532,62622 | 0,09402 | 0,08711 | 0,08898 | 0,09961 | 0,0977 |
| 532,66341 | 0,0938 | 0,08661 | 0,08861 | 0,09899 | 0,09738 |
| 532,70059 | 0,09358 | 0,08614 | 0,08823 | 0,09838 | 0,09708 |
| 532,73777 | 0,09336 | 0,08569 | 0,08786 | 0,09777 | 0,09678 |
| 532,77495 | 0,09314 | 0,08526 | 0,08747 | 0,09717 | 0,09648 |
| 532,81213 | 0,09292 | 0,08485 | 0,08709 | 0,09657 | 0,09619 |
| 532,84932 | 0,0927 | 0,08446 | 0,0867 | 0,09599 | 0,0959 |
| 532,8865 | 0,09248 | 0,08409 | 0,0863 | 0,0954 | 0,09562 |
| 532,92368 | 0,09225 | 0,08374 | 0,08591 | 0,09483 | 0,09534 |
| 532,96086 | 0,09203 | 0,08342 | 0,08551 | 0,09427 | 0,09506 |
| 532,99804 | 0,0918 | 0,08311 | 0,08511 | 0,09372 | 0,09479 |
| 533,03523 | 0,09156 | 0,08282 | 0,08471 | 0,09317 | 0,09451 |
| 533,07241 | 0,09133 | 0,08255 | 0,0843 | 0,09263 | 0,09423 |
| 533,10959 | 0,09108 | 0,08231 | 0,08389 | 0,09211 | 0,09395 |
| 533,14677 | 0,09083 | 0,08208 | 0,08348 | 0,09159 | 0,09367 |
| 533,18395 | 0,09057 | 0,08187 | 0,08307 | 0,09108 | 0,09339 |
| 533,22114 | 0,0903 | 0,08168 | 0,08265 | 0,09058 | 0,0931 |
| 533,25832 | 0,09002 | 0,08151 | 0,08223 | 0,09009 | 0,0928 |
| 533,2955 | 0,08973 | 0,08135 | 0,08181 | 0,08961 | 0,0925 |
| 533,33268 | 0,08943 | 0,0812 | 0,08138 | 0,08913 | 0,09219 |
| 533,36986 | 0,08911 | 0,08108 | 0,08096 | 0,08866 | 0,09188 |
| 533,40705 | 0,08878 | 0,08096 | 0,08053 | 0,08819 | 0,09155 |
| 533,44423 | 0,08844 | 0,08086 | 0,0801 | 0,08773 | 0,09122 |
| 533,48141 | 0,08809 | 0,08078 | 0,07966 | 0,08728 | 0,09087 |
| 533,51859 | 0,08771 | 0,0807 | 0,07922 | 0,08682 | 0,09052 |
| 533,55577 | 0,08732 | 0,08064 | 0,07878 | 0,08637 | 0,09015 |
| 533,59295 | 0,08691 | 0,08058 | 0,07834 | 0,08593 | 0,08976 |
| 533,63014 | 0,08649 | 0,08053 | 0,07789 | 0,08548 | 0,08937 |
| 533,66732 | 0,08604 | 0,08049 | 0,07744 | 0,08503 | 0,08896 |
| 533,7045 | 0,08558 | 0,08046 | 0,07699 | 0,08459 | 0,08853 |
| 533,74168 | 0,0851 | 0,08043 | 0,07653 | 0,08414 | 0,08809 |
| 533,77886 | 0,0846 | 0,08041 | 0,07608 | 0,0837 | 0,08764 |
| 533,81605 | 0,08408 | 0,08039 | 0,07562 | 0,08325 | 0,08716 |
| 533,85323 | 0,08354 | 0,08038 | 0,07515 | 0,0828 | 0,08667 |
| 533,89041 | 0,08298 | 0,08036 | 0,07468 | 0,08234 | 0,08616 |
| 533,92759 | 0,08241 | 0,08035 | 0,07422 | 0,08189 | 0,08564 |
| 533,96477 | 0,08181 | 0,08033 | 0,07374 | 0,08143 | 0,08509 |
| 534,00196 | 0,0812 | 0,08031 | 0,07327 | 0,08096 | 0,08453 |
| 534,03914 | 0,08057 | 0,08029 | 0,0728 | 0,0805 | 0,08395 |
| 534,07632 | 0,07993 | 0,08026 | 0,07232 | 0,08003 | 0,08336 |
| 534,1135 | 0,07926 | 0,08023 | 0,07184 | 0,07956 | 0,08274 |
| 534,15068 | 0,07858 | 0,08019 | 0,07136 | 0,07908 | 0,0821 |
| 534,18787 | 0,07789 | 0,08014 | 0,07088 | 0,07861 | 0,08146 |
| 534,22505 | 0,07719 | 0,08009 | 0,07041 | 0,07813 | 0,08079 |
| 534,26223 | 0,07647 | 0,08002 | 0,06993 | 0,07765 | 0,08011 |
| 534,29941 | 0,07573 | 0,07994 | 0,06945 | 0,07717 | 0,07942 |
| 534,33659 | 0,075 | 0,07986 | 0,06898 | 0,07669 | 0,07871 |
| 534,37378 | 0,07425 | 0,07975 | 0,06851 | 0,07621 | 0,07799 |
| 534,41096 | 0,07349 | 0,07963 | 0,06804 | 0,07573 | 0,07726 |
| 534,44814 | 0,07273 | 0,0795 | 0,06757 | 0,07525 | 0,07652 |
| 534,48532 | 0,07196 | 0,07936 | 0,06711 | 0,07478 | 0,07578 |
| 534,5225 | 0,07119 | 0,07919 | 0,06666 | 0,07431 | 0,07503 |
| 534,55969 | 0,07041 | 0,07901 | 0,06622 | 0,07385 | 0,07428 |
| 534,59687 | 0,06963 | 0,07881 | 0,06578 | 0,07339 | 0,07352 |
| 534,63405 | 0,06886 | 0,07859 | 0,06535 | 0,07294 | 0,07277 |
| 534,67123 | 0,06808 | 0,07835 | 0,06493 | 0,0725 | 0,07202 |
| 534,70841 | 0,06731 | 0,0781 | 0,06452 | 0,07207 | 0,07128 |
| 534,7456 | 0,06654 | 0,07782 | 0,06413 | 0,07164 | 0,07054 |
| 534,78278 | 0,06578 | 0,07753 | 0,06374 | 0,07123 | 0,06981 |
| 534,81996 | 0,06502 | 0,07721 | 0,06337 | 0,07083 | 0,06909 |
| 534,85714 | 0,06427 | 0,07688 | 0,06302 | 0,07045 | 0,06839 |
| 534,89432 | 0,06353 | 0,07653 | 0,06268 | 0,07008 | 0,0677 |
| 534,93151 | 0,0628 | 0,07616 | 0,06236 | 0,06972 | 0,06703 |
| 534,96869 | 0,06208 | 0,07577 | 0,06206 | 0,06938 | 0,06638 |
| 535,00587 | 0,06138 | 0,07536 | 0,06177 | 0,06906 | 0,06575 |
| 535,04305 | 0,06068 | 0,07494 | 0,0615 | 0,06875 | 0,06514 |
| 535,08023 | 0,06 | 0,07449 | 0,06126 | 0,06846 | 0,06456 |
| 535,11742 | 0,05933 | 0,07403 | 0,06103 | 0,06819 | 0,06401 |
| 535,1546 | 0,05868 | 0,07356 | 0,06083 | 0,06793 | 0,06349 |
| 535,19178 | 0,05804 | 0,07307 | 0,06065 | 0,06769 | 0,06299 |
| 535,22896 | 0,05742 | 0,07257 | 0,06049 | 0,06747 | 0,06252 |
| 535,26614 | 0,05682 | 0,07205 | 0,06036 | 0,06727 | 0,06209 |
| 535,30333 | 0,05624 | 0,07152 | 0,06024 | 0,06708 | 0,06168 |
| 535,34051 | 0,05567 | 0,07098 | 0,06016 | 0,06691 | 0,06131 |
| 535,37769 | 0,05512 | 0,07043 | 0,0601 | 0,06675 | 0,06096 |
| 535,41487 | 0,05459 | 0,06988 | 0,06005 | 0,06661 | 0,06065 |
| 535,45205 | 0,05408 | 0,06931 | 0,06003 | 0,06648 | 0,06038 |
| 535,48924 | 0,05358 | 0,06874 | 0,06004 | 0,06636 | 0,06012 |
| 535,52642 | 0,0531 | 0,06816 | 0,06007 | 0,06625 | 0,0599 |
| 535,5636 | 0,05265 | 0,06757 | 0,06012 | 0,06616 | 0,05971 |
| 535,60078 | 0,05221 | 0,06698 | 0,06019 | 0,06608 | 0,05955 |
| 535,63796 | 0,05179 | 0,06639 | 0,06028 | 0,066 | 0,05941 |
| 535,67515 | 0,05139 | 0,0658 | 0,0604 | 0,06593 | 0,05929 |
| 535,71233 | 0,05101 | 0,06521 | 0,06052 | 0,06586 | 0,0592 |
| 535,74951 | 0,05065 | 0,06461 | 0,06067 | 0,0658 | 0,05913 |
| 535,78669 | 0,05031 | 0,06402 | 0,06084 | 0,06574 | 0,05907 |
| 535,82387 | 0,04998 | 0,06343 | 0,06101 | 0,06568 | 0,05904 |
| 535,86106 | 0,04967 | 0,06284 | 0,0612 | 0,06561 | 0,05901 |
| 535,89824 | 0,04938 | 0,06225 | 0,06141 | 0,06555 | 0,059 |
| 535,93542 | 0,0491 | 0,06167 | 0,06162 | 0,06548 | 0,059 |
| 535,9726 | 0,04885 | 0,06109 | 0,06185 | 0,06541 | 0,05901 |
| 536,00978 | 0,04861 | 0,06051 | 0,06208 | 0,06533 | 0,05902 |
| 536,04697 | 0,04838 | 0,05994 | 0,06231 | 0,06524 | 0,05904 |
| 536,08415 | 0,04817 | 0,05938 | 0,06255 | 0,06514 | 0,05905 |
| 536,12133 | 0,04798 | 0,05882 | 0,06279 | 0,06503 | 0,05907 |
| 536,15851 | 0,0478 | 0,05828 | 0,06304 | 0,06491 | 0,05908 |
| 536,19569 | 0,04764 | 0,05773 | 0,06328 | 0,06478 | 0,05908 |
| 536,23288 | 0,04749 | 0,0572 | 0,06352 | 0,06464 | 0,05909 |
| 536,27006 | 0,04735 | 0,05668 | 0,06376 | 0,06448 | 0,05908 |
| 536,30724 | 0,04723 | 0,05616 | 0,06399 | 0,06431 | 0,05906 |
| 536,34442 | 0,04712 | 0,05565 | 0,06421 | 0,06412 | 0,05903 |
| 536,3816 | 0,04702 | 0,05516 | 0,06443 | 0,06392 | 0,05899 |
| 536,41879 | 0,04693 | 0,05467 | 0,06463 | 0,06371 | 0,05894 |
| 536,45597 | 0,04686 | 0,05419 | 0,06483 | 0,06347 | 0,05887 |
| 536,49315 | 0,04679 | 0,05373 | 0,06501 | 0,06323 | 0,05879 |
| 536,53033 | 0,04673 | 0,05328 | 0,06518 | 0,06298 | 0,05869 |
| 536,56751 | 0,04668 | 0,05284 | 0,06534 | 0,06271 | 0,05858 |
| 536,6047 | 0,04664 | 0,0524 | 0,06549 | 0,06242 | 0,05846 |
| 536,64188 | 0,0466 | 0,05199 | 0,06561 | 0,06213 | 0,05832 |
| 536,67906 | 0,04657 | 0,05159 | 0,06573 | 0,06183 | 0,05817 |
| 536,71624 | 0,04655 | 0,0512 | 0,06583 | 0,06151 | 0,058 |
| 536,75342 | 0,04652 | 0,05082 | 0,06591 | 0,06119 | 0,05782 |
| 536,79061 | 0,0465 | 0,05046 | 0,06597 | 0,06086 | 0,05763 |
| 536,82779 | 0,04648 | 0,05011 | 0,06602 | 0,06052 | 0,05743 |
| 536,86497 | 0,04647 | 0,04978 | 0,06605 | 0,06018 | 0,05723 |
| 536,90215 | 0,04645 | 0,04946 | 0,06607 | 0,05984 | 0,05701 |
| 536,93933 | 0,04642 | 0,04916 | 0,06606 | 0,05949 | 0,05679 |
| 536,97652 | 0,0464 | 0,04887 | 0,06605 | 0,05914 | 0,05656 |
| 537,0137 | 0,04637 | 0,0486 | 0,06601 | 0,05879 | 0,05633 |
| 537,05088 | 0,04633 | 0,04835 | 0,06596 | 0,05844 | 0,05609 |
| 537,08806 | 0,04628 | 0,04811 | 0,0659 | 0,05809 | 0,05586 |
| 537,12524 | 0,04623 | 0,04789 | 0,06582 | 0,05775 | 0,05563 |
| 537,16243 | 0,04617 | 0,04768 | 0,06573 | 0,05741 | 0,05539 |
| 537,19961 | 0,04609 | 0,04749 | 0,06562 | 0,05708 | 0,05517 |
| 537,23679 | 0,04601 | 0,04732 | 0,0655 | 0,05676 | 0,05495 |
| 537,27397 | 0,04591 | 0,04716 | 0,06537 | 0,05644 | 0,05473 |
| 537,31115 | 0,04579 | 0,04702 | 0,06523 | 0,05613 | 0,05453 |
| 537,34834 | 0,04566 | 0,0469 | 0,06507 | 0,05584 | 0,05433 |
| 537,38552 | 0,04552 | 0,04678 | 0,06491 | 0,05555 | 0,05414 |
| 537,4227 | 0,04536 | 0,04669 | 0,06474 | 0,05527 | 0,05397 |
| 537,45988 | 0,04518 | 0,0466 | 0,06455 | 0,055 | 0,0538 |
| 537,49706 | 0,04498 | 0,04654 | 0,06437 | 0,05475 | 0,05365 |
| 537,53425 | 0,04476 | 0,04648 | 0,06417 | 0,0545 | 0,05351 |
| 537,57143 | 0,04453 | 0,04643 | 0,06397 | 0,05427 | 0,05339 |
| 537,60861 | 0,04427 | 0,0464 | 0,06376 | 0,05405 | 0,05328 |
| 537,64579 | 0,044 | 0,04637 | 0,06355 | 0,05384 | 0,05319 |
| 537,68297 | 0,04371 | 0,04636 | 0,06333 | 0,05365 | 0,05311 |
| 537,72016 | 0,04339 | 0,04635 | 0,06311 | 0,05346 | 0,05304 |
| 537,75734 | 0,04306 | 0,04635 | 0,06288 | 0,05328 | 0,05299 |
| 537,79452 | 0,04271 | 0,04636 | 0,06266 | 0,05312 | 0,05295 |
| 537,8317 | 0,04234 | 0,04636 | 0,06243 | 0,05296 | 0,05292 |
| 537,86888 | 0,04196 | 0,04638 | 0,06219 | 0,05281 | 0,0529 |
| 537,90607 | 0,04155 | 0,04639 | 0,06196 | 0,05267 | 0,0529 |
| 537,94325 | 0,04114 | 0,0464 | 0,06173 | 0,05253 | 0,0529 |
| 537,98043 | 0,04071 | 0,04642 | 0,06149 | 0,0524 | 0,05291 |
| 538,01761 | 0,04026 | 0,04643 | 0,06125 | 0,05227 | 0,05293 |
| 538,05479 | 0,0398 | 0,04643 | 0,06101 | 0,05215 | 0,05295 |
| 538,09198 | 0,03933 | 0,04643 | 0,06078 | 0,05202 | 0,05298 |
| 538,12916 | 0,03885 | 0,04642 | 0,06053 | 0,0519 | 0,05301 |
| 538,16634 | 0,03836 | 0,04641 | 0,06029 | 0,05178 | 0,05303 |
| 538,20352 | 0,03786 | 0,04638 | 0,06005 | 0,05165 | 0,05306 |
| 538,2407 | 0,03736 | 0,04634 | 0,0598 | 0,05152 | 0,05309 |
| 538,27789 | 0,03685 | 0,0463 | 0,05955 | 0,05139 | 0,05311 |
| 538,31507 | 0,03634 | 0,04623 | 0,0593 | 0,05125 | 0,05312 |
| 538,35225 | 0,03582 | 0,04615 | 0,05905 | 0,0511 | 0,05312 |
| 538,38943 | 0,03531 | 0,04606 | 0,05879 | 0,05095 | 0,05311 |
| 538,42661 | 0,03479 | 0,04594 | 0,05853 | 0,05078 | 0,0531 |
| 538,4638 | 0,03428 | 0,04581 | 0,05826 | 0,0506 | 0,05306 |
| 538,50098 | 0,03377 | 0,04566 | 0,05798 | 0,05041 | 0,05301 |
| 538,53816 | 0,03326 | 0,04549 | 0,0577 | 0,05021 | 0,05295 |
| 538,57534 | 0,03276 | 0,0453 | 0,05741 | 0,05 | 0,05286 |
| 538,61252 | 0,03226 | 0,04508 | 0,05711 | 0,04976 | 0,05276 |
| 538,64971 | 0,03177 | 0,04484 | 0,0568 | 0,04951 | 0,05263 |
| 538,68689 | 0,03129 | 0,04458 | 0,05648 | 0,04925 | 0,05249 |
| 538,72407 | 0,03082 | 0,0443 | 0,05615 | 0,04897 | 0,05231 |
| 538,76125 | 0,03036 | 0,04399 | 0,0558 | 0,04867 | 0,05211 |
| 538,79843 | 0,02991 | 0,04366 | 0,05545 | 0,04835 | 0,05189 |
| 538,83562 | 0,02947 | 0,0433 | 0,05507 | 0,04801 | 0,05165 |
| 538,8728 | 0,02904 | 0,04293 | 0,05468 | 0,04766 | 0,05137 |
| 538,90998 | 0,02862 | 0,04252 | 0,05428 | 0,04728 | 0,05106 |
| 538,94716 | 0,02822 | 0,0421 | 0,05386 | 0,04689 | 0,05073 |
| 538,98434 | 0,02782 | 0,04165 | 0,05342 | 0,04648 | 0,05038 |
| 539,02153 | 0,02744 | 0,04119 | 0,05296 | 0,04605 | 0,04998 |
| 539,05871 | 0,02708 | 0,0407 | 0,05248 | 0,0456 | 0,04957 |
| 539,09589 | 0,02672 | 0,04019 | 0,05198 | 0,04513 | 0,04913 |
| 539,13307 | 0,02638 | 0,03966 | 0,05146 | 0,04464 | 0,04866 |
| 539,17025 | 0,02604 | 0,03911 | 0,05092 | 0,04414 | 0,04816 |
| 539,20744 | 0,02572 | 0,03854 | 0,05036 | 0,04362 | 0,04763 |
| 539,24462 | 0,02542 | 0,03796 | 0,04977 | 0,04308 | 0,04708 |
| 539,2818 | 0,02512 | 0,03737 | 0,04916 | 0,04254 | 0,04651 |
| 539,31898 | 0,02483 | 0,03675 | 0,04854 | 0,04197 | 0,0459 |
| 539,35616 | 0,02455 | 0,03613 | 0,04789 | 0,04139 | 0,04528 |
| 539,39335 | 0,02428 | 0,03549 | 0,04722 | 0,0408 | 0,04464 |
| 539,43053 | 0,02402 | 0,03485 | 0,04653 | 0,04019 | 0,04397 |
| 539,46771 | 0,02377 | 0,03419 | 0,04582 | 0,03958 | 0,04328 |
| 539,50489 | 0,02353 | 0,03352 | 0,04509 | 0,03895 | 0,04258 |
| 539,54207 | 0,02329 | 0,03285 | 0,04434 | 0,03832 | 0,04186 |
| 539,57926 | 0,02306 | 0,03218 | 0,04358 | 0,03768 | 0,04112 |
| 539,61644 | 0,02283 | 0,03149 | 0,0428 | 0,03703 | 0,04036 |
| 539,65362 | 0,02261 | 0,03081 | 0,042 | 0,03638 | 0,0396 |
| 539,6908 | 0,02239 | 0,03012 | 0,04118 | 0,03572 | 0,03882 |
| 539,72798 | 0,02218 | 0,02944 | 0,04036 | 0,03506 | 0,03803 |
| 539,76517 | 0,02196 | 0,02875 | 0,03952 | 0,03439 | 0,03723 |
| 539,80235 | 0,02175 | 0,02806 | 0,03867 | 0,03372 | 0,03643 |
| 539,83953 | 0,02155 | 0,02738 | 0,03781 | 0,03305 | 0,03562 |
| 539,87671 | 0,02134 | 0,0267 | 0,03694 | 0,03238 | 0,03481 |
| 539,91389 | 0,02113 | 0,02603 | 0,03606 | 0,03171 | 0,03399 |
| 539,95108 | 0,02092 | 0,02536 | 0,03518 | 0,03105 | 0,03317 |
| 539,98826 | 0,02071 | 0,0247 | 0,0343 | 0,03038 | 0,03236 |
| 540,02544 | 0,0205 | 0,02404 | 0,03341 | 0,02972 | 0,03154 |
| 540,06262 | 0,02029 | 0,0234 | 0,03253 | 0,02905 | 0,03073 |
| 540,0998 | 0,02007 | 0,02276 | 0,03164 | 0,0284 | 0,02992 |
| 540,13699 | 0,01986 | 0,02213 | 0,03076 | 0,02775 | 0,02911 |
| 540,17417 | 0,01964 | 0,02151 | 0,02988 | 0,0271 | 0,02832 |
| 540,21135 | 0,01941 | 0,0209 | 0,02901 | 0,02646 | 0,02753 |
| 540,24853 | 0,01918 | 0,0203 | 0,02814 | 0,02582 | 0,02674 |
| 540,28571 | 0,01895 | 0,01971 | 0,02728 | 0,02519 | 0,02597 |
| 540,3229 | 0,01872 | 0,01913 | 0,02643 | 0,02456 | 0,02521 |
| 540,36008 | 0,01848 | 0,01856 | 0,0256 | 0,02395 | 0,02446 |
| 540,39726 | 0,01823 | 0,01801 | 0,02477 | 0,02334 | 0,02372 |
| 540,43444 | 0,01798 | 0,01746 | 0,02395 | 0,02273 | 0,02299 |
| 540,47162 | 0,01773 | 0,01693 | 0,02315 | 0,02214 | 0,02228 |
| 540,50881 | 0,01747 | 0,01641 | 0,02237 | 0,02155 | 0,02158 |
| 540,54599 | 0,01721 | 0,0159 | 0,02159 | 0,02097 | 0,02089 |
| 540,58317 | 0,01695 | 0,01541 | 0,02084 | 0,02039 | 0,02022 |
| 540,62035 | 0,01667 | 0,01492 | 0,0201 | 0,01983 | 0,01957 |
| 540,65753 | 0,0164 | 0,01445 | 0,01937 | 0,01927 | 0,01892 |
| 540,69472 | 0,01612 | 0,01398 | 0,01867 | 0,01872 | 0,01829 |
| 540,7319 | 0,01584 | 0,01353 | 0,01798 | 0,01818 | 0,01768 |
| 540,76908 | 0,01555 | 0,01309 | 0,01731 | 0,01765 | 0,01708 |
| 540,80626 | 0,01526 | 0,01266 | 0,01666 | 0,01712 | 0,0165 |
| 540,84344 | 0,01496 | 0,01224 | 0,01602 | 0,01661 | 0,01593 |
| 540,88063 | 0,01466 | 0,01184 | 0,0154 | 0,0161 | 0,01538 |
| 540,91781 | 0,01436 | 0,01144 | 0,0148 | 0,0156 | 0,01484 |
| 540,95499 | 0,01406 | 0,01105 | 0,01422 | 0,01512 | 0,01431 |
| 540,99217 | 0,01375 | 0,01067 | 0,01366 | 0,01464 | 0,0138 |
| 541,02935 | 0,01344 | 0,0103 | 0,01311 | 0,01417 | 0,0133 |
| 541,06654 | 0,01312 | 0,00994 | 0,01258 | 0,01371 | 0,01281 |
| 541,10372 | 0,01281 | 0,00959 | 0,01207 | 0,01326 | 0,01234 |
| 541,1409 | 0,01249 | 0,00925 | 0,01157 | 0,01281 | 0,01188 |
| 541,17808 | 0,01217 | 0,00892 | 0,01109 | 0,01238 | 0,01143 |
| 541,21526 | 0,01185 | 0,00859 | 0,01063 | 0,01196 | 0,01099 |
| 541,25245 | 0,01153 | 0,00827 | 0,01018 | 0,01155 | 0,01057 |
| 541,28963 | 0,01121 | 0,00796 | 0,00974 | 0,01115 | 0,01015 |
| 541,32681 | 0,01089 | 0,00766 | 0,00933 | 0,01075 | 0,00975 |
| 541,36399 | 0,01057 | 0,00737 | 0,00892 | 0,01037 | 0,00936 |
| 541,40117 | 0,01024 | 0,00708 | 0,00853 | 0,01 | 0,00898 |
| 541,43836 | 0,00992 | 0,0068 | 0,00815 | 0,00964 | 0,0086 |
| 541,47554 | 0,0096 | 0,00653 | 0,00779 | 0,00928 | 0,00824 |
| 541,51272 | 0,00928 | 0,00626 | 0,00744 | 0,00894 | 0,00789 |
| 541,5499 | 0,00897 | 0,006 | 0,00709 | 0,00861 | 0,00755 |
| 541,58708 | 0,00865 | 0,00575 | 0,00676 | 0,00829 | 0,00721 |
| 541,62427 | 0,00834 | 0,0055 | 0,00645 | 0,00798 | 0,00689 |
| 541,66145 | 0,00803 | 0,00526 | 0,00614 | 0,00768 | 0,00657 |
| 541,69863 | 0,00772 | 0,00503 | 0,00585 | 0,00739 | 0,00626 |
| 541,73581 | 0,00742 | 0,0048 | 0,00556 | 0,00711 | 0,00596 |
| 541,77299 | 0,00712 | 0,00458 | 0,00529 | 0,00683 | 0,00568 |
| 541,81018 | 0,00683 | 0,00437 | 0,00502 | 0,00657 | 0,00539 |
| 541,84736 | 0,00654 | 0,00416 | 0,00476 | 0,00632 | 0,00512 |
| 541,88454 | 0,00625 | 0,00396 | 0,00452 | 0,00608 | 0,00486 |
| 541,92172 | 0,00597 | 0,00376 | 0,00428 | 0,00584 | 0,0046 |
| 541,9589 | 0,0057 | 0,00357 | 0,00405 | 0,00561 | 0,00435 |
| 541,99609 | 0,00543 | 0,00339 | 0,00383 | 0,00539 | 0,00411 |
| 542,03327 | 0,00517 | 0,00321 | 0,00362 | 0,00518 | 0,00388 |
| 542,07045 | 0,00491 | 0,00304 | 0,00342 | 0,00498 | 0,00366 |
| 542,10763 | 0,00467 | 0,00287 | 0,00322 | 0,00478 | 0,00345 |
| 542,14481 | 0,00442 | 0,00271 | 0,00303 | 0,00459 | 0,00324 |
| 542,182 | 0,00419 | 0,00256 | 0,00286 | 0,00441 | 0,00304 |
| 542,21918 | 0,00396 | 0,00241 | 0,00268 | 0,00423 | 0,00285 |
| 542,25636 | 0,00374 | 0,00227 | 0,00252 | 0,00406 | 0,00267 |
| 542,29354 | 0,00353 | 0,00213 | 0,00236 | 0,0039 | 0,0025 |
| 542,33072 | 0,00332 | 0,002 | 0,00221 | 0,00374 | 0,00233 |
| 542,36791 | 0,00313 | 0,00187 | 0,00207 | 0,00358 | 0,00218 |
| 542,40509 | 0,00294 | 0,00175 | 0,00193 | 0,00344 | 0,00202 |
| 542,44227 | 0,00275 | 0,00164 | 0,0018 | 0,00329 | 0,00188 |
| 542,47945 | 0,00258 | 0,00153 | 0,00168 | 0,00315 | 0,00175 |
| 542,51663 | 0,00241 | 0,00143 | 0,00156 | 0,00302 | 0,00162 |
| 542,55382 | 0,00225 | 0,00133 | 0,00145 | 0,00289 | 0,0015 |
| 542,591 | 0,0021 | 0,00124 | 0,00135 | 0,00276 | 0,00138 |
| 542,62818 | 0,00196 | 0,00115 | 0,00125 | 0,00264 | 0,00127 |
| 542,66536 | 0,00182 | 0,00106 | 0,00116 | 0,00252 | 0,00117 |
| 542,70254 | 0,00169 | 0,00098 | 0,00107 | 0,0024 | 0,00108 |
| 542,73973 | 0,00157 | 0,00091 | 0,00099 | 0,00229 | 0,00099 |
| 542,77691 | 0,00145 | 0,00084 | 0,00091 | 0,00218 | 0,00091 |
| 542,81409 | 0,00134 | 0,00077 | 0,00084 | 0,00208 | 0,00083 |
| 542,85127 | 0,00124 | 0,00071 | 0,00077 | 0,00198 | 0,00076 |
| 542,88845 | 0,00114 | 0,00065 | 0,00071 | 0,00188 | 0,00069 |
| 542,92564 | 0,00105 | 6e-04 | 0,00065 | 0,00178 | 0,00063 |
| 542,96282 | 0,00097 | 0,00055 | 0,00059 | 0,00169 | 0,00057 |
| 543 | 0,00089 | 5e-04 | 0,00054 | 0,0016 | 0,00052 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00098 | 0,00145 | 5e-04 | 0,00028 | 0,00028 |
| 524,03718 | 0,00101 | 0,00149 | 5e-04 | 0,00032 | 0,00031 |
| 524,07436 | 0,00103 | 0,00153 | 0,00049 | 0,00036 | 0,00034 |
| 524,11155 | 0,00105 | 0,00156 | 0,00049 | 4e-04 | 0,00038 |
| 524,14873 | 0,00106 | 0,00158 | 0,00049 | 0,00043 | 0,00041 |
| 524,18591 | 0,00107 | 0,0016 | 0,00049 | 0,00047 | 0,00045 |
| 524,22309 | 0,00107 | 0,00161 | 5e-04 | 0,00051 | 0,00048 |
| 524,26027 | 0,00107 | 0,00161 | 0,00051 | 0,00054 | 0,00051 |
| 524,29746 | 0,00108 | 0,0016 | 0,00053 | 0,00057 | 0,00054 |
| 524,33464 | 0,00108 | 0,00158 | 0,00055 | 0,00059 | 0,00056 |
| 524,37182 | 0,0011 | 0,00156 | 0,00058 | 0,00061 | 0,00059 |
| 524,409 | 0,00112 | 0,00154 | 0,00062 | 0,00063 | 0,00061 |
| 524,44618 | 0,00115 | 0,00152 | 0,00066 | 0,00064 | 0,00062 |
| 524,48337 | 0,00119 | 0,0015 | 0,00071 | 0,00065 | 0,00063 |
| 524,52055 | 0,00124 | 0,00148 | 0,00077 | 0,00065 | 0,00064 |
| 524,55773 | 0,00131 | 0,00146 | 0,00082 | 0,00065 | 0,00064 |
| 524,59491 | 0,00139 | 0,00146 | 0,00089 | 0,00065 | 0,00063 |
| 524,63209 | 0,00147 | 0,00146 | 0,00095 | 0,00064 | 0,00063 |
| 524,66928 | 0,00157 | 0,00148 | 0,00102 | 0,00063 | 0,00062 |
| 524,70646 | 0,00167 | 0,00151 | 0,00109 | 0,00063 | 6e-04 |
| 524,74364 | 0,00177 | 0,00154 | 0,00116 | 0,00062 | 0,00059 |
| 524,78082 | 0,00188 | 0,0016 | 0,00123 | 0,00061 | 0,00058 |
| 524,818 | 0,00197 | 0,00166 | 0,00129 | 0,00061 | 0,00056 |
| 524,85519 | 0,00207 | 0,00173 | 0,00136 | 0,00061 | 0,00055 |
| 524,89237 | 0,00215 | 0,00181 | 0,00143 | 0,00061 | 0,00054 |
| 524,92955 | 0,00223 | 0,00191 | 0,00149 | 0,00062 | 0,00054 |
| 524,96673 | 0,00229 | 0,00201 | 0,00156 | 0,00062 | 0,00054 |
| 525,00391 | 0,00235 | 0,00212 | 0,00163 | 0,00064 | 0,00055 |
| 525,0411 | 0,00239 | 0,00224 | 0,0017 | 0,00066 | 0,00057 |
| 525,07828 | 0,00243 | 0,00237 | 0,00177 | 0,00068 | 6e-04 |
| 525,11546 | 0,00247 | 0,0025 | 0,00186 | 0,00072 | 0,00065 |
| 525,15264 | 0,00252 | 0,00265 | 0,00195 | 0,00076 | 7e-04 |
| 525,18982 | 0,00257 | 0,00281 | 0,00206 | 0,00082 | 0,00077 |
| 525,22701 | 0,00265 | 0,00299 | 0,00218 | 9e-04 | 0,00085 |
| 525,26419 | 0,00276 | 0,00319 | 0,00234 | 0,001 | 0,00096 |
| 525,30137 | 0,00291 | 0,00343 | 0,00253 | 0,00112 | 0,00109 |
| 525,33855 | 0,00313 | 0,00369 | 0,00275 | 0,00129 | 0,00124 |
| 525,37573 | 0,00342 | 0,00401 | 0,00302 | 0,00149 | 0,00143 |
| 525,41292 | 0,00381 | 0,00437 | 0,00335 | 0,00174 | 0,00165 |
| 525,4501 | 0,0043 | 0,00479 | 0,00375 | 0,00205 | 0,00193 |
| 525,48728 | 0,00492 | 0,00528 | 0,00422 | 0,00243 | 0,00226 |
| 525,52446 | 0,00567 | 0,00585 | 0,00477 | 0,00289 | 0,00266 |
| 525,56164 | 0,00658 | 0,00651 | 0,00543 | 0,00344 | 0,00315 |
| 525,59883 | 0,00764 | 0,00728 | 0,00619 | 0,00413 | 0,00376 |
| 525,63601 | 0,00886 | 0,00814 | 0,00704 | 0,00495 | 0,00449 |
| 525,67319 | 0,01025 | 0,0091 | 0,008 | 0,00591 | 0,00536 |
| 525,71037 | 0,01178 | 0,01016 | 0,00905 | 0,00704 | 0,0064 |
| 525,74755 | 0,01344 | 0,01132 | 0,0102 | 0,00834 | 0,00761 |
| 525,78474 | 0,01519 | 0,01256 | 0,01143 | 0,00984 | 0,00902 |
| 525,82192 | 0,01702 | 0,01387 | 0,01273 | 0,01155 | 0,01063 |
| 525,8591 | 0,01888 | 0,01525 | 0,0141 | 0,01347 | 0,01246 |
| 525,89628 | 0,02074 | 0,01669 | 0,01551 | 0,01563 | 0,01452 |
| 525,93346 | 0,02258 | 0,01817 | 0,01695 | 0,01804 | 0,01684 |
| 525,97065 | 0,02436 | 0,01967 | 0,0184 | 0,02069 | 0,01937 |
| 526,00783 | 0,02605 | 0,02119 | 0,01985 | 0,02355 | 0,0221 |
| 526,04501 | 0,02765 | 0,02273 | 0,02129 | 0,02662 | 0,02502 |
| 526,08219 | 0,02916 | 0,02429 | 0,02273 | 0,02988 | 0,0281 |
| 526,11937 | 0,03061 | 0,02587 | 0,02416 | 0,0333 | 0,03129 |
| 526,15656 | 0,03201 | 0,02748 | 0,0256 | 0,03685 | 0,03457 |
| 526,19374 | 0,03341 | 0,02915 | 0,02707 | 0,04048 | 0,03787 |
| 526,23092 | 0,03485 | 0,0309 | 0,02857 | 0,04413 | 0,04115 |
| 526,2681 | 0,03638 | 0,03274 | 0,03014 | 0,04774 | 0,04431 |
| 526,30528 | 0,03805 | 0,0347 | 0,0318 | 0,05122 | 0,0473 |
| 526,34247 | 0,03992 | 0,0368 | 0,03355 | 0,0545 | 0,05005 |
| 526,37965 | 0,04202 | 0,03904 | 0,03542 | 0,0575 | 0,05249 |
| 526,41683 | 0,04435 | 0,04143 | 0,03741 | 0,06015 | 0,05454 |
| 526,45401 | 0,04691 | 0,04398 | 0,03953 | 0,06236 | 0,05617 |
| 526,49119 | 0,04968 | 0,04667 | 0,04177 | 0,06408 | 0,05731 |
| 526,52838 | 0,05262 | 0,04949 | 0,04412 | 0,06526 | 0,05793 |
| 526,56556 | 0,05568 | 0,0524 | 0,04655 | 0,06581 | 0,05799 |
| 526,60274 | 0,05882 | 0,05537 | 0,04901 | 0,0657 | 0,05744 |
| 526,63992 | 0,06195 | 0,05835 | 0,05147 | 0,06498 | 0,05636 |
| 526,6771 | 0,06502 | 0,0613 | 0,05389 | 0,06371 | 0,05481 |
| 526,71429 | 0,06795 | 0,0642 | 0,05625 | 0,06192 | 0,05282 |
| 526,75147 | 0,07071 | 0,06699 | 0,05849 | 0,05969 | 0,05049 |
| 526,78865 | 0,07328 | 0,06965 | 0,06061 | 0,05712 | 0,04789 |
| 526,82583 | 0,07564 | 0,07216 | 0,06255 | 0,0543 | 0,04512 |
| 526,86301 | 0,07782 | 0,07449 | 0,06434 | 0,05134 | 0,04228 |
| 526,9002 | 0,07982 | 0,07665 | 0,06597 | 0,04837 | 0,03948 |
| 526,93738 | 0,08168 | 0,07866 | 0,06747 | 0,04554 | 0,03685 |
| 526,97456 | 0,08345 | 0,08053 | 0,06887 | 0,04295 | 0,0345 |
| 527,01174 | 0,08518 | 0,08229 | 0,0702 | 0,0407 | 0,03249 |
| 527,04892 | 0,08692 | 0,08397 | 0,0715 | 0,0389 | 0,03091 |
| 527,08611 | 0,08873 | 0,08561 | 0,07283 | 0,0376 | 0,02983 |
| 527,12329 | 0,09064 | 0,08725 | 0,07425 | 0,03688 | 0,02931 |
| 527,16047 | 0,09269 | 0,08894 | 0,07583 | 0,0368 | 0,02937 |
| 527,19765 | 0,09492 | 0,09075 | 0,07763 | 0,03739 | 0,03007 |
| 527,23483 | 0,09735 | 0,09271 | 0,0797 | 0,03873 | 0,03145 |
| 527,27202 | 0,10002 | 0,09489 | 0,08211 | 0,04084 | 0,03356 |
| 527,3092 | 0,10297 | 0,09734 | 0,0849 | 0,04365 | 0,03633 |
| 527,34638 | 0,10625 | 0,10012 | 0,08814 | 0,04717 | 0,03976 |
| 527,38356 | 0,10996 | 0,10326 | 0,09186 | 0,05137 | 0,04384 |
| 527,42074 | 0,1141 | 0,10684 | 0,09612 | 0,05623 | 0,04855 |
| 527,45793 | 0,11874 | 0,11089 | 0,10103 | 0,06171 | 0,05387 |
| 527,49511 | 0,12391 | 0,11553 | 0,10656 | 0,0678 | 0,05977 |
| 527,53229 | 0,12967 | 0,12072 | 0,11272 | 0,07445 | 0,06624 |
| 527,56947 | 0,13602 | 0,12644 | 0,11948 | 0,08167 | 0,07329 |
| 527,60665 | 0,14296 | 0,13269 | 0,12683 | 0,0894 | 0,08089 |
| 527,64384 | 0,15046 | 0,13942 | 0,13471 | 0,09758 | 0,08898 |
| 527,68102 | 0,15845 | 0,14659 | 0,14305 | 0,10618 | 0,09754 |
| 527,7182 | 0,16686 | 0,1541 | 0,15178 | 0,11517 | 0,10655 |
| 527,75538 | 0,17549 | 0,16186 | 0,16079 | 0,12452 | 0,11599 |
| 527,79256 | 0,18417 | 0,16975 | 0,16992 | 0,13419 | 0,12583 |
| 527,82975 | 0,19272 | 0,1776 | 0,17901 | 0,14415 | 0,13605 |
| 527,86693 | 0,20096 | 0,18528 | 0,18789 | 0,15434 | 0,14659 |
| 527,90411 | 0,20871 | 0,19264 | 0,19642 | 0,16472 | 0,15743 |
| 527,94129 | 0,21583 | 0,19956 | 0,20447 | 0,17519 | 0,16846 |
| 527,97847 | 0,22218 | 0,20594 | 0,21189 | 0,18565 | 0,17959 |
| 528,01566 | 0,22766 | 0,21168 | 0,21859 | 0,19601 | 0,1907 |
| 528,05284 | 0,23212 | 0,21672 | 0,22447 | 0,20615 | 0,20168 |
| 528,09002 | 0,23562 | 0,22102 | 0,22941 | 0,21595 | 0,21239 |
| 528,1272 | 0,23822 | 0,22446 | 0,23338 | 0,22527 | 0,22268 |
| 528,16438 | 0,24 | 0,22716 | 0,23645 | 0,23398 | 0,23241 |
| 528,20157 | 0,24104 | 0,22916 | 0,23867 | 0,24194 | 0,24141 |
| 528,23875 | 0,24145 | 0,23052 | 0,24009 | 0,24889 | 0,24941 |
| 528,27593 | 0,24133 | 0,23131 | 0,24078 | 0,2548 | 0,25631 |
| 528,31311 | 0,2408 | 0,2316 | 0,24084 | 0,25958 | 0,26202 |
| 528,35029 | 0,23994 | 0,23146 | 0,24034 | 0,26318 | 0,26646 |
| 528,38748 | 0,23883 | 0,23096 | 0,23938 | 0,26556 | 0,26957 |
| 528,42466 | 0,23753 | 0,23014 | 0,23801 | 0,26672 | 0,27131 |
| 528,46184 | 0,23609 | 0,22906 | 0,23636 | 0,26668 | 0,27172 |
| 528,49902 | 0,23453 | 0,22777 | 0,23451 | 0,2655 | 0,27084 |
| 528,5362 | 0,23285 | 0,22631 | 0,23249 | 0,26329 | 0,26877 |
| 528,57339 | 0,23104 | 0,22469 | 0,23034 | 0,26006 | 0,26552 |
| 528,61057 | 0,2291 | 0,22292 | 0,2281 | 0,2561 | 0,26141 |
| 528,64775 | 0,22701 | 0,221 | 0,22577 | 0,2516 | 0,25663 |
| 528,68493 | 0,22476 | 0,21894 | 0,22336 | 0,2467 | 0,25137 |
| 528,72211 | 0,22236 | 0,21675 | 0,22087 | 0,24156 | 0,24582 |
| 528,7593 | 0,2198 | 0,21442 | 0,21828 | 0,23632 | 0,24013 |
| 528,79648 | 0,21712 | 0,21197 | 0,21561 | 0,23111 | 0,23447 |
| 528,83366 | 0,21435 | 0,20943 | 0,21285 | 0,22602 | 0,22895 |
| 528,87084 | 0,21153 | 0,20682 | 0,20999 | 0,22112 | 0,22367 |
| 528,90802 | 0,2087 | 0,20417 | 0,20705 | 0,21648 | 0,21874 |
| 528,94521 | 0,2059 | 0,2015 | 0,20402 | 0,21208 | 0,21414 |
| 528,98239 | 0,20318 | 0,19885 | 0,20091 | 0,20792 | 0,20988 |
| 529,01957 | 0,20058 | 0,19624 | 0,19776 | 0,20395 | 0,20594 |
| 529,05675 | 0,19813 | 0,19371 | 0,19457 | 0,20017 | 0,20229 |
| 529,09393 | 0,19589 | 0,1913 | 0,19138 | 0,19654 | 0,19889 |
| 529,13112 | 0,19385 | 0,18903 | 0,18823 | 0,19304 | 0,19572 |
| 529,1683 | 0,19204 | 0,18691 | 0,18515 | 0,18967 | 0,19276 |
| 529,20548 | 0,19046 | 0,18497 | 0,18218 | 0,18643 | 0,19001 |
| 529,24266 | 0,18911 | 0,18322 | 0,17937 | 0,18338 | 0,18749 |
| 529,27984 | 0,18799 | 0,18169 | 0,17676 | 0,18055 | 0,18521 |
| 529,31703 | 0,18711 | 0,18038 | 0,17439 | 0,178 | 0,18321 |
| 529,35421 | 0,18647 | 0,17932 | 0,17232 | 0,1758 | 0,18156 |
| 529,39139 | 0,18605 | 0,17855 | 0,17063 | 0,17403 | 0,18029 |
| 529,42857 | 0,18591 | 0,17807 | 0,16932 | 0,17275 | 0,17947 |
| 529,46575 | 0,186 | 0,17788 | 0,16843 | 0,17202 | 0,17915 |
| 529,50294 | 0,18633 | 0,178 | 0,16797 | 0,17189 | 0,17936 |
| 529,54012 | 0,1869 | 0,17842 | 0,16796 | 0,17238 | 0,18014 |
| 529,5773 | 0,18769 | 0,17914 | 0,1684 | 0,17354 | 0,18153 |
| 529,61448 | 0,18869 | 0,18014 | 0,16928 | 0,17523 | 0,18342 |
| 529,65166 | 0,18988 | 0,18141 | 0,17056 | 0,17738 | 0,18572 |
| 529,68885 | 0,19122 | 0,1829 | 0,17225 | 0,17987 | 0,18834 |
| 529,72603 | 0,19267 | 0,18458 | 0,17424 | 0,18256 | 0,19114 |
| 529,76321 | 0,19416 | 0,18634 | 0,17645 | 0,1853 | 0,19398 |
| 529,80039 | 0,19558 | 0,18811 | 0,17877 | 0,18792 | 0,19669 |
| 529,83757 | 0,19687 | 0,18978 | 0,18111 | 0,19026 | 0,19911 |
| 529,87476 | 0,19792 | 0,19128 | 0,18336 | 0,1921 | 0,20104 |
| 529,91194 | 0,19864 | 0,1925 | 0,18543 | 0,19327 | 0,20228 |
| 529,94912 | 0,19894 | 0,19335 | 0,1872 | 0,19371 | 0,20277 |
| 529,9863 | 0,19874 | 0,19373 | 0,18857 | 0,19335 | 0,20244 |
| 530,02348 | 0,19797 | 0,19352 | 0,18938 | 0,19217 | 0,20126 |
| 530,06067 | 0,19657 | 0,19266 | 0,1896 | 0,19019 | 0,19925 |
| 530,09785 | 0,19447 | 0,19114 | 0,1892 | 0,18748 | 0,19645 |
| 530,13503 | 0,19166 | 0,18897 | 0,18816 | 0,18412 | 0,19297 |
| 530,17221 | 0,18822 | 0,18614 | 0,18646 | 0,18025 | 0,18892 |
| 530,20939 | 0,18418 | 0,18269 | 0,18412 | 0,176 | 0,18444 |
| 530,24658 | 0,17962 | 0,17868 | 0,18118 | 0,17158 | 0,17973 |
| 530,28376 | 0,17461 | 0,17418 | 0,17769 | 0,16718 | 0,17499 |
| 530,32094 | 0,16926 | 0,16927 | 0,1737 | 0,16294 | 0,17037 |
| 530,35812 | 0,16365 | 0,16404 | 0,16931 | 0,15898 | 0,16599 |
| 530,3953 | 0,15791 | 0,15865 | 0,16466 | 0,15542 | 0,16198 |
| 530,43249 | 0,15213 | 0,15322 | 0,15984 | 0,15232 | 0,15839 |
| 530,46967 | 0,14645 | 0,14784 | 0,15496 | 0,14973 | 0,15529 |
| 530,50685 | 0,14096 | 0,14262 | 0,1501 | 0,14764 | 0,15267 |
| 530,54403 | 0,13573 | 0,13764 | 0,14537 | 0,14608 | 0,15057 |
| 530,58121 | 0,13082 | 0,13298 | 0,14084 | 0,14497 | 0,14893 |
| 530,6184 | 0,12629 | 0,12872 | 0,13658 | 0,14421 | 0,14765 |
| 530,65558 | 0,12219 | 0,12492 | 0,13271 | 0,14373 | 0,14666 |
| 530,69276 | 0,11853 | 0,12165 | 0,12925 | 0,14343 | 0,1459 |
| 530,72994 | 0,11534 | 0,11889 | 0,12622 | 0,14323 | 0,14529 |
| 530,76712 | 0,11263 | 0,11663 | 0,12365 | 0,14308 | 0,14477 |
| 530,80431 | 0,11046 | 0,11489 | 0,12153 | 0,14291 | 0,14431 |
| 530,84149 | 0,10877 | 0,11364 | 0,11989 | 0,14267 | 0,14386 |
| 530,87867 | 0,10752 | 0,11287 | 0,1187 | 0,14234 | 0,14341 |
| 530,91585 | 0,10672 | 0,11254 | 0,11794 | 0,14191 | 0,14295 |
| 530,95303 | 0,10632 | 0,11263 | 0,11761 | 0,14139 | 0,14249 |
| 530,99022 | 0,10631 | 0,11312 | 0,1177 | 0,14081 | 0,14206 |
| 531,0274 | 0,10663 | 0,11393 | 0,1181 | 0,14019 | 0,14166 |
| 531,06458 | 0,10725 | 0,11497 | 0,11877 | 0,13955 | 0,14131 |
| 531,10176 | 0,10811 | 0,11619 | 0,11964 | 0,13891 | 0,141 |
| 531,13894 | 0,10916 | 0,11751 | 0,12066 | 0,13828 | 0,14074 |
| 531,17613 | 0,11031 | 0,11888 | 0,12175 | 0,13766 | 0,14048 |
| 531,21331 | 0,11147 | 0,1202 | 0,12285 | 0,13701 | 0,14019 |
| 531,25049 | 0,11256 | 0,12141 | 0,12389 | 0,1363 | 0,13979 |
| 531,28767 | 0,1135 | 0,12242 | 0,12477 | 0,13546 | 0,1392 |
| 531,32485 | 0,11422 | 0,12312 | 0,12542 | 0,13443 | 0,13835 |
| 531,36204 | 0,11465 | 0,12348 | 0,12578 | 0,13314 | 0,13715 |
| 531,39922 | 0,11471 | 0,12343 | 0,12582 | 0,13152 | 0,13553 |
| 531,4364 | 0,11436 | 0,12294 | 0,12547 | 0,12951 | 0,13341 |
| 531,47358 | 0,11351 | 0,12198 | 0,12472 | 0,12706 | 0,13077 |
| 531,51076 | 0,11217 | 0,12052 | 0,12354 | 0,12413 | 0,12755 |
| 531,54795 | 0,11034 | 0,11857 | 0,12193 | 0,12066 | 0,1237 |
| 531,58513 | 0,10806 | 0,11613 | 0,11988 | 0,11671 | 0,11931 |
| 531,62231 | 0,10536 | 0,11318 | 0,11738 | 0,11234 | 0,11445 |
| 531,65949 | 0,10227 | 0,10982 | 0,1145 | 0,10761 | 0,10919 |
| 531,69667 | 0,09887 | 0,1061 | 0,11131 | 0,10261 | 0,10363 |
| 531,73386 | 0,09522 | 0,10209 | 0,10784 | 0,09742 | 0,09788 |
| 531,77104 | 0,09138 | 0,09785 | 0,10416 | 0,09214 | 0,09204 |
| 531,80822 | 0,08742 | 0,09346 | 0,10031 | 0,08687 | 0,08621 |
| 531,8454 | 0,08342 | 0,08899 | 0,09637 | 0,08172 | 0,0805 |
| 531,88258 | 0,07946 | 0,0845 | 0,09237 | 0,07681 | 0,07505 |
| 531,91977 | 0,07556 | 0,08007 | 0,08839 | 0,0722 | 0,06991 |
| 531,95695 | 0,07179 | 0,07576 | 0,08448 | 0,06795 | 0,06513 |
| 531,99413 | 0,06816 | 0,07163 | 0,08067 | 0,06411 | 0,06075 |
| 532,03131 | 0,06471 | 0,06771 | 0,077 | 0,06069 | 0,05679 |
| 532,06849 | 0,06144 | 0,06404 | 0,0735 | 0,05772 | 0,05328 |
| 532,10568 | 0,05837 | 0,06064 | 0,07018 | 0,05517 | 0,05019 |
| 532,14286 | 0,05551 | 0,05753 | 0,06707 | 0,05305 | 0,04753 |
| 532,18004 | 0,05287 | 0,05472 | 0,06418 | 0,05133 | 0,04527 |
| 532,21722 | 0,05042 | 0,05221 | 0,06151 | 0,05001 | 0,04344 |
| 532,2544 | 0,04818 | 0,05004 | 0,0591 | 0,049 | 0,04195 |
| 532,29159 | 0,04613 | 0,04817 | 0,05693 | 0,04825 | 0,04077 |
| 532,32877 | 0,04427 | 0,04659 | 0,05499 | 0,04772 | 0,03987 |
| 532,36595 | 0,0426 | 0,04529 | 0,05329 | 0,04738 | 0,03921 |
| 532,40313 | 0,04112 | 0,04424 | 0,05183 | 0,04718 | 0,03877 |
| 532,44031 | 0,03983 | 0,04343 | 0,05058 | 0,04709 | 0,03852 |
| 532,4775 | 0,03873 | 0,04284 | 0,04956 | 0,04707 | 0,03842 |
| 532,51468 | 0,03783 | 0,04246 | 0,04875 | 0,04711 | 0,03847 |
| 532,55186 | 0,03711 | 0,04226 | 0,04815 | 0,04719 | 0,03864 |
| 532,58904 | 0,03655 | 0,04225 | 0,04775 | 0,0473 | 0,03891 |
| 532,62622 | 0,03614 | 0,04236 | 0,04752 | 0,04742 | 0,03926 |
| 532,66341 | 0,03588 | 0,04258 | 0,04744 | 0,04757 | 0,03968 |
| 532,70059 | 0,03574 | 0,04289 | 0,04748 | 0,04775 | 0,04018 |
| 532,73777 | 0,03571 | 0,04325 | 0,04762 | 0,04795 | 0,04075 |
| 532,77495 | 0,03578 | 0,04364 | 0,04786 | 0,0482 | 0,04139 |
| 532,81213 | 0,03591 | 0,04404 | 0,04815 | 0,0485 | 0,04211 |
| 532,84932 | 0,0361 | 0,04442 | 0,04847 | 0,04886 | 0,0429 |
| 532,8865 | 0,03631 | 0,04476 | 0,04881 | 0,04928 | 0,04378 |
| 532,92368 | 0,03652 | 0,04502 | 0,04913 | 0,04978 | 0,04474 |
| 532,96086 | 0,03672 | 0,0452 | 0,04942 | 0,05033 | 0,04577 |
| 532,99804 | 0,03688 | 0,04528 | 0,04965 | 0,05093 | 0,04687 |
| 533,03523 | 0,03699 | 0,04525 | 0,04981 | 0,05157 | 0,04801 |
| 533,07241 | 0,03703 | 0,04511 | 0,04987 | 0,05223 | 0,04918 |
| 533,10959 | 0,037 | 0,04484 | 0,04984 | 0,05289 | 0,05037 |
| 533,14677 | 0,03689 | 0,04446 | 0,04969 | 0,05353 | 0,05154 |
| 533,18395 | 0,03668 | 0,04398 | 0,04943 | 0,05412 | 0,05268 |
| 533,22114 | 0,03638 | 0,04338 | 0,04903 | 0,05464 | 0,05375 |
| 533,25832 | 0,03601 | 0,04272 | 0,04851 | 0,05508 | 0,05473 |
| 533,2955 | 0,03558 | 0,042 | 0,0479 | 0,05542 | 0,05563 |
| 533,33268 | 0,0351 | 0,04125 | 0,04719 | 0,05566 | 0,05642 |
| 533,36986 | 0,03459 | 0,04051 | 0,04641 | 0,0558 | 0,05713 |
| 533,40705 | 0,0341 | 0,03979 | 0,04558 | 0,05586 | 0,05775 |
| 533,44423 | 0,03363 | 0,03913 | 0,04472 | 0,05585 | 0,05831 |
| 533,48141 | 0,03322 | 0,03856 | 0,04388 | 0,0558 | 0,05882 |
| 533,51859 | 0,03292 | 0,03812 | 0,04307 | 0,05573 | 0,05932 |
| 533,55577 | 0,03276 | 0,03784 | 0,04235 | 0,05568 | 0,05983 |
| 533,59295 | 0,03276 | 0,03773 | 0,04173 | 0,05568 | 0,06038 |
| 533,63014 | 0,03294 | 0,0378 | 0,04124 | 0,05575 | 0,06098 |
| 533,66732 | 0,03332 | 0,03807 | 0,0409 | 0,05588 | 0,06163 |
| 533,7045 | 0,0339 | 0,03855 | 0,04073 | 0,05609 | 0,06232 |
| 533,74168 | 0,03468 | 0,03922 | 0,04073 | 0,05636 | 0,06302 |
| 533,77886 | 0,03565 | 0,04008 | 0,04089 | 0,05666 | 0,06371 |
| 533,81605 | 0,03679 | 0,04112 | 0,04122 | 0,05695 | 0,06433 |
| 533,85323 | 0,03807 | 0,0423 | 0,0417 | 0,05719 | 0,0648 |
| 533,89041 | 0,03944 | 0,04359 | 0,04229 | 0,05729 | 0,06506 |
| 533,92759 | 0,04084 | 0,04492 | 0,04295 | 0,05721 | 0,06505 |
| 533,96477 | 0,04221 | 0,04626 | 0,04365 | 0,05689 | 0,06472 |
| 534,00196 | 0,04348 | 0,04754 | 0,04433 | 0,0563 | 0,06401 |
| 534,03914 | 0,04461 | 0,04872 | 0,04496 | 0,05539 | 0,06291 |
| 534,07632 | 0,04553 | 0,04975 | 0,0455 | 0,05415 | 0,06141 |
| 534,1135 | 0,04618 | 0,05057 | 0,04589 | 0,05258 | 0,05951 |
| 534,15068 | 0,04654 | 0,05112 | 0,0461 | 0,0507 | 0,05724 |
| 534,18787 | 0,04656 | 0,05134 | 0,04608 | 0,0485 | 0,05462 |
| 534,22505 | 0,04618 | 0,05124 | 0,04583 | 0,04608 | 0,05175 |
| 534,26223 | 0,04545 | 0,0508 | 0,04533 | 0,0435 | 0,04871 |
| 534,29941 | 0,04437 | 0,05003 | 0,04458 | 0,04084 | 0,0456 |
| 534,33659 | 0,04299 | 0,04892 | 0,0436 | 0,03816 | 0,04249 |
| 534,37378 | 0,04133 | 0,04751 | 0,04238 | 0,03554 | 0,03947 |
| 534,41096 | 0,03944 | 0,04582 | 0,04097 | 0,03304 | 0,0366 |
| 534,44814 | 0,03737 | 0,04389 | 0,03938 | 0,03071 | 0,03396 |
| 534,48532 | 0,03519 | 0,04176 | 0,03764 | 0,02862 | 0,03158 |
| 534,5225 | 0,03294 | 0,03951 | 0,0358 | 0,02681 | 0,02955 |
| 534,55969 | 0,0307 | 0,0372 | 0,03393 | 0,02531 | 0,02786 |
| 534,59687 | 0,02852 | 0,03488 | 0,03205 | 0,02409 | 0,0265 |
| 534,63405 | 0,02646 | 0,03261 | 0,0302 | 0,02315 | 0,02545 |
| 534,67123 | 0,02454 | 0,03042 | 0,02842 | 0,02248 | 0,02469 |
| 534,70841 | 0,02279 | 0,02836 | 0,02675 | 0,02205 | 0,0242 |
| 534,7456 | 0,02125 | 0,02646 | 0,02521 | 0,02182 | 0,02392 |
| 534,78278 | 0,01992 | 0,02476 | 0,02382 | 0,02176 | 0,02381 |
| 534,81996 | 0,0188 | 0,02328 | 0,02261 | 0,02182 | 0,02383 |
| 534,85714 | 0,0179 | 0,02201 | 0,02158 | 0,02197 | 0,02392 |
| 534,89432 | 0,01722 | 0,02094 | 0,02072 | 0,02214 | 0,02403 |
| 534,93151 | 0,01673 | 0,02006 | 0,02002 | 0,0223 | 0,02411 |
| 534,96869 | 0,01639 | 0,01936 | 0,01947 | 0,02241 | 0,02412 |
| 535,00587 | 0,0162 | 0,01882 | 0,01906 | 0,02245 | 0,02404 |
| 535,04305 | 0,0161 | 0,0184 | 0,01876 | 0,02238 | 0,02384 |
| 535,08023 | 0,01609 | 0,01809 | 0,01855 | 0,02219 | 0,02351 |
| 535,11742 | 0,01612 | 0,01787 | 0,01841 | 0,02189 | 0,02305 |
| 535,1546 | 0,01618 | 0,01769 | 0,01832 | 0,02145 | 0,02245 |
| 535,19178 | 0,01623 | 0,01753 | 0,01824 | 0,02087 | 0,02171 |
| 535,22896 | 0,01624 | 0,01738 | 0,01815 | 0,02019 | 0,02086 |
| 535,26614 | 0,0162 | 0,0172 | 0,01804 | 0,01942 | 0,01994 |
| 535,30333 | 0,0161 | 0,01699 | 0,01789 | 0,01857 | 0,01895 |
| 535,34051 | 0,01591 | 0,01674 | 0,01769 | 0,01768 | 0,01792 |
| 535,37769 | 0,01564 | 0,01644 | 0,01743 | 0,01675 | 0,01688 |
| 535,41487 | 0,01528 | 0,01608 | 0,0171 | 0,01581 | 0,01584 |
| 535,45205 | 0,01484 | 0,01566 | 0,01669 | 0,01488 | 0,01483 |
| 535,48924 | 0,01432 | 0,01519 | 0,01621 | 0,01398 | 0,01386 |
| 535,52642 | 0,01373 | 0,01468 | 0,01568 | 0,01313 | 0,01294 |
| 535,5636 | 0,01308 | 0,01413 | 0,01509 | 0,01233 | 0,01209 |
| 535,60078 | 0,01239 | 0,01354 | 0,01446 | 0,0116 | 0,0113 |
| 535,63796 | 0,01167 | 0,01294 | 0,01379 | 0,01093 | 0,01059 |
| 535,67515 | 0,01093 | 0,01233 | 0,01311 | 0,01032 | 0,00993 |
| 535,71233 | 0,0102 | 0,01171 | 0,0124 | 0,00978 | 0,00934 |
| 535,74951 | 0,00948 | 0,01109 | 0,0117 | 0,00931 | 0,00882 |
| 535,78669 | 0,00878 | 0,01049 | 0,01101 | 0,00889 | 0,00835 |
| 535,82387 | 0,00812 | 0,00991 | 0,01033 | 0,00852 | 0,00793 |
| 535,86106 | 0,00749 | 0,00936 | 0,00968 | 0,00821 | 0,00757 |
| 535,89824 | 0,0069 | 0,00882 | 0,00906 | 0,00793 | 0,00725 |
| 535,93542 | 0,00637 | 0,00832 | 0,00847 | 0,00768 | 0,00697 |
| 535,9726 | 0,00588 | 0,00785 | 0,00792 | 0,00746 | 0,00672 |
| 536,00978 | 0,00543 | 0,00741 | 0,00741 | 0,00727 | 0,00651 |
| 536,04697 | 0,00503 | 0,007 | 0,00693 | 0,00709 | 0,00633 |
| 536,08415 | 0,00466 | 0,00662 | 0,00649 | 0,00693 | 0,00617 |
| 536,12133 | 0,00433 | 0,00628 | 0,00609 | 0,00677 | 0,00604 |
| 536,15851 | 0,00403 | 0,00596 | 0,00573 | 0,00663 | 0,00593 |
| 536,19569 | 0,00375 | 0,00568 | 0,00539 | 0,0065 | 0,00584 |
| 536,23288 | 0,0035 | 0,00541 | 0,00508 | 0,00638 | 0,00577 |
| 536,27006 | 0,00328 | 0,00518 | 0,00479 | 0,00626 | 0,00571 |
| 536,30724 | 0,00307 | 0,00496 | 0,00453 | 0,00614 | 0,00566 |
| 536,34442 | 0,00288 | 0,00477 | 0,00428 | 0,00603 | 0,00562 |
| 536,3816 | 0,0027 | 0,00461 | 0,00406 | 0,00592 | 0,00558 |
| 536,41879 | 0,00254 | 0,00446 | 0,00385 | 0,00581 | 0,00555 |
| 536,45597 | 0,0024 | 0,00433 | 0,00365 | 0,0057 | 0,00552 |
| 536,49315 | 0,00227 | 0,00422 | 0,00347 | 0,00558 | 0,00548 |
| 536,53033 | 0,00216 | 0,00411 | 0,0033 | 0,00545 | 0,00543 |
| 536,56751 | 0,00206 | 0,00403 | 0,00314 | 0,00532 | 0,00538 |
| 536,6047 | 0,00198 | 0,00395 | 0,00299 | 0,00517 | 0,00531 |
| 536,64188 | 0,00192 | 0,00388 | 0,00285 | 0,00502 | 0,00523 |
| 536,67906 | 0,00188 | 0,00381 | 0,00272 | 0,00485 | 0,00514 |
| 536,71624 | 0,00185 | 0,00375 | 0,0026 | 0,00467 | 0,00503 |
| 536,75342 | 0,00184 | 0,00369 | 0,00248 | 0,00449 | 0,00491 |
| 536,79061 | 0,00184 | 0,00364 | 0,00238 | 0,0043 | 0,00478 |
| 536,82779 | 0,00185 | 0,00358 | 0,00227 | 0,00412 | 0,00463 |
| 536,86497 | 0,00187 | 0,00351 | 0,00218 | 0,00393 | 0,00447 |
| 536,90215 | 0,0019 | 0,00345 | 0,00209 | 0,00375 | 0,00431 |
| 536,93933 | 0,00193 | 0,00338 | 0,002 | 0,00357 | 0,00413 |
| 536,97652 | 0,00196 | 0,0033 | 0,00193 | 0,00341 | 0,00395 |
| 537,0137 | 0,00199 | 0,00323 | 0,00185 | 0,00326 | 0,00376 |
| 537,05088 | 0,00201 | 0,00314 | 0,00179 | 0,00312 | 0,00357 |
| 537,08806 | 0,00203 | 0,00306 | 0,00173 | 0,003 | 0,00338 |
| 537,12524 | 0,00204 | 0,00297 | 0,00169 | 0,00289 | 0,00319 |
| 537,16243 | 0,00205 | 0,00288 | 0,00165 | 0,0028 | 0,003 |
| 537,19961 | 0,00205 | 0,00279 | 0,00162 | 0,00271 | 0,00281 |
| 537,23679 | 0,00204 | 0,0027 | 0,0016 | 0,00264 | 0,00263 |
| 537,27397 | 0,00202 | 0,00261 | 0,0016 | 0,00258 | 0,00246 |
| 537,31115 | 0,00201 | 0,00252 | 0,00161 | 0,00252 | 0,00229 |
| 537,34834 | 0,00199 | 0,00244 | 0,00162 | 0,00246 | 0,00213 |
| 537,38552 | 0,00197 | 0,00237 | 0,00165 | 0,00241 | 0,00198 |
| 537,4227 | 0,00195 | 0,00229 | 0,00168 | 0,00237 | 0,00184 |
| 537,45988 | 0,00193 | 0,00223 | 0,00172 | 0,00232 | 0,0017 |
| 537,49706 | 0,00191 | 0,00216 | 0,00177 | 0,00228 | 0,00158 |
| 537,53425 | 0,0019 | 0,00211 | 0,00181 | 0,00223 | 0,00146 |
| 537,57143 | 0,00189 | 0,00205 | 0,00186 | 0,00219 | 0,00136 |
| 537,60861 | 0,00187 | 0,002 | 0,0019 | 0,00214 | 0,00126 |
| 537,64579 | 0,00186 | 0,00195 | 0,00194 | 0,0021 | 0,00117 |
| 537,68297 | 0,00185 | 0,0019 | 0,00196 | 0,00206 | 0,00109 |
| 537,72016 | 0,00183 | 0,00186 | 0,00197 | 0,00202 | 0,00102 |
| 537,75734 | 0,00181 | 0,00181 | 0,00198 | 0,00197 | 0,00096 |
| 537,79452 | 0,00179 | 0,00176 | 0,00196 | 0,00193 | 9e-04 |
| 537,8317 | 0,00176 | 0,00172 | 0,00194 | 0,00188 | 0,00085 |
| 537,86888 | 0,00173 | 0,00167 | 0,0019 | 0,00184 | 0,00081 |
| 537,90607 | 0,0017 | 0,00161 | 0,00184 | 0,00179 | 0,00078 |
| 537,94325 | 0,00166 | 0,00156 | 0,00177 | 0,00174 | 0,00075 |
| 537,98043 | 0,00162 | 0,0015 | 0,00169 | 0,00169 | 0,00074 |
| 538,01761 | 0,00157 | 0,00144 | 0,00161 | 0,00164 | 0,00072 |
| 538,05479 | 0,00153 | 0,00138 | 0,00151 | 0,00158 | 0,00071 |
| 538,09198 | 0,00149 | 0,00132 | 0,00141 | 0,00152 | 0,00071 |
| 538,12916 | 0,00144 | 0,00125 | 0,0013 | 0,00145 | 7e-04 |
| 538,16634 | 0,0014 | 0,00118 | 0,0012 | 0,00139 | 7e-04 |
| 538,20352 | 0,00137 | 0,00112 | 0,0011 | 0,00131 | 7e-04 |
| 538,2407 | 0,00133 | 0,00105 | 0,001 | 0,00124 | 0,00069 |
| 538,27789 | 0,0013 | 0,00099 | 9e-04 | 0,00117 | 0,00068 |
| 538,31507 | 0,00127 | 0,00093 | 0,00081 | 0,00109 | 0,00067 |
| 538,35225 | 0,00125 | 0,00087 | 0,00073 | 0,00101 | 0,00065 |
| 538,38943 | 0,00122 | 0,00081 | 0,00066 | 0,00093 | 0,00063 |
| 538,42661 | 0,0012 | 0,00076 | 6e-04 | 0,00085 | 6e-04 |
| 538,4638 | 0,00117 | 0,00072 | 0,00054 | 0,00077 | 0,00057 |
| 538,50098 | 0,00115 | 0,00068 | 0,00049 | 7e-04 | 0,00053 |
| 538,53816 | 0,00112 | 0,00064 | 0,00045 | 0,00062 | 0,00049 |
| 538,57534 | 0,00108 | 0,00061 | 0,00042 | 0,00055 | 0,00045 |
| 538,61252 | 0,00104 | 0,00059 | 0,00039 | 0,00048 | 0,00041 |
| 538,64971 | 0,001 | 0,00057 | 0,00036 | 0,00042 | 0,00036 |
| 538,68689 | 0,00095 | 0,00055 | 0,00034 | 0,00036 | 0,00032 |
| 538,72407 | 9e-04 | 0,00053 | 0,00033 | 0,00031 | 0,00029 |
| 538,76125 | 0,00085 | 0,00052 | 0,00032 | 0,00026 | 0,00025 |
| 538,79843 | 8e-04 | 0,00051 | 0,00031 | 0,00022 | 0,00022 |
| 538,83562 | 0,00074 | 0,00049 | 3e-04 | 0,00018 | 0,00019 |
| 538,8728 | 0,00069 | 0,00048 | 3e-04 | 0,00015 | 0,00017 |
| 538,90998 | 0,00064 | 0,00047 | 0,00029 | 0,00012 | 0,00016 |
| 538,94716 | 0,00059 | 0,00046 | 3e-04 | 1e-04 | 0,00014 |
| 538,98434 | 0,00054 | 0,00046 | 3e-04 | 8e-05 | 0,00014 |
| 539,02153 | 5e-04 | 0,00045 | 3e-04 | 6e-05 | 0,00013 |
| 539,05871 | 0,00046 | 0,00045 | 0,00031 | 5e-05 | 0,00013 |
| 539,09589 | 0,00043 | 0,00044 | 0,00031 | 5e-05 | 0,00013 |
| 539,13307 | 4e-04 | 0,00044 | 0,00032 | 4e-05 | 0,00014 |
| 539,17025 | 0,00038 | 0,00044 | 0,00032 | 4e-05 | 0,00014 |
| 539,20744 | 0,00036 | 0,00045 | 0,00033 | 4e-05 | 0,00015 |
| 539,24462 | 0,00034 | 0,00046 | 0,00033 | 4e-05 | 0,00015 |
| 539,2818 | 0,00033 | 0,00047 | 0,00034 | 5e-05 | 0,00016 |
| 539,31898 | 0,00031 | 0,00048 | 0,00034 | 6e-05 | 0,00016 |
| 539,35616 | 3e-04 | 0,00049 | 0,00034 | 6e-05 | 0,00016 |
| 539,39335 | 0,00029 | 0,00051 | 0,00033 | 7e-05 | 0,00016 |
| 539,43053 | 0,00028 | 0,00053 | 0,00032 | 8e-05 | 0,00016 |
| 539,46771 | 0,00027 | 0,00054 | 0,00031 | 9e-05 | 0,00015 |
| 539,50489 | 0,00025 | 0,00056 | 3e-04 | 0,00011 | 0,00015 |
| 539,54207 | 0,00024 | 0,00057 | 0,00028 | 0,00012 | 0,00014 |
| 539,57926 | 0,00023 | 0,00059 | 0,00026 | 0,00013 | 0,00013 |
| 539,61644 | 0,00021 | 0,00059 | 0,00024 | 0,00014 | 0,00012 |
| 539,65362 | 0,00019 | 6e-04 | 0,00022 | 0,00015 | 0,00011 |
| 539,6908 | 0,00018 | 6e-04 | 2e-04 | 0,00015 | 9e-05 |
| 539,72798 | 0,00016 | 0,00059 | 0,00017 | 0,00016 | 8e-05 |
| 539,76517 | 0,00014 | 0,00058 | 0,00015 | 0,00016 | 7e-05 |
| 539,80235 | 0,00013 | 0,00056 | 0,00013 | 0,00016 | 6e-05 |
| 539,83953 | 0,00011 | 0,00054 | 0,00011 | 0,00015 | 5e-05 |
| 539,87671 | 9e-05 | 0,00051 | 9e-05 | 0,00015 | 4e-05 |
| 539,91389 | 8e-05 | 0,00048 | 8e-05 | 0,00014 | 3e-05 |
| 539,95108 | 7e-05 | 0,00045 | 6e-05 | 0,00014 | 3e-05 |
| 539,98826 | 5e-05 | 0,00041 | 5e-05 | 0,00013 | 2e-05 |
| 540,02544 | 4e-05 | 0,00037 | 4e-05 | 0,00012 | 2e-05 |
| 540,06262 | 3e-05 | 0,00034 | 3e-05 | 0,00011 | 1e-05 |
| 540,0998 | 3e-05 | 3e-04 | 2e-05 | 1e-04 | 1e-05 |
| 540,13699 | 2e-05 | 0,00026 | 2e-05 | 9e-05 | 1e-05 |
| 540,17417 | 2e-05 | 0,00023 | 1e-05 | 8e-05 | 0 |
| 540,21135 | 1e-05 | 0,00019 | 1e-05 | 8e-05 | 0 |
| 540,24853 | 1e-05 | 0,00016 | 1e-05 | 8e-05 | 0 |
| 540,28571 | 1e-05 | 0,00014 | 1e-05 | 7e-05 | 0 |
| 540,3229 | 0 | 0,00011 | 0 | 8e-05 | 0 |
| 540,36008 | 0 | 9e-05 | 0 | 8e-05 | 0 |
| 540,39726 | 0 | 7e-05 | 0 | 8e-05 | 0 |
| 540,43444 | 0 | 6e-05 | 0 | 9e-05 | 0 |
| 540,47162 | 0 | 5e-05 | 0 | 1e-04 | 0 |
| 540,50881 | 0 | 4e-05 | 0 | 0,00011 | 0 |
| 540,54599 | 0 | 3e-05 | 0 | 0,00012 | 0 |
| 540,58317 | 0 | 2e-05 | 0 | 0,00013 | 0 |
| 540,62035 | 0 | 2e-05 | 0 | 0,00014 | 0 |
| 540,65753 | 0 | 1e-05 | 0 | 0,00014 | 0 |
| 540,69472 | 0 | 1e-05 | 0 | 0,00015 | 0 |
| 540,7319 | 0 | 1e-05 | 0 | 0,00015 | 0 |
| 540,76908 | 0 | 0 | 0 | 0,00016 | 0 |
| 540,80626 | 0 | 0 | 0 | 0,00016 | 0 |
| 540,84344 | 0 | 0 | 0 | 0,00016 | 0 |
| 540,88063 | 0 | 0 | 0 | 0,00015 | 0 |
| 540,91781 | 0 | 0 | 0 | 0,00015 | 0 |
| 540,95499 | 0 | 0 | 0 | 0,00014 | 0 |
| 540,99217 | 0 | 0 | 0 | 0,00013 | 0 |
| 541,02935 | 0 | 0 | 0 | 0,00012 | 0 |
| 541,06654 | 0 | 0 | 0 | 0,00011 | 0 |
| 541,10372 | 0 | 0 | 0 | 9e-05 | 0 |
| 541,1409 | 0 | 0 | 0 | 8e-05 | 0 |
| 541,17808 | 0 | 0 | 0 | 7e-05 | 0 |
| 541,21526 | 0 | 0 | 0 | 6e-05 | 0 |
| 541,25245 | 0 | 0 | 0 | 5e-05 | 0 |
| 541,28963 | 0 | 0 | 0 | 4e-05 | 0 |
| 541,32681 | 0 | 0 | 0 | 3e-05 | 0 |
| 541,36399 | 0 | 0 | 0 | 3e-05 | 0 |
| 541,40117 | 0 | 0 | 0 | 2e-05 | 0 |
| 541,43836 | 0 | 0 | 0 | 2e-05 | 0 |
| 541,47554 | 0 | 0 | 0 | 1e-05 | 0 |
| 541,51272 | 0 | 0 | 0 | 1e-05 | 0 |
| 541,5499 | 0 | 0 | 0 | 1e-05 | 0 |
| 541,58708 | 0 | 0 | 0 | 1e-05 | 0 |
| 541,62427 | 0 | 0 | 0 | 0 | 0 |
| 541,66145 | 0 | 0 | 0 | 0 | 0 |
| 541,69863 | 0 | 0 | 0 | 0 | 0 |
| 541,73581 | 0 | 0 | 0 | 0 | 0 |
| 541,77299 | 0 | 0 | 0 | 0 | 0 |
| 541,81018 | 0 | 0 | 0 | 0 | 0 |
| 541,84736 | 0 | 0 | 0 | 0 | 0 |
| 541,88454 | 0 | 0 | 0 | 0 | 0 |
| 541,92172 | 0 | 0 | 0 | 0 | 0 |
| 541,9589 | 0 | 0 | 0 | 0 | 0 |
| 541,99609 | 0 | 0 | 0 | 0 | 0 |
| 542,03327 | 0 | 0 | 0 | 0 | 0 |
| 542,07045 | 0 | 0 | 0 | 0 | 0 |
| 542,10763 | 0 | 0 | 0 | 0 | 0 |
| 542,14481 | 0 | 0 | 0 | 0 | 0 |
| 542,182 | 0 | 0 | 0 | 0 | 0 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 8e-04 | 0,00051 | 0,00033 | 0 | 0 |
| 524,03718 | 0,00086 | 0,00053 | 0,00036 | 0 | 0 |
| 524,07436 | 0,00092 | 0,00055 | 0,00039 | 1e-05 | 0 |
| 524,11155 | 0,00097 | 0,00056 | 0,00042 | 1e-05 | 0 |
| 524,14873 | 0,00101 | 0,00057 | 0,00045 | 1e-05 | 0 |
| 524,18591 | 0,00104 | 0,00057 | 0,00048 | 2e-05 | 0 |
| 524,22309 | 0,00106 | 0,00056 | 5e-04 | 3e-05 | 1e-05 |
| 524,26027 | 0,00108 | 0,00055 | 0,00052 | 4e-05 | 1e-05 |
| 524,29746 | 0,00108 | 0,00053 | 0,00054 | 5e-05 | 1e-05 |
| 524,33464 | 0,00108 | 0,00051 | 0,00057 | 6e-05 | 2e-05 |
| 524,37182 | 0,00107 | 0,00049 | 0,00059 | 8e-05 | 2e-05 |
| 524,409 | 0,00105 | 0,00047 | 0,00061 | 0,00011 | 3e-05 |
| 524,44618 | 0,00102 | 0,00044 | 0,00064 | 0,00014 | 4e-05 |
| 524,48337 | 0,001 | 0,00042 | 0,00067 | 0,00018 | 5e-05 |
| 524,52055 | 0,00097 | 4e-04 | 7e-04 | 0,00022 | 6e-05 |
| 524,55773 | 0,00094 | 0,00039 | 0,00073 | 0,00027 | 8e-05 |
| 524,59491 | 0,00091 | 0,00037 | 0,00076 | 0,00032 | 1e-04 |
| 524,63209 | 0,00088 | 0,00037 | 0,00079 | 0,00038 | 0,00013 |
| 524,66928 | 0,00085 | 0,00037 | 0,00082 | 0,00045 | 0,00015 |
| 524,70646 | 0,00083 | 0,00037 | 0,00084 | 0,00052 | 0,00018 |
| 524,74364 | 0,00081 | 0,00039 | 0,00087 | 0,00059 | 0,00021 |
| 524,78082 | 8e-04 | 4e-04 | 0,00089 | 0,00066 | 0,00024 |
| 524,818 | 0,00079 | 0,00043 | 9e-04 | 0,00074 | 0,00028 |
| 524,85519 | 0,00079 | 0,00046 | 0,00091 | 0,00081 | 0,00031 |
| 524,89237 | 0,00079 | 0,00049 | 0,00092 | 0,00087 | 0,00035 |
| 524,92955 | 8e-04 | 0,00053 | 0,00092 | 0,00093 | 0,00038 |
| 524,96673 | 0,00082 | 0,00057 | 0,00092 | 0,00098 | 0,00041 |
| 525,00391 | 0,00084 | 0,00061 | 0,00092 | 0,00102 | 0,00043 |
| 525,0411 | 0,00087 | 0,00065 | 0,00092 | 0,00105 | 0,00045 |
| 525,07828 | 9e-04 | 0,00069 | 0,00091 | 0,00106 | 0,00046 |
| 525,11546 | 0,00094 | 0,00073 | 0,00091 | 0,00107 | 0,00047 |
| 525,15264 | 0,00098 | 0,00076 | 0,00091 | 0,00106 | 0,00047 |
| 525,18982 | 0,00102 | 0,00079 | 0,00091 | 0,00104 | 0,00046 |
| 525,22701 | 0,00107 | 0,00082 | 0,00091 | 0,001 | 0,00045 |
| 525,26419 | 0,00113 | 0,00084 | 0,00092 | 0,00096 | 0,00043 |
| 525,30137 | 0,00118 | 0,00085 | 0,00093 | 0,00091 | 4e-04 |
| 525,33855 | 0,00124 | 0,00086 | 0,00095 | 0,00086 | 0,00037 |
| 525,37573 | 0,0013 | 0,00087 | 0,00098 | 8e-04 | 0,00034 |
| 525,41292 | 0,00136 | 0,00087 | 0,00101 | 0,00074 | 0,00031 |
| 525,4501 | 0,00143 | 0,00087 | 0,00105 | 0,00068 | 0,00028 |
| 525,48728 | 0,0015 | 0,00087 | 0,0011 | 0,00063 | 0,00024 |
| 525,52446 | 0,00157 | 0,00087 | 0,00115 | 0,00057 | 0,00021 |
| 525,56164 | 0,00165 | 0,00088 | 0,00122 | 0,00052 | 0,00019 |
| 525,59883 | 0,00173 | 0,00089 | 0,00128 | 0,00048 | 0,00017 |
| 525,63601 | 0,00182 | 9e-04 | 0,00136 | 0,00044 | 0,00015 |
| 525,67319 | 0,00192 | 0,00092 | 0,00144 | 0,00041 | 0,00014 |
| 525,71037 | 0,00203 | 0,00096 | 0,00154 | 0,00039 | 0,00013 |
| 525,74755 | 0,00216 | 0,00101 | 0,00163 | 0,00038 | 0,00013 |
| 525,78474 | 0,0023 | 0,00107 | 0,00174 | 0,00037 | 0,00014 |
| 525,82192 | 0,00247 | 0,00117 | 0,00186 | 0,00037 | 0,00016 |
| 525,8591 | 0,00268 | 0,00129 | 0,00199 | 0,00038 | 2e-04 |
| 525,89628 | 0,00291 | 0,00144 | 0,00214 | 0,00041 | 0,00024 |
| 525,93346 | 0,00319 | 0,00164 | 0,00232 | 0,00044 | 3e-04 |
| 525,97065 | 0,00351 | 0,00188 | 0,00251 | 5e-04 | 0,00037 |
| 526,00783 | 0,00389 | 0,00216 | 0,00274 | 0,00057 | 0,00046 |
| 526,04501 | 0,00433 | 0,00251 | 0,00301 | 0,00065 | 0,00057 |
| 526,08219 | 0,00483 | 0,00291 | 0,00331 | 0,00076 | 0,00071 |
| 526,11937 | 0,0054 | 0,00338 | 0,00367 | 9e-04 | 0,00087 |
| 526,15656 | 0,00606 | 0,00391 | 0,00408 | 0,00106 | 0,00107 |
| 526,19374 | 0,00679 | 0,00452 | 0,00455 | 0,00126 | 0,00131 |
| 526,23092 | 0,0076 | 0,00519 | 0,00508 | 0,0015 | 0,00159 |
| 526,2681 | 0,00848 | 0,00592 | 0,00567 | 0,00179 | 0,00192 |
| 526,30528 | 0,00943 | 0,0067 | 0,00633 | 0,00213 | 0,00232 |
| 526,34247 | 0,01043 | 0,00753 | 0,00703 | 0,00253 | 0,00278 |
| 526,37965 | 0,01148 | 0,00839 | 0,00779 | 0,003 | 0,00331 |
| 526,41683 | 0,01255 | 0,00927 | 0,00858 | 0,00355 | 0,00393 |
| 526,45401 | 0,01365 | 0,01017 | 0,00941 | 0,00418 | 0,00464 |
| 526,49119 | 0,01475 | 0,01106 | 0,01024 | 0,00491 | 0,00545 |
| 526,52838 | 0,01582 | 0,01194 | 0,01108 | 0,00574 | 0,00638 |
| 526,56556 | 0,01687 | 0,01279 | 0,01191 | 0,00669 | 0,00741 |
| 526,60274 | 0,01788 | 0,0136 | 0,01272 | 0,00778 | 0,00856 |
| 526,63992 | 0,01884 | 0,01438 | 0,01349 | 0,00899 | 0,00982 |
| 526,6771 | 0,01974 | 0,01511 | 0,01421 | 0,01033 | 0,0112 |
| 526,71429 | 0,0206 | 0,01581 | 0,0149 | 0,01179 | 0,01267 |
| 526,75147 | 0,0214 | 0,01648 | 0,01555 | 0,01338 | 0,01423 |
| 526,78865 | 0,02217 | 0,01713 | 0,01616 | 0,01508 | 0,01586 |
| 526,82583 | 0,02291 | 0,01776 | 0,01674 | 0,01687 | 0,01756 |
| 526,86301 | 0,02364 | 0,01841 | 0,01731 | 0,01873 | 0,01928 |
| 526,9002 | 0,02437 | 0,01908 | 0,01788 | 0,02064 | 0,021 |
| 526,93738 | 0,02512 | 0,01978 | 0,01847 | 0,02256 | 0,02267 |
| 526,97456 | 0,0259 | 0,02053 | 0,01909 | 0,02444 | 0,02428 |
| 527,01174 | 0,02672 | 0,02132 | 0,01975 | 0,02624 | 0,02578 |
| 527,04892 | 0,02757 | 0,02216 | 0,02046 | 0,02792 | 0,02714 |
| 527,08611 | 0,02847 | 0,02305 | 0,02123 | 0,02943 | 0,02832 |
| 527,12329 | 0,02941 | 0,02397 | 0,02204 | 0,03073 | 0,0293 |
| 527,16047 | 0,03038 | 0,02493 | 0,0229 | 0,03179 | 0,03002 |
| 527,19765 | 0,03136 | 0,0259 | 0,02379 | 0,03257 | 0,03048 |
| 527,23483 | 0,03234 | 0,02687 | 0,02471 | 0,03306 | 0,03067 |
| 527,27202 | 0,03332 | 0,02782 | 0,02564 | 0,03322 | 0,03059 |
| 527,3092 | 0,03427 | 0,02875 | 0,02656 | 0,03306 | 0,03026 |
| 527,34638 | 0,03519 | 0,02965 | 0,02745 | 0,03261 | 0,02968 |
| 527,38356 | 0,03608 | 0,03051 | 0,02832 | 0,0319 | 0,02889 |
| 527,42074 | 0,03693 | 0,03133 | 0,02916 | 0,03097 | 0,02792 |
| 527,45793 | 0,03775 | 0,03213 | 0,02996 | 0,02986 | 0,02681 |
| 527,49511 | 0,03854 | 0,03292 | 0,03074 | 0,02862 | 0,02559 |
| 527,53229 | 0,03932 | 0,0337 | 0,0315 | 0,0273 | 0,02432 |
| 527,56947 | 0,0401 | 0,03452 | 0,03225 | 0,02595 | 0,02307 |
| 527,60665 | 0,0409 | 0,03537 | 0,03302 | 0,02464 | 0,02188 |
| 527,64384 | 0,04173 | 0,03629 | 0,03382 | 0,02342 | 0,02078 |
| 527,68102 | 0,04261 | 0,03728 | 0,03467 | 0,02234 | 0,01984 |
| 527,7182 | 0,04355 | 0,03837 | 0,03558 | 0,02145 | 0,01908 |
| 527,75538 | 0,04457 | 0,03957 | 0,03658 | 0,02077 | 0,01853 |
| 527,79256 | 0,04567 | 0,04089 | 0,03768 | 0,02035 | 0,01824 |
| 527,82975 | 0,04686 | 0,04234 | 0,03887 | 0,0202 | 0,01824 |
| 527,86693 | 0,04817 | 0,04392 | 0,04017 | 0,02036 | 0,01856 |
| 527,90411 | 0,04957 | 0,04563 | 0,04159 | 0,02084 | 0,01918 |
| 527,94129 | 0,05109 | 0,04746 | 0,04313 | 0,02165 | 0,02011 |
| 527,97847 | 0,05271 | 0,0494 | 0,0448 | 0,02284 | 0,02136 |
| 528,01566 | 0,05444 | 0,05146 | 0,04659 | 0,02437 | 0,02292 |
| 528,05284 | 0,05627 | 0,05363 | 0,0485 | 0,02623 | 0,02478 |
| 528,09002 | 0,05822 | 0,05589 | 0,05053 | 0,0284 | 0,02692 |
| 528,1272 | 0,06027 | 0,05825 | 0,05267 | 0,03086 | 0,02932 |
| 528,16438 | 0,06243 | 0,06069 | 0,05493 | 0,03358 | 0,03199 |
| 528,20157 | 0,06468 | 0,06322 | 0,05731 | 0,03654 | 0,03488 |
| 528,23875 | 0,06702 | 0,0658 | 0,05979 | 0,03971 | 0,03796 |
| 528,27593 | 0,06944 | 0,06845 | 0,06237 | 0,04304 | 0,0412 |
| 528,31311 | 0,07193 | 0,07113 | 0,06506 | 0,04653 | 0,04459 |
| 528,35029 | 0,07449 | 0,07386 | 0,06784 | 0,05014 | 0,04812 |
| 528,38748 | 0,07711 | 0,07662 | 0,07071 | 0,05384 | 0,05177 |
| 528,42466 | 0,07979 | 0,07941 | 0,07366 | 0,05763 | 0,05555 |
| 528,46184 | 0,08254 | 0,08224 | 0,0767 | 0,06151 | 0,05948 |
| 528,49902 | 0,08536 | 0,08511 | 0,07983 | 0,06551 | 0,06359 |
| 528,5362 | 0,08829 | 0,08803 | 0,08306 | 0,06964 | 0,06791 |
| 528,57339 | 0,09132 | 0,09103 | 0,0864 | 0,07394 | 0,07247 |
| 528,61057 | 0,09448 | 0,09412 | 0,08988 | 0,07845 | 0,07732 |
| 528,64775 | 0,09779 | 0,09732 | 0,09352 | 0,08322 | 0,08249 |
| 528,68493 | 0,10124 | 0,10063 | 0,09734 | 0,08832 | 0,08801 |
| 528,72211 | 0,10486 | 0,10408 | 0,10134 | 0,09376 | 0,09391 |
| 528,7593 | 0,10864 | 0,10765 | 0,10552 | 0,09953 | 0,10017 |
| 528,79648 | 0,11256 | 0,11135 | 0,10985 | 0,10564 | 0,1068 |
| 528,83366 | 0,1166 | 0,11515 | 0,11432 | 0,11204 | 0,11375 |
| 528,87084 | 0,1207 | 0,11902 | 0,11887 | 0,11867 | 0,12093 |
| 528,90802 | 0,12479 | 0,12288 | 0,12345 | 0,12544 | 0,12821 |
| 528,94521 | 0,12881 | 0,12668 | 0,12796 | 0,13223 | 0,13545 |
| 528,98239 | 0,13268 | 0,13034 | 0,13232 | 0,13889 | 0,14251 |
| 529,01957 | 0,13632 | 0,1338 | 0,13638 | 0,14522 | 0,1492 |
| 529,05675 | 0,13965 | 0,13697 | 0,14007 | 0,15104 | 0,15538 |
| 529,09393 | 0,14261 | 0,1398 | 0,1433 | 0,15621 | 0,16087 |
| 529,13112 | 0,14514 | 0,14223 | 0,14599 | 0,1606 | 0,16554 |
| 529,1683 | 0,14715 | 0,14416 | 0,1481 | 0,16411 | 0,16919 |
| 529,20548 | 0,14862 | 0,14558 | 0,14958 | 0,16666 | 0,17173 |
| 529,24266 | 0,1496 | 0,14653 | 0,15045 | 0,16823 | 0,17321 |
| 529,27984 | 0,1501 | 0,14702 | 0,15071 | 0,16883 | 0,17363 |
| 529,31703 | 0,15016 | 0,14709 | 0,15042 | 0,16851 | 0,17307 |
| 529,35421 | 0,14983 | 0,14677 | 0,14962 | 0,16733 | 0,1716 |
| 529,39139 | 0,14917 | 0,14614 | 0,14842 | 0,16543 | 0,16936 |
| 529,42857 | 0,14826 | 0,14526 | 0,14695 | 0,16301 | 0,16647 |
| 529,46575 | 0,14715 | 0,14419 | 0,14532 | 0,1602 | 0,1631 |
| 529,50294 | 0,14592 | 0,143 | 0,1436 | 0,15716 | 0,15938 |
| 529,54012 | 0,14465 | 0,14177 | 0,14189 | 0,154 | 0,1555 |
| 529,5773 | 0,1434 | 0,14055 | 0,14027 | 0,15083 | 0,15161 |
| 529,61448 | 0,1422 | 0,13939 | 0,13878 | 0,14775 | 0,14783 |
| 529,65166 | 0,14111 | 0,13833 | 0,13748 | 0,14482 | 0,14424 |
| 529,68885 | 0,14013 | 0,1374 | 0,13641 | 0,1421 | 0,14093 |
| 529,72603 | 0,13932 | 0,13663 | 0,13561 | 0,13965 | 0,13795 |
| 529,76321 | 0,13869 | 0,13605 | 0,13508 | 0,13749 | 0,13536 |
| 529,80039 | 0,13827 | 0,13569 | 0,13485 | 0,13564 | 0,1332 |
| 529,83757 | 0,13812 | 0,13561 | 0,13494 | 0,13415 | 0,13155 |
| 529,87476 | 0,1383 | 0,13587 | 0,13539 | 0,13304 | 0,13045 |
| 529,91194 | 0,13883 | 0,13649 | 0,13626 | 0,13238 | 0,12993 |
| 529,94912 | 0,13979 | 0,13755 | 0,13759 | 0,13224 | 0,13004 |
| 529,9863 | 0,14122 | 0,1391 | 0,13946 | 0,1327 | 0,13087 |
| 530,02348 | 0,14318 | 0,14121 | 0,14195 | 0,13385 | 0,13247 |
| 530,06067 | 0,14575 | 0,14393 | 0,14521 | 0,13589 | 0,13493 |
| 530,09785 | 0,14895 | 0,14733 | 0,14925 | 0,13885 | 0,13831 |
| 530,13503 | 0,15281 | 0,15142 | 0,15408 | 0,1428 | 0,14266 |
| 530,17221 | 0,15739 | 0,15627 | 0,15971 | 0,14778 | 0,14811 |
| 530,20939 | 0,16264 | 0,16184 | 0,16613 | 0,15382 | 0,15462 |
| 530,24658 | 0,16844 | 0,16801 | 0,17326 | 0,16087 | 0,16207 |
| 530,28376 | 0,17469 | 0,17468 | 0,18099 | 0,16887 | 0,17035 |
| 530,32094 | 0,18124 | 0,18171 | 0,18918 | 0,17766 | 0,17927 |
| 530,35812 | 0,18792 | 0,18892 | 0,19761 | 0,18704 | 0,18863 |
| 530,3953 | 0,19456 | 0,19611 | 0,20604 | 0,19676 | 0,19814 |
| 530,43249 | 0,20093 | 0,20308 | 0,21414 | 0,2064 | 0,20751 |
| 530,46967 | 0,20683 | 0,20958 | 0,22161 | 0,21558 | 0,21637 |
| 530,50685 | 0,21197 | 0,21532 | 0,22819 | 0,22391 | 0,2243 |
| 530,54403 | 0,21611 | 0,22004 | 0,2336 | 0,23105 | 0,23088 |
| 530,58121 | 0,21915 | 0,22362 | 0,23763 | 0,23664 | 0,23588 |
| 530,6184 | 0,22097 | 0,22591 | 0,2401 | 0,24044 | 0,23908 |
| 530,65558 | 0,22148 | 0,22682 | 0,24087 | 0,24222 | 0,24031 |
| 530,69276 | 0,22066 | 0,22632 | 0,23989 | 0,2419 | 0,23953 |
| 530,72994 | 0,21852 | 0,22441 | 0,23709 | 0,23941 | 0,23676 |
| 530,76712 | 0,21513 | 0,22116 | 0,2325 | 0,23472 | 0,2321 |
| 530,80431 | 0,21059 | 0,21668 | 0,22645 | 0,2283 | 0,22576 |
| 530,84149 | 0,20499 | 0,21106 | 0,21917 | 0,22047 | 0,21793 |
| 530,87867 | 0,19858 | 0,20456 | 0,21091 | 0,21159 | 0,20906 |
| 530,91585 | 0,19164 | 0,19747 | 0,20197 | 0,20208 | 0,1996 |
| 530,95303 | 0,18438 | 0,19003 | 0,19263 | 0,19232 | 0,18993 |
| 530,99022 | 0,17702 | 0,18247 | 0,18319 | 0,18272 | 0,18041 |
| 531,0274 | 0,16975 | 0,175 | 0,17394 | 0,17362 | 0,17136 |
| 531,06458 | 0,16279 | 0,16783 | 0,16513 | 0,16533 | 0,16306 |
| 531,10176 | 0,15629 | 0,16114 | 0,15709 | 0,15823 | 0,15572 |
| 531,13894 | 0,15042 | 0,15508 | 0,14996 | 0,15242 | 0,14951 |
| 531,17613 | 0,14536 | 0,14986 | 0,14386 | 0,14791 | 0,14461 |
| 531,21331 | 0,1412 | 0,14557 | 0,13887 | 0,14473 | 0,14105 |
| 531,25049 | 0,13797 | 0,14221 | 0,13506 | 0,14281 | 0,13871 |
| 531,28767 | 0,13569 | 0,13983 | 0,13246 | 0,14207 | 0,13751 |
| 531,32485 | 0,13438 | 0,13844 | 0,13106 | 0,14239 | 0,13736 |
| 531,36204 | 0,13403 | 0,13804 | 0,13087 | 0,14364 | 0,13816 |
| 531,39922 | 0,13462 | 0,13861 | 0,13184 | 0,14567 | 0,1398 |
| 531,4364 | 0,13612 | 0,14013 | 0,13403 | 0,14838 | 0,14217 |
| 531,47358 | 0,13848 | 0,14255 | 0,13733 | 0,15165 | 0,14519 |
| 531,51076 | 0,14169 | 0,14588 | 0,14161 | 0,15534 | 0,14881 |
| 531,54795 | 0,14564 | 0,15 | 0,14679 | 0,15941 | 0,15298 |
| 531,58513 | 0,15019 | 0,15479 | 0,15278 | 0,16381 | 0,15762 |
| 531,62231 | 0,15524 | 0,16013 | 0,15946 | 0,16855 | 0,1627 |
| 531,65949 | 0,16066 | 0,1659 | 0,16671 | 0,17361 | 0,16819 |
| 531,69667 | 0,16633 | 0,17197 | 0,17437 | 0,17899 | 0,17407 |
| 531,73386 | 0,17211 | 0,17816 | 0,18227 | 0,18468 | 0,18026 |
| 531,77104 | 0,17785 | 0,18433 | 0,19021 | 0,19064 | 0,1867 |
| 531,80822 | 0,18338 | 0,19028 | 0,19792 | 0,19681 | 0,19328 |
| 531,8454 | 0,1885 | 0,1958 | 0,20516 | 0,203 | 0,19983 |
| 531,88258 | 0,19302 | 0,20065 | 0,2117 | 0,20906 | 0,20612 |
| 531,91977 | 0,19681 | 0,2047 | 0,21731 | 0,21476 | 0,21193 |
| 531,95695 | 0,19975 | 0,20779 | 0,22178 | 0,21986 | 0,217 |
| 531,99413 | 0,20172 | 0,20979 | 0,22492 | 0,22409 | 0,22111 |
| 532,03131 | 0,20264 | 0,21061 | 0,22659 | 0,2272 | 0,22401 |
| 532,06849 | 0,20245 | 0,21019 | 0,22668 | 0,22895 | 0,2255 |
| 532,10568 | 0,20114 | 0,2085 | 0,22513 | 0,22913 | 0,2254 |
| 532,14286 | 0,19872 | 0,20555 | 0,22175 | 0,22739 | 0,22361 |
| 532,18004 | 0,19517 | 0,20131 | 0,21681 | 0,22382 | 0,21993 |
| 532,21722 | 0,19061 | 0,19592 | 0,21046 | 0,21851 | 0,21442 |
| 532,2544 | 0,18524 | 0,1896 | 0,20288 | 0,21157 | 0,20733 |
| 532,29159 | 0,17919 | 0,18252 | 0,19429 | 0,20319 | 0,19885 |
| 532,32877 | 0,17263 | 0,17484 | 0,18492 | 0,19362 | 0,18922 |
| 532,36595 | 0,16572 | 0,16675 | 0,17501 | 0,18315 | 0,17871 |
| 532,40313 | 0,15861 | 0,15845 | 0,16482 | 0,1721 | 0,16761 |
| 532,44031 | 0,15145 | 0,1501 | 0,15459 | 0,16078 | 0,15622 |
| 532,4775 | 0,14438 | 0,14188 | 0,14456 | 0,14954 | 0,14485 |
| 532,51468 | 0,13755 | 0,13396 | 0,13496 | 0,13872 | 0,1338 |
| 532,55186 | 0,13107 | 0,1265 | 0,12591 | 0,12852 | 0,12336 |
| 532,58904 | 0,125 | 0,11955 | 0,11753 | 0,1191 | 0,11367 |
| 532,62622 | 0,11939 | 0,11319 | 0,10989 | 0,1106 | 0,10486 |
| 532,66341 | 0,11425 | 0,10744 | 0,10302 | 0,10306 | 0,09699 |
| 532,70059 | 0,1096 | 0,10234 | 0,09693 | 0,09651 | 0,09012 |
| 532,73777 | 0,10545 | 0,09787 | 0,09163 | 0,09093 | 0,08422 |
| 532,77495 | 0,10176 | 0,09402 | 0,08707 | 0,08626 | 0,07928 |
| 532,81213 | 0,09854 | 0,09077 | 0,08322 | 0,08246 | 0,07522 |
| 532,84932 | 0,09576 | 0,08811 | 0,08009 | 0,07946 | 0,07203 |
| 532,8865 | 0,0934 | 0,08598 | 0,07752 | 0,07708 | 0,06959 |
| 532,92368 | 0,09139 | 0,08429 | 0,07547 | 0,07522 | 0,06775 |
| 532,96086 | 0,0897 | 0,08301 | 0,07387 | 0,07377 | 0,06641 |
| 532,99804 | 0,08831 | 0,08208 | 0,07267 | 0,07266 | 0,0655 |
| 533,03523 | 0,08718 | 0,08146 | 0,07183 | 0,07179 | 0,06492 |
| 533,07241 | 0,08629 | 0,08112 | 0,07131 | 0,0711 | 0,0646 |
| 533,10959 | 0,08561 | 0,081 | 0,07105 | 0,07053 | 0,06448 |
| 533,14677 | 0,08513 | 0,08109 | 0,07104 | 0,07003 | 0,0645 |
| 533,18395 | 0,08482 | 0,08134 | 0,07125 | 0,06956 | 0,06463 |
| 533,22114 | 0,08466 | 0,08173 | 0,07163 | 0,0691 | 0,06481 |
| 533,25832 | 0,08461 | 0,08222 | 0,07216 | 0,06863 | 0,06503 |
| 533,2955 | 0,08464 | 0,08276 | 0,07281 | 0,06815 | 0,06526 |
| 533,33268 | 0,08474 | 0,08332 | 0,07355 | 0,06766 | 0,06551 |
| 533,36986 | 0,08486 | 0,08389 | 0,07435 | 0,06719 | 0,06578 |
| 533,40705 | 0,08498 | 0,08441 | 0,07518 | 0,06674 | 0,06607 |
| 533,44423 | 0,08507 | 0,08486 | 0,07601 | 0,06634 | 0,06641 |
| 533,48141 | 0,08509 | 0,08521 | 0,07681 | 0,06602 | 0,0668 |
| 533,51859 | 0,08501 | 0,08541 | 0,07751 | 0,06582 | 0,06727 |
| 533,55577 | 0,08478 | 0,08542 | 0,07809 | 0,06576 | 0,06785 |
| 533,59295 | 0,08438 | 0,08523 | 0,07849 | 0,06587 | 0,06853 |
| 533,63014 | 0,08379 | 0,08481 | 0,07868 | 0,06615 | 0,06934 |
| 533,66732 | 0,083 | 0,08415 | 0,07864 | 0,06661 | 0,07027 |
| 533,7045 | 0,08199 | 0,08324 | 0,07833 | 0,06727 | 0,07132 |
| 533,74168 | 0,08076 | 0,08209 | 0,07774 | 0,0681 | 0,07248 |
| 533,77886 | 0,07933 | 0,08069 | 0,07687 | 0,0691 | 0,07374 |
| 533,81605 | 0,07771 | 0,07908 | 0,07572 | 0,07024 | 0,07509 |
| 533,85323 | 0,07592 | 0,07727 | 0,07433 | 0,07149 | 0,07651 |
| 533,89041 | 0,07402 | 0,07532 | 0,07272 | 0,07284 | 0,07798 |
| 533,92759 | 0,07207 | 0,0733 | 0,071 | 0,07424 | 0,07947 |
| 533,96477 | 0,07013 | 0,07128 | 0,06923 | 0,07568 | 0,081 |
| 534,00196 | 0,06828 | 0,06932 | 0,06752 | 0,07714 | 0,08257 |
| 534,03914 | 0,06659 | 0,06751 | 0,06596 | 0,07863 | 0,08419 |
| 534,07632 | 0,06512 | 0,06593 | 0,06464 | 0,08018 | 0,0859 |
| 534,1135 | 0,06394 | 0,06466 | 0,06368 | 0,08181 | 0,08773 |
| 534,15068 | 0,06313 | 0,06376 | 0,06316 | 0,08358 | 0,08973 |
| 534,18787 | 0,06275 | 0,06335 | 0,06318 | 0,08553 | 0,09198 |
| 534,22505 | 0,06287 | 0,06348 | 0,06386 | 0,08775 | 0,09452 |
| 534,26223 | 0,06347 | 0,06416 | 0,06521 | 0,09027 | 0,09736 |
| 534,29941 | 0,06454 | 0,06539 | 0,06722 | 0,09309 | 0,1005 |
| 534,33659 | 0,06606 | 0,06716 | 0,06985 | 0,09622 | 0,10392 |
| 534,37378 | 0,06799 | 0,06942 | 0,07305 | 0,09959 | 0,10755 |
| 534,41096 | 0,07027 | 0,07211 | 0,07675 | 0,10312 | 0,11131 |
| 534,44814 | 0,07281 | 0,07515 | 0,0808 | 0,1067 | 0,11506 |
| 534,48532 | 0,07551 | 0,07842 | 0,08508 | 0,11017 | 0,11866 |
| 534,5225 | 0,07824 | 0,08181 | 0,08941 | 0,11334 | 0,12189 |
| 534,55969 | 0,08087 | 0,08512 | 0,09359 | 0,11598 | 0,12451 |
| 534,59687 | 0,08325 | 0,08821 | 0,09738 | 0,11784 | 0,12637 |
| 534,63405 | 0,08526 | 0,09093 | 0,10061 | 0,11878 | 0,1273 |
| 534,67123 | 0,08682 | 0,09316 | 0,10313 | 0,11867 | 0,12719 |
| 534,70841 | 0,08781 | 0,09476 | 0,10479 | 0,11742 | 0,12595 |
| 534,7456 | 0,08818 | 0,09566 | 0,1055 | 0,115 | 0,12354 |
| 534,78278 | 0,08788 | 0,09578 | 0,10519 | 0,11143 | 0,11998 |
| 534,81996 | 0,0869 | 0,09509 | 0,10384 | 0,1068 | 0,11535 |
| 534,85714 | 0,0852 | 0,09353 | 0,10148 | 0,10124 | 0,10972 |
| 534,89432 | 0,08283 | 0,09115 | 0,09815 | 0,09491 | 0,10329 |
| 534,93151 | 0,07992 | 0,08808 | 0,0939 | 0,08802 | 0,09634 |
| 534,96869 | 0,07656 | 0,08442 | 0,08898 | 0,08089 | 0,08911 |
| 535,00587 | 0,07284 | 0,08028 | 0,08358 | 0,07375 | 0,08181 |
| 535,04305 | 0,0689 | 0,0758 | 0,07785 | 0,0668 | 0,07465 |
| 535,08023 | 0,06482 | 0,07112 | 0,07197 | 0,06024 | 0,06783 |
| 535,11742 | 0,06074 | 0,06636 | 0,06612 | 0,05422 | 0,06152 |
| 535,1546 | 0,05674 | 0,06165 | 0,06045 | 0,04886 | 0,05584 |
| 535,19178 | 0,05294 | 0,05714 | 0,05509 | 0,04424 | 0,05095 |
| 535,22896 | 0,04943 | 0,05294 | 0,05015 | 0,04042 | 0,04693 |
| 535,26614 | 0,04625 | 0,04913 | 0,04578 | 0,03748 | 0,04371 |
| 535,30333 | 0,04344 | 0,04573 | 0,04201 | 0,03533 | 0,04127 |
| 535,34051 | 0,04101 | 0,0428 | 0,03883 | 0,03388 | 0,03957 |
| 535,37769 | 0,03896 | 0,04033 | 0,03625 | 0,03306 | 0,03852 |
| 535,41487 | 0,03728 | 0,03833 | 0,03423 | 0,03279 | 0,03804 |
| 535,45205 | 0,03595 | 0,03677 | 0,03274 | 0,03296 | 0,03802 |
| 535,48924 | 0,03492 | 0,0356 | 0,03172 | 0,03348 | 0,03836 |
| 535,52642 | 0,03418 | 0,03481 | 0,03111 | 0,03423 | 0,03894 |
| 535,5636 | 0,03367 | 0,03432 | 0,03084 | 0,03511 | 0,03963 |
| 535,60078 | 0,0333 | 0,03404 | 0,03084 | 0,03602 | 0,04032 |
| 535,63796 | 0,03304 | 0,03391 | 0,03101 | 0,03684 | 0,04092 |
| 535,67515 | 0,03283 | 0,03387 | 0,03128 | 0,03751 | 0,04134 |
| 535,71233 | 0,03263 | 0,03386 | 0,03155 | 0,03796 | 0,04154 |
| 535,74951 | 0,03241 | 0,03383 | 0,03179 | 0,03816 | 0,04146 |
| 535,78669 | 0,03213 | 0,03373 | 0,03192 | 0,03806 | 0,04108 |
| 535,82387 | 0,03176 | 0,03353 | 0,03193 | 0,03765 | 0,04039 |
| 535,86106 | 0,03128 | 0,03319 | 0,03177 | 0,03695 | 0,03938 |
| 535,89824 | 0,03067 | 0,03269 | 0,03142 | 0,03597 | 0,03807 |
| 535,93542 | 0,02994 | 0,03204 | 0,03088 | 0,03473 | 0,03653 |
| 535,9726 | 0,0291 | 0,03125 | 0,03013 | 0,03326 | 0,0348 |
| 536,00978 | 0,02816 | 0,03031 | 0,0292 | 0,03163 | 0,03293 |
| 536,04697 | 0,02713 | 0,02926 | 0,02814 | 0,0299 | 0,03097 |
| 536,08415 | 0,02603 | 0,0281 | 0,02695 | 0,02811 | 0,02896 |
| 536,12133 | 0,02487 | 0,02687 | 0,02568 | 0,02631 | 0,02696 |
| 536,15851 | 0,02369 | 0,02559 | 0,02435 | 0,02452 | 0,025 |
| 536,19569 | 0,02249 | 0,02427 | 0,023 | 0,0228 | 0,02313 |
| 536,23288 | 0,0213 | 0,02296 | 0,02165 | 0,02115 | 0,02136 |
| 536,27006 | 0,02013 | 0,02167 | 0,02034 | 0,0196 | 0,01971 |
| 536,30724 | 0,01901 | 0,02042 | 0,01909 | 0,01816 | 0,01819 |
| 536,34442 | 0,01793 | 0,01923 | 0,01793 | 0,01685 | 0,0168 |
| 536,3816 | 0,01691 | 0,0181 | 0,01685 | 0,01565 | 0,01553 |
| 536,41879 | 0,01596 | 0,01703 | 0,01586 | 0,01455 | 0,01438 |
| 536,45597 | 0,01506 | 0,01605 | 0,01497 | 0,01356 | 0,01334 |
| 536,49315 | 0,01423 | 0,01514 | 0,01417 | 0,01266 | 0,0124 |
| 536,53033 | 0,01347 | 0,01432 | 0,01346 | 0,01184 | 0,01155 |
| 536,56751 | 0,01277 | 0,01358 | 0,01283 | 0,0111 | 0,01078 |
| 536,6047 | 0,01212 | 0,0129 | 0,01227 | 0,01044 | 0,01008 |
| 536,64188 | 0,01152 | 0,01229 | 0,01177 | 0,00984 | 0,00943 |
| 536,67906 | 0,01097 | 0,01174 | 0,01132 | 0,0093 | 0,00884 |
| 536,71624 | 0,01045 | 0,01124 | 0,01091 | 0,00881 | 0,00829 |
| 536,75342 | 0,00998 | 0,01078 | 0,01052 | 0,00837 | 0,00778 |
| 536,79061 | 0,00954 | 0,01036 | 0,01014 | 0,00797 | 0,00731 |
| 536,82779 | 0,00912 | 0,00996 | 0,00978 | 0,00761 | 0,00688 |
| 536,86497 | 0,00874 | 0,00959 | 0,00942 | 0,00729 | 0,00647 |
| 536,90215 | 0,00839 | 0,00924 | 0,00906 | 0,00699 | 0,00611 |
| 536,93933 | 0,00805 | 0,0089 | 0,00869 | 0,00673 | 0,00576 |
| 536,97652 | 0,00774 | 0,00857 | 0,00832 | 0,00648 | 0,00545 |
| 537,0137 | 0,00744 | 0,00825 | 0,00795 | 0,00625 | 0,00516 |
| 537,05088 | 0,00716 | 0,00793 | 0,00757 | 0,00603 | 0,00489 |
| 537,08806 | 0,00689 | 0,00761 | 0,0072 | 0,00583 | 0,00464 |
| 537,12524 | 0,00662 | 0,0073 | 0,00682 | 0,00563 | 0,00441 |
| 537,16243 | 0,00637 | 0,00699 | 0,00645 | 0,00544 | 0,00419 |
| 537,19961 | 0,00612 | 0,00668 | 0,00609 | 0,00525 | 0,00399 |
| 537,23679 | 0,00587 | 0,00637 | 0,00574 | 0,00507 | 0,00381 |
| 537,27397 | 0,00563 | 0,00608 | 0,0054 | 0,00489 | 0,00363 |
| 537,31115 | 0,00538 | 0,00579 | 0,00507 | 0,00472 | 0,00347 |
| 537,34834 | 0,00515 | 0,00551 | 0,00476 | 0,00456 | 0,00332 |
| 537,38552 | 0,00491 | 0,00524 | 0,00447 | 0,0044 | 0,00317 |
| 537,4227 | 0,00468 | 0,00499 | 0,00419 | 0,00425 | 0,00303 |
| 537,45988 | 0,00445 | 0,00474 | 0,00393 | 0,0041 | 0,0029 |
| 537,49706 | 0,00423 | 0,00451 | 0,00369 | 0,00395 | 0,00277 |
| 537,53425 | 0,00401 | 0,00429 | 0,00346 | 0,00381 | 0,00265 |
| 537,57143 | 0,0038 | 0,00408 | 0,00325 | 0,00367 | 0,00253 |
| 537,60861 | 0,00359 | 0,00387 | 0,00305 | 0,00353 | 0,00241 |
| 537,64579 | 0,00339 | 0,00368 | 0,00287 | 0,00338 | 0,0023 |
| 537,68297 | 0,00319 | 0,0035 | 0,0027 | 0,00323 | 0,0022 |
| 537,72016 | 0,003 | 0,00332 | 0,00255 | 0,00307 | 0,00209 |
| 537,75734 | 0,00281 | 0,00314 | 0,00241 | 0,0029 | 0,00199 |
| 537,79452 | 0,00263 | 0,00297 | 0,00229 | 0,00273 | 0,00189 |
| 537,8317 | 0,00245 | 0,0028 | 0,00217 | 0,00255 | 0,0018 |
| 537,86888 | 0,00228 | 0,00264 | 0,00206 | 0,00237 | 0,0017 |
| 537,90607 | 0,00211 | 0,00248 | 0,00197 | 0,00218 | 0,00161 |
| 537,94325 | 0,00195 | 0,00232 | 0,00188 | 0,002 | 0,00152 |
| 537,98043 | 0,00179 | 0,00217 | 0,00181 | 0,00182 | 0,00144 |
| 538,01761 | 0,00164 | 0,00202 | 0,00174 | 0,00164 | 0,00136 |
| 538,05479 | 0,0015 | 0,00187 | 0,00167 | 0,00148 | 0,00128 |
| 538,09198 | 0,00136 | 0,00174 | 0,00161 | 0,00132 | 0,00121 |
| 538,12916 | 0,00124 | 0,00161 | 0,00156 | 0,00118 | 0,00113 |
| 538,16634 | 0,00113 | 0,00148 | 0,00151 | 0,00104 | 0,00107 |
| 538,20352 | 0,00103 | 0,00137 | 0,00146 | 0,00092 | 0,001 |
| 538,2407 | 0,00094 | 0,00127 | 0,00142 | 0,00081 | 0,00094 |
| 538,27789 | 0,00086 | 0,00117 | 0,00138 | 0,00071 | 0,00088 |
| 538,31507 | 0,00079 | 0,00109 | 0,00134 | 0,00062 | 0,00083 |
| 538,35225 | 0,00073 | 0,00101 | 0,0013 | 0,00055 | 0,00077 |
| 538,38943 | 0,00068 | 0,00094 | 0,00126 | 0,00048 | 0,00072 |
| 538,42661 | 0,00064 | 0,00087 | 0,00123 | 0,00042 | 0,00067 |
| 538,4638 | 6e-04 | 0,00081 | 0,00119 | 0,00036 | 0,00063 |
| 538,50098 | 0,00057 | 0,00076 | 0,00115 | 0,00031 | 0,00058 |
| 538,53816 | 0,00054 | 0,00071 | 0,00111 | 0,00027 | 0,00054 |
| 538,57534 | 0,00051 | 0,00066 | 0,00107 | 0,00023 | 5e-04 |
| 538,61252 | 0,00049 | 0,00062 | 0,00103 | 0,00019 | 0,00046 |
| 538,64971 | 0,00047 | 0,00058 | 0,00098 | 0,00016 | 0,00042 |
| 538,68689 | 0,00044 | 0,00053 | 0,00093 | 0,00013 | 0,00038 |
| 538,72407 | 0,00042 | 0,00049 | 0,00088 | 0,00011 | 0,00035 |
| 538,76125 | 4e-04 | 0,00045 | 0,00082 | 9e-05 | 0,00032 |
| 538,79843 | 0,00038 | 0,00041 | 0,00076 | 7e-05 | 0,00029 |
| 538,83562 | 0,00035 | 0,00038 | 7e-04 | 6e-05 | 0,00027 |
| 538,8728 | 0,00033 | 0,00034 | 0,00064 | 4e-05 | 0,00025 |
| 538,90998 | 3e-04 | 3e-04 | 0,00058 | 3e-05 | 0,00023 |
| 538,94716 | 0,00028 | 0,00027 | 0,00052 | 3e-05 | 0,00022 |
| 538,98434 | 0,00026 | 0,00024 | 0,00045 | 2e-05 | 2e-04 |
| 539,02153 | 0,00023 | 0,00021 | 4e-04 | 1e-05 | 0,00019 |
| 539,05871 | 0,00021 | 0,00018 | 0,00034 | 1e-05 | 0,00019 |
| 539,09589 | 0,00019 | 0,00015 | 0,00029 | 1e-05 | 0,00018 |
| 539,13307 | 0,00017 | 0,00013 | 0,00024 | 0 | 0,00017 |
| 539,17025 | 0,00015 | 0,00011 | 2e-04 | 0 | 0,00017 |
| 539,20744 | 0,00013 | 9e-05 | 0,00016 | 0 | 0,00017 |
| 539,24462 | 0,00011 | 8e-05 | 0,00013 | 0 | 0,00016 |
| 539,2818 | 1e-04 | 7e-05 | 0,00011 | 0 | 0,00016 |
| 539,31898 | 8e-05 | 6e-05 | 8e-05 | 0 | 0,00016 |
| 539,35616 | 7e-05 | 5e-05 | 6e-05 | 0 | 0,00016 |
| 539,39335 | 6e-05 | 5e-05 | 5e-05 | 0 | 0,00017 |
| 539,43053 | 5e-05 | 5e-05 | 4e-05 | 0 | 0,00017 |
| 539,46771 | 4e-05 | 5e-05 | 3e-05 | 0 | 0,00018 |
| 539,50489 | 3e-05 | 5e-05 | 2e-05 | 0 | 0,00018 |
| 539,54207 | 3e-05 | 6e-05 | 1e-05 | 0 | 0,00019 |
| 539,57926 | 2e-05 | 6e-05 | 1e-05 | 0 | 2e-04 |
| 539,61644 | 2e-05 | 7e-05 | 1e-05 | 0 | 0,00021 |
| 539,65362 | 1e-05 | 7e-05 | 0 | 0 | 0,00022 |
| 539,6908 | 1e-05 | 8e-05 | 0 | 0 | 0,00023 |
| 539,72798 | 1e-05 | 9e-05 | 0 | 0 | 0,00024 |
| 539,76517 | 0 | 1e-04 | 0 | 0 | 0,00024 |
| 539,80235 | 0 | 1e-04 | 0 | 0 | 0,00025 |
| 539,83953 | 0 | 0,00011 | 0 | 1e-05 | 0,00025 |
| 539,87671 | 0 | 0,00011 | 0 | 1e-05 | 0,00024 |
| 539,91389 | 0 | 0,00011 | 0 | 1e-05 | 0,00024 |
| 539,95108 | 0 | 0,00011 | 0 | 2e-05 | 0,00023 |
| 539,98826 | 0 | 0,00011 | 0 | 3e-05 | 0,00022 |
| 540,02544 | 0 | 0,00011 | 0 | 4e-05 | 0,00021 |
| 540,06262 | 0 | 1e-04 | 0 | 5e-05 | 0,00019 |
| 540,0998 | 0 | 1e-04 | 0 | 6e-05 | 0,00018 |
| 540,13699 | 0 | 9e-05 | 0 | 8e-05 | 0,00016 |
| 540,17417 | 0 | 8e-05 | 0 | 1e-04 | 0,00014 |
| 540,21135 | 0 | 8e-05 | 0 | 0,00012 | 0,00012 |
| 540,24853 | 0 | 7e-05 | 0 | 0,00014 | 0,00011 |
| 540,28571 | 0 | 6e-05 | 0 | 0,00017 | 9e-05 |
| 540,3229 | 0 | 5e-05 | 0 | 2e-04 | 7e-05 |
| 540,36008 | 0 | 4e-05 | 0 | 0,00023 | 6e-05 |
| 540,39726 | 0 | 4e-05 | 0 | 0,00026 | 5e-05 |
| 540,43444 | 0 | 3e-05 | 0 | 0,00028 | 4e-05 |
| 540,47162 | 0 | 2e-05 | 1e-05 | 0,00031 | 3e-05 |
| 540,50881 | 0 | 2e-05 | 1e-05 | 0,00033 | 2e-05 |
| 540,54599 | 0 | 1e-05 | 1e-05 | 0,00035 | 2e-05 |
| 540,58317 | 0 | 1e-05 | 1e-05 | 0,00037 | 1e-05 |
| 540,62035 | 0 | 1e-05 | 2e-05 | 0,00037 | 1e-05 |
| 540,65753 | 0 | 1e-05 | 2e-05 | 0,00038 | 1e-05 |
| 540,69472 | 0 | 0 | 3e-05 | 0,00037 | 1e-05 |
| 540,7319 | 0 | 0 | 3e-05 | 0,00036 | 0 |
| 540,76908 | 0 | 0 | 4e-05 | 0,00034 | 0 |
| 540,80626 | 0 | 0 | 5e-05 | 0,00032 | 0 |
| 540,84344 | 0 | 0 | 6e-05 | 3e-04 | 0 |
| 540,88063 | 0 | 0 | 7e-05 | 0,00027 | 0 |
| 540,91781 | 0 | 0 | 8e-05 | 0,00024 | 0 |
| 540,95499 | 0 | 0 | 9e-05 | 0,00021 | 0 |
| 540,99217 | 0 | 0 | 1e-04 | 0,00018 | 0 |
| 541,02935 | 0 | 0 | 0,00011 | 0,00016 | 0 |
| 541,06654 | 0 | 0 | 0,00012 | 0,00013 | 0 |
| 541,10372 | 0 | 0 | 0,00012 | 0,00011 | 0 |
| 541,1409 | 0 | 0 | 0,00013 | 9e-05 | 0 |
| 541,17808 | 0 | 0 | 0,00013 | 7e-05 | 0 |
| 541,21526 | 0 | 0 | 0,00013 | 5e-05 | 0 |
| 541,25245 | 0 | 0 | 0,00012 | 4e-05 | 0 |
| 541,28963 | 0 | 0 | 0,00012 | 3e-05 | 0 |
| 541,32681 | 0 | 0 | 0,00011 | 2e-05 | 0 |
| 541,36399 | 0 | 0 | 0,00011 | 2e-05 | 0 |
| 541,40117 | 0 | 0 | 1e-04 | 1e-05 | 0 |
| 541,43836 | 0 | 0 | 9e-05 | 1e-05 | 0 |
| 541,47554 | 0 | 0 | 8e-05 | 1e-05 | 0 |
| 541,51272 | 0 | 0 | 7e-05 | 0 | 0 |
| 541,5499 | 0 | 0 | 6e-05 | 0 | 0 |
| 541,58708 | 0 | 0 | 5e-05 | 0 | 0 |
| 541,62427 | 0 | 0 | 4e-05 | 0 | 0 |
| 541,66145 | 0 | 0 | 3e-05 | 0 | 0 |
| 541,69863 | 0 | 0 | 3e-05 | 0 | 0 |
| 541,73581 | 0 | 0 | 2e-05 | 0 | 0 |
| 541,77299 | 0 | 0 | 2e-05 | 0 | 0 |
| 541,81018 | 0 | 0 | 1e-05 | 0 | 0 |
| 541,84736 | 0 | 0 | 1e-05 | 0 | 0 |
| 541,88454 | 0 | 0 | 1e-05 | 0 | 0 |
| 541,92172 | 0 | 0 | 0 | 0 | 0 |
| 541,9589 | 0 | 0 | 0 | 0 | 0 |
| 541,99609 | 0 | 0 | 0 | 0 | 0 |
| 542,03327 | 0 | 0 | 0 | 0 | 0 |
| 542,07045 | 0 | 0 | 0 | 0 | 0 |
| 542,10763 | 0 | 0 | 0 | 0 | 0 |
| 542,14481 | 0 | 0 | 0 | 0 | 0 |
| 542,182 | 0 | 0 | 0 | 0 | 0 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 0 | 0 | 0 |
| 524,74364 | 0 | 0 | 0 | 0 | 0 |
| 524,78082 | 0 | 0 | 0 | 0 | 0 |
| 524,818 | 0 | 0 | 0 | 0 | 0 |
| 524,85519 | 0 | 0 | 0 | 0 | 0 |
| 524,89237 | 1e-05 | 0 | 0 | 0 | 0 |
| 524,92955 | 1e-05 | 0 | 0 | 0 | 0 |
| 524,96673 | 1e-05 | 0 | 0 | 0 | 0 |
| 525,00391 | 1e-05 | 0 | 1e-05 | 0 | 0 |
| 525,0411 | 2e-05 | 0 | 1e-05 | 0 | 0 |
| 525,07828 | 2e-05 | 0 | 1e-05 | 0 | 0 |
| 525,11546 | 3e-05 | 1e-05 | 1e-05 | 0 | 0 |
| 525,15264 | 3e-05 | 1e-05 | 1e-05 | 0 | 0 |
| 525,18982 | 4e-05 | 1e-05 | 2e-05 | 0 | 0 |
| 525,22701 | 5e-05 | 1e-05 | 2e-05 | 0 | 0 |
| 525,26419 | 6e-05 | 2e-05 | 3e-05 | 0 | 0 |
| 525,30137 | 8e-05 | 2e-05 | 3e-05 | 0 | 0 |
| 525,33855 | 9e-05 | 2e-05 | 4e-05 | 0 | 0 |
| 525,37573 | 0,00011 | 3e-05 | 5e-05 | 0 | 0 |
| 525,41292 | 0,00014 | 4e-05 | 6e-05 | 0 | 0 |
| 525,4501 | 0,00016 | 4e-05 | 7e-05 | 0 | 0 |
| 525,48728 | 0,00019 | 5e-05 | 8e-05 | 0 | 0 |
| 525,52446 | 0,00022 | 7e-05 | 1e-04 | 0 | 0 |
| 525,56164 | 0,00026 | 8e-05 | 0,00011 | 0 | 0 |
| 525,59883 | 3e-04 | 9e-05 | 0,00013 | 0 | 0 |
| 525,63601 | 0,00035 | 0,00011 | 0,00015 | 0 | 0 |
| 525,67319 | 4e-04 | 0,00012 | 0,00017 | 0 | 0 |
| 525,71037 | 0,00046 | 0,00014 | 0,00019 | 0 | 0 |
| 525,74755 | 0,00052 | 0,00016 | 0,00022 | 0 | 0 |
| 525,78474 | 0,00058 | 0,00019 | 0,00024 | 0 | 0 |
| 525,82192 | 0,00065 | 0,00021 | 0,00027 | 0 | 0 |
| 525,8591 | 0,00072 | 0,00024 | 3e-04 | 0 | 0 |
| 525,89628 | 8e-04 | 0,00027 | 0,00033 | 1e-05 | 0 |
| 525,93346 | 0,00088 | 3e-04 | 0,00037 | 1e-05 | 0 |
| 525,97065 | 0,00096 | 0,00033 | 4e-04 | 1e-05 | 0 |
| 526,00783 | 0,00104 | 0,00036 | 0,00043 | 1e-05 | 0 |
| 526,04501 | 0,00112 | 4e-04 | 0,00047 | 2e-05 | 0 |
| 526,08219 | 0,00119 | 0,00043 | 0,00051 | 2e-05 | 0 |
| 526,11937 | 0,00127 | 0,00047 | 0,00054 | 2e-05 | 0 |
| 526,15656 | 0,00134 | 0,00051 | 0,00058 | 3e-05 | 0 |
| 526,19374 | 0,00141 | 0,00055 | 0,00063 | 4e-05 | 0 |
| 526,23092 | 0,00147 | 0,00059 | 0,00067 | 4e-05 | 0 |
| 526,2681 | 0,00152 | 0,00063 | 0,00071 | 5e-05 | 0 |
| 526,30528 | 0,00157 | 0,00067 | 0,00076 | 6e-05 | 0 |
| 526,34247 | 0,00161 | 0,00071 | 0,00081 | 7e-05 | 0 |
| 526,37965 | 0,00163 | 0,00075 | 0,00086 | 9e-05 | 0 |
| 526,41683 | 0,00165 | 8e-04 | 0,00092 | 1e-04 | 0 |
| 526,45401 | 0,00166 | 0,00084 | 0,00098 | 0,00011 | 0 |
| 526,49119 | 0,00166 | 0,00089 | 0,00104 | 0,00013 | 0 |
| 526,52838 | 0,00165 | 0,00094 | 0,00111 | 0,00015 | 0 |
| 526,56556 | 0,00162 | 0,00099 | 0,00119 | 0,00017 | 1e-05 |
| 526,60274 | 0,00159 | 0,00105 | 0,00127 | 0,00018 | 1e-05 |
| 526,63992 | 0,00156 | 0,0011 | 0,00136 | 2e-04 | 1e-05 |
| 526,6771 | 0,00151 | 0,00116 | 0,00145 | 0,00022 | 1e-05 |
| 526,71429 | 0,00146 | 0,00123 | 0,00154 | 0,00024 | 2e-05 |
| 526,75147 | 0,0014 | 0,00129 | 0,00165 | 0,00026 | 3e-05 |
| 526,78865 | 0,00134 | 0,00136 | 0,00175 | 0,00028 | 3e-05 |
| 526,82583 | 0,00128 | 0,00144 | 0,00186 | 3e-04 | 4e-05 |
| 526,86301 | 0,00122 | 0,00151 | 0,00198 | 0,00031 | 6e-05 |
| 526,9002 | 0,00116 | 0,00159 | 0,0021 | 0,00033 | 8e-05 |
| 526,93738 | 0,0011 | 0,00168 | 0,00222 | 0,00034 | 1e-04 |
| 526,97456 | 0,00105 | 0,00177 | 0,00234 | 0,00036 | 0,00013 |
| 527,01174 | 0,00101 | 0,00186 | 0,00246 | 0,00038 | 0,00016 |
| 527,04892 | 0,00097 | 0,00196 | 0,00259 | 0,00039 | 0,00021 |
| 527,08611 | 0,00095 | 0,00206 | 0,00271 | 0,00041 | 0,00026 |
| 527,12329 | 0,00094 | 0,00216 | 0,00284 | 0,00043 | 0,00033 |
| 527,16047 | 0,00095 | 0,00227 | 0,00296 | 0,00045 | 0,00041 |
| 527,19765 | 0,00098 | 0,00239 | 0,00309 | 0,00047 | 5e-04 |
| 527,23483 | 0,00103 | 0,00251 | 0,00321 | 0,00051 | 0,00061 |
| 527,27202 | 0,00111 | 0,00264 | 0,00334 | 0,00054 | 0,00074 |
| 527,3092 | 0,00121 | 0,00277 | 0,00347 | 0,00059 | 0,00089 |
| 527,34638 | 0,00134 | 0,00292 | 0,0036 | 0,00065 | 0,00106 |
| 527,38356 | 0,00151 | 0,00308 | 0,00373 | 0,00072 | 0,00126 |
| 527,42074 | 0,00171 | 0,00325 | 0,00387 | 8e-04 | 0,00148 |
| 527,45793 | 0,00195 | 0,00343 | 0,00402 | 9e-04 | 0,00174 |
| 527,49511 | 0,00223 | 0,00364 | 0,00418 | 0,00102 | 0,00202 |
| 527,53229 | 0,00256 | 0,00387 | 0,00435 | 0,00115 | 0,00233 |
| 527,56947 | 0,00294 | 0,00412 | 0,00452 | 0,00131 | 0,00266 |
| 527,60665 | 0,00337 | 0,0044 | 0,00472 | 0,0015 | 0,00303 |
| 527,64384 | 0,00385 | 0,0047 | 0,00492 | 0,0017 | 0,00343 |
| 527,68102 | 0,00437 | 0,00504 | 0,00515 | 0,00194 | 0,00387 |
| 527,7182 | 0,00496 | 0,00542 | 0,0054 | 0,0022 | 0,00433 |
| 527,75538 | 0,0056 | 0,00584 | 0,00567 | 0,00248 | 0,00482 |
| 527,79256 | 0,00631 | 0,00629 | 0,00596 | 0,0028 | 0,00534 |
| 527,82975 | 0,00706 | 0,0068 | 0,00628 | 0,00315 | 0,00588 |
| 527,86693 | 0,00787 | 0,00734 | 0,00663 | 0,00353 | 0,00645 |
| 527,90411 | 0,00872 | 0,00793 | 0,007 | 0,00395 | 0,00704 |
| 527,94129 | 0,00962 | 0,00856 | 0,0074 | 0,0044 | 0,00767 |
| 527,97847 | 0,01057 | 0,00924 | 0,00784 | 0,00488 | 0,00832 |
| 528,01566 | 0,01156 | 0,00997 | 0,00831 | 0,0054 | 0,00899 |
| 528,05284 | 0,01259 | 0,01074 | 0,00881 | 0,00596 | 0,00969 |
| 528,09002 | 0,01364 | 0,01155 | 0,00933 | 0,00656 | 0,01041 |
| 528,1272 | 0,01471 | 0,01239 | 0,00989 | 0,00721 | 0,01116 |
| 528,16438 | 0,01581 | 0,01326 | 0,01048 | 0,0079 | 0,01194 |
| 528,20157 | 0,01692 | 0,01416 | 0,0111 | 0,00863 | 0,01276 |
| 528,23875 | 0,01803 | 0,01509 | 0,01176 | 0,00941 | 0,0136 |
| 528,27593 | 0,01915 | 0,01603 | 0,01244 | 0,01024 | 0,01447 |
| 528,31311 | 0,02026 | 0,01699 | 0,01315 | 0,01111 | 0,01537 |
| 528,35029 | 0,02137 | 0,01795 | 0,01389 | 0,01205 | 0,0163 |
| 528,38748 | 0,02247 | 0,01891 | 0,01466 | 0,01303 | 0,01725 |
| 528,42466 | 0,02356 | 0,01987 | 0,01546 | 0,01406 | 0,01824 |
| 528,46184 | 0,02463 | 0,02083 | 0,01629 | 0,01514 | 0,01923 |
| 528,49902 | 0,02569 | 0,02176 | 0,01714 | 0,01625 | 0,02024 |
| 528,5362 | 0,02674 | 0,02268 | 0,01803 | 0,0174 | 0,02125 |
| 528,57339 | 0,02778 | 0,02359 | 0,01895 | 0,01857 | 0,02226 |
| 528,61057 | 0,0288 | 0,02446 | 0,01989 | 0,01977 | 0,02325 |
| 528,64775 | 0,02982 | 0,02532 | 0,02086 | 0,02097 | 0,02422 |
| 528,68493 | 0,03083 | 0,02615 | 0,02187 | 0,02216 | 0,02515 |
| 528,72211 | 0,03184 | 0,02695 | 0,0229 | 0,02333 | 0,02602 |
| 528,7593 | 0,03285 | 0,02773 | 0,02396 | 0,02446 | 0,02684 |
| 528,79648 | 0,03386 | 0,02847 | 0,02505 | 0,02554 | 0,02758 |
| 528,83366 | 0,03488 | 0,0292 | 0,02616 | 0,02656 | 0,02824 |
| 528,87084 | 0,03591 | 0,02991 | 0,02729 | 0,02749 | 0,02882 |
| 528,90802 | 0,03695 | 0,03059 | 0,02844 | 0,02832 | 0,02929 |
| 528,94521 | 0,038 | 0,03127 | 0,02961 | 0,02904 | 0,02965 |
| 528,98239 | 0,03907 | 0,03194 | 0,0308 | 0,02964 | 0,0299 |
| 529,01957 | 0,04016 | 0,0326 | 0,03199 | 0,03013 | 0,03006 |
| 529,05675 | 0,04126 | 0,03327 | 0,03319 | 0,03049 | 0,03011 |
| 529,09393 | 0,04238 | 0,03395 | 0,03439 | 0,03073 | 0,03008 |
| 529,13112 | 0,04352 | 0,03466 | 0,03559 | 0,03084 | 0,02997 |
| 529,1683 | 0,04468 | 0,03539 | 0,03679 | 0,03084 | 0,02978 |
| 529,20548 | 0,04586 | 0,03616 | 0,03799 | 0,03074 | 0,02954 |
| 529,24266 | 0,04706 | 0,03699 | 0,03919 | 0,03058 | 0,02926 |
| 529,27984 | 0,04829 | 0,03788 | 0,04039 | 0,03037 | 0,02898 |
| 529,31703 | 0,04955 | 0,03883 | 0,04159 | 0,03012 | 0,02871 |
| 529,35421 | 0,05084 | 0,03986 | 0,0428 | 0,02986 | 0,02847 |
| 529,39139 | 0,05215 | 0,04097 | 0,04401 | 0,02964 | 0,02829 |
| 529,42857 | 0,0535 | 0,04217 | 0,04524 | 0,02948 | 0,02819 |
| 529,46575 | 0,05489 | 0,04347 | 0,04648 | 0,0294 | 0,02821 |
| 529,50294 | 0,05632 | 0,04488 | 0,04775 | 0,02943 | 0,02835 |
| 529,54012 | 0,05779 | 0,0464 | 0,04905 | 0,02959 | 0,02865 |
| 529,5773 | 0,05932 | 0,04802 | 0,05039 | 0,02991 | 0,02911 |
| 529,61448 | 0,0609 | 0,04975 | 0,05177 | 0,0304 | 0,02976 |
| 529,65166 | 0,06253 | 0,05157 | 0,0532 | 0,03113 | 0,03059 |
| 529,68885 | 0,06422 | 0,05349 | 0,05468 | 0,03207 | 0,03165 |
| 529,72603 | 0,06598 | 0,05551 | 0,05624 | 0,03323 | 0,03295 |
| 529,76321 | 0,06781 | 0,05762 | 0,05786 | 0,03461 | 0,03446 |
| 529,80039 | 0,06971 | 0,05981 | 0,05955 | 0,03621 | 0,03618 |
| 529,83757 | 0,07169 | 0,06207 | 0,06132 | 0,03803 | 0,03812 |
| 529,87476 | 0,07374 | 0,06439 | 0,06317 | 0,04008 | 0,04026 |
| 529,91194 | 0,07587 | 0,06676 | 0,06509 | 0,04237 | 0,0426 |
| 529,94912 | 0,07807 | 0,06917 | 0,0671 | 0,04487 | 0,04516 |
| 529,9863 | 0,08034 | 0,07162 | 0,06921 | 0,04755 | 0,0479 |
| 530,02348 | 0,08271 | 0,07409 | 0,0714 | 0,05041 | 0,0508 |
| 530,06067 | 0,08514 | 0,07658 | 0,07367 | 0,05344 | 0,05385 |
| 530,09785 | 0,08764 | 0,07909 | 0,07602 | 0,05662 | 0,05703 |
| 530,13503 | 0,0902 | 0,08159 | 0,07845 | 0,05994 | 0,06032 |
| 530,17221 | 0,09282 | 0,0841 | 0,08095 | 0,06342 | 0,06371 |
| 530,20939 | 0,09548 | 0,08661 | 0,08351 | 0,06701 | 0,06721 |
| 530,24658 | 0,0982 | 0,08911 | 0,08615 | 0,0707 | 0,07077 |
| 530,28376 | 0,10096 | 0,0916 | 0,08883 | 0,07448 | 0,07439 |
| 530,32094 | 0,10374 | 0,09408 | 0,09156 | 0,07835 | 0,07804 |
| 530,35812 | 0,10653 | 0,09654 | 0,09431 | 0,08228 | 0,08172 |
| 530,3953 | 0,10933 | 0,09898 | 0,09707 | 0,08627 | 0,08542 |
| 530,43249 | 0,11213 | 0,10139 | 0,09983 | 0,0903 | 0,08911 |
| 530,46967 | 0,11492 | 0,10378 | 0,10258 | 0,09434 | 0,09279 |
| 530,50685 | 0,11767 | 0,10612 | 0,10528 | 0,09838 | 0,09643 |
| 530,54403 | 0,12037 | 0,1084 | 0,10792 | 0,10238 | 0,10001 |
| 530,58121 | 0,12301 | 0,11063 | 0,11048 | 0,10633 | 0,10353 |
| 530,6184 | 0,12558 | 0,11279 | 0,11294 | 0,1102 | 0,10696 |
| 530,65558 | 0,12805 | 0,11486 | 0,11528 | 0,11394 | 0,11028 |
| 530,69276 | 0,13043 | 0,11684 | 0,11748 | 0,1175 | 0,11348 |
| 530,72994 | 0,13269 | 0,1187 | 0,11951 | 0,12086 | 0,11649 |
| 530,76712 | 0,13478 | 0,12041 | 0,12133 | 0,12399 | 0,11932 |
| 530,80431 | 0,13672 | 0,12197 | 0,12295 | 0,12684 | 0,12196 |
| 530,84149 | 0,13849 | 0,12337 | 0,12437 | 0,1294 | 0,12437 |
| 530,87867 | 0,14007 | 0,12459 | 0,12555 | 0,13163 | 0,12655 |
| 530,91585 | 0,14146 | 0,12564 | 0,12651 | 0,1335 | 0,12847 |
| 530,95303 | 0,14265 | 0,1265 | 0,12723 | 0,13492 | 0,13012 |
| 530,99022 | 0,14363 | 0,12716 | 0,12768 | 0,13596 | 0,13145 |
| 531,0274 | 0,14434 | 0,12759 | 0,12788 | 0,1366 | 0,1325 |
| 531,06458 | 0,14484 | 0,12783 | 0,12785 | 0,13684 | 0,13327 |
| 531,10176 | 0,14512 | 0,12788 | 0,1276 | 0,13671 | 0,13377 |
| 531,13894 | 0,1452 | 0,12777 | 0,12716 | 0,13622 | 0,134 |
| 531,17613 | 0,14507 | 0,12749 | 0,12654 | 0,13537 | 0,13399 |
| 531,21331 | 0,14475 | 0,12708 | 0,12576 | 0,13418 | 0,13373 |
| 531,25049 | 0,14424 | 0,12653 | 0,12483 | 0,13273 | 0,13324 |
| 531,28767 | 0,14357 | 0,12589 | 0,1238 | 0,13108 | 0,13259 |
| 531,32485 | 0,14278 | 0,12519 | 0,12271 | 0,12927 | 0,13179 |
| 531,36204 | 0,14189 | 0,12447 | 0,12159 | 0,12734 | 0,1309 |
| 531,39922 | 0,14095 | 0,12375 | 0,12048 | 0,12536 | 0,12993 |
| 531,4364 | 0,13996 | 0,12307 | 0,11941 | 0,12337 | 0,12892 |
| 531,47358 | 0,13898 | 0,12246 | 0,11842 | 0,12145 | 0,12792 |
| 531,51076 | 0,13805 | 0,12198 | 0,11759 | 0,11966 | 0,12698 |
| 531,54795 | 0,13721 | 0,12166 | 0,11693 | 0,11805 | 0,12613 |
| 531,58513 | 0,13648 | 0,12153 | 0,11648 | 0,11666 | 0,12542 |
| 531,62231 | 0,13592 | 0,12162 | 0,11627 | 0,11553 | 0,12487 |
| 531,65949 | 0,13553 | 0,12196 | 0,11634 | 0,11471 | 0,12451 |
| 531,69667 | 0,13536 | 0,12257 | 0,11671 | 0,11427 | 0,12439 |
| 531,73386 | 0,13542 | 0,12346 | 0,11741 | 0,11426 | 0,12457 |
| 531,77104 | 0,13578 | 0,12473 | 0,11853 | 0,11468 | 0,12506 |
| 531,80822 | 0,13641 | 0,12632 | 0,12001 | 0,11553 | 0,12587 |
| 531,8454 | 0,13732 | 0,12822 | 0,12184 | 0,11682 | 0,127 |
| 531,88258 | 0,13848 | 0,13043 | 0,12403 | 0,11856 | 0,12846 |
| 531,91977 | 0,1399 | 0,13292 | 0,12656 | 0,12073 | 0,13025 |
| 531,95695 | 0,14155 | 0,13569 | 0,1294 | 0,12335 | 0,13237 |
| 531,99413 | 0,1434 | 0,13869 | 0,13254 | 0,1264 | 0,13483 |
| 532,03131 | 0,14544 | 0,14191 | 0,13595 | 0,12978 | 0,13757 |
| 532,06849 | 0,14759 | 0,14525 | 0,13951 | 0,13344 | 0,14054 |
| 532,10568 | 0,14979 | 0,14865 | 0,14319 | 0,13731 | 0,14368 |
| 532,14286 | 0,15199 | 0,15206 | 0,14691 | 0,14133 | 0,14693 |
| 532,18004 | 0,15414 | 0,15542 | 0,1506 | 0,14543 | 0,15025 |
| 532,21722 | 0,15619 | 0,15865 | 0,15421 | 0,14952 | 0,15356 |
| 532,2544 | 0,15806 | 0,16168 | 0,15763 | 0,15348 | 0,15677 |
| 532,29159 | 0,15968 | 0,16441 | 0,16077 | 0,15724 | 0,15979 |
| 532,32877 | 0,16102 | 0,16682 | 0,1636 | 0,16072 | 0,16257 |
| 532,36595 | 0,16205 | 0,16885 | 0,16605 | 0,16385 | 0,16504 |
| 532,40313 | 0,16274 | 0,17048 | 0,1681 | 0,16658 | 0,16715 |
| 532,44031 | 0,16308 | 0,17167 | 0,1697 | 0,16887 | 0,16886 |
| 532,4775 | 0,16305 | 0,17242 | 0,17082 | 0,17063 | 0,17013 |
| 532,51468 | 0,16261 | 0,17264 | 0,1714 | 0,17183 | 0,17084 |
| 532,55186 | 0,1618 | 0,1724 | 0,17148 | 0,17253 | 0,17109 |
| 532,58904 | 0,16069 | 0,17174 | 0,17111 | 0,17275 | 0,17088 |
| 532,62622 | 0,15929 | 0,17072 | 0,17032 | 0,17254 | 0,17026 |
| 532,66341 | 0,15768 | 0,16937 | 0,16917 | 0,17195 | 0,16925 |
| 532,70059 | 0,15589 | 0,16776 | 0,1677 | 0,17102 | 0,1679 |
| 532,73777 | 0,15399 | 0,16594 | 0,16598 | 0,16983 | 0,16629 |
| 532,77495 | 0,15205 | 0,16399 | 0,16407 | 0,16846 | 0,16446 |
| 532,81213 | 0,15017 | 0,16202 | 0,16208 | 0,16703 | 0,16255 |
| 532,84932 | 0,14841 | 0,1601 | 0,1601 | 0,16562 | 0,16063 |
| 532,8865 | 0,14683 | 0,15832 | 0,15822 | 0,16431 | 0,15879 |
| 532,92368 | 0,14551 | 0,15674 | 0,15649 | 0,16318 | 0,15711 |
| 532,96086 | 0,14449 | 0,15543 | 0,155 | 0,16227 | 0,15564 |
| 532,99804 | 0,14383 | 0,15446 | 0,15382 | 0,16169 | 0,15449 |
| 533,03523 | 0,14367 | 0,15395 | 0,15308 | 0,16151 | 0,15377 |
| 533,07241 | 0,14396 | 0,15388 | 0,15277 | 0,1617 | 0,15346 |
| 533,10959 | 0,14472 | 0,15427 | 0,15293 | 0,1623 | 0,15362 |
| 533,14677 | 0,14595 | 0,15514 | 0,15357 | 0,16331 | 0,15425 |
| 533,18395 | 0,14766 | 0,15648 | 0,15471 | 0,16472 | 0,15537 |
| 533,22114 | 0,14982 | 0,15828 | 0,15635 | 0,16652 | 0,15698 |
| 533,25832 | 0,15244 | 0,16055 | 0,1585 | 0,16873 | 0,15912 |
| 533,2955 | 0,15551 | 0,16328 | 0,16117 | 0,1713 | 0,16178 |
| 533,33268 | 0,1589 | 0,16635 | 0,16424 | 0,17415 | 0,16486 |
| 533,36986 | 0,16256 | 0,16969 | 0,16765 | 0,17725 | 0,16831 |
| 533,40705 | 0,16641 | 0,17324 | 0,17133 | 0,18053 | 0,17207 |
| 533,44423 | 0,17039 | 0,17693 | 0,17523 | 0,18394 | 0,1761 |
| 533,48141 | 0,17441 | 0,18067 | 0,17925 | 0,18743 | 0,18032 |
| 533,51859 | 0,17838 | 0,18437 | 0,1833 | 0,19093 | 0,18465 |
| 533,55577 | 0,18217 | 0,1879 | 0,18726 | 0,19434 | 0,18899 |
| 533,59295 | 0,18571 | 0,19119 | 0,19104 | 0,19759 | 0,19322 |
| 533,63014 | 0,18892 | 0,19414 | 0,19453 | 0,20062 | 0,19725 |
| 533,66732 | 0,19171 | 0,19669 | 0,19765 | 0,20335 | 0,201 |
| 533,7045 | 0,19403 | 0,19876 | 0,20031 | 0,2057 | 0,20437 |
| 533,74168 | 0,19579 | 0,20028 | 0,20245 | 0,20762 | 0,20727 |
| 533,77886 | 0,19686 | 0,2011 | 0,20388 | 0,20897 | 0,20953 |
| 533,81605 | 0,19722 | 0,20121 | 0,20459 | 0,20967 | 0,21108 |
| 533,85323 | 0,1969 | 0,20062 | 0,20458 | 0,20972 | 0,21189 |
| 533,89041 | 0,19588 | 0,19932 | 0,20382 | 0,20908 | 0,21193 |
| 533,92759 | 0,19416 | 0,19731 | 0,2023 | 0,20772 | 0,21115 |
| 533,96477 | 0,19175 | 0,19459 | 0,20002 | 0,20562 | 0,20952 |
| 534,00196 | 0,18867 | 0,19118 | 0,197 | 0,20277 | 0,20705 |
| 534,03914 | 0,18483 | 0,18701 | 0,19314 | 0,19909 | 0,20362 |
| 534,07632 | 0,18043 | 0,18225 | 0,18862 | 0,19463 | 0,19934 |
| 534,1135 | 0,17553 | 0,17696 | 0,18351 | 0,18952 | 0,19433 |
| 534,15068 | 0,17018 | 0,17122 | 0,17788 | 0,1838 | 0,18863 |
| 534,18787 | 0,16446 | 0,16509 | 0,1718 | 0,17754 | 0,18233 |
| 534,22505 | 0,15843 | 0,15865 | 0,16535 | 0,17081 | 0,17551 |
| 534,26223 | 0,15218 | 0,15198 | 0,15862 | 0,16371 | 0,16825 |
| 534,29941 | 0,14577 | 0,14515 | 0,15167 | 0,15629 | 0,16063 |
| 534,33659 | 0,13933 | 0,13829 | 0,14465 | 0,14869 | 0,15281 |
| 534,37378 | 0,13291 | 0,13146 | 0,13763 | 0,14104 | 0,14491 |
| 534,41096 | 0,12657 | 0,12474 | 0,13069 | 0,13341 | 0,13701 |
| 534,44814 | 0,12039 | 0,1182 | 0,1239 | 0,12589 | 0,1292 |
| 534,48532 | 0,11441 | 0,11188 | 0,11732 | 0,11856 | 0,12157 |
| 534,5225 | 0,1087 | 0,10588 | 0,11103 | 0,11149 | 0,11418 |
| 534,55969 | 0,10333 | 0,10027 | 0,10512 | 0,10479 | 0,10719 |
| 534,59687 | 0,0983 | 0,09504 | 0,09958 | 0,09851 | 0,10058 |
| 534,63405 | 0,09362 | 0,09022 | 0,09445 | 0,09264 | 0,09439 |
| 534,67123 | 0,08931 | 0,08584 | 0,08974 | 0,08723 | 0,08864 |
| 534,70841 | 0,08538 | 0,08189 | 0,08547 | 0,08228 | 0,08336 |
| 534,7456 | 0,08183 | 0,07839 | 0,08164 | 0,07781 | 0,07855 |
| 534,78278 | 0,07873 | 0,07541 | 0,07829 | 0,07381 | 0,07423 |
| 534,81996 | 0,07602 | 0,07289 | 0,07544 | 0,07033 | 0,07046 |
| 534,85714 | 0,07368 | 0,0708 | 0,07301 | 0,06734 | 0,06714 |
| 534,89432 | 0,07168 | 0,06913 | 0,07098 | 0,06479 | 0,06426 |
| 534,93151 | 0,07001 | 0,06783 | 0,06935 | 0,06264 | 0,06179 |
| 534,96869 | 0,06864 | 0,06691 | 0,06808 | 0,06088 | 0,05972 |
| 535,00587 | 0,06755 | 0,06632 | 0,06715 | 0,0595 | 0,05802 |
| 535,04305 | 0,06676 | 0,06608 | 0,06657 | 0,05846 | 0,05669 |
| 535,08023 | 0,0662 | 0,06612 | 0,06628 | 0,0578 | 0,05573 |
| 535,11742 | 0,06583 | 0,06639 | 0,06624 | 0,05745 | 0,05507 |
| 535,1546 | 0,06562 | 0,06687 | 0,0664 | 0,05737 | 0,05469 |
| 535,19178 | 0,06556 | 0,06751 | 0,06674 | 0,05757 | 0,05457 |
| 535,22896 | 0,06561 | 0,06828 | 0,06723 | 0,05801 | 0,05471 |
| 535,26614 | 0,06576 | 0,06917 | 0,06785 | 0,05869 | 0,05508 |
| 535,30333 | 0,06599 | 0,07015 | 0,06857 | 0,05959 | 0,05569 |
| 535,34051 | 0,06626 | 0,07117 | 0,06936 | 0,06074 | 0,05654 |
| 535,37769 | 0,06657 | 0,07221 | 0,07018 | 0,0621 | 0,0576 |
| 535,41487 | 0,06691 | 0,07326 | 0,07103 | 0,06365 | 0,05885 |
| 535,45205 | 0,06726 | 0,0743 | 0,07189 | 0,0654 | 0,0603 |
| 535,48924 | 0,06762 | 0,07533 | 0,07275 | 0,06734 | 0,06195 |
| 535,52642 | 0,068 | 0,07633 | 0,07361 | 0,06945 | 0,06379 |
| 535,5636 | 0,0684 | 0,07731 | 0,07447 | 0,07175 | 0,06585 |
| 535,60078 | 0,06884 | 0,07828 | 0,07534 | 0,07424 | 0,06812 |
| 535,63796 | 0,06932 | 0,07925 | 0,07624 | 0,07692 | 0,07059 |
| 535,67515 | 0,06986 | 0,08022 | 0,07717 | 0,07977 | 0,07327 |
| 535,71233 | 0,07047 | 0,08123 | 0,07815 | 0,08279 | 0,07614 |
| 535,74951 | 0,07117 | 0,08228 | 0,07922 | 0,08597 | 0,07922 |
| 535,78669 | 0,072 | 0,0834 | 0,08039 | 0,08932 | 0,08251 |
| 535,82387 | 0,07297 | 0,08463 | 0,08171 | 0,09281 | 0,08602 |
| 535,86106 | 0,07408 | 0,08596 | 0,08319 | 0,09648 | 0,08974 |
| 535,89824 | 0,07535 | 0,08742 | 0,08483 | 0,10028 | 0,09363 |
| 535,93542 | 0,07676 | 0,08901 | 0,08665 | 0,10418 | 0,09769 |
| 535,9726 | 0,07834 | 0,09074 | 0,08866 | 0,10818 | 0,10188 |
| 536,00978 | 0,08006 | 0,09261 | 0,09086 | 0,11222 | 0,10617 |
| 536,04697 | 0,08193 | 0,09463 | 0,09325 | 0,11629 | 0,11053 |
| 536,08415 | 0,08392 | 0,09676 | 0,09581 | 0,12033 | 0,11491 |
| 536,12133 | 0,08598 | 0,09897 | 0,0985 | 0,12428 | 0,11923 |
| 536,15851 | 0,08808 | 0,10122 | 0,10127 | 0,12808 | 0,12343 |
| 536,19569 | 0,09018 | 0,10348 | 0,10409 | 0,13166 | 0,12745 |
| 536,23288 | 0,09224 | 0,10571 | 0,10689 | 0,13496 | 0,13122 |
| 536,27006 | 0,09421 | 0,10784 | 0,10962 | 0,13792 | 0,13465 |
| 536,30724 | 0,09601 | 0,10979 | 0,1122 | 0,14047 | 0,13769 |
| 536,34442 | 0,09759 | 0,11152 | 0,11455 | 0,14254 | 0,14015 |
| 536,3816 | 0,09893 | 0,11298 | 0,11662 | 0,14397 | 0,14204 |
| 536,41879 | 0,09997 | 0,11411 | 0,11835 | 0,14477 | 0,1433 |
| 536,45597 | 0,10068 | 0,11488 | 0,11968 | 0,14493 | 0,14391 |
| 536,49315 | 0,10102 | 0,11525 | 0,12057 | 0,14441 | 0,14382 |
| 536,53033 | 0,10095 | 0,11517 | 0,12099 | 0,14321 | 0,14302 |
| 536,56751 | 0,10041 | 0,11455 | 0,1208 | 0,14133 | 0,14149 |
| 536,6047 | 0,09946 | 0,11346 | 0,12007 | 0,13877 | 0,13912 |
| 536,64188 | 0,0981 | 0,11191 | 0,11881 | 0,13548 | 0,1361 |
| 536,67906 | 0,09635 | 0,10991 | 0,11704 | 0,13162 | 0,13247 |
| 536,71624 | 0,09424 | 0,10749 | 0,11478 | 0,12727 | 0,1283 |
| 536,75342 | 0,09178 | 0,10468 | 0,11207 | 0,1225 | 0,12366 |
| 536,79061 | 0,08899 | 0,1015 | 0,10894 | 0,11741 | 0,11863 |
| 536,82779 | 0,08594 | 0,098 | 0,10539 | 0,11207 | 0,11329 |
| 536,86497 | 0,0827 | 0,09429 | 0,10157 | 0,10658 | 0,10775 |
| 536,90215 | 0,07932 | 0,09042 | 0,09755 | 0,10105 | 0,10214 |
| 536,93933 | 0,07586 | 0,08645 | 0,09338 | 0,09558 | 0,09655 |
| 536,97652 | 0,07236 | 0,08244 | 0,08913 | 0,09026 | 0,09106 |
| 537,0137 | 0,06887 | 0,07845 | 0,08487 | 0,08515 | 0,08576 |
| 537,05088 | 0,06546 | 0,07455 | 0,08065 | 0,08031 | 0,08069 |
| 537,08806 | 0,06217 | 0,07078 | 0,07656 | 0,07578 | 0,07594 |
| 537,12524 | 0,05901 | 0,06719 | 0,07263 | 0,07159 | 0,07158 |
| 537,16243 | 0,05603 | 0,06381 | 0,0689 | 0,06784 | 0,06759 |
| 537,19961 | 0,05323 | 0,06064 | 0,06538 | 0,06444 | 0,06396 |
| 537,23679 | 0,05063 | 0,05771 | 0,06209 | 0,0614 | 0,06071 |
| 537,27397 | 0,04824 | 0,05502 | 0,05905 | 0,05869 | 0,0578 |
| 537,31115 | 0,04609 | 0,05262 | 0,05628 | 0,05626 | 0,05523 |
| 537,34834 | 0,04412 | 0,05046 | 0,05377 | 0,0541 | 0,05297 |
| 537,38552 | 0,04233 | 0,0485 | 0,05147 | 0,05215 | 0,05098 |
| 537,4227 | 0,0407 | 0,04674 | 0,04938 | 0,0504 | 0,04919 |
| 537,45988 | 0,03921 | 0,04514 | 0,04746 | 0,04876 | 0,04756 |
| 537,49706 | 0,03784 | 0,04368 | 0,04569 | 0,04719 | 0,04603 |
| 537,53425 | 0,03656 | 0,04234 | 0,04405 | 0,04564 | 0,04458 |
| 537,57143 | 0,03536 | 0,04109 | 0,04251 | 0,0441 | 0,04316 |
| 537,60861 | 0,0342 | 0,03989 | 0,04103 | 0,04252 | 0,04175 |
| 537,64579 | 0,03306 | 0,03872 | 0,03959 | 0,04089 | 0,04031 |
| 537,68297 | 0,03193 | 0,03755 | 0,03817 | 0,03919 | 0,03882 |
| 537,72016 | 0,03079 | 0,03636 | 0,03675 | 0,03741 | 0,03728 |
| 537,75734 | 0,02964 | 0,03515 | 0,03531 | 0,03556 | 0,03569 |
| 537,79452 | 0,02845 | 0,03389 | 0,03385 | 0,03364 | 0,03403 |
| 537,8317 | 0,02723 | 0,03258 | 0,03236 | 0,03168 | 0,03233 |
| 537,86888 | 0,02597 | 0,03123 | 0,03083 | 0,02967 | 0,03058 |
| 537,90607 | 0,02469 | 0,02982 | 0,02928 | 0,02764 | 0,02881 |
| 537,94325 | 0,02338 | 0,02838 | 0,02769 | 0,02562 | 0,02703 |
| 537,98043 | 0,02205 | 0,02689 | 0,02609 | 0,02362 | 0,02526 |
| 538,01761 | 0,02071 | 0,02538 | 0,02449 | 0,02167 | 0,02352 |
| 538,05479 | 0,01938 | 0,02386 | 0,02288 | 0,01979 | 0,02182 |
| 538,09198 | 0,01805 | 0,02233 | 0,02129 | 0,01798 | 0,02018 |
| 538,12916 | 0,01675 | 0,02081 | 0,01972 | 0,01627 | 0,01863 |
| 538,16634 | 0,01548 | 0,01931 | 0,0182 | 0,01467 | 0,01716 |
| 538,20352 | 0,01426 | 0,01785 | 0,01672 | 0,01321 | 0,01578 |
| 538,2407 | 0,01308 | 0,01642 | 0,01529 | 0,01186 | 0,01449 |
| 538,27789 | 0,01196 | 0,01505 | 0,01393 | 0,01064 | 0,0133 |
| 538,31507 | 0,01091 | 0,01375 | 0,01264 | 0,00955 | 0,01221 |
| 538,35225 | 0,00993 | 0,01253 | 0,01144 | 0,00857 | 0,01121 |
| 538,38943 | 0,00902 | 0,01137 | 0,01032 | 0,0077 | 0,01032 |
| 538,42661 | 0,00818 | 0,01029 | 0,00927 | 0,00695 | 0,00951 |
| 538,4638 | 0,00741 | 0,00928 | 0,00831 | 0,00631 | 0,00878 |
| 538,50098 | 0,00671 | 0,00835 | 0,00742 | 0,00576 | 0,00811 |
| 538,53816 | 0,00608 | 0,0075 | 0,00661 | 0,00528 | 0,00751 |
| 538,57534 | 0,00552 | 0,00673 | 0,00588 | 0,00488 | 0,00696 |
| 538,61252 | 0,00502 | 0,00603 | 0,00523 | 0,00453 | 0,00647 |
| 538,64971 | 0,00457 | 0,0054 | 0,00465 | 0,00424 | 0,00602 |
| 538,68689 | 0,00417 | 0,00482 | 0,00412 | 0,004 | 0,00561 |
| 538,72407 | 0,00382 | 0,0043 | 0,00365 | 0,00379 | 0,00523 |
| 538,76125 | 0,0035 | 0,00384 | 0,00323 | 0,00361 | 0,00488 |
| 538,79843 | 0,00322 | 0,00342 | 0,00286 | 0,00345 | 0,00455 |
| 538,83562 | 0,00298 | 0,00305 | 0,00254 | 0,0033 | 0,00424 |
| 538,8728 | 0,00276 | 0,00272 | 0,00225 | 0,00316 | 0,00395 |
| 538,90998 | 0,00256 | 0,00242 | 0,002 | 0,00303 | 0,00367 |
| 538,94716 | 0,00238 | 0,00215 | 0,00178 | 0,00291 | 0,00341 |
| 538,98434 | 0,00221 | 0,00191 | 0,00158 | 0,00278 | 0,00317 |
| 539,02153 | 0,00205 | 0,00169 | 0,00141 | 0,00266 | 0,00293 |
| 539,05871 | 0,00191 | 0,0015 | 0,00126 | 0,00253 | 0,00271 |
| 539,09589 | 0,00178 | 0,00132 | 0,00113 | 0,0024 | 0,0025 |
| 539,13307 | 0,00165 | 0,00117 | 0,00101 | 0,00227 | 0,0023 |
| 539,17025 | 0,00152 | 0,00103 | 9e-04 | 0,00214 | 0,00211 |
| 539,20744 | 0,00141 | 9e-04 | 0,00081 | 0,002 | 0,00193 |
| 539,24462 | 0,00129 | 0,00079 | 0,00073 | 0,00186 | 0,00176 |
| 539,2818 | 0,00118 | 0,00069 | 0,00065 | 0,00173 | 0,0016 |
| 539,31898 | 0,00108 | 6e-04 | 0,00059 | 0,00159 | 0,00145 |
| 539,35616 | 0,00098 | 0,00052 | 0,00053 | 0,00146 | 0,00131 |
| 539,39335 | 0,00089 | 0,00045 | 0,00048 | 0,00132 | 0,00118 |
| 539,43053 | 8e-04 | 0,00038 | 0,00043 | 0,0012 | 0,00107 |
| 539,46771 | 0,00071 | 0,00033 | 0,00038 | 0,00107 | 0,00096 |
| 539,50489 | 0,00063 | 0,00028 | 0,00034 | 0,00096 | 0,00087 |
| 539,54207 | 0,00056 | 0,00023 | 3e-04 | 0,00085 | 0,00078 |
| 539,57926 | 0,00049 | 2e-04 | 0,00027 | 0,00075 | 7e-04 |
| 539,61644 | 0,00043 | 0,00017 | 0,00024 | 0,00065 | 0,00063 |
| 539,65362 | 0,00037 | 0,00014 | 0,00021 | 0,00057 | 0,00058 |
| 539,6908 | 0,00032 | 0,00011 | 0,00018 | 0,00049 | 0,00053 |
| 539,72798 | 0,00028 | 9e-05 | 0,00016 | 0,00042 | 0,00049 |
| 539,76517 | 0,00023 | 8e-05 | 0,00014 | 0,00035 | 0,00045 |
| 539,80235 | 2e-04 | 6e-05 | 0,00012 | 3e-04 | 0,00043 |
| 539,83953 | 0,00017 | 5e-05 | 1e-04 | 0,00025 | 4e-04 |
| 539,87671 | 0,00014 | 4e-05 | 9e-05 | 0,00021 | 0,00039 |
| 539,91389 | 0,00012 | 3e-05 | 7e-05 | 0,00017 | 0,00038 |
| 539,95108 | 9e-05 | 3e-05 | 6e-05 | 0,00014 | 0,00037 |
| 539,98826 | 8e-05 | 2e-05 | 5e-05 | 0,00011 | 0,00036 |
| 540,02544 | 6e-05 | 2e-05 | 4e-05 | 9e-05 | 0,00036 |
| 540,06262 | 5e-05 | 1e-05 | 4e-05 | 7e-05 | 0,00035 |
| 540,0998 | 4e-05 | 1e-05 | 3e-05 | 6e-05 | 0,00035 |
| 540,13699 | 3e-05 | 1e-05 | 2e-05 | 5e-05 | 0,00035 |
| 540,17417 | 3e-05 | 1e-05 | 2e-05 | 4e-05 | 0,00035 |
| 540,21135 | 2e-05 | 0 | 2e-05 | 3e-05 | 0,00034 |
| 540,24853 | 2e-05 | 0 | 1e-05 | 2e-05 | 0,00033 |
| 540,28571 | 1e-05 | 0 | 1e-05 | 2e-05 | 0,00033 |
| 540,3229 | 1e-05 | 0 | 1e-05 | 1e-05 | 0,00032 |
| 540,36008 | 1e-05 | 0 | 1e-05 | 1e-05 | 0,00031 |
| 540,39726 | 1e-05 | 0 | 0 | 1e-05 | 0,00029 |
| 540,43444 | 0 | 0 | 0 | 0 | 0,00028 |
| 540,47162 | 0 | 0 | 0 | 0 | 0,00026 |
| 540,50881 | 0 | 0 | 0 | 0 | 0,00025 |
| 540,54599 | 0 | 0 | 0 | 0 | 0,00023 |
| 540,58317 | 0 | 0 | 0 | 0 | 0,00021 |
| 540,62035 | 0 | 0 | 0 | 0 | 0,00019 |
| 540,65753 | 0 | 0 | 0 | 0 | 0,00017 |
| 540,69472 | 0 | 0 | 0 | 0 | 0,00016 |
| 540,7319 | 0 | 0 | 0 | 0 | 0,00014 |
| 540,76908 | 0 | 0 | 0 | 0 | 0,00012 |
| 540,80626 | 0 | 0 | 0 | 0 | 0,00011 |
| 540,84344 | 0 | 0 | 0 | 0 | 9e-05 |
| 540,88063 | 0 | 0 | 0 | 0 | 8e-05 |
| 540,91781 | 0 | 0 | 0 | 0 | 7e-05 |
| 540,95499 | 0 | 0 | 0 | 0 | 6e-05 |
| 540,99217 | 0 | 0 | 0 | 0 | 5e-05 |
| 541,02935 | 0 | 0 | 0 | 0 | 4e-05 |
| 541,06654 | 0 | 0 | 0 | 0 | 3e-05 |
| 541,10372 | 0 | 0 | 0 | 0 | 3e-05 |
| 541,1409 | 0 | 0 | 0 | 0 | 2e-05 |
| 541,17808 | 0 | 0 | 0 | 0 | 2e-05 |
| 541,21526 | 0 | 0 | 0 | 0 | 1e-05 |
| 541,25245 | 0 | 0 | 0 | 0 | 1e-05 |
| 541,28963 | 0 | 0 | 0 | 0 | 1e-05 |
| 541,32681 | 0 | 0 | 0 | 0 | 1e-05 |
| 541,36399 | 0 | 0 | 0 | 0 | 1e-05 |
| 541,40117 | 0 | 0 | 0 | 0 | 0 |
| 541,43836 | 0 | 0 | 0 | 0 | 0 |
| 541,47554 | 0 | 0 | 0 | 0 | 0 |
| 541,51272 | 0 | 0 | 0 | 0 | 0 |
| 541,5499 | 0 | 0 | 0 | 0 | 0 |
| 541,58708 | 0 | 0 | 0 | 0 | 0 |
| 541,62427 | 0 | 0 | 0 | 0 | 0 |
| 541,66145 | 0 | 0 | 0 | 0 | 0 |
| 541,69863 | 0 | 0 | 0 | 0 | 0 |
| 541,73581 | 0 | 0 | 0 | 0 | 0 |
| 541,77299 | 0 | 0 | 0 | 0 | 0 |
| 541,81018 | 0 | 0 | 0 | 0 | 0 |
| 541,84736 | 0 | 0 | 0 | 0 | 0 |
| 541,88454 | 0 | 0 | 0 | 0 | 0 |
| 541,92172 | 0 | 0 | 0 | 0 | 0 |
| 541,9589 | 0 | 0 | 0 | 0 | 0 |
| 541,99609 | 0 | 0 | 0 | 0 | 0 |
| 542,03327 | 0 | 0 | 0 | 0 | 0 |
| 542,07045 | 0 | 0 | 0 | 0 | 0 |
| 542,10763 | 0 | 0 | 0 | 0 | 0 |
| 542,14481 | 0 | 0 | 0 | 0 | 0 |
| 542,182 | 0 | 0 | 0 | 0 | 0 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 1e-05 | 0 | 0 | 0 |
| 524,22309 | 0 | 1e-05 | 0 | 0 | 0 |
| 524,26027 | 0 | 1e-05 | 0 | 0 | 0 |
| 524,29746 | 0 | 2e-05 | 1e-05 | 0 | 0 |
| 524,33464 | 0 | 2e-05 | 1e-05 | 0 | 0 |
| 524,37182 | 0 | 3e-05 | 1e-05 | 0 | 0 |
| 524,409 | 0 | 4e-05 | 2e-05 | 0 | 0 |
| 524,44618 | 0 | 5e-05 | 2e-05 | 0 | 0 |
| 524,48337 | 0 | 6e-05 | 3e-05 | 0 | 0 |
| 524,52055 | 0 | 8e-05 | 3e-05 | 0 | 0 |
| 524,55773 | 0 | 9e-05 | 4e-05 | 0 | 0 |
| 524,59491 | 0 | 1e-04 | 5e-05 | 0 | 0 |
| 524,63209 | 1e-05 | 0,00011 | 6e-05 | 0 | 0 |
| 524,66928 | 1e-05 | 0,00012 | 7e-05 | 0 | 0 |
| 524,70646 | 1e-05 | 0,00013 | 8e-05 | 0 | 0 |
| 524,74364 | 2e-05 | 0,00014 | 9e-05 | 0 | 0 |
| 524,78082 | 3e-05 | 0,00014 | 1e-04 | 0 | 0 |
| 524,818 | 5e-05 | 0,00014 | 0,00012 | 0 | 0 |
| 524,85519 | 6e-05 | 0,00014 | 0,00013 | 0 | 0 |
| 524,89237 | 9e-05 | 0,00014 | 0,00015 | 0 | 0 |
| 524,92955 | 0,00011 | 0,00014 | 0,00017 | 0 | 0 |
| 524,96673 | 0,00014 | 0,00014 | 0,00019 | 0 | 0 |
| 525,00391 | 0,00018 | 0,00014 | 0,00021 | 0 | 0 |
| 525,0411 | 0,00022 | 0,00015 | 0,00023 | 0 | 0 |
| 525,07828 | 0,00026 | 0,00016 | 0,00025 | 0 | 0 |
| 525,11546 | 3e-04 | 0,00017 | 0,00026 | 0 | 0 |
| 525,15264 | 0,00034 | 0,00018 | 0,00028 | 0 | 0 |
| 525,18982 | 0,00037 | 2e-04 | 0,00029 | 0 | 0 |
| 525,22701 | 4e-04 | 0,00022 | 0,00029 | 0 | 0 |
| 525,26419 | 0,00042 | 0,00024 | 0,00029 | 0 | 0 |
| 525,30137 | 0,00043 | 0,00026 | 0,00028 | 0 | 0 |
| 525,33855 | 0,00044 | 0,00027 | 0,00028 | 0 | 0 |
| 525,37573 | 0,00044 | 0,00029 | 0,00027 | 0 | 1e-05 |
| 525,41292 | 0,00044 | 0,00029 | 0,00025 | 0 | 1e-05 |
| 525,4501 | 0,00044 | 0,00029 | 0,00024 | 1e-05 | 2e-05 |
| 525,48728 | 0,00044 | 0,00029 | 0,00024 | 1e-05 | 2e-05 |
| 525,52446 | 0,00044 | 0,00028 | 0,00023 | 1e-05 | 3e-05 |
| 525,56164 | 0,00044 | 0,00027 | 0,00023 | 2e-05 | 4e-05 |
| 525,59883 | 0,00045 | 0,00025 | 0,00023 | 2e-05 | 5e-05 |
| 525,63601 | 0,00045 | 0,00023 | 0,00024 | 3e-05 | 7e-05 |
| 525,67319 | 0,00047 | 0,00021 | 0,00025 | 4e-05 | 8e-05 |
| 525,71037 | 0,00048 | 2e-04 | 0,00026 | 5e-05 | 1e-04 |
| 525,74755 | 0,00049 | 0,00018 | 0,00028 | 6e-05 | 0,00012 |
| 525,78474 | 0,00049 | 0,00016 | 0,00029 | 8e-05 | 0,00014 |
| 525,82192 | 5e-04 | 0,00015 | 3e-04 | 1e-04 | 0,00017 |
| 525,8591 | 5e-04 | 0,00015 | 0,00031 | 0,00012 | 0,00019 |
| 525,89628 | 0,00049 | 0,00015 | 0,00032 | 0,00014 | 0,00021 |
| 525,93346 | 0,00048 | 0,00015 | 0,00032 | 0,00017 | 0,00023 |
| 525,97065 | 0,00047 | 0,00016 | 0,00032 | 2e-04 | 0,00025 |
| 526,00783 | 0,00046 | 0,00017 | 0,00031 | 0,00023 | 0,00027 |
| 526,04501 | 0,00045 | 0,00018 | 3e-04 | 0,00026 | 0,00028 |
| 526,08219 | 0,00044 | 2e-04 | 0,00029 | 3e-04 | 0,00029 |
| 526,11937 | 0,00043 | 0,00022 | 0,00029 | 0,00033 | 3e-04 |
| 526,15656 | 0,00043 | 0,00024 | 0,00028 | 0,00036 | 3e-04 |
| 526,19374 | 0,00043 | 0,00027 | 0,00028 | 4e-04 | 3e-04 |
| 526,23092 | 0,00044 | 0,00029 | 0,00029 | 0,00043 | 3e-04 |
| 526,2681 | 0,00046 | 0,00032 | 3e-04 | 0,00045 | 0,00029 |
| 526,30528 | 0,00048 | 0,00035 | 0,00032 | 0,00048 | 0,00029 |
| 526,34247 | 0,00051 | 0,00039 | 0,00035 | 0,00049 | 0,00028 |
| 526,37965 | 0,00055 | 0,00042 | 0,00039 | 5e-04 | 0,00027 |
| 526,41683 | 6e-04 | 0,00046 | 0,00044 | 5e-04 | 0,00025 |
| 526,45401 | 0,00065 | 5e-04 | 0,00049 | 5e-04 | 0,00024 |
| 526,49119 | 0,00071 | 0,00054 | 0,00056 | 0,00048 | 0,00022 |
| 526,52838 | 0,00076 | 0,00058 | 0,00062 | 0,00046 | 0,00021 |
| 526,56556 | 0,00082 | 0,00062 | 0,00068 | 0,00043 | 0,00019 |
| 526,60274 | 0,00087 | 0,00065 | 0,00075 | 4e-04 | 0,00018 |
| 526,63992 | 0,00091 | 0,00069 | 8e-04 | 0,00036 | 0,00017 |
| 526,6771 | 0,00095 | 0,00073 | 0,00086 | 0,00032 | 0,00016 |
| 526,71429 | 0,00098 | 0,00077 | 9e-04 | 0,00028 | 0,00015 |
| 526,75147 | 0,001 | 8e-04 | 0,00094 | 0,00024 | 0,00014 |
| 526,78865 | 0,00101 | 0,00085 | 0,00098 | 0,00021 | 0,00014 |
| 526,82583 | 0,00102 | 9e-04 | 0,00101 | 0,00018 | 0,00014 |
| 526,86301 | 0,00103 | 0,00096 | 0,00104 | 0,00015 | 0,00015 |
| 526,9002 | 0,00104 | 0,00103 | 0,00106 | 0,00013 | 0,00016 |
| 526,93738 | 0,00107 | 0,00111 | 0,00109 | 0,00013 | 0,00018 |
| 526,97456 | 0,00112 | 0,00121 | 0,00113 | 0,00013 | 2e-04 |
| 527,01174 | 0,0012 | 0,00133 | 0,00117 | 0,00014 | 0,00023 |
| 527,04892 | 0,00131 | 0,00148 | 0,00122 | 0,00016 | 0,00027 |
| 527,08611 | 0,00147 | 0,00164 | 0,00129 | 0,00019 | 0,00031 |
| 527,12329 | 0,00167 | 0,00184 | 0,00138 | 0,00024 | 0,00036 |
| 527,16047 | 0,00192 | 0,00206 | 0,00149 | 3e-04 | 0,00042 |
| 527,19765 | 0,00223 | 0,00232 | 0,00163 | 0,00038 | 0,00049 |
| 527,23483 | 0,00262 | 0,00263 | 0,00181 | 0,00048 | 0,00057 |
| 527,27202 | 0,00307 | 0,00297 | 0,00204 | 0,00059 | 0,00065 |
| 527,3092 | 0,00359 | 0,00336 | 0,00232 | 0,00072 | 0,00074 |
| 527,34638 | 0,00418 | 0,0038 | 0,00267 | 0,00087 | 0,00084 |
| 527,38356 | 0,00484 | 0,0043 | 0,00307 | 0,00104 | 0,00094 |
| 527,42074 | 0,00557 | 0,00485 | 0,00355 | 0,00123 | 0,00106 |
| 527,45793 | 0,00635 | 0,00546 | 0,00411 | 0,00144 | 0,00119 |
| 527,49511 | 0,00717 | 0,00612 | 0,00473 | 0,00168 | 0,00134 |
| 527,53229 | 0,00802 | 0,00683 | 0,00541 | 0,00195 | 0,00152 |
| 527,56947 | 0,00888 | 0,00757 | 0,00614 | 0,00225 | 0,00172 |
| 527,60665 | 0,00971 | 0,00834 | 0,0069 | 0,0026 | 0,00196 |
| 527,64384 | 0,01049 | 0,0091 | 0,00766 | 0,003 | 0,00225 |
| 527,68102 | 0,0112 | 0,00985 | 0,00839 | 0,00346 | 0,00259 |
| 527,7182 | 0,01181 | 0,01056 | 0,00909 | 0,00399 | 0,00299 |
| 527,75538 | 0,01231 | 0,01122 | 0,00971 | 0,00459 | 0,00346 |
| 527,79256 | 0,01268 | 0,01182 | 0,01025 | 0,00527 | 0,004 |
| 527,82975 | 0,01293 | 0,01233 | 0,01069 | 0,00603 | 0,00462 |
| 527,86693 | 0,01307 | 0,01275 | 0,01103 | 0,00688 | 0,00532 |
| 527,90411 | 0,01312 | 0,0131 | 0,01127 | 0,00781 | 0,00608 |
| 527,94129 | 0,0131 | 0,01336 | 0,01143 | 0,00882 | 0,00692 |
| 527,97847 | 0,01305 | 0,01355 | 0,01152 | 0,00991 | 0,00781 |
| 528,01566 | 0,01301 | 0,01369 | 0,01159 | 0,01108 | 0,00875 |
| 528,05284 | 0,01302 | 0,0138 | 0,01166 | 0,0123 | 0,00973 |
| 528,09002 | 0,01312 | 0,01392 | 0,01177 | 0,01357 | 0,01074 |
| 528,1272 | 0,01334 | 0,01404 | 0,01194 | 0,01486 | 0,01175 |
| 528,16438 | 0,01371 | 0,01419 | 0,0122 | 0,01615 | 0,01276 |
| 528,20157 | 0,01423 | 0,01438 | 0,01255 | 0,01739 | 0,01374 |
| 528,23875 | 0,01488 | 0,01462 | 0,01301 | 0,01856 | 0,01465 |
| 528,27593 | 0,01564 | 0,01489 | 0,01357 | 0,01961 | 0,01548 |
| 528,31311 | 0,01648 | 0,01519 | 0,01419 | 0,02049 | 0,0162 |
| 528,35029 | 0,01736 | 0,01552 | 0,01488 | 0,02117 | 0,01677 |
| 528,38748 | 0,01822 | 0,01586 | 0,01558 | 0,0216 | 0,01718 |
| 528,42466 | 0,01902 | 0,01619 | 0,01627 | 0,02177 | 0,0174 |
| 528,46184 | 0,01974 | 0,01651 | 0,01691 | 0,02162 | 0,01742 |
| 528,49902 | 0,02034 | 0,01681 | 0,0175 | 0,02118 | 0,01725 |
| 528,5362 | 0,02083 | 0,01711 | 0,01802 | 0,02048 | 0,01687 |
| 528,57339 | 0,02121 | 0,0174 | 0,01847 | 0,01955 | 0,01631 |
| 528,61057 | 0,02152 | 0,01771 | 0,01887 | 0,01843 | 0,01558 |
| 528,64775 | 0,02181 | 0,01806 | 0,01923 | 0,0172 | 0,01472 |
| 528,68493 | 0,02211 | 0,01847 | 0,01959 | 0,01589 | 0,01377 |
| 528,72211 | 0,02248 | 0,01896 | 0,01995 | 0,01458 | 0,01277 |
| 528,7593 | 0,02293 | 0,01955 | 0,02037 | 0,01331 | 0,01176 |
| 528,79648 | 0,02351 | 0,02025 | 0,02085 | 0,01214 | 0,01078 |
| 528,83366 | 0,02421 | 0,02106 | 0,02142 | 0,01109 | 0,00988 |
| 528,87084 | 0,02504 | 0,02198 | 0,02209 | 0,01021 | 0,00907 |
| 528,90802 | 0,02598 | 0,02299 | 0,02287 | 0,00953 | 0,0084 |
| 528,94521 | 0,02702 | 0,02407 | 0,02373 | 0,00905 | 0,00789 |
| 528,98239 | 0,02812 | 0,0252 | 0,02469 | 0,00879 | 0,00756 |
| 529,01957 | 0,02927 | 0,02634 | 0,02572 | 0,00875 | 0,00744 |
| 529,05675 | 0,03044 | 0,02749 | 0,02681 | 0,00894 | 0,00757 |
| 529,09393 | 0,03161 | 0,0286 | 0,02794 | 0,00938 | 0,00795 |
| 529,13112 | 0,03277 | 0,02968 | 0,02911 | 0,01006 | 0,00858 |
| 529,1683 | 0,03393 | 0,03071 | 0,0303 | 0,01101 | 0,00948 |
| 529,20548 | 0,03509 | 0,0317 | 0,0315 | 0,01222 | 0,01064 |
| 529,24266 | 0,03626 | 0,03264 | 0,03271 | 0,01369 | 0,01207 |
| 529,27984 | 0,03745 | 0,03357 | 0,03393 | 0,01543 | 0,01376 |
| 529,31703 | 0,03868 | 0,0345 | 0,03517 | 0,01743 | 0,01568 |
| 529,35421 | 0,03995 | 0,03545 | 0,03643 | 0,01966 | 0,01782 |
| 529,39139 | 0,04127 | 0,03646 | 0,03773 | 0,02207 | 0,02015 |
| 529,42857 | 0,04263 | 0,03755 | 0,03909 | 0,02464 | 0,02262 |
| 529,46575 | 0,04403 | 0,03873 | 0,04051 | 0,02731 | 0,02521 |
| 529,50294 | 0,04548 | 0,04003 | 0,04201 | 0,03004 | 0,02787 |
| 529,54012 | 0,04697 | 0,04146 | 0,0436 | 0,03278 | 0,03055 |
| 529,5773 | 0,04853 | 0,04304 | 0,04531 | 0,03551 | 0,03323 |
| 529,61448 | 0,05017 | 0,0448 | 0,04715 | 0,03819 | 0,03588 |
| 529,65166 | 0,05196 | 0,04676 | 0,04917 | 0,0408 | 0,03851 |
| 529,68885 | 0,05397 | 0,049 | 0,05141 | 0,04335 | 0,04112 |
| 529,72603 | 0,05627 | 0,05155 | 0,05393 | 0,04586 | 0,04373 |
| 529,76321 | 0,05895 | 0,05447 | 0,05677 | 0,04839 | 0,0464 |
| 529,80039 | 0,06211 | 0,05783 | 0,06 | 0,05101 | 0,04918 |
| 529,83757 | 0,06581 | 0,06167 | 0,06366 | 0,05382 | 0,05215 |
| 529,87476 | 0,0701 | 0,06603 | 0,06778 | 0,05692 | 0,05546 |
| 529,91194 | 0,07501 | 0,07092 | 0,07236 | 0,06042 | 0,05919 |
| 529,94912 | 0,08051 | 0,07631 | 0,07739 | 0,06445 | 0,06343 |
| 529,9863 | 0,08647 | 0,08215 | 0,08279 | 0,06909 | 0,06827 |
| 530,02348 | 0,09272 | 0,08833 | 0,08847 | 0,0744 | 0,07375 |
| 530,06067 | 0,09909 | 0,0947 | 0,09428 | 0,08041 | 0,07988 |
| 530,09785 | 0,10534 | 0,10108 | 0,10003 | 0,08707 | 0,08661 |
| 530,13503 | 0,11123 | 0,1072 | 0,1055 | 0,09428 | 0,09383 |
| 530,17221 | 0,11652 | 0,11284 | 0,1105 | 0,10182 | 0,10136 |
| 530,20939 | 0,121 | 0,11778 | 0,11483 | 0,10938 | 0,10896 |
| 530,24658 | 0,12447 | 0,12181 | 0,11833 | 0,11662 | 0,11635 |
| 530,28376 | 0,1268 | 0,12481 | 0,12089 | 0,1232 | 0,12311 |
| 530,32094 | 0,12792 | 0,12666 | 0,12243 | 0,12879 | 0,12896 |
| 530,35812 | 0,12782 | 0,12734 | 0,12293 | 0,13311 | 0,13363 |
| 530,3953 | 0,12653 | 0,12688 | 0,12244 | 0,13594 | 0,13692 |
| 530,43249 | 0,1243 | 0,12536 | 0,12104 | 0,13717 | 0,13872 |
| 530,46967 | 0,12136 | 0,12295 | 0,11888 | 0,13679 | 0,13899 |
| 530,50685 | 0,11792 | 0,11982 | 0,1161 | 0,1349 | 0,13781 |
| 530,54403 | 0,11423 | 0,11615 | 0,1129 | 0,1317 | 0,13534 |
| 530,58121 | 0,11049 | 0,11221 | 0,1095 | 0,12739 | 0,13178 |
| 530,6184 | 0,10688 | 0,1082 | 0,10607 | 0,12241 | 0,12741 |
| 530,65558 | 0,10352 | 0,10427 | 0,10272 | 0,11707 | 0,12249 |
| 530,69276 | 0,10049 | 0,10053 | 0,09954 | 0,11165 | 0,11732 |
| 530,72994 | 0,09781 | 0,09705 | 0,09659 | 0,10637 | 0,11216 |
| 530,76712 | 0,09546 | 0,09387 | 0,09388 | 0,10137 | 0,10718 |
| 530,80431 | 0,09339 | 0,09099 | 0,09139 | 0,09675 | 0,1025 |
| 530,84149 | 0,09154 | 0,0884 | 0,0891 | 0,09255 | 0,09819 |
| 530,87867 | 0,08982 | 0,08607 | 0,08697 | 0,08877 | 0,09428 |
| 530,91585 | 0,08818 | 0,08397 | 0,08499 | 0,08538 | 0,09076 |
| 530,95303 | 0,08662 | 0,08213 | 0,08318 | 0,08233 | 0,08762 |
| 530,99022 | 0,08516 | 0,08057 | 0,08157 | 0,07959 | 0,08484 |
| 531,0274 | 0,08386 | 0,07937 | 0,08026 | 0,07715 | 0,08241 |
| 531,06458 | 0,08282 | 0,07862 | 0,07939 | 0,07498 | 0,08035 |
| 531,10176 | 0,0822 | 0,07847 | 0,07914 | 0,07312 | 0,07871 |
| 531,13894 | 0,08217 | 0,07911 | 0,07973 | 0,07163 | 0,07754 |
| 531,17613 | 0,08293 | 0,08071 | 0,08138 | 0,07064 | 0,07695 |
| 531,21331 | 0,08469 | 0,08348 | 0,08435 | 0,07028 | 0,07711 |
| 531,25049 | 0,08768 | 0,0876 | 0,08883 | 0,07075 | 0,07821 |
| 531,28767 | 0,09222 | 0,09323 | 0,09503 | 0,07228 | 0,08048 |
| 531,32485 | 0,09832 | 0,10048 | 0,10304 | 0,07513 | 0,08417 |
| 531,36204 | 0,10604 | 0,10939 | 0,11296 | 0,0796 | 0,08955 |
| 531,39922 | 0,11533 | 0,12004 | 0,1248 | 0,08601 | 0,09688 |
| 531,4364 | 0,12605 | 0,13213 | 0,13819 | 0,09479 | 0,10636 |
| 531,47358 | 0,13795 | 0,14534 | 0,15278 | 0,10592 | 0,11819 |
| 531,51076 | 0,15068 | 0,1593 | 0,16815 | 0,11942 | 0,13249 |
| 531,54795 | 0,16381 | 0,17354 | 0,18375 | 0,13515 | 0,14887 |
| 531,58513 | 0,17682 | 0,18755 | 0,199 | 0,15278 | 0,16696 |
| 531,62231 | 0,18917 | 0,20079 | 0,21329 | 0,17178 | 0,18618 |
| 531,65949 | 0,20033 | 0,21272 | 0,22602 | 0,19147 | 0,20582 |
| 531,69667 | 0,20982 | 0,22284 | 0,23666 | 0,21098 | 0,22505 |
| 531,73386 | 0,21701 | 0,23075 | 0,24476 | 0,22938 | 0,24294 |
| 531,77104 | 0,22179 | 0,23615 | 0,25001 | 0,24572 | 0,25859 |
| 531,80822 | 0,22411 | 0,23876 | 0,25206 | 0,25911 | 0,27117 |
| 531,8454 | 0,22404 | 0,23853 | 0,25103 | 0,26841 | 0,28 |
| 531,88258 | 0,22182 | 0,23582 | 0,24727 | 0,27342 | 0,28447 |
| 531,91977 | 0,21777 | 0,23094 | 0,24114 | 0,27409 | 0,28418 |
| 531,95695 | 0,21232 | 0,22428 | 0,23307 | 0,2706 | 0,27966 |
| 531,99413 | 0,20592 | 0,21632 | 0,22359 | 0,2634 | 0,27137 |
| 532,03131 | 0,19904 | 0,20754 | 0,21323 | 0,25317 | 0,25996 |
| 532,06849 | 0,19211 | 0,1984 | 0,20248 | 0,24072 | 0,24621 |
| 532,10568 | 0,18549 | 0,18935 | 0,19182 | 0,22693 | 0,231 |
| 532,14286 | 0,17946 | 0,18075 | 0,18163 | 0,21267 | 0,21517 |
| 532,18004 | 0,17428 | 0,17289 | 0,17221 | 0,19872 | 0,19955 |
| 532,21722 | 0,17001 | 0,16599 | 0,16378 | 0,18575 | 0,1848 |
| 532,2544 | 0,16665 | 0,16028 | 0,15656 | 0,17436 | 0,17147 |
| 532,29159 | 0,16417 | 0,15573 | 0,15051 | 0,16487 | 0,16 |
| 532,32877 | 0,16251 | 0,1523 | 0,14561 | 0,15731 | 0,15068 |
| 532,36595 | 0,1616 | 0,14996 | 0,14182 | 0,15166 | 0,14339 |
| 532,40313 | 0,16138 | 0,14864 | 0,13911 | 0,1478 | 0,13802 |
| 532,44031 | 0,16181 | 0,14828 | 0,13744 | 0,14555 | 0,13441 |
| 532,4775 | 0,16288 | 0,14882 | 0,13678 | 0,14467 | 0,13235 |
| 532,51468 | 0,16459 | 0,15023 | 0,13712 | 0,14493 | 0,13158 |
| 532,55186 | 0,16696 | 0,15247 | 0,13849 | 0,1461 | 0,13188 |
| 532,58904 | 0,17004 | 0,15556 | 0,14092 | 0,14796 | 0,13302 |
| 532,62622 | 0,17393 | 0,1595 | 0,14448 | 0,15031 | 0,13482 |
| 532,66341 | 0,17866 | 0,16437 | 0,14929 | 0,15304 | 0,13715 |
| 532,70059 | 0,18426 | 0,17023 | 0,15543 | 0,15604 | 0,13994 |
| 532,73777 | 0,19075 | 0,17705 | 0,16287 | 0,1593 | 0,1432 |
| 532,77495 | 0,19811 | 0,18482 | 0,17163 | 0,16289 | 0,147 |
| 532,81213 | 0,20629 | 0,19351 | 0,18166 | 0,16693 | 0,15146 |
| 532,84932 | 0,2152 | 0,20301 | 0,19285 | 0,17162 | 0,15678 |
| 532,8865 | 0,22467 | 0,21316 | 0,20503 | 0,17719 | 0,16317 |
| 532,92368 | 0,23447 | 0,22374 | 0,21791 | 0,18388 | 0,17081 |
| 532,96086 | 0,24433 | 0,23445 | 0,23116 | 0,19189 | 0,17986 |
| 532,99804 | 0,25391 | 0,24494 | 0,24434 | 0,20135 | 0,19038 |
| 533,03523 | 0,26282 | 0,25481 | 0,25697 | 0,21229 | 0,20233 |
| 533,07241 | 0,27056 | 0,26365 | 0,2685 | 0,22455 | 0,21551 |
| 533,10959 | 0,27672 | 0,27083 | 0,27817 | 0,23787 | 0,22958 |
| 533,14677 | 0,28098 | 0,2761 | 0,28562 | 0,25156 | 0,24389 |
| 533,18395 | 0,28311 | 0,27918 | 0,29046 | 0,26491 | 0,2577 |
| 533,22114 | 0,28294 | 0,27988 | 0,29243 | 0,27712 | 0,27027 |
| 533,25832 | 0,28044 | 0,27815 | 0,29142 | 0,2874 | 0,28084 |
| 533,2955 | 0,27569 | 0,27403 | 0,28747 | 0,29502 | 0,28874 |
| 533,33268 | 0,2689 | 0,26772 | 0,28078 | 0,2994 | 0,29343 |
| 533,36986 | 0,26036 | 0,25949 | 0,27168 | 0,30013 | 0,29456 |
| 533,40705 | 0,25044 | 0,2497 | 0,26061 | 0,29708 | 0,292 |
| 533,44423 | 0,23955 | 0,23876 | 0,24808 | 0,29036 | 0,28583 |
| 533,48141 | 0,2281 | 0,22709 | 0,23465 | 0,28034 | 0,27639 |
| 533,51859 | 0,21649 | 0,21513 | 0,22086 | 0,26746 | 0,26406 |
| 533,55577 | 0,20511 | 0,20329 | 0,20725 | 0,25258 | 0,24964 |
| 533,59295 | 0,19422 | 0,19188 | 0,19422 | 0,2366 | 0,234 |
| 533,63014 | 0,18399 | 0,18109 | 0,18204 | 0,22026 | 0,21783 |
| 533,66732 | 0,17454 | 0,17107 | 0,17088 | 0,20418 | 0,20175 |
| 533,7045 | 0,16592 | 0,16188 | 0,16082 | 0,18885 | 0,18629 |
| 533,74168 | 0,15811 | 0,15354 | 0,15185 | 0,17464 | 0,17181 |
| 533,77886 | 0,15109 | 0,14602 | 0,14392 | 0,16174 | 0,15859 |
| 533,81605 | 0,14476 | 0,13925 | 0,13692 | 0,15024 | 0,14674 |
| 533,85323 | 0,13906 | 0,13317 | 0,13071 | 0,14011 | 0,13629 |
| 533,89041 | 0,13389 | 0,12769 | 0,12516 | 0,13125 | 0,12718 |
| 533,92759 | 0,12916 | 0,12274 | 0,12012 | 0,12355 | 0,11935 |
| 533,96477 | 0,12481 | 0,11826 | 0,11552 | 0,11688 | 0,11261 |
| 534,00196 | 0,12075 | 0,11416 | 0,1112 | 0,11101 | 0,10674 |
| 534,03914 | 0,11691 | 0,11037 | 0,10711 | 0,1058 | 0,1016 |
| 534,07632 | 0,11325 | 0,10687 | 0,10322 | 0,10114 | 0,09704 |
| 534,1135 | 0,10976 | 0,10362 | 0,0995 | 0,09695 | 0,09296 |
| 534,15068 | 0,1064 | 0,10061 | 0,09597 | 0,09316 | 0,08927 |
| 534,18787 | 0,10319 | 0,09782 | 0,09265 | 0,08972 | 0,0859 |
| 534,22505 | 0,10013 | 0,09527 | 0,08957 | 0,08659 | 0,08279 |
| 534,26223 | 0,09724 | 0,09296 | 0,08677 | 0,08374 | 0,07991 |
| 534,29941 | 0,09454 | 0,0909 | 0,0843 | 0,08113 | 0,07722 |
| 534,33659 | 0,09207 | 0,08911 | 0,08219 | 0,07874 | 0,07471 |
| 534,37378 | 0,08986 | 0,08761 | 0,08048 | 0,07656 | 0,07235 |
| 534,41096 | 0,08794 | 0,08642 | 0,07921 | 0,07454 | 0,07013 |
| 534,44814 | 0,08636 | 0,08553 | 0,07836 | 0,07267 | 0,06805 |
| 534,48532 | 0,08511 | 0,08494 | 0,07791 | 0,07092 | 0,06611 |
| 534,5225 | 0,0842 | 0,08462 | 0,07783 | 0,06929 | 0,06431 |
| 534,55969 | 0,08362 | 0,08457 | 0,0781 | 0,06777 | 0,06266 |
| 534,59687 | 0,08332 | 0,08472 | 0,07865 | 0,06635 | 0,06118 |
| 534,63405 | 0,08327 | 0,08505 | 0,07942 | 0,06505 | 0,05989 |
| 534,67123 | 0,08339 | 0,08548 | 0,08033 | 0,06388 | 0,05882 |
| 534,70841 | 0,08359 | 0,08595 | 0,08127 | 0,06287 | 0,058 |
| 534,7456 | 0,08378 | 0,08636 | 0,08216 | 0,06204 | 0,05747 |
| 534,78278 | 0,08385 | 0,08663 | 0,08288 | 0,06145 | 0,05726 |
| 534,81996 | 0,08371 | 0,08663 | 0,08331 | 0,06115 | 0,05739 |
| 534,85714 | 0,08326 | 0,08631 | 0,08335 | 0,06115 | 0,05788 |
| 534,89432 | 0,08238 | 0,0856 | 0,08296 | 0,06149 | 0,05872 |
| 534,93151 | 0,08106 | 0,08445 | 0,08207 | 0,0622 | 0,05993 |
| 534,96869 | 0,07931 | 0,08285 | 0,0807 | 0,06327 | 0,06147 |
| 535,00587 | 0,07713 | 0,08082 | 0,07885 | 0,06468 | 0,06331 |
| 535,04305 | 0,0746 | 0,07841 | 0,07659 | 0,0664 | 0,0654 |
| 535,08023 | 0,0718 | 0,07572 | 0,07402 | 0,06837 | 0,06767 |
| 535,11742 | 0,06886 | 0,07285 | 0,07126 | 0,0705 | 0,07004 |
| 535,1546 | 0,06594 | 0,06995 | 0,06849 | 0,07271 | 0,07243 |
| 535,19178 | 0,06318 | 0,0672 | 0,06588 | 0,07492 | 0,07478 |
| 535,22896 | 0,06077 | 0,06482 | 0,06364 | 0,07705 | 0,07704 |
| 535,26614 | 0,05888 | 0,06302 | 0,06204 | 0,07909 | 0,07923 |
| 535,30333 | 0,0577 | 0,06197 | 0,06125 | 0,08108 | 0,08142 |
| 535,34051 | 0,05747 | 0,06183 | 0,06144 | 0,08312 | 0,0837 |
| 535,37769 | 0,05826 | 0,06276 | 0,06276 | 0,08537 | 0,08626 |
| 535,41487 | 0,06017 | 0,06486 | 0,06532 | 0,08805 | 0,08929 |
| 535,45205 | 0,06325 | 0,06817 | 0,06918 | 0,09137 | 0,093 |
| 535,48924 | 0,06749 | 0,07272 | 0,07433 | 0,09557 | 0,09763 |
| 535,52642 | 0,07282 | 0,07843 | 0,08071 | 0,10083 | 0,10333 |
| 535,5636 | 0,07911 | 0,08518 | 0,08818 | 0,10725 | 0,11032 |
| 535,60078 | 0,08615 | 0,09276 | 0,09651 | 0,11484 | 0,11847 |
| 535,63796 | 0,09364 | 0,10091 | 0,10539 | 0,12348 | 0,12756 |
| 535,67515 | 0,10124 | 0,10925 | 0,11445 | 0,13277 | 0,13726 |
| 535,71233 | 0,10856 | 0,11734 | 0,1232 | 0,14218 | 0,14712 |
| 535,74951 | 0,11519 | 0,12476 | 0,13118 | 0,15115 | 0,15659 |
| 535,78669 | 0,12058 | 0,13114 | 0,13799 | 0,15908 | 0,16509 |
| 535,82387 | 0,12448 | 0,13613 | 0,14324 | 0,16537 | 0,17203 |
| 535,86106 | 0,12664 | 0,13944 | 0,14664 | 0,16952 | 0,17691 |
| 535,89824 | 0,12694 | 0,14089 | 0,14799 | 0,17117 | 0,1793 |
| 535,93542 | 0,12537 | 0,1404 | 0,14721 | 0,17011 | 0,17897 |
| 535,9726 | 0,12203 | 0,13799 | 0,14434 | 0,16636 | 0,17561 |
| 536,00978 | 0,11717 | 0,13381 | 0,13956 | 0,16009 | 0,16962 |
| 536,04697 | 0,11106 | 0,12809 | 0,13312 | 0,15162 | 0,16143 |
| 536,08415 | 0,10409 | 0,12108 | 0,12535 | 0,14153 | 0,1515 |
| 536,12133 | 0,09662 | 0,11326 | 0,11668 | 0,13054 | 0,14041 |
| 536,15851 | 0,08904 | 0,10502 | 0,10763 | 0,11922 | 0,12874 |
| 536,19569 | 0,08166 | 0,09674 | 0,09858 | 0,10809 | 0,11703 |
| 536,23288 | 0,07485 | 0,08872 | 0,08988 | 0,09761 | 0,10578 |
| 536,27006 | 0,06876 | 0,08122 | 0,08181 | 0,08809 | 0,0954 |
| 536,30724 | 0,06351 | 0,07445 | 0,07457 | 0,07976 | 0,08619 |
| 536,34442 | 0,05912 | 0,06854 | 0,0683 | 0,07272 | 0,07832 |
| 536,3816 | 0,05559 | 0,06355 | 0,06307 | 0,06701 | 0,07202 |
| 536,41879 | 0,05287 | 0,05951 | 0,05887 | 0,06256 | 0,06715 |
| 536,45597 | 0,05088 | 0,0564 | 0,05568 | 0,0593 | 0,0636 |
| 536,49315 | 0,04953 | 0,05416 | 0,05342 | 0,05717 | 0,06122 |
| 536,53033 | 0,04872 | 0,05273 | 0,05204 | 0,05593 | 0,05988 |
| 536,56751 | 0,04835 | 0,05193 | 0,05137 | 0,05544 | 0,0594 |
| 536,6047 | 0,04832 | 0,05163 | 0,05125 | 0,05557 | 0,0596 |
| 536,64188 | 0,04854 | 0,05172 | 0,05156 | 0,05618 | 0,06031 |
| 536,67906 | 0,04893 | 0,05205 | 0,05216 | 0,05713 | 0,06136 |
| 536,71624 | 0,04937 | 0,05251 | 0,05291 | 0,05828 | 0,06256 |
| 536,75342 | 0,04979 | 0,05297 | 0,05369 | 0,05946 | 0,06375 |
| 536,79061 | 0,05009 | 0,05333 | 0,05436 | 0,06054 | 0,06473 |
| 536,82779 | 0,05022 | 0,05348 | 0,05482 | 0,06134 | 0,06534 |
| 536,86497 | 0,05009 | 0,05334 | 0,05497 | 0,06174 | 0,06546 |
| 536,90215 | 0,04966 | 0,05286 | 0,05473 | 0,06154 | 0,06499 |
| 536,93933 | 0,04889 | 0,05195 | 0,05403 | 0,06069 | 0,06387 |
| 536,97652 | 0,04775 | 0,05063 | 0,05284 | 0,05917 | 0,06208 |
| 537,0137 | 0,04625 | 0,04893 | 0,05118 | 0,05699 | 0,05964 |
| 537,05088 | 0,04441 | 0,04689 | 0,04911 | 0,05421 | 0,05661 |
| 537,08806 | 0,04227 | 0,04457 | 0,04666 | 0,05093 | 0,05309 |
| 537,12524 | 0,03987 | 0,04202 | 0,04393 | 0,04728 | 0,04919 |
| 537,16243 | 0,03729 | 0,03933 | 0,04097 | 0,04339 | 0,04506 |
| 537,19961 | 0,03461 | 0,03658 | 0,0379 | 0,03941 | 0,04084 |
| 537,23679 | 0,0319 | 0,03382 | 0,03478 | 0,03549 | 0,03671 |
| 537,27397 | 0,02923 | 0,03113 | 0,03169 | 0,03173 | 0,03277 |
| 537,31115 | 0,02664 | 0,02856 | 0,02871 | 0,02825 | 0,02912 |
| 537,34834 | 0,02419 | 0,02615 | 0,0259 | 0,02513 | 0,02582 |
| 537,38552 | 0,02191 | 0,02394 | 0,0233 | 0,02236 | 0,02289 |
| 537,4227 | 0,01982 | 0,02193 | 0,02095 | 0,01995 | 0,02036 |
| 537,45988 | 0,01794 | 0,02011 | 0,01883 | 0,01788 | 0,01821 |
| 537,49706 | 0,01626 | 0,01849 | 0,01696 | 0,01612 | 0,01642 |
| 537,53425 | 0,01479 | 0,01704 | 0,01532 | 0,01461 | 0,01494 |
| 537,57143 | 0,01351 | 0,01576 | 0,01388 | 0,01334 | 0,01373 |
| 537,60861 | 0,01242 | 0,01462 | 0,01264 | 0,01224 | 0,01276 |
| 537,64579 | 0,01147 | 0,0136 | 0,01156 | 0,01129 | 0,01196 |
| 537,68297 | 0,01066 | 0,01269 | 0,01063 | 0,01046 | 0,0113 |
| 537,72016 | 0,00996 | 0,01187 | 0,00982 | 0,00973 | 0,01073 |
| 537,75734 | 0,00937 | 0,01113 | 0,00912 | 0,00907 | 0,01023 |
| 537,79452 | 0,00887 | 0,01045 | 0,0085 | 0,00849 | 0,00978 |
| 537,8317 | 0,00844 | 0,00982 | 0,00797 | 0,00796 | 0,00937 |
| 537,86888 | 0,00808 | 0,00924 | 0,00749 | 0,00749 | 0,00898 |
| 537,90607 | 0,00778 | 0,00869 | 0,00706 | 0,00707 | 0,00861 |
| 537,94325 | 0,00753 | 0,00818 | 0,00668 | 0,00671 | 0,00827 |
| 537,98043 | 0,00733 | 0,00769 | 0,00634 | 0,0064 | 0,00793 |
| 538,01761 | 0,00715 | 0,00723 | 0,00603 | 0,00613 | 0,00761 |
| 538,05479 | 0,00701 | 0,0068 | 0,00575 | 0,0059 | 0,00729 |
| 538,09198 | 0,00687 | 0,0064 | 0,0055 | 0,00571 | 0,00699 |
| 538,12916 | 0,00674 | 0,00602 | 0,00527 | 0,00554 | 0,00669 |
| 538,16634 | 0,0066 | 0,00567 | 0,00505 | 0,00539 | 0,0064 |
| 538,20352 | 0,00645 | 0,00535 | 0,00485 | 0,00525 | 0,0061 |
| 538,2407 | 0,00628 | 0,00506 | 0,00467 | 0,00511 | 0,0058 |
| 538,27789 | 0,00608 | 0,00478 | 0,00449 | 0,00496 | 0,00551 |
| 538,31507 | 0,00586 | 0,00453 | 0,00432 | 0,00481 | 0,0052 |
| 538,35225 | 0,00562 | 0,0043 | 0,00415 | 0,00464 | 0,0049 |
| 538,38943 | 0,00536 | 0,00409 | 0,00399 | 0,00446 | 0,00459 |
| 538,42661 | 0,00509 | 0,00388 | 0,00382 | 0,00427 | 0,00428 |
| 538,4638 | 0,0048 | 0,00369 | 0,00366 | 0,00407 | 0,00397 |
| 538,50098 | 0,00451 | 0,0035 | 0,0035 | 0,00386 | 0,00367 |
| 538,53816 | 0,00422 | 0,00332 | 0,00334 | 0,00364 | 0,00338 |
| 538,57534 | 0,00394 | 0,00314 | 0,00317 | 0,00342 | 0,0031 |
| 538,61252 | 0,00367 | 0,00295 | 0,003 | 0,00318 | 0,00283 |
| 538,64971 | 0,00341 | 0,00277 | 0,00283 | 0,00295 | 0,00258 |
| 538,68689 | 0,00316 | 0,00259 | 0,00266 | 0,00271 | 0,00235 |
| 538,72407 | 0,00293 | 0,00241 | 0,00248 | 0,00248 | 0,00213 |
| 538,76125 | 0,0027 | 0,00223 | 0,0023 | 0,00225 | 0,00194 |
| 538,79843 | 0,00249 | 0,00204 | 0,00211 | 0,00203 | 0,00176 |
| 538,83562 | 0,00228 | 0,00187 | 0,00193 | 0,00181 | 0,0016 |
| 538,8728 | 0,00209 | 0,00169 | 0,00175 | 0,00161 | 0,00145 |
| 538,90998 | 0,0019 | 0,00153 | 0,00158 | 0,00142 | 0,00132 |
| 538,94716 | 0,00172 | 0,00136 | 0,00141 | 0,00124 | 0,00119 |
| 538,98434 | 0,00156 | 0,00121 | 0,00126 | 0,00107 | 0,00108 |
| 539,02153 | 0,00141 | 0,00107 | 0,00111 | 0,00093 | 0,00098 |
| 539,05871 | 0,00127 | 0,00094 | 0,00098 | 0,00079 | 0,00088 |
| 539,09589 | 0,00114 | 0,00082 | 0,00087 | 0,00068 | 0,00079 |
| 539,13307 | 0,00102 | 0,00071 | 0,00077 | 0,00057 | 7e-04 |
| 539,17025 | 0,00092 | 0,00062 | 0,00068 | 0,00048 | 0,00063 |
| 539,20744 | 0,00083 | 0,00054 | 6e-04 | 0,00041 | 0,00056 |
| 539,24462 | 0,00075 | 0,00046 | 0,00053 | 0,00034 | 0,00049 |
| 539,2818 | 0,00067 | 4e-04 | 0,00046 | 0,00029 | 0,00044 |
| 539,31898 | 6e-04 | 0,00034 | 4e-04 | 0,00025 | 0,00039 |
| 539,35616 | 0,00054 | 0,00029 | 0,00034 | 0,00022 | 0,00035 |
| 539,39335 | 0,00049 | 0,00024 | 0,00029 | 0,00019 | 0,00031 |
| 539,43053 | 0,00043 | 2e-04 | 0,00025 | 0,00018 | 0,00028 |
| 539,46771 | 0,00039 | 0,00017 | 2e-04 | 0,00016 | 0,00026 |
| 539,50489 | 0,00035 | 0,00014 | 0,00016 | 0,00016 | 0,00025 |
| 539,54207 | 0,00032 | 0,00011 | 0,00013 | 0,00015 | 0,00023 |
| 539,57926 | 0,00029 | 9e-05 | 1e-04 | 0,00015 | 0,00023 |
| 539,61644 | 0,00027 | 7e-05 | 8e-05 | 0,00015 | 0,00022 |
| 539,65362 | 0,00025 | 5e-05 | 6e-05 | 0,00015 | 0,00022 |
| 539,6908 | 0,00024 | 4e-05 | 4e-05 | 0,00015 | 0,00022 |
| 539,72798 | 0,00024 | 3e-05 | 3e-05 | 0,00014 | 0,00022 |
| 539,76517 | 0,00024 | 2e-05 | 2e-05 | 0,00014 | 0,00021 |
| 539,80235 | 0,00025 | 2e-05 | 1e-05 | 0,00013 | 0,00021 |
| 539,83953 | 0,00025 | 2e-05 | 1e-05 | 0,00013 | 2e-04 |
| 539,87671 | 0,00025 | 1e-05 | 1e-05 | 0,00012 | 0,00019 |
| 539,91389 | 0,00026 | 1e-05 | 0 | 1e-04 | 0,00017 |
| 539,95108 | 0,00026 | 2e-05 | 0 | 9e-05 | 0,00016 |
| 539,98826 | 0,00026 | 2e-05 | 0 | 8e-05 | 0,00014 |
| 540,02544 | 0,00025 | 2e-05 | 0 | 7e-05 | 0,00012 |
| 540,06262 | 0,00025 | 3e-05 | 0 | 5e-05 | 1e-04 |
| 540,0998 | 0,00024 | 4e-05 | 0 | 4e-05 | 9e-05 |
| 540,13699 | 0,00022 | 4e-05 | 0 | 3e-05 | 7e-05 |
| 540,17417 | 0,00021 | 5e-05 | 0 | 3e-05 | 6e-05 |
| 540,21135 | 0,00019 | 5e-05 | 0 | 2e-05 | 4e-05 |
| 540,24853 | 0,00018 | 6e-05 | 0 | 1e-05 | 3e-05 |
| 540,28571 | 0,00016 | 6e-05 | 0 | 1e-05 | 2e-05 |
| 540,3229 | 0,00014 | 7e-05 | 0 | 1e-05 | 2e-05 |
| 540,36008 | 0,00013 | 7e-05 | 0 | 0 | 1e-05 |
| 540,39726 | 0,00011 | 6e-05 | 0 | 0 | 1e-05 |
| 540,43444 | 9e-05 | 6e-05 | 0 | 0 | 1e-05 |
| 540,47162 | 8e-05 | 6e-05 | 0 | 0 | 0 |
| 540,50881 | 6e-05 | 5e-05 | 0 | 0 | 0 |
| 540,54599 | 5e-05 | 5e-05 | 0 | 0 | 0 |
| 540,58317 | 4e-05 | 4e-05 | 0 | 0 | 0 |
| 540,62035 | 3e-05 | 3e-05 | 0 | 0 | 0 |
| 540,65753 | 2e-05 | 3e-05 | 0 | 0 | 0 |
| 540,69472 | 2e-05 | 2e-05 | 0 | 0 | 0 |
| 540,7319 | 1e-05 | 2e-05 | 0 | 0 | 0 |
| 540,76908 | 1e-05 | 1e-05 | 0 | 0 | 0 |
| 540,80626 | 1e-05 | 1e-05 | 0 | 0 | 0 |
| 540,84344 | 0 | 1e-05 | 0 | 0 | 0 |
| 540,88063 | 0 | 0 | 0 | 0 | 0 |
| 540,91781 | 0 | 0 | 0 | 0 | 0 |
| 540,95499 | 0 | 0 | 0 | 0 | 0 |
| 540,99217 | 0 | 0 | 0 | 0 | 0 |
| 541,02935 | 0 | 0 | 0 | 0 | 0 |
| 541,06654 | 0 | 0 | 0 | 0 | 0 |
| 541,10372 | 0 | 0 | 0 | 0 | 0 |
| 541,1409 | 0 | 0 | 0 | 0 | 0 |
| 541,17808 | 0 | 0 | 0 | 0 | 0 |
| 541,21526 | 0 | 0 | 0 | 0 | 0 |
| 541,25245 | 0 | 0 | 0 | 0 | 0 |
| 541,28963 | 0 | 0 | 0 | 0 | 0 |
| 541,32681 | 0 | 0 | 0 | 0 | 0 |
| 541,36399 | 0 | 0 | 0 | 0 | 0 |
| 541,40117 | 0 | 0 | 0 | 0 | 0 |
| 541,43836 | 0 | 0 | 0 | 0 | 0 |
| 541,47554 | 0 | 0 | 0 | 0 | 0 |
| 541,51272 | 0 | 0 | 0 | 0 | 0 |
| 541,5499 | 0 | 0 | 0 | 0 | 0 |
| 541,58708 | 0 | 0 | 0 | 0 | 0 |
| 541,62427 | 0 | 0 | 0 | 0 | 0 |
| 541,66145 | 0 | 0 | 0 | 0 | 0 |
| 541,69863 | 0 | 0 | 0 | 0 | 0 |
| 541,73581 | 0 | 0 | 0 | 0 | 0 |
| 541,77299 | 0 | 0 | 0 | 0 | 0 |
| 541,81018 | 0 | 0 | 0 | 0 | 0 |
| 541,84736 | 0 | 0 | 0 | 0 | 0 |
| 541,88454 | 0 | 0 | 0 | 0 | 0 |
| 541,92172 | 0 | 0 | 0 | 0 | 0 |
| 541,9589 | 0 | 0 | 0 | 0 | 0 |
| 541,99609 | 0 | 0 | 0 | 0 | 0 |
| 542,03327 | 0 | 0 | 0 | 0 | 0 |
| 542,07045 | 0 | 0 | 0 | 0 | 0 |
| 542,10763 | 0 | 0 | 0 | 0 | 0 |
| 542,14481 | 0 | 0 | 0 | 0 | 0 |
| 542,182 | 0 | 0 | 0 | 0 | 0 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 0 | 0 | 0 |
| 524,74364 | 0 | 0 | 0 | 0 | 0 |
| 524,78082 | 0 | 0 | 0 | 0 | 0 |
| 524,818 | 0 | 0 | 0 | 0 | 0 |
| 524,85519 | 0 | 0 | 0 | 0 | 0 |
| 524,89237 | 0 | 0 | 0 | 0 | 0 |
| 524,92955 | 0 | 0 | 0 | 0 | 0 |
| 524,96673 | 0 | 0 | 0 | 0 | 0 |
| 525,00391 | 0 | 0 | 0 | 0 | 0 |
| 525,0411 | 0 | 0 | 0 | 0 | 0 |
| 525,07828 | 0 | 0 | 0 | 0 | 0 |
| 525,11546 | 0 | 0 | 0 | 0 | 0 |
| 525,15264 | 0 | 0 | 0 | 0 | 0 |
| 525,18982 | 0 | 0 | 0 | 0 | 0 |
| 525,22701 | 0 | 0 | 0 | 0 | 0 |
| 525,26419 | 0 | 0 | 0 | 0 | 0 |
| 525,30137 | 0 | 0 | 0 | 0 | 0 |
| 525,33855 | 0 | 0 | 0 | 0 | 0 |
| 525,37573 | 1e-05 | 0 | 0 | 0 | 0 |
| 525,41292 | 1e-05 | 0 | 0 | 0 | 0 |
| 525,4501 | 1e-05 | 0 | 0 | 0 | 0 |
| 525,48728 | 1e-05 | 0 | 0 | 0 | 0 |
| 525,52446 | 2e-05 | 0 | 0 | 0 | 0 |
| 525,56164 | 2e-05 | 0 | 0 | 0 | 0 |
| 525,59883 | 3e-05 | 0 | 0 | 0 | 0 |
| 525,63601 | 3e-05 | 0 | 0 | 0 | 0 |
| 525,67319 | 4e-05 | 0 | 0 | 0 | 0 |
| 525,71037 | 4e-05 | 0 | 0 | 0 | 0 |
| 525,74755 | 4e-05 | 0 | 0 | 0 | 0 |
| 525,78474 | 5e-05 | 0 | 0 | 0 | 0 |
| 525,82192 | 5e-05 | 0 | 0 | 0 | 0 |
| 525,8591 | 5e-05 | 0 | 0 | 0 | 0 |
| 525,89628 | 4e-05 | 0 | 0 | 0 | 0 |
| 525,93346 | 4e-05 | 0 | 0 | 0 | 0 |
| 525,97065 | 4e-05 | 0 | 0 | 0 | 0 |
| 526,00783 | 3e-05 | 0 | 0 | 0 | 0 |
| 526,04501 | 3e-05 | 0 | 0 | 0 | 0 |
| 526,08219 | 2e-05 | 0 | 0 | 0 | 0 |
| 526,11937 | 2e-05 | 0 | 1e-05 | 0 | 0 |
| 526,15656 | 2e-05 | 0 | 1e-05 | 0 | 0 |
| 526,19374 | 2e-05 | 1e-05 | 1e-05 | 0 | 0 |
| 526,23092 | 1e-05 | 1e-05 | 2e-05 | 0 | 0 |
| 526,2681 | 2e-05 | 1e-05 | 2e-05 | 0 | 0 |
| 526,30528 | 2e-05 | 2e-05 | 3e-05 | 0 | 0 |
| 526,34247 | 2e-05 | 3e-05 | 5e-05 | 0 | 0 |
| 526,37965 | 3e-05 | 4e-05 | 6e-05 | 0 | 0 |
| 526,41683 | 4e-05 | 5e-05 | 8e-05 | 0 | 0 |
| 526,45401 | 4e-05 | 6e-05 | 9e-05 | 0 | 0 |
| 526,49119 | 5e-05 | 8e-05 | 0,00011 | 0 | 0 |
| 526,52838 | 7e-05 | 1e-04 | 0,00014 | 1e-05 | 0 |
| 526,56556 | 8e-05 | 0,00011 | 0,00016 | 1e-05 | 0 |
| 526,60274 | 9e-05 | 0,00013 | 0,00018 | 1e-05 | 0 |
| 526,63992 | 1e-04 | 0,00015 | 2e-04 | 2e-05 | 0 |
| 526,6771 | 0,00011 | 0,00017 | 0,00021 | 3e-05 | 0 |
| 526,71429 | 0,00012 | 0,00018 | 0,00022 | 4e-05 | 0 |
| 526,75147 | 0,00012 | 0,00019 | 0,00023 | 5e-05 | 0 |
| 526,78865 | 0,00013 | 2e-04 | 0,00023 | 7e-05 | 0 |
| 526,82583 | 0,00013 | 0,00021 | 0,00023 | 9e-05 | 0 |
| 526,86301 | 0,00014 | 0,00022 | 0,00022 | 0,00011 | 1e-05 |
| 526,9002 | 0,00014 | 0,00022 | 0,00021 | 0,00013 | 1e-05 |
| 526,93738 | 0,00014 | 0,00022 | 0,00019 | 0,00015 | 1e-05 |
| 526,97456 | 0,00014 | 0,00023 | 0,00018 | 0,00018 | 2e-05 |
| 527,01174 | 0,00014 | 0,00024 | 0,00016 | 2e-04 | 3e-05 |
| 527,04892 | 0,00014 | 0,00024 | 0,00014 | 0,00022 | 4e-05 |
| 527,08611 | 0,00014 | 0,00026 | 0,00012 | 0,00023 | 5e-05 |
| 527,12329 | 0,00014 | 0,00027 | 0,00011 | 0,00024 | 6e-05 |
| 527,16047 | 0,00014 | 0,00028 | 1e-04 | 0,00025 | 8e-05 |
| 527,19765 | 0,00014 | 0,00029 | 1e-04 | 0,00025 | 1e-04 |
| 527,23483 | 0,00014 | 3e-04 | 1e-04 | 0,00024 | 0,00011 |
| 527,27202 | 0,00014 | 0,00031 | 1e-04 | 0,00024 | 0,00013 |
| 527,3092 | 0,00014 | 0,00031 | 0,00011 | 0,00023 | 0,00015 |
| 527,34638 | 0,00014 | 0,00031 | 0,00012 | 0,00021 | 0,00016 |
| 527,38356 | 0,00015 | 0,00031 | 0,00013 | 2e-04 | 0,00018 |
| 527,42074 | 0,00016 | 3e-04 | 0,00015 | 0,00019 | 0,00019 |
| 527,45793 | 0,00017 | 0,00029 | 0,00017 | 0,00018 | 0,00019 |
| 527,49511 | 0,00018 | 0,00028 | 0,00019 | 0,00018 | 2e-04 |
| 527,53229 | 2e-04 | 0,00027 | 0,00021 | 0,00017 | 2e-04 |
| 527,56947 | 0,00022 | 0,00026 | 0,00023 | 0,00018 | 2e-04 |
| 527,60665 | 0,00024 | 0,00026 | 0,00025 | 0,00018 | 0,00019 |
| 527,64384 | 0,00026 | 0,00026 | 0,00027 | 0,00019 | 0,00019 |
| 527,68102 | 0,00029 | 0,00026 | 0,00028 | 2e-04 | 0,00019 |
| 527,7182 | 0,00031 | 0,00027 | 3e-04 | 0,00022 | 0,00019 |
| 527,75538 | 0,00034 | 0,00029 | 0,00031 | 0,00024 | 0,00019 |
| 527,79256 | 0,00036 | 0,00031 | 0,00032 | 0,00026 | 2e-04 |
| 527,82975 | 0,00038 | 0,00034 | 0,00033 | 0,00029 | 0,00021 |
| 527,86693 | 0,00039 | 0,00037 | 0,00034 | 0,00032 | 0,00023 |
| 527,90411 | 0,00041 | 4e-04 | 0,00034 | 0,00035 | 0,00025 |
| 527,94129 | 0,00042 | 0,00044 | 0,00035 | 0,00039 | 0,00027 |
| 527,97847 | 0,00043 | 0,00047 | 0,00036 | 0,00043 | 0,00031 |
| 528,01566 | 0,00044 | 0,00051 | 0,00037 | 0,00048 | 0,00034 |
| 528,05284 | 0,00045 | 0,00055 | 0,00038 | 0,00053 | 0,00038 |
| 528,09002 | 0,00046 | 6e-04 | 4e-04 | 0,00059 | 0,00043 |
| 528,1272 | 0,00048 | 0,00064 | 0,00043 | 0,00065 | 0,00049 |
| 528,16438 | 0,00051 | 0,00068 | 0,00046 | 0,00071 | 0,00055 |
| 528,20157 | 0,00053 | 0,00072 | 0,00049 | 0,00078 | 0,00062 |
| 528,23875 | 0,00057 | 0,00076 | 0,00053 | 0,00085 | 0,00069 |
| 528,27593 | 0,00061 | 8e-04 | 0,00057 | 0,00092 | 0,00077 |
| 528,31311 | 0,00065 | 0,00084 | 0,00061 | 0,00099 | 0,00085 |
| 528,35029 | 0,00069 | 0,00087 | 0,00066 | 0,00107 | 0,00094 |
| 528,38748 | 0,00074 | 0,00091 | 7e-04 | 0,00114 | 0,00103 |
| 528,42466 | 0,00078 | 0,00094 | 0,00075 | 0,00121 | 0,00112 |
| 528,46184 | 0,00082 | 0,00098 | 8e-04 | 0,00128 | 0,0012 |
| 528,49902 | 0,00086 | 0,00102 | 0,00085 | 0,00135 | 0,00129 |
| 528,5362 | 9e-04 | 0,00106 | 9e-04 | 0,00141 | 0,00138 |
| 528,57339 | 0,00094 | 0,00111 | 0,00095 | 0,00148 | 0,00146 |
| 528,61057 | 0,00099 | 0,00117 | 0,00101 | 0,00155 | 0,00153 |
| 528,64775 | 0,00104 | 0,00123 | 0,00107 | 0,00163 | 0,00161 |
| 528,68493 | 0,00111 | 0,00131 | 0,00114 | 0,0017 | 0,00169 |
| 528,72211 | 0,0012 | 0,0014 | 0,00122 | 0,00179 | 0,00177 |
| 528,7593 | 0,0013 | 0,00151 | 0,00131 | 0,00188 | 0,00187 |
| 528,79648 | 0,00144 | 0,00164 | 0,00141 | 0,00199 | 0,00199 |
| 528,83366 | 0,0016 | 0,00178 | 0,00152 | 0,00212 | 0,00214 |
| 528,87084 | 0,00178 | 0,00194 | 0,00166 | 0,00227 | 0,00231 |
| 528,90802 | 0,002 | 0,00212 | 0,00181 | 0,00244 | 0,00252 |
| 528,94521 | 0,00224 | 0,00232 | 0,00199 | 0,00265 | 0,00277 |
| 528,98239 | 0,00251 | 0,00253 | 0,00218 | 0,00289 | 0,00306 |
| 529,01957 | 0,00279 | 0,00277 | 0,0024 | 0,00316 | 0,00339 |
| 529,05675 | 0,00309 | 0,00301 | 0,00263 | 0,00347 | 0,00375 |
| 529,09393 | 0,00338 | 0,00327 | 0,00288 | 0,00382 | 0,00413 |
| 529,13112 | 0,00368 | 0,00354 | 0,00315 | 0,00421 | 0,00455 |
| 529,1683 | 0,00396 | 0,00381 | 0,00342 | 0,00462 | 0,00497 |
| 529,20548 | 0,00422 | 0,00409 | 0,00369 | 0,00506 | 0,00541 |
| 529,24266 | 0,00445 | 0,00436 | 0,00396 | 0,00551 | 0,00583 |
| 529,27984 | 0,00466 | 0,00462 | 0,00422 | 0,00597 | 0,00624 |
| 529,31703 | 0,00485 | 0,00486 | 0,00447 | 0,0064 | 0,00661 |
| 529,35421 | 0,00501 | 0,0051 | 0,0047 | 0,0068 | 0,00694 |
| 529,39139 | 0,00515 | 0,00531 | 0,00492 | 0,00714 | 0,00722 |
| 529,42857 | 0,00527 | 0,0055 | 0,00513 | 0,00741 | 0,00742 |
| 529,46575 | 0,00539 | 0,00567 | 0,00532 | 0,00759 | 0,00755 |
| 529,50294 | 0,0055 | 0,00583 | 0,00551 | 0,00767 | 0,0076 |
| 529,54012 | 0,00563 | 0,00597 | 0,00569 | 0,00763 | 0,00756 |
| 529,5773 | 0,00577 | 0,00611 | 0,00588 | 0,00748 | 0,00744 |
| 529,61448 | 0,00594 | 0,00624 | 0,00607 | 0,00725 | 0,00724 |
| 529,65166 | 0,00614 | 0,00637 | 0,00628 | 0,00694 | 0,00699 |
| 529,68885 | 0,00637 | 0,00651 | 0,00651 | 0,00659 | 0,0067 |
| 529,72603 | 0,00665 | 0,00667 | 0,00675 | 0,00622 | 0,0064 |
| 529,76321 | 0,00696 | 0,00684 | 0,00702 | 0,00585 | 0,00609 |
| 529,80039 | 0,0073 | 0,00704 | 0,0073 | 0,00553 | 0,00581 |
| 529,83757 | 0,00767 | 0,00726 | 0,00758 | 0,00527 | 0,00557 |
| 529,87476 | 0,00807 | 0,00752 | 0,00787 | 0,0051 | 0,00539 |
| 529,91194 | 0,00847 | 0,00781 | 0,00815 | 0,00503 | 0,00529 |
| 529,94912 | 0,00889 | 0,00813 | 0,00843 | 0,00507 | 0,00527 |
| 529,9863 | 0,00931 | 0,00851 | 0,0087 | 0,00525 | 0,00536 |
| 530,02348 | 0,00974 | 0,00893 | 0,00897 | 0,00555 | 0,00556 |
| 530,06067 | 0,01018 | 0,00941 | 0,00924 | 0,00599 | 0,00588 |
| 530,09785 | 0,01063 | 0,00995 | 0,00954 | 0,00655 | 0,00633 |
| 530,13503 | 0,01112 | 0,01057 | 0,00988 | 0,00724 | 0,00691 |
| 530,17221 | 0,01164 | 0,01126 | 0,01027 | 0,00805 | 0,00762 |
| 530,20939 | 0,01222 | 0,01202 | 0,01074 | 0,00898 | 0,00846 |
| 530,24658 | 0,01286 | 0,01286 | 0,0113 | 0,01004 | 0,00944 |
| 530,28376 | 0,01356 | 0,01378 | 0,01195 | 0,01122 | 0,01054 |
| 530,32094 | 0,01434 | 0,01477 | 0,01271 | 0,01251 | 0,01176 |
| 530,35812 | 0,01519 | 0,01582 | 0,01356 | 0,01392 | 0,01308 |
| 530,3953 | 0,01611 | 0,01691 | 0,01449 | 0,01542 | 0,01449 |
| 530,43249 | 0,01709 | 0,01803 | 0,01549 | 0,017 | 0,01596 |
| 530,46967 | 0,01811 | 0,01916 | 0,01654 | 0,01865 | 0,01748 |
| 530,50685 | 0,01915 | 0,02028 | 0,01761 | 0,02032 | 0,01899 |
| 530,54403 | 0,02019 | 0,02136 | 0,01867 | 0,02198 | 0,02047 |
| 530,58121 | 0,02121 | 0,02239 | 0,0197 | 0,0236 | 0,02189 |
| 530,6184 | 0,02219 | 0,02335 | 0,02068 | 0,02514 | 0,02321 |
| 530,65558 | 0,02311 | 0,02423 | 0,0216 | 0,02656 | 0,0244 |
| 530,69276 | 0,02397 | 0,02502 | 0,02244 | 0,02784 | 0,02545 |
| 530,72994 | 0,02475 | 0,02571 | 0,0232 | 0,02895 | 0,02633 |
| 530,76712 | 0,02544 | 0,02632 | 0,02388 | 0,02989 | 0,02705 |
| 530,80431 | 0,02605 | 0,02683 | 0,02447 | 0,03064 | 0,02762 |
| 530,84149 | 0,02657 | 0,02727 | 0,02497 | 0,03122 | 0,02805 |
| 530,87867 | 0,02702 | 0,02763 | 0,0254 | 0,03165 | 0,02839 |
| 530,91585 | 0,02739 | 0,02792 | 0,02575 | 0,032 | 0,02869 |
| 530,95303 | 0,02771 | 0,02816 | 0,02604 | 0,03231 | 0,02904 |
| 530,99022 | 0,02797 | 0,02834 | 0,02626 | 0,03267 | 0,0295 |
| 531,0274 | 0,02818 | 0,02848 | 0,02645 | 0,03315 | 0,03015 |
| 531,06458 | 0,02837 | 0,02859 | 0,02659 | 0,03383 | 0,03108 |
| 531,10176 | 0,02854 | 0,02868 | 0,02673 | 0,03479 | 0,03234 |
| 531,13894 | 0,0287 | 0,02877 | 0,02687 | 0,03607 | 0,03398 |
| 531,17613 | 0,02889 | 0,02889 | 0,02704 | 0,03771 | 0,03601 |
| 531,21331 | 0,02914 | 0,02907 | 0,02729 | 0,0397 | 0,03841 |
| 531,25049 | 0,02947 | 0,02934 | 0,02764 | 0,04201 | 0,04113 |
| 531,28767 | 0,02993 | 0,02977 | 0,02815 | 0,04455 | 0,04406 |
| 531,32485 | 0,03057 | 0,03039 | 0,02886 | 0,0472 | 0,04707 |
| 531,36204 | 0,03142 | 0,03128 | 0,02982 | 0,04978 | 0,04999 |
| 531,39922 | 0,0325 | 0,03247 | 0,03108 | 0,05213 | 0,05265 |
| 531,4364 | 0,03383 | 0,03397 | 0,03264 | 0,05411 | 0,0549 |
| 531,47358 | 0,03542 | 0,03581 | 0,03452 | 0,05562 | 0,05666 |
| 531,51076 | 0,03724 | 0,03797 | 0,03669 | 0,05658 | 0,05786 |
| 531,54795 | 0,03927 | 0,04042 | 0,03912 | 0,05701 | 0,05849 |
| 531,58513 | 0,04147 | 0,04312 | 0,04177 | 0,05694 | 0,05863 |
| 531,62231 | 0,04378 | 0,04599 | 0,04458 | 0,05648 | 0,05836 |
| 531,65949 | 0,04613 | 0,04895 | 0,04747 | 0,05577 | 0,05781 |
| 531,69667 | 0,04846 | 0,05193 | 0,05036 | 0,05496 | 0,05715 |
| 531,73386 | 0,05069 | 0,05481 | 0,05316 | 0,05423 | 0,05651 |
| 531,77104 | 0,05277 | 0,05752 | 0,05581 | 0,05373 | 0,05605 |
| 531,80822 | 0,05465 | 0,05997 | 0,05821 | 0,05355 | 0,05585 |
| 531,8454 | 0,05634 | 0,06212 | 0,06033 | 0,05373 | 0,05596 |
| 531,88258 | 0,05783 | 0,06397 | 0,06216 | 0,05429 | 0,05637 |
| 531,91977 | 0,05917 | 0,06552 | 0,06369 | 0,05518 | 0,05704 |
| 531,95695 | 0,06039 | 0,06681 | 0,06495 | 0,05634 | 0,05793 |
| 531,99413 | 0,06156 | 0,0679 | 0,06599 | 0,05771 | 0,05896 |
| 532,03131 | 0,06274 | 0,06884 | 0,06684 | 0,0592 | 0,06008 |
| 532,06849 | 0,06399 | 0,0697 | 0,06756 | 0,06073 | 0,06122 |
| 532,10568 | 0,06536 | 0,07054 | 0,06822 | 0,06225 | 0,06234 |
| 532,14286 | 0,06687 | 0,07143 | 0,06885 | 0,06371 | 0,0634 |
| 532,18004 | 0,06855 | 0,07237 | 0,06949 | 0,06508 | 0,0644 |
| 532,21722 | 0,07037 | 0,0734 | 0,07016 | 0,06635 | 0,06533 |
| 532,2544 | 0,07229 | 0,07448 | 0,07085 | 0,06756 | 0,06624 |
| 532,29159 | 0,07424 | 0,07559 | 0,07155 | 0,06876 | 0,0672 |
| 532,32877 | 0,07617 | 0,07667 | 0,07222 | 0,07003 | 0,06829 |
| 532,36595 | 0,07801 | 0,07767 | 0,07284 | 0,0715 | 0,06963 |
| 532,40313 | 0,07971 | 0,07856 | 0,07337 | 0,0733 | 0,07138 |
| 532,44031 | 0,08122 | 0,07928 | 0,0738 | 0,0756 | 0,07372 |
| 532,4775 | 0,08254 | 0,07984 | 0,07411 | 0,07859 | 0,07683 |
| 532,51468 | 0,08368 | 0,08022 | 0,07435 | 0,08246 | 0,0809 |
| 532,55186 | 0,08467 | 0,08047 | 0,07454 | 0,08736 | 0,08612 |
| 532,58904 | 0,08559 | 0,08066 | 0,07477 | 0,09342 | 0,09259 |
| 532,62622 | 0,08656 | 0,08086 | 0,07514 | 0,10071 | 0,10036 |
| 532,66341 | 0,08774 | 0,08124 | 0,07579 | 0,10919 | 0,10942 |
| 532,70059 | 0,08929 | 0,08195 | 0,0769 | 0,11853 | 0,1194 |
| 532,73777 | 0,09137 | 0,08312 | 0,0786 | 0,12838 | 0,1299 |
| 532,77495 | 0,09413 | 0,08491 | 0,08104 | 0,13827 | 0,14041 |
| 532,81213 | 0,09771 | 0,08745 | 0,08434 | 0,14766 | 0,15035 |
| 532,84932 | 0,10221 | 0,09085 | 0,08858 | 0,15598 | 0,1591 |
| 532,8865 | 0,10768 | 0,09518 | 0,09382 | 0,16273 | 0,16611 |
| 532,92368 | 0,11411 | 0,10043 | 0,10005 | 0,16748 | 0,17091 |
| 532,96086 | 0,12143 | 0,10657 | 0,10718 | 0,16994 | 0,17318 |
| 532,99804 | 0,12949 | 0,11349 | 0,11507 | 0,17003 | 0,17281 |
| 533,03523 | 0,1381 | 0,12101 | 0,12352 | 0,16785 | 0,1699 |
| 533,07241 | 0,14697 | 0,12892 | 0,13226 | 0,16364 | 0,16469 |
| 533,10959 | 0,15576 | 0,13691 | 0,14092 | 0,15791 | 0,15771 |
| 533,14677 | 0,16413 | 0,14466 | 0,14914 | 0,15137 | 0,14974 |
| 533,18395 | 0,17178 | 0,15188 | 0,15659 | 0,14461 | 0,14144 |
| 533,22114 | 0,17847 | 0,15833 | 0,16298 | 0,13818 | 0,13343 |
| 533,25832 | 0,18399 | 0,16379 | 0,16808 | 0,13258 | 0,12627 |
| 533,2955 | 0,18823 | 0,16814 | 0,17173 | 0,12817 | 0,12037 |
| 533,33268 | 0,19116 | 0,17133 | 0,17388 | 0,1252 | 0,11603 |
| 533,36986 | 0,19285 | 0,17336 | 0,17456 | 0,1238 | 0,1134 |
| 533,40705 | 0,19342 | 0,17435 | 0,17389 | 0,124 | 0,11252 |
| 533,44423 | 0,19309 | 0,17444 | 0,17208 | 0,12574 | 0,1133 |
| 533,48141 | 0,19208 | 0,17383 | 0,1694 | 0,12887 | 0,11559 |
| 533,51859 | 0,19064 | 0,17274 | 0,16613 | 0,13329 | 0,11922 |
| 533,55577 | 0,18907 | 0,17144 | 0,16265 | 0,13876 | 0,12392 |
| 533,59295 | 0,18758 | 0,17016 | 0,15926 | 0,14501 | 0,12937 |
| 533,63014 | 0,18634 | 0,16907 | 0,15622 | 0,1518 | 0,13533 |
| 533,66732 | 0,18546 | 0,16831 | 0,15373 | 0,15895 | 0,14159 |
| 533,7045 | 0,185 | 0,16796 | 0,15192 | 0,16626 | 0,14797 |
| 533,74168 | 0,18497 | 0,16807 | 0,15086 | 0,17354 | 0,15435 |
| 533,77886 | 0,18536 | 0,16866 | 0,1506 | 0,18069 | 0,16064 |
| 533,81605 | 0,18614 | 0,16972 | 0,15111 | 0,1876 | 0,16684 |
| 533,85323 | 0,18725 | 0,17121 | 0,15235 | 0,19428 | 0,17301 |
| 533,89041 | 0,18866 | 0,17309 | 0,15425 | 0,20079 | 0,17927 |
| 533,92759 | 0,19033 | 0,1753 | 0,15674 | 0,20726 | 0,18584 |
| 533,96477 | 0,19226 | 0,17783 | 0,15978 | 0,21394 | 0,19304 |
| 534,00196 | 0,19447 | 0,18064 | 0,16328 | 0,22112 | 0,20118 |
| 534,03914 | 0,19696 | 0,1837 | 0,1672 | 0,22905 | 0,21049 |
| 534,07632 | 0,1998 | 0,18704 | 0,17153 | 0,23793 | 0,22116 |
| 534,1135 | 0,20305 | 0,19069 | 0,1763 | 0,24783 | 0,23322 |
| 534,15068 | 0,20676 | 0,19472 | 0,18154 | 0,25867 | 0,24653 |
| 534,18787 | 0,211 | 0,19918 | 0,18732 | 0,27018 | 0,26073 |
| 534,22505 | 0,21581 | 0,20415 | 0,19368 | 0,28188 | 0,27528 |
| 534,26223 | 0,22123 | 0,20969 | 0,20068 | 0,29313 | 0,28942 |
| 534,29941 | 0,22724 | 0,21584 | 0,20837 | 0,30316 | 0,30228 |
| 534,33659 | 0,23382 | 0,22261 | 0,21673 | 0,31115 | 0,31293 |
| 534,37378 | 0,24087 | 0,22994 | 0,22573 | 0,31628 | 0,32048 |
| 534,41096 | 0,24825 | 0,23775 | 0,23523 | 0,31762 | 0,32374 |
| 534,44814 | 0,25572 | 0,24579 | 0,24498 | 0,31486 | 0,32256 |
| 534,48532 | 0,26298 | 0,25377 | 0,25466 | 0,30805 | 0,31686 |
| 534,5225 | 0,26968 | 0,26136 | 0,26392 | 0,29744 | 0,30688 |
| 534,55969 | 0,27546 | 0,26819 | 0,27234 | 0,28353 | 0,29315 |
| 534,59687 | 0,27993 | 0,27386 | 0,27948 | 0,26707 | 0,27643 |
| 534,63405 | 0,28271 | 0,27796 | 0,2849 | 0,24888 | 0,25762 |
| 534,67123 | 0,28349 | 0,28017 | 0,28824 | 0,22986 | 0,2377 |
| 534,70841 | 0,28203 | 0,28018 | 0,28917 | 0,21086 | 0,21758 |
| 534,7456 | 0,27818 | 0,27782 | 0,28749 | 0,1926 | 0,19806 |
| 534,78278 | 0,27195 | 0,27303 | 0,28312 | 0,17564 | 0,1798 |
| 534,81996 | 0,26347 | 0,26579 | 0,27596 | 0,16037 | 0,16325 |
| 534,85714 | 0,2529 | 0,25629 | 0,26638 | 0,14714 | 0,1488 |
| 534,89432 | 0,24069 | 0,24503 | 0,25484 | 0,13581 | 0,13629 |
| 534,93151 | 0,22739 | 0,23242 | 0,24175 | 0,12623 | 0,12562 |
| 534,96869 | 0,21349 | 0,21892 | 0,22762 | 0,1182 | 0,11659 |
| 535,00587 | 0,19944 | 0,205 | 0,21292 | 0,11149 | 0,10897 |
| 535,04305 | 0,18565 | 0,19109 | 0,19811 | 0,10587 | 0,10254 |
| 535,08023 | 0,17248 | 0,17759 | 0,18361 | 0,10113 | 0,09706 |
| 535,11742 | 0,16018 | 0,16479 | 0,16974 | 0,09706 | 0,09236 |
| 535,1546 | 0,1489 | 0,15293 | 0,15676 | 0,09353 | 0,08829 |
| 535,19178 | 0,13874 | 0,14216 | 0,14482 | 0,0904 | 0,08472 |
| 535,22896 | 0,12971 | 0,13252 | 0,13404 | 0,08758 | 0,08157 |
| 535,26614 | 0,12176 | 0,1241 | 0,12451 | 0,08502 | 0,0788 |
| 535,30333 | 0,11483 | 0,11677 | 0,11607 | 0,08269 | 0,07635 |
| 535,34051 | 0,10882 | 0,11039 | 0,10865 | 0,08055 | 0,07418 |
| 535,37769 | 0,10356 | 0,10486 | 0,10218 | 0,07858 | 0,07227 |
| 535,41487 | 0,09894 | 0,10005 | 0,09656 | 0,07678 | 0,0706 |
| 535,45205 | 0,09487 | 0,09587 | 0,09171 | 0,07517 | 0,06917 |
| 535,48924 | 0,09128 | 0,09224 | 0,08756 | 0,07375 | 0,06796 |
| 535,52642 | 0,08811 | 0,08908 | 0,08403 | 0,07253 | 0,06698 |
| 535,5636 | 0,08532 | 0,08635 | 0,0811 | 0,07152 | 0,06623 |
| 535,60078 | 0,08288 | 0,08401 | 0,0787 | 0,07074 | 0,0657 |
| 535,63796 | 0,08078 | 0,08206 | 0,07681 | 0,07019 | 0,06541 |
| 535,67515 | 0,07902 | 0,08048 | 0,07543 | 0,0699 | 0,06537 |
| 535,71233 | 0,07759 | 0,07931 | 0,07451 | 0,06988 | 0,0656 |
| 535,74951 | 0,07652 | 0,07851 | 0,07401 | 0,07017 | 0,06612 |
| 535,78669 | 0,0758 | 0,07807 | 0,0739 | 0,07076 | 0,06695 |
| 535,82387 | 0,07543 | 0,07799 | 0,07418 | 0,07169 | 0,0681 |
| 535,86106 | 0,0754 | 0,07828 | 0,0748 | 0,07299 | 0,06961 |
| 535,89824 | 0,07573 | 0,07891 | 0,07577 | 0,0747 | 0,07152 |
| 535,93542 | 0,0764 | 0,07989 | 0,07705 | 0,07686 | 0,07385 |
| 535,9726 | 0,07743 | 0,08121 | 0,07865 | 0,07951 | 0,07664 |
| 536,00978 | 0,07881 | 0,08287 | 0,08055 | 0,08267 | 0,07991 |
| 536,04697 | 0,08053 | 0,08484 | 0,08274 | 0,08636 | 0,08367 |
| 536,08415 | 0,08259 | 0,08712 | 0,08519 | 0,09056 | 0,08792 |
| 536,12133 | 0,08495 | 0,08968 | 0,08791 | 0,09523 | 0,09261 |
| 536,15851 | 0,08757 | 0,09249 | 0,09083 | 0,10029 | 0,09773 |
| 536,19569 | 0,09042 | 0,09545 | 0,09389 | 0,10564 | 0,10313 |
| 536,23288 | 0,09338 | 0,09848 | 0,09702 | 0,1111 | 0,1087 |
| 536,27006 | 0,09636 | 0,10149 | 0,10014 | 0,11653 | 0,11434 |
| 536,30724 | 0,09925 | 0,10437 | 0,10315 | 0,12183 | 0,11995 |
| 536,34442 | 0,10194 | 0,10701 | 0,10596 | 0,12694 | 0,1255 |
| 536,3816 | 0,10432 | 0,10931 | 0,10847 | 0,13189 | 0,13104 |
| 536,41879 | 0,1063 | 0,11118 | 0,11062 | 0,1368 | 0,13669 |
| 536,45597 | 0,10782 | 0,11257 | 0,11234 | 0,14191 | 0,14268 |
| 536,49315 | 0,10886 | 0,11344 | 0,1136 | 0,14753 | 0,14932 |
| 536,53033 | 0,10942 | 0,11381 | 0,11439 | 0,15405 | 0,15701 |
| 536,56751 | 0,10956 | 0,1137 | 0,11476 | 0,16189 | 0,16617 |
| 536,6047 | 0,10935 | 0,11323 | 0,11483 | 0,1715 | 0,17738 |
| 536,64188 | 0,10894 | 0,11258 | 0,11473 | 0,18323 | 0,19072 |
| 536,67906 | 0,10851 | 0,11192 | 0,11461 | 0,19698 | 0,20618 |
| 536,71624 | 0,10825 | 0,11145 | 0,11466 | 0,21249 | 0,22348 |
| 536,75342 | 0,10838 | 0,11141 | 0,11509 | 0,22923 | 0,24205 |
| 536,79061 | 0,10911 | 0,11201 | 0,11611 | 0,2464 | 0,26104 |
| 536,82779 | 0,11066 | 0,11351 | 0,11795 | 0,26299 | 0,27939 |
| 536,86497 | 0,11324 | 0,11611 | 0,12084 | 0,27788 | 0,29589 |
| 536,90215 | 0,11703 | 0,12001 | 0,12497 | 0,28992 | 0,30933 |
| 536,93933 | 0,12218 | 0,12537 | 0,13051 | 0,29807 | 0,31857 |
| 536,97652 | 0,12879 | 0,13229 | 0,13773 | 0,30154 | 0,32275 |
| 537,0137 | 0,13689 | 0,14091 | 0,14654 | 0,29982 | 0,32123 |
| 537,05088 | 0,14641 | 0,15105 | 0,15686 | 0,29264 | 0,31353 |
| 537,08806 | 0,15719 | 0,16244 | 0,1685 | 0,28032 | 0,3006 |
| 537,12524 | 0,16889 | 0,17476 | 0,18115 | 0,26395 | 0,28325 |
| 537,16243 | 0,18098 | 0,18756 | 0,19439 | 0,24455 | 0,26253 |
| 537,19961 | 0,19291 | 0,20032 | 0,20771 | 0,22324 | 0,23965 |
| 537,23679 | 0,20405 | 0,21244 | 0,22049 | 0,20117 | 0,21583 |
| 537,27397 | 0,21377 | 0,22328 | 0,23212 | 0,17936 | 0,19221 |
| 537,31115 | 0,22147 | 0,23224 | 0,24193 | 0,15871 | 0,16973 |
| 537,34834 | 0,22662 | 0,23875 | 0,24933 | 0,13985 | 0,14915 |
| 537,38552 | 0,22884 | 0,24238 | 0,25375 | 0,12324 | 0,13095 |
| 537,4227 | 0,22788 | 0,24279 | 0,25463 | 0,10909 | 0,11542 |
| 537,45988 | 0,22372 | 0,23958 | 0,25211 | 0,09743 | 0,10273 |
| 537,49706 | 0,21651 | 0,23318 | 0,24625 | 0,0883 | 0,09285 |
| 537,53425 | 0,20649 | 0,22389 | 0,23733 | 0,08149 | 0,08543 |
| 537,57143 | 0,19417 | 0,21215 | 0,22576 | 0,07664 | 0,08024 |
| 537,60861 | 0,18032 | 0,19851 | 0,21208 | 0,07356 | 0,07707 |
| 537,64579 | 0,16555 | 0,18355 | 0,19688 | 0,07201 | 0,07567 |
| 537,68297 | 0,15047 | 0,1679 | 0,1808 | 0,0718 | 0,07584 |
| 537,72016 | 0,1356 | 0,15213 | 0,16447 | 0,07272 | 0,07732 |
| 537,75734 | 0,12141 | 0,13678 | 0,14843 | 0,07455 | 0,07986 |
| 537,79452 | 0,10826 | 0,12227 | 0,13319 | 0,07703 | 0,08316 |
| 537,8317 | 0,09641 | 0,10896 | 0,11922 | 0,07989 | 0,08692 |
| 537,86888 | 0,08603 | 0,09716 | 0,10678 | 0,08282 | 0,09074 |
| 537,90607 | 0,0772 | 0,08706 | 0,09599 | 0,08549 | 0,09422 |
| 537,94325 | 0,06993 | 0,07863 | 0,0869 | 0,08752 | 0,0969 |
| 537,98043 | 0,06423 | 0,07184 | 0,07952 | 0,08859 | 0,09848 |
| 538,01761 | 0,06005 | 0,06662 | 0,07377 | 0,0885 | 0,09868 |
| 538,05479 | 0,05716 | 0,06287 | 0,06955 | 0,08713 | 0,09736 |
| 538,09198 | 0,05541 | 0,06045 | 0,06672 | 0,08444 | 0,09447 |
| 538,12916 | 0,05464 | 0,05919 | 0,0651 | 0,08052 | 0,0901 |
| 538,16634 | 0,05467 | 0,05892 | 0,06451 | 0,07552 | 0,08442 |
| 538,20352 | 0,05529 | 0,05942 | 0,06474 | 0,06969 | 0,07773 |
| 538,2407 | 0,05632 | 0,06049 | 0,06557 | 0,0633 | 0,07034 |
| 538,27789 | 0,05753 | 0,06189 | 0,06679 | 0,05666 | 0,06262 |
| 538,31507 | 0,05873 | 0,0634 | 0,0681 | 0,05006 | 0,05492 |
| 538,35225 | 0,05973 | 0,06476 | 0,0693 | 0,04374 | 0,04759 |
| 538,38943 | 0,06035 | 0,06579 | 0,07021 | 0,03796 | 0,04087 |
| 538,42661 | 0,06045 | 0,06631 | 0,07066 | 0,03284 | 0,0349 |
| 538,4638 | 0,05991 | 0,06622 | 0,07053 | 0,0284 | 0,02973 |
| 538,50098 | 0,05872 | 0,06544 | 0,06974 | 0,02464 | 0,02538 |
| 538,53816 | 0,0569 | 0,06394 | 0,06825 | 0,02154 | 0,0218 |
| 538,57534 | 0,05449 | 0,06175 | 0,06607 | 0,01902 | 0,01891 |
| 538,61252 | 0,05158 | 0,05893 | 0,06324 | 0,017 | 0,01661 |
| 538,64971 | 0,04827 | 0,05556 | 0,05985 | 0,01538 | 0,0148 |
| 538,68689 | 0,04469 | 0,05177 | 0,05598 | 0,0141 | 0,01337 |
| 538,72407 | 0,04095 | 0,04769 | 0,05177 | 0,01306 | 0,01224 |
| 538,76125 | 0,03716 | 0,04345 | 0,04739 | 0,01221 | 0,01132 |
| 538,79843 | 0,03344 | 0,0392 | 0,04296 | 0,01148 | 0,01055 |
| 538,83562 | 0,02986 | 0,03506 | 0,03859 | 0,01084 | 0,00988 |
| 538,8728 | 0,02651 | 0,0311 | 0,03437 | 0,01024 | 0,00927 |
| 538,90998 | 0,02343 | 0,02741 | 0,0304 | 0,00967 | 0,00869 |
| 538,94716 | 0,02064 | 0,02402 | 0,02672 | 0,00911 | 0,00814 |
| 538,98434 | 0,01815 | 0,02097 | 0,02338 | 0,00854 | 0,0076 |
| 539,02153 | 0,01595 | 0,01826 | 0,02039 | 0,00796 | 0,00707 |
| 539,05871 | 0,01403 | 0,01589 | 0,01775 | 0,00738 | 0,00656 |
| 539,09589 | 0,01236 | 0,01385 | 0,01546 | 0,0068 | 0,00605 |
| 539,13307 | 0,01092 | 0,0121 | 0,01352 | 0,00621 | 0,00555 |
| 539,17025 | 0,00968 | 0,01062 | 0,01187 | 0,00563 | 0,00508 |
| 539,20744 | 0,00862 | 0,00939 | 0,01046 | 0,00506 | 0,00462 |
| 539,24462 | 0,0077 | 0,00836 | 0,00927 | 0,00452 | 0,00419 |
| 539,2818 | 0,00691 | 0,00748 | 0,00826 | 0,00401 | 0,00379 |
| 539,31898 | 0,00622 | 0,00673 | 0,0074 | 0,00354 | 0,00342 |
| 539,35616 | 0,00561 | 0,00609 | 0,00666 | 0,00311 | 0,00307 |
| 539,39335 | 0,00507 | 0,00552 | 0,00602 | 0,00272 | 0,00275 |
| 539,43053 | 0,00458 | 0,00502 | 0,00546 | 0,00237 | 0,00246 |
| 539,46771 | 0,00413 | 0,00457 | 0,00496 | 0,00207 | 0,00219 |
| 539,50489 | 0,00372 | 0,00415 | 0,00452 | 0,00181 | 0,00194 |
| 539,54207 | 0,00335 | 0,00375 | 0,00411 | 0,00158 | 0,00172 |
| 539,57926 | 0,003 | 0,00338 | 0,00375 | 0,00138 | 0,00151 |
| 539,61644 | 0,00269 | 0,00303 | 0,00341 | 0,00121 | 0,00133 |
| 539,65362 | 0,0024 | 0,0027 | 0,00309 | 0,00107 | 0,00115 |
| 539,6908 | 0,00213 | 0,00239 | 0,0028 | 0,00094 | 0,001 |
| 539,72798 | 0,00189 | 0,0021 | 0,00252 | 0,00082 | 0,00086 |
| 539,76517 | 0,00167 | 0,00183 | 0,00226 | 0,00072 | 0,00073 |
| 539,80235 | 0,00148 | 0,00159 | 0,00202 | 0,00063 | 0,00062 |
| 539,83953 | 0,0013 | 0,00138 | 0,0018 | 0,00055 | 0,00052 |
| 539,87671 | 0,00114 | 0,00119 | 0,00159 | 0,00048 | 0,00043 |
| 539,91389 | 0,001 | 0,00103 | 0,0014 | 0,00041 | 0,00035 |
| 539,95108 | 0,00088 | 9e-04 | 0,00123 | 0,00035 | 0,00029 |
| 539,98826 | 0,00077 | 0,00079 | 0,00108 | 3e-04 | 0,00023 |
| 540,02544 | 0,00068 | 7e-04 | 0,00095 | 0,00026 | 0,00019 |
| 540,06262 | 0,00059 | 0,00062 | 0,00083 | 0,00022 | 0,00016 |
| 540,0998 | 0,00053 | 0,00056 | 0,00072 | 0,00019 | 0,00014 |
| 540,13699 | 0,00047 | 0,00051 | 0,00063 | 0,00017 | 0,00012 |
| 540,17417 | 0,00042 | 0,00047 | 0,00055 | 0,00015 | 0,00011 |
| 540,21135 | 0,00037 | 0,00043 | 0,00048 | 0,00013 | 0,00011 |
| 540,24853 | 0,00034 | 0,00039 | 0,00042 | 0,00012 | 1e-04 |
| 540,28571 | 3e-04 | 0,00036 | 0,00036 | 0,00011 | 0,00011 |
| 540,3229 | 0,00027 | 0,00032 | 0,00032 | 1e-04 | 0,00011 |
| 540,36008 | 0,00024 | 0,00029 | 0,00027 | 9e-05 | 0,00011 |
| 540,39726 | 0,00021 | 0,00026 | 0,00023 | 8e-05 | 0,00012 |
| 540,43444 | 0,00018 | 0,00023 | 2e-04 | 7e-05 | 0,00012 |
| 540,47162 | 0,00015 | 0,00021 | 0,00017 | 6e-05 | 0,00013 |
| 540,50881 | 0,00013 | 0,00019 | 0,00014 | 6e-05 | 0,00013 |
| 540,54599 | 1e-04 | 0,00016 | 0,00012 | 5e-05 | 0,00013 |
| 540,58317 | 8e-05 | 0,00014 | 1e-04 | 5e-05 | 0,00013 |
| 540,62035 | 7e-05 | 0,00012 | 8e-05 | 4e-05 | 0,00012 |
| 540,65753 | 5e-05 | 0,00011 | 7e-05 | 4e-05 | 0,00011 |
| 540,69472 | 4e-05 | 9e-05 | 5e-05 | 4e-05 | 0,00011 |
| 540,7319 | 3e-05 | 7e-05 | 4e-05 | 4e-05 | 1e-04 |
| 540,76908 | 2e-05 | 6e-05 | 3e-05 | 4e-05 | 8e-05 |
| 540,80626 | 1e-05 | 5e-05 | 3e-05 | 4e-05 | 7e-05 |
| 540,84344 | 1e-05 | 4e-05 | 2e-05 | 4e-05 | 6e-05 |
| 540,88063 | 1e-05 | 3e-05 | 2e-05 | 5e-05 | 5e-05 |
| 540,91781 | 0 | 2e-05 | 1e-05 | 5e-05 | 4e-05 |
| 540,95499 | 0 | 2e-05 | 1e-05 | 6e-05 | 3e-05 |
| 540,99217 | 0 | 1e-05 | 1e-05 | 6e-05 | 2e-05 |
| 541,02935 | 0 | 1e-05 | 0 | 6e-05 | 2e-05 |
| 541,06654 | 0 | 1e-05 | 0 | 6e-05 | 1e-05 |
| 541,10372 | 0 | 0 | 0 | 7e-05 | 1e-05 |
| 541,1409 | 0 | 0 | 0 | 7e-05 | 1e-05 |
| 541,17808 | 0 | 0 | 0 | 7e-05 | 0 |
| 541,21526 | 0 | 0 | 0 | 7e-05 | 0 |
| 541,25245 | 0 | 0 | 0 | 7e-05 | 0 |
| 541,28963 | 0 | 0 | 0 | 7e-05 | 0 |
| 541,32681 | 0 | 0 | 0 | 7e-05 | 0 |
| 541,36399 | 0 | 0 | 0 | 7e-05 | 0 |
| 541,40117 | 0 | 0 | 0 | 6e-05 | 0 |
| 541,43836 | 0 | 0 | 0 | 6e-05 | 0 |
| 541,47554 | 0 | 0 | 0 | 6e-05 | 0 |
| 541,51272 | 0 | 0 | 0 | 5e-05 | 0 |
| 541,5499 | 0 | 0 | 0 | 5e-05 | 0 |
| 541,58708 | 0 | 0 | 0 | 4e-05 | 0 |
| 541,62427 | 0 | 0 | 0 | 3e-05 | 0 |
| 541,66145 | 0 | 0 | 0 | 3e-05 | 0 |
| 541,69863 | 0 | 0 | 0 | 2e-05 | 0 |
| 541,73581 | 0 | 0 | 0 | 2e-05 | 0 |
| 541,77299 | 0 | 0 | 0 | 1e-05 | 0 |
| 541,81018 | 0 | 0 | 0 | 1e-05 | 0 |
| 541,84736 | 0 | 0 | 0 | 1e-05 | 0 |
| 541,88454 | 0 | 0 | 0 | 1e-05 | 0 |
| 541,92172 | 0 | 0 | 0 | 0 | 0 |
| 541,9589 | 0 | 0 | 0 | 0 | 0 |
| 541,99609 | 0 | 0 | 0 | 0 | 0 |
| 542,03327 | 0 | 0 | 0 | 0 | 0 |
| 542,07045 | 0 | 0 | 0 | 0 | 0 |
| 542,10763 | 0 | 0 | 0 | 0 | 0 |
| 542,14481 | 0 | 0 | 0 | 0 | 0 |
| 542,182 | 0 | 0 | 0 | 0 | 0 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 0 | 0 | 0 |
| 524,74364 | 0 | 0 | 0 | 0 | 0 |
| 524,78082 | 0 | 0 | 0 | 0 | 0 |
| 524,818 | 0 | 0 | 0 | 0 | 0 |
| 524,85519 | 0 | 0 | 0 | 0 | 0 |
| 524,89237 | 0 | 0 | 0 | 0 | 0 |
| 524,92955 | 0 | 0 | 0 | 0 | 0 |
| 524,96673 | 0 | 0 | 0 | 0 | 0 |
| 525,00391 | 0 | 0 | 0 | 0 | 0 |
| 525,0411 | 0 | 0 | 0 | 0 | 0 |
| 525,07828 | 0 | 0 | 0 | 0 | 0 |
| 525,11546 | 0 | 0 | 0 | 0 | 0 |
| 525,15264 | 0 | 0 | 0 | 0 | 0 |
| 525,18982 | 0 | 0 | 0 | 0 | 0 |
| 525,22701 | 0 | 0 | 0 | 0 | 0 |
| 525,26419 | 0 | 0 | 0 | 0 | 0 |
| 525,30137 | 0 | 0 | 0 | 0 | 0 |
| 525,33855 | 0 | 0 | 0 | 0 | 0 |
| 525,37573 | 0 | 0 | 0 | 0 | 0 |
| 525,41292 | 0 | 0 | 0 | 0 | 0 |
| 525,4501 | 0 | 0 | 0 | 0 | 0 |
| 525,48728 | 0 | 0 | 0 | 0 | 0 |
| 525,52446 | 0 | 0 | 0 | 0 | 0 |
| 525,56164 | 0 | 0 | 0 | 0 | 0 |
| 525,59883 | 0 | 0 | 0 | 0 | 0 |
| 525,63601 | 0 | 0 | 0 | 0 | 0 |
| 525,67319 | 0 | 1e-05 | 0 | 0 | 0 |
| 525,71037 | 1e-05 | 1e-05 | 0 | 0 | 0 |
| 525,74755 | 1e-05 | 1e-05 | 0 | 0 | 0 |
| 525,78474 | 1e-05 | 1e-05 | 0 | 0 | 0 |
| 525,82192 | 1e-05 | 2e-05 | 1e-05 | 0 | 0 |
| 525,8591 | 2e-05 | 2e-05 | 1e-05 | 0 | 0 |
| 525,89628 | 2e-05 | 3e-05 | 1e-05 | 0 | 0 |
| 525,93346 | 2e-05 | 3e-05 | 1e-05 | 0 | 0 |
| 525,97065 | 3e-05 | 4e-05 | 2e-05 | 0 | 1e-05 |
| 526,00783 | 3e-05 | 5e-05 | 2e-05 | 0 | 1e-05 |
| 526,04501 | 4e-05 | 6e-05 | 3e-05 | 0 | 1e-05 |
| 526,08219 | 4e-05 | 7e-05 | 3e-05 | 0 | 1e-05 |
| 526,11937 | 5e-05 | 9e-05 | 4e-05 | 0 | 2e-05 |
| 526,15656 | 6e-05 | 1e-04 | 5e-05 | 0 | 2e-05 |
| 526,19374 | 6e-05 | 0,00012 | 6e-05 | 1e-05 | 3e-05 |
| 526,23092 | 7e-05 | 0,00014 | 7e-05 | 1e-05 | 3e-05 |
| 526,2681 | 8e-05 | 0,00016 | 8e-05 | 1e-05 | 4e-05 |
| 526,30528 | 9e-05 | 0,00018 | 1e-04 | 1e-05 | 5e-05 |
| 526,34247 | 9e-05 | 0,00021 | 0,00011 | 2e-05 | 6e-05 |
| 526,37965 | 1e-04 | 0,00023 | 0,00013 | 2e-05 | 7e-05 |
| 526,41683 | 1e-04 | 0,00025 | 0,00014 | 3e-05 | 8e-05 |
| 526,45401 | 0,00011 | 0,00028 | 0,00016 | 3e-05 | 9e-05 |
| 526,49119 | 0,00011 | 3e-04 | 0,00017 | 4e-05 | 1e-04 |
| 526,52838 | 0,00012 | 0,00033 | 0,00018 | 5e-05 | 0,00011 |
| 526,56556 | 0,00012 | 0,00035 | 2e-04 | 6e-05 | 0,00012 |
| 526,60274 | 0,00012 | 0,00037 | 0,00021 | 6e-05 | 0,00012 |
| 526,63992 | 0,00012 | 0,00038 | 0,00022 | 7e-05 | 0,00013 |
| 526,6771 | 0,00013 | 4e-04 | 0,00022 | 8e-05 | 0,00013 |
| 526,71429 | 0,00013 | 0,00041 | 0,00023 | 9e-05 | 0,00013 |
| 526,75147 | 0,00013 | 0,00042 | 0,00023 | 1e-04 | 0,00013 |
| 526,78865 | 0,00013 | 0,00042 | 0,00023 | 0,00011 | 0,00013 |
| 526,82583 | 0,00014 | 0,00043 | 0,00023 | 0,00011 | 0,00013 |
| 526,86301 | 0,00014 | 0,00042 | 0,00022 | 0,00012 | 0,00012 |
| 526,9002 | 0,00015 | 0,00042 | 0,00021 | 0,00012 | 0,00012 |
| 526,93738 | 0,00015 | 0,00041 | 2e-04 | 0,00013 | 0,00011 |
| 526,97456 | 0,00016 | 4e-04 | 0,00019 | 0,00013 | 1e-04 |
| 527,01174 | 0,00017 | 0,00039 | 0,00018 | 0,00013 | 9e-05 |
| 527,04892 | 0,00019 | 0,00038 | 0,00017 | 0,00013 | 8e-05 |
| 527,08611 | 2e-04 | 0,00037 | 0,00015 | 0,00013 | 7e-05 |
| 527,12329 | 0,00022 | 0,00035 | 0,00014 | 0,00012 | 6e-05 |
| 527,16047 | 0,00023 | 0,00034 | 0,00012 | 0,00012 | 5e-05 |
| 527,19765 | 0,00025 | 0,00034 | 0,00011 | 0,00011 | 4e-05 |
| 527,23483 | 0,00027 | 0,00033 | 1e-04 | 0,00011 | 4e-05 |
| 527,27202 | 0,00029 | 0,00033 | 9e-05 | 0,00011 | 3e-05 |
| 527,3092 | 0,00031 | 0,00033 | 8e-05 | 0,00011 | 2e-05 |
| 527,34638 | 0,00033 | 0,00033 | 7e-05 | 0,00011 | 2e-05 |
| 527,38356 | 0,00036 | 0,00033 | 6e-05 | 0,00011 | 2e-05 |
| 527,42074 | 0,00038 | 0,00034 | 6e-05 | 0,00011 | 2e-05 |
| 527,45793 | 4e-04 | 0,00035 | 6e-05 | 0,00012 | 2e-05 |
| 527,49511 | 0,00042 | 0,00037 | 6e-05 | 0,00013 | 2e-05 |
| 527,53229 | 0,00045 | 0,00038 | 6e-05 | 0,00014 | 2e-05 |
| 527,56947 | 0,00047 | 4e-04 | 7e-05 | 0,00016 | 2e-05 |
| 527,60665 | 5e-04 | 0,00042 | 8e-05 | 0,00018 | 3e-05 |
| 527,64384 | 0,00053 | 0,00044 | 9e-05 | 2e-04 | 4e-05 |
| 527,68102 | 0,00056 | 0,00046 | 1e-04 | 0,00023 | 5e-05 |
| 527,7182 | 0,00059 | 0,00047 | 0,00012 | 0,00026 | 6e-05 |
| 527,75538 | 0,00063 | 0,00049 | 0,00014 | 3e-04 | 8e-05 |
| 527,79256 | 0,00067 | 0,00051 | 0,00016 | 0,00035 | 9e-05 |
| 527,82975 | 0,00071 | 0,00052 | 0,00019 | 4e-04 | 0,00011 |
| 527,86693 | 0,00076 | 0,00054 | 0,00022 | 0,00046 | 0,00014 |
| 527,90411 | 0,00081 | 0,00056 | 0,00025 | 0,00053 | 0,00017 |
| 527,94129 | 0,00087 | 0,00057 | 0,00029 | 6e-04 | 2e-04 |
| 527,97847 | 0,00094 | 0,00059 | 0,00033 | 0,00069 | 0,00023 |
| 528,01566 | 0,00101 | 0,00061 | 0,00037 | 0,00078 | 0,00027 |
| 528,05284 | 0,00108 | 0,00063 | 0,00042 | 0,00088 | 0,00032 |
| 528,09002 | 0,00117 | 0,00065 | 0,00047 | 0,00099 | 0,00036 |
| 528,1272 | 0,00126 | 0,00068 | 0,00053 | 0,0011 | 0,00042 |
| 528,16438 | 0,00135 | 0,00071 | 0,00059 | 0,00123 | 0,00047 |
| 528,20157 | 0,00145 | 0,00075 | 0,00066 | 0,00135 | 0,00054 |
| 528,23875 | 0,00156 | 0,00079 | 0,00073 | 0,00149 | 0,00061 |
| 528,27593 | 0,00167 | 0,00084 | 0,00081 | 0,00162 | 0,00068 |
| 528,31311 | 0,00178 | 0,00091 | 9e-04 | 0,00176 | 0,00077 |
| 528,35029 | 0,00191 | 0,00098 | 0,00099 | 0,0019 | 0,00086 |
| 528,38748 | 0,00204 | 0,00106 | 0,00109 | 0,00204 | 0,00097 |
| 528,42466 | 0,00218 | 0,00115 | 0,00119 | 0,00218 | 0,00108 |
| 528,46184 | 0,00232 | 0,00125 | 0,00131 | 0,00232 | 0,0012 |
| 528,49902 | 0,00247 | 0,00136 | 0,00143 | 0,00245 | 0,00134 |
| 528,5362 | 0,00262 | 0,00147 | 0,00155 | 0,00258 | 0,00148 |
| 528,57339 | 0,00278 | 0,0016 | 0,00169 | 0,00271 | 0,00164 |
| 528,61057 | 0,00294 | 0,00174 | 0,00183 | 0,00284 | 0,00181 |
| 528,64775 | 0,00311 | 0,00188 | 0,00197 | 0,00295 | 0,00199 |
| 528,68493 | 0,00328 | 0,00203 | 0,00211 | 0,00307 | 0,00218 |
| 528,72211 | 0,00345 | 0,00218 | 0,00226 | 0,00317 | 0,00238 |
| 528,7593 | 0,00363 | 0,00233 | 0,00241 | 0,00327 | 0,00258 |
| 528,79648 | 0,0038 | 0,00249 | 0,00255 | 0,00337 | 0,00278 |
| 528,83366 | 0,00397 | 0,00265 | 0,0027 | 0,00345 | 0,00297 |
| 528,87084 | 0,00414 | 0,00281 | 0,00284 | 0,00352 | 0,00316 |
| 528,90802 | 0,0043 | 0,00297 | 0,00297 | 0,00358 | 0,00334 |
| 528,94521 | 0,00446 | 0,00313 | 0,0031 | 0,00363 | 0,0035 |
| 528,98239 | 0,00461 | 0,00328 | 0,00322 | 0,00367 | 0,00365 |
| 529,01957 | 0,00475 | 0,00344 | 0,00333 | 0,0037 | 0,00378 |
| 529,05675 | 0,00488 | 0,00359 | 0,00344 | 0,00372 | 0,00389 |
| 529,09393 | 0,00501 | 0,00374 | 0,00353 | 0,00373 | 0,00398 |
| 529,13112 | 0,00512 | 0,00388 | 0,00362 | 0,00373 | 0,00404 |
| 529,1683 | 0,00523 | 0,00403 | 0,00369 | 0,00372 | 0,00409 |
| 529,20548 | 0,00532 | 0,00417 | 0,00376 | 0,00371 | 0,00411 |
| 529,24266 | 0,00541 | 0,00431 | 0,00382 | 0,00369 | 0,00412 |
| 529,27984 | 0,00549 | 0,00445 | 0,00387 | 0,00367 | 0,0041 |
| 529,31703 | 0,00555 | 0,00459 | 0,00392 | 0,00365 | 0,00408 |
| 529,35421 | 0,00562 | 0,00474 | 0,00396 | 0,00364 | 0,00404 |
| 529,39139 | 0,00568 | 0,00488 | 0,004 | 0,00362 | 0,00399 |
| 529,42857 | 0,00573 | 0,00502 | 0,00403 | 0,00361 | 0,00393 |
| 529,46575 | 0,00579 | 0,00517 | 0,00407 | 0,00361 | 0,00387 |
| 529,50294 | 0,00584 | 0,00531 | 0,0041 | 0,00362 | 0,00381 |
| 529,54012 | 0,00589 | 0,00546 | 0,00413 | 0,00363 | 0,00375 |
| 529,5773 | 0,00595 | 0,0056 | 0,00417 | 0,00366 | 0,00369 |
| 529,61448 | 0,00601 | 0,00574 | 0,00421 | 0,00369 | 0,00363 |
| 529,65166 | 0,00607 | 0,00588 | 0,00425 | 0,00375 | 0,00359 |
| 529,68885 | 0,00614 | 0,00602 | 0,0043 | 0,00382 | 0,00356 |
| 529,72603 | 0,00621 | 0,00616 | 0,00436 | 0,00391 | 0,00355 |
| 529,76321 | 0,00629 | 0,0063 | 0,00443 | 0,00403 | 0,00357 |
| 529,80039 | 0,00638 | 0,00643 | 0,0045 | 0,00418 | 0,0036 |
| 529,83757 | 0,00649 | 0,00656 | 0,00458 | 0,00436 | 0,00367 |
| 529,87476 | 0,0066 | 0,00669 | 0,00468 | 0,00457 | 0,00376 |
| 529,91194 | 0,00672 | 0,00682 | 0,00478 | 0,00482 | 0,0039 |
| 529,94912 | 0,00685 | 0,00694 | 0,0049 | 0,00512 | 0,00407 |
| 529,9863 | 0,007 | 0,00707 | 0,00503 | 0,00546 | 0,00428 |
| 530,02348 | 0,00716 | 0,00721 | 0,00518 | 0,00585 | 0,00453 |
| 530,06067 | 0,00734 | 0,00735 | 0,00535 | 0,0063 | 0,00483 |
| 530,09785 | 0,00755 | 0,0075 | 0,00554 | 0,00679 | 0,00516 |
| 530,13503 | 0,00777 | 0,00766 | 0,00575 | 0,00733 | 0,00553 |
| 530,17221 | 0,00801 | 0,00783 | 0,00598 | 0,00791 | 0,00595 |
| 530,20939 | 0,00828 | 0,00801 | 0,00624 | 0,00853 | 0,0064 |
| 530,24658 | 0,00856 | 0,00822 | 0,00653 | 0,00919 | 0,00689 |
| 530,28376 | 0,00887 | 0,00843 | 0,00684 | 0,00987 | 0,00742 |
| 530,32094 | 0,0092 | 0,00867 | 0,00719 | 0,01058 | 0,00797 |
| 530,35812 | 0,00955 | 0,00892 | 0,00756 | 0,01131 | 0,00855 |
| 530,3953 | 0,00992 | 0,00918 | 0,00795 | 0,01203 | 0,00916 |
| 530,43249 | 0,0103 | 0,00946 | 0,00837 | 0,01275 | 0,00978 |
| 530,46967 | 0,0107 | 0,00975 | 0,0088 | 0,01346 | 0,01042 |
| 530,50685 | 0,0111 | 0,01005 | 0,00924 | 0,01414 | 0,01107 |
| 530,54403 | 0,0115 | 0,01036 | 0,00969 | 0,01478 | 0,01172 |
| 530,58121 | 0,0119 | 0,01067 | 0,01014 | 0,01538 | 0,01235 |
| 530,6184 | 0,01229 | 0,01098 | 0,01058 | 0,01592 | 0,01297 |
| 530,65558 | 0,01268 | 0,01129 | 0,01101 | 0,0164 | 0,01356 |
| 530,69276 | 0,01305 | 0,0116 | 0,01143 | 0,0168 | 0,0141 |
| 530,72994 | 0,01341 | 0,0119 | 0,01182 | 0,01712 | 0,0146 |
| 530,76712 | 0,01375 | 0,0122 | 0,01219 | 0,01736 | 0,01503 |
| 530,80431 | 0,01408 | 0,0125 | 0,01252 | 0,0175 | 0,01538 |
| 530,84149 | 0,01439 | 0,01279 | 0,01283 | 0,01756 | 0,01565 |
| 530,87867 | 0,01468 | 0,01307 | 0,0131 | 0,01753 | 0,01583 |
| 530,91585 | 0,01496 | 0,01335 | 0,01335 | 0,01742 | 0,01591 |
| 530,95303 | 0,01523 | 0,01364 | 0,01356 | 0,01721 | 0,01589 |
| 530,99022 | 0,01549 | 0,01392 | 0,01376 | 0,01692 | 0,01579 |
| 531,0274 | 0,01574 | 0,01421 | 0,01394 | 0,01657 | 0,01561 |
| 531,06458 | 0,01599 | 0,01451 | 0,01411 | 0,01616 | 0,01536 |
| 531,10176 | 0,01624 | 0,01481 | 0,01427 | 0,01571 | 0,01505 |
| 531,13894 | 0,01649 | 0,01512 | 0,01443 | 0,01523 | 0,01471 |
| 531,17613 | 0,01674 | 0,01544 | 0,0146 | 0,01474 | 0,01435 |
| 531,21331 | 0,01699 | 0,01577 | 0,01478 | 0,01426 | 0,014 |
| 531,25049 | 0,01725 | 0,01611 | 0,01497 | 0,0138 | 0,01368 |
| 531,28767 | 0,01751 | 0,01646 | 0,01519 | 0,01338 | 0,01342 |
| 531,32485 | 0,01778 | 0,01682 | 0,01542 | 0,01302 | 0,01324 |
| 531,36204 | 0,01805 | 0,01718 | 0,01567 | 0,01273 | 0,01314 |
| 531,39922 | 0,01832 | 0,01755 | 0,01595 | 0,01254 | 0,01316 |
| 531,4364 | 0,0186 | 0,01793 | 0,01625 | 0,01244 | 0,0133 |
| 531,47358 | 0,01889 | 0,01831 | 0,01657 | 0,01244 | 0,01358 |
| 531,51076 | 0,01917 | 0,01869 | 0,01692 | 0,01257 | 0,014 |
| 531,54795 | 0,01947 | 0,01909 | 0,01729 | 0,01281 | 0,01457 |
| 531,58513 | 0,01978 | 0,01948 | 0,01767 | 0,01317 | 0,01529 |
| 531,62231 | 0,02009 | 0,01989 | 0,01808 | 0,01366 | 0,01614 |
| 531,65949 | 0,02043 | 0,0203 | 0,0185 | 0,01428 | 0,0171 |
| 531,69667 | 0,02077 | 0,02073 | 0,01894 | 0,015 | 0,01817 |
| 531,73386 | 0,02114 | 0,02116 | 0,0194 | 0,01582 | 0,01932 |
| 531,77104 | 0,02154 | 0,02161 | 0,01988 | 0,01673 | 0,02054 |
| 531,80822 | 0,02197 | 0,02207 | 0,02038 | 0,01772 | 0,0218 |
| 531,8454 | 0,02242 | 0,02255 | 0,0209 | 0,01876 | 0,02308 |
| 531,88258 | 0,02292 | 0,02305 | 0,02143 | 0,01986 | 0,02436 |
| 531,91977 | 0,02345 | 0,02356 | 0,02198 | 0,021 | 0,0256 |
| 531,95695 | 0,02401 | 0,02408 | 0,02254 | 0,02216 | 0,0268 |
| 531,99413 | 0,02462 | 0,02461 | 0,02312 | 0,02333 | 0,02794 |
| 532,03131 | 0,02527 | 0,02516 | 0,02371 | 0,02451 | 0,02902 |
| 532,06849 | 0,02596 | 0,02571 | 0,02431 | 0,02569 | 0,03003 |
| 532,10568 | 0,02669 | 0,02628 | 0,02492 | 0,02688 | 0,03098 |
| 532,14286 | 0,02745 | 0,02684 | 0,02553 | 0,02809 | 0,03188 |
| 532,18004 | 0,02824 | 0,02741 | 0,02615 | 0,02931 | 0,03273 |
| 532,21722 | 0,02907 | 0,02798 | 0,02676 | 0,03055 | 0,03357 |
| 532,2544 | 0,02991 | 0,02856 | 0,02738 | 0,03185 | 0,03441 |
| 532,29159 | 0,03078 | 0,02914 | 0,028 | 0,0332 | 0,03529 |
| 532,32877 | 0,03166 | 0,02973 | 0,02861 | 0,03462 | 0,03623 |
| 532,36595 | 0,03256 | 0,03032 | 0,02923 | 0,03611 | 0,03723 |
| 532,40313 | 0,03347 | 0,03093 | 0,02986 | 0,03769 | 0,03833 |
| 532,44031 | 0,03438 | 0,03157 | 0,0305 | 0,03934 | 0,03953 |
| 532,4775 | 0,03529 | 0,03223 | 0,03115 | 0,04107 | 0,04084 |
| 532,51468 | 0,03621 | 0,03293 | 0,03183 | 0,04286 | 0,04224 |
| 532,55186 | 0,03714 | 0,03367 | 0,03253 | 0,0447 | 0,04375 |
| 532,58904 | 0,03808 | 0,03447 | 0,03328 | 0,04656 | 0,04531 |
| 532,62622 | 0,03902 | 0,03533 | 0,03407 | 0,0484 | 0,04691 |
| 532,66341 | 0,04 | 0,03628 | 0,03492 | 0,05019 | 0,04849 |
| 532,70059 | 0,04099 | 0,03731 | 0,03584 | 0,05191 | 0,05004 |
| 532,73777 | 0,04202 | 0,03843 | 0,03683 | 0,0535 | 0,0515 |
| 532,77495 | 0,04308 | 0,03964 | 0,0379 | 0,05496 | 0,05284 |
| 532,81213 | 0,04418 | 0,04095 | 0,03904 | 0,05625 | 0,05403 |
| 532,84932 | 0,04532 | 0,04235 | 0,04026 | 0,05735 | 0,05502 |
| 532,8865 | 0,04651 | 0,04384 | 0,04155 | 0,05824 | 0,0558 |
| 532,92368 | 0,04774 | 0,04541 | 0,04292 | 0,05892 | 0,05636 |
| 532,96086 | 0,04901 | 0,04705 | 0,04436 | 0,05941 | 0,05671 |
| 532,99804 | 0,05031 | 0,04874 | 0,04585 | 0,05973 | 0,05687 |
| 533,03523 | 0,05163 | 0,05046 | 0,04737 | 0,05989 | 0,05684 |
| 533,07241 | 0,05296 | 0,05218 | 0,04891 | 0,05993 | 0,05666 |
| 533,10959 | 0,05429 | 0,05388 | 0,05044 | 0,05985 | 0,05635 |
| 533,14677 | 0,05559 | 0,05553 | 0,05196 | 0,0597 | 0,05593 |
| 533,18395 | 0,05685 | 0,05711 | 0,05343 | 0,05948 | 0,05544 |
| 533,22114 | 0,05805 | 0,05858 | 0,05484 | 0,05922 | 0,0549 |
| 533,25832 | 0,05917 | 0,05991 | 0,05615 | 0,05894 | 0,05433 |
| 533,2955 | 0,06019 | 0,06109 | 0,05736 | 0,05864 | 0,05376 |
| 533,33268 | 0,06111 | 0,0621 | 0,05844 | 0,05833 | 0,05317 |
| 533,36986 | 0,06191 | 0,06293 | 0,05939 | 0,05801 | 0,0526 |
| 533,40705 | 0,06258 | 0,06357 | 0,0602 | 0,0577 | 0,05204 |
| 533,44423 | 0,06311 | 0,06401 | 0,06086 | 0,05738 | 0,0515 |
| 533,48141 | 0,06352 | 0,06426 | 0,06136 | 0,05708 | 0,05099 |
| 533,51859 | 0,06377 | 0,0643 | 0,06169 | 0,05681 | 0,05053 |
| 533,55577 | 0,06388 | 0,06416 | 0,06187 | 0,05658 | 0,05016 |
| 533,59295 | 0,06386 | 0,06386 | 0,0619 | 0,05644 | 0,0499 |
| 533,63014 | 0,06374 | 0,06343 | 0,0618 | 0,05641 | 0,04979 |
| 533,66732 | 0,06351 | 0,06289 | 0,06159 | 0,05652 | 0,04988 |
| 533,7045 | 0,0632 | 0,06227 | 0,06127 | 0,05683 | 0,05024 |
| 533,74168 | 0,06282 | 0,06159 | 0,06088 | 0,05738 | 0,0509 |
| 533,77886 | 0,0624 | 0,06088 | 0,06042 | 0,0582 | 0,05192 |
| 533,81605 | 0,06195 | 0,06018 | 0,05993 | 0,05933 | 0,05335 |
| 533,85323 | 0,06151 | 0,05953 | 0,05944 | 0,06084 | 0,05526 |
| 533,89041 | 0,06111 | 0,05896 | 0,05898 | 0,0627 | 0,05767 |
| 533,92759 | 0,06077 | 0,0585 | 0,05859 | 0,06489 | 0,06052 |
| 533,96477 | 0,06053 | 0,05818 | 0,0583 | 0,06738 | 0,06378 |
| 534,00196 | 0,06041 | 0,05803 | 0,05814 | 0,07012 | 0,06739 |
| 534,03914 | 0,06043 | 0,05807 | 0,05814 | 0,07304 | 0,07127 |
| 534,07632 | 0,06064 | 0,05832 | 0,05834 | 0,07606 | 0,07529 |
| 534,1135 | 0,0611 | 0,05885 | 0,0588 | 0,07908 | 0,07933 |
| 534,15068 | 0,06178 | 0,05965 | 0,05953 | 0,08198 | 0,08325 |
| 534,18787 | 0,06272 | 0,0607 | 0,06054 | 0,08462 | 0,08684 |
| 534,22505 | 0,0639 | 0,06203 | 0,06183 | 0,08689 | 0,08994 |
| 534,26223 | 0,06535 | 0,06361 | 0,06341 | 0,08871 | 0,09244 |
| 534,29941 | 0,06704 | 0,06545 | 0,06527 | 0,09001 | 0,09424 |
| 534,33659 | 0,06897 | 0,06751 | 0,06739 | 0,09072 | 0,09526 |
| 534,37378 | 0,07111 | 0,06978 | 0,06973 | 0,09083 | 0,09547 |
| 534,41096 | 0,07344 | 0,07222 | 0,07229 | 0,09034 | 0,09486 |
| 534,44814 | 0,07589 | 0,07477 | 0,07496 | 0,08926 | 0,09347 |
| 534,48532 | 0,0784 | 0,07736 | 0,0777 | 0,0876 | 0,09138 |
| 534,5225 | 0,08091 | 0,07994 | 0,08042 | 0,08552 | 0,08865 |
| 534,55969 | 0,08338 | 0,08244 | 0,08306 | 0,08313 | 0,08549 |
| 534,59687 | 0,08574 | 0,08482 | 0,08554 | 0,08055 | 0,08207 |
| 534,63405 | 0,08793 | 0,08699 | 0,08781 | 0,07789 | 0,07855 |
| 534,67123 | 0,08988 | 0,08891 | 0,08979 | 0,07529 | 0,07509 |
| 534,70841 | 0,09152 | 0,09047 | 0,09136 | 0,07285 | 0,07182 |
| 534,7456 | 0,09284 | 0,09167 | 0,09251 | 0,07068 | 0,06887 |
| 534,78278 | 0,09382 | 0,09249 | 0,09323 | 0,06888 | 0,06635 |
| 534,81996 | 0,09444 | 0,0929 | 0,09349 | 0,06759 | 0,06434 |
| 534,85714 | 0,09471 | 0,09292 | 0,09331 | 0,0668 | 0,06298 |
| 534,89432 | 0,09465 | 0,09254 | 0,09268 | 0,06655 | 0,06224 |
| 534,93151 | 0,09426 | 0,09179 | 0,09163 | 0,06687 | 0,06212 |
| 534,96869 | 0,09357 | 0,09071 | 0,09021 | 0,06777 | 0,06264 |
| 535,00587 | 0,09265 | 0,08932 | 0,08844 | 0,06926 | 0,06378 |
| 535,04305 | 0,09158 | 0,08773 | 0,08644 | 0,07134 | 0,06554 |
| 535,08023 | 0,09042 | 0,08603 | 0,0843 | 0,07402 | 0,06792 |
| 535,11742 | 0,08924 | 0,08427 | 0,08209 | 0,07735 | 0,07091 |
| 535,1546 | 0,08812 | 0,08255 | 0,0799 | 0,0813 | 0,07454 |
| 535,19178 | 0,08711 | 0,08095 | 0,07782 | 0,08585 | 0,07889 |
| 535,22896 | 0,0863 | 0,07953 | 0,07592 | 0,09099 | 0,0839 |
| 535,26614 | 0,08581 | 0,07842 | 0,07431 | 0,09672 | 0,0896 |
| 535,30333 | 0,08567 | 0,07771 | 0,0731 | 0,10303 | 0,09598 |
| 535,34051 | 0,08594 | 0,07743 | 0,07235 | 0,1099 | 0,10304 |
| 535,37769 | 0,08666 | 0,07766 | 0,07209 | 0,11727 | 0,11075 |
| 535,41487 | 0,08788 | 0,07843 | 0,07239 | 0,12509 | 0,11906 |
| 535,45205 | 0,08962 | 0,07979 | 0,07328 | 0,13329 | 0,12787 |
| 535,48924 | 0,09192 | 0,08177 | 0,07481 | 0,14168 | 0,13708 |
| 535,52642 | 0,09481 | 0,08438 | 0,07699 | 0,15009 | 0,14648 |
| 535,5636 | 0,09834 | 0,08769 | 0,07987 | 0,15835 | 0,15583 |
| 535,60078 | 0,10244 | 0,09169 | 0,0835 | 0,16627 | 0,16486 |
| 535,63796 | 0,10706 | 0,09629 | 0,08778 | 0,17363 | 0,17333 |
| 535,67515 | 0,11218 | 0,10146 | 0,09267 | 0,18025 | 0,18097 |
| 535,71233 | 0,11773 | 0,10714 | 0,09812 | 0,18591 | 0,18752 |
| 535,74951 | 0,12367 | 0,11328 | 0,10409 | 0,19031 | 0,19276 |
| 535,78669 | 0,1299 | 0,11979 | 0,11049 | 0,19332 | 0,19648 |
| 535,82387 | 0,13635 | 0,12657 | 0,11723 | 0,19491 | 0,19848 |
| 535,86106 | 0,14289 | 0,13355 | 0,12423 | 0,19505 | 0,19854 |
| 535,89824 | 0,14939 | 0,14054 | 0,13133 | 0,19374 | 0,19686 |
| 535,93542 | 0,15572 | 0,14744 | 0,13839 | 0,19103 | 0,19351 |
| 535,9726 | 0,16177 | 0,1541 | 0,14528 | 0,18702 | 0,18865 |
| 536,00978 | 0,16742 | 0,1604 | 0,15185 | 0,18185 | 0,18245 |
| 536,04697 | 0,17255 | 0,16622 | 0,15797 | 0,17568 | 0,17515 |
| 536,08415 | 0,17706 | 0,17145 | 0,16353 | 0,16865 | 0,167 |
| 536,12133 | 0,18074 | 0,17597 | 0,1684 | 0,16109 | 0,15828 |
| 536,15851 | 0,18354 | 0,17956 | 0,1724 | 0,15323 | 0,14925 |
| 536,19569 | 0,18546 | 0,18223 | 0,17542 | 0,14526 | 0,14023 |
| 536,23288 | 0,18644 | 0,18397 | 0,17748 | 0,13734 | 0,13145 |
| 536,27006 | 0,18648 | 0,18474 | 0,17856 | 0,12964 | 0,12308 |
| 536,30724 | 0,18558 | 0,18455 | 0,17864 | 0,12227 | 0,11528 |
| 536,34442 | 0,18376 | 0,18341 | 0,17774 | 0,11534 | 0,10812 |
| 536,3816 | 0,18107 | 0,18135 | 0,17589 | 0,10897 | 0,10168 |
| 536,41879 | 0,17746 | 0,17844 | 0,17317 | 0,10319 | 0,09598 |
| 536,45597 | 0,17315 | 0,17465 | 0,16957 | 0,09798 | 0,09101 |
| 536,49315 | 0,16824 | 0,17021 | 0,16526 | 0,09334 | 0,08678 |
| 536,53033 | 0,16285 | 0,16523 | 0,1604 | 0,08924 | 0,08325 |
| 536,56751 | 0,15707 | 0,15982 | 0,1551 | 0,08566 | 0,08029 |
| 536,6047 | 0,15102 | 0,15408 | 0,14948 | 0,08257 | 0,07784 |
| 536,64188 | 0,14481 | 0,14813 | 0,14366 | 0,07992 | 0,07583 |
| 536,67906 | 0,13853 | 0,14206 | 0,13774 | 0,07769 | 0,0742 |
| 536,71624 | 0,13231 | 0,13598 | 0,13183 | 0,07588 | 0,07289 |
| 536,75342 | 0,12623 | 0,13001 | 0,12605 | 0,0744 | 0,07186 |
| 536,79061 | 0,12037 | 0,12421 | 0,12049 | 0,07323 | 0,07107 |
| 536,82779 | 0,11479 | 0,11867 | 0,1152 | 0,07234 | 0,0705 |
| 536,86497 | 0,10953 | 0,11342 | 0,11024 | 0,0717 | 0,07014 |
| 536,90215 | 0,10463 | 0,10851 | 0,10565 | 0,07132 | 0,06995 |
| 536,93933 | 0,10013 | 0,10398 | 0,10145 | 0,07116 | 0,06994 |
| 536,97652 | 0,09607 | 0,09986 | 0,09768 | 0,07124 | 0,07012 |
| 537,0137 | 0,0925 | 0,09618 | 0,09433 | 0,07156 | 0,07049 |
| 537,05088 | 0,08937 | 0,09299 | 0,09149 | 0,07214 | 0,07109 |
| 537,08806 | 0,0867 | 0,09024 | 0,08909 | 0,07297 | 0,07193 |
| 537,12524 | 0,08447 | 0,08793 | 0,08713 | 0,07405 | 0,07304 |
| 537,16243 | 0,08269 | 0,08607 | 0,08558 | 0,07541 | 0,07447 |
| 537,19961 | 0,08136 | 0,08464 | 0,08443 | 0,07707 | 0,07625 |
| 537,23679 | 0,08047 | 0,08365 | 0,08369 | 0,07906 | 0,0784 |
| 537,27397 | 0,08006 | 0,08307 | 0,08332 | 0,08138 | 0,08093 |
| 537,31115 | 0,08009 | 0,08294 | 0,08331 | 0,08408 | 0,08387 |
| 537,34834 | 0,08051 | 0,08322 | 0,08369 | 0,08721 | 0,08723 |
| 537,38552 | 0,08131 | 0,08386 | 0,08439 | 0,09077 | 0,09103 |
| 537,4227 | 0,08246 | 0,08484 | 0,08537 | 0,09477 | 0,09527 |
| 537,45988 | 0,08393 | 0,08612 | 0,08662 | 0,09922 | 0,09996 |
| 537,49706 | 0,08569 | 0,08768 | 0,08809 | 0,10415 | 0,10515 |
| 537,53425 | 0,08769 | 0,08948 | 0,08977 | 0,10957 | 0,11082 |
| 537,57143 | 0,08992 | 0,09147 | 0,09161 | 0,11552 | 0,11695 |
| 537,60861 | 0,09228 | 0,09364 | 0,09357 | 0,12203 | 0,12358 |
| 537,64579 | 0,09472 | 0,0959 | 0,09564 | 0,12916 | 0,13073 |
| 537,68297 | 0,09719 | 0,09821 | 0,09774 | 0,13703 | 0,13847 |
| 537,72016 | 0,09966 | 0,10053 | 0,09985 | 0,14562 | 0,14685 |
| 537,75734 | 0,10206 | 0,10283 | 0,10193 | 0,15499 | 0,15597 |
| 537,79452 | 0,10438 | 0,10507 | 0,10397 | 0,16521 | 0,16592 |
| 537,8317 | 0,10657 | 0,10722 | 0,10594 | 0,17632 | 0,17691 |
| 537,86888 | 0,10861 | 0,10929 | 0,10784 | 0,18834 | 0,18895 |
| 537,90607 | 0,11052 | 0,11126 | 0,10968 | 0,20126 | 0,20205 |
| 537,94325 | 0,11233 | 0,11315 | 0,11149 | 0,21504 | 0,21621 |
| 537,98043 | 0,11407 | 0,11503 | 0,11331 | 0,22964 | 0,23135 |
| 538,01761 | 0,11581 | 0,11693 | 0,1152 | 0,24478 | 0,24732 |
| 538,05479 | 0,1176 | 0,11893 | 0,11724 | 0,26018 | 0,26388 |
| 538,09198 | 0,11952 | 0,1211 | 0,11951 | 0,2755 | 0,28071 |
| 538,12916 | 0,1217 | 0,12353 | 0,12211 | 0,29038 | 0,2974 |
| 538,16634 | 0,12428 | 0,12631 | 0,12515 | 0,30438 | 0,31328 |
| 538,20352 | 0,12731 | 0,12966 | 0,12875 | 0,31705 | 0,32777 |
| 538,2407 | 0,1309 | 0,1336 | 0,13308 | 0,32795 | 0,34032 |
| 538,27789 | 0,13513 | 0,13821 | 0,13818 | 0,33656 | 0,35037 |
| 538,31507 | 0,14006 | 0,14355 | 0,1441 | 0,34215 | 0,35742 |
| 538,35225 | 0,14573 | 0,14968 | 0,15089 | 0,34473 | 0,36108 |
| 538,38943 | 0,15217 | 0,15661 | 0,15856 | 0,34412 | 0,36106 |
| 538,42661 | 0,15943 | 0,16433 | 0,16709 | 0,34026 | 0,35721 |
| 538,4638 | 0,16742 | 0,17281 | 0,17644 | 0,33322 | 0,34952 |
| 538,50098 | 0,17597 | 0,18203 | 0,18655 | 0,32319 | 0,33775 |
| 538,53816 | 0,18497 | 0,19172 | 0,19724 | 0,31045 | 0,32285 |
| 538,57534 | 0,19425 | 0,20172 | 0,20827 | 0,29541 | 0,30535 |
| 538,61252 | 0,20362 | 0,21183 | 0,21941 | 0,27846 | 0,2859 |
| 538,64971 | 0,21287 | 0,22182 | 0,23043 | 0,26038 | 0,26519 |
| 538,68689 | 0,22178 | 0,23146 | 0,24106 | 0,24188 | 0,24396 |
| 538,72407 | 0,22998 | 0,2405 | 0,25103 | 0,22354 | 0,22295 |
| 538,76125 | 0,23727 | 0,24861 | 0,26009 | 0,20594 | 0,20286 |
| 538,79843 | 0,24345 | 0,25545 | 0,26782 | 0,18958 | 0,18437 |
| 538,83562 | 0,24835 | 0,26089 | 0,27398 | 0,17491 | 0,16834 |
| 538,8728 | 0,25181 | 0,26477 | 0,27846 | 0,16229 | 0,15497 |
| 538,90998 | 0,25371 | 0,26698 | 0,28114 | 0,15202 | 0,1445 |
| 538,94716 | 0,25399 | 0,26741 | 0,28193 | 0,1446 | 0,13706 |
| 538,98434 | 0,25257 | 0,26605 | 0,28079 | 0,13971 | 0,13268 |
| 539,02153 | 0,2493 | 0,26291 | 0,27775 | 0,13724 | 0,13123 |
| 539,05871 | 0,24453 | 0,25793 | 0,27287 | 0,13702 | 0,13251 |
| 539,09589 | 0,23841 | 0,25128 | 0,26613 | 0,13878 | 0,1362 |
| 539,13307 | 0,23112 | 0,24332 | 0,25787 | 0,1422 | 0,14196 |
| 539,17025 | 0,22287 | 0,23427 | 0,24843 | 0,1469 | 0,1493 |
| 539,20744 | 0,2139 | 0,22439 | 0,23808 | 0,15246 | 0,15748 |
| 539,24462 | 0,20446 | 0,21396 | 0,22711 | 0,15842 | 0,16594 |
| 539,2818 | 0,19483 | 0,20324 | 0,21583 | 0,16421 | 0,17414 |
| 539,31898 | 0,18535 | 0,19254 | 0,20452 | 0,1694 | 0,18156 |
| 539,35616 | 0,17626 | 0,18218 | 0,19347 | 0,17361 | 0,18772 |
| 539,39335 | 0,16778 | 0,17246 | 0,18308 | 0,17653 | 0,19224 |
| 539,43053 | 0,1601 | 0,16357 | 0,17356 | 0,1779 | 0,19477 |
| 539,46771 | 0,15335 | 0,15567 | 0,16508 | 0,17755 | 0,19497 |
| 539,50489 | 0,14764 | 0,14889 | 0,15776 | 0,17538 | 0,19263 |
| 539,54207 | 0,14304 | 0,14331 | 0,15169 | 0,17137 | 0,188 |
| 539,57926 | 0,1397 | 0,13897 | 0,14691 | 0,16537 | 0,18122 |
| 539,61644 | 0,1375 | 0,13585 | 0,14341 | 0,15779 | 0,17251 |
| 539,65362 | 0,13629 | 0,13406 | 0,14114 | 0,14889 | 0,16217 |
| 539,6908 | 0,13596 | 0,13334 | 0,14015 | 0,13893 | 0,15055 |
| 539,72798 | 0,13636 | 0,13351 | 0,14011 | 0,12819 | 0,13802 |
| 539,76517 | 0,13732 | 0,13439 | 0,14082 | 0,11697 | 0,12496 |
| 539,80235 | 0,13865 | 0,1358 | 0,14208 | 0,10556 | 0,11176 |
| 539,83953 | 0,14018 | 0,13753 | 0,14368 | 0,09423 | 0,09885 |
| 539,87671 | 0,14165 | 0,13939 | 0,14541 | 0,08327 | 0,0865 |
| 539,91389 | 0,14286 | 0,14118 | 0,14707 | 0,07293 | 0,07493 |
| 539,95108 | 0,14364 | 0,1426 | 0,14844 | 0,06333 | 0,0643 |
| 539,98826 | 0,14384 | 0,1435 | 0,14923 | 0,05455 | 0,0547 |
| 540,02544 | 0,14335 | 0,14375 | 0,14935 | 0,04666 | 0,04619 |
| 540,06262 | 0,14208 | 0,14322 | 0,14867 | 0,03966 | 0,03875 |
| 540,0998 | 0,13997 | 0,14185 | 0,14713 | 0,03355 | 0,03237 |
| 540,13699 | 0,13697 | 0,13957 | 0,14467 | 0,02829 | 0,02702 |
| 540,17417 | 0,13297 | 0,13638 | 0,14127 | 0,02381 | 0,02259 |
| 540,21135 | 0,12815 | 0,13225 | 0,13695 | 0,02012 | 0,01891 |
| 540,24853 | 0,12259 | 0,12715 | 0,13174 | 0,01706 | 0,01587 |
| 540,28571 | 0,11638 | 0,12129 | 0,12564 | 0,01452 | 0,01338 |
| 540,3229 | 0,10961 | 0,11478 | 0,11888 | 0,01242 | 0,01134 |
| 540,36008 | 0,10242 | 0,10774 | 0,11159 | 0,01071 | 0,00969 |
| 540,39726 | 0,09491 | 0,1003 | 0,10391 | 0,0093 | 0,00834 |
| 540,43444 | 0,08723 | 0,09259 | 0,09596 | 0,00816 | 0,00724 |
| 540,47162 | 0,07952 | 0,08474 | 0,08788 | 0,00723 | 0,00636 |
| 540,50881 | 0,07191 | 0,07689 | 0,0798 | 0,00648 | 0,00564 |
| 540,54599 | 0,06451 | 0,0692 | 0,07186 | 0,00587 | 0,00506 |
| 540,58317 | 0,05741 | 0,06178 | 0,06421 | 0,00538 | 0,00458 |
| 540,62035 | 0,05068 | 0,0547 | 0,05693 | 0,00498 | 0,00418 |
| 540,65753 | 0,04438 | 0,04804 | 0,05008 | 0,00465 | 0,00387 |
| 540,69472 | 0,03856 | 0,04185 | 0,04372 | 0,00438 | 0,00362 |
| 540,7319 | 0,03329 | 0,03616 | 0,03788 | 0,00416 | 0,00342 |
| 540,76908 | 0,02858 | 0,03101 | 0,03257 | 0,00398 | 0,00326 |
| 540,80626 | 0,02438 | 0,02643 | 0,02782 | 0,00382 | 0,00313 |
| 540,84344 | 0,02068 | 0,02242 | 0,02364 | 0,00369 | 0,00303 |
| 540,88063 | 0,01745 | 0,01891 | 0,02004 | 0,00357 | 0,00294 |
| 540,91781 | 0,01467 | 0,01587 | 0,01692 | 0,00346 | 0,00285 |
| 540,95499 | 0,0123 | 0,01326 | 0,01424 | 0,00334 | 0,00276 |
| 540,99217 | 0,01031 | 0,01105 | 0,01197 | 0,00322 | 0,00267 |
| 541,02935 | 0,0087 | 0,00919 | 0,01007 | 0,00309 | 0,00256 |
| 541,06654 | 0,00738 | 0,00765 | 0,0085 | 0,00295 | 0,00244 |
| 541,10372 | 0,0063 | 0,0064 | 0,00721 | 0,0028 | 0,00232 |
| 541,1409 | 0,00544 | 0,0054 | 0,00619 | 0,00264 | 0,00217 |
| 541,17808 | 0,00476 | 0,00459 | 0,00538 | 0,00247 | 0,00202 |
| 541,21526 | 0,00422 | 0,00394 | 0,00474 | 0,00229 | 0,00186 |
| 541,25245 | 0,0038 | 0,00342 | 0,00424 | 0,00211 | 0,0017 |
| 541,28963 | 0,00349 | 0,00301 | 0,00384 | 0,00193 | 0,00153 |
| 541,32681 | 0,00325 | 0,00269 | 0,00354 | 0,00176 | 0,00137 |
| 541,36399 | 0,00307 | 0,00243 | 0,00331 | 0,00159 | 0,00122 |
| 541,40117 | 0,00293 | 0,00224 | 0,00313 | 0,00143 | 0,00107 |
| 541,43836 | 0,00281 | 0,00209 | 0,00299 | 0,00128 | 0,00093 |
| 541,47554 | 0,00271 | 0,00196 | 0,00287 | 0,00114 | 8e-04 |
| 541,51272 | 0,00262 | 0,00185 | 0,00278 | 0,00102 | 0,00069 |
| 541,5499 | 0,00253 | 0,00176 | 0,00269 | 0,00092 | 0,00059 |
| 541,58708 | 0,00244 | 0,00168 | 0,0026 | 0,00082 | 0,00051 |
| 541,62427 | 0,00235 | 0,0016 | 0,00251 | 0,00074 | 0,00043 |
| 541,66145 | 0,00225 | 0,00153 | 0,00242 | 0,00067 | 0,00037 |
| 541,69863 | 0,00214 | 0,00145 | 0,00232 | 0,00062 | 0,00031 |
| 541,73581 | 0,00202 | 0,00137 | 0,00222 | 0,00056 | 0,00027 |
| 541,77299 | 0,0019 | 0,00129 | 0,00211 | 0,00052 | 0,00023 |
| 541,81018 | 0,00177 | 0,00121 | 0,002 | 0,00048 | 2e-04 |
| 541,84736 | 0,00164 | 0,00113 | 0,00188 | 0,00044 | 0,00017 |
| 541,88454 | 0,00151 | 0,00105 | 0,00175 | 0,00041 | 0,00014 |
| 541,92172 | 0,00138 | 0,00096 | 0,00163 | 0,00038 | 0,00012 |
| 541,9589 | 0,00124 | 0,00087 | 0,0015 | 0,00034 | 1e-04 |
| 541,99609 | 0,00111 | 0,00079 | 0,00137 | 0,00031 | 9e-05 |
| 542,03327 | 0,00099 | 0,00071 | 0,00125 | 0,00028 | 7e-05 |
| 542,07045 | 0,00087 | 0,00063 | 0,00113 | 0,00025 | 6e-05 |
| 542,10763 | 0,00076 | 0,00056 | 0,00101 | 0,00022 | 5e-05 |
| 542,14481 | 0,00066 | 0,00048 | 9e-04 | 2e-04 | 4e-05 |
| 542,182 | 0,00056 | 0,00042 | 8e-04 | 0,00017 | 3e-05 |
| 542,21918 | 0,00048 | 0,00036 | 0,00071 | 0,00015 | 3e-05 |
| 542,25636 | 4e-04 | 3e-04 | 0,00062 | 0,00012 | 2e-05 |
| 542,29354 | 0,00034 | 0,00026 | 0,00053 | 1e-04 | 2e-05 |
| 542,33072 | 0,00028 | 0,00021 | 0,00046 | 9e-05 | 1e-05 |
| 542,36791 | 0,00023 | 0,00018 | 4e-04 | 7e-05 | 1e-05 |
| 542,40509 | 0,00018 | 0,00014 | 0,00034 | 6e-05 | 1e-05 |
| 542,44227 | 0,00015 | 0,00012 | 0,00029 | 4e-05 | 0 |
| 542,47945 | 0,00012 | 9e-05 | 0,00024 | 4e-05 | 0 |
| 542,51663 | 9e-05 | 7e-05 | 2e-04 | 3e-05 | 0 |
| 542,55382 | 7e-05 | 6e-05 | 0,00016 | 2e-05 | 0 |
| 542,591 | 6e-05 | 4e-05 | 0,00014 | 2e-05 | 0 |
| 542,62818 | 4e-05 | 3e-05 | 0,00011 | 1e-05 | 0 |
| 542,66536 | 3e-05 | 3e-05 | 9e-05 | 1e-05 | 0 |
| 542,70254 | 2e-05 | 2e-05 | 7e-05 | 1e-05 | 0 |
| 542,73973 | 2e-05 | 1e-05 | 6e-05 | 0 | 0 |
| 542,77691 | 1e-05 | 1e-05 | 5e-05 | 0 | 0 |
| 542,81409 | 1e-05 | 1e-05 | 4e-05 | 0 | 0 |
| 542,85127 | 1e-05 | 1e-05 | 3e-05 | 0 | 0 |
| 542,88845 | 0 | 0 | 2e-05 | 0 | 0 |
| 542,92564 | 0 | 0 | 2e-05 | 0 | 0 |
| 542,96282 | 0 | 0 | 1e-05 | 0 | 0 |
| 543 | 0 | 0 | 1e-05 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 0 | 0 | 0 |
| 524,74364 | 0 | 0 | 0 | 0 | 0 |
| 524,78082 | 0 | 0 | 0 | 0 | 0 |
| 524,818 | 0 | 0 | 0 | 0 | 0 |
| 524,85519 | 0 | 0 | 0 | 0 | 0 |
| 524,89237 | 0 | 0 | 0 | 0 | 0 |
| 524,92955 | 0 | 0 | 0 | 0 | 0 |
| 524,96673 | 0 | 0 | 0 | 0 | 0 |
| 525,00391 | 0 | 0 | 0 | 0 | 0 |
| 525,0411 | 0 | 0 | 0 | 0 | 0 |
| 525,07828 | 0 | 0 | 0 | 0 | 0 |
| 525,11546 | 0 | 0 | 0 | 0 | 0 |
| 525,15264 | 0 | 0 | 0 | 0 | 0 |
| 525,18982 | 0 | 0 | 0 | 0 | 0 |
| 525,22701 | 0 | 0 | 0 | 0 | 0 |
| 525,26419 | 0 | 0 | 0 | 0 | 0 |
| 525,30137 | 0 | 0 | 0 | 0 | 0 |
| 525,33855 | 0 | 0 | 0 | 0 | 0 |
| 525,37573 | 0 | 0 | 0 | 0 | 0 |
| 525,41292 | 0 | 0 | 0 | 0 | 0 |
| 525,4501 | 0 | 0 | 0 | 0 | 0 |
| 525,48728 | 0 | 0 | 0 | 0 | 0 |
| 525,52446 | 0 | 0 | 0 | 0 | 0 |
| 525,56164 | 0 | 0 | 0 | 0 | 0 |
| 525,59883 | 0 | 0 | 0 | 0 | 0 |
| 525,63601 | 0 | 0 | 0 | 0 | 0 |
| 525,67319 | 0 | 0 | 0 | 0 | 0 |
| 525,71037 | 0 | 0 | 0 | 0 | 0 |
| 525,74755 | 0 | 0 | 0 | 0 | 0 |
| 525,78474 | 0 | 0 | 0 | 0 | 0 |
| 525,82192 | 0 | 0 | 0 | 0 | 0 |
| 525,8591 | 0 | 0 | 0 | 0 | 0 |
| 525,89628 | 0 | 0 | 0 | 0 | 0 |
| 525,93346 | 0 | 0 | 0 | 0 | 0 |
| 525,97065 | 0 | 0 | 0 | 0 | 0 |
| 526,00783 | 0 | 0 | 0 | 0 | 0 |
| 526,04501 | 0 | 0 | 0 | 0 | 0 |
| 526,08219 | 0 | 0 | 0 | 0 | 0 |
| 526,11937 | 0 | 0 | 0 | 0 | 0 |
| 526,15656 | 0 | 0 | 0 | 0 | 0 |
| 526,19374 | 0 | 0 | 1e-05 | 0 | 0 |
| 526,23092 | 0 | 0 | 1e-05 | 0 | 0 |
| 526,2681 | 0 | 0 | 1e-05 | 0 | 0 |
| 526,30528 | 0 | 0 | 2e-05 | 0 | 0 |
| 526,34247 | 0 | 0 | 2e-05 | 0 | 0 |
| 526,37965 | 0 | 0 | 2e-05 | 0 | 0 |
| 526,41683 | 0 | 0 | 3e-05 | 0 | 0 |
| 526,45401 | 0 | 0 | 3e-05 | 0 | 0 |
| 526,49119 | 0 | 0 | 4e-05 | 0 | 0 |
| 526,52838 | 0 | 0 | 4e-05 | 0 | 0 |
| 526,56556 | 0 | 0 | 4e-05 | 0 | 0 |
| 526,60274 | 0 | 0 | 5e-05 | 0 | 0 |
| 526,63992 | 0 | 0 | 5e-05 | 0 | 0 |
| 526,6771 | 0 | 0 | 4e-05 | 0 | 0 |
| 526,71429 | 0 | 0 | 4e-05 | 0 | 0 |
| 526,75147 | 0 | 0 | 4e-05 | 0 | 0 |
| 526,78865 | 1e-05 | 0 | 4e-05 | 0 | 0 |
| 526,82583 | 1e-05 | 0 | 3e-05 | 0 | 0 |
| 526,86301 | 1e-05 | 0 | 3e-05 | 0 | 0 |
| 526,9002 | 2e-05 | 0 | 3e-05 | 0 | 0 |
| 526,93738 | 2e-05 | 0 | 3e-05 | 0 | 0 |
| 526,97456 | 2e-05 | 0 | 3e-05 | 0 | 0 |
| 527,01174 | 3e-05 | 0 | 3e-05 | 0 | 0 |
| 527,04892 | 3e-05 | 0 | 3e-05 | 0 | 0 |
| 527,08611 | 4e-05 | 0 | 4e-05 | 0 | 0 |
| 527,12329 | 4e-05 | 0 | 4e-05 | 0 | 0 |
| 527,16047 | 5e-05 | 0 | 4e-05 | 0 | 0 |
| 527,19765 | 5e-05 | 0 | 4e-05 | 0 | 0 |
| 527,23483 | 5e-05 | 0 | 5e-05 | 0 | 0 |
| 527,27202 | 5e-05 | 0 | 5e-05 | 0 | 0 |
| 527,3092 | 4e-05 | 1e-05 | 5e-05 | 0 | 0 |
| 527,34638 | 4e-05 | 1e-05 | 4e-05 | 0 | 0 |
| 527,38356 | 4e-05 | 1e-05 | 4e-05 | 0 | 0 |
| 527,42074 | 3e-05 | 2e-05 | 4e-05 | 0 | 0 |
| 527,45793 | 3e-05 | 2e-05 | 4e-05 | 0 | 0 |
| 527,49511 | 2e-05 | 2e-05 | 3e-05 | 0 | 1e-05 |
| 527,53229 | 2e-05 | 3e-05 | 3e-05 | 0 | 1e-05 |
| 527,56947 | 1e-05 | 4e-05 | 3e-05 | 0 | 1e-05 |
| 527,60665 | 1e-05 | 4e-05 | 3e-05 | 0 | 2e-05 |
| 527,64384 | 1e-05 | 5e-05 | 3e-05 | 0 | 2e-05 |
| 527,68102 | 1e-05 | 5e-05 | 4e-05 | 1e-05 | 3e-05 |
| 527,7182 | 0 | 6e-05 | 4e-05 | 1e-05 | 4e-05 |
| 527,75538 | 0 | 6e-05 | 5e-05 | 1e-05 | 5e-05 |
| 527,79256 | 1e-05 | 7e-05 | 5e-05 | 2e-05 | 6e-05 |
| 527,82975 | 1e-05 | 7e-05 | 5e-05 | 2e-05 | 7e-05 |
| 527,86693 | 1e-05 | 7e-05 | 6e-05 | 3e-05 | 8e-05 |
| 527,90411 | 1e-05 | 7e-05 | 7e-05 | 4e-05 | 9e-05 |
| 527,94129 | 1e-05 | 8e-05 | 7e-05 | 5e-05 | 1e-04 |
| 527,97847 | 2e-05 | 8e-05 | 8e-05 | 6e-05 | 0,00011 |
| 528,01566 | 2e-05 | 8e-05 | 8e-05 | 7e-05 | 0,00012 |
| 528,05284 | 3e-05 | 8e-05 | 9e-05 | 8e-05 | 0,00012 |
| 528,09002 | 3e-05 | 9e-05 | 1e-04 | 9e-05 | 0,00013 |
| 528,1272 | 4e-05 | 9e-05 | 0,00011 | 1e-04 | 0,00013 |
| 528,16438 | 4e-05 | 9e-05 | 0,00012 | 1e-04 | 0,00014 |
| 528,20157 | 5e-05 | 1e-04 | 0,00013 | 1e-04 | 0,00015 |
| 528,23875 | 5e-05 | 1e-04 | 0,00014 | 1e-04 | 0,00016 |
| 528,27593 | 5e-05 | 0,00011 | 0,00015 | 1e-04 | 0,00017 |
| 528,31311 | 5e-05 | 0,00011 | 0,00016 | 1e-04 | 0,00018 |
| 528,35029 | 5e-05 | 0,00012 | 0,00017 | 9e-05 | 2e-04 |
| 528,38748 | 5e-05 | 0,00012 | 0,00017 | 9e-05 | 0,00021 |
| 528,42466 | 5e-05 | 0,00013 | 0,00018 | 9e-05 | 0,00022 |
| 528,46184 | 5e-05 | 0,00013 | 0,00018 | 9e-05 | 0,00023 |
| 528,49902 | 5e-05 | 0,00014 | 0,00018 | 9e-05 | 0,00023 |
| 528,5362 | 6e-05 | 0,00014 | 0,00018 | 1e-04 | 0,00023 |
| 528,57339 | 6e-05 | 0,00015 | 0,00017 | 1e-04 | 0,00023 |
| 528,61057 | 7e-05 | 0,00015 | 0,00017 | 0,00011 | 0,00022 |
| 528,64775 | 8e-05 | 0,00016 | 0,00017 | 0,00012 | 0,00022 |
| 528,68493 | 1e-04 | 0,00016 | 0,00016 | 0,00012 | 0,00021 |
| 528,72211 | 0,00011 | 0,00016 | 0,00016 | 0,00013 | 0,00021 |
| 528,7593 | 0,00013 | 0,00017 | 0,00016 | 0,00014 | 2e-04 |
| 528,79648 | 0,00016 | 0,00017 | 0,00016 | 0,00015 | 2e-04 |
| 528,83366 | 0,00018 | 0,00017 | 0,00017 | 0,00016 | 2e-04 |
| 528,87084 | 0,00021 | 0,00018 | 0,00018 | 0,00017 | 0,00021 |
| 528,90802 | 0,00023 | 0,00018 | 0,00019 | 0,00018 | 0,00021 |
| 528,94521 | 0,00026 | 0,00019 | 2e-04 | 0,00019 | 0,00021 |
| 528,98239 | 0,00028 | 2e-04 | 0,00022 | 2e-04 | 0,00021 |
| 529,01957 | 3e-04 | 0,00021 | 0,00023 | 0,00022 | 0,00021 |
| 529,05675 | 0,00032 | 0,00022 | 0,00025 | 0,00023 | 0,00021 |
| 529,09393 | 0,00033 | 0,00023 | 0,00026 | 0,00025 | 2e-04 |
| 529,13112 | 0,00034 | 0,00025 | 0,00027 | 0,00026 | 2e-04 |
| 529,1683 | 0,00035 | 0,00027 | 0,00027 | 0,00028 | 0,00019 |
| 529,20548 | 0,00035 | 0,00029 | 0,00027 | 3e-04 | 0,00018 |
| 529,24266 | 0,00035 | 0,00032 | 0,00027 | 0,00032 | 0,00017 |
| 529,27984 | 0,00035 | 0,00035 | 0,00026 | 0,00035 | 0,00016 |
| 529,31703 | 0,00036 | 0,00038 | 0,00025 | 0,00037 | 0,00015 |
| 529,35421 | 0,00036 | 0,00041 | 0,00024 | 0,00038 | 0,00015 |
| 529,39139 | 0,00037 | 0,00044 | 0,00024 | 4e-04 | 0,00015 |
| 529,42857 | 0,00039 | 0,00047 | 0,00023 | 0,00041 | 0,00016 |
| 529,46575 | 0,00041 | 0,00051 | 0,00023 | 0,00042 | 0,00017 |
| 529,50294 | 0,00044 | 0,00055 | 0,00023 | 0,00043 | 0,00018 |
| 529,54012 | 0,00048 | 0,00058 | 0,00024 | 0,00044 | 2e-04 |
| 529,5773 | 0,00052 | 0,00062 | 0,00025 | 0,00045 | 0,00023 |
| 529,61448 | 0,00057 | 0,00065 | 0,00027 | 0,00045 | 0,00025 |
| 529,65166 | 0,00062 | 0,00068 | 0,00029 | 0,00046 | 0,00028 |
| 529,68885 | 0,00067 | 0,00071 | 0,00031 | 0,00047 | 0,00031 |
| 529,72603 | 0,00072 | 0,00074 | 0,00033 | 0,00048 | 0,00034 |
| 529,76321 | 0,00076 | 0,00077 | 0,00036 | 5e-04 | 0,00038 |
| 529,80039 | 8e-04 | 8e-04 | 0,00038 | 0,00051 | 0,00041 |
| 529,83757 | 0,00084 | 0,00083 | 0,00041 | 0,00054 | 0,00043 |
| 529,87476 | 0,00086 | 0,00086 | 0,00044 | 0,00056 | 0,00046 |
| 529,91194 | 0,00088 | 0,00088 | 0,00047 | 0,00058 | 0,00049 |
| 529,94912 | 0,00089 | 0,00091 | 0,00051 | 0,00061 | 0,00051 |
| 529,9863 | 9e-04 | 0,00094 | 0,00055 | 0,00064 | 0,00053 |
| 530,02348 | 0,00091 | 0,00096 | 6e-04 | 0,00067 | 0,00055 |
| 530,06067 | 0,00091 | 0,001 | 0,00066 | 7e-04 | 0,00057 |
| 530,09785 | 0,00092 | 0,00103 | 0,00073 | 0,00073 | 0,00059 |
| 530,13503 | 0,00094 | 0,00107 | 0,00081 | 0,00075 | 6e-04 |
| 530,17221 | 0,00097 | 0,00112 | 9e-04 | 0,00078 | 0,00062 |
| 530,20939 | 0,00101 | 0,00118 | 0,001 | 0,00081 | 0,00063 |
| 530,24658 | 0,00107 | 0,00125 | 0,0011 | 0,00083 | 0,00064 |
| 530,28376 | 0,00114 | 0,00134 | 0,0012 | 0,00086 | 0,00065 |
| 530,32094 | 0,00124 | 0,00144 | 0,0013 | 0,00088 | 0,00067 |
| 530,35812 | 0,00136 | 0,00155 | 0,00141 | 0,00091 | 7e-04 |
| 530,3953 | 0,00151 | 0,00167 | 0,00151 | 0,00095 | 0,00073 |
| 530,43249 | 0,00168 | 0,00181 | 0,00162 | 0,00099 | 0,00078 |
| 530,46967 | 0,00187 | 0,00195 | 0,00173 | 0,00103 | 0,00084 |
| 530,50685 | 0,00208 | 0,0021 | 0,00184 | 0,00109 | 0,00093 |
| 530,54403 | 0,0023 | 0,00225 | 0,00196 | 0,00116 | 0,00104 |
| 530,58121 | 0,00252 | 0,0024 | 0,00208 | 0,00125 | 0,00117 |
| 530,6184 | 0,00274 | 0,00255 | 0,00222 | 0,00136 | 0,00133 |
| 530,65558 | 0,00296 | 0,0027 | 0,00235 | 0,0015 | 0,00153 |
| 530,69276 | 0,00317 | 0,00284 | 0,0025 | 0,00166 | 0,00175 |
| 530,72994 | 0,00336 | 0,00297 | 0,00264 | 0,00186 | 0,00199 |
| 530,76712 | 0,00353 | 0,0031 | 0,00279 | 0,0021 | 0,00227 |
| 530,80431 | 0,00369 | 0,00321 | 0,00294 | 0,00237 | 0,00256 |
| 530,84149 | 0,00382 | 0,00331 | 0,00308 | 0,00267 | 0,00287 |
| 530,87867 | 0,00394 | 0,0034 | 0,00322 | 0,003 | 0,00318 |
| 530,91585 | 0,00405 | 0,00348 | 0,00337 | 0,00335 | 0,00349 |
| 530,95303 | 0,00416 | 0,00354 | 0,00351 | 0,00373 | 0,0038 |
| 530,99022 | 0,00426 | 0,00361 | 0,00365 | 0,00411 | 0,00411 |
| 531,0274 | 0,00438 | 0,00367 | 0,00379 | 0,0045 | 0,0044 |
| 531,06458 | 0,0045 | 0,00373 | 0,00394 | 0,00488 | 0,00467 |
| 531,10176 | 0,00463 | 0,00381 | 0,00409 | 0,00525 | 0,00492 |
| 531,13894 | 0,00478 | 0,0039 | 0,00425 | 0,00559 | 0,00514 |
| 531,17613 | 0,00494 | 0,00401 | 0,00443 | 0,00591 | 0,00533 |
| 531,21331 | 0,00511 | 0,00414 | 0,00461 | 0,00618 | 0,00548 |
| 531,25049 | 0,00529 | 0,0043 | 0,0048 | 0,0064 | 0,0056 |
| 531,28767 | 0,00547 | 0,00447 | 0,005 | 0,00659 | 0,00567 |
| 531,32485 | 0,00565 | 0,00467 | 0,00521 | 0,00672 | 0,00569 |
| 531,36204 | 0,00583 | 0,00488 | 0,00543 | 0,0068 | 0,00567 |
| 531,39922 | 0,006 | 0,00509 | 0,00565 | 0,00685 | 0,00561 |
| 531,4364 | 0,00617 | 0,00531 | 0,00587 | 0,00685 | 0,00552 |
| 531,47358 | 0,00633 | 0,00553 | 0,0061 | 0,00683 | 0,0054 |
| 531,51076 | 0,00649 | 0,00574 | 0,00633 | 0,00679 | 0,00526 |
| 531,54795 | 0,00665 | 0,00596 | 0,00656 | 0,00673 | 0,00513 |
| 531,58513 | 0,00681 | 0,00617 | 0,0068 | 0,00667 | 0,00501 |
| 531,62231 | 0,00698 | 0,00639 | 0,00703 | 0,00661 | 0,0049 |
| 531,65949 | 0,00715 | 0,00662 | 0,00726 | 0,00656 | 0,00483 |
| 531,69667 | 0,00732 | 0,00685 | 0,00749 | 0,00652 | 0,00478 |
| 531,73386 | 0,0075 | 0,0071 | 0,00772 | 0,00649 | 0,00476 |
| 531,77104 | 0,00769 | 0,00736 | 0,00795 | 0,00647 | 0,00478 |
| 531,80822 | 0,00787 | 0,00763 | 0,00818 | 0,00646 | 0,00482 |
| 531,8454 | 0,00806 | 0,00792 | 0,0084 | 0,00646 | 0,00489 |
| 531,88258 | 0,00825 | 0,0082 | 0,00862 | 0,00648 | 0,00498 |
| 531,91977 | 0,00845 | 0,00849 | 0,00884 | 0,0065 | 0,0051 |
| 531,95695 | 0,00866 | 0,00878 | 0,00905 | 0,00655 | 0,00523 |
| 531,99413 | 0,00887 | 0,00907 | 0,00927 | 0,00662 | 0,00539 |
| 532,03131 | 0,0091 | 0,00936 | 0,00949 | 0,00673 | 0,00558 |
| 532,06849 | 0,00934 | 0,00966 | 0,00971 | 0,00688 | 0,00581 |
| 532,10568 | 0,00959 | 0,00995 | 0,00995 | 0,0071 | 0,00608 |
| 532,14286 | 0,00987 | 0,01025 | 0,01021 | 0,00738 | 0,0064 |
| 532,18004 | 0,01016 | 0,01057 | 0,01049 | 0,00773 | 0,00677 |
| 532,21722 | 0,01046 | 0,01089 | 0,01079 | 0,00814 | 0,0072 |
| 532,2544 | 0,01079 | 0,01122 | 0,01113 | 0,0086 | 0,00768 |
| 532,29159 | 0,01112 | 0,01156 | 0,0115 | 0,00912 | 0,00822 |
| 532,32877 | 0,01146 | 0,0119 | 0,01189 | 0,00966 | 0,0088 |
| 532,36595 | 0,01181 | 0,01225 | 0,0123 | 0,01021 | 0,00943 |
| 532,40313 | 0,01214 | 0,01259 | 0,01272 | 0,01077 | 0,01008 |
| 532,44031 | 0,01247 | 0,01293 | 0,01315 | 0,01133 | 0,01075 |
| 532,4775 | 0,01277 | 0,01325 | 0,01356 | 0,01186 | 0,01142 |
| 532,51468 | 0,01306 | 0,01357 | 0,01395 | 0,01238 | 0,01208 |
| 532,55186 | 0,01333 | 0,01388 | 0,01433 | 0,01289 | 0,01273 |
| 532,58904 | 0,0136 | 0,01419 | 0,01468 | 0,01338 | 0,01335 |
| 532,62622 | 0,01389 | 0,01453 | 0,01501 | 0,01387 | 0,01395 |
| 532,66341 | 0,01421 | 0,01493 | 0,01535 | 0,01436 | 0,01453 |
| 532,70059 | 0,01461 | 0,01541 | 0,01572 | 0,01488 | 0,01509 |
| 532,73777 | 0,01511 | 0,016 | 0,01615 | 0,01543 | 0,01567 |
| 532,77495 | 0,01575 | 0,01674 | 0,01667 | 0,01603 | 0,01628 |
| 532,81213 | 0,01656 | 0,01765 | 0,0173 | 0,0167 | 0,01697 |
| 532,84932 | 0,01756 | 0,01875 | 0,01808 | 0,01748 | 0,01777 |
| 532,8865 | 0,01875 | 0,02005 | 0,01901 | 0,01839 | 0,01872 |
| 532,92368 | 0,02016 | 0,02155 | 0,02012 | 0,01946 | 0,01985 |
| 532,96086 | 0,02174 | 0,02323 | 0,0214 | 0,02073 | 0,0212 |
| 532,99804 | 0,02349 | 0,02506 | 0,02283 | 0,02219 | 0,02278 |
| 533,03523 | 0,02534 | 0,02698 | 0,02438 | 0,02386 | 0,02457 |
| 533,07241 | 0,02725 | 0,02894 | 0,02601 | 0,02571 | 0,02654 |
| 533,10959 | 0,02915 | 0,03087 | 0,02765 | 0,02766 | 0,02859 |
| 533,14677 | 0,03095 | 0,03268 | 0,02925 | 0,02963 | 0,03063 |
| 533,18395 | 0,03261 | 0,0343 | 0,03074 | 0,03152 | 0,03253 |
| 533,22114 | 0,03407 | 0,03569 | 0,03207 | 0,03321 | 0,03418 |
| 533,25832 | 0,03528 | 0,0368 | 0,03318 | 0,03463 | 0,03548 |
| 533,2955 | 0,03623 | 0,03759 | 0,03405 | 0,03568 | 0,03637 |
| 533,33268 | 0,03692 | 0,03807 | 0,03466 | 0,03634 | 0,0368 |
| 533,36986 | 0,03735 | 0,03825 | 0,03501 | 0,03659 | 0,03679 |
| 533,40705 | 0,03756 | 0,03816 | 0,03512 | 0,03647 | 0,03639 |
| 533,44423 | 0,03758 | 0,03785 | 0,03502 | 0,03606 | 0,03571 |
| 533,48141 | 0,03747 | 0,03737 | 0,03475 | 0,03546 | 0,03485 |
| 533,51859 | 0,03727 | 0,03678 | 0,03438 | 0,03476 | 0,03394 |
| 533,55577 | 0,03703 | 0,03616 | 0,03394 | 0,03409 | 0,03313 |
| 533,59295 | 0,03681 | 0,03555 | 0,03351 | 0,03351 | 0,03248 |
| 533,63014 | 0,03662 | 0,035 | 0,03311 | 0,03308 | 0,03204 |
| 533,66732 | 0,03649 | 0,03454 | 0,03278 | 0,0328 | 0,03183 |
| 533,7045 | 0,03642 | 0,03417 | 0,03253 | 0,03268 | 0,03182 |
| 533,74168 | 0,03642 | 0,03389 | 0,03236 | 0,03268 | 0,03196 |
| 533,77886 | 0,03647 | 0,03371 | 0,03226 | 0,03277 | 0,0322 |
| 533,81605 | 0,03657 | 0,03361 | 0,03222 | 0,03292 | 0,03248 |
| 533,85323 | 0,03671 | 0,03358 | 0,03223 | 0,03307 | 0,03274 |
| 533,89041 | 0,03688 | 0,0336 | 0,03228 | 0,03323 | 0,03295 |
| 533,92759 | 0,03708 | 0,03367 | 0,03235 | 0,03336 | 0,03308 |
| 533,96477 | 0,03734 | 0,03381 | 0,03245 | 0,03346 | 0,03311 |
| 534,00196 | 0,03768 | 0,03403 | 0,0326 | 0,03354 | 0,03307 |
| 534,03914 | 0,03815 | 0,03438 | 0,03286 | 0,03361 | 0,03297 |
| 534,07632 | 0,0388 | 0,03492 | 0,03327 | 0,0337 | 0,03286 |
| 534,1135 | 0,03972 | 0,03569 | 0,03391 | 0,03385 | 0,03279 |
| 534,15068 | 0,04096 | 0,03679 | 0,03486 | 0,03411 | 0,03284 |
| 534,18787 | 0,0426 | 0,03827 | 0,03619 | 0,03456 | 0,03309 |
| 534,22505 | 0,04472 | 0,04022 | 0,03799 | 0,0353 | 0,03364 |
| 534,26223 | 0,04735 | 0,0427 | 0,04032 | 0,03645 | 0,03463 |
| 534,29941 | 0,05054 | 0,04574 | 0,04322 | 0,03814 | 0,03618 |
| 534,33659 | 0,05426 | 0,04936 | 0,04671 | 0,0405 | 0,03844 |
| 534,37378 | 0,05848 | 0,05352 | 0,05077 | 0,04365 | 0,04154 |
| 534,41096 | 0,06313 | 0,05816 | 0,05532 | 0,04769 | 0,04556 |
| 534,44814 | 0,06807 | 0,06317 | 0,06028 | 0,05266 | 0,05057 |
| 534,48532 | 0,07308 | 0,06835 | 0,06542 | 0,0585 | 0,05653 |
| 534,5225 | 0,07797 | 0,07349 | 0,07055 | 0,06497 | 0,06319 |
| 534,55969 | 0,08251 | 0,07836 | 0,07543 | 0,07176 | 0,07028 |
| 534,59687 | 0,08648 | 0,08273 | 0,07984 | 0,07851 | 0,0774 |
| 534,63405 | 0,08969 | 0,08641 | 0,08355 | 0,08477 | 0,0841 |
| 534,67123 | 0,09197 | 0,0892 | 0,08637 | 0,0901 | 0,08993 |
| 534,70841 | 0,09321 | 0,09098 | 0,08818 | 0,09411 | 0,09445 |
| 534,7456 | 0,09336 | 0,09168 | 0,08888 | 0,09647 | 0,0973 |
| 534,78278 | 0,09243 | 0,09128 | 0,08847 | 0,09699 | 0,09827 |
| 534,81996 | 0,0905 | 0,08984 | 0,08701 | 0,09563 | 0,09729 |
| 534,85714 | 0,08769 | 0,08747 | 0,08462 | 0,09252 | 0,09446 |
| 534,89432 | 0,08417 | 0,08428 | 0,08143 | 0,08792 | 0,09004 |
| 534,93151 | 0,08023 | 0,08056 | 0,07771 | 0,08217 | 0,08438 |
| 534,96869 | 0,07608 | 0,0765 | 0,0737 | 0,07585 | 0,07802 |
| 535,00587 | 0,07192 | 0,07231 | 0,0696 | 0,06941 | 0,07148 |
| 535,04305 | 0,06793 | 0,06817 | 0,06558 | 0,06327 | 0,06518 |
| 535,08023 | 0,06426 | 0,06423 | 0,06178 | 0,05773 | 0,05945 |
| 535,11742 | 0,061 | 0,06062 | 0,05832 | 0,05301 | 0,05452 |
| 535,1546 | 0,05824 | 0,05742 | 0,05526 | 0,04923 | 0,05054 |
| 535,19178 | 0,05602 | 0,0547 | 0,05264 | 0,04642 | 0,04753 |
| 535,22896 | 0,05436 | 0,0525 | 0,05047 | 0,04454 | 0,04545 |
| 535,26614 | 0,05325 | 0,05085 | 0,04876 | 0,04351 | 0,04423 |
| 535,30333 | 0,0527 | 0,04975 | 0,0475 | 0,04319 | 0,04372 |
| 535,34051 | 0,05275 | 0,04926 | 0,04669 | 0,04346 | 0,04381 |
| 535,37769 | 0,05335 | 0,04935 | 0,04636 | 0,04421 | 0,04435 |
| 535,41487 | 0,05452 | 0,05003 | 0,0465 | 0,04531 | 0,04525 |
| 535,45205 | 0,05628 | 0,05132 | 0,04715 | 0,04667 | 0,04637 |
| 535,48924 | 0,05869 | 0,05326 | 0,04837 | 0,04821 | 0,04765 |
| 535,52642 | 0,06181 | 0,05591 | 0,05026 | 0,04991 | 0,04905 |
| 535,5636 | 0,06572 | 0,05934 | 0,05291 | 0,05175 | 0,05057 |
| 535,60078 | 0,07051 | 0,06364 | 0,05644 | 0,05378 | 0,05224 |
| 535,63796 | 0,07627 | 0,06891 | 0,06099 | 0,05608 | 0,05416 |
| 535,67515 | 0,08308 | 0,07524 | 0,06668 | 0,05878 | 0,05645 |
| 535,71233 | 0,09102 | 0,08271 | 0,07361 | 0,06208 | 0,05932 |
| 535,74951 | 0,10012 | 0,09138 | 0,08187 | 0,06624 | 0,06305 |
| 535,78669 | 0,11042 | 0,1013 | 0,0915 | 0,07155 | 0,06794 |
| 535,82387 | 0,12172 | 0,11237 | 0,1025 | 0,07835 | 0,07434 |
| 535,86106 | 0,13378 | 0,12436 | 0,1146 | 0,08707 | 0,08265 |
| 535,89824 | 0,14631 | 0,13698 | 0,1275 | 0,09786 | 0,09318 |
| 535,93542 | 0,15893 | 0,14984 | 0,14082 | 0,11071 | 0,10588 |
| 535,9726 | 0,17119 | 0,1625 | 0,15407 | 0,12542 | 0,12057 |
| 536,00978 | 0,18261 | 0,17443 | 0,16672 | 0,14155 | 0,13683 |
| 536,04697 | 0,19271 | 0,18512 | 0,1782 | 0,15845 | 0,15397 |
| 536,08415 | 0,20104 | 0,19406 | 0,18796 | 0,1752 | 0,17108 |
| 536,12133 | 0,20722 | 0,20081 | 0,19551 | 0,19081 | 0,18709 |
| 536,15851 | 0,21098 | 0,20505 | 0,20047 | 0,2042 | 0,20089 |
| 536,19569 | 0,2122 | 0,20659 | 0,20263 | 0,21441 | 0,21144 |
| 536,23288 | 0,21063 | 0,20533 | 0,20192 | 0,22068 | 0,21793 |
| 536,27006 | 0,20675 | 0,20133 | 0,19825 | 0,22254 | 0,21984 |
| 536,30724 | 0,20084 | 0,1951 | 0,19217 | 0,21984 | 0,21705 |
| 536,34442 | 0,1933 | 0,18706 | 0,18417 | 0,2127 | 0,20956 |
| 536,3816 | 0,18456 | 0,17771 | 0,17476 | 0,20222 | 0,19844 |
| 536,41879 | 0,17505 | 0,16752 | 0,16446 | 0,18933 | 0,18473 |
| 536,45597 | 0,16521 | 0,15699 | 0,1538 | 0,17507 | 0,16953 |
| 536,49315 | 0,15538 | 0,14653 | 0,14322 | 0,16042 | 0,15388 |
| 536,53033 | 0,14589 | 0,1365 | 0,1331 | 0,14627 | 0,13871 |
| 536,56751 | 0,13696 | 0,12716 | 0,12372 | 0,13328 | 0,12473 |
| 536,6047 | 0,12875 | 0,11869 | 0,11525 | 0,12191 | 0,11244 |
| 536,64188 | 0,12136 | 0,11119 | 0,10778 | 0,11238 | 0,10209 |
| 536,67906 | 0,11489 | 0,10468 | 0,10132 | 0,10471 | 0,09372 |
| 536,71624 | 0,10927 | 0,09923 | 0,0959 | 0,09878 | 0,08723 |
| 536,75342 | 0,10442 | 0,09466 | 0,09138 | 0,09437 | 0,08239 |
| 536,79061 | 0,10028 | 0,0909 | 0,08765 | 0,09126 | 0,07896 |
| 536,82779 | 0,09678 | 0,08785 | 0,08461 | 0,0891 | 0,07671 |
| 536,86497 | 0,09382 | 0,08544 | 0,08218 | 0,08764 | 0,07528 |
| 536,90215 | 0,09133 | 0,08358 | 0,08029 | 0,08668 | 0,07447 |
| 536,93933 | 0,08926 | 0,08222 | 0,07889 | 0,08609 | 0,07412 |
| 536,97652 | 0,08754 | 0,08129 | 0,07793 | 0,08577 | 0,07413 |
| 537,0137 | 0,08613 | 0,08076 | 0,07739 | 0,08565 | 0,07439 |
| 537,05088 | 0,08501 | 0,08059 | 0,07724 | 0,08569 | 0,07484 |
| 537,08806 | 0,08417 | 0,08075 | 0,07746 | 0,08585 | 0,07546 |
| 537,12524 | 0,08363 | 0,08121 | 0,07803 | 0,0861 | 0,07621 |
| 537,16243 | 0,08339 | 0,08199 | 0,07896 | 0,08642 | 0,07707 |
| 537,19961 | 0,08345 | 0,08306 | 0,08022 | 0,08677 | 0,07803 |
| 537,23679 | 0,08385 | 0,08441 | 0,08177 | 0,08714 | 0,07908 |
| 537,27397 | 0,0846 | 0,08604 | 0,08361 | 0,0875 | 0,0802 |
| 537,31115 | 0,08572 | 0,08796 | 0,08571 | 0,08783 | 0,08138 |
| 537,34834 | 0,08726 | 0,09018 | 0,08805 | 0,08813 | 0,08259 |
| 537,38552 | 0,08922 | 0,09271 | 0,09064 | 0,08839 | 0,08381 |
| 537,4227 | 0,09163 | 0,09558 | 0,09346 | 0,08864 | 0,085 |
| 537,45988 | 0,09448 | 0,09878 | 0,09651 | 0,08889 | 0,08617 |
| 537,49706 | 0,09778 | 0,1023 | 0,09976 | 0,08916 | 0,08729 |
| 537,53425 | 0,10148 | 0,10613 | 0,10321 | 0,08949 | 0,08839 |
| 537,57143 | 0,10554 | 0,11021 | 0,10683 | 0,08991 | 0,08947 |
| 537,60861 | 0,10985 | 0,11448 | 0,11055 | 0,09046 | 0,09058 |
| 537,64579 | 0,11424 | 0,11879 | 0,11431 | 0,0912 | 0,09175 |
| 537,68297 | 0,11856 | 0,123 | 0,11799 | 0,09217 | 0,09306 |
| 537,72016 | 0,12262 | 0,12693 | 0,12147 | 0,09347 | 0,09455 |
| 537,75734 | 0,12623 | 0,1304 | 0,12462 | 0,09516 | 0,09633 |
| 537,79452 | 0,12921 | 0,13324 | 0,1273 | 0,09732 | 0,09846 |
| 537,8317 | 0,13141 | 0,13529 | 0,12937 | 0,1 | 0,101 |
| 537,86888 | 0,13271 | 0,13644 | 0,13074 | 0,10326 | 0,10398 |
| 537,90607 | 0,13306 | 0,13662 | 0,13134 | 0,1071 | 0,10744 |
| 537,94325 | 0,13247 | 0,13585 | 0,13115 | 0,11149 | 0,11133 |
| 537,98043 | 0,13105 | 0,1342 | 0,13023 | 0,11637 | 0,11561 |
| 538,01761 | 0,12895 | 0,13186 | 0,12869 | 0,12159 | 0,12017 |
| 538,05479 | 0,12653 | 0,12907 | 0,12674 | 0,12701 | 0,12488 |
| 538,09198 | 0,12418 | 0,12625 | 0,12468 | 0,13247 | 0,12964 |
| 538,12916 | 0,12237 | 0,12386 | 0,12296 | 0,13788 | 0,1344 |
| 538,16634 | 0,12163 | 0,12241 | 0,12205 | 0,14325 | 0,1392 |
| 538,20352 | 0,12253 | 0,12246 | 0,1225 | 0,14883 | 0,14432 |
| 538,2407 | 0,12569 | 0,12463 | 0,12491 | 0,15518 | 0,15036 |
| 538,27789 | 0,13172 | 0,12953 | 0,12993 | 0,16307 | 0,15813 |
| 538,31507 | 0,14123 | 0,13778 | 0,13819 | 0,17359 | 0,16873 |
| 538,35225 | 0,15472 | 0,14994 | 0,15027 | 0,18792 | 0,18338 |
| 538,38943 | 0,17259 | 0,16645 | 0,16668 | 0,20732 | 0,20335 |
| 538,42661 | 0,19504 | 0,1876 | 0,18775 | 0,23283 | 0,22971 |
| 538,4638 | 0,22224 | 0,21346 | 0,21359 | 0,26514 | 0,26316 |
| 538,50098 | 0,25366 | 0,24388 | 0,244 | 0,30433 | 0,30377 |
| 538,53816 | 0,28826 | 0,27832 | 0,27864 | 0,34968 | 0,35081 |
| 538,57534 | 0,32486 | 0,31538 | 0,3163 | 0,39961 | 0,40265 |
| 538,61252 | 0,36199 | 0,35366 | 0,35546 | 0,45164 | 0,45675 |
| 538,64971 | 0,39795 | 0,39147 | 0,39442 | 0,50234 | 0,50981 |
| 538,68689 | 0,43092 | 0,42698 | 0,43135 | 0,54737 | 0,55735 |
| 538,72407 | 0,45911 | 0,45832 | 0,46432 | 0,58313 | 0,59523 |
| 538,76125 | 0,48092 | 0,48374 | 0,49154 | 0,60649 | 0,6203 |
| 538,79843 | 0,49503 | 0,50176 | 0,51144 | 0,61527 | 0,63025 |
| 538,83562 | 0,50054 | 0,51127 | 0,52283 | 0,60847 | 0,62402 |
| 538,8728 | 0,49705 | 0,51166 | 0,52499 | 0,58641 | 0,60192 |
| 538,90998 | 0,48432 | 0,50287 | 0,51776 | 0,55067 | 0,56557 |
| 538,94716 | 0,46316 | 0,48528 | 0,5015 | 0,50384 | 0,5177 |
| 538,98434 | 0,43526 | 0,45939 | 0,47689 | 0,44925 | 0,46173 |
| 539,02153 | 0,40213 | 0,42742 | 0,44524 | 0,39053 | 0,40147 |
| 539,05871 | 0,36543 | 0,39105 | 0,40876 | 0,33123 | 0,34059 |
| 539,09589 | 0,32688 | 0,352 | 0,36923 | 0,2745 | 0,28236 |
| 539,13307 | 0,2881 | 0,312 | 0,32842 | 0,22339 | 0,22942 |
| 539,17025 | 0,25056 | 0,27261 | 0,28799 | 0,17926 | 0,18415 |
| 539,20744 | 0,21551 | 0,23524 | 0,2494 | 0,14278 | 0,14684 |
| 539,24462 | 0,18395 | 0,20101 | 0,21388 | 0,11408 | 0,11761 |
| 539,2818 | 0,15662 | 0,17082 | 0,18239 | 0,09292 | 0,09616 |
| 539,31898 | 0,13403 | 0,14528 | 0,15561 | 0,07881 | 0,08198 |
| 539,35616 | 0,11663 | 0,12478 | 0,134 | 0,07119 | 0,07448 |
| 539,39335 | 0,1046 | 0,1095 | 0,11775 | 0,06951 | 0,07309 |
| 539,43053 | 0,09748 | 0,09985 | 0,10692 | 0,07332 | 0,07734 |
| 539,46771 | 0,09501 | 0,09521 | 0,10175 | 0,08218 | 0,08683 |
| 539,50489 | 0,09679 | 0,0952 | 0,10141 | 0,09572 | 0,10115 |
| 539,54207 | 0,10234 | 0,09934 | 0,10542 | 0,11347 | 0,11985 |
| 539,57926 | 0,11106 | 0,10707 | 0,11323 | 0,13489 | 0,14228 |
| 539,61644 | 0,12227 | 0,11773 | 0,12415 | 0,15904 | 0,16762 |
| 539,65362 | 0,1352 | 0,13058 | 0,13742 | 0,18445 | 0,19443 |
| 539,6908 | 0,14905 | 0,14482 | 0,1522 | 0,20962 | 0,22098 |
| 539,72798 | 0,16298 | 0,15958 | 0,1676 | 0,23289 | 0,2455 |
| 539,76517 | 0,17615 | 0,17402 | 0,18273 | 0,2526 | 0,2662 |
| 539,80235 | 0,1877 | 0,18728 | 0,19671 | 0,26722 | 0,28147 |
| 539,83953 | 0,19679 | 0,1986 | 0,20873 | 0,27555 | 0,29003 |
| 539,87671 | 0,20301 | 0,2071 | 0,21808 | 0,27685 | 0,2911 |
| 539,91389 | 0,20603 | 0,21233 | 0,22393 | 0,27093 | 0,2845 |
| 539,95108 | 0,20571 | 0,21409 | 0,22608 | 0,25818 | 0,27068 |
| 539,98826 | 0,20206 | 0,2123 | 0,2245 | 0,23952 | 0,25065 |
| 540,02544 | 0,19528 | 0,20705 | 0,21926 | 0,21632 | 0,22587 |
| 540,06262 | 0,1857 | 0,19861 | 0,21061 | 0,19011 | 0,19809 |
| 540,0998 | 0,17376 | 0,18738 | 0,19895 | 0,16292 | 0,16917 |
| 540,13699 | 0,15999 | 0,17387 | 0,18482 | 0,13631 | 0,14099 |
| 540,17417 | 0,14494 | 0,15866 | 0,1688 | 0,11148 | 0,11484 |
| 540,21135 | 0,12918 | 0,14237 | 0,15155 | 0,08927 | 0,09161 |
| 540,24853 | 0,11325 | 0,1256 | 0,13371 | 0,07018 | 0,07176 |
| 540,28571 | 0,09773 | 0,10893 | 0,1159 | 0,05436 | 0,05544 |
| 540,3229 | 0,08302 | 0,09291 | 0,09868 | 0,04169 | 0,04249 |
| 540,36008 | 0,06943 | 0,07801 | 0,08258 | 0,03185 | 0,03254 |
| 540,39726 | 0,05717 | 0,06449 | 0,068 | 0,02443 | 0,02513 |
| 540,43444 | 0,04638 | 0,05251 | 0,05509 | 0,01896 | 0,01975 |
| 540,47162 | 0,03709 | 0,04214 | 0,04394 | 0,01499 | 0,01591 |
| 540,50881 | 0,02926 | 0,03337 | 0,03454 | 0,01214 | 0,01319 |
| 540,54599 | 0,02282 | 0,02612 | 0,0268 | 0,01009 | 0,01124 |
| 540,58317 | 0,01763 | 0,02024 | 0,02058 | 0,00855 | 0,0098 |
| 540,62035 | 0,01353 | 0,01557 | 0,01569 | 0,00733 | 0,00864 |
| 540,65753 | 0,01035 | 0,01193 | 0,01191 | 0,00634 | 0,00766 |
| 540,69472 | 0,00794 | 0,00913 | 0,00905 | 0,00551 | 0,0068 |
| 540,7319 | 0,00616 | 0,007 | 0,00691 | 0,00479 | 0,00601 |
| 540,76908 | 0,00482 | 0,00541 | 0,00533 | 0,00415 | 0,00527 |
| 540,80626 | 0,00383 | 0,00425 | 0,00418 | 0,00359 | 0,0046 |
| 540,84344 | 0,0031 | 0,00338 | 0,00335 | 0,0031 | 0,00399 |
| 540,88063 | 0,00256 | 0,00273 | 0,00274 | 0,00269 | 0,00345 |
| 540,91781 | 0,00217 | 0,00227 | 0,00229 | 0,00234 | 0,003 |
| 540,95499 | 0,0019 | 0,00194 | 0,00197 | 0,00208 | 0,00265 |
| 540,99217 | 0,00171 | 0,00172 | 0,00175 | 0,00189 | 0,0024 |
| 541,02935 | 0,0016 | 0,00159 | 0,00162 | 0,00178 | 0,00225 |
| 541,06654 | 0,00155 | 0,00153 | 0,00155 | 0,00175 | 0,00221 |
| 541,10372 | 0,00154 | 0,00153 | 0,00154 | 0,00179 | 0,00226 |
| 541,1409 | 0,00156 | 0,00157 | 0,00157 | 0,00188 | 0,00238 |
| 541,17808 | 0,00162 | 0,00164 | 0,00164 | 0,00202 | 0,00256 |
| 541,21526 | 0,00169 | 0,00174 | 0,00172 | 0,00219 | 0,00277 |
| 541,25245 | 0,00176 | 0,00186 | 0,00182 | 0,00237 | 0,00299 |
| 541,28963 | 0,00184 | 0,00197 | 0,00192 | 0,00253 | 0,0032 |
| 541,32681 | 0,00192 | 0,00207 | 0,00201 | 0,00268 | 0,00336 |
| 541,36399 | 0,00198 | 0,00216 | 0,00208 | 0,00277 | 0,00347 |
| 541,40117 | 0,00202 | 0,00223 | 0,00212 | 0,00281 | 0,00351 |
| 541,43836 | 0,00205 | 0,00227 | 0,00214 | 0,00279 | 0,00347 |
| 541,47554 | 0,00205 | 0,00228 | 0,00213 | 0,00269 | 0,00334 |
| 541,51272 | 0,00202 | 0,00225 | 0,00209 | 0,00253 | 0,00313 |
| 541,5499 | 0,00197 | 0,0022 | 0,00202 | 0,00232 | 0,00286 |
| 541,58708 | 0,00189 | 0,0021 | 0,00192 | 0,00208 | 0,00255 |
| 541,62427 | 0,00178 | 0,00198 | 0,0018 | 0,00181 | 0,00222 |
| 541,66145 | 0,00165 | 0,00183 | 0,00166 | 0,00153 | 0,00187 |
| 541,69863 | 0,00151 | 0,00166 | 0,00151 | 0,00127 | 0,00154 |
| 541,73581 | 0,00135 | 0,00147 | 0,00134 | 0,00102 | 0,00124 |
| 541,77299 | 0,00119 | 0,00129 | 0,00118 | 8e-04 | 0,00097 |
| 541,81018 | 0,00103 | 0,0011 | 0,00101 | 6e-04 | 0,00073 |
| 541,84736 | 0,00087 | 0,00093 | 0,00085 | 0,00045 | 0,00054 |
| 541,88454 | 0,00073 | 0,00076 | 7e-04 | 0,00032 | 0,00039 |
| 541,92172 | 0,00059 | 0,00062 | 0,00057 | 0,00022 | 0,00027 |
| 541,9589 | 0,00048 | 0,00049 | 0,00045 | 0,00015 | 0,00019 |
| 541,99609 | 0,00037 | 0,00038 | 0,00034 | 1e-04 | 0,00013 |
| 542,03327 | 0,00029 | 3e-04 | 0,00026 | 7e-05 | 8e-05 |
| 542,07045 | 0,00022 | 0,00023 | 0,00019 | 4e-05 | 6e-05 |
| 542,10763 | 0,00016 | 0,00017 | 0,00014 | 2e-05 | 4e-05 |
| 542,14481 | 0,00012 | 0,00013 | 1e-04 | 1e-05 | 3e-05 |
| 542,182 | 9e-05 | 1e-04 | 7e-05 | 1e-05 | 3e-05 |
| 542,21918 | 6e-05 | 7e-05 | 4e-05 | 0 | 3e-05 |
| 542,25636 | 4e-05 | 6e-05 | 3e-05 | 0 | 3e-05 |
| 542,29354 | 3e-05 | 4e-05 | 2e-05 | 0 | 3e-05 |
| 542,33072 | 2e-05 | 3e-05 | 1e-05 | 0 | 4e-05 |
| 542,36791 | 1e-05 | 2e-05 | 1e-05 | 0 | 4e-05 |
| 542,40509 | 1e-05 | 2e-05 | 0 | 0 | 4e-05 |
| 542,44227 | 1e-05 | 1e-05 | 0 | 0 | 5e-05 |
| 542,47945 | 0 | 1e-05 | 0 | 0 | 5e-05 |
| 542,51663 | 0 | 1e-05 | 0 | 0 | 5e-05 |
| 542,55382 | 0 | 0 | 0 | 0 | 4e-05 |
| 542,591 | 0 | 0 | 0 | 0 | 4e-05 |
| 542,62818 | 0 | 0 | 0 | 0 | 4e-05 |
| 542,66536 | 0 | 0 | 0 | 0 | 3e-05 |
| 542,70254 | 0 | 0 | 0 | 0 | 3e-05 |
| 542,73973 | 0 | 0 | 0 | 0 | 2e-05 |
| 542,77691 | 0 | 0 | 0 | 0 | 2e-05 |
| 542,81409 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,85127 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,88845 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 0 | 0 | 0 |
| 524,74364 | 0 | 0 | 0 | 0 | 0 |
| 524,78082 | 0 | 0 | 0 | 0 | 0 |
| 524,818 | 0 | 0 | 0 | 0 | 0 |
| 524,85519 | 0 | 0 | 0 | 0 | 0 |
| 524,89237 | 0 | 0 | 0 | 0 | 0 |
| 524,92955 | 0 | 0 | 0 | 0 | 0 |
| 524,96673 | 0 | 0 | 0 | 0 | 0 |
| 525,00391 | 0 | 0 | 0 | 0 | 0 |
| 525,0411 | 0 | 0 | 0 | 0 | 0 |
| 525,07828 | 0 | 0 | 0 | 0 | 0 |
| 525,11546 | 0 | 0 | 0 | 0 | 0 |
| 525,15264 | 0 | 0 | 0 | 0 | 0 |
| 525,18982 | 0 | 0 | 0 | 0 | 0 |
| 525,22701 | 0 | 0 | 0 | 0 | 0 |
| 525,26419 | 0 | 0 | 0 | 0 | 0 |
| 525,30137 | 0 | 0 | 0 | 0 | 0 |
| 525,33855 | 0 | 0 | 0 | 0 | 0 |
| 525,37573 | 0 | 0 | 0 | 0 | 0 |
| 525,41292 | 0 | 0 | 0 | 0 | 0 |
| 525,4501 | 0 | 0 | 0 | 0 | 0 |
| 525,48728 | 0 | 0 | 0 | 0 | 0 |
| 525,52446 | 0 | 0 | 0 | 0 | 0 |
| 525,56164 | 0 | 0 | 0 | 0 | 0 |
| 525,59883 | 0 | 0 | 0 | 0 | 0 |
| 525,63601 | 0 | 0 | 0 | 0 | 0 |
| 525,67319 | 0 | 0 | 0 | 0 | 0 |
| 525,71037 | 0 | 0 | 0 | 0 | 0 |
| 525,74755 | 0 | 0 | 0 | 0 | 0 |
| 525,78474 | 0 | 0 | 0 | 0 | 0 |
| 525,82192 | 0 | 0 | 0 | 0 | 0 |
| 525,8591 | 0 | 0 | 0 | 0 | 0 |
| 525,89628 | 0 | 0 | 0 | 0 | 0 |
| 525,93346 | 0 | 0 | 0 | 0 | 0 |
| 525,97065 | 0 | 0 | 0 | 0 | 0 |
| 526,00783 | 0 | 0 | 0 | 0 | 0 |
| 526,04501 | 0 | 0 | 0 | 1e-05 | 0 |
| 526,08219 | 0 | 0 | 0 | 1e-05 | 0 |
| 526,11937 | 0 | 0 | 0 | 2e-05 | 0 |
| 526,15656 | 0 | 0 | 0 | 3e-05 | 0 |
| 526,19374 | 0 | 0 | 0 | 4e-05 | 0 |
| 526,23092 | 0 | 0 | 0 | 6e-05 | 0 |
| 526,2681 | 0 | 0 | 0 | 7e-05 | 0 |
| 526,30528 | 0 | 0 | 0 | 9e-05 | 0 |
| 526,34247 | 0 | 0 | 0 | 1e-04 | 0 |
| 526,37965 | 0 | 0 | 0 | 0,00011 | 0 |
| 526,41683 | 0 | 0 | 0 | 1e-04 | 0 |
| 526,45401 | 0 | 0 | 0 | 1e-04 | 0 |
| 526,49119 | 0 | 0 | 0 | 8e-05 | 1e-05 |
| 526,52838 | 0 | 0 | 0 | 7e-05 | 1e-05 |
| 526,56556 | 0 | 0 | 0 | 5e-05 | 2e-05 |
| 526,60274 | 0 | 0 | 0 | 4e-05 | 3e-05 |
| 526,63992 | 0 | 0 | 0 | 2e-05 | 5e-05 |
| 526,6771 | 0 | 0 | 0 | 2e-05 | 6e-05 |
| 526,71429 | 0 | 0 | 0 | 1e-05 | 8e-05 |
| 526,75147 | 0 | 0 | 0 | 1e-05 | 9e-05 |
| 526,78865 | 0 | 0 | 0 | 0 | 1e-04 |
| 526,82583 | 0 | 0 | 0 | 0 | 0,00011 |
| 526,86301 | 0 | 0 | 0 | 0 | 1e-04 |
| 526,9002 | 0 | 0 | 0 | 0 | 9e-05 |
| 526,93738 | 0 | 0 | 0 | 0 | 8e-05 |
| 526,97456 | 0 | 0 | 0 | 0 | 6e-05 |
| 527,01174 | 0 | 0 | 0 | 0 | 5e-05 |
| 527,04892 | 0 | 0 | 0 | 0 | 3e-05 |
| 527,08611 | 0 | 0 | 0 | 0 | 2e-05 |
| 527,12329 | 0 | 0 | 0 | 0 | 1e-05 |
| 527,16047 | 0 | 0 | 0 | 0 | 1e-05 |
| 527,19765 | 0 | 0 | 0 | 0 | 0 |
| 527,23483 | 0 | 0 | 1e-05 | 0 | 0 |
| 527,27202 | 0 | 0 | 1e-05 | 0 | 0 |
| 527,3092 | 0 | 0 | 2e-05 | 0 | 0 |
| 527,34638 | 0 | 0 | 2e-05 | 0 | 0 |
| 527,38356 | 0 | 0 | 3e-05 | 0 | 0 |
| 527,42074 | 0 | 0 | 4e-05 | 0 | 0 |
| 527,45793 | 0 | 0 | 5e-05 | 0 | 0 |
| 527,49511 | 0 | 0 | 7e-05 | 0 | 0 |
| 527,53229 | 0 | 0 | 8e-05 | 0 | 0 |
| 527,56947 | 0 | 1e-05 | 8e-05 | 0 | 0 |
| 527,60665 | 0 | 1e-05 | 9e-05 | 0 | 0 |
| 527,64384 | 0 | 2e-05 | 9e-05 | 0 | 0 |
| 527,68102 | 0 | 3e-05 | 8e-05 | 0 | 0 |
| 527,7182 | 0 | 4e-05 | 8e-05 | 0 | 0 |
| 527,75538 | 0 | 6e-05 | 7e-05 | 0 | 0 |
| 527,79256 | 1e-05 | 8e-05 | 6e-05 | 0 | 0 |
| 527,82975 | 1e-05 | 1e-04 | 5e-05 | 0 | 0 |
| 527,86693 | 1e-05 | 0,00012 | 4e-05 | 0 | 0 |
| 527,90411 | 2e-05 | 0,00014 | 4e-05 | 0 | 0 |
| 527,94129 | 2e-05 | 0,00016 | 4e-05 | 0 | 0 |
| 527,97847 | 3e-05 | 0,00017 | 4e-05 | 0 | 0 |
| 528,01566 | 4e-05 | 0,00018 | 5e-05 | 0 | 0 |
| 528,05284 | 5e-05 | 0,00018 | 6e-05 | 0 | 0 |
| 528,09002 | 6e-05 | 0,00018 | 7e-05 | 0 | 0 |
| 528,1272 | 7e-05 | 0,00017 | 7e-05 | 0 | 0 |
| 528,16438 | 8e-05 | 0,00016 | 8e-05 | 0 | 0 |
| 528,20157 | 8e-05 | 0,00015 | 9e-05 | 0 | 0 |
| 528,23875 | 8e-05 | 0,00014 | 9e-05 | 0 | 0 |
| 528,27593 | 8e-05 | 0,00013 | 9e-05 | 0 | 0 |
| 528,31311 | 8e-05 | 0,00012 | 8e-05 | 0 | 0 |
| 528,35029 | 7e-05 | 0,00011 | 7e-05 | 0 | 0 |
| 528,38748 | 6e-05 | 0,00011 | 6e-05 | 0 | 0 |
| 528,42466 | 6e-05 | 1e-04 | 5e-05 | 0 | 0 |
| 528,46184 | 5e-05 | 1e-04 | 4e-05 | 0 | 0 |
| 528,49902 | 4e-05 | 9e-05 | 3e-05 | 1e-05 | 0 |
| 528,5362 | 4e-05 | 8e-05 | 2e-05 | 1e-05 | 0 |
| 528,57339 | 4e-05 | 7e-05 | 1e-05 | 2e-05 | 0 |
| 528,61057 | 4e-05 | 6e-05 | 1e-05 | 4e-05 | 0 |
| 528,64775 | 4e-05 | 5e-05 | 1e-05 | 5e-05 | 0 |
| 528,68493 | 5e-05 | 3e-05 | 0 | 7e-05 | 0 |
| 528,72211 | 5e-05 | 3e-05 | 0 | 1e-04 | 0 |
| 528,7593 | 6e-05 | 2e-05 | 0 | 0,00012 | 0 |
| 528,79648 | 7e-05 | 1e-05 | 0 | 0,00014 | 0 |
| 528,83366 | 8e-05 | 1e-05 | 1e-05 | 0,00016 | 0 |
| 528,87084 | 8e-05 | 1e-05 | 1e-05 | 0,00017 | 0 |
| 528,90802 | 8e-05 | 0 | 2e-05 | 0,00018 | 1e-05 |
| 528,94521 | 8e-05 | 0 | 3e-05 | 0,00018 | 1e-05 |
| 528,98239 | 8e-05 | 1e-05 | 4e-05 | 0,00017 | 2e-05 |
| 529,01957 | 8e-05 | 1e-05 | 6e-05 | 0,00015 | 3e-05 |
| 529,05675 | 8e-05 | 1e-05 | 8e-05 | 0,00013 | 4e-05 |
| 529,09393 | 7e-05 | 2e-05 | 0,00011 | 0,00011 | 6e-05 |
| 529,13112 | 8e-05 | 3e-05 | 0,00014 | 9e-05 | 7e-05 |
| 529,1683 | 8e-05 | 4e-05 | 0,00017 | 7e-05 | 9e-05 |
| 529,20548 | 1e-04 | 5e-05 | 2e-04 | 5e-05 | 1e-04 |
| 529,24266 | 0,00012 | 6e-05 | 0,00023 | 4e-05 | 0,00011 |
| 529,27984 | 0,00016 | 7e-05 | 0,00025 | 4e-05 | 1e-04 |
| 529,31703 | 2e-04 | 8e-05 | 0,00026 | 4e-05 | 1e-04 |
| 529,35421 | 0,00025 | 9e-05 | 0,00026 | 5e-05 | 8e-05 |
| 529,39139 | 0,00032 | 1e-04 | 0,00026 | 7e-05 | 7e-05 |
| 529,42857 | 0,00039 | 1e-04 | 0,00026 | 9e-05 | 5e-05 |
| 529,46575 | 0,00046 | 0,00011 | 0,00025 | 0,00012 | 4e-05 |
| 529,50294 | 0,00053 | 0,00011 | 0,00025 | 0,00014 | 3e-05 |
| 529,54012 | 0,00059 | 0,00011 | 0,00025 | 0,00017 | 2e-05 |
| 529,5773 | 0,00065 | 0,00012 | 0,00028 | 0,00018 | 3e-05 |
| 529,61448 | 0,00068 | 0,00013 | 0,00031 | 2e-04 | 3e-05 |
| 529,65166 | 7e-04 | 0,00014 | 0,00036 | 2e-04 | 5e-05 |
| 529,68885 | 0,00071 | 0,00016 | 0,00043 | 0,00019 | 7e-05 |
| 529,72603 | 0,00069 | 0,00018 | 0,00051 | 0,00019 | 9e-05 |
| 529,76321 | 0,00066 | 2e-04 | 6e-04 | 0,00018 | 0,00012 |
| 529,80039 | 0,00062 | 0,00022 | 0,00069 | 0,00018 | 0,00015 |
| 529,83757 | 0,00056 | 0,00025 | 0,00076 | 0,00018 | 0,00018 |
| 529,87476 | 0,00051 | 0,00027 | 0,00083 | 0,00019 | 0,00021 |
| 529,91194 | 0,00045 | 3e-04 | 0,00087 | 2e-04 | 0,00023 |
| 529,94912 | 4e-04 | 0,00032 | 0,00089 | 0,00021 | 0,00025 |
| 529,9863 | 0,00036 | 0,00033 | 0,00089 | 0,00023 | 0,00026 |
| 530,02348 | 0,00034 | 0,00035 | 0,00088 | 0,00025 | 0,00027 |
| 530,06067 | 0,00032 | 0,00037 | 0,00084 | 0,00026 | 0,00027 |
| 530,09785 | 0,00033 | 0,00038 | 8e-04 | 0,00027 | 0,00026 |
| 530,13503 | 0,00034 | 4e-04 | 0,00075 | 0,00027 | 0,00026 |
| 530,17221 | 0,00037 | 0,00043 | 7e-04 | 0,00027 | 0,00026 |
| 530,20939 | 4e-04 | 0,00046 | 0,00066 | 0,00026 | 0,00027 |
| 530,24658 | 0,00045 | 0,00049 | 0,00063 | 0,00026 | 3e-04 |
| 530,28376 | 0,00049 | 0,00054 | 6e-04 | 0,00025 | 0,00034 |
| 530,32094 | 0,00054 | 6e-04 | 0,00059 | 0,00025 | 0,00039 |
| 530,35812 | 0,00058 | 0,00066 | 0,00059 | 0,00026 | 0,00044 |
| 530,3953 | 0,00062 | 0,00073 | 0,00059 | 0,00027 | 0,00048 |
| 530,43249 | 0,00065 | 0,00081 | 0,00061 | 0,00029 | 0,00052 |
| 530,46967 | 0,00068 | 0,00088 | 0,00062 | 0,00032 | 0,00054 |
| 530,50685 | 7e-04 | 0,00094 | 0,00065 | 0,00035 | 0,00054 |
| 530,54403 | 0,00071 | 0,001 | 0,00067 | 0,00039 | 0,00053 |
| 530,58121 | 0,00071 | 0,00104 | 7e-04 | 0,00043 | 0,00052 |
| 530,6184 | 0,00072 | 0,00107 | 0,00073 | 0,00047 | 5e-04 |
| 530,65558 | 0,00072 | 0,00109 | 0,00077 | 0,00052 | 0,00049 |
| 530,69276 | 0,00072 | 0,0011 | 0,00081 | 0,00057 | 5e-04 |
| 530,72994 | 0,00073 | 0,0011 | 0,00085 | 0,00064 | 0,00052 |
| 530,76712 | 0,00074 | 0,0011 | 0,00089 | 0,00071 | 0,00056 |
| 530,80431 | 0,00076 | 0,0011 | 0,00093 | 0,00079 | 0,00061 |
| 530,84149 | 8e-04 | 0,00111 | 0,00096 | 0,00088 | 0,00066 |
| 530,87867 | 0,00084 | 0,00112 | 0,00097 | 0,00098 | 0,00073 |
| 530,91585 | 9e-04 | 0,00114 | 0,00098 | 0,00109 | 0,00079 |
| 530,95303 | 0,00097 | 0,00117 | 0,00097 | 0,00121 | 0,00086 |
| 530,99022 | 0,00105 | 0,0012 | 0,00095 | 0,00132 | 0,00092 |
| 531,0274 | 0,00114 | 0,00123 | 0,00093 | 0,00142 | 0,00097 |
| 531,06458 | 0,00124 | 0,00125 | 0,00092 | 0,00151 | 0,00102 |
| 531,10176 | 0,00135 | 0,00128 | 0,00092 | 0,00158 | 0,00106 |
| 531,13894 | 0,00146 | 0,00131 | 0,00094 | 0,00163 | 0,00108 |
| 531,17613 | 0,00157 | 0,00134 | 0,00098 | 0,00167 | 0,00109 |
| 531,21331 | 0,00167 | 0,00137 | 0,00105 | 0,0017 | 0,00109 |
| 531,25049 | 0,00177 | 0,00141 | 0,00113 | 0,00173 | 0,00109 |
| 531,28767 | 0,00187 | 0,00147 | 0,00124 | 0,00177 | 0,00109 |
| 531,32485 | 0,00196 | 0,00154 | 0,00136 | 0,00183 | 0,00111 |
| 531,36204 | 0,00204 | 0,00163 | 0,00148 | 0,00192 | 0,00114 |
| 531,39922 | 0,00212 | 0,00174 | 0,00161 | 0,00204 | 0,0012 |
| 531,4364 | 0,00219 | 0,00185 | 0,00174 | 0,00217 | 0,00127 |
| 531,47358 | 0,00227 | 0,00197 | 0,00186 | 0,00231 | 0,00136 |
| 531,51076 | 0,00234 | 0,00208 | 0,00199 | 0,00245 | 0,00146 |
| 531,54795 | 0,00242 | 0,00219 | 0,0021 | 0,00258 | 0,00158 |
| 531,58513 | 0,00249 | 0,00229 | 0,00222 | 0,00269 | 0,0017 |
| 531,62231 | 0,00258 | 0,00238 | 0,00233 | 0,00278 | 0,00184 |
| 531,65949 | 0,00266 | 0,00245 | 0,00243 | 0,00286 | 0,00199 |
| 531,69667 | 0,00274 | 0,00251 | 0,00252 | 0,00293 | 0,00215 |
| 531,73386 | 0,00282 | 0,00255 | 0,00259 | 0,003 | 0,00231 |
| 531,77104 | 0,0029 | 0,00257 | 0,00264 | 0,00308 | 0,00245 |
| 531,80822 | 0,00297 | 0,00258 | 0,00267 | 0,00317 | 0,00257 |
| 531,8454 | 0,00303 | 0,00258 | 0,00269 | 0,00328 | 0,00267 |
| 531,88258 | 0,00309 | 0,00255 | 0,00269 | 0,00342 | 0,00274 |
| 531,91977 | 0,00314 | 0,0025 | 0,0027 | 0,0036 | 0,0028 |
| 531,95695 | 0,00319 | 0,00245 | 0,00272 | 0,0038 | 0,00287 |
| 531,99413 | 0,00324 | 0,00238 | 0,00278 | 0,00402 | 0,00295 |
| 532,03131 | 0,00328 | 0,00231 | 0,00286 | 0,00424 | 0,00307 |
| 532,06849 | 0,00334 | 0,00225 | 0,00299 | 0,00443 | 0,00321 |
| 532,10568 | 0,00341 | 0,00221 | 0,00317 | 0,00456 | 0,00336 |
| 532,14286 | 0,00349 | 0,0022 | 0,00337 | 0,00462 | 0,00352 |
| 532,18004 | 0,00359 | 0,00222 | 0,0036 | 0,00458 | 0,00367 |
| 532,21722 | 0,0037 | 0,00226 | 0,00384 | 0,00445 | 0,00379 |
| 532,2544 | 0,00381 | 0,00235 | 0,00407 | 0,00424 | 0,0039 |
| 532,29159 | 0,00392 | 0,00246 | 0,00427 | 0,004 | 0,00399 |
| 532,32877 | 0,00404 | 0,00259 | 0,00444 | 0,00375 | 0,00405 |
| 532,36595 | 0,00414 | 0,00274 | 0,00457 | 0,00352 | 0,0041 |
| 532,40313 | 0,00423 | 0,0029 | 0,00464 | 0,00334 | 0,00413 |
| 532,44031 | 0,0043 | 0,00306 | 0,00467 | 0,00322 | 0,00414 |
| 532,4775 | 0,00437 | 0,00323 | 0,00467 | 0,00314 | 0,00415 |
| 532,51468 | 0,00443 | 0,00338 | 0,00463 | 0,00311 | 0,00414 |
| 532,55186 | 0,00449 | 0,00354 | 0,00458 | 0,0031 | 0,00413 |
| 532,58904 | 0,00455 | 0,0037 | 0,00453 | 0,00309 | 0,00412 |
| 532,62622 | 0,00463 | 0,00387 | 0,00448 | 0,00307 | 0,00411 |
| 532,66341 | 0,00472 | 0,00404 | 0,00445 | 0,00305 | 0,00409 |
| 532,70059 | 0,00482 | 0,00423 | 0,00444 | 0,003 | 0,00405 |
| 532,73777 | 0,00493 | 0,00443 | 0,00446 | 0,00295 | 0,004 |
| 532,77495 | 0,00504 | 0,00463 | 0,00451 | 0,0029 | 0,00392 |
| 532,81213 | 0,00515 | 0,00484 | 0,0046 | 0,00285 | 0,00384 |
| 532,84932 | 0,00525 | 0,00505 | 0,00471 | 0,00284 | 0,00375 |
| 532,8865 | 0,00535 | 0,00525 | 0,00484 | 0,00287 | 0,00369 |
| 532,92368 | 0,00544 | 0,00544 | 0,00499 | 0,00295 | 0,00367 |
| 532,96086 | 0,00552 | 0,00562 | 0,00514 | 0,00309 | 0,00371 |
| 532,99804 | 0,0056 | 0,00577 | 0,00529 | 0,00331 | 0,00382 |
| 533,03523 | 0,0057 | 0,0059 | 0,00543 | 0,00361 | 0,00401 |
| 533,07241 | 0,00582 | 0,00601 | 0,00555 | 0,004 | 0,00426 |
| 533,10959 | 0,00596 | 0,00611 | 0,00567 | 0,00444 | 0,00456 |
| 533,14677 | 0,00613 | 0,00619 | 0,00578 | 0,00494 | 0,00489 |
| 533,18395 | 0,00633 | 0,00628 | 0,00589 | 0,00547 | 0,00523 |
| 533,22114 | 0,00657 | 0,00638 | 0,00602 | 0,00598 | 0,00559 |
| 533,25832 | 0,00685 | 0,00651 | 0,00616 | 0,00645 | 0,00595 |
| 533,2955 | 0,00719 | 0,00666 | 0,00632 | 0,00685 | 0,00632 |
| 533,33268 | 0,00757 | 0,00686 | 0,00651 | 0,00717 | 0,0067 |
| 533,36986 | 0,008 | 0,00709 | 0,00673 | 0,00741 | 0,00709 |
| 533,40705 | 0,00848 | 0,00737 | 0,00697 | 0,00761 | 0,0075 |
| 533,44423 | 0,00898 | 0,00768 | 0,00725 | 0,0078 | 0,00791 |
| 533,48141 | 0,00951 | 0,00802 | 0,00754 | 0,008 | 0,00833 |
| 533,51859 | 0,01002 | 0,00836 | 0,00786 | 0,00828 | 0,00874 |
| 533,55577 | 0,0105 | 0,0087 | 0,00819 | 0,00864 | 0,00915 |
| 533,59295 | 0,01092 | 0,00901 | 0,00853 | 0,00908 | 0,00954 |
| 533,63014 | 0,01128 | 0,00929 | 0,00886 | 0,0096 | 0,00992 |
| 533,66732 | 0,01156 | 0,00953 | 0,00918 | 0,01016 | 0,01027 |
| 533,7045 | 0,01177 | 0,00973 | 0,00947 | 0,01071 | 0,01057 |
| 533,74168 | 0,01193 | 0,00989 | 0,00974 | 0,01124 | 0,01082 |
| 533,77886 | 0,01206 | 0,01003 | 0,01 | 0,01173 | 0,01102 |
| 533,81605 | 0,01217 | 0,01017 | 0,01024 | 0,0122 | 0,01122 |
| 533,85323 | 0,01231 | 0,01033 | 0,0105 | 0,0127 | 0,01146 |
| 533,89041 | 0,01249 | 0,01053 | 0,01079 | 0,0133 | 0,01181 |
| 533,92759 | 0,01274 | 0,01081 | 0,01112 | 0,01406 | 0,01234 |
| 533,96477 | 0,01308 | 0,01117 | 0,01153 | 0,01502 | 0,01309 |
| 534,00196 | 0,01352 | 0,01163 | 0,01202 | 0,01617 | 0,01405 |
| 534,03914 | 0,01407 | 0,01218 | 0,0126 | 0,01741 | 0,01516 |
| 534,07632 | 0,01473 | 0,01285 | 0,01327 | 0,01863 | 0,0163 |
| 534,1135 | 0,01548 | 0,01359 | 0,01403 | 0,01965 | 0,01732 |
| 534,15068 | 0,0163 | 0,0144 | 0,01486 | 0,0203 | 0,01805 |
| 534,18787 | 0,01716 | 0,01524 | 0,01573 | 0,02046 | 0,01835 |
| 534,22505 | 0,01803 | 0,01609 | 0,01662 | 0,02016 | 0,01821 |
| 534,26223 | 0,01888 | 0,01692 | 0,01749 | 0,01949 | 0,0177 |
| 534,29941 | 0,01968 | 0,01769 | 0,0183 | 0,01863 | 0,01697 |
| 534,33659 | 0,02039 | 0,0184 | 0,01903 | 0,01778 | 0,01622 |
| 534,37378 | 0,021 | 0,01901 | 0,01966 | 0,01711 | 0,01565 |
| 534,41096 | 0,0215 | 0,01954 | 0,02015 | 0,01677 | 0,0154 |
| 534,44814 | 0,02188 | 0,01997 | 0,02052 | 0,01683 | 0,01556 |
| 534,48532 | 0,02217 | 0,02031 | 0,02079 | 0,01726 | 0,01613 |
| 534,5225 | 0,02237 | 0,02057 | 0,02097 | 0,018 | 0,01703 |
| 534,55969 | 0,02252 | 0,02076 | 0,0211 | 0,01892 | 0,01811 |
| 534,59687 | 0,02265 | 0,02087 | 0,02121 | 0,0199 | 0,01923 |
| 534,63405 | 0,02278 | 0,02093 | 0,02134 | 0,02082 | 0,02023 |
| 534,67123 | 0,02293 | 0,02093 | 0,02151 | 0,02158 | 0,02099 |
| 534,70841 | 0,02311 | 0,02088 | 0,0217 | 0,02213 | 0,02144 |
| 534,7456 | 0,02333 | 0,0208 | 0,02191 | 0,02245 | 0,02158 |
| 534,78278 | 0,02358 | 0,02071 | 0,02213 | 0,02256 | 0,02144 |
| 534,81996 | 0,02384 | 0,02062 | 0,02235 | 0,0225 | 0,02108 |
| 534,85714 | 0,02411 | 0,02055 | 0,02254 | 0,02231 | 0,02059 |
| 534,89432 | 0,02437 | 0,02052 | 0,02268 | 0,02206 | 0,02005 |
| 534,93151 | 0,02459 | 0,02053 | 0,02278 | 0,02176 | 0,01951 |
| 534,96869 | 0,02478 | 0,0206 | 0,02282 | 0,02142 | 0,01901 |
| 535,00587 | 0,0249 | 0,02071 | 0,02279 | 0,02105 | 0,01857 |
| 535,04305 | 0,02495 | 0,02087 | 0,02269 | 0,02062 | 0,01818 |
| 535,08023 | 0,02496 | 0,02106 | 0,02252 | 0,02014 | 0,01786 |
| 535,11742 | 0,02492 | 0,02127 | 0,02227 | 0,01964 | 0,01762 |
| 535,1546 | 0,02488 | 0,02151 | 0,02197 | 0,01919 | 0,0175 |
| 535,19178 | 0,02486 | 0,02178 | 0,02164 | 0,01889 | 0,01756 |
| 535,22896 | 0,0249 | 0,02209 | 0,02131 | 0,0189 | 0,0179 |
| 535,26614 | 0,02506 | 0,02246 | 0,02103 | 0,01937 | 0,01864 |
| 535,30333 | 0,02537 | 0,02292 | 0,02085 | 0,02045 | 0,01992 |
| 535,34051 | 0,02588 | 0,02349 | 0,02081 | 0,02226 | 0,02184 |
| 535,37769 | 0,02663 | 0,02421 | 0,02099 | 0,02486 | 0,0245 |
| 535,41487 | 0,02763 | 0,02511 | 0,02141 | 0,02817 | 0,02789 |
| 535,45205 | 0,02889 | 0,02622 | 0,02213 | 0,03205 | 0,03188 |
| 535,48924 | 0,0304 | 0,02754 | 0,02317 | 0,03613 | 0,03617 |
| 535,52642 | 0,03212 | 0,02909 | 0,02454 | 0,03997 | 0,04028 |
| 535,5636 | 0,03399 | 0,03085 | 0,02621 | 0,04313 | 0,0437 |
| 535,60078 | 0,03591 | 0,03278 | 0,02814 | 0,04518 | 0,04597 |
| 535,63796 | 0,03776 | 0,0348 | 0,03024 | 0,04587 | 0,04676 |
| 535,67515 | 0,03946 | 0,03683 | 0,03242 | 0,0451 | 0,046 |
| 535,71233 | 0,04089 | 0,03872 | 0,03452 | 0,04301 | 0,04383 |
| 535,74951 | 0,04197 | 0,04036 | 0,0364 | 0,03989 | 0,0406 |
| 535,78669 | 0,04263 | 0,04164 | 0,03793 | 0,03616 | 0,03678 |
| 535,82387 | 0,04285 | 0,04248 | 0,03903 | 0,03225 | 0,03286 |
| 535,86106 | 0,04262 | 0,04281 | 0,03964 | 0,02855 | 0,02925 |
| 535,89824 | 0,04199 | 0,04264 | 0,03974 | 0,02536 | 0,02624 |
| 535,93542 | 0,04103 | 0,042 | 0,03935 | 0,02285 | 0,02396 |
| 535,9726 | 0,03983 | 0,04095 | 0,03855 | 0,02108 | 0,02243 |
| 536,00978 | 0,03848 | 0,0396 | 0,0374 | 0,02001 | 0,02156 |
| 536,04697 | 0,0371 | 0,03803 | 0,03601 | 0,01954 | 0,0212 |
| 536,08415 | 0,03576 | 0,03636 | 0,03448 | 0,01956 | 0,02122 |
| 536,12133 | 0,03453 | 0,03468 | 0,03288 | 0,01993 | 0,02147 |
| 536,15851 | 0,03343 | 0,03305 | 0,0313 | 0,0205 | 0,02187 |
| 536,19569 | 0,03247 | 0,03155 | 0,02978 | 0,02117 | 0,02233 |
| 536,23288 | 0,03166 | 0,0302 | 0,02837 | 0,02188 | 0,02284 |
| 536,27006 | 0,03098 | 0,02902 | 0,02709 | 0,0226 | 0,02337 |
| 536,30724 | 0,03041 | 0,02801 | 0,02597 | 0,02333 | 0,02394 |
| 536,34442 | 0,02995 | 0,02716 | 0,025 | 0,02412 | 0,02454 |
| 536,3816 | 0,02958 | 0,02647 | 0,0242 | 0,02497 | 0,02515 |
| 536,41879 | 0,0293 | 0,02592 | 0,02357 | 0,0259 | 0,02575 |
| 536,45597 | 0,02911 | 0,02549 | 0,02313 | 0,02687 | 0,02631 |
| 536,49315 | 0,02904 | 0,02518 | 0,0229 | 0,02783 | 0,0268 |
| 536,53033 | 0,02911 | 0,02499 | 0,02291 | 0,02869 | 0,02721 |
| 536,56751 | 0,02934 | 0,02493 | 0,02318 | 0,02939 | 0,02752 |
| 536,6047 | 0,02979 | 0,02503 | 0,02373 | 0,02992 | 0,02782 |
| 536,64188 | 0,0305 | 0,02532 | 0,02459 | 0,03038 | 0,02823 |
| 536,67906 | 0,03153 | 0,02587 | 0,02578 | 0,03098 | 0,02898 |
| 536,71624 | 0,03295 | 0,02675 | 0,02731 | 0,03205 | 0,0304 |
| 536,75342 | 0,03483 | 0,02808 | 0,02919 | 0,0341 | 0,03287 |
| 536,79061 | 0,03723 | 0,02992 | 0,03145 | 0,03765 | 0,03687 |
| 536,82779 | 0,04022 | 0,03234 | 0,03414 | 0,04307 | 0,04287 |
| 536,86497 | 0,04382 | 0,03543 | 0,03725 | 0,0506 | 0,05099 |
| 536,90215 | 0,04804 | 0,0392 | 0,04083 | 0,06015 | 0,0611 |
| 536,93933 | 0,05286 | 0,04365 | 0,04486 | 0,07123 | 0,07269 |
| 536,97652 | 0,05818 | 0,04876 | 0,04933 | 0,08298 | 0,08485 |
| 537,0137 | 0,06389 | 0,0544 | 0,05418 | 0,09423 | 0,09635 |
| 537,05088 | 0,0698 | 0,06042 | 0,05929 | 0,1037 | 0,10583 |
| 537,08806 | 0,07566 | 0,06661 | 0,06449 | 0,11023 | 0,11211 |
| 537,12524 | 0,08121 | 0,0727 | 0,06956 | 0,11302 | 0,11438 |
| 537,16243 | 0,08621 | 0,0784 | 0,07427 | 0,11182 | 0,11245 |
| 537,19961 | 0,09042 | 0,0834 | 0,07836 | 0,10694 | 0,10676 |
| 537,23679 | 0,09364 | 0,08744 | 0,0816 | 0,0992 | 0,09825 |
| 537,27397 | 0,09573 | 0,0902 | 0,08384 | 0,08971 | 0,08817 |
| 537,31115 | 0,09661 | 0,09163 | 0,08498 | 0,07967 | 0,07779 |
| 537,34834 | 0,0963 | 0,09173 | 0,08499 | 0,07011 | 0,06819 |
| 537,38552 | 0,09486 | 0,09059 | 0,0839 | 0,06181 | 0,06008 |
| 537,4227 | 0,09246 | 0,0884 | 0,08194 | 0,05524 | 0,05378 |
| 537,45988 | 0,08928 | 0,08537 | 0,07929 | 0,05037 | 0,04937 |
| 537,49706 | 0,08556 | 0,08178 | 0,07615 | 0,04702 | 0,04656 |
| 537,53425 | 0,08152 | 0,07788 | 0,07273 | 0,04493 | 0,04497 |
| 537,57143 | 0,07743 | 0,07393 | 0,06921 | 0,04379 | 0,04428 |
| 537,60861 | 0,07349 | 0,07013 | 0,06575 | 0,04334 | 0,04421 |
| 537,64579 | 0,06982 | 0,06666 | 0,06249 | 0,04338 | 0,04455 |
| 537,68297 | 0,06656 | 0,06363 | 0,05954 | 0,04378 | 0,04515 |
| 537,72016 | 0,06377 | 0,0611 | 0,05698 | 0,04448 | 0,04593 |
| 537,75734 | 0,06148 | 0,0591 | 0,05487 | 0,04544 | 0,04685 |
| 537,79452 | 0,05972 | 0,05762 | 0,05324 | 0,04664 | 0,04787 |
| 537,8317 | 0,05846 | 0,05662 | 0,05207 | 0,04805 | 0,04899 |
| 537,86888 | 0,05769 | 0,056 | 0,05132 | 0,04963 | 0,05022 |
| 537,90607 | 0,05736 | 0,05569 | 0,05094 | 0,05132 | 0,05153 |
| 537,94325 | 0,05742 | 0,05564 | 0,05084 | 0,05311 | 0,05292 |
| 537,98043 | 0,05782 | 0,05578 | 0,05095 | 0,05497 | 0,05437 |
| 538,01761 | 0,05852 | 0,05608 | 0,05118 | 0,05691 | 0,05586 |
| 538,05479 | 0,05945 | 0,0565 | 0,05152 | 0,05894 | 0,05736 |
| 538,09198 | 0,06056 | 0,05702 | 0,05193 | 0,06102 | 0,05886 |
| 538,12916 | 0,06179 | 0,05765 | 0,05244 | 0,06312 | 0,06032 |
| 538,16634 | 0,06312 | 0,05838 | 0,05306 | 0,06515 | 0,06175 |
| 538,20352 | 0,0645 | 0,05922 | 0,05383 | 0,06702 | 0,06315 |
| 538,2407 | 0,06593 | 0,0602 | 0,05478 | 0,06863 | 0,06454 |
| 538,27789 | 0,06738 | 0,06133 | 0,05595 | 0,0699 | 0,06597 |
| 538,31507 | 0,06886 | 0,06264 | 0,05736 | 0,07081 | 0,06748 |
| 538,35225 | 0,07038 | 0,06417 | 0,05902 | 0,07136 | 0,06908 |
| 538,38943 | 0,07195 | 0,0659 | 0,06093 | 0,07162 | 0,07078 |
| 538,42661 | 0,07362 | 0,06784 | 0,06309 | 0,07169 | 0,07255 |
| 538,4638 | 0,0754 | 0,06999 | 0,06551 | 0,07171 | 0,07431 |
| 538,50098 | 0,07735 | 0,07233 | 0,06818 | 0,07182 | 0,07599 |
| 538,53816 | 0,07952 | 0,07484 | 0,07109 | 0,07217 | 0,07748 |
| 538,57534 | 0,08192 | 0,07752 | 0,07427 | 0,07285 | 0,07872 |
| 538,61252 | 0,08457 | 0,08033 | 0,07771 | 0,07391 | 0,07968 |
| 538,64971 | 0,08748 | 0,08327 | 0,0814 | 0,07538 | 0,08037 |
| 538,68689 | 0,0906 | 0,08631 | 0,08532 | 0,07726 | 0,08088 |
| 538,72407 | 0,09388 | 0,08941 | 0,08942 | 0,07954 | 0,08137 |
| 538,76125 | 0,09724 | 0,09253 | 0,0936 | 0,08223 | 0,08206 |
| 538,79843 | 0,10056 | 0,09561 | 0,09773 | 0,08542 | 0,08326 |
| 538,83562 | 0,10372 | 0,09855 | 0,10164 | 0,08921 | 0,08523 |
| 538,8728 | 0,10655 | 0,10124 | 0,10514 | 0,09367 | 0,08818 |
| 538,90998 | 0,10893 | 0,10356 | 0,10806 | 0,09875 | 0,09217 |
| 538,94716 | 0,11071 | 0,10542 | 0,11022 | 0,10427 | 0,09707 |
| 538,98434 | 0,1118 | 0,1067 | 0,1115 | 0,10983 | 0,10252 |
| 539,02153 | 0,11209 | 0,10734 | 0,11179 | 0,11492 | 0,10798 |
| 539,05871 | 0,11159 | 0,1073 | 0,11114 | 0,11897 | 0,11279 |
| 539,09589 | 0,11038 | 0,10659 | 0,10966 | 0,12158 | 0,11639 |
| 539,13307 | 0,10859 | 0,10526 | 0,1075 | 0,12267 | 0,11847 |
| 539,17025 | 0,10637 | 0,10344 | 0,10485 | 0,12267 | 0,11922 |
| 539,20744 | 0,10396 | 0,10132 | 0,10197 | 0,12268 | 0,11947 |
| 539,24462 | 0,10166 | 0,09915 | 0,09912 | 0,12446 | 0,12086 |
| 539,2818 | 0,0998 | 0,09728 | 0,09666 | 0,13041 | 0,12574 |
| 539,31898 | 0,09883 | 0,09611 | 0,09495 | 0,14339 | 0,13706 |
| 539,35616 | 0,09921 | 0,09613 | 0,09445 | 0,16707 | 0,15792 |
| 539,39335 | 0,10146 | 0,09794 | 0,09566 | 0,20316 | 0,19104 |
| 539,43053 | 0,10614 | 0,10227 | 0,09913 | 0,25241 | 0,23847 |
| 539,46771 | 0,11378 | 0,10961 | 0,10543 | 0,31351 | 0,29922 |
| 539,50489 | 0,1249 | 0,12049 | 0,11513 | 0,3827 | 0,36934 |
| 539,54207 | 0,14008 | 0,13533 | 0,12874 | 0,45392 | 0,4426 |
| 539,57926 | 0,15917 | 0,15434 | 0,14694 | 0,5195 | 0,51091 |
| 539,61644 | 0,18196 | 0,17749 | 0,16951 | 0,57138 | 0,56567 |
| 539,65362 | 0,20799 | 0,20444 | 0,19623 | 0,60263 | 0,59939 |
| 539,6908 | 0,23645 | 0,23451 | 0,22647 | 0,60879 | 0,60732 |
| 539,72798 | 0,26625 | 0,26668 | 0,25927 | 0,58887 | 0,58835 |
| 539,76517 | 0,2961 | 0,29964 | 0,29329 | 0,54553 | 0,5453 |
| 539,80235 | 0,32457 | 0,33184 | 0,32697 | 0,48447 | 0,48416 |
| 539,83953 | 0,3502 | 0,36163 | 0,35858 | 0,41324 | 0,41277 |
| 539,87671 | 0,37162 | 0,3874 | 0,38641 | 0,33976 | 0,33926 |
| 539,91389 | 0,38769 | 0,40769 | 0,40892 | 0,27088 | 0,27058 |
| 539,95108 | 0,39757 | 0,42084 | 0,42487 | 0,21149 | 0,21155 |
| 539,98826 | 0,40078 | 0,42653 | 0,43341 | 0,16459 | 0,16459 |
| 540,02544 | 0,39681 | 0,42465 | 0,43413 | 0,13011 | 0,1299 |
| 540,06262 | 0,38634 | 0,41544 | 0,42709 | 0,10636 | 0,10613 |
| 540,0998 | 0,37022 | 0,39955 | 0,4126 | 0,09124 | 0,09151 |
| 540,13699 | 0,34939 | 0,37793 | 0,39139 | 0,08261 | 0,08314 |
| 540,17417 | 0,32497 | 0,35174 | 0,36503 | 0,07875 | 0,0792 |
| 540,21135 | 0,29818 | 0,32233 | 0,33488 | 0,07858 | 0,07862 |
| 540,24853 | 0,27026 | 0,29112 | 0,30243 | 0,08189 | 0,0812 |
| 540,28571 | 0,24246 | 0,25955 | 0,26923 | 0,08942 | 0,08773 |
| 540,3229 | 0,216 | 0,22904 | 0,23682 | 0,10285 | 0,10004 |
| 540,36008 | 0,19199 | 0,20093 | 0,20666 | 0,12478 | 0,12092 |
| 540,39726 | 0,17145 | 0,1764 | 0,18007 | 0,15837 | 0,15386 |
| 540,43444 | 0,15527 | 0,15652 | 0,15817 | 0,20686 | 0,20246 |
| 540,47162 | 0,14422 | 0,14239 | 0,14184 | 0,27276 | 0,26963 |
| 540,50881 | 0,13906 | 0,13474 | 0,13177 | 0,35685 | 0,35643 |
| 540,54599 | 0,14051 | 0,13381 | 0,12845 | 0,4572 | 0,46099 |
| 540,58317 | 0,14846 | 0,13987 | 0,1322 | 0,56842 | 0,57766 |
| 540,62035 | 0,16295 | 0,15304 | 0,14321 | 0,68134 | 0,69692 |
| 540,65753 | 0,18383 | 0,17324 | 0,1618 | 0,7827 | 0,80612 |
| 540,69472 | 0,21074 | 0,20017 | 0,18781 | 0,85965 | 0,89137 |
| 540,7319 | 0,24305 | 0,23329 | 0,22055 | 0,90144 | 0,93927 |
| 540,76908 | 0,27986 | 0,27177 | 0,25933 | 0,90157 | 0,9401 |
| 540,80626 | 0,32005 | 0,31447 | 0,30313 | 0,85939 | 0,8949 |
| 540,84344 | 0,36225 | 0,36 | 0,3506 | 0,78026 | 0,80987 |
| 540,88063 | 0,40491 | 0,40673 | 0,4001 | 0,67446 | 0,69665 |
| 540,91781 | 0,44635 | 0,45285 | 0,4497 | 0,55503 | 0,56971 |
| 540,95499 | 0,48482 | 0,49643 | 0,49733 | 0,43512 | 0,44331 |
| 540,99217 | 0,51859 | 0,53549 | 0,54082 | 0,32572 | 0,32903 |
| 541,02935 | 0,54541 | 0,56754 | 0,57799 | 0,23414 | 0,23426 |
| 541,06654 | 0,56406 | 0,59117 | 0,60676 | 0,16353 | 0,16187 |
| 541,10372 | 0,57348 | 0,60489 | 0,62525 | 0,11346 | 0,11099 |
| 541,1409 | 0,57289 | 0,60754 | 0,63193 | 0,08095 | 0,07824 |
| 541,17808 | 0,56195 | 0,59842 | 0,62572 | 0,06181 | 0,05913 |
| 541,21526 | 0,54084 | 0,57744 | 0,60548 | 0,05169 | 0,04914 |
| 541,25245 | 0,5103 | 0,5452 | 0,57232 | 0,04683 | 0,04448 |
| 541,28963 | 0,47159 | 0,50304 | 0,52802 | 0,04445 | 0,04231 |
| 541,32681 | 0,42649 | 0,453 | 0,47494 | 0,04257 | 0,04081 |
| 541,36399 | 0,37713 | 0,39765 | 0,41606 | 0,04033 | 0,03898 |
| 541,40117 | 0,32582 | 0,3399 | 0,35466 | 0,03745 | 0,03643 |
| 541,43836 | 0,27487 | 0,28266 | 0,29404 | 0,034 | 0,03324 |
| 541,47554 | 0,22639 | 0,22857 | 0,23707 | 0,03023 | 0,02967 |
| 541,51272 | 0,18228 | 0,17975 | 0,186 | 0,02642 | 0,02601 |
| 541,5499 | 0,14388 | 0,13803 | 0,14223 | 0,02278 | 0,02249 |
| 541,58708 | 0,11145 | 0,10374 | 0,10632 | 0,01943 | 0,01925 |
| 541,62427 | 0,08495 | 0,07652 | 0,0781 | 0,01642 | 0,01634 |
| 541,66145 | 0,06396 | 0,05569 | 0,05678 | 0,01376 | 0,01377 |
| 541,69863 | 0,04781 | 0,04027 | 0,04125 | 0,01143 | 0,01152 |
| 541,73581 | 0,0357 | 0,02919 | 0,03028 | 0,00944 | 0,00959 |
| 541,77299 | 0,0268 | 0,02142 | 0,02286 | 0,0078 | 0,00799 |
| 541,81018 | 0,02035 | 0,01606 | 0,01769 | 0,00657 | 0,00677 |
| 541,84736 | 0,01572 | 0,0124 | 0,01405 | 0,00578 | 0,00597 |
| 541,88454 | 0,0124 | 0,00992 | 0,01143 | 0,00549 | 0,00565 |
| 541,92172 | 0,01001 | 0,00823 | 0,0095 | 0,00574 | 0,00587 |
| 541,9589 | 0,00829 | 0,00711 | 0,00806 | 0,0066 | 0,00668 |
| 541,99609 | 0,00708 | 0,00641 | 0,007 | 0,00807 | 0,00815 |
| 542,03327 | 0,0063 | 0,00605 | 0,00627 | 0,01019 | 0,0103 |
| 542,07045 | 0,00585 | 0,00598 | 0,00585 | 0,01291 | 0,01315 |
| 542,10763 | 0,0057 | 0,00615 | 0,00573 | 0,01615 | 0,01655 |
| 542,14481 | 0,00581 | 0,00653 | 0,0059 | 0,01968 | 0,02028 |
| 542,182 | 0,00617 | 0,00709 | 0,00635 | 0,02322 | 0,02402 |
| 542,21918 | 0,00675 | 0,00781 | 0,00706 | 0,02636 | 0,02737 |
| 542,25636 | 0,00751 | 0,00868 | 0,00801 | 0,0287 | 0,02988 |
| 542,29354 | 0,00843 | 0,00967 | 0,00917 | 0,02987 | 0,03119 |
| 542,33072 | 0,00946 | 0,01079 | 0,0105 | 0,02967 | 0,03105 |
| 542,36791 | 0,01057 | 0,01202 | 0,01194 | 0,02805 | 0,02942 |
| 542,40509 | 0,01171 | 0,01334 | 0,01345 | 0,0252 | 0,02648 |
| 542,44227 | 0,01282 | 0,01471 | 0,01496 | 0,02147 | 0,02262 |
| 542,47945 | 0,01387 | 0,01608 | 0,01642 | 0,01733 | 0,0183 |
| 542,51663 | 0,01477 | 0,0174 | 0,01776 | 0,01324 | 0,01401 |
| 542,55382 | 0,01548 | 0,01857 | 0,0189 | 0,00956 | 0,01014 |
| 542,591 | 0,01595 | 0,0195 | 0,01975 | 0,00658 | 0,00695 |
| 542,62818 | 0,01614 | 0,02007 | 0,02024 | 0,00431 | 0,00452 |
| 542,66536 | 0,01601 | 0,02021 | 0,0203 | 0,00271 | 0,00282 |
| 542,70254 | 0,01555 | 0,01988 | 0,01988 | 0,00165 | 0,00173 |
| 542,73973 | 0,01478 | 0,01906 | 0,01898 | 0,001 | 0,00109 |
| 542,77691 | 0,01373 | 0,01779 | 0,01762 | 0,00063 | 0,00073 |
| 542,81409 | 0,01244 | 0,01614 | 0,01589 | 0,00044 | 0,00054 |
| 542,85127 | 0,011 | 0,01421 | 0,01388 | 0,00037 | 0,00045 |
| 542,88845 | 0,00947 | 0,01213 | 0,01174 | 0,00036 | 4e-04 |
| 542,92564 | 0,00795 | 0,01004 | 0,00962 | 0,00039 | 0,00038 |
| 542,96282 | 0,0065 | 0,00804 | 0,00765 | 0,00044 | 0,00036 |
| 543 | 0,00517 | 0,00623 | 0,00589 | 0,00049 | 0,00034 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00014 | 0,00021 | 0,00027 | 0 | 0,00021 |
| 524,03718 | 0,00014 | 0,00022 | 0,00028 | 0 | 0,00022 |
| 524,07436 | 0,00015 | 0,00024 | 3e-04 | 0 | 0,00023 |
| 524,11155 | 0,00016 | 0,00025 | 0,00031 | 0 | 0,00024 |
| 524,14873 | 0,00017 | 0,00027 | 0,00033 | 1e-05 | 0,00024 |
| 524,18591 | 0,00018 | 0,00029 | 0,00035 | 1e-05 | 0,00025 |
| 524,22309 | 2e-04 | 3e-04 | 0,00036 | 1e-05 | 0,00026 |
| 524,26027 | 0,00021 | 0,00032 | 0,00038 | 1e-05 | 0,00027 |
| 524,29746 | 0,00023 | 0,00035 | 0,00041 | 1e-05 | 0,00028 |
| 524,33464 | 0,00025 | 0,00037 | 0,00043 | 2e-05 | 0,00028 |
| 524,37182 | 0,00028 | 0,00039 | 0,00046 | 2e-05 | 0,00029 |
| 524,409 | 3e-04 | 0,00042 | 0,00048 | 2e-05 | 0,00029 |
| 524,44618 | 0,00033 | 0,00045 | 0,00051 | 3e-05 | 3e-04 |
| 524,48337 | 0,00036 | 0,00048 | 0,00054 | 3e-05 | 3e-04 |
| 524,52055 | 0,00039 | 0,00051 | 0,00057 | 4e-05 | 0,00031 |
| 524,55773 | 0,00043 | 0,00055 | 0,00061 | 5e-05 | 0,00031 |
| 524,59491 | 0,00047 | 0,00058 | 0,00064 | 6e-05 | 0,00031 |
| 524,63209 | 0,00052 | 0,00062 | 0,00068 | 7e-05 | 0,00032 |
| 524,66928 | 0,00057 | 0,00066 | 0,00073 | 8e-05 | 0,00032 |
| 524,70646 | 0,00062 | 0,00071 | 0,00077 | 1e-04 | 0,00032 |
| 524,74364 | 0,00068 | 0,00076 | 0,00082 | 0,00012 | 0,00033 |
| 524,78082 | 0,00075 | 0,00081 | 0,00086 | 0,00014 | 0,00033 |
| 524,818 | 0,00082 | 0,00086 | 0,00092 | 0,00016 | 0,00034 |
| 524,85519 | 9e-04 | 0,00092 | 0,00097 | 0,00019 | 0,00035 |
| 524,89237 | 0,00098 | 0,00098 | 0,00103 | 0,00022 | 0,00036 |
| 524,92955 | 0,00108 | 0,00105 | 0,00109 | 0,00025 | 0,00037 |
| 524,96673 | 0,00118 | 0,00112 | 0,00116 | 0,00029 | 0,00039 |
| 525,00391 | 0,00129 | 0,00119 | 0,00123 | 0,00034 | 0,00041 |
| 525,0411 | 0,00141 | 0,00128 | 0,00131 | 0,00039 | 0,00043 |
| 525,07828 | 0,00154 | 0,00136 | 0,00139 | 0,00045 | 0,00046 |
| 525,11546 | 0,00168 | 0,00146 | 0,00148 | 0,00051 | 0,00049 |
| 525,15264 | 0,00184 | 0,00155 | 0,00157 | 0,00059 | 0,00053 |
| 525,18982 | 0,002 | 0,00166 | 0,00167 | 0,00067 | 0,00058 |
| 525,22701 | 0,00218 | 0,00178 | 0,00177 | 0,00076 | 0,00063 |
| 525,26419 | 0,00237 | 0,0019 | 0,00189 | 0,00087 | 0,00069 |
| 525,30137 | 0,00258 | 0,00204 | 0,00201 | 0,00098 | 0,00076 |
| 525,33855 | 0,0028 | 0,00218 | 0,00214 | 0,00111 | 0,00084 |
| 525,37573 | 0,00303 | 0,00234 | 0,00228 | 0,00124 | 0,00093 |
| 525,41292 | 0,00328 | 0,00251 | 0,00243 | 0,00139 | 0,00104 |
| 525,4501 | 0,00354 | 0,00269 | 0,00259 | 0,00156 | 0,00115 |
| 525,48728 | 0,00382 | 0,00288 | 0,00276 | 0,00174 | 0,00128 |
| 525,52446 | 0,00412 | 0,00309 | 0,00295 | 0,00193 | 0,00142 |
| 525,56164 | 0,00443 | 0,00331 | 0,00315 | 0,00213 | 0,00157 |
| 525,59883 | 0,00476 | 0,00355 | 0,00336 | 0,00235 | 0,00174 |
| 525,63601 | 0,0051 | 0,00381 | 0,00358 | 0,00259 | 0,00193 |
| 525,67319 | 0,00545 | 0,00408 | 0,00382 | 0,00284 | 0,00212 |
| 525,71037 | 0,00583 | 0,00438 | 0,00407 | 0,0031 | 0,00234 |
| 525,74755 | 0,00622 | 0,00468 | 0,00434 | 0,00338 | 0,00257 |
| 525,78474 | 0,00662 | 0,00501 | 0,00463 | 0,00367 | 0,00281 |
| 525,82192 | 0,00704 | 0,00536 | 0,00493 | 0,00397 | 0,00307 |
| 525,8591 | 0,00746 | 0,00572 | 0,00524 | 0,00428 | 0,00335 |
| 525,89628 | 0,00791 | 0,00611 | 0,00558 | 0,0046 | 0,00364 |
| 525,93346 | 0,00836 | 0,00652 | 0,00592 | 0,00493 | 0,00394 |
| 525,97065 | 0,00883 | 0,00694 | 0,00629 | 0,00527 | 0,00426 |
| 526,00783 | 0,00931 | 0,00738 | 0,00666 | 0,00561 | 0,00459 |
| 526,04501 | 0,00979 | 0,00785 | 0,00706 | 0,00596 | 0,00492 |
| 526,08219 | 0,01029 | 0,00834 | 0,00746 | 0,00631 | 0,00527 |
| 526,11937 | 0,01079 | 0,00884 | 0,00788 | 0,00666 | 0,00563 |
| 526,15656 | 0,0113 | 0,00936 | 0,00832 | 0,00702 | 0,006 |
| 526,19374 | 0,01182 | 0,0099 | 0,00877 | 0,00737 | 0,00637 |
| 526,23092 | 0,01234 | 0,01046 | 0,00923 | 0,00772 | 0,00675 |
| 526,2681 | 0,01287 | 0,01104 | 0,0097 | 0,00807 | 0,00714 |
| 526,30528 | 0,0134 | 0,01163 | 0,01019 | 0,00841 | 0,00752 |
| 526,34247 | 0,01394 | 0,01224 | 0,01068 | 0,00874 | 0,00791 |
| 526,37965 | 0,01448 | 0,01287 | 0,01119 | 0,00908 | 0,0083 |
| 526,41683 | 0,01503 | 0,01351 | 0,01171 | 0,0094 | 0,00869 |
| 526,45401 | 0,01558 | 0,01417 | 0,01225 | 0,00972 | 0,00909 |
| 526,49119 | 0,01614 | 0,01484 | 0,01279 | 0,01004 | 0,00948 |
| 526,52838 | 0,01671 | 0,01553 | 0,01335 | 0,01035 | 0,00986 |
| 526,56556 | 0,01729 | 0,01622 | 0,01392 | 0,01066 | 0,01025 |
| 526,60274 | 0,01787 | 0,01694 | 0,01451 | 0,01096 | 0,01064 |
| 526,63992 | 0,01847 | 0,01767 | 0,01511 | 0,01127 | 0,01102 |
| 526,6771 | 0,01909 | 0,01841 | 0,01573 | 0,01158 | 0,01141 |
| 526,71429 | 0,01972 | 0,01917 | 0,01637 | 0,01189 | 0,0118 |
| 526,75147 | 0,02038 | 0,01994 | 0,01704 | 0,0122 | 0,01219 |
| 526,78865 | 0,02106 | 0,02072 | 0,01773 | 0,01253 | 0,01258 |
| 526,82583 | 0,02177 | 0,02153 | 0,01844 | 0,01287 | 0,01299 |
| 526,86301 | 0,0225 | 0,02236 | 0,01918 | 0,01322 | 0,0134 |
| 526,9002 | 0,02327 | 0,0232 | 0,01996 | 0,01359 | 0,01382 |
| 526,93738 | 0,02408 | 0,02406 | 0,02076 | 0,01398 | 0,01425 |
| 526,97456 | 0,02493 | 0,02495 | 0,02161 | 0,0144 | 0,01471 |
| 527,01174 | 0,02582 | 0,02586 | 0,02249 | 0,01485 | 0,01519 |
| 527,04892 | 0,02676 | 0,0268 | 0,02342 | 0,01532 | 0,01569 |
| 527,08611 | 0,02775 | 0,02777 | 0,02438 | 0,01584 | 0,01622 |
| 527,12329 | 0,02879 | 0,02877 | 0,02538 | 0,0164 | 0,01678 |
| 527,16047 | 0,02989 | 0,02979 | 0,02644 | 0,01701 | 0,01739 |
| 527,19765 | 0,03104 | 0,03085 | 0,02755 | 0,01766 | 0,01803 |
| 527,23483 | 0,03225 | 0,03195 | 0,0287 | 0,01836 | 0,01873 |
| 527,27202 | 0,03351 | 0,03308 | 0,0299 | 0,01912 | 0,01946 |
| 527,3092 | 0,03483 | 0,03425 | 0,03114 | 0,01994 | 0,02025 |
| 527,34638 | 0,03621 | 0,03546 | 0,03243 | 0,02083 | 0,0211 |
| 527,38356 | 0,03766 | 0,0367 | 0,03377 | 0,02178 | 0,02202 |
| 527,42074 | 0,03915 | 0,03797 | 0,03515 | 0,02279 | 0,023 |
| 527,45793 | 0,04069 | 0,03929 | 0,03657 | 0,02387 | 0,02405 |
| 527,49511 | 0,04229 | 0,04065 | 0,03803 | 0,02504 | 0,02516 |
| 527,53229 | 0,04393 | 0,04203 | 0,03953 | 0,02628 | 0,02633 |
| 527,56947 | 0,04562 | 0,04345 | 0,04106 | 0,02759 | 0,0276 |
| 527,60665 | 0,04736 | 0,0449 | 0,04262 | 0,02898 | 0,02893 |
| 527,64384 | 0,04913 | 0,04638 | 0,0442 | 0,03043 | 0,03033 |
| 527,68102 | 0,05093 | 0,04788 | 0,04581 | 0,03196 | 0,0318 |
| 527,7182 | 0,05276 | 0,04941 | 0,04743 | 0,03357 | 0,03334 |
| 527,75538 | 0,05462 | 0,05095 | 0,04906 | 0,03524 | 0,03494 |
| 527,79256 | 0,05651 | 0,05251 | 0,05071 | 0,03697 | 0,03662 |
| 527,82975 | 0,05842 | 0,05408 | 0,05235 | 0,03876 | 0,03835 |
| 527,86693 | 0,06033 | 0,05565 | 0,054 | 0,0406 | 0,04013 |
| 527,90411 | 0,06226 | 0,05723 | 0,05564 | 0,0425 | 0,04196 |
| 527,94129 | 0,0642 | 0,05881 | 0,05728 | 0,04443 | 0,04383 |
| 527,97847 | 0,06614 | 0,06039 | 0,0589 | 0,04639 | 0,04574 |
| 528,01566 | 0,06808 | 0,06196 | 0,06051 | 0,04838 | 0,04767 |
| 528,05284 | 0,07001 | 0,06352 | 0,0621 | 0,05039 | 0,04962 |
| 528,09002 | 0,07194 | 0,06507 | 0,06368 | 0,0524 | 0,05158 |
| 528,1272 | 0,07385 | 0,0666 | 0,06523 | 0,05442 | 0,05355 |
| 528,16438 | 0,07576 | 0,06812 | 0,06677 | 0,05642 | 0,05552 |
| 528,20157 | 0,07764 | 0,06962 | 0,06828 | 0,05842 | 0,05747 |
| 528,23875 | 0,0795 | 0,0711 | 0,06976 | 0,06039 | 0,0594 |
| 528,27593 | 0,08134 | 0,07256 | 0,07123 | 0,06233 | 0,06131 |
| 528,31311 | 0,08315 | 0,074 | 0,07268 | 0,06424 | 0,06318 |
| 528,35029 | 0,08493 | 0,07542 | 0,0741 | 0,0661 | 0,06502 |
| 528,38748 | 0,08668 | 0,07682 | 0,07549 | 0,06791 | 0,06682 |
| 528,42466 | 0,08839 | 0,0782 | 0,07687 | 0,06968 | 0,06856 |
| 528,46184 | 0,09005 | 0,07955 | 0,07823 | 0,0714 | 0,07026 |
| 528,49902 | 0,09168 | 0,08089 | 0,07957 | 0,07307 | 0,0719 |
| 528,5362 | 0,09326 | 0,0822 | 0,08089 | 0,07468 | 0,0735 |
| 528,57339 | 0,0948 | 0,08351 | 0,0822 | 0,07623 | 0,07504 |
| 528,61057 | 0,09627 | 0,08479 | 0,08349 | 0,07773 | 0,07651 |
| 528,64775 | 0,09769 | 0,08606 | 0,08476 | 0,07919 | 0,07793 |
| 528,68493 | 0,09905 | 0,08731 | 0,08603 | 0,08059 | 0,0793 |
| 528,72211 | 0,10036 | 0,08855 | 0,08728 | 0,08195 | 0,08062 |
| 528,7593 | 0,1016 | 0,08977 | 0,08851 | 0,08326 | 0,0819 |
| 528,79648 | 0,10277 | 0,09098 | 0,08973 | 0,08454 | 0,08312 |
| 528,83366 | 0,10387 | 0,09217 | 0,09094 | 0,08578 | 0,0843 |
| 528,87084 | 0,10491 | 0,09334 | 0,09214 | 0,08699 | 0,08544 |
| 528,90802 | 0,10588 | 0,0945 | 0,09332 | 0,08817 | 0,08654 |
| 528,94521 | 0,10679 | 0,09564 | 0,09449 | 0,08932 | 0,08762 |
| 528,98239 | 0,10762 | 0,09676 | 0,09564 | 0,09046 | 0,08866 |
| 529,01957 | 0,10837 | 0,09787 | 0,09677 | 0,09157 | 0,08968 |
| 529,05675 | 0,10906 | 0,09895 | 0,09789 | 0,09267 | 0,09067 |
| 529,09393 | 0,10969 | 0,10001 | 0,09898 | 0,09376 | 0,09165 |
| 529,13112 | 0,11025 | 0,10104 | 0,10006 | 0,09483 | 0,09262 |
| 529,1683 | 0,11075 | 0,10206 | 0,10111 | 0,09589 | 0,09357 |
| 529,20548 | 0,11119 | 0,10305 | 0,10214 | 0,09695 | 0,09451 |
| 529,24266 | 0,11157 | 0,10401 | 0,10314 | 0,09799 | 0,09545 |
| 529,27984 | 0,1119 | 0,10494 | 0,10412 | 0,09902 | 0,09638 |
| 529,31703 | 0,11218 | 0,10584 | 0,10508 | 0,10004 | 0,09732 |
| 529,35421 | 0,11243 | 0,10672 | 0,10601 | 0,10105 | 0,09825 |
| 529,39139 | 0,11264 | 0,10757 | 0,1069 | 0,10205 | 0,09919 |
| 529,42857 | 0,11281 | 0,10839 | 0,10777 | 0,10304 | 0,10014 |
| 529,46575 | 0,11296 | 0,10918 | 0,10862 | 0,10402 | 0,10109 |
| 529,50294 | 0,11309 | 0,10995 | 0,10944 | 0,10498 | 0,10205 |
| 529,54012 | 0,11321 | 0,11068 | 0,11023 | 0,10594 | 0,10302 |
| 529,5773 | 0,11331 | 0,11139 | 0,11099 | 0,10688 | 0,104 |
| 529,61448 | 0,11342 | 0,11208 | 0,11172 | 0,1078 | 0,105 |
| 529,65166 | 0,11352 | 0,11274 | 0,11243 | 0,10871 | 0,106 |
| 529,68885 | 0,11363 | 0,11338 | 0,11312 | 0,10961 | 0,10702 |
| 529,72603 | 0,11375 | 0,11399 | 0,11378 | 0,1105 | 0,10804 |
| 529,76321 | 0,11388 | 0,11457 | 0,11441 | 0,11138 | 0,10908 |
| 529,80039 | 0,11402 | 0,11514 | 0,11501 | 0,11224 | 0,11012 |
| 529,83757 | 0,11419 | 0,11569 | 0,1156 | 0,11308 | 0,11117 |
| 529,87476 | 0,11438 | 0,1162 | 0,11616 | 0,11392 | 0,11222 |
| 529,91194 | 0,11458 | 0,1167 | 0,1167 | 0,11474 | 0,11328 |
| 529,94912 | 0,11481 | 0,11717 | 0,11721 | 0,11554 | 0,11433 |
| 529,9863 | 0,11505 | 0,11761 | 0,11769 | 0,11633 | 0,11538 |
| 530,02348 | 0,11531 | 0,11803 | 0,11815 | 0,1171 | 0,11641 |
| 530,06067 | 0,11559 | 0,11843 | 0,11859 | 0,11785 | 0,11742 |
| 530,09785 | 0,11588 | 0,11878 | 0,119 | 0,11858 | 0,11842 |
| 530,13503 | 0,11617 | 0,11911 | 0,11937 | 0,11928 | 0,11938 |
| 530,17221 | 0,11648 | 0,11941 | 0,11971 | 0,11996 | 0,12032 |
| 530,20939 | 0,11678 | 0,11968 | 0,12002 | 0,1206 | 0,12122 |
| 530,24658 | 0,11708 | 0,11991 | 0,1203 | 0,1212 | 0,12206 |
| 530,28376 | 0,11736 | 0,1201 | 0,12054 | 0,12177 | 0,12286 |
| 530,32094 | 0,11763 | 0,12025 | 0,12074 | 0,12229 | 0,12359 |
| 530,35812 | 0,11789 | 0,12037 | 0,12089 | 0,12277 | 0,12427 |
| 530,3953 | 0,11812 | 0,12045 | 0,12101 | 0,12319 | 0,12489 |
| 530,43249 | 0,11831 | 0,1205 | 0,12108 | 0,12355 | 0,12543 |
| 530,46967 | 0,11847 | 0,1205 | 0,1211 | 0,12385 | 0,12589 |
| 530,50685 | 0,1186 | 0,12047 | 0,12109 | 0,12409 | 0,12628 |
| 530,54403 | 0,11868 | 0,1204 | 0,12102 | 0,12427 | 0,12659 |
| 530,58121 | 0,11873 | 0,1203 | 0,1209 | 0,12439 | 0,12682 |
| 530,6184 | 0,11873 | 0,12018 | 0,12074 | 0,12444 | 0,12698 |
| 530,65558 | 0,11867 | 0,12003 | 0,12054 | 0,12442 | 0,12704 |
| 530,69276 | 0,11857 | 0,11985 | 0,1203 | 0,12434 | 0,12703 |
| 530,72994 | 0,11844 | 0,11966 | 0,12002 | 0,12421 | 0,12695 |
| 530,76712 | 0,11826 | 0,11945 | 0,1197 | 0,12402 | 0,12681 |
| 530,80431 | 0,11804 | 0,11923 | 0,11935 | 0,12378 | 0,1266 |
| 530,84149 | 0,11779 | 0,11901 | 0,11897 | 0,1235 | 0,12633 |
| 530,87867 | 0,1175 | 0,11879 | 0,11857 | 0,12318 | 0,126 |
| 530,91585 | 0,11719 | 0,11857 | 0,11815 | 0,12284 | 0,12563 |
| 530,95303 | 0,11686 | 0,11836 | 0,11771 | 0,12248 | 0,12523 |
| 530,99022 | 0,11651 | 0,11816 | 0,11726 | 0,12211 | 0,12479 |
| 531,0274 | 0,11616 | 0,11798 | 0,11681 | 0,12173 | 0,12433 |
| 531,06458 | 0,1158 | 0,11781 | 0,11635 | 0,12136 | 0,12385 |
| 531,10176 | 0,11545 | 0,11767 | 0,1159 | 0,12101 | 0,12337 |
| 531,13894 | 0,11511 | 0,11754 | 0,11546 | 0,12067 | 0,12288 |
| 531,17613 | 0,11478 | 0,11744 | 0,11502 | 0,12036 | 0,1224 |
| 531,21331 | 0,11446 | 0,11736 | 0,1146 | 0,12009 | 0,12193 |
| 531,25049 | 0,11417 | 0,11729 | 0,11419 | 0,11985 | 0,12146 |
| 531,28767 | 0,11391 | 0,11725 | 0,11379 | 0,11965 | 0,12102 |
| 531,32485 | 0,11367 | 0,11722 | 0,11341 | 0,11949 | 0,1206 |
| 531,36204 | 0,11346 | 0,1172 | 0,11304 | 0,11936 | 0,1202 |
| 531,39922 | 0,11327 | 0,11719 | 0,11269 | 0,11927 | 0,11982 |
| 531,4364 | 0,1131 | 0,11718 | 0,11234 | 0,11922 | 0,11947 |
| 531,47358 | 0,11296 | 0,11717 | 0,112 | 0,1192 | 0,11913 |
| 531,51076 | 0,11283 | 0,11715 | 0,11167 | 0,1192 | 0,11882 |
| 531,54795 | 0,11272 | 0,11711 | 0,11134 | 0,11921 | 0,11852 |
| 531,58513 | 0,11261 | 0,11705 | 0,11101 | 0,11924 | 0,11824 |
| 531,62231 | 0,11251 | 0,11696 | 0,11067 | 0,11926 | 0,11796 |
| 531,65949 | 0,1124 | 0,11684 | 0,11032 | 0,11927 | 0,11769 |
| 531,69667 | 0,11228 | 0,11667 | 0,10996 | 0,11927 | 0,11743 |
| 531,73386 | 0,11215 | 0,11645 | 0,10957 | 0,11923 | 0,11716 |
| 531,77104 | 0,112 | 0,11619 | 0,10917 | 0,11917 | 0,11688 |
| 531,80822 | 0,11182 | 0,11588 | 0,10874 | 0,11906 | 0,11659 |
| 531,8454 | 0,11161 | 0,11551 | 0,10829 | 0,11891 | 0,11629 |
| 531,88258 | 0,11136 | 0,11508 | 0,10781 | 0,1187 | 0,11597 |
| 531,91977 | 0,11108 | 0,11459 | 0,1073 | 0,11842 | 0,11562 |
| 531,95695 | 0,11075 | 0,11403 | 0,10675 | 0,11809 | 0,11526 |
| 531,99413 | 0,11038 | 0,11343 | 0,10619 | 0,1177 | 0,11487 |
| 532,03131 | 0,10997 | 0,11277 | 0,10559 | 0,11725 | 0,11446 |
| 532,06849 | 0,10951 | 0,11205 | 0,10498 | 0,11673 | 0,11403 |
| 532,10568 | 0,10901 | 0,11129 | 0,10434 | 0,11615 | 0,11357 |
| 532,14286 | 0,10847 | 0,11048 | 0,10369 | 0,11552 | 0,11309 |
| 532,18004 | 0,1079 | 0,10964 | 0,10302 | 0,11484 | 0,11259 |
| 532,21722 | 0,1073 | 0,10877 | 0,10235 | 0,11411 | 0,11208 |
| 532,2544 | 0,10667 | 0,10788 | 0,10167 | 0,11335 | 0,11155 |
| 532,29159 | 0,10602 | 0,10697 | 0,10099 | 0,11255 | 0,11101 |
| 532,32877 | 0,10535 | 0,10606 | 0,10033 | 0,11173 | 0,11046 |
| 532,36595 | 0,10468 | 0,10514 | 0,09967 | 0,1109 | 0,10991 |
| 532,40313 | 0,10401 | 0,10424 | 0,09904 | 0,11006 | 0,10935 |
| 532,44031 | 0,10334 | 0,10335 | 0,09843 | 0,10921 | 0,1088 |
| 532,4775 | 0,10268 | 0,10248 | 0,09784 | 0,10837 | 0,10825 |
| 532,51468 | 0,10204 | 0,10164 | 0,09729 | 0,10755 | 0,10771 |
| 532,55186 | 0,10142 | 0,10083 | 0,09677 | 0,10674 | 0,10718 |
| 532,58904 | 0,10082 | 0,10006 | 0,0963 | 0,10595 | 0,10665 |
| 532,62622 | 0,10025 | 0,09933 | 0,09586 | 0,10519 | 0,10614 |
| 532,66341 | 0,09971 | 0,09864 | 0,09545 | 0,10445 | 0,10564 |
| 532,70059 | 0,0992 | 0,098 | 0,09509 | 0,10374 | 0,10515 |
| 532,73777 | 0,09872 | 0,0974 | 0,09477 | 0,10307 | 0,10468 |
| 532,77495 | 0,09828 | 0,09685 | 0,09448 | 0,10242 | 0,10421 |
| 532,81213 | 0,09786 | 0,09633 | 0,09423 | 0,1018 | 0,10375 |
| 532,84932 | 0,09746 | 0,09585 | 0,09401 | 0,10121 | 0,1033 |
| 532,8865 | 0,09709 | 0,0954 | 0,09381 | 0,10065 | 0,10285 |
| 532,92368 | 0,09674 | 0,09499 | 0,09363 | 0,10011 | 0,1024 |
| 532,96086 | 0,0964 | 0,09459 | 0,09347 | 0,09959 | 0,10195 |
| 532,99804 | 0,09607 | 0,09421 | 0,09332 | 0,09908 | 0,1015 |
| 533,03523 | 0,09574 | 0,09384 | 0,09318 | 0,09859 | 0,10104 |
| 533,07241 | 0,09541 | 0,09347 | 0,09303 | 0,09811 | 0,10058 |
| 533,10959 | 0,09507 | 0,0931 | 0,09287 | 0,09764 | 0,1001 |
| 533,14677 | 0,09471 | 0,09271 | 0,09269 | 0,09717 | 0,0996 |
| 533,18395 | 0,09433 | 0,09231 | 0,09249 | 0,0967 | 0,09909 |
| 533,22114 | 0,09393 | 0,09189 | 0,09226 | 0,09624 | 0,09856 |
| 533,25832 | 0,0935 | 0,09143 | 0,09201 | 0,09577 | 0,09801 |
| 533,2955 | 0,09304 | 0,09095 | 0,09172 | 0,0953 | 0,09744 |
| 533,33268 | 0,09254 | 0,09043 | 0,09138 | 0,09482 | 0,09685 |
| 533,36986 | 0,092 | 0,08987 | 0,09099 | 0,09434 | 0,09624 |
| 533,40705 | 0,09143 | 0,08927 | 0,09057 | 0,09385 | 0,0956 |
| 533,44423 | 0,09082 | 0,08863 | 0,09009 | 0,09335 | 0,09495 |
| 533,48141 | 0,09019 | 0,08796 | 0,08957 | 0,09285 | 0,09428 |
| 533,51859 | 0,08951 | 0,08724 | 0,089 | 0,09234 | 0,09359 |
| 533,55577 | 0,08881 | 0,08649 | 0,08838 | 0,09182 | 0,09288 |
| 533,59295 | 0,08809 | 0,08572 | 0,08772 | 0,09129 | 0,09215 |
| 533,63014 | 0,08735 | 0,08492 | 0,08702 | 0,09077 | 0,09141 |
| 533,66732 | 0,0866 | 0,0841 | 0,08628 | 0,09023 | 0,09066 |
| 533,7045 | 0,08584 | 0,08327 | 0,0855 | 0,08969 | 0,0899 |
| 533,74168 | 0,08509 | 0,08243 | 0,0847 | 0,08915 | 0,08913 |
| 533,77886 | 0,08434 | 0,0816 | 0,08387 | 0,0886 | 0,08835 |
| 533,81605 | 0,08361 | 0,08078 | 0,08302 | 0,08804 | 0,08756 |
| 533,85323 | 0,0829 | 0,07997 | 0,08216 | 0,08748 | 0,08677 |
| 533,89041 | 0,08221 | 0,07918 | 0,08129 | 0,08691 | 0,08597 |
| 533,92759 | 0,08155 | 0,07843 | 0,08042 | 0,08634 | 0,08516 |
| 533,96477 | 0,08093 | 0,07771 | 0,07955 | 0,08575 | 0,08435 |
| 534,00196 | 0,08035 | 0,07704 | 0,07869 | 0,08515 | 0,08353 |
| 534,03914 | 0,07981 | 0,07641 | 0,07784 | 0,08453 | 0,0827 |
| 534,07632 | 0,07931 | 0,07583 | 0,077 | 0,0839 | 0,08187 |
| 534,1135 | 0,07884 | 0,07529 | 0,07618 | 0,08326 | 0,08104 |
| 534,15068 | 0,07842 | 0,07482 | 0,07539 | 0,08259 | 0,08019 |
| 534,18787 | 0,07804 | 0,0744 | 0,07462 | 0,0819 | 0,07933 |
| 534,22505 | 0,07769 | 0,07402 | 0,07388 | 0,08119 | 0,07847 |
| 534,26223 | 0,07737 | 0,07369 | 0,07315 | 0,08045 | 0,0776 |
| 534,29941 | 0,07707 | 0,0734 | 0,07245 | 0,07969 | 0,07672 |
| 534,33659 | 0,07679 | 0,07316 | 0,07178 | 0,0789 | 0,07582 |
| 534,37378 | 0,07651 | 0,07295 | 0,07113 | 0,07808 | 0,07492 |
| 534,41096 | 0,07624 | 0,07276 | 0,0705 | 0,07724 | 0,074 |
| 534,44814 | 0,07596 | 0,0726 | 0,06989 | 0,07636 | 0,07308 |
| 534,48532 | 0,07567 | 0,07245 | 0,06929 | 0,07547 | 0,07215 |
| 534,5225 | 0,07536 | 0,0723 | 0,06871 | 0,07455 | 0,07122 |
| 534,55969 | 0,07502 | 0,07215 | 0,06814 | 0,07361 | 0,07028 |
| 534,59687 | 0,07464 | 0,07198 | 0,06757 | 0,07265 | 0,06934 |
| 534,63405 | 0,07422 | 0,0718 | 0,067 | 0,07168 | 0,0684 |
| 534,67123 | 0,07376 | 0,0716 | 0,06643 | 0,0707 | 0,06747 |
| 534,70841 | 0,07325 | 0,07137 | 0,06587 | 0,06971 | 0,06655 |
| 534,7456 | 0,07269 | 0,0711 | 0,06529 | 0,06873 | 0,06564 |
| 534,78278 | 0,07207 | 0,07079 | 0,06471 | 0,06775 | 0,06476 |
| 534,81996 | 0,0714 | 0,07044 | 0,06412 | 0,06679 | 0,06389 |
| 534,85714 | 0,07069 | 0,07005 | 0,06353 | 0,06585 | 0,06306 |
| 534,89432 | 0,06992 | 0,06962 | 0,06293 | 0,06493 | 0,06225 |
| 534,93151 | 0,06912 | 0,06914 | 0,06232 | 0,06405 | 0,06148 |
| 534,96869 | 0,06827 | 0,06862 | 0,06171 | 0,0632 | 0,06075 |
| 535,00587 | 0,06738 | 0,06806 | 0,06109 | 0,0624 | 0,06007 |
| 535,04305 | 0,06648 | 0,06748 | 0,06048 | 0,06164 | 0,05944 |
| 535,08023 | 0,06555 | 0,06687 | 0,05987 | 0,06094 | 0,05886 |
| 535,11742 | 0,06462 | 0,06623 | 0,05926 | 0,06029 | 0,05833 |
| 535,1546 | 0,06369 | 0,06558 | 0,05867 | 0,0597 | 0,05785 |
| 535,19178 | 0,06276 | 0,06493 | 0,0581 | 0,05918 | 0,05745 |
| 535,22896 | 0,06185 | 0,06427 | 0,05754 | 0,05872 | 0,05711 |
| 535,26614 | 0,06097 | 0,06362 | 0,05701 | 0,05833 | 0,05683 |
| 535,30333 | 0,06012 | 0,06299 | 0,05651 | 0,058 | 0,0566 |
| 535,34051 | 0,0593 | 0,06237 | 0,05605 | 0,05774 | 0,05643 |
| 535,37769 | 0,05854 | 0,06178 | 0,05562 | 0,05753 | 0,05634 |
| 535,41487 | 0,05783 | 0,06123 | 0,05524 | 0,05741 | 0,0563 |
| 535,45205 | 0,05718 | 0,06071 | 0,05489 | 0,05733 | 0,05631 |
| 535,48924 | 0,05658 | 0,06023 | 0,05459 | 0,05731 | 0,05637 |
| 535,52642 | 0,05604 | 0,05978 | 0,05435 | 0,05735 | 0,05649 |
| 535,5636 | 0,05556 | 0,0594 | 0,05415 | 0,05742 | 0,05664 |
| 535,60078 | 0,05516 | 0,05905 | 0,054 | 0,05755 | 0,05685 |
| 535,63796 | 0,05481 | 0,05875 | 0,05389 | 0,05771 | 0,05708 |
| 535,67515 | 0,05451 | 0,05848 | 0,05383 | 0,0579 | 0,05735 |
| 535,71233 | 0,05426 | 0,05826 | 0,05381 | 0,05812 | 0,05764 |
| 535,74951 | 0,05406 | 0,05807 | 0,05384 | 0,05836 | 0,05794 |
| 535,78669 | 0,05391 | 0,05792 | 0,0539 | 0,05862 | 0,05827 |
| 535,82387 | 0,0538 | 0,05779 | 0,05399 | 0,05888 | 0,0586 |
| 535,86106 | 0,05371 | 0,05769 | 0,0541 | 0,05915 | 0,05894 |
| 535,89824 | 0,05365 | 0,0576 | 0,05423 | 0,05941 | 0,05927 |
| 535,93542 | 0,0536 | 0,05752 | 0,05438 | 0,05966 | 0,05959 |
| 535,9726 | 0,05356 | 0,05744 | 0,05454 | 0,05991 | 0,05991 |
| 536,00978 | 0,05352 | 0,05736 | 0,05469 | 0,06013 | 0,0602 |
| 536,04697 | 0,05348 | 0,05727 | 0,05484 | 0,06033 | 0,06048 |
| 536,08415 | 0,05342 | 0,05717 | 0,05499 | 0,06051 | 0,06073 |
| 536,12133 | 0,05335 | 0,05706 | 0,05511 | 0,06065 | 0,06095 |
| 536,15851 | 0,05326 | 0,05691 | 0,05522 | 0,06077 | 0,06115 |
| 536,19569 | 0,05314 | 0,05674 | 0,0553 | 0,06085 | 0,0613 |
| 536,23288 | 0,05299 | 0,05654 | 0,05535 | 0,06089 | 0,06142 |
| 536,27006 | 0,0528 | 0,05631 | 0,05537 | 0,06089 | 0,0615 |
| 536,30724 | 0,05259 | 0,05605 | 0,05535 | 0,06086 | 0,06153 |
| 536,34442 | 0,05234 | 0,05576 | 0,05529 | 0,06078 | 0,06153 |
| 536,3816 | 0,05206 | 0,05542 | 0,0552 | 0,06067 | 0,06149 |
| 536,41879 | 0,05174 | 0,05505 | 0,05507 | 0,06052 | 0,06139 |
| 536,45597 | 0,05138 | 0,05466 | 0,05491 | 0,06032 | 0,06125 |
| 536,49315 | 0,05101 | 0,05424 | 0,05471 | 0,06008 | 0,06106 |
| 536,53033 | 0,0506 | 0,05379 | 0,05447 | 0,05982 | 0,06083 |
| 536,56751 | 0,05018 | 0,05332 | 0,0542 | 0,05951 | 0,06056 |
| 536,6047 | 0,04974 | 0,05283 | 0,05391 | 0,05918 | 0,06023 |
| 536,64188 | 0,04928 | 0,05232 | 0,05359 | 0,05881 | 0,05986 |
| 536,67906 | 0,04882 | 0,05181 | 0,05326 | 0,05842 | 0,05945 |
| 536,71624 | 0,04835 | 0,05129 | 0,05291 | 0,058 | 0,059 |
| 536,75342 | 0,04789 | 0,05077 | 0,05255 | 0,05755 | 0,05852 |
| 536,79061 | 0,04743 | 0,05026 | 0,05218 | 0,05709 | 0,058 |
| 536,82779 | 0,04697 | 0,04975 | 0,05181 | 0,05662 | 0,05743 |
| 536,86497 | 0,04654 | 0,04925 | 0,05145 | 0,05612 | 0,05685 |
| 536,90215 | 0,04612 | 0,04876 | 0,0511 | 0,05562 | 0,05623 |
| 536,93933 | 0,04571 | 0,04829 | 0,05075 | 0,05512 | 0,0556 |
| 536,97652 | 0,04533 | 0,04784 | 0,05042 | 0,05461 | 0,05495 |
| 537,0137 | 0,04497 | 0,04741 | 0,05011 | 0,0541 | 0,05428 |
| 537,05088 | 0,04463 | 0,04699 | 0,04981 | 0,05359 | 0,05361 |
| 537,08806 | 0,04432 | 0,0466 | 0,04953 | 0,0531 | 0,05293 |
| 537,12524 | 0,04402 | 0,04623 | 0,04927 | 0,05261 | 0,05226 |
| 537,16243 | 0,04375 | 0,04588 | 0,04903 | 0,05214 | 0,0516 |
| 537,19961 | 0,04349 | 0,04555 | 0,04881 | 0,05168 | 0,05096 |
| 537,23679 | 0,04325 | 0,04524 | 0,04861 | 0,05125 | 0,05034 |
| 537,27397 | 0,04302 | 0,04495 | 0,04843 | 0,05084 | 0,04974 |
| 537,31115 | 0,04281 | 0,04467 | 0,04826 | 0,05046 | 0,04918 |
| 537,34834 | 0,04259 | 0,0444 | 0,04811 | 0,0501 | 0,04866 |
| 537,38552 | 0,04238 | 0,04415 | 0,04796 | 0,04978 | 0,04818 |
| 537,4227 | 0,04217 | 0,0439 | 0,04783 | 0,04948 | 0,04774 |
| 537,45988 | 0,04195 | 0,04367 | 0,0477 | 0,04922 | 0,04737 |
| 537,49706 | 0,04173 | 0,04344 | 0,04758 | 0,04901 | 0,04704 |
| 537,53425 | 0,0415 | 0,04321 | 0,04746 | 0,04882 | 0,04677 |
| 537,57143 | 0,04126 | 0,04299 | 0,04734 | 0,04867 | 0,04656 |
| 537,60861 | 0,04101 | 0,04277 | 0,04722 | 0,04856 | 0,0464 |
| 537,64579 | 0,04074 | 0,04256 | 0,04711 | 0,04847 | 0,04632 |
| 537,68297 | 0,04046 | 0,04234 | 0,04699 | 0,04843 | 0,0463 |
| 537,72016 | 0,04017 | 0,04213 | 0,04687 | 0,04841 | 0,04633 |
| 537,75734 | 0,03986 | 0,04193 | 0,04675 | 0,04843 | 0,04641 |
| 537,79452 | 0,03955 | 0,04173 | 0,04663 | 0,04847 | 0,04655 |
| 537,8317 | 0,03923 | 0,04154 | 0,04652 | 0,04853 | 0,04674 |
| 537,86888 | 0,03891 | 0,04135 | 0,04641 | 0,04862 | 0,04699 |
| 537,90607 | 0,03859 | 0,04118 | 0,0463 | 0,04872 | 0,04727 |
| 537,94325 | 0,03827 | 0,04101 | 0,04621 | 0,04884 | 0,04759 |
| 537,98043 | 0,03795 | 0,04087 | 0,04612 | 0,04896 | 0,04794 |
| 538,01761 | 0,03765 | 0,04074 | 0,04605 | 0,04909 | 0,04832 |
| 538,05479 | 0,03736 | 0,04062 | 0,04599 | 0,04922 | 0,04871 |
| 538,09198 | 0,03709 | 0,04052 | 0,04595 | 0,04934 | 0,04912 |
| 538,12916 | 0,03683 | 0,04045 | 0,04593 | 0,04945 | 0,04953 |
| 538,16634 | 0,0366 | 0,04039 | 0,04593 | 0,04955 | 0,04994 |
| 538,20352 | 0,03639 | 0,04035 | 0,04595 | 0,04963 | 0,05033 |
| 538,2407 | 0,03621 | 0,04034 | 0,04598 | 0,04969 | 0,05071 |
| 538,27789 | 0,03605 | 0,04034 | 0,04603 | 0,04973 | 0,05107 |
| 538,31507 | 0,03592 | 0,04035 | 0,0461 | 0,04973 | 0,05139 |
| 538,35225 | 0,03581 | 0,04038 | 0,04619 | 0,04969 | 0,05167 |
| 538,38943 | 0,03572 | 0,04042 | 0,04628 | 0,04962 | 0,05191 |
| 538,42661 | 0,03564 | 0,04047 | 0,04638 | 0,04951 | 0,0521 |
| 538,4638 | 0,03559 | 0,04052 | 0,04649 | 0,04937 | 0,05223 |
| 538,50098 | 0,03554 | 0,04057 | 0,0466 | 0,04917 | 0,05229 |
| 538,53816 | 0,03551 | 0,04061 | 0,0467 | 0,04893 | 0,05229 |
| 538,57534 | 0,03547 | 0,04064 | 0,04679 | 0,04864 | 0,05223 |
| 538,61252 | 0,03543 | 0,04065 | 0,04687 | 0,04831 | 0,0521 |
| 538,64971 | 0,03538 | 0,04064 | 0,04693 | 0,04794 | 0,05189 |
| 538,68689 | 0,03532 | 0,04061 | 0,04696 | 0,04752 | 0,0516 |
| 538,72407 | 0,03523 | 0,04054 | 0,04696 | 0,04706 | 0,05124 |
| 538,76125 | 0,03513 | 0,04044 | 0,04692 | 0,04655 | 0,05081 |
| 538,79843 | 0,035 | 0,0403 | 0,04685 | 0,04601 | 0,05031 |
| 538,83562 | 0,03484 | 0,04012 | 0,04675 | 0,04543 | 0,04976 |
| 538,8728 | 0,03465 | 0,03989 | 0,0466 | 0,04483 | 0,04912 |
| 538,90998 | 0,03442 | 0,03962 | 0,0464 | 0,0442 | 0,04843 |
| 538,94716 | 0,03416 | 0,03931 | 0,04615 | 0,04355 | 0,04769 |
| 538,98434 | 0,03386 | 0,03895 | 0,04587 | 0,04288 | 0,04691 |
| 539,02153 | 0,03353 | 0,03854 | 0,04554 | 0,04219 | 0,04608 |
| 539,05871 | 0,03317 | 0,03809 | 0,04517 | 0,0415 | 0,04522 |
| 539,09589 | 0,03277 | 0,0376 | 0,04475 | 0,0408 | 0,04433 |
| 539,13307 | 0,03235 | 0,03708 | 0,0443 | 0,0401 | 0,04341 |
| 539,17025 | 0,0319 | 0,03653 | 0,04381 | 0,0394 | 0,04248 |
| 539,20744 | 0,03143 | 0,03595 | 0,04329 | 0,0387 | 0,04154 |
| 539,24462 | 0,03094 | 0,03534 | 0,04275 | 0,03801 | 0,04059 |
| 539,2818 | 0,03044 | 0,03471 | 0,04219 | 0,03733 | 0,03964 |
| 539,31898 | 0,02993 | 0,03407 | 0,0416 | 0,03666 | 0,03869 |
| 539,35616 | 0,02942 | 0,03342 | 0,041 | 0,036 | 0,03775 |
| 539,39335 | 0,02891 | 0,03277 | 0,04038 | 0,03534 | 0,03682 |
| 539,43053 | 0,02839 | 0,03211 | 0,03976 | 0,0347 | 0,0359 |
| 539,46771 | 0,02789 | 0,03146 | 0,03914 | 0,03406 | 0,03499 |
| 539,50489 | 0,02739 | 0,03081 | 0,03851 | 0,03343 | 0,0341 |
| 539,54207 | 0,0269 | 0,03016 | 0,03788 | 0,0328 | 0,03323 |
| 539,57926 | 0,02642 | 0,02953 | 0,03724 | 0,03217 | 0,03237 |
| 539,61644 | 0,02595 | 0,02891 | 0,03661 | 0,03154 | 0,03152 |
| 539,65362 | 0,0255 | 0,0283 | 0,03598 | 0,03091 | 0,03069 |
| 539,6908 | 0,02505 | 0,0277 | 0,03535 | 0,03027 | 0,02987 |
| 539,72798 | 0,02462 | 0,02712 | 0,03472 | 0,02963 | 0,02907 |
| 539,76517 | 0,02419 | 0,02654 | 0,03408 | 0,02897 | 0,02828 |
| 539,80235 | 0,02377 | 0,02597 | 0,03344 | 0,0283 | 0,02751 |
| 539,83953 | 0,02335 | 0,02541 | 0,0328 | 0,02762 | 0,02674 |
| 539,87671 | 0,02294 | 0,02486 | 0,03215 | 0,02693 | 0,02599 |
| 539,91389 | 0,02252 | 0,02432 | 0,03149 | 0,02622 | 0,02525 |
| 539,95108 | 0,0221 | 0,02377 | 0,03083 | 0,02551 | 0,02452 |
| 539,98826 | 0,02168 | 0,02323 | 0,03015 | 0,02478 | 0,0238 |
| 540,02544 | 0,02125 | 0,02269 | 0,02946 | 0,02404 | 0,02309 |
| 540,06262 | 0,02081 | 0,02215 | 0,02876 | 0,02329 | 0,0224 |
| 540,0998 | 0,02037 | 0,0216 | 0,02804 | 0,02254 | 0,02173 |
| 540,13699 | 0,01992 | 0,02106 | 0,02732 | 0,02179 | 0,02106 |
| 540,17417 | 0,01945 | 0,02051 | 0,02658 | 0,02103 | 0,02042 |
| 540,21135 | 0,01898 | 0,01996 | 0,02583 | 0,02028 | 0,01979 |
| 540,24853 | 0,0185 | 0,01941 | 0,02507 | 0,01953 | 0,01918 |
| 540,28571 | 0,01802 | 0,01886 | 0,02431 | 0,01879 | 0,01858 |
| 540,3229 | 0,01753 | 0,01831 | 0,02354 | 0,01806 | 0,01801 |
| 540,36008 | 0,01704 | 0,01776 | 0,02277 | 0,01734 | 0,01746 |
| 540,39726 | 0,01654 | 0,01721 | 0,022 | 0,01664 | 0,01692 |
| 540,43444 | 0,01605 | 0,01667 | 0,02123 | 0,01595 | 0,01641 |
| 540,47162 | 0,01556 | 0,01614 | 0,02047 | 0,01528 | 0,01591 |
| 540,50881 | 0,01508 | 0,01561 | 0,01972 | 0,01462 | 0,01542 |
| 540,54599 | 0,01461 | 0,0151 | 0,01898 | 0,01398 | 0,01496 |
| 540,58317 | 0,01415 | 0,01459 | 0,01825 | 0,01336 | 0,01451 |
| 540,62035 | 0,01369 | 0,0141 | 0,01754 | 0,01276 | 0,01407 |
| 540,65753 | 0,01326 | 0,01362 | 0,01685 | 0,01218 | 0,01364 |
| 540,69472 | 0,01283 | 0,01316 | 0,01618 | 0,01161 | 0,01322 |
| 540,7319 | 0,01242 | 0,01271 | 0,01553 | 0,01106 | 0,01282 |
| 540,76908 | 0,01203 | 0,01228 | 0,01491 | 0,01053 | 0,01241 |
| 540,80626 | 0,01165 | 0,01186 | 0,01431 | 0,01001 | 0,01202 |
| 540,84344 | 0,01129 | 0,01146 | 0,01372 | 0,00951 | 0,01162 |
| 540,88063 | 0,01094 | 0,01107 | 0,01316 | 0,00902 | 0,01123 |
| 540,91781 | 0,0106 | 0,01069 | 0,01263 | 0,00854 | 0,01084 |
| 540,95499 | 0,01027 | 0,01032 | 0,01212 | 0,00808 | 0,01045 |
| 540,99217 | 0,00996 | 0,00996 | 0,01162 | 0,00763 | 0,01006 |
| 541,02935 | 0,00965 | 0,00962 | 0,01115 | 0,00719 | 0,00967 |
| 541,06654 | 0,00935 | 0,00928 | 0,01069 | 0,00676 | 0,00928 |
| 541,10372 | 0,00905 | 0,00895 | 0,01024 | 0,00635 | 0,00889 |
| 541,1409 | 0,00876 | 0,00862 | 0,00982 | 0,00595 | 0,0085 |
| 541,17808 | 0,00847 | 0,0083 | 0,0094 | 0,00556 | 0,00811 |
| 541,21526 | 0,00818 | 0,00798 | 0,00899 | 0,00519 | 0,00772 |
| 541,25245 | 0,00789 | 0,00767 | 0,0086 | 0,00483 | 0,00733 |
| 541,28963 | 0,0076 | 0,00735 | 0,00821 | 0,00449 | 0,00694 |
| 541,32681 | 0,00731 | 0,00704 | 0,00783 | 0,00416 | 0,00656 |
| 541,36399 | 0,00701 | 0,00673 | 0,00746 | 0,00384 | 0,00619 |
| 541,40117 | 0,00671 | 0,00642 | 0,0071 | 0,00354 | 0,00582 |
| 541,43836 | 0,00641 | 0,00611 | 0,00674 | 0,00326 | 0,00546 |
| 541,47554 | 0,00611 | 0,0058 | 0,00638 | 0,00299 | 0,00511 |
| 541,51272 | 0,00581 | 0,00549 | 0,00603 | 0,00274 | 0,00477 |
| 541,5499 | 0,00551 | 0,00519 | 0,00569 | 0,00251 | 0,00444 |
| 541,58708 | 0,0052 | 0,00489 | 0,00535 | 0,00229 | 0,00412 |
| 541,62427 | 0,0049 | 0,0046 | 0,00502 | 0,00209 | 0,00382 |
| 541,66145 | 0,0046 | 0,00431 | 0,0047 | 0,0019 | 0,00352 |
| 541,69863 | 0,00431 | 0,00403 | 0,00439 | 0,00173 | 0,00324 |
| 541,73581 | 0,00402 | 0,00376 | 0,00408 | 0,00157 | 0,00297 |
| 541,77299 | 0,00374 | 0,00349 | 0,00379 | 0,00143 | 0,00272 |
| 541,81018 | 0,00346 | 0,00323 | 0,0035 | 0,0013 | 0,00249 |
| 541,84736 | 0,0032 | 0,00298 | 0,00323 | 0,00118 | 0,00226 |
| 541,88454 | 0,00294 | 0,00275 | 0,00296 | 0,00107 | 0,00205 |
| 541,92172 | 0,0027 | 0,00252 | 0,00271 | 0,00097 | 0,00185 |
| 541,9589 | 0,00246 | 0,00231 | 0,00248 | 0,00089 | 0,00167 |
| 541,99609 | 0,00224 | 0,00211 | 0,00225 | 0,00081 | 0,0015 |
| 542,03327 | 0,00203 | 0,00192 | 0,00204 | 0,00074 | 0,00135 |
| 542,07045 | 0,00184 | 0,00174 | 0,00184 | 0,00067 | 0,0012 |
| 542,10763 | 0,00165 | 0,00158 | 0,00166 | 0,00062 | 0,00107 |
| 542,14481 | 0,00148 | 0,00143 | 0,00148 | 0,00057 | 0,00095 |
| 542,182 | 0,00132 | 0,00129 | 0,00133 | 0,00052 | 0,00084 |
| 542,21918 | 0,00118 | 0,00116 | 0,00118 | 0,00048 | 0,00074 |
| 542,25636 | 0,00104 | 0,00104 | 0,00104 | 0,00044 | 0,00065 |
| 542,29354 | 0,00092 | 0,00093 | 0,00092 | 0,00041 | 0,00057 |
| 542,33072 | 0,00081 | 0,00084 | 0,00081 | 0,00038 | 5e-04 |
| 542,36791 | 0,00071 | 0,00075 | 0,00071 | 0,00035 | 0,00044 |
| 542,40509 | 0,00062 | 0,00067 | 0,00062 | 0,00033 | 0,00038 |
| 542,44227 | 0,00054 | 6e-04 | 0,00054 | 3e-04 | 0,00033 |
| 542,47945 | 0,00047 | 0,00054 | 0,00047 | 0,00028 | 0,00028 |
| 542,51663 | 0,00041 | 0,00048 | 4e-04 | 0,00026 | 0,00024 |
| 542,55382 | 0,00035 | 0,00043 | 0,00035 | 0,00024 | 0,00021 |
| 542,591 | 3e-04 | 0,00039 | 3e-04 | 0,00022 | 0,00018 |
| 542,62818 | 0,00026 | 0,00035 | 0,00025 | 2e-04 | 0,00015 |
| 542,66536 | 0,00022 | 0,00032 | 0,00022 | 0,00019 | 0,00013 |
| 542,70254 | 0,00019 | 0,00029 | 0,00018 | 0,00017 | 0,00011 |
| 542,73973 | 0,00016 | 0,00026 | 0,00016 | 0,00016 | 9e-05 |
| 542,77691 | 0,00013 | 0,00024 | 0,00013 | 0,00014 | 8e-05 |
| 542,81409 | 0,00011 | 0,00022 | 0,00011 | 0,00013 | 6e-05 |
| 542,85127 | 9e-05 | 2e-04 | 9e-05 | 0,00012 | 5e-05 |
| 542,88845 | 8e-05 | 0,00018 | 8e-05 | 0,00011 | 4e-05 |
| 542,92564 | 6e-05 | 0,00017 | 6e-05 | 1e-04 | 4e-05 |
| 542,96282 | 5e-05 | 0,00015 | 5e-05 | 9e-05 | 3e-05 |
| 543 | 4e-05 | 0,00014 | 4e-05 | 8e-05 | 2e-05 |
Uit de figuren 3.2.1 tot en met 3.2.18 kunnen we aflezen dat de verdeling van de onderwijsscores over de schooljaren heen stabiel is voor alle opleidingsniveaus van de ouders. Na oktober 2021 verschillen met name bij opleidingsniveaus van de moeders met de voorgaande jaren. Deze verschillen zitten vooral in de positie van de pieken, maar deze verschillen zijn relatief klein. Dit is een gevolg van de herijking van het model in 2022 zoals beschreven in de inleiding: in het herijkte model hebben onder andere de opleidingsniveaus van de moeders andere effecten op de onderwijsscores. De verschillen in de frequentiedichtheid tussen de moeders en vaders zijn een gevolg van het verschil in bijdrage aan de onderwijsscore voor de betreffende opleidingsniveaus van de moeders en vaders, zoals te zien is in figuren 1.1.1 en 1.1.2 weergegeven.
Verblijfsduur van de moeder
De figuren 3.2.19 tot en met 3.2.21 geven de frequentiedichtheid weer van de onderwijsscore per verblijfsduur van de moeder van het kind uitgesplitst naar schooljaar.
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 2e-05 | 5e-05 | 2e-05 | 0 | 0 |
| 524,03718 | 3e-05 | 5e-05 | 2e-05 | 0 | 0 |
| 524,07436 | 3e-05 | 6e-05 | 2e-05 | 0 | 0 |
| 524,11155 | 4e-05 | 7e-05 | 3e-05 | 0 | 0 |
| 524,14873 | 5e-05 | 8e-05 | 3e-05 | 0 | 0 |
| 524,18591 | 5e-05 | 8e-05 | 4e-05 | 0 | 0 |
| 524,22309 | 6e-05 | 9e-05 | 4e-05 | 0 | 0 |
| 524,26027 | 7e-05 | 1e-04 | 5e-05 | 0 | 0 |
| 524,29746 | 8e-05 | 0,00012 | 5e-05 | 0 | 1e-05 |
| 524,33464 | 1e-04 | 0,00013 | 6e-05 | 1e-05 | 1e-05 |
| 524,37182 | 0,00011 | 0,00014 | 7e-05 | 1e-05 | 1e-05 |
| 524,409 | 0,00013 | 0,00015 | 8e-05 | 1e-05 | 1e-05 |
| 524,44618 | 0,00014 | 0,00017 | 9e-05 | 1e-05 | 1e-05 |
| 524,48337 | 0,00017 | 0,00019 | 1e-04 | 1e-05 | 1e-05 |
| 524,52055 | 0,00019 | 2e-04 | 0,00011 | 1e-05 | 1e-05 |
| 524,55773 | 0,00022 | 0,00022 | 0,00012 | 1e-05 | 2e-05 |
| 524,59491 | 0,00024 | 0,00024 | 0,00014 | 2e-05 | 2e-05 |
| 524,63209 | 0,00028 | 0,00026 | 0,00016 | 2e-05 | 2e-05 |
| 524,66928 | 0,00031 | 0,00029 | 0,00017 | 2e-05 | 3e-05 |
| 524,70646 | 0,00035 | 0,00031 | 0,00019 | 3e-05 | 3e-05 |
| 524,74364 | 4e-04 | 0,00034 | 0,00021 | 3e-05 | 3e-05 |
| 524,78082 | 0,00045 | 0,00036 | 0,00024 | 4e-05 | 4e-05 |
| 524,818 | 5e-04 | 0,00039 | 0,00026 | 4e-05 | 4e-05 |
| 524,85519 | 0,00056 | 0,00042 | 0,00029 | 5e-05 | 5e-05 |
| 524,89237 | 0,00062 | 0,00046 | 0,00032 | 6e-05 | 6e-05 |
| 524,92955 | 0,00069 | 0,00049 | 0,00035 | 6e-05 | 7e-05 |
| 524,96673 | 0,00077 | 0,00053 | 0,00039 | 7e-05 | 7e-05 |
| 525,00391 | 0,00085 | 0,00057 | 0,00043 | 8e-05 | 8e-05 |
| 525,0411 | 0,00094 | 0,00061 | 0,00047 | 1e-04 | 9e-05 |
| 525,07828 | 0,00104 | 0,00066 | 0,00051 | 0,00011 | 0,00011 |
| 525,11546 | 0,00114 | 7e-04 | 0,00056 | 0,00012 | 0,00012 |
| 525,15264 | 0,00125 | 0,00075 | 0,00061 | 0,00014 | 0,00013 |
| 525,18982 | 0,00137 | 0,00081 | 0,00066 | 0,00016 | 0,00015 |
| 525,22701 | 0,0015 | 0,00086 | 0,00072 | 0,00018 | 0,00017 |
| 525,26419 | 0,00164 | 0,00092 | 0,00078 | 2e-04 | 0,00019 |
| 525,30137 | 0,00178 | 0,00099 | 0,00084 | 0,00022 | 0,00021 |
| 525,33855 | 0,00194 | 0,00106 | 0,00091 | 0,00025 | 0,00023 |
| 525,37573 | 0,0021 | 0,00113 | 0,00098 | 0,00028 | 0,00025 |
| 525,41292 | 0,00227 | 0,0012 | 0,00106 | 0,00031 | 0,00028 |
| 525,4501 | 0,00246 | 0,00129 | 0,00114 | 0,00034 | 0,00031 |
| 525,48728 | 0,00265 | 0,00137 | 0,00123 | 0,00038 | 0,00034 |
| 525,52446 | 0,00285 | 0,00146 | 0,00132 | 0,00042 | 0,00037 |
| 525,56164 | 0,00306 | 0,00156 | 0,00141 | 0,00046 | 0,00041 |
| 525,59883 | 0,00328 | 0,00166 | 0,00151 | 0,00051 | 0,00044 |
| 525,63601 | 0,00351 | 0,00177 | 0,00162 | 0,00056 | 0,00048 |
| 525,67319 | 0,00375 | 0,00189 | 0,00173 | 0,00061 | 0,00053 |
| 525,71037 | 0,004 | 0,00201 | 0,00185 | 0,00067 | 0,00057 |
| 525,74755 | 0,00426 | 0,00214 | 0,00197 | 0,00073 | 0,00062 |
| 525,78474 | 0,00453 | 0,00227 | 0,0021 | 0,00079 | 0,00067 |
| 525,82192 | 0,00481 | 0,00242 | 0,00223 | 0,00086 | 0,00073 |
| 525,8591 | 0,0051 | 0,00257 | 0,00237 | 0,00093 | 0,00078 |
| 525,89628 | 0,0054 | 0,00273 | 0,00252 | 0,00101 | 0,00085 |
| 525,93346 | 0,00571 | 0,0029 | 0,00268 | 0,00109 | 0,00091 |
| 525,97065 | 0,00602 | 0,00308 | 0,00284 | 0,00118 | 0,00098 |
| 526,00783 | 0,00635 | 0,00327 | 0,00301 | 0,00127 | 0,00105 |
| 526,04501 | 0,00668 | 0,00346 | 0,00319 | 0,00136 | 0,00112 |
| 526,08219 | 0,00703 | 0,00367 | 0,00338 | 0,00147 | 0,0012 |
| 526,11937 | 0,00739 | 0,00389 | 0,00358 | 0,00157 | 0,00129 |
| 526,15656 | 0,00775 | 0,00412 | 0,00378 | 0,00168 | 0,00137 |
| 526,19374 | 0,00812 | 0,00436 | 0,004 | 0,0018 | 0,00146 |
| 526,23092 | 0,0085 | 0,00461 | 0,00423 | 0,00192 | 0,00156 |
| 526,2681 | 0,0089 | 0,00487 | 0,00447 | 0,00205 | 0,00166 |
| 526,30528 | 0,0093 | 0,00515 | 0,00472 | 0,00218 | 0,00176 |
| 526,34247 | 0,00972 | 0,00544 | 0,00499 | 0,00232 | 0,00187 |
| 526,37965 | 0,01014 | 0,00573 | 0,00527 | 0,00247 | 0,00199 |
| 526,41683 | 0,01057 | 0,00605 | 0,00556 | 0,00262 | 0,00211 |
| 526,45401 | 0,01102 | 0,00637 | 0,00587 | 0,00278 | 0,00224 |
| 526,49119 | 0,01148 | 0,00671 | 0,00619 | 0,00295 | 0,00237 |
| 526,52838 | 0,01195 | 0,00706 | 0,00653 | 0,00312 | 0,00251 |
| 526,56556 | 0,01243 | 0,00743 | 0,00688 | 0,0033 | 0,00265 |
| 526,60274 | 0,01292 | 0,00781 | 0,00725 | 0,00349 | 0,0028 |
| 526,63992 | 0,01343 | 0,00821 | 0,00764 | 0,00369 | 0,00296 |
| 526,6771 | 0,01395 | 0,00862 | 0,00805 | 0,00389 | 0,00313 |
| 526,71429 | 0,01449 | 0,00905 | 0,00847 | 0,00411 | 0,0033 |
| 526,75147 | 0,01504 | 0,00949 | 0,00892 | 0,00433 | 0,00348 |
| 526,78865 | 0,0156 | 0,00995 | 0,00938 | 0,00456 | 0,00367 |
| 526,82583 | 0,01618 | 0,01042 | 0,00987 | 0,00481 | 0,00387 |
| 526,86301 | 0,01678 | 0,01091 | 0,01037 | 0,00506 | 0,00407 |
| 526,9002 | 0,01739 | 0,01142 | 0,01089 | 0,00533 | 0,00429 |
| 526,93738 | 0,01802 | 0,01195 | 0,01144 | 0,0056 | 0,00452 |
| 526,97456 | 0,01866 | 0,01249 | 0,012 | 0,00589 | 0,00475 |
| 527,01174 | 0,01932 | 0,01305 | 0,01259 | 0,00619 | 0,005 |
| 527,04892 | 0,02 | 0,01362 | 0,01319 | 0,0065 | 0,00526 |
| 527,08611 | 0,0207 | 0,01422 | 0,01381 | 0,00682 | 0,00553 |
| 527,12329 | 0,0214 | 0,01483 | 0,01445 | 0,00716 | 0,00581 |
| 527,16047 | 0,02213 | 0,01546 | 0,01511 | 0,00751 | 0,0061 |
| 527,19765 | 0,02287 | 0,01611 | 0,01578 | 0,00788 | 0,00641 |
| 527,23483 | 0,02362 | 0,01677 | 0,01648 | 0,00826 | 0,00673 |
| 527,27202 | 0,02439 | 0,01745 | 0,01718 | 0,00865 | 0,00706 |
| 527,3092 | 0,02517 | 0,01815 | 0,01791 | 0,00906 | 0,00741 |
| 527,34638 | 0,02596 | 0,01886 | 0,01864 | 0,00949 | 0,00777 |
| 527,38356 | 0,02677 | 0,01958 | 0,01939 | 0,00993 | 0,00814 |
| 527,42074 | 0,02759 | 0,02033 | 0,02015 | 0,01039 | 0,00853 |
| 527,45793 | 0,02841 | 0,02108 | 0,02092 | 0,01086 | 0,00894 |
| 527,49511 | 0,02924 | 0,02185 | 0,0217 | 0,01134 | 0,00936 |
| 527,53229 | 0,03008 | 0,02262 | 0,02248 | 0,01185 | 0,00979 |
| 527,56947 | 0,03092 | 0,02341 | 0,02327 | 0,01236 | 0,01024 |
| 527,60665 | 0,03177 | 0,02421 | 0,02406 | 0,01289 | 0,01071 |
| 527,64384 | 0,03262 | 0,02502 | 0,02486 | 0,01344 | 0,01119 |
| 527,68102 | 0,03347 | 0,02583 | 0,02566 | 0,014 | 0,01169 |
| 527,7182 | 0,03432 | 0,02665 | 0,02645 | 0,01458 | 0,01221 |
| 527,75538 | 0,03516 | 0,02747 | 0,02725 | 0,01516 | 0,01274 |
| 527,79256 | 0,036 | 0,02829 | 0,02804 | 0,01577 | 0,01329 |
| 527,82975 | 0,03684 | 0,02912 | 0,02883 | 0,01638 | 0,01385 |
| 527,86693 | 0,03767 | 0,02994 | 0,02961 | 0,01701 | 0,01443 |
| 527,90411 | 0,03848 | 0,03076 | 0,03039 | 0,01764 | 0,01502 |
| 527,94129 | 0,03929 | 0,03158 | 0,03116 | 0,01829 | 0,01563 |
| 527,97847 | 0,04009 | 0,03239 | 0,03192 | 0,01895 | 0,01626 |
| 528,01566 | 0,04088 | 0,0332 | 0,03267 | 0,01962 | 0,01689 |
| 528,05284 | 0,04165 | 0,03399 | 0,03341 | 0,0203 | 0,01754 |
| 528,09002 | 0,0424 | 0,03478 | 0,03414 | 0,02098 | 0,01821 |
| 528,1272 | 0,04314 | 0,03555 | 0,03486 | 0,02167 | 0,01889 |
| 528,16438 | 0,04387 | 0,03631 | 0,03556 | 0,02237 | 0,01958 |
| 528,20157 | 0,04457 | 0,03706 | 0,03626 | 0,02307 | 0,02028 |
| 528,23875 | 0,04526 | 0,03779 | 0,03694 | 0,02378 | 0,021 |
| 528,27593 | 0,04594 | 0,0385 | 0,03761 | 0,0245 | 0,02172 |
| 528,31311 | 0,04659 | 0,0392 | 0,03827 | 0,02521 | 0,02246 |
| 528,35029 | 0,04722 | 0,03988 | 0,03892 | 0,02593 | 0,0232 |
| 528,38748 | 0,04784 | 0,04054 | 0,03955 | 0,02666 | 0,02395 |
| 528,42466 | 0,04843 | 0,04118 | 0,04018 | 0,02738 | 0,02471 |
| 528,46184 | 0,04901 | 0,0418 | 0,04079 | 0,02811 | 0,02547 |
| 528,49902 | 0,04957 | 0,0424 | 0,04139 | 0,02884 | 0,02624 |
| 528,5362 | 0,0501 | 0,04299 | 0,04198 | 0,02956 | 0,02701 |
| 528,57339 | 0,05062 | 0,04355 | 0,04256 | 0,03029 | 0,02778 |
| 528,61057 | 0,05112 | 0,04408 | 0,04313 | 0,03102 | 0,02856 |
| 528,64775 | 0,05161 | 0,0446 | 0,04369 | 0,03174 | 0,02934 |
| 528,68493 | 0,05207 | 0,04511 | 0,04424 | 0,03246 | 0,03012 |
| 528,72211 | 0,05252 | 0,04559 | 0,04478 | 0,03319 | 0,03089 |
| 528,7593 | 0,05295 | 0,04605 | 0,04531 | 0,03391 | 0,03167 |
| 528,79648 | 0,05336 | 0,04649 | 0,04583 | 0,03462 | 0,03244 |
| 528,83366 | 0,05376 | 0,04692 | 0,04634 | 0,03534 | 0,03321 |
| 528,87084 | 0,05413 | 0,04733 | 0,04685 | 0,03605 | 0,03397 |
| 528,90802 | 0,0545 | 0,04772 | 0,04735 | 0,03675 | 0,03473 |
| 528,94521 | 0,05484 | 0,0481 | 0,04784 | 0,03745 | 0,03548 |
| 528,98239 | 0,05518 | 0,04847 | 0,04832 | 0,03815 | 0,03623 |
| 529,01957 | 0,05549 | 0,04882 | 0,04879 | 0,03885 | 0,03696 |
| 529,05675 | 0,05579 | 0,04916 | 0,04926 | 0,03953 | 0,03769 |
| 529,09393 | 0,05608 | 0,04949 | 0,04971 | 0,04022 | 0,03841 |
| 529,13112 | 0,05635 | 0,04981 | 0,05016 | 0,04089 | 0,03911 |
| 529,1683 | 0,05661 | 0,05013 | 0,0506 | 0,04157 | 0,03981 |
| 529,20548 | 0,05685 | 0,05044 | 0,05103 | 0,04223 | 0,04049 |
| 529,24266 | 0,05708 | 0,05074 | 0,05146 | 0,04289 | 0,04117 |
| 529,27984 | 0,0573 | 0,05103 | 0,05187 | 0,04354 | 0,04182 |
| 529,31703 | 0,0575 | 0,05132 | 0,05228 | 0,04418 | 0,04247 |
| 529,35421 | 0,05769 | 0,05161 | 0,05268 | 0,04482 | 0,0431 |
| 529,39139 | 0,05786 | 0,0519 | 0,05307 | 0,04545 | 0,04372 |
| 529,42857 | 0,05803 | 0,05219 | 0,05346 | 0,04607 | 0,04433 |
| 529,46575 | 0,05818 | 0,05248 | 0,05383 | 0,04668 | 0,04492 |
| 529,50294 | 0,05833 | 0,05277 | 0,0542 | 0,04728 | 0,0455 |
| 529,54012 | 0,05846 | 0,05306 | 0,05456 | 0,04788 | 0,04606 |
| 529,5773 | 0,05858 | 0,05335 | 0,05492 | 0,04847 | 0,04661 |
| 529,61448 | 0,0587 | 0,05365 | 0,05527 | 0,04904 | 0,04714 |
| 529,65166 | 0,0588 | 0,05395 | 0,05561 | 0,04962 | 0,04766 |
| 529,68885 | 0,0589 | 0,05425 | 0,05595 | 0,05017 | 0,04817 |
| 529,72603 | 0,05899 | 0,05456 | 0,05629 | 0,05073 | 0,04866 |
| 529,76321 | 0,05908 | 0,05488 | 0,05662 | 0,05127 | 0,04914 |
| 529,80039 | 0,05916 | 0,0552 | 0,05695 | 0,0518 | 0,0496 |
| 529,83757 | 0,05924 | 0,05552 | 0,05728 | 0,05233 | 0,05004 |
| 529,87476 | 0,05931 | 0,05585 | 0,0576 | 0,05285 | 0,05048 |
| 529,91194 | 0,05938 | 0,05618 | 0,05792 | 0,05335 | 0,0509 |
| 529,94912 | 0,05946 | 0,05652 | 0,05824 | 0,05385 | 0,0513 |
| 529,9863 | 0,05953 | 0,05687 | 0,05856 | 0,05435 | 0,05169 |
| 530,02348 | 0,0596 | 0,05721 | 0,05889 | 0,05483 | 0,05207 |
| 530,06067 | 0,05968 | 0,05756 | 0,05921 | 0,05531 | 0,05244 |
| 530,09785 | 0,05975 | 0,05792 | 0,05953 | 0,05578 | 0,0528 |
| 530,13503 | 0,05984 | 0,05828 | 0,05985 | 0,05624 | 0,05314 |
| 530,17221 | 0,05992 | 0,05864 | 0,06018 | 0,0567 | 0,05347 |
| 530,20939 | 0,06001 | 0,059 | 0,06051 | 0,05715 | 0,05379 |
| 530,24658 | 0,06011 | 0,05936 | 0,06084 | 0,05759 | 0,0541 |
| 530,28376 | 0,06022 | 0,05972 | 0,06116 | 0,05803 | 0,05439 |
| 530,32094 | 0,06033 | 0,06008 | 0,0615 | 0,05846 | 0,05468 |
| 530,35812 | 0,06045 | 0,06044 | 0,06183 | 0,05888 | 0,05495 |
| 530,3953 | 0,06058 | 0,0608 | 0,06216 | 0,0593 | 0,05522 |
| 530,43249 | 0,06071 | 0,06116 | 0,06249 | 0,05971 | 0,05548 |
| 530,46967 | 0,06086 | 0,06151 | 0,06282 | 0,06011 | 0,05573 |
| 530,50685 | 0,06101 | 0,06186 | 0,06315 | 0,06051 | 0,05598 |
| 530,54403 | 0,06117 | 0,06221 | 0,06348 | 0,0609 | 0,05622 |
| 530,58121 | 0,06134 | 0,06255 | 0,0638 | 0,06128 | 0,05645 |
| 530,6184 | 0,06153 | 0,06288 | 0,06412 | 0,06166 | 0,05667 |
| 530,65558 | 0,06172 | 0,06321 | 0,06444 | 0,06203 | 0,0569 |
| 530,69276 | 0,06191 | 0,06353 | 0,06475 | 0,06239 | 0,05711 |
| 530,72994 | 0,06212 | 0,06384 | 0,06506 | 0,06274 | 0,05733 |
| 530,76712 | 0,06233 | 0,06415 | 0,06536 | 0,06309 | 0,05754 |
| 530,80431 | 0,06256 | 0,06445 | 0,06565 | 0,06343 | 0,05775 |
| 530,84149 | 0,06278 | 0,06474 | 0,06594 | 0,06376 | 0,05796 |
| 530,87867 | 0,06302 | 0,06502 | 0,06621 | 0,06408 | 0,05817 |
| 530,91585 | 0,06326 | 0,06529 | 0,06648 | 0,06439 | 0,05839 |
| 530,95303 | 0,06351 | 0,06555 | 0,06674 | 0,0647 | 0,0586 |
| 530,99022 | 0,06376 | 0,06581 | 0,06698 | 0,065 | 0,05881 |
| 531,0274 | 0,06402 | 0,06605 | 0,06722 | 0,06529 | 0,05903 |
| 531,06458 | 0,06429 | 0,06629 | 0,06745 | 0,06557 | 0,05925 |
| 531,10176 | 0,06455 | 0,06651 | 0,06767 | 0,06584 | 0,05947 |
| 531,13894 | 0,06483 | 0,06672 | 0,06787 | 0,06611 | 0,0597 |
| 531,17613 | 0,0651 | 0,06693 | 0,06807 | 0,06636 | 0,05993 |
| 531,21331 | 0,06538 | 0,06712 | 0,06825 | 0,06661 | 0,06016 |
| 531,25049 | 0,06566 | 0,0673 | 0,06842 | 0,06686 | 0,0604 |
| 531,28767 | 0,06594 | 0,06747 | 0,06859 | 0,06709 | 0,06064 |
| 531,32485 | 0,06623 | 0,06764 | 0,06874 | 0,06732 | 0,06089 |
| 531,36204 | 0,06652 | 0,06779 | 0,06888 | 0,06754 | 0,06114 |
| 531,39922 | 0,06681 | 0,06793 | 0,06901 | 0,06776 | 0,0614 |
| 531,4364 | 0,0671 | 0,06806 | 0,06913 | 0,06797 | 0,06166 |
| 531,47358 | 0,06739 | 0,06818 | 0,06924 | 0,06818 | 0,06192 |
| 531,51076 | 0,06768 | 0,06829 | 0,06935 | 0,06838 | 0,06219 |
| 531,54795 | 0,06798 | 0,06838 | 0,06944 | 0,06858 | 0,06246 |
| 531,58513 | 0,06828 | 0,06847 | 0,06952 | 0,06877 | 0,06274 |
| 531,62231 | 0,06858 | 0,06855 | 0,0696 | 0,06897 | 0,06301 |
| 531,65949 | 0,06888 | 0,06862 | 0,06966 | 0,06916 | 0,06329 |
| 531,69667 | 0,06918 | 0,06869 | 0,06972 | 0,06934 | 0,06358 |
| 531,73386 | 0,06949 | 0,06874 | 0,06977 | 0,06953 | 0,06386 |
| 531,77104 | 0,0698 | 0,06879 | 0,06982 | 0,06971 | 0,06414 |
| 531,80822 | 0,07011 | 0,06883 | 0,06985 | 0,06989 | 0,06442 |
| 531,8454 | 0,07042 | 0,06886 | 0,06988 | 0,07007 | 0,06471 |
| 531,88258 | 0,07074 | 0,06889 | 0,0699 | 0,07025 | 0,06499 |
| 531,91977 | 0,07107 | 0,06892 | 0,06991 | 0,07043 | 0,06528 |
| 531,95695 | 0,07139 | 0,06895 | 0,06992 | 0,0706 | 0,06556 |
| 531,99413 | 0,07173 | 0,06897 | 0,06992 | 0,07078 | 0,06584 |
| 532,03131 | 0,07206 | 0,06899 | 0,06992 | 0,07095 | 0,06612 |
| 532,06849 | 0,07241 | 0,06902 | 0,06991 | 0,07112 | 0,0664 |
| 532,10568 | 0,07276 | 0,06904 | 0,0699 | 0,07128 | 0,06668 |
| 532,14286 | 0,07311 | 0,06907 | 0,06988 | 0,07145 | 0,06696 |
| 532,18004 | 0,07347 | 0,06911 | 0,06986 | 0,07161 | 0,06724 |
| 532,21722 | 0,07384 | 0,06916 | 0,06984 | 0,07176 | 0,06752 |
| 532,2544 | 0,07422 | 0,06921 | 0,06982 | 0,07191 | 0,0678 |
| 532,29159 | 0,07461 | 0,06927 | 0,06979 | 0,07205 | 0,06808 |
| 532,32877 | 0,075 | 0,06935 | 0,06977 | 0,07219 | 0,06836 |
| 532,36595 | 0,0754 | 0,06944 | 0,06974 | 0,07232 | 0,06864 |
| 532,40313 | 0,07581 | 0,06955 | 0,06972 | 0,07244 | 0,06893 |
| 532,44031 | 0,07623 | 0,06967 | 0,0697 | 0,07256 | 0,06921 |
| 532,4775 | 0,07666 | 0,0698 | 0,06968 | 0,07266 | 0,0695 |
| 532,51468 | 0,07709 | 0,06996 | 0,06967 | 0,07276 | 0,06978 |
| 532,55186 | 0,07754 | 0,07014 | 0,06966 | 0,07284 | 0,07007 |
| 532,58904 | 0,07799 | 0,07033 | 0,06965 | 0,07291 | 0,07036 |
| 532,62622 | 0,07845 | 0,07055 | 0,06965 | 0,07298 | 0,07066 |
| 532,66341 | 0,07891 | 0,07079 | 0,06966 | 0,07303 | 0,07096 |
| 532,70059 | 0,07938 | 0,07105 | 0,06968 | 0,07307 | 0,07125 |
| 532,73777 | 0,07986 | 0,07134 | 0,0697 | 0,0731 | 0,07156 |
| 532,77495 | 0,08034 | 0,07164 | 0,06973 | 0,07312 | 0,07186 |
| 532,81213 | 0,08083 | 0,07197 | 0,06977 | 0,07313 | 0,07216 |
| 532,84932 | 0,08131 | 0,07232 | 0,06982 | 0,07314 | 0,07247 |
| 532,8865 | 0,08181 | 0,07269 | 0,06988 | 0,07313 | 0,07277 |
| 532,92368 | 0,0823 | 0,07308 | 0,06995 | 0,07311 | 0,07308 |
| 532,96086 | 0,0828 | 0,07349 | 0,07003 | 0,07309 | 0,07339 |
| 532,99804 | 0,08329 | 0,07392 | 0,07012 | 0,07306 | 0,07369 |
| 533,03523 | 0,08379 | 0,07437 | 0,07022 | 0,07302 | 0,074 |
| 533,07241 | 0,08428 | 0,07483 | 0,07034 | 0,07299 | 0,0743 |
| 533,10959 | 0,08476 | 0,07531 | 0,07046 | 0,07295 | 0,0746 |
| 533,14677 | 0,08524 | 0,0758 | 0,07059 | 0,07291 | 0,0749 |
| 533,18395 | 0,08572 | 0,07631 | 0,07073 | 0,07287 | 0,07519 |
| 533,22114 | 0,08619 | 0,07682 | 0,07088 | 0,07284 | 0,07548 |
| 533,25832 | 0,08664 | 0,07734 | 0,07105 | 0,07281 | 0,07576 |
| 533,2955 | 0,08709 | 0,07787 | 0,07122 | 0,07279 | 0,07604 |
| 533,33268 | 0,08753 | 0,07841 | 0,0714 | 0,07277 | 0,07632 |
| 533,36986 | 0,08795 | 0,07895 | 0,0716 | 0,07277 | 0,07658 |
| 533,40705 | 0,08836 | 0,07949 | 0,07181 | 0,07278 | 0,07685 |
| 533,44423 | 0,08876 | 0,08003 | 0,07202 | 0,0728 | 0,0771 |
| 533,48141 | 0,08914 | 0,08057 | 0,07225 | 0,07283 | 0,07735 |
| 533,51859 | 0,0895 | 0,08111 | 0,07248 | 0,07289 | 0,0776 |
| 533,55577 | 0,08983 | 0,08165 | 0,07273 | 0,07296 | 0,07784 |
| 533,59295 | 0,09015 | 0,08218 | 0,07299 | 0,07305 | 0,07807 |
| 533,63014 | 0,09045 | 0,08271 | 0,07326 | 0,07316 | 0,0783 |
| 533,66732 | 0,09073 | 0,08322 | 0,07354 | 0,07328 | 0,07853 |
| 533,7045 | 0,09098 | 0,08373 | 0,07383 | 0,07343 | 0,07874 |
| 533,74168 | 0,09121 | 0,08423 | 0,07413 | 0,0736 | 0,07896 |
| 533,77886 | 0,09142 | 0,08472 | 0,07444 | 0,07379 | 0,07917 |
| 533,81605 | 0,0916 | 0,08521 | 0,07476 | 0,074 | 0,07938 |
| 533,85323 | 0,09175 | 0,08567 | 0,07509 | 0,07423 | 0,07959 |
| 533,89041 | 0,09188 | 0,08613 | 0,07544 | 0,07449 | 0,07979 |
| 533,92759 | 0,09198 | 0,08657 | 0,07579 | 0,07476 | 0,07999 |
| 533,96477 | 0,09206 | 0,087 | 0,07615 | 0,07504 | 0,08019 |
| 534,00196 | 0,09211 | 0,08742 | 0,07653 | 0,07535 | 0,0804 |
| 534,03914 | 0,09213 | 0,08782 | 0,07691 | 0,07567 | 0,0806 |
| 534,07632 | 0,09212 | 0,0882 | 0,0773 | 0,07601 | 0,0808 |
| 534,1135 | 0,09209 | 0,08857 | 0,07769 | 0,07636 | 0,081 |
| 534,15068 | 0,09203 | 0,08893 | 0,07809 | 0,07673 | 0,0812 |
| 534,18787 | 0,09195 | 0,08927 | 0,0785 | 0,0771 | 0,0814 |
| 534,22505 | 0,09184 | 0,08958 | 0,07891 | 0,07748 | 0,0816 |
| 534,26223 | 0,0917 | 0,08989 | 0,07932 | 0,07787 | 0,0818 |
| 534,29941 | 0,09155 | 0,09017 | 0,07974 | 0,07827 | 0,082 |
| 534,33659 | 0,09137 | 0,09044 | 0,08015 | 0,07867 | 0,0822 |
| 534,37378 | 0,09116 | 0,09068 | 0,08056 | 0,07907 | 0,08241 |
| 534,41096 | 0,09094 | 0,09091 | 0,08098 | 0,07947 | 0,08261 |
| 534,44814 | 0,0907 | 0,09112 | 0,08138 | 0,07987 | 0,08281 |
| 534,48532 | 0,09043 | 0,0913 | 0,08178 | 0,08027 | 0,08301 |
| 534,5225 | 0,09015 | 0,09147 | 0,08218 | 0,08066 | 0,08321 |
| 534,55969 | 0,08986 | 0,09161 | 0,08256 | 0,08105 | 0,08341 |
| 534,59687 | 0,08955 | 0,09174 | 0,08293 | 0,08142 | 0,0836 |
| 534,63405 | 0,08923 | 0,09184 | 0,0833 | 0,0818 | 0,0838 |
| 534,67123 | 0,08889 | 0,09192 | 0,08365 | 0,08216 | 0,08399 |
| 534,70841 | 0,08855 | 0,09198 | 0,08398 | 0,08251 | 0,08418 |
| 534,7456 | 0,0882 | 0,09202 | 0,0843 | 0,08284 | 0,08437 |
| 534,78278 | 0,08784 | 0,09205 | 0,08461 | 0,08317 | 0,08455 |
| 534,81996 | 0,08748 | 0,09205 | 0,0849 | 0,08348 | 0,08474 |
| 534,85714 | 0,08711 | 0,09203 | 0,08517 | 0,08378 | 0,08492 |
| 534,89432 | 0,08674 | 0,09199 | 0,08543 | 0,08406 | 0,0851 |
| 534,93151 | 0,08637 | 0,09193 | 0,08566 | 0,08433 | 0,08527 |
| 534,96869 | 0,086 | 0,09186 | 0,08589 | 0,08459 | 0,08544 |
| 535,00587 | 0,08563 | 0,09177 | 0,08609 | 0,08483 | 0,08562 |
| 535,04305 | 0,08526 | 0,09166 | 0,08627 | 0,08505 | 0,08579 |
| 535,08023 | 0,0849 | 0,09154 | 0,08643 | 0,08526 | 0,08596 |
| 535,11742 | 0,08454 | 0,09141 | 0,08658 | 0,08545 | 0,08613 |
| 535,1546 | 0,08419 | 0,09126 | 0,08672 | 0,08563 | 0,08629 |
| 535,19178 | 0,08385 | 0,0911 | 0,08683 | 0,0858 | 0,08646 |
| 535,22896 | 0,08351 | 0,09094 | 0,08693 | 0,08594 | 0,08663 |
| 535,26614 | 0,08318 | 0,09076 | 0,08702 | 0,08608 | 0,0868 |
| 535,30333 | 0,08285 | 0,09058 | 0,08709 | 0,08621 | 0,08697 |
| 535,34051 | 0,08254 | 0,09039 | 0,08715 | 0,08632 | 0,08714 |
| 535,37769 | 0,08223 | 0,09019 | 0,08719 | 0,08642 | 0,08731 |
| 535,41487 | 0,08193 | 0,08999 | 0,08723 | 0,08651 | 0,08748 |
| 535,45205 | 0,08164 | 0,08978 | 0,08726 | 0,08659 | 0,08765 |
| 535,48924 | 0,08135 | 0,08958 | 0,08728 | 0,08666 | 0,08783 |
| 535,52642 | 0,08107 | 0,08937 | 0,08728 | 0,08672 | 0,088 |
| 535,5636 | 0,0808 | 0,08916 | 0,08728 | 0,08677 | 0,08818 |
| 535,60078 | 0,08053 | 0,08894 | 0,08727 | 0,08682 | 0,08836 |
| 535,63796 | 0,08027 | 0,08873 | 0,08726 | 0,08686 | 0,08854 |
| 535,67515 | 0,08001 | 0,08852 | 0,08724 | 0,08689 | 0,08871 |
| 535,71233 | 0,07975 | 0,0883 | 0,08721 | 0,08691 | 0,08889 |
| 535,74951 | 0,07949 | 0,08809 | 0,08717 | 0,08693 | 0,08906 |
| 535,78669 | 0,07924 | 0,08787 | 0,08713 | 0,08695 | 0,08923 |
| 535,82387 | 0,07899 | 0,08766 | 0,08708 | 0,08696 | 0,08939 |
| 535,86106 | 0,07873 | 0,08744 | 0,08702 | 0,08696 | 0,08955 |
| 535,89824 | 0,07847 | 0,08722 | 0,08696 | 0,08697 | 0,0897 |
| 535,93542 | 0,07821 | 0,087 | 0,08688 | 0,08696 | 0,08985 |
| 535,9726 | 0,07795 | 0,08677 | 0,0868 | 0,08696 | 0,08998 |
| 536,00978 | 0,07768 | 0,08654 | 0,08671 | 0,08695 | 0,0901 |
| 536,04697 | 0,0774 | 0,08631 | 0,08661 | 0,08693 | 0,09022 |
| 536,08415 | 0,07712 | 0,08608 | 0,08649 | 0,08692 | 0,09031 |
| 536,12133 | 0,07683 | 0,08584 | 0,08637 | 0,08689 | 0,09039 |
| 536,15851 | 0,07654 | 0,08559 | 0,08623 | 0,08686 | 0,09046 |
| 536,19569 | 0,07623 | 0,08534 | 0,08607 | 0,08683 | 0,09051 |
| 536,23288 | 0,07592 | 0,08508 | 0,0859 | 0,08679 | 0,09054 |
| 536,27006 | 0,07561 | 0,08481 | 0,08572 | 0,08674 | 0,09054 |
| 536,30724 | 0,07528 | 0,08454 | 0,08552 | 0,08669 | 0,09053 |
| 536,34442 | 0,07495 | 0,08425 | 0,08531 | 0,08663 | 0,09049 |
| 536,3816 | 0,0746 | 0,08396 | 0,08507 | 0,08656 | 0,09044 |
| 536,41879 | 0,07426 | 0,08366 | 0,08482 | 0,08648 | 0,09036 |
| 536,45597 | 0,0739 | 0,08335 | 0,08456 | 0,08638 | 0,09025 |
| 536,49315 | 0,07354 | 0,08304 | 0,08427 | 0,08628 | 0,09011 |
| 536,53033 | 0,07317 | 0,08271 | 0,08397 | 0,08617 | 0,08996 |
| 536,56751 | 0,0728 | 0,08237 | 0,08365 | 0,08605 | 0,08978 |
| 536,6047 | 0,07243 | 0,08203 | 0,08331 | 0,08591 | 0,08957 |
| 536,64188 | 0,07205 | 0,08168 | 0,08296 | 0,08576 | 0,08934 |
| 536,67906 | 0,07167 | 0,08132 | 0,08259 | 0,08559 | 0,08909 |
| 536,71624 | 0,07128 | 0,08095 | 0,08221 | 0,08541 | 0,08882 |
| 536,75342 | 0,0709 | 0,08057 | 0,08181 | 0,08522 | 0,08852 |
| 536,79061 | 0,07052 | 0,08019 | 0,08141 | 0,08501 | 0,0882 |
| 536,82779 | 0,07014 | 0,0798 | 0,08099 | 0,08479 | 0,08786 |
| 536,86497 | 0,06976 | 0,07941 | 0,08056 | 0,08455 | 0,0875 |
| 536,90215 | 0,06939 | 0,07901 | 0,08012 | 0,0843 | 0,08713 |
| 536,93933 | 0,06902 | 0,0786 | 0,07968 | 0,08403 | 0,08674 |
| 536,97652 | 0,06865 | 0,0782 | 0,07923 | 0,08375 | 0,08633 |
| 537,0137 | 0,0683 | 0,07779 | 0,07877 | 0,08346 | 0,08591 |
| 537,05088 | 0,06794 | 0,07737 | 0,07832 | 0,08316 | 0,08549 |
| 537,08806 | 0,0676 | 0,07696 | 0,07786 | 0,08284 | 0,08505 |
| 537,12524 | 0,06727 | 0,07655 | 0,0774 | 0,08251 | 0,08461 |
| 537,16243 | 0,06695 | 0,07614 | 0,07695 | 0,08218 | 0,08416 |
| 537,19961 | 0,06663 | 0,07573 | 0,07651 | 0,08184 | 0,08371 |
| 537,23679 | 0,06633 | 0,07532 | 0,07607 | 0,08149 | 0,08326 |
| 537,27397 | 0,06605 | 0,07492 | 0,07563 | 0,08113 | 0,08281 |
| 537,31115 | 0,06577 | 0,07452 | 0,07521 | 0,08078 | 0,08237 |
| 537,34834 | 0,06551 | 0,07414 | 0,0748 | 0,08042 | 0,08192 |
| 537,38552 | 0,06525 | 0,07376 | 0,0744 | 0,08006 | 0,08149 |
| 537,4227 | 0,06502 | 0,07338 | 0,07401 | 0,07971 | 0,08106 |
| 537,45988 | 0,0648 | 0,07302 | 0,07364 | 0,07935 | 0,08065 |
| 537,49706 | 0,0646 | 0,07267 | 0,07328 | 0,07901 | 0,08025 |
| 537,53425 | 0,0644 | 0,07234 | 0,07295 | 0,07867 | 0,07986 |
| 537,57143 | 0,06423 | 0,07202 | 0,07263 | 0,07835 | 0,07948 |
| 537,60861 | 0,06407 | 0,07171 | 0,07232 | 0,07803 | 0,07913 |
| 537,64579 | 0,06393 | 0,07142 | 0,07204 | 0,07773 | 0,0788 |
| 537,68297 | 0,0638 | 0,07115 | 0,07179 | 0,07744 | 0,07848 |
| 537,72016 | 0,06369 | 0,0709 | 0,07155 | 0,07717 | 0,07819 |
| 537,75734 | 0,0636 | 0,07066 | 0,07133 | 0,07692 | 0,07792 |
| 537,79452 | 0,06352 | 0,07045 | 0,07114 | 0,07669 | 0,07768 |
| 537,8317 | 0,06346 | 0,07026 | 0,07097 | 0,07648 | 0,07747 |
| 537,86888 | 0,0634 | 0,07008 | 0,07083 | 0,07629 | 0,07728 |
| 537,90607 | 0,06337 | 0,06993 | 0,0707 | 0,07613 | 0,07712 |
| 537,94325 | 0,06335 | 0,0698 | 0,0706 | 0,07599 | 0,07698 |
| 537,98043 | 0,06334 | 0,06969 | 0,07053 | 0,07588 | 0,07689 |
| 538,01761 | 0,06335 | 0,06961 | 0,07048 | 0,07579 | 0,07682 |
| 538,05479 | 0,06336 | 0,06954 | 0,07045 | 0,07572 | 0,07677 |
| 538,09198 | 0,06339 | 0,06949 | 0,07044 | 0,07569 | 0,07676 |
| 538,12916 | 0,06343 | 0,06945 | 0,07045 | 0,07567 | 0,07679 |
| 538,16634 | 0,06347 | 0,06944 | 0,07049 | 0,07568 | 0,07684 |
| 538,20352 | 0,06352 | 0,06945 | 0,07054 | 0,07571 | 0,07693 |
| 538,2407 | 0,06358 | 0,06946 | 0,07061 | 0,07577 | 0,07704 |
| 538,27789 | 0,06364 | 0,06949 | 0,07069 | 0,07585 | 0,07718 |
| 538,31507 | 0,0637 | 0,06953 | 0,07079 | 0,07595 | 0,07735 |
| 538,35225 | 0,06376 | 0,06958 | 0,07091 | 0,07607 | 0,07755 |
| 538,38943 | 0,06383 | 0,06963 | 0,07103 | 0,07621 | 0,07778 |
| 538,42661 | 0,06389 | 0,06969 | 0,07116 | 0,07637 | 0,07802 |
| 538,4638 | 0,06394 | 0,06975 | 0,07131 | 0,07653 | 0,0783 |
| 538,50098 | 0,064 | 0,06981 | 0,07145 | 0,07672 | 0,07859 |
| 538,53816 | 0,06405 | 0,06987 | 0,0716 | 0,07691 | 0,0789 |
| 538,57534 | 0,06408 | 0,06992 | 0,07176 | 0,07711 | 0,07923 |
| 538,61252 | 0,06412 | 0,06997 | 0,07191 | 0,07733 | 0,07957 |
| 538,64971 | 0,06414 | 0,07001 | 0,07205 | 0,07754 | 0,07993 |
| 538,68689 | 0,06415 | 0,07003 | 0,0722 | 0,07776 | 0,08029 |
| 538,72407 | 0,06415 | 0,07005 | 0,07234 | 0,07798 | 0,08066 |
| 538,76125 | 0,06414 | 0,07005 | 0,07247 | 0,07821 | 0,08103 |
| 538,79843 | 0,06412 | 0,07004 | 0,07258 | 0,07843 | 0,08141 |
| 538,83562 | 0,06408 | 0,07001 | 0,07269 | 0,07865 | 0,08178 |
| 538,8728 | 0,06403 | 0,06997 | 0,07279 | 0,07886 | 0,08215 |
| 538,90998 | 0,06397 | 0,06991 | 0,07287 | 0,07907 | 0,08252 |
| 538,94716 | 0,0639 | 0,06984 | 0,07294 | 0,07927 | 0,08287 |
| 538,98434 | 0,06382 | 0,06974 | 0,073 | 0,07946 | 0,08322 |
| 539,02153 | 0,06373 | 0,06963 | 0,07304 | 0,07965 | 0,08355 |
| 539,05871 | 0,06362 | 0,06951 | 0,07306 | 0,07982 | 0,08386 |
| 539,09589 | 0,06351 | 0,06937 | 0,07307 | 0,07998 | 0,08416 |
| 539,13307 | 0,06339 | 0,06922 | 0,07306 | 0,08013 | 0,08444 |
| 539,17025 | 0,06327 | 0,06906 | 0,07304 | 0,08027 | 0,08469 |
| 539,20744 | 0,06314 | 0,06888 | 0,07301 | 0,0804 | 0,08492 |
| 539,24462 | 0,06301 | 0,0687 | 0,07296 | 0,08051 | 0,08513 |
| 539,2818 | 0,06287 | 0,06851 | 0,0729 | 0,08061 | 0,08532 |
| 539,31898 | 0,06274 | 0,06831 | 0,07283 | 0,0807 | 0,08548 |
| 539,35616 | 0,0626 | 0,06811 | 0,07275 | 0,08078 | 0,0856 |
| 539,39335 | 0,06247 | 0,0679 | 0,07265 | 0,08084 | 0,08571 |
| 539,43053 | 0,06234 | 0,0677 | 0,07255 | 0,0809 | 0,08579 |
| 539,46771 | 0,06222 | 0,06749 | 0,07245 | 0,08094 | 0,08584 |
| 539,50489 | 0,0621 | 0,06729 | 0,07233 | 0,08097 | 0,08586 |
| 539,54207 | 0,06199 | 0,06709 | 0,07221 | 0,08099 | 0,08585 |
| 539,57926 | 0,06189 | 0,0669 | 0,07209 | 0,08099 | 0,08582 |
| 539,61644 | 0,0618 | 0,06671 | 0,07197 | 0,08099 | 0,08576 |
| 539,65362 | 0,06171 | 0,06652 | 0,07184 | 0,08098 | 0,08568 |
| 539,6908 | 0,06165 | 0,06635 | 0,07172 | 0,08096 | 0,08557 |
| 539,72798 | 0,06159 | 0,06618 | 0,07159 | 0,08093 | 0,08544 |
| 539,76517 | 0,06154 | 0,06603 | 0,07147 | 0,08089 | 0,08528 |
| 539,80235 | 0,0615 | 0,06588 | 0,07135 | 0,08085 | 0,08511 |
| 539,83953 | 0,06148 | 0,06574 | 0,07124 | 0,08079 | 0,08492 |
| 539,87671 | 0,06147 | 0,06561 | 0,07113 | 0,08073 | 0,08471 |
| 539,91389 | 0,06147 | 0,06549 | 0,07102 | 0,08066 | 0,08448 |
| 539,95108 | 0,06148 | 0,06538 | 0,07092 | 0,08058 | 0,08424 |
| 539,98826 | 0,0615 | 0,06528 | 0,07082 | 0,0805 | 0,08399 |
| 540,02544 | 0,06153 | 0,06519 | 0,07073 | 0,08041 | 0,08372 |
| 540,06262 | 0,06157 | 0,06511 | 0,07064 | 0,08032 | 0,08344 |
| 540,0998 | 0,06162 | 0,06503 | 0,07056 | 0,08021 | 0,08316 |
| 540,13699 | 0,06167 | 0,06497 | 0,07048 | 0,08011 | 0,08286 |
| 540,17417 | 0,06173 | 0,0649 | 0,07041 | 0,07999 | 0,08256 |
| 540,21135 | 0,06179 | 0,06484 | 0,07034 | 0,07987 | 0,08226 |
| 540,24853 | 0,06186 | 0,06479 | 0,07027 | 0,07974 | 0,08194 |
| 540,28571 | 0,06192 | 0,06473 | 0,0702 | 0,0796 | 0,08163 |
| 540,3229 | 0,06198 | 0,06468 | 0,07013 | 0,07946 | 0,08131 |
| 540,36008 | 0,06204 | 0,06462 | 0,07006 | 0,0793 | 0,08099 |
| 540,39726 | 0,06209 | 0,06456 | 0,06998 | 0,07914 | 0,08066 |
| 540,43444 | 0,06213 | 0,0645 | 0,0699 | 0,07896 | 0,08032 |
| 540,47162 | 0,06216 | 0,06442 | 0,06981 | 0,07876 | 0,07998 |
| 540,50881 | 0,06218 | 0,06433 | 0,0697 | 0,07856 | 0,07963 |
| 540,54599 | 0,06217 | 0,06423 | 0,06959 | 0,07833 | 0,07927 |
| 540,58317 | 0,06215 | 0,06412 | 0,06945 | 0,07808 | 0,0789 |
| 540,62035 | 0,0621 | 0,06398 | 0,06929 | 0,0778 | 0,07852 |
| 540,65753 | 0,06201 | 0,06382 | 0,06911 | 0,0775 | 0,07811 |
| 540,69472 | 0,0619 | 0,06363 | 0,06889 | 0,07718 | 0,07768 |
| 540,7319 | 0,06176 | 0,06342 | 0,06865 | 0,07681 | 0,07723 |
| 540,76908 | 0,06158 | 0,06317 | 0,06836 | 0,0764 | 0,07675 |
| 540,80626 | 0,06135 | 0,06288 | 0,06804 | 0,07595 | 0,07624 |
| 540,84344 | 0,06107 | 0,06255 | 0,06767 | 0,07547 | 0,07569 |
| 540,88063 | 0,06075 | 0,06217 | 0,06725 | 0,07493 | 0,07509 |
| 540,91781 | 0,06038 | 0,06175 | 0,06678 | 0,07433 | 0,07444 |
| 540,95499 | 0,05995 | 0,06128 | 0,06625 | 0,07367 | 0,07375 |
| 540,99217 | 0,05946 | 0,06074 | 0,06566 | 0,07296 | 0,07301 |
| 541,02935 | 0,05891 | 0,06015 | 0,06501 | 0,07219 | 0,07219 |
| 541,06654 | 0,0583 | 0,0595 | 0,0643 | 0,07134 | 0,07131 |
| 541,10372 | 0,05763 | 0,05879 | 0,06351 | 0,07042 | 0,07037 |
| 541,1409 | 0,05689 | 0,05801 | 0,06265 | 0,06943 | 0,06937 |
| 541,17808 | 0,05608 | 0,05716 | 0,06172 | 0,06837 | 0,06829 |
| 541,21526 | 0,05521 | 0,05625 | 0,06074 | 0,06724 | 0,06712 |
| 541,25245 | 0,05428 | 0,05527 | 0,05966 | 0,06601 | 0,06589 |
| 541,28963 | 0,05327 | 0,05423 | 0,05852 | 0,06472 | 0,06458 |
| 541,32681 | 0,0522 | 0,05311 | 0,05731 | 0,06336 | 0,06321 |
| 541,36399 | 0,05107 | 0,05194 | 0,05604 | 0,06193 | 0,06175 |
| 541,40117 | 0,04989 | 0,0507 | 0,0547 | 0,06041 | 0,06022 |
| 541,43836 | 0,04864 | 0,04941 | 0,05329 | 0,05883 | 0,05862 |
| 541,47554 | 0,04734 | 0,04805 | 0,05182 | 0,05719 | 0,05697 |
| 541,51272 | 0,04599 | 0,04665 | 0,0503 | 0,05549 | 0,05525 |
| 541,5499 | 0,0446 | 0,0452 | 0,04874 | 0,05374 | 0,05347 |
| 541,58708 | 0,04317 | 0,04371 | 0,04713 | 0,05193 | 0,05164 |
| 541,62427 | 0,04169 | 0,04218 | 0,04547 | 0,05008 | 0,04977 |
| 541,66145 | 0,04019 | 0,04061 | 0,04379 | 0,04819 | 0,04787 |
| 541,69863 | 0,03866 | 0,03902 | 0,04208 | 0,04628 | 0,04593 |
| 541,73581 | 0,03712 | 0,03742 | 0,04036 | 0,04434 | 0,04397 |
| 541,77299 | 0,03556 | 0,0358 | 0,03861 | 0,04239 | 0,04201 |
| 541,81018 | 0,03399 | 0,03417 | 0,03686 | 0,04044 | 0,04003 |
| 541,84736 | 0,03242 | 0,03254 | 0,03512 | 0,03848 | 0,03806 |
| 541,88454 | 0,03086 | 0,03092 | 0,03337 | 0,03653 | 0,03609 |
| 541,92172 | 0,0293 | 0,0293 | 0,03165 | 0,0346 | 0,03415 |
| 541,9589 | 0,02777 | 0,02771 | 0,02994 | 0,03269 | 0,03223 |
| 541,99609 | 0,02625 | 0,02615 | 0,02826 | 0,03081 | 0,03033 |
| 542,03327 | 0,02476 | 0,02461 | 0,02661 | 0,02896 | 0,02848 |
| 542,07045 | 0,02329 | 0,0231 | 0,02499 | 0,02717 | 0,02668 |
| 542,10763 | 0,02187 | 0,02163 | 0,02342 | 0,02542 | 0,02493 |
| 542,14481 | 0,02049 | 0,02021 | 0,0219 | 0,02371 | 0,02322 |
| 542,182 | 0,01914 | 0,01883 | 0,02042 | 0,02207 | 0,02157 |
| 542,21918 | 0,01784 | 0,0175 | 0,01899 | 0,02048 | 0,02 |
| 542,25636 | 0,01659 | 0,01622 | 0,01762 | 0,01897 | 0,0185 |
| 542,29354 | 0,01539 | 0,015 | 0,01632 | 0,01752 | 0,01705 |
| 542,33072 | 0,01424 | 0,01384 | 0,01506 | 0,01613 | 0,01568 |
| 542,36791 | 0,01314 | 0,01273 | 0,01387 | 0,01481 | 0,01438 |
| 542,40509 | 0,0121 | 0,01168 | 0,01274 | 0,01358 | 0,01316 |
| 542,44227 | 0,01112 | 0,01068 | 0,01168 | 0,01241 | 0,01201 |
| 542,47945 | 0,01019 | 0,00976 | 0,01068 | 0,01131 | 0,01092 |
| 542,51663 | 0,00931 | 0,00888 | 0,00973 | 0,01028 | 0,0099 |
| 542,55382 | 0,00848 | 0,00806 | 0,00884 | 0,00932 | 0,00897 |
| 542,591 | 0,00772 | 0,00729 | 0,00803 | 0,00843 | 0,0081 |
| 542,62818 | 0,007 | 0,00659 | 0,00726 | 0,0076 | 0,00729 |
| 542,66536 | 0,00634 | 0,00594 | 0,00655 | 0,00683 | 0,00654 |
| 542,70254 | 0,00571 | 0,00534 | 0,00589 | 0,00612 | 0,00585 |
| 542,73973 | 0,00514 | 0,00478 | 0,00529 | 0,00548 | 0,00523 |
| 542,77691 | 0,00462 | 0,00427 | 0,00474 | 0,00489 | 0,00466 |
| 542,81409 | 0,00414 | 0,00381 | 0,00423 | 0,00435 | 0,00414 |
| 542,85127 | 0,00369 | 0,00338 | 0,00377 | 0,00386 | 0,00366 |
| 542,88845 | 0,00329 | 0,003 | 0,00335 | 0,00342 | 0,00324 |
| 542,92564 | 0,00293 | 0,00264 | 0,00297 | 0,00302 | 0,00286 |
| 542,96282 | 0,0026 | 0,00233 | 0,00262 | 0,00266 | 0,00251 |
| 543 | 0,00229 | 0,00205 | 0,00231 | 0,00233 | 0,0022 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 4e-05 | 6e-05 | 2e-05 | 0 | 0 |
| 524,03718 | 4e-05 | 6e-05 | 2e-05 | 0 | 0 |
| 524,07436 | 5e-05 | 7e-05 | 3e-05 | 0 | 0 |
| 524,11155 | 5e-05 | 7e-05 | 3e-05 | 0 | 0 |
| 524,14873 | 6e-05 | 8e-05 | 3e-05 | 0 | 0 |
| 524,18591 | 6e-05 | 8e-05 | 3e-05 | 0 | 0 |
| 524,22309 | 7e-05 | 9e-05 | 4e-05 | 0 | 0 |
| 524,26027 | 7e-05 | 1e-04 | 4e-05 | 0 | 0 |
| 524,29746 | 8e-05 | 1e-04 | 5e-05 | 0 | 0 |
| 524,33464 | 9e-05 | 0,00011 | 5e-05 | 0 | 0 |
| 524,37182 | 1e-04 | 0,00012 | 6e-05 | 0 | 1e-05 |
| 524,409 | 0,00011 | 0,00013 | 6e-05 | 0 | 1e-05 |
| 524,44618 | 0,00012 | 0,00014 | 7e-05 | 0 | 1e-05 |
| 524,48337 | 0,00013 | 0,00014 | 7e-05 | 0 | 1e-05 |
| 524,52055 | 0,00014 | 0,00015 | 8e-05 | 0 | 1e-05 |
| 524,55773 | 0,00015 | 0,00016 | 8e-05 | 0 | 1e-05 |
| 524,59491 | 0,00016 | 0,00017 | 9e-05 | 1e-05 | 1e-05 |
| 524,63209 | 0,00017 | 0,00018 | 1e-04 | 1e-05 | 1e-05 |
| 524,66928 | 0,00018 | 0,00019 | 0,00011 | 1e-05 | 2e-05 |
| 524,70646 | 0,00019 | 2e-04 | 0,00011 | 1e-05 | 2e-05 |
| 524,74364 | 0,00021 | 0,00021 | 0,00012 | 1e-05 | 2e-05 |
| 524,78082 | 0,00022 | 0,00022 | 0,00013 | 1e-05 | 3e-05 |
| 524,818 | 0,00024 | 0,00023 | 0,00014 | 1e-05 | 3e-05 |
| 524,85519 | 0,00025 | 0,00025 | 0,00015 | 2e-05 | 3e-05 |
| 524,89237 | 0,00027 | 0,00026 | 0,00016 | 2e-05 | 4e-05 |
| 524,92955 | 0,00028 | 0,00027 | 0,00017 | 2e-05 | 4e-05 |
| 524,96673 | 3e-04 | 0,00028 | 0,00018 | 2e-05 | 5e-05 |
| 525,00391 | 0,00031 | 0,00029 | 2e-04 | 3e-05 | 6e-05 |
| 525,0411 | 0,00033 | 0,00031 | 0,00021 | 3e-05 | 6e-05 |
| 525,07828 | 0,00035 | 0,00032 | 0,00022 | 4e-05 | 7e-05 |
| 525,11546 | 0,00036 | 0,00034 | 0,00024 | 4e-05 | 8e-05 |
| 525,15264 | 0,00038 | 0,00035 | 0,00025 | 5e-05 | 9e-05 |
| 525,18982 | 4e-04 | 0,00037 | 0,00027 | 5e-05 | 1e-04 |
| 525,22701 | 0,00042 | 0,00038 | 0,00028 | 6e-05 | 0,00011 |
| 525,26419 | 0,00043 | 4e-04 | 3e-04 | 7e-05 | 0,00012 |
| 525,30137 | 0,00045 | 0,00042 | 0,00032 | 7e-05 | 0,00013 |
| 525,33855 | 0,00047 | 0,00043 | 0,00034 | 8e-05 | 0,00014 |
| 525,37573 | 0,00049 | 0,00045 | 0,00036 | 9e-05 | 0,00016 |
| 525,41292 | 0,00051 | 0,00047 | 0,00038 | 1e-04 | 0,00017 |
| 525,4501 | 0,00052 | 0,00049 | 4e-04 | 0,00011 | 0,00019 |
| 525,48728 | 0,00054 | 0,00052 | 0,00043 | 0,00012 | 0,00021 |
| 525,52446 | 0,00056 | 0,00054 | 0,00045 | 0,00014 | 0,00022 |
| 525,56164 | 0,00058 | 0,00056 | 0,00047 | 0,00015 | 0,00024 |
| 525,59883 | 6e-04 | 0,00059 | 5e-04 | 0,00017 | 0,00026 |
| 525,63601 | 0,00062 | 0,00061 | 0,00053 | 0,00018 | 0,00029 |
| 525,67319 | 0,00065 | 0,00064 | 0,00056 | 2e-04 | 0,00031 |
| 525,71037 | 0,00067 | 0,00067 | 0,00059 | 0,00022 | 0,00033 |
| 525,74755 | 0,00069 | 7e-04 | 0,00062 | 0,00024 | 0,00036 |
| 525,78474 | 0,00072 | 0,00074 | 0,00066 | 0,00026 | 0,00038 |
| 525,82192 | 0,00074 | 0,00077 | 0,00069 | 0,00028 | 0,00041 |
| 525,8591 | 0,00077 | 0,00081 | 0,00073 | 3e-04 | 0,00044 |
| 525,89628 | 8e-04 | 0,00084 | 0,00077 | 0,00033 | 0,00047 |
| 525,93346 | 0,00083 | 0,00089 | 0,00081 | 0,00035 | 5e-04 |
| 525,97065 | 0,00086 | 0,00093 | 0,00085 | 0,00038 | 0,00054 |
| 526,00783 | 9e-04 | 0,00097 | 9e-04 | 0,00041 | 0,00057 |
| 526,04501 | 0,00094 | 0,00102 | 0,00095 | 0,00044 | 0,00061 |
| 526,08219 | 0,00098 | 0,00107 | 0,001 | 0,00047 | 0,00065 |
| 526,11937 | 0,00102 | 0,00112 | 0,00105 | 5e-04 | 0,00069 |
| 526,15656 | 0,00107 | 0,00118 | 0,0011 | 0,00054 | 0,00073 |
| 526,19374 | 0,00112 | 0,00124 | 0,00116 | 0,00058 | 0,00077 |
| 526,23092 | 0,00118 | 0,0013 | 0,00122 | 0,00062 | 0,00082 |
| 526,2681 | 0,00124 | 0,00137 | 0,00128 | 0,00066 | 0,00087 |
| 526,30528 | 0,0013 | 0,00144 | 0,00135 | 7e-04 | 0,00092 |
| 526,34247 | 0,00137 | 0,00152 | 0,00142 | 0,00075 | 0,00098 |
| 526,37965 | 0,00145 | 0,0016 | 0,00149 | 0,00079 | 0,00104 |
| 526,41683 | 0,00153 | 0,00168 | 0,00157 | 0,00084 | 0,0011 |
| 526,45401 | 0,00161 | 0,00177 | 0,00165 | 9e-04 | 0,00117 |
| 526,49119 | 0,00171 | 0,00187 | 0,00173 | 0,00095 | 0,00124 |
| 526,52838 | 0,00181 | 0,00197 | 0,00182 | 0,00102 | 0,00131 |
| 526,56556 | 0,00192 | 0,00207 | 0,00192 | 0,00108 | 0,00139 |
| 526,60274 | 0,00203 | 0,00219 | 0,00202 | 0,00115 | 0,00148 |
| 526,63992 | 0,00215 | 0,00231 | 0,00212 | 0,00122 | 0,00157 |
| 526,6771 | 0,00229 | 0,00244 | 0,00223 | 0,0013 | 0,00166 |
| 526,71429 | 0,00243 | 0,00257 | 0,00234 | 0,00138 | 0,00176 |
| 526,75147 | 0,00257 | 0,00271 | 0,00246 | 0,00147 | 0,00187 |
| 526,78865 | 0,00273 | 0,00287 | 0,00259 | 0,00157 | 0,00199 |
| 526,82583 | 0,0029 | 0,00303 | 0,00272 | 0,00167 | 0,00211 |
| 526,86301 | 0,00308 | 0,0032 | 0,00286 | 0,00178 | 0,00223 |
| 526,9002 | 0,00327 | 0,00338 | 0,00301 | 0,00189 | 0,00237 |
| 526,93738 | 0,00347 | 0,00358 | 0,00317 | 0,00202 | 0,00251 |
| 526,97456 | 0,00368 | 0,00378 | 0,00333 | 0,00215 | 0,00266 |
| 527,01174 | 0,0039 | 0,004 | 0,0035 | 0,00229 | 0,00281 |
| 527,04892 | 0,00414 | 0,00423 | 0,00368 | 0,00244 | 0,00298 |
| 527,08611 | 0,00439 | 0,00447 | 0,00387 | 0,00261 | 0,00315 |
| 527,12329 | 0,00465 | 0,00472 | 0,00407 | 0,00278 | 0,00333 |
| 527,16047 | 0,00492 | 0,00499 | 0,00427 | 0,00296 | 0,00352 |
| 527,19765 | 0,00521 | 0,00528 | 0,00449 | 0,00315 | 0,00371 |
| 527,23483 | 0,00551 | 0,00557 | 0,00472 | 0,00336 | 0,00392 |
| 527,27202 | 0,00583 | 0,00589 | 0,00496 | 0,00357 | 0,00413 |
| 527,3092 | 0,00617 | 0,00622 | 0,0052 | 0,0038 | 0,00435 |
| 527,34638 | 0,00652 | 0,00657 | 0,00547 | 0,00404 | 0,00457 |
| 527,38356 | 0,00688 | 0,00693 | 0,00574 | 0,00429 | 0,00481 |
| 527,42074 | 0,00727 | 0,00732 | 0,00602 | 0,00455 | 0,00505 |
| 527,45793 | 0,00767 | 0,00772 | 0,00632 | 0,00482 | 0,0053 |
| 527,49511 | 0,0081 | 0,00815 | 0,00663 | 0,00511 | 0,00555 |
| 527,53229 | 0,00854 | 0,00859 | 0,00695 | 0,00541 | 0,00581 |
| 527,56947 | 0,009 | 0,00905 | 0,00729 | 0,00571 | 0,00608 |
| 527,60665 | 0,00949 | 0,00953 | 0,00764 | 0,00603 | 0,00635 |
| 527,64384 | 0,01001 | 0,01004 | 0,008 | 0,00636 | 0,00663 |
| 527,68102 | 0,01054 | 0,01056 | 0,00839 | 0,0067 | 0,00691 |
| 527,7182 | 0,0111 | 0,01111 | 0,00879 | 0,00705 | 0,00719 |
| 527,75538 | 0,0117 | 0,01169 | 0,0092 | 0,00741 | 0,00749 |
| 527,79256 | 0,01233 | 0,01229 | 0,00963 | 0,00778 | 0,00778 |
| 527,82975 | 0,01298 | 0,01291 | 0,01009 | 0,00815 | 0,00808 |
| 527,86693 | 0,01366 | 0,01356 | 0,01056 | 0,00854 | 0,00839 |
| 527,90411 | 0,01438 | 0,01423 | 0,01105 | 0,00893 | 0,0087 |
| 527,94129 | 0,01514 | 0,01494 | 0,01156 | 0,00933 | 0,00901 |
| 527,97847 | 0,01594 | 0,01567 | 0,01209 | 0,00974 | 0,00933 |
| 528,01566 | 0,01677 | 0,01642 | 0,01266 | 0,01016 | 0,00965 |
| 528,05284 | 0,01764 | 0,01721 | 0,01324 | 0,01058 | 0,00998 |
| 528,09002 | 0,01856 | 0,01803 | 0,01384 | 0,01101 | 0,01032 |
| 528,1272 | 0,01953 | 0,01887 | 0,01447 | 0,01144 | 0,01065 |
| 528,16438 | 0,02054 | 0,01975 | 0,01513 | 0,01189 | 0,011 |
| 528,20157 | 0,02159 | 0,02066 | 0,01582 | 0,01234 | 0,01135 |
| 528,23875 | 0,0227 | 0,0216 | 0,01654 | 0,0128 | 0,01171 |
| 528,27593 | 0,02386 | 0,02258 | 0,01728 | 0,01327 | 0,01208 |
| 528,31311 | 0,02507 | 0,02358 | 0,01806 | 0,01375 | 0,01245 |
| 528,35029 | 0,02633 | 0,02462 | 0,01887 | 0,01424 | 0,01284 |
| 528,38748 | 0,02765 | 0,0257 | 0,01971 | 0,01475 | 0,01324 |
| 528,42466 | 0,02902 | 0,02681 | 0,02058 | 0,01526 | 0,01365 |
| 528,46184 | 0,03045 | 0,02795 | 0,02148 | 0,01579 | 0,01407 |
| 528,49902 | 0,03192 | 0,02912 | 0,02243 | 0,01633 | 0,0145 |
| 528,5362 | 0,03345 | 0,03032 | 0,0234 | 0,0169 | 0,01495 |
| 528,57339 | 0,03504 | 0,03156 | 0,0244 | 0,01748 | 0,01541 |
| 528,61057 | 0,03667 | 0,03283 | 0,02544 | 0,01808 | 0,0159 |
| 528,64775 | 0,03835 | 0,03412 | 0,02651 | 0,0187 | 0,0164 |
| 528,68493 | 0,04007 | 0,03544 | 0,02762 | 0,01935 | 0,01691 |
| 528,72211 | 0,04184 | 0,0368 | 0,02875 | 0,02002 | 0,01745 |
| 528,7593 | 0,04366 | 0,03818 | 0,02991 | 0,02072 | 0,01801 |
| 528,79648 | 0,0455 | 0,03957 | 0,0311 | 0,02144 | 0,01859 |
| 528,83366 | 0,04738 | 0,04099 | 0,03232 | 0,02219 | 0,01919 |
| 528,87084 | 0,04929 | 0,04243 | 0,03356 | 0,02298 | 0,01981 |
| 528,90802 | 0,05123 | 0,04388 | 0,03483 | 0,0238 | 0,02046 |
| 528,94521 | 0,05317 | 0,04535 | 0,03611 | 0,02464 | 0,02113 |
| 528,98239 | 0,05514 | 0,04682 | 0,03741 | 0,02552 | 0,02182 |
| 529,01957 | 0,0571 | 0,04829 | 0,03872 | 0,02644 | 0,02254 |
| 529,05675 | 0,05907 | 0,04977 | 0,04005 | 0,02738 | 0,02327 |
| 529,09393 | 0,06103 | 0,05125 | 0,04138 | 0,02836 | 0,02403 |
| 529,13112 | 0,06298 | 0,05272 | 0,04271 | 0,02936 | 0,02481 |
| 529,1683 | 0,06492 | 0,05418 | 0,04405 | 0,03041 | 0,02561 |
| 529,20548 | 0,06681 | 0,05562 | 0,04538 | 0,03148 | 0,02643 |
| 529,24266 | 0,06868 | 0,05705 | 0,04671 | 0,03258 | 0,02727 |
| 529,27984 | 0,07051 | 0,05845 | 0,04802 | 0,0337 | 0,02813 |
| 529,31703 | 0,0723 | 0,05983 | 0,04931 | 0,03485 | 0,029 |
| 529,35421 | 0,07402 | 0,06117 | 0,05059 | 0,03602 | 0,02988 |
| 529,39139 | 0,07568 | 0,06248 | 0,05184 | 0,03721 | 0,03078 |
| 529,42857 | 0,07728 | 0,06375 | 0,05307 | 0,03841 | 0,03168 |
| 529,46575 | 0,07882 | 0,06498 | 0,05426 | 0,03963 | 0,0326 |
| 529,50294 | 0,08027 | 0,06616 | 0,05542 | 0,04085 | 0,03351 |
| 529,54012 | 0,08164 | 0,06729 | 0,05654 | 0,04208 | 0,03443 |
| 529,5773 | 0,08292 | 0,06836 | 0,05762 | 0,04331 | 0,03535 |
| 529,61448 | 0,08413 | 0,06939 | 0,05865 | 0,04454 | 0,03626 |
| 529,65166 | 0,08525 | 0,07036 | 0,05963 | 0,04576 | 0,03717 |
| 529,68885 | 0,08625 | 0,07126 | 0,06057 | 0,04697 | 0,03807 |
| 529,72603 | 0,08717 | 0,0721 | 0,06145 | 0,04816 | 0,03896 |
| 529,76321 | 0,088 | 0,07289 | 0,06229 | 0,04934 | 0,03983 |
| 529,80039 | 0,08874 | 0,07362 | 0,06305 | 0,0505 | 0,04069 |
| 529,83757 | 0,08937 | 0,07426 | 0,06376 | 0,05162 | 0,04153 |
| 529,87476 | 0,0899 | 0,07485 | 0,06442 | 0,05271 | 0,04234 |
| 529,91194 | 0,09036 | 0,07538 | 0,06502 | 0,05377 | 0,04314 |
| 529,94912 | 0,09073 | 0,07585 | 0,06555 | 0,0548 | 0,0439 |
| 529,9863 | 0,09101 | 0,07625 | 0,06602 | 0,05579 | 0,04464 |
| 530,02348 | 0,09119 | 0,07659 | 0,06644 | 0,05673 | 0,04535 |
| 530,06067 | 0,09131 | 0,07687 | 0,0668 | 0,05762 | 0,04603 |
| 530,09785 | 0,09136 | 0,07711 | 0,06711 | 0,05847 | 0,04668 |
| 530,13503 | 0,09134 | 0,07728 | 0,06735 | 0,05928 | 0,04728 |
| 530,17221 | 0,09125 | 0,0774 | 0,06754 | 0,06003 | 0,04786 |
| 530,20939 | 0,0911 | 0,07747 | 0,06768 | 0,06073 | 0,0484 |
| 530,24658 | 0,09091 | 0,0775 | 0,06778 | 0,06138 | 0,04892 |
| 530,28376 | 0,09067 | 0,07749 | 0,06781 | 0,06199 | 0,04939 |
| 530,32094 | 0,09038 | 0,07742 | 0,06781 | 0,06254 | 0,04983 |
| 530,35812 | 0,09006 | 0,07733 | 0,06776 | 0,06304 | 0,05023 |
| 530,3953 | 0,08971 | 0,07721 | 0,06768 | 0,06349 | 0,05061 |
| 530,43249 | 0,08934 | 0,07706 | 0,06756 | 0,06389 | 0,05095 |
| 530,46967 | 0,08895 | 0,07688 | 0,0674 | 0,06425 | 0,05126 |
| 530,50685 | 0,08854 | 0,07667 | 0,06722 | 0,06456 | 0,05154 |
| 530,54403 | 0,08813 | 0,07645 | 0,06701 | 0,06482 | 0,0518 |
| 530,58121 | 0,08771 | 0,07622 | 0,06678 | 0,06505 | 0,05203 |
| 530,6184 | 0,0873 | 0,07597 | 0,06652 | 0,06524 | 0,05224 |
| 530,65558 | 0,08688 | 0,07571 | 0,06625 | 0,06539 | 0,05242 |
| 530,69276 | 0,08647 | 0,07545 | 0,06597 | 0,06551 | 0,05259 |
| 530,72994 | 0,08607 | 0,07518 | 0,06568 | 0,06559 | 0,05274 |
| 530,76712 | 0,08568 | 0,07492 | 0,06538 | 0,06565 | 0,05288 |
| 530,80431 | 0,08531 | 0,07465 | 0,06508 | 0,06569 | 0,05301 |
| 530,84149 | 0,08495 | 0,07439 | 0,06478 | 0,0657 | 0,05312 |
| 530,87867 | 0,08461 | 0,07413 | 0,06448 | 0,06569 | 0,05323 |
| 530,91585 | 0,08428 | 0,07388 | 0,06418 | 0,06566 | 0,05334 |
| 530,95303 | 0,08397 | 0,07364 | 0,0639 | 0,06563 | 0,05344 |
| 530,99022 | 0,08368 | 0,07341 | 0,06362 | 0,06557 | 0,05354 |
| 531,0274 | 0,08341 | 0,07319 | 0,06336 | 0,06551 | 0,05364 |
| 531,06458 | 0,08315 | 0,07298 | 0,06311 | 0,06544 | 0,05375 |
| 531,10176 | 0,0829 | 0,07278 | 0,06288 | 0,06537 | 0,05385 |
| 531,13894 | 0,08267 | 0,0726 | 0,06266 | 0,06529 | 0,05397 |
| 531,17613 | 0,08245 | 0,07243 | 0,06247 | 0,06522 | 0,05409 |
| 531,21331 | 0,08224 | 0,07227 | 0,06229 | 0,06514 | 0,05422 |
| 531,25049 | 0,08204 | 0,07212 | 0,06213 | 0,06507 | 0,05435 |
| 531,28767 | 0,08185 | 0,07198 | 0,062 | 0,065 | 0,0545 |
| 531,32485 | 0,08166 | 0,07186 | 0,06189 | 0,06493 | 0,05465 |
| 531,36204 | 0,08148 | 0,07175 | 0,06179 | 0,06487 | 0,05482 |
| 531,39922 | 0,0813 | 0,07164 | 0,06172 | 0,06482 | 0,05499 |
| 531,4364 | 0,08112 | 0,07155 | 0,06168 | 0,06478 | 0,05517 |
| 531,47358 | 0,08093 | 0,07146 | 0,06165 | 0,06474 | 0,05537 |
| 531,51076 | 0,08074 | 0,07138 | 0,06164 | 0,06471 | 0,05557 |
| 531,54795 | 0,08055 | 0,0713 | 0,06166 | 0,06469 | 0,05578 |
| 531,58513 | 0,08035 | 0,07123 | 0,06169 | 0,06468 | 0,056 |
| 531,62231 | 0,08014 | 0,07116 | 0,06174 | 0,06467 | 0,05622 |
| 531,65949 | 0,07993 | 0,0711 | 0,0618 | 0,06467 | 0,05645 |
| 531,69667 | 0,0797 | 0,07103 | 0,06188 | 0,06469 | 0,05669 |
| 531,73386 | 0,07947 | 0,07097 | 0,06198 | 0,0647 | 0,05693 |
| 531,77104 | 0,07922 | 0,07091 | 0,06209 | 0,06473 | 0,05717 |
| 531,80822 | 0,07896 | 0,07084 | 0,0622 | 0,06476 | 0,05741 |
| 531,8454 | 0,07869 | 0,07077 | 0,06233 | 0,06479 | 0,05766 |
| 531,88258 | 0,07842 | 0,0707 | 0,06246 | 0,06483 | 0,05791 |
| 531,91977 | 0,07813 | 0,07062 | 0,06261 | 0,06488 | 0,05816 |
| 531,95695 | 0,07783 | 0,07054 | 0,06275 | 0,06492 | 0,0584 |
| 531,99413 | 0,07752 | 0,07045 | 0,06291 | 0,06497 | 0,05865 |
| 532,03131 | 0,07721 | 0,07036 | 0,06306 | 0,06502 | 0,05889 |
| 532,06849 | 0,07689 | 0,07026 | 0,06322 | 0,06507 | 0,05913 |
| 532,10568 | 0,07657 | 0,07016 | 0,06337 | 0,06513 | 0,05936 |
| 532,14286 | 0,07624 | 0,07005 | 0,06353 | 0,06518 | 0,05959 |
| 532,18004 | 0,07591 | 0,06994 | 0,06368 | 0,06522 | 0,05981 |
| 532,21722 | 0,07558 | 0,06982 | 0,06384 | 0,06527 | 0,06003 |
| 532,2544 | 0,07525 | 0,06969 | 0,06399 | 0,06532 | 0,06024 |
| 532,29159 | 0,07492 | 0,06956 | 0,06414 | 0,06536 | 0,06045 |
| 532,32877 | 0,07459 | 0,06943 | 0,06428 | 0,0654 | 0,06064 |
| 532,36595 | 0,07428 | 0,06929 | 0,06442 | 0,06543 | 0,06083 |
| 532,40313 | 0,07396 | 0,06915 | 0,06456 | 0,06546 | 0,06101 |
| 532,44031 | 0,07366 | 0,06901 | 0,06469 | 0,06549 | 0,06119 |
| 532,4775 | 0,07337 | 0,06886 | 0,06481 | 0,06551 | 0,06136 |
| 532,51468 | 0,07309 | 0,06872 | 0,06493 | 0,06552 | 0,06152 |
| 532,55186 | 0,07282 | 0,06857 | 0,06505 | 0,06553 | 0,06167 |
| 532,58904 | 0,07257 | 0,06843 | 0,06516 | 0,06554 | 0,06181 |
| 532,62622 | 0,07233 | 0,06828 | 0,06526 | 0,06554 | 0,06195 |
| 532,66341 | 0,0721 | 0,06814 | 0,06536 | 0,06554 | 0,06208 |
| 532,70059 | 0,07189 | 0,068 | 0,06546 | 0,06553 | 0,0622 |
| 532,73777 | 0,0717 | 0,06786 | 0,06554 | 0,06552 | 0,06231 |
| 532,77495 | 0,07153 | 0,06773 | 0,06563 | 0,0655 | 0,06242 |
| 532,81213 | 0,07137 | 0,0676 | 0,0657 | 0,06548 | 0,06252 |
| 532,84932 | 0,07123 | 0,06747 | 0,06578 | 0,06546 | 0,06261 |
| 532,8865 | 0,07111 | 0,06735 | 0,06584 | 0,06543 | 0,0627 |
| 532,92368 | 0,071 | 0,06723 | 0,0659 | 0,0654 | 0,06278 |
| 532,96086 | 0,07091 | 0,06712 | 0,06596 | 0,06536 | 0,06286 |
| 532,99804 | 0,07084 | 0,06701 | 0,06601 | 0,06533 | 0,06293 |
| 533,03523 | 0,07078 | 0,06691 | 0,06605 | 0,06529 | 0,063 |
| 533,07241 | 0,07074 | 0,06681 | 0,06608 | 0,06526 | 0,06307 |
| 533,10959 | 0,07071 | 0,06672 | 0,06611 | 0,06522 | 0,06313 |
| 533,14677 | 0,07069 | 0,06663 | 0,06614 | 0,06518 | 0,06319 |
| 533,18395 | 0,07069 | 0,06655 | 0,06616 | 0,06515 | 0,06325 |
| 533,22114 | 0,0707 | 0,06648 | 0,06617 | 0,06511 | 0,0633 |
| 533,25832 | 0,07072 | 0,06641 | 0,06617 | 0,06508 | 0,06336 |
| 533,2955 | 0,07074 | 0,06635 | 0,06617 | 0,06505 | 0,06342 |
| 533,33268 | 0,07078 | 0,06629 | 0,06617 | 0,06502 | 0,06349 |
| 533,36986 | 0,07083 | 0,06624 | 0,06615 | 0,065 | 0,06355 |
| 533,40705 | 0,07089 | 0,06619 | 0,06613 | 0,06498 | 0,06362 |
| 533,44423 | 0,07095 | 0,06614 | 0,06611 | 0,06497 | 0,0637 |
| 533,48141 | 0,07102 | 0,0661 | 0,06608 | 0,06496 | 0,06378 |
| 533,51859 | 0,07109 | 0,06607 | 0,06605 | 0,06496 | 0,06387 |
| 533,55577 | 0,07117 | 0,06604 | 0,06601 | 0,06496 | 0,06396 |
| 533,59295 | 0,07126 | 0,06601 | 0,06597 | 0,06497 | 0,06407 |
| 533,63014 | 0,07135 | 0,06599 | 0,06593 | 0,06498 | 0,06418 |
| 533,66732 | 0,07144 | 0,06597 | 0,06589 | 0,06501 | 0,0643 |
| 533,7045 | 0,07154 | 0,06596 | 0,06584 | 0,06503 | 0,06443 |
| 533,74168 | 0,07164 | 0,06595 | 0,0658 | 0,06507 | 0,06457 |
| 533,77886 | 0,07174 | 0,06594 | 0,06576 | 0,06511 | 0,06472 |
| 533,81605 | 0,07185 | 0,06594 | 0,06571 | 0,06516 | 0,06488 |
| 533,85323 | 0,07196 | 0,06594 | 0,06568 | 0,06522 | 0,06505 |
| 533,89041 | 0,07207 | 0,06594 | 0,06564 | 0,06528 | 0,06523 |
| 533,92759 | 0,07219 | 0,06595 | 0,06561 | 0,06535 | 0,06542 |
| 533,96477 | 0,0723 | 0,06596 | 0,06558 | 0,06542 | 0,06561 |
| 534,00196 | 0,07242 | 0,06597 | 0,06557 | 0,0655 | 0,06581 |
| 534,03914 | 0,07254 | 0,06598 | 0,06555 | 0,06559 | 0,06602 |
| 534,07632 | 0,07266 | 0,066 | 0,06555 | 0,06568 | 0,06623 |
| 534,1135 | 0,07278 | 0,06602 | 0,06556 | 0,06577 | 0,06645 |
| 534,15068 | 0,0729 | 0,06604 | 0,06557 | 0,06587 | 0,06667 |
| 534,18787 | 0,07303 | 0,06606 | 0,0656 | 0,06597 | 0,06689 |
| 534,22505 | 0,07315 | 0,06608 | 0,06563 | 0,06607 | 0,06711 |
| 534,26223 | 0,07327 | 0,0661 | 0,06568 | 0,06618 | 0,06733 |
| 534,29941 | 0,07338 | 0,06613 | 0,06573 | 0,06629 | 0,06754 |
| 534,33659 | 0,0735 | 0,06615 | 0,0658 | 0,0664 | 0,06775 |
| 534,37378 | 0,07361 | 0,06618 | 0,06588 | 0,06652 | 0,06796 |
| 534,41096 | 0,07372 | 0,06621 | 0,06598 | 0,06664 | 0,06816 |
| 534,44814 | 0,07382 | 0,06623 | 0,06608 | 0,06675 | 0,06836 |
| 534,48532 | 0,07392 | 0,06626 | 0,06619 | 0,06687 | 0,06855 |
| 534,5225 | 0,07402 | 0,06629 | 0,06632 | 0,067 | 0,06873 |
| 534,55969 | 0,07411 | 0,06632 | 0,06646 | 0,06712 | 0,0689 |
| 534,59687 | 0,07419 | 0,06636 | 0,0666 | 0,06724 | 0,06907 |
| 534,63405 | 0,07426 | 0,06639 | 0,06676 | 0,06737 | 0,06923 |
| 534,67123 | 0,07433 | 0,06643 | 0,06693 | 0,0675 | 0,06938 |
| 534,70841 | 0,07439 | 0,06647 | 0,06711 | 0,06763 | 0,06952 |
| 534,7456 | 0,07444 | 0,06651 | 0,0673 | 0,06777 | 0,06966 |
| 534,78278 | 0,07448 | 0,06656 | 0,0675 | 0,0679 | 0,06979 |
| 534,81996 | 0,07451 | 0,06661 | 0,0677 | 0,06804 | 0,06992 |
| 534,85714 | 0,07453 | 0,06666 | 0,06792 | 0,06819 | 0,07005 |
| 534,89432 | 0,07454 | 0,06673 | 0,06814 | 0,06833 | 0,07018 |
| 534,93151 | 0,07454 | 0,06679 | 0,06837 | 0,06849 | 0,07031 |
| 534,96869 | 0,07453 | 0,06686 | 0,06861 | 0,06864 | 0,07044 |
| 535,00587 | 0,07451 | 0,06695 | 0,06885 | 0,06881 | 0,07058 |
| 535,04305 | 0,07448 | 0,06703 | 0,06911 | 0,06897 | 0,07072 |
| 535,08023 | 0,07444 | 0,06713 | 0,06936 | 0,06915 | 0,07087 |
| 535,11742 | 0,0744 | 0,06723 | 0,06962 | 0,06933 | 0,07104 |
| 535,1546 | 0,07434 | 0,06735 | 0,06989 | 0,06951 | 0,07121 |
| 535,19178 | 0,07427 | 0,06747 | 0,07017 | 0,0697 | 0,0714 |
| 535,22896 | 0,0742 | 0,0676 | 0,07044 | 0,0699 | 0,07161 |
| 535,26614 | 0,07412 | 0,06774 | 0,07072 | 0,07011 | 0,07183 |
| 535,30333 | 0,07403 | 0,0679 | 0,07101 | 0,07032 | 0,07207 |
| 535,34051 | 0,07394 | 0,06806 | 0,07129 | 0,07053 | 0,07233 |
| 535,37769 | 0,07384 | 0,06823 | 0,07158 | 0,07075 | 0,07261 |
| 535,41487 | 0,07373 | 0,06841 | 0,07187 | 0,07098 | 0,07291 |
| 535,45205 | 0,07362 | 0,06859 | 0,07216 | 0,07121 | 0,07323 |
| 535,48924 | 0,0735 | 0,06879 | 0,07245 | 0,07145 | 0,07358 |
| 535,52642 | 0,07337 | 0,06899 | 0,07274 | 0,07169 | 0,07394 |
| 535,5636 | 0,07324 | 0,0692 | 0,07303 | 0,07193 | 0,07432 |
| 535,60078 | 0,07311 | 0,06941 | 0,07331 | 0,07217 | 0,07472 |
| 535,63796 | 0,07297 | 0,06962 | 0,07359 | 0,07242 | 0,07514 |
| 535,67515 | 0,07283 | 0,06984 | 0,07387 | 0,07267 | 0,07558 |
| 535,71233 | 0,07269 | 0,07007 | 0,07414 | 0,07292 | 0,07603 |
| 535,74951 | 0,07254 | 0,07029 | 0,0744 | 0,07317 | 0,0765 |
| 535,78669 | 0,07238 | 0,07051 | 0,07466 | 0,07342 | 0,07698 |
| 535,82387 | 0,07222 | 0,07073 | 0,0749 | 0,07367 | 0,07747 |
| 535,86106 | 0,07206 | 0,07095 | 0,07514 | 0,07392 | 0,07796 |
| 535,89824 | 0,07189 | 0,07117 | 0,07537 | 0,07417 | 0,07847 |
| 535,93542 | 0,07172 | 0,07138 | 0,07559 | 0,07441 | 0,07897 |
| 535,9726 | 0,07154 | 0,07158 | 0,07579 | 0,07465 | 0,07948 |
| 536,00978 | 0,07136 | 0,07178 | 0,07598 | 0,07489 | 0,07998 |
| 536,04697 | 0,07117 | 0,07198 | 0,07616 | 0,07512 | 0,08048 |
| 536,08415 | 0,07098 | 0,07216 | 0,07632 | 0,07536 | 0,08098 |
| 536,12133 | 0,07078 | 0,07234 | 0,07647 | 0,07558 | 0,08146 |
| 536,15851 | 0,07058 | 0,07251 | 0,07661 | 0,07581 | 0,08194 |
| 536,19569 | 0,07036 | 0,07267 | 0,07673 | 0,07603 | 0,08241 |
| 536,23288 | 0,07015 | 0,07282 | 0,07684 | 0,07625 | 0,08286 |
| 536,27006 | 0,06992 | 0,07296 | 0,07693 | 0,07646 | 0,08329 |
| 536,30724 | 0,06969 | 0,07309 | 0,07701 | 0,07667 | 0,08371 |
| 536,34442 | 0,06945 | 0,07321 | 0,07708 | 0,07688 | 0,08411 |
| 536,3816 | 0,06921 | 0,07333 | 0,07713 | 0,07709 | 0,08449 |
| 536,41879 | 0,06896 | 0,07343 | 0,07717 | 0,07729 | 0,08484 |
| 536,45597 | 0,0687 | 0,07353 | 0,0772 | 0,0775 | 0,08518 |
| 536,49315 | 0,06844 | 0,07362 | 0,07722 | 0,0777 | 0,08549 |
| 536,53033 | 0,06817 | 0,0737 | 0,07723 | 0,0779 | 0,08578 |
| 536,56751 | 0,0679 | 0,07378 | 0,07724 | 0,0781 | 0,08605 |
| 536,6047 | 0,06762 | 0,07385 | 0,07723 | 0,0783 | 0,08628 |
| 536,64188 | 0,06733 | 0,07392 | 0,07722 | 0,0785 | 0,0865 |
| 536,67906 | 0,06705 | 0,07398 | 0,0772 | 0,0787 | 0,08669 |
| 536,71624 | 0,06676 | 0,07403 | 0,07717 | 0,0789 | 0,08686 |
| 536,75342 | 0,06646 | 0,07408 | 0,07714 | 0,0791 | 0,08701 |
| 536,79061 | 0,06616 | 0,07413 | 0,07711 | 0,0793 | 0,08713 |
| 536,82779 | 0,06587 | 0,07417 | 0,07708 | 0,0795 | 0,08723 |
| 536,86497 | 0,06557 | 0,07422 | 0,07705 | 0,07971 | 0,08731 |
| 536,90215 | 0,06526 | 0,07425 | 0,07701 | 0,07991 | 0,08738 |
| 536,93933 | 0,06496 | 0,07429 | 0,07698 | 0,08012 | 0,08742 |
| 536,97652 | 0,06466 | 0,07432 | 0,07694 | 0,08033 | 0,08744 |
| 537,0137 | 0,06436 | 0,07435 | 0,07691 | 0,08053 | 0,08745 |
| 537,05088 | 0,06406 | 0,07438 | 0,07687 | 0,08075 | 0,08744 |
| 537,08806 | 0,06376 | 0,07441 | 0,07684 | 0,08096 | 0,08742 |
| 537,12524 | 0,06346 | 0,07443 | 0,07682 | 0,08117 | 0,08738 |
| 537,16243 | 0,06317 | 0,07445 | 0,07679 | 0,08138 | 0,08734 |
| 537,19961 | 0,06288 | 0,07446 | 0,07677 | 0,08159 | 0,08728 |
| 537,23679 | 0,06259 | 0,07447 | 0,07674 | 0,0818 | 0,08722 |
| 537,27397 | 0,0623 | 0,07447 | 0,07672 | 0,08201 | 0,08714 |
| 537,31115 | 0,06202 | 0,07447 | 0,0767 | 0,08222 | 0,08706 |
| 537,34834 | 0,06173 | 0,07446 | 0,07669 | 0,08243 | 0,08698 |
| 537,38552 | 0,06146 | 0,07445 | 0,07667 | 0,08263 | 0,08689 |
| 537,4227 | 0,06118 | 0,07442 | 0,07665 | 0,08283 | 0,0868 |
| 537,45988 | 0,06091 | 0,07439 | 0,07664 | 0,08303 | 0,08671 |
| 537,49706 | 0,06064 | 0,07435 | 0,07662 | 0,08322 | 0,08661 |
| 537,53425 | 0,06038 | 0,0743 | 0,07661 | 0,08341 | 0,08652 |
| 537,57143 | 0,06012 | 0,07424 | 0,07659 | 0,08359 | 0,08642 |
| 537,60861 | 0,05986 | 0,07417 | 0,07658 | 0,08376 | 0,08633 |
| 537,64579 | 0,0596 | 0,07408 | 0,07656 | 0,08392 | 0,08624 |
| 537,68297 | 0,05935 | 0,07399 | 0,07654 | 0,08408 | 0,08614 |
| 537,72016 | 0,0591 | 0,07388 | 0,07652 | 0,08422 | 0,08605 |
| 537,75734 | 0,05886 | 0,07376 | 0,0765 | 0,08435 | 0,08596 |
| 537,79452 | 0,05861 | 0,07363 | 0,07648 | 0,08447 | 0,08587 |
| 537,8317 | 0,05837 | 0,07349 | 0,07645 | 0,08458 | 0,08579 |
| 537,86888 | 0,05813 | 0,07334 | 0,07643 | 0,08467 | 0,0857 |
| 537,90607 | 0,05789 | 0,07317 | 0,07639 | 0,08474 | 0,08562 |
| 537,94325 | 0,05766 | 0,07299 | 0,07636 | 0,0848 | 0,08553 |
| 537,98043 | 0,05743 | 0,07279 | 0,07632 | 0,08484 | 0,08545 |
| 538,01761 | 0,0572 | 0,07259 | 0,07628 | 0,08486 | 0,08536 |
| 538,05479 | 0,05697 | 0,07237 | 0,07624 | 0,08485 | 0,08527 |
| 538,09198 | 0,05674 | 0,07214 | 0,07619 | 0,08483 | 0,08519 |
| 538,12916 | 0,05652 | 0,0719 | 0,07614 | 0,08478 | 0,0851 |
| 538,16634 | 0,0563 | 0,07165 | 0,07608 | 0,08471 | 0,08501 |
| 538,20352 | 0,05608 | 0,07138 | 0,07602 | 0,08461 | 0,08491 |
| 538,2407 | 0,05586 | 0,07111 | 0,07596 | 0,08449 | 0,08481 |
| 538,27789 | 0,05564 | 0,07082 | 0,07588 | 0,08434 | 0,08471 |
| 538,31507 | 0,05542 | 0,07053 | 0,07581 | 0,08417 | 0,08461 |
| 538,35225 | 0,05521 | 0,07023 | 0,07572 | 0,08398 | 0,0845 |
| 538,38943 | 0,055 | 0,06992 | 0,07563 | 0,08375 | 0,08438 |
| 538,42661 | 0,05479 | 0,0696 | 0,07553 | 0,0835 | 0,08427 |
| 538,4638 | 0,05458 | 0,06928 | 0,07543 | 0,08323 | 0,08414 |
| 538,50098 | 0,05437 | 0,06895 | 0,07531 | 0,08294 | 0,08402 |
| 538,53816 | 0,05417 | 0,06861 | 0,07519 | 0,08262 | 0,08388 |
| 538,57534 | 0,05397 | 0,06827 | 0,07506 | 0,08228 | 0,08375 |
| 538,61252 | 0,05377 | 0,06793 | 0,07491 | 0,08192 | 0,08361 |
| 538,64971 | 0,05357 | 0,06758 | 0,07476 | 0,08155 | 0,08347 |
| 538,68689 | 0,05339 | 0,06723 | 0,0746 | 0,08116 | 0,08332 |
| 538,72407 | 0,0532 | 0,06688 | 0,07443 | 0,08075 | 0,08317 |
| 538,76125 | 0,05302 | 0,06654 | 0,07424 | 0,08034 | 0,08302 |
| 538,79843 | 0,05285 | 0,06619 | 0,07405 | 0,07991 | 0,08287 |
| 538,83562 | 0,05268 | 0,06585 | 0,07385 | 0,07948 | 0,08271 |
| 538,8728 | 0,05252 | 0,06551 | 0,07364 | 0,07905 | 0,08256 |
| 538,90998 | 0,05237 | 0,06517 | 0,07341 | 0,07862 | 0,0824 |
| 538,94716 | 0,05223 | 0,06485 | 0,07318 | 0,07818 | 0,08225 |
| 538,98434 | 0,05209 | 0,06453 | 0,07294 | 0,07776 | 0,0821 |
| 539,02153 | 0,05197 | 0,06422 | 0,07269 | 0,07734 | 0,08195 |
| 539,05871 | 0,05186 | 0,06392 | 0,07243 | 0,07693 | 0,0818 |
| 539,09589 | 0,05177 | 0,06363 | 0,07217 | 0,07654 | 0,08165 |
| 539,13307 | 0,05168 | 0,06336 | 0,0719 | 0,07616 | 0,08151 |
| 539,17025 | 0,05161 | 0,0631 | 0,07163 | 0,07579 | 0,08138 |
| 539,20744 | 0,05156 | 0,06285 | 0,07136 | 0,07545 | 0,08125 |
| 539,24462 | 0,05152 | 0,06262 | 0,07108 | 0,07513 | 0,08112 |
| 539,2818 | 0,05149 | 0,06241 | 0,07081 | 0,07484 | 0,08101 |
| 539,31898 | 0,05149 | 0,06221 | 0,07053 | 0,07456 | 0,08089 |
| 539,35616 | 0,0515 | 0,06204 | 0,07026 | 0,07431 | 0,08079 |
| 539,39335 | 0,05152 | 0,06188 | 0,06999 | 0,0741 | 0,08069 |
| 539,43053 | 0,05157 | 0,06173 | 0,06973 | 0,07391 | 0,08061 |
| 539,46771 | 0,05163 | 0,06161 | 0,06947 | 0,07375 | 0,08052 |
| 539,50489 | 0,0517 | 0,06151 | 0,06922 | 0,07361 | 0,08045 |
| 539,54207 | 0,0518 | 0,06142 | 0,06898 | 0,0735 | 0,08039 |
| 539,57926 | 0,0519 | 0,06135 | 0,06875 | 0,07343 | 0,08033 |
| 539,61644 | 0,05203 | 0,0613 | 0,06853 | 0,07338 | 0,08028 |
| 539,65362 | 0,05216 | 0,06126 | 0,06831 | 0,07336 | 0,08025 |
| 539,6908 | 0,05231 | 0,06124 | 0,06811 | 0,07335 | 0,08022 |
| 539,72798 | 0,05247 | 0,06123 | 0,06793 | 0,07338 | 0,0802 |
| 539,76517 | 0,05264 | 0,06123 | 0,06775 | 0,07343 | 0,08018 |
| 539,80235 | 0,05283 | 0,06125 | 0,06759 | 0,0735 | 0,08018 |
| 539,83953 | 0,05302 | 0,06127 | 0,06744 | 0,07359 | 0,08018 |
| 539,87671 | 0,05321 | 0,0613 | 0,0673 | 0,0737 | 0,0802 |
| 539,91389 | 0,05341 | 0,06134 | 0,06718 | 0,07383 | 0,08022 |
| 539,95108 | 0,05362 | 0,06138 | 0,06707 | 0,07397 | 0,08025 |
| 539,98826 | 0,05383 | 0,06142 | 0,06697 | 0,07412 | 0,08029 |
| 540,02544 | 0,05404 | 0,06147 | 0,06688 | 0,07429 | 0,08033 |
| 540,06262 | 0,05425 | 0,06151 | 0,06681 | 0,07446 | 0,08039 |
| 540,0998 | 0,05445 | 0,06155 | 0,06675 | 0,07464 | 0,08045 |
| 540,13699 | 0,05466 | 0,06159 | 0,06669 | 0,07483 | 0,08052 |
| 540,17417 | 0,05486 | 0,06162 | 0,06665 | 0,07502 | 0,08059 |
| 540,21135 | 0,05506 | 0,06164 | 0,06662 | 0,07522 | 0,08067 |
| 540,24853 | 0,05525 | 0,06166 | 0,0666 | 0,07541 | 0,08076 |
| 540,28571 | 0,05543 | 0,06167 | 0,06658 | 0,07561 | 0,08086 |
| 540,3229 | 0,05561 | 0,06167 | 0,06658 | 0,0758 | 0,08096 |
| 540,36008 | 0,05578 | 0,06166 | 0,06658 | 0,076 | 0,08106 |
| 540,39726 | 0,05595 | 0,06164 | 0,06659 | 0,07618 | 0,08117 |
| 540,43444 | 0,0561 | 0,06161 | 0,0666 | 0,07637 | 0,08128 |
| 540,47162 | 0,05625 | 0,06156 | 0,06662 | 0,07655 | 0,0814 |
| 540,50881 | 0,05639 | 0,06151 | 0,06665 | 0,07672 | 0,08152 |
| 540,54599 | 0,05653 | 0,06144 | 0,06668 | 0,07688 | 0,08163 |
| 540,58317 | 0,05665 | 0,06137 | 0,06672 | 0,07704 | 0,08175 |
| 540,62035 | 0,05677 | 0,06128 | 0,06676 | 0,07719 | 0,08187 |
| 540,65753 | 0,05688 | 0,06119 | 0,0668 | 0,07733 | 0,08199 |
| 540,69472 | 0,05699 | 0,06109 | 0,06685 | 0,07746 | 0,0821 |
| 540,7319 | 0,05709 | 0,06098 | 0,0669 | 0,07758 | 0,08221 |
| 540,76908 | 0,05718 | 0,06087 | 0,06695 | 0,07769 | 0,08232 |
| 540,80626 | 0,05727 | 0,06075 | 0,06701 | 0,07779 | 0,08242 |
| 540,84344 | 0,05735 | 0,06063 | 0,06706 | 0,07788 | 0,08252 |
| 540,88063 | 0,05742 | 0,06051 | 0,06712 | 0,07796 | 0,0826 |
| 540,91781 | 0,0575 | 0,06038 | 0,06718 | 0,07803 | 0,08268 |
| 540,95499 | 0,05756 | 0,06026 | 0,06723 | 0,07809 | 0,08275 |
| 540,99217 | 0,05762 | 0,06013 | 0,06729 | 0,07814 | 0,08282 |
| 541,02935 | 0,05768 | 0,06001 | 0,06734 | 0,07817 | 0,08287 |
| 541,06654 | 0,05773 | 0,0599 | 0,0674 | 0,0782 | 0,08291 |
| 541,10372 | 0,05778 | 0,05979 | 0,06745 | 0,07821 | 0,08294 |
| 541,1409 | 0,05782 | 0,05968 | 0,0675 | 0,07822 | 0,08296 |
| 541,17808 | 0,05786 | 0,05958 | 0,06754 | 0,07821 | 0,08297 |
| 541,21526 | 0,05789 | 0,05949 | 0,06758 | 0,07819 | 0,08296 |
| 541,25245 | 0,05792 | 0,05941 | 0,06762 | 0,07816 | 0,08294 |
| 541,28963 | 0,05793 | 0,05934 | 0,06766 | 0,07812 | 0,08291 |
| 541,32681 | 0,05795 | 0,05928 | 0,06768 | 0,07806 | 0,08287 |
| 541,36399 | 0,05795 | 0,05923 | 0,06771 | 0,07799 | 0,08281 |
| 541,40117 | 0,05795 | 0,05919 | 0,06772 | 0,07791 | 0,08273 |
| 541,43836 | 0,05793 | 0,05916 | 0,06773 | 0,0778 | 0,08263 |
| 541,47554 | 0,05791 | 0,05914 | 0,06773 | 0,07768 | 0,08252 |
| 541,51272 | 0,05788 | 0,05913 | 0,06773 | 0,07754 | 0,08239 |
| 541,5499 | 0,05783 | 0,05913 | 0,06771 | 0,07739 | 0,08223 |
| 541,58708 | 0,05778 | 0,05913 | 0,06769 | 0,0772 | 0,08205 |
| 541,62427 | 0,05771 | 0,05915 | 0,06766 | 0,07698 | 0,08184 |
| 541,66145 | 0,05763 | 0,05917 | 0,06762 | 0,07674 | 0,0816 |
| 541,69863 | 0,05753 | 0,05919 | 0,06756 | 0,07647 | 0,08132 |
| 541,73581 | 0,05742 | 0,05922 | 0,06749 | 0,07616 | 0,081 |
| 541,77299 | 0,05728 | 0,05924 | 0,06741 | 0,0758 | 0,08064 |
| 541,81018 | 0,05714 | 0,05926 | 0,06731 | 0,0754 | 0,08024 |
| 541,84736 | 0,05697 | 0,05928 | 0,06719 | 0,07496 | 0,07979 |
| 541,88454 | 0,05678 | 0,05929 | 0,06705 | 0,07447 | 0,07928 |
| 541,92172 | 0,05656 | 0,05929 | 0,0669 | 0,07392 | 0,0787 |
| 541,9589 | 0,05633 | 0,05927 | 0,06672 | 0,0733 | 0,07806 |
| 541,99609 | 0,05607 | 0,05924 | 0,0665 | 0,07263 | 0,07736 |
| 542,03327 | 0,05577 | 0,05918 | 0,06626 | 0,07189 | 0,0766 |
| 542,07045 | 0,05545 | 0,05909 | 0,06599 | 0,07109 | 0,07574 |
| 542,10763 | 0,0551 | 0,05898 | 0,0657 | 0,0702 | 0,0748 |
| 542,14481 | 0,05472 | 0,05884 | 0,06535 | 0,06924 | 0,07378 |
| 542,182 | 0,0543 | 0,05866 | 0,06497 | 0,06821 | 0,07269 |
| 542,21918 | 0,05384 | 0,05843 | 0,06454 | 0,06711 | 0,07151 |
| 542,25636 | 0,05334 | 0,05817 | 0,06407 | 0,06592 | 0,07022 |
| 542,29354 | 0,05281 | 0,05785 | 0,06356 | 0,06465 | 0,06886 |
| 542,33072 | 0,05224 | 0,0575 | 0,06298 | 0,06331 | 0,06741 |
| 542,36791 | 0,05161 | 0,05707 | 0,06235 | 0,0619 | 0,06589 |
| 542,40509 | 0,05095 | 0,05659 | 0,06167 | 0,06041 | 0,06427 |
| 542,44227 | 0,05024 | 0,05605 | 0,06094 | 0,05884 | 0,06257 |
| 542,47945 | 0,0495 | 0,05546 | 0,06013 | 0,05722 | 0,0608 |
| 542,51663 | 0,0487 | 0,0548 | 0,05926 | 0,05553 | 0,05897 |
| 542,55382 | 0,04785 | 0,05407 | 0,05834 | 0,0538 | 0,05707 |
| 542,591 | 0,04696 | 0,05328 | 0,05737 | 0,052 | 0,05511 |
| 542,62818 | 0,04603 | 0,05243 | 0,05632 | 0,05016 | 0,0531 |
| 542,66536 | 0,04505 | 0,05151 | 0,0552 | 0,04829 | 0,05105 |
| 542,70254 | 0,04403 | 0,05052 | 0,05403 | 0,04639 | 0,04897 |
| 542,73973 | 0,04297 | 0,04948 | 0,05281 | 0,04446 | 0,04686 |
| 542,77691 | 0,04187 | 0,04838 | 0,05153 | 0,04252 | 0,04473 |
| 542,81409 | 0,04073 | 0,04722 | 0,05018 | 0,04057 | 0,0426 |
| 542,85127 | 0,03956 | 0,046 | 0,0488 | 0,03862 | 0,04047 |
| 542,88845 | 0,03835 | 0,04473 | 0,04736 | 0,03668 | 0,03834 |
| 542,92564 | 0,03712 | 0,04342 | 0,04589 | 0,03475 | 0,03624 |
| 542,96282 | 0,03587 | 0,04207 | 0,04438 | 0,03285 | 0,03417 |
| 543 | 0,03459 | 0,04068 | 0,04283 | 0,03097 | 0,03213 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00011 | 0,00012 | 6e-05 | 1e-05 | 2e-05 |
| 524,03718 | 0,00012 | 0,00013 | 6e-05 | 2e-05 | 3e-05 |
| 524,07436 | 0,00013 | 0,00013 | 6e-05 | 2e-05 | 3e-05 |
| 524,11155 | 0,00013 | 0,00013 | 6e-05 | 2e-05 | 3e-05 |
| 524,14873 | 0,00013 | 0,00014 | 6e-05 | 2e-05 | 3e-05 |
| 524,18591 | 0,00014 | 0,00014 | 7e-05 | 3e-05 | 4e-05 |
| 524,22309 | 0,00014 | 0,00014 | 7e-05 | 3e-05 | 4e-05 |
| 524,26027 | 0,00014 | 0,00014 | 7e-05 | 3e-05 | 4e-05 |
| 524,29746 | 0,00014 | 0,00013 | 8e-05 | 3e-05 | 4e-05 |
| 524,33464 | 0,00014 | 0,00013 | 8e-05 | 4e-05 | 5e-05 |
| 524,37182 | 0,00014 | 0,00013 | 9e-05 | 4e-05 | 5e-05 |
| 524,409 | 0,00014 | 0,00013 | 9e-05 | 4e-05 | 5e-05 |
| 524,44618 | 0,00014 | 0,00013 | 1e-04 | 4e-05 | 5e-05 |
| 524,48337 | 0,00015 | 0,00012 | 1e-04 | 5e-05 | 5e-05 |
| 524,52055 | 0,00015 | 0,00012 | 0,00011 | 5e-05 | 5e-05 |
| 524,55773 | 0,00015 | 0,00012 | 0,00012 | 5e-05 | 5e-05 |
| 524,59491 | 0,00015 | 0,00012 | 0,00013 | 6e-05 | 5e-05 |
| 524,63209 | 0,00016 | 0,00012 | 0,00014 | 6e-05 | 6e-05 |
| 524,66928 | 0,00016 | 0,00013 | 0,00014 | 6e-05 | 6e-05 |
| 524,70646 | 0,00017 | 0,00013 | 0,00015 | 7e-05 | 6e-05 |
| 524,74364 | 0,00018 | 0,00014 | 0,00016 | 7e-05 | 6e-05 |
| 524,78082 | 0,00018 | 0,00014 | 0,00017 | 8e-05 | 6e-05 |
| 524,818 | 0,00019 | 0,00015 | 0,00018 | 8e-05 | 6e-05 |
| 524,85519 | 2e-04 | 0,00016 | 0,00019 | 9e-05 | 6e-05 |
| 524,89237 | 0,00021 | 0,00017 | 0,00019 | 9e-05 | 6e-05 |
| 524,92955 | 0,00022 | 0,00018 | 2e-04 | 1e-04 | 7e-05 |
| 524,96673 | 0,00023 | 0,00019 | 0,00021 | 1e-04 | 7e-05 |
| 525,00391 | 0,00024 | 2e-04 | 0,00022 | 0,00011 | 7e-05 |
| 525,0411 | 0,00025 | 0,00021 | 0,00022 | 0,00011 | 7e-05 |
| 525,07828 | 0,00026 | 0,00022 | 0,00023 | 0,00011 | 7e-05 |
| 525,11546 | 0,00027 | 0,00024 | 0,00024 | 0,00011 | 7e-05 |
| 525,15264 | 0,00028 | 0,00025 | 0,00024 | 0,00012 | 8e-05 |
| 525,18982 | 0,00029 | 0,00026 | 0,00025 | 0,00012 | 8e-05 |
| 525,22701 | 0,00031 | 0,00027 | 0,00026 | 0,00012 | 8e-05 |
| 525,26419 | 0,00032 | 0,00028 | 0,00027 | 0,00012 | 8e-05 |
| 525,30137 | 0,00034 | 3e-04 | 0,00028 | 0,00013 | 9e-05 |
| 525,33855 | 0,00036 | 0,00031 | 0,00029 | 0,00013 | 9e-05 |
| 525,37573 | 0,00039 | 0,00032 | 0,00031 | 0,00014 | 1e-04 |
| 525,41292 | 0,00042 | 0,00034 | 0,00033 | 0,00015 | 0,00011 |
| 525,4501 | 0,00046 | 0,00036 | 0,00035 | 0,00016 | 0,00012 |
| 525,48728 | 5e-04 | 0,00038 | 0,00038 | 0,00018 | 0,00013 |
| 525,52446 | 0,00056 | 0,00041 | 0,00041 | 2e-04 | 0,00015 |
| 525,56164 | 0,00062 | 0,00045 | 0,00045 | 0,00023 | 0,00017 |
| 525,59883 | 0,00069 | 0,00049 | 0,00049 | 0,00026 | 2e-04 |
| 525,63601 | 0,00077 | 0,00054 | 0,00055 | 0,00031 | 0,00024 |
| 525,67319 | 0,00086 | 0,00059 | 0,00061 | 0,00036 | 0,00028 |
| 525,71037 | 0,00096 | 0,00066 | 0,00068 | 0,00042 | 0,00034 |
| 525,74755 | 0,00106 | 0,00073 | 0,00075 | 5e-04 | 4e-04 |
| 525,78474 | 0,00118 | 0,00081 | 0,00083 | 0,00059 | 0,00048 |
| 525,82192 | 0,0013 | 9e-04 | 0,00092 | 0,00069 | 0,00058 |
| 525,8591 | 0,00142 | 0,001 | 0,00102 | 0,00081 | 0,00068 |
| 525,89628 | 0,00154 | 0,0011 | 0,00111 | 0,00095 | 0,00081 |
| 525,93346 | 0,00167 | 0,00121 | 0,00122 | 0,0011 | 0,00094 |
| 525,97065 | 0,0018 | 0,00132 | 0,00132 | 0,00126 | 0,0011 |
| 526,00783 | 0,00193 | 0,00144 | 0,00143 | 0,00144 | 0,00126 |
| 526,04501 | 0,00206 | 0,00156 | 0,00154 | 0,00164 | 0,00144 |
| 526,08219 | 0,00219 | 0,00168 | 0,00165 | 0,00185 | 0,00163 |
| 526,11937 | 0,00233 | 0,00181 | 0,00176 | 0,00207 | 0,00184 |
| 526,15656 | 0,00246 | 0,00194 | 0,00188 | 0,00231 | 0,00205 |
| 526,19374 | 0,00261 | 0,00208 | 0,00201 | 0,00255 | 0,00227 |
| 526,23092 | 0,00277 | 0,00223 | 0,00214 | 0,0028 | 0,00249 |
| 526,2681 | 0,00294 | 0,0024 | 0,00228 | 0,00304 | 0,00271 |
| 526,30528 | 0,00313 | 0,00257 | 0,00243 | 0,00329 | 0,00293 |
| 526,34247 | 0,00333 | 0,00276 | 0,0026 | 0,00352 | 0,00314 |
| 526,37965 | 0,00355 | 0,00296 | 0,00278 | 0,00374 | 0,00333 |
| 526,41683 | 0,00378 | 0,00318 | 0,00297 | 0,00395 | 0,00352 |
| 526,45401 | 0,00403 | 0,00341 | 0,00318 | 0,00413 | 0,00368 |
| 526,49119 | 0,00428 | 0,00366 | 0,0034 | 0,00429 | 0,00382 |
| 526,52838 | 0,00455 | 0,00391 | 0,00362 | 0,00441 | 0,00393 |
| 526,56556 | 0,00481 | 0,00417 | 0,00385 | 0,00451 | 0,00402 |
| 526,60274 | 0,00507 | 0,00443 | 0,00408 | 0,00457 | 0,00408 |
| 526,63992 | 0,00533 | 0,00469 | 0,00431 | 0,00461 | 0,00412 |
| 526,6771 | 0,00557 | 0,00495 | 0,00453 | 0,00461 | 0,00413 |
| 526,71429 | 0,00579 | 0,0052 | 0,00474 | 0,00459 | 0,00412 |
| 526,75147 | 0,006 | 0,00543 | 0,00493 | 0,00456 | 0,0041 |
| 526,78865 | 0,0062 | 0,00565 | 0,00511 | 0,00451 | 0,00406 |
| 526,82583 | 0,00638 | 0,00586 | 0,00527 | 0,00446 | 0,00402 |
| 526,86301 | 0,00655 | 0,00606 | 0,00541 | 0,0044 | 0,00398 |
| 526,9002 | 0,00671 | 0,00625 | 0,00554 | 0,00436 | 0,00394 |
| 526,93738 | 0,00687 | 0,00642 | 0,00567 | 0,00432 | 0,00392 |
| 526,97456 | 0,00703 | 0,0066 | 0,00578 | 0,00431 | 0,0039 |
| 527,01174 | 0,0072 | 0,00677 | 0,00589 | 0,00431 | 0,00389 |
| 527,04892 | 0,00739 | 0,00694 | 0,00601 | 0,00433 | 0,0039 |
| 527,08611 | 0,00759 | 0,00713 | 0,00614 | 0,00437 | 0,00393 |
| 527,12329 | 0,00781 | 0,00731 | 0,00628 | 0,00444 | 0,00398 |
| 527,16047 | 0,00806 | 0,00751 | 0,00644 | 0,00452 | 0,00404 |
| 527,19765 | 0,00833 | 0,00772 | 0,00662 | 0,00464 | 0,00412 |
| 527,23483 | 0,00862 | 0,00795 | 0,00683 | 0,00477 | 0,00421 |
| 527,27202 | 0,00894 | 0,00819 | 0,00707 | 0,00492 | 0,00433 |
| 527,3092 | 0,00928 | 0,00845 | 0,00734 | 0,0051 | 0,00446 |
| 527,34638 | 0,00965 | 0,00873 | 0,00765 | 0,00529 | 0,00462 |
| 527,38356 | 0,01005 | 0,00904 | 0,008 | 0,00551 | 0,0048 |
| 527,42074 | 0,01047 | 0,00938 | 0,00839 | 0,00576 | 0,005 |
| 527,45793 | 0,01093 | 0,00975 | 0,00883 | 0,00603 | 0,00523 |
| 527,49511 | 0,01141 | 0,01016 | 0,0093 | 0,00633 | 0,00549 |
| 527,53229 | 0,01192 | 0,0106 | 0,00983 | 0,00667 | 0,00579 |
| 527,56947 | 0,01247 | 0,01109 | 0,01039 | 0,00704 | 0,00613 |
| 527,60665 | 0,01305 | 0,01162 | 0,011 | 0,00746 | 0,00651 |
| 527,64384 | 0,01365 | 0,01219 | 0,01165 | 0,00791 | 0,00694 |
| 527,68102 | 0,01428 | 0,0128 | 0,01233 | 0,00841 | 0,00742 |
| 527,7182 | 0,01493 | 0,01345 | 0,01304 | 0,00896 | 0,00795 |
| 527,75538 | 0,01559 | 0,01411 | 0,01378 | 0,00955 | 0,00854 |
| 527,79256 | 0,01625 | 0,01479 | 0,01452 | 0,01021 | 0,00918 |
| 527,82975 | 0,01691 | 0,01548 | 0,01526 | 0,01092 | 0,00989 |
| 527,86693 | 0,01756 | 0,01616 | 0,01599 | 0,01168 | 0,01065 |
| 527,90411 | 0,01818 | 0,01682 | 0,0167 | 0,01251 | 0,01148 |
| 527,94129 | 0,01878 | 0,01746 | 0,01739 | 0,01339 | 0,01237 |
| 527,97847 | 0,01935 | 0,01806 | 0,01804 | 0,01431 | 0,0133 |
| 528,01566 | 0,01988 | 0,01862 | 0,01864 | 0,01527 | 0,01427 |
| 528,05284 | 0,02037 | 0,01914 | 0,01919 | 0,01625 | 0,01527 |
| 528,09002 | 0,02084 | 0,01961 | 0,0197 | 0,01725 | 0,0163 |
| 528,1272 | 0,02127 | 0,02004 | 0,02016 | 0,01826 | 0,01732 |
| 528,16438 | 0,02169 | 0,02043 | 0,02058 | 0,01924 | 0,01834 |
| 528,20157 | 0,02208 | 0,02078 | 0,02096 | 0,0202 | 0,01933 |
| 528,23875 | 0,02246 | 0,0211 | 0,02131 | 0,0211 | 0,02027 |
| 528,27593 | 0,02282 | 0,0214 | 0,02163 | 0,02192 | 0,02114 |
| 528,31311 | 0,02317 | 0,02168 | 0,02192 | 0,02266 | 0,02192 |
| 528,35029 | 0,02352 | 0,02194 | 0,0222 | 0,02331 | 0,02262 |
| 528,38748 | 0,02387 | 0,02219 | 0,02246 | 0,02385 | 0,02321 |
| 528,42466 | 0,0242 | 0,02243 | 0,02272 | 0,02429 | 0,02369 |
| 528,46184 | 0,02454 | 0,02267 | 0,02298 | 0,02461 | 0,02406 |
| 528,49902 | 0,02487 | 0,02291 | 0,02323 | 0,02484 | 0,02432 |
| 528,5362 | 0,0252 | 0,02315 | 0,02349 | 0,02497 | 0,02449 |
| 528,57339 | 0,02553 | 0,0234 | 0,02375 | 0,02503 | 0,02458 |
| 528,61057 | 0,02586 | 0,02366 | 0,02402 | 0,02503 | 0,02461 |
| 528,64775 | 0,02619 | 0,02392 | 0,02431 | 0,025 | 0,0246 |
| 528,68493 | 0,02653 | 0,0242 | 0,0246 | 0,02497 | 0,02459 |
| 528,72211 | 0,02688 | 0,0245 | 0,02491 | 0,02495 | 0,02459 |
| 528,7593 | 0,02723 | 0,02481 | 0,02524 | 0,02497 | 0,02462 |
| 528,79648 | 0,0276 | 0,02514 | 0,02558 | 0,02503 | 0,02471 |
| 528,83366 | 0,02797 | 0,02549 | 0,02593 | 0,02516 | 0,02485 |
| 528,87084 | 0,02836 | 0,02585 | 0,02629 | 0,02535 | 0,02507 |
| 528,90802 | 0,02874 | 0,02622 | 0,02666 | 0,0256 | 0,02535 |
| 528,94521 | 0,02912 | 0,02659 | 0,02702 | 0,02592 | 0,02569 |
| 528,98239 | 0,02949 | 0,02697 | 0,02737 | 0,02627 | 0,02608 |
| 529,01957 | 0,02985 | 0,02733 | 0,02771 | 0,02665 | 0,02649 |
| 529,05675 | 0,03017 | 0,02768 | 0,02802 | 0,02704 | 0,02692 |
| 529,09393 | 0,03046 | 0,028 | 0,0283 | 0,02742 | 0,02733 |
| 529,13112 | 0,03072 | 0,02829 | 0,02855 | 0,02777 | 0,02771 |
| 529,1683 | 0,03093 | 0,02854 | 0,02876 | 0,0281 | 0,02805 |
| 529,20548 | 0,0311 | 0,02876 | 0,02893 | 0,02837 | 0,02835 |
| 529,24266 | 0,03124 | 0,02894 | 0,02906 | 0,02861 | 0,02858 |
| 529,27984 | 0,03133 | 0,02909 | 0,02916 | 0,02879 | 0,02876 |
| 529,31703 | 0,0314 | 0,02922 | 0,02925 | 0,02893 | 0,02889 |
| 529,35421 | 0,03145 | 0,02932 | 0,02932 | 0,02904 | 0,02898 |
| 529,39139 | 0,03149 | 0,02942 | 0,02939 | 0,02914 | 0,02905 |
| 529,42857 | 0,03155 | 0,02954 | 0,02948 | 0,02924 | 0,02911 |
| 529,46575 | 0,03163 | 0,02967 | 0,0296 | 0,02934 | 0,02918 |
| 529,50294 | 0,03174 | 0,02984 | 0,02976 | 0,02947 | 0,02927 |
| 529,54012 | 0,03191 | 0,03007 | 0,02998 | 0,02963 | 0,0294 |
| 529,5773 | 0,03214 | 0,03035 | 0,03027 | 0,02983 | 0,02957 |
| 529,61448 | 0,03245 | 0,0307 | 0,03064 | 0,03008 | 0,02981 |
| 529,65166 | 0,03283 | 0,03114 | 0,03109 | 0,0304 | 0,03012 |
| 529,68885 | 0,0333 | 0,03166 | 0,03163 | 0,03077 | 0,0305 |
| 529,72603 | 0,03388 | 0,03229 | 0,03225 | 0,03121 | 0,03095 |
| 529,76321 | 0,03455 | 0,033 | 0,03298 | 0,03171 | 0,03148 |
| 529,80039 | 0,0353 | 0,03382 | 0,03379 | 0,03226 | 0,03208 |
| 529,83757 | 0,03615 | 0,03471 | 0,03468 | 0,03289 | 0,03276 |
| 529,87476 | 0,03707 | 0,03569 | 0,03564 | 0,03358 | 0,03351 |
| 529,91194 | 0,03806 | 0,03674 | 0,03666 | 0,03434 | 0,03433 |
| 529,94912 | 0,0391 | 0,03784 | 0,03774 | 0,03517 | 0,03524 |
| 529,9863 | 0,0402 | 0,039 | 0,03885 | 0,03609 | 0,03624 |
| 530,02348 | 0,04132 | 0,04019 | 0,03999 | 0,0371 | 0,03733 |
| 530,06067 | 0,04247 | 0,04139 | 0,04114 | 0,0382 | 0,03851 |
| 530,09785 | 0,04361 | 0,04259 | 0,04229 | 0,03938 | 0,03977 |
| 530,13503 | 0,04474 | 0,04376 | 0,04343 | 0,04064 | 0,04112 |
| 530,17221 | 0,04584 | 0,0449 | 0,04453 | 0,04198 | 0,04255 |
| 530,20939 | 0,0469 | 0,04599 | 0,04558 | 0,04338 | 0,04405 |
| 530,24658 | 0,0479 | 0,047 | 0,04658 | 0,04482 | 0,04558 |
| 530,28376 | 0,04883 | 0,04793 | 0,04751 | 0,04629 | 0,04714 |
| 530,32094 | 0,04967 | 0,04877 | 0,04835 | 0,04775 | 0,04869 |
| 530,35812 | 0,05042 | 0,0495 | 0,0491 | 0,04917 | 0,05018 |
| 530,3953 | 0,05107 | 0,05011 | 0,04975 | 0,05051 | 0,05159 |
| 530,43249 | 0,0516 | 0,05058 | 0,05028 | 0,05175 | 0,05287 |
| 530,46967 | 0,052 | 0,05093 | 0,05067 | 0,05284 | 0,05398 |
| 530,50685 | 0,05227 | 0,05114 | 0,05094 | 0,05375 | 0,05491 |
| 530,54403 | 0,05242 | 0,05122 | 0,05108 | 0,05447 | 0,05561 |
| 530,58121 | 0,05245 | 0,05118 | 0,05108 | 0,05497 | 0,05607 |
| 530,6184 | 0,05234 | 0,051 | 0,05095 | 0,05524 | 0,05627 |
| 530,65558 | 0,05211 | 0,05071 | 0,05069 | 0,05528 | 0,05623 |
| 530,69276 | 0,05177 | 0,05031 | 0,05032 | 0,05507 | 0,05592 |
| 530,72994 | 0,05132 | 0,04981 | 0,04983 | 0,05463 | 0,05538 |
| 530,76712 | 0,05077 | 0,04922 | 0,04924 | 0,05401 | 0,05464 |
| 530,80431 | 0,05015 | 0,04857 | 0,04857 | 0,05322 | 0,05374 |
| 530,84149 | 0,04948 | 0,04788 | 0,04786 | 0,05231 | 0,05274 |
| 530,87867 | 0,04879 | 0,04719 | 0,04713 | 0,05133 | 0,05167 |
| 530,91585 | 0,04809 | 0,0465 | 0,0464 | 0,05031 | 0,05058 |
| 530,95303 | 0,04743 | 0,04587 | 0,04572 | 0,04929 | 0,04952 |
| 530,99022 | 0,04683 | 0,04531 | 0,04512 | 0,04834 | 0,04854 |
| 531,0274 | 0,04632 | 0,04485 | 0,04463 | 0,04748 | 0,04769 |
| 531,06458 | 0,04593 | 0,04454 | 0,0443 | 0,04679 | 0,04704 |
| 531,10176 | 0,04571 | 0,04441 | 0,04415 | 0,0463 | 0,04659 |
| 531,13894 | 0,04568 | 0,0445 | 0,04425 | 0,04602 | 0,04639 |
| 531,17613 | 0,04586 | 0,04481 | 0,0446 | 0,04598 | 0,04645 |
| 531,21331 | 0,04626 | 0,04538 | 0,04522 | 0,04621 | 0,04679 |
| 531,25049 | 0,0469 | 0,04622 | 0,04613 | 0,04672 | 0,04741 |
| 531,28767 | 0,04779 | 0,04732 | 0,04733 | 0,0475 | 0,04833 |
| 531,32485 | 0,04891 | 0,04868 | 0,04881 | 0,04857 | 0,04953 |
| 531,36204 | 0,05026 | 0,05031 | 0,05055 | 0,04991 | 0,05102 |
| 531,39922 | 0,05182 | 0,05216 | 0,05254 | 0,05153 | 0,05279 |
| 531,4364 | 0,05357 | 0,05423 | 0,05475 | 0,05341 | 0,05483 |
| 531,47358 | 0,05549 | 0,05647 | 0,05712 | 0,05549 | 0,05708 |
| 531,51076 | 0,0575 | 0,05881 | 0,0596 | 0,05776 | 0,05951 |
| 531,54795 | 0,05957 | 0,06121 | 0,06212 | 0,06015 | 0,06208 |
| 531,58513 | 0,06164 | 0,06359 | 0,06461 | 0,06264 | 0,06474 |
| 531,62231 | 0,06367 | 0,0659 | 0,06701 | 0,06516 | 0,06743 |
| 531,65949 | 0,06561 | 0,06809 | 0,06927 | 0,06766 | 0,07009 |
| 531,69667 | 0,06743 | 0,0701 | 0,07133 | 0,07008 | 0,07264 |
| 531,73386 | 0,06908 | 0,07189 | 0,07314 | 0,07236 | 0,07502 |
| 531,77104 | 0,07053 | 0,07342 | 0,07466 | 0,07439 | 0,07712 |
| 531,80822 | 0,07174 | 0,07462 | 0,07584 | 0,07615 | 0,07888 |
| 531,8454 | 0,07272 | 0,07551 | 0,07666 | 0,0776 | 0,08027 |
| 531,88258 | 0,07346 | 0,07609 | 0,07715 | 0,07869 | 0,08124 |
| 531,91977 | 0,07399 | 0,07638 | 0,07732 | 0,07941 | 0,08178 |
| 531,95695 | 0,0743 | 0,07639 | 0,07719 | 0,07975 | 0,08187 |
| 531,99413 | 0,07443 | 0,07615 | 0,07678 | 0,07972 | 0,08153 |
| 532,03131 | 0,0744 | 0,07569 | 0,07612 | 0,07934 | 0,08078 |
| 532,06849 | 0,07424 | 0,07506 | 0,07527 | 0,07866 | 0,07968 |
| 532,10568 | 0,07397 | 0,07429 | 0,07426 | 0,0777 | 0,07827 |
| 532,14286 | 0,07362 | 0,07342 | 0,07312 | 0,07654 | 0,07664 |
| 532,18004 | 0,07323 | 0,07251 | 0,07191 | 0,07527 | 0,07489 |
| 532,21722 | 0,07282 | 0,07158 | 0,07068 | 0,07395 | 0,0731 |
| 532,2544 | 0,07242 | 0,07067 | 0,06946 | 0,07264 | 0,07135 |
| 532,29159 | 0,07206 | 0,06981 | 0,06829 | 0,07142 | 0,06972 |
| 532,32877 | 0,07174 | 0,06903 | 0,06719 | 0,07034 | 0,06827 |
| 532,36595 | 0,07149 | 0,06834 | 0,06621 | 0,06945 | 0,06705 |
| 532,40313 | 0,07133 | 0,06777 | 0,06535 | 0,0688 | 0,06613 |
| 532,44031 | 0,07127 | 0,06734 | 0,06466 | 0,06842 | 0,06553 |
| 532,4775 | 0,07134 | 0,06708 | 0,06417 | 0,06838 | 0,06533 |
| 532,51468 | 0,07157 | 0,06701 | 0,06391 | 0,06865 | 0,06548 |
| 532,55186 | 0,07197 | 0,06714 | 0,0639 | 0,06922 | 0,06599 |
| 532,58904 | 0,07256 | 0,0675 | 0,06415 | 0,07009 | 0,06683 |
| 532,62622 | 0,07335 | 0,06809 | 0,06469 | 0,07124 | 0,06797 |
| 532,66341 | 0,07437 | 0,06894 | 0,06553 | 0,07263 | 0,0694 |
| 532,70059 | 0,07564 | 0,07005 | 0,0667 | 0,07423 | 0,07106 |
| 532,73777 | 0,07714 | 0,07144 | 0,06818 | 0,07601 | 0,07291 |
| 532,77495 | 0,0789 | 0,07311 | 0,06998 | 0,07792 | 0,07491 |
| 532,81213 | 0,0809 | 0,07506 | 0,07209 | 0,07993 | 0,07701 |
| 532,84932 | 0,08315 | 0,07728 | 0,07452 | 0,08198 | 0,07917 |
| 532,8865 | 0,08558 | 0,07972 | 0,07718 | 0,08404 | 0,08133 |
| 532,92368 | 0,08816 | 0,08232 | 0,08002 | 0,08609 | 0,08346 |
| 532,96086 | 0,09084 | 0,08504 | 0,08299 | 0,08808 | 0,08552 |
| 532,99804 | 0,09355 | 0,08781 | 0,08599 | 0,08999 | 0,0875 |
| 533,03523 | 0,09623 | 0,09056 | 0,08897 | 0,09181 | 0,08937 |
| 533,07241 | 0,09882 | 0,09322 | 0,09183 | 0,09352 | 0,09111 |
| 533,10959 | 0,10124 | 0,09573 | 0,09449 | 0,09509 | 0,09268 |
| 533,14677 | 0,10345 | 0,098 | 0,09688 | 0,09651 | 0,09408 |
| 533,18395 | 0,10534 | 0,09994 | 0,09889 | 0,09772 | 0,09525 |
| 533,22114 | 0,10688 | 0,10151 | 0,10046 | 0,09873 | 0,09619 |
| 533,25832 | 0,10806 | 0,1027 | 0,10159 | 0,09953 | 0,09688 |
| 533,2955 | 0,10887 | 0,10348 | 0,10226 | 0,10009 | 0,09732 |
| 533,33268 | 0,10929 | 0,10386 | 0,10246 | 0,10041 | 0,0975 |
| 533,36986 | 0,10936 | 0,10385 | 0,10222 | 0,10049 | 0,09742 |
| 533,40705 | 0,10909 | 0,10348 | 0,10158 | 0,10035 | 0,09711 |
| 533,44423 | 0,10853 | 0,10279 | 0,10058 | 0,1 | 0,09657 |
| 533,48141 | 0,10771 | 0,10183 | 0,09928 | 0,09948 | 0,09586 |
| 533,51859 | 0,10669 | 0,10064 | 0,09775 | 0,09883 | 0,095 |
| 533,55577 | 0,10551 | 0,09931 | 0,09606 | 0,0981 | 0,09407 |
| 533,59295 | 0,10425 | 0,09789 | 0,0943 | 0,09735 | 0,09313 |
| 533,63014 | 0,10295 | 0,09645 | 0,09254 | 0,09664 | 0,09223 |
| 533,66732 | 0,10166 | 0,09502 | 0,09082 | 0,09601 | 0,09143 |
| 533,7045 | 0,10041 | 0,09365 | 0,0892 | 0,09549 | 0,09077 |
| 533,74168 | 0,09922 | 0,09237 | 0,0877 | 0,09513 | 0,09029 |
| 533,77886 | 0,09812 | 0,0912 | 0,08636 | 0,09496 | 0,09003 |
| 533,81605 | 0,09713 | 0,09017 | 0,08519 | 0,09497 | 0,08999 |
| 533,85323 | 0,09627 | 0,0893 | 0,08423 | 0,09519 | 0,09021 |
| 533,89041 | 0,09557 | 0,08861 | 0,08347 | 0,09565 | 0,0907 |
| 533,92759 | 0,09502 | 0,08809 | 0,08293 | 0,0963 | 0,09145 |
| 533,96477 | 0,09463 | 0,08775 | 0,08259 | 0,09713 | 0,09243 |
| 534,00196 | 0,09442 | 0,08761 | 0,08247 | 0,09813 | 0,09362 |
| 534,03914 | 0,09441 | 0,08766 | 0,08258 | 0,09928 | 0,09501 |
| 534,07632 | 0,09459 | 0,08793 | 0,08292 | 0,10054 | 0,09657 |
| 534,1135 | 0,09499 | 0,08843 | 0,0835 | 0,10188 | 0,09824 |
| 534,15068 | 0,09561 | 0,08915 | 0,08434 | 0,10327 | 0,09999 |
| 534,18787 | 0,09647 | 0,09012 | 0,08544 | 0,10465 | 0,10177 |
| 534,22505 | 0,09758 | 0,09136 | 0,08684 | 0,10597 | 0,1035 |
| 534,26223 | 0,09891 | 0,09284 | 0,08849 | 0,10716 | 0,1051 |
| 534,29941 | 0,10044 | 0,09454 | 0,09037 | 0,10816 | 0,1065 |
| 534,33659 | 0,10214 | 0,09643 | 0,09247 | 0,10892 | 0,10765 |
| 534,37378 | 0,10396 | 0,09846 | 0,09472 | 0,10938 | 0,10846 |
| 534,41096 | 0,10584 | 0,1006 | 0,09709 | 0,10949 | 0,10889 |
| 534,44814 | 0,10772 | 0,10278 | 0,0995 | 0,10921 | 0,10889 |
| 534,48532 | 0,10953 | 0,10492 | 0,10188 | 0,10852 | 0,10843 |
| 534,5225 | 0,11119 | 0,10694 | 0,10413 | 0,1074 | 0,1075 |
| 534,55969 | 0,11259 | 0,10874 | 0,10615 | 0,10585 | 0,10608 |
| 534,59687 | 0,11363 | 0,11021 | 0,10783 | 0,10383 | 0,10415 |
| 534,63405 | 0,11427 | 0,11129 | 0,1091 | 0,10144 | 0,1018 |
| 534,67123 | 0,11444 | 0,11191 | 0,1099 | 0,09872 | 0,09908 |
| 534,70841 | 0,1141 | 0,11202 | 0,11015 | 0,09571 | 0,09605 |
| 534,7456 | 0,11323 | 0,11157 | 0,10984 | 0,0925 | 0,09278 |
| 534,78278 | 0,11181 | 0,11056 | 0,10893 | 0,08913 | 0,08933 |
| 534,81996 | 0,10986 | 0,10899 | 0,10743 | 0,08568 | 0,08579 |
| 534,85714 | 0,10741 | 0,10687 | 0,10535 | 0,08221 | 0,08222 |
| 534,89432 | 0,1045 | 0,10423 | 0,10272 | 0,07881 | 0,07869 |
| 534,93151 | 0,10121 | 0,10114 | 0,09962 | 0,07553 | 0,07529 |
| 534,96869 | 0,09765 | 0,09772 | 0,09617 | 0,07246 | 0,07208 |
| 535,00587 | 0,09391 | 0,09407 | 0,09246 | 0,06962 | 0,06911 |
| 535,04305 | 0,09011 | 0,09029 | 0,0886 | 0,06707 | 0,06643 |
| 535,08023 | 0,08632 | 0,08648 | 0,08469 | 0,06483 | 0,06406 |
| 535,11742 | 0,08264 | 0,08272 | 0,08081 | 0,06292 | 0,06203 |
| 535,1546 | 0,07916 | 0,07913 | 0,07708 | 0,06136 | 0,06036 |
| 535,19178 | 0,07595 | 0,07578 | 0,07358 | 0,06017 | 0,05906 |
| 535,22896 | 0,07307 | 0,07275 | 0,07041 | 0,05935 | 0,05815 |
| 535,26614 | 0,07065 | 0,07016 | 0,06765 | 0,0589 | 0,05763 |
| 535,30333 | 0,06866 | 0,06803 | 0,06534 | 0,05886 | 0,05755 |
| 535,34051 | 0,06713 | 0,06637 | 0,06351 | 0,05919 | 0,05785 |
| 535,37769 | 0,06608 | 0,06522 | 0,06218 | 0,05986 | 0,05852 |
| 535,41487 | 0,06551 | 0,06458 | 0,06138 | 0,06088 | 0,05956 |
| 535,45205 | 0,06542 | 0,06446 | 0,0611 | 0,06222 | 0,06095 |
| 535,48924 | 0,06579 | 0,06485 | 0,06135 | 0,06387 | 0,06268 |
| 535,52642 | 0,06661 | 0,06572 | 0,0621 | 0,06581 | 0,06471 |
| 535,5636 | 0,06784 | 0,06707 | 0,06336 | 0,068 | 0,06701 |
| 535,60078 | 0,06949 | 0,06887 | 0,0651 | 0,07041 | 0,06956 |
| 535,63796 | 0,07147 | 0,07107 | 0,06723 | 0,07303 | 0,07232 |
| 535,67515 | 0,07373 | 0,07357 | 0,0697 | 0,07578 | 0,07522 |
| 535,71233 | 0,07621 | 0,07633 | 0,07244 | 0,07861 | 0,07821 |
| 535,74951 | 0,07886 | 0,07928 | 0,0754 | 0,08149 | 0,08122 |
| 535,78669 | 0,08161 | 0,08235 | 0,07849 | 0,08435 | 0,08421 |
| 535,82387 | 0,08439 | 0,08546 | 0,08165 | 0,08716 | 0,08713 |
| 535,86106 | 0,08715 | 0,08854 | 0,0848 | 0,08988 | 0,08992 |
| 535,89824 | 0,08982 | 0,09152 | 0,08785 | 0,09246 | 0,09254 |
| 535,93542 | 0,09232 | 0,0943 | 0,09071 | 0,09487 | 0,09496 |
| 535,9726 | 0,09458 | 0,09681 | 0,09331 | 0,09708 | 0,09713 |
| 536,00978 | 0,09656 | 0,09899 | 0,0956 | 0,09902 | 0,099 |
| 536,04697 | 0,0982 | 0,10079 | 0,09752 | 0,10069 | 0,10056 |
| 536,08415 | 0,09949 | 0,10218 | 0,09902 | 0,10207 | 0,1018 |
| 536,12133 | 0,10039 | 0,10313 | 0,10009 | 0,10314 | 0,10271 |
| 536,15851 | 0,10088 | 0,10362 | 0,1007 | 0,10389 | 0,10329 |
| 536,19569 | 0,10097 | 0,10366 | 0,10086 | 0,1043 | 0,10353 |
| 536,23288 | 0,10067 | 0,10324 | 0,10056 | 0,1044 | 0,10347 |
| 536,27006 | 0,09997 | 0,10238 | 0,0998 | 0,10419 | 0,10311 |
| 536,30724 | 0,09889 | 0,1011 | 0,09864 | 0,10372 | 0,10251 |
| 536,34442 | 0,09751 | 0,09948 | 0,09716 | 0,10302 | 0,10171 |
| 536,3816 | 0,09588 | 0,09759 | 0,09541 | 0,10216 | 0,1008 |
| 536,41879 | 0,09405 | 0,09548 | 0,09345 | 0,10126 | 0,09988 |
| 536,45597 | 0,09209 | 0,09322 | 0,09134 | 0,10038 | 0,09903 |
| 536,49315 | 0,09004 | 0,09088 | 0,08915 | 0,09961 | 0,09834 |
| 536,53033 | 0,08798 | 0,08853 | 0,08696 | 0,09904 | 0,09788 |
| 536,56751 | 0,08595 | 0,08622 | 0,08481 | 0,09871 | 0,09771 |
| 536,6047 | 0,08401 | 0,08402 | 0,08279 | 0,09869 | 0,09788 |
| 536,64188 | 0,08225 | 0,08202 | 0,08096 | 0,09899 | 0,0984 |
| 536,67906 | 0,08069 | 0,08026 | 0,07935 | 0,09961 | 0,09927 |
| 536,71624 | 0,07939 | 0,07877 | 0,07801 | 0,10052 | 0,10044 |
| 536,75342 | 0,07836 | 0,0776 | 0,07696 | 0,10162 | 0,1018 |
| 536,79061 | 0,07763 | 0,07676 | 0,07624 | 0,1028 | 0,10324 |
| 536,82779 | 0,07722 | 0,07629 | 0,07585 | 0,10393 | 0,10462 |
| 536,86497 | 0,07714 | 0,07617 | 0,07581 | 0,10491 | 0,10581 |
| 536,90215 | 0,07739 | 0,07643 | 0,07612 | 0,1056 | 0,10669 |
| 536,93933 | 0,07795 | 0,07705 | 0,07678 | 0,1059 | 0,10713 |
| 536,97652 | 0,07882 | 0,07802 | 0,07778 | 0,10571 | 0,10704 |
| 537,0137 | 0,07994 | 0,0793 | 0,07906 | 0,10495 | 0,10635 |
| 537,05088 | 0,08127 | 0,08082 | 0,08057 | 0,10357 | 0,10496 |
| 537,08806 | 0,08273 | 0,08253 | 0,08226 | 0,10155 | 0,10291 |
| 537,12524 | 0,08427 | 0,08436 | 0,08406 | 0,09899 | 0,10028 |
| 537,16243 | 0,08582 | 0,08623 | 0,08592 | 0,09597 | 0,09715 |
| 537,19961 | 0,08731 | 0,08807 | 0,08775 | 0,09257 | 0,09363 |
| 537,23679 | 0,08868 | 0,08981 | 0,08949 | 0,08892 | 0,08984 |
| 537,27397 | 0,08985 | 0,09137 | 0,09107 | 0,08512 | 0,08592 |
| 537,31115 | 0,09077 | 0,09269 | 0,09237 | 0,08131 | 0,08199 |
| 537,34834 | 0,09136 | 0,09366 | 0,09336 | 0,07759 | 0,07818 |
| 537,38552 | 0,09161 | 0,09428 | 0,09401 | 0,07409 | 0,0746 |
| 537,4227 | 0,09151 | 0,09452 | 0,09427 | 0,07094 | 0,0714 |
| 537,45988 | 0,09106 | 0,09437 | 0,09415 | 0,06817 | 0,06862 |
| 537,49706 | 0,09027 | 0,09383 | 0,09364 | 0,06583 | 0,0663 |
| 537,53425 | 0,08916 | 0,09294 | 0,09276 | 0,06396 | 0,06447 |
| 537,57143 | 0,08776 | 0,0917 | 0,09153 | 0,06254 | 0,06312 |
| 537,60861 | 0,08613 | 0,09017 | 0,08999 | 0,0616 | 0,06227 |
| 537,64579 | 0,08429 | 0,08839 | 0,08817 | 0,0611 | 0,06187 |
| 537,68297 | 0,08231 | 0,0864 | 0,08617 | 0,06103 | 0,06191 |
| 537,72016 | 0,08024 | 0,08428 | 0,08404 | 0,06135 | 0,06235 |
| 537,75734 | 0,07814 | 0,0821 | 0,08184 | 0,06206 | 0,06318 |
| 537,79452 | 0,07607 | 0,0799 | 0,07963 | 0,0631 | 0,06432 |
| 537,8317 | 0,07406 | 0,07774 | 0,07747 | 0,06442 | 0,06573 |
| 537,86888 | 0,07216 | 0,07567 | 0,07541 | 0,06599 | 0,06736 |
| 537,90607 | 0,07041 | 0,07374 | 0,07351 | 0,06778 | 0,06919 |
| 537,94325 | 0,06886 | 0,07199 | 0,07181 | 0,06975 | 0,07118 |
| 537,98043 | 0,06755 | 0,07048 | 0,07039 | 0,07189 | 0,07331 |
| 538,01761 | 0,06657 | 0,0693 | 0,06931 | 0,07419 | 0,07558 |
| 538,05479 | 0,06594 | 0,06849 | 0,06861 | 0,07665 | 0,07798 |
| 538,09198 | 0,06573 | 0,0681 | 0,06834 | 0,07926 | 0,08053 |
| 538,12916 | 0,06597 | 0,06819 | 0,06856 | 0,08206 | 0,08327 |
| 538,16634 | 0,06673 | 0,06882 | 0,06933 | 0,08507 | 0,08623 |
| 538,20352 | 0,06805 | 0,07004 | 0,0707 | 0,08832 | 0,08943 |
| 538,2407 | 0,06996 | 0,07189 | 0,07272 | 0,09184 | 0,09294 |
| 538,27789 | 0,07252 | 0,07443 | 0,07543 | 0,09567 | 0,09679 |
| 538,31507 | 0,07572 | 0,07767 | 0,07889 | 0,09985 | 0,10102 |
| 538,35225 | 0,07961 | 0,08165 | 0,08312 | 0,10439 | 0,10565 |
| 538,38943 | 0,08416 | 0,08636 | 0,08803 | 0,10928 | 0,11067 |
| 538,42661 | 0,08926 | 0,09169 | 0,09356 | 0,11448 | 0,11604 |
| 538,4638 | 0,0948 | 0,09754 | 0,09963 | 0,11995 | 0,1217 |
| 538,50098 | 0,10067 | 0,10378 | 0,10611 | 0,12554 | 0,12751 |
| 538,53816 | 0,10671 | 0,11027 | 0,11285 | 0,13108 | 0,13327 |
| 538,57534 | 0,11276 | 0,11683 | 0,11969 | 0,13636 | 0,13878 |
| 538,61252 | 0,11862 | 0,12327 | 0,12641 | 0,14118 | 0,14382 |
| 538,64971 | 0,1241 | 0,12936 | 0,1328 | 0,1453 | 0,14815 |
| 538,68689 | 0,12898 | 0,13489 | 0,13855 | 0,14852 | 0,15153 |
| 538,72407 | 0,13296 | 0,13952 | 0,14348 | 0,15064 | 0,15378 |
| 538,76125 | 0,13594 | 0,14314 | 0,14741 | 0,15149 | 0,15471 |
| 538,79843 | 0,13779 | 0,1456 | 0,15018 | 0,15095 | 0,1542 |
| 538,83562 | 0,13844 | 0,14679 | 0,15168 | 0,14882 | 0,15205 |
| 538,8728 | 0,13782 | 0,14665 | 0,15182 | 0,14535 | 0,1485 |
| 538,90998 | 0,13596 | 0,14516 | 0,15059 | 0,14068 | 0,1437 |
| 538,94716 | 0,1329 | 0,14235 | 0,14801 | 0,135 | 0,13787 |
| 538,98434 | 0,12873 | 0,13833 | 0,14416 | 0,1286 | 0,13127 |
| 539,02153 | 0,12361 | 0,13322 | 0,13904 | 0,12176 | 0,12421 |
| 539,05871 | 0,11765 | 0,12713 | 0,13303 | 0,1148 | 0,11702 |
| 539,09589 | 0,11117 | 0,12039 | 0,12633 | 0,10806 | 0,11003 |
| 539,13307 | 0,10443 | 0,11328 | 0,1192 | 0,10184 | 0,10358 |
| 539,17025 | 0,09766 | 0,10603 | 0,11188 | 0,0965 | 0,09803 |
| 539,20744 | 0,09108 | 0,0989 | 0,10463 | 0,0923 | 0,09364 |
| 539,24462 | 0,08491 | 0,09213 | 0,09769 | 0,08933 | 0,0905 |
| 539,2818 | 0,07934 | 0,08593 | 0,09128 | 0,08765 | 0,0887 |
| 539,31898 | 0,07456 | 0,08049 | 0,08562 | 0,08727 | 0,08825 |
| 539,35616 | 0,07068 | 0,07597 | 0,08099 | 0,08814 | 0,08907 |
| 539,39335 | 0,0679 | 0,07257 | 0,07746 | 0,09011 | 0,09106 |
| 539,43053 | 0,06625 | 0,07038 | 0,07506 | 0,09303 | 0,09403 |
| 539,46771 | 0,06567 | 0,06933 | 0,07384 | 0,09666 | 0,09775 |
| 539,50489 | 0,06612 | 0,06941 | 0,07376 | 0,10074 | 0,10197 |
| 539,54207 | 0,06753 | 0,07053 | 0,07476 | 0,10497 | 0,10637 |
| 539,57926 | 0,06979 | 0,07261 | 0,07676 | 0,10901 | 0,1106 |
| 539,61644 | 0,07274 | 0,07549 | 0,07961 | 0,11258 | 0,11438 |
| 539,65362 | 0,07622 | 0,07901 | 0,08316 | 0,11544 | 0,11745 |
| 539,6908 | 0,08004 | 0,08297 | 0,08721 | 0,11738 | 0,1196 |
| 539,72798 | 0,084 | 0,08718 | 0,09152 | 0,11824 | 0,12066 |
| 539,76517 | 0,08785 | 0,09137 | 0,09581 | 0,11793 | 0,12051 |
| 539,80235 | 0,09138 | 0,0953 | 0,09989 | 0,1164 | 0,11912 |
| 539,83953 | 0,09441 | 0,09879 | 0,10354 | 0,11366 | 0,11647 |
| 539,87671 | 0,09678 | 0,10164 | 0,10657 | 0,10972 | 0,11258 |
| 539,91389 | 0,09837 | 0,10372 | 0,10884 | 0,10479 | 0,10764 |
| 539,95108 | 0,09908 | 0,10492 | 0,11021 | 0,09913 | 0,10194 |
| 539,98826 | 0,09887 | 0,10515 | 0,1106 | 0,09298 | 0,09572 |
| 540,02544 | 0,09772 | 0,10437 | 0,10989 | 0,08661 | 0,08924 |
| 540,06262 | 0,09564 | 0,10261 | 0,10807 | 0,08028 | 0,08277 |
| 540,0998 | 0,0926 | 0,09979 | 0,10529 | 0,07426 | 0,0766 |
| 540,13699 | 0,08885 | 0,09614 | 0,10163 | 0,06879 | 0,07098 |
| 540,17417 | 0,08451 | 0,09179 | 0,09723 | 0,0641 | 0,06614 |
| 540,21135 | 0,07974 | 0,08692 | 0,09223 | 0,06039 | 0,0623 |
| 540,24853 | 0,07471 | 0,08169 | 0,08682 | 0,05792 | 0,05974 |
| 540,28571 | 0,06958 | 0,07627 | 0,08118 | 0,05664 | 0,05839 |
| 540,3229 | 0,06454 | 0,07087 | 0,0755 | 0,05655 | 0,05826 |
| 540,36008 | 0,05974 | 0,06564 | 0,06997 | 0,05758 | 0,0593 |
| 540,39726 | 0,05533 | 0,06077 | 0,06484 | 0,05962 | 0,06138 |
| 540,43444 | 0,05152 | 0,05645 | 0,06023 | 0,06252 | 0,06435 |
| 540,47162 | 0,04838 | 0,05283 | 0,05628 | 0,06604 | 0,06798 |
| 540,50881 | 0,04598 | 0,04994 | 0,05308 | 0,06996 | 0,07203 |
| 540,54599 | 0,04434 | 0,04785 | 0,05069 | 0,074 | 0,07621 |
| 540,58317 | 0,04349 | 0,04659 | 0,04916 | 0,07784 | 0,08019 |
| 540,62035 | 0,0434 | 0,04614 | 0,04848 | 0,08117 | 0,08364 |
| 540,65753 | 0,04404 | 0,04648 | 0,04864 | 0,08374 | 0,08632 |
| 540,69472 | 0,04533 | 0,04753 | 0,04957 | 0,08537 | 0,08803 |
| 540,7319 | 0,04719 | 0,04922 | 0,05127 | 0,08591 | 0,08862 |
| 540,76908 | 0,04953 | 0,05144 | 0,05351 | 0,08527 | 0,08799 |
| 540,80626 | 0,0522 | 0,05406 | 0,05615 | 0,08344 | 0,08612 |
| 540,84344 | 0,05502 | 0,05688 | 0,05905 | 0,08044 | 0,08305 |
| 540,88063 | 0,05784 | 0,05975 | 0,06205 | 0,07639 | 0,07888 |
| 540,91781 | 0,06052 | 0,06253 | 0,06499 | 0,07141 | 0,07375 |
| 540,95499 | 0,06293 | 0,06505 | 0,06771 | 0,06564 | 0,06781 |
| 540,99217 | 0,06494 | 0,0672 | 0,07007 | 0,05943 | 0,0614 |
| 541,02935 | 0,06645 | 0,06884 | 0,07194 | 0,05299 | 0,05475 |
| 541,06654 | 0,06735 | 0,06988 | 0,07313 | 0,04652 | 0,04807 |
| 541,10372 | 0,06756 | 0,07024 | 0,07357 | 0,04021 | 0,04155 |
| 541,1409 | 0,06698 | 0,06976 | 0,07325 | 0,03422 | 0,03537 |
| 541,17808 | 0,06567 | 0,06853 | 0,07214 | 0,02868 | 0,02964 |
| 541,21526 | 0,06367 | 0,06657 | 0,07026 | 0,02368 | 0,02446 |
| 541,25245 | 0,06102 | 0,06393 | 0,06765 | 0,01926 | 0,0199 |
| 541,28963 | 0,0578 | 0,06067 | 0,06438 | 0,01549 | 0,016 |
| 541,32681 | 0,0541 | 0,05689 | 0,06053 | 0,01234 | 0,01275 |
| 541,36399 | 0,05001 | 0,05269 | 0,05622 | 0,00974 | 0,01005 |
| 541,40117 | 0,04566 | 0,0482 | 0,05154 | 0,00763 | 0,00786 |
| 541,43836 | 0,04116 | 0,04352 | 0,04666 | 0,00594 | 0,00611 |
| 541,47554 | 0,03663 | 0,03879 | 0,04173 | 0,00462 | 0,00474 |
| 541,51272 | 0,0322 | 0,03415 | 0,03685 | 0,0036 | 0,00368 |
| 541,5499 | 0,02795 | 0,02968 | 0,03213 | 0,00282 | 0,00288 |
| 541,58708 | 0,02395 | 0,02546 | 0,02766 | 0,00224 | 0,00227 |
| 541,62427 | 0,02027 | 0,02156 | 0,0235 | 0,0018 | 0,00181 |
| 541,66145 | 0,01693 | 0,01802 | 0,0197 | 0,00148 | 0,00148 |
| 541,69863 | 0,01395 | 0,01486 | 0,0163 | 0,00123 | 0,00122 |
| 541,73581 | 0,01135 | 0,01209 | 0,01332 | 0,00103 | 0,00102 |
| 541,77299 | 0,00912 | 0,0097 | 0,01078 | 0,00087 | 0,00085 |
| 541,81018 | 0,00725 | 0,0077 | 0,00862 | 0,00074 | 0,00072 |
| 541,84736 | 0,00572 | 0,00606 | 0,00681 | 0,00063 | 0,00061 |
| 541,88454 | 0,00446 | 0,00471 | 0,00532 | 0,00053 | 0,00051 |
| 541,92172 | 0,00344 | 0,00362 | 0,0041 | 0,00045 | 0,00042 |
| 541,9589 | 0,00262 | 0,00275 | 0,00313 | 0,00037 | 0,00035 |
| 541,99609 | 0,00198 | 0,00206 | 0,00236 | 0,00031 | 0,00029 |
| 542,03327 | 0,00148 | 0,00153 | 0,00177 | 0,00025 | 0,00023 |
| 542,07045 | 0,0011 | 0,00113 | 0,00131 | 2e-04 | 0,00018 |
| 542,10763 | 0,00081 | 0,00082 | 0,00097 | 0,00016 | 0,00015 |
| 542,14481 | 6e-04 | 6e-04 | 0,00072 | 0,00013 | 0,00011 |
| 542,182 | 0,00044 | 0,00044 | 0,00052 | 0,00011 | 9e-05 |
| 542,21918 | 0,00032 | 0,00032 | 0,00038 | 8e-05 | 6e-05 |
| 542,25636 | 0,00024 | 0,00023 | 0,00028 | 7e-05 | 5e-05 |
| 542,29354 | 0,00017 | 0,00016 | 2e-04 | 5e-05 | 3e-05 |
| 542,33072 | 0,00012 | 0,00012 | 0,00014 | 4e-05 | 2e-05 |
| 542,36791 | 9e-05 | 9e-05 | 1e-04 | 4e-05 | 2e-05 |
| 542,40509 | 6e-05 | 6e-05 | 7e-05 | 3e-05 | 1e-05 |
| 542,44227 | 4e-05 | 5e-05 | 5e-05 | 3e-05 | 1e-05 |
| 542,47945 | 3e-05 | 3e-05 | 4e-05 | 2e-05 | 1e-05 |
| 542,51663 | 2e-05 | 3e-05 | 3e-05 | 2e-05 | 0 |
| 542,55382 | 2e-05 | 2e-05 | 2e-05 | 2e-05 | 0 |
| 542,591 | 1e-05 | 2e-05 | 1e-05 | 1e-05 | 0 |
| 542,62818 | 1e-05 | 1e-05 | 1e-05 | 1e-05 | 0 |
| 542,66536 | 0 | 1e-05 | 1e-05 | 1e-05 | 0 |
| 542,70254 | 0 | 1e-05 | 0 | 1e-05 | 0 |
| 542,73973 | 0 | 1e-05 | 0 | 1e-05 | 0 |
| 542,77691 | 0 | 1e-05 | 0 | 1e-05 | 0 |
| 542,81409 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,85127 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,88845 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,92564 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,96282 | 0 | 1e-05 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
We zien dat kinderen met een moeder met een verblijfsduur tussen de vijf en tien jaar gemiddeld een lagere onderwijsscore krijgen ten opzichte van kinderen met een moeder met een verblijfsduur van nul tot vijf jaar of van tien jaar of langer. Dit patroon is te verklaren door de interactie met de andere modelvariabelen. De coëfficiënten in figuren 1.1.1 en 1.1.2 geven aan dat kinderen met een moeder met een kortere verblijfsduur het relatief goed doen in relatie tot hun andere achtergrondvariabelen; met name het opleidingsniveau van de ouders en de herkomst. Zoals in het eerste onderzoeksrapport is te zien, is de categorie van de groep met een verblijfsduur van de moeder van 5 tot 10 jaar licht negatief gecorreleerd met de meeste andere variabelen en sterker positief gecorreleerd met herkomst7). Het gevolg hiervan is dat het positieve effect van verblijfsduur vaak teniet wordt gedaan door de negatieve coëfficiënten van herkomst. In de groep waar de verblijfsduur van de moeder tussen de vijf en tien jaar is, zijn kinderen met een niet-Nederlandse herkomst oververtegenwoordigd. Zoals in figuren 1.1.1 en 1.1.2 is te zien, hebben deze veelal een negatieve bijdrage aan de onderwijsscore. De groep kinderen met een moeder met een verblijfsduur van langer dan tien jaar is veruit het grootst in de onderzoekspopulatie: voor ongeveer 96 procent van de kinderen heeft de moeder een verblijfsduur van langer dan tien jaar.
Na het schooljaar 2020/’21 liggen de onderwijsscores voor kinderen met een moeder met een verblijfsduur van nul tot vijf jaar of van vijf tot tien jaar gemiddeld genomen hoger dan in het schooljaar 2019/’20. Dit verschil wordt verklaard door verschillen in achtergrondkenmerken van deze groepen tussen de schooljaren. We zien dat de dichtheid vanaf oktober 2021 iets afwijkt van de voorgaande jaren. Aangezien dit dezelfde data betreft als februari 2022, kunnen we opmaken dat dit wederom een gevolg is van de herijking van het model en de instroom van kinderen in groep 1 tussen oktober en februari.
Herkomst
De figuren 3.2.22 tot en met 3.2.30 laten de frequentiedichtheid zien van de onderwijsscore per herkomstcategorie uitgesplitst naar schooljaar. De verwachting is dat kinderen met Nederland als land van herkomst een hogere onderwijsscore hebben dan kinderen met een ander land van herkomst en dat dit stabiel is over de schooljaren heen. Hierbij is het van belang om te beseffen dat bij de afleiding van de herkomstvariabele een kind waarvan één van de ouders als herkomst Nederland heeft, ook Nederland als herkomst krijgt.
Uit de figuren 3.2.22 tot en met 3.2.30 is op te maken dat kinderen met Nederland, EU-15 en andere ontwikkelde economieën of Oost-Azië als herkomstcategorie vaker een hogere onderwijsscore hebben dan kinderen met een andere herkomstcategorie. De frequentiedichtheid-verdeling van deze categorieën is scheef met een staart naar links. Kinderen met Noord-Afrika, Overig Afrika, overig Azië, overig Latijns-Amerika, Suriname en (voormalige) Nederlandse Antillen en Turkije als herkomstcategorie hebben daarentegen vaker een relatief lage onderwijsscore. De frequentiedichtheid-verdeling van deze categorieën is fors scheef met een staart naar rechts. Hoewel minder scheef verdeeld, hebben ook kinderen uit Nieuwe EU-landen en economieën in transitie vaker een lagere onderwijsscore dan kinderen met Nederland of EU-15 en andere ontwikkelde economieën als referentiecategorie, dit verschil wordt minder over de jaren heen. Dit is wederom te verklaren door de herijking: deze categorie heeft een minder groot negatief effect dan voor de herijking.
De onderwijsscores voor diverse herkomstcategorieën, waaronder Europese herkomst, zijn gemiddeld genomen hoger vanaf het schooljaar 2020/’21 ten op zichtte van het schooljaar 2019/’20. Deze bevinding is consistent met de bevinding dat kinderen met een moeder die minder dan tien jaar in Nederland verblijft in het schooljaar 2020/’21 gemiddeld genomen hogere onderwijsscores hadden dan in schooljaar 2019/’20. Wat we ook zien is dat er voor de herkomstcategorie Nederland een verschil is tussen de meetmomenten oktober 2021 en februari 2022. Dit is wederom te wijten aan de herijking van het model.
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 0 | 0 | 0 |
| 524,74364 | 0 | 0 | 0 | 0 | 0 |
| 524,78082 | 0 | 0 | 0 | 0 | 0 |
| 524,818 | 0 | 0 | 0 | 0 | 0 |
| 524,85519 | 0 | 0 | 0 | 0 | 0 |
| 524,89237 | 0 | 0 | 0 | 0 | 0 |
| 524,92955 | 0 | 0 | 0 | 0 | 0 |
| 524,96673 | 0 | 0 | 0 | 0 | 0 |
| 525,00391 | 0 | 0 | 0 | 0 | 0 |
| 525,0411 | 0 | 0 | 0 | 0 | 0 |
| 525,07828 | 0 | 0 | 0 | 0 | 0 |
| 525,11546 | 1e-05 | 0 | 0 | 0 | 0 |
| 525,15264 | 1e-05 | 0 | 0 | 0 | 0 |
| 525,18982 | 1e-05 | 0 | 1e-05 | 0 | 0 |
| 525,22701 | 1e-05 | 1e-05 | 1e-05 | 0 | 0 |
| 525,26419 | 2e-05 | 1e-05 | 1e-05 | 0 | 0 |
| 525,30137 | 2e-05 | 1e-05 | 1e-05 | 0 | 0 |
| 525,33855 | 3e-05 | 2e-05 | 2e-05 | 0 | 0 |
| 525,37573 | 4e-05 | 2e-05 | 2e-05 | 0 | 0 |
| 525,41292 | 5e-05 | 3e-05 | 3e-05 | 0 | 0 |
| 525,4501 | 6e-05 | 3e-05 | 4e-05 | 0 | 0 |
| 525,48728 | 8e-05 | 4e-05 | 5e-05 | 0 | 0 |
| 525,52446 | 1e-04 | 5e-05 | 6e-05 | 0 | 0 |
| 525,56164 | 0,00011 | 6e-05 | 7e-05 | 0 | 0 |
| 525,59883 | 0,00014 | 7e-05 | 8e-05 | 0 | 0 |
| 525,63601 | 0,00016 | 8e-05 | 9e-05 | 0 | 0 |
| 525,67319 | 0,00018 | 9e-05 | 1e-04 | 1e-05 | 0 |
| 525,71037 | 0,00021 | 0,00011 | 0,00011 | 1e-05 | 1e-05 |
| 525,74755 | 0,00024 | 0,00012 | 0,00012 | 1e-05 | 1e-05 |
| 525,78474 | 0,00026 | 0,00014 | 0,00014 | 1e-05 | 1e-05 |
| 525,82192 | 0,00029 | 0,00015 | 0,00015 | 2e-05 | 2e-05 |
| 525,8591 | 0,00032 | 0,00017 | 0,00016 | 3e-05 | 2e-05 |
| 525,89628 | 0,00035 | 0,00018 | 0,00017 | 3e-05 | 3e-05 |
| 525,93346 | 0,00038 | 2e-04 | 0,00019 | 4e-05 | 3e-05 |
| 525,97065 | 4e-04 | 0,00021 | 2e-04 | 5e-05 | 4e-05 |
| 526,00783 | 0,00043 | 0,00023 | 0,00021 | 7e-05 | 5e-05 |
| 526,04501 | 0,00046 | 0,00024 | 0,00022 | 8e-05 | 6e-05 |
| 526,08219 | 0,00048 | 0,00026 | 0,00024 | 1e-04 | 8e-05 |
| 526,11937 | 5e-04 | 0,00028 | 0,00025 | 0,00011 | 9e-05 |
| 526,15656 | 0,00053 | 0,00029 | 0,00026 | 0,00013 | 1e-04 |
| 526,19374 | 0,00055 | 0,00031 | 0,00028 | 0,00015 | 0,00012 |
| 526,23092 | 0,00057 | 0,00033 | 3e-04 | 0,00017 | 0,00013 |
| 526,2681 | 6e-04 | 0,00035 | 0,00032 | 0,00019 | 0,00014 |
| 526,30528 | 0,00062 | 0,00038 | 0,00033 | 0,00021 | 0,00015 |
| 526,34247 | 0,00064 | 4e-04 | 0,00035 | 0,00022 | 0,00016 |
| 526,37965 | 0,00066 | 0,00042 | 0,00037 | 0,00024 | 0,00017 |
| 526,41683 | 0,00068 | 0,00044 | 0,00038 | 0,00025 | 0,00018 |
| 526,45401 | 0,00069 | 0,00046 | 4e-04 | 0,00026 | 0,00018 |
| 526,49119 | 0,00071 | 0,00047 | 0,00041 | 0,00027 | 0,00019 |
| 526,52838 | 0,00072 | 0,00049 | 0,00042 | 0,00028 | 0,00019 |
| 526,56556 | 0,00073 | 5e-04 | 0,00043 | 0,00029 | 0,00019 |
| 526,60274 | 0,00074 | 5e-04 | 0,00043 | 0,00029 | 2e-04 |
| 526,63992 | 0,00075 | 0,00051 | 0,00043 | 3e-04 | 2e-04 |
| 526,6771 | 0,00075 | 0,00051 | 0,00043 | 0,00031 | 2e-04 |
| 526,71429 | 0,00076 | 0,00051 | 0,00043 | 0,00032 | 0,00021 |
| 526,75147 | 0,00076 | 5e-04 | 0,00042 | 0,00033 | 0,00022 |
| 526,78865 | 0,00076 | 5e-04 | 0,00042 | 0,00034 | 0,00023 |
| 526,82583 | 0,00076 | 0,00049 | 0,00041 | 0,00036 | 0,00024 |
| 526,86301 | 0,00076 | 0,00049 | 0,00041 | 0,00037 | 0,00025 |
| 526,9002 | 0,00077 | 0,00048 | 4e-04 | 0,00039 | 0,00026 |
| 526,93738 | 0,00077 | 0,00048 | 4e-04 | 4e-04 | 0,00027 |
| 526,97456 | 0,00079 | 0,00048 | 4e-04 | 0,00042 | 0,00028 |
| 527,01174 | 8e-04 | 0,00049 | 0,00041 | 0,00043 | 0,00029 |
| 527,04892 | 0,00083 | 0,00049 | 0,00041 | 0,00044 | 3e-04 |
| 527,08611 | 0,00086 | 5e-04 | 0,00043 | 0,00045 | 0,00031 |
| 527,12329 | 0,00089 | 0,00052 | 0,00044 | 0,00045 | 0,00031 |
| 527,16047 | 0,00093 | 0,00053 | 0,00046 | 0,00046 | 0,00031 |
| 527,19765 | 0,00097 | 0,00056 | 0,00048 | 0,00045 | 3e-04 |
| 527,23483 | 0,00102 | 0,00058 | 0,00051 | 0,00045 | 3e-04 |
| 527,27202 | 0,00107 | 0,00061 | 0,00053 | 0,00044 | 0,00029 |
| 527,3092 | 0,00113 | 0,00065 | 0,00056 | 0,00043 | 0,00028 |
| 527,34638 | 0,00118 | 0,00068 | 6e-04 | 0,00043 | 0,00027 |
| 527,38356 | 0,00123 | 0,00072 | 0,00063 | 0,00042 | 0,00026 |
| 527,42074 | 0,00128 | 0,00076 | 0,00066 | 0,00041 | 0,00025 |
| 527,45793 | 0,00133 | 8e-04 | 0,00069 | 4e-04 | 0,00025 |
| 527,49511 | 0,00137 | 0,00085 | 0,00073 | 4e-04 | 0,00024 |
| 527,53229 | 0,00141 | 0,00089 | 0,00076 | 0,00039 | 0,00024 |
| 527,56947 | 0,00144 | 0,00093 | 0,00079 | 4e-04 | 0,00023 |
| 527,60665 | 0,00147 | 0,00098 | 0,00082 | 4e-04 | 0,00024 |
| 527,64384 | 0,0015 | 0,00102 | 0,00085 | 0,00042 | 0,00024 |
| 527,68102 | 0,00152 | 0,00106 | 0,00088 | 0,00044 | 0,00026 |
| 527,7182 | 0,00154 | 0,00111 | 0,00092 | 0,00047 | 0,00028 |
| 527,75538 | 0,00157 | 0,00116 | 0,00096 | 0,00051 | 0,00031 |
| 527,79256 | 0,00159 | 0,00121 | 0,001 | 0,00056 | 0,00036 |
| 527,82975 | 0,00163 | 0,00127 | 0,00105 | 0,00063 | 0,00042 |
| 527,86693 | 0,00168 | 0,00134 | 0,00112 | 0,00072 | 5e-04 |
| 527,90411 | 0,00174 | 0,00141 | 0,00119 | 0,00083 | 0,00061 |
| 527,94129 | 0,00183 | 0,00151 | 0,00128 | 0,00098 | 0,00074 |
| 527,97847 | 0,00193 | 0,00161 | 0,00139 | 0,00115 | 0,00091 |
| 528,01566 | 0,00206 | 0,00174 | 0,00152 | 0,00136 | 0,00111 |
| 528,05284 | 0,00222 | 0,0019 | 0,00168 | 0,00161 | 0,00135 |
| 528,09002 | 0,0024 | 0,00207 | 0,00186 | 0,0019 | 0,00162 |
| 528,1272 | 0,00262 | 0,00227 | 0,00207 | 0,00223 | 0,00194 |
| 528,16438 | 0,00286 | 0,00249 | 0,0023 | 0,00259 | 0,00229 |
| 528,20157 | 0,00313 | 0,00274 | 0,00255 | 0,00299 | 0,00268 |
| 528,23875 | 0,00342 | 0,003 | 0,00282 | 0,00341 | 0,00309 |
| 528,27593 | 0,00374 | 0,00329 | 0,00311 | 0,00386 | 0,00352 |
| 528,31311 | 0,00407 | 0,00359 | 0,00342 | 0,0043 | 0,00396 |
| 528,35029 | 0,00443 | 0,00391 | 0,00375 | 0,00474 | 0,0044 |
| 528,38748 | 0,00479 | 0,00425 | 0,00408 | 0,00517 | 0,00482 |
| 528,42466 | 0,00517 | 0,00459 | 0,00443 | 0,00558 | 0,00523 |
| 528,46184 | 0,00556 | 0,00494 | 0,00478 | 0,00595 | 0,00562 |
| 528,49902 | 0,00595 | 0,0053 | 0,00514 | 0,0063 | 0,00598 |
| 528,5362 | 0,00636 | 0,00566 | 0,00551 | 0,00661 | 0,00632 |
| 528,57339 | 0,00678 | 0,00604 | 0,0059 | 0,0069 | 0,00664 |
| 528,61057 | 0,00722 | 0,00643 | 0,0063 | 0,00717 | 0,00694 |
| 528,64775 | 0,00768 | 0,00684 | 0,00671 | 0,00743 | 0,00725 |
| 528,68493 | 0,00816 | 0,00727 | 0,00715 | 0,00771 | 0,00757 |
| 528,72211 | 0,00866 | 0,00772 | 0,00761 | 0,008 | 0,00792 |
| 528,7593 | 0,00919 | 0,00819 | 0,00809 | 0,00833 | 0,00832 |
| 528,79648 | 0,00974 | 0,00869 | 0,0086 | 0,00871 | 0,00875 |
| 528,83366 | 0,01031 | 0,0092 | 0,00912 | 0,00912 | 0,00924 |
| 528,87084 | 0,01089 | 0,00973 | 0,00965 | 0,00958 | 0,00977 |
| 528,90802 | 0,01146 | 0,01026 | 0,01018 | 0,01009 | 0,01035 |
| 528,94521 | 0,01202 | 0,01078 | 0,0107 | 0,01062 | 0,01095 |
| 528,98239 | 0,01255 | 0,01128 | 0,0112 | 0,01116 | 0,01156 |
| 529,01957 | 0,01304 | 0,01175 | 0,01166 | 0,0117 | 0,01217 |
| 529,05675 | 0,01347 | 0,01217 | 0,01207 | 0,01222 | 0,01273 |
| 529,09393 | 0,01383 | 0,01252 | 0,01243 | 0,01269 | 0,01323 |
| 529,13112 | 0,0141 | 0,01281 | 0,0127 | 0,01309 | 0,01366 |
| 529,1683 | 0,0143 | 0,01301 | 0,0129 | 0,01343 | 0,01399 |
| 529,20548 | 0,01441 | 0,01314 | 0,01303 | 0,01368 | 0,01423 |
| 529,24266 | 0,01445 | 0,0132 | 0,01308 | 0,01385 | 0,01436 |
| 529,27984 | 0,01443 | 0,01319 | 0,01308 | 0,01395 | 0,0144 |
| 529,31703 | 0,01437 | 0,01312 | 0,01303 | 0,01398 | 0,01435 |
| 529,35421 | 0,01428 | 0,01303 | 0,01296 | 0,01396 | 0,01423 |
| 529,39139 | 0,01419 | 0,01291 | 0,01288 | 0,01392 | 0,01407 |
| 529,42857 | 0,01412 | 0,01281 | 0,01282 | 0,01386 | 0,01389 |
| 529,46575 | 0,01411 | 0,01275 | 0,01281 | 0,01383 | 0,01372 |
| 529,50294 | 0,01419 | 0,01275 | 0,01287 | 0,01382 | 0,01359 |
| 529,54012 | 0,01436 | 0,01284 | 0,01303 | 0,01387 | 0,01351 |
| 529,5773 | 0,01466 | 0,01304 | 0,01331 | 0,01398 | 0,01351 |
| 529,61448 | 0,01509 | 0,01337 | 0,01372 | 0,01417 | 0,0136 |
| 529,65166 | 0,01567 | 0,01384 | 0,01426 | 0,01444 | 0,0138 |
| 529,68885 | 0,01639 | 0,01446 | 0,01496 | 0,01479 | 0,01409 |
| 529,72603 | 0,01726 | 0,01523 | 0,0158 | 0,01523 | 0,01451 |
| 529,76321 | 0,01828 | 0,01617 | 0,01679 | 0,01576 | 0,01503 |
| 529,80039 | 0,01943 | 0,01726 | 0,01792 | 0,0164 | 0,01568 |
| 529,83757 | 0,02072 | 0,01851 | 0,01918 | 0,01713 | 0,01645 |
| 529,87476 | 0,02211 | 0,01989 | 0,02056 | 0,01796 | 0,01735 |
| 529,91194 | 0,02358 | 0,02138 | 0,02204 | 0,0189 | 0,01836 |
| 529,94912 | 0,02512 | 0,02297 | 0,02358 | 0,01995 | 0,01951 |
| 529,9863 | 0,02669 | 0,02462 | 0,02517 | 0,02113 | 0,02079 |
| 530,02348 | 0,02828 | 0,02631 | 0,02677 | 0,02244 | 0,02221 |
| 530,06067 | 0,02987 | 0,02802 | 0,02837 | 0,02387 | 0,02378 |
| 530,09785 | 0,03142 | 0,02971 | 0,02994 | 0,02545 | 0,02549 |
| 530,13503 | 0,03293 | 0,03135 | 0,03147 | 0,02714 | 0,02733 |
| 530,17221 | 0,03437 | 0,03293 | 0,03291 | 0,02897 | 0,02931 |
| 530,20939 | 0,0357 | 0,03439 | 0,03426 | 0,03088 | 0,03139 |
| 530,24658 | 0,03692 | 0,03574 | 0,03549 | 0,03285 | 0,03352 |
| 530,28376 | 0,03802 | 0,03694 | 0,03658 | 0,03484 | 0,03568 |
| 530,32094 | 0,03898 | 0,03799 | 0,03753 | 0,03681 | 0,0378 |
| 530,35812 | 0,0398 | 0,03887 | 0,03832 | 0,0387 | 0,03983 |
| 530,3953 | 0,04047 | 0,03958 | 0,03896 | 0,04048 | 0,04172 |
| 530,43249 | 0,04099 | 0,04012 | 0,03943 | 0,04207 | 0,04342 |
| 530,46967 | 0,04135 | 0,04049 | 0,03974 | 0,04345 | 0,04485 |
| 530,50685 | 0,04155 | 0,04068 | 0,03987 | 0,04456 | 0,04598 |
| 530,54403 | 0,0416 | 0,04071 | 0,03984 | 0,04534 | 0,04674 |
| 530,58121 | 0,04147 | 0,04056 | 0,03964 | 0,04578 | 0,04711 |
| 530,6184 | 0,04121 | 0,04026 | 0,03927 | 0,04589 | 0,0471 |
| 530,65558 | 0,04081 | 0,03983 | 0,03875 | 0,04566 | 0,04673 |
| 530,69276 | 0,04029 | 0,03928 | 0,03811 | 0,04511 | 0,046 |
| 530,72994 | 0,03967 | 0,03863 | 0,03736 | 0,04427 | 0,04495 |
| 530,76712 | 0,03896 | 0,03789 | 0,03653 | 0,04317 | 0,04364 |
| 530,80431 | 0,03819 | 0,0371 | 0,03564 | 0,04186 | 0,04212 |
| 530,84149 | 0,03737 | 0,03628 | 0,03472 | 0,04039 | 0,04046 |
| 530,87867 | 0,03655 | 0,03545 | 0,0338 | 0,03884 | 0,03872 |
| 530,91585 | 0,03575 | 0,03465 | 0,03293 | 0,03727 | 0,03699 |
| 530,95303 | 0,03501 | 0,03393 | 0,03215 | 0,03576 | 0,03536 |
| 530,99022 | 0,03438 | 0,03333 | 0,03152 | 0,03438 | 0,03389 |
| 531,0274 | 0,03388 | 0,03288 | 0,03107 | 0,03319 | 0,03264 |
| 531,06458 | 0,03356 | 0,03262 | 0,03084 | 0,03225 | 0,03167 |
| 531,10176 | 0,03346 | 0,03259 | 0,03087 | 0,03161 | 0,03104 |
| 531,13894 | 0,0336 | 0,03283 | 0,03121 | 0,0313 | 0,03076 |
| 531,17613 | 0,03401 | 0,03336 | 0,03187 | 0,03137 | 0,03088 |
| 531,21331 | 0,03472 | 0,03422 | 0,0329 | 0,03182 | 0,03141 |
| 531,25049 | 0,03575 | 0,03542 | 0,03429 | 0,03267 | 0,03236 |
| 531,28767 | 0,0371 | 0,03697 | 0,03606 | 0,03397 | 0,03376 |
| 531,32485 | 0,0388 | 0,03892 | 0,03822 | 0,03566 | 0,03558 |
| 531,36204 | 0,0408 | 0,04121 | 0,04075 | 0,03773 | 0,03779 |
| 531,39922 | 0,04307 | 0,04379 | 0,04358 | 0,04014 | 0,04037 |
| 531,4364 | 0,04556 | 0,04663 | 0,04666 | 0,04286 | 0,04327 |
| 531,47358 | 0,04822 | 0,04966 | 0,04992 | 0,04585 | 0,04647 |
| 531,51076 | 0,05099 | 0,05282 | 0,05329 | 0,04906 | 0,04991 |
| 531,54795 | 0,0538 | 0,05604 | 0,05668 | 0,05244 | 0,05353 |
| 531,58513 | 0,05659 | 0,05922 | 0,06001 | 0,05592 | 0,05727 |
| 531,62231 | 0,05927 | 0,06229 | 0,06319 | 0,05943 | 0,06104 |
| 531,65949 | 0,06178 | 0,06514 | 0,06613 | 0,06289 | 0,06475 |
| 531,69667 | 0,06403 | 0,06768 | 0,06872 | 0,06618 | 0,06827 |
| 531,73386 | 0,06599 | 0,06985 | 0,0709 | 0,06924 | 0,07152 |
| 531,77104 | 0,06761 | 0,07162 | 0,07263 | 0,07197 | 0,07438 |
| 531,80822 | 0,06889 | 0,07295 | 0,0739 | 0,0743 | 0,07678 |
| 531,8454 | 0,06982 | 0,07382 | 0,07468 | 0,07616 | 0,07863 |
| 531,88258 | 0,0704 | 0,07426 | 0,07499 | 0,07752 | 0,07989 |
| 531,91977 | 0,07066 | 0,07426 | 0,07484 | 0,07833 | 0,08051 |
| 531,95695 | 0,07063 | 0,07389 | 0,07428 | 0,0786 | 0,08049 |
| 531,99413 | 0,07035 | 0,07317 | 0,07336 | 0,07834 | 0,07986 |
| 532,03131 | 0,06986 | 0,07217 | 0,07212 | 0,07754 | 0,07861 |
| 532,06849 | 0,06921 | 0,07094 | 0,07063 | 0,07632 | 0,07686 |
| 532,10568 | 0,06847 | 0,06958 | 0,06897 | 0,07477 | 0,07474 |
| 532,14286 | 0,06769 | 0,06815 | 0,06722 | 0,07298 | 0,07235 |
| 532,18004 | 0,0669 | 0,06671 | 0,06544 | 0,07105 | 0,0698 |
| 532,21722 | 0,06615 | 0,0653 | 0,06367 | 0,06907 | 0,06722 |
| 532,2544 | 0,06547 | 0,06397 | 0,06198 | 0,06715 | 0,06471 |
| 532,29159 | 0,06488 | 0,06276 | 0,0604 | 0,06536 | 0,06239 |
| 532,32877 | 0,06441 | 0,0617 | 0,05897 | 0,0638 | 0,06034 |
| 532,36595 | 0,06407 | 0,06081 | 0,05773 | 0,06253 | 0,05865 |
| 532,40313 | 0,06389 | 0,06013 | 0,05671 | 0,06165 | 0,05741 |
| 532,44031 | 0,06391 | 0,05968 | 0,05597 | 0,0612 | 0,05668 |
| 532,4775 | 0,06412 | 0,05946 | 0,05551 | 0,06117 | 0,05645 |
| 532,51468 | 0,06455 | 0,0595 | 0,05536 | 0,06159 | 0,05674 |
| 532,55186 | 0,06521 | 0,05982 | 0,05554 | 0,06244 | 0,05753 |
| 532,58904 | 0,06614 | 0,06044 | 0,05608 | 0,06372 | 0,05881 |
| 532,62622 | 0,06734 | 0,06137 | 0,05701 | 0,06538 | 0,06052 |
| 532,66341 | 0,06885 | 0,06264 | 0,05834 | 0,06738 | 0,06263 |
| 532,70059 | 0,07068 | 0,06427 | 0,0601 | 0,06967 | 0,06507 |
| 532,73777 | 0,07284 | 0,06627 | 0,06229 | 0,07219 | 0,06777 |
| 532,77495 | 0,07535 | 0,06866 | 0,06491 | 0,07488 | 0,07066 |
| 532,81213 | 0,0782 | 0,07143 | 0,06799 | 0,07766 | 0,07366 |
| 532,84932 | 0,08135 | 0,07453 | 0,07144 | 0,08046 | 0,07668 |
| 532,8865 | 0,08473 | 0,07792 | 0,0752 | 0,08324 | 0,07968 |
| 532,92368 | 0,08831 | 0,08153 | 0,0792 | 0,08596 | 0,08259 |
| 532,96086 | 0,092 | 0,08527 | 0,08334 | 0,08858 | 0,08538 |
| 532,99804 | 0,09571 | 0,08907 | 0,08752 | 0,09107 | 0,08802 |
| 533,03523 | 0,09935 | 0,09281 | 0,09161 | 0,09341 | 0,09048 |
| 533,07241 | 0,10283 | 0,09639 | 0,09551 | 0,09558 | 0,09273 |
| 533,10959 | 0,10603 | 0,09969 | 0,09908 | 0,09757 | 0,09476 |
| 533,14677 | 0,10886 | 0,1026 | 0,10219 | 0,09933 | 0,09651 |
| 533,18395 | 0,11119 | 0,105 | 0,10469 | 0,10083 | 0,09797 |
| 533,22114 | 0,11301 | 0,10684 | 0,10655 | 0,10206 | 0,09911 |
| 533,25832 | 0,11429 | 0,1081 | 0,10774 | 0,10297 | 0,09991 |
| 533,2955 | 0,11501 | 0,10877 | 0,10823 | 0,10356 | 0,10034 |
| 533,33268 | 0,11519 | 0,10885 | 0,10805 | 0,1038 | 0,10039 |
| 533,36986 | 0,11486 | 0,10839 | 0,10724 | 0,10369 | 0,10007 |
| 533,40705 | 0,1141 | 0,10745 | 0,10588 | 0,10325 | 0,0994 |
| 533,44423 | 0,11296 | 0,1061 | 0,10406 | 0,10251 | 0,0984 |
| 533,48141 | 0,11154 | 0,10444 | 0,10188 | 0,10152 | 0,09715 |
| 533,51859 | 0,10991 | 0,10256 | 0,09946 | 0,10035 | 0,0957 |
| 533,55577 | 0,10819 | 0,10057 | 0,09694 | 0,09909 | 0,09416 |
| 533,59295 | 0,10645 | 0,09857 | 0,09444 | 0,09784 | 0,09263 |
| 533,63014 | 0,10477 | 0,09664 | 0,09204 | 0,09668 | 0,09119 |
| 533,66732 | 0,10319 | 0,09484 | 0,08982 | 0,09567 | 0,08994 |
| 533,7045 | 0,10176 | 0,09321 | 0,08783 | 0,09489 | 0,08893 |
| 533,74168 | 0,10049 | 0,09178 | 0,08612 | 0,09438 | 0,08822 |
| 533,77886 | 0,09942 | 0,09057 | 0,0847 | 0,09416 | 0,08785 |
| 533,81605 | 0,09853 | 0,08959 | 0,08357 | 0,09426 | 0,08784 |
| 533,85323 | 0,09784 | 0,08884 | 0,08274 | 0,09467 | 0,08821 |
| 533,89041 | 0,09734 | 0,08833 | 0,0822 | 0,09541 | 0,08897 |
| 533,92759 | 0,09704 | 0,08804 | 0,08194 | 0,09647 | 0,09012 |
| 533,96477 | 0,09692 | 0,08796 | 0,08193 | 0,0978 | 0,09162 |
| 534,00196 | 0,09699 | 0,0881 | 0,08216 | 0,09938 | 0,09344 |
| 534,03914 | 0,09725 | 0,08845 | 0,08264 | 0,10118 | 0,09556 |
| 534,07632 | 0,09773 | 0,08903 | 0,08337 | 0,10316 | 0,09792 |
| 534,1135 | 0,09843 | 0,08986 | 0,08435 | 0,10529 | 0,10049 |
| 534,15068 | 0,09938 | 0,09094 | 0,08562 | 0,10749 | 0,1032 |
| 534,18787 | 0,10059 | 0,0923 | 0,08717 | 0,10972 | 0,10598 |
| 534,22505 | 0,10206 | 0,09395 | 0,08903 | 0,1119 | 0,10873 |
| 534,26223 | 0,10383 | 0,09591 | 0,09124 | 0,11393 | 0,11135 |
| 534,29941 | 0,10585 | 0,09818 | 0,09375 | 0,1157 | 0,11371 |
| 534,33659 | 0,10811 | 0,1007 | 0,09654 | 0,11713 | 0,1157 |
| 534,37378 | 0,11053 | 0,10344 | 0,09955 | 0,11813 | 0,11723 |
| 534,41096 | 0,11305 | 0,10633 | 0,10272 | 0,11863 | 0,11821 |
| 534,44814 | 0,1156 | 0,10929 | 0,10597 | 0,11857 | 0,11857 |
| 534,48532 | 0,11808 | 0,11222 | 0,10918 | 0,11791 | 0,11826 |
| 534,5225 | 0,12036 | 0,11501 | 0,11225 | 0,11663 | 0,11725 |
| 534,55969 | 0,12235 | 0,11754 | 0,11504 | 0,11475 | 0,11556 |
| 534,59687 | 0,12393 | 0,11968 | 0,11744 | 0,11227 | 0,1132 |
| 534,63405 | 0,12493 | 0,12127 | 0,11922 | 0,10924 | 0,1102 |
| 534,67123 | 0,12527 | 0,1222 | 0,12034 | 0,10571 | 0,10664 |
| 534,70841 | 0,12491 | 0,12241 | 0,12071 | 0,10181 | 0,10264 |
| 534,7456 | 0,12381 | 0,12185 | 0,12028 | 0,09764 | 0,09832 |
| 534,78278 | 0,12196 | 0,12049 | 0,11902 | 0,09329 | 0,09378 |
| 534,81996 | 0,1194 | 0,11837 | 0,11695 | 0,08886 | 0,08913 |
| 534,85714 | 0,11618 | 0,1155 | 0,11412 | 0,08444 | 0,08446 |
| 534,89432 | 0,11237 | 0,11198 | 0,11059 | 0,08014 | 0,07988 |
| 534,93151 | 0,10809 | 0,10789 | 0,10647 | 0,07604 | 0,07549 |
| 534,96869 | 0,10345 | 0,10337 | 0,10187 | 0,0722 | 0,07136 |
| 535,00587 | 0,09859 | 0,09853 | 0,09693 | 0,0687 | 0,06758 |
| 535,04305 | 0,09369 | 0,09356 | 0,09185 | 0,06563 | 0,06424 |
| 535,08023 | 0,08887 | 0,08862 | 0,08677 | 0,06299 | 0,06133 |
| 535,11742 | 0,08427 | 0,08384 | 0,08182 | 0,06079 | 0,05889 |
| 535,1546 | 0,07999 | 0,07935 | 0,07714 | 0,05903 | 0,05693 |
| 535,19178 | 0,07612 | 0,07524 | 0,07283 | 0,05774 | 0,05546 |
| 535,22896 | 0,07274 | 0,07161 | 0,06898 | 0,05689 | 0,05447 |
| 535,26614 | 0,0699 | 0,06853 | 0,06567 | 0,05649 | 0,05397 |
| 535,30333 | 0,06765 | 0,06606 | 0,06295 | 0,05653 | 0,05394 |
| 535,34051 | 0,06601 | 0,06422 | 0,06091 | 0,05699 | 0,05437 |
| 535,37769 | 0,06506 | 0,06312 | 0,05959 | 0,05789 | 0,05529 |
| 535,41487 | 0,06474 | 0,0627 | 0,05895 | 0,05923 | 0,05668 |
| 535,45205 | 0,06502 | 0,06294 | 0,05898 | 0,06098 | 0,05851 |
| 535,48924 | 0,06588 | 0,06381 | 0,05966 | 0,0631 | 0,06075 |
| 535,52642 | 0,06728 | 0,06529 | 0,06098 | 0,06558 | 0,06338 |
| 535,5636 | 0,06919 | 0,06732 | 0,06288 | 0,06838 | 0,06635 |
| 535,60078 | 0,07155 | 0,06988 | 0,06533 | 0,07146 | 0,06962 |
| 535,63796 | 0,07432 | 0,07288 | 0,06827 | 0,07477 | 0,07314 |
| 535,67515 | 0,07742 | 0,07627 | 0,07163 | 0,07825 | 0,07684 |
| 535,71233 | 0,0808 | 0,07998 | 0,07535 | 0,08184 | 0,08064 |
| 535,74951 | 0,08439 | 0,08392 | 0,07932 | 0,08546 | 0,08448 |
| 535,78669 | 0,08808 | 0,08799 | 0,08343 | 0,08906 | 0,08826 |
| 535,82387 | 0,09177 | 0,09207 | 0,08758 | 0,09255 | 0,09192 |
| 535,86106 | 0,09539 | 0,09607 | 0,09166 | 0,0959 | 0,09539 |
| 535,89824 | 0,09885 | 0,09989 | 0,09558 | 0,09905 | 0,09863 |
| 535,93542 | 0,10207 | 0,10344 | 0,09924 | 0,10197 | 0,10159 |
| 535,9726 | 0,10497 | 0,10663 | 0,10255 | 0,10462 | 0,10424 |
| 536,00978 | 0,10747 | 0,10938 | 0,10542 | 0,10697 | 0,10654 |
| 536,04697 | 0,10952 | 0,11162 | 0,10778 | 0,109 | 0,10847 |
| 536,08415 | 0,11108 | 0,1133 | 0,10953 | 0,11067 | 0,11001 |
| 536,12133 | 0,11202 | 0,1143 | 0,11064 | 0,11195 | 0,11113 |
| 536,15851 | 0,11242 | 0,11467 | 0,11112 | 0,11277 | 0,11178 |
| 536,19569 | 0,11226 | 0,11443 | 0,11098 | 0,11316 | 0,11201 |
| 536,23288 | 0,11158 | 0,1136 | 0,11026 | 0,11311 | 0,11181 |
| 536,27006 | 0,11041 | 0,11222 | 0,10898 | 0,11265 | 0,11123 |
| 536,30724 | 0,10879 | 0,11035 | 0,10722 | 0,11182 | 0,11031 |
| 536,34442 | 0,1068 | 0,10806 | 0,10504 | 0,11068 | 0,10912 |
| 536,3816 | 0,1045 | 0,10545 | 0,10252 | 0,10933 | 0,10777 |
| 536,41879 | 0,10197 | 0,10258 | 0,09976 | 0,10787 | 0,10636 |
| 536,45597 | 0,09928 | 0,09957 | 0,09685 | 0,10643 | 0,10503 |
| 536,49315 | 0,09654 | 0,0965 | 0,0939 | 0,10515 | 0,10392 |
| 536,53033 | 0,09383 | 0,09348 | 0,09101 | 0,10421 | 0,10321 |
| 536,56751 | 0,09124 | 0,0906 | 0,08826 | 0,10371 | 0,10298 |
| 536,6047 | 0,08882 | 0,08793 | 0,08573 | 0,10373 | 0,1033 |
| 536,64188 | 0,08665 | 0,08553 | 0,08347 | 0,10428 | 0,10419 |
| 536,67906 | 0,08478 | 0,08347 | 0,08155 | 0,10537 | 0,10564 |
| 536,71624 | 0,08325 | 0,08179 | 0,08 | 0,10692 | 0,10757 |
| 536,75342 | 0,0821 | 0,08053 | 0,07887 | 0,10884 | 0,10987 |
| 536,79061 | 0,08136 | 0,07972 | 0,07817 | 0,11097 | 0,11237 |
| 536,82779 | 0,08105 | 0,07939 | 0,07799 | 0,11313 | 0,11488 |
| 536,86497 | 0,08122 | 0,07958 | 0,07827 | 0,11512 | 0,11718 |
| 536,90215 | 0,08182 | 0,08025 | 0,079 | 0,11668 | 0,11898 |
| 536,93933 | 0,08282 | 0,08136 | 0,08017 | 0,11762 | 0,12011 |
| 536,97652 | 0,08419 | 0,08289 | 0,08173 | 0,11782 | 0,12043 |
| 537,0137 | 0,08587 | 0,08479 | 0,08365 | 0,11717 | 0,11983 |
| 537,05088 | 0,08781 | 0,087 | 0,08587 | 0,11563 | 0,11827 |
| 537,08806 | 0,08993 | 0,08945 | 0,08831 | 0,11322 | 0,11576 |
| 537,12524 | 0,09215 | 0,09203 | 0,0909 | 0,11 | 0,11238 |
| 537,16243 | 0,09437 | 0,09467 | 0,09354 | 0,10607 | 0,10825 |
| 537,19961 | 0,0965 | 0,09724 | 0,09611 | 0,10159 | 0,10353 |
| 537,23679 | 0,0984 | 0,09962 | 0,0985 | 0,09672 | 0,0984 |
| 537,27397 | 0,1 | 0,1017 | 0,10061 | 0,09166 | 0,09309 |
| 537,31115 | 0,10121 | 0,10341 | 0,10236 | 0,08663 | 0,08782 |
| 537,34834 | 0,102 | 0,10466 | 0,10367 | 0,08181 | 0,08278 |
| 537,38552 | 0,10231 | 0,10541 | 0,10447 | 0,07732 | 0,07811 |
| 537,4227 | 0,10213 | 0,10562 | 0,10474 | 0,07328 | 0,07394 |
| 537,45988 | 0,10147 | 0,10529 | 0,10446 | 0,06978 | 0,07034 |
| 537,49706 | 0,10035 | 0,10443 | 0,10365 | 0,06686 | 0,06738 |
| 537,53425 | 0,09881 | 0,10309 | 0,10231 | 0,06456 | 0,06508 |
| 537,57143 | 0,09691 | 0,1013 | 0,10049 | 0,06288 | 0,06344 |
| 537,60861 | 0,09471 | 0,09913 | 0,09832 | 0,0618 | 0,06245 |
| 537,64579 | 0,09232 | 0,0967 | 0,09586 | 0,06135 | 0,06213 |
| 537,68297 | 0,08981 | 0,09409 | 0,09321 | 0,06145 | 0,06235 |
| 537,72016 | 0,08725 | 0,09138 | 0,09045 | 0,06202 | 0,06307 |
| 537,75734 | 0,08471 | 0,08863 | 0,08766 | 0,06303 | 0,06422 |
| 537,79452 | 0,08222 | 0,08592 | 0,08492 | 0,06442 | 0,06575 |
| 537,8317 | 0,07985 | 0,0833 | 0,08228 | 0,06616 | 0,0676 |
| 537,86888 | 0,07764 | 0,08082 | 0,0798 | 0,0682 | 0,06973 |
| 537,90607 | 0,07562 | 0,07853 | 0,07755 | 0,0705 | 0,07209 |
| 537,94325 | 0,07383 | 0,07648 | 0,0756 | 0,07302 | 0,07462 |
| 537,98043 | 0,07235 | 0,07473 | 0,07396 | 0,07573 | 0,07731 |
| 538,01761 | 0,07118 | 0,07332 | 0,07268 | 0,07862 | 0,08013 |
| 538,05479 | 0,0704 | 0,07231 | 0,07183 | 0,08166 | 0,08308 |
| 538,09198 | 0,07006 | 0,07175 | 0,07146 | 0,08484 | 0,08615 |
| 538,12916 | 0,07022 | 0,07172 | 0,07163 | 0,08819 | 0,08937 |
| 538,16634 | 0,07096 | 0,0723 | 0,07242 | 0,09172 | 0,0928 |
| 538,20352 | 0,07235 | 0,07356 | 0,0739 | 0,0955 | 0,09649 |
| 538,2407 | 0,07448 | 0,07559 | 0,07616 | 0,09958 | 0,10052 |
| 538,27789 | 0,07739 | 0,07845 | 0,07933 | 0,10402 | 0,10497 |
| 538,31507 | 0,08119 | 0,08225 | 0,08344 | 0,1089 | 0,1099 |
| 538,35225 | 0,08591 | 0,08705 | 0,08848 | 0,11427 | 0,1154 |
| 538,38943 | 0,09149 | 0,09277 | 0,09445 | 0,12022 | 0,12156 |
| 538,42661 | 0,09785 | 0,09937 | 0,10129 | 0,12671 | 0,1283 |
| 538,4638 | 0,10491 | 0,10675 | 0,10892 | 0,13364 | 0,13552 |
| 538,50098 | 0,11251 | 0,11477 | 0,11721 | 0,14088 | 0,14309 |
| 538,53816 | 0,12047 | 0,12324 | 0,12596 | 0,14822 | 0,15078 |
| 538,57534 | 0,12856 | 0,13193 | 0,13496 | 0,15541 | 0,15832 |
| 538,61252 | 0,13651 | 0,14058 | 0,14394 | 0,16213 | 0,1654 |
| 538,64971 | 0,14405 | 0,14888 | 0,15253 | 0,16805 | 0,17165 |
| 538,68689 | 0,1508 | 0,15646 | 0,1604 | 0,17282 | 0,17671 |
| 538,72407 | 0,15642 | 0,16295 | 0,16724 | 0,17612 | 0,18026 |
| 538,76125 | 0,16072 | 0,1681 | 0,17278 | 0,17753 | 0,18176 |
| 538,79843 | 0,16349 | 0,1717 | 0,17678 | 0,17689 | 0,18122 |
| 538,83562 | 0,16459 | 0,17356 | 0,17905 | 0,17424 | 0,17861 |
| 538,8728 | 0,16395 | 0,17358 | 0,17946 | 0,16967 | 0,17401 |
| 538,90998 | 0,16156 | 0,17173 | 0,17799 | 0,16337 | 0,16761 |
| 538,94716 | 0,15749 | 0,16806 | 0,17465 | 0,15564 | 0,15972 |
| 538,98434 | 0,1519 | 0,1627 | 0,16955 | 0,14686 | 0,15073 |
| 539,02153 | 0,14498 | 0,15583 | 0,16273 | 0,13747 | 0,14108 |
| 539,05871 | 0,13694 | 0,14766 | 0,15466 | 0,12795 | 0,13128 |
| 539,09589 | 0,12818 | 0,13858 | 0,14567 | 0,11878 | 0,12181 |
| 539,13307 | 0,11908 | 0,12899 | 0,1361 | 0,11049 | 0,11327 |
| 539,17025 | 0,10996 | 0,11926 | 0,1263 | 0,10353 | 0,10605 |
| 539,20744 | 0,10115 | 0,10972 | 0,11663 | 0,09813 | 0,1004 |
| 539,24462 | 0,09294 | 0,10071 | 0,10741 | 0,09447 | 0,09653 |
| 539,2818 | 0,08559 | 0,09252 | 0,09897 | 0,09265 | 0,09453 |
| 539,31898 | 0,07933 | 0,0854 | 0,09158 | 0,09264 | 0,0944 |
| 539,35616 | 0,07434 | 0,07957 | 0,08549 | 0,09436 | 0,09605 |
| 539,39335 | 0,07075 | 0,07519 | 0,08103 | 0,09761 | 0,09929 |
| 539,43053 | 0,06875 | 0,07246 | 0,07815 | 0,10215 | 0,10387 |
| 539,46771 | 0,06831 | 0,07141 | 0,07688 | 0,10765 | 0,10947 |
| 539,50489 | 0,06929 | 0,0719 | 0,0772 | 0,11378 | 0,11575 |
| 539,54207 | 0,07159 | 0,07384 | 0,07903 | 0,12005 | 0,1222 |
| 539,57926 | 0,07506 | 0,07709 | 0,08222 | 0,12605 | 0,1284 |
| 539,61644 | 0,07949 | 0,08145 | 0,0866 | 0,13139 | 0,13397 |
| 539,65362 | 0,08466 | 0,08669 | 0,09192 | 0,13574 | 0,13856 |
| 539,6908 | 0,0903 | 0,09254 | 0,09793 | 0,13881 | 0,14187 |
| 539,72798 | 0,09614 | 0,09873 | 0,10432 | 0,14038 | 0,14367 |
| 539,76517 | 0,10188 | 0,10494 | 0,11074 | 0,14032 | 0,1438 |
| 539,80235 | 0,10717 | 0,11082 | 0,11684 | 0,13855 | 0,14218 |
| 539,83953 | 0,11174 | 0,11605 | 0,12233 | 0,13511 | 0,13885 |
| 539,87671 | 0,11537 | 0,12039 | 0,12694 | 0,13006 | 0,13375 |
| 539,91389 | 0,11789 | 0,12363 | 0,13045 | 0,1236 | 0,12728 |
| 539,95108 | 0,11917 | 0,12561 | 0,13269 | 0,11614 | 0,11975 |
| 539,98826 | 0,11914 | 0,12624 | 0,13353 | 0,10803 | 0,1115 |
| 540,02544 | 0,11778 | 0,12545 | 0,13291 | 0,09962 | 0,10292 |
| 540,06262 | 0,11514 | 0,12328 | 0,13084 | 0,09128 | 0,09436 |
| 540,0998 | 0,11131 | 0,1198 | 0,12729 | 0,08338 | 0,08623 |
| 540,13699 | 0,10644 | 0,11513 | 0,12242 | 0,07625 | 0,07885 |
| 540,17417 | 0,10064 | 0,10938 | 0,11652 | 0,07019 | 0,07256 |
| 540,21135 | 0,09424 | 0,10287 | 0,10982 | 0,06546 | 0,0676 |
| 540,24853 | 0,08751 | 0,09589 | 0,10255 | 0,06229 | 0,06434 |
| 540,28571 | 0,08068 | 0,08868 | 0,095 | 0,06087 | 0,0628 |
| 540,3229 | 0,07399 | 0,08152 | 0,08743 | 0,06108 | 0,06293 |
| 540,36008 | 0,06767 | 0,07464 | 0,08009 | 0,06285 | 0,06467 |
| 540,39726 | 0,06191 | 0,06828 | 0,07325 | 0,06603 | 0,06787 |
| 540,43444 | 0,0569 | 0,06263 | 0,0671 | 0,07038 | 0,07229 |
| 540,47162 | 0,05278 | 0,05787 | 0,06194 | 0,07562 | 0,07765 |
| 540,50881 | 0,04965 | 0,05411 | 0,05788 | 0,08142 | 0,0836 |
| 540,54599 | 0,04771 | 0,05157 | 0,05498 | 0,08739 | 0,08976 |
| 540,58317 | 0,04687 | 0,0502 | 0,05327 | 0,09316 | 0,09572 |
| 540,62035 | 0,04708 | 0,04996 | 0,05275 | 0,09829 | 0,10097 |
| 540,65753 | 0,04829 | 0,05078 | 0,05339 | 0,1023 | 0,10513 |
| 540,69472 | 0,0504 | 0,05259 | 0,05508 | 0,10498 | 0,10793 |
| 540,7319 | 0,05328 | 0,05525 | 0,05772 | 0,10611 | 0,10914 |
| 540,76908 | 0,05678 | 0,05861 | 0,06115 | 0,10559 | 0,10867 |
| 540,80626 | 0,06073 | 0,0625 | 0,06519 | 0,1034 | 0,10647 |
| 540,84344 | 0,06494 | 0,06672 | 0,06966 | 0,09962 | 0,10262 |
| 540,88063 | 0,0692 | 0,07106 | 0,07428 | 0,0944 | 0,0973 |
| 540,91781 | 0,07329 | 0,07528 | 0,07879 | 0,08798 | 0,09072 |
| 540,95499 | 0,07698 | 0,07913 | 0,083 | 0,08065 | 0,08319 |
| 540,99217 | 0,0801 | 0,08245 | 0,08668 | 0,07271 | 0,075 |
| 541,02935 | 0,0825 | 0,08505 | 0,08965 | 0,06451 | 0,06658 |
| 541,06654 | 0,08406 | 0,0868 | 0,09176 | 0,0564 | 0,05823 |
| 541,10372 | 0,08467 | 0,08758 | 0,09286 | 0,04863 | 0,05021 |
| 541,1409 | 0,08428 | 0,08734 | 0,09289 | 0,04138 | 0,04273 |
| 541,17808 | 0,08287 | 0,08604 | 0,09178 | 0,03479 | 0,03592 |
| 541,21526 | 0,08046 | 0,08369 | 0,08942 | 0,02894 | 0,02986 |
| 541,25245 | 0,07712 | 0,08035 | 0,08601 | 0,02385 | 0,0246 |
| 541,28963 | 0,07286 | 0,07604 | 0,08167 | 0,01953 | 0,02012 |
| 541,32681 | 0,06793 | 0,071 | 0,07652 | 0,01591 | 0,01638 |
| 541,36399 | 0,0625 | 0,06541 | 0,07075 | 0,01294 | 0,01335 |
| 541,40117 | 0,05674 | 0,05944 | 0,06452 | 0,01057 | 0,0109 |
| 541,43836 | 0,0508 | 0,05327 | 0,05804 | 0,00865 | 0,00891 |
| 541,47554 | 0,04486 | 0,04707 | 0,05148 | 0,00711 | 0,00732 |
| 541,51272 | 0,03906 | 0,04101 | 0,04501 | 0,00586 | 0,00604 |
| 541,5499 | 0,03352 | 0,03521 | 0,03879 | 0,00486 | 0,00502 |
| 541,58708 | 0,02837 | 0,02979 | 0,03302 | 0,00406 | 0,00419 |
| 541,62427 | 0,02367 | 0,02484 | 0,02773 | 0,00342 | 0,00354 |
| 541,66145 | 0,01953 | 0,02048 | 0,02298 | 0,00291 | 0,00302 |
| 541,69863 | 0,01592 | 0,01668 | 0,0188 | 0,00251 | 0,00261 |
| 541,73581 | 0,01282 | 0,01342 | 0,0152 | 0,00221 | 0,00231 |
| 541,77299 | 0,01022 | 0,01068 | 0,01214 | 0,002 | 0,0021 |
| 541,81018 | 0,00806 | 0,00842 | 0,0096 | 0,00188 | 0,00198 |
| 541,84736 | 0,00631 | 0,00659 | 0,00754 | 0,00183 | 0,00193 |
| 541,88454 | 0,00493 | 0,00515 | 0,00589 | 0,00184 | 0,00194 |
| 541,92172 | 0,00385 | 0,00403 | 0,00461 | 0,00191 | 0,00202 |
| 541,9589 | 0,00303 | 0,00319 | 0,00366 | 0,00203 | 0,00214 |
| 541,99609 | 0,00243 | 0,00259 | 0,00295 | 0,00219 | 0,00231 |
| 542,03327 | 0,00201 | 0,00218 | 0,00244 | 0,00238 | 0,0025 |
| 542,07045 | 0,00173 | 0,00191 | 0,0021 | 0,00258 | 0,00271 |
| 542,10763 | 0,00156 | 0,00175 | 0,00188 | 0,00278 | 0,00293 |
| 542,14481 | 0,00147 | 0,00168 | 0,00177 | 0,00298 | 0,00313 |
| 542,182 | 0,00144 | 0,00167 | 0,00174 | 0,00314 | 0,0033 |
| 542,21918 | 0,00147 | 0,00172 | 0,00177 | 0,00327 | 0,00344 |
| 542,25636 | 0,00153 | 0,0018 | 0,00185 | 0,00335 | 0,00352 |
| 542,29354 | 0,00162 | 0,00191 | 0,00196 | 0,00338 | 0,00356 |
| 542,33072 | 0,00172 | 0,00204 | 0,0021 | 0,00335 | 0,00353 |
| 542,36791 | 0,00184 | 0,00218 | 0,00224 | 0,00327 | 0,00345 |
| 542,40509 | 0,00195 | 0,00232 | 0,00239 | 0,00313 | 0,00331 |
| 542,44227 | 0,00206 | 0,00246 | 0,00253 | 0,00295 | 0,00312 |
| 542,47945 | 0,00215 | 0,00258 | 0,00266 | 0,00273 | 0,00288 |
| 542,51663 | 0,00223 | 0,00269 | 0,00276 | 0,00247 | 0,00262 |
| 542,55382 | 0,00228 | 0,00277 | 0,00284 | 0,0022 | 0,00234 |
| 542,591 | 0,00231 | 0,00282 | 0,00289 | 0,00192 | 0,00205 |
| 542,62818 | 0,00231 | 0,00283 | 0,00291 | 0,00165 | 0,00176 |
| 542,66536 | 0,00228 | 0,00282 | 0,00288 | 0,00139 | 0,00149 |
| 542,70254 | 0,00222 | 0,00276 | 0,00281 | 0,00115 | 0,00123 |
| 542,73973 | 0,00213 | 0,00267 | 0,00271 | 0,00093 | 0,001 |
| 542,77691 | 0,00202 | 0,00254 | 0,00258 | 0,00074 | 8e-04 |
| 542,81409 | 0,00188 | 0,00239 | 0,00242 | 0,00058 | 0,00063 |
| 542,85127 | 0,00173 | 0,00221 | 0,00223 | 0,00044 | 0,00048 |
| 542,88845 | 0,00156 | 0,00201 | 0,00203 | 0,00033 | 0,00036 |
| 542,92564 | 0,00139 | 0,0018 | 0,00182 | 0,00025 | 0,00027 |
| 542,96282 | 0,00122 | 0,00159 | 0,00161 | 0,00018 | 2e-04 |
| 543 | 0,00105 | 0,00138 | 0,00139 | 0,00013 | 0,00014 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 2e-05 | 0,00019 | 3e-05 | 0 | 0 |
| 524,03718 | 2e-05 | 0,00021 | 4e-05 | 1e-05 | 0 |
| 524,07436 | 3e-05 | 0,00023 | 4e-05 | 1e-05 | 0 |
| 524,11155 | 3e-05 | 0,00025 | 5e-05 | 1e-05 | 0 |
| 524,14873 | 3e-05 | 0,00027 | 5e-05 | 1e-05 | 0 |
| 524,18591 | 4e-05 | 0,00029 | 6e-05 | 1e-05 | 0 |
| 524,22309 | 5e-05 | 0,00031 | 6e-05 | 1e-05 | 0 |
| 524,26027 | 5e-05 | 0,00033 | 7e-05 | 1e-05 | 0 |
| 524,29746 | 6e-05 | 0,00036 | 8e-05 | 2e-05 | 0 |
| 524,33464 | 7e-05 | 0,00038 | 9e-05 | 2e-05 | 0 |
| 524,37182 | 8e-05 | 0,00041 | 1e-04 | 2e-05 | 1e-05 |
| 524,409 | 9e-05 | 0,00043 | 0,00011 | 2e-05 | 1e-05 |
| 524,44618 | 0,00011 | 0,00046 | 0,00012 | 3e-05 | 1e-05 |
| 524,48337 | 0,00012 | 0,00049 | 0,00013 | 3e-05 | 1e-05 |
| 524,52055 | 0,00014 | 0,00051 | 0,00014 | 4e-05 | 1e-05 |
| 524,55773 | 0,00015 | 0,00054 | 0,00016 | 4e-05 | 1e-05 |
| 524,59491 | 0,00017 | 0,00057 | 0,00017 | 5e-05 | 1e-05 |
| 524,63209 | 0,00019 | 6e-04 | 0,00019 | 5e-05 | 2e-05 |
| 524,66928 | 0,00022 | 0,00063 | 0,00021 | 6e-05 | 2e-05 |
| 524,70646 | 0,00024 | 0,00065 | 0,00023 | 7e-05 | 2e-05 |
| 524,74364 | 0,00027 | 0,00068 | 0,00025 | 7e-05 | 2e-05 |
| 524,78082 | 3e-04 | 0,00071 | 0,00027 | 8e-05 | 3e-05 |
| 524,818 | 0,00034 | 0,00074 | 0,00029 | 9e-05 | 3e-05 |
| 524,85519 | 0,00038 | 0,00077 | 0,00032 | 1e-04 | 3e-05 |
| 524,89237 | 0,00041 | 0,00079 | 0,00035 | 0,00011 | 4e-05 |
| 524,92955 | 0,00046 | 0,00082 | 0,00038 | 0,00013 | 5e-05 |
| 524,96673 | 5e-04 | 0,00085 | 0,00041 | 0,00014 | 5e-05 |
| 525,00391 | 0,00055 | 0,00088 | 0,00044 | 0,00015 | 6e-05 |
| 525,0411 | 0,00061 | 9e-04 | 0,00048 | 0,00017 | 6e-05 |
| 525,07828 | 0,00066 | 0,00093 | 0,00052 | 0,00019 | 7e-05 |
| 525,11546 | 0,00073 | 0,00095 | 0,00056 | 2e-04 | 8e-05 |
| 525,15264 | 0,00079 | 0,00098 | 6e-04 | 0,00022 | 9e-05 |
| 525,18982 | 0,00086 | 0,001 | 0,00065 | 0,00024 | 1e-04 |
| 525,22701 | 0,00093 | 0,00103 | 7e-04 | 0,00026 | 0,00011 |
| 525,26419 | 0,00101 | 0,00105 | 0,00075 | 0,00029 | 0,00013 |
| 525,30137 | 0,00109 | 0,00108 | 0,00081 | 0,00031 | 0,00014 |
| 525,33855 | 0,00118 | 0,0011 | 0,00087 | 0,00034 | 0,00016 |
| 525,37573 | 0,00127 | 0,00113 | 0,00094 | 0,00036 | 0,00018 |
| 525,41292 | 0,00137 | 0,00115 | 0,00101 | 0,00039 | 0,00019 |
| 525,4501 | 0,00147 | 0,00118 | 0,00108 | 0,00043 | 0,00022 |
| 525,48728 | 0,00158 | 0,00121 | 0,00116 | 0,00046 | 0,00024 |
| 525,52446 | 0,00169 | 0,00124 | 0,00125 | 0,00049 | 0,00026 |
| 525,56164 | 0,00181 | 0,00127 | 0,00134 | 0,00053 | 0,00029 |
| 525,59883 | 0,00193 | 0,0013 | 0,00143 | 0,00057 | 0,00032 |
| 525,63601 | 0,00206 | 0,00134 | 0,00153 | 0,00061 | 0,00035 |
| 525,67319 | 0,0022 | 0,00137 | 0,00164 | 0,00066 | 0,00039 |
| 525,71037 | 0,00234 | 0,00142 | 0,00175 | 0,00071 | 0,00043 |
| 525,74755 | 0,00249 | 0,00146 | 0,00187 | 0,00076 | 0,00047 |
| 525,78474 | 0,00265 | 0,00151 | 0,002 | 0,00081 | 0,00051 |
| 525,82192 | 0,00282 | 0,00157 | 0,00213 | 0,00087 | 0,00056 |
| 525,8591 | 0,00299 | 0,00163 | 0,00227 | 0,00093 | 0,00062 |
| 525,89628 | 0,00317 | 0,0017 | 0,00242 | 0,001 | 0,00068 |
| 525,93346 | 0,00337 | 0,00177 | 0,00257 | 0,00107 | 0,00074 |
| 525,97065 | 0,00358 | 0,00185 | 0,00274 | 0,00115 | 0,00081 |
| 526,00783 | 0,00379 | 0,00194 | 0,00291 | 0,00123 | 0,00089 |
| 526,04501 | 0,00402 | 0,00204 | 0,00309 | 0,00132 | 0,00097 |
| 526,08219 | 0,00426 | 0,00215 | 0,00328 | 0,00141 | 0,00106 |
| 526,11937 | 0,00452 | 0,00227 | 0,00348 | 0,00152 | 0,00116 |
| 526,15656 | 0,0048 | 0,00241 | 0,00369 | 0,00163 | 0,00127 |
| 526,19374 | 0,00508 | 0,00256 | 0,00391 | 0,00175 | 0,00138 |
| 526,23092 | 0,00539 | 0,00271 | 0,00413 | 0,00188 | 0,00151 |
| 526,2681 | 0,00572 | 0,00289 | 0,00438 | 0,00202 | 0,00164 |
| 526,30528 | 0,00607 | 0,00308 | 0,00463 | 0,00217 | 0,00179 |
| 526,34247 | 0,00644 | 0,00329 | 0,00489 | 0,00234 | 0,00195 |
| 526,37965 | 0,00683 | 0,00351 | 0,00516 | 0,00251 | 0,00212 |
| 526,41683 | 0,00725 | 0,00375 | 0,00545 | 0,0027 | 0,00231 |
| 526,45401 | 0,0077 | 0,00402 | 0,00575 | 0,00291 | 0,00251 |
| 526,49119 | 0,00817 | 0,0043 | 0,00607 | 0,00313 | 0,00272 |
| 526,52838 | 0,00866 | 0,0046 | 0,00639 | 0,00337 | 0,00295 |
| 526,56556 | 0,00919 | 0,00493 | 0,00673 | 0,00362 | 0,0032 |
| 526,60274 | 0,00975 | 0,00527 | 0,00709 | 0,00389 | 0,00347 |
| 526,63992 | 0,01034 | 0,00565 | 0,00747 | 0,00418 | 0,00375 |
| 526,6771 | 0,01096 | 0,00604 | 0,00786 | 0,0045 | 0,00405 |
| 526,71429 | 0,01161 | 0,00646 | 0,00826 | 0,00483 | 0,00437 |
| 526,75147 | 0,01231 | 0,0069 | 0,00868 | 0,00518 | 0,00471 |
| 526,78865 | 0,01303 | 0,00737 | 0,00912 | 0,00556 | 0,00507 |
| 526,82583 | 0,01379 | 0,00786 | 0,00958 | 0,00595 | 0,00545 |
| 526,86301 | 0,01457 | 0,00838 | 0,01006 | 0,00637 | 0,00585 |
| 526,9002 | 0,01541 | 0,00892 | 0,01055 | 0,00681 | 0,00628 |
| 526,93738 | 0,01627 | 0,00948 | 0,01107 | 0,00728 | 0,00672 |
| 526,97456 | 0,01716 | 0,01008 | 0,0116 | 0,00777 | 0,00719 |
| 527,01174 | 0,01808 | 0,01069 | 0,01216 | 0,00828 | 0,00767 |
| 527,04892 | 0,01904 | 0,01133 | 0,01273 | 0,00882 | 0,00817 |
| 527,08611 | 0,02004 | 0,01199 | 0,01332 | 0,00938 | 0,0087 |
| 527,12329 | 0,02106 | 0,01268 | 0,01393 | 0,00996 | 0,00925 |
| 527,16047 | 0,0221 | 0,01338 | 0,01457 | 0,01057 | 0,00981 |
| 527,19765 | 0,02317 | 0,01411 | 0,01522 | 0,01119 | 0,01039 |
| 527,23483 | 0,02427 | 0,01485 | 0,01588 | 0,01183 | 0,011 |
| 527,27202 | 0,02539 | 0,01561 | 0,01658 | 0,0125 | 0,01161 |
| 527,3092 | 0,02653 | 0,0164 | 0,01728 | 0,01318 | 0,01225 |
| 527,34638 | 0,02768 | 0,01719 | 0,01801 | 0,01388 | 0,01289 |
| 527,38356 | 0,02886 | 0,018 | 0,01875 | 0,01459 | 0,01355 |
| 527,42074 | 0,03004 | 0,01882 | 0,01951 | 0,01532 | 0,01422 |
| 527,45793 | 0,03123 | 0,01966 | 0,02028 | 0,01606 | 0,0149 |
| 527,49511 | 0,03243 | 0,0205 | 0,02107 | 0,01681 | 0,01559 |
| 527,53229 | 0,03364 | 0,02135 | 0,02187 | 0,01758 | 0,01628 |
| 527,56947 | 0,03484 | 0,02221 | 0,02269 | 0,01834 | 0,01698 |
| 527,60665 | 0,03604 | 0,02307 | 0,02352 | 0,01912 | 0,01768 |
| 527,64384 | 0,03724 | 0,02394 | 0,02435 | 0,0199 | 0,01839 |
| 527,68102 | 0,03843 | 0,02481 | 0,0252 | 0,02069 | 0,01909 |
| 527,7182 | 0,03961 | 0,02568 | 0,02605 | 0,02147 | 0,01979 |
| 527,75538 | 0,04078 | 0,02656 | 0,02691 | 0,02226 | 0,02049 |
| 527,79256 | 0,04194 | 0,02743 | 0,02777 | 0,02304 | 0,02119 |
| 527,82975 | 0,04308 | 0,0283 | 0,02864 | 0,02383 | 0,02188 |
| 527,86693 | 0,04419 | 0,02916 | 0,02951 | 0,02461 | 0,02256 |
| 527,90411 | 0,04529 | 0,03003 | 0,03038 | 0,02538 | 0,02323 |
| 527,94129 | 0,04636 | 0,03088 | 0,03125 | 0,02615 | 0,0239 |
| 527,97847 | 0,04742 | 0,03173 | 0,03212 | 0,02692 | 0,02456 |
| 528,01566 | 0,04844 | 0,03258 | 0,03298 | 0,02768 | 0,02521 |
| 528,05284 | 0,04944 | 0,03341 | 0,03384 | 0,02843 | 0,02585 |
| 528,09002 | 0,05041 | 0,03424 | 0,0347 | 0,02918 | 0,02648 |
| 528,1272 | 0,05136 | 0,03506 | 0,03555 | 0,02992 | 0,0271 |
| 528,16438 | 0,05228 | 0,03587 | 0,03639 | 0,03066 | 0,02771 |
| 528,20157 | 0,05317 | 0,03668 | 0,03723 | 0,03139 | 0,02831 |
| 528,23875 | 0,05403 | 0,03747 | 0,03805 | 0,03211 | 0,0289 |
| 528,27593 | 0,05486 | 0,03825 | 0,03886 | 0,03284 | 0,02949 |
| 528,31311 | 0,05567 | 0,03902 | 0,03967 | 0,03355 | 0,03007 |
| 528,35029 | 0,05645 | 0,03978 | 0,04046 | 0,03427 | 0,03064 |
| 528,38748 | 0,0572 | 0,04053 | 0,04124 | 0,03498 | 0,03121 |
| 528,42466 | 0,05792 | 0,04127 | 0,04201 | 0,03569 | 0,03177 |
| 528,46184 | 0,05863 | 0,042 | 0,04276 | 0,0364 | 0,03234 |
| 528,49902 | 0,0593 | 0,04271 | 0,0435 | 0,03711 | 0,0329 |
| 528,5362 | 0,05995 | 0,04342 | 0,04423 | 0,03782 | 0,03346 |
| 528,57339 | 0,06058 | 0,04411 | 0,04494 | 0,03853 | 0,03403 |
| 528,61057 | 0,0612 | 0,04479 | 0,04564 | 0,03924 | 0,0346 |
| 528,64775 | 0,06179 | 0,04546 | 0,04633 | 0,03996 | 0,03517 |
| 528,68493 | 0,06236 | 0,04611 | 0,047 | 0,04068 | 0,03575 |
| 528,72211 | 0,06291 | 0,04676 | 0,04766 | 0,0414 | 0,03633 |
| 528,7593 | 0,06344 | 0,04739 | 0,04831 | 0,04213 | 0,03693 |
| 528,79648 | 0,06397 | 0,048 | 0,04894 | 0,04286 | 0,03753 |
| 528,83366 | 0,06447 | 0,04861 | 0,04956 | 0,04359 | 0,03814 |
| 528,87084 | 0,06496 | 0,0492 | 0,05017 | 0,04432 | 0,03875 |
| 528,90802 | 0,06543 | 0,04978 | 0,05077 | 0,04506 | 0,03938 |
| 528,94521 | 0,0659 | 0,05034 | 0,05136 | 0,04579 | 0,04001 |
| 528,98239 | 0,06635 | 0,05089 | 0,05194 | 0,04653 | 0,04066 |
| 529,01957 | 0,06679 | 0,05143 | 0,05251 | 0,04726 | 0,04131 |
| 529,05675 | 0,06722 | 0,05196 | 0,05307 | 0,04799 | 0,04197 |
| 529,09393 | 0,06763 | 0,05247 | 0,05362 | 0,04872 | 0,04264 |
| 529,13112 | 0,06804 | 0,05298 | 0,05416 | 0,04945 | 0,04331 |
| 529,1683 | 0,06844 | 0,05346 | 0,0547 | 0,05016 | 0,04399 |
| 529,20548 | 0,06882 | 0,05394 | 0,05524 | 0,05087 | 0,04468 |
| 529,24266 | 0,0692 | 0,05441 | 0,05577 | 0,05157 | 0,04537 |
| 529,27984 | 0,06957 | 0,05486 | 0,05629 | 0,05226 | 0,04606 |
| 529,31703 | 0,06993 | 0,0553 | 0,05681 | 0,05293 | 0,04675 |
| 529,35421 | 0,07027 | 0,05574 | 0,05733 | 0,05359 | 0,04745 |
| 529,39139 | 0,07061 | 0,05616 | 0,05785 | 0,05424 | 0,04814 |
| 529,42857 | 0,07094 | 0,05657 | 0,05836 | 0,05487 | 0,04883 |
| 529,46575 | 0,07125 | 0,05697 | 0,05887 | 0,05548 | 0,04952 |
| 529,50294 | 0,07155 | 0,05737 | 0,05938 | 0,05607 | 0,05021 |
| 529,54012 | 0,07185 | 0,05775 | 0,05988 | 0,05664 | 0,05089 |
| 529,5773 | 0,07213 | 0,05813 | 0,06038 | 0,05719 | 0,05156 |
| 529,61448 | 0,07239 | 0,0585 | 0,06088 | 0,05773 | 0,05223 |
| 529,65166 | 0,07264 | 0,05886 | 0,06138 | 0,05823 | 0,05289 |
| 529,68885 | 0,07288 | 0,05921 | 0,06187 | 0,05872 | 0,05354 |
| 529,72603 | 0,07311 | 0,05956 | 0,06235 | 0,05919 | 0,05418 |
| 529,76321 | 0,07331 | 0,05989 | 0,06283 | 0,05964 | 0,05481 |
| 529,80039 | 0,0735 | 0,06022 | 0,06329 | 0,06007 | 0,05544 |
| 529,83757 | 0,07368 | 0,06054 | 0,06375 | 0,06047 | 0,05605 |
| 529,87476 | 0,07383 | 0,06086 | 0,0642 | 0,06086 | 0,05665 |
| 529,91194 | 0,07397 | 0,06116 | 0,06463 | 0,06123 | 0,05725 |
| 529,94912 | 0,07409 | 0,06146 | 0,06505 | 0,06159 | 0,05783 |
| 529,9863 | 0,07418 | 0,06174 | 0,06546 | 0,06192 | 0,0584 |
| 530,02348 | 0,07426 | 0,06202 | 0,06584 | 0,06223 | 0,05896 |
| 530,06067 | 0,07432 | 0,06228 | 0,06621 | 0,06254 | 0,05951 |
| 530,09785 | 0,07436 | 0,06254 | 0,06654 | 0,06282 | 0,06005 |
| 530,13503 | 0,07437 | 0,06278 | 0,06686 | 0,0631 | 0,06057 |
| 530,17221 | 0,07436 | 0,06301 | 0,06715 | 0,06336 | 0,06108 |
| 530,20939 | 0,07434 | 0,06322 | 0,06742 | 0,0636 | 0,06159 |
| 530,24658 | 0,07429 | 0,06342 | 0,06765 | 0,06384 | 0,06208 |
| 530,28376 | 0,07422 | 0,06361 | 0,06785 | 0,06406 | 0,06255 |
| 530,32094 | 0,07413 | 0,06378 | 0,06802 | 0,06427 | 0,06301 |
| 530,35812 | 0,07402 | 0,06394 | 0,06816 | 0,06447 | 0,06346 |
| 530,3953 | 0,0739 | 0,06407 | 0,06826 | 0,06466 | 0,06389 |
| 530,43249 | 0,07376 | 0,0642 | 0,06832 | 0,06484 | 0,06431 |
| 530,46967 | 0,0736 | 0,0643 | 0,06835 | 0,06501 | 0,06471 |
| 530,50685 | 0,07343 | 0,06439 | 0,06836 | 0,06516 | 0,06509 |
| 530,54403 | 0,07324 | 0,06447 | 0,06832 | 0,06531 | 0,06545 |
| 530,58121 | 0,07305 | 0,06452 | 0,06825 | 0,06545 | 0,0658 |
| 530,6184 | 0,07285 | 0,06456 | 0,06815 | 0,06557 | 0,06612 |
| 530,65558 | 0,07264 | 0,06459 | 0,06802 | 0,06569 | 0,06642 |
| 530,69276 | 0,07243 | 0,0646 | 0,06786 | 0,06579 | 0,06671 |
| 530,72994 | 0,07222 | 0,0646 | 0,06767 | 0,06588 | 0,06697 |
| 530,76712 | 0,07201 | 0,06459 | 0,06745 | 0,06596 | 0,06721 |
| 530,80431 | 0,07181 | 0,06456 | 0,06721 | 0,06603 | 0,06742 |
| 530,84149 | 0,07161 | 0,06453 | 0,06696 | 0,06609 | 0,06761 |
| 530,87867 | 0,07142 | 0,06448 | 0,06668 | 0,06614 | 0,06779 |
| 530,91585 | 0,07124 | 0,06443 | 0,06639 | 0,06618 | 0,06794 |
| 530,95303 | 0,07108 | 0,06438 | 0,06609 | 0,06622 | 0,06807 |
| 530,99022 | 0,07094 | 0,06432 | 0,06578 | 0,06624 | 0,06818 |
| 531,0274 | 0,07081 | 0,06425 | 0,06547 | 0,06625 | 0,06826 |
| 531,06458 | 0,0707 | 0,06419 | 0,06515 | 0,06626 | 0,06834 |
| 531,10176 | 0,07062 | 0,06412 | 0,06483 | 0,06627 | 0,06839 |
| 531,13894 | 0,07056 | 0,06406 | 0,06452 | 0,06627 | 0,06843 |
| 531,17613 | 0,07053 | 0,06401 | 0,06421 | 0,06627 | 0,06845 |
| 531,21331 | 0,07051 | 0,06395 | 0,06391 | 0,06627 | 0,06847 |
| 531,25049 | 0,07053 | 0,06391 | 0,06363 | 0,06627 | 0,06847 |
| 531,28767 | 0,07058 | 0,06387 | 0,06335 | 0,06626 | 0,06846 |
| 531,32485 | 0,07066 | 0,06384 | 0,06309 | 0,06627 | 0,06845 |
| 531,36204 | 0,07076 | 0,06382 | 0,06285 | 0,06628 | 0,06843 |
| 531,39922 | 0,07088 | 0,06381 | 0,06263 | 0,06629 | 0,06841 |
| 531,4364 | 0,07104 | 0,06381 | 0,06242 | 0,06631 | 0,06838 |
| 531,47358 | 0,07122 | 0,06382 | 0,06224 | 0,06634 | 0,06835 |
| 531,51076 | 0,07143 | 0,06384 | 0,06207 | 0,06638 | 0,06833 |
| 531,54795 | 0,07166 | 0,06388 | 0,06193 | 0,06643 | 0,0683 |
| 531,58513 | 0,07191 | 0,06393 | 0,06181 | 0,06649 | 0,06828 |
| 531,62231 | 0,07218 | 0,06399 | 0,06171 | 0,06656 | 0,06826 |
| 531,65949 | 0,07247 | 0,06406 | 0,06162 | 0,06664 | 0,06824 |
| 531,69667 | 0,07278 | 0,06414 | 0,06156 | 0,06674 | 0,06822 |
| 531,73386 | 0,0731 | 0,06424 | 0,06152 | 0,06685 | 0,06821 |
| 531,77104 | 0,07343 | 0,06435 | 0,0615 | 0,06696 | 0,0682 |
| 531,80822 | 0,07378 | 0,06446 | 0,06149 | 0,06709 | 0,0682 |
| 531,8454 | 0,07413 | 0,06459 | 0,0615 | 0,06724 | 0,06819 |
| 531,88258 | 0,07448 | 0,06473 | 0,06153 | 0,06739 | 0,06819 |
| 531,91977 | 0,07484 | 0,06488 | 0,06156 | 0,06755 | 0,06819 |
| 531,95695 | 0,0752 | 0,06503 | 0,06162 | 0,06772 | 0,06819 |
| 531,99413 | 0,07557 | 0,0652 | 0,06168 | 0,0679 | 0,06819 |
| 532,03131 | 0,07593 | 0,06537 | 0,06175 | 0,06808 | 0,06819 |
| 532,06849 | 0,07628 | 0,06555 | 0,06184 | 0,06827 | 0,06818 |
| 532,10568 | 0,07663 | 0,06573 | 0,06193 | 0,06846 | 0,06817 |
| 532,14286 | 0,07698 | 0,06592 | 0,06203 | 0,06865 | 0,06815 |
| 532,18004 | 0,07732 | 0,06612 | 0,06214 | 0,06885 | 0,06813 |
| 532,21722 | 0,07765 | 0,06632 | 0,06226 | 0,06904 | 0,0681 |
| 532,2544 | 0,07796 | 0,06653 | 0,06238 | 0,06923 | 0,06807 |
| 532,29159 | 0,07827 | 0,06674 | 0,06251 | 0,06942 | 0,06803 |
| 532,32877 | 0,07857 | 0,06695 | 0,06264 | 0,06961 | 0,06798 |
| 532,36595 | 0,07886 | 0,06717 | 0,06278 | 0,06979 | 0,06792 |
| 532,40313 | 0,07914 | 0,06739 | 0,06293 | 0,06996 | 0,06785 |
| 532,44031 | 0,0794 | 0,06762 | 0,06309 | 0,07013 | 0,06778 |
| 532,4775 | 0,07966 | 0,06785 | 0,06325 | 0,07029 | 0,06769 |
| 532,51468 | 0,0799 | 0,06808 | 0,06342 | 0,07044 | 0,0676 |
| 532,55186 | 0,08013 | 0,06831 | 0,0636 | 0,07058 | 0,06751 |
| 532,58904 | 0,08035 | 0,06854 | 0,06378 | 0,07071 | 0,0674 |
| 532,62622 | 0,08055 | 0,06878 | 0,06397 | 0,07084 | 0,0673 |
| 532,66341 | 0,08075 | 0,06901 | 0,06418 | 0,07095 | 0,06718 |
| 532,70059 | 0,08093 | 0,06925 | 0,06439 | 0,07105 | 0,06707 |
| 532,73777 | 0,0811 | 0,06949 | 0,06461 | 0,07114 | 0,06695 |
| 532,77495 | 0,08126 | 0,06972 | 0,06484 | 0,07122 | 0,06683 |
| 532,81213 | 0,08141 | 0,06996 | 0,06507 | 0,07129 | 0,06671 |
| 532,84932 | 0,08155 | 0,07019 | 0,06532 | 0,07135 | 0,06659 |
| 532,8865 | 0,08167 | 0,07042 | 0,06558 | 0,07139 | 0,06648 |
| 532,92368 | 0,08178 | 0,07065 | 0,06585 | 0,07143 | 0,06636 |
| 532,96086 | 0,08188 | 0,07087 | 0,06612 | 0,07146 | 0,06625 |
| 532,99804 | 0,08197 | 0,07109 | 0,06641 | 0,07147 | 0,06615 |
| 533,03523 | 0,08204 | 0,0713 | 0,0667 | 0,07148 | 0,06605 |
| 533,07241 | 0,0821 | 0,07151 | 0,067 | 0,07147 | 0,06596 |
| 533,10959 | 0,08215 | 0,07171 | 0,06731 | 0,07146 | 0,06587 |
| 533,14677 | 0,08219 | 0,07191 | 0,06762 | 0,07143 | 0,06579 |
| 533,18395 | 0,08221 | 0,0721 | 0,06795 | 0,0714 | 0,06572 |
| 533,22114 | 0,08221 | 0,07228 | 0,06827 | 0,07137 | 0,06566 |
| 533,25832 | 0,0822 | 0,07246 | 0,0686 | 0,07132 | 0,06561 |
| 533,2955 | 0,08218 | 0,07263 | 0,06894 | 0,07127 | 0,06557 |
| 533,33268 | 0,08215 | 0,07279 | 0,06928 | 0,07122 | 0,06554 |
| 533,36986 | 0,0821 | 0,07294 | 0,06962 | 0,07116 | 0,06552 |
| 533,40705 | 0,08204 | 0,07308 | 0,06996 | 0,07109 | 0,06551 |
| 533,44423 | 0,08197 | 0,07322 | 0,07031 | 0,07103 | 0,06552 |
| 533,48141 | 0,08188 | 0,07336 | 0,07066 | 0,07097 | 0,06553 |
| 533,51859 | 0,08179 | 0,07349 | 0,071 | 0,07091 | 0,06557 |
| 533,55577 | 0,08168 | 0,07361 | 0,07135 | 0,07085 | 0,06561 |
| 533,59295 | 0,08157 | 0,07373 | 0,07169 | 0,0708 | 0,06568 |
| 533,63014 | 0,08145 | 0,07385 | 0,07204 | 0,07075 | 0,06575 |
| 533,66732 | 0,08132 | 0,07396 | 0,07238 | 0,07071 | 0,06584 |
| 533,7045 | 0,08118 | 0,07408 | 0,07272 | 0,07068 | 0,06596 |
| 533,74168 | 0,08105 | 0,07419 | 0,07305 | 0,07067 | 0,06609 |
| 533,77886 | 0,08091 | 0,07431 | 0,07339 | 0,07066 | 0,06623 |
| 533,81605 | 0,08077 | 0,07443 | 0,07372 | 0,07067 | 0,0664 |
| 533,85323 | 0,08064 | 0,07456 | 0,07404 | 0,0707 | 0,06658 |
| 533,89041 | 0,0805 | 0,07469 | 0,07437 | 0,07075 | 0,06679 |
| 533,92759 | 0,08038 | 0,07483 | 0,07468 | 0,07082 | 0,06702 |
| 533,96477 | 0,08026 | 0,07497 | 0,075 | 0,0709 | 0,06726 |
| 534,00196 | 0,08014 | 0,07512 | 0,0753 | 0,07101 | 0,06752 |
| 534,03914 | 0,08004 | 0,07529 | 0,07561 | 0,07115 | 0,06781 |
| 534,07632 | 0,07995 | 0,07546 | 0,0759 | 0,07131 | 0,06812 |
| 534,1135 | 0,07987 | 0,07564 | 0,07619 | 0,07149 | 0,06845 |
| 534,15068 | 0,0798 | 0,07583 | 0,07647 | 0,0717 | 0,06879 |
| 534,18787 | 0,07975 | 0,07603 | 0,07674 | 0,07193 | 0,06915 |
| 534,22505 | 0,07971 | 0,07624 | 0,077 | 0,07219 | 0,06953 |
| 534,26223 | 0,07968 | 0,07646 | 0,07725 | 0,07247 | 0,06993 |
| 534,29941 | 0,07967 | 0,07669 | 0,07749 | 0,07278 | 0,07033 |
| 534,33659 | 0,07968 | 0,07693 | 0,07772 | 0,07311 | 0,07075 |
| 534,37378 | 0,0797 | 0,07718 | 0,07793 | 0,07346 | 0,07118 |
| 534,41096 | 0,07974 | 0,07743 | 0,07813 | 0,07383 | 0,07162 |
| 534,44814 | 0,07978 | 0,07769 | 0,07832 | 0,07423 | 0,07207 |
| 534,48532 | 0,07985 | 0,07796 | 0,07849 | 0,07464 | 0,07252 |
| 534,5225 | 0,07992 | 0,07823 | 0,07864 | 0,07506 | 0,07297 |
| 534,55969 | 0,08001 | 0,0785 | 0,07878 | 0,0755 | 0,07342 |
| 534,59687 | 0,0801 | 0,07878 | 0,07891 | 0,07595 | 0,07387 |
| 534,63405 | 0,0802 | 0,07906 | 0,07902 | 0,07641 | 0,07432 |
| 534,67123 | 0,08031 | 0,07933 | 0,07911 | 0,07687 | 0,07476 |
| 534,70841 | 0,08043 | 0,07961 | 0,07918 | 0,07734 | 0,07519 |
| 534,7456 | 0,08055 | 0,07989 | 0,07924 | 0,07782 | 0,07561 |
| 534,78278 | 0,08067 | 0,08016 | 0,07929 | 0,07829 | 0,07602 |
| 534,81996 | 0,0808 | 0,08044 | 0,07932 | 0,07876 | 0,07643 |
| 534,85714 | 0,08093 | 0,08071 | 0,07934 | 0,07923 | 0,07682 |
| 534,89432 | 0,08105 | 0,08098 | 0,07935 | 0,07968 | 0,07719 |
| 534,93151 | 0,08118 | 0,08124 | 0,07935 | 0,08013 | 0,07755 |
| 534,96869 | 0,0813 | 0,0815 | 0,07934 | 0,08058 | 0,0779 |
| 535,00587 | 0,08141 | 0,08176 | 0,07933 | 0,08101 | 0,07824 |
| 535,04305 | 0,08153 | 0,08202 | 0,07931 | 0,08142 | 0,07857 |
| 535,08023 | 0,08163 | 0,08228 | 0,0793 | 0,08183 | 0,07888 |
| 535,11742 | 0,08174 | 0,08253 | 0,07928 | 0,08221 | 0,07919 |
| 535,1546 | 0,08183 | 0,08279 | 0,07927 | 0,08259 | 0,07948 |
| 535,19178 | 0,08192 | 0,08304 | 0,07927 | 0,08295 | 0,07977 |
| 535,22896 | 0,08201 | 0,0833 | 0,07927 | 0,08329 | 0,08005 |
| 535,26614 | 0,08208 | 0,08356 | 0,07929 | 0,08362 | 0,08033 |
| 535,30333 | 0,08216 | 0,08382 | 0,07933 | 0,08393 | 0,08061 |
| 535,34051 | 0,08222 | 0,08408 | 0,07938 | 0,08423 | 0,08088 |
| 535,37769 | 0,08229 | 0,08435 | 0,07945 | 0,08451 | 0,08116 |
| 535,41487 | 0,08235 | 0,08463 | 0,07955 | 0,08478 | 0,08144 |
| 535,45205 | 0,08241 | 0,08491 | 0,07967 | 0,08503 | 0,08173 |
| 535,48924 | 0,08246 | 0,0852 | 0,07981 | 0,08528 | 0,08203 |
| 535,52642 | 0,08251 | 0,08549 | 0,07999 | 0,08552 | 0,08233 |
| 535,5636 | 0,08257 | 0,0858 | 0,0802 | 0,08574 | 0,08265 |
| 535,60078 | 0,08262 | 0,08611 | 0,08044 | 0,08596 | 0,08299 |
| 535,63796 | 0,08268 | 0,08642 | 0,08071 | 0,08618 | 0,08333 |
| 535,67515 | 0,08274 | 0,08675 | 0,08101 | 0,08639 | 0,08369 |
| 535,71233 | 0,0828 | 0,08708 | 0,08135 | 0,08659 | 0,08407 |
| 535,74951 | 0,08286 | 0,08742 | 0,08172 | 0,0868 | 0,08448 |
| 535,78669 | 0,08294 | 0,08777 | 0,08212 | 0,08701 | 0,0849 |
| 535,82387 | 0,08302 | 0,08813 | 0,08255 | 0,08722 | 0,08534 |
| 535,86106 | 0,0831 | 0,08849 | 0,08302 | 0,08744 | 0,0858 |
| 535,89824 | 0,0832 | 0,08886 | 0,08352 | 0,08766 | 0,08629 |
| 535,93542 | 0,0833 | 0,08924 | 0,08405 | 0,08789 | 0,0868 |
| 535,9726 | 0,08341 | 0,08962 | 0,0846 | 0,08813 | 0,08733 |
| 536,00978 | 0,08353 | 0,09 | 0,08518 | 0,08838 | 0,08789 |
| 536,04697 | 0,08366 | 0,09039 | 0,08578 | 0,08864 | 0,08847 |
| 536,08415 | 0,0838 | 0,09079 | 0,0864 | 0,08892 | 0,08908 |
| 536,12133 | 0,08396 | 0,09119 | 0,08705 | 0,08922 | 0,08971 |
| 536,15851 | 0,08412 | 0,09159 | 0,08771 | 0,08953 | 0,09037 |
| 536,19569 | 0,08429 | 0,09199 | 0,08838 | 0,08985 | 0,09104 |
| 536,23288 | 0,08448 | 0,0924 | 0,08907 | 0,0902 | 0,09175 |
| 536,27006 | 0,08467 | 0,09282 | 0,08977 | 0,09057 | 0,09248 |
| 536,30724 | 0,08488 | 0,09323 | 0,09047 | 0,09096 | 0,09323 |
| 536,34442 | 0,0851 | 0,09365 | 0,09119 | 0,09137 | 0,09401 |
| 536,3816 | 0,08532 | 0,09408 | 0,0919 | 0,09181 | 0,09481 |
| 536,41879 | 0,08555 | 0,0945 | 0,09262 | 0,09227 | 0,09563 |
| 536,45597 | 0,0858 | 0,09494 | 0,09334 | 0,09275 | 0,09648 |
| 536,49315 | 0,08605 | 0,09538 | 0,09405 | 0,09326 | 0,09735 |
| 536,53033 | 0,0863 | 0,09582 | 0,09477 | 0,09379 | 0,09823 |
| 536,56751 | 0,08657 | 0,09627 | 0,09547 | 0,09435 | 0,09914 |
| 536,6047 | 0,08683 | 0,09672 | 0,09617 | 0,09493 | 0,10007 |
| 536,64188 | 0,08711 | 0,09719 | 0,09687 | 0,09554 | 0,10101 |
| 536,67906 | 0,08738 | 0,09766 | 0,09755 | 0,09616 | 0,10198 |
| 536,71624 | 0,08765 | 0,09813 | 0,09822 | 0,09681 | 0,10295 |
| 536,75342 | 0,08793 | 0,09861 | 0,09888 | 0,09749 | 0,10394 |
| 536,79061 | 0,0882 | 0,0991 | 0,09953 | 0,09818 | 0,10494 |
| 536,82779 | 0,08848 | 0,0996 | 0,10016 | 0,09889 | 0,10594 |
| 536,86497 | 0,08874 | 0,1001 | 0,10078 | 0,09962 | 0,10696 |
| 536,90215 | 0,089 | 0,10061 | 0,10138 | 0,10036 | 0,10797 |
| 536,93933 | 0,08925 | 0,10113 | 0,10196 | 0,10112 | 0,10899 |
| 536,97652 | 0,0895 | 0,10164 | 0,10253 | 0,10189 | 0,11 |
| 537,0137 | 0,08973 | 0,10216 | 0,10308 | 0,10266 | 0,11101 |
| 537,05088 | 0,08995 | 0,10268 | 0,10361 | 0,10344 | 0,11201 |
| 537,08806 | 0,09015 | 0,1032 | 0,10412 | 0,10423 | 0,113 |
| 537,12524 | 0,09033 | 0,10372 | 0,10461 | 0,10501 | 0,11398 |
| 537,16243 | 0,0905 | 0,10423 | 0,10507 | 0,10579 | 0,11493 |
| 537,19961 | 0,09065 | 0,10473 | 0,10551 | 0,10657 | 0,11587 |
| 537,23679 | 0,09077 | 0,10523 | 0,10593 | 0,10733 | 0,11679 |
| 537,27397 | 0,09087 | 0,10572 | 0,10632 | 0,10809 | 0,11767 |
| 537,31115 | 0,09095 | 0,1062 | 0,10669 | 0,10882 | 0,11852 |
| 537,34834 | 0,091 | 0,10666 | 0,10703 | 0,10955 | 0,11934 |
| 537,38552 | 0,09103 | 0,10711 | 0,10735 | 0,11025 | 0,12013 |
| 537,4227 | 0,09103 | 0,10754 | 0,10764 | 0,11092 | 0,12088 |
| 537,45988 | 0,09099 | 0,10795 | 0,10791 | 0,11156 | 0,12158 |
| 537,49706 | 0,09093 | 0,10833 | 0,10814 | 0,11218 | 0,12224 |
| 537,53425 | 0,09085 | 0,1087 | 0,10835 | 0,11277 | 0,12286 |
| 537,57143 | 0,09073 | 0,10904 | 0,10854 | 0,11332 | 0,12343 |
| 537,60861 | 0,09058 | 0,10936 | 0,1087 | 0,11382 | 0,12396 |
| 537,64579 | 0,0904 | 0,10964 | 0,10883 | 0,11429 | 0,12443 |
| 537,68297 | 0,0902 | 0,1099 | 0,10894 | 0,11473 | 0,12485 |
| 537,72016 | 0,08997 | 0,11014 | 0,10902 | 0,11512 | 0,12523 |
| 537,75734 | 0,08971 | 0,11035 | 0,10908 | 0,11546 | 0,12556 |
| 537,79452 | 0,08943 | 0,11053 | 0,10912 | 0,11576 | 0,12584 |
| 537,8317 | 0,08912 | 0,11068 | 0,10913 | 0,11602 | 0,12606 |
| 537,86888 | 0,0888 | 0,1108 | 0,10913 | 0,11623 | 0,12624 |
| 537,90607 | 0,08844 | 0,1109 | 0,1091 | 0,11639 | 0,12638 |
| 537,94325 | 0,08807 | 0,11097 | 0,10906 | 0,1165 | 0,12646 |
| 537,98043 | 0,08768 | 0,11101 | 0,10901 | 0,11657 | 0,12649 |
| 538,01761 | 0,08728 | 0,11102 | 0,10893 | 0,1166 | 0,12648 |
| 538,05479 | 0,08686 | 0,11101 | 0,10884 | 0,11658 | 0,12643 |
| 538,09198 | 0,08643 | 0,11097 | 0,10874 | 0,11651 | 0,12634 |
| 538,12916 | 0,08599 | 0,11091 | 0,10863 | 0,1164 | 0,1262 |
| 538,16634 | 0,08554 | 0,11082 | 0,10851 | 0,11625 | 0,12602 |
| 538,20352 | 0,08508 | 0,11071 | 0,10837 | 0,11605 | 0,1258 |
| 538,2407 | 0,08461 | 0,11057 | 0,10822 | 0,11583 | 0,12554 |
| 538,27789 | 0,08414 | 0,11041 | 0,10807 | 0,11555 | 0,12525 |
| 538,31507 | 0,08367 | 0,11022 | 0,1079 | 0,11523 | 0,12491 |
| 538,35225 | 0,08319 | 0,11 | 0,10772 | 0,11489 | 0,12454 |
| 538,38943 | 0,08271 | 0,10976 | 0,10754 | 0,11451 | 0,12413 |
| 538,42661 | 0,08223 | 0,1095 | 0,10734 | 0,1141 | 0,12369 |
| 538,4638 | 0,08175 | 0,10921 | 0,10713 | 0,11365 | 0,12321 |
| 538,50098 | 0,08126 | 0,10888 | 0,1069 | 0,11318 | 0,12269 |
| 538,53816 | 0,08078 | 0,10853 | 0,10666 | 0,11267 | 0,12214 |
| 538,57534 | 0,08029 | 0,10816 | 0,10641 | 0,11215 | 0,12155 |
| 538,61252 | 0,07981 | 0,10775 | 0,10614 | 0,11159 | 0,12092 |
| 538,64971 | 0,07932 | 0,1073 | 0,10584 | 0,111 | 0,12025 |
| 538,68689 | 0,07883 | 0,10682 | 0,10553 | 0,11039 | 0,11954 |
| 538,72407 | 0,07833 | 0,10631 | 0,10519 | 0,10976 | 0,1188 |
| 538,76125 | 0,07783 | 0,10577 | 0,10483 | 0,10911 | 0,11802 |
| 538,79843 | 0,07733 | 0,10518 | 0,10444 | 0,10842 | 0,11719 |
| 538,83562 | 0,07682 | 0,10455 | 0,10401 | 0,10772 | 0,11631 |
| 538,8728 | 0,0763 | 0,10388 | 0,10355 | 0,10699 | 0,11539 |
| 538,90998 | 0,07577 | 0,10318 | 0,10306 | 0,10624 | 0,11443 |
| 538,94716 | 0,07523 | 0,10243 | 0,10254 | 0,10546 | 0,11342 |
| 538,98434 | 0,07468 | 0,10163 | 0,10196 | 0,10466 | 0,11236 |
| 539,02153 | 0,07412 | 0,10079 | 0,10134 | 0,10382 | 0,11124 |
| 539,05871 | 0,07353 | 0,0999 | 0,10068 | 0,10296 | 0,11008 |
| 539,09589 | 0,07293 | 0,09898 | 0,09998 | 0,10207 | 0,10887 |
| 539,13307 | 0,07231 | 0,09799 | 0,09922 | 0,10114 | 0,1076 |
| 539,17025 | 0,07167 | 0,09696 | 0,0984 | 0,10018 | 0,10627 |
| 539,20744 | 0,071 | 0,09588 | 0,09754 | 0,09918 | 0,1049 |
| 539,24462 | 0,07031 | 0,09475 | 0,09662 | 0,09814 | 0,10347 |
| 539,2818 | 0,06959 | 0,09357 | 0,09565 | 0,09705 | 0,10198 |
| 539,31898 | 0,06885 | 0,09234 | 0,09461 | 0,09592 | 0,10043 |
| 539,35616 | 0,06807 | 0,09105 | 0,09351 | 0,09474 | 0,09882 |
| 539,39335 | 0,06725 | 0,08972 | 0,09236 | 0,09352 | 0,09717 |
| 539,43053 | 0,0664 | 0,08835 | 0,09115 | 0,09224 | 0,09546 |
| 539,46771 | 0,06553 | 0,08691 | 0,08987 | 0,0909 | 0,09369 |
| 539,50489 | 0,06461 | 0,08542 | 0,08853 | 0,08951 | 0,09186 |
| 539,54207 | 0,06365 | 0,08389 | 0,08713 | 0,08806 | 0,08998 |
| 539,57926 | 0,06266 | 0,08231 | 0,08568 | 0,08657 | 0,08806 |
| 539,61644 | 0,06163 | 0,08068 | 0,08417 | 0,085 | 0,08609 |
| 539,65362 | 0,06057 | 0,079 | 0,08258 | 0,08337 | 0,08407 |
| 539,6908 | 0,05946 | 0,07729 | 0,08095 | 0,08168 | 0,082 |
| 539,72798 | 0,05831 | 0,07553 | 0,07927 | 0,07995 | 0,0799 |
| 539,76517 | 0,05713 | 0,07373 | 0,07754 | 0,07815 | 0,07776 |
| 539,80235 | 0,05591 | 0,07189 | 0,07576 | 0,0763 | 0,07559 |
| 539,83953 | 0,05466 | 0,07001 | 0,07392 | 0,07439 | 0,07339 |
| 539,87671 | 0,05337 | 0,06811 | 0,07205 | 0,07244 | 0,07117 |
| 539,91389 | 0,05205 | 0,06618 | 0,07015 | 0,07045 | 0,06893 |
| 539,95108 | 0,05071 | 0,06422 | 0,06821 | 0,06841 | 0,06667 |
| 539,98826 | 0,04934 | 0,06224 | 0,06623 | 0,06633 | 0,06441 |
| 540,02544 | 0,04793 | 0,06024 | 0,06424 | 0,06423 | 0,06214 |
| 540,06262 | 0,04652 | 0,05823 | 0,06222 | 0,0621 | 0,05988 |
| 540,0998 | 0,04508 | 0,05622 | 0,06019 | 0,05996 | 0,05762 |
| 540,13699 | 0,04363 | 0,05419 | 0,05815 | 0,0578 | 0,05537 |
| 540,17417 | 0,04217 | 0,05217 | 0,0561 | 0,05564 | 0,05315 |
| 540,21135 | 0,0407 | 0,05016 | 0,05406 | 0,05347 | 0,05095 |
| 540,24853 | 0,03922 | 0,04815 | 0,05202 | 0,05132 | 0,04878 |
| 540,28571 | 0,03775 | 0,04617 | 0,05 | 0,04918 | 0,04665 |
| 540,3229 | 0,03628 | 0,0442 | 0,04799 | 0,04706 | 0,04455 |
| 540,36008 | 0,03482 | 0,04225 | 0,04601 | 0,04496 | 0,0425 |
| 540,39726 | 0,03337 | 0,04034 | 0,04405 | 0,0429 | 0,0405 |
| 540,43444 | 0,03194 | 0,03846 | 0,04212 | 0,04087 | 0,03855 |
| 540,47162 | 0,03052 | 0,03662 | 0,04023 | 0,0389 | 0,03664 |
| 540,50881 | 0,02913 | 0,03482 | 0,03838 | 0,03697 | 0,03481 |
| 540,54599 | 0,02777 | 0,03306 | 0,03658 | 0,03509 | 0,03303 |
| 540,58317 | 0,02643 | 0,03134 | 0,03481 | 0,03327 | 0,03132 |
| 540,62035 | 0,02512 | 0,02969 | 0,03311 | 0,0315 | 0,02966 |
| 540,65753 | 0,02385 | 0,02809 | 0,03146 | 0,02981 | 0,02807 |
| 540,69472 | 0,02261 | 0,02655 | 0,02986 | 0,02818 | 0,02655 |
| 540,7319 | 0,02141 | 0,02505 | 0,02831 | 0,02661 | 0,0251 |
| 540,76908 | 0,02025 | 0,02362 | 0,02682 | 0,0251 | 0,02371 |
| 540,80626 | 0,01913 | 0,02226 | 0,0254 | 0,02368 | 0,02237 |
| 540,84344 | 0,01805 | 0,02095 | 0,02404 | 0,02232 | 0,02112 |
| 540,88063 | 0,01702 | 0,0197 | 0,02273 | 0,02102 | 0,01992 |
| 540,91781 | 0,01602 | 0,01851 | 0,02147 | 0,01978 | 0,01879 |
| 540,95499 | 0,01507 | 0,01738 | 0,02028 | 0,01861 | 0,0177 |
| 540,99217 | 0,01417 | 0,01632 | 0,01915 | 0,01752 | 0,01668 |
| 541,02935 | 0,0133 | 0,0153 | 0,01808 | 0,01648 | 0,01572 |
| 541,06654 | 0,01248 | 0,01434 | 0,01705 | 0,01549 | 0,0148 |
| 541,10372 | 0,01169 | 0,01345 | 0,01608 | 0,01456 | 0,01394 |
| 541,1409 | 0,01095 | 0,01261 | 0,01517 | 0,01369 | 0,01312 |
| 541,17808 | 0,01025 | 0,01181 | 0,0143 | 0,01287 | 0,01235 |
| 541,21526 | 0,00959 | 0,01106 | 0,01347 | 0,0121 | 0,01162 |
| 541,25245 | 0,00896 | 0,01036 | 0,01269 | 0,01137 | 0,01094 |
| 541,28963 | 0,00837 | 0,0097 | 0,01196 | 0,01068 | 0,01028 |
| 541,32681 | 0,00781 | 0,00909 | 0,01127 | 0,01004 | 0,00966 |
| 541,36399 | 0,00729 | 0,00851 | 0,01061 | 0,00944 | 0,00909 |
| 541,40117 | 0,00679 | 0,00797 | 0,00999 | 0,00886 | 0,00854 |
| 541,43836 | 0,00633 | 0,00747 | 0,0094 | 0,00832 | 0,00802 |
| 541,47554 | 0,00589 | 0,007 | 0,00885 | 0,00781 | 0,00752 |
| 541,51272 | 0,00549 | 0,00656 | 0,00832 | 0,00734 | 0,00705 |
| 541,5499 | 0,0051 | 0,00614 | 0,00782 | 0,00688 | 0,00661 |
| 541,58708 | 0,00474 | 0,00575 | 0,00735 | 0,00645 | 0,00619 |
| 541,62427 | 0,0044 | 0,00539 | 0,0069 | 0,00604 | 0,00579 |
| 541,66145 | 0,00409 | 0,00505 | 0,00648 | 0,00566 | 0,00541 |
| 541,69863 | 0,00379 | 0,00473 | 0,00608 | 0,00529 | 0,00505 |
| 541,73581 | 0,00351 | 0,00442 | 0,00569 | 0,00494 | 0,00471 |
| 541,77299 | 0,00325 | 0,00414 | 0,00533 | 0,00461 | 0,00439 |
| 541,81018 | 0,00301 | 0,00387 | 0,00499 | 0,0043 | 0,00408 |
| 541,84736 | 0,00278 | 0,00362 | 0,00466 | 0,004 | 0,00378 |
| 541,88454 | 0,00257 | 0,00338 | 0,00435 | 0,00372 | 0,00351 |
| 541,92172 | 0,00237 | 0,00315 | 0,00405 | 0,00345 | 0,00325 |
| 541,9589 | 0,00219 | 0,00294 | 0,00377 | 0,0032 | 0,003 |
| 541,99609 | 0,00201 | 0,00274 | 0,0035 | 0,00296 | 0,00277 |
| 542,03327 | 0,00185 | 0,00255 | 0,00325 | 0,00273 | 0,00255 |
| 542,07045 | 0,0017 | 0,00237 | 0,00301 | 0,00252 | 0,00234 |
| 542,10763 | 0,00156 | 0,0022 | 0,00278 | 0,00232 | 0,00215 |
| 542,14481 | 0,00143 | 0,00204 | 0,00257 | 0,00213 | 0,00196 |
| 542,182 | 0,00131 | 0,00189 | 0,00237 | 0,00195 | 0,00179 |
| 542,21918 | 0,00119 | 0,00174 | 0,00218 | 0,00178 | 0,00163 |
| 542,25636 | 0,00109 | 0,00161 | 0,002 | 0,00162 | 0,00149 |
| 542,29354 | 0,00099 | 0,00148 | 0,00183 | 0,00148 | 0,00135 |
| 542,33072 | 9e-04 | 0,00136 | 0,00168 | 0,00134 | 0,00122 |
| 542,36791 | 0,00081 | 0,00125 | 0,00153 | 0,00121 | 0,0011 |
| 542,40509 | 0,00074 | 0,00114 | 0,00139 | 0,0011 | 0,00099 |
| 542,44227 | 0,00067 | 0,00104 | 0,00126 | 0,00099 | 0,00089 |
| 542,47945 | 6e-04 | 0,00095 | 0,00115 | 0,00089 | 8e-04 |
| 542,51663 | 0,00054 | 0,00087 | 0,00104 | 8e-04 | 0,00071 |
| 542,55382 | 0,00049 | 0,00078 | 0,00093 | 0,00071 | 0,00064 |
| 542,591 | 0,00044 | 0,00071 | 0,00084 | 0,00063 | 0,00057 |
| 542,62818 | 0,00039 | 0,00064 | 0,00076 | 0,00056 | 5e-04 |
| 542,66536 | 0,00035 | 0,00058 | 0,00068 | 5e-04 | 0,00044 |
| 542,70254 | 0,00031 | 0,00052 | 6e-04 | 0,00044 | 0,00039 |
| 542,73973 | 0,00028 | 0,00047 | 0,00054 | 0,00039 | 0,00034 |
| 542,77691 | 0,00024 | 0,00042 | 0,00048 | 0,00034 | 3e-04 |
| 542,81409 | 0,00022 | 0,00038 | 0,00043 | 3e-04 | 0,00026 |
| 542,85127 | 0,00019 | 0,00033 | 0,00038 | 0,00026 | 0,00023 |
| 542,88845 | 0,00017 | 3e-04 | 0,00033 | 0,00023 | 2e-04 |
| 542,92564 | 0,00015 | 0,00026 | 0,00029 | 2e-04 | 0,00017 |
| 542,96282 | 0,00013 | 0,00023 | 0,00026 | 0,00017 | 0,00015 |
| 543 | 0,00011 | 0,00021 | 0,00022 | 0,00015 | 0,00013 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 5e-05 | 2e-05 | 0 | 0 | 0 |
| 524,03718 | 6e-05 | 2e-05 | 0 | 0 | 0 |
| 524,07436 | 7e-05 | 2e-05 | 0 | 0 | 0 |
| 524,11155 | 8e-05 | 3e-05 | 0 | 0 | 0 |
| 524,14873 | 9e-05 | 3e-05 | 0 | 0 | 0 |
| 524,18591 | 1e-04 | 3e-05 | 0 | 0 | 0 |
| 524,22309 | 0,00011 | 4e-05 | 0 | 0 | 0 |
| 524,26027 | 0,00012 | 4e-05 | 0 | 0 | 0 |
| 524,29746 | 0,00013 | 5e-05 | 0 | 0 | 0 |
| 524,33464 | 0,00014 | 5e-05 | 0 | 0 | 0 |
| 524,37182 | 0,00016 | 6e-05 | 0 | 0 | 0 |
| 524,409 | 0,00017 | 6e-05 | 1e-05 | 0 | 0 |
| 524,44618 | 0,00019 | 7e-05 | 1e-05 | 0 | 0 |
| 524,48337 | 2e-04 | 8e-05 | 1e-05 | 0 | 0 |
| 524,52055 | 0,00022 | 8e-05 | 1e-05 | 0 | 0 |
| 524,55773 | 0,00023 | 9e-05 | 1e-05 | 0 | 0 |
| 524,59491 | 0,00025 | 1e-04 | 2e-05 | 0 | 0 |
| 524,63209 | 0,00026 | 0,00011 | 2e-05 | 0 | 0 |
| 524,66928 | 0,00028 | 0,00012 | 2e-05 | 0 | 0 |
| 524,70646 | 0,00029 | 0,00012 | 3e-05 | 0 | 0 |
| 524,74364 | 0,00031 | 0,00013 | 3e-05 | 0 | 0 |
| 524,78082 | 0,00032 | 0,00014 | 3e-05 | 0 | 0 |
| 524,818 | 0,00034 | 0,00015 | 4e-05 | 0 | 0 |
| 524,85519 | 0,00035 | 0,00016 | 5e-05 | 0 | 0 |
| 524,89237 | 0,00036 | 0,00017 | 5e-05 | 0 | 0 |
| 524,92955 | 0,00037 | 0,00018 | 6e-05 | 0 | 0 |
| 524,96673 | 0,00038 | 0,00019 | 7e-05 | 0 | 0 |
| 525,00391 | 0,00039 | 2e-04 | 8e-05 | 0 | 1e-05 |
| 525,0411 | 4e-04 | 0,00021 | 9e-05 | 0 | 1e-05 |
| 525,07828 | 4e-04 | 0,00023 | 0,00011 | 0 | 1e-05 |
| 525,11546 | 0,00041 | 0,00024 | 0,00012 | 0 | 1e-05 |
| 525,15264 | 0,00041 | 0,00025 | 0,00014 | 0 | 1e-05 |
| 525,18982 | 0,00041 | 0,00026 | 0,00015 | 0 | 1e-05 |
| 525,22701 | 0,00041 | 0,00028 | 0,00017 | 1e-05 | 1e-05 |
| 525,26419 | 0,00041 | 0,00029 | 0,00019 | 1e-05 | 2e-05 |
| 525,30137 | 0,00041 | 0,00031 | 0,00021 | 1e-05 | 2e-05 |
| 525,33855 | 0,00041 | 0,00032 | 0,00024 | 1e-05 | 2e-05 |
| 525,37573 | 0,00041 | 0,00034 | 0,00026 | 1e-05 | 3e-05 |
| 525,41292 | 0,00041 | 0,00036 | 0,00029 | 1e-05 | 3e-05 |
| 525,4501 | 4e-04 | 0,00038 | 0,00031 | 2e-05 | 3e-05 |
| 525,48728 | 4e-04 | 4e-04 | 0,00034 | 2e-05 | 4e-05 |
| 525,52446 | 4e-04 | 0,00042 | 0,00038 | 2e-05 | 4e-05 |
| 525,56164 | 4e-04 | 0,00044 | 0,00041 | 3e-05 | 5e-05 |
| 525,59883 | 4e-04 | 0,00047 | 0,00044 | 3e-05 | 5e-05 |
| 525,63601 | 4e-04 | 5e-04 | 0,00048 | 4e-05 | 6e-05 |
| 525,67319 | 4e-04 | 0,00052 | 0,00052 | 4e-05 | 6e-05 |
| 525,71037 | 4e-04 | 0,00055 | 0,00056 | 5e-05 | 7e-05 |
| 525,74755 | 0,00041 | 0,00059 | 6e-04 | 5e-05 | 7e-05 |
| 525,78474 | 0,00041 | 0,00062 | 0,00064 | 6e-05 | 8e-05 |
| 525,82192 | 0,00042 | 0,00066 | 0,00068 | 7e-05 | 9e-05 |
| 525,8591 | 0,00043 | 0,00069 | 0,00073 | 8e-05 | 9e-05 |
| 525,89628 | 0,00045 | 0,00073 | 0,00077 | 9e-05 | 1e-04 |
| 525,93346 | 0,00047 | 0,00077 | 0,00082 | 1e-04 | 0,00011 |
| 525,97065 | 0,00049 | 0,00082 | 0,00087 | 0,00011 | 0,00011 |
| 526,00783 | 0,00051 | 0,00086 | 0,00092 | 0,00012 | 0,00012 |
| 526,04501 | 0,00054 | 0,00091 | 0,00097 | 0,00014 | 0,00013 |
| 526,08219 | 0,00058 | 0,00096 | 0,00103 | 0,00015 | 0,00013 |
| 526,11937 | 0,00062 | 0,00101 | 0,00109 | 0,00017 | 0,00014 |
| 526,15656 | 0,00066 | 0,00106 | 0,00115 | 0,00018 | 0,00015 |
| 526,19374 | 0,00071 | 0,00112 | 0,00121 | 2e-04 | 0,00015 |
| 526,23092 | 0,00076 | 0,00117 | 0,00128 | 0,00022 | 0,00016 |
| 526,2681 | 0,00081 | 0,00124 | 0,00135 | 0,00024 | 0,00017 |
| 526,30528 | 0,00088 | 0,0013 | 0,00143 | 0,00026 | 0,00017 |
| 526,34247 | 0,00095 | 0,00137 | 0,00151 | 0,00028 | 0,00018 |
| 526,37965 | 0,00102 | 0,00144 | 0,00159 | 3e-04 | 0,00019 |
| 526,41683 | 0,0011 | 0,00151 | 0,00169 | 0,00033 | 0,00019 |
| 526,45401 | 0,00119 | 0,00159 | 0,00179 | 0,00035 | 2e-04 |
| 526,49119 | 0,00129 | 0,00168 | 0,0019 | 0,00038 | 0,00021 |
| 526,52838 | 0,00139 | 0,00177 | 0,00202 | 0,00041 | 0,00022 |
| 526,56556 | 0,00151 | 0,00187 | 0,00216 | 0,00044 | 0,00023 |
| 526,60274 | 0,00163 | 0,00198 | 0,0023 | 0,00047 | 0,00024 |
| 526,63992 | 0,00177 | 0,0021 | 0,00246 | 0,00051 | 0,00025 |
| 526,6771 | 0,00191 | 0,00224 | 0,00263 | 0,00055 | 0,00026 |
| 526,71429 | 0,00208 | 0,00238 | 0,00282 | 0,00059 | 0,00028 |
| 526,75147 | 0,00225 | 0,00254 | 0,00303 | 0,00064 | 3e-04 |
| 526,78865 | 0,00245 | 0,00271 | 0,00326 | 0,00069 | 0,00032 |
| 526,82583 | 0,00265 | 0,0029 | 0,00351 | 0,00074 | 0,00035 |
| 526,86301 | 0,00288 | 0,00311 | 0,00378 | 0,00081 | 0,00039 |
| 526,9002 | 0,00314 | 0,00335 | 0,00407 | 0,00088 | 0,00043 |
| 526,93738 | 0,00341 | 0,0036 | 0,00439 | 0,00096 | 0,00048 |
| 526,97456 | 0,00371 | 0,00388 | 0,00475 | 0,00105 | 0,00054 |
| 527,01174 | 0,00404 | 0,0042 | 0,00512 | 0,00115 | 0,00061 |
| 527,04892 | 0,0044 | 0,00454 | 0,00553 | 0,00126 | 0,00069 |
| 527,08611 | 0,00479 | 0,00492 | 0,00597 | 0,00139 | 0,00078 |
| 527,12329 | 0,00522 | 0,00532 | 0,00645 | 0,00154 | 0,00089 |
| 527,16047 | 0,00568 | 0,00577 | 0,00696 | 0,0017 | 0,00101 |
| 527,19765 | 0,00619 | 0,00627 | 0,00751 | 0,00188 | 0,00115 |
| 527,23483 | 0,00673 | 0,0068 | 0,0081 | 0,00208 | 0,00132 |
| 527,27202 | 0,00732 | 0,00738 | 0,00872 | 0,00232 | 0,0015 |
| 527,3092 | 0,00796 | 0,008 | 0,00939 | 0,00258 | 0,00171 |
| 527,34638 | 0,00864 | 0,00867 | 0,01011 | 0,00287 | 0,00195 |
| 527,38356 | 0,00938 | 0,0094 | 0,01087 | 0,00319 | 0,00222 |
| 527,42074 | 0,01016 | 0,01018 | 0,01166 | 0,00354 | 0,00252 |
| 527,45793 | 0,011 | 0,01101 | 0,0125 | 0,00394 | 0,00286 |
| 527,49511 | 0,01189 | 0,0119 | 0,01339 | 0,00438 | 0,00323 |
| 527,53229 | 0,01284 | 0,01284 | 0,01433 | 0,00486 | 0,00364 |
| 527,56947 | 0,01384 | 0,01385 | 0,01531 | 0,00538 | 0,0041 |
| 527,60665 | 0,01489 | 0,0149 | 0,01634 | 0,00595 | 0,0046 |
| 527,64384 | 0,01601 | 0,01602 | 0,0174 | 0,00658 | 0,00516 |
| 527,68102 | 0,01717 | 0,01718 | 0,01851 | 0,00727 | 0,00576 |
| 527,7182 | 0,01839 | 0,0184 | 0,01967 | 0,008 | 0,00641 |
| 527,75538 | 0,01966 | 0,01969 | 0,02087 | 0,00879 | 0,00712 |
| 527,79256 | 0,02097 | 0,02102 | 0,0221 | 0,00963 | 0,00789 |
| 527,82975 | 0,02233 | 0,02239 | 0,02337 | 0,01054 | 0,00871 |
| 527,86693 | 0,02375 | 0,02382 | 0,02468 | 0,01151 | 0,00959 |
| 527,90411 | 0,02519 | 0,02528 | 0,02602 | 0,01254 | 0,01053 |
| 527,94129 | 0,02668 | 0,02679 | 0,02739 | 0,01362 | 0,01152 |
| 527,97847 | 0,0282 | 0,02834 | 0,02879 | 0,01475 | 0,01259 |
| 528,01566 | 0,02974 | 0,02991 | 0,0302 | 0,01595 | 0,01371 |
| 528,05284 | 0,03132 | 0,03151 | 0,03164 | 0,0172 | 0,01488 |
| 528,09002 | 0,03292 | 0,03313 | 0,0331 | 0,0185 | 0,0161 |
| 528,1272 | 0,03453 | 0,03477 | 0,03457 | 0,01984 | 0,01737 |
| 528,16438 | 0,03616 | 0,03642 | 0,03604 | 0,02122 | 0,0187 |
| 528,20157 | 0,03779 | 0,03808 | 0,03752 | 0,02265 | 0,02007 |
| 528,23875 | 0,03943 | 0,03974 | 0,03901 | 0,02411 | 0,02147 |
| 528,27593 | 0,04108 | 0,0414 | 0,04049 | 0,02559 | 0,02291 |
| 528,31311 | 0,04271 | 0,04304 | 0,04196 | 0,0271 | 0,02437 |
| 528,35029 | 0,04434 | 0,04468 | 0,04343 | 0,02862 | 0,02586 |
| 528,38748 | 0,04596 | 0,0463 | 0,04489 | 0,03014 | 0,02737 |
| 528,42466 | 0,04757 | 0,04789 | 0,04633 | 0,03167 | 0,02887 |
| 528,46184 | 0,04915 | 0,04947 | 0,04775 | 0,0332 | 0,03038 |
| 528,49902 | 0,05072 | 0,051 | 0,04915 | 0,03471 | 0,03189 |
| 528,5362 | 0,05227 | 0,05251 | 0,05053 | 0,0362 | 0,03337 |
| 528,57339 | 0,05379 | 0,05399 | 0,05189 | 0,03766 | 0,03483 |
| 528,61057 | 0,05528 | 0,05543 | 0,05323 | 0,03909 | 0,03627 |
| 528,64775 | 0,05675 | 0,05684 | 0,05453 | 0,04048 | 0,03767 |
| 528,68493 | 0,05819 | 0,0582 | 0,05581 | 0,04183 | 0,03903 |
| 528,72211 | 0,05961 | 0,05952 | 0,05706 | 0,04313 | 0,04034 |
| 528,7593 | 0,061 | 0,06081 | 0,05829 | 0,04438 | 0,04159 |
| 528,79648 | 0,06235 | 0,06206 | 0,05949 | 0,04556 | 0,04278 |
| 528,83366 | 0,06367 | 0,06327 | 0,06066 | 0,04669 | 0,04392 |
| 528,87084 | 0,06497 | 0,06445 | 0,0618 | 0,04776 | 0,04499 |
| 528,90802 | 0,06624 | 0,06559 | 0,06291 | 0,04877 | 0,046 |
| 528,94521 | 0,06749 | 0,0667 | 0,06401 | 0,04972 | 0,04693 |
| 528,98239 | 0,0687 | 0,06778 | 0,06507 | 0,0506 | 0,0478 |
| 529,01957 | 0,06988 | 0,06884 | 0,06611 | 0,05143 | 0,0486 |
| 529,05675 | 0,07103 | 0,06986 | 0,06713 | 0,0522 | 0,04935 |
| 529,09393 | 0,07216 | 0,07086 | 0,06812 | 0,05293 | 0,05003 |
| 529,13112 | 0,07327 | 0,07184 | 0,06909 | 0,05361 | 0,05064 |
| 529,1683 | 0,07434 | 0,0728 | 0,07004 | 0,05424 | 0,05121 |
| 529,20548 | 0,07538 | 0,07375 | 0,07096 | 0,05484 | 0,05174 |
| 529,24266 | 0,07639 | 0,07468 | 0,07186 | 0,05541 | 0,05222 |
| 529,27984 | 0,07737 | 0,07559 | 0,07273 | 0,05595 | 0,05268 |
| 529,31703 | 0,07833 | 0,07649 | 0,07358 | 0,05648 | 0,0531 |
| 529,35421 | 0,07925 | 0,07737 | 0,07441 | 0,057 | 0,05351 |
| 529,39139 | 0,08013 | 0,07825 | 0,07521 | 0,05751 | 0,0539 |
| 529,42857 | 0,08098 | 0,0791 | 0,07598 | 0,05803 | 0,0543 |
| 529,46575 | 0,0818 | 0,07995 | 0,07672 | 0,05855 | 0,05469 |
| 529,50294 | 0,08259 | 0,08078 | 0,07744 | 0,05908 | 0,05511 |
| 529,54012 | 0,08334 | 0,0816 | 0,07813 | 0,05963 | 0,05554 |
| 529,5773 | 0,08405 | 0,08241 | 0,07879 | 0,06021 | 0,05599 |
| 529,61448 | 0,08472 | 0,08319 | 0,07941 | 0,06081 | 0,05648 |
| 529,65166 | 0,08536 | 0,08395 | 0,08001 | 0,06144 | 0,057 |
| 529,68885 | 0,08596 | 0,0847 | 0,08057 | 0,0621 | 0,05757 |
| 529,72603 | 0,08652 | 0,08543 | 0,0811 | 0,0628 | 0,05818 |
| 529,76321 | 0,08704 | 0,08613 | 0,08159 | 0,06352 | 0,05883 |
| 529,80039 | 0,08753 | 0,0868 | 0,08205 | 0,06428 | 0,05953 |
| 529,83757 | 0,08799 | 0,08744 | 0,08248 | 0,06507 | 0,06028 |
| 529,87476 | 0,08842 | 0,08806 | 0,08287 | 0,06589 | 0,06108 |
| 529,91194 | 0,08881 | 0,08865 | 0,08323 | 0,06673 | 0,06193 |
| 529,94912 | 0,08917 | 0,0892 | 0,08356 | 0,0676 | 0,06282 |
| 529,9863 | 0,08951 | 0,08971 | 0,08385 | 0,06848 | 0,06375 |
| 530,02348 | 0,08982 | 0,09019 | 0,08412 | 0,06938 | 0,06472 |
| 530,06067 | 0,09012 | 0,09064 | 0,08435 | 0,07029 | 0,06572 |
| 530,09785 | 0,09039 | 0,09105 | 0,08456 | 0,0712 | 0,06674 |
| 530,13503 | 0,09065 | 0,09143 | 0,08474 | 0,07211 | 0,06779 |
| 530,17221 | 0,0909 | 0,09175 | 0,08488 | 0,073 | 0,06884 |
| 530,20939 | 0,09114 | 0,09204 | 0,08501 | 0,07389 | 0,06991 |
| 530,24658 | 0,09138 | 0,0923 | 0,08511 | 0,07475 | 0,07097 |
| 530,28376 | 0,09161 | 0,09252 | 0,0852 | 0,07559 | 0,07202 |
| 530,32094 | 0,09185 | 0,0927 | 0,08525 | 0,07638 | 0,07306 |
| 530,35812 | 0,09209 | 0,09284 | 0,08529 | 0,07714 | 0,07408 |
| 530,3953 | 0,09234 | 0,09295 | 0,08531 | 0,07786 | 0,07507 |
| 530,43249 | 0,09259 | 0,09302 | 0,08531 | 0,07854 | 0,07603 |
| 530,46967 | 0,09286 | 0,09306 | 0,08529 | 0,07916 | 0,07694 |
| 530,50685 | 0,09314 | 0,09307 | 0,08525 | 0,07971 | 0,07781 |
| 530,54403 | 0,09343 | 0,09304 | 0,08519 | 0,08021 | 0,07864 |
| 530,58121 | 0,09374 | 0,09298 | 0,08511 | 0,08066 | 0,07941 |
| 530,6184 | 0,09406 | 0,09289 | 0,08502 | 0,08104 | 0,08014 |
| 530,65558 | 0,09439 | 0,09278 | 0,08491 | 0,08137 | 0,08081 |
| 530,69276 | 0,09474 | 0,09264 | 0,08477 | 0,08162 | 0,08142 |
| 530,72994 | 0,09511 | 0,09247 | 0,08462 | 0,08181 | 0,08199 |
| 530,76712 | 0,09549 | 0,09228 | 0,08444 | 0,08195 | 0,0825 |
| 530,80431 | 0,09587 | 0,09206 | 0,08425 | 0,08204 | 0,08297 |
| 530,84149 | 0,09627 | 0,09183 | 0,08403 | 0,08208 | 0,08339 |
| 530,87867 | 0,09668 | 0,09158 | 0,0838 | 0,08206 | 0,08376 |
| 530,91585 | 0,09709 | 0,09131 | 0,08353 | 0,082 | 0,08409 |
| 530,95303 | 0,0975 | 0,09102 | 0,08325 | 0,0819 | 0,08439 |
| 530,99022 | 0,09791 | 0,09072 | 0,08295 | 0,08177 | 0,08466 |
| 531,0274 | 0,09832 | 0,0904 | 0,08263 | 0,08161 | 0,0849 |
| 531,06458 | 0,09872 | 0,09008 | 0,08229 | 0,08142 | 0,08511 |
| 531,10176 | 0,09912 | 0,08975 | 0,08193 | 0,08122 | 0,08531 |
| 531,13894 | 0,0995 | 0,08941 | 0,08155 | 0,081 | 0,08548 |
| 531,17613 | 0,09987 | 0,08907 | 0,08116 | 0,08078 | 0,08564 |
| 531,21331 | 0,10023 | 0,08873 | 0,08076 | 0,08055 | 0,08579 |
| 531,25049 | 0,10058 | 0,08839 | 0,08035 | 0,08032 | 0,08593 |
| 531,28767 | 0,1009 | 0,08805 | 0,07994 | 0,0801 | 0,08605 |
| 531,32485 | 0,1012 | 0,08771 | 0,07952 | 0,07989 | 0,08617 |
| 531,36204 | 0,10148 | 0,08739 | 0,07911 | 0,07969 | 0,08627 |
| 531,39922 | 0,10175 | 0,08707 | 0,07871 | 0,0795 | 0,08637 |
| 531,4364 | 0,10199 | 0,08677 | 0,07831 | 0,07933 | 0,08645 |
| 531,47358 | 0,10221 | 0,08648 | 0,07794 | 0,07917 | 0,08651 |
| 531,51076 | 0,10241 | 0,08622 | 0,07758 | 0,07904 | 0,08656 |
| 531,54795 | 0,10259 | 0,08597 | 0,07725 | 0,07892 | 0,08659 |
| 531,58513 | 0,10276 | 0,08573 | 0,07695 | 0,07882 | 0,08661 |
| 531,62231 | 0,1029 | 0,08552 | 0,07668 | 0,07874 | 0,08659 |
| 531,65949 | 0,10303 | 0,08534 | 0,07645 | 0,07869 | 0,08656 |
| 531,69667 | 0,10314 | 0,08518 | 0,07626 | 0,07865 | 0,08649 |
| 531,73386 | 0,10325 | 0,08505 | 0,07612 | 0,07863 | 0,0864 |
| 531,77104 | 0,10334 | 0,08494 | 0,07602 | 0,07862 | 0,08629 |
| 531,80822 | 0,10342 | 0,08486 | 0,07597 | 0,07863 | 0,08614 |
| 531,8454 | 0,1035 | 0,08481 | 0,07598 | 0,07867 | 0,08597 |
| 531,88258 | 0,10357 | 0,08478 | 0,07604 | 0,07871 | 0,08577 |
| 531,91977 | 0,10364 | 0,08478 | 0,07615 | 0,07878 | 0,08554 |
| 531,95695 | 0,10371 | 0,0848 | 0,07632 | 0,07885 | 0,0853 |
| 531,99413 | 0,10377 | 0,08485 | 0,07653 | 0,07895 | 0,08504 |
| 532,03131 | 0,10384 | 0,08492 | 0,07681 | 0,07907 | 0,08476 |
| 532,06849 | 0,1039 | 0,08501 | 0,07713 | 0,0792 | 0,08447 |
| 532,10568 | 0,10397 | 0,08512 | 0,0775 | 0,07935 | 0,08418 |
| 532,14286 | 0,10404 | 0,08525 | 0,07791 | 0,07953 | 0,08389 |
| 532,18004 | 0,10412 | 0,08539 | 0,07836 | 0,07972 | 0,08361 |
| 532,21722 | 0,10419 | 0,08554 | 0,07886 | 0,07994 | 0,08334 |
| 532,2544 | 0,10427 | 0,08571 | 0,07938 | 0,08019 | 0,08309 |
| 532,29159 | 0,10435 | 0,08589 | 0,07993 | 0,08046 | 0,08286 |
| 532,32877 | 0,10443 | 0,08607 | 0,0805 | 0,08075 | 0,08265 |
| 532,36595 | 0,10451 | 0,08625 | 0,08109 | 0,08107 | 0,08249 |
| 532,40313 | 0,10459 | 0,08644 | 0,0817 | 0,08143 | 0,08236 |
| 532,44031 | 0,10467 | 0,08663 | 0,08231 | 0,0818 | 0,08227 |
| 532,4775 | 0,10475 | 0,08682 | 0,08292 | 0,08221 | 0,08222 |
| 532,51468 | 0,10482 | 0,08701 | 0,08353 | 0,08264 | 0,08222 |
| 532,55186 | 0,10489 | 0,0872 | 0,08413 | 0,08309 | 0,08226 |
| 532,58904 | 0,10495 | 0,08738 | 0,08472 | 0,08357 | 0,08236 |
| 532,62622 | 0,105 | 0,08755 | 0,08529 | 0,08407 | 0,0825 |
| 532,66341 | 0,10505 | 0,08773 | 0,08584 | 0,08459 | 0,08268 |
| 532,70059 | 0,10509 | 0,08789 | 0,08637 | 0,08512 | 0,08289 |
| 532,73777 | 0,10512 | 0,08805 | 0,08688 | 0,08566 | 0,08315 |
| 532,77495 | 0,10514 | 0,08821 | 0,08736 | 0,0862 | 0,08345 |
| 532,81213 | 0,10515 | 0,08836 | 0,0878 | 0,08675 | 0,08377 |
| 532,84932 | 0,10516 | 0,0885 | 0,08822 | 0,0873 | 0,08412 |
| 532,8865 | 0,10516 | 0,08864 | 0,0886 | 0,08784 | 0,08448 |
| 532,92368 | 0,10515 | 0,08878 | 0,08896 | 0,08836 | 0,08486 |
| 532,96086 | 0,10513 | 0,08892 | 0,08928 | 0,08887 | 0,08525 |
| 532,99804 | 0,1051 | 0,08905 | 0,08957 | 0,08936 | 0,08564 |
| 533,03523 | 0,10507 | 0,08918 | 0,08983 | 0,08982 | 0,08603 |
| 533,07241 | 0,10504 | 0,08932 | 0,09007 | 0,09025 | 0,08641 |
| 533,10959 | 0,105 | 0,08945 | 0,09028 | 0,09066 | 0,08678 |
| 533,14677 | 0,10496 | 0,08959 | 0,09046 | 0,09103 | 0,08713 |
| 533,18395 | 0,10491 | 0,08973 | 0,09062 | 0,09135 | 0,08746 |
| 533,22114 | 0,10487 | 0,08987 | 0,09077 | 0,09164 | 0,08777 |
| 533,25832 | 0,10483 | 0,09001 | 0,09089 | 0,09189 | 0,08805 |
| 533,2955 | 0,10479 | 0,09015 | 0,09101 | 0,09211 | 0,08831 |
| 533,33268 | 0,10475 | 0,0903 | 0,09111 | 0,09227 | 0,08854 |
| 533,36986 | 0,10471 | 0,09046 | 0,0912 | 0,0924 | 0,08873 |
| 533,40705 | 0,10468 | 0,09061 | 0,09129 | 0,09249 | 0,08891 |
| 533,44423 | 0,10465 | 0,09077 | 0,09138 | 0,09255 | 0,08905 |
| 533,48141 | 0,10462 | 0,09093 | 0,09146 | 0,09257 | 0,08918 |
| 533,51859 | 0,1046 | 0,09109 | 0,09155 | 0,09256 | 0,08927 |
| 533,55577 | 0,10458 | 0,09125 | 0,09164 | 0,09251 | 0,08934 |
| 533,59295 | 0,10456 | 0,09141 | 0,09174 | 0,09245 | 0,0894 |
| 533,63014 | 0,10454 | 0,09157 | 0,09185 | 0,09236 | 0,08944 |
| 533,66732 | 0,10452 | 0,09173 | 0,09196 | 0,09226 | 0,08947 |
| 533,7045 | 0,10449 | 0,09188 | 0,09209 | 0,09214 | 0,08949 |
| 533,74168 | 0,10446 | 0,09204 | 0,09223 | 0,09201 | 0,0895 |
| 533,77886 | 0,10443 | 0,09218 | 0,09238 | 0,09187 | 0,0895 |
| 533,81605 | 0,10439 | 0,09232 | 0,09255 | 0,09173 | 0,08951 |
| 533,85323 | 0,10433 | 0,09246 | 0,09273 | 0,09158 | 0,08951 |
| 533,89041 | 0,10427 | 0,09259 | 0,09292 | 0,09144 | 0,08951 |
| 533,92759 | 0,10419 | 0,09271 | 0,09313 | 0,09131 | 0,08952 |
| 533,96477 | 0,10409 | 0,09282 | 0,09335 | 0,09117 | 0,08954 |
| 534,00196 | 0,10398 | 0,09292 | 0,09359 | 0,09105 | 0,08955 |
| 534,03914 | 0,10385 | 0,09302 | 0,09383 | 0,09094 | 0,08958 |
| 534,07632 | 0,1037 | 0,09311 | 0,09409 | 0,09083 | 0,08961 |
| 534,1135 | 0,10352 | 0,09319 | 0,09436 | 0,09074 | 0,08965 |
| 534,15068 | 0,10333 | 0,09326 | 0,09463 | 0,09066 | 0,08969 |
| 534,18787 | 0,10311 | 0,09333 | 0,09492 | 0,09059 | 0,08974 |
| 534,22505 | 0,10287 | 0,09339 | 0,09521 | 0,09053 | 0,08979 |
| 534,26223 | 0,10261 | 0,09344 | 0,09551 | 0,09048 | 0,08984 |
| 534,29941 | 0,10232 | 0,09349 | 0,09581 | 0,09044 | 0,0899 |
| 534,33659 | 0,10201 | 0,09354 | 0,09612 | 0,09041 | 0,08996 |
| 534,37378 | 0,10169 | 0,09358 | 0,09642 | 0,0904 | 0,09001 |
| 534,41096 | 0,10134 | 0,09362 | 0,09673 | 0,09038 | 0,09007 |
| 534,44814 | 0,10098 | 0,09365 | 0,09703 | 0,09038 | 0,09013 |
| 534,48532 | 0,1006 | 0,09369 | 0,09733 | 0,09039 | 0,09018 |
| 534,5225 | 0,10021 | 0,09372 | 0,09762 | 0,0904 | 0,09024 |
| 534,55969 | 0,09981 | 0,09376 | 0,09791 | 0,09042 | 0,09029 |
| 534,59687 | 0,09941 | 0,09379 | 0,0982 | 0,09044 | 0,09034 |
| 534,63405 | 0,09899 | 0,09382 | 0,09847 | 0,09047 | 0,0904 |
| 534,67123 | 0,09856 | 0,09386 | 0,09874 | 0,09051 | 0,09045 |
| 534,70841 | 0,09814 | 0,09389 | 0,09899 | 0,09055 | 0,09051 |
| 534,7456 | 0,09771 | 0,09393 | 0,09923 | 0,0906 | 0,09058 |
| 534,78278 | 0,09727 | 0,09396 | 0,09946 | 0,09066 | 0,09066 |
| 534,81996 | 0,09684 | 0,09399 | 0,09968 | 0,09073 | 0,09074 |
| 534,85714 | 0,09641 | 0,09402 | 0,09988 | 0,09081 | 0,09083 |
| 534,89432 | 0,09598 | 0,09405 | 0,10007 | 0,09089 | 0,09095 |
| 534,93151 | 0,09554 | 0,09407 | 0,10024 | 0,09099 | 0,09108 |
| 534,96869 | 0,09511 | 0,09408 | 0,10039 | 0,0911 | 0,09123 |
| 535,00587 | 0,09468 | 0,09409 | 0,10053 | 0,09123 | 0,0914 |
| 535,04305 | 0,09424 | 0,09409 | 0,10065 | 0,09136 | 0,09159 |
| 535,08023 | 0,09381 | 0,09408 | 0,10076 | 0,09152 | 0,09181 |
| 535,11742 | 0,09337 | 0,09406 | 0,10084 | 0,09168 | 0,09206 |
| 535,1546 | 0,09292 | 0,09402 | 0,10091 | 0,09187 | 0,09234 |
| 535,19178 | 0,09248 | 0,09397 | 0,10096 | 0,09206 | 0,09264 |
| 535,22896 | 0,09202 | 0,0939 | 0,101 | 0,09228 | 0,09297 |
| 535,26614 | 0,09156 | 0,09381 | 0,10101 | 0,09251 | 0,09333 |
| 535,30333 | 0,09109 | 0,09371 | 0,10101 | 0,09275 | 0,09372 |
| 535,34051 | 0,09062 | 0,09359 | 0,10099 | 0,09301 | 0,09414 |
| 535,37769 | 0,09013 | 0,09344 | 0,10096 | 0,09328 | 0,09457 |
| 535,41487 | 0,08964 | 0,09328 | 0,10091 | 0,09356 | 0,09503 |
| 535,45205 | 0,08914 | 0,09309 | 0,10084 | 0,09386 | 0,09551 |
| 535,48924 | 0,08862 | 0,09289 | 0,10076 | 0,09416 | 0,09601 |
| 535,52642 | 0,0881 | 0,09267 | 0,10066 | 0,09447 | 0,09652 |
| 535,5636 | 0,08758 | 0,09242 | 0,10055 | 0,09479 | 0,09704 |
| 535,60078 | 0,08704 | 0,09216 | 0,10043 | 0,09511 | 0,09756 |
| 535,63796 | 0,0865 | 0,09188 | 0,10029 | 0,09543 | 0,09809 |
| 535,67515 | 0,08595 | 0,09158 | 0,10014 | 0,09575 | 0,09861 |
| 535,71233 | 0,0854 | 0,09126 | 0,09998 | 0,09607 | 0,09912 |
| 535,74951 | 0,08485 | 0,09093 | 0,09981 | 0,09639 | 0,09963 |
| 535,78669 | 0,0843 | 0,09058 | 0,09962 | 0,09671 | 0,10012 |
| 535,82387 | 0,08375 | 0,09023 | 0,09942 | 0,09702 | 0,10059 |
| 535,86106 | 0,08321 | 0,08986 | 0,09921 | 0,09732 | 0,10104 |
| 535,89824 | 0,08266 | 0,08948 | 0,09899 | 0,09762 | 0,10146 |
| 535,93542 | 0,08213 | 0,0891 | 0,09875 | 0,09791 | 0,10185 |
| 535,9726 | 0,0816 | 0,0887 | 0,0985 | 0,09819 | 0,10222 |
| 536,00978 | 0,08107 | 0,0883 | 0,09824 | 0,09846 | 0,10255 |
| 536,04697 | 0,08056 | 0,0879 | 0,09796 | 0,09872 | 0,10284 |
| 536,08415 | 0,08005 | 0,08749 | 0,09767 | 0,09897 | 0,10309 |
| 536,12133 | 0,07955 | 0,08708 | 0,09737 | 0,09921 | 0,10331 |
| 536,15851 | 0,07907 | 0,08667 | 0,09705 | 0,09944 | 0,10349 |
| 536,19569 | 0,07859 | 0,08626 | 0,09671 | 0,09965 | 0,10362 |
| 536,23288 | 0,07811 | 0,08585 | 0,09635 | 0,09985 | 0,1037 |
| 536,27006 | 0,07765 | 0,08544 | 0,09598 | 0,10003 | 0,10374 |
| 536,30724 | 0,07719 | 0,08503 | 0,09559 | 0,1002 | 0,10374 |
| 536,34442 | 0,07673 | 0,08461 | 0,09517 | 0,10036 | 0,10369 |
| 536,3816 | 0,07628 | 0,0842 | 0,09473 | 0,10049 | 0,1036 |
| 536,41879 | 0,07582 | 0,08379 | 0,09428 | 0,10061 | 0,10345 |
| 536,45597 | 0,07537 | 0,08338 | 0,0938 | 0,10071 | 0,10326 |
| 536,49315 | 0,07492 | 0,08296 | 0,09331 | 0,10078 | 0,10302 |
| 536,53033 | 0,07446 | 0,08255 | 0,09279 | 0,10084 | 0,10274 |
| 536,56751 | 0,074 | 0,08213 | 0,09225 | 0,10087 | 0,10241 |
| 536,6047 | 0,07353 | 0,08172 | 0,09169 | 0,10087 | 0,10203 |
| 536,64188 | 0,07306 | 0,0813 | 0,09111 | 0,10084 | 0,10161 |
| 536,67906 | 0,07258 | 0,08088 | 0,09051 | 0,10078 | 0,10115 |
| 536,71624 | 0,07209 | 0,08046 | 0,0899 | 0,1007 | 0,10064 |
| 536,75342 | 0,07158 | 0,08004 | 0,08926 | 0,10058 | 0,1001 |
| 536,79061 | 0,07107 | 0,07962 | 0,08862 | 0,10042 | 0,09951 |
| 536,82779 | 0,07054 | 0,07919 | 0,08796 | 0,10023 | 0,09888 |
| 536,86497 | 0,07 | 0,07876 | 0,08729 | 0,1 | 0,09822 |
| 536,90215 | 0,06946 | 0,07834 | 0,08662 | 0,09975 | 0,09754 |
| 536,93933 | 0,0689 | 0,07791 | 0,08593 | 0,09945 | 0,09682 |
| 536,97652 | 0,06833 | 0,07749 | 0,08524 | 0,09911 | 0,09608 |
| 537,0137 | 0,06776 | 0,07706 | 0,08455 | 0,09873 | 0,09531 |
| 537,05088 | 0,06717 | 0,07664 | 0,08386 | 0,09833 | 0,09453 |
| 537,08806 | 0,06658 | 0,07622 | 0,08316 | 0,09789 | 0,09374 |
| 537,12524 | 0,06599 | 0,07581 | 0,08248 | 0,09742 | 0,09294 |
| 537,16243 | 0,06539 | 0,0754 | 0,08179 | 0,09691 | 0,09213 |
| 537,19961 | 0,06479 | 0,075 | 0,08111 | 0,09638 | 0,09133 |
| 537,23679 | 0,06419 | 0,0746 | 0,08044 | 0,09583 | 0,09053 |
| 537,27397 | 0,06359 | 0,07422 | 0,07978 | 0,09525 | 0,08974 |
| 537,31115 | 0,06299 | 0,07384 | 0,07913 | 0,09465 | 0,08896 |
| 537,34834 | 0,0624 | 0,07348 | 0,07849 | 0,09403 | 0,0882 |
| 537,38552 | 0,06182 | 0,07312 | 0,07786 | 0,0934 | 0,08746 |
| 537,4227 | 0,06124 | 0,07277 | 0,07724 | 0,09276 | 0,08675 |
| 537,45988 | 0,06066 | 0,07244 | 0,07664 | 0,09212 | 0,08606 |
| 537,49706 | 0,0601 | 0,07211 | 0,07605 | 0,09146 | 0,08541 |
| 537,53425 | 0,05955 | 0,0718 | 0,07547 | 0,09081 | 0,08478 |
| 537,57143 | 0,05901 | 0,07149 | 0,07491 | 0,09015 | 0,0842 |
| 537,60861 | 0,05848 | 0,07119 | 0,07435 | 0,0895 | 0,08365 |
| 537,64579 | 0,05795 | 0,07091 | 0,07381 | 0,08885 | 0,08314 |
| 537,68297 | 0,05744 | 0,07063 | 0,07329 | 0,08821 | 0,08266 |
| 537,72016 | 0,05694 | 0,07035 | 0,07278 | 0,08758 | 0,08221 |
| 537,75734 | 0,05645 | 0,07008 | 0,07227 | 0,08695 | 0,08181 |
| 537,79452 | 0,05597 | 0,06982 | 0,07178 | 0,08634 | 0,08144 |
| 537,8317 | 0,0555 | 0,06955 | 0,0713 | 0,08574 | 0,0811 |
| 537,86888 | 0,05503 | 0,06929 | 0,07083 | 0,08515 | 0,08079 |
| 537,90607 | 0,05458 | 0,06902 | 0,07037 | 0,08457 | 0,08051 |
| 537,94325 | 0,05413 | 0,06876 | 0,06992 | 0,084 | 0,08026 |
| 537,98043 | 0,05368 | 0,06849 | 0,06948 | 0,08344 | 0,08003 |
| 538,01761 | 0,05324 | 0,06821 | 0,06904 | 0,08289 | 0,07982 |
| 538,05479 | 0,05281 | 0,06793 | 0,06862 | 0,08235 | 0,07962 |
| 538,09198 | 0,05238 | 0,06764 | 0,0682 | 0,08182 | 0,07944 |
| 538,12916 | 0,05195 | 0,06734 | 0,06778 | 0,08129 | 0,07927 |
| 538,16634 | 0,05153 | 0,06703 | 0,06738 | 0,08077 | 0,0791 |
| 538,20352 | 0,05111 | 0,06671 | 0,06697 | 0,08026 | 0,07893 |
| 538,2407 | 0,0507 | 0,06638 | 0,06658 | 0,07974 | 0,07876 |
| 538,27789 | 0,05029 | 0,06603 | 0,06619 | 0,07923 | 0,07859 |
| 538,31507 | 0,04988 | 0,06568 | 0,0658 | 0,07872 | 0,07841 |
| 538,35225 | 0,04948 | 0,06532 | 0,06542 | 0,07821 | 0,07822 |
| 538,38943 | 0,04908 | 0,06495 | 0,06504 | 0,0777 | 0,07802 |
| 538,42661 | 0,04869 | 0,06456 | 0,06466 | 0,07718 | 0,0778 |
| 538,4638 | 0,04831 | 0,06417 | 0,06429 | 0,07666 | 0,07756 |
| 538,50098 | 0,04793 | 0,06377 | 0,06391 | 0,07614 | 0,0773 |
| 538,53816 | 0,04756 | 0,06337 | 0,06354 | 0,0756 | 0,07702 |
| 538,57534 | 0,0472 | 0,06295 | 0,06317 | 0,07507 | 0,07672 |
| 538,61252 | 0,04684 | 0,06253 | 0,0628 | 0,07452 | 0,07639 |
| 538,64971 | 0,0465 | 0,06211 | 0,06243 | 0,07397 | 0,07604 |
| 538,68689 | 0,04616 | 0,06168 | 0,06205 | 0,07341 | 0,07567 |
| 538,72407 | 0,04583 | 0,06124 | 0,06167 | 0,07284 | 0,07527 |
| 538,76125 | 0,04551 | 0,06081 | 0,06129 | 0,07227 | 0,07484 |
| 538,79843 | 0,0452 | 0,06037 | 0,0609 | 0,07168 | 0,0744 |
| 538,83562 | 0,04489 | 0,05993 | 0,06051 | 0,0711 | 0,07394 |
| 538,8728 | 0,04459 | 0,0595 | 0,06011 | 0,0705 | 0,07346 |
| 538,90998 | 0,0443 | 0,05906 | 0,0597 | 0,0699 | 0,07295 |
| 538,94716 | 0,04401 | 0,05862 | 0,05928 | 0,0693 | 0,07243 |
| 538,98434 | 0,04373 | 0,05818 | 0,05885 | 0,06869 | 0,0719 |
| 539,02153 | 0,04345 | 0,05774 | 0,0584 | 0,06808 | 0,07135 |
| 539,05871 | 0,04318 | 0,0573 | 0,05795 | 0,06747 | 0,0708 |
| 539,09589 | 0,04291 | 0,05686 | 0,05748 | 0,06685 | 0,07023 |
| 539,13307 | 0,04264 | 0,05642 | 0,05699 | 0,06624 | 0,06966 |
| 539,17025 | 0,04237 | 0,05598 | 0,05649 | 0,06563 | 0,06908 |
| 539,20744 | 0,0421 | 0,05553 | 0,05596 | 0,06502 | 0,06849 |
| 539,24462 | 0,04183 | 0,05509 | 0,05543 | 0,0644 | 0,0679 |
| 539,2818 | 0,04156 | 0,05464 | 0,05487 | 0,0638 | 0,0673 |
| 539,31898 | 0,04129 | 0,05419 | 0,0543 | 0,06319 | 0,06671 |
| 539,35616 | 0,04101 | 0,05373 | 0,0537 | 0,06259 | 0,06611 |
| 539,39335 | 0,04074 | 0,05327 | 0,05309 | 0,06199 | 0,0655 |
| 539,43053 | 0,04046 | 0,0528 | 0,05245 | 0,06139 | 0,0649 |
| 539,46771 | 0,04018 | 0,05232 | 0,0518 | 0,06079 | 0,06429 |
| 539,50489 | 0,0399 | 0,05184 | 0,05114 | 0,0602 | 0,06368 |
| 539,54207 | 0,03962 | 0,05135 | 0,05045 | 0,05961 | 0,06306 |
| 539,57926 | 0,03934 | 0,05085 | 0,04974 | 0,05902 | 0,06244 |
| 539,61644 | 0,03905 | 0,05033 | 0,04902 | 0,05843 | 0,06181 |
| 539,65362 | 0,03877 | 0,04981 | 0,04829 | 0,05783 | 0,06117 |
| 539,6908 | 0,03848 | 0,04927 | 0,04754 | 0,05724 | 0,06053 |
| 539,72798 | 0,03818 | 0,04872 | 0,04677 | 0,05664 | 0,05988 |
| 539,76517 | 0,03789 | 0,04815 | 0,04599 | 0,05604 | 0,05922 |
| 539,80235 | 0,03758 | 0,04757 | 0,0452 | 0,05543 | 0,05855 |
| 539,83953 | 0,03728 | 0,04697 | 0,04439 | 0,05481 | 0,05787 |
| 539,87671 | 0,03696 | 0,04635 | 0,04358 | 0,05418 | 0,05718 |
| 539,91389 | 0,03664 | 0,04571 | 0,04275 | 0,05354 | 0,05648 |
| 539,95108 | 0,0363 | 0,04504 | 0,04191 | 0,0529 | 0,05576 |
| 539,98826 | 0,03595 | 0,04436 | 0,04106 | 0,05223 | 0,05504 |
| 540,02544 | 0,03559 | 0,04365 | 0,0402 | 0,05155 | 0,0543 |
| 540,06262 | 0,03521 | 0,04291 | 0,03934 | 0,05085 | 0,05354 |
| 540,0998 | 0,03481 | 0,04215 | 0,03846 | 0,05013 | 0,05277 |
| 540,13699 | 0,03439 | 0,04136 | 0,03758 | 0,0494 | 0,05199 |
| 540,17417 | 0,03394 | 0,04055 | 0,03669 | 0,04864 | 0,05119 |
| 540,21135 | 0,03347 | 0,03971 | 0,03579 | 0,04785 | 0,05038 |
| 540,24853 | 0,03297 | 0,03885 | 0,03488 | 0,04704 | 0,04955 |
| 540,28571 | 0,03244 | 0,03795 | 0,03397 | 0,0462 | 0,0487 |
| 540,3229 | 0,03188 | 0,03703 | 0,03304 | 0,04534 | 0,04784 |
| 540,36008 | 0,03128 | 0,03608 | 0,03212 | 0,04445 | 0,04695 |
| 540,39726 | 0,03065 | 0,03511 | 0,03118 | 0,04352 | 0,04605 |
| 540,43444 | 0,02999 | 0,03412 | 0,03025 | 0,04257 | 0,04513 |
| 540,47162 | 0,0293 | 0,0331 | 0,02931 | 0,04159 | 0,04418 |
| 540,50881 | 0,02858 | 0,03207 | 0,02836 | 0,04058 | 0,04321 |
| 540,54599 | 0,02781 | 0,03102 | 0,02742 | 0,03955 | 0,04222 |
| 540,58317 | 0,02702 | 0,02996 | 0,02648 | 0,03848 | 0,0412 |
| 540,62035 | 0,02621 | 0,02888 | 0,02553 | 0,03739 | 0,04016 |
| 540,65753 | 0,02537 | 0,02779 | 0,0246 | 0,03627 | 0,0391 |
| 540,69472 | 0,02451 | 0,02671 | 0,02366 | 0,03514 | 0,03802 |
| 540,7319 | 0,02362 | 0,02562 | 0,02274 | 0,03398 | 0,03691 |
| 540,76908 | 0,02273 | 0,02453 | 0,02182 | 0,03281 | 0,03579 |
| 540,80626 | 0,02182 | 0,02344 | 0,02092 | 0,03163 | 0,03464 |
| 540,84344 | 0,0209 | 0,02237 | 0,02003 | 0,03043 | 0,03348 |
| 540,88063 | 0,01998 | 0,02131 | 0,01915 | 0,02923 | 0,03231 |
| 540,91781 | 0,01906 | 0,02026 | 0,0183 | 0,02803 | 0,03112 |
| 540,95499 | 0,01815 | 0,01923 | 0,01746 | 0,02683 | 0,02992 |
| 540,99217 | 0,01724 | 0,01822 | 0,01664 | 0,02564 | 0,02872 |
| 541,02935 | 0,01635 | 0,01723 | 0,01585 | 0,02446 | 0,02752 |
| 541,06654 | 0,01547 | 0,01628 | 0,01508 | 0,02329 | 0,02632 |
| 541,10372 | 0,01462 | 0,01535 | 0,01434 | 0,02214 | 0,02512 |
| 541,1409 | 0,01378 | 0,01444 | 0,01362 | 0,02102 | 0,02394 |
| 541,17808 | 0,01298 | 0,01357 | 0,01293 | 0,01992 | 0,02276 |
| 541,21526 | 0,0122 | 0,01274 | 0,01227 | 0,01885 | 0,02161 |
| 541,25245 | 0,01145 | 0,01194 | 0,01164 | 0,01781 | 0,02048 |
| 541,28963 | 0,01073 | 0,01118 | 0,01103 | 0,0168 | 0,01937 |
| 541,32681 | 0,01005 | 0,01044 | 0,01046 | 0,01584 | 0,01828 |
| 541,36399 | 0,0094 | 0,00975 | 0,00991 | 0,01492 | 0,01723 |
| 541,40117 | 0,00879 | 0,00909 | 0,00939 | 0,01404 | 0,01621 |
| 541,43836 | 0,0082 | 0,00846 | 0,0089 | 0,01319 | 0,01523 |
| 541,47554 | 0,00766 | 0,00787 | 0,00843 | 0,01239 | 0,01428 |
| 541,51272 | 0,00715 | 0,00731 | 0,00799 | 0,01164 | 0,01338 |
| 541,5499 | 0,00667 | 0,00678 | 0,00757 | 0,01093 | 0,0125 |
| 541,58708 | 0,00622 | 0,00629 | 0,00718 | 0,01026 | 0,01168 |
| 541,62427 | 0,00581 | 0,00583 | 0,0068 | 0,00962 | 0,0109 |
| 541,66145 | 0,00542 | 0,0054 | 0,00645 | 0,00903 | 0,01015 |
| 541,69863 | 0,00506 | 0,00499 | 0,00612 | 0,00848 | 0,00945 |
| 541,73581 | 0,00473 | 0,00461 | 0,0058 | 0,00797 | 0,00878 |
| 541,77299 | 0,00442 | 0,00425 | 0,0055 | 0,00749 | 0,00816 |
| 541,81018 | 0,00413 | 0,00392 | 0,00522 | 0,00704 | 0,00758 |
| 541,84736 | 0,00387 | 0,00362 | 0,00494 | 0,00662 | 0,00704 |
| 541,88454 | 0,00362 | 0,00333 | 0,00469 | 0,00624 | 0,00652 |
| 541,92172 | 0,00339 | 0,00306 | 0,00444 | 0,00588 | 0,00604 |
| 541,9589 | 0,00318 | 0,00281 | 0,0042 | 0,00555 | 0,0056 |
| 541,99609 | 0,00298 | 0,00258 | 0,00397 | 0,00523 | 0,00519 |
| 542,03327 | 0,00279 | 0,00237 | 0,00375 | 0,00494 | 0,0048 |
| 542,07045 | 0,00262 | 0,00217 | 0,00354 | 0,00466 | 0,00445 |
| 542,10763 | 0,00246 | 0,00198 | 0,00334 | 0,00441 | 0,00411 |
| 542,14481 | 0,0023 | 0,00181 | 0,00315 | 0,00417 | 0,0038 |
| 542,182 | 0,00215 | 0,00165 | 0,00296 | 0,00394 | 0,00352 |
| 542,21918 | 0,00202 | 0,00151 | 0,00278 | 0,00372 | 0,00325 |
| 542,25636 | 0,00188 | 0,00137 | 0,0026 | 0,00351 | 0,003 |
| 542,29354 | 0,00176 | 0,00124 | 0,00244 | 0,00332 | 0,00277 |
| 542,33072 | 0,00164 | 0,00113 | 0,00227 | 0,00313 | 0,00256 |
| 542,36791 | 0,00153 | 0,00102 | 0,00212 | 0,00295 | 0,00236 |
| 542,40509 | 0,00142 | 0,00092 | 0,00197 | 0,00277 | 0,00217 |
| 542,44227 | 0,00132 | 0,00083 | 0,00182 | 0,00261 | 0,002 |
| 542,47945 | 0,00122 | 0,00075 | 0,00169 | 0,00245 | 0,00184 |
| 542,51663 | 0,00112 | 0,00067 | 0,00156 | 0,0023 | 0,00169 |
| 542,55382 | 0,00104 | 6e-04 | 0,00143 | 0,00215 | 0,00155 |
| 542,591 | 0,00095 | 0,00054 | 0,00131 | 0,002 | 0,00142 |
| 542,62818 | 0,00087 | 0,00048 | 0,0012 | 0,00187 | 0,0013 |
| 542,66536 | 8e-04 | 0,00043 | 0,0011 | 0,00174 | 0,00118 |
| 542,70254 | 0,00073 | 0,00038 | 0,001 | 0,00161 | 0,00108 |
| 542,73973 | 0,00066 | 0,00034 | 0,00091 | 0,00149 | 0,00098 |
| 542,77691 | 6e-04 | 3e-04 | 0,00082 | 0,00137 | 0,00089 |
| 542,81409 | 0,00054 | 0,00026 | 0,00074 | 0,00126 | 0,00081 |
| 542,85127 | 0,00049 | 0,00023 | 0,00066 | 0,00116 | 0,00073 |
| 542,88845 | 0,00044 | 2e-04 | 0,00059 | 0,00106 | 0,00066 |
| 542,92564 | 0,00039 | 0,00018 | 0,00053 | 0,00097 | 0,00059 |
| 542,96282 | 0,00035 | 0,00016 | 0,00047 | 0,00088 | 0,00053 |
| 543 | 0,00031 | 0,00014 | 0,00042 | 0,00079 | 0,00047 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 1e-05 | 0 | 0 |
| 524,74364 | 0 | 0 | 1e-05 | 0 | 0 |
| 524,78082 | 0 | 0 | 1e-05 | 0 | 0 |
| 524,818 | 0 | 0 | 1e-05 | 0 | 0 |
| 524,85519 | 0 | 0 | 1e-05 | 0 | 0 |
| 524,89237 | 0 | 0 | 1e-05 | 0 | 0 |
| 524,92955 | 0 | 0 | 1e-05 | 0 | 0 |
| 524,96673 | 0 | 0 | 1e-05 | 0 | 0 |
| 525,00391 | 0 | 0 | 2e-05 | 0 | 0 |
| 525,0411 | 0 | 0 | 2e-05 | 0 | 0 |
| 525,07828 | 0 | 0 | 2e-05 | 0 | 0 |
| 525,11546 | 0 | 0 | 2e-05 | 0 | 0 |
| 525,15264 | 1e-05 | 0 | 3e-05 | 0 | 1e-05 |
| 525,18982 | 1e-05 | 0 | 3e-05 | 0 | 1e-05 |
| 525,22701 | 1e-05 | 0 | 3e-05 | 0 | 1e-05 |
| 525,26419 | 1e-05 | 0 | 4e-05 | 0 | 1e-05 |
| 525,30137 | 1e-05 | 0 | 4e-05 | 0 | 1e-05 |
| 525,33855 | 1e-05 | 0 | 5e-05 | 0 | 1e-05 |
| 525,37573 | 1e-05 | 0 | 5e-05 | 0 | 1e-05 |
| 525,41292 | 2e-05 | 0 | 6e-05 | 0 | 2e-05 |
| 525,4501 | 2e-05 | 0 | 6e-05 | 1e-05 | 2e-05 |
| 525,48728 | 2e-05 | 0 | 7e-05 | 1e-05 | 2e-05 |
| 525,52446 | 3e-05 | 0 | 8e-05 | 1e-05 | 2e-05 |
| 525,56164 | 3e-05 | 0 | 9e-05 | 1e-05 | 3e-05 |
| 525,59883 | 3e-05 | 0 | 9e-05 | 1e-05 | 3e-05 |
| 525,63601 | 4e-05 | 0 | 1e-04 | 1e-05 | 4e-05 |
| 525,67319 | 5e-05 | 0 | 0,00011 | 1e-05 | 4e-05 |
| 525,71037 | 5e-05 | 0 | 0,00012 | 1e-05 | 5e-05 |
| 525,74755 | 6e-05 | 0 | 0,00013 | 2e-05 | 5e-05 |
| 525,78474 | 7e-05 | 0 | 0,00013 | 2e-05 | 6e-05 |
| 525,82192 | 8e-05 | 0 | 0,00014 | 2e-05 | 7e-05 |
| 525,8591 | 9e-05 | 0 | 0,00015 | 2e-05 | 7e-05 |
| 525,89628 | 1e-04 | 0 | 0,00016 | 3e-05 | 8e-05 |
| 525,93346 | 0,00011 | 0 | 0,00017 | 3e-05 | 9e-05 |
| 525,97065 | 0,00012 | 0 | 0,00018 | 4e-05 | 1e-04 |
| 526,00783 | 0,00013 | 0 | 0,00019 | 4e-05 | 0,00011 |
| 526,04501 | 0,00015 | 0 | 2e-04 | 4e-05 | 0,00012 |
| 526,08219 | 0,00016 | 0 | 0,00021 | 5e-05 | 0,00013 |
| 526,11937 | 0,00018 | 0 | 0,00022 | 6e-05 | 0,00015 |
| 526,15656 | 2e-04 | 0 | 0,00023 | 6e-05 | 0,00016 |
| 526,19374 | 0,00022 | 0 | 0,00024 | 7e-05 | 0,00018 |
| 526,23092 | 0,00024 | 0 | 0,00025 | 7e-05 | 0,00019 |
| 526,2681 | 0,00026 | 0 | 0,00026 | 8e-05 | 0,00021 |
| 526,30528 | 0,00028 | 0 | 0,00027 | 9e-05 | 0,00022 |
| 526,34247 | 0,00031 | 0 | 0,00028 | 1e-04 | 0,00024 |
| 526,37965 | 0,00034 | 0 | 0,00029 | 0,00011 | 0,00026 |
| 526,41683 | 0,00036 | 0 | 3e-04 | 0,00012 | 0,00028 |
| 526,45401 | 0,00039 | 0 | 0,00031 | 0,00012 | 3e-04 |
| 526,49119 | 0,00042 | 1e-05 | 0,00032 | 0,00013 | 0,00032 |
| 526,52838 | 0,00045 | 1e-05 | 0,00033 | 0,00015 | 0,00034 |
| 526,56556 | 0,00048 | 1e-05 | 0,00035 | 0,00016 | 0,00036 |
| 526,60274 | 0,00052 | 1e-05 | 0,00036 | 0,00017 | 0,00038 |
| 526,63992 | 0,00055 | 1e-05 | 0,00037 | 0,00018 | 4e-04 |
| 526,6771 | 0,00059 | 2e-05 | 0,00038 | 0,00019 | 0,00042 |
| 526,71429 | 0,00062 | 2e-05 | 4e-04 | 2e-04 | 0,00045 |
| 526,75147 | 0,00066 | 2e-05 | 0,00041 | 0,00021 | 0,00047 |
| 526,78865 | 7e-04 | 3e-05 | 0,00043 | 0,00023 | 0,00049 |
| 526,82583 | 0,00074 | 4e-05 | 0,00045 | 0,00024 | 0,00052 |
| 526,86301 | 0,00079 | 4e-05 | 0,00047 | 0,00025 | 0,00054 |
| 526,9002 | 0,00083 | 5e-05 | 0,00049 | 0,00027 | 0,00057 |
| 526,93738 | 0,00088 | 6e-05 | 0,00051 | 0,00028 | 0,00059 |
| 526,97456 | 0,00093 | 7e-05 | 0,00054 | 0,00029 | 0,00062 |
| 527,01174 | 0,00098 | 9e-05 | 0,00057 | 0,00031 | 0,00064 |
| 527,04892 | 0,00103 | 1e-04 | 6e-04 | 0,00032 | 0,00067 |
| 527,08611 | 0,00108 | 0,00012 | 0,00064 | 0,00034 | 7e-04 |
| 527,12329 | 0,00114 | 0,00014 | 0,00068 | 0,00036 | 0,00073 |
| 527,16047 | 0,0012 | 0,00017 | 0,00072 | 0,00037 | 0,00076 |
| 527,19765 | 0,00127 | 2e-04 | 0,00077 | 0,00039 | 8e-04 |
| 527,23483 | 0,00134 | 0,00023 | 0,00082 | 0,00041 | 0,00083 |
| 527,27202 | 0,00141 | 0,00027 | 0,00087 | 0,00043 | 0,00087 |
| 527,3092 | 0,00149 | 0,00031 | 0,00093 | 0,00046 | 0,00091 |
| 527,34638 | 0,00158 | 0,00036 | 0,001 | 0,00048 | 0,00096 |
| 527,38356 | 0,00167 | 0,00041 | 0,00107 | 0,00051 | 0,00101 |
| 527,42074 | 0,00177 | 0,00048 | 0,00115 | 0,00054 | 0,00106 |
| 527,45793 | 0,00188 | 0,00055 | 0,00124 | 0,00058 | 0,00112 |
| 527,49511 | 0,00199 | 0,00063 | 0,00133 | 0,00061 | 0,00118 |
| 527,53229 | 0,00211 | 0,00072 | 0,00143 | 0,00066 | 0,00125 |
| 527,56947 | 0,00225 | 0,00082 | 0,00154 | 0,00071 | 0,00133 |
| 527,60665 | 0,00239 | 0,00094 | 0,00165 | 0,00076 | 0,00142 |
| 527,64384 | 0,00255 | 0,00106 | 0,00177 | 0,00082 | 0,00151 |
| 527,68102 | 0,00272 | 0,0012 | 0,00191 | 0,00089 | 0,00161 |
| 527,7182 | 0,0029 | 0,00136 | 0,00205 | 0,00096 | 0,00173 |
| 527,75538 | 0,0031 | 0,00154 | 0,00221 | 0,00105 | 0,00185 |
| 527,79256 | 0,00331 | 0,00173 | 0,00237 | 0,00114 | 0,00199 |
| 527,82975 | 0,00354 | 0,00194 | 0,00255 | 0,00125 | 0,00215 |
| 527,86693 | 0,00379 | 0,00217 | 0,00274 | 0,00138 | 0,00231 |
| 527,90411 | 0,00405 | 0,00243 | 0,00295 | 0,00151 | 0,00249 |
| 527,94129 | 0,00434 | 0,00271 | 0,00317 | 0,00166 | 0,0027 |
| 527,97847 | 0,00465 | 0,00301 | 0,00341 | 0,00182 | 0,00291 |
| 528,01566 | 0,00497 | 0,00334 | 0,00366 | 0,00201 | 0,00315 |
| 528,05284 | 0,00532 | 0,0037 | 0,00394 | 0,00222 | 0,00341 |
| 528,09002 | 0,0057 | 0,00409 | 0,00423 | 0,00244 | 0,0037 |
| 528,1272 | 0,0061 | 0,00451 | 0,00454 | 0,00269 | 0,00401 |
| 528,16438 | 0,00652 | 0,00496 | 0,00487 | 0,00296 | 0,00434 |
| 528,20157 | 0,00697 | 0,00545 | 0,00523 | 0,00327 | 0,0047 |
| 528,23875 | 0,00745 | 0,00597 | 0,00561 | 0,00359 | 0,00509 |
| 528,27593 | 0,00795 | 0,00653 | 0,00602 | 0,00395 | 0,00552 |
| 528,31311 | 0,00849 | 0,00712 | 0,00645 | 0,00434 | 0,00598 |
| 528,35029 | 0,00906 | 0,00774 | 0,0069 | 0,00476 | 0,00646 |
| 528,38748 | 0,00966 | 0,00842 | 0,0074 | 0,00522 | 0,00698 |
| 528,42466 | 0,01028 | 0,00913 | 0,00792 | 0,00571 | 0,00755 |
| 528,46184 | 0,01094 | 0,00987 | 0,00847 | 0,00624 | 0,00815 |
| 528,49902 | 0,01164 | 0,01065 | 0,00905 | 0,00681 | 0,00879 |
| 528,5362 | 0,01236 | 0,01148 | 0,00966 | 0,00742 | 0,00946 |
| 528,57339 | 0,01311 | 0,01235 | 0,01031 | 0,00807 | 0,01017 |
| 528,61057 | 0,0139 | 0,01326 | 0,011 | 0,00875 | 0,01093 |
| 528,64775 | 0,01472 | 0,0142 | 0,01171 | 0,00948 | 0,01173 |
| 528,68493 | 0,01557 | 0,01517 | 0,01246 | 0,01026 | 0,01257 |
| 528,72211 | 0,01645 | 0,01619 | 0,01325 | 0,01107 | 0,01344 |
| 528,7593 | 0,01736 | 0,01725 | 0,01408 | 0,01193 | 0,01436 |
| 528,79648 | 0,01829 | 0,01833 | 0,01494 | 0,01282 | 0,01532 |
| 528,83366 | 0,01926 | 0,01945 | 0,01583 | 0,01376 | 0,01631 |
| 528,87084 | 0,02025 | 0,02059 | 0,01675 | 0,01474 | 0,01734 |
| 528,90802 | 0,02126 | 0,02177 | 0,01771 | 0,01576 | 0,01839 |
| 528,94521 | 0,02229 | 0,02297 | 0,0187 | 0,01681 | 0,01949 |
| 528,98239 | 0,02335 | 0,02419 | 0,01972 | 0,01789 | 0,02061 |
| 529,01957 | 0,02442 | 0,02543 | 0,02076 | 0,01901 | 0,02175 |
| 529,05675 | 0,0255 | 0,02669 | 0,02184 | 0,02016 | 0,02292 |
| 529,09393 | 0,0266 | 0,02796 | 0,02293 | 0,02133 | 0,0241 |
| 529,13112 | 0,0277 | 0,02924 | 0,02405 | 0,02252 | 0,0253 |
| 529,1683 | 0,02881 | 0,03052 | 0,02519 | 0,02374 | 0,02651 |
| 529,20548 | 0,02993 | 0,03181 | 0,02634 | 0,02497 | 0,02773 |
| 529,24266 | 0,03104 | 0,0331 | 0,0275 | 0,02622 | 0,02894 |
| 529,27984 | 0,03215 | 0,03439 | 0,02868 | 0,02747 | 0,03016 |
| 529,31703 | 0,03326 | 0,03567 | 0,02986 | 0,02872 | 0,03137 |
| 529,35421 | 0,03435 | 0,03694 | 0,03104 | 0,02998 | 0,03256 |
| 529,39139 | 0,03544 | 0,03819 | 0,03223 | 0,03124 | 0,03375 |
| 529,42857 | 0,03651 | 0,03943 | 0,03341 | 0,03248 | 0,03491 |
| 529,46575 | 0,03757 | 0,04065 | 0,03458 | 0,03372 | 0,03604 |
| 529,50294 | 0,03861 | 0,04184 | 0,03575 | 0,03494 | 0,03715 |
| 529,54012 | 0,03963 | 0,04302 | 0,0369 | 0,03614 | 0,03823 |
| 529,5773 | 0,04062 | 0,04417 | 0,03803 | 0,03732 | 0,03928 |
| 529,61448 | 0,0416 | 0,04528 | 0,03914 | 0,03848 | 0,04029 |
| 529,65166 | 0,04256 | 0,04637 | 0,04023 | 0,0396 | 0,04125 |
| 529,68885 | 0,04349 | 0,04743 | 0,0413 | 0,0407 | 0,04218 |
| 529,72603 | 0,04439 | 0,04846 | 0,04234 | 0,04176 | 0,04306 |
| 529,76321 | 0,04528 | 0,04946 | 0,04335 | 0,04278 | 0,0439 |
| 529,80039 | 0,04614 | 0,05042 | 0,04433 | 0,04377 | 0,04469 |
| 529,83757 | 0,04699 | 0,05135 | 0,04527 | 0,04472 | 0,04543 |
| 529,87476 | 0,0478 | 0,05225 | 0,04619 | 0,04563 | 0,04613 |
| 529,91194 | 0,0486 | 0,05312 | 0,04706 | 0,04649 | 0,04679 |
| 529,94912 | 0,04939 | 0,05396 | 0,0479 | 0,04731 | 0,0474 |
| 529,9863 | 0,05016 | 0,05477 | 0,04871 | 0,0481 | 0,04796 |
| 530,02348 | 0,05092 | 0,05555 | 0,04948 | 0,04885 | 0,04849 |
| 530,06067 | 0,05166 | 0,05632 | 0,05022 | 0,04954 | 0,04898 |
| 530,09785 | 0,05239 | 0,05705 | 0,05091 | 0,0502 | 0,04943 |
| 530,13503 | 0,05312 | 0,05776 | 0,05158 | 0,05082 | 0,04984 |
| 530,17221 | 0,05384 | 0,05845 | 0,05221 | 0,05141 | 0,05023 |
| 530,20939 | 0,05456 | 0,05913 | 0,05282 | 0,05196 | 0,05058 |
| 530,24658 | 0,05528 | 0,05978 | 0,05339 | 0,05246 | 0,05091 |
| 530,28376 | 0,056 | 0,06043 | 0,05394 | 0,05294 | 0,05122 |
| 530,32094 | 0,05672 | 0,06106 | 0,05445 | 0,05338 | 0,05151 |
| 530,35812 | 0,05744 | 0,06168 | 0,05495 | 0,0538 | 0,05178 |
| 530,3953 | 0,05817 | 0,06229 | 0,05543 | 0,05419 | 0,05203 |
| 530,43249 | 0,0589 | 0,06289 | 0,05588 | 0,05454 | 0,05228 |
| 530,46967 | 0,05964 | 0,06349 | 0,05631 | 0,05488 | 0,05251 |
| 530,50685 | 0,06038 | 0,06408 | 0,05673 | 0,05519 | 0,05274 |
| 530,54403 | 0,06113 | 0,06467 | 0,05714 | 0,05549 | 0,05295 |
| 530,58121 | 0,06189 | 0,06526 | 0,05753 | 0,05576 | 0,05317 |
| 530,6184 | 0,06265 | 0,06584 | 0,05792 | 0,05601 | 0,05338 |
| 530,65558 | 0,06341 | 0,06642 | 0,05829 | 0,05625 | 0,05359 |
| 530,69276 | 0,06418 | 0,067 | 0,05866 | 0,05648 | 0,0538 |
| 530,72994 | 0,06494 | 0,06757 | 0,05902 | 0,05669 | 0,054 |
| 530,76712 | 0,06571 | 0,06814 | 0,05938 | 0,05689 | 0,05421 |
| 530,80431 | 0,06648 | 0,0687 | 0,05974 | 0,05707 | 0,05441 |
| 530,84149 | 0,06724 | 0,06926 | 0,06009 | 0,05725 | 0,05461 |
| 530,87867 | 0,068 | 0,06982 | 0,06045 | 0,05742 | 0,0548 |
| 530,91585 | 0,06876 | 0,07037 | 0,0608 | 0,05757 | 0,05499 |
| 530,95303 | 0,0695 | 0,0709 | 0,06115 | 0,05772 | 0,05518 |
| 530,99022 | 0,07023 | 0,07143 | 0,0615 | 0,05786 | 0,05535 |
| 531,0274 | 0,07096 | 0,07194 | 0,06185 | 0,05799 | 0,05552 |
| 531,06458 | 0,07167 | 0,07244 | 0,0622 | 0,05812 | 0,05568 |
| 531,10176 | 0,07236 | 0,07293 | 0,06254 | 0,05823 | 0,05583 |
| 531,13894 | 0,07304 | 0,0734 | 0,06288 | 0,05834 | 0,05597 |
| 531,17613 | 0,07371 | 0,07384 | 0,06322 | 0,05843 | 0,05609 |
| 531,21331 | 0,07435 | 0,07427 | 0,06356 | 0,05852 | 0,0562 |
| 531,25049 | 0,07498 | 0,07468 | 0,06389 | 0,05861 | 0,0563 |
| 531,28767 | 0,07558 | 0,07506 | 0,06422 | 0,05868 | 0,05638 |
| 531,32485 | 0,07616 | 0,07541 | 0,06453 | 0,05874 | 0,05644 |
| 531,36204 | 0,07673 | 0,07573 | 0,06484 | 0,0588 | 0,05649 |
| 531,39922 | 0,07727 | 0,07603 | 0,06514 | 0,05884 | 0,05652 |
| 531,4364 | 0,07779 | 0,0763 | 0,06542 | 0,05888 | 0,05653 |
| 531,47358 | 0,07829 | 0,07653 | 0,0657 | 0,05891 | 0,05653 |
| 531,51076 | 0,07876 | 0,07673 | 0,06595 | 0,05893 | 0,05651 |
| 531,54795 | 0,07921 | 0,0769 | 0,06619 | 0,05894 | 0,05648 |
| 531,58513 | 0,07965 | 0,07703 | 0,06642 | 0,05895 | 0,05644 |
| 531,62231 | 0,08005 | 0,07713 | 0,06663 | 0,05895 | 0,05638 |
| 531,65949 | 0,08044 | 0,07719 | 0,06681 | 0,05894 | 0,05632 |
| 531,69667 | 0,0808 | 0,07722 | 0,06698 | 0,05892 | 0,05624 |
| 531,73386 | 0,08115 | 0,07721 | 0,06712 | 0,0589 | 0,05616 |
| 531,77104 | 0,08147 | 0,07718 | 0,06725 | 0,05887 | 0,05608 |
| 531,80822 | 0,08177 | 0,0771 | 0,06735 | 0,05883 | 0,05599 |
| 531,8454 | 0,08205 | 0,07699 | 0,06742 | 0,0588 | 0,05591 |
| 531,88258 | 0,08232 | 0,07686 | 0,06747 | 0,05876 | 0,05583 |
| 531,91977 | 0,08257 | 0,07669 | 0,0675 | 0,05871 | 0,05575 |
| 531,95695 | 0,08279 | 0,0765 | 0,0675 | 0,05866 | 0,05567 |
| 531,99413 | 0,083 | 0,07628 | 0,06747 | 0,05862 | 0,05561 |
| 532,03131 | 0,08319 | 0,07604 | 0,06742 | 0,05857 | 0,05555 |
| 532,06849 | 0,08337 | 0,07578 | 0,06735 | 0,05851 | 0,05551 |
| 532,10568 | 0,08353 | 0,0755 | 0,06726 | 0,05846 | 0,05547 |
| 532,14286 | 0,08368 | 0,07521 | 0,06714 | 0,05841 | 0,05545 |
| 532,18004 | 0,08381 | 0,0749 | 0,067 | 0,05836 | 0,05545 |
| 532,21722 | 0,08393 | 0,07459 | 0,06684 | 0,05831 | 0,05546 |
| 532,2544 | 0,08404 | 0,07428 | 0,06667 | 0,05827 | 0,05549 |
| 532,29159 | 0,08414 | 0,07396 | 0,06648 | 0,05822 | 0,05553 |
| 532,32877 | 0,08423 | 0,07365 | 0,06627 | 0,05818 | 0,05559 |
| 532,36595 | 0,08431 | 0,07335 | 0,06605 | 0,05814 | 0,05567 |
| 532,40313 | 0,08439 | 0,07306 | 0,06582 | 0,0581 | 0,05576 |
| 532,44031 | 0,08447 | 0,07278 | 0,06558 | 0,05806 | 0,05588 |
| 532,4775 | 0,08453 | 0,07253 | 0,06534 | 0,05803 | 0,056 |
| 532,51468 | 0,0846 | 0,07229 | 0,0651 | 0,058 | 0,05615 |
| 532,55186 | 0,08467 | 0,07209 | 0,06486 | 0,05797 | 0,05632 |
| 532,58904 | 0,08474 | 0,07191 | 0,06462 | 0,05795 | 0,0565 |
| 532,62622 | 0,08481 | 0,07176 | 0,06438 | 0,05794 | 0,05669 |
| 532,66341 | 0,08488 | 0,07166 | 0,06416 | 0,05794 | 0,05691 |
| 532,70059 | 0,08496 | 0,07159 | 0,06395 | 0,05794 | 0,05714 |
| 532,73777 | 0,08504 | 0,07156 | 0,06375 | 0,05795 | 0,05739 |
| 532,77495 | 0,08513 | 0,07157 | 0,06357 | 0,05798 | 0,05765 |
| 532,81213 | 0,08523 | 0,07162 | 0,0634 | 0,05801 | 0,05793 |
| 532,84932 | 0,08533 | 0,07172 | 0,06326 | 0,05806 | 0,05823 |
| 532,8865 | 0,08544 | 0,07187 | 0,06315 | 0,05813 | 0,05855 |
| 532,92368 | 0,08557 | 0,07206 | 0,06306 | 0,05822 | 0,05888 |
| 532,96086 | 0,0857 | 0,07229 | 0,06299 | 0,05832 | 0,05923 |
| 532,99804 | 0,08584 | 0,07257 | 0,06296 | 0,05845 | 0,0596 |
| 533,03523 | 0,08599 | 0,07289 | 0,06296 | 0,05861 | 0,06 |
| 533,07241 | 0,08615 | 0,07326 | 0,06299 | 0,05879 | 0,06041 |
| 533,10959 | 0,08631 | 0,07365 | 0,06304 | 0,059 | 0,06084 |
| 533,14677 | 0,08649 | 0,07409 | 0,06314 | 0,05923 | 0,06129 |
| 533,18395 | 0,08667 | 0,07456 | 0,06326 | 0,05951 | 0,06176 |
| 533,22114 | 0,08687 | 0,07507 | 0,06343 | 0,05981 | 0,06226 |
| 533,25832 | 0,08707 | 0,0756 | 0,06362 | 0,06015 | 0,06277 |
| 533,2955 | 0,08727 | 0,07615 | 0,06385 | 0,06053 | 0,06331 |
| 533,33268 | 0,08749 | 0,07672 | 0,06411 | 0,06094 | 0,06386 |
| 533,36986 | 0,08771 | 0,07731 | 0,06441 | 0,0614 | 0,06444 |
| 533,40705 | 0,08793 | 0,07792 | 0,06473 | 0,06189 | 0,06504 |
| 533,44423 | 0,08816 | 0,07853 | 0,06509 | 0,06242 | 0,06566 |
| 533,48141 | 0,0884 | 0,07915 | 0,06547 | 0,06298 | 0,0663 |
| 533,51859 | 0,08864 | 0,07977 | 0,06589 | 0,06358 | 0,06695 |
| 533,55577 | 0,08888 | 0,08039 | 0,06633 | 0,06422 | 0,06762 |
| 533,59295 | 0,08914 | 0,08101 | 0,0668 | 0,0649 | 0,06831 |
| 533,63014 | 0,08939 | 0,08161 | 0,06729 | 0,0656 | 0,06901 |
| 533,66732 | 0,08966 | 0,08221 | 0,06781 | 0,06633 | 0,06972 |
| 533,7045 | 0,08993 | 0,08279 | 0,06835 | 0,0671 | 0,07044 |
| 533,74168 | 0,09021 | 0,08335 | 0,06891 | 0,06789 | 0,07117 |
| 533,77886 | 0,09049 | 0,0839 | 0,06949 | 0,06871 | 0,07191 |
| 533,81605 | 0,09079 | 0,08443 | 0,07008 | 0,06954 | 0,07265 |
| 533,85323 | 0,09109 | 0,08494 | 0,0707 | 0,07039 | 0,07339 |
| 533,89041 | 0,09141 | 0,08542 | 0,07133 | 0,07126 | 0,07414 |
| 533,92759 | 0,09173 | 0,08588 | 0,07197 | 0,07213 | 0,07488 |
| 533,96477 | 0,09207 | 0,08632 | 0,07263 | 0,07301 | 0,07562 |
| 534,00196 | 0,09242 | 0,08673 | 0,0733 | 0,0739 | 0,07636 |
| 534,03914 | 0,09278 | 0,08712 | 0,07398 | 0,07478 | 0,07709 |
| 534,07632 | 0,09315 | 0,08748 | 0,07467 | 0,07567 | 0,07781 |
| 534,1135 | 0,09354 | 0,08782 | 0,07537 | 0,07655 | 0,07853 |
| 534,15068 | 0,09393 | 0,08815 | 0,07608 | 0,07741 | 0,07923 |
| 534,18787 | 0,09434 | 0,08845 | 0,07679 | 0,07827 | 0,07992 |
| 534,22505 | 0,09476 | 0,08872 | 0,07751 | 0,07912 | 0,0806 |
| 534,26223 | 0,09519 | 0,08898 | 0,07823 | 0,07994 | 0,08126 |
| 534,29941 | 0,09563 | 0,08923 | 0,07896 | 0,08075 | 0,08191 |
| 534,33659 | 0,09608 | 0,08946 | 0,07969 | 0,08153 | 0,08254 |
| 534,37378 | 0,09653 | 0,08967 | 0,08042 | 0,0823 | 0,08316 |
| 534,41096 | 0,09699 | 0,08987 | 0,08115 | 0,08303 | 0,08375 |
| 534,44814 | 0,09744 | 0,09005 | 0,08187 | 0,08374 | 0,08433 |
| 534,48532 | 0,0979 | 0,09023 | 0,0826 | 0,08442 | 0,08489 |
| 534,5225 | 0,09835 | 0,0904 | 0,08332 | 0,08508 | 0,08543 |
| 534,55969 | 0,09879 | 0,09056 | 0,08403 | 0,08571 | 0,08595 |
| 534,59687 | 0,09922 | 0,09072 | 0,08474 | 0,0863 | 0,08644 |
| 534,63405 | 0,09964 | 0,09086 | 0,08543 | 0,08686 | 0,08691 |
| 534,67123 | 0,10005 | 0,09101 | 0,08612 | 0,08739 | 0,08736 |
| 534,70841 | 0,10043 | 0,09115 | 0,0868 | 0,08789 | 0,08778 |
| 534,7456 | 0,1008 | 0,09128 | 0,08746 | 0,08836 | 0,08817 |
| 534,78278 | 0,10113 | 0,09142 | 0,0881 | 0,08879 | 0,08854 |
| 534,81996 | 0,10144 | 0,09155 | 0,08873 | 0,08919 | 0,08887 |
| 534,85714 | 0,10172 | 0,09168 | 0,08934 | 0,08957 | 0,08919 |
| 534,89432 | 0,10197 | 0,09181 | 0,08994 | 0,08991 | 0,08946 |
| 534,93151 | 0,10218 | 0,09194 | 0,09051 | 0,09022 | 0,08971 |
| 534,96869 | 0,10236 | 0,09207 | 0,09106 | 0,09051 | 0,08992 |
| 535,00587 | 0,1025 | 0,0922 | 0,09159 | 0,09077 | 0,0901 |
| 535,04305 | 0,10261 | 0,09232 | 0,09211 | 0,091 | 0,09026 |
| 535,08023 | 0,10268 | 0,09245 | 0,09259 | 0,09121 | 0,09037 |
| 535,11742 | 0,1027 | 0,09258 | 0,09305 | 0,09139 | 0,09044 |
| 535,1546 | 0,10269 | 0,0927 | 0,09349 | 0,09155 | 0,09049 |
| 535,19178 | 0,10265 | 0,09283 | 0,09392 | 0,0917 | 0,09051 |
| 535,22896 | 0,10257 | 0,09295 | 0,09431 | 0,09183 | 0,09049 |
| 535,26614 | 0,10245 | 0,09308 | 0,09469 | 0,09194 | 0,09044 |
| 535,30333 | 0,1023 | 0,0932 | 0,09504 | 0,09204 | 0,09035 |
| 535,34051 | 0,10213 | 0,09333 | 0,09538 | 0,09213 | 0,09024 |
| 535,37769 | 0,10193 | 0,09346 | 0,0957 | 0,09221 | 0,09011 |
| 535,41487 | 0,1017 | 0,09358 | 0,096 | 0,09229 | 0,08994 |
| 535,45205 | 0,10145 | 0,09371 | 0,09628 | 0,09237 | 0,08975 |
| 535,48924 | 0,10118 | 0,09384 | 0,09655 | 0,09245 | 0,08955 |
| 535,52642 | 0,1009 | 0,09397 | 0,09681 | 0,09253 | 0,08932 |
| 535,5636 | 0,1006 | 0,09411 | 0,09706 | 0,09262 | 0,08908 |
| 535,60078 | 0,1003 | 0,09424 | 0,09729 | 0,09273 | 0,08883 |
| 535,63796 | 0,09998 | 0,09438 | 0,09752 | 0,09284 | 0,08857 |
| 535,67515 | 0,09966 | 0,09451 | 0,09774 | 0,09297 | 0,0883 |
| 535,71233 | 0,09934 | 0,09465 | 0,09795 | 0,09312 | 0,08803 |
| 535,74951 | 0,09902 | 0,09479 | 0,09816 | 0,09328 | 0,08777 |
| 535,78669 | 0,0987 | 0,09493 | 0,09837 | 0,09347 | 0,0875 |
| 535,82387 | 0,09839 | 0,09508 | 0,09857 | 0,09368 | 0,08725 |
| 535,86106 | 0,09808 | 0,09522 | 0,09878 | 0,09392 | 0,08701 |
| 535,89824 | 0,09777 | 0,09536 | 0,09897 | 0,09417 | 0,08678 |
| 535,93542 | 0,09747 | 0,0955 | 0,09917 | 0,09446 | 0,08657 |
| 535,9726 | 0,09718 | 0,09564 | 0,09937 | 0,09478 | 0,08638 |
| 536,00978 | 0,09689 | 0,09578 | 0,09956 | 0,09512 | 0,0862 |
| 536,04697 | 0,09661 | 0,09591 | 0,09975 | 0,09548 | 0,08605 |
| 536,08415 | 0,09633 | 0,09604 | 0,09993 | 0,09587 | 0,08593 |
| 536,12133 | 0,09606 | 0,09616 | 0,10011 | 0,09628 | 0,08584 |
| 536,15851 | 0,09579 | 0,09628 | 0,10028 | 0,09672 | 0,08577 |
| 536,19569 | 0,09553 | 0,09638 | 0,10045 | 0,09717 | 0,08573 |
| 536,23288 | 0,09526 | 0,09647 | 0,10061 | 0,09764 | 0,08571 |
| 536,27006 | 0,095 | 0,09655 | 0,10075 | 0,09813 | 0,08573 |
| 536,30724 | 0,09473 | 0,09662 | 0,10088 | 0,09863 | 0,08577 |
| 536,34442 | 0,09446 | 0,09667 | 0,101 | 0,09913 | 0,08584 |
| 536,3816 | 0,09418 | 0,0967 | 0,1011 | 0,09965 | 0,08593 |
| 536,41879 | 0,0939 | 0,09671 | 0,10119 | 0,10016 | 0,08605 |
| 536,45597 | 0,0936 | 0,0967 | 0,10125 | 0,10068 | 0,0862 |
| 536,49315 | 0,0933 | 0,09667 | 0,10129 | 0,10118 | 0,08636 |
| 536,53033 | 0,09299 | 0,09662 | 0,10132 | 0,10168 | 0,08654 |
| 536,56751 | 0,09267 | 0,09655 | 0,10132 | 0,10217 | 0,08674 |
| 536,6047 | 0,09234 | 0,09645 | 0,1013 | 0,10264 | 0,08695 |
| 536,64188 | 0,092 | 0,09633 | 0,10125 | 0,10309 | 0,08718 |
| 536,67906 | 0,09164 | 0,09618 | 0,10117 | 0,10352 | 0,08742 |
| 536,71624 | 0,09127 | 0,09601 | 0,10108 | 0,10392 | 0,08766 |
| 536,75342 | 0,09089 | 0,09581 | 0,10096 | 0,10429 | 0,08791 |
| 536,79061 | 0,09051 | 0,09559 | 0,10081 | 0,10463 | 0,08817 |
| 536,82779 | 0,09011 | 0,09535 | 0,10065 | 0,10493 | 0,08842 |
| 536,86497 | 0,0897 | 0,09508 | 0,10046 | 0,1052 | 0,08867 |
| 536,90215 | 0,08928 | 0,0948 | 0,10025 | 0,10543 | 0,08892 |
| 536,93933 | 0,08886 | 0,09449 | 0,10002 | 0,10562 | 0,08917 |
| 536,97652 | 0,08843 | 0,09417 | 0,09977 | 0,10576 | 0,0894 |
| 537,0137 | 0,088 | 0,09383 | 0,0995 | 0,10586 | 0,08963 |
| 537,05088 | 0,08757 | 0,09348 | 0,09922 | 0,10592 | 0,08984 |
| 537,08806 | 0,08713 | 0,09311 | 0,09893 | 0,10594 | 0,09005 |
| 537,12524 | 0,0867 | 0,09274 | 0,09863 | 0,10591 | 0,09023 |
| 537,16243 | 0,08627 | 0,09235 | 0,09832 | 0,10584 | 0,0904 |
| 537,19961 | 0,08584 | 0,09196 | 0,098 | 0,10572 | 0,09056 |
| 537,23679 | 0,08541 | 0,09157 | 0,09768 | 0,10557 | 0,0907 |
| 537,27397 | 0,08499 | 0,09117 | 0,09735 | 0,10538 | 0,09082 |
| 537,31115 | 0,08458 | 0,09078 | 0,09702 | 0,10515 | 0,09092 |
| 537,34834 | 0,08418 | 0,09039 | 0,0967 | 0,10488 | 0,091 |
| 537,38552 | 0,08378 | 0,09 | 0,09637 | 0,10457 | 0,09107 |
| 537,4227 | 0,08339 | 0,08961 | 0,09605 | 0,10424 | 0,09111 |
| 537,45988 | 0,08302 | 0,08923 | 0,09573 | 0,10388 | 0,09114 |
| 537,49706 | 0,08265 | 0,08886 | 0,09542 | 0,10349 | 0,09114 |
| 537,53425 | 0,08229 | 0,08851 | 0,09512 | 0,10307 | 0,09113 |
| 537,57143 | 0,08194 | 0,08816 | 0,09483 | 0,10264 | 0,09111 |
| 537,60861 | 0,0816 | 0,08782 | 0,09454 | 0,1022 | 0,09107 |
| 537,64579 | 0,08127 | 0,08749 | 0,09427 | 0,10174 | 0,09102 |
| 537,68297 | 0,08095 | 0,08718 | 0,09401 | 0,10128 | 0,09095 |
| 537,72016 | 0,08064 | 0,08688 | 0,09375 | 0,10081 | 0,09088 |
| 537,75734 | 0,08034 | 0,08659 | 0,09352 | 0,10034 | 0,09079 |
| 537,79452 | 0,08005 | 0,08632 | 0,09329 | 0,09987 | 0,09071 |
| 537,8317 | 0,07977 | 0,08606 | 0,09308 | 0,09941 | 0,09062 |
| 537,86888 | 0,07949 | 0,08582 | 0,09288 | 0,09896 | 0,09053 |
| 537,90607 | 0,07923 | 0,08559 | 0,0927 | 0,09853 | 0,09044 |
| 537,94325 | 0,07897 | 0,08537 | 0,09253 | 0,09811 | 0,09035 |
| 537,98043 | 0,07872 | 0,08517 | 0,09238 | 0,09771 | 0,09028 |
| 538,01761 | 0,07848 | 0,08498 | 0,09225 | 0,09734 | 0,09022 |
| 538,05479 | 0,07825 | 0,08481 | 0,09214 | 0,097 | 0,09018 |
| 538,09198 | 0,07803 | 0,08465 | 0,09204 | 0,09668 | 0,09015 |
| 538,12916 | 0,07782 | 0,0845 | 0,09196 | 0,0964 | 0,09014 |
| 538,16634 | 0,07762 | 0,08437 | 0,0919 | 0,09615 | 0,09016 |
| 538,20352 | 0,07742 | 0,08425 | 0,09186 | 0,09594 | 0,09021 |
| 538,2407 | 0,07725 | 0,08414 | 0,09183 | 0,09576 | 0,09028 |
| 538,27789 | 0,07708 | 0,08405 | 0,09183 | 0,09563 | 0,09039 |
| 538,31507 | 0,07692 | 0,08397 | 0,09184 | 0,09552 | 0,09054 |
| 538,35225 | 0,07678 | 0,0839 | 0,09188 | 0,09545 | 0,09072 |
| 538,38943 | 0,07665 | 0,08384 | 0,09193 | 0,09543 | 0,09094 |
| 538,42661 | 0,07653 | 0,08379 | 0,09201 | 0,09544 | 0,09119 |
| 538,4638 | 0,07643 | 0,08375 | 0,09209 | 0,09549 | 0,09149 |
| 538,50098 | 0,07634 | 0,08372 | 0,0922 | 0,09557 | 0,09184 |
| 538,53816 | 0,07626 | 0,0837 | 0,09232 | 0,09567 | 0,09222 |
| 538,57534 | 0,0762 | 0,08369 | 0,09245 | 0,09582 | 0,09264 |
| 538,61252 | 0,07615 | 0,08368 | 0,09259 | 0,09598 | 0,0931 |
| 538,64971 | 0,07611 | 0,08368 | 0,09274 | 0,09617 | 0,09361 |
| 538,68689 | 0,07608 | 0,08368 | 0,0929 | 0,09637 | 0,09415 |
| 538,72407 | 0,07606 | 0,08368 | 0,09306 | 0,0966 | 0,09473 |
| 538,76125 | 0,07604 | 0,08368 | 0,09322 | 0,09683 | 0,09533 |
| 538,79843 | 0,07604 | 0,08367 | 0,09337 | 0,09707 | 0,09597 |
| 538,83562 | 0,07603 | 0,08366 | 0,09352 | 0,09732 | 0,09664 |
| 538,8728 | 0,07602 | 0,08364 | 0,09366 | 0,09757 | 0,09733 |
| 538,90998 | 0,07602 | 0,08361 | 0,09379 | 0,09781 | 0,09803 |
| 538,94716 | 0,076 | 0,08357 | 0,09389 | 0,09804 | 0,09875 |
| 538,98434 | 0,07598 | 0,08351 | 0,09398 | 0,09826 | 0,09949 |
| 539,02153 | 0,07595 | 0,08343 | 0,09404 | 0,09847 | 0,10022 |
| 539,05871 | 0,07591 | 0,08334 | 0,09408 | 0,09865 | 0,10096 |
| 539,09589 | 0,07586 | 0,08322 | 0,09408 | 0,09881 | 0,10169 |
| 539,13307 | 0,07578 | 0,08307 | 0,09405 | 0,09894 | 0,10242 |
| 539,17025 | 0,07568 | 0,08291 | 0,09399 | 0,09904 | 0,10312 |
| 539,20744 | 0,07556 | 0,08271 | 0,09389 | 0,09911 | 0,10381 |
| 539,24462 | 0,07542 | 0,08248 | 0,09374 | 0,09914 | 0,10448 |
| 539,2818 | 0,07525 | 0,08222 | 0,09356 | 0,09913 | 0,10512 |
| 539,31898 | 0,07505 | 0,08193 | 0,09334 | 0,09908 | 0,10572 |
| 539,35616 | 0,07482 | 0,08161 | 0,09307 | 0,09899 | 0,10628 |
| 539,39335 | 0,07457 | 0,08125 | 0,09276 | 0,09886 | 0,10681 |
| 539,43053 | 0,07428 | 0,08087 | 0,09242 | 0,09868 | 0,10729 |
| 539,46771 | 0,07396 | 0,08046 | 0,09203 | 0,09845 | 0,10773 |
| 539,50489 | 0,07361 | 0,08001 | 0,09161 | 0,09819 | 0,10811 |
| 539,54207 | 0,07323 | 0,07954 | 0,09114 | 0,09788 | 0,10843 |
| 539,57926 | 0,07282 | 0,07903 | 0,09064 | 0,09752 | 0,10871 |
| 539,61644 | 0,07239 | 0,07851 | 0,09012 | 0,09712 | 0,10893 |
| 539,65362 | 0,07192 | 0,07796 | 0,08956 | 0,09668 | 0,10908 |
| 539,6908 | 0,07143 | 0,07739 | 0,08898 | 0,0962 | 0,10917 |
| 539,72798 | 0,07092 | 0,0768 | 0,08836 | 0,09569 | 0,10921 |
| 539,76517 | 0,07039 | 0,0762 | 0,08773 | 0,09514 | 0,10918 |
| 539,80235 | 0,06983 | 0,07558 | 0,08709 | 0,09454 | 0,1091 |
| 539,83953 | 0,06926 | 0,07495 | 0,08642 | 0,09392 | 0,10894 |
| 539,87671 | 0,06867 | 0,07431 | 0,08574 | 0,09327 | 0,10872 |
| 539,91389 | 0,06806 | 0,07367 | 0,08505 | 0,0926 | 0,10844 |
| 539,95108 | 0,06744 | 0,07302 | 0,08436 | 0,09189 | 0,1081 |
| 539,98826 | 0,06681 | 0,07237 | 0,08365 | 0,09116 | 0,1077 |
| 540,02544 | 0,06617 | 0,07172 | 0,08295 | 0,09041 | 0,10724 |
| 540,06262 | 0,06552 | 0,07107 | 0,08223 | 0,08964 | 0,10672 |
| 540,0998 | 0,06486 | 0,07042 | 0,08152 | 0,08886 | 0,10614 |
| 540,13699 | 0,06419 | 0,06978 | 0,0808 | 0,08806 | 0,10552 |
| 540,17417 | 0,06352 | 0,06914 | 0,08009 | 0,08724 | 0,10483 |
| 540,21135 | 0,06284 | 0,0685 | 0,07937 | 0,08641 | 0,10408 |
| 540,24853 | 0,06216 | 0,06787 | 0,07865 | 0,08558 | 0,10329 |
| 540,28571 | 0,06148 | 0,06725 | 0,07793 | 0,08473 | 0,10245 |
| 540,3229 | 0,06079 | 0,06663 | 0,0772 | 0,08388 | 0,10156 |
| 540,36008 | 0,06011 | 0,06602 | 0,07648 | 0,08302 | 0,10061 |
| 540,39726 | 0,05942 | 0,06541 | 0,07575 | 0,08215 | 0,09962 |
| 540,43444 | 0,05872 | 0,0648 | 0,07502 | 0,08128 | 0,0986 |
| 540,47162 | 0,05803 | 0,06419 | 0,07428 | 0,0804 | 0,09753 |
| 540,50881 | 0,05734 | 0,06359 | 0,07354 | 0,07952 | 0,09641 |
| 540,54599 | 0,05665 | 0,06298 | 0,07279 | 0,07863 | 0,09525 |
| 540,58317 | 0,05596 | 0,06238 | 0,07203 | 0,07774 | 0,09406 |
| 540,62035 | 0,05527 | 0,06177 | 0,07126 | 0,07685 | 0,09284 |
| 540,65753 | 0,05458 | 0,06115 | 0,07049 | 0,07595 | 0,09158 |
| 540,69472 | 0,0539 | 0,06054 | 0,0697 | 0,07504 | 0,09028 |
| 540,7319 | 0,05321 | 0,05991 | 0,0689 | 0,07413 | 0,08895 |
| 540,76908 | 0,05254 | 0,05927 | 0,06809 | 0,07321 | 0,08759 |
| 540,80626 | 0,05186 | 0,05863 | 0,06727 | 0,07229 | 0,08621 |
| 540,84344 | 0,05119 | 0,05797 | 0,06644 | 0,07135 | 0,08479 |
| 540,88063 | 0,05052 | 0,05731 | 0,06559 | 0,07041 | 0,08335 |
| 540,91781 | 0,04985 | 0,05662 | 0,06473 | 0,06945 | 0,08189 |
| 540,95499 | 0,04919 | 0,05593 | 0,06385 | 0,06849 | 0,0804 |
| 540,99217 | 0,04853 | 0,05521 | 0,06296 | 0,0675 | 0,07889 |
| 541,02935 | 0,04787 | 0,05448 | 0,06206 | 0,0665 | 0,07736 |
| 541,06654 | 0,04721 | 0,05373 | 0,06114 | 0,06548 | 0,0758 |
| 541,10372 | 0,04655 | 0,05296 | 0,0602 | 0,06444 | 0,07423 |
| 541,1409 | 0,04589 | 0,05217 | 0,05924 | 0,06338 | 0,07264 |
| 541,17808 | 0,04523 | 0,05136 | 0,05827 | 0,0623 | 0,07103 |
| 541,21526 | 0,04456 | 0,05052 | 0,05729 | 0,06119 | 0,0694 |
| 541,25245 | 0,04388 | 0,04966 | 0,05628 | 0,06005 | 0,06776 |
| 541,28963 | 0,04319 | 0,04878 | 0,05525 | 0,05889 | 0,0661 |
| 541,32681 | 0,04249 | 0,04787 | 0,0542 | 0,05769 | 0,06443 |
| 541,36399 | 0,04178 | 0,04694 | 0,05313 | 0,05646 | 0,06274 |
| 541,40117 | 0,04105 | 0,04598 | 0,05205 | 0,0552 | 0,06103 |
| 541,43836 | 0,0403 | 0,045 | 0,05093 | 0,05391 | 0,05932 |
| 541,47554 | 0,03953 | 0,04399 | 0,0498 | 0,05259 | 0,05759 |
| 541,51272 | 0,03875 | 0,04295 | 0,04865 | 0,05123 | 0,05585 |
| 541,5499 | 0,03794 | 0,04189 | 0,04748 | 0,04985 | 0,05411 |
| 541,58708 | 0,0371 | 0,04081 | 0,04628 | 0,04843 | 0,05236 |
| 541,62427 | 0,03624 | 0,03971 | 0,04506 | 0,04699 | 0,0506 |
| 541,66145 | 0,03536 | 0,03858 | 0,04383 | 0,04552 | 0,04885 |
| 541,69863 | 0,03445 | 0,03744 | 0,04257 | 0,04403 | 0,04709 |
| 541,73581 | 0,03352 | 0,03628 | 0,0413 | 0,04252 | 0,04533 |
| 541,77299 | 0,03256 | 0,0351 | 0,04001 | 0,04099 | 0,04358 |
| 541,81018 | 0,03158 | 0,0339 | 0,03871 | 0,03945 | 0,04184 |
| 541,84736 | 0,03058 | 0,0327 | 0,0374 | 0,0379 | 0,04011 |
| 541,88454 | 0,02956 | 0,03149 | 0,03608 | 0,03635 | 0,0384 |
| 541,92172 | 0,02852 | 0,03028 | 0,03475 | 0,0348 | 0,0367 |
| 541,9589 | 0,02748 | 0,02906 | 0,03342 | 0,03325 | 0,03502 |
| 541,99609 | 0,02642 | 0,02785 | 0,03209 | 0,03171 | 0,03336 |
| 542,03327 | 0,02535 | 0,02664 | 0,03076 | 0,03018 | 0,03174 |
| 542,07045 | 0,02428 | 0,02544 | 0,02944 | 0,02868 | 0,03015 |
| 542,10763 | 0,02321 | 0,02425 | 0,02812 | 0,0272 | 0,02859 |
| 542,14481 | 0,02215 | 0,02307 | 0,02683 | 0,02574 | 0,02706 |
| 542,182 | 0,02109 | 0,02191 | 0,02555 | 0,02432 | 0,02557 |
| 542,21918 | 0,02004 | 0,02078 | 0,02429 | 0,02294 | 0,02413 |
| 542,25636 | 0,01901 | 0,01966 | 0,02305 | 0,02159 | 0,02274 |
| 542,29354 | 0,018 | 0,01858 | 0,02184 | 0,02029 | 0,02138 |
| 542,33072 | 0,01701 | 0,01752 | 0,02067 | 0,01903 | 0,02008 |
| 542,36791 | 0,01604 | 0,0165 | 0,01952 | 0,01782 | 0,01882 |
| 542,40509 | 0,0151 | 0,0155 | 0,01841 | 0,01667 | 0,01763 |
| 542,44227 | 0,0142 | 0,01454 | 0,01733 | 0,01557 | 0,01648 |
| 542,47945 | 0,01332 | 0,01363 | 0,0163 | 0,01451 | 0,01538 |
| 542,51663 | 0,01248 | 0,01275 | 0,01531 | 0,01351 | 0,01433 |
| 542,55382 | 0,01167 | 0,01191 | 0,01435 | 0,01257 | 0,01334 |
| 542,591 | 0,0109 | 0,0111 | 0,01344 | 0,01169 | 0,01241 |
| 542,62818 | 0,01018 | 0,01034 | 0,01258 | 0,01085 | 0,01152 |
| 542,66536 | 0,00948 | 0,00962 | 0,01175 | 0,01006 | 0,01068 |
| 542,70254 | 0,00883 | 0,00894 | 0,01097 | 0,00933 | 0,00989 |
| 542,73973 | 0,00821 | 0,00829 | 0,01023 | 0,00865 | 0,00916 |
| 542,77691 | 0,00763 | 0,00768 | 0,00954 | 0,00802 | 0,00847 |
| 542,81409 | 0,00709 | 0,00712 | 0,00889 | 0,00743 | 0,00782 |
| 542,85127 | 0,00659 | 0,00659 | 0,00828 | 0,00688 | 0,00722 |
| 542,88845 | 0,00611 | 0,00609 | 0,0077 | 0,00638 | 0,00666 |
| 542,92564 | 0,00567 | 0,00563 | 0,00716 | 0,00592 | 0,00614 |
| 542,96282 | 0,00527 | 0,0052 | 0,00666 | 0,00549 | 0,00565 |
| 543 | 0,00489 | 0,0048 | 0,0062 | 0,0051 | 0,0052 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 9e-05 | 3e-05 | 8e-05 | 0 | 0 |
| 524,03718 | 0,00011 | 4e-05 | 9e-05 | 0 | 0 |
| 524,07436 | 0,00013 | 5e-05 | 0,00011 | 0 | 0 |
| 524,11155 | 0,00015 | 6e-05 | 0,00012 | 0 | 0 |
| 524,14873 | 0,00017 | 7e-05 | 0,00014 | 0 | 0 |
| 524,18591 | 0,00019 | 8e-05 | 0,00016 | 0 | 0 |
| 524,22309 | 0,00022 | 9e-05 | 0,00018 | 0 | 0 |
| 524,26027 | 0,00025 | 0,00011 | 2e-04 | 0 | 0 |
| 524,29746 | 0,00028 | 0,00013 | 0,00022 | 0 | 0 |
| 524,33464 | 0,00032 | 0,00015 | 0,00024 | 0 | 0 |
| 524,37182 | 0,00035 | 0,00017 | 0,00027 | 1e-05 | 0 |
| 524,409 | 0,00039 | 2e-04 | 0,00029 | 1e-05 | 0 |
| 524,44618 | 0,00043 | 0,00023 | 0,00032 | 1e-05 | 0 |
| 524,48337 | 0,00048 | 0,00026 | 0,00035 | 1e-05 | 1e-05 |
| 524,52055 | 0,00052 | 3e-04 | 0,00037 | 2e-05 | 1e-05 |
| 524,55773 | 0,00056 | 0,00033 | 4e-04 | 2e-05 | 1e-05 |
| 524,59491 | 0,00061 | 0,00037 | 0,00043 | 2e-05 | 1e-05 |
| 524,63209 | 0,00066 | 0,00042 | 0,00046 | 3e-05 | 1e-05 |
| 524,66928 | 0,00071 | 0,00046 | 0,00049 | 3e-05 | 1e-05 |
| 524,70646 | 0,00075 | 0,00051 | 0,00052 | 4e-05 | 2e-05 |
| 524,74364 | 8e-04 | 0,00056 | 0,00055 | 5e-05 | 2e-05 |
| 524,78082 | 0,00085 | 0,00061 | 0,00057 | 6e-05 | 3e-05 |
| 524,818 | 9e-04 | 0,00066 | 6e-04 | 7e-05 | 3e-05 |
| 524,85519 | 0,00094 | 0,00072 | 0,00063 | 8e-05 | 4e-05 |
| 524,89237 | 0,00099 | 0,00077 | 0,00066 | 1e-04 | 4e-05 |
| 524,92955 | 0,00103 | 0,00082 | 0,00068 | 0,00011 | 5e-05 |
| 524,96673 | 0,00107 | 0,00088 | 0,00071 | 0,00013 | 6e-05 |
| 525,00391 | 0,00111 | 0,00093 | 0,00073 | 0,00015 | 7e-05 |
| 525,0411 | 0,00115 | 0,00098 | 0,00076 | 0,00017 | 8e-05 |
| 525,07828 | 0,00118 | 0,00102 | 0,00078 | 2e-04 | 9e-05 |
| 525,11546 | 0,00121 | 0,00107 | 8e-04 | 0,00022 | 0,00011 |
| 525,15264 | 0,00124 | 0,00111 | 0,00082 | 0,00025 | 0,00012 |
| 525,18982 | 0,00127 | 0,00114 | 0,00085 | 0,00028 | 0,00014 |
| 525,22701 | 0,0013 | 0,00117 | 0,00086 | 0,00032 | 0,00016 |
| 525,26419 | 0,00132 | 0,0012 | 0,00088 | 0,00035 | 0,00018 |
| 525,30137 | 0,00135 | 0,00122 | 9e-04 | 0,00039 | 2e-04 |
| 525,33855 | 0,00137 | 0,00124 | 0,00092 | 0,00043 | 0,00023 |
| 525,37573 | 0,00139 | 0,00125 | 0,00093 | 0,00047 | 0,00025 |
| 525,41292 | 0,00141 | 0,00126 | 0,00094 | 0,00051 | 0,00028 |
| 525,4501 | 0,00143 | 0,00126 | 0,00096 | 0,00055 | 0,00031 |
| 525,48728 | 0,00145 | 0,00126 | 0,00097 | 6e-04 | 0,00034 |
| 525,52446 | 0,00146 | 0,00126 | 0,00098 | 0,00065 | 0,00037 |
| 525,56164 | 0,00148 | 0,00126 | 0,00098 | 0,00069 | 4e-04 |
| 525,59883 | 0,00151 | 0,00125 | 0,00099 | 0,00074 | 0,00044 |
| 525,63601 | 0,00153 | 0,00125 | 0,001 | 0,00079 | 0,00047 |
| 525,67319 | 0,00155 | 0,00124 | 0,001 | 0,00084 | 0,00051 |
| 525,71037 | 0,00158 | 0,00124 | 0,00101 | 0,00088 | 0,00055 |
| 525,74755 | 0,00161 | 0,00124 | 0,00101 | 0,00093 | 0,00058 |
| 525,78474 | 0,00164 | 0,00124 | 0,00102 | 0,00098 | 0,00062 |
| 525,82192 | 0,00168 | 0,00125 | 0,00103 | 0,00102 | 0,00066 |
| 525,8591 | 0,00172 | 0,00126 | 0,00104 | 0,00106 | 0,00069 |
| 525,89628 | 0,00177 | 0,00129 | 0,00106 | 0,0011 | 0,00073 |
| 525,93346 | 0,00183 | 0,00132 | 0,00108 | 0,00114 | 0,00077 |
| 525,97065 | 0,00189 | 0,00137 | 0,00112 | 0,00118 | 8e-04 |
| 526,00783 | 0,00197 | 0,00144 | 0,00116 | 0,00121 | 0,00083 |
| 526,04501 | 0,00206 | 0,00152 | 0,00122 | 0,00124 | 0,00087 |
| 526,08219 | 0,00216 | 0,00162 | 0,00129 | 0,00128 | 9e-04 |
| 526,11937 | 0,00228 | 0,00175 | 0,00139 | 0,00131 | 0,00093 |
| 526,15656 | 0,00242 | 0,0019 | 0,0015 | 0,00134 | 0,00096 |
| 526,19374 | 0,00258 | 0,00208 | 0,00165 | 0,00137 | 0,00099 |
| 526,23092 | 0,00278 | 0,00231 | 0,00183 | 0,0014 | 0,00103 |
| 526,2681 | 0,003 | 0,00257 | 0,00204 | 0,00143 | 0,00107 |
| 526,30528 | 0,00327 | 0,00288 | 0,00229 | 0,00147 | 0,00111 |
| 526,34247 | 0,00358 | 0,00324 | 0,00259 | 0,00151 | 0,00116 |
| 526,37965 | 0,00394 | 0,00365 | 0,00294 | 0,00156 | 0,00122 |
| 526,41683 | 0,00436 | 0,00413 | 0,00336 | 0,00163 | 0,00128 |
| 526,45401 | 0,00483 | 0,00468 | 0,00383 | 0,00171 | 0,00137 |
| 526,49119 | 0,00537 | 0,00531 | 0,00438 | 0,00181 | 0,00147 |
| 526,52838 | 0,006 | 0,00602 | 0,00499 | 0,00193 | 0,00159 |
| 526,56556 | 0,00672 | 0,00681 | 0,00568 | 0,00209 | 0,00175 |
| 526,60274 | 0,00752 | 0,00769 | 0,00647 | 0,00228 | 0,00194 |
| 526,63992 | 0,00841 | 0,00866 | 0,00735 | 0,00252 | 0,00217 |
| 526,6771 | 0,00941 | 0,00976 | 0,00833 | 0,00281 | 0,00244 |
| 526,71429 | 0,01051 | 0,01097 | 0,00941 | 0,00316 | 0,00277 |
| 526,75147 | 0,01175 | 0,01228 | 0,0106 | 0,00358 | 0,00317 |
| 526,78865 | 0,01311 | 0,01371 | 0,0119 | 0,00408 | 0,00365 |
| 526,82583 | 0,01461 | 0,01526 | 0,01332 | 0,00467 | 0,00421 |
| 526,86301 | 0,01624 | 0,01692 | 0,01489 | 0,00538 | 0,00487 |
| 526,9002 | 0,01801 | 0,01873 | 0,01658 | 0,00621 | 0,00563 |
| 526,93738 | 0,01992 | 0,02068 | 0,01839 | 0,00717 | 0,00651 |
| 526,97456 | 0,02199 | 0,02276 | 0,02035 | 0,00827 | 0,00753 |
| 527,01174 | 0,02425 | 0,02497 | 0,02244 | 0,00952 | 0,00872 |
| 527,04892 | 0,02668 | 0,02732 | 0,02469 | 0,01095 | 0,01006 |
| 527,08611 | 0,02928 | 0,0298 | 0,0271 | 0,01259 | 0,01158 |
| 527,12329 | 0,03205 | 0,03243 | 0,02966 | 0,01442 | 0,01327 |
| 527,16047 | 0,03501 | 0,03523 | 0,03238 | 0,01646 | 0,01516 |
| 527,19765 | 0,03815 | 0,03816 | 0,03524 | 0,01872 | 0,01724 |
| 527,23483 | 0,0415 | 0,04124 | 0,03826 | 0,02119 | 0,01958 |
| 527,27202 | 0,04506 | 0,04446 | 0,04143 | 0,0239 | 0,02214 |
| 527,3092 | 0,0488 | 0,04782 | 0,04478 | 0,02689 | 0,02491 |
| 527,34638 | 0,05272 | 0,05131 | 0,04827 | 0,0301 | 0,0279 |
| 527,38356 | 0,05682 | 0,05496 | 0,05189 | 0,03354 | 0,0311 |
| 527,42074 | 0,06109 | 0,05873 | 0,05564 | 0,0372 | 0,03451 |
| 527,45793 | 0,06552 | 0,06261 | 0,0595 | 0,04107 | 0,03816 |
| 527,49511 | 0,07011 | 0,06658 | 0,06346 | 0,04513 | 0,04199 |
| 527,53229 | 0,07481 | 0,07063 | 0,06752 | 0,04941 | 0,04599 |
| 527,56947 | 0,0796 | 0,07475 | 0,07163 | 0,05383 | 0,05012 |
| 527,60665 | 0,08445 | 0,07891 | 0,07579 | 0,05837 | 0,05438 |
| 527,64384 | 0,08934 | 0,08309 | 0,07997 | 0,063 | 0,05872 |
| 527,68102 | 0,09423 | 0,08726 | 0,08413 | 0,06768 | 0,06312 |
| 527,7182 | 0,09909 | 0,09139 | 0,08827 | 0,0724 | 0,06754 |
| 527,75538 | 0,10387 | 0,09546 | 0,09234 | 0,07709 | 0,07193 |
| 527,79256 | 0,10854 | 0,09945 | 0,09632 | 0,08172 | 0,07626 |
| 527,82975 | 0,11307 | 0,10333 | 0,10018 | 0,08624 | 0,08049 |
| 527,86693 | 0,11743 | 0,10704 | 0,1039 | 0,09062 | 0,08459 |
| 527,90411 | 0,1216 | 0,11058 | 0,10747 | 0,09482 | 0,08851 |
| 527,94129 | 0,12554 | 0,11394 | 0,11086 | 0,09882 | 0,09218 |
| 527,97847 | 0,12919 | 0,1171 | 0,11402 | 0,10255 | 0,09559 |
| 528,01566 | 0,13258 | 0,12006 | 0,11695 | 0,10598 | 0,09874 |
| 528,05284 | 0,13569 | 0,12279 | 0,11966 | 0,1091 | 0,10159 |
| 528,09002 | 0,13851 | 0,12524 | 0,12213 | 0,11191 | 0,10414 |
| 528,1272 | 0,14105 | 0,12746 | 0,12437 | 0,11441 | 0,10636 |
| 528,16438 | 0,14331 | 0,12945 | 0,12638 | 0,11657 | 0,10819 |
| 528,20157 | 0,14525 | 0,13121 | 0,12813 | 0,11839 | 0,10968 |
| 528,23875 | 0,14689 | 0,13276 | 0,12961 | 0,11983 | 0,11086 |
| 528,27593 | 0,14827 | 0,13409 | 0,13087 | 0,12097 | 0,11173 |
| 528,31311 | 0,14941 | 0,1352 | 0,13192 | 0,12183 | 0,11232 |
| 528,35029 | 0,15032 | 0,13611 | 0,13277 | 0,12242 | 0,11264 |
| 528,38748 | 0,15101 | 0,13685 | 0,13342 | 0,12277 | 0,11269 |
| 528,42466 | 0,15149 | 0,13743 | 0,1339 | 0,1229 | 0,11252 |
| 528,46184 | 0,15175 | 0,13787 | 0,13417 | 0,12281 | 0,11218 |
| 528,49902 | 0,15185 | 0,13817 | 0,1343 | 0,12259 | 0,1117 |
| 528,5362 | 0,15181 | 0,13836 | 0,13429 | 0,12225 | 0,11111 |
| 528,57339 | 0,15163 | 0,13843 | 0,13417 | 0,12182 | 0,11045 |
| 528,61057 | 0,15132 | 0,13841 | 0,13393 | 0,12134 | 0,10973 |
| 528,64775 | 0,15092 | 0,13831 | 0,13359 | 0,12082 | 0,109 |
| 528,68493 | 0,15041 | 0,13815 | 0,13315 | 0,1203 | 0,10828 |
| 528,72211 | 0,14982 | 0,13793 | 0,13264 | 0,11979 | 0,1076 |
| 528,7593 | 0,14917 | 0,13766 | 0,13206 | 0,11931 | 0,10696 |
| 528,79648 | 0,14847 | 0,13735 | 0,13144 | 0,11888 | 0,10639 |
| 528,83366 | 0,14774 | 0,13701 | 0,13077 | 0,1185 | 0,1059 |
| 528,87084 | 0,14698 | 0,13665 | 0,13007 | 0,11818 | 0,10552 |
| 528,90802 | 0,14621 | 0,13627 | 0,12936 | 0,11793 | 0,10523 |
| 528,94521 | 0,14545 | 0,1359 | 0,12863 | 0,11776 | 0,10504 |
| 528,98239 | 0,1447 | 0,13553 | 0,12791 | 0,11766 | 0,10494 |
| 529,01957 | 0,14397 | 0,13517 | 0,12721 | 0,11762 | 0,10494 |
| 529,05675 | 0,14327 | 0,13483 | 0,12653 | 0,11764 | 0,10504 |
| 529,09393 | 0,14261 | 0,13452 | 0,12588 | 0,11773 | 0,10525 |
| 529,13112 | 0,142 | 0,13424 | 0,12528 | 0,11787 | 0,10555 |
| 529,1683 | 0,14144 | 0,134 | 0,12474 | 0,11807 | 0,10594 |
| 529,20548 | 0,14095 | 0,13379 | 0,12427 | 0,11832 | 0,10641 |
| 529,24266 | 0,14051 | 0,13363 | 0,12386 | 0,1186 | 0,10695 |
| 529,27984 | 0,14012 | 0,13353 | 0,12352 | 0,11892 | 0,10758 |
| 529,31703 | 0,13979 | 0,13347 | 0,12326 | 0,11927 | 0,10828 |
| 529,35421 | 0,1395 | 0,13345 | 0,12309 | 0,11965 | 0,10906 |
| 529,39139 | 0,13927 | 0,13347 | 0,12301 | 0,12005 | 0,10989 |
| 529,42857 | 0,13908 | 0,13354 | 0,12301 | 0,12047 | 0,11078 |
| 529,46575 | 0,13893 | 0,13364 | 0,12309 | 0,12089 | 0,11172 |
| 529,50294 | 0,13881 | 0,13377 | 0,12325 | 0,12132 | 0,1127 |
| 529,54012 | 0,13872 | 0,13393 | 0,12348 | 0,12175 | 0,11373 |
| 529,5773 | 0,13864 | 0,1341 | 0,12378 | 0,12218 | 0,11478 |
| 529,61448 | 0,13857 | 0,13428 | 0,12416 | 0,12258 | 0,11584 |
| 529,65166 | 0,13851 | 0,13447 | 0,12459 | 0,12296 | 0,11691 |
| 529,68885 | 0,13844 | 0,13465 | 0,12506 | 0,12332 | 0,11798 |
| 529,72603 | 0,13838 | 0,13483 | 0,12557 | 0,12364 | 0,11903 |
| 529,76321 | 0,13831 | 0,13498 | 0,12611 | 0,12393 | 0,12006 |
| 529,80039 | 0,13822 | 0,13512 | 0,12667 | 0,12418 | 0,12104 |
| 529,83757 | 0,13812 | 0,13522 | 0,12725 | 0,12437 | 0,12197 |
| 529,87476 | 0,13801 | 0,13529 | 0,12783 | 0,12452 | 0,12285 |
| 529,91194 | 0,13787 | 0,13532 | 0,1284 | 0,12462 | 0,12366 |
| 529,94912 | 0,1377 | 0,13531 | 0,12895 | 0,12468 | 0,1244 |
| 529,9863 | 0,13751 | 0,13524 | 0,12948 | 0,1247 | 0,12507 |
| 530,02348 | 0,1373 | 0,13511 | 0,12998 | 0,12467 | 0,12564 |
| 530,06067 | 0,13705 | 0,13494 | 0,13043 | 0,12461 | 0,12614 |
| 530,09785 | 0,13676 | 0,13471 | 0,13082 | 0,12453 | 0,12656 |
| 530,13503 | 0,13644 | 0,13442 | 0,13116 | 0,12442 | 0,1269 |
| 530,17221 | 0,13606 | 0,13406 | 0,13144 | 0,12431 | 0,12718 |
| 530,20939 | 0,13565 | 0,13364 | 0,13164 | 0,12419 | 0,1274 |
| 530,24658 | 0,13518 | 0,13315 | 0,13177 | 0,12408 | 0,12756 |
| 530,28376 | 0,13467 | 0,13259 | 0,13181 | 0,12399 | 0,12766 |
| 530,32094 | 0,1341 | 0,13196 | 0,13175 | 0,12391 | 0,12772 |
| 530,35812 | 0,13347 | 0,13127 | 0,1316 | 0,12387 | 0,12776 |
| 530,3953 | 0,13278 | 0,13052 | 0,13136 | 0,12385 | 0,12776 |
| 530,43249 | 0,13204 | 0,12969 | 0,13102 | 0,12386 | 0,12775 |
| 530,46967 | 0,13124 | 0,12879 | 0,13059 | 0,1239 | 0,12772 |
| 530,50685 | 0,13038 | 0,12784 | 0,13005 | 0,12398 | 0,12768 |
| 530,54403 | 0,12948 | 0,12682 | 0,12941 | 0,12408 | 0,12762 |
| 530,58121 | 0,12853 | 0,12576 | 0,12867 | 0,1242 | 0,12756 |
| 530,6184 | 0,12753 | 0,12465 | 0,12785 | 0,12433 | 0,12748 |
| 530,65558 | 0,1265 | 0,1235 | 0,12694 | 0,12446 | 0,12738 |
| 530,69276 | 0,12543 | 0,12231 | 0,12596 | 0,12458 | 0,12726 |
| 530,72994 | 0,12434 | 0,1211 | 0,12492 | 0,12468 | 0,1271 |
| 530,76712 | 0,12324 | 0,11987 | 0,12381 | 0,12475 | 0,12691 |
| 530,80431 | 0,12213 | 0,11864 | 0,12265 | 0,12477 | 0,12668 |
| 530,84149 | 0,12102 | 0,11741 | 0,12146 | 0,12474 | 0,12639 |
| 530,87867 | 0,11991 | 0,1162 | 0,12026 | 0,12465 | 0,12604 |
| 530,91585 | 0,11882 | 0,11501 | 0,11904 | 0,12448 | 0,12563 |
| 530,95303 | 0,11776 | 0,11386 | 0,11783 | 0,12424 | 0,12515 |
| 530,99022 | 0,11673 | 0,11277 | 0,11665 | 0,1239 | 0,12458 |
| 531,0274 | 0,11574 | 0,11173 | 0,1155 | 0,12348 | 0,12393 |
| 531,06458 | 0,1148 | 0,11076 | 0,11441 | 0,12296 | 0,12321 |
| 531,10176 | 0,11392 | 0,10986 | 0,11337 | 0,12236 | 0,12241 |
| 531,13894 | 0,11311 | 0,10906 | 0,11241 | 0,12168 | 0,12154 |
| 531,17613 | 0,11238 | 0,10837 | 0,11154 | 0,12092 | 0,1206 |
| 531,21331 | 0,11172 | 0,10778 | 0,11077 | 0,12008 | 0,1196 |
| 531,25049 | 0,11114 | 0,1073 | 0,11012 | 0,11918 | 0,11855 |
| 531,28767 | 0,11064 | 0,10693 | 0,10958 | 0,11824 | 0,11748 |
| 531,32485 | 0,11024 | 0,10667 | 0,10915 | 0,11726 | 0,11638 |
| 531,36204 | 0,10995 | 0,10653 | 0,10885 | 0,11627 | 0,11528 |
| 531,39922 | 0,10975 | 0,10652 | 0,10866 | 0,11527 | 0,11419 |
| 531,4364 | 0,10965 | 0,10663 | 0,1086 | 0,11429 | 0,11315 |
| 531,47358 | 0,10964 | 0,10684 | 0,10867 | 0,11334 | 0,11215 |
| 531,51076 | 0,10972 | 0,10716 | 0,10885 | 0,11243 | 0,11123 |
| 531,54795 | 0,10987 | 0,10756 | 0,10912 | 0,11158 | 0,11038 |
| 531,58513 | 0,11012 | 0,10805 | 0,10947 | 0,11081 | 0,10964 |
| 531,62231 | 0,11043 | 0,10862 | 0,1099 | 0,11012 | 0,10901 |
| 531,65949 | 0,1108 | 0,10925 | 0,1104 | 0,10953 | 0,10852 |
| 531,69667 | 0,11121 | 0,10992 | 0,11095 | 0,10906 | 0,10818 |
| 531,73386 | 0,11165 | 0,11062 | 0,11152 | 0,10871 | 0,10797 |
| 531,77104 | 0,1121 | 0,11133 | 0,11211 | 0,10846 | 0,10792 |
| 531,80822 | 0,11256 | 0,11205 | 0,11269 | 0,10834 | 0,10801 |
| 531,8454 | 0,11301 | 0,11274 | 0,11325 | 0,10832 | 0,10824 |
| 531,88258 | 0,11342 | 0,1134 | 0,11378 | 0,10842 | 0,10862 |
| 531,91977 | 0,1138 | 0,114 | 0,11425 | 0,10864 | 0,10915 |
| 531,95695 | 0,11412 | 0,11454 | 0,11464 | 0,10896 | 0,1098 |
| 531,99413 | 0,11437 | 0,11502 | 0,11497 | 0,10937 | 0,11055 |
| 532,03131 | 0,11456 | 0,11541 | 0,1152 | 0,10985 | 0,11139 |
| 532,06849 | 0,11464 | 0,11571 | 0,11535 | 0,11039 | 0,11229 |
| 532,10568 | 0,11463 | 0,1159 | 0,11539 | 0,11097 | 0,11326 |
| 532,14286 | 0,11452 | 0,11598 | 0,11532 | 0,11159 | 0,11426 |
| 532,18004 | 0,11431 | 0,11597 | 0,11514 | 0,11222 | 0,11526 |
| 532,21722 | 0,11399 | 0,11585 | 0,11486 | 0,11285 | 0,11626 |
| 532,2544 | 0,11358 | 0,11563 | 0,11448 | 0,11346 | 0,11722 |
| 532,29159 | 0,11306 | 0,11531 | 0,114 | 0,11403 | 0,11813 |
| 532,32877 | 0,11242 | 0,1149 | 0,11344 | 0,11456 | 0,11897 |
| 532,36595 | 0,1117 | 0,1144 | 0,11279 | 0,11502 | 0,11971 |
| 532,40313 | 0,11088 | 0,11383 | 0,11206 | 0,1154 | 0,12036 |
| 532,44031 | 0,10999 | 0,11319 | 0,11128 | 0,11569 | 0,12089 |
| 532,4775 | 0,10903 | 0,1125 | 0,11045 | 0,1159 | 0,12131 |
| 532,51468 | 0,10801 | 0,11177 | 0,10958 | 0,11602 | 0,1216 |
| 532,55186 | 0,10694 | 0,11101 | 0,10869 | 0,11604 | 0,12178 |
| 532,58904 | 0,10582 | 0,11023 | 0,10778 | 0,11596 | 0,12181 |
| 532,62622 | 0,10468 | 0,10945 | 0,10687 | 0,11577 | 0,12171 |
| 532,66341 | 0,10353 | 0,10867 | 0,10597 | 0,11549 | 0,12151 |
| 532,70059 | 0,10237 | 0,1079 | 0,10509 | 0,11513 | 0,1212 |
| 532,73777 | 0,10122 | 0,10716 | 0,10423 | 0,11469 | 0,12079 |
| 532,77495 | 0,10009 | 0,10645 | 0,1034 | 0,11418 | 0,1203 |
| 532,81213 | 0,09899 | 0,10577 | 0,10261 | 0,1136 | 0,11973 |
| 532,84932 | 0,09793 | 0,10514 | 0,10186 | 0,11296 | 0,11909 |
| 532,8865 | 0,09691 | 0,10456 | 0,10116 | 0,11229 | 0,11841 |
| 532,92368 | 0,09594 | 0,10401 | 0,1005 | 0,11158 | 0,11768 |
| 532,96086 | 0,09502 | 0,1035 | 0,09987 | 0,11084 | 0,11694 |
| 532,99804 | 0,09415 | 0,10303 | 0,09928 | 0,1101 | 0,11617 |
| 533,03523 | 0,09335 | 0,10259 | 0,09872 | 0,10934 | 0,1154 |
| 533,07241 | 0,09259 | 0,10217 | 0,09817 | 0,10857 | 0,11462 |
| 533,10959 | 0,09187 | 0,10176 | 0,09764 | 0,10781 | 0,11384 |
| 533,14677 | 0,09119 | 0,10134 | 0,0971 | 0,10704 | 0,11306 |
| 533,18395 | 0,09054 | 0,10091 | 0,09655 | 0,10628 | 0,11227 |
| 533,22114 | 0,0899 | 0,10046 | 0,09598 | 0,10551 | 0,11149 |
| 533,25832 | 0,08927 | 0,09997 | 0,09537 | 0,10474 | 0,11069 |
| 533,2955 | 0,08863 | 0,09941 | 0,09471 | 0,10396 | 0,10988 |
| 533,33268 | 0,08797 | 0,09878 | 0,09399 | 0,10315 | 0,10904 |
| 533,36986 | 0,08728 | 0,09807 | 0,09319 | 0,10232 | 0,10817 |
| 533,40705 | 0,08655 | 0,09727 | 0,09233 | 0,10146 | 0,10726 |
| 533,44423 | 0,08577 | 0,09638 | 0,09138 | 0,10056 | 0,1063 |
| 533,48141 | 0,08495 | 0,09538 | 0,09035 | 0,09961 | 0,10527 |
| 533,51859 | 0,08405 | 0,09427 | 0,08923 | 0,09859 | 0,10417 |
| 533,55577 | 0,0831 | 0,09305 | 0,08801 | 0,0975 | 0,10299 |
| 533,59295 | 0,08208 | 0,09172 | 0,08672 | 0,09634 | 0,10171 |
| 533,63014 | 0,08101 | 0,09031 | 0,08535 | 0,0951 | 0,10035 |
| 533,66732 | 0,07989 | 0,08881 | 0,08392 | 0,09379 | 0,0989 |
| 533,7045 | 0,07874 | 0,08724 | 0,08245 | 0,0924 | 0,09736 |
| 533,74168 | 0,07755 | 0,0856 | 0,08093 | 0,09093 | 0,09573 |
| 533,77886 | 0,07635 | 0,08392 | 0,07938 | 0,08938 | 0,094 |
| 533,81605 | 0,07515 | 0,08222 | 0,07784 | 0,08776 | 0,0922 |
| 533,85323 | 0,07398 | 0,08053 | 0,07632 | 0,08609 | 0,09033 |
| 533,89041 | 0,07284 | 0,07885 | 0,07482 | 0,08438 | 0,08842 |
| 533,92759 | 0,07174 | 0,07721 | 0,07338 | 0,08263 | 0,08646 |
| 533,96477 | 0,07071 | 0,07562 | 0,072 | 0,08087 | 0,08448 |
| 534,00196 | 0,06977 | 0,07412 | 0,07073 | 0,0791 | 0,0825 |
| 534,03914 | 0,06894 | 0,07273 | 0,06956 | 0,07735 | 0,08054 |
| 534,07632 | 0,0682 | 0,07144 | 0,0685 | 0,07564 | 0,07862 |
| 534,1135 | 0,06758 | 0,07027 | 0,06756 | 0,07398 | 0,07676 |
| 534,15068 | 0,06707 | 0,06923 | 0,06676 | 0,07239 | 0,07498 |
| 534,18787 | 0,06668 | 0,06832 | 0,06609 | 0,07088 | 0,0733 |
| 534,22505 | 0,06639 | 0,06757 | 0,06558 | 0,06949 | 0,07175 |
| 534,26223 | 0,06624 | 0,06696 | 0,06521 | 0,06821 | 0,07034 |
| 534,29941 | 0,06619 | 0,06648 | 0,06497 | 0,06706 | 0,06909 |
| 534,33659 | 0,06623 | 0,06613 | 0,06485 | 0,06605 | 0,068 |
| 534,37378 | 0,06633 | 0,06588 | 0,06485 | 0,06517 | 0,06708 |
| 534,41096 | 0,0665 | 0,06574 | 0,06495 | 0,06444 | 0,06634 |
| 534,44814 | 0,06671 | 0,06569 | 0,06514 | 0,06388 | 0,06579 |
| 534,48532 | 0,06695 | 0,06572 | 0,06541 | 0,06348 | 0,06545 |
| 534,5225 | 0,0672 | 0,06579 | 0,06573 | 0,06322 | 0,06529 |
| 534,55969 | 0,06742 | 0,06589 | 0,06608 | 0,06309 | 0,06529 |
| 534,59687 | 0,06762 | 0,066 | 0,06645 | 0,0631 | 0,06546 |
| 534,63405 | 0,06776 | 0,0661 | 0,06681 | 0,06322 | 0,06578 |
| 534,67123 | 0,06784 | 0,06618 | 0,06715 | 0,06347 | 0,06624 |
| 534,70841 | 0,06784 | 0,0662 | 0,06744 | 0,06382 | 0,06683 |
| 534,7456 | 0,06773 | 0,06616 | 0,06768 | 0,06424 | 0,06753 |
| 534,78278 | 0,06752 | 0,06603 | 0,06784 | 0,06473 | 0,06829 |
| 534,81996 | 0,0672 | 0,06582 | 0,06792 | 0,06526 | 0,06912 |
| 534,85714 | 0,06677 | 0,06552 | 0,06791 | 0,06583 | 0,06998 |
| 534,89432 | 0,06623 | 0,06511 | 0,0678 | 0,06642 | 0,07085 |
| 534,93151 | 0,06557 | 0,06459 | 0,06756 | 0,067 | 0,07172 |
| 534,96869 | 0,0648 | 0,06395 | 0,06722 | 0,06756 | 0,07255 |
| 535,00587 | 0,06391 | 0,0632 | 0,06677 | 0,06809 | 0,07334 |
| 535,04305 | 0,06294 | 0,06236 | 0,06623 | 0,06858 | 0,07406 |
| 535,08023 | 0,06187 | 0,06143 | 0,06558 | 0,06901 | 0,0747 |
| 535,11742 | 0,06074 | 0,06041 | 0,06485 | 0,06937 | 0,07526 |
| 535,1546 | 0,05954 | 0,05932 | 0,06401 | 0,06965 | 0,0757 |
| 535,19178 | 0,0583 | 0,05816 | 0,06311 | 0,06984 | 0,07601 |
| 535,22896 | 0,05701 | 0,05696 | 0,06216 | 0,06995 | 0,07621 |
| 535,26614 | 0,0557 | 0,05574 | 0,06115 | 0,06997 | 0,0763 |
| 535,30333 | 0,05439 | 0,0545 | 0,06012 | 0,0699 | 0,07626 |
| 535,34051 | 0,05308 | 0,05327 | 0,05906 | 0,06974 | 0,07611 |
| 535,37769 | 0,05178 | 0,05205 | 0,05799 | 0,06948 | 0,07584 |
| 535,41487 | 0,05051 | 0,05086 | 0,05693 | 0,06912 | 0,07545 |
| 535,45205 | 0,04928 | 0,04972 | 0,05588 | 0,06869 | 0,07495 |
| 535,48924 | 0,04809 | 0,04864 | 0,05485 | 0,06817 | 0,07437 |
| 535,52642 | 0,04696 | 0,04761 | 0,05386 | 0,06759 | 0,0737 |
| 535,5636 | 0,04588 | 0,04665 | 0,05291 | 0,06694 | 0,07295 |
| 535,60078 | 0,04486 | 0,04576 | 0,052 | 0,06622 | 0,07214 |
| 535,63796 | 0,04389 | 0,04495 | 0,05114 | 0,06544 | 0,07125 |
| 535,67515 | 0,04299 | 0,04422 | 0,05034 | 0,06461 | 0,07032 |
| 535,71233 | 0,04216 | 0,04357 | 0,04958 | 0,06374 | 0,06934 |
| 535,74951 | 0,04138 | 0,04298 | 0,04887 | 0,06283 | 0,06832 |
| 535,78669 | 0,04066 | 0,04245 | 0,04821 | 0,06189 | 0,06728 |
| 535,82387 | 0,04 | 0,04198 | 0,04759 | 0,06092 | 0,0662 |
| 535,86106 | 0,03937 | 0,04156 | 0,04702 | 0,05991 | 0,0651 |
| 535,89824 | 0,0388 | 0,04118 | 0,04648 | 0,05888 | 0,06397 |
| 535,93542 | 0,03826 | 0,04083 | 0,04597 | 0,05783 | 0,06281 |
| 535,9726 | 0,03775 | 0,04051 | 0,04548 | 0,05676 | 0,06163 |
| 536,00978 | 0,03727 | 0,0402 | 0,045 | 0,05567 | 0,06043 |
| 536,04697 | 0,0368 | 0,03989 | 0,04454 | 0,05456 | 0,05921 |
| 536,08415 | 0,03635 | 0,03957 | 0,04409 | 0,05342 | 0,05795 |
| 536,12133 | 0,03591 | 0,03925 | 0,04364 | 0,05228 | 0,05667 |
| 536,15851 | 0,03548 | 0,0389 | 0,04318 | 0,05111 | 0,05536 |
| 536,19569 | 0,03504 | 0,03854 | 0,04272 | 0,04993 | 0,05402 |
| 536,23288 | 0,0346 | 0,03815 | 0,04225 | 0,04875 | 0,05267 |
| 536,27006 | 0,03415 | 0,03773 | 0,04178 | 0,04755 | 0,05129 |
| 536,30724 | 0,0337 | 0,03729 | 0,04129 | 0,04635 | 0,0499 |
| 536,34442 | 0,03324 | 0,03681 | 0,04079 | 0,04515 | 0,0485 |
| 536,3816 | 0,03277 | 0,03632 | 0,04028 | 0,04396 | 0,0471 |
| 536,41879 | 0,0323 | 0,0358 | 0,03977 | 0,04278 | 0,0457 |
| 536,45597 | 0,03182 | 0,03527 | 0,03926 | 0,04162 | 0,04432 |
| 536,49315 | 0,03135 | 0,03473 | 0,03875 | 0,04048 | 0,04296 |
| 536,53033 | 0,03088 | 0,03419 | 0,03825 | 0,03939 | 0,04163 |
| 536,56751 | 0,03042 | 0,03366 | 0,03776 | 0,03834 | 0,04035 |
| 536,6047 | 0,02997 | 0,03314 | 0,03728 | 0,03733 | 0,03913 |
| 536,64188 | 0,02954 | 0,03264 | 0,03683 | 0,03639 | 0,03797 |
| 536,67906 | 0,02914 | 0,03218 | 0,03641 | 0,0355 | 0,03688 |
| 536,71624 | 0,02877 | 0,03175 | 0,03602 | 0,03469 | 0,03588 |
| 536,75342 | 0,02844 | 0,03136 | 0,03567 | 0,03395 | 0,03496 |
| 536,79061 | 0,02815 | 0,03103 | 0,03537 | 0,0333 | 0,03414 |
| 536,82779 | 0,0279 | 0,03075 | 0,03511 | 0,03273 | 0,03344 |
| 536,86497 | 0,0277 | 0,03053 | 0,0349 | 0,03225 | 0,03283 |
| 536,90215 | 0,02754 | 0,03038 | 0,03473 | 0,03185 | 0,03233 |
| 536,93933 | 0,02745 | 0,03028 | 0,03462 | 0,03153 | 0,03192 |
| 536,97652 | 0,02739 | 0,03024 | 0,03455 | 0,0313 | 0,03162 |
| 537,0137 | 0,02739 | 0,03026 | 0,03454 | 0,03116 | 0,03143 |
| 537,05088 | 0,02742 | 0,03033 | 0,03457 | 0,03111 | 0,03135 |
| 537,08806 | 0,02749 | 0,03046 | 0,03463 | 0,03112 | 0,03136 |
| 537,12524 | 0,0276 | 0,03062 | 0,03473 | 0,0312 | 0,03145 |
| 537,16243 | 0,02773 | 0,03081 | 0,03484 | 0,03135 | 0,03162 |
| 537,19961 | 0,02787 | 0,03102 | 0,03498 | 0,03155 | 0,03186 |
| 537,23679 | 0,02803 | 0,03125 | 0,03512 | 0,03182 | 0,03216 |
| 537,27397 | 0,02817 | 0,03147 | 0,03527 | 0,03213 | 0,03253 |
| 537,31115 | 0,02831 | 0,03168 | 0,0354 | 0,03247 | 0,03295 |
| 537,34834 | 0,02843 | 0,03187 | 0,03551 | 0,03284 | 0,0334 |
| 537,38552 | 0,02851 | 0,03203 | 0,0356 | 0,03323 | 0,03387 |
| 537,4227 | 0,02855 | 0,03214 | 0,03566 | 0,03363 | 0,03437 |
| 537,45988 | 0,02854 | 0,0322 | 0,03566 | 0,03404 | 0,03487 |
| 537,49706 | 0,02848 | 0,03221 | 0,03562 | 0,03444 | 0,03537 |
| 537,53425 | 0,02836 | 0,03215 | 0,03553 | 0,03484 | 0,03586 |
| 537,57143 | 0,02819 | 0,03202 | 0,03539 | 0,03521 | 0,03632 |
| 537,60861 | 0,02795 | 0,03181 | 0,03519 | 0,03555 | 0,03676 |
| 537,64579 | 0,02764 | 0,03154 | 0,03494 | 0,03587 | 0,03716 |
| 537,68297 | 0,02727 | 0,0312 | 0,03462 | 0,03614 | 0,03751 |
| 537,72016 | 0,02685 | 0,0308 | 0,03426 | 0,03636 | 0,03781 |
| 537,75734 | 0,02638 | 0,03034 | 0,03386 | 0,03654 | 0,03804 |
| 537,79452 | 0,02586 | 0,02981 | 0,03342 | 0,03666 | 0,0382 |
| 537,8317 | 0,0253 | 0,02924 | 0,03294 | 0,03674 | 0,03829 |
| 537,86888 | 0,02471 | 0,02863 | 0,03245 | 0,03676 | 0,03831 |
| 537,90607 | 0,02411 | 0,028 | 0,03194 | 0,03672 | 0,03825 |
| 537,94325 | 0,02349 | 0,02735 | 0,03143 | 0,03662 | 0,03812 |
| 537,98043 | 0,02287 | 0,02669 | 0,03092 | 0,03647 | 0,03789 |
| 538,01761 | 0,02226 | 0,02603 | 0,03042 | 0,03627 | 0,0376 |
| 538,05479 | 0,02166 | 0,02538 | 0,02994 | 0,03603 | 0,03723 |
| 538,09198 | 0,02108 | 0,02475 | 0,02949 | 0,03575 | 0,0368 |
| 538,12916 | 0,02053 | 0,02414 | 0,02907 | 0,03544 | 0,03631 |
| 538,16634 | 0,02002 | 0,02356 | 0,02868 | 0,03509 | 0,03576 |
| 538,20352 | 0,01953 | 0,02301 | 0,02834 | 0,03473 | 0,03516 |
| 538,2407 | 0,01909 | 0,0225 | 0,02803 | 0,03435 | 0,03452 |
| 538,27789 | 0,01868 | 0,02203 | 0,02776 | 0,03396 | 0,03386 |
| 538,31507 | 0,0183 | 0,0216 | 0,02752 | 0,03356 | 0,03317 |
| 538,35225 | 0,01796 | 0,0212 | 0,02732 | 0,03316 | 0,03247 |
| 538,38943 | 0,01764 | 0,02082 | 0,02714 | 0,03277 | 0,03177 |
| 538,42661 | 0,01735 | 0,02048 | 0,02698 | 0,03238 | 0,03106 |
| 538,4638 | 0,01707 | 0,02015 | 0,02682 | 0,03199 | 0,03037 |
| 538,50098 | 0,0168 | 0,01985 | 0,02667 | 0,03161 | 0,02968 |
| 538,53816 | 0,01654 | 0,01955 | 0,02651 | 0,03124 | 0,02901 |
| 538,57534 | 0,01627 | 0,01925 | 0,02634 | 0,03086 | 0,02835 |
| 538,61252 | 0,01599 | 0,01895 | 0,02614 | 0,03048 | 0,02771 |
| 538,64971 | 0,0157 | 0,01865 | 0,02591 | 0,03009 | 0,02709 |
| 538,68689 | 0,0154 | 0,01834 | 0,02563 | 0,02969 | 0,02649 |
| 538,72407 | 0,01506 | 0,018 | 0,02531 | 0,02927 | 0,0259 |
| 538,76125 | 0,01471 | 0,01765 | 0,02495 | 0,02883 | 0,02532 |
| 538,79843 | 0,01433 | 0,01728 | 0,02453 | 0,02836 | 0,02474 |
| 538,83562 | 0,01392 | 0,01689 | 0,02404 | 0,02785 | 0,02417 |
| 538,8728 | 0,01349 | 0,01647 | 0,0235 | 0,02731 | 0,02359 |
| 538,90998 | 0,01303 | 0,01604 | 0,02291 | 0,02672 | 0,02301 |
| 538,94716 | 0,01255 | 0,01559 | 0,02227 | 0,02609 | 0,02243 |
| 538,98434 | 0,01205 | 0,01512 | 0,02158 | 0,02543 | 0,02183 |
| 539,02153 | 0,01154 | 0,01465 | 0,02085 | 0,02472 | 0,02123 |
| 539,05871 | 0,01102 | 0,01416 | 0,02008 | 0,02397 | 0,02061 |
| 539,09589 | 0,0105 | 0,01367 | 0,01928 | 0,02318 | 0,01999 |
| 539,13307 | 0,00998 | 0,01318 | 0,01846 | 0,02236 | 0,01935 |
| 539,17025 | 0,00947 | 0,0127 | 0,01763 | 0,02151 | 0,01871 |
| 539,20744 | 0,00897 | 0,01222 | 0,0168 | 0,02065 | 0,01806 |
| 539,24462 | 0,00848 | 0,01176 | 0,01597 | 0,01977 | 0,01741 |
| 539,2818 | 0,00802 | 0,01131 | 0,01514 | 0,01889 | 0,01677 |
| 539,31898 | 0,00758 | 0,01087 | 0,01434 | 0,01801 | 0,01613 |
| 539,35616 | 0,00717 | 0,01045 | 0,01356 | 0,01714 | 0,0155 |
| 539,39335 | 0,00679 | 0,01005 | 0,01281 | 0,01629 | 0,01489 |
| 539,43053 | 0,00643 | 0,00968 | 0,01209 | 0,01546 | 0,01429 |
| 539,46771 | 0,00611 | 0,00932 | 0,0114 | 0,01466 | 0,01371 |
| 539,50489 | 0,00581 | 0,00898 | 0,01075 | 0,01388 | 0,01316 |
| 539,54207 | 0,00554 | 0,00865 | 0,01015 | 0,01315 | 0,01262 |
| 539,57926 | 0,0053 | 0,00834 | 0,00958 | 0,01245 | 0,01212 |
| 539,61644 | 0,00509 | 0,00804 | 0,00904 | 0,01179 | 0,01163 |
| 539,65362 | 0,00489 | 0,00776 | 0,00854 | 0,01117 | 0,01118 |
| 539,6908 | 0,00471 | 0,00748 | 0,00807 | 0,01058 | 0,01074 |
| 539,72798 | 0,00455 | 0,00721 | 0,00764 | 0,01003 | 0,01032 |
| 539,76517 | 0,00439 | 0,00694 | 0,00723 | 0,00951 | 0,00993 |
| 539,80235 | 0,00425 | 0,00667 | 0,00685 | 0,00903 | 0,00954 |
| 539,83953 | 0,00411 | 0,00641 | 0,00649 | 0,00857 | 0,00917 |
| 539,87671 | 0,00397 | 0,00614 | 0,00615 | 0,00814 | 0,00882 |
| 539,91389 | 0,00383 | 0,00588 | 0,00582 | 0,00773 | 0,00846 |
| 539,95108 | 0,0037 | 0,00561 | 0,00551 | 0,00733 | 0,00812 |
| 539,98826 | 0,00355 | 0,00534 | 0,00521 | 0,00695 | 0,00777 |
| 540,02544 | 0,00341 | 0,00507 | 0,00492 | 0,00659 | 0,00743 |
| 540,06262 | 0,00326 | 0,00481 | 0,00464 | 0,00623 | 0,00709 |
| 540,0998 | 0,0031 | 0,00454 | 0,00437 | 0,00588 | 0,00675 |
| 540,13699 | 0,00294 | 0,00427 | 0,0041 | 0,00554 | 0,0064 |
| 540,17417 | 0,00278 | 0,00401 | 0,00384 | 0,00521 | 0,00606 |
| 540,21135 | 0,00261 | 0,00375 | 0,00358 | 0,00488 | 0,00572 |
| 540,24853 | 0,00244 | 0,0035 | 0,00334 | 0,00456 | 0,00538 |
| 540,28571 | 0,00227 | 0,00325 | 0,0031 | 0,00425 | 0,00504 |
| 540,3229 | 0,0021 | 0,00302 | 0,00286 | 0,00394 | 0,0047 |
| 540,36008 | 0,00193 | 0,00279 | 0,00264 | 0,00364 | 0,00437 |
| 540,39726 | 0,00177 | 0,00257 | 0,00242 | 0,00335 | 0,00405 |
| 540,43444 | 0,00161 | 0,00237 | 0,00221 | 0,00307 | 0,00374 |
| 540,47162 | 0,00145 | 0,00218 | 0,00202 | 0,0028 | 0,00344 |
| 540,50881 | 0,0013 | 0,002 | 0,00183 | 0,00254 | 0,00315 |
| 540,54599 | 0,00116 | 0,00184 | 0,00166 | 0,0023 | 0,00288 |
| 540,58317 | 0,00103 | 0,00168 | 0,00149 | 0,00207 | 0,00262 |
| 540,62035 | 0,00091 | 0,00154 | 0,00134 | 0,00185 | 0,00237 |
| 540,65753 | 8e-04 | 0,00142 | 0,0012 | 0,00165 | 0,00214 |
| 540,69472 | 7e-04 | 0,0013 | 0,00107 | 0,00146 | 0,00193 |
| 540,7319 | 6e-04 | 0,00119 | 0,00095 | 0,00129 | 0,00173 |
| 540,76908 | 0,00052 | 0,0011 | 0,00084 | 0,00113 | 0,00155 |
| 540,80626 | 0,00044 | 0,00101 | 0,00075 | 0,00099 | 0,00139 |
| 540,84344 | 0,00038 | 0,00093 | 0,00066 | 0,00086 | 0,00124 |
| 540,88063 | 0,00032 | 0,00086 | 0,00058 | 0,00075 | 0,0011 |
| 540,91781 | 0,00027 | 8e-04 | 0,00051 | 0,00064 | 0,00098 |
| 540,95499 | 0,00022 | 0,00074 | 0,00045 | 0,00055 | 0,00087 |
| 540,99217 | 0,00018 | 0,00068 | 4e-04 | 0,00047 | 0,00077 |
| 541,02935 | 0,00015 | 0,00063 | 0,00035 | 4e-04 | 0,00068 |
| 541,06654 | 0,00012 | 0,00059 | 0,00031 | 0,00034 | 6e-04 |
| 541,10372 | 1e-04 | 0,00055 | 0,00027 | 0,00029 | 0,00053 |
| 541,1409 | 8e-05 | 0,00051 | 0,00024 | 0,00024 | 0,00046 |
| 541,17808 | 7e-05 | 0,00047 | 0,00021 | 2e-04 | 0,00041 |
| 541,21526 | 5e-05 | 0,00044 | 0,00019 | 0,00017 | 0,00036 |
| 541,25245 | 4e-05 | 0,00041 | 0,00017 | 0,00014 | 0,00031 |
| 541,28963 | 3e-05 | 0,00037 | 0,00015 | 0,00012 | 0,00027 |
| 541,32681 | 3e-05 | 0,00034 | 0,00013 | 9e-05 | 0,00024 |
| 541,36399 | 2e-05 | 0,00032 | 0,00011 | 8e-05 | 0,00021 |
| 541,40117 | 2e-05 | 0,00029 | 1e-04 | 6e-05 | 0,00018 |
| 541,43836 | 1e-05 | 0,00026 | 9e-05 | 5e-05 | 0,00016 |
| 541,47554 | 1e-05 | 0,00024 | 8e-05 | 4e-05 | 0,00014 |
| 541,51272 | 1e-05 | 0,00022 | 7e-05 | 3e-05 | 0,00012 |
| 541,5499 | 0 | 2e-04 | 6e-05 | 3e-05 | 1e-04 |
| 541,58708 | 0 | 0,00018 | 5e-05 | 2e-05 | 9e-05 |
| 541,62427 | 0 | 0,00016 | 5e-05 | 2e-05 | 7e-05 |
| 541,66145 | 0 | 0,00014 | 4e-05 | 1e-05 | 6e-05 |
| 541,69863 | 0 | 0,00012 | 3e-05 | 1e-05 | 5e-05 |
| 541,73581 | 0 | 0,00011 | 3e-05 | 1e-05 | 4e-05 |
| 541,77299 | 0 | 9e-05 | 3e-05 | 1e-05 | 4e-05 |
| 541,81018 | 0 | 8e-05 | 2e-05 | 1e-05 | 3e-05 |
| 541,84736 | 0 | 7e-05 | 2e-05 | 0 | 3e-05 |
| 541,88454 | 0 | 6e-05 | 2e-05 | 0 | 2e-05 |
| 541,92172 | 0 | 5e-05 | 1e-05 | 0 | 2e-05 |
| 541,9589 | 0 | 4e-05 | 1e-05 | 0 | 1e-05 |
| 541,99609 | 0 | 4e-05 | 1e-05 | 0 | 1e-05 |
| 542,03327 | 0 | 3e-05 | 1e-05 | 0 | 1e-05 |
| 542,07045 | 0 | 3e-05 | 1e-05 | 0 | 1e-05 |
| 542,10763 | 0 | 2e-05 | 0 | 0 | 1e-05 |
| 542,14481 | 0 | 2e-05 | 0 | 0 | 0 |
| 542,182 | 0 | 2e-05 | 0 | 0 | 0 |
| 542,21918 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,25636 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,29354 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,33072 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,36791 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00011 | 9e-05 | 2e-05 | 0 | 0 |
| 524,03718 | 0,00012 | 1e-04 | 2e-05 | 0 | 0 |
| 524,07436 | 0,00014 | 0,00012 | 2e-05 | 0 | 0 |
| 524,11155 | 0,00015 | 0,00013 | 3e-05 | 0 | 0 |
| 524,14873 | 0,00017 | 0,00015 | 3e-05 | 0 | 0 |
| 524,18591 | 0,00019 | 0,00017 | 4e-05 | 0 | 0 |
| 524,22309 | 2e-04 | 0,00019 | 5e-05 | 0 | 0 |
| 524,26027 | 0,00022 | 0,00021 | 5e-05 | 0 | 0 |
| 524,29746 | 0,00024 | 0,00023 | 6e-05 | 0 | 0 |
| 524,33464 | 0,00026 | 0,00026 | 7e-05 | 0 | 0 |
| 524,37182 | 0,00029 | 0,00028 | 8e-05 | 0 | 0 |
| 524,409 | 0,00031 | 0,00031 | 9e-05 | 0 | 0 |
| 524,44618 | 0,00033 | 0,00034 | 1e-04 | 0 | 0 |
| 524,48337 | 0,00036 | 0,00038 | 0,00012 | 0 | 0 |
| 524,52055 | 0,00038 | 0,00041 | 0,00013 | 0 | 0 |
| 524,55773 | 0,00041 | 0,00044 | 0,00015 | 0 | 0 |
| 524,59491 | 0,00044 | 0,00048 | 0,00017 | 1e-05 | 0 |
| 524,63209 | 0,00046 | 0,00052 | 0,00019 | 1e-05 | 0 |
| 524,66928 | 0,00049 | 0,00056 | 0,00021 | 1e-05 | 0 |
| 524,70646 | 0,00052 | 6e-04 | 0,00024 | 1e-05 | 1e-05 |
| 524,74364 | 0,00056 | 0,00064 | 0,00026 | 1e-05 | 1e-05 |
| 524,78082 | 0,00059 | 0,00069 | 0,00029 | 1e-05 | 1e-05 |
| 524,818 | 0,00062 | 0,00073 | 0,00032 | 2e-05 | 1e-05 |
| 524,85519 | 0,00066 | 0,00077 | 0,00035 | 2e-05 | 1e-05 |
| 524,89237 | 0,00069 | 0,00082 | 0,00038 | 2e-05 | 2e-05 |
| 524,92955 | 0,00073 | 0,00086 | 0,00042 | 3e-05 | 2e-05 |
| 524,96673 | 0,00077 | 0,00091 | 0,00045 | 4e-05 | 2e-05 |
| 525,00391 | 0,00081 | 0,00095 | 0,00049 | 4e-05 | 3e-05 |
| 525,0411 | 0,00086 | 0,001 | 0,00053 | 5e-05 | 3e-05 |
| 525,07828 | 9e-04 | 0,00104 | 0,00057 | 6e-05 | 4e-05 |
| 525,11546 | 0,00095 | 0,00108 | 0,00061 | 7e-05 | 4e-05 |
| 525,15264 | 0,001 | 0,00112 | 0,00066 | 8e-05 | 5e-05 |
| 525,18982 | 0,00105 | 0,00117 | 7e-04 | 9e-05 | 6e-05 |
| 525,22701 | 0,00111 | 0,00121 | 0,00075 | 1e-04 | 7e-05 |
| 525,26419 | 0,00116 | 0,00125 | 8e-04 | 0,00012 | 8e-05 |
| 525,30137 | 0,00122 | 0,00129 | 0,00085 | 0,00014 | 9e-05 |
| 525,33855 | 0,00128 | 0,00133 | 9e-04 | 0,00016 | 1e-04 |
| 525,37573 | 0,00135 | 0,00137 | 0,00095 | 0,00018 | 0,00011 |
| 525,41292 | 0,00142 | 0,00141 | 0,001 | 2e-04 | 0,00013 |
| 525,4501 | 0,00149 | 0,00145 | 0,00106 | 0,00022 | 0,00014 |
| 525,48728 | 0,00156 | 0,00149 | 0,00111 | 0,00025 | 0,00016 |
| 525,52446 | 0,00164 | 0,00153 | 0,00117 | 0,00028 | 0,00018 |
| 525,56164 | 0,00172 | 0,00157 | 0,00123 | 0,00031 | 2e-04 |
| 525,59883 | 0,0018 | 0,00162 | 0,00129 | 0,00035 | 0,00022 |
| 525,63601 | 0,00189 | 0,00166 | 0,00135 | 0,00038 | 0,00024 |
| 525,67319 | 0,00198 | 0,00171 | 0,00141 | 0,00042 | 0,00027 |
| 525,71037 | 0,00207 | 0,00177 | 0,00147 | 0,00046 | 0,00029 |
| 525,74755 | 0,00217 | 0,00183 | 0,00154 | 5e-04 | 0,00032 |
| 525,78474 | 0,00227 | 0,00189 | 0,00161 | 0,00055 | 0,00035 |
| 525,82192 | 0,00237 | 0,00196 | 0,00168 | 6e-04 | 0,00038 |
| 525,8591 | 0,00248 | 0,00204 | 0,00176 | 0,00064 | 0,00041 |
| 525,89628 | 0,0026 | 0,00212 | 0,00184 | 0,00069 | 0,00044 |
| 525,93346 | 0,00272 | 0,00221 | 0,00193 | 0,00075 | 0,00047 |
| 525,97065 | 0,00285 | 0,00232 | 0,00202 | 8e-04 | 0,00051 |
| 526,00783 | 0,00299 | 0,00243 | 0,00212 | 0,00086 | 0,00054 |
| 526,04501 | 0,00313 | 0,00256 | 0,00223 | 0,00091 | 0,00058 |
| 526,08219 | 0,00329 | 0,00271 | 0,00236 | 0,00097 | 0,00061 |
| 526,11937 | 0,00346 | 0,00287 | 0,0025 | 0,00103 | 0,00065 |
| 526,15656 | 0,00365 | 0,00305 | 0,00265 | 0,00109 | 0,00069 |
| 526,19374 | 0,00386 | 0,00325 | 0,00282 | 0,00116 | 0,00074 |
| 526,23092 | 0,00409 | 0,00348 | 0,00301 | 0,00122 | 0,00078 |
| 526,2681 | 0,00434 | 0,00374 | 0,00323 | 0,00129 | 0,00083 |
| 526,30528 | 0,00461 | 0,00402 | 0,00348 | 0,00136 | 0,00089 |
| 526,34247 | 0,00493 | 0,00434 | 0,00376 | 0,00144 | 0,00094 |
| 526,37965 | 0,00527 | 0,00469 | 0,00407 | 0,00152 | 0,00101 |
| 526,41683 | 0,00566 | 0,00509 | 0,00441 | 0,00161 | 0,00108 |
| 526,45401 | 0,00609 | 0,00554 | 0,00481 | 0,00171 | 0,00116 |
| 526,49119 | 0,00657 | 0,00603 | 0,00526 | 0,00182 | 0,00126 |
| 526,52838 | 0,0071 | 0,00657 | 0,00576 | 0,00194 | 0,00136 |
| 526,56556 | 0,0077 | 0,00717 | 0,00632 | 0,00208 | 0,00148 |
| 526,60274 | 0,00836 | 0,00785 | 0,00695 | 0,00223 | 0,00162 |
| 526,63992 | 0,0091 | 0,0086 | 0,00764 | 0,0024 | 0,00179 |
| 526,6771 | 0,0099 | 0,00942 | 0,00843 | 0,0026 | 0,00198 |
| 526,71429 | 0,01079 | 0,01031 | 0,00931 | 0,00283 | 0,0022 |
| 526,75147 | 0,01178 | 0,01129 | 0,01027 | 0,00309 | 0,00245 |
| 526,78865 | 0,01288 | 0,01238 | 0,01133 | 0,00339 | 0,00274 |
| 526,82583 | 0,01407 | 0,01358 | 0,01249 | 0,00374 | 0,00309 |
| 526,86301 | 0,01537 | 0,01487 | 0,0138 | 0,00414 | 0,00348 |
| 526,9002 | 0,01678 | 0,01627 | 0,01522 | 0,0046 | 0,00394 |
| 526,93738 | 0,01831 | 0,01779 | 0,01677 | 0,00513 | 0,00445 |
| 526,97456 | 0,01999 | 0,01943 | 0,01845 | 0,00572 | 0,00503 |
| 527,01174 | 0,0218 | 0,02122 | 0,02026 | 0,00639 | 0,00571 |
| 527,04892 | 0,02374 | 0,02314 | 0,02225 | 0,00716 | 0,00648 |
| 527,08611 | 0,02582 | 0,02519 | 0,02439 | 0,00804 | 0,00735 |
| 527,12329 | 0,02803 | 0,02737 | 0,02669 | 0,00903 | 0,00831 |
| 527,16047 | 0,03042 | 0,0297 | 0,02913 | 0,01013 | 0,00939 |
| 527,19765 | 0,03296 | 0,0322 | 0,03173 | 0,01134 | 0,0106 |
| 527,23483 | 0,03564 | 0,03484 | 0,03451 | 0,0127 | 0,01197 |
| 527,27202 | 0,03846 | 0,03761 | 0,03746 | 0,01423 | 0,01347 |
| 527,3092 | 0,04142 | 0,04052 | 0,04057 | 0,0159 | 0,01511 |
| 527,34638 | 0,04452 | 0,04357 | 0,04382 | 0,01773 | 0,01691 |
| 527,38356 | 0,04778 | 0,04677 | 0,04721 | 0,01973 | 0,01887 |
| 527,42074 | 0,05117 | 0,05009 | 0,05074 | 0,02188 | 0,02103 |
| 527,45793 | 0,05466 | 0,05353 | 0,05442 | 0,02425 | 0,02337 |
| 527,49511 | 0,05826 | 0,05706 | 0,05821 | 0,02681 | 0,02587 |
| 527,53229 | 0,06195 | 0,06069 | 0,06209 | 0,02953 | 0,02855 |
| 527,56947 | 0,06574 | 0,06441 | 0,06606 | 0,03243 | 0,0314 |
| 527,60665 | 0,06959 | 0,06821 | 0,0701 | 0,0355 | 0,03447 |
| 527,64384 | 0,07348 | 0,07204 | 0,0742 | 0,03877 | 0,0377 |
| 527,68102 | 0,0774 | 0,07591 | 0,07832 | 0,04221 | 0,0411 |
| 527,7182 | 0,08134 | 0,07979 | 0,08245 | 0,04581 | 0,04464 |
| 527,75538 | 0,08527 | 0,08367 | 0,08657 | 0,04954 | 0,04832 |
| 527,79256 | 0,08916 | 0,08752 | 0,09066 | 0,05339 | 0,05215 |
| 527,82975 | 0,093 | 0,09133 | 0,09469 | 0,05737 | 0,0561 |
| 527,86693 | 0,09677 | 0,09507 | 0,09862 | 0,06145 | 0,06014 |
| 527,90411 | 0,10045 | 0,09873 | 0,10246 | 0,06559 | 0,06425 |
| 527,94129 | 0,10404 | 0,1023 | 0,10618 | 0,06978 | 0,06841 |
| 527,97847 | 0,10748 | 0,10573 | 0,10976 | 0,074 | 0,0726 |
| 528,01566 | 0,11077 | 0,10902 | 0,11318 | 0,07822 | 0,07679 |
| 528,05284 | 0,11391 | 0,11216 | 0,11639 | 0,0824 | 0,08095 |
| 528,09002 | 0,11689 | 0,11514 | 0,11941 | 0,08652 | 0,08506 |
| 528,1272 | 0,11969 | 0,11796 | 0,12224 | 0,09056 | 0,08909 |
| 528,16438 | 0,12232 | 0,12058 | 0,12486 | 0,0945 | 0,09302 |
| 528,20157 | 0,12472 | 0,12299 | 0,12727 | 0,09831 | 0,0968 |
| 528,23875 | 0,12693 | 0,1252 | 0,1294 | 0,10194 | 0,1004 |
| 528,27593 | 0,12896 | 0,12723 | 0,1313 | 0,10537 | 0,10384 |
| 528,31311 | 0,13081 | 0,12907 | 0,13299 | 0,1086 | 0,10708 |
| 528,35029 | 0,13248 | 0,13072 | 0,13447 | 0,11163 | 0,11011 |
| 528,38748 | 0,13396 | 0,13214 | 0,13572 | 0,11443 | 0,11287 |
| 528,42466 | 0,13527 | 0,13339 | 0,13673 | 0,11695 | 0,11537 |
| 528,46184 | 0,13643 | 0,13447 | 0,13753 | 0,11919 | 0,11762 |
| 528,49902 | 0,13746 | 0,13539 | 0,13814 | 0,12117 | 0,11961 |
| 528,5362 | 0,13837 | 0,13617 | 0,13858 | 0,12291 | 0,12136 |
| 528,57339 | 0,13917 | 0,13679 | 0,13886 | 0,12439 | 0,12282 |
| 528,61057 | 0,13986 | 0,13728 | 0,13896 | 0,1256 | 0,12399 |
| 528,64775 | 0,14048 | 0,13767 | 0,13892 | 0,12652 | 0,12491 |
| 528,68493 | 0,14105 | 0,13797 | 0,13877 | 0,12721 | 0,12561 |
| 528,72211 | 0,14157 | 0,13819 | 0,13852 | 0,12769 | 0,12608 |
| 528,7593 | 0,14207 | 0,13834 | 0,13818 | 0,12796 | 0,12635 |
| 528,79648 | 0,14254 | 0,13843 | 0,13776 | 0,12805 | 0,12638 |
| 528,83366 | 0,14301 | 0,13849 | 0,13727 | 0,12792 | 0,12625 |
| 528,87084 | 0,14348 | 0,13852 | 0,13675 | 0,12765 | 0,12597 |
| 528,90802 | 0,14397 | 0,13854 | 0,13619 | 0,12726 | 0,12557 |
| 528,94521 | 0,14448 | 0,13855 | 0,13562 | 0,12677 | 0,12505 |
| 528,98239 | 0,14501 | 0,13856 | 0,13503 | 0,1262 | 0,12444 |
| 529,01957 | 0,14557 | 0,13858 | 0,13445 | 0,12555 | 0,12375 |
| 529,05675 | 0,14615 | 0,13861 | 0,13387 | 0,12486 | 0,12302 |
| 529,09393 | 0,14675 | 0,13865 | 0,13331 | 0,12416 | 0,12227 |
| 529,13112 | 0,14737 | 0,13871 | 0,13277 | 0,12345 | 0,12151 |
| 529,1683 | 0,14801 | 0,13879 | 0,13224 | 0,12276 | 0,12075 |
| 529,20548 | 0,14865 | 0,13888 | 0,13175 | 0,1221 | 0,12002 |
| 529,24266 | 0,14927 | 0,13898 | 0,13128 | 0,12149 | 0,11932 |
| 529,27984 | 0,14989 | 0,13908 | 0,13084 | 0,12093 | 0,11867 |
| 529,31703 | 0,15047 | 0,13919 | 0,13042 | 0,12043 | 0,11807 |
| 529,35421 | 0,15102 | 0,1393 | 0,13002 | 0,12 | 0,11753 |
| 529,39139 | 0,15151 | 0,13939 | 0,12964 | 0,11965 | 0,11707 |
| 529,42857 | 0,15193 | 0,13946 | 0,12927 | 0,11939 | 0,11668 |
| 529,46575 | 0,15227 | 0,13951 | 0,12892 | 0,11921 | 0,11635 |
| 529,50294 | 0,15252 | 0,13953 | 0,12857 | 0,11909 | 0,11609 |
| 529,54012 | 0,15268 | 0,13951 | 0,12822 | 0,11905 | 0,1159 |
| 529,5773 | 0,15273 | 0,13943 | 0,12786 | 0,11908 | 0,11578 |
| 529,61448 | 0,15265 | 0,13931 | 0,1275 | 0,11918 | 0,11572 |
| 529,65166 | 0,15243 | 0,13913 | 0,12712 | 0,11933 | 0,11571 |
| 529,68885 | 0,15208 | 0,13889 | 0,12672 | 0,11952 | 0,11574 |
| 529,72603 | 0,15161 | 0,13859 | 0,1263 | 0,11974 | 0,11581 |
| 529,76321 | 0,151 | 0,13821 | 0,12585 | 0,11999 | 0,11592 |
| 529,80039 | 0,15026 | 0,13776 | 0,12536 | 0,12025 | 0,11604 |
| 529,83757 | 0,14935 | 0,13724 | 0,12484 | 0,12051 | 0,11618 |
| 529,87476 | 0,14832 | 0,13665 | 0,12429 | 0,12076 | 0,11632 |
| 529,91194 | 0,14716 | 0,136 | 0,12369 | 0,12099 | 0,11645 |
| 529,94912 | 0,14589 | 0,13526 | 0,12306 | 0,12119 | 0,11658 |
| 529,9863 | 0,1445 | 0,13445 | 0,12238 | 0,12135 | 0,11667 |
| 530,02348 | 0,143 | 0,13357 | 0,12166 | 0,12145 | 0,11674 |
| 530,06067 | 0,1414 | 0,13264 | 0,12089 | 0,12149 | 0,11678 |
| 530,09785 | 0,13971 | 0,13164 | 0,12008 | 0,12147 | 0,11678 |
| 530,13503 | 0,13794 | 0,13058 | 0,11923 | 0,12138 | 0,11675 |
| 530,17221 | 0,13612 | 0,12945 | 0,11833 | 0,12123 | 0,11665 |
| 530,20939 | 0,13424 | 0,12828 | 0,11739 | 0,12097 | 0,11651 |
| 530,24658 | 0,1323 | 0,12705 | 0,11641 | 0,12064 | 0,11632 |
| 530,28376 | 0,13033 | 0,12578 | 0,11539 | 0,12024 | 0,11608 |
| 530,32094 | 0,12834 | 0,12447 | 0,11434 | 0,11975 | 0,11579 |
| 530,35812 | 0,12633 | 0,1231 | 0,11325 | 0,1192 | 0,11545 |
| 530,3953 | 0,12431 | 0,1217 | 0,11212 | 0,11856 | 0,11507 |
| 530,43249 | 0,12229 | 0,12026 | 0,11096 | 0,11785 | 0,11464 |
| 530,46967 | 0,12028 | 0,11879 | 0,10977 | 0,11708 | 0,11417 |
| 530,50685 | 0,11828 | 0,1173 | 0,10856 | 0,11625 | 0,11367 |
| 530,54403 | 0,1163 | 0,11577 | 0,10733 | 0,11538 | 0,11314 |
| 530,58121 | 0,11435 | 0,11421 | 0,10608 | 0,11445 | 0,11257 |
| 530,6184 | 0,11242 | 0,11263 | 0,10481 | 0,11348 | 0,11199 |
| 530,65558 | 0,11052 | 0,11104 | 0,10353 | 0,11248 | 0,11138 |
| 530,69276 | 0,10867 | 0,10943 | 0,10224 | 0,11145 | 0,11076 |
| 530,72994 | 0,10685 | 0,10781 | 0,10095 | 0,11041 | 0,11012 |
| 530,76712 | 0,10508 | 0,10618 | 0,09967 | 0,10935 | 0,10947 |
| 530,80431 | 0,10335 | 0,10455 | 0,09839 | 0,10827 | 0,10882 |
| 530,84149 | 0,10167 | 0,10292 | 0,09712 | 0,1072 | 0,10815 |
| 530,87867 | 0,10006 | 0,1013 | 0,09588 | 0,10612 | 0,10747 |
| 530,91585 | 0,0985 | 0,09969 | 0,09466 | 0,10505 | 0,10679 |
| 530,95303 | 0,097 | 0,09811 | 0,09347 | 0,10397 | 0,1061 |
| 530,99022 | 0,09556 | 0,09655 | 0,09232 | 0,10291 | 0,1054 |
| 531,0274 | 0,09418 | 0,09502 | 0,09122 | 0,10186 | 0,10468 |
| 531,06458 | 0,09289 | 0,09353 | 0,09016 | 0,10082 | 0,10395 |
| 531,10176 | 0,09167 | 0,09209 | 0,08916 | 0,09978 | 0,10321 |
| 531,13894 | 0,09053 | 0,09069 | 0,08822 | 0,09876 | 0,10246 |
| 531,17613 | 0,08947 | 0,08937 | 0,08736 | 0,09775 | 0,10168 |
| 531,21331 | 0,08849 | 0,0881 | 0,08657 | 0,09676 | 0,10088 |
| 531,25049 | 0,0876 | 0,0869 | 0,08585 | 0,09578 | 0,10007 |
| 531,28767 | 0,08681 | 0,08577 | 0,0852 | 0,09482 | 0,09924 |
| 531,32485 | 0,08611 | 0,08472 | 0,08464 | 0,09387 | 0,09839 |
| 531,36204 | 0,0855 | 0,08376 | 0,08416 | 0,09295 | 0,09752 |
| 531,39922 | 0,08498 | 0,08289 | 0,08378 | 0,09204 | 0,09663 |
| 531,4364 | 0,08455 | 0,0821 | 0,08348 | 0,09116 | 0,09573 |
| 531,47358 | 0,08422 | 0,08139 | 0,08326 | 0,09031 | 0,09483 |
| 531,51076 | 0,08399 | 0,08077 | 0,08311 | 0,08949 | 0,09392 |
| 531,54795 | 0,08384 | 0,08025 | 0,08305 | 0,0887 | 0,09301 |
| 531,58513 | 0,08377 | 0,07982 | 0,08307 | 0,08795 | 0,09212 |
| 531,62231 | 0,08378 | 0,07947 | 0,08316 | 0,08725 | 0,09123 |
| 531,65949 | 0,08386 | 0,0792 | 0,08331 | 0,0866 | 0,09037 |
| 531,69667 | 0,08402 | 0,07901 | 0,08352 | 0,08599 | 0,08954 |
| 531,73386 | 0,08424 | 0,07889 | 0,08378 | 0,08544 | 0,08874 |
| 531,77104 | 0,08452 | 0,07885 | 0,08409 | 0,08497 | 0,08799 |
| 531,80822 | 0,08484 | 0,07887 | 0,08444 | 0,08456 | 0,08729 |
| 531,8454 | 0,0852 | 0,07895 | 0,08481 | 0,08422 | 0,08664 |
| 531,88258 | 0,08559 | 0,07907 | 0,0852 | 0,08395 | 0,08606 |
| 531,91977 | 0,08602 | 0,07924 | 0,08561 | 0,08375 | 0,08554 |
| 531,95695 | 0,08645 | 0,07946 | 0,08603 | 0,08363 | 0,0851 |
| 531,99413 | 0,0869 | 0,0797 | 0,08644 | 0,0836 | 0,08474 |
| 532,03131 | 0,08734 | 0,07997 | 0,08684 | 0,08364 | 0,08446 |
| 532,06849 | 0,08778 | 0,08025 | 0,08723 | 0,08375 | 0,08424 |
| 532,10568 | 0,08821 | 0,08055 | 0,0876 | 0,08393 | 0,08411 |
| 532,14286 | 0,08862 | 0,08086 | 0,08794 | 0,08418 | 0,08405 |
| 532,18004 | 0,089 | 0,08117 | 0,08824 | 0,0845 | 0,08408 |
| 532,21722 | 0,08936 | 0,08147 | 0,08851 | 0,08488 | 0,08417 |
| 532,2544 | 0,08969 | 0,08177 | 0,08875 | 0,08531 | 0,08432 |
| 532,29159 | 0,08998 | 0,08205 | 0,08895 | 0,08578 | 0,08453 |
| 532,32877 | 0,09023 | 0,08232 | 0,0891 | 0,08629 | 0,0848 |
| 532,36595 | 0,09045 | 0,08258 | 0,08921 | 0,08684 | 0,08511 |
| 532,40313 | 0,09062 | 0,08281 | 0,08928 | 0,0874 | 0,08546 |
| 532,44031 | 0,09076 | 0,08302 | 0,08931 | 0,08797 | 0,08584 |
| 532,4775 | 0,09087 | 0,08322 | 0,08931 | 0,08854 | 0,08624 |
| 532,51468 | 0,09093 | 0,08339 | 0,08927 | 0,08911 | 0,08665 |
| 532,55186 | 0,09095 | 0,08353 | 0,08919 | 0,08965 | 0,08706 |
| 532,58904 | 0,09095 | 0,08366 | 0,08908 | 0,09018 | 0,08748 |
| 532,62622 | 0,09092 | 0,08376 | 0,08895 | 0,09067 | 0,08788 |
| 532,66341 | 0,09086 | 0,08384 | 0,0888 | 0,09113 | 0,08826 |
| 532,70059 | 0,09078 | 0,08391 | 0,08862 | 0,09154 | 0,08862 |
| 532,73777 | 0,09068 | 0,08395 | 0,08843 | 0,09191 | 0,08895 |
| 532,77495 | 0,09056 | 0,08398 | 0,08823 | 0,09221 | 0,08924 |
| 532,81213 | 0,09042 | 0,08399 | 0,08801 | 0,09246 | 0,0895 |
| 532,84932 | 0,09028 | 0,08399 | 0,08779 | 0,09265 | 0,08972 |
| 532,8865 | 0,09012 | 0,08398 | 0,08756 | 0,09278 | 0,08989 |
| 532,92368 | 0,08995 | 0,08395 | 0,08733 | 0,09285 | 0,09003 |
| 532,96086 | 0,08978 | 0,08391 | 0,08709 | 0,09286 | 0,09011 |
| 532,99804 | 0,0896 | 0,08385 | 0,08685 | 0,0928 | 0,09015 |
| 533,03523 | 0,08942 | 0,08379 | 0,08661 | 0,0927 | 0,09016 |
| 533,07241 | 0,08922 | 0,08371 | 0,08636 | 0,09254 | 0,09012 |
| 533,10959 | 0,08902 | 0,08362 | 0,08611 | 0,09234 | 0,09004 |
| 533,14677 | 0,08881 | 0,08352 | 0,08585 | 0,09208 | 0,08992 |
| 533,18395 | 0,08858 | 0,0834 | 0,08558 | 0,09179 | 0,08977 |
| 533,22114 | 0,08834 | 0,08327 | 0,0853 | 0,09146 | 0,08959 |
| 533,25832 | 0,08808 | 0,08312 | 0,08501 | 0,0911 | 0,08938 |
| 533,2955 | 0,08781 | 0,08295 | 0,0847 | 0,09071 | 0,08915 |
| 533,33268 | 0,0875 | 0,08277 | 0,08437 | 0,0903 | 0,08888 |
| 533,36986 | 0,08717 | 0,08256 | 0,08401 | 0,08987 | 0,08859 |
| 533,40705 | 0,08681 | 0,08234 | 0,08363 | 0,08943 | 0,08828 |
| 533,44423 | 0,08642 | 0,08209 | 0,08322 | 0,08897 | 0,08795 |
| 533,48141 | 0,08599 | 0,08182 | 0,08278 | 0,08851 | 0,0876 |
| 533,51859 | 0,08553 | 0,08153 | 0,0823 | 0,08804 | 0,08723 |
| 533,55577 | 0,08502 | 0,08121 | 0,08179 | 0,08756 | 0,08684 |
| 533,59295 | 0,08448 | 0,08086 | 0,08124 | 0,08708 | 0,08643 |
| 533,63014 | 0,0839 | 0,0805 | 0,08066 | 0,08659 | 0,086 |
| 533,66732 | 0,08329 | 0,08011 | 0,08005 | 0,0861 | 0,08555 |
| 533,7045 | 0,08265 | 0,07971 | 0,0794 | 0,08561 | 0,08508 |
| 533,74168 | 0,08196 | 0,07928 | 0,07872 | 0,08511 | 0,08458 |
| 533,77886 | 0,08126 | 0,07884 | 0,07802 | 0,08461 | 0,08406 |
| 533,81605 | 0,08053 | 0,07839 | 0,07729 | 0,0841 | 0,08351 |
| 533,85323 | 0,07979 | 0,07793 | 0,07654 | 0,08358 | 0,08295 |
| 533,89041 | 0,07903 | 0,07746 | 0,07578 | 0,08305 | 0,08236 |
| 533,92759 | 0,07827 | 0,077 | 0,075 | 0,08251 | 0,08174 |
| 533,96477 | 0,07751 | 0,07653 | 0,07423 | 0,08196 | 0,08109 |
| 534,00196 | 0,07675 | 0,07607 | 0,07345 | 0,08139 | 0,08043 |
| 534,03914 | 0,076 | 0,07562 | 0,07268 | 0,08082 | 0,07974 |
| 534,07632 | 0,07527 | 0,07518 | 0,07193 | 0,08023 | 0,07904 |
| 534,1135 | 0,07456 | 0,07476 | 0,07119 | 0,07963 | 0,07832 |
| 534,15068 | 0,07388 | 0,07436 | 0,07048 | 0,07902 | 0,07758 |
| 534,18787 | 0,07323 | 0,07399 | 0,0698 | 0,0784 | 0,07684 |
| 534,22505 | 0,07261 | 0,07363 | 0,06914 | 0,07778 | 0,07609 |
| 534,26223 | 0,07202 | 0,0733 | 0,06852 | 0,07714 | 0,07534 |
| 534,29941 | 0,07147 | 0,073 | 0,06793 | 0,0765 | 0,07459 |
| 534,33659 | 0,07095 | 0,07273 | 0,06739 | 0,07586 | 0,07385 |
| 534,37378 | 0,07046 | 0,07248 | 0,06689 | 0,07522 | 0,07312 |
| 534,41096 | 0,07001 | 0,07225 | 0,06643 | 0,07459 | 0,07241 |
| 534,44814 | 0,06958 | 0,07204 | 0,066 | 0,07396 | 0,07172 |
| 534,48532 | 0,06917 | 0,07185 | 0,0656 | 0,07334 | 0,07105 |
| 534,5225 | 0,06879 | 0,07168 | 0,06525 | 0,07273 | 0,07042 |
| 534,55969 | 0,06842 | 0,07151 | 0,06492 | 0,07213 | 0,06983 |
| 534,59687 | 0,06806 | 0,07135 | 0,06463 | 0,07155 | 0,06928 |
| 534,63405 | 0,0677 | 0,07119 | 0,06435 | 0,07098 | 0,06876 |
| 534,67123 | 0,06734 | 0,07102 | 0,06409 | 0,07043 | 0,06829 |
| 534,70841 | 0,06698 | 0,07085 | 0,06385 | 0,06991 | 0,06786 |
| 534,7456 | 0,0666 | 0,07065 | 0,06361 | 0,0694 | 0,06749 |
| 534,78278 | 0,0662 | 0,07044 | 0,06338 | 0,06891 | 0,06716 |
| 534,81996 | 0,06577 | 0,07021 | 0,06315 | 0,06844 | 0,06687 |
| 534,85714 | 0,06533 | 0,06994 | 0,06291 | 0,06799 | 0,06663 |
| 534,89432 | 0,06485 | 0,06965 | 0,06266 | 0,06755 | 0,06643 |
| 534,93151 | 0,06435 | 0,06931 | 0,0624 | 0,06713 | 0,06628 |
| 534,96869 | 0,0638 | 0,06894 | 0,06213 | 0,06673 | 0,06617 |
| 535,00587 | 0,06322 | 0,06853 | 0,06183 | 0,06633 | 0,06609 |
| 535,04305 | 0,06261 | 0,06809 | 0,06152 | 0,06595 | 0,06603 |
| 535,08023 | 0,06196 | 0,06761 | 0,06118 | 0,06557 | 0,06601 |
| 535,11742 | 0,06128 | 0,06708 | 0,06083 | 0,0652 | 0,06601 |
| 535,1546 | 0,06058 | 0,06652 | 0,06045 | 0,06483 | 0,06602 |
| 535,19178 | 0,05984 | 0,06592 | 0,06005 | 0,06447 | 0,06605 |
| 535,22896 | 0,05908 | 0,06529 | 0,05963 | 0,0641 | 0,06608 |
| 535,26614 | 0,0583 | 0,06464 | 0,05919 | 0,06373 | 0,06612 |
| 535,30333 | 0,05751 | 0,06396 | 0,05874 | 0,06336 | 0,06616 |
| 535,34051 | 0,05671 | 0,06327 | 0,05827 | 0,06299 | 0,06619 |
| 535,37769 | 0,05591 | 0,06256 | 0,0578 | 0,06261 | 0,06622 |
| 535,41487 | 0,0551 | 0,06184 | 0,05732 | 0,06222 | 0,06623 |
| 535,45205 | 0,0543 | 0,06111 | 0,05684 | 0,06183 | 0,06623 |
| 535,48924 | 0,05351 | 0,06039 | 0,05636 | 0,06143 | 0,06621 |
| 535,52642 | 0,05274 | 0,05968 | 0,05588 | 0,06104 | 0,06617 |
| 535,5636 | 0,05198 | 0,05897 | 0,0554 | 0,06063 | 0,0661 |
| 535,60078 | 0,05126 | 0,05828 | 0,05494 | 0,06023 | 0,06602 |
| 535,63796 | 0,05055 | 0,05761 | 0,05449 | 0,05983 | 0,06592 |
| 535,67515 | 0,04988 | 0,05696 | 0,05405 | 0,05942 | 0,06579 |
| 535,71233 | 0,04924 | 0,05634 | 0,05363 | 0,05902 | 0,06563 |
| 535,74951 | 0,04864 | 0,05575 | 0,05322 | 0,05863 | 0,06545 |
| 535,78669 | 0,04808 | 0,05519 | 0,05283 | 0,05824 | 0,06525 |
| 535,82387 | 0,04756 | 0,05466 | 0,05246 | 0,05786 | 0,06503 |
| 535,86106 | 0,04707 | 0,05415 | 0,05211 | 0,05748 | 0,06479 |
| 535,89824 | 0,04663 | 0,05368 | 0,05178 | 0,05712 | 0,06452 |
| 535,93542 | 0,04622 | 0,05324 | 0,05146 | 0,05678 | 0,06423 |
| 535,9726 | 0,04585 | 0,05283 | 0,05116 | 0,05644 | 0,06393 |
| 536,00978 | 0,04553 | 0,05245 | 0,05088 | 0,05612 | 0,06361 |
| 536,04697 | 0,04524 | 0,05209 | 0,05061 | 0,05581 | 0,06327 |
| 536,08415 | 0,04498 | 0,05176 | 0,05035 | 0,05552 | 0,06291 |
| 536,12133 | 0,04476 | 0,05145 | 0,05011 | 0,05524 | 0,06254 |
| 536,15851 | 0,04456 | 0,05115 | 0,04987 | 0,05497 | 0,06216 |
| 536,19569 | 0,0444 | 0,05087 | 0,04964 | 0,05472 | 0,06177 |
| 536,23288 | 0,04426 | 0,0506 | 0,04942 | 0,05447 | 0,06137 |
| 536,27006 | 0,04415 | 0,05033 | 0,04921 | 0,05425 | 0,06095 |
| 536,30724 | 0,04405 | 0,05008 | 0,049 | 0,05403 | 0,06053 |
| 536,34442 | 0,04397 | 0,04982 | 0,04879 | 0,05382 | 0,0601 |
| 536,3816 | 0,0439 | 0,04957 | 0,04859 | 0,05361 | 0,05966 |
| 536,41879 | 0,04384 | 0,04931 | 0,04839 | 0,05342 | 0,05922 |
| 536,45597 | 0,04379 | 0,04905 | 0,0482 | 0,05323 | 0,05878 |
| 536,49315 | 0,04375 | 0,04878 | 0,04801 | 0,05304 | 0,05833 |
| 536,53033 | 0,04371 | 0,04851 | 0,04782 | 0,05286 | 0,05789 |
| 536,56751 | 0,04367 | 0,04823 | 0,04765 | 0,05269 | 0,05744 |
| 536,6047 | 0,04363 | 0,04794 | 0,04748 | 0,05251 | 0,05701 |
| 536,64188 | 0,04359 | 0,04765 | 0,04731 | 0,05234 | 0,05658 |
| 536,67906 | 0,04354 | 0,04735 | 0,04716 | 0,05218 | 0,05615 |
| 536,71624 | 0,04348 | 0,04705 | 0,04703 | 0,05201 | 0,05575 |
| 536,75342 | 0,04342 | 0,04674 | 0,04691 | 0,05186 | 0,05535 |
| 536,79061 | 0,04335 | 0,04643 | 0,0468 | 0,0517 | 0,05497 |
| 536,82779 | 0,04327 | 0,04612 | 0,04671 | 0,05156 | 0,05461 |
| 536,86497 | 0,04318 | 0,04581 | 0,04664 | 0,05142 | 0,05427 |
| 536,90215 | 0,04308 | 0,0455 | 0,0466 | 0,05129 | 0,05396 |
| 536,93933 | 0,04297 | 0,0452 | 0,04658 | 0,05118 | 0,05367 |
| 536,97652 | 0,04285 | 0,0449 | 0,04657 | 0,05107 | 0,05341 |
| 537,0137 | 0,04272 | 0,04461 | 0,04659 | 0,05097 | 0,05318 |
| 537,05088 | 0,04258 | 0,04433 | 0,04663 | 0,0509 | 0,05297 |
| 537,08806 | 0,04242 | 0,04406 | 0,0467 | 0,05083 | 0,0528 |
| 537,12524 | 0,04226 | 0,0438 | 0,04679 | 0,05079 | 0,05265 |
| 537,16243 | 0,04209 | 0,04355 | 0,0469 | 0,05076 | 0,05254 |
| 537,19961 | 0,0419 | 0,04331 | 0,04702 | 0,05074 | 0,05245 |
| 537,23679 | 0,0417 | 0,04309 | 0,04716 | 0,05075 | 0,05239 |
| 537,27397 | 0,04148 | 0,04287 | 0,04732 | 0,05077 | 0,05236 |
| 537,31115 | 0,04126 | 0,04267 | 0,04748 | 0,05081 | 0,05236 |
| 537,34834 | 0,04101 | 0,04247 | 0,04766 | 0,05087 | 0,05238 |
| 537,38552 | 0,04076 | 0,04228 | 0,04783 | 0,05095 | 0,05242 |
| 537,4227 | 0,04048 | 0,0421 | 0,04801 | 0,05104 | 0,05247 |
| 537,45988 | 0,04019 | 0,04192 | 0,04818 | 0,05115 | 0,05254 |
| 537,49706 | 0,03988 | 0,04174 | 0,04834 | 0,05126 | 0,05263 |
| 537,53425 | 0,03955 | 0,04156 | 0,04849 | 0,05139 | 0,05272 |
| 537,57143 | 0,0392 | 0,04139 | 0,04863 | 0,05153 | 0,05281 |
| 537,60861 | 0,03883 | 0,04121 | 0,04875 | 0,05167 | 0,05291 |
| 537,64579 | 0,03843 | 0,04102 | 0,04884 | 0,05182 | 0,05301 |
| 537,68297 | 0,03802 | 0,04083 | 0,04892 | 0,05197 | 0,05309 |
| 537,72016 | 0,03759 | 0,04063 | 0,04896 | 0,05212 | 0,05317 |
| 537,75734 | 0,03714 | 0,04043 | 0,04898 | 0,05226 | 0,05324 |
| 537,79452 | 0,03667 | 0,04022 | 0,04898 | 0,0524 | 0,05329 |
| 537,8317 | 0,03619 | 0,04 | 0,04894 | 0,05253 | 0,05333 |
| 537,86888 | 0,03569 | 0,03977 | 0,04888 | 0,05265 | 0,05335 |
| 537,90607 | 0,03519 | 0,03954 | 0,04878 | 0,05275 | 0,05334 |
| 537,94325 | 0,03467 | 0,0393 | 0,04866 | 0,05283 | 0,05331 |
| 537,98043 | 0,03415 | 0,03905 | 0,04851 | 0,0529 | 0,05325 |
| 538,01761 | 0,03363 | 0,0388 | 0,04833 | 0,05295 | 0,05318 |
| 538,05479 | 0,0331 | 0,03855 | 0,04813 | 0,05298 | 0,05307 |
| 538,09198 | 0,03258 | 0,03829 | 0,0479 | 0,05298 | 0,05293 |
| 538,12916 | 0,03207 | 0,03803 | 0,04766 | 0,05295 | 0,05277 |
| 538,16634 | 0,03156 | 0,03777 | 0,04739 | 0,05291 | 0,05258 |
| 538,20352 | 0,03107 | 0,03751 | 0,04711 | 0,05283 | 0,05237 |
| 538,2407 | 0,03059 | 0,03725 | 0,04682 | 0,05273 | 0,05213 |
| 538,27789 | 0,03013 | 0,03699 | 0,0465 | 0,05259 | 0,05186 |
| 538,31507 | 0,02969 | 0,03673 | 0,04618 | 0,05243 | 0,05157 |
| 538,35225 | 0,02926 | 0,03648 | 0,04584 | 0,05225 | 0,05125 |
| 538,38943 | 0,02885 | 0,03622 | 0,04549 | 0,05204 | 0,05092 |
| 538,42661 | 0,02846 | 0,03597 | 0,04513 | 0,05179 | 0,05057 |
| 538,4638 | 0,0281 | 0,03571 | 0,04475 | 0,05152 | 0,05019 |
| 538,50098 | 0,02775 | 0,03545 | 0,04437 | 0,05123 | 0,0498 |
| 538,53816 | 0,02742 | 0,03519 | 0,04397 | 0,05091 | 0,04939 |
| 538,57534 | 0,0271 | 0,03493 | 0,04356 | 0,05057 | 0,04898 |
| 538,61252 | 0,0268 | 0,03466 | 0,04314 | 0,0502 | 0,04854 |
| 538,64971 | 0,02652 | 0,03438 | 0,04269 | 0,04981 | 0,0481 |
| 538,68689 | 0,02624 | 0,03409 | 0,04224 | 0,0494 | 0,04764 |
| 538,72407 | 0,02598 | 0,03379 | 0,04176 | 0,04897 | 0,04718 |
| 538,76125 | 0,02572 | 0,03348 | 0,04127 | 0,04852 | 0,04671 |
| 538,79843 | 0,02547 | 0,03316 | 0,04076 | 0,04804 | 0,04622 |
| 538,83562 | 0,02522 | 0,03282 | 0,04022 | 0,04755 | 0,04573 |
| 538,8728 | 0,02497 | 0,03247 | 0,03967 | 0,04704 | 0,04523 |
| 538,90998 | 0,02473 | 0,0321 | 0,03909 | 0,04651 | 0,04473 |
| 538,94716 | 0,02448 | 0,03171 | 0,0385 | 0,04597 | 0,04421 |
| 538,98434 | 0,02424 | 0,03132 | 0,03789 | 0,04541 | 0,04369 |
| 539,02153 | 0,02399 | 0,03091 | 0,03726 | 0,04483 | 0,04316 |
| 539,05871 | 0,02374 | 0,03048 | 0,03661 | 0,04423 | 0,04262 |
| 539,09589 | 0,02349 | 0,03005 | 0,03594 | 0,04363 | 0,04207 |
| 539,13307 | 0,02324 | 0,0296 | 0,03526 | 0,04301 | 0,04152 |
| 539,17025 | 0,02298 | 0,02915 | 0,03457 | 0,04238 | 0,04095 |
| 539,20744 | 0,02272 | 0,02868 | 0,03387 | 0,04173 | 0,04038 |
| 539,24462 | 0,02246 | 0,02822 | 0,03317 | 0,04108 | 0,0398 |
| 539,2818 | 0,0222 | 0,02775 | 0,03246 | 0,04042 | 0,03922 |
| 539,31898 | 0,02194 | 0,02728 | 0,03175 | 0,03975 | 0,03862 |
| 539,35616 | 0,02167 | 0,0268 | 0,03104 | 0,03907 | 0,03802 |
| 539,39335 | 0,0214 | 0,02633 | 0,03034 | 0,0384 | 0,03742 |
| 539,43053 | 0,02113 | 0,02586 | 0,02964 | 0,03772 | 0,03681 |
| 539,46771 | 0,02086 | 0,0254 | 0,02895 | 0,03703 | 0,0362 |
| 539,50489 | 0,02059 | 0,02493 | 0,02827 | 0,03635 | 0,03558 |
| 539,54207 | 0,0203 | 0,02448 | 0,0276 | 0,03567 | 0,03496 |
| 539,57926 | 0,02002 | 0,02402 | 0,02694 | 0,035 | 0,03434 |
| 539,61644 | 0,01972 | 0,02357 | 0,02629 | 0,03432 | 0,03372 |
| 539,65362 | 0,01942 | 0,02312 | 0,02566 | 0,03366 | 0,03311 |
| 539,6908 | 0,0191 | 0,02267 | 0,02504 | 0,03299 | 0,03249 |
| 539,72798 | 0,01878 | 0,02222 | 0,02443 | 0,03233 | 0,03187 |
| 539,76517 | 0,01844 | 0,02178 | 0,02383 | 0,03168 | 0,03125 |
| 539,80235 | 0,01808 | 0,02133 | 0,02324 | 0,03103 | 0,03064 |
| 539,83953 | 0,01771 | 0,02087 | 0,02266 | 0,03039 | 0,03003 |
| 539,87671 | 0,01732 | 0,02042 | 0,02208 | 0,02975 | 0,02941 |
| 539,91389 | 0,01692 | 0,01995 | 0,02152 | 0,02911 | 0,0288 |
| 539,95108 | 0,01649 | 0,01948 | 0,02095 | 0,02847 | 0,02818 |
| 539,98826 | 0,01604 | 0,019 | 0,02039 | 0,02784 | 0,02757 |
| 540,02544 | 0,01558 | 0,01851 | 0,01983 | 0,0272 | 0,02695 |
| 540,06262 | 0,01509 | 0,01801 | 0,01926 | 0,02655 | 0,02632 |
| 540,0998 | 0,01459 | 0,01749 | 0,0187 | 0,02591 | 0,02569 |
| 540,13699 | 0,01407 | 0,01697 | 0,01813 | 0,02525 | 0,02505 |
| 540,17417 | 0,01354 | 0,01644 | 0,01755 | 0,0246 | 0,02441 |
| 540,21135 | 0,01299 | 0,0159 | 0,01698 | 0,02393 | 0,02376 |
| 540,24853 | 0,01243 | 0,01535 | 0,01639 | 0,02325 | 0,0231 |
| 540,28571 | 0,01187 | 0,01478 | 0,01581 | 0,02256 | 0,02243 |
| 540,3229 | 0,01129 | 0,01422 | 0,01521 | 0,02186 | 0,02175 |
| 540,36008 | 0,01072 | 0,01365 | 0,01462 | 0,02116 | 0,02106 |
| 540,39726 | 0,01015 | 0,01307 | 0,01402 | 0,02044 | 0,02036 |
| 540,43444 | 0,00957 | 0,0125 | 0,01342 | 0,01971 | 0,01965 |
| 540,47162 | 0,00901 | 0,01193 | 0,01282 | 0,01897 | 0,01894 |
| 540,50881 | 0,00845 | 0,01136 | 0,01222 | 0,01823 | 0,01822 |
| 540,54599 | 0,00791 | 0,01079 | 0,01163 | 0,01749 | 0,0175 |
| 540,58317 | 0,00738 | 0,01024 | 0,01104 | 0,01674 | 0,01678 |
| 540,62035 | 0,00687 | 0,00969 | 0,01046 | 0,01599 | 0,01606 |
| 540,65753 | 0,00637 | 0,00916 | 0,00988 | 0,01524 | 0,01534 |
| 540,69472 | 0,0059 | 0,00864 | 0,00932 | 0,01449 | 0,01462 |
| 540,7319 | 0,00545 | 0,00814 | 0,00877 | 0,01375 | 0,01391 |
| 540,76908 | 0,00502 | 0,00766 | 0,00823 | 0,01302 | 0,01322 |
| 540,80626 | 0,00462 | 0,00719 | 0,00771 | 0,0123 | 0,01253 |
| 540,84344 | 0,00424 | 0,00675 | 0,00721 | 0,0116 | 0,01186 |
| 540,88063 | 0,00389 | 0,00633 | 0,00673 | 0,01091 | 0,01121 |
| 540,91781 | 0,00356 | 0,00593 | 0,00626 | 0,01024 | 0,01057 |
| 540,95499 | 0,00326 | 0,00555 | 0,00582 | 0,00959 | 0,00996 |
| 540,99217 | 0,00299 | 0,00519 | 0,0054 | 0,00897 | 0,00936 |
| 541,02935 | 0,00273 | 0,00485 | 0,005 | 0,00837 | 0,00879 |
| 541,06654 | 0,0025 | 0,00454 | 0,00462 | 0,00779 | 0,00825 |
| 541,10372 | 0,00229 | 0,00424 | 0,00426 | 0,00724 | 0,00773 |
| 541,1409 | 0,0021 | 0,00397 | 0,00392 | 0,00671 | 0,00724 |
| 541,17808 | 0,00193 | 0,00371 | 0,00361 | 0,00622 | 0,00677 |
| 541,21526 | 0,00178 | 0,00348 | 0,00332 | 0,00576 | 0,00634 |
| 541,25245 | 0,00164 | 0,00326 | 0,00304 | 0,00532 | 0,00593 |
| 541,28963 | 0,00151 | 0,00306 | 0,00279 | 0,00491 | 0,00554 |
| 541,32681 | 0,0014 | 0,00287 | 0,00255 | 0,00453 | 0,00518 |
| 541,36399 | 0,0013 | 0,0027 | 0,00233 | 0,00418 | 0,00484 |
| 541,40117 | 0,00121 | 0,00253 | 0,00213 | 0,00385 | 0,00453 |
| 541,43836 | 0,00113 | 0,00238 | 0,00195 | 0,00355 | 0,00424 |
| 541,47554 | 0,00106 | 0,00225 | 0,00178 | 0,00327 | 0,00397 |
| 541,51272 | 0,00099 | 0,00212 | 0,00162 | 0,00301 | 0,00372 |
| 541,5499 | 0,00093 | 0,00199 | 0,00148 | 0,00278 | 0,00349 |
| 541,58708 | 0,00087 | 0,00188 | 0,00135 | 0,00257 | 0,00327 |
| 541,62427 | 0,00082 | 0,00177 | 0,00123 | 0,00237 | 0,00307 |
| 541,66145 | 0,00077 | 0,00167 | 0,00112 | 0,00219 | 0,00289 |
| 541,69863 | 0,00073 | 0,00157 | 0,00102 | 0,00203 | 0,00272 |
| 541,73581 | 0,00068 | 0,00148 | 0,00092 | 0,00188 | 0,00256 |
| 541,77299 | 0,00064 | 0,00139 | 0,00084 | 0,00175 | 0,00241 |
| 541,81018 | 6e-04 | 0,0013 | 0,00076 | 0,00163 | 0,00226 |
| 541,84736 | 0,00056 | 0,00122 | 0,00069 | 0,00152 | 0,00213 |
| 541,88454 | 0,00052 | 0,00114 | 0,00063 | 0,00142 | 0,00201 |
| 541,92172 | 0,00049 | 0,00107 | 0,00057 | 0,00132 | 0,00189 |
| 541,9589 | 0,00045 | 0,001 | 0,00052 | 0,00124 | 0,00177 |
| 541,99609 | 0,00042 | 0,00093 | 0,00047 | 0,00116 | 0,00166 |
| 542,03327 | 0,00039 | 0,00086 | 0,00042 | 0,00109 | 0,00156 |
| 542,07045 | 0,00036 | 8e-04 | 0,00038 | 0,00102 | 0,00146 |
| 542,10763 | 0,00033 | 0,00074 | 0,00034 | 0,00096 | 0,00136 |
| 542,14481 | 3e-04 | 0,00068 | 0,00031 | 9e-04 | 0,00127 |
| 542,182 | 0,00027 | 0,00062 | 0,00028 | 0,00084 | 0,00118 |
| 542,21918 | 0,00025 | 0,00057 | 0,00025 | 0,00079 | 0,0011 |
| 542,25636 | 0,00022 | 0,00052 | 0,00022 | 0,00074 | 0,00102 |
| 542,29354 | 2e-04 | 0,00047 | 2e-04 | 0,00069 | 0,00094 |
| 542,33072 | 0,00018 | 0,00043 | 0,00018 | 0,00065 | 0,00087 |
| 542,36791 | 0,00016 | 0,00039 | 0,00016 | 0,00061 | 8e-04 |
| 542,40509 | 0,00014 | 0,00035 | 0,00014 | 0,00057 | 0,00073 |
| 542,44227 | 0,00013 | 0,00031 | 0,00013 | 0,00053 | 0,00067 |
| 542,47945 | 0,00011 | 0,00028 | 0,00011 | 0,00049 | 0,00061 |
| 542,51663 | 1e-04 | 0,00025 | 1e-04 | 0,00045 | 0,00055 |
| 542,55382 | 8e-05 | 0,00022 | 9e-05 | 0,00042 | 5e-04 |
| 542,591 | 7e-05 | 0,00019 | 8e-05 | 0,00039 | 0,00045 |
| 542,62818 | 6e-05 | 0,00017 | 7e-05 | 0,00036 | 4e-04 |
| 542,66536 | 5e-05 | 0,00015 | 6e-05 | 0,00033 | 0,00036 |
| 542,70254 | 5e-05 | 0,00013 | 5e-05 | 3e-04 | 0,00032 |
| 542,73973 | 4e-05 | 0,00011 | 4e-05 | 0,00028 | 0,00028 |
| 542,77691 | 3e-05 | 1e-04 | 4e-05 | 0,00025 | 0,00025 |
| 542,81409 | 3e-05 | 8e-05 | 3e-05 | 0,00023 | 0,00022 |
| 542,85127 | 2e-05 | 7e-05 | 3e-05 | 0,00021 | 0,00019 |
| 542,88845 | 2e-05 | 6e-05 | 2e-05 | 0,00019 | 0,00017 |
| 542,92564 | 2e-05 | 5e-05 | 2e-05 | 0,00017 | 0,00015 |
| 542,96282 | 1e-05 | 5e-05 | 2e-05 | 0,00015 | 0,00013 |
| 543 | 1e-05 | 4e-05 | 1e-05 | 0,00014 | 0,00011 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00109 | 0,00173 | 0,00144 | 0,00042 | 0,00056 |
| 524,03718 | 0,00114 | 0,00179 | 0,0015 | 0,00045 | 0,00059 |
| 524,07436 | 0,00119 | 0,00184 | 0,00157 | 5e-04 | 0,00063 |
| 524,11155 | 0,00124 | 0,00189 | 0,00163 | 0,00054 | 0,00067 |
| 524,14873 | 0,00129 | 0,00195 | 0,0017 | 0,00058 | 0,00071 |
| 524,18591 | 0,00134 | 0,002 | 0,00177 | 0,00063 | 0,00074 |
| 524,22309 | 0,0014 | 0,00205 | 0,00184 | 0,00068 | 0,00078 |
| 524,26027 | 0,00145 | 0,0021 | 0,00192 | 0,00073 | 0,00081 |
| 524,29746 | 0,00152 | 0,00214 | 0,002 | 0,00078 | 0,00085 |
| 524,33464 | 0,00158 | 0,00219 | 0,00209 | 0,00083 | 0,00088 |
| 524,37182 | 0,00165 | 0,00224 | 0,00217 | 0,00088 | 0,00091 |
| 524,409 | 0,00172 | 0,00229 | 0,00227 | 0,00094 | 0,00094 |
| 524,44618 | 0,0018 | 0,00234 | 0,00236 | 0,00099 | 0,00097 |
| 524,48337 | 0,00188 | 0,00239 | 0,00246 | 0,00105 | 0,001 |
| 524,52055 | 0,00196 | 0,00244 | 0,00257 | 0,0011 | 0,00102 |
| 524,55773 | 0,00206 | 0,0025 | 0,00268 | 0,00116 | 0,00104 |
| 524,59491 | 0,00215 | 0,00255 | 0,00279 | 0,00121 | 0,00107 |
| 524,63209 | 0,00226 | 0,00261 | 0,00291 | 0,00127 | 0,00109 |
| 524,66928 | 0,00237 | 0,00268 | 0,00303 | 0,00133 | 0,0011 |
| 524,70646 | 0,00249 | 0,00275 | 0,00316 | 0,00139 | 0,00112 |
| 524,74364 | 0,00262 | 0,00282 | 0,00329 | 0,00145 | 0,00114 |
| 524,78082 | 0,00276 | 0,0029 | 0,00342 | 0,00151 | 0,00116 |
| 524,818 | 0,00291 | 0,00298 | 0,00355 | 0,00157 | 0,00117 |
| 524,85519 | 0,00306 | 0,00308 | 0,00369 | 0,00164 | 0,00119 |
| 524,89237 | 0,00323 | 0,00318 | 0,00384 | 0,00171 | 0,00121 |
| 524,92955 | 0,00341 | 0,00328 | 0,00398 | 0,00178 | 0,00123 |
| 524,96673 | 0,0036 | 0,0034 | 0,00414 | 0,00186 | 0,00126 |
| 525,00391 | 0,0038 | 0,00353 | 0,00429 | 0,00194 | 0,0013 |
| 525,0411 | 0,00402 | 0,00367 | 0,00445 | 0,00204 | 0,00134 |
| 525,07828 | 0,00425 | 0,00383 | 0,00462 | 0,00213 | 0,00138 |
| 525,11546 | 0,0045 | 0,004 | 0,00479 | 0,00224 | 0,00144 |
| 525,15264 | 0,00476 | 0,00418 | 0,00497 | 0,00236 | 0,00151 |
| 525,18982 | 0,00504 | 0,00438 | 0,00516 | 0,0025 | 0,0016 |
| 525,22701 | 0,00535 | 0,00461 | 0,00536 | 0,00264 | 0,0017 |
| 525,26419 | 0,00567 | 0,00485 | 0,00557 | 0,00281 | 0,00182 |
| 525,30137 | 0,00602 | 0,00511 | 0,00579 | 0,00299 | 0,00196 |
| 525,33855 | 0,00639 | 0,0054 | 0,00603 | 0,00319 | 0,00212 |
| 525,37573 | 0,00678 | 0,00572 | 0,00629 | 0,00341 | 0,0023 |
| 525,41292 | 0,0072 | 0,00606 | 0,00656 | 0,00366 | 0,00252 |
| 525,4501 | 0,00766 | 0,00643 | 0,00686 | 0,00393 | 0,00277 |
| 525,48728 | 0,00815 | 0,00684 | 0,00717 | 0,00422 | 0,00305 |
| 525,52446 | 0,00867 | 0,00728 | 0,00752 | 0,00454 | 0,00336 |
| 525,56164 | 0,00922 | 0,00776 | 0,00789 | 0,0049 | 0,00371 |
| 525,59883 | 0,0098 | 0,00827 | 0,00829 | 0,00528 | 0,0041 |
| 525,63601 | 0,01043 | 0,00883 | 0,00873 | 0,0057 | 0,00453 |
| 525,67319 | 0,0111 | 0,00942 | 0,00919 | 0,00615 | 0,005 |
| 525,71037 | 0,0118 | 0,01005 | 0,00969 | 0,00663 | 0,00552 |
| 525,74755 | 0,01255 | 0,01073 | 0,01024 | 0,00714 | 0,00607 |
| 525,78474 | 0,01333 | 0,01146 | 0,01082 | 0,00769 | 0,00667 |
| 525,82192 | 0,01416 | 0,01223 | 0,01144 | 0,00828 | 0,00732 |
| 525,8591 | 0,01503 | 0,01304 | 0,01209 | 0,0089 | 0,00801 |
| 525,89628 | 0,01595 | 0,0139 | 0,01279 | 0,00955 | 0,00875 |
| 525,93346 | 0,0169 | 0,0148 | 0,01353 | 0,01023 | 0,00953 |
| 525,97065 | 0,01789 | 0,01576 | 0,01431 | 0,01094 | 0,01034 |
| 526,00783 | 0,01892 | 0,01676 | 0,01514 | 0,01169 | 0,0112 |
| 526,04501 | 0,01998 | 0,01779 | 0,016 | 0,01246 | 0,01209 |
| 526,08219 | 0,02108 | 0,01887 | 0,01689 | 0,01326 | 0,01303 |
| 526,11937 | 0,02221 | 0,01999 | 0,01782 | 0,01408 | 0,01399 |
| 526,15656 | 0,02337 | 0,02114 | 0,01878 | 0,01493 | 0,01498 |
| 526,19374 | 0,02455 | 0,02234 | 0,01978 | 0,0158 | 0,01599 |
| 526,23092 | 0,02575 | 0,02356 | 0,0208 | 0,01669 | 0,01703 |
| 526,2681 | 0,02697 | 0,02481 | 0,02185 | 0,01759 | 0,01809 |
| 526,30528 | 0,0282 | 0,02609 | 0,02291 | 0,01852 | 0,01916 |
| 526,34247 | 0,02944 | 0,02738 | 0,024 | 0,01945 | 0,02024 |
| 526,37965 | 0,03069 | 0,02871 | 0,0251 | 0,0204 | 0,02134 |
| 526,41683 | 0,03194 | 0,03004 | 0,02621 | 0,02135 | 0,02243 |
| 526,45401 | 0,03319 | 0,03139 | 0,02733 | 0,02232 | 0,02353 |
| 526,49119 | 0,03444 | 0,03274 | 0,02845 | 0,02329 | 0,02462 |
| 526,52838 | 0,03568 | 0,03411 | 0,02958 | 0,02427 | 0,0257 |
| 526,56556 | 0,03691 | 0,03547 | 0,0307 | 0,02525 | 0,02678 |
| 526,60274 | 0,03812 | 0,03684 | 0,03183 | 0,02624 | 0,02784 |
| 526,63992 | 0,03933 | 0,0382 | 0,03295 | 0,02723 | 0,02888 |
| 526,6771 | 0,04052 | 0,03956 | 0,03407 | 0,02822 | 0,02991 |
| 526,71429 | 0,0417 | 0,04092 | 0,03519 | 0,02922 | 0,03092 |
| 526,75147 | 0,04286 | 0,04227 | 0,0363 | 0,03021 | 0,0319 |
| 526,78865 | 0,04402 | 0,04361 | 0,03742 | 0,03122 | 0,03287 |
| 526,82583 | 0,04516 | 0,04495 | 0,03853 | 0,03222 | 0,03381 |
| 526,86301 | 0,04629 | 0,04629 | 0,03965 | 0,03323 | 0,03472 |
| 526,9002 | 0,04742 | 0,04762 | 0,04077 | 0,03425 | 0,03561 |
| 526,93738 | 0,04854 | 0,04895 | 0,04191 | 0,03527 | 0,03647 |
| 526,97456 | 0,04967 | 0,05028 | 0,04305 | 0,0363 | 0,03732 |
| 527,01174 | 0,0508 | 0,05161 | 0,04421 | 0,03734 | 0,03815 |
| 527,04892 | 0,05193 | 0,05295 | 0,04539 | 0,03839 | 0,03896 |
| 527,08611 | 0,05307 | 0,05429 | 0,04659 | 0,03945 | 0,03975 |
| 527,12329 | 0,05423 | 0,05564 | 0,04782 | 0,04053 | 0,04053 |
| 527,16047 | 0,0554 | 0,057 | 0,04907 | 0,04162 | 0,04131 |
| 527,19765 | 0,05659 | 0,05838 | 0,05035 | 0,04273 | 0,04208 |
| 527,23483 | 0,0578 | 0,05977 | 0,05166 | 0,04385 | 0,04286 |
| 527,27202 | 0,05902 | 0,06117 | 0,053 | 0,045 | 0,04365 |
| 527,3092 | 0,06027 | 0,06259 | 0,05437 | 0,04617 | 0,04445 |
| 527,34638 | 0,06154 | 0,06402 | 0,05577 | 0,04736 | 0,04527 |
| 527,38356 | 0,06283 | 0,06547 | 0,0572 | 0,04858 | 0,04612 |
| 527,42074 | 0,06413 | 0,06693 | 0,05865 | 0,04981 | 0,04699 |
| 527,45793 | 0,06545 | 0,06839 | 0,06011 | 0,05108 | 0,0479 |
| 527,49511 | 0,06678 | 0,06986 | 0,06159 | 0,05237 | 0,04886 |
| 527,53229 | 0,06812 | 0,07132 | 0,06307 | 0,05368 | 0,04987 |
| 527,56947 | 0,06947 | 0,07278 | 0,06455 | 0,05501 | 0,05092 |
| 527,60665 | 0,07082 | 0,07423 | 0,06603 | 0,05636 | 0,05203 |
| 527,64384 | 0,07216 | 0,07565 | 0,06748 | 0,05774 | 0,05318 |
| 527,68102 | 0,0735 | 0,07705 | 0,06892 | 0,05913 | 0,0544 |
| 527,7182 | 0,07482 | 0,07842 | 0,07032 | 0,06054 | 0,05569 |
| 527,75538 | 0,07612 | 0,07975 | 0,07169 | 0,06195 | 0,05703 |
| 527,79256 | 0,07741 | 0,08103 | 0,073 | 0,06338 | 0,05842 |
| 527,82975 | 0,07867 | 0,08225 | 0,07425 | 0,0648 | 0,05986 |
| 527,86693 | 0,07991 | 0,08341 | 0,07545 | 0,06622 | 0,06136 |
| 527,90411 | 0,08112 | 0,08452 | 0,07659 | 0,06764 | 0,0629 |
| 527,94129 | 0,0823 | 0,08556 | 0,07766 | 0,06904 | 0,06448 |
| 527,97847 | 0,08344 | 0,08653 | 0,07866 | 0,07042 | 0,06609 |
| 528,01566 | 0,08455 | 0,08742 | 0,07957 | 0,07178 | 0,06772 |
| 528,05284 | 0,08564 | 0,08824 | 0,08042 | 0,07311 | 0,06936 |
| 528,09002 | 0,0867 | 0,08899 | 0,0812 | 0,07441 | 0,07101 |
| 528,1272 | 0,08774 | 0,08969 | 0,08191 | 0,07566 | 0,07265 |
| 528,16438 | 0,08874 | 0,09032 | 0,08257 | 0,07686 | 0,07428 |
| 528,20157 | 0,08974 | 0,09089 | 0,08317 | 0,07802 | 0,07587 |
| 528,23875 | 0,09072 | 0,09141 | 0,08371 | 0,07914 | 0,07744 |
| 528,27593 | 0,0917 | 0,0919 | 0,08423 | 0,08019 | 0,07897 |
| 528,31311 | 0,09267 | 0,09236 | 0,08472 | 0,08119 | 0,08043 |
| 528,35029 | 0,09365 | 0,0928 | 0,08519 | 0,08213 | 0,08184 |
| 528,38748 | 0,09464 | 0,09323 | 0,08566 | 0,08301 | 0,08318 |
| 528,42466 | 0,09564 | 0,09367 | 0,08613 | 0,08385 | 0,08446 |
| 528,46184 | 0,09667 | 0,09414 | 0,08663 | 0,08465 | 0,08568 |
| 528,49902 | 0,09773 | 0,09463 | 0,08717 | 0,0854 | 0,08682 |
| 528,5362 | 0,09882 | 0,09516 | 0,08774 | 0,08611 | 0,08788 |
| 528,57339 | 0,09995 | 0,09575 | 0,08837 | 0,0868 | 0,08888 |
| 528,61057 | 0,10112 | 0,0964 | 0,08907 | 0,08747 | 0,08982 |
| 528,64775 | 0,10234 | 0,09713 | 0,08984 | 0,08814 | 0,09071 |
| 528,68493 | 0,10359 | 0,09794 | 0,0907 | 0,0888 | 0,09155 |
| 528,72211 | 0,10489 | 0,09883 | 0,09163 | 0,08948 | 0,09235 |
| 528,7593 | 0,10623 | 0,09981 | 0,09265 | 0,09019 | 0,09312 |
| 528,79648 | 0,10761 | 0,10087 | 0,09375 | 0,09094 | 0,09388 |
| 528,83366 | 0,10902 | 0,10205 | 0,09496 | 0,09173 | 0,09463 |
| 528,87084 | 0,11045 | 0,1033 | 0,09624 | 0,09258 | 0,09539 |
| 528,90802 | 0,1119 | 0,10463 | 0,09759 | 0,09348 | 0,09615 |
| 528,94521 | 0,11336 | 0,10603 | 0,09901 | 0,09448 | 0,09695 |
| 528,98239 | 0,11481 | 0,1075 | 0,10048 | 0,09554 | 0,09778 |
| 529,01957 | 0,11624 | 0,10902 | 0,10199 | 0,09668 | 0,09865 |
| 529,05675 | 0,11765 | 0,11059 | 0,10354 | 0,0979 | 0,09956 |
| 529,09393 | 0,11901 | 0,11217 | 0,10509 | 0,09919 | 0,10052 |
| 529,13112 | 0,12033 | 0,11376 | 0,10663 | 0,10056 | 0,10153 |
| 529,1683 | 0,12156 | 0,11534 | 0,10815 | 0,10201 | 0,1026 |
| 529,20548 | 0,12271 | 0,1169 | 0,10963 | 0,1035 | 0,1037 |
| 529,24266 | 0,12375 | 0,11841 | 0,11104 | 0,10505 | 0,10484 |
| 529,27984 | 0,12469 | 0,11985 | 0,11238 | 0,10663 | 0,10601 |
| 529,31703 | 0,12552 | 0,12121 | 0,11362 | 0,10823 | 0,1072 |
| 529,35421 | 0,12623 | 0,12249 | 0,11476 | 0,10983 | 0,1084 |
| 529,39139 | 0,12676 | 0,12366 | 0,11579 | 0,11142 | 0,1096 |
| 529,42857 | 0,12716 | 0,1247 | 0,11667 | 0,11298 | 0,11077 |
| 529,46575 | 0,12742 | 0,1256 | 0,1174 | 0,11449 | 0,1119 |
| 529,50294 | 0,12754 | 0,12635 | 0,11799 | 0,11594 | 0,11299 |
| 529,54012 | 0,12752 | 0,12697 | 0,11845 | 0,11731 | 0,11402 |
| 529,5773 | 0,12735 | 0,12745 | 0,11876 | 0,11857 | 0,11495 |
| 529,61448 | 0,12704 | 0,12778 | 0,11894 | 0,11971 | 0,11579 |
| 529,65166 | 0,12662 | 0,12792 | 0,11895 | 0,12074 | 0,11652 |
| 529,68885 | 0,12609 | 0,12793 | 0,11884 | 0,12164 | 0,11714 |
| 529,72603 | 0,12547 | 0,12781 | 0,11863 | 0,12241 | 0,11765 |
| 529,76321 | 0,12477 | 0,12756 | 0,11833 | 0,12302 | 0,11802 |
| 529,80039 | 0,12401 | 0,1272 | 0,11795 | 0,12347 | 0,11824 |
| 529,83757 | 0,1232 | 0,12671 | 0,1175 | 0,12379 | 0,11833 |
| 529,87476 | 0,12238 | 0,12614 | 0,11701 | 0,12398 | 0,1183 |
| 529,91194 | 0,12156 | 0,12549 | 0,1165 | 0,12404 | 0,11816 |
| 529,94912 | 0,12075 | 0,12479 | 0,116 | 0,12399 | 0,11791 |
| 529,9863 | 0,11998 | 0,12405 | 0,11552 | 0,12381 | 0,11754 |
| 530,02348 | 0,11927 | 0,12328 | 0,11508 | 0,12355 | 0,11708 |
| 530,06067 | 0,11864 | 0,1225 | 0,11472 | 0,12322 | 0,11656 |
| 530,09785 | 0,11809 | 0,12173 | 0,11444 | 0,12284 | 0,11599 |
| 530,13503 | 0,11763 | 0,12099 | 0,11426 | 0,12242 | 0,11539 |
| 530,17221 | 0,11728 | 0,12028 | 0,11417 | 0,12199 | 0,11477 |
| 530,20939 | 0,11705 | 0,11962 | 0,11421 | 0,12157 | 0,11416 |
| 530,24658 | 0,11695 | 0,11902 | 0,11438 | 0,12117 | 0,11358 |
| 530,28376 | 0,11696 | 0,1185 | 0,11469 | 0,12081 | 0,11305 |
| 530,32094 | 0,11708 | 0,11805 | 0,11513 | 0,12051 | 0,11257 |
| 530,35812 | 0,1173 | 0,11767 | 0,11569 | 0,12028 | 0,11217 |
| 530,3953 | 0,11763 | 0,11737 | 0,11636 | 0,12015 | 0,11187 |
| 530,43249 | 0,11806 | 0,11714 | 0,11714 | 0,12012 | 0,11168 |
| 530,46967 | 0,11855 | 0,11701 | 0,11803 | 0,12018 | 0,1116 |
| 530,50685 | 0,1191 | 0,11694 | 0,11899 | 0,12034 | 0,11164 |
| 530,54403 | 0,11968 | 0,11692 | 0,12001 | 0,1206 | 0,11178 |
| 530,58121 | 0,12029 | 0,11697 | 0,12107 | 0,12096 | 0,11204 |
| 530,6184 | 0,12091 | 0,11705 | 0,12215 | 0,12144 | 0,11244 |
| 530,65558 | 0,12149 | 0,11717 | 0,12323 | 0,12199 | 0,11295 |
| 530,69276 | 0,12204 | 0,11732 | 0,12428 | 0,12261 | 0,11354 |
| 530,72994 | 0,12254 | 0,11748 | 0,12528 | 0,1233 | 0,11421 |
| 530,76712 | 0,12296 | 0,11763 | 0,12621 | 0,12403 | 0,11496 |
| 530,80431 | 0,1233 | 0,11778 | 0,12707 | 0,12479 | 0,11577 |
| 530,84149 | 0,12352 | 0,1179 | 0,12782 | 0,12556 | 0,11662 |
| 530,87867 | 0,12362 | 0,11799 | 0,12843 | 0,12633 | 0,11748 |
| 530,91585 | 0,12361 | 0,11803 | 0,12891 | 0,12707 | 0,11835 |
| 530,95303 | 0,12347 | 0,11803 | 0,12926 | 0,12778 | 0,11921 |
| 530,99022 | 0,12322 | 0,11798 | 0,12947 | 0,12844 | 0,12004 |
| 531,0274 | 0,12283 | 0,11788 | 0,12953 | 0,12902 | 0,12082 |
| 531,06458 | 0,1223 | 0,11772 | 0,12942 | 0,12952 | 0,12154 |
| 531,10176 | 0,12166 | 0,11749 | 0,12917 | 0,12993 | 0,12219 |
| 531,13894 | 0,12093 | 0,1172 | 0,12878 | 0,13025 | 0,12277 |
| 531,17613 | 0,12011 | 0,11687 | 0,12827 | 0,13047 | 0,12327 |
| 531,21331 | 0,11921 | 0,11649 | 0,12764 | 0,13059 | 0,12368 |
| 531,25049 | 0,11824 | 0,11607 | 0,12692 | 0,1306 | 0,12398 |
| 531,28767 | 0,11724 | 0,11561 | 0,12609 | 0,13051 | 0,12421 |
| 531,32485 | 0,11621 | 0,11512 | 0,1252 | 0,13033 | 0,12435 |
| 531,36204 | 0,11518 | 0,11462 | 0,12427 | 0,13007 | 0,12442 |
| 531,39922 | 0,11417 | 0,11412 | 0,12331 | 0,12974 | 0,12442 |
| 531,4364 | 0,11319 | 0,11362 | 0,12234 | 0,12933 | 0,12435 |
| 531,47358 | 0,11227 | 0,11314 | 0,12137 | 0,12887 | 0,12423 |
| 531,51076 | 0,11142 | 0,11269 | 0,12042 | 0,12837 | 0,12407 |
| 531,54795 | 0,11064 | 0,11226 | 0,11952 | 0,12784 | 0,12389 |
| 531,58513 | 0,10996 | 0,11188 | 0,11867 | 0,12728 | 0,12369 |
| 531,62231 | 0,10938 | 0,11155 | 0,11787 | 0,12672 | 0,12348 |
| 531,65949 | 0,10892 | 0,11126 | 0,11715 | 0,12614 | 0,12327 |
| 531,69667 | 0,10857 | 0,11104 | 0,11651 | 0,12557 | 0,12307 |
| 531,73386 | 0,10834 | 0,11088 | 0,11596 | 0,12501 | 0,12289 |
| 531,77104 | 0,10821 | 0,11077 | 0,11547 | 0,12446 | 0,12272 |
| 531,80822 | 0,10818 | 0,11072 | 0,11507 | 0,12391 | 0,12257 |
| 531,8454 | 0,10825 | 0,11071 | 0,11473 | 0,12337 | 0,12244 |
| 531,88258 | 0,10842 | 0,11074 | 0,11446 | 0,12284 | 0,12232 |
| 531,91977 | 0,10866 | 0,11082 | 0,11424 | 0,12229 | 0,12221 |
| 531,95695 | 0,10895 | 0,11091 | 0,11406 | 0,12174 | 0,1221 |
| 531,99413 | 0,10928 | 0,11102 | 0,1139 | 0,12117 | 0,12198 |
| 532,03131 | 0,10963 | 0,11112 | 0,11376 | 0,12056 | 0,12185 |
| 532,06849 | 0,10998 | 0,11122 | 0,11361 | 0,11991 | 0,12167 |
| 532,10568 | 0,11032 | 0,11127 | 0,11343 | 0,1192 | 0,12145 |
| 532,14286 | 0,11061 | 0,11129 | 0,11321 | 0,11843 | 0,12117 |
| 532,18004 | 0,11086 | 0,11124 | 0,11294 | 0,11758 | 0,12082 |
| 532,21722 | 0,11103 | 0,11113 | 0,1126 | 0,11665 | 0,12039 |
| 532,2544 | 0,11113 | 0,11094 | 0,11218 | 0,11563 | 0,11988 |
| 532,29159 | 0,11111 | 0,11065 | 0,11166 | 0,11449 | 0,11923 |
| 532,32877 | 0,11098 | 0,11024 | 0,11102 | 0,11325 | 0,11849 |
| 532,36595 | 0,11073 | 0,10973 | 0,11028 | 0,11191 | 0,11763 |
| 532,40313 | 0,11036 | 0,1091 | 0,10943 | 0,11048 | 0,11665 |
| 532,44031 | 0,10988 | 0,10837 | 0,10848 | 0,10895 | 0,11557 |
| 532,4775 | 0,10925 | 0,10752 | 0,10741 | 0,10732 | 0,11435 |
| 532,51468 | 0,10849 | 0,10654 | 0,10622 | 0,1056 | 0,11302 |
| 532,55186 | 0,10762 | 0,10545 | 0,10493 | 0,10383 | 0,1116 |
| 532,58904 | 0,10665 | 0,10427 | 0,10357 | 0,102 | 0,11009 |
| 532,62622 | 0,10558 | 0,103 | 0,10213 | 0,10013 | 0,10851 |
| 532,66341 | 0,10442 | 0,10167 | 0,10064 | 0,09824 | 0,10686 |
| 532,70059 | 0,10319 | 0,10026 | 0,09911 | 0,09636 | 0,10517 |
| 532,73777 | 0,10191 | 0,09881 | 0,09755 | 0,0945 | 0,10346 |
| 532,77495 | 0,10059 | 0,09735 | 0,096 | 0,09269 | 0,10174 |
| 532,81213 | 0,09926 | 0,09587 | 0,09447 | 0,09094 | 0,10005 |
| 532,84932 | 0,09793 | 0,09441 | 0,09298 | 0,08926 | 0,09839 |
| 532,8865 | 0,09662 | 0,09297 | 0,09154 | 0,0877 | 0,09678 |
| 532,92368 | 0,09535 | 0,09159 | 0,0902 | 0,08628 | 0,09527 |
| 532,96086 | 0,09413 | 0,09028 | 0,08895 | 0,08499 | 0,09386 |
| 532,99804 | 0,09298 | 0,08905 | 0,08781 | 0,08385 | 0,09255 |
| 533,03523 | 0,09191 | 0,08791 | 0,08678 | 0,08287 | 0,09137 |
| 533,07241 | 0,09092 | 0,08687 | 0,08588 | 0,08206 | 0,09032 |
| 533,10959 | 0,09004 | 0,08595 | 0,08513 | 0,08145 | 0,08944 |
| 533,14677 | 0,08928 | 0,08517 | 0,08453 | 0,08103 | 0,08872 |
| 533,18395 | 0,08861 | 0,08451 | 0,08407 | 0,08079 | 0,08816 |
| 533,22114 | 0,08805 | 0,08397 | 0,08374 | 0,08071 | 0,08775 |
| 533,25832 | 0,08759 | 0,08355 | 0,08354 | 0,0808 | 0,08749 |
| 533,2955 | 0,08723 | 0,08325 | 0,08347 | 0,08105 | 0,08739 |
| 533,33268 | 0,08699 | 0,08308 | 0,08353 | 0,08148 | 0,08746 |
| 533,36986 | 0,08683 | 0,08302 | 0,08369 | 0,08204 | 0,08766 |
| 533,40705 | 0,08673 | 0,08304 | 0,08393 | 0,08271 | 0,08798 |
| 533,44423 | 0,0867 | 0,08314 | 0,08424 | 0,08348 | 0,0884 |
| 533,48141 | 0,08672 | 0,08331 | 0,08459 | 0,08432 | 0,08891 |
| 533,51859 | 0,08678 | 0,08354 | 0,08499 | 0,08524 | 0,08951 |
| 533,55577 | 0,08687 | 0,0838 | 0,0854 | 0,0862 | 0,09016 |
| 533,59295 | 0,08696 | 0,08408 | 0,0858 | 0,08717 | 0,09086 |
| 533,63014 | 0,08704 | 0,08436 | 0,08617 | 0,08814 | 0,09157 |
| 533,66732 | 0,08711 | 0,08463 | 0,08651 | 0,0891 | 0,09228 |
| 533,7045 | 0,08715 | 0,08488 | 0,0868 | 0,09002 | 0,09299 |
| 533,74168 | 0,08714 | 0,08508 | 0,087 | 0,09087 | 0,09365 |
| 533,77886 | 0,08707 | 0,08523 | 0,08712 | 0,09164 | 0,09426 |
| 533,81605 | 0,08694 | 0,08532 | 0,08715 | 0,09234 | 0,09481 |
| 533,85323 | 0,08675 | 0,08533 | 0,08708 | 0,09294 | 0,09529 |
| 533,89041 | 0,08648 | 0,08528 | 0,08692 | 0,09344 | 0,09568 |
| 533,92759 | 0,08614 | 0,08513 | 0,08663 | 0,09382 | 0,09598 |
| 533,96477 | 0,0857 | 0,08488 | 0,08623 | 0,09406 | 0,09616 |
| 534,00196 | 0,08519 | 0,08455 | 0,08573 | 0,09418 | 0,09624 |
| 534,03914 | 0,08461 | 0,08414 | 0,08513 | 0,09419 | 0,09621 |
| 534,07632 | 0,08396 | 0,08365 | 0,08445 | 0,09407 | 0,09608 |
| 534,1135 | 0,08324 | 0,08308 | 0,08368 | 0,09384 | 0,09584 |
| 534,15068 | 0,08245 | 0,08242 | 0,08281 | 0,09347 | 0,09547 |
| 534,18787 | 0,08162 | 0,0817 | 0,08189 | 0,09299 | 0,095 |
| 534,22505 | 0,08073 | 0,08093 | 0,08092 | 0,0924 | 0,09442 |
| 534,26223 | 0,07982 | 0,08011 | 0,07991 | 0,09172 | 0,09376 |
| 534,29941 | 0,07888 | 0,07925 | 0,07888 | 0,09095 | 0,09301 |
| 534,33659 | 0,07791 | 0,07836 | 0,07783 | 0,09009 | 0,09218 |
| 534,37378 | 0,07694 | 0,07745 | 0,07678 | 0,08914 | 0,09126 |
| 534,41096 | 0,07597 | 0,07653 | 0,07574 | 0,08812 | 0,09028 |
| 534,44814 | 0,07501 | 0,07562 | 0,07473 | 0,08704 | 0,08923 |
| 534,48532 | 0,07405 | 0,07471 | 0,07374 | 0,08591 | 0,08814 |
| 534,5225 | 0,07312 | 0,07382 | 0,07279 | 0,08473 | 0,08699 |
| 534,55969 | 0,07221 | 0,07296 | 0,0719 | 0,0835 | 0,0858 |
| 534,59687 | 0,07132 | 0,07212 | 0,07107 | 0,08223 | 0,08457 |
| 534,63405 | 0,07047 | 0,07132 | 0,07028 | 0,08093 | 0,08331 |
| 534,67123 | 0,06965 | 0,07056 | 0,06955 | 0,07961 | 0,08203 |
| 534,70841 | 0,06885 | 0,06983 | 0,06888 | 0,07826 | 0,08073 |
| 534,7456 | 0,06808 | 0,06915 | 0,06826 | 0,07689 | 0,07941 |
| 534,78278 | 0,06734 | 0,06851 | 0,0677 | 0,07551 | 0,07807 |
| 534,81996 | 0,06663 | 0,06791 | 0,06719 | 0,07413 | 0,07673 |
| 534,85714 | 0,06594 | 0,06734 | 0,06672 | 0,07274 | 0,07539 |
| 534,89432 | 0,06526 | 0,0668 | 0,06629 | 0,07136 | 0,07406 |
| 534,93151 | 0,06459 | 0,06628 | 0,06589 | 0,06998 | 0,07272 |
| 534,96869 | 0,06394 | 0,0658 | 0,06552 | 0,06862 | 0,07141 |
| 535,00587 | 0,06329 | 0,06534 | 0,06517 | 0,06728 | 0,07011 |
| 535,04305 | 0,06264 | 0,06488 | 0,06483 | 0,06597 | 0,06884 |
| 535,08023 | 0,062 | 0,06444 | 0,06449 | 0,0647 | 0,06761 |
| 535,11742 | 0,06135 | 0,064 | 0,06415 | 0,06347 | 0,0664 |
| 535,1546 | 0,06069 | 0,06357 | 0,06382 | 0,06228 | 0,06525 |
| 535,19178 | 0,06004 | 0,06313 | 0,06347 | 0,06117 | 0,06415 |
| 535,22896 | 0,05938 | 0,06269 | 0,06312 | 0,06012 | 0,06311 |
| 535,26614 | 0,05871 | 0,06224 | 0,06276 | 0,05915 | 0,06215 |
| 535,30333 | 0,05805 | 0,06179 | 0,06239 | 0,05826 | 0,06125 |
| 535,34051 | 0,05739 | 0,06133 | 0,06202 | 0,05746 | 0,06043 |
| 535,37769 | 0,05675 | 0,06087 | 0,06165 | 0,05675 | 0,05969 |
| 535,41487 | 0,05611 | 0,0604 | 0,06127 | 0,05616 | 0,05906 |
| 535,45205 | 0,0555 | 0,05994 | 0,06091 | 0,05569 | 0,05852 |
| 535,48924 | 0,05491 | 0,05947 | 0,06055 | 0,05532 | 0,05807 |
| 535,52642 | 0,05435 | 0,05902 | 0,06022 | 0,05506 | 0,05772 |
| 535,5636 | 0,05382 | 0,05857 | 0,05991 | 0,05491 | 0,05747 |
| 535,60078 | 0,05335 | 0,05814 | 0,05965 | 0,05489 | 0,05732 |
| 535,63796 | 0,05293 | 0,05774 | 0,05942 | 0,055 | 0,05729 |
| 535,67515 | 0,05256 | 0,05735 | 0,05924 | 0,05521 | 0,05734 |
| 535,71233 | 0,05226 | 0,057 | 0,05911 | 0,05553 | 0,05748 |
| 535,74951 | 0,05201 | 0,05667 | 0,05904 | 0,05595 | 0,0577 |
| 535,78669 | 0,05182 | 0,05639 | 0,05905 | 0,05646 | 0,05801 |
| 535,82387 | 0,05172 | 0,05614 | 0,05912 | 0,05708 | 0,05839 |
| 535,86106 | 0,05168 | 0,05593 | 0,05926 | 0,05778 | 0,05885 |
| 535,89824 | 0,0517 | 0,05575 | 0,05946 | 0,05854 | 0,05935 |
| 535,93542 | 0,05177 | 0,05561 | 0,05972 | 0,05935 | 0,0599 |
| 535,9726 | 0,05191 | 0,05551 | 0,06005 | 0,06021 | 0,06048 |
| 536,00978 | 0,05209 | 0,05545 | 0,06044 | 0,0611 | 0,06109 |
| 536,04697 | 0,05232 | 0,05541 | 0,06088 | 0,06201 | 0,06171 |
| 536,08415 | 0,05259 | 0,05538 | 0,06135 | 0,06293 | 0,06233 |
| 536,12133 | 0,05287 | 0,05538 | 0,06185 | 0,06383 | 0,06294 |
| 536,15851 | 0,05316 | 0,05538 | 0,06236 | 0,06471 | 0,06353 |
| 536,19569 | 0,05346 | 0,05538 | 0,06288 | 0,06555 | 0,06409 |
| 536,23288 | 0,05374 | 0,05537 | 0,06339 | 0,06634 | 0,06461 |
| 536,27006 | 0,05399 | 0,05534 | 0,06387 | 0,06706 | 0,06506 |
| 536,30724 | 0,05421 | 0,05529 | 0,06432 | 0,0677 | 0,06545 |
| 536,34442 | 0,05438 | 0,0552 | 0,06471 | 0,06826 | 0,06577 |
| 536,3816 | 0,0545 | 0,05507 | 0,06504 | 0,06872 | 0,06602 |
| 536,41879 | 0,05455 | 0,05489 | 0,06529 | 0,06909 | 0,06618 |
| 536,45597 | 0,05451 | 0,05465 | 0,06544 | 0,06932 | 0,06623 |
| 536,49315 | 0,05439 | 0,05436 | 0,0655 | 0,06943 | 0,06618 |
| 536,53033 | 0,05418 | 0,05401 | 0,06546 | 0,06942 | 0,06603 |
| 536,56751 | 0,05389 | 0,05359 | 0,06532 | 0,06929 | 0,06579 |
| 536,6047 | 0,05351 | 0,0531 | 0,06503 | 0,06904 | 0,06545 |
| 536,64188 | 0,05302 | 0,05254 | 0,06463 | 0,06866 | 0,065 |
| 536,67906 | 0,05244 | 0,05192 | 0,06411 | 0,06814 | 0,06444 |
| 536,71624 | 0,05178 | 0,05124 | 0,06349 | 0,06751 | 0,06378 |
| 536,75342 | 0,05104 | 0,05051 | 0,06275 | 0,06677 | 0,06305 |
| 536,79061 | 0,05023 | 0,04972 | 0,0619 | 0,06593 | 0,06223 |
| 536,82779 | 0,04934 | 0,04888 | 0,06094 | 0,065 | 0,06134 |
| 536,86497 | 0,04839 | 0,04802 | 0,0599 | 0,06398 | 0,06037 |
| 536,90215 | 0,0474 | 0,04712 | 0,05878 | 0,06287 | 0,05934 |
| 536,93933 | 0,04637 | 0,0462 | 0,05759 | 0,0617 | 0,05826 |
| 536,97652 | 0,04532 | 0,04527 | 0,05634 | 0,06047 | 0,05715 |
| 537,0137 | 0,04424 | 0,04434 | 0,05504 | 0,0592 | 0,056 |
| 537,05088 | 0,04316 | 0,04341 | 0,05371 | 0,0579 | 0,05484 |
| 537,08806 | 0,04207 | 0,04249 | 0,05236 | 0,05657 | 0,05366 |
| 537,12524 | 0,041 | 0,04159 | 0,051 | 0,05522 | 0,05247 |
| 537,16243 | 0,03994 | 0,0407 | 0,04963 | 0,05387 | 0,05129 |
| 537,19961 | 0,0389 | 0,03984 | 0,04827 | 0,05252 | 0,05012 |
| 537,23679 | 0,03789 | 0,03902 | 0,04693 | 0,05117 | 0,04896 |
| 537,27397 | 0,03692 | 0,03822 | 0,04562 | 0,04984 | 0,04782 |
| 537,31115 | 0,03598 | 0,03746 | 0,04433 | 0,04853 | 0,04671 |
| 537,34834 | 0,03507 | 0,03672 | 0,04307 | 0,04724 | 0,04562 |
| 537,38552 | 0,0342 | 0,03602 | 0,04184 | 0,04597 | 0,04456 |
| 537,4227 | 0,03336 | 0,03534 | 0,04066 | 0,04473 | 0,04353 |
| 537,45988 | 0,03256 | 0,0347 | 0,03952 | 0,04352 | 0,04252 |
| 537,49706 | 0,03179 | 0,03407 | 0,03841 | 0,04233 | 0,04155 |
| 537,53425 | 0,03105 | 0,03346 | 0,03734 | 0,04117 | 0,0406 |
| 537,57143 | 0,03033 | 0,03287 | 0,0363 | 0,04004 | 0,03968 |
| 537,60861 | 0,02964 | 0,03229 | 0,0353 | 0,03893 | 0,03878 |
| 537,64579 | 0,02897 | 0,03171 | 0,03434 | 0,03785 | 0,0379 |
| 537,68297 | 0,02832 | 0,03114 | 0,0334 | 0,03679 | 0,03705 |
| 537,72016 | 0,02768 | 0,03057 | 0,03249 | 0,03576 | 0,03622 |
| 537,75734 | 0,02705 | 0,02999 | 0,03161 | 0,03476 | 0,03541 |
| 537,79452 | 0,02643 | 0,02941 | 0,03074 | 0,03378 | 0,03462 |
| 537,8317 | 0,02583 | 0,02882 | 0,0299 | 0,03282 | 0,03385 |
| 537,86888 | 0,02523 | 0,02823 | 0,02909 | 0,03188 | 0,0331 |
| 537,90607 | 0,02464 | 0,02762 | 0,02829 | 0,03098 | 0,03238 |
| 537,94325 | 0,02405 | 0,02701 | 0,02751 | 0,0301 | 0,03168 |
| 537,98043 | 0,02348 | 0,02639 | 0,02675 | 0,02925 | 0,031 |
| 538,01761 | 0,02291 | 0,02577 | 0,02602 | 0,02843 | 0,03034 |
| 538,05479 | 0,02236 | 0,02514 | 0,02531 | 0,02764 | 0,02971 |
| 538,09198 | 0,02181 | 0,02451 | 0,02462 | 0,02687 | 0,0291 |
| 538,12916 | 0,02128 | 0,02388 | 0,02395 | 0,02614 | 0,02853 |
| 538,16634 | 0,02076 | 0,02326 | 0,02331 | 0,02545 | 0,02797 |
| 538,20352 | 0,02026 | 0,02264 | 0,0227 | 0,02478 | 0,02744 |
| 538,2407 | 0,01977 | 0,02204 | 0,02212 | 0,02414 | 0,02693 |
| 538,27789 | 0,01929 | 0,02145 | 0,02157 | 0,02353 | 0,02644 |
| 538,31507 | 0,01884 | 0,02086 | 0,02104 | 0,02294 | 0,02597 |
| 538,35225 | 0,0184 | 0,0203 | 0,02054 | 0,02238 | 0,02552 |
| 538,38943 | 0,01797 | 0,01974 | 0,02007 | 0,02184 | 0,02507 |
| 538,42661 | 0,01756 | 0,01921 | 0,01962 | 0,02132 | 0,02464 |
| 538,4638 | 0,01716 | 0,01869 | 0,0192 | 0,02081 | 0,0242 |
| 538,50098 | 0,01678 | 0,01819 | 0,0188 | 0,02031 | 0,02376 |
| 538,53816 | 0,0164 | 0,0177 | 0,01842 | 0,01982 | 0,02332 |
| 538,57534 | 0,01603 | 0,01722 | 0,01805 | 0,01934 | 0,02286 |
| 538,61252 | 0,01566 | 0,01676 | 0,0177 | 0,01885 | 0,02239 |
| 538,64971 | 0,0153 | 0,0163 | 0,01735 | 0,01835 | 0,02191 |
| 538,68689 | 0,01494 | 0,01586 | 0,01701 | 0,01785 | 0,0214 |
| 538,72407 | 0,01457 | 0,01542 | 0,01667 | 0,01735 | 0,02086 |
| 538,76125 | 0,0142 | 0,01498 | 0,01633 | 0,01682 | 0,0203 |
| 538,79843 | 0,01382 | 0,01454 | 0,01598 | 0,01629 | 0,01971 |
| 538,83562 | 0,01344 | 0,0141 | 0,01562 | 0,01574 | 0,0191 |
| 538,8728 | 0,01304 | 0,01366 | 0,01525 | 0,01518 | 0,01846 |
| 538,90998 | 0,01264 | 0,01321 | 0,01486 | 0,0146 | 0,01779 |
| 538,94716 | 0,01222 | 0,01276 | 0,01446 | 0,01401 | 0,0171 |
| 538,98434 | 0,01179 | 0,0123 | 0,01404 | 0,01341 | 0,01639 |
| 539,02153 | 0,01135 | 0,01184 | 0,0136 | 0,0128 | 0,01566 |
| 539,05871 | 0,0109 | 0,01136 | 0,01314 | 0,01218 | 0,01492 |
| 539,09589 | 0,01044 | 0,01089 | 0,01267 | 0,01156 | 0,01416 |
| 539,13307 | 0,00997 | 0,0104 | 0,01218 | 0,01094 | 0,01341 |
| 539,17025 | 0,00949 | 0,00991 | 0,01167 | 0,01032 | 0,01265 |
| 539,20744 | 0,00901 | 0,00942 | 0,01115 | 0,0097 | 0,0119 |
| 539,24462 | 0,00854 | 0,00893 | 0,01063 | 0,00909 | 0,01116 |
| 539,2818 | 0,00806 | 0,00844 | 0,01009 | 0,00849 | 0,01043 |
| 539,31898 | 0,00758 | 0,00796 | 0,00955 | 0,00791 | 0,00972 |
| 539,35616 | 0,00711 | 0,00747 | 0,00901 | 0,00734 | 0,00904 |
| 539,39335 | 0,00665 | 0,007 | 0,00847 | 0,00679 | 0,00838 |
| 539,43053 | 0,0062 | 0,00653 | 0,00793 | 0,00626 | 0,00774 |
| 539,46771 | 0,00576 | 0,00608 | 0,0074 | 0,00576 | 0,00714 |
| 539,50489 | 0,00534 | 0,00564 | 0,00689 | 0,00528 | 0,00657 |
| 539,54207 | 0,00493 | 0,00522 | 0,00639 | 0,00482 | 0,00602 |
| 539,57926 | 0,00454 | 0,00481 | 0,0059 | 0,00439 | 0,00552 |
| 539,61644 | 0,00417 | 0,00442 | 0,00543 | 0,00399 | 0,00506 |
| 539,65362 | 0,00382 | 0,00405 | 0,00498 | 0,00362 | 0,00462 |
| 539,6908 | 0,00349 | 0,00371 | 0,00456 | 0,00327 | 0,00422 |
| 539,72798 | 0,00319 | 0,00338 | 0,00416 | 0,00295 | 0,00385 |
| 539,76517 | 0,0029 | 0,00308 | 0,00378 | 0,00265 | 0,00351 |
| 539,80235 | 0,00264 | 0,00279 | 0,00343 | 0,00238 | 0,00321 |
| 539,83953 | 0,0024 | 0,00253 | 0,00309 | 0,00214 | 0,00293 |
| 539,87671 | 0,00217 | 0,00229 | 0,00279 | 0,00191 | 0,00268 |
| 539,91389 | 0,00197 | 0,00207 | 0,00251 | 0,00171 | 0,00246 |
| 539,95108 | 0,00178 | 0,00187 | 0,00226 | 0,00153 | 0,00225 |
| 539,98826 | 0,00162 | 0,00168 | 0,00202 | 0,00136 | 0,00207 |
| 540,02544 | 0,00146 | 0,00152 | 0,00181 | 0,00122 | 0,00191 |
| 540,06262 | 0,00133 | 0,00137 | 0,00162 | 0,00109 | 0,00177 |
| 540,0998 | 0,00121 | 0,00124 | 0,00145 | 0,00097 | 0,00164 |
| 540,13699 | 0,0011 | 0,00113 | 0,00129 | 0,00087 | 0,00152 |
| 540,17417 | 0,001 | 0,00102 | 0,00116 | 0,00077 | 0,00141 |
| 540,21135 | 0,00092 | 0,00093 | 0,00103 | 0,00069 | 0,00132 |
| 540,24853 | 0,00084 | 0,00086 | 0,00092 | 0,00062 | 0,00123 |
| 540,28571 | 0,00077 | 0,00079 | 0,00083 | 0,00056 | 0,00115 |
| 540,3229 | 0,00071 | 0,00073 | 0,00074 | 5e-04 | 0,00108 |
| 540,36008 | 0,00065 | 0,00068 | 0,00067 | 0,00045 | 0,00101 |
| 540,39726 | 6e-04 | 0,00064 | 6e-04 | 0,00041 | 0,00095 |
| 540,43444 | 0,00056 | 0,00061 | 0,00054 | 0,00037 | 0,00089 |
| 540,47162 | 0,00052 | 0,00058 | 0,00049 | 0,00034 | 0,00083 |
| 540,50881 | 0,00048 | 0,00055 | 0,00045 | 0,00031 | 0,00078 |
| 540,54599 | 0,00044 | 0,00053 | 0,00041 | 0,00028 | 0,00073 |
| 540,58317 | 0,00041 | 0,00052 | 0,00037 | 0,00025 | 0,00068 |
| 540,62035 | 0,00038 | 5e-04 | 0,00034 | 0,00023 | 0,00064 |
| 540,65753 | 0,00036 | 0,00049 | 0,00031 | 0,00021 | 0,00059 |
| 540,69472 | 0,00033 | 0,00048 | 0,00029 | 0,00019 | 0,00055 |
| 540,7319 | 3e-04 | 0,00047 | 0,00026 | 0,00017 | 0,00051 |
| 540,76908 | 0,00028 | 0,00047 | 0,00024 | 0,00016 | 0,00047 |
| 540,80626 | 0,00026 | 0,00046 | 0,00022 | 0,00014 | 0,00043 |
| 540,84344 | 0,00024 | 0,00046 | 2e-04 | 0,00013 | 0,00039 |
| 540,88063 | 0,00022 | 0,00045 | 0,00019 | 0,00012 | 0,00036 |
| 540,91781 | 2e-04 | 0,00045 | 0,00017 | 0,00011 | 0,00032 |
| 540,95499 | 0,00018 | 0,00044 | 0,00016 | 9e-05 | 0,00029 |
| 540,99217 | 0,00017 | 0,00044 | 0,00014 | 8e-05 | 0,00026 |
| 541,02935 | 0,00015 | 0,00043 | 0,00013 | 8e-05 | 0,00024 |
| 541,06654 | 0,00014 | 0,00042 | 0,00012 | 7e-05 | 0,00021 |
| 541,10372 | 0,00012 | 0,00041 | 0,00011 | 6e-05 | 0,00019 |
| 541,1409 | 0,00011 | 0,00041 | 1e-04 | 5e-05 | 0,00017 |
| 541,17808 | 1e-04 | 4e-04 | 9e-05 | 5e-05 | 0,00015 |
| 541,21526 | 9e-05 | 0,00039 | 8e-05 | 4e-05 | 0,00013 |
| 541,25245 | 8e-05 | 0,00037 | 7e-05 | 4e-05 | 0,00011 |
| 541,28963 | 7e-05 | 0,00036 | 6e-05 | 3e-05 | 1e-04 |
| 541,32681 | 6e-05 | 0,00035 | 5e-05 | 3e-05 | 8e-05 |
| 541,36399 | 5e-05 | 0,00034 | 5e-05 | 2e-05 | 7e-05 |
| 541,40117 | 4e-05 | 0,00032 | 4e-05 | 2e-05 | 6e-05 |
| 541,43836 | 4e-05 | 0,00031 | 4e-05 | 2e-05 | 5e-05 |
| 541,47554 | 3e-05 | 0,00029 | 3e-05 | 1e-05 | 5e-05 |
| 541,51272 | 3e-05 | 0,00028 | 3e-05 | 1e-05 | 4e-05 |
| 541,5499 | 2e-05 | 0,00026 | 2e-05 | 1e-05 | 3e-05 |
| 541,58708 | 2e-05 | 0,00024 | 2e-05 | 1e-05 | 3e-05 |
| 541,62427 | 2e-05 | 0,00023 | 2e-05 | 1e-05 | 2e-05 |
| 541,66145 | 1e-05 | 0,00021 | 2e-05 | 1e-05 | 2e-05 |
| 541,69863 | 1e-05 | 2e-04 | 1e-05 | 0 | 2e-05 |
| 541,73581 | 1e-05 | 0,00018 | 1e-05 | 0 | 1e-05 |
| 541,77299 | 1e-05 | 0,00017 | 1e-05 | 0 | 1e-05 |
| 541,81018 | 1e-05 | 0,00015 | 1e-05 | 0 | 1e-05 |
| 541,84736 | 1e-05 | 0,00014 | 1e-05 | 0 | 1e-05 |
| 541,88454 | 0 | 0,00013 | 1e-05 | 0 | 1e-05 |
| 541,92172 | 0 | 0,00012 | 0 | 0 | 0 |
| 541,9589 | 0 | 1e-04 | 0 | 0 | 0 |
| 541,99609 | 0 | 9e-05 | 0 | 0 | 0 |
| 542,03327 | 0 | 8e-05 | 0 | 0 | 0 |
| 542,07045 | 0 | 7e-05 | 0 | 0 | 0 |
| 542,10763 | 0 | 7e-05 | 0 | 0 | 0 |
| 542,14481 | 0 | 6e-05 | 0 | 0 | 0 |
| 542,182 | 0 | 5e-05 | 0 | 0 | 0 |
| 542,21918 | 0 | 4e-05 | 0 | 0 | 0 |
| 542,25636 | 0 | 4e-05 | 0 | 0 | 0 |
| 542,29354 | 0 | 3e-05 | 0 | 0 | 0 |
| 542,33072 | 0 | 3e-05 | 0 | 0 | 0 |
| 542,36791 | 0 | 2e-05 | 0 | 0 | 0 |
| 542,40509 | 0 | 2e-05 | 0 | 0 | 0 |
| 542,44227 | 0 | 2e-05 | 0 | 0 | 0 |
| 542,47945 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,51663 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,55382 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,591 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,62818 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,66536 | 0 | 1e-05 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00216 | 0,00185 | 0,00073 | 0,00035 | 0,00035 |
| 524,03718 | 0,00222 | 0,00188 | 0,00077 | 0,00038 | 0,00038 |
| 524,07436 | 0,00228 | 0,00191 | 0,00081 | 0,00041 | 4e-04 |
| 524,11155 | 0,00233 | 0,00194 | 0,00085 | 0,00044 | 0,00043 |
| 524,14873 | 0,00238 | 0,00196 | 9e-04 | 0,00047 | 0,00046 |
| 524,18591 | 0,00241 | 0,00197 | 0,00094 | 0,00051 | 0,00048 |
| 524,22309 | 0,00245 | 0,00198 | 0,00099 | 0,00054 | 0,00051 |
| 524,26027 | 0,00248 | 0,00198 | 0,00104 | 0,00058 | 0,00054 |
| 524,29746 | 0,0025 | 0,00198 | 0,00108 | 0,00062 | 0,00057 |
| 524,33464 | 0,00252 | 0,00198 | 0,00113 | 0,00067 | 6e-04 |
| 524,37182 | 0,00253 | 0,00197 | 0,00118 | 0,00071 | 0,00064 |
| 524,409 | 0,00254 | 0,00196 | 0,00124 | 0,00076 | 0,00067 |
| 524,44618 | 0,00255 | 0,00195 | 0,00129 | 0,00081 | 0,00072 |
| 524,48337 | 0,00256 | 0,00194 | 0,00134 | 0,00087 | 0,00076 |
| 524,52055 | 0,00257 | 0,00194 | 0,0014 | 0,00093 | 0,00081 |
| 524,55773 | 0,00258 | 0,00193 | 0,00146 | 0,00099 | 0,00086 |
| 524,59491 | 0,0026 | 0,00193 | 0,00152 | 0,00106 | 0,00092 |
| 524,63209 | 0,00262 | 0,00194 | 0,00158 | 0,00114 | 0,00099 |
| 524,66928 | 0,00265 | 0,00195 | 0,00166 | 0,00122 | 0,00107 |
| 524,70646 | 0,00269 | 0,00198 | 0,00173 | 0,00132 | 0,00116 |
| 524,74364 | 0,00275 | 0,00202 | 0,00182 | 0,00142 | 0,00126 |
| 524,78082 | 0,00282 | 0,00207 | 0,00191 | 0,00153 | 0,00137 |
| 524,818 | 0,0029 | 0,00214 | 0,00202 | 0,00166 | 0,0015 |
| 524,85519 | 0,00302 | 0,00223 | 0,00214 | 0,00181 | 0,00166 |
| 524,89237 | 0,00315 | 0,00234 | 0,00228 | 0,00198 | 0,00183 |
| 524,92955 | 0,00332 | 0,00249 | 0,00243 | 0,00217 | 0,00204 |
| 524,96673 | 0,00352 | 0,00266 | 0,00262 | 0,00239 | 0,00227 |
| 525,00391 | 0,00376 | 0,00287 | 0,00282 | 0,00263 | 0,00253 |
| 525,0411 | 0,00404 | 0,00311 | 0,00306 | 0,00292 | 0,00283 |
| 525,07828 | 0,00437 | 0,00339 | 0,00333 | 0,00325 | 0,00319 |
| 525,11546 | 0,00475 | 0,00372 | 0,00365 | 0,00363 | 0,00359 |
| 525,15264 | 0,00519 | 0,0041 | 0,00401 | 0,00406 | 0,00404 |
| 525,18982 | 0,00569 | 0,00454 | 0,00442 | 0,00456 | 0,00456 |
| 525,22701 | 0,00626 | 0,00503 | 0,00487 | 0,00512 | 0,00513 |
| 525,26419 | 0,00689 | 0,00559 | 0,00539 | 0,00577 | 0,00579 |
| 525,30137 | 0,00762 | 0,00621 | 0,00597 | 0,00652 | 0,00653 |
| 525,33855 | 0,00842 | 0,00691 | 0,00663 | 0,00735 | 0,00736 |
| 525,37573 | 0,00931 | 0,00769 | 0,00736 | 0,00829 | 0,00827 |
| 525,41292 | 0,01029 | 0,00855 | 0,00816 | 0,00934 | 0,00928 |
| 525,4501 | 0,01136 | 0,0095 | 0,00905 | 0,01051 | 0,01039 |
| 525,48728 | 0,01253 | 0,01054 | 0,01001 | 0,01183 | 0,01163 |
| 525,52446 | 0,01382 | 0,01167 | 0,01108 | 0,01329 | 0,01299 |
| 525,56164 | 0,01522 | 0,01292 | 0,01225 | 0,01489 | 0,01446 |
| 525,59883 | 0,01672 | 0,01428 | 0,01351 | 0,01664 | 0,01605 |
| 525,63601 | 0,01833 | 0,01575 | 0,01487 | 0,01853 | 0,01776 |
| 525,67319 | 0,02006 | 0,01733 | 0,01632 | 0,02059 | 0,0196 |
| 525,71037 | 0,0219 | 0,01902 | 0,01788 | 0,02283 | 0,02158 |
| 525,74755 | 0,02389 | 0,02083 | 0,01956 | 0,02522 | 0,02368 |
| 525,78474 | 0,02599 | 0,02279 | 0,02134 | 0,02776 | 0,0259 |
| 525,82192 | 0,02822 | 0,02487 | 0,02323 | 0,03045 | 0,02822 |
| 525,8591 | 0,03057 | 0,02707 | 0,02523 | 0,03327 | 0,03064 |
| 525,89628 | 0,03303 | 0,0294 | 0,02732 | 0,03623 | 0,03317 |
| 525,93346 | 0,03562 | 0,03186 | 0,02952 | 0,03932 | 0,03579 |
| 525,97065 | 0,03836 | 0,03445 | 0,03184 | 0,04251 | 0,03848 |
| 526,00783 | 0,04122 | 0,03718 | 0,03425 | 0,04578 | 0,04123 |
| 526,04501 | 0,04419 | 0,04003 | 0,03675 | 0,04912 | 0,04401 |
| 526,08219 | 0,04727 | 0,043 | 0,03934 | 0,0525 | 0,04682 |
| 526,11937 | 0,05045 | 0,04608 | 0,042 | 0,05591 | 0,04964 |
| 526,15656 | 0,05374 | 0,04927 | 0,04475 | 0,05932 | 0,05245 |
| 526,19374 | 0,05714 | 0,05256 | 0,04758 | 0,06269 | 0,05523 |
| 526,23092 | 0,06063 | 0,05595 | 0,05045 | 0,06602 | 0,05796 |
| 526,2681 | 0,06418 | 0,05941 | 0,05338 | 0,06928 | 0,06062 |
| 526,30528 | 0,06778 | 0,06294 | 0,05634 | 0,07245 | 0,06321 |
| 526,34247 | 0,07144 | 0,06651 | 0,05932 | 0,07548 | 0,06568 |
| 526,37965 | 0,07513 | 0,07013 | 0,06232 | 0,07837 | 0,06803 |
| 526,41683 | 0,07883 | 0,07377 | 0,06531 | 0,08111 | 0,07026 |
| 526,45401 | 0,08253 | 0,07741 | 0,06829 | 0,08368 | 0,07236 |
| 526,49119 | 0,08621 | 0,08103 | 0,07124 | 0,08608 | 0,07432 |
| 526,52838 | 0,08985 | 0,08463 | 0,07415 | 0,08829 | 0,07611 |
| 526,56556 | 0,09344 | 0,08818 | 0,077 | 0,09027 | 0,07773 |
| 526,60274 | 0,09697 | 0,09166 | 0,07978 | 0,09205 | 0,07919 |
| 526,63992 | 0,10039 | 0,09505 | 0,08246 | 0,09364 | 0,0805 |
| 526,6771 | 0,10371 | 0,09833 | 0,08506 | 0,09504 | 0,08167 |
| 526,71429 | 0,10691 | 0,1015 | 0,08755 | 0,09627 | 0,0827 |
| 526,75147 | 0,11 | 0,10455 | 0,08993 | 0,09733 | 0,08356 |
| 526,78865 | 0,11295 | 0,10746 | 0,0922 | 0,09819 | 0,0843 |
| 526,82583 | 0,11577 | 0,11022 | 0,09432 | 0,09892 | 0,08494 |
| 526,86301 | 0,11841 | 0,1128 | 0,09631 | 0,09952 | 0,08547 |
| 526,9002 | 0,1209 | 0,11521 | 0,09818 | 0,10002 | 0,08593 |
| 526,93738 | 0,12325 | 0,11747 | 0,09992 | 0,10042 | 0,08631 |
| 526,97456 | 0,12545 | 0,11956 | 0,10154 | 0,10075 | 0,08663 |
| 527,01174 | 0,1275 | 0,12148 | 0,10303 | 0,10102 | 0,08693 |
| 527,04892 | 0,12941 | 0,12324 | 0,10438 | 0,10126 | 0,0872 |
| 527,08611 | 0,13116 | 0,1248 | 0,10561 | 0,10148 | 0,08747 |
| 527,12329 | 0,13277 | 0,12622 | 0,10675 | 0,1017 | 0,08775 |
| 527,16047 | 0,13425 | 0,12749 | 0,10778 | 0,10194 | 0,08806 |
| 527,19765 | 0,13562 | 0,12863 | 0,10873 | 0,1022 | 0,08841 |
| 527,23483 | 0,13687 | 0,12964 | 0,10959 | 0,10251 | 0,08881 |
| 527,27202 | 0,13802 | 0,13051 | 0,11036 | 0,10286 | 0,08928 |
| 527,3092 | 0,13904 | 0,13127 | 0,11107 | 0,10328 | 0,08981 |
| 527,34638 | 0,13997 | 0,13192 | 0,11172 | 0,10376 | 0,09041 |
| 527,38356 | 0,14081 | 0,1325 | 0,11232 | 0,10432 | 0,09112 |
| 527,42074 | 0,14158 | 0,13299 | 0,11289 | 0,10496 | 0,09192 |
| 527,45793 | 0,14227 | 0,13342 | 0,11341 | 0,10569 | 0,09281 |
| 527,49511 | 0,14288 | 0,13378 | 0,1139 | 0,10651 | 0,0938 |
| 527,53229 | 0,14342 | 0,1341 | 0,11438 | 0,10742 | 0,09488 |
| 527,56947 | 0,14391 | 0,13438 | 0,11484 | 0,10842 | 0,09605 |
| 527,60665 | 0,14435 | 0,13462 | 0,11529 | 0,1095 | 0,09735 |
| 527,64384 | 0,14474 | 0,13485 | 0,11574 | 0,11068 | 0,09873 |
| 527,68102 | 0,14509 | 0,13506 | 0,11619 | 0,11196 | 0,1002 |
| 527,7182 | 0,14541 | 0,13525 | 0,11664 | 0,11332 | 0,10175 |
| 527,75538 | 0,14569 | 0,13544 | 0,11712 | 0,11475 | 0,10338 |
| 527,79256 | 0,14596 | 0,13563 | 0,1176 | 0,11625 | 0,10508 |
| 527,82975 | 0,14621 | 0,13581 | 0,11811 | 0,11783 | 0,10685 |
| 527,86693 | 0,14645 | 0,136 | 0,11864 | 0,11946 | 0,10866 |
| 527,90411 | 0,14668 | 0,1362 | 0,1192 | 0,12115 | 0,11051 |
| 527,94129 | 0,14691 | 0,13639 | 0,11979 | 0,12287 | 0,11239 |
| 527,97847 | 0,14714 | 0,13659 | 0,12042 | 0,1246 | 0,11428 |
| 528,01566 | 0,14738 | 0,13679 | 0,12107 | 0,12635 | 0,11617 |
| 528,05284 | 0,14761 | 0,13699 | 0,12176 | 0,1281 | 0,11804 |
| 528,09002 | 0,14786 | 0,13718 | 0,12248 | 0,12981 | 0,11989 |
| 528,1272 | 0,1481 | 0,13737 | 0,12325 | 0,13149 | 0,1217 |
| 528,16438 | 0,14836 | 0,13755 | 0,12404 | 0,13311 | 0,12346 |
| 528,20157 | 0,14861 | 0,13771 | 0,12487 | 0,13467 | 0,12516 |
| 528,23875 | 0,14886 | 0,13786 | 0,12572 | 0,13615 | 0,12678 |
| 528,27593 | 0,14911 | 0,13799 | 0,1266 | 0,13753 | 0,1283 |
| 528,31311 | 0,14934 | 0,1381 | 0,1275 | 0,13878 | 0,12974 |
| 528,35029 | 0,14957 | 0,13818 | 0,12842 | 0,13991 | 0,13108 |
| 528,38748 | 0,14978 | 0,13823 | 0,12935 | 0,14092 | 0,13232 |
| 528,42466 | 0,14997 | 0,13825 | 0,13029 | 0,1418 | 0,13345 |
| 528,46184 | 0,15013 | 0,13823 | 0,13124 | 0,14255 | 0,13446 |
| 528,49902 | 0,15026 | 0,13819 | 0,13218 | 0,14316 | 0,13537 |
| 528,5362 | 0,15036 | 0,13812 | 0,13311 | 0,1436 | 0,13617 |
| 528,57339 | 0,15042 | 0,138 | 0,13403 | 0,14392 | 0,13688 |
| 528,61057 | 0,15044 | 0,13785 | 0,13493 | 0,14412 | 0,1375 |
| 528,64775 | 0,15041 | 0,13767 | 0,1358 | 0,1442 | 0,13802 |
| 528,68493 | 0,15034 | 0,13746 | 0,13664 | 0,14418 | 0,13844 |
| 528,72211 | 0,15021 | 0,13721 | 0,13744 | 0,14404 | 0,1388 |
| 528,7593 | 0,15004 | 0,13693 | 0,13819 | 0,1438 | 0,13909 |
| 528,79648 | 0,14982 | 0,13662 | 0,13889 | 0,14349 | 0,13932 |
| 528,83366 | 0,14953 | 0,13627 | 0,13952 | 0,1431 | 0,13949 |
| 528,87084 | 0,14918 | 0,1359 | 0,1401 | 0,14265 | 0,13961 |
| 528,90802 | 0,14877 | 0,13549 | 0,1406 | 0,14215 | 0,13968 |
| 528,94521 | 0,14831 | 0,13506 | 0,14102 | 0,1416 | 0,1397 |
| 528,98239 | 0,14778 | 0,13459 | 0,14135 | 0,14099 | 0,13969 |
| 529,01957 | 0,14718 | 0,13409 | 0,14158 | 0,14035 | 0,13963 |
| 529,05675 | 0,14652 | 0,13357 | 0,14172 | 0,13968 | 0,13953 |
| 529,09393 | 0,14579 | 0,13301 | 0,14175 | 0,13896 | 0,13937 |
| 529,13112 | 0,14498 | 0,13242 | 0,14169 | 0,13822 | 0,13916 |
| 529,1683 | 0,14411 | 0,1318 | 0,14152 | 0,13743 | 0,1389 |
| 529,20548 | 0,14318 | 0,13115 | 0,14121 | 0,13659 | 0,13858 |
| 529,24266 | 0,14218 | 0,13046 | 0,14079 | 0,13571 | 0,13819 |
| 529,27984 | 0,14112 | 0,12974 | 0,14027 | 0,13479 | 0,13773 |
| 529,31703 | 0,14 | 0,129 | 0,13963 | 0,13382 | 0,13718 |
| 529,35421 | 0,13881 | 0,12823 | 0,13889 | 0,13279 | 0,13654 |
| 529,39139 | 0,13759 | 0,12743 | 0,13805 | 0,13171 | 0,13583 |
| 529,42857 | 0,13632 | 0,1266 | 0,13709 | 0,13057 | 0,13502 |
| 529,46575 | 0,13501 | 0,12575 | 0,13605 | 0,12939 | 0,13413 |
| 529,50294 | 0,13368 | 0,12489 | 0,13493 | 0,12816 | 0,13313 |
| 529,54012 | 0,13232 | 0,12401 | 0,13375 | 0,12689 | 0,13205 |
| 529,5773 | 0,13096 | 0,12312 | 0,13251 | 0,12558 | 0,13088 |
| 529,61448 | 0,12961 | 0,12222 | 0,13122 | 0,12425 | 0,12965 |
| 529,65166 | 0,12827 | 0,12133 | 0,1299 | 0,1229 | 0,12835 |
| 529,68885 | 0,12695 | 0,12044 | 0,12857 | 0,12155 | 0,12699 |
| 529,72603 | 0,12567 | 0,11956 | 0,12724 | 0,12022 | 0,12559 |
| 529,76321 | 0,12444 | 0,11871 | 0,12593 | 0,11891 | 0,12416 |
| 529,80039 | 0,12328 | 0,11787 | 0,12465 | 0,11764 | 0,12272 |
| 529,83757 | 0,12219 | 0,11707 | 0,12341 | 0,11645 | 0,12129 |
| 529,87476 | 0,12117 | 0,11631 | 0,12225 | 0,11532 | 0,11988 |
| 529,91194 | 0,12024 | 0,11559 | 0,12117 | 0,11429 | 0,1185 |
| 529,94912 | 0,11942 | 0,11492 | 0,12018 | 0,11336 | 0,1172 |
| 529,9863 | 0,11871 | 0,11431 | 0,11928 | 0,11255 | 0,11597 |
| 530,02348 | 0,11811 | 0,11375 | 0,11849 | 0,11186 | 0,11483 |
| 530,06067 | 0,11763 | 0,11325 | 0,11783 | 0,11133 | 0,11379 |
| 530,09785 | 0,11725 | 0,11284 | 0,1173 | 0,11095 | 0,11286 |
| 530,13503 | 0,11699 | 0,11249 | 0,1169 | 0,11072 | 0,11207 |
| 530,17221 | 0,11685 | 0,11221 | 0,11662 | 0,11062 | 0,11142 |
| 530,20939 | 0,11683 | 0,11199 | 0,11647 | 0,11068 | 0,11091 |
| 530,24658 | 0,11692 | 0,11185 | 0,11644 | 0,11089 | 0,11054 |
| 530,28376 | 0,11709 | 0,11177 | 0,11655 | 0,11126 | 0,1103 |
| 530,32094 | 0,11735 | 0,11176 | 0,11677 | 0,11175 | 0,1102 |
| 530,35812 | 0,11768 | 0,11181 | 0,11708 | 0,11236 | 0,11026 |
| 530,3953 | 0,11808 | 0,11191 | 0,11748 | 0,11307 | 0,11044 |
| 530,43249 | 0,11854 | 0,11205 | 0,11794 | 0,11387 | 0,11073 |
| 530,46967 | 0,11902 | 0,11222 | 0,11847 | 0,11475 | 0,11111 |
| 530,50685 | 0,11951 | 0,11242 | 0,11905 | 0,11568 | 0,11159 |
| 530,54403 | 0,12 | 0,11265 | 0,11965 | 0,11665 | 0,11213 |
| 530,58121 | 0,12048 | 0,11287 | 0,12025 | 0,11763 | 0,11275 |
| 530,6184 | 0,12092 | 0,1131 | 0,12084 | 0,1186 | 0,11339 |
| 530,65558 | 0,1213 | 0,11331 | 0,12141 | 0,11955 | 0,11406 |
| 530,69276 | 0,12161 | 0,11349 | 0,12193 | 0,12046 | 0,11473 |
| 530,72994 | 0,12185 | 0,11364 | 0,12239 | 0,1213 | 0,1154 |
| 530,76712 | 0,12199 | 0,11374 | 0,12277 | 0,12206 | 0,11603 |
| 530,80431 | 0,12204 | 0,1138 | 0,12308 | 0,12274 | 0,11662 |
| 530,84149 | 0,12197 | 0,11379 | 0,12329 | 0,12331 | 0,11716 |
| 530,87867 | 0,12176 | 0,11373 | 0,1234 | 0,12378 | 0,11763 |
| 530,91585 | 0,12143 | 0,11359 | 0,12341 | 0,12411 | 0,11804 |
| 530,95303 | 0,12098 | 0,11337 | 0,12329 | 0,12431 | 0,11837 |
| 530,99022 | 0,1204 | 0,11308 | 0,12306 | 0,12439 | 0,1186 |
| 531,0274 | 0,11971 | 0,11272 | 0,12273 | 0,12434 | 0,11875 |
| 531,06458 | 0,11888 | 0,11228 | 0,1223 | 0,12417 | 0,11881 |
| 531,10176 | 0,11793 | 0,11177 | 0,12177 | 0,12388 | 0,1188 |
| 531,13894 | 0,11687 | 0,1112 | 0,12113 | 0,12345 | 0,1187 |
| 531,17613 | 0,11572 | 0,11055 | 0,12041 | 0,12291 | 0,11853 |
| 531,21331 | 0,11448 | 0,10985 | 0,11961 | 0,12227 | 0,11827 |
| 531,25049 | 0,11317 | 0,10911 | 0,11875 | 0,12154 | 0,11794 |
| 531,28767 | 0,11178 | 0,10832 | 0,11784 | 0,12073 | 0,11756 |
| 531,32485 | 0,11034 | 0,1075 | 0,11689 | 0,11984 | 0,11713 |
| 531,36204 | 0,10886 | 0,10665 | 0,1159 | 0,11887 | 0,11666 |
| 531,39922 | 0,10736 | 0,10578 | 0,11488 | 0,11785 | 0,11613 |
| 531,4364 | 0,10583 | 0,1049 | 0,11386 | 0,11678 | 0,11557 |
| 531,47358 | 0,1043 | 0,10403 | 0,11284 | 0,11568 | 0,11497 |
| 531,51076 | 0,10278 | 0,10315 | 0,11182 | 0,11454 | 0,11434 |
| 531,54795 | 0,10128 | 0,10229 | 0,11082 | 0,11337 | 0,11369 |
| 531,58513 | 0,0998 | 0,10144 | 0,10984 | 0,11217 | 0,113 |
| 531,62231 | 0,09835 | 0,10062 | 0,10888 | 0,11095 | 0,11228 |
| 531,65949 | 0,09693 | 0,09982 | 0,10795 | 0,1097 | 0,11152 |
| 531,69667 | 0,09556 | 0,09904 | 0,10705 | 0,10844 | 0,11073 |
| 531,73386 | 0,09423 | 0,09829 | 0,10618 | 0,10716 | 0,10989 |
| 531,77104 | 0,09294 | 0,09756 | 0,10533 | 0,10585 | 0,10901 |
| 531,80822 | 0,0917 | 0,09685 | 0,10451 | 0,10451 | 0,10807 |
| 531,8454 | 0,0905 | 0,09615 | 0,10371 | 0,10314 | 0,10707 |
| 531,88258 | 0,08933 | 0,09547 | 0,10292 | 0,10174 | 0,10599 |
| 531,91977 | 0,08819 | 0,09479 | 0,10213 | 0,1003 | 0,10485 |
| 531,95695 | 0,08707 | 0,09411 | 0,10134 | 0,09883 | 0,10364 |
| 531,99413 | 0,08597 | 0,09342 | 0,10053 | 0,09731 | 0,10235 |
| 532,03131 | 0,08489 | 0,09271 | 0,09971 | 0,09575 | 0,10098 |
| 532,06849 | 0,0838 | 0,09197 | 0,09885 | 0,09415 | 0,09951 |
| 532,10568 | 0,0827 | 0,0912 | 0,09796 | 0,09251 | 0,09797 |
| 532,14286 | 0,0816 | 0,09039 | 0,09702 | 0,09084 | 0,09636 |
| 532,18004 | 0,08047 | 0,08954 | 0,09604 | 0,08913 | 0,09468 |
| 532,21722 | 0,07932 | 0,08864 | 0,09499 | 0,0874 | 0,09293 |
| 532,2544 | 0,07814 | 0,08767 | 0,09387 | 0,08564 | 0,09113 |
| 532,29159 | 0,07693 | 0,08666 | 0,09269 | 0,08387 | 0,08927 |
| 532,32877 | 0,07568 | 0,08559 | 0,09146 | 0,0821 | 0,08739 |
| 532,36595 | 0,07441 | 0,08447 | 0,09016 | 0,08034 | 0,0855 |
| 532,40313 | 0,07311 | 0,08331 | 0,0888 | 0,0786 | 0,0836 |
| 532,44031 | 0,07179 | 0,08209 | 0,08738 | 0,07689 | 0,0817 |
| 532,4775 | 0,07045 | 0,08084 | 0,08592 | 0,07523 | 0,07984 |
| 532,51468 | 0,06911 | 0,07956 | 0,08443 | 0,07362 | 0,07802 |
| 532,55186 | 0,06777 | 0,07827 | 0,08291 | 0,07208 | 0,07627 |
| 532,58904 | 0,06644 | 0,07697 | 0,08138 | 0,07061 | 0,07458 |
| 532,62622 | 0,06515 | 0,07567 | 0,07985 | 0,06923 | 0,07298 |
| 532,66341 | 0,06389 | 0,07439 | 0,07834 | 0,06797 | 0,07148 |
| 532,70059 | 0,06269 | 0,07314 | 0,07687 | 0,06681 | 0,07011 |
| 532,73777 | 0,06155 | 0,07194 | 0,07544 | 0,06577 | 0,06886 |
| 532,77495 | 0,06048 | 0,07079 | 0,07408 | 0,06484 | 0,06773 |
| 532,81213 | 0,0595 | 0,0697 | 0,07278 | 0,06402 | 0,06674 |
| 532,84932 | 0,05861 | 0,06868 | 0,07156 | 0,06333 | 0,06588 |
| 532,8865 | 0,05784 | 0,06776 | 0,07046 | 0,06279 | 0,06518 |
| 532,92368 | 0,05717 | 0,06693 | 0,06947 | 0,06237 | 0,06463 |
| 532,96086 | 0,0566 | 0,06619 | 0,06859 | 0,06206 | 0,06422 |
| 532,99804 | 0,05614 | 0,06555 | 0,06782 | 0,06185 | 0,06393 |
| 533,03523 | 0,05578 | 0,065 | 0,06716 | 0,06174 | 0,06377 |
| 533,07241 | 0,05553 | 0,06455 | 0,06662 | 0,06173 | 0,06372 |
| 533,10959 | 0,05538 | 0,0642 | 0,06621 | 0,06182 | 0,06381 |
| 533,14677 | 0,05531 | 0,06394 | 0,06591 | 0,06198 | 0,06398 |
| 533,18395 | 0,05531 | 0,06375 | 0,06571 | 0,06218 | 0,06424 |
| 533,22114 | 0,05537 | 0,06363 | 0,06559 | 0,06244 | 0,06456 |
| 533,25832 | 0,05548 | 0,06356 | 0,06555 | 0,06272 | 0,06493 |
| 533,2955 | 0,05562 | 0,06355 | 0,06557 | 0,06303 | 0,06535 |
| 533,33268 | 0,05577 | 0,06357 | 0,06565 | 0,06333 | 0,0658 |
| 533,36986 | 0,05592 | 0,06361 | 0,06575 | 0,06363 | 0,06625 |
| 533,40705 | 0,05604 | 0,06366 | 0,06587 | 0,0639 | 0,0667 |
| 533,44423 | 0,05613 | 0,06371 | 0,06598 | 0,06414 | 0,06712 |
| 533,48141 | 0,05618 | 0,06374 | 0,06608 | 0,06433 | 0,06752 |
| 533,51859 | 0,05616 | 0,06374 | 0,06614 | 0,06447 | 0,06787 |
| 533,55577 | 0,05605 | 0,06369 | 0,06615 | 0,06454 | 0,06815 |
| 533,59295 | 0,05586 | 0,06359 | 0,06609 | 0,06454 | 0,06837 |
| 533,63014 | 0,05558 | 0,06343 | 0,06596 | 0,06446 | 0,06852 |
| 533,66732 | 0,05521 | 0,06321 | 0,06575 | 0,06431 | 0,06859 |
| 533,7045 | 0,05473 | 0,06293 | 0,06544 | 0,06408 | 0,06857 |
| 533,74168 | 0,05415 | 0,06256 | 0,06503 | 0,06375 | 0,06846 |
| 533,77886 | 0,05345 | 0,06211 | 0,0645 | 0,06334 | 0,06825 |
| 533,81605 | 0,05266 | 0,06158 | 0,06388 | 0,06285 | 0,06795 |
| 533,85323 | 0,05178 | 0,06099 | 0,06315 | 0,06229 | 0,06757 |
| 533,89041 | 0,05082 | 0,06032 | 0,06234 | 0,06165 | 0,06711 |
| 533,92759 | 0,04978 | 0,05959 | 0,06142 | 0,06095 | 0,06656 |
| 533,96477 | 0,04868 | 0,05879 | 0,06041 | 0,06017 | 0,06592 |
| 534,00196 | 0,04752 | 0,05793 | 0,05932 | 0,05934 | 0,06521 |
| 534,03914 | 0,04632 | 0,05703 | 0,05817 | 0,05846 | 0,06444 |
| 534,07632 | 0,0451 | 0,05609 | 0,05696 | 0,05754 | 0,06361 |
| 534,1135 | 0,04387 | 0,05512 | 0,05571 | 0,05658 | 0,06274 |
| 534,15068 | 0,04264 | 0,05413 | 0,05442 | 0,0556 | 0,06181 |
| 534,18787 | 0,04142 | 0,05312 | 0,05311 | 0,05458 | 0,06085 |
| 534,22505 | 0,04024 | 0,0521 | 0,0518 | 0,05355 | 0,05985 |
| 534,26223 | 0,03909 | 0,05109 | 0,0505 | 0,0525 | 0,05884 |
| 534,29941 | 0,03799 | 0,0501 | 0,04921 | 0,05145 | 0,0578 |
| 534,33659 | 0,03694 | 0,04911 | 0,04795 | 0,05039 | 0,05676 |
| 534,37378 | 0,03596 | 0,04816 | 0,04672 | 0,04934 | 0,05571 |
| 534,41096 | 0,03505 | 0,04724 | 0,04554 | 0,04829 | 0,05466 |
| 534,44814 | 0,03423 | 0,04635 | 0,04442 | 0,04724 | 0,05361 |
| 534,48532 | 0,03348 | 0,0455 | 0,04335 | 0,04621 | 0,05257 |
| 534,5225 | 0,0328 | 0,04469 | 0,04234 | 0,0452 | 0,05154 |
| 534,55969 | 0,0322 | 0,04391 | 0,04139 | 0,04419 | 0,05052 |
| 534,59687 | 0,03167 | 0,04319 | 0,04051 | 0,04321 | 0,04952 |
| 534,63405 | 0,03122 | 0,04252 | 0,0397 | 0,04225 | 0,04854 |
| 534,67123 | 0,03085 | 0,04189 | 0,03895 | 0,04132 | 0,04758 |
| 534,70841 | 0,03053 | 0,04129 | 0,03827 | 0,04041 | 0,04665 |
| 534,7456 | 0,03027 | 0,04074 | 0,03764 | 0,03953 | 0,04574 |
| 534,78278 | 0,03005 | 0,04022 | 0,03707 | 0,03869 | 0,04485 |
| 534,81996 | 0,02988 | 0,03974 | 0,03655 | 0,03788 | 0,04401 |
| 534,85714 | 0,02974 | 0,03929 | 0,03609 | 0,03712 | 0,0432 |
| 534,89432 | 0,02964 | 0,03887 | 0,03567 | 0,03641 | 0,04242 |
| 534,93151 | 0,02955 | 0,03848 | 0,03529 | 0,03574 | 0,04168 |
| 534,96869 | 0,02948 | 0,0381 | 0,03494 | 0,03512 | 0,04098 |
| 535,00587 | 0,02942 | 0,03774 | 0,03463 | 0,03456 | 0,04034 |
| 535,04305 | 0,02936 | 0,0374 | 0,03435 | 0,03407 | 0,03975 |
| 535,08023 | 0,0293 | 0,03708 | 0,0341 | 0,03365 | 0,03921 |
| 535,11742 | 0,02923 | 0,03677 | 0,03387 | 0,03329 | 0,03873 |
| 535,1546 | 0,02916 | 0,03646 | 0,03367 | 0,03301 | 0,0383 |
| 535,19178 | 0,02908 | 0,03618 | 0,03348 | 0,0328 | 0,03793 |
| 535,22896 | 0,02899 | 0,0359 | 0,03332 | 0,03265 | 0,03764 |
| 535,26614 | 0,0289 | 0,03564 | 0,03318 | 0,0326 | 0,03741 |
| 535,30333 | 0,02879 | 0,0354 | 0,03307 | 0,03262 | 0,03725 |
| 535,34051 | 0,02868 | 0,03517 | 0,03298 | 0,03272 | 0,03715 |
| 535,37769 | 0,02858 | 0,03497 | 0,03291 | 0,03288 | 0,03712 |
| 535,41487 | 0,02847 | 0,03479 | 0,03288 | 0,03312 | 0,03715 |
| 535,45205 | 0,02838 | 0,03463 | 0,03287 | 0,03341 | 0,03726 |
| 535,48924 | 0,02829 | 0,03452 | 0,0329 | 0,03378 | 0,03744 |
| 535,52642 | 0,02822 | 0,03444 | 0,03296 | 0,0342 | 0,03767 |
| 535,5636 | 0,02818 | 0,03439 | 0,03306 | 0,03468 | 0,03795 |
| 535,60078 | 0,02817 | 0,03439 | 0,0332 | 0,03519 | 0,03829 |
| 535,63796 | 0,02818 | 0,03442 | 0,03337 | 0,03573 | 0,03868 |
| 535,67515 | 0,02823 | 0,03451 | 0,03359 | 0,03631 | 0,03912 |
| 535,71233 | 0,02831 | 0,03464 | 0,03385 | 0,03691 | 0,03959 |
| 535,74951 | 0,02843 | 0,03482 | 0,03415 | 0,03751 | 0,04009 |
| 535,78669 | 0,02859 | 0,03504 | 0,03448 | 0,03812 | 0,04062 |
| 535,82387 | 0,02879 | 0,03529 | 0,03484 | 0,03872 | 0,04116 |
| 535,86106 | 0,02901 | 0,03558 | 0,03524 | 0,03931 | 0,04171 |
| 535,89824 | 0,02927 | 0,03591 | 0,03566 | 0,03988 | 0,04227 |
| 535,93542 | 0,02955 | 0,03626 | 0,0361 | 0,04041 | 0,04282 |
| 535,9726 | 0,02986 | 0,03662 | 0,03655 | 0,0409 | 0,04335 |
| 536,00978 | 0,03017 | 0,03699 | 0,037 | 0,04135 | 0,04387 |
| 536,04697 | 0,03049 | 0,03737 | 0,03745 | 0,04174 | 0,04436 |
| 536,08415 | 0,0308 | 0,03773 | 0,03789 | 0,04208 | 0,0448 |
| 536,12133 | 0,0311 | 0,03807 | 0,0383 | 0,04236 | 0,0452 |
| 536,15851 | 0,03138 | 0,03838 | 0,03868 | 0,04256 | 0,04555 |
| 536,19569 | 0,03163 | 0,03865 | 0,03902 | 0,04269 | 0,04584 |
| 536,23288 | 0,03183 | 0,03888 | 0,03931 | 0,04275 | 0,04608 |
| 536,27006 | 0,03198 | 0,03905 | 0,03955 | 0,04274 | 0,04624 |
| 536,30724 | 0,03209 | 0,03916 | 0,03972 | 0,04265 | 0,04633 |
| 536,34442 | 0,03213 | 0,03919 | 0,03982 | 0,04249 | 0,04635 |
| 536,3816 | 0,03211 | 0,03914 | 0,03983 | 0,04224 | 0,0463 |
| 536,41879 | 0,03202 | 0,03901 | 0,03978 | 0,04193 | 0,04618 |
| 536,45597 | 0,03185 | 0,03881 | 0,03964 | 0,04155 | 0,04598 |
| 536,49315 | 0,03161 | 0,03853 | 0,03943 | 0,04111 | 0,04571 |
| 536,53033 | 0,03131 | 0,03816 | 0,03914 | 0,04061 | 0,04536 |
| 536,56751 | 0,03095 | 0,0377 | 0,03876 | 0,04006 | 0,04496 |
| 536,6047 | 0,03053 | 0,03718 | 0,03831 | 0,03945 | 0,04449 |
| 536,64188 | 0,03004 | 0,03659 | 0,03779 | 0,03881 | 0,04397 |
| 536,67906 | 0,02951 | 0,03594 | 0,03722 | 0,03814 | 0,04341 |
| 536,71624 | 0,02895 | 0,03524 | 0,0366 | 0,03744 | 0,04279 |
| 536,75342 | 0,02835 | 0,03449 | 0,03593 | 0,03672 | 0,04213 |
| 536,79061 | 0,02773 | 0,03371 | 0,03523 | 0,03598 | 0,04145 |
| 536,82779 | 0,02709 | 0,0329 | 0,03449 | 0,03523 | 0,04074 |
| 536,86497 | 0,02645 | 0,03208 | 0,03375 | 0,03449 | 0,04002 |
| 536,90215 | 0,02582 | 0,03125 | 0,03299 | 0,03374 | 0,03928 |
| 536,93933 | 0,02519 | 0,03042 | 0,03224 | 0,033 | 0,03853 |
| 536,97652 | 0,02458 | 0,0296 | 0,03149 | 0,03227 | 0,03778 |
| 537,0137 | 0,024 | 0,0288 | 0,03076 | 0,03155 | 0,03703 |
| 537,05088 | 0,02343 | 0,02802 | 0,03005 | 0,03084 | 0,03628 |
| 537,08806 | 0,0229 | 0,02728 | 0,02937 | 0,03015 | 0,03554 |
| 537,12524 | 0,0224 | 0,02656 | 0,02871 | 0,02946 | 0,0348 |
| 537,16243 | 0,02193 | 0,02587 | 0,02808 | 0,02879 | 0,03408 |
| 537,19961 | 0,02149 | 0,02523 | 0,02749 | 0,02813 | 0,03336 |
| 537,23679 | 0,02108 | 0,02462 | 0,02693 | 0,02749 | 0,03266 |
| 537,27397 | 0,02069 | 0,02404 | 0,0264 | 0,02685 | 0,03196 |
| 537,31115 | 0,02032 | 0,02349 | 0,0259 | 0,02622 | 0,03128 |
| 537,34834 | 0,01998 | 0,02297 | 0,02543 | 0,0256 | 0,0306 |
| 537,38552 | 0,01964 | 0,02248 | 0,02497 | 0,02498 | 0,02994 |
| 537,4227 | 0,01932 | 0,02201 | 0,02454 | 0,02437 | 0,02929 |
| 537,45988 | 0,019 | 0,02155 | 0,02412 | 0,02376 | 0,02864 |
| 537,49706 | 0,01868 | 0,02111 | 0,02371 | 0,02316 | 0,028 |
| 537,53425 | 0,01835 | 0,02067 | 0,0233 | 0,02256 | 0,02738 |
| 537,57143 | 0,01802 | 0,02023 | 0,0229 | 0,02197 | 0,02676 |
| 537,60861 | 0,01768 | 0,0198 | 0,0225 | 0,02139 | 0,02616 |
| 537,64579 | 0,01733 | 0,01936 | 0,0221 | 0,02081 | 0,02556 |
| 537,68297 | 0,01697 | 0,01891 | 0,02169 | 0,02025 | 0,02498 |
| 537,72016 | 0,0166 | 0,01845 | 0,02127 | 0,01969 | 0,02441 |
| 537,75734 | 0,01622 | 0,01799 | 0,02084 | 0,01916 | 0,02386 |
| 537,79452 | 0,01583 | 0,01751 | 0,02041 | 0,01863 | 0,02332 |
| 537,8317 | 0,01543 | 0,01702 | 0,01997 | 0,01812 | 0,0228 |
| 537,86888 | 0,01502 | 0,01652 | 0,01952 | 0,01763 | 0,02229 |
| 537,90607 | 0,01462 | 0,01601 | 0,01907 | 0,01716 | 0,02179 |
| 537,94325 | 0,01421 | 0,0155 | 0,01862 | 0,01671 | 0,02131 |
| 537,98043 | 0,01381 | 0,01497 | 0,01816 | 0,01628 | 0,02085 |
| 538,01761 | 0,01341 | 0,01445 | 0,0177 | 0,01586 | 0,02039 |
| 538,05479 | 0,01303 | 0,01392 | 0,01725 | 0,01545 | 0,01995 |
| 538,09198 | 0,01265 | 0,0134 | 0,0168 | 0,01506 | 0,01951 |
| 538,12916 | 0,01229 | 0,01288 | 0,01636 | 0,01468 | 0,01908 |
| 538,16634 | 0,01194 | 0,01237 | 0,01593 | 0,01431 | 0,01865 |
| 538,20352 | 0,01161 | 0,01187 | 0,01551 | 0,01394 | 0,01822 |
| 538,2407 | 0,01129 | 0,01138 | 0,0151 | 0,01358 | 0,01779 |
| 538,27789 | 0,01099 | 0,01091 | 0,0147 | 0,01321 | 0,01735 |
| 538,31507 | 0,01071 | 0,01045 | 0,01431 | 0,01285 | 0,0169 |
| 538,35225 | 0,01044 | 0,01 | 0,01393 | 0,01247 | 0,01644 |
| 538,38943 | 0,01018 | 0,00957 | 0,01357 | 0,01209 | 0,01597 |
| 538,42661 | 0,00993 | 0,00916 | 0,01321 | 0,0117 | 0,01548 |
| 538,4638 | 0,00968 | 0,00876 | 0,01286 | 0,0113 | 0,01498 |
| 538,50098 | 0,00945 | 0,00839 | 0,01251 | 0,01089 | 0,01446 |
| 538,53816 | 0,00921 | 0,00802 | 0,01217 | 0,01047 | 0,01393 |
| 538,57534 | 0,00897 | 0,00767 | 0,01183 | 0,01004 | 0,01339 |
| 538,61252 | 0,00873 | 0,00733 | 0,01149 | 0,00959 | 0,01282 |
| 538,64971 | 0,00849 | 0,00701 | 0,01116 | 0,00914 | 0,01225 |
| 538,68689 | 0,00824 | 0,00669 | 0,01081 | 0,00868 | 0,01166 |
| 538,72407 | 0,00798 | 0,00639 | 0,01046 | 0,00821 | 0,01107 |
| 538,76125 | 0,00771 | 0,00609 | 0,01011 | 0,00774 | 0,01048 |
| 538,79843 | 0,00743 | 0,0058 | 0,00975 | 0,00728 | 0,00988 |
| 538,83562 | 0,00714 | 0,00552 | 0,00938 | 0,00681 | 0,00928 |
| 538,8728 | 0,00684 | 0,00524 | 0,00901 | 0,00635 | 0,00869 |
| 538,90998 | 0,00653 | 0,00497 | 0,00863 | 0,0059 | 0,0081 |
| 538,94716 | 0,00622 | 0,0047 | 0,00824 | 0,00546 | 0,00753 |
| 538,98434 | 0,0059 | 0,00444 | 0,00785 | 0,00503 | 0,00697 |
| 539,02153 | 0,00557 | 0,00418 | 0,00746 | 0,00462 | 0,00643 |
| 539,05871 | 0,00524 | 0,00393 | 0,00706 | 0,00423 | 0,0059 |
| 539,09589 | 0,0049 | 0,00368 | 0,00666 | 0,00386 | 0,0054 |
| 539,13307 | 0,00457 | 0,00344 | 0,00626 | 0,0035 | 0,00493 |
| 539,17025 | 0,00425 | 0,0032 | 0,00586 | 0,00317 | 0,00447 |
| 539,20744 | 0,00393 | 0,00297 | 0,00547 | 0,00286 | 0,00404 |
| 539,24462 | 0,00361 | 0,00275 | 0,00508 | 0,00257 | 0,00364 |
| 539,2818 | 0,00331 | 0,00254 | 0,00471 | 0,00231 | 0,00327 |
| 539,31898 | 0,00301 | 0,00233 | 0,00434 | 0,00206 | 0,00293 |
| 539,35616 | 0,00273 | 0,00213 | 0,00399 | 0,00183 | 0,00261 |
| 539,39335 | 0,00247 | 0,00195 | 0,00365 | 0,00163 | 0,00231 |
| 539,43053 | 0,00222 | 0,00177 | 0,00332 | 0,00144 | 0,00204 |
| 539,46771 | 0,00198 | 0,0016 | 0,00301 | 0,00128 | 0,0018 |
| 539,50489 | 0,00176 | 0,00144 | 0,00272 | 0,00112 | 0,00158 |
| 539,54207 | 0,00156 | 0,00129 | 0,00245 | 0,00099 | 0,00138 |
| 539,57926 | 0,00137 | 0,00116 | 0,00219 | 0,00087 | 0,0012 |
| 539,61644 | 0,0012 | 0,00103 | 0,00195 | 0,00076 | 0,00104 |
| 539,65362 | 0,00105 | 0,00091 | 0,00173 | 0,00067 | 9e-04 |
| 539,6908 | 9e-04 | 8e-04 | 0,00153 | 0,00058 | 0,00077 |
| 539,72798 | 0,00078 | 0,00071 | 0,00135 | 0,00051 | 0,00067 |
| 539,76517 | 0,00067 | 0,00062 | 0,00118 | 0,00044 | 0,00057 |
| 539,80235 | 0,00057 | 0,00054 | 0,00103 | 0,00038 | 0,00048 |
| 539,83953 | 0,00048 | 0,00047 | 0,00089 | 0,00033 | 0,00041 |
| 539,87671 | 0,00041 | 4e-04 | 0,00077 | 0,00029 | 0,00035 |
| 539,91389 | 0,00034 | 0,00035 | 0,00066 | 0,00025 | 0,00029 |
| 539,95108 | 0,00029 | 3e-04 | 0,00056 | 0,00022 | 0,00025 |
| 539,98826 | 0,00024 | 0,00025 | 0,00048 | 0,00019 | 0,00021 |
| 540,02544 | 2e-04 | 0,00021 | 0,00041 | 0,00016 | 0,00017 |
| 540,06262 | 0,00016 | 0,00018 | 0,00034 | 0,00014 | 0,00014 |
| 540,0998 | 0,00013 | 0,00015 | 0,00029 | 0,00012 | 0,00012 |
| 540,13699 | 0,00011 | 0,00013 | 0,00024 | 1e-04 | 1e-04 |
| 540,17417 | 9e-05 | 1e-04 | 2e-04 | 9e-05 | 8e-05 |
| 540,21135 | 7e-05 | 9e-05 | 0,00017 | 7e-05 | 7e-05 |
| 540,24853 | 6e-05 | 7e-05 | 0,00014 | 6e-05 | 5e-05 |
| 540,28571 | 4e-05 | 6e-05 | 0,00011 | 5e-05 | 4e-05 |
| 540,3229 | 4e-05 | 5e-05 | 9e-05 | 4e-05 | 3e-05 |
| 540,36008 | 3e-05 | 4e-05 | 7e-05 | 4e-05 | 3e-05 |
| 540,39726 | 2e-05 | 3e-05 | 6e-05 | 3e-05 | 2e-05 |
| 540,43444 | 2e-05 | 3e-05 | 5e-05 | 3e-05 | 2e-05 |
| 540,47162 | 1e-05 | 2e-05 | 4e-05 | 2e-05 | 1e-05 |
| 540,50881 | 1e-05 | 2e-05 | 3e-05 | 2e-05 | 1e-05 |
| 540,54599 | 1e-05 | 1e-05 | 2e-05 | 1e-05 | 1e-05 |
| 540,58317 | 1e-05 | 1e-05 | 2e-05 | 1e-05 | 1e-05 |
| 540,62035 | 0 | 1e-05 | 2e-05 | 1e-05 | 1e-05 |
| 540,65753 | 0 | 1e-05 | 1e-05 | 1e-05 | 0 |
| 540,69472 | 0 | 0 | 1e-05 | 1e-05 | 0 |
| 540,7319 | 0 | 0 | 1e-05 | 1e-05 | 0 |
| 540,76908 | 0 | 0 | 1e-05 | 0 | 0 |
| 540,80626 | 0 | 0 | 0 | 0 | 0 |
| 540,84344 | 0 | 0 | 0 | 0 | 0 |
| 540,88063 | 0 | 0 | 0 | 0 | 0 |
| 540,91781 | 0 | 0 | 0 | 0 | 0 |
| 540,95499 | 0 | 0 | 0 | 0 | 0 |
| 540,99217 | 0 | 0 | 0 | 0 | 0 |
| 541,02935 | 0 | 0 | 0 | 0 | 0 |
| 541,06654 | 0 | 0 | 0 | 0 | 0 |
| 541,10372 | 0 | 0 | 0 | 0 | 0 |
| 541,1409 | 0 | 0 | 0 | 0 | 0 |
| 541,17808 | 0 | 0 | 0 | 0 | 0 |
| 541,21526 | 0 | 0 | 0 | 0 | 0 |
| 541,25245 | 0 | 0 | 0 | 0 | 0 |
| 541,28963 | 0 | 0 | 0 | 0 | 0 |
| 541,32681 | 0 | 0 | 0 | 0 | 0 |
| 541,36399 | 0 | 0 | 0 | 0 | 0 |
| 541,40117 | 0 | 0 | 0 | 0 | 0 |
| 541,43836 | 0 | 0 | 0 | 0 | 0 |
| 541,47554 | 0 | 0 | 0 | 0 | 0 |
| 541,51272 | 0 | 0 | 0 | 0 | 0 |
| 541,5499 | 0 | 0 | 0 | 0 | 0 |
| 541,58708 | 0 | 0 | 0 | 0 | 0 |
| 541,62427 | 0 | 0 | 0 | 0 | 0 |
| 541,66145 | 0 | 0 | 0 | 0 | 0 |
| 541,69863 | 0 | 0 | 0 | 0 | 0 |
| 541,73581 | 0 | 0 | 0 | 0 | 0 |
| 541,77299 | 0 | 0 | 0 | 0 | 0 |
| 541,81018 | 0 | 0 | 0 | 0 | 0 |
| 541,84736 | 0 | 0 | 0 | 0 | 0 |
| 541,88454 | 0 | 0 | 0 | 0 | 0 |
| 541,92172 | 0 | 0 | 0 | 0 | 0 |
| 541,9589 | 0 | 0 | 0 | 0 | 0 |
| 541,99609 | 0 | 0 | 0 | 0 | 0 |
| 542,03327 | 0 | 0 | 0 | 0 | 0 |
| 542,07045 | 0 | 0 | 0 | 0 | 0 |
| 542,10763 | 0 | 0 | 0 | 0 | 0 |
| 542,14481 | 0 | 0 | 0 | 0 | 0 |
| 542,182 | 0 | 0 | 0 | 0 | 0 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00232 | 0 | 0,00268 | 0,00255 | 0,00115 |
| 524,03718 | 0,00244 | 0 | 0,00282 | 0,00269 | 0,00123 |
| 524,07436 | 0,00256 | 0 | 0,00297 | 0,00283 | 0,00131 |
| 524,11155 | 0,00269 | 1e-05 | 0,00313 | 0,00298 | 0,00139 |
| 524,14873 | 0,00282 | 1e-05 | 0,0033 | 0,00313 | 0,00148 |
| 524,18591 | 0,00295 | 1e-05 | 0,00347 | 0,00329 | 0,00158 |
| 524,22309 | 0,00309 | 1e-05 | 0,00364 | 0,00346 | 0,00168 |
| 524,26027 | 0,00324 | 1e-05 | 0,00383 | 0,00363 | 0,00178 |
| 524,29746 | 0,00339 | 1e-05 | 0,00402 | 0,00381 | 0,00189 |
| 524,33464 | 0,00354 | 1e-05 | 0,00422 | 0,004 | 0,00201 |
| 524,37182 | 0,0037 | 1e-05 | 0,00443 | 0,00419 | 0,00213 |
| 524,409 | 0,00386 | 2e-05 | 0,00464 | 0,00439 | 0,00226 |
| 524,44618 | 0,00402 | 2e-05 | 0,00486 | 0,0046 | 0,00239 |
| 524,48337 | 0,00419 | 2e-05 | 0,0051 | 0,00482 | 0,00254 |
| 524,52055 | 0,00437 | 2e-05 | 0,00533 | 0,00504 | 0,00268 |
| 524,55773 | 0,00455 | 3e-05 | 0,00558 | 0,00528 | 0,00284 |
| 524,59491 | 0,00473 | 3e-05 | 0,00583 | 0,00552 | 0,003 |
| 524,63209 | 0,00492 | 3e-05 | 0,00609 | 0,00577 | 0,00317 |
| 524,66928 | 0,00511 | 4e-05 | 0,00637 | 0,00602 | 0,00335 |
| 524,70646 | 0,0053 | 4e-05 | 0,00665 | 0,00629 | 0,00354 |
| 524,74364 | 0,0055 | 5e-05 | 0,00693 | 0,00657 | 0,00374 |
| 524,78082 | 0,00571 | 5e-05 | 0,00723 | 0,00685 | 0,00394 |
| 524,818 | 0,00592 | 6e-05 | 0,00754 | 0,00714 | 0,00416 |
| 524,85519 | 0,00613 | 6e-05 | 0,00785 | 0,00745 | 0,00438 |
| 524,89237 | 0,00635 | 7e-05 | 0,00818 | 0,00776 | 0,00461 |
| 524,92955 | 0,00658 | 8e-05 | 0,00851 | 0,00808 | 0,00486 |
| 524,96673 | 0,0068 | 9e-05 | 0,00885 | 0,00841 | 0,00511 |
| 525,00391 | 0,00704 | 1e-04 | 0,00921 | 0,00875 | 0,00537 |
| 525,0411 | 0,00727 | 0,00011 | 0,00956 | 0,00911 | 0,00565 |
| 525,07828 | 0,00751 | 0,00013 | 0,00994 | 0,00947 | 0,00593 |
| 525,11546 | 0,00776 | 0,00014 | 0,01031 | 0,00984 | 0,00623 |
| 525,15264 | 0,00801 | 0,00016 | 0,0107 | 0,01022 | 0,00654 |
| 525,18982 | 0,00827 | 0,00017 | 0,0111 | 0,01062 | 0,00686 |
| 525,22701 | 0,00853 | 0,00019 | 0,01151 | 0,01102 | 0,00719 |
| 525,26419 | 0,00879 | 0,00022 | 0,01192 | 0,01144 | 0,00754 |
| 525,30137 | 0,00906 | 0,00024 | 0,01235 | 0,01186 | 0,0079 |
| 525,33855 | 0,00934 | 0,00026 | 0,01278 | 0,0123 | 0,00827 |
| 525,37573 | 0,00962 | 0,00029 | 0,01323 | 0,01275 | 0,00865 |
| 525,41292 | 0,0099 | 0,00032 | 0,01368 | 0,01321 | 0,00905 |
| 525,4501 | 0,0102 | 0,00036 | 0,01414 | 0,01368 | 0,00946 |
| 525,48728 | 0,01049 | 0,00039 | 0,01461 | 0,01416 | 0,00989 |
| 525,52446 | 0,0108 | 0,00043 | 0,01508 | 0,01466 | 0,01033 |
| 525,56164 | 0,01111 | 0,00048 | 0,01557 | 0,01517 | 0,01078 |
| 525,59883 | 0,01142 | 0,00052 | 0,01607 | 0,01568 | 0,01126 |
| 525,63601 | 0,01174 | 0,00058 | 0,01657 | 0,01622 | 0,01174 |
| 525,67319 | 0,01207 | 0,00063 | 0,01709 | 0,01676 | 0,01224 |
| 525,71037 | 0,0124 | 0,00069 | 0,0176 | 0,01732 | 0,01276 |
| 525,74755 | 0,01274 | 0,00076 | 0,01813 | 0,01789 | 0,01329 |
| 525,78474 | 0,01309 | 0,00083 | 0,01867 | 0,01846 | 0,01384 |
| 525,82192 | 0,01345 | 0,00091 | 0,01921 | 0,01906 | 0,01441 |
| 525,8591 | 0,01381 | 0,00099 | 0,01977 | 0,01966 | 0,01498 |
| 525,89628 | 0,01418 | 0,00108 | 0,02032 | 0,02028 | 0,01558 |
| 525,93346 | 0,01456 | 0,00118 | 0,02089 | 0,02091 | 0,0162 |
| 525,97065 | 0,01495 | 0,00128 | 0,02146 | 0,02155 | 0,01682 |
| 526,00783 | 0,01535 | 0,00139 | 0,02204 | 0,02221 | 0,01747 |
| 526,04501 | 0,01575 | 0,00152 | 0,02263 | 0,02287 | 0,01813 |
| 526,08219 | 0,01616 | 0,00165 | 0,02322 | 0,02355 | 0,01881 |
| 526,11937 | 0,01659 | 0,00178 | 0,02382 | 0,02425 | 0,01951 |
| 526,15656 | 0,01702 | 0,00194 | 0,02443 | 0,02495 | 0,02022 |
| 526,19374 | 0,01746 | 0,00209 | 0,02504 | 0,02567 | 0,02095 |
| 526,23092 | 0,01792 | 0,00226 | 0,02565 | 0,0264 | 0,0217 |
| 526,2681 | 0,01838 | 0,00245 | 0,02627 | 0,02714 | 0,02246 |
| 526,30528 | 0,01885 | 0,00264 | 0,0269 | 0,0279 | 0,02324 |
| 526,34247 | 0,01934 | 0,00285 | 0,02753 | 0,02867 | 0,02404 |
| 526,37965 | 0,01984 | 0,00307 | 0,02817 | 0,02945 | 0,02485 |
| 526,41683 | 0,02035 | 0,0033 | 0,02881 | 0,03024 | 0,02568 |
| 526,45401 | 0,02087 | 0,00355 | 0,02945 | 0,03105 | 0,02653 |
| 526,49119 | 0,02141 | 0,00382 | 0,0301 | 0,03186 | 0,02738 |
| 526,52838 | 0,02195 | 0,0041 | 0,03075 | 0,03269 | 0,02826 |
| 526,56556 | 0,02251 | 0,00439 | 0,03141 | 0,03353 | 0,02916 |
| 526,60274 | 0,02308 | 0,00471 | 0,03207 | 0,03439 | 0,03006 |
| 526,63992 | 0,02367 | 0,00504 | 0,03273 | 0,03525 | 0,03098 |
| 526,6771 | 0,02427 | 0,00539 | 0,03339 | 0,03612 | 0,03192 |
| 526,71429 | 0,02488 | 0,00576 | 0,03406 | 0,03701 | 0,03287 |
| 526,75147 | 0,0255 | 0,00615 | 0,03473 | 0,03791 | 0,03383 |
| 526,78865 | 0,02615 | 0,00655 | 0,0354 | 0,03882 | 0,03481 |
| 526,82583 | 0,0268 | 0,00698 | 0,03607 | 0,03974 | 0,0358 |
| 526,86301 | 0,02747 | 0,00744 | 0,03675 | 0,04067 | 0,0368 |
| 526,9002 | 0,02815 | 0,00791 | 0,03743 | 0,04161 | 0,03782 |
| 526,93738 | 0,02885 | 0,00841 | 0,0381 | 0,04256 | 0,03884 |
| 526,97456 | 0,02956 | 0,00893 | 0,03878 | 0,04352 | 0,03988 |
| 527,01174 | 0,03028 | 0,00947 | 0,03946 | 0,04449 | 0,04092 |
| 527,04892 | 0,03102 | 0,01003 | 0,04014 | 0,04546 | 0,04198 |
| 527,08611 | 0,03177 | 0,01063 | 0,04082 | 0,04645 | 0,04304 |
| 527,12329 | 0,03254 | 0,01125 | 0,0415 | 0,04744 | 0,04412 |
| 527,16047 | 0,03332 | 0,01189 | 0,04218 | 0,04844 | 0,0452 |
| 527,19765 | 0,03412 | 0,01256 | 0,04286 | 0,04945 | 0,04628 |
| 527,23483 | 0,03493 | 0,01325 | 0,04354 | 0,05047 | 0,04738 |
| 527,27202 | 0,03575 | 0,01397 | 0,04422 | 0,05149 | 0,04848 |
| 527,3092 | 0,03658 | 0,01473 | 0,0449 | 0,05252 | 0,04958 |
| 527,34638 | 0,03743 | 0,0155 | 0,04558 | 0,05355 | 0,05069 |
| 527,38356 | 0,03829 | 0,0163 | 0,04625 | 0,05459 | 0,0518 |
| 527,42074 | 0,03916 | 0,01714 | 0,04693 | 0,05563 | 0,05291 |
| 527,45793 | 0,04005 | 0,018 | 0,0476 | 0,05668 | 0,05403 |
| 527,49511 | 0,04094 | 0,01888 | 0,04828 | 0,05773 | 0,05515 |
| 527,53229 | 0,04185 | 0,0198 | 0,04895 | 0,05879 | 0,05626 |
| 527,56947 | 0,04277 | 0,02074 | 0,04962 | 0,05984 | 0,05738 |
| 527,60665 | 0,04369 | 0,0217 | 0,05028 | 0,0609 | 0,05849 |
| 527,64384 | 0,04463 | 0,0227 | 0,05095 | 0,06196 | 0,0596 |
| 527,68102 | 0,04557 | 0,02373 | 0,05161 | 0,06302 | 0,06071 |
| 527,7182 | 0,04652 | 0,02477 | 0,05227 | 0,06407 | 0,06182 |
| 527,75538 | 0,04748 | 0,02585 | 0,05293 | 0,06513 | 0,06292 |
| 527,79256 | 0,04845 | 0,02696 | 0,05359 | 0,06619 | 0,06401 |
| 527,82975 | 0,04942 | 0,02808 | 0,05424 | 0,06724 | 0,0651 |
| 527,86693 | 0,0504 | 0,02924 | 0,05489 | 0,06829 | 0,06618 |
| 527,90411 | 0,05139 | 0,03042 | 0,05554 | 0,06934 | 0,06725 |
| 527,94129 | 0,05237 | 0,03162 | 0,05618 | 0,07038 | 0,06832 |
| 527,97847 | 0,05336 | 0,03285 | 0,05682 | 0,07141 | 0,06937 |
| 528,01566 | 0,05436 | 0,0341 | 0,05746 | 0,07244 | 0,07041 |
| 528,05284 | 0,05535 | 0,03537 | 0,0581 | 0,07347 | 0,07145 |
| 528,09002 | 0,05635 | 0,03666 | 0,05873 | 0,07448 | 0,07247 |
| 528,1272 | 0,05734 | 0,03798 | 0,05935 | 0,07549 | 0,07348 |
| 528,16438 | 0,05834 | 0,03931 | 0,05998 | 0,07649 | 0,07448 |
| 528,20157 | 0,05933 | 0,04066 | 0,0606 | 0,07748 | 0,07546 |
| 528,23875 | 0,06032 | 0,04203 | 0,06121 | 0,07845 | 0,07643 |
| 528,27593 | 0,0613 | 0,04342 | 0,06182 | 0,07942 | 0,07738 |
| 528,31311 | 0,06228 | 0,04482 | 0,06243 | 0,08037 | 0,07832 |
| 528,35029 | 0,06326 | 0,04623 | 0,06303 | 0,08131 | 0,07925 |
| 528,38748 | 0,06423 | 0,04766 | 0,06363 | 0,08224 | 0,08015 |
| 528,42466 | 0,06519 | 0,0491 | 0,06422 | 0,08315 | 0,08105 |
| 528,46184 | 0,06614 | 0,05055 | 0,06481 | 0,08404 | 0,08192 |
| 528,49902 | 0,06709 | 0,05201 | 0,06539 | 0,08492 | 0,08278 |
| 528,5362 | 0,06803 | 0,05348 | 0,06597 | 0,08579 | 0,08362 |
| 528,57339 | 0,06895 | 0,05496 | 0,06655 | 0,08663 | 0,08444 |
| 528,61057 | 0,06986 | 0,05644 | 0,06711 | 0,08746 | 0,08525 |
| 528,64775 | 0,07076 | 0,05792 | 0,06768 | 0,08826 | 0,08604 |
| 528,68493 | 0,07165 | 0,05941 | 0,06823 | 0,08905 | 0,0868 |
| 528,72211 | 0,07253 | 0,06089 | 0,06878 | 0,08982 | 0,08755 |
| 528,7593 | 0,07338 | 0,06238 | 0,06933 | 0,09056 | 0,08829 |
| 528,79648 | 0,07423 | 0,06387 | 0,06987 | 0,09128 | 0,08899 |
| 528,83366 | 0,07506 | 0,06535 | 0,0704 | 0,09199 | 0,08969 |
| 528,87084 | 0,07587 | 0,06683 | 0,07092 | 0,09266 | 0,09037 |
| 528,90802 | 0,07666 | 0,0683 | 0,07144 | 0,09332 | 0,09102 |
| 528,94521 | 0,07744 | 0,06976 | 0,07196 | 0,09394 | 0,09166 |
| 528,98239 | 0,07819 | 0,07122 | 0,07246 | 0,09454 | 0,09228 |
| 529,01957 | 0,07893 | 0,07266 | 0,07296 | 0,09513 | 0,09287 |
| 529,05675 | 0,07965 | 0,07409 | 0,07345 | 0,09567 | 0,09346 |
| 529,09393 | 0,08035 | 0,07551 | 0,07394 | 0,0962 | 0,09402 |
| 529,13112 | 0,08102 | 0,07691 | 0,07441 | 0,0967 | 0,09457 |
| 529,1683 | 0,08168 | 0,07829 | 0,07488 | 0,09716 | 0,0951 |
| 529,20548 | 0,08231 | 0,07966 | 0,07534 | 0,09761 | 0,09561 |
| 529,24266 | 0,08293 | 0,08101 | 0,0758 | 0,09802 | 0,0961 |
| 529,27984 | 0,08352 | 0,08233 | 0,07624 | 0,09841 | 0,09658 |
| 529,31703 | 0,08409 | 0,08364 | 0,07668 | 0,09877 | 0,09704 |
| 529,35421 | 0,08464 | 0,08492 | 0,07711 | 0,09909 | 0,09749 |
| 529,39139 | 0,08517 | 0,08617 | 0,07753 | 0,0994 | 0,09792 |
| 529,42857 | 0,08567 | 0,0874 | 0,07794 | 0,09966 | 0,09833 |
| 529,46575 | 0,08615 | 0,0886 | 0,07834 | 0,0999 | 0,09873 |
| 529,50294 | 0,08661 | 0,08977 | 0,07874 | 0,10012 | 0,09911 |
| 529,54012 | 0,08705 | 0,09091 | 0,07912 | 0,10029 | 0,09948 |
| 529,5773 | 0,08746 | 0,09202 | 0,07949 | 0,10045 | 0,09983 |
| 529,61448 | 0,08786 | 0,09309 | 0,07986 | 0,10057 | 0,10017 |
| 529,65166 | 0,08823 | 0,09413 | 0,08022 | 0,10066 | 0,1005 |
| 529,68885 | 0,08858 | 0,09514 | 0,08057 | 0,10073 | 0,10082 |
| 529,72603 | 0,08891 | 0,0961 | 0,08091 | 0,10075 | 0,10112 |
| 529,76321 | 0,08922 | 0,09703 | 0,08124 | 0,10076 | 0,10141 |
| 529,80039 | 0,0895 | 0,09794 | 0,08156 | 0,10073 | 0,10168 |
| 529,83757 | 0,08978 | 0,09879 | 0,08187 | 0,10067 | 0,10195 |
| 529,87476 | 0,09002 | 0,0996 | 0,08217 | 0,10059 | 0,1022 |
| 529,91194 | 0,09025 | 0,10038 | 0,08246 | 0,10048 | 0,10245 |
| 529,94912 | 0,09047 | 0,10111 | 0,08274 | 0,10034 | 0,10268 |
| 529,9863 | 0,09066 | 0,1018 | 0,08301 | 0,10018 | 0,1029 |
| 530,02348 | 0,09084 | 0,10246 | 0,08327 | 0,09998 | 0,10311 |
| 530,06067 | 0,091 | 0,10306 | 0,08353 | 0,09976 | 0,10331 |
| 530,09785 | 0,09115 | 0,10363 | 0,08377 | 0,09951 | 0,10351 |
| 530,13503 | 0,09128 | 0,10415 | 0,084 | 0,09924 | 0,10369 |
| 530,17221 | 0,0914 | 0,10463 | 0,08423 | 0,09894 | 0,10386 |
| 530,20939 | 0,0915 | 0,10507 | 0,08444 | 0,09862 | 0,10403 |
| 530,24658 | 0,09159 | 0,10546 | 0,08465 | 0,09827 | 0,10418 |
| 530,28376 | 0,09167 | 0,10582 | 0,08484 | 0,0979 | 0,10432 |
| 530,32094 | 0,09174 | 0,10612 | 0,08503 | 0,0975 | 0,10446 |
| 530,35812 | 0,09179 | 0,10639 | 0,08521 | 0,09709 | 0,10458 |
| 530,3953 | 0,09184 | 0,10662 | 0,08538 | 0,09665 | 0,1047 |
| 530,43249 | 0,09188 | 0,1068 | 0,08554 | 0,09619 | 0,10481 |
| 530,46967 | 0,09191 | 0,10694 | 0,08569 | 0,09572 | 0,10491 |
| 530,50685 | 0,09194 | 0,10705 | 0,08584 | 0,09522 | 0,105 |
| 530,54403 | 0,09196 | 0,10711 | 0,08597 | 0,0947 | 0,10508 |
| 530,58121 | 0,09197 | 0,10713 | 0,0861 | 0,09417 | 0,10516 |
| 530,6184 | 0,09198 | 0,10713 | 0,08622 | 0,09362 | 0,10522 |
| 530,65558 | 0,09199 | 0,10707 | 0,08633 | 0,09306 | 0,10528 |
| 530,69276 | 0,09199 | 0,10699 | 0,08644 | 0,09248 | 0,10532 |
| 530,72994 | 0,09199 | 0,10688 | 0,08653 | 0,09188 | 0,10536 |
| 530,76712 | 0,09199 | 0,10673 | 0,08662 | 0,09128 | 0,10538 |
| 530,80431 | 0,09199 | 0,10655 | 0,08671 | 0,09065 | 0,1054 |
| 530,84149 | 0,09199 | 0,10634 | 0,08679 | 0,09002 | 0,10541 |
| 530,87867 | 0,092 | 0,1061 | 0,08686 | 0,08938 | 0,1054 |
| 530,91585 | 0,092 | 0,10583 | 0,08692 | 0,08873 | 0,10539 |
| 530,95303 | 0,092 | 0,10555 | 0,08698 | 0,08807 | 0,10537 |
| 530,99022 | 0,09201 | 0,10523 | 0,08704 | 0,0874 | 0,10533 |
| 531,0274 | 0,09202 | 0,1049 | 0,08708 | 0,08672 | 0,10529 |
| 531,06458 | 0,09204 | 0,10455 | 0,08713 | 0,08604 | 0,10523 |
| 531,10176 | 0,09206 | 0,10417 | 0,08717 | 0,08535 | 0,10517 |
| 531,13894 | 0,09208 | 0,10378 | 0,0872 | 0,08466 | 0,10509 |
| 531,17613 | 0,09211 | 0,10338 | 0,08723 | 0,08396 | 0,105 |
| 531,21331 | 0,09215 | 0,10297 | 0,08725 | 0,08327 | 0,1049 |
| 531,25049 | 0,09219 | 0,10254 | 0,08727 | 0,08257 | 0,10479 |
| 531,28767 | 0,09224 | 0,10211 | 0,08729 | 0,08187 | 0,10466 |
| 531,32485 | 0,0923 | 0,10166 | 0,08731 | 0,08117 | 0,10453 |
| 531,36204 | 0,09236 | 0,10122 | 0,08732 | 0,08047 | 0,10438 |
| 531,39922 | 0,09243 | 0,10077 | 0,08733 | 0,07977 | 0,10422 |
| 531,4364 | 0,0925 | 0,10031 | 0,08733 | 0,07907 | 0,10405 |
| 531,47358 | 0,09258 | 0,09986 | 0,08734 | 0,07838 | 0,10386 |
| 531,51076 | 0,09267 | 0,09941 | 0,08734 | 0,07769 | 0,10366 |
| 531,54795 | 0,09277 | 0,09897 | 0,08734 | 0,07701 | 0,10345 |
| 531,58513 | 0,09287 | 0,09853 | 0,08734 | 0,07633 | 0,10323 |
| 531,62231 | 0,09298 | 0,0981 | 0,08733 | 0,07566 | 0,10299 |
| 531,65949 | 0,0931 | 0,09767 | 0,08733 | 0,07499 | 0,10274 |
| 531,69667 | 0,09322 | 0,09726 | 0,08732 | 0,07434 | 0,10248 |
| 531,73386 | 0,09335 | 0,09686 | 0,08731 | 0,07369 | 0,10221 |
| 531,77104 | 0,09348 | 0,09646 | 0,0873 | 0,07305 | 0,10192 |
| 531,80822 | 0,09362 | 0,09609 | 0,08729 | 0,07242 | 0,10162 |
| 531,8454 | 0,09376 | 0,09574 | 0,08728 | 0,07179 | 0,10131 |
| 531,88258 | 0,09391 | 0,09539 | 0,08727 | 0,07118 | 0,10098 |
| 531,91977 | 0,09406 | 0,09507 | 0,08726 | 0,07058 | 0,10064 |
| 531,95695 | 0,09421 | 0,09477 | 0,08725 | 0,06999 | 0,1003 |
| 531,99413 | 0,09437 | 0,09448 | 0,08724 | 0,06941 | 0,09993 |
| 532,03131 | 0,09453 | 0,09422 | 0,08722 | 0,06884 | 0,09956 |
| 532,06849 | 0,09469 | 0,09399 | 0,08721 | 0,06829 | 0,09917 |
| 532,10568 | 0,09485 | 0,09377 | 0,08719 | 0,06775 | 0,09877 |
| 532,14286 | 0,09501 | 0,09358 | 0,08718 | 0,06722 | 0,09836 |
| 532,18004 | 0,09517 | 0,09341 | 0,08717 | 0,06671 | 0,09794 |
| 532,21722 | 0,09533 | 0,09327 | 0,08715 | 0,06621 | 0,09751 |
| 532,2544 | 0,09548 | 0,09315 | 0,08714 | 0,06572 | 0,09707 |
| 532,29159 | 0,09564 | 0,09306 | 0,08712 | 0,06525 | 0,09661 |
| 532,32877 | 0,09579 | 0,093 | 0,0871 | 0,06479 | 0,09615 |
| 532,36595 | 0,09594 | 0,09296 | 0,08709 | 0,06435 | 0,09568 |
| 532,40313 | 0,09608 | 0,09296 | 0,08707 | 0,06392 | 0,09519 |
| 532,44031 | 0,09622 | 0,09298 | 0,08705 | 0,0635 | 0,0947 |
| 532,4775 | 0,09635 | 0,09302 | 0,08703 | 0,06311 | 0,0942 |
| 532,51468 | 0,09647 | 0,0931 | 0,08701 | 0,06272 | 0,09368 |
| 532,55186 | 0,09659 | 0,09321 | 0,08699 | 0,06235 | 0,09316 |
| 532,58904 | 0,0967 | 0,09334 | 0,08697 | 0,06199 | 0,09264 |
| 532,62622 | 0,0968 | 0,0935 | 0,08695 | 0,06165 | 0,0921 |
| 532,66341 | 0,09689 | 0,09369 | 0,08692 | 0,06133 | 0,09156 |
| 532,70059 | 0,09697 | 0,0939 | 0,0869 | 0,06101 | 0,09101 |
| 532,73777 | 0,09704 | 0,09415 | 0,08687 | 0,06072 | 0,09045 |
| 532,77495 | 0,09709 | 0,09443 | 0,08684 | 0,06043 | 0,08989 |
| 532,81213 | 0,09714 | 0,09472 | 0,08681 | 0,06016 | 0,08932 |
| 532,84932 | 0,09718 | 0,09505 | 0,08677 | 0,05991 | 0,08874 |
| 532,8865 | 0,0972 | 0,0954 | 0,08673 | 0,05967 | 0,08816 |
| 532,92368 | 0,09721 | 0,09578 | 0,08669 | 0,05944 | 0,08757 |
| 532,96086 | 0,0972 | 0,09619 | 0,08665 | 0,05924 | 0,08698 |
| 532,99804 | 0,09718 | 0,09661 | 0,0866 | 0,05904 | 0,08639 |
| 533,03523 | 0,09715 | 0,09706 | 0,08655 | 0,05885 | 0,08579 |
| 533,07241 | 0,09711 | 0,09754 | 0,0865 | 0,05868 | 0,08519 |
| 533,10959 | 0,09704 | 0,09804 | 0,08644 | 0,05852 | 0,08458 |
| 533,14677 | 0,09697 | 0,09856 | 0,08638 | 0,05838 | 0,08398 |
| 533,18395 | 0,09688 | 0,09911 | 0,08631 | 0,05824 | 0,08337 |
| 533,22114 | 0,09677 | 0,09967 | 0,08624 | 0,05812 | 0,08275 |
| 533,25832 | 0,09664 | 0,10025 | 0,08616 | 0,05802 | 0,08214 |
| 533,2955 | 0,09651 | 0,10085 | 0,08608 | 0,05792 | 0,08152 |
| 533,33268 | 0,09635 | 0,10147 | 0,08599 | 0,05784 | 0,08091 |
| 533,36986 | 0,09618 | 0,1021 | 0,0859 | 0,05776 | 0,08029 |
| 533,40705 | 0,096 | 0,10275 | 0,08581 | 0,0577 | 0,07967 |
| 533,44423 | 0,0958 | 0,10342 | 0,0857 | 0,05765 | 0,07905 |
| 533,48141 | 0,09558 | 0,1041 | 0,08559 | 0,05761 | 0,07844 |
| 533,51859 | 0,09535 | 0,10479 | 0,08548 | 0,05759 | 0,07782 |
| 533,55577 | 0,0951 | 0,10549 | 0,08536 | 0,05757 | 0,0772 |
| 533,59295 | 0,09484 | 0,1062 | 0,08523 | 0,05756 | 0,07659 |
| 533,63014 | 0,09456 | 0,10691 | 0,0851 | 0,05756 | 0,07598 |
| 533,66732 | 0,09427 | 0,10764 | 0,08495 | 0,05758 | 0,07536 |
| 533,7045 | 0,09397 | 0,10837 | 0,08481 | 0,0576 | 0,07475 |
| 533,74168 | 0,09365 | 0,1091 | 0,08465 | 0,05763 | 0,07415 |
| 533,77886 | 0,09331 | 0,10983 | 0,08449 | 0,05767 | 0,07355 |
| 533,81605 | 0,09297 | 0,11057 | 0,08432 | 0,05772 | 0,07294 |
| 533,85323 | 0,09261 | 0,11131 | 0,08414 | 0,05778 | 0,07235 |
| 533,89041 | 0,09223 | 0,11204 | 0,08396 | 0,05785 | 0,07175 |
| 533,92759 | 0,09185 | 0,11277 | 0,08377 | 0,05793 | 0,07116 |
| 533,96477 | 0,09145 | 0,11349 | 0,08357 | 0,05801 | 0,07058 |
| 534,00196 | 0,09104 | 0,1142 | 0,08336 | 0,05811 | 0,07 |
| 534,03914 | 0,09062 | 0,11491 | 0,08315 | 0,05821 | 0,06942 |
| 534,07632 | 0,09019 | 0,11561 | 0,08293 | 0,05832 | 0,06885 |
| 534,1135 | 0,08975 | 0,11629 | 0,0827 | 0,05844 | 0,06828 |
| 534,15068 | 0,0893 | 0,11696 | 0,08246 | 0,05856 | 0,06773 |
| 534,18787 | 0,08884 | 0,11762 | 0,08222 | 0,0587 | 0,06717 |
| 534,22505 | 0,08837 | 0,11825 | 0,08196 | 0,05884 | 0,06662 |
| 534,26223 | 0,08789 | 0,11887 | 0,08171 | 0,05899 | 0,06608 |
| 534,29941 | 0,0874 | 0,11947 | 0,08144 | 0,05914 | 0,06554 |
| 534,33659 | 0,08691 | 0,12004 | 0,08117 | 0,0593 | 0,06502 |
| 534,37378 | 0,08641 | 0,12059 | 0,08089 | 0,05947 | 0,0645 |
| 534,41096 | 0,0859 | 0,12112 | 0,0806 | 0,05965 | 0,06398 |
| 534,44814 | 0,08539 | 0,12161 | 0,0803 | 0,05983 | 0,06347 |
| 534,48532 | 0,08488 | 0,12208 | 0,08 | 0,06002 | 0,06298 |
| 534,5225 | 0,08435 | 0,12252 | 0,0797 | 0,06021 | 0,06248 |
| 534,55969 | 0,08383 | 0,12293 | 0,07938 | 0,06041 | 0,062 |
| 534,59687 | 0,0833 | 0,1233 | 0,07906 | 0,06062 | 0,06153 |
| 534,63405 | 0,08276 | 0,12364 | 0,07873 | 0,06083 | 0,06106 |
| 534,67123 | 0,08223 | 0,12394 | 0,0784 | 0,06105 | 0,0606 |
| 534,70841 | 0,08169 | 0,1242 | 0,07807 | 0,06127 | 0,06015 |
| 534,7456 | 0,08115 | 0,12443 | 0,07772 | 0,0615 | 0,05971 |
| 534,78278 | 0,08061 | 0,12462 | 0,07738 | 0,06173 | 0,05929 |
| 534,81996 | 0,08006 | 0,12475 | 0,07702 | 0,06197 | 0,05886 |
| 534,85714 | 0,07952 | 0,12486 | 0,07666 | 0,06221 | 0,05845 |
| 534,89432 | 0,07898 | 0,12492 | 0,0763 | 0,06245 | 0,05805 |
| 534,93151 | 0,07844 | 0,12493 | 0,07594 | 0,0627 | 0,05766 |
| 534,96869 | 0,0779 | 0,1249 | 0,07557 | 0,06295 | 0,05728 |
| 535,00587 | 0,07736 | 0,12483 | 0,07519 | 0,06321 | 0,05691 |
| 535,04305 | 0,07683 | 0,1247 | 0,07482 | 0,06347 | 0,05655 |
| 535,08023 | 0,0763 | 0,12453 | 0,07444 | 0,06373 | 0,0562 |
| 535,11742 | 0,07577 | 0,12432 | 0,07406 | 0,064 | 0,05586 |
| 535,1546 | 0,07524 | 0,12404 | 0,07367 | 0,06426 | 0,05553 |
| 535,19178 | 0,07472 | 0,12372 | 0,07328 | 0,06453 | 0,05521 |
| 535,22896 | 0,07421 | 0,12337 | 0,0729 | 0,0648 | 0,05491 |
| 535,26614 | 0,0737 | 0,12294 | 0,07251 | 0,06507 | 0,05461 |
| 535,30333 | 0,0732 | 0,12248 | 0,07211 | 0,06534 | 0,05432 |
| 535,34051 | 0,0727 | 0,12197 | 0,07172 | 0,06561 | 0,05405 |
| 535,37769 | 0,07221 | 0,1214 | 0,07133 | 0,06589 | 0,05379 |
| 535,41487 | 0,07173 | 0,12078 | 0,07094 | 0,06616 | 0,05353 |
| 535,45205 | 0,07126 | 0,12013 | 0,07054 | 0,06643 | 0,05329 |
| 535,48924 | 0,07079 | 0,11941 | 0,07015 | 0,0667 | 0,05306 |
| 535,52642 | 0,07034 | 0,11865 | 0,06976 | 0,06696 | 0,05284 |
| 535,5636 | 0,06989 | 0,11785 | 0,06937 | 0,06723 | 0,05263 |
| 535,60078 | 0,06945 | 0,11699 | 0,06898 | 0,06749 | 0,05244 |
| 535,63796 | 0,06902 | 0,11608 | 0,06859 | 0,06775 | 0,05225 |
| 535,67515 | 0,06861 | 0,11514 | 0,0682 | 0,068 | 0,05207 |
| 535,71233 | 0,0682 | 0,11414 | 0,06782 | 0,06826 | 0,05191 |
| 535,74951 | 0,0678 | 0,1131 | 0,06743 | 0,0685 | 0,05175 |
| 535,78669 | 0,06742 | 0,11203 | 0,06705 | 0,06875 | 0,0516 |
| 535,82387 | 0,06704 | 0,11091 | 0,06668 | 0,06898 | 0,05147 |
| 535,86106 | 0,06668 | 0,10974 | 0,0663 | 0,06921 | 0,05134 |
| 535,89824 | 0,06633 | 0,10854 | 0,06593 | 0,06944 | 0,05123 |
| 535,93542 | 0,06599 | 0,1073 | 0,06556 | 0,06966 | 0,05113 |
| 535,9726 | 0,06567 | 0,10602 | 0,06519 | 0,06987 | 0,05103 |
| 536,00978 | 0,06535 | 0,10471 | 0,06483 | 0,07007 | 0,05095 |
| 536,04697 | 0,06505 | 0,10337 | 0,06448 | 0,07027 | 0,05087 |
| 536,08415 | 0,06476 | 0,10198 | 0,06412 | 0,07045 | 0,0508 |
| 536,12133 | 0,06449 | 0,10058 | 0,06377 | 0,07063 | 0,05074 |
| 536,15851 | 0,06422 | 0,09915 | 0,06343 | 0,0708 | 0,05069 |
| 536,19569 | 0,06397 | 0,09768 | 0,06309 | 0,07096 | 0,05065 |
| 536,23288 | 0,06373 | 0,09619 | 0,06275 | 0,07111 | 0,05062 |
| 536,27006 | 0,0635 | 0,09469 | 0,06242 | 0,07124 | 0,05059 |
| 536,30724 | 0,06328 | 0,09316 | 0,0621 | 0,07137 | 0,05057 |
| 536,34442 | 0,06308 | 0,09161 | 0,06178 | 0,07149 | 0,05056 |
| 536,3816 | 0,06288 | 0,09004 | 0,06146 | 0,07159 | 0,05056 |
| 536,41879 | 0,0627 | 0,08846 | 0,06115 | 0,07168 | 0,05056 |
| 536,45597 | 0,06252 | 0,08687 | 0,06084 | 0,07176 | 0,05057 |
| 536,49315 | 0,06236 | 0,08527 | 0,06054 | 0,07183 | 0,05058 |
| 536,53033 | 0,06221 | 0,08365 | 0,06025 | 0,07189 | 0,0506 |
| 536,56751 | 0,06206 | 0,08204 | 0,05996 | 0,07192 | 0,05062 |
| 536,6047 | 0,06192 | 0,08041 | 0,05967 | 0,07195 | 0,05065 |
| 536,64188 | 0,06179 | 0,07879 | 0,0594 | 0,07197 | 0,05068 |
| 536,67906 | 0,06167 | 0,07716 | 0,05912 | 0,07197 | 0,05072 |
| 536,71624 | 0,06156 | 0,07554 | 0,05886 | 0,07196 | 0,05076 |
| 536,75342 | 0,06145 | 0,07392 | 0,05859 | 0,07192 | 0,0508 |
| 536,79061 | 0,06134 | 0,07231 | 0,05834 | 0,07188 | 0,05085 |
| 536,82779 | 0,06124 | 0,0707 | 0,05809 | 0,07183 | 0,0509 |
| 536,86497 | 0,06115 | 0,06911 | 0,05784 | 0,07175 | 0,05095 |
| 536,90215 | 0,06106 | 0,06752 | 0,0576 | 0,07167 | 0,051 |
| 536,93933 | 0,06097 | 0,06595 | 0,05737 | 0,07157 | 0,05105 |
| 536,97652 | 0,06088 | 0,06439 | 0,05713 | 0,07145 | 0,05111 |
| 537,0137 | 0,06079 | 0,06285 | 0,05691 | 0,07133 | 0,05116 |
| 537,05088 | 0,0607 | 0,06133 | 0,05669 | 0,07118 | 0,05121 |
| 537,08806 | 0,06061 | 0,05982 | 0,05648 | 0,07102 | 0,05126 |
| 537,12524 | 0,06052 | 0,05835 | 0,05627 | 0,07085 | 0,05131 |
| 537,16243 | 0,06042 | 0,05689 | 0,05606 | 0,07065 | 0,05136 |
| 537,19961 | 0,06033 | 0,05545 | 0,05586 | 0,07045 | 0,05141 |
| 537,23679 | 0,06022 | 0,05404 | 0,05567 | 0,07023 | 0,05145 |
| 537,27397 | 0,06012 | 0,05266 | 0,05548 | 0,07 | 0,05149 |
| 537,31115 | 0,06 | 0,0513 | 0,05529 | 0,06976 | 0,05153 |
| 537,34834 | 0,05988 | 0,04998 | 0,05511 | 0,06949 | 0,05156 |
| 537,38552 | 0,05975 | 0,04868 | 0,05493 | 0,06922 | 0,05159 |
| 537,4227 | 0,05961 | 0,04741 | 0,05475 | 0,06893 | 0,05162 |
| 537,45988 | 0,05947 | 0,04618 | 0,05458 | 0,06863 | 0,05163 |
| 537,49706 | 0,05931 | 0,04497 | 0,05442 | 0,06831 | 0,05165 |
| 537,53425 | 0,05914 | 0,04379 | 0,05425 | 0,06798 | 0,05166 |
| 537,57143 | 0,05896 | 0,04266 | 0,05409 | 0,06764 | 0,05166 |
| 537,60861 | 0,05877 | 0,04155 | 0,05393 | 0,06729 | 0,05165 |
| 537,64579 | 0,05857 | 0,04048 | 0,05378 | 0,06692 | 0,05164 |
| 537,68297 | 0,05835 | 0,03944 | 0,05362 | 0,06654 | 0,05162 |
| 537,72016 | 0,05813 | 0,03844 | 0,05347 | 0,06615 | 0,05159 |
| 537,75734 | 0,05788 | 0,03746 | 0,05332 | 0,06574 | 0,05155 |
| 537,79452 | 0,05762 | 0,03653 | 0,05317 | 0,06533 | 0,0515 |
| 537,8317 | 0,05735 | 0,03562 | 0,05303 | 0,0649 | 0,05145 |
| 537,86888 | 0,05706 | 0,03475 | 0,05288 | 0,06447 | 0,05139 |
| 537,90607 | 0,05676 | 0,03391 | 0,05274 | 0,06402 | 0,05131 |
| 537,94325 | 0,05644 | 0,03312 | 0,0526 | 0,06356 | 0,05123 |
| 537,98043 | 0,0561 | 0,03234 | 0,05245 | 0,0631 | 0,05114 |
| 538,01761 | 0,05575 | 0,0316 | 0,05231 | 0,06262 | 0,05103 |
| 538,05479 | 0,05538 | 0,0309 | 0,05216 | 0,06213 | 0,05092 |
| 538,09198 | 0,055 | 0,03022 | 0,05202 | 0,06164 | 0,05079 |
| 538,12916 | 0,0546 | 0,02957 | 0,05188 | 0,06114 | 0,05066 |
| 538,16634 | 0,05419 | 0,02896 | 0,05173 | 0,06063 | 0,05051 |
| 538,20352 | 0,05375 | 0,02838 | 0,05158 | 0,06011 | 0,05035 |
| 538,2407 | 0,05331 | 0,02782 | 0,05143 | 0,05958 | 0,05018 |
| 538,27789 | 0,05285 | 0,02729 | 0,05128 | 0,05905 | 0,05 |
| 538,31507 | 0,05237 | 0,02679 | 0,05112 | 0,05851 | 0,0498 |
| 538,35225 | 0,05188 | 0,02631 | 0,05097 | 0,05796 | 0,0496 |
| 538,38943 | 0,05138 | 0,02586 | 0,05081 | 0,05741 | 0,04938 |
| 538,42661 | 0,05086 | 0,02543 | 0,05064 | 0,05685 | 0,04915 |
| 538,4638 | 0,05033 | 0,02502 | 0,05047 | 0,05628 | 0,04891 |
| 538,50098 | 0,04978 | 0,02464 | 0,0503 | 0,05571 | 0,04865 |
| 538,53816 | 0,04922 | 0,02428 | 0,05012 | 0,05514 | 0,04839 |
| 538,57534 | 0,04865 | 0,02393 | 0,04994 | 0,05456 | 0,04811 |
| 538,61252 | 0,04807 | 0,02361 | 0,04975 | 0,05398 | 0,04782 |
| 538,64971 | 0,04748 | 0,0233 | 0,04956 | 0,05339 | 0,04753 |
| 538,68689 | 0,04688 | 0,02301 | 0,04936 | 0,0528 | 0,04721 |
| 538,72407 | 0,04627 | 0,02274 | 0,04915 | 0,0522 | 0,04689 |
| 538,76125 | 0,04566 | 0,02248 | 0,04894 | 0,05161 | 0,04655 |
| 538,79843 | 0,04503 | 0,02223 | 0,04872 | 0,05101 | 0,0462 |
| 538,83562 | 0,0444 | 0,02199 | 0,0485 | 0,0504 | 0,04585 |
| 538,8728 | 0,04376 | 0,02177 | 0,04827 | 0,0498 | 0,04548 |
| 538,90998 | 0,04311 | 0,02155 | 0,04802 | 0,04919 | 0,0451 |
| 538,94716 | 0,04246 | 0,02135 | 0,04777 | 0,04859 | 0,04471 |
| 538,98434 | 0,04181 | 0,02115 | 0,04752 | 0,04798 | 0,04431 |
| 539,02153 | 0,04115 | 0,02096 | 0,04725 | 0,04737 | 0,04389 |
| 539,05871 | 0,04049 | 0,02078 | 0,04698 | 0,04676 | 0,04348 |
| 539,09589 | 0,03983 | 0,0206 | 0,0467 | 0,04614 | 0,04304 |
| 539,13307 | 0,03917 | 0,02042 | 0,0464 | 0,04553 | 0,0426 |
| 539,17025 | 0,0385 | 0,02025 | 0,04611 | 0,04492 | 0,04216 |
| 539,20744 | 0,03784 | 0,02008 | 0,04579 | 0,04431 | 0,0417 |
| 539,24462 | 0,03717 | 0,01991 | 0,04548 | 0,0437 | 0,04123 |
| 539,2818 | 0,03651 | 0,01974 | 0,04515 | 0,04309 | 0,04076 |
| 539,31898 | 0,03585 | 0,01957 | 0,04481 | 0,04248 | 0,04028 |
| 539,35616 | 0,03519 | 0,0194 | 0,04446 | 0,04187 | 0,03979 |
| 539,39335 | 0,03454 | 0,01923 | 0,0441 | 0,04126 | 0,03929 |
| 539,43053 | 0,03389 | 0,01905 | 0,04374 | 0,04066 | 0,03879 |
| 539,46771 | 0,03324 | 0,01888 | 0,04336 | 0,04005 | 0,03828 |
| 539,50489 | 0,0326 | 0,0187 | 0,04297 | 0,03945 | 0,03777 |
| 539,54207 | 0,03197 | 0,01851 | 0,04258 | 0,03885 | 0,03725 |
| 539,57926 | 0,03133 | 0,01833 | 0,04217 | 0,03826 | 0,03672 |
| 539,61644 | 0,03071 | 0,01814 | 0,04176 | 0,03766 | 0,03619 |
| 539,65362 | 0,03009 | 0,01794 | 0,04133 | 0,03707 | 0,03565 |
| 539,6908 | 0,02948 | 0,01773 | 0,0409 | 0,03648 | 0,03511 |
| 539,72798 | 0,02888 | 0,01753 | 0,04046 | 0,0359 | 0,03457 |
| 539,76517 | 0,02828 | 0,01731 | 0,04001 | 0,03531 | 0,03402 |
| 539,80235 | 0,02769 | 0,01709 | 0,03955 | 0,03473 | 0,03347 |
| 539,83953 | 0,02711 | 0,01687 | 0,03908 | 0,03416 | 0,03292 |
| 539,87671 | 0,02654 | 0,01664 | 0,0386 | 0,03359 | 0,03237 |
| 539,91389 | 0,02598 | 0,0164 | 0,03812 | 0,03302 | 0,03181 |
| 539,95108 | 0,02542 | 0,01616 | 0,03763 | 0,03246 | 0,03125 |
| 539,98826 | 0,02488 | 0,01591 | 0,03713 | 0,0319 | 0,03069 |
| 540,02544 | 0,02434 | 0,01565 | 0,03662 | 0,03134 | 0,03013 |
| 540,06262 | 0,02381 | 0,01539 | 0,03611 | 0,03079 | 0,02957 |
| 540,0998 | 0,02329 | 0,01512 | 0,03559 | 0,03024 | 0,02901 |
| 540,13699 | 0,02278 | 0,01485 | 0,03506 | 0,0297 | 0,02845 |
| 540,17417 | 0,02228 | 0,01457 | 0,03453 | 0,02916 | 0,02789 |
| 540,21135 | 0,02179 | 0,01429 | 0,034 | 0,02863 | 0,02733 |
| 540,24853 | 0,0213 | 0,014 | 0,03345 | 0,0281 | 0,02677 |
| 540,28571 | 0,02083 | 0,01371 | 0,03291 | 0,02758 | 0,02622 |
| 540,3229 | 0,02036 | 0,01342 | 0,03236 | 0,02706 | 0,02566 |
| 540,36008 | 0,01991 | 0,01312 | 0,03181 | 0,02655 | 0,02511 |
| 540,39726 | 0,01946 | 0,01281 | 0,03125 | 0,02605 | 0,02456 |
| 540,43444 | 0,01902 | 0,01251 | 0,03069 | 0,02555 | 0,02401 |
| 540,47162 | 0,01859 | 0,0122 | 0,03013 | 0,02505 | 0,02347 |
| 540,50881 | 0,01817 | 0,01189 | 0,02957 | 0,02456 | 0,02293 |
| 540,54599 | 0,01775 | 0,01158 | 0,029 | 0,02408 | 0,02239 |
| 540,58317 | 0,01734 | 0,01127 | 0,02843 | 0,0236 | 0,02186 |
| 540,62035 | 0,01695 | 0,01096 | 0,02787 | 0,02313 | 0,02133 |
| 540,65753 | 0,01656 | 0,01064 | 0,0273 | 0,02266 | 0,02081 |
| 540,69472 | 0,01617 | 0,01033 | 0,02674 | 0,0222 | 0,02029 |
| 540,7319 | 0,0158 | 0,01002 | 0,02617 | 0,02175 | 0,01977 |
| 540,76908 | 0,01543 | 0,00971 | 0,02561 | 0,0213 | 0,01926 |
| 540,80626 | 0,01506 | 0,0094 | 0,02504 | 0,02085 | 0,01876 |
| 540,84344 | 0,01471 | 0,00909 | 0,02448 | 0,02042 | 0,01826 |
| 540,88063 | 0,01436 | 0,00878 | 0,02392 | 0,01999 | 0,01777 |
| 540,91781 | 0,01402 | 0,00848 | 0,02337 | 0,01956 | 0,01728 |
| 540,95499 | 0,01368 | 0,00818 | 0,02282 | 0,01914 | 0,0168 |
| 540,99217 | 0,01336 | 0,00789 | 0,02227 | 0,01873 | 0,01632 |
| 541,02935 | 0,01303 | 0,00759 | 0,02173 | 0,01833 | 0,01585 |
| 541,06654 | 0,01271 | 0,00731 | 0,02118 | 0,01793 | 0,01539 |
| 541,10372 | 0,0124 | 0,00702 | 0,02065 | 0,01753 | 0,01494 |
| 541,1409 | 0,01209 | 0,00674 | 0,02012 | 0,01714 | 0,01449 |
| 541,17808 | 0,01179 | 0,00647 | 0,01959 | 0,01676 | 0,01405 |
| 541,21526 | 0,0115 | 0,0062 | 0,01908 | 0,01639 | 0,01362 |
| 541,25245 | 0,0112 | 0,00594 | 0,01856 | 0,01602 | 0,01319 |
| 541,28963 | 0,01092 | 0,00568 | 0,01805 | 0,01565 | 0,01277 |
| 541,32681 | 0,01064 | 0,00543 | 0,01755 | 0,0153 | 0,01236 |
| 541,36399 | 0,01036 | 0,00519 | 0,01706 | 0,01495 | 0,01196 |
| 541,40117 | 0,01009 | 0,00495 | 0,01657 | 0,0146 | 0,01156 |
| 541,43836 | 0,00982 | 0,00472 | 0,01609 | 0,01426 | 0,01118 |
| 541,47554 | 0,00955 | 0,00449 | 0,01562 | 0,01393 | 0,0108 |
| 541,51272 | 0,00929 | 0,00428 | 0,01516 | 0,0136 | 0,01042 |
| 541,5499 | 0,00904 | 0,00406 | 0,0147 | 0,01328 | 0,01006 |
| 541,58708 | 0,00879 | 0,00386 | 0,01425 | 0,01296 | 0,0097 |
| 541,62427 | 0,00854 | 0,00366 | 0,01381 | 0,01265 | 0,00935 |
| 541,66145 | 0,0083 | 0,00347 | 0,01338 | 0,01234 | 0,00902 |
| 541,69863 | 0,00806 | 0,00328 | 0,01295 | 0,01204 | 0,00868 |
| 541,73581 | 0,00782 | 0,00311 | 0,01254 | 0,01175 | 0,00836 |
| 541,77299 | 0,00759 | 0,00294 | 0,01213 | 0,01146 | 0,00804 |
| 541,81018 | 0,00736 | 0,00277 | 0,01173 | 0,01118 | 0,00773 |
| 541,84736 | 0,00714 | 0,00262 | 0,01134 | 0,0109 | 0,00743 |
| 541,88454 | 0,00692 | 0,00246 | 0,01096 | 0,01063 | 0,00714 |
| 541,92172 | 0,0067 | 0,00232 | 0,01058 | 0,01036 | 0,00686 |
| 541,9589 | 0,00649 | 0,00218 | 0,01022 | 0,0101 | 0,00658 |
| 541,99609 | 0,00628 | 0,00205 | 0,00986 | 0,00984 | 0,00631 |
| 542,03327 | 0,00608 | 0,00192 | 0,00951 | 0,00959 | 0,00605 |
| 542,07045 | 0,00588 | 0,0018 | 0,00917 | 0,00935 | 0,0058 |
| 542,10763 | 0,00568 | 0,00169 | 0,00884 | 0,0091 | 0,00555 |
| 542,14481 | 0,00548 | 0,00158 | 0,00852 | 0,00887 | 0,00531 |
| 542,182 | 0,0053 | 0,00148 | 0,00821 | 0,00863 | 0,00508 |
| 542,21918 | 0,00511 | 0,00138 | 0,0079 | 0,00841 | 0,00486 |
| 542,25636 | 0,00493 | 0,00129 | 0,00761 | 0,00818 | 0,00464 |
| 542,29354 | 0,00475 | 0,0012 | 0,00732 | 0,00796 | 0,00443 |
| 542,33072 | 0,00457 | 0,00112 | 0,00704 | 0,00775 | 0,00423 |
| 542,36791 | 0,0044 | 0,00104 | 0,00676 | 0,00754 | 0,00404 |
| 542,40509 | 0,00424 | 0,00097 | 0,0065 | 0,00734 | 0,00385 |
| 542,44227 | 0,00407 | 9e-04 | 0,00624 | 0,00713 | 0,00367 |
| 542,47945 | 0,00391 | 0,00083 | 0,006 | 0,00694 | 0,00349 |
| 542,51663 | 0,00376 | 0,00077 | 0,00576 | 0,00675 | 0,00332 |
| 542,55382 | 0,00361 | 0,00071 | 0,00552 | 0,00656 | 0,00316 |
| 542,591 | 0,00346 | 0,00066 | 0,0053 | 0,00637 | 0,003 |
| 542,62818 | 0,00332 | 0,00061 | 0,00508 | 0,00619 | 0,00285 |
| 542,66536 | 0,00318 | 0,00056 | 0,00486 | 0,00601 | 0,00271 |
| 542,70254 | 0,00304 | 0,00052 | 0,00466 | 0,00584 | 0,00257 |
| 542,73973 | 0,00291 | 0,00048 | 0,00446 | 0,00567 | 0,00244 |
| 542,77691 | 0,00278 | 0,00044 | 0,00427 | 0,0055 | 0,00231 |
| 542,81409 | 0,00266 | 4e-04 | 0,00409 | 0,00534 | 0,00219 |
| 542,85127 | 0,00254 | 0,00037 | 0,00391 | 0,00518 | 0,00207 |
| 542,88845 | 0,00242 | 0,00034 | 0,00374 | 0,00503 | 0,00196 |
| 542,92564 | 0,00231 | 0,00031 | 0,00357 | 0,00488 | 0,00185 |
| 542,96282 | 0,0022 | 0,00028 | 0,00341 | 0,00473 | 0,00175 |
| 543 | 0,00209 | 0,00026 | 0,00326 | 0,00458 | 0,00165 |
Schuldsanering
De figuren 3.2.31 en 3.2.32 tonen de frequentiedichtheid van de onderwijsscores naar de status van de ouders wat betreft de schuldsanering uitgesplitst naar schooljaar. De verwachting is dat kinderen met ouders in de schuldsanering een lagere onderwijsscore hebben dan kinderen met ouders die niet in de schuldsanering zitten en dat dit stabiel is over de schooljaren heen. Bij kinderen met ouders in de schuldsanering wordt de onderwijsscore immers verlaagd (zie figuren 1.1.1 en 1.1.2).
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 0 | 0 | 0 |
| 524,74364 | 0 | 0 | 0 | 0 | 0 |
| 524,78082 | 0 | 0 | 0 | 0 | 0 |
| 524,818 | 0 | 0 | 0 | 0 | 0 |
| 524,85519 | 0 | 0 | 0 | 0 | 0 |
| 524,89237 | 0 | 0 | 0 | 0 | 0 |
| 524,92955 | 0 | 0 | 0 | 0 | 0 |
| 524,96673 | 0 | 0 | 0 | 0 | 0 |
| 525,00391 | 0 | 0 | 0 | 0 | 0 |
| 525,0411 | 0 | 0 | 0 | 0 | 0 |
| 525,07828 | 1e-05 | 0 | 0 | 0 | 0 |
| 525,11546 | 1e-05 | 0 | 1e-05 | 0 | 0 |
| 525,15264 | 1e-05 | 1e-05 | 1e-05 | 0 | 0 |
| 525,18982 | 1e-05 | 1e-05 | 1e-05 | 0 | 0 |
| 525,22701 | 2e-05 | 1e-05 | 1e-05 | 0 | 0 |
| 525,26419 | 3e-05 | 2e-05 | 2e-05 | 0 | 0 |
| 525,30137 | 4e-05 | 2e-05 | 2e-05 | 1e-05 | 1e-05 |
| 525,33855 | 5e-05 | 3e-05 | 3e-05 | 1e-05 | 1e-05 |
| 525,37573 | 7e-05 | 4e-05 | 4e-05 | 2e-05 | 1e-05 |
| 525,41292 | 9e-05 | 5e-05 | 5e-05 | 2e-05 | 2e-05 |
| 525,4501 | 0,00011 | 7e-05 | 6e-05 | 3e-05 | 3e-05 |
| 525,48728 | 0,00014 | 9e-05 | 8e-05 | 5e-05 | 4e-05 |
| 525,52446 | 0,00018 | 0,00012 | 1e-04 | 6e-05 | 5e-05 |
| 525,56164 | 0,00022 | 0,00015 | 0,00013 | 8e-05 | 7e-05 |
| 525,59883 | 0,00028 | 0,00019 | 0,00016 | 0,00011 | 9e-05 |
| 525,63601 | 0,00034 | 0,00023 | 0,00021 | 0,00015 | 0,00013 |
| 525,67319 | 0,00041 | 0,00028 | 0,00025 | 0,00019 | 0,00016 |
| 525,71037 | 0,00048 | 0,00034 | 0,00031 | 0,00024 | 0,00021 |
| 525,74755 | 0,00057 | 0,00041 | 0,00037 | 0,00031 | 0,00027 |
| 525,78474 | 0,00066 | 0,00048 | 0,00044 | 0,00039 | 0,00034 |
| 525,82192 | 0,00076 | 0,00056 | 0,00051 | 0,00047 | 0,00042 |
| 525,8591 | 0,00086 | 0,00064 | 0,00059 | 0,00058 | 0,00052 |
| 525,89628 | 0,00097 | 0,00073 | 0,00068 | 0,00069 | 0,00063 |
| 525,93346 | 0,00108 | 0,00082 | 0,00077 | 0,00082 | 0,00075 |
| 525,97065 | 0,00119 | 0,00092 | 0,00086 | 0,00096 | 0,00088 |
| 526,00783 | 0,0013 | 0,00102 | 0,00096 | 0,00112 | 0,00103 |
| 526,04501 | 0,00141 | 0,00112 | 0,00106 | 0,00129 | 0,00119 |
| 526,08219 | 0,00152 | 0,00122 | 0,00116 | 0,00147 | 0,00136 |
| 526,11937 | 0,00164 | 0,00132 | 0,00126 | 0,00166 | 0,00154 |
| 526,15656 | 0,00176 | 0,00143 | 0,00137 | 0,00187 | 0,00173 |
| 526,19374 | 0,00189 | 0,00155 | 0,00148 | 0,00208 | 0,00193 |
| 526,23092 | 0,00202 | 0,00167 | 0,0016 | 0,0023 | 0,00213 |
| 526,2681 | 0,00217 | 0,00181 | 0,00172 | 0,00252 | 0,00233 |
| 526,30528 | 0,00234 | 0,00195 | 0,00186 | 0,00273 | 0,00253 |
| 526,34247 | 0,00252 | 0,00211 | 0,00201 | 0,00295 | 0,00272 |
| 526,37965 | 0,00271 | 0,00229 | 0,00217 | 0,00316 | 0,00291 |
| 526,41683 | 0,00293 | 0,00248 | 0,00234 | 0,00335 | 0,00308 |
| 526,45401 | 0,00316 | 0,00269 | 0,00252 | 0,00352 | 0,00324 |
| 526,49119 | 0,0034 | 0,00291 | 0,00272 | 0,00367 | 0,00337 |
| 526,52838 | 0,00365 | 0,00314 | 0,00292 | 0,00379 | 0,00348 |
| 526,56556 | 0,0039 | 0,00339 | 0,00313 | 0,00388 | 0,00357 |
| 526,60274 | 0,00416 | 0,00364 | 0,00335 | 0,00395 | 0,00364 |
| 526,63992 | 0,00441 | 0,00389 | 0,00357 | 0,00398 | 0,00368 |
| 526,6771 | 0,00465 | 0,00414 | 0,00378 | 0,00399 | 0,00369 |
| 526,71429 | 0,00487 | 0,00438 | 0,00398 | 0,00398 | 0,00369 |
| 526,75147 | 0,00509 | 0,00461 | 0,00417 | 0,00394 | 0,00367 |
| 526,78865 | 0,00528 | 0,00483 | 0,00435 | 0,00389 | 0,00364 |
| 526,82583 | 0,00547 | 0,00505 | 0,00451 | 0,00383 | 0,0036 |
| 526,86301 | 0,00564 | 0,00525 | 0,00466 | 0,00378 | 0,00355 |
| 526,9002 | 0,00581 | 0,00544 | 0,0048 | 0,00373 | 0,00352 |
| 526,93738 | 0,00597 | 0,00562 | 0,00494 | 0,00369 | 0,00349 |
| 526,97456 | 0,00613 | 0,00579 | 0,00506 | 0,00366 | 0,00346 |
| 527,01174 | 0,0063 | 0,00597 | 0,00519 | 0,00365 | 0,00346 |
| 527,04892 | 0,00648 | 0,00614 | 0,00532 | 0,00367 | 0,00347 |
| 527,08611 | 0,00667 | 0,00632 | 0,00546 | 0,0037 | 0,00349 |
| 527,12329 | 0,00688 | 0,00651 | 0,00562 | 0,00376 | 0,00353 |
| 527,16047 | 0,00711 | 0,00671 | 0,00579 | 0,00385 | 0,0036 |
| 527,19765 | 0,00737 | 0,00691 | 0,00598 | 0,00396 | 0,00368 |
| 527,23483 | 0,00764 | 0,00713 | 0,0062 | 0,00409 | 0,00378 |
| 527,27202 | 0,00794 | 0,00736 | 0,00645 | 0,00425 | 0,00389 |
| 527,3092 | 0,00826 | 0,00761 | 0,00672 | 0,00442 | 0,00403 |
| 527,34638 | 0,00861 | 0,00788 | 0,00704 | 0,00463 | 0,00419 |
| 527,38356 | 0,00899 | 0,00818 | 0,00739 | 0,00485 | 0,00437 |
| 527,42074 | 0,0094 | 0,0085 | 0,00778 | 0,00511 | 0,00458 |
| 527,45793 | 0,00983 | 0,00886 | 0,00821 | 0,00539 | 0,00482 |
| 527,49511 | 0,01031 | 0,00925 | 0,00868 | 0,0057 | 0,00508 |
| 527,53229 | 0,01081 | 0,00969 | 0,0092 | 0,00605 | 0,00539 |
| 527,56947 | 0,01136 | 0,01017 | 0,00976 | 0,00643 | 0,00573 |
| 527,60665 | 0,01194 | 0,01069 | 0,01037 | 0,00684 | 0,00611 |
| 527,64384 | 0,01256 | 0,01127 | 0,01102 | 0,0073 | 0,00654 |
| 527,68102 | 0,0132 | 0,01188 | 0,01172 | 0,0078 | 0,00701 |
| 527,7182 | 0,01387 | 0,01253 | 0,01244 | 0,00835 | 0,00754 |
| 527,75538 | 0,01456 | 0,01321 | 0,01319 | 0,00895 | 0,00812 |
| 527,79256 | 0,01525 | 0,0139 | 0,01395 | 0,0096 | 0,00876 |
| 527,82975 | 0,01594 | 0,01461 | 0,01471 | 0,01031 | 0,00945 |
| 527,86693 | 0,01663 | 0,01531 | 0,01547 | 0,01107 | 0,01021 |
| 527,90411 | 0,01729 | 0,016 | 0,01621 | 0,01189 | 0,01103 |
| 527,94129 | 0,01793 | 0,01667 | 0,01692 | 0,01275 | 0,0119 |
| 527,97847 | 0,01853 | 0,01731 | 0,0176 | 0,01366 | 0,01281 |
| 528,01566 | 0,01909 | 0,0179 | 0,01823 | 0,01461 | 0,01376 |
| 528,05284 | 0,01963 | 0,01845 | 0,01882 | 0,01558 | 0,01475 |
| 528,09002 | 0,02013 | 0,01896 | 0,01935 | 0,01656 | 0,01575 |
| 528,1272 | 0,0206 | 0,01942 | 0,01984 | 0,01755 | 0,01676 |
| 528,16438 | 0,02104 | 0,01985 | 0,02028 | 0,01852 | 0,01775 |
| 528,20157 | 0,02146 | 0,02024 | 0,02068 | 0,01945 | 0,01872 |
| 528,23875 | 0,02186 | 0,0206 | 0,02104 | 0,02033 | 0,01964 |
| 528,27593 | 0,02224 | 0,02093 | 0,02137 | 0,02115 | 0,02049 |
| 528,31311 | 0,02262 | 0,02123 | 0,02167 | 0,02188 | 0,02126 |
| 528,35029 | 0,02298 | 0,02153 | 0,02195 | 0,02252 | 0,02194 |
| 528,38748 | 0,02334 | 0,02181 | 0,02221 | 0,02305 | 0,02253 |
| 528,42466 | 0,02369 | 0,02208 | 0,02246 | 0,02349 | 0,023 |
| 528,46184 | 0,02404 | 0,02235 | 0,0227 | 0,02382 | 0,02337 |
| 528,49902 | 0,02438 | 0,02261 | 0,02294 | 0,02405 | 0,02364 |
| 528,5362 | 0,02472 | 0,02287 | 0,02317 | 0,02419 | 0,02382 |
| 528,57339 | 0,02505 | 0,02313 | 0,02341 | 0,02426 | 0,02392 |
| 528,61057 | 0,02537 | 0,0234 | 0,02366 | 0,02428 | 0,02397 |
| 528,64775 | 0,0257 | 0,02367 | 0,02391 | 0,02428 | 0,02399 |
| 528,68493 | 0,02603 | 0,02394 | 0,02418 | 0,02427 | 0,02401 |
| 528,72211 | 0,02637 | 0,02423 | 0,02447 | 0,02428 | 0,02404 |
| 528,7593 | 0,02672 | 0,02454 | 0,02477 | 0,02433 | 0,02411 |
| 528,79648 | 0,02708 | 0,02486 | 0,02509 | 0,02442 | 0,02423 |
| 528,83366 | 0,02745 | 0,02519 | 0,02543 | 0,02457 | 0,02442 |
| 528,87084 | 0,02784 | 0,02554 | 0,02578 | 0,02479 | 0,02467 |
| 528,90802 | 0,02823 | 0,0259 | 0,02615 | 0,02507 | 0,02499 |
| 528,94521 | 0,02863 | 0,02628 | 0,02652 | 0,02541 | 0,02537 |
| 528,98239 | 0,02904 | 0,02665 | 0,0269 | 0,02579 | 0,02578 |
| 529,01957 | 0,02945 | 0,02703 | 0,02727 | 0,02618 | 0,02623 |
| 529,05675 | 0,02984 | 0,0274 | 0,02764 | 0,02658 | 0,02667 |
| 529,09393 | 0,03022 | 0,02776 | 0,02798 | 0,02698 | 0,0271 |
| 529,13112 | 0,03059 | 0,0281 | 0,0283 | 0,02735 | 0,0275 |
| 529,1683 | 0,03093 | 0,02842 | 0,02859 | 0,02768 | 0,02786 |
| 529,20548 | 0,03125 | 0,02871 | 0,02885 | 0,02797 | 0,02816 |
| 529,24266 | 0,03154 | 0,02898 | 0,02909 | 0,02821 | 0,0284 |
| 529,27984 | 0,03181 | 0,02923 | 0,02931 | 0,0284 | 0,02858 |
| 529,31703 | 0,03207 | 0,02946 | 0,0295 | 0,02856 | 0,02871 |
| 529,35421 | 0,03231 | 0,02968 | 0,02969 | 0,02869 | 0,02881 |
| 529,39139 | 0,03254 | 0,02991 | 0,02987 | 0,02881 | 0,02887 |
| 529,42857 | 0,03278 | 0,03014 | 0,03007 | 0,02893 | 0,02894 |
| 529,46575 | 0,03304 | 0,03039 | 0,0303 | 0,02906 | 0,02901 |
| 529,50294 | 0,03332 | 0,03067 | 0,03057 | 0,02923 | 0,02911 |
| 529,54012 | 0,03363 | 0,03099 | 0,03088 | 0,02943 | 0,02924 |
| 529,5773 | 0,03399 | 0,03137 | 0,03125 | 0,02968 | 0,02943 |
| 529,61448 | 0,0344 | 0,0318 | 0,03168 | 0,02999 | 0,02969 |
| 529,65166 | 0,03486 | 0,0323 | 0,03219 | 0,03036 | 0,03002 |
| 529,68885 | 0,03539 | 0,03287 | 0,03277 | 0,03079 | 0,03042 |
| 529,72603 | 0,03599 | 0,03353 | 0,03343 | 0,03129 | 0,0309 |
| 529,76321 | 0,03665 | 0,03426 | 0,03417 | 0,03185 | 0,03145 |
| 529,80039 | 0,03738 | 0,03507 | 0,03498 | 0,03247 | 0,03208 |
| 529,83757 | 0,03817 | 0,03595 | 0,03586 | 0,03315 | 0,03278 |
| 529,87476 | 0,03902 | 0,03689 | 0,0368 | 0,0339 | 0,03356 |
| 529,91194 | 0,03992 | 0,0379 | 0,03778 | 0,0347 | 0,03441 |
| 529,94912 | 0,04086 | 0,03895 | 0,03881 | 0,03558 | 0,03534 |
| 529,9863 | 0,04183 | 0,04004 | 0,03986 | 0,03653 | 0,03636 |
| 530,02348 | 0,04283 | 0,04116 | 0,04094 | 0,03756 | 0,03746 |
| 530,06067 | 0,04383 | 0,04228 | 0,04203 | 0,03867 | 0,03864 |
| 530,09785 | 0,04483 | 0,0434 | 0,0431 | 0,03985 | 0,03991 |
| 530,13503 | 0,04581 | 0,04449 | 0,04416 | 0,0411 | 0,04126 |
| 530,17221 | 0,04676 | 0,04555 | 0,04519 | 0,04242 | 0,04268 |
| 530,20939 | 0,04767 | 0,04655 | 0,04617 | 0,0438 | 0,04416 |
| 530,24658 | 0,04853 | 0,04748 | 0,0471 | 0,04522 | 0,04568 |
| 530,28376 | 0,04932 | 0,04834 | 0,04796 | 0,04665 | 0,04722 |
| 530,32094 | 0,05004 | 0,04911 | 0,04875 | 0,04808 | 0,04874 |
| 530,35812 | 0,05068 | 0,04977 | 0,04946 | 0,04947 | 0,05021 |
| 530,3953 | 0,05122 | 0,05032 | 0,05007 | 0,05078 | 0,05159 |
| 530,43249 | 0,05165 | 0,05075 | 0,05056 | 0,05199 | 0,05284 |
| 530,46967 | 0,05198 | 0,05106 | 0,05095 | 0,05306 | 0,05393 |
| 530,50685 | 0,0522 | 0,05125 | 0,05121 | 0,05395 | 0,05482 |
| 530,54403 | 0,05232 | 0,05132 | 0,05136 | 0,05466 | 0,05549 |
| 530,58121 | 0,05232 | 0,05127 | 0,05138 | 0,05515 | 0,05592 |
| 530,6184 | 0,05221 | 0,0511 | 0,05128 | 0,05542 | 0,0561 |
| 530,65558 | 0,052 | 0,05082 | 0,05105 | 0,05546 | 0,05603 |
| 530,69276 | 0,05169 | 0,05044 | 0,05071 | 0,05525 | 0,05569 |
| 530,72994 | 0,05128 | 0,04995 | 0,05026 | 0,05482 | 0,05512 |
| 530,76712 | 0,05079 | 0,04939 | 0,0497 | 0,05421 | 0,05437 |
| 530,80431 | 0,05024 | 0,04877 | 0,04907 | 0,05344 | 0,05347 |
| 530,84149 | 0,04964 | 0,04812 | 0,04839 | 0,05255 | 0,05246 |
| 530,87867 | 0,04902 | 0,04746 | 0,04768 | 0,05158 | 0,05139 |
| 530,91585 | 0,0484 | 0,04681 | 0,04697 | 0,05057 | 0,05031 |
| 530,95303 | 0,04782 | 0,0462 | 0,0463 | 0,04957 | 0,04926 |
| 530,99022 | 0,04728 | 0,04567 | 0,0457 | 0,04863 | 0,0483 |
| 531,0274 | 0,04684 | 0,04524 | 0,04521 | 0,04778 | 0,04747 |
| 531,06458 | 0,0465 | 0,04495 | 0,04485 | 0,0471 | 0,04683 |
| 531,10176 | 0,04633 | 0,04485 | 0,04468 | 0,0466 | 0,04641 |
| 531,13894 | 0,04634 | 0,04496 | 0,04475 | 0,04632 | 0,04622 |
| 531,17613 | 0,04655 | 0,04528 | 0,04506 | 0,04627 | 0,04629 |
| 531,21331 | 0,04697 | 0,04586 | 0,04563 | 0,04648 | 0,04663 |
| 531,25049 | 0,04763 | 0,04669 | 0,04648 | 0,04696 | 0,04726 |
| 531,28767 | 0,04851 | 0,04778 | 0,04762 | 0,04772 | 0,04816 |
| 531,32485 | 0,04963 | 0,04913 | 0,04903 | 0,04875 | 0,04935 |
| 531,36204 | 0,05097 | 0,05074 | 0,05072 | 0,05006 | 0,05082 |
| 531,39922 | 0,05252 | 0,05257 | 0,05265 | 0,05165 | 0,05257 |
| 531,4364 | 0,05426 | 0,05462 | 0,05479 | 0,05348 | 0,05457 |
| 531,47358 | 0,05615 | 0,05683 | 0,05712 | 0,05552 | 0,05679 |
| 531,51076 | 0,05814 | 0,05914 | 0,05954 | 0,05773 | 0,05918 |
| 531,54795 | 0,06018 | 0,0615 | 0,06201 | 0,06008 | 0,0617 |
| 531,58513 | 0,06222 | 0,06385 | 0,06445 | 0,06252 | 0,06432 |
| 531,62231 | 0,06422 | 0,06613 | 0,06682 | 0,065 | 0,06696 |
| 531,65949 | 0,06614 | 0,06829 | 0,06905 | 0,06745 | 0,06958 |
| 531,69667 | 0,06792 | 0,07027 | 0,07108 | 0,06983 | 0,07209 |
| 531,73386 | 0,06953 | 0,07203 | 0,07287 | 0,07206 | 0,07444 |
| 531,77104 | 0,07094 | 0,07352 | 0,07438 | 0,07407 | 0,07651 |
| 531,80822 | 0,0721 | 0,0747 | 0,07554 | 0,07579 | 0,07826 |
| 531,8454 | 0,07303 | 0,07557 | 0,07636 | 0,07721 | 0,07964 |
| 531,88258 | 0,07373 | 0,07613 | 0,07686 | 0,07828 | 0,08061 |
| 531,91977 | 0,07421 | 0,07641 | 0,07704 | 0,07897 | 0,08115 |
| 531,95695 | 0,07447 | 0,07641 | 0,07692 | 0,0793 | 0,08126 |
| 531,99413 | 0,07456 | 0,07616 | 0,07653 | 0,07925 | 0,08093 |
| 532,03131 | 0,07448 | 0,07571 | 0,0759 | 0,07887 | 0,08022 |
| 532,06849 | 0,07427 | 0,07508 | 0,07508 | 0,07818 | 0,07915 |
| 532,10568 | 0,07396 | 0,07431 | 0,0741 | 0,07722 | 0,07777 |
| 532,14286 | 0,07358 | 0,07345 | 0,07299 | 0,07607 | 0,07618 |
| 532,18004 | 0,07316 | 0,07254 | 0,07182 | 0,07482 | 0,07447 |
| 532,21722 | 0,07273 | 0,07162 | 0,07063 | 0,07351 | 0,07271 |
| 532,2544 | 0,07232 | 0,07072 | 0,06944 | 0,07223 | 0,071 |
| 532,29159 | 0,07195 | 0,06987 | 0,0683 | 0,07104 | 0,0694 |
| 532,32877 | 0,07163 | 0,06909 | 0,06723 | 0,06999 | 0,06798 |
| 532,36595 | 0,07138 | 0,0684 | 0,06626 | 0,06913 | 0,06679 |
| 532,40313 | 0,07122 | 0,06783 | 0,06542 | 0,06851 | 0,06589 |
| 532,44031 | 0,07117 | 0,06739 | 0,06474 | 0,06817 | 0,0653 |
| 532,4775 | 0,07125 | 0,06711 | 0,06424 | 0,06815 | 0,0651 |
| 532,51468 | 0,07148 | 0,06702 | 0,06396 | 0,06844 | 0,06525 |
| 532,55186 | 0,07188 | 0,06712 | 0,06392 | 0,06903 | 0,06575 |
| 532,58904 | 0,07246 | 0,06743 | 0,06414 | 0,06991 | 0,06657 |
| 532,62622 | 0,07324 | 0,06798 | 0,06464 | 0,07106 | 0,0677 |
| 532,66341 | 0,07424 | 0,06878 | 0,06543 | 0,07244 | 0,06911 |
| 532,70059 | 0,07548 | 0,06984 | 0,06653 | 0,07404 | 0,07074 |
| 532,73777 | 0,07696 | 0,07117 | 0,06794 | 0,0758 | 0,07256 |
| 532,77495 | 0,07868 | 0,07278 | 0,06968 | 0,07769 | 0,07453 |
| 532,81213 | 0,08065 | 0,07467 | 0,07172 | 0,07967 | 0,0766 |
| 532,84932 | 0,08286 | 0,07683 | 0,07408 | 0,08169 | 0,07872 |
| 532,8865 | 0,08526 | 0,07921 | 0,07668 | 0,08371 | 0,08085 |
| 532,92368 | 0,0878 | 0,08177 | 0,07946 | 0,0857 | 0,08294 |
| 532,96086 | 0,09045 | 0,08444 | 0,08237 | 0,08764 | 0,08498 |
| 532,99804 | 0,09313 | 0,08716 | 0,08533 | 0,0895 | 0,08692 |
| 533,03523 | 0,09579 | 0,08988 | 0,08826 | 0,09126 | 0,08876 |
| 533,07241 | 0,09836 | 0,09251 | 0,09108 | 0,0929 | 0,09046 |
| 533,10959 | 0,10077 | 0,09498 | 0,09372 | 0,09441 | 0,09201 |
| 533,14677 | 0,10297 | 0,09723 | 0,09608 | 0,09576 | 0,09338 |
| 533,18395 | 0,10485 | 0,09915 | 0,09806 | 0,09692 | 0,09453 |
| 533,22114 | 0,10639 | 0,10072 | 0,09963 | 0,09787 | 0,09545 |
| 533,25832 | 0,10757 | 0,1019 | 0,10075 | 0,09861 | 0,09613 |
| 533,2955 | 0,10837 | 0,10268 | 0,1014 | 0,09912 | 0,09655 |
| 533,33268 | 0,1088 | 0,10306 | 0,1016 | 0,0994 | 0,09672 |
| 533,36986 | 0,10887 | 0,10306 | 0,10136 | 0,09945 | 0,09664 |
| 533,40705 | 0,1086 | 0,1027 | 0,10072 | 0,09927 | 0,09631 |
| 533,44423 | 0,10804 | 0,10203 | 0,09973 | 0,0989 | 0,09577 |
| 533,48141 | 0,10724 | 0,10109 | 0,09844 | 0,09835 | 0,09504 |
| 533,51859 | 0,10622 | 0,09994 | 0,09691 | 0,09768 | 0,09418 |
| 533,55577 | 0,10506 | 0,09863 | 0,09524 | 0,09693 | 0,09324 |
| 533,59295 | 0,10381 | 0,09725 | 0,0935 | 0,09617 | 0,09229 |
| 533,63014 | 0,10254 | 0,09584 | 0,09176 | 0,09545 | 0,09138 |
| 533,66732 | 0,10127 | 0,09445 | 0,09006 | 0,09481 | 0,09056 |
| 533,7045 | 0,10004 | 0,09311 | 0,08846 | 0,0943 | 0,08988 |
| 533,74168 | 0,09889 | 0,09187 | 0,08699 | 0,09394 | 0,08939 |
| 533,77886 | 0,09782 | 0,09074 | 0,08568 | 0,09376 | 0,0891 |
| 533,81605 | 0,09687 | 0,08974 | 0,08454 | 0,09377 | 0,08904 |
| 533,85323 | 0,09605 | 0,0889 | 0,08359 | 0,094 | 0,08922 |
| 533,89041 | 0,09538 | 0,08823 | 0,08286 | 0,09445 | 0,08969 |
| 533,92759 | 0,09485 | 0,08773 | 0,08232 | 0,0951 | 0,0904 |
| 533,96477 | 0,09449 | 0,0874 | 0,08199 | 0,09593 | 0,09135 |
| 534,00196 | 0,0943 | 0,08727 | 0,08187 | 0,09693 | 0,09251 |
| 534,03914 | 0,09429 | 0,08732 | 0,08197 | 0,09807 | 0,09387 |
| 534,07632 | 0,09447 | 0,08759 | 0,0823 | 0,09933 | 0,0954 |
| 534,1135 | 0,09486 | 0,08807 | 0,08286 | 0,10068 | 0,09705 |
| 534,15068 | 0,09547 | 0,08879 | 0,08367 | 0,10206 | 0,09879 |
| 534,18787 | 0,09631 | 0,08974 | 0,08473 | 0,10345 | 0,10057 |
| 534,22505 | 0,09739 | 0,09096 | 0,08609 | 0,10478 | 0,1023 |
| 534,26223 | 0,09869 | 0,09242 | 0,0877 | 0,10599 | 0,10392 |
| 534,29941 | 0,10018 | 0,0941 | 0,08955 | 0,10701 | 0,10536 |
| 534,33659 | 0,10185 | 0,09598 | 0,0916 | 0,10779 | 0,10653 |
| 534,37378 | 0,10363 | 0,09801 | 0,09382 | 0,10828 | 0,10739 |
| 534,41096 | 0,10549 | 0,10014 | 0,09616 | 0,10843 | 0,10788 |
| 534,44814 | 0,10735 | 0,10232 | 0,09855 | 0,1082 | 0,10794 |
| 534,48532 | 0,10914 | 0,10446 | 0,10092 | 0,10757 | 0,10756 |
| 534,5225 | 0,11079 | 0,10649 | 0,10317 | 0,10651 | 0,1067 |
| 534,55969 | 0,1122 | 0,10831 | 0,1052 | 0,10503 | 0,10537 |
| 534,59687 | 0,11325 | 0,10981 | 0,10691 | 0,1031 | 0,10353 |
| 534,63405 | 0,11391 | 0,11092 | 0,10822 | 0,10079 | 0,10127 |
| 534,67123 | 0,11411 | 0,11157 | 0,10907 | 0,09815 | 0,09864 |
| 534,70841 | 0,1138 | 0,1117 | 0,10938 | 0,09524 | 0,09571 |
| 534,7456 | 0,11296 | 0,11129 | 0,10913 | 0,09212 | 0,09253 |
| 534,78278 | 0,11158 | 0,11031 | 0,1083 | 0,08885 | 0,08918 |
| 534,81996 | 0,10968 | 0,10876 | 0,10687 | 0,0855 | 0,08573 |
| 534,85714 | 0,10728 | 0,10667 | 0,10489 | 0,08214 | 0,08225 |
| 534,89432 | 0,10444 | 0,10408 | 0,10236 | 0,07884 | 0,07882 |
| 534,93151 | 0,1012 | 0,10102 | 0,09935 | 0,07566 | 0,0755 |
| 534,96869 | 0,09769 | 0,09763 | 0,09599 | 0,07268 | 0,07237 |
| 535,00587 | 0,09401 | 0,09401 | 0,09237 | 0,06994 | 0,06948 |
| 535,04305 | 0,09026 | 0,09027 | 0,0886 | 0,06747 | 0,06686 |
| 535,08023 | 0,08653 | 0,08649 | 0,08477 | 0,06531 | 0,06456 |
| 535,11742 | 0,08292 | 0,08278 | 0,08099 | 0,06348 | 0,06258 |
| 535,1546 | 0,07949 | 0,07923 | 0,07734 | 0,06199 | 0,06096 |
| 535,19178 | 0,07633 | 0,07592 | 0,07391 | 0,06086 | 0,05971 |
| 535,22896 | 0,0735 | 0,07294 | 0,07079 | 0,06008 | 0,05883 |
| 535,26614 | 0,0711 | 0,07038 | 0,0681 | 0,05967 | 0,05833 |
| 535,30333 | 0,06914 | 0,06829 | 0,06584 | 0,05964 | 0,05824 |
| 535,34051 | 0,06764 | 0,06667 | 0,06405 | 0,05998 | 0,05853 |
| 535,37769 | 0,06661 | 0,06556 | 0,06277 | 0,06066 | 0,05918 |
| 535,41487 | 0,06605 | 0,06495 | 0,06199 | 0,06166 | 0,06019 |
| 535,45205 | 0,06596 | 0,06486 | 0,06174 | 0,06298 | 0,06154 |
| 535,48924 | 0,06632 | 0,06526 | 0,062 | 0,0646 | 0,06322 |
| 535,52642 | 0,06712 | 0,06615 | 0,06275 | 0,06649 | 0,06519 |
| 535,5636 | 0,06832 | 0,0675 | 0,06398 | 0,06863 | 0,06743 |
| 535,60078 | 0,06991 | 0,06927 | 0,06569 | 0,07098 | 0,06992 |
| 535,63796 | 0,07186 | 0,07145 | 0,0678 | 0,07351 | 0,0726 |
| 535,67515 | 0,07407 | 0,07393 | 0,07023 | 0,07619 | 0,07543 |
| 535,71233 | 0,0765 | 0,07667 | 0,07293 | 0,07895 | 0,07835 |
| 535,74951 | 0,0791 | 0,07958 | 0,07584 | 0,08174 | 0,08131 |
| 535,78669 | 0,08179 | 0,08261 | 0,07888 | 0,08452 | 0,08424 |
| 535,82387 | 0,08452 | 0,08568 | 0,08199 | 0,08725 | 0,0871 |
| 535,86106 | 0,08722 | 0,08872 | 0,08507 | 0,08989 | 0,08984 |
| 535,89824 | 0,08984 | 0,09165 | 0,08808 | 0,0924 | 0,09243 |
| 535,93542 | 0,0923 | 0,09441 | 0,0909 | 0,09474 | 0,09481 |
| 535,9726 | 0,09451 | 0,09688 | 0,09346 | 0,09689 | 0,09697 |
| 536,00978 | 0,09645 | 0,09902 | 0,0957 | 0,09879 | 0,09883 |
| 536,04697 | 0,09806 | 0,1008 | 0,09759 | 0,10042 | 0,10039 |
| 536,08415 | 0,09932 | 0,10216 | 0,09908 | 0,10176 | 0,10163 |
| 536,12133 | 0,10019 | 0,10308 | 0,10013 | 0,10281 | 0,10255 |
| 536,15851 | 0,10067 | 0,10355 | 0,10074 | 0,10354 | 0,10314 |
| 536,19569 | 0,10076 | 0,10357 | 0,1009 | 0,10395 | 0,1034 |
| 536,23288 | 0,10045 | 0,10314 | 0,10061 | 0,10404 | 0,10335 |
| 536,27006 | 0,09976 | 0,10229 | 0,0999 | 0,10384 | 0,10301 |
| 536,30724 | 0,09871 | 0,10102 | 0,09877 | 0,10337 | 0,10243 |
| 536,34442 | 0,09734 | 0,09941 | 0,09732 | 0,10269 | 0,10165 |
| 536,3816 | 0,09573 | 0,09753 | 0,0956 | 0,10183 | 0,10075 |
| 536,41879 | 0,09392 | 0,09544 | 0,09368 | 0,10093 | 0,09984 |
| 536,45597 | 0,09198 | 0,09321 | 0,09161 | 0,10004 | 0,09899 |
| 536,49315 | 0,08996 | 0,09089 | 0,08946 | 0,09927 | 0,09829 |
| 536,53033 | 0,08791 | 0,08857 | 0,0873 | 0,09869 | 0,09783 |
| 536,56751 | 0,0859 | 0,08629 | 0,08518 | 0,09836 | 0,09766 |
| 536,6047 | 0,08398 | 0,08413 | 0,08317 | 0,09833 | 0,09782 |
| 536,64188 | 0,08221 | 0,08214 | 0,08134 | 0,09863 | 0,09833 |
| 536,67906 | 0,08065 | 0,08039 | 0,07973 | 0,09923 | 0,09917 |
| 536,71624 | 0,07934 | 0,07892 | 0,07838 | 0,10013 | 0,10032 |
| 536,75342 | 0,0783 | 0,07776 | 0,07732 | 0,10124 | 0,10168 |
| 536,79061 | 0,07756 | 0,07693 | 0,07657 | 0,10242 | 0,1031 |
| 536,82779 | 0,07714 | 0,07645 | 0,07615 | 0,10358 | 0,10448 |
| 536,86497 | 0,07704 | 0,07634 | 0,07607 | 0,10458 | 0,10567 |
| 536,90215 | 0,07726 | 0,07658 | 0,07633 | 0,1053 | 0,10654 |
| 536,93933 | 0,07778 | 0,07718 | 0,07692 | 0,10563 | 0,10698 |
| 536,97652 | 0,0786 | 0,07811 | 0,07785 | 0,10548 | 0,10689 |
| 537,0137 | 0,0797 | 0,07936 | 0,07907 | 0,10478 | 0,1062 |
| 537,05088 | 0,08099 | 0,08086 | 0,08053 | 0,10349 | 0,10488 |
| 537,08806 | 0,08243 | 0,08255 | 0,08216 | 0,10155 | 0,10285 |
| 537,12524 | 0,08394 | 0,08435 | 0,08392 | 0,09906 | 0,10025 |
| 537,16243 | 0,08547 | 0,08621 | 0,08573 | 0,09611 | 0,09716 |
| 537,19961 | 0,08694 | 0,08803 | 0,08753 | 0,09278 | 0,09369 |
| 537,23679 | 0,08829 | 0,08976 | 0,08925 | 0,08921 | 0,08996 |
| 537,27397 | 0,08946 | 0,09132 | 0,09081 | 0,0855 | 0,08611 |
| 537,31115 | 0,09038 | 0,09264 | 0,09213 | 0,08177 | 0,08225 |
| 537,34834 | 0,09099 | 0,09365 | 0,09313 | 0,07814 | 0,07853 |
| 537,38552 | 0,09125 | 0,09428 | 0,0938 | 0,07472 | 0,07504 |
| 537,4227 | 0,09116 | 0,09453 | 0,09409 | 0,07161 | 0,0719 |
| 537,45988 | 0,09072 | 0,0944 | 0,094 | 0,0689 | 0,0692 |
| 537,49706 | 0,08995 | 0,09389 | 0,09352 | 0,06662 | 0,06696 |
| 537,53425 | 0,08887 | 0,09302 | 0,09268 | 0,06479 | 0,0652 |
| 537,57143 | 0,08751 | 0,09181 | 0,09149 | 0,06342 | 0,06393 |
| 537,60861 | 0,08591 | 0,09031 | 0,09 | 0,0625 | 0,06312 |
| 537,64579 | 0,08411 | 0,08856 | 0,08825 | 0,06202 | 0,06277 |
| 537,68297 | 0,08218 | 0,08662 | 0,08628 | 0,06195 | 0,06283 |
| 537,72016 | 0,08015 | 0,08452 | 0,08419 | 0,06227 | 0,06328 |
| 537,75734 | 0,07809 | 0,08236 | 0,08203 | 0,06294 | 0,06407 |
| 537,79452 | 0,07604 | 0,08018 | 0,07985 | 0,06395 | 0,06519 |
| 537,8317 | 0,07406 | 0,07804 | 0,07772 | 0,06524 | 0,06656 |
| 537,86888 | 0,07218 | 0,07597 | 0,07568 | 0,06677 | 0,06814 |
| 537,90607 | 0,07045 | 0,07405 | 0,07378 | 0,0685 | 0,0699 |
| 537,94325 | 0,06891 | 0,0723 | 0,07209 | 0,07042 | 0,0718 |
| 537,98043 | 0,0676 | 0,07078 | 0,07063 | 0,0725 | 0,07385 |
| 538,01761 | 0,06657 | 0,06954 | 0,06952 | 0,07473 | 0,07601 |
| 538,05479 | 0,06591 | 0,06868 | 0,06878 | 0,0771 | 0,0783 |
| 538,09198 | 0,06565 | 0,06825 | 0,06846 | 0,07962 | 0,08073 |
| 538,12916 | 0,06583 | 0,06828 | 0,06863 | 0,08232 | 0,08332 |
| 538,16634 | 0,06652 | 0,06884 | 0,06932 | 0,08522 | 0,08613 |
| 538,20352 | 0,06776 | 0,06998 | 0,07061 | 0,08835 | 0,08919 |
| 538,2407 | 0,0696 | 0,07175 | 0,07253 | 0,09175 | 0,09254 |
| 538,27789 | 0,07206 | 0,0742 | 0,07513 | 0,09545 | 0,09623 |
| 538,31507 | 0,07517 | 0,07733 | 0,07843 | 0,09949 | 0,1003 |
| 538,35225 | 0,07892 | 0,08117 | 0,08249 | 0,10388 | 0,10475 |
| 538,38943 | 0,08332 | 0,08572 | 0,08727 | 0,10862 | 0,1096 |
| 538,42661 | 0,08832 | 0,09095 | 0,09267 | 0,11367 | 0,1148 |
| 538,4638 | 0,09377 | 0,09669 | 0,09861 | 0,11898 | 0,12029 |
| 538,50098 | 0,09955 | 0,10284 | 0,10496 | 0,12443 | 0,12595 |
| 538,53816 | 0,10552 | 0,10923 | 0,11158 | 0,12985 | 0,13158 |
| 538,57534 | 0,1115 | 0,1157 | 0,11829 | 0,13502 | 0,13698 |
| 538,61252 | 0,1173 | 0,12204 | 0,1249 | 0,13974 | 0,14192 |
| 538,64971 | 0,12272 | 0,12806 | 0,1312 | 0,14379 | 0,14616 |
| 538,68689 | 0,12756 | 0,13352 | 0,13695 | 0,14694 | 0,14948 |
| 538,72407 | 0,13163 | 0,13822 | 0,14184 | 0,149 | 0,15169 |
| 538,76125 | 0,13461 | 0,14182 | 0,14575 | 0,14982 | 0,15261 |
| 538,79843 | 0,13646 | 0,14426 | 0,14851 | 0,14929 | 0,15213 |
| 538,83562 | 0,13711 | 0,14543 | 0,15001 | 0,14733 | 0,15017 |
| 538,8728 | 0,1365 | 0,14528 | 0,15017 | 0,14389 | 0,14669 |
| 538,90998 | 0,13465 | 0,14378 | 0,14898 | 0,13926 | 0,14199 |
| 538,94716 | 0,13161 | 0,14099 | 0,14646 | 0,13365 | 0,13628 |
| 538,98434 | 0,12748 | 0,13699 | 0,14269 | 0,12732 | 0,12982 |
| 539,02153 | 0,1224 | 0,13192 | 0,13779 | 0,12057 | 0,12292 |
| 539,05871 | 0,11655 | 0,12596 | 0,13185 | 0,11373 | 0,11591 |
| 539,09589 | 0,11011 | 0,11928 | 0,12524 | 0,1071 | 0,10912 |
| 539,13307 | 0,10339 | 0,1122 | 0,1182 | 0,10101 | 0,10286 |
| 539,17025 | 0,09664 | 0,10499 | 0,11097 | 0,0957 | 0,0974 |
| 539,20744 | 0,09009 | 0,09791 | 0,10382 | 0,09153 | 0,09312 |
| 539,24462 | 0,08396 | 0,0912 | 0,09697 | 0,08862 | 0,0901 |
| 539,2818 | 0,07844 | 0,08505 | 0,09066 | 0,087 | 0,0884 |
| 539,31898 | 0,07369 | 0,07967 | 0,08507 | 0,08666 | 0,08802 |
| 539,35616 | 0,06985 | 0,0752 | 0,08039 | 0,08754 | 0,08888 |
| 539,39335 | 0,06701 | 0,07177 | 0,07684 | 0,0895 | 0,09086 |
| 539,43053 | 0,06528 | 0,06949 | 0,07447 | 0,09238 | 0,09379 |
| 539,46771 | 0,06472 | 0,06847 | 0,07324 | 0,09595 | 0,09745 |
| 539,50489 | 0,0652 | 0,06856 | 0,07316 | 0,09996 | 0,10157 |
| 539,54207 | 0,06662 | 0,06969 | 0,07415 | 0,10413 | 0,10588 |
| 539,57926 | 0,06889 | 0,07177 | 0,07612 | 0,10812 | 0,11002 |
| 539,61644 | 0,07185 | 0,07465 | 0,07892 | 0,11164 | 0,11371 |
| 539,65362 | 0,07534 | 0,07816 | 0,08241 | 0,11447 | 0,1167 |
| 539,6908 | 0,07918 | 0,08212 | 0,08639 | 0,11639 | 0,11878 |
| 539,72798 | 0,08315 | 0,08631 | 0,09065 | 0,11726 | 0,11979 |
| 539,76517 | 0,08707 | 0,09053 | 0,09493 | 0,11698 | 0,11963 |
| 539,80235 | 0,09066 | 0,09451 | 0,099 | 0,11551 | 0,11825 |
| 539,83953 | 0,09376 | 0,09804 | 0,10264 | 0,11286 | 0,11567 |
| 539,87671 | 0,0962 | 0,10095 | 0,10568 | 0,10913 | 0,11196 |
| 539,91389 | 0,09786 | 0,10309 | 0,10796 | 0,1044 | 0,10718 |
| 539,95108 | 0,09865 | 0,10435 | 0,10936 | 0,0989 | 0,10162 |
| 539,98826 | 0,09853 | 0,10465 | 0,10979 | 0,09294 | 0,09556 |
| 540,02544 | 0,09746 | 0,10396 | 0,1092 | 0,08677 | 0,08926 |
| 540,06262 | 0,09549 | 0,10229 | 0,10758 | 0,08065 | 0,083 |
| 540,0998 | 0,09266 | 0,09969 | 0,10488 | 0,07483 | 0,07702 |
| 540,13699 | 0,08903 | 0,09617 | 0,10131 | 0,06957 | 0,07159 |
| 540,17417 | 0,08477 | 0,09192 | 0,09701 | 0,06505 | 0,06693 |
| 540,21135 | 0,08008 | 0,08714 | 0,09212 | 0,06147 | 0,06322 |
| 540,24853 | 0,07512 | 0,08199 | 0,08682 | 0,05895 | 0,06061 |
| 540,28571 | 0,07006 | 0,07666 | 0,08129 | 0,05772 | 0,05931 |
| 540,3229 | 0,06508 | 0,07133 | 0,07571 | 0,05764 | 0,0592 |
| 540,36008 | 0,06034 | 0,06618 | 0,07028 | 0,05865 | 0,06022 |
| 540,39726 | 0,05597 | 0,06137 | 0,06516 | 0,06063 | 0,06224 |
| 540,43444 | 0,05212 | 0,05704 | 0,06059 | 0,06342 | 0,06511 |
| 540,47162 | 0,04891 | 0,05335 | 0,05667 | 0,06681 | 0,06861 |
| 540,50881 | 0,0465 | 0,05046 | 0,0535 | 0,07058 | 0,0725 |
| 540,54599 | 0,04484 | 0,04836 | 0,05113 | 0,07445 | 0,07652 |
| 540,58317 | 0,04396 | 0,04708 | 0,0496 | 0,07816 | 0,08037 |
| 540,62035 | 0,04385 | 0,04661 | 0,04892 | 0,0814 | 0,08374 |
| 540,65753 | 0,04446 | 0,04691 | 0,04906 | 0,08388 | 0,08633 |
| 540,69472 | 0,04572 | 0,04793 | 0,04997 | 0,08544 | 0,08798 |
| 540,7319 | 0,04756 | 0,04957 | 0,05157 | 0,08595 | 0,08853 |
| 540,76908 | 0,04985 | 0,05174 | 0,05378 | 0,08532 | 0,08792 |
| 540,80626 | 0,05249 | 0,0543 | 0,05644 | 0,08355 | 0,08613 |
| 540,84344 | 0,05533 | 0,05713 | 0,05936 | 0,08068 | 0,08319 |
| 540,88063 | 0,05819 | 0,06002 | 0,06239 | 0,0768 | 0,07921 |
| 540,91781 | 0,06093 | 0,06283 | 0,06537 | 0,07206 | 0,07433 |
| 540,95499 | 0,0634 | 0,0654 | 0,06815 | 0,06664 | 0,06875 |
| 540,99217 | 0,06549 | 0,0676 | 0,07058 | 0,06072 | 0,06265 |
| 541,02935 | 0,06707 | 0,06931 | 0,07253 | 0,0546 | 0,05633 |
| 541,06654 | 0,06807 | 0,07043 | 0,07388 | 0,04847 | 0,05001 |
| 541,10372 | 0,06841 | 0,07088 | 0,07452 | 0,0425 | 0,04385 |
| 541,1409 | 0,06804 | 0,07061 | 0,07432 | 0,03685 | 0,03801 |
| 541,17808 | 0,0669 | 0,06954 | 0,07334 | 0,03162 | 0,03261 |
| 541,21526 | 0,06501 | 0,06768 | 0,07158 | 0,02688 | 0,02771 |
| 541,25245 | 0,06248 | 0,06513 | 0,06909 | 0,02268 | 0,02337 |
| 541,28963 | 0,05935 | 0,06196 | 0,06593 | 0,01902 | 0,0196 |
| 541,32681 | 0,05574 | 0,05826 | 0,06218 | 0,01592 | 0,0164 |
| 541,36399 | 0,05174 | 0,05413 | 0,05796 | 0,01334 | 0,01374 |
| 541,40117 | 0,04745 | 0,0497 | 0,05338 | 0,01119 | 0,01153 |
| 541,43836 | 0,043 | 0,04507 | 0,04856 | 0,00942 | 0,0097 |
| 541,47554 | 0,03849 | 0,04037 | 0,04364 | 0,00796 | 0,0082 |
| 541,51272 | 0,03404 | 0,03571 | 0,03877 | 0,00677 | 0,00697 |
| 541,5499 | 0,02977 | 0,03122 | 0,03404 | 0,00579 | 0,00597 |
| 541,58708 | 0,02574 | 0,02698 | 0,02955 | 0,005 | 0,00515 |
| 541,62427 | 0,02201 | 0,02305 | 0,02535 | 0,00434 | 0,00448 |
| 541,66145 | 0,01861 | 0,01947 | 0,02151 | 0,00381 | 0,00393 |
| 541,69863 | 0,01557 | 0,01627 | 0,01806 | 0,00338 | 0,0035 |
| 541,73581 | 0,0129 | 0,01345 | 0,015 | 0,00304 | 0,00315 |
| 541,77299 | 0,01059 | 0,01102 | 0,01234 | 0,00277 | 0,00287 |
| 541,81018 | 0,00863 | 0,00895 | 0,01011 | 0,00257 | 0,00266 |
| 541,84736 | 0,00698 | 0,00723 | 0,00824 | 0,00243 | 0,00252 |
| 541,88454 | 0,00566 | 0,00584 | 0,00669 | 0,00234 | 0,00242 |
| 541,92172 | 0,00459 | 0,00473 | 0,00544 | 0,0023 | 0,00238 |
| 541,9589 | 0,00373 | 0,00385 | 0,00443 | 0,00231 | 0,00239 |
| 541,99609 | 0,00306 | 0,00317 | 0,00364 | 0,00234 | 0,00243 |
| 542,03327 | 0,00255 | 0,00266 | 0,00304 | 0,00241 | 0,00249 |
| 542,07045 | 0,00217 | 0,00228 | 0,00259 | 0,0025 | 0,00258 |
| 542,10763 | 0,00189 | 0,00202 | 0,00226 | 0,00259 | 0,00268 |
| 542,14481 | 0,00171 | 0,00185 | 0,00205 | 0,00267 | 0,00277 |
| 542,182 | 0,00159 | 0,00176 | 0,00192 | 0,00275 | 0,00285 |
| 542,21918 | 0,00153 | 0,00172 | 0,00186 | 0,0028 | 0,00291 |
| 542,25636 | 0,00152 | 0,00173 | 0,00185 | 0,00283 | 0,00294 |
| 542,29354 | 0,00153 | 0,00177 | 0,00187 | 0,00282 | 0,00294 |
| 542,33072 | 0,00157 | 0,00183 | 0,00192 | 0,00278 | 0,0029 |
| 542,36791 | 0,00162 | 0,00191 | 0,00198 | 0,00271 | 0,00282 |
| 542,40509 | 0,00168 | 0,00199 | 0,00206 | 0,00259 | 0,00271 |
| 542,44227 | 0,00174 | 0,00207 | 0,00214 | 0,00244 | 0,00256 |
| 542,47945 | 0,00179 | 0,00215 | 0,00221 | 0,00227 | 0,00238 |
| 542,51663 | 0,00183 | 0,00221 | 0,00227 | 0,00208 | 0,00218 |
| 542,55382 | 0,00187 | 0,00226 | 0,00231 | 0,00187 | 0,00197 |
| 542,591 | 0,00188 | 0,00229 | 0,00234 | 0,00166 | 0,00175 |
| 542,62818 | 0,00187 | 0,00229 | 0,00234 | 0,00145 | 0,00153 |
| 542,66536 | 0,00185 | 0,00227 | 0,00231 | 0,00125 | 0,00132 |
| 542,70254 | 0,0018 | 0,00222 | 0,00226 | 0,00106 | 0,00112 |
| 542,73973 | 0,00174 | 0,00215 | 0,00219 | 0,00089 | 0,00094 |
| 542,77691 | 0,00165 | 0,00206 | 0,00209 | 0,00073 | 0,00078 |
| 542,81409 | 0,00156 | 0,00195 | 0,00198 | 6e-04 | 0,00063 |
| 542,85127 | 0,00145 | 0,00182 | 0,00184 | 0,00048 | 0,00051 |
| 542,88845 | 0,00133 | 0,00167 | 0,0017 | 0,00039 | 0,00041 |
| 542,92564 | 0,0012 | 0,00152 | 0,00154 | 0,00031 | 0,00032 |
| 542,96282 | 0,00107 | 0,00136 | 0,00138 | 0,00025 | 0,00025 |
| 543 | 0,00095 | 0,0012 | 0,00122 | 2e-04 | 0,00019 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,01099 | 0,01388 | 0,01184 | 0,00405 | 0,00621 |
| 524,03718 | 0,01146 | 0,01436 | 0,01246 | 0,00437 | 0,00656 |
| 524,07436 | 0,01193 | 0,01483 | 0,0131 | 0,0047 | 0,00692 |
| 524,11155 | 0,01241 | 0,0153 | 0,01377 | 0,00504 | 0,00728 |
| 524,14873 | 0,0129 | 0,01577 | 0,01446 | 0,0054 | 0,00765 |
| 524,18591 | 0,0134 | 0,01624 | 0,01518 | 0,00578 | 0,00803 |
| 524,22309 | 0,0139 | 0,01671 | 0,01592 | 0,00617 | 0,00841 |
| 524,26027 | 0,01441 | 0,01718 | 0,01669 | 0,00658 | 0,0088 |
| 524,29746 | 0,01494 | 0,01766 | 0,01749 | 0,00699 | 0,00919 |
| 524,33464 | 0,01548 | 0,01815 | 0,01832 | 0,00742 | 0,00958 |
| 524,37182 | 0,01603 | 0,01865 | 0,01917 | 0,00787 | 0,00998 |
| 524,409 | 0,01659 | 0,01916 | 0,02005 | 0,00832 | 0,01039 |
| 524,44618 | 0,01718 | 0,01968 | 0,02096 | 0,00879 | 0,0108 |
| 524,48337 | 0,01778 | 0,02023 | 0,0219 | 0,00928 | 0,01122 |
| 524,52055 | 0,0184 | 0,02079 | 0,02287 | 0,00977 | 0,01165 |
| 524,55773 | 0,01905 | 0,02137 | 0,02386 | 0,01028 | 0,01209 |
| 524,59491 | 0,01972 | 0,02198 | 0,02488 | 0,0108 | 0,01253 |
| 524,63209 | 0,02042 | 0,02261 | 0,02594 | 0,01133 | 0,01299 |
| 524,66928 | 0,02115 | 0,02327 | 0,02702 | 0,01187 | 0,01345 |
| 524,70646 | 0,02191 | 0,02395 | 0,02812 | 0,01243 | 0,01393 |
| 524,74364 | 0,02271 | 0,02466 | 0,02925 | 0,013 | 0,01443 |
| 524,78082 | 0,02354 | 0,0254 | 0,03041 | 0,01359 | 0,01494 |
| 524,818 | 0,0244 | 0,02617 | 0,03161 | 0,0142 | 0,01547 |
| 524,85519 | 0,0253 | 0,02696 | 0,03282 | 0,01482 | 0,01602 |
| 524,89237 | 0,02625 | 0,02778 | 0,03407 | 0,01546 | 0,0166 |
| 524,92955 | 0,02724 | 0,02862 | 0,03534 | 0,01612 | 0,01719 |
| 524,96673 | 0,02828 | 0,02949 | 0,03664 | 0,01681 | 0,01782 |
| 525,00391 | 0,02935 | 0,03038 | 0,03797 | 0,01752 | 0,01848 |
| 525,0411 | 0,03047 | 0,0313 | 0,03933 | 0,01826 | 0,01918 |
| 525,07828 | 0,03165 | 0,03224 | 0,04072 | 0,01903 | 0,0199 |
| 525,11546 | 0,03287 | 0,0332 | 0,04213 | 0,01984 | 0,02067 |
| 525,15264 | 0,03414 | 0,03419 | 0,04358 | 0,02068 | 0,02147 |
| 525,18982 | 0,03546 | 0,0352 | 0,04506 | 0,02157 | 0,02233 |
| 525,22701 | 0,03683 | 0,03623 | 0,04657 | 0,0225 | 0,02322 |
| 525,26419 | 0,03825 | 0,03729 | 0,0481 | 0,02348 | 0,02416 |
| 525,30137 | 0,03973 | 0,03837 | 0,04967 | 0,02451 | 0,02514 |
| 525,33855 | 0,04125 | 0,03948 | 0,05128 | 0,0256 | 0,02618 |
| 525,37573 | 0,04281 | 0,04062 | 0,05291 | 0,02675 | 0,02728 |
| 525,41292 | 0,04442 | 0,0418 | 0,05458 | 0,02796 | 0,02842 |
| 525,4501 | 0,04609 | 0,04301 | 0,05627 | 0,02923 | 0,02962 |
| 525,48728 | 0,04779 | 0,04425 | 0,058 | 0,03056 | 0,03086 |
| 525,52446 | 0,04954 | 0,04553 | 0,05976 | 0,03198 | 0,03217 |
| 525,56164 | 0,05132 | 0,04686 | 0,06155 | 0,03346 | 0,03352 |
| 525,59883 | 0,05314 | 0,04824 | 0,06336 | 0,03501 | 0,03493 |
| 525,63601 | 0,055 | 0,04966 | 0,0652 | 0,03662 | 0,03638 |
| 525,67319 | 0,05688 | 0,05114 | 0,06706 | 0,0383 | 0,03788 |
| 525,71037 | 0,05879 | 0,05266 | 0,06895 | 0,04006 | 0,03944 |
| 525,74755 | 0,06072 | 0,05424 | 0,07086 | 0,04189 | 0,04103 |
| 525,78474 | 0,06267 | 0,05589 | 0,07279 | 0,04377 | 0,04266 |
| 525,82192 | 0,06463 | 0,05758 | 0,07472 | 0,04571 | 0,04432 |
| 525,8591 | 0,0666 | 0,05933 | 0,07667 | 0,0477 | 0,04602 |
| 525,89628 | 0,06858 | 0,06113 | 0,07863 | 0,04975 | 0,04775 |
| 525,93346 | 0,07055 | 0,06298 | 0,08059 | 0,05184 | 0,0495 |
| 525,97065 | 0,07252 | 0,06489 | 0,08255 | 0,05396 | 0,05126 |
| 526,00783 | 0,07449 | 0,06685 | 0,08451 | 0,05612 | 0,05304 |
| 526,04501 | 0,07643 | 0,06884 | 0,08645 | 0,0583 | 0,05483 |
| 526,08219 | 0,07837 | 0,07086 | 0,08838 | 0,06049 | 0,05663 |
| 526,11937 | 0,08028 | 0,07292 | 0,09029 | 0,06269 | 0,05842 |
| 526,15656 | 0,08217 | 0,075 | 0,09218 | 0,06489 | 0,0602 |
| 526,19374 | 0,08403 | 0,0771 | 0,09405 | 0,06708 | 0,06198 |
| 526,23092 | 0,08586 | 0,07921 | 0,09588 | 0,06926 | 0,06374 |
| 526,2681 | 0,08766 | 0,08132 | 0,09767 | 0,07141 | 0,06548 |
| 526,30528 | 0,08943 | 0,08343 | 0,09942 | 0,07352 | 0,0672 |
| 526,34247 | 0,09117 | 0,08552 | 0,10113 | 0,0756 | 0,0689 |
| 526,37965 | 0,09288 | 0,0876 | 0,1028 | 0,07763 | 0,07056 |
| 526,41683 | 0,09454 | 0,08965 | 0,10441 | 0,07962 | 0,07219 |
| 526,45401 | 0,09618 | 0,09167 | 0,10596 | 0,08154 | 0,07379 |
| 526,49119 | 0,09778 | 0,09365 | 0,10746 | 0,08339 | 0,07535 |
| 526,52838 | 0,09936 | 0,0956 | 0,10891 | 0,08518 | 0,07688 |
| 526,56556 | 0,10091 | 0,09749 | 0,1103 | 0,0869 | 0,07837 |
| 526,60274 | 0,10244 | 0,09934 | 0,11163 | 0,08855 | 0,07982 |
| 526,63992 | 0,10393 | 0,10115 | 0,11289 | 0,09012 | 0,08123 |
| 526,6771 | 0,10542 | 0,1029 | 0,11409 | 0,09161 | 0,08261 |
| 526,71429 | 0,10688 | 0,10461 | 0,11524 | 0,09303 | 0,08395 |
| 526,75147 | 0,10833 | 0,10626 | 0,11633 | 0,09437 | 0,08526 |
| 526,78865 | 0,10977 | 0,10786 | 0,11736 | 0,09564 | 0,08652 |
| 526,82583 | 0,11119 | 0,10942 | 0,11833 | 0,09684 | 0,08776 |
| 526,86301 | 0,11261 | 0,11094 | 0,11924 | 0,09796 | 0,08897 |
| 526,9002 | 0,11403 | 0,11242 | 0,12011 | 0,09901 | 0,09015 |
| 526,93738 | 0,11544 | 0,11386 | 0,12093 | 0,10001 | 0,0913 |
| 526,97456 | 0,11684 | 0,11526 | 0,12169 | 0,10095 | 0,09243 |
| 527,01174 | 0,11824 | 0,11664 | 0,1224 | 0,10184 | 0,09354 |
| 527,04892 | 0,11963 | 0,11798 | 0,12307 | 0,10267 | 0,09463 |
| 527,08611 | 0,12101 | 0,11931 | 0,1237 | 0,10347 | 0,0957 |
| 527,12329 | 0,12238 | 0,12061 | 0,12429 | 0,10424 | 0,09675 |
| 527,16047 | 0,12374 | 0,12189 | 0,12483 | 0,10498 | 0,0978 |
| 527,19765 | 0,12508 | 0,12315 | 0,12534 | 0,10569 | 0,09883 |
| 527,23483 | 0,1264 | 0,1244 | 0,12581 | 0,1064 | 0,09986 |
| 527,27202 | 0,12769 | 0,12562 | 0,12625 | 0,1071 | 0,10088 |
| 527,3092 | 0,12895 | 0,12683 | 0,12666 | 0,1078 | 0,1019 |
| 527,34638 | 0,13018 | 0,12801 | 0,12703 | 0,1085 | 0,10291 |
| 527,38356 | 0,13135 | 0,12916 | 0,12738 | 0,10922 | 0,10392 |
| 527,42074 | 0,13248 | 0,13029 | 0,12769 | 0,10997 | 0,10492 |
| 527,45793 | 0,13355 | 0,13139 | 0,12799 | 0,11074 | 0,10593 |
| 527,49511 | 0,13457 | 0,13246 | 0,12826 | 0,11153 | 0,10693 |
| 527,53229 | 0,13552 | 0,13349 | 0,1285 | 0,11236 | 0,10793 |
| 527,56947 | 0,1364 | 0,13448 | 0,12873 | 0,11323 | 0,10893 |
| 527,60665 | 0,13721 | 0,13542 | 0,12894 | 0,11414 | 0,10993 |
| 527,64384 | 0,13794 | 0,13631 | 0,12913 | 0,11508 | 0,11092 |
| 527,68102 | 0,13861 | 0,13715 | 0,12932 | 0,11607 | 0,11191 |
| 527,7182 | 0,13921 | 0,13795 | 0,12949 | 0,11709 | 0,11289 |
| 527,75538 | 0,13972 | 0,13868 | 0,12967 | 0,11814 | 0,11386 |
| 527,79256 | 0,14015 | 0,13935 | 0,12985 | 0,11923 | 0,11482 |
| 527,82975 | 0,14052 | 0,13997 | 0,13003 | 0,12035 | 0,11577 |
| 527,86693 | 0,14083 | 0,14054 | 0,13023 | 0,12148 | 0,1167 |
| 527,90411 | 0,14108 | 0,14106 | 0,13045 | 0,12263 | 0,11762 |
| 527,94129 | 0,14128 | 0,14153 | 0,13069 | 0,12378 | 0,11852 |
| 527,97847 | 0,14142 | 0,14195 | 0,13096 | 0,12494 | 0,1194 |
| 528,01566 | 0,14153 | 0,14234 | 0,13126 | 0,12608 | 0,12025 |
| 528,05284 | 0,1416 | 0,1427 | 0,13161 | 0,12721 | 0,12107 |
| 528,09002 | 0,14166 | 0,14303 | 0,13201 | 0,12831 | 0,12187 |
| 528,1272 | 0,1417 | 0,14334 | 0,13246 | 0,12937 | 0,12265 |
| 528,16438 | 0,14173 | 0,14365 | 0,13295 | 0,1304 | 0,1234 |
| 528,20157 | 0,14176 | 0,14395 | 0,1335 | 0,13137 | 0,12411 |
| 528,23875 | 0,1418 | 0,14427 | 0,13412 | 0,13229 | 0,1248 |
| 528,27593 | 0,14186 | 0,1446 | 0,13481 | 0,13315 | 0,12546 |
| 528,31311 | 0,14194 | 0,14494 | 0,13555 | 0,13395 | 0,12609 |
| 528,35029 | 0,14204 | 0,14532 | 0,13635 | 0,13469 | 0,1267 |
| 528,38748 | 0,14218 | 0,14574 | 0,1372 | 0,13535 | 0,12729 |
| 528,42466 | 0,14235 | 0,1462 | 0,13811 | 0,13595 | 0,12786 |
| 528,46184 | 0,14255 | 0,14669 | 0,13908 | 0,1365 | 0,12842 |
| 528,49902 | 0,14278 | 0,14722 | 0,14008 | 0,13698 | 0,12897 |
| 528,5362 | 0,14305 | 0,1478 | 0,14112 | 0,13742 | 0,12951 |
| 528,57339 | 0,14334 | 0,14842 | 0,14218 | 0,1378 | 0,13005 |
| 528,61057 | 0,14365 | 0,14907 | 0,14326 | 0,13815 | 0,1306 |
| 528,64775 | 0,14398 | 0,14975 | 0,14435 | 0,13847 | 0,13115 |
| 528,68493 | 0,14432 | 0,15045 | 0,14542 | 0,13877 | 0,13172 |
| 528,72211 | 0,14466 | 0,15116 | 0,14648 | 0,13907 | 0,13231 |
| 528,7593 | 0,14499 | 0,15188 | 0,14751 | 0,13936 | 0,13293 |
| 528,79648 | 0,1453 | 0,15259 | 0,14849 | 0,13968 | 0,13358 |
| 528,83366 | 0,14559 | 0,15327 | 0,14941 | 0,14001 | 0,13426 |
| 528,87084 | 0,14584 | 0,15392 | 0,15026 | 0,14038 | 0,13497 |
| 528,90802 | 0,14604 | 0,15453 | 0,15104 | 0,14078 | 0,13573 |
| 528,94521 | 0,14618 | 0,15508 | 0,15173 | 0,14124 | 0,13653 |
| 528,98239 | 0,14625 | 0,15554 | 0,1523 | 0,14176 | 0,13737 |
| 529,01957 | 0,14625 | 0,15593 | 0,15277 | 0,14233 | 0,13825 |
| 529,05675 | 0,14618 | 0,15623 | 0,15312 | 0,14296 | 0,13917 |
| 529,09393 | 0,14601 | 0,15644 | 0,15336 | 0,14364 | 0,14014 |
| 529,13112 | 0,14575 | 0,15653 | 0,15348 | 0,1444 | 0,14113 |
| 529,1683 | 0,1454 | 0,1565 | 0,15345 | 0,14521 | 0,14215 |
| 529,20548 | 0,14496 | 0,15636 | 0,15329 | 0,14607 | 0,1432 |
| 529,24266 | 0,14443 | 0,15612 | 0,15302 | 0,14697 | 0,14426 |
| 529,27984 | 0,14382 | 0,15577 | 0,15263 | 0,14791 | 0,14533 |
| 529,31703 | 0,14311 | 0,15531 | 0,15212 | 0,14887 | 0,14641 |
| 529,35421 | 0,14233 | 0,15474 | 0,15147 | 0,14985 | 0,14747 |
| 529,39139 | 0,14148 | 0,15409 | 0,15073 | 0,15082 | 0,14853 |
| 529,42857 | 0,14058 | 0,15337 | 0,1499 | 0,15178 | 0,14955 |
| 529,46575 | 0,13963 | 0,15258 | 0,14898 | 0,15272 | 0,15054 |
| 529,50294 | 0,13864 | 0,15175 | 0,14799 | 0,15362 | 0,15148 |
| 529,54012 | 0,13763 | 0,15088 | 0,14692 | 0,15446 | 0,15237 |
| 529,5773 | 0,13661 | 0,14999 | 0,1458 | 0,15523 | 0,15321 |
| 529,61448 | 0,13559 | 0,1491 | 0,14464 | 0,15592 | 0,15396 |
| 529,65166 | 0,13458 | 0,14823 | 0,14346 | 0,15653 | 0,15464 |
| 529,68885 | 0,1336 | 0,14738 | 0,14224 | 0,15704 | 0,15524 |
| 529,72603 | 0,13266 | 0,14657 | 0,14102 | 0,15743 | 0,15575 |
| 529,76321 | 0,13177 | 0,14582 | 0,1398 | 0,1577 | 0,15618 |
| 529,80039 | 0,13092 | 0,14514 | 0,13858 | 0,15785 | 0,15649 |
| 529,83757 | 0,13014 | 0,14452 | 0,13737 | 0,15789 | 0,15671 |
| 529,87476 | 0,12944 | 0,14397 | 0,13619 | 0,15781 | 0,15684 |
| 529,91194 | 0,12881 | 0,1435 | 0,13503 | 0,15757 | 0,15688 |
| 529,94912 | 0,12825 | 0,14313 | 0,1339 | 0,15722 | 0,15682 |
| 529,9863 | 0,12777 | 0,14283 | 0,13279 | 0,15676 | 0,15666 |
| 530,02348 | 0,12735 | 0,1426 | 0,13171 | 0,15619 | 0,15641 |
| 530,06067 | 0,12701 | 0,14242 | 0,13067 | 0,15552 | 0,15608 |
| 530,09785 | 0,12673 | 0,1423 | 0,12965 | 0,15472 | 0,15568 |
| 530,13503 | 0,12651 | 0,14223 | 0,12865 | 0,15384 | 0,15519 |
| 530,17221 | 0,12632 | 0,14219 | 0,12768 | 0,15288 | 0,15463 |
| 530,20939 | 0,12617 | 0,14215 | 0,12671 | 0,15185 | 0,15401 |
| 530,24658 | 0,12605 | 0,14211 | 0,12576 | 0,15076 | 0,15333 |
| 530,28376 | 0,12594 | 0,14204 | 0,12481 | 0,14961 | 0,15261 |
| 530,32094 | 0,12583 | 0,14194 | 0,12386 | 0,14841 | 0,15183 |
| 530,35812 | 0,1257 | 0,14178 | 0,1229 | 0,14718 | 0,15102 |
| 530,3953 | 0,12555 | 0,14154 | 0,12193 | 0,14593 | 0,15016 |
| 530,43249 | 0,12536 | 0,14121 | 0,12093 | 0,14466 | 0,14928 |
| 530,46967 | 0,12511 | 0,14079 | 0,11991 | 0,14337 | 0,14838 |
| 530,50685 | 0,1248 | 0,14026 | 0,11885 | 0,14207 | 0,14744 |
| 530,54403 | 0,12442 | 0,13958 | 0,11777 | 0,14077 | 0,14647 |
| 530,58121 | 0,12397 | 0,13877 | 0,11665 | 0,13948 | 0,14549 |
| 530,6184 | 0,12344 | 0,13782 | 0,11549 | 0,13819 | 0,14449 |
| 530,65558 | 0,12279 | 0,13674 | 0,11428 | 0,1369 | 0,14346 |
| 530,69276 | 0,12205 | 0,13552 | 0,11304 | 0,13562 | 0,14241 |
| 530,72994 | 0,12123 | 0,13415 | 0,11177 | 0,13435 | 0,14134 |
| 530,76712 | 0,12031 | 0,13262 | 0,11046 | 0,13308 | 0,14025 |
| 530,80431 | 0,11931 | 0,13097 | 0,10911 | 0,13182 | 0,13913 |
| 530,84149 | 0,1182 | 0,1292 | 0,10773 | 0,13057 | 0,13798 |
| 530,87867 | 0,11701 | 0,12732 | 0,10633 | 0,12932 | 0,13679 |
| 530,91585 | 0,11575 | 0,12534 | 0,10491 | 0,12807 | 0,13558 |
| 530,95303 | 0,11443 | 0,12325 | 0,10348 | 0,12682 | 0,13433 |
| 530,99022 | 0,11305 | 0,12109 | 0,10204 | 0,12556 | 0,13305 |
| 531,0274 | 0,11162 | 0,11888 | 0,1006 | 0,12431 | 0,13173 |
| 531,06458 | 0,11015 | 0,11662 | 0,09917 | 0,12305 | 0,13037 |
| 531,10176 | 0,10867 | 0,11432 | 0,09774 | 0,12179 | 0,12897 |
| 531,13894 | 0,10716 | 0,11201 | 0,09634 | 0,12052 | 0,12753 |
| 531,17613 | 0,10566 | 0,10969 | 0,09496 | 0,11925 | 0,12606 |
| 531,21331 | 0,10416 | 0,10739 | 0,09362 | 0,11797 | 0,12454 |
| 531,25049 | 0,10267 | 0,10511 | 0,0923 | 0,1167 | 0,12299 |
| 531,28767 | 0,10122 | 0,10286 | 0,09102 | 0,11542 | 0,12141 |
| 531,32485 | 0,09979 | 0,10065 | 0,08978 | 0,11415 | 0,11979 |
| 531,36204 | 0,0984 | 0,0985 | 0,0886 | 0,11289 | 0,11815 |
| 531,39922 | 0,09706 | 0,09641 | 0,08745 | 0,11163 | 0,11648 |
| 531,4364 | 0,09577 | 0,09437 | 0,08635 | 0,11038 | 0,1148 |
| 531,47358 | 0,09452 | 0,0924 | 0,08529 | 0,10915 | 0,11309 |
| 531,51076 | 0,09332 | 0,09049 | 0,08428 | 0,10793 | 0,11138 |
| 531,54795 | 0,09217 | 0,08866 | 0,08332 | 0,10673 | 0,10965 |
| 531,58513 | 0,09107 | 0,0869 | 0,08239 | 0,10554 | 0,10793 |
| 531,62231 | 0,09002 | 0,0852 | 0,08149 | 0,10438 | 0,1062 |
| 531,65949 | 0,08901 | 0,08355 | 0,08063 | 0,10324 | 0,10448 |
| 531,69667 | 0,08804 | 0,08196 | 0,07979 | 0,10212 | 0,10276 |
| 531,73386 | 0,08709 | 0,08043 | 0,07898 | 0,10102 | 0,10106 |
| 531,77104 | 0,08617 | 0,07894 | 0,07819 | 0,09993 | 0,09937 |
| 531,80822 | 0,08527 | 0,0775 | 0,07741 | 0,09886 | 0,09769 |
| 531,8454 | 0,08438 | 0,07608 | 0,07663 | 0,09781 | 0,09603 |
| 531,88258 | 0,08349 | 0,0747 | 0,07586 | 0,09676 | 0,0944 |
| 531,91977 | 0,08261 | 0,07335 | 0,07509 | 0,09572 | 0,09278 |
| 531,95695 | 0,08172 | 0,07201 | 0,07431 | 0,09468 | 0,09119 |
| 531,99413 | 0,08081 | 0,0707 | 0,07353 | 0,09363 | 0,08961 |
| 532,03131 | 0,07989 | 0,0694 | 0,07273 | 0,09257 | 0,08806 |
| 532,06849 | 0,07895 | 0,06811 | 0,07191 | 0,0915 | 0,08652 |
| 532,10568 | 0,07799 | 0,06684 | 0,07108 | 0,0904 | 0,08501 |
| 532,14286 | 0,077 | 0,06558 | 0,07023 | 0,08929 | 0,08352 |
| 532,18004 | 0,07599 | 0,06434 | 0,06937 | 0,08814 | 0,08205 |
| 532,21722 | 0,07494 | 0,06311 | 0,06849 | 0,08695 | 0,0806 |
| 532,2544 | 0,07388 | 0,0619 | 0,06759 | 0,08572 | 0,07916 |
| 532,29159 | 0,07279 | 0,06071 | 0,06667 | 0,08446 | 0,07774 |
| 532,32877 | 0,07168 | 0,05956 | 0,06575 | 0,08315 | 0,07634 |
| 532,36595 | 0,07055 | 0,05844 | 0,06482 | 0,08181 | 0,07495 |
| 532,40313 | 0,06941 | 0,05736 | 0,06389 | 0,08041 | 0,07358 |
| 532,44031 | 0,06826 | 0,05632 | 0,06295 | 0,07898 | 0,07222 |
| 532,4775 | 0,06711 | 0,05533 | 0,06202 | 0,07751 | 0,07089 |
| 532,51468 | 0,06595 | 0,05439 | 0,0611 | 0,07601 | 0,06958 |
| 532,55186 | 0,06481 | 0,05353 | 0,06019 | 0,07447 | 0,06828 |
| 532,58904 | 0,06367 | 0,05272 | 0,0593 | 0,07291 | 0,06701 |
| 532,62622 | 0,06256 | 0,05198 | 0,05843 | 0,07134 | 0,06577 |
| 532,66341 | 0,06147 | 0,0513 | 0,05759 | 0,06975 | 0,06456 |
| 532,70059 | 0,0604 | 0,05068 | 0,05678 | 0,06816 | 0,06338 |
| 532,73777 | 0,05936 | 0,05016 | 0,056 | 0,06658 | 0,06224 |
| 532,77495 | 0,05836 | 0,0497 | 0,05525 | 0,06502 | 0,06113 |
| 532,81213 | 0,05739 | 0,0493 | 0,05455 | 0,06348 | 0,06007 |
| 532,84932 | 0,05647 | 0,04896 | 0,05389 | 0,06197 | 0,05907 |
| 532,8865 | 0,05558 | 0,04867 | 0,05327 | 0,0605 | 0,0581 |
| 532,92368 | 0,05473 | 0,04845 | 0,05268 | 0,05908 | 0,05719 |
| 532,96086 | 0,05392 | 0,04827 | 0,05214 | 0,05773 | 0,05634 |
| 532,99804 | 0,05316 | 0,04812 | 0,05164 | 0,05644 | 0,05555 |
| 533,03523 | 0,05243 | 0,04801 | 0,05118 | 0,05523 | 0,05483 |
| 533,07241 | 0,05174 | 0,04791 | 0,05076 | 0,05409 | 0,05416 |
| 533,10959 | 0,05108 | 0,04783 | 0,05036 | 0,05303 | 0,05356 |
| 533,14677 | 0,05045 | 0,04775 | 0,05 | 0,05207 | 0,05302 |
| 533,18395 | 0,04985 | 0,04766 | 0,04966 | 0,0512 | 0,05256 |
| 533,22114 | 0,04927 | 0,04755 | 0,04935 | 0,05042 | 0,05217 |
| 533,25832 | 0,0487 | 0,04742 | 0,04905 | 0,04974 | 0,05183 |
| 533,2955 | 0,04816 | 0,04727 | 0,04877 | 0,04913 | 0,05155 |
| 533,33268 | 0,04762 | 0,04707 | 0,04851 | 0,04864 | 0,05134 |
| 533,36986 | 0,0471 | 0,04682 | 0,04825 | 0,04823 | 0,05119 |
| 533,40705 | 0,04657 | 0,04652 | 0,04799 | 0,04791 | 0,05109 |
| 533,44423 | 0,04605 | 0,04618 | 0,04774 | 0,04766 | 0,05103 |
| 533,48141 | 0,04553 | 0,04578 | 0,04748 | 0,04748 | 0,05102 |
| 533,51859 | 0,045 | 0,04532 | 0,04722 | 0,04738 | 0,05105 |
| 533,55577 | 0,04447 | 0,0448 | 0,04695 | 0,04734 | 0,05111 |
| 533,59295 | 0,04393 | 0,04422 | 0,04667 | 0,04735 | 0,0512 |
| 533,63014 | 0,04339 | 0,04359 | 0,04638 | 0,0474 | 0,05131 |
| 533,66732 | 0,04283 | 0,04291 | 0,04608 | 0,04749 | 0,05143 |
| 533,7045 | 0,04227 | 0,04217 | 0,04577 | 0,04761 | 0,05156 |
| 533,74168 | 0,04171 | 0,04139 | 0,04544 | 0,04775 | 0,05169 |
| 533,77886 | 0,04113 | 0,04057 | 0,04511 | 0,0479 | 0,05182 |
| 533,81605 | 0,04056 | 0,03971 | 0,04476 | 0,04805 | 0,05193 |
| 533,85323 | 0,03998 | 0,03883 | 0,04441 | 0,0482 | 0,05203 |
| 533,89041 | 0,0394 | 0,03793 | 0,04404 | 0,04834 | 0,0521 |
| 533,92759 | 0,03882 | 0,03701 | 0,04366 | 0,04845 | 0,05214 |
| 533,96477 | 0,03825 | 0,03609 | 0,04328 | 0,04854 | 0,05215 |
| 534,00196 | 0,03768 | 0,03516 | 0,04289 | 0,0486 | 0,05212 |
| 534,03914 | 0,03711 | 0,03424 | 0,04249 | 0,04862 | 0,05206 |
| 534,07632 | 0,03655 | 0,03332 | 0,04209 | 0,04861 | 0,05194 |
| 534,1135 | 0,03601 | 0,03243 | 0,04169 | 0,04854 | 0,05179 |
| 534,15068 | 0,03547 | 0,03156 | 0,04128 | 0,04843 | 0,05158 |
| 534,18787 | 0,03495 | 0,03071 | 0,04088 | 0,04828 | 0,05133 |
| 534,22505 | 0,03444 | 0,02989 | 0,04047 | 0,04808 | 0,05103 |
| 534,26223 | 0,03394 | 0,0291 | 0,04005 | 0,04783 | 0,05068 |
| 534,29941 | 0,03346 | 0,02835 | 0,03963 | 0,04752 | 0,05028 |
| 534,33659 | 0,033 | 0,02764 | 0,03921 | 0,04717 | 0,04984 |
| 534,37378 | 0,03254 | 0,02697 | 0,03879 | 0,04678 | 0,04935 |
| 534,41096 | 0,0321 | 0,02633 | 0,03836 | 0,04634 | 0,04882 |
| 534,44814 | 0,03166 | 0,02573 | 0,03792 | 0,04587 | 0,04825 |
| 534,48532 | 0,03125 | 0,02517 | 0,03747 | 0,04535 | 0,04765 |
| 534,5225 | 0,03084 | 0,02465 | 0,03702 | 0,04479 | 0,04701 |
| 534,55969 | 0,03044 | 0,02417 | 0,03655 | 0,0442 | 0,04635 |
| 534,59687 | 0,03005 | 0,02371 | 0,03607 | 0,04358 | 0,04567 |
| 534,63405 | 0,02966 | 0,02329 | 0,03557 | 0,04293 | 0,04496 |
| 534,67123 | 0,02929 | 0,0229 | 0,03506 | 0,04226 | 0,04424 |
| 534,70841 | 0,02892 | 0,02254 | 0,03453 | 0,04157 | 0,04351 |
| 534,7456 | 0,02856 | 0,02221 | 0,03398 | 0,04086 | 0,04277 |
| 534,78278 | 0,0282 | 0,02189 | 0,03342 | 0,04013 | 0,04203 |
| 534,81996 | 0,02785 | 0,0216 | 0,03283 | 0,0394 | 0,04129 |
| 534,85714 | 0,02751 | 0,02133 | 0,03222 | 0,03865 | 0,04056 |
| 534,89432 | 0,02718 | 0,02107 | 0,0316 | 0,0379 | 0,03983 |
| 534,93151 | 0,02685 | 0,02083 | 0,03097 | 0,03714 | 0,03911 |
| 534,96869 | 0,02654 | 0,02061 | 0,03031 | 0,03639 | 0,03842 |
| 535,00587 | 0,02623 | 0,02039 | 0,02964 | 0,03563 | 0,03774 |
| 535,04305 | 0,02594 | 0,02019 | 0,02895 | 0,03488 | 0,03707 |
| 535,08023 | 0,02566 | 0,02 | 0,02825 | 0,03413 | 0,03643 |
| 535,11742 | 0,0254 | 0,01983 | 0,02754 | 0,03339 | 0,03581 |
| 535,1546 | 0,02515 | 0,01967 | 0,02683 | 0,03265 | 0,03522 |
| 535,19178 | 0,02492 | 0,01951 | 0,02611 | 0,03193 | 0,03465 |
| 535,22896 | 0,02471 | 0,01937 | 0,02538 | 0,03122 | 0,0341 |
| 535,26614 | 0,02452 | 0,01925 | 0,02466 | 0,03052 | 0,03357 |
| 535,30333 | 0,02436 | 0,01913 | 0,02394 | 0,02983 | 0,03307 |
| 535,34051 | 0,02421 | 0,01903 | 0,02322 | 0,02916 | 0,0326 |
| 535,37769 | 0,02408 | 0,01895 | 0,02251 | 0,0285 | 0,03214 |
| 535,41487 | 0,02398 | 0,01888 | 0,02182 | 0,02785 | 0,03171 |
| 535,45205 | 0,0239 | 0,01882 | 0,02113 | 0,02723 | 0,03129 |
| 535,48924 | 0,02383 | 0,01877 | 0,02046 | 0,02661 | 0,0309 |
| 535,52642 | 0,02379 | 0,01875 | 0,01981 | 0,02602 | 0,03051 |
| 535,5636 | 0,02376 | 0,01873 | 0,01918 | 0,02544 | 0,03014 |
| 535,60078 | 0,02374 | 0,01873 | 0,01857 | 0,02487 | 0,02978 |
| 535,63796 | 0,02373 | 0,01874 | 0,01797 | 0,02432 | 0,02943 |
| 535,67515 | 0,02373 | 0,01876 | 0,0174 | 0,02379 | 0,02909 |
| 535,71233 | 0,02374 | 0,01879 | 0,01686 | 0,02327 | 0,02875 |
| 535,74951 | 0,02374 | 0,01883 | 0,01634 | 0,02276 | 0,02841 |
| 535,78669 | 0,02375 | 0,01887 | 0,01585 | 0,02227 | 0,02807 |
| 535,82387 | 0,02374 | 0,01892 | 0,01537 | 0,02179 | 0,02774 |
| 535,86106 | 0,02372 | 0,01896 | 0,01492 | 0,02133 | 0,02739 |
| 535,89824 | 0,02369 | 0,01901 | 0,0145 | 0,02087 | 0,02704 |
| 535,93542 | 0,02365 | 0,01905 | 0,0141 | 0,02043 | 0,02669 |
| 535,9726 | 0,02358 | 0,01909 | 0,01373 | 0,01999 | 0,02633 |
| 536,00978 | 0,02349 | 0,01911 | 0,01337 | 0,01957 | 0,02596 |
| 536,04697 | 0,02336 | 0,01913 | 0,01304 | 0,01916 | 0,02558 |
| 536,08415 | 0,02321 | 0,01913 | 0,01273 | 0,01875 | 0,02519 |
| 536,12133 | 0,02303 | 0,01912 | 0,01244 | 0,01835 | 0,02479 |
| 536,15851 | 0,02282 | 0,01909 | 0,01216 | 0,01796 | 0,02438 |
| 536,19569 | 0,02258 | 0,01904 | 0,01191 | 0,01758 | 0,02396 |
| 536,23288 | 0,0223 | 0,01897 | 0,01166 | 0,01721 | 0,02353 |
| 536,27006 | 0,02199 | 0,01888 | 0,01144 | 0,01684 | 0,02309 |
| 536,30724 | 0,02165 | 0,01877 | 0,01123 | 0,01648 | 0,02264 |
| 536,34442 | 0,02128 | 0,01864 | 0,01104 | 0,01613 | 0,02219 |
| 536,3816 | 0,02088 | 0,01848 | 0,01085 | 0,01578 | 0,02172 |
| 536,41879 | 0,02045 | 0,0183 | 0,01068 | 0,01545 | 0,02126 |
| 536,45597 | 0,02 | 0,0181 | 0,01052 | 0,01512 | 0,02078 |
| 536,49315 | 0,01952 | 0,01789 | 0,01037 | 0,0148 | 0,02031 |
| 536,53033 | 0,01903 | 0,01764 | 0,01023 | 0,01448 | 0,01983 |
| 536,56751 | 0,01853 | 0,01738 | 0,01009 | 0,01418 | 0,01935 |
| 536,6047 | 0,01801 | 0,0171 | 0,00997 | 0,01388 | 0,01887 |
| 536,64188 | 0,01748 | 0,01681 | 0,00985 | 0,0136 | 0,01839 |
| 536,67906 | 0,01695 | 0,0165 | 0,00974 | 0,01332 | 0,01791 |
| 536,71624 | 0,01641 | 0,01618 | 0,00963 | 0,01305 | 0,01744 |
| 536,75342 | 0,01587 | 0,01584 | 0,00953 | 0,01279 | 0,01697 |
| 536,79061 | 0,01533 | 0,01549 | 0,00943 | 0,01254 | 0,01651 |
| 536,82779 | 0,0148 | 0,01513 | 0,00933 | 0,0123 | 0,01605 |
| 536,86497 | 0,01428 | 0,01476 | 0,00924 | 0,01207 | 0,0156 |
| 536,90215 | 0,01376 | 0,01439 | 0,00915 | 0,01184 | 0,01515 |
| 536,93933 | 0,01326 | 0,014 | 0,00906 | 0,01163 | 0,01472 |
| 536,97652 | 0,01276 | 0,01361 | 0,00897 | 0,01142 | 0,01429 |
| 537,0137 | 0,01228 | 0,01322 | 0,00888 | 0,01122 | 0,01387 |
| 537,05088 | 0,01181 | 0,01282 | 0,00879 | 0,01103 | 0,01346 |
| 537,08806 | 0,01135 | 0,01241 | 0,00869 | 0,01084 | 0,01306 |
| 537,12524 | 0,01091 | 0,012 | 0,00859 | 0,01065 | 0,01267 |
| 537,16243 | 0,01048 | 0,01159 | 0,00849 | 0,01047 | 0,01229 |
| 537,19961 | 0,01006 | 0,01117 | 0,00838 | 0,01029 | 0,01191 |
| 537,23679 | 0,00966 | 0,01075 | 0,00827 | 0,01012 | 0,01155 |
| 537,27397 | 0,00928 | 0,01033 | 0,00815 | 0,00994 | 0,01119 |
| 537,31115 | 0,0089 | 0,00991 | 0,00803 | 0,00976 | 0,01085 |
| 537,34834 | 0,00854 | 0,00949 | 0,00789 | 0,00959 | 0,01051 |
| 537,38552 | 0,00819 | 0,00906 | 0,00775 | 0,00941 | 0,01018 |
| 537,4227 | 0,00785 | 0,00864 | 0,00761 | 0,00923 | 0,00985 |
| 537,45988 | 0,00752 | 0,00822 | 0,00745 | 0,00904 | 0,00954 |
| 537,49706 | 0,00721 | 0,0078 | 0,00729 | 0,00885 | 0,00923 |
| 537,53425 | 0,0069 | 0,00739 | 0,00712 | 0,00866 | 0,00893 |
| 537,57143 | 0,00661 | 0,00698 | 0,00695 | 0,00846 | 0,00864 |
| 537,60861 | 0,00633 | 0,00657 | 0,00677 | 0,00826 | 0,00835 |
| 537,64579 | 0,00606 | 0,00617 | 0,00658 | 0,00805 | 0,00807 |
| 537,68297 | 0,00579 | 0,00578 | 0,00638 | 0,00784 | 0,0078 |
| 537,72016 | 0,00554 | 0,0054 | 0,00618 | 0,00763 | 0,00753 |
| 537,75734 | 0,0053 | 0,00503 | 0,00598 | 0,00741 | 0,00727 |
| 537,79452 | 0,00507 | 0,00467 | 0,00577 | 0,00719 | 0,00701 |
| 537,8317 | 0,00485 | 0,00432 | 0,00555 | 0,00696 | 0,00676 |
| 537,86888 | 0,00463 | 0,00399 | 0,00534 | 0,00673 | 0,00652 |
| 537,90607 | 0,00443 | 0,00367 | 0,00512 | 0,00651 | 0,00628 |
| 537,94325 | 0,00424 | 0,00336 | 0,0049 | 0,00628 | 0,00605 |
| 537,98043 | 0,00406 | 0,00307 | 0,00468 | 0,00605 | 0,00582 |
| 538,01761 | 0,00388 | 0,0028 | 0,00446 | 0,00582 | 0,0056 |
| 538,05479 | 0,00372 | 0,00253 | 0,00424 | 0,00559 | 0,00539 |
| 538,09198 | 0,00356 | 0,00229 | 0,00403 | 0,00537 | 0,00518 |
| 538,12916 | 0,00341 | 0,00206 | 0,00382 | 0,00515 | 0,00498 |
| 538,16634 | 0,00327 | 0,00185 | 0,00361 | 0,00493 | 0,00479 |
| 538,20352 | 0,00314 | 0,00165 | 0,0034 | 0,00472 | 0,0046 |
| 538,2407 | 0,00301 | 0,00147 | 0,0032 | 0,00451 | 0,00442 |
| 538,27789 | 0,00289 | 0,0013 | 0,003 | 0,0043 | 0,00424 |
| 538,31507 | 0,00277 | 0,00115 | 0,00281 | 0,0041 | 0,00407 |
| 538,35225 | 0,00267 | 0,00102 | 0,00263 | 0,00391 | 0,00391 |
| 538,38943 | 0,00256 | 0,00089 | 0,00245 | 0,00372 | 0,00375 |
| 538,42661 | 0,00246 | 0,00078 | 0,00228 | 0,00354 | 0,0036 |
| 538,4638 | 0,00236 | 0,00068 | 0,00212 | 0,00336 | 0,00346 |
| 538,50098 | 0,00227 | 0,00059 | 0,00196 | 0,00319 | 0,00332 |
| 538,53816 | 0,00218 | 0,00051 | 0,00181 | 0,00303 | 0,00319 |
| 538,57534 | 0,00209 | 0,00044 | 0,00167 | 0,00287 | 0,00306 |
| 538,61252 | 0,002 | 0,00038 | 0,00153 | 0,00271 | 0,00294 |
| 538,64971 | 0,00192 | 0,00032 | 0,00141 | 0,00256 | 0,00283 |
| 538,68689 | 0,00184 | 0,00028 | 0,00129 | 0,00242 | 0,00272 |
| 538,72407 | 0,00175 | 0,00024 | 0,00117 | 0,00228 | 0,00261 |
| 538,76125 | 0,00167 | 0,00021 | 0,00107 | 0,00214 | 0,00251 |
| 538,79843 | 0,00159 | 0,00018 | 0,00097 | 0,00201 | 0,00241 |
| 538,83562 | 0,00151 | 0,00016 | 0,00088 | 0,00189 | 0,00231 |
| 538,8728 | 0,00144 | 0,00014 | 0,00079 | 0,00177 | 0,00222 |
| 538,90998 | 0,00136 | 0,00012 | 0,00071 | 0,00165 | 0,00213 |
| 538,94716 | 0,00129 | 0,00011 | 0,00064 | 0,00154 | 0,00205 |
| 538,98434 | 0,00121 | 0,00011 | 0,00057 | 0,00143 | 0,00196 |
| 539,02153 | 0,00114 | 1e-04 | 0,00051 | 0,00133 | 0,00188 |
| 539,05871 | 0,00107 | 1e-04 | 0,00046 | 0,00123 | 0,0018 |
| 539,09589 | 0,001 | 1e-04 | 0,00041 | 0,00114 | 0,00173 |
| 539,13307 | 0,00093 | 1e-04 | 0,00036 | 0,00105 | 0,00165 |
| 539,17025 | 0,00087 | 0,00011 | 0,00032 | 0,00097 | 0,00158 |
| 539,20744 | 8e-04 | 0,00012 | 0,00028 | 0,00088 | 0,00151 |
| 539,24462 | 0,00074 | 0,00013 | 0,00025 | 0,00081 | 0,00144 |
| 539,2818 | 0,00069 | 0,00014 | 0,00021 | 0,00074 | 0,00137 |
| 539,31898 | 0,00063 | 0,00015 | 0,00019 | 0,00067 | 0,0013 |
| 539,35616 | 0,00058 | 0,00017 | 0,00016 | 0,00061 | 0,00124 |
| 539,39335 | 0,00053 | 0,00019 | 0,00014 | 0,00055 | 0,00117 |
| 539,43053 | 0,00048 | 0,00021 | 0,00012 | 0,00049 | 0,00111 |
| 539,46771 | 0,00043 | 0,00023 | 0,00011 | 0,00044 | 0,00105 |
| 539,50489 | 0,00039 | 0,00025 | 9e-05 | 0,00039 | 0,00099 |
| 539,54207 | 0,00035 | 0,00027 | 8e-05 | 0,00035 | 0,00093 |
| 539,57926 | 0,00032 | 0,00029 | 7e-05 | 0,00031 | 0,00087 |
| 539,61644 | 0,00028 | 0,00032 | 6e-05 | 0,00028 | 0,00081 |
| 539,65362 | 0,00025 | 0,00034 | 5e-05 | 0,00024 | 0,00076 |
| 539,6908 | 0,00022 | 0,00037 | 4e-05 | 0,00021 | 0,00071 |
| 539,72798 | 2e-04 | 0,00039 | 3e-05 | 0,00019 | 0,00066 |
| 539,76517 | 0,00017 | 0,00042 | 3e-05 | 0,00016 | 0,00061 |
| 539,80235 | 0,00015 | 0,00044 | 2e-05 | 0,00014 | 0,00056 |
| 539,83953 | 0,00013 | 0,00047 | 2e-05 | 0,00012 | 0,00052 |
| 539,87671 | 0,00012 | 0,00049 | 2e-05 | 1e-04 | 0,00048 |
| 539,91389 | 1e-04 | 0,00051 | 1e-05 | 9e-05 | 0,00044 |
| 539,95108 | 9e-05 | 0,00053 | 1e-05 | 8e-05 | 4e-04 |
| 539,98826 | 8e-05 | 0,00055 | 1e-05 | 7e-05 | 0,00037 |
| 540,02544 | 6e-05 | 0,00056 | 1e-05 | 6e-05 | 0,00033 |
| 540,06262 | 6e-05 | 0,00058 | 1e-05 | 5e-05 | 3e-04 |
| 540,0998 | 5e-05 | 0,00059 | 1e-05 | 4e-05 | 0,00027 |
| 540,13699 | 4e-05 | 6e-04 | 0 | 3e-05 | 0,00025 |
| 540,17417 | 3e-05 | 0,00061 | 0 | 3e-05 | 0,00022 |
| 540,21135 | 3e-05 | 0,00061 | 0 | 2e-05 | 2e-04 |
| 540,24853 | 2e-05 | 0,00061 | 0 | 2e-05 | 0,00018 |
| 540,28571 | 2e-05 | 0,00061 | 0 | 2e-05 | 0,00016 |
| 540,3229 | 2e-05 | 0,00061 | 0 | 1e-05 | 0,00014 |
| 540,36008 | 1e-05 | 6e-04 | 0 | 1e-05 | 0,00012 |
| 540,39726 | 1e-05 | 0,00059 | 0 | 1e-05 | 0,00011 |
| 540,43444 | 1e-05 | 0,00058 | 0 | 1e-05 | 1e-04 |
| 540,47162 | 1e-05 | 0,00056 | 0 | 1e-05 | 8e-05 |
| 540,50881 | 1e-05 | 0,00054 | 0 | 0 | 7e-05 |
| 540,54599 | 1e-05 | 0,00052 | 0 | 0 | 6e-05 |
| 540,58317 | 0 | 5e-04 | 0 | 0 | 5e-05 |
| 540,62035 | 0 | 0,00048 | 0 | 0 | 5e-05 |
| 540,65753 | 0 | 0,00046 | 0 | 0 | 4e-05 |
| 540,69472 | 0 | 0,00043 | 0 | 0 | 4e-05 |
| 540,7319 | 0 | 0,00041 | 0 | 0 | 3e-05 |
| 540,76908 | 0 | 0,00038 | 0 | 0 | 3e-05 |
| 540,80626 | 0 | 0,00036 | 0 | 0 | 2e-05 |
| 540,84344 | 0 | 0,00033 | 0 | 0 | 2e-05 |
| 540,88063 | 0 | 0,00031 | 0 | 0 | 2e-05 |
| 540,91781 | 0 | 0,00029 | 0 | 0 | 1e-05 |
| 540,95499 | 0 | 0,00026 | 0 | 0 | 1e-05 |
| 540,99217 | 0 | 0,00024 | 0 | 0 | 1e-05 |
| 541,02935 | 0 | 0,00022 | 0 | 0 | 1e-05 |
| 541,06654 | 0 | 2e-04 | 0 | 0 | 1e-05 |
| 541,10372 | 0 | 0,00018 | 0 | 0 | 1e-05 |
| 541,1409 | 0 | 0,00016 | 0 | 0 | 0 |
| 541,17808 | 0 | 0,00014 | 0 | 0 | 0 |
| 541,21526 | 0 | 0,00013 | 0 | 0 | 0 |
| 541,25245 | 0 | 0,00011 | 0 | 0 | 0 |
| 541,28963 | 0 | 1e-04 | 0 | 0 | 0 |
| 541,32681 | 0 | 9e-05 | 0 | 0 | 0 |
| 541,36399 | 0 | 7e-05 | 0 | 0 | 0 |
| 541,40117 | 0 | 6e-05 | 0 | 0 | 0 |
| 541,43836 | 0 | 6e-05 | 0 | 0 | 0 |
| 541,47554 | 0 | 5e-05 | 0 | 0 | 0 |
| 541,51272 | 0 | 4e-05 | 0 | 0 | 0 |
| 541,5499 | 0 | 4e-05 | 0 | 0 | 0 |
| 541,58708 | 0 | 3e-05 | 0 | 0 | 0 |
| 541,62427 | 0 | 3e-05 | 0 | 0 | 0 |
| 541,66145 | 0 | 2e-05 | 0 | 0 | 0 |
| 541,69863 | 0 | 2e-05 | 0 | 0 | 0 |
| 541,73581 | 0 | 1e-05 | 0 | 0 | 0 |
| 541,77299 | 0 | 1e-05 | 0 | 0 | 0 |
| 541,81018 | 0 | 1e-05 | 0 | 0 | 0 |
| 541,84736 | 0 | 1e-05 | 0 | 0 | 0 |
| 541,88454 | 0 | 1e-05 | 0 | 0 | 0 |
| 541,92172 | 0 | 1e-05 | 0 | 0 | 0 |
| 541,9589 | 0 | 0 | 0 | 0 | 0 |
| 541,99609 | 0 | 0 | 0 | 0 | 0 |
| 542,03327 | 0 | 0 | 0 | 0 | 0 |
| 542,07045 | 0 | 0 | 0 | 0 | 0 |
| 542,10763 | 0 | 0 | 0 | 0 | 0 |
| 542,14481 | 0 | 0 | 0 | 0 | 0 |
| 542,182 | 0 | 0 | 0 | 0 | 0 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
In de figuren 3.2.31 en 3.2.32 is – conform de verwachting – te zien dat kinderen met ouders in de schuldsanering vaker een lage onderwijsscore hebben dan kinderen waarvan de ouders niet in de schuldsanering zitten. Voor kinderen met ouders in de schuldsanering zijn de onderwijsscores scheef verdeeld met een staart naar rechts. Voor kinderen waarvan de ouders niet in de schuldsanering zitten, zijn de onderwijsscores daarentegen scheef verdeeld met een staart naar links. Het percentage kinderen met ouders in de schuldsanering is met minder dan 1 procent in alle vier de schooljaren behoorlijk kleiner dan de groep kinderen waarvan de ouders niet in de schuldsanering zitten, met grofweg 99 procent in alle vier de schooljaren. De frequentieverdeling van onderwijsscores is voor kinderen met ouders in de schuldsanering stabiel over de schooljaren met een kleine verschuiving naar rechts. Voor kinderen waarvan de ouders niet in de schuldsanering zitten, zien we tussen de meetmomenten oktober 2021 en februari 2022 een verschil. Dit verschil is wederom te verklaren door de herijking.
Gemiddeld opleidingsniveau van moeders op school
Figuur 3.2.33 laat de relatieve frequentiedichtheid zien van de onderwijsscores en het gemiddelde hoogste opleidingsniveau van de moeders op school uitgesplitst naar schooljaar. De frequentiedichtheid loopt van lichtblauw (laag) naar donkerblauw (hoog). Op basis van het model van de onderwijsachterstandenindicator kunnen we verwachten dat een lager gemiddeld opleidingsniveau van de moeders op school resulteert in een lagere onderwijsscore.
De frequentiedichtheidswolken zoals getoond in figuur 3.2.33 laten voor ieder schooljaar een licht oplopend effect zien. Dit geeft aan dat er een zwakke, maar positieve relatie is tussen het gemiddelde opleidingsniveau van de moeder op school en de onderwijsscore. De spreiding in de data is stabiel gebleven.
3.2.33 Frequentiedichtheidswolken van de onderwijsscore en het gemiddelde hoogste opleidingsniveau van de moeders
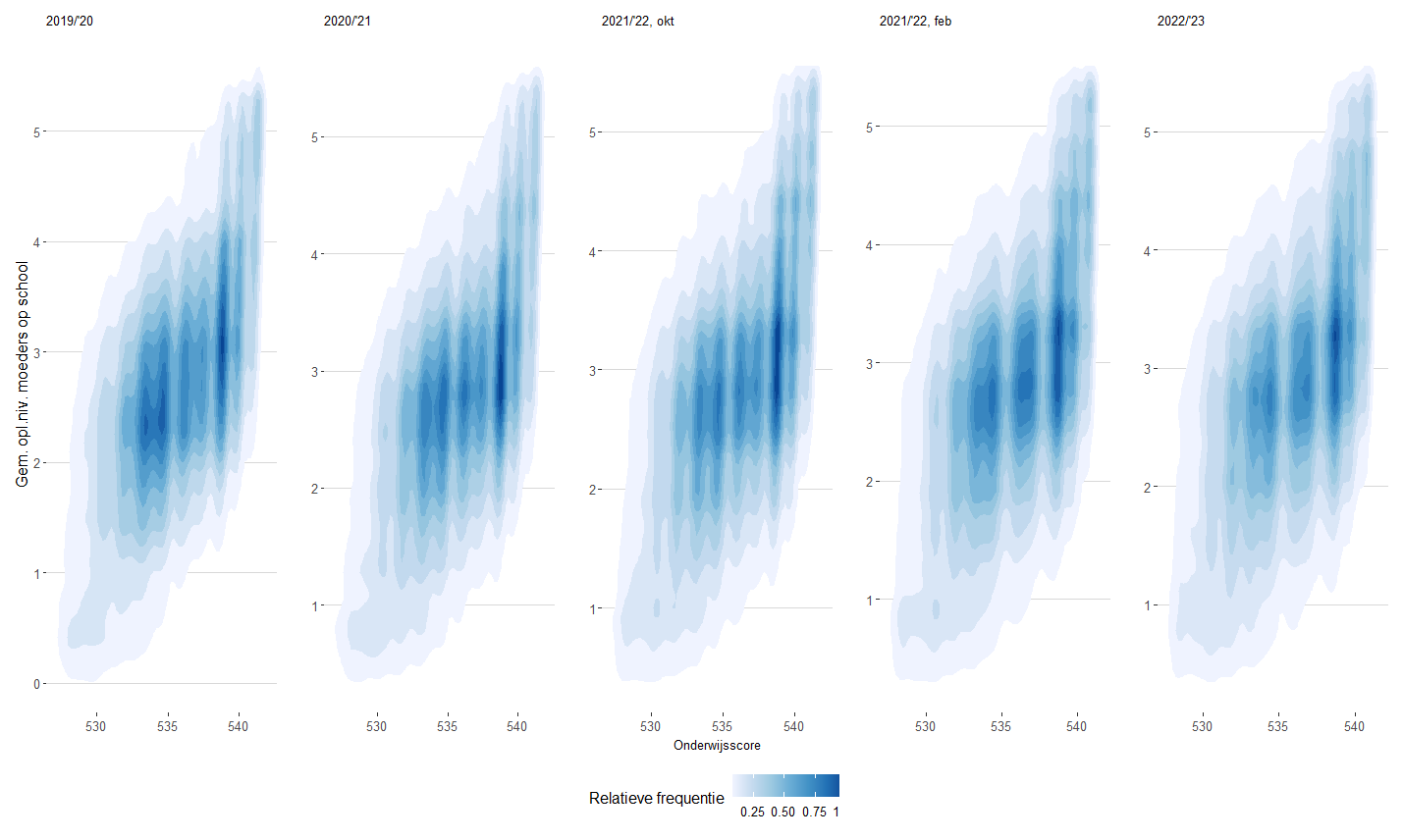
3.3 Onderwijsscores per schooljaar naar methoden van imputeren
Niet alle achtergrondkenmerken waarop het model van de onderwijsachterstandenindicator is geschat zijn bekend voor alle kinderen. Zo ontbreekt het hoogste opleidingsniveau van de moeder, de vader of beide ouders voor een deel van de populatie. Voor het deel dat ontbreekt is het hoogste opleidingsniveau geïmputeerd. Naast het imputeren van het hoogste opleidingsniveau, is voor kinderen waarvan geen onderwijsscore berekend kan worden, omdat één of beide ouders of het kind zelf onbekend is in de Basisregistratie Personen (BRP), de onderwijsscore geïmputeerd.
Imputatie van het opleidingsniveau van vader, moeder of beide ouders
De figuren 3.3.1 tot en met 3.3.4 geven de frequentiedichtheid weer van de onderwijsscore per deelpopulatie voor wat betreft de beschikbaarheid van het hoogste opleidingsniveau van de vader en moeder van het kind uitgesplitst naar de schooljaren. De registratie van het hoogste opleidingsniveau in het SSB is incompleet voor een substantieel en selectief deel van de Nederlandse bevolking. Het opleidingsniveau is vaker onbekend voor oudere mensen, mensen met een lager opleidingsniveau en mensen die (een deel van) hun opleiding in het buitenland hebben gevolgd. Er bestaan statistische methoden om de ontbrekende gegevens aan te vullen; dit wordt ook wel imputatie genoemd. Voor de onderwijsachterstandenindicator wordt aan de hand van een aantal andere kenmerken die wel bekend zijn, het opleidingsniveau geschat. Deze geïmputeerde opleidingsniveaus bevatten relatief vaak de lagere opleidingsniveaus. Hierdoor wordt de selectieve onbekendheid gecorrigeerd.
De volgende deelpopulaties worden onderscheden:
- A: Het hoogste opleidingsniveau van beide ouders is niet bekend
- B: Het hoogste opleidingsniveau is bekend voor de moeder maar niet voor de vader
- C: Het hoogste opleidingsniveau is bekend voor de vader maar niet voor de moeder
- D: Het hoogste opleidingsniveau van beide ouders is bekend
De verwachting is dan ook dat de onderwijsscore van kinderen waarvan het hoogste opleidingsniveau van beide ouders bekend is, gemiddeld hoger is dan van de kinderen waarvan het hoogste opleidingsniveau van één of beide ouders niet bekend is.
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 0 | 0 | 0 | 0 | 0 |
| 524,07436 | 0 | 0 | 0 | 0 | 0 |
| 524,11155 | 0 | 0 | 0 | 0 | 0 |
| 524,14873 | 0 | 0 | 0 | 0 | 0 |
| 524,18591 | 0 | 0 | 0 | 0 | 0 |
| 524,22309 | 0 | 0 | 0 | 0 | 0 |
| 524,26027 | 0 | 0 | 0 | 0 | 0 |
| 524,29746 | 0 | 0 | 0 | 0 | 0 |
| 524,33464 | 0 | 0 | 0 | 0 | 0 |
| 524,37182 | 0 | 0 | 0 | 0 | 0 |
| 524,409 | 0 | 0 | 0 | 0 | 0 |
| 524,44618 | 0 | 0 | 0 | 0 | 0 |
| 524,48337 | 0 | 0 | 0 | 0 | 0 |
| 524,52055 | 0 | 0 | 0 | 0 | 0 |
| 524,55773 | 0 | 0 | 0 | 0 | 0 |
| 524,59491 | 0 | 0 | 0 | 0 | 0 |
| 524,63209 | 0 | 0 | 0 | 0 | 0 |
| 524,66928 | 0 | 0 | 0 | 0 | 0 |
| 524,70646 | 0 | 0 | 0 | 0 | 0 |
| 524,74364 | 0 | 0 | 0 | 0 | 0 |
| 524,78082 | 0 | 0 | 0 | 0 | 0 |
| 524,818 | 0 | 0 | 0 | 0 | 0 |
| 524,85519 | 0 | 0 | 0 | 0 | 0 |
| 524,89237 | 0 | 0 | 0 | 0 | 0 |
| 524,92955 | 0 | 0 | 0 | 0 | 0 |
| 524,96673 | 0 | 0 | 0 | 0 | 0 |
| 525,00391 | 0 | 0 | 0 | 0 | 0 |
| 525,0411 | 0 | 0 | 0 | 0 | 0 |
| 525,07828 | 0 | 0 | 0 | 0 | 0 |
| 525,11546 | 0 | 0 | 0 | 0 | 0 |
| 525,15264 | 0 | 0 | 0 | 0 | 0 |
| 525,18982 | 1e-05 | 0 | 0 | 0 | 0 |
| 525,22701 | 1e-05 | 0 | 0 | 0 | 0 |
| 525,26419 | 1e-05 | 0 | 0 | 0 | 0 |
| 525,30137 | 2e-05 | 0 | 0 | 0 | 0 |
| 525,33855 | 3e-05 | 0 | 0 | 0 | 0 |
| 525,37573 | 5e-05 | 0 | 0 | 0 | 0 |
| 525,41292 | 6e-05 | 0 | 0 | 0 | 0 |
| 525,4501 | 8e-05 | 0 | 0 | 0 | 0 |
| 525,48728 | 1e-04 | 0 | 0 | 0 | 0 |
| 525,52446 | 0,00013 | 0 | 0 | 0 | 0 |
| 525,56164 | 0,00015 | 0 | 1e-05 | 1e-05 | 0 |
| 525,59883 | 0,00017 | 0 | 1e-05 | 1e-05 | 1e-05 |
| 525,63601 | 2e-04 | 0 | 1e-05 | 1e-05 | 1e-05 |
| 525,67319 | 0,00022 | 1e-05 | 2e-05 | 2e-05 | 1e-05 |
| 525,71037 | 0,00024 | 1e-05 | 3e-05 | 3e-05 | 2e-05 |
| 525,74755 | 0,00027 | 1e-05 | 5e-05 | 4e-05 | 3e-05 |
| 525,78474 | 3e-04 | 2e-05 | 7e-05 | 5e-05 | 4e-05 |
| 525,82192 | 0,00035 | 2e-05 | 9e-05 | 7e-05 | 5e-05 |
| 525,8591 | 4e-04 | 3e-05 | 0,00012 | 9e-05 | 6e-05 |
| 525,89628 | 0,00048 | 4e-05 | 0,00016 | 0,00012 | 8e-05 |
| 525,93346 | 0,00056 | 5e-05 | 0,00021 | 0,00015 | 1e-04 |
| 525,97065 | 0,00066 | 6e-05 | 0,00027 | 0,00018 | 0,00012 |
| 526,00783 | 0,00076 | 7e-05 | 0,00033 | 0,00022 | 0,00015 |
| 526,04501 | 0,00086 | 8e-05 | 4e-04 | 0,00026 | 0,00017 |
| 526,08219 | 0,00095 | 9e-05 | 0,00048 | 0,00031 | 2e-04 |
| 526,11937 | 0,00103 | 1e-04 | 0,00056 | 0,00035 | 0,00023 |
| 526,15656 | 0,00108 | 0,00011 | 0,00065 | 4e-04 | 0,00026 |
| 526,19374 | 0,00111 | 0,00012 | 0,00073 | 0,00045 | 0,00029 |
| 526,23092 | 0,00112 | 0,00013 | 0,00082 | 5e-04 | 0,00032 |
| 526,2681 | 0,0011 | 0,00014 | 9e-04 | 0,00055 | 0,00035 |
| 526,30528 | 0,00107 | 0,00015 | 0,00097 | 6e-04 | 0,00038 |
| 526,34247 | 0,00102 | 0,00016 | 0,00103 | 0,00064 | 0,00041 |
| 526,37965 | 0,00098 | 0,00018 | 0,00108 | 0,00068 | 0,00043 |
| 526,41683 | 0,00095 | 0,00021 | 0,00112 | 0,00071 | 0,00046 |
| 526,45401 | 0,00092 | 0,00024 | 0,00115 | 0,00073 | 0,00048 |
| 526,49119 | 0,00091 | 0,00028 | 0,00116 | 0,00075 | 5e-04 |
| 526,52838 | 0,00092 | 0,00033 | 0,00117 | 0,00077 | 0,00052 |
| 526,56556 | 0,00094 | 0,00038 | 0,00116 | 0,00078 | 0,00054 |
| 526,60274 | 0,00098 | 0,00044 | 0,00114 | 0,00078 | 0,00056 |
| 526,63992 | 0,00102 | 5e-04 | 0,00112 | 0,00078 | 0,00058 |
| 526,6771 | 0,00108 | 0,00057 | 0,00109 | 0,00078 | 0,00061 |
| 526,71429 | 0,00113 | 0,00064 | 0,00107 | 0,00079 | 0,00064 |
| 526,75147 | 0,00118 | 7e-04 | 0,00105 | 0,00079 | 0,00067 |
| 526,78865 | 0,00123 | 0,00077 | 0,00103 | 0,00079 | 0,00071 |
| 526,82583 | 0,00127 | 0,00083 | 0,00103 | 8e-04 | 0,00075 |
| 526,86301 | 0,00131 | 0,00089 | 0,00103 | 0,00081 | 8e-04 |
| 526,9002 | 0,00135 | 0,00096 | 0,00104 | 0,00082 | 0,00085 |
| 526,93738 | 0,0014 | 0,00102 | 0,00107 | 0,00083 | 9e-04 |
| 526,97456 | 0,00145 | 0,00108 | 0,00111 | 0,00084 | 0,00096 |
| 527,01174 | 0,00151 | 0,00115 | 0,00116 | 0,00086 | 0,00102 |
| 527,04892 | 0,00158 | 0,00122 | 0,00122 | 0,00087 | 0,00107 |
| 527,08611 | 0,00166 | 0,0013 | 0,00129 | 0,00088 | 0,00113 |
| 527,12329 | 0,00175 | 0,00138 | 0,00136 | 0,00088 | 0,00119 |
| 527,16047 | 0,00186 | 0,00147 | 0,00145 | 0,00089 | 0,00125 |
| 527,19765 | 0,00197 | 0,00155 | 0,00153 | 0,00089 | 0,00131 |
| 527,23483 | 0,00209 | 0,00163 | 0,00163 | 9e-04 | 0,00137 |
| 527,27202 | 0,00222 | 0,00171 | 0,00173 | 0,00091 | 0,00143 |
| 527,3092 | 0,00235 | 0,00178 | 0,00183 | 0,00093 | 0,00149 |
| 527,34638 | 0,00249 | 0,00184 | 0,00194 | 0,00096 | 0,00155 |
| 527,38356 | 0,00264 | 0,00189 | 0,00206 | 0,00099 | 0,00161 |
| 527,42074 | 0,00279 | 0,00194 | 0,0022 | 0,00104 | 0,00166 |
| 527,45793 | 0,00296 | 0,00198 | 0,00236 | 0,00111 | 0,00172 |
| 527,49511 | 0,00314 | 0,00202 | 0,00253 | 0,00118 | 0,00178 |
| 527,53229 | 0,00333 | 0,00207 | 0,00274 | 0,00128 | 0,00185 |
| 527,56947 | 0,00354 | 0,00213 | 0,00296 | 0,00139 | 0,00191 |
| 527,60665 | 0,00376 | 0,00222 | 0,00322 | 0,00151 | 0,00197 |
| 527,64384 | 0,00398 | 0,00232 | 0,00349 | 0,00164 | 0,00204 |
| 527,68102 | 0,00421 | 0,00245 | 0,00379 | 0,00179 | 0,00212 |
| 527,7182 | 0,00443 | 0,00261 | 0,00411 | 0,00196 | 0,00221 |
| 527,75538 | 0,00465 | 0,0028 | 0,00443 | 0,00214 | 0,00231 |
| 527,79256 | 0,00485 | 0,00302 | 0,00476 | 0,00234 | 0,00242 |
| 527,82975 | 0,00504 | 0,00326 | 0,00508 | 0,00256 | 0,00256 |
| 527,86693 | 0,00522 | 0,00352 | 0,0054 | 0,00281 | 0,00272 |
| 527,90411 | 0,00539 | 0,0038 | 0,00569 | 0,00309 | 0,0029 |
| 527,94129 | 0,00555 | 0,00408 | 0,00597 | 0,0034 | 0,00311 |
| 527,97847 | 0,00572 | 0,00435 | 0,00621 | 0,00374 | 0,00336 |
| 528,01566 | 0,0059 | 0,0046 | 0,00643 | 0,0041 | 0,00363 |
| 528,05284 | 0,00609 | 0,00484 | 0,00661 | 0,0045 | 0,00393 |
| 528,09002 | 0,00629 | 0,00504 | 0,00675 | 0,00491 | 0,00425 |
| 528,1272 | 0,0065 | 0,00521 | 0,00687 | 0,00533 | 0,00458 |
| 528,16438 | 0,00671 | 0,00536 | 0,00697 | 0,00576 | 0,00492 |
| 528,20157 | 0,00693 | 0,00547 | 0,00704 | 0,00618 | 0,00526 |
| 528,23875 | 0,00715 | 0,00557 | 0,00711 | 0,00659 | 0,00558 |
| 528,27593 | 0,00737 | 0,00566 | 0,00716 | 0,00698 | 0,00588 |
| 528,31311 | 0,00759 | 0,00575 | 0,00722 | 0,00733 | 0,00616 |
| 528,35029 | 0,0078 | 0,00584 | 0,00728 | 0,00765 | 0,00639 |
| 528,38748 | 0,00801 | 0,00594 | 0,00734 | 0,00792 | 0,00658 |
| 528,42466 | 0,00822 | 0,00606 | 0,00742 | 0,00814 | 0,00672 |
| 528,46184 | 0,00843 | 0,0062 | 0,00751 | 0,00831 | 0,00683 |
| 528,49902 | 0,00864 | 0,00635 | 0,0076 | 0,00844 | 0,0069 |
| 528,5362 | 0,00885 | 0,00651 | 0,0077 | 0,00852 | 0,00695 |
| 528,57339 | 0,00905 | 0,00667 | 0,00781 | 0,00858 | 0,00699 |
| 528,61057 | 0,00925 | 0,00682 | 0,00791 | 0,0086 | 0,00702 |
| 528,64775 | 0,00944 | 0,00697 | 0,00802 | 0,00862 | 0,00706 |
| 528,68493 | 0,00962 | 0,00709 | 0,00813 | 0,00863 | 0,00713 |
| 528,72211 | 0,00979 | 0,0072 | 0,00824 | 0,00866 | 0,00722 |
| 528,7593 | 0,00994 | 0,0073 | 0,00834 | 0,00871 | 0,00735 |
| 528,79648 | 0,01009 | 0,00738 | 0,00845 | 0,00879 | 0,00752 |
| 528,83366 | 0,01023 | 0,00746 | 0,00856 | 0,00892 | 0,00772 |
| 528,87084 | 0,01036 | 0,00755 | 0,00869 | 0,00908 | 0,00796 |
| 528,90802 | 0,0105 | 0,00764 | 0,00884 | 0,00929 | 0,00822 |
| 528,94521 | 0,01064 | 0,00776 | 0,009 | 0,00952 | 0,0085 |
| 528,98239 | 0,01079 | 0,0079 | 0,00919 | 0,00978 | 0,00878 |
| 529,01957 | 0,01094 | 0,00807 | 0,00941 | 0,01005 | 0,00906 |
| 529,05675 | 0,01109 | 0,00827 | 0,00966 | 0,01031 | 0,00932 |
| 529,09393 | 0,01124 | 0,00849 | 0,00993 | 0,01056 | 0,00955 |
| 529,13112 | 0,01139 | 0,00875 | 0,01023 | 0,01079 | 0,00975 |
| 529,1683 | 0,01155 | 0,00903 | 0,01055 | 0,01099 | 0,00992 |
| 529,20548 | 0,01171 | 0,00933 | 0,01089 | 0,01116 | 0,01004 |
| 529,24266 | 0,01188 | 0,00965 | 0,01125 | 0,0113 | 0,01013 |
| 529,27984 | 0,01207 | 0,00997 | 0,01162 | 0,01142 | 0,01019 |
| 529,31703 | 0,01227 | 0,0103 | 0,01199 | 0,01153 | 0,01022 |
| 529,35421 | 0,01249 | 0,01063 | 0,01237 | 0,01165 | 0,01024 |
| 529,39139 | 0,01271 | 0,01094 | 0,01274 | 0,01179 | 0,01025 |
| 529,42857 | 0,01294 | 0,01124 | 0,01312 | 0,01197 | 0,01027 |
| 529,46575 | 0,01315 | 0,01152 | 0,01348 | 0,01219 | 0,0103 |
| 529,50294 | 0,01334 | 0,01177 | 0,01384 | 0,01246 | 0,01036 |
| 529,54012 | 0,0135 | 0,012 | 0,01418 | 0,01279 | 0,01045 |
| 529,5773 | 0,01363 | 0,01221 | 0,01451 | 0,01317 | 0,01058 |
| 529,61448 | 0,01374 | 0,0124 | 0,01482 | 0,0136 | 0,01075 |
| 529,65166 | 0,01384 | 0,01258 | 0,01511 | 0,01406 | 0,01097 |
| 529,68885 | 0,01393 | 0,01277 | 0,01538 | 0,01453 | 0,01124 |
| 529,72603 | 0,01404 | 0,01298 | 0,01563 | 0,01501 | 0,01154 |
| 529,76321 | 0,01418 | 0,0132 | 0,01587 | 0,01547 | 0,01188 |
| 529,80039 | 0,01437 | 0,01346 | 0,01609 | 0,01589 | 0,01224 |
| 529,83757 | 0,01461 | 0,01375 | 0,01631 | 0,01627 | 0,01264 |
| 529,87476 | 0,01492 | 0,01408 | 0,01653 | 0,0166 | 0,01305 |
| 529,91194 | 0,01529 | 0,01445 | 0,01674 | 0,01686 | 0,01347 |
| 529,94912 | 0,01572 | 0,01484 | 0,01696 | 0,01707 | 0,01391 |
| 529,9863 | 0,01619 | 0,01525 | 0,0172 | 0,01723 | 0,01436 |
| 530,02348 | 0,0167 | 0,01567 | 0,01745 | 0,01734 | 0,01483 |
| 530,06067 | 0,01722 | 0,0161 | 0,01772 | 0,01741 | 0,01531 |
| 530,09785 | 0,01774 | 0,01651 | 0,01802 | 0,01748 | 0,01581 |
| 530,13503 | 0,01826 | 0,01692 | 0,01834 | 0,01754 | 0,01634 |
| 530,17221 | 0,01875 | 0,01732 | 0,0187 | 0,01762 | 0,0169 |
| 530,20939 | 0,01922 | 0,0177 | 0,01909 | 0,01772 | 0,0175 |
| 530,24658 | 0,01967 | 0,01808 | 0,01951 | 0,01787 | 0,01812 |
| 530,28376 | 0,02008 | 0,01845 | 0,01995 | 0,01807 | 0,01877 |
| 530,32094 | 0,02048 | 0,01882 | 0,02042 | 0,01831 | 0,01945 |
| 530,35812 | 0,02084 | 0,01918 | 0,02091 | 0,0186 | 0,02013 |
| 530,3953 | 0,02117 | 0,01955 | 0,02142 | 0,01893 | 0,02081 |
| 530,43249 | 0,02147 | 0,0199 | 0,02193 | 0,0193 | 0,02146 |
| 530,46967 | 0,02175 | 0,02024 | 0,02244 | 0,01971 | 0,02207 |
| 530,50685 | 0,022 | 0,02055 | 0,02295 | 0,02013 | 0,02262 |
| 530,54403 | 0,02225 | 0,02085 | 0,02344 | 0,02058 | 0,02311 |
| 530,58121 | 0,0225 | 0,02111 | 0,02392 | 0,02102 | 0,02351 |
| 530,6184 | 0,02276 | 0,02134 | 0,02437 | 0,02147 | 0,02383 |
| 530,65558 | 0,02303 | 0,02154 | 0,02478 | 0,0219 | 0,02406 |
| 530,69276 | 0,02333 | 0,02172 | 0,02517 | 0,02232 | 0,02421 |
| 530,72994 | 0,02364 | 0,02189 | 0,0255 | 0,02271 | 0,02428 |
| 530,76712 | 0,02396 | 0,02205 | 0,0258 | 0,02307 | 0,02428 |
| 530,80431 | 0,02428 | 0,02222 | 0,02604 | 0,0234 | 0,02424 |
| 530,84149 | 0,02458 | 0,02241 | 0,02623 | 0,0237 | 0,02418 |
| 530,87867 | 0,02485 | 0,02263 | 0,02637 | 0,02396 | 0,02412 |
| 530,91585 | 0,02508 | 0,02288 | 0,02646 | 0,02418 | 0,02407 |
| 530,95303 | 0,02528 | 0,02317 | 0,02651 | 0,02437 | 0,02405 |
| 530,99022 | 0,02544 | 0,02349 | 0,02651 | 0,02453 | 0,02407 |
| 531,0274 | 0,02557 | 0,02384 | 0,02648 | 0,02468 | 0,02414 |
| 531,06458 | 0,02568 | 0,02423 | 0,02644 | 0,02483 | 0,02428 |
| 531,10176 | 0,02578 | 0,02463 | 0,0264 | 0,02497 | 0,02447 |
| 531,13894 | 0,02589 | 0,02505 | 0,02638 | 0,02513 | 0,02473 |
| 531,17613 | 0,02601 | 0,02549 | 0,0264 | 0,02531 | 0,02504 |
| 531,21331 | 0,02615 | 0,02594 | 0,02647 | 0,02552 | 0,0254 |
| 531,25049 | 0,02634 | 0,02641 | 0,02661 | 0,02579 | 0,02581 |
| 531,28767 | 0,02657 | 0,02691 | 0,02684 | 0,02611 | 0,02625 |
| 531,32485 | 0,02687 | 0,02744 | 0,02716 | 0,0265 | 0,02672 |
| 531,36204 | 0,02725 | 0,02803 | 0,02759 | 0,02697 | 0,02722 |
| 531,39922 | 0,02775 | 0,02868 | 0,02814 | 0,02754 | 0,02776 |
| 531,4364 | 0,02838 | 0,02941 | 0,02879 | 0,0282 | 0,02833 |
| 531,47358 | 0,0292 | 0,03024 | 0,02954 | 0,02897 | 0,02894 |
| 531,51076 | 0,0302 | 0,03118 | 0,03038 | 0,02984 | 0,02959 |
| 531,54795 | 0,03139 | 0,03223 | 0,03131 | 0,03081 | 0,0303 |
| 531,58513 | 0,03277 | 0,03341 | 0,03231 | 0,03187 | 0,03106 |
| 531,62231 | 0,03432 | 0,0347 | 0,03337 | 0,03301 | 0,03188 |
| 531,65949 | 0,036 | 0,03612 | 0,0345 | 0,03422 | 0,03275 |
| 531,69667 | 0,03777 | 0,03764 | 0,03569 | 0,03549 | 0,03368 |
| 531,73386 | 0,03961 | 0,03926 | 0,03694 | 0,03679 | 0,03467 |
| 531,77104 | 0,04147 | 0,04096 | 0,03825 | 0,03812 | 0,03569 |
| 531,80822 | 0,04334 | 0,04273 | 0,03964 | 0,03947 | 0,03676 |
| 531,8454 | 0,04524 | 0,04455 | 0,0411 | 0,04084 | 0,03786 |
| 531,88258 | 0,04717 | 0,04642 | 0,04264 | 0,04223 | 0,039 |
| 531,91977 | 0,04919 | 0,04835 | 0,04427 | 0,04366 | 0,04016 |
| 531,95695 | 0,05136 | 0,05034 | 0,04598 | 0,04514 | 0,04136 |
| 531,99413 | 0,05376 | 0,05241 | 0,04779 | 0,04669 | 0,0426 |
| 532,03131 | 0,05642 | 0,05457 | 0,0497 | 0,04835 | 0,04389 |
| 532,06849 | 0,05938 | 0,05685 | 0,05171 | 0,05013 | 0,04525 |
| 532,10568 | 0,06265 | 0,05928 | 0,05383 | 0,05206 | 0,0467 |
| 532,14286 | 0,06621 | 0,06187 | 0,05606 | 0,05417 | 0,04826 |
| 532,18004 | 0,07004 | 0,06467 | 0,0584 | 0,05647 | 0,04994 |
| 532,21722 | 0,0741 | 0,06769 | 0,06087 | 0,05898 | 0,05178 |
| 532,2544 | 0,07833 | 0,07094 | 0,06348 | 0,06175 | 0,05378 |
| 532,29159 | 0,08271 | 0,07442 | 0,06622 | 0,06474 | 0,05597 |
| 532,32877 | 0,0872 | 0,07813 | 0,0691 | 0,06796 | 0,05837 |
| 532,36595 | 0,09179 | 0,08206 | 0,07212 | 0,0714 | 0,06098 |
| 532,40313 | 0,09648 | 0,08619 | 0,07527 | 0,07506 | 0,06381 |
| 532,44031 | 0,10128 | 0,09049 | 0,07856 | 0,07893 | 0,06685 |
| 532,4775 | 0,10623 | 0,09493 | 0,082 | 0,08299 | 0,07009 |
| 532,51468 | 0,11134 | 0,09947 | 0,08557 | 0,08723 | 0,07352 |
| 532,55186 | 0,11662 | 0,10406 | 0,08927 | 0,09164 | 0,07714 |
| 532,58904 | 0,12207 | 0,10869 | 0,09311 | 0,0962 | 0,08092 |
| 532,62622 | 0,12767 | 0,11332 | 0,09709 | 0,10089 | 0,08487 |
| 532,66341 | 0,13342 | 0,11792 | 0,10121 | 0,1057 | 0,08896 |
| 532,70059 | 0,13931 | 0,12252 | 0,10547 | 0,11061 | 0,09318 |
| 532,73777 | 0,14532 | 0,1271 | 0,10986 | 0,11558 | 0,09754 |
| 532,77495 | 0,15145 | 0,13169 | 0,11438 | 0,12059 | 0,10201 |
| 532,81213 | 0,15768 | 0,13631 | 0,11902 | 0,12561 | 0,10656 |
| 532,84932 | 0,16401 | 0,14098 | 0,12379 | 0,13062 | 0,1112 |
| 532,8865 | 0,17042 | 0,14572 | 0,12867 | 0,13559 | 0,1159 |
| 532,92368 | 0,1769 | 0,15055 | 0,13365 | 0,1405 | 0,12065 |
| 532,96086 | 0,18339 | 0,15547 | 0,13872 | 0,14534 | 0,12543 |
| 532,99804 | 0,18986 | 0,16048 | 0,14386 | 0,15009 | 0,13022 |
| 533,03523 | 0,19623 | 0,16557 | 0,14904 | 0,15475 | 0,135 |
| 533,07241 | 0,20244 | 0,17073 | 0,15422 | 0,15931 | 0,13975 |
| 533,10959 | 0,20843 | 0,17594 | 0,15935 | 0,16377 | 0,14446 |
| 533,14677 | 0,21416 | 0,18117 | 0,16438 | 0,16813 | 0,1491 |
| 533,18395 | 0,21959 | 0,18641 | 0,16925 | 0,17239 | 0,15365 |
| 533,22114 | 0,22473 | 0,19163 | 0,1739 | 0,17654 | 0,15811 |
| 533,25832 | 0,22958 | 0,19683 | 0,1783 | 0,18061 | 0,16248 |
| 533,2955 | 0,23418 | 0,20197 | 0,1824 | 0,18459 | 0,16673 |
| 533,33268 | 0,23856 | 0,20705 | 0,18618 | 0,18849 | 0,17088 |
| 533,36986 | 0,24272 | 0,21202 | 0,18963 | 0,19234 | 0,17493 |
| 533,40705 | 0,24669 | 0,21686 | 0,19276 | 0,19613 | 0,17889 |
| 533,44423 | 0,25046 | 0,22153 | 0,1956 | 0,1999 | 0,18276 |
| 533,48141 | 0,25401 | 0,22598 | 0,1982 | 0,20366 | 0,18654 |
| 533,51859 | 0,25731 | 0,23015 | 0,20061 | 0,20741 | 0,19024 |
| 533,55577 | 0,26031 | 0,23401 | 0,20291 | 0,21114 | 0,19386 |
| 533,59295 | 0,26303 | 0,23753 | 0,20519 | 0,21484 | 0,19738 |
| 533,63014 | 0,26544 | 0,24069 | 0,20751 | 0,21847 | 0,2008 |
| 533,66732 | 0,26757 | 0,24349 | 0,20993 | 0,222 | 0,20409 |
| 533,7045 | 0,26944 | 0,24594 | 0,21246 | 0,22537 | 0,20724 |
| 533,74168 | 0,27104 | 0,24805 | 0,21512 | 0,22854 | 0,21021 |
| 533,77886 | 0,2724 | 0,24985 | 0,2179 | 0,23146 | 0,21298 |
| 533,81605 | 0,27352 | 0,25137 | 0,22078 | 0,23408 | 0,21552 |
| 533,85323 | 0,27438 | 0,25263 | 0,22369 | 0,23637 | 0,21783 |
| 533,89041 | 0,27497 | 0,25365 | 0,22658 | 0,23832 | 0,21988 |
| 533,92759 | 0,27527 | 0,25446 | 0,22938 | 0,23993 | 0,22166 |
| 533,96477 | 0,27525 | 0,25505 | 0,23198 | 0,24116 | 0,22319 |
| 534,00196 | 0,27493 | 0,25543 | 0,23435 | 0,24208 | 0,22448 |
| 534,03914 | 0,27431 | 0,2556 | 0,23641 | 0,24271 | 0,22557 |
| 534,07632 | 0,27344 | 0,25558 | 0,23815 | 0,24309 | 0,22647 |
| 534,1135 | 0,27236 | 0,25536 | 0,23954 | 0,24324 | 0,22721 |
| 534,15068 | 0,27112 | 0,25495 | 0,24057 | 0,24319 | 0,2278 |
| 534,18787 | 0,26977 | 0,25437 | 0,24125 | 0,24296 | 0,22826 |
| 534,22505 | 0,26831 | 0,25361 | 0,24159 | 0,24256 | 0,22859 |
| 534,26223 | 0,26675 | 0,25268 | 0,24162 | 0,24199 | 0,2288 |
| 534,29941 | 0,26507 | 0,25159 | 0,24137 | 0,24127 | 0,22888 |
| 534,33659 | 0,26322 | 0,25034 | 0,24085 | 0,24038 | 0,22881 |
| 534,37378 | 0,26117 | 0,24892 | 0,24009 | 0,23934 | 0,22858 |
| 534,41096 | 0,25886 | 0,24732 | 0,23912 | 0,23814 | 0,22818 |
| 534,44814 | 0,25626 | 0,24551 | 0,23798 | 0,23679 | 0,2276 |
| 534,48532 | 0,25335 | 0,24348 | 0,23669 | 0,2353 | 0,22683 |
| 534,5225 | 0,25013 | 0,24122 | 0,23527 | 0,23368 | 0,22586 |
| 534,55969 | 0,24661 | 0,23871 | 0,23374 | 0,23194 | 0,2247 |
| 534,59687 | 0,24285 | 0,23595 | 0,23214 | 0,23007 | 0,22336 |
| 534,63405 | 0,2389 | 0,23295 | 0,23048 | 0,22809 | 0,22183 |
| 534,67123 | 0,23483 | 0,22972 | 0,22879 | 0,226 | 0,22015 |
| 534,70841 | 0,23069 | 0,22627 | 0,22707 | 0,22379 | 0,21833 |
| 534,7456 | 0,22654 | 0,22264 | 0,22535 | 0,22147 | 0,21637 |
| 534,78278 | 0,22241 | 0,21886 | 0,22361 | 0,21904 | 0,21433 |
| 534,81996 | 0,21832 | 0,21497 | 0,22183 | 0,21648 | 0,2122 |
| 534,85714 | 0,2143 | 0,21103 | 0,22001 | 0,21383 | 0,20999 |
| 534,89432 | 0,21035 | 0,20708 | 0,2181 | 0,21109 | 0,20772 |
| 534,93151 | 0,20646 | 0,20316 | 0,21606 | 0,20827 | 0,2054 |
| 534,96869 | 0,20262 | 0,19932 | 0,21387 | 0,20541 | 0,20302 |
| 535,00587 | 0,19883 | 0,19559 | 0,21149 | 0,2025 | 0,20058 |
| 535,04305 | 0,19506 | 0,19198 | 0,20888 | 0,19959 | 0,19809 |
| 535,08023 | 0,19128 | 0,1885 | 0,20603 | 0,19668 | 0,19555 |
| 535,11742 | 0,18748 | 0,18518 | 0,20293 | 0,19379 | 0,19297 |
| 535,1546 | 0,18364 | 0,18199 | 0,19959 | 0,19093 | 0,19035 |
| 535,19178 | 0,17975 | 0,17894 | 0,19604 | 0,1881 | 0,18771 |
| 535,22896 | 0,17581 | 0,176 | 0,19228 | 0,1853 | 0,18506 |
| 535,26614 | 0,17182 | 0,17317 | 0,1884 | 0,18252 | 0,18243 |
| 535,30333 | 0,1678 | 0,17043 | 0,18444 | 0,17975 | 0,17982 |
| 535,34051 | 0,16377 | 0,16777 | 0,18047 | 0,17698 | 0,17726 |
| 535,37769 | 0,15977 | 0,16519 | 0,17654 | 0,17421 | 0,17476 |
| 535,41487 | 0,15583 | 0,16269 | 0,17272 | 0,17143 | 0,17234 |
| 535,45205 | 0,152 | 0,16026 | 0,16904 | 0,16866 | 0,17002 |
| 535,48924 | 0,1483 | 0,15792 | 0,16556 | 0,1659 | 0,16781 |
| 535,52642 | 0,14477 | 0,15568 | 0,1623 | 0,16316 | 0,16573 |
| 535,5636 | 0,14142 | 0,15353 | 0,1593 | 0,16046 | 0,16378 |
| 535,60078 | 0,13827 | 0,15149 | 0,15656 | 0,15781 | 0,16195 |
| 535,63796 | 0,13532 | 0,14955 | 0,15409 | 0,15522 | 0,16023 |
| 535,67515 | 0,13255 | 0,14769 | 0,15187 | 0,1527 | 0,15861 |
| 535,71233 | 0,12995 | 0,14591 | 0,14986 | 0,15025 | 0,15708 |
| 535,74951 | 0,1275 | 0,14417 | 0,14802 | 0,14786 | 0,15561 |
| 535,78669 | 0,12518 | 0,14246 | 0,14631 | 0,14553 | 0,15419 |
| 535,82387 | 0,12296 | 0,14073 | 0,14467 | 0,14325 | 0,15279 |
| 535,86106 | 0,12083 | 0,13898 | 0,14305 | 0,14102 | 0,15137 |
| 535,89824 | 0,11876 | 0,13717 | 0,14143 | 0,13884 | 0,14993 |
| 535,93542 | 0,11674 | 0,1353 | 0,13976 | 0,1367 | 0,14844 |
| 535,9726 | 0,11476 | 0,13338 | 0,13802 | 0,13462 | 0,14688 |
| 536,00978 | 0,11279 | 0,13141 | 0,13618 | 0,13258 | 0,14526 |
| 536,04697 | 0,11085 | 0,1294 | 0,13425 | 0,13059 | 0,14358 |
| 536,08415 | 0,10893 | 0,12735 | 0,13221 | 0,12866 | 0,14184 |
| 536,12133 | 0,10703 | 0,12529 | 0,13011 | 0,12676 | 0,14005 |
| 536,15851 | 0,10515 | 0,12321 | 0,12794 | 0,12489 | 0,13823 |
| 536,19569 | 0,10326 | 0,12111 | 0,12574 | 0,12302 | 0,13638 |
| 536,23288 | 0,10136 | 0,11898 | 0,12353 | 0,12115 | 0,13452 |
| 536,27006 | 0,09942 | 0,11681 | 0,12133 | 0,11926 | 0,13267 |
| 536,30724 | 0,09744 | 0,11459 | 0,11916 | 0,11735 | 0,13084 |
| 536,34442 | 0,09539 | 0,11232 | 0,11704 | 0,1154 | 0,12903 |
| 536,3816 | 0,09327 | 0,10998 | 0,11497 | 0,11342 | 0,12725 |
| 536,41879 | 0,09109 | 0,10758 | 0,11297 | 0,11142 | 0,12551 |
| 536,45597 | 0,08887 | 0,10513 | 0,11105 | 0,10941 | 0,1238 |
| 536,49315 | 0,08662 | 0,10265 | 0,10921 | 0,10742 | 0,12212 |
| 536,53033 | 0,08439 | 0,10016 | 0,10743 | 0,10545 | 0,12049 |
| 536,56751 | 0,0822 | 0,09767 | 0,10571 | 0,10352 | 0,11889 |
| 536,6047 | 0,08008 | 0,09521 | 0,10402 | 0,10165 | 0,11733 |
| 536,64188 | 0,07808 | 0,09281 | 0,10235 | 0,09983 | 0,1158 |
| 536,67906 | 0,07619 | 0,09049 | 0,10068 | 0,09808 | 0,11429 |
| 536,71624 | 0,07441 | 0,08827 | 0,09899 | 0,0964 | 0,1128 |
| 536,75342 | 0,07276 | 0,08617 | 0,09724 | 0,09478 | 0,1113 |
| 536,79061 | 0,07121 | 0,08419 | 0,09544 | 0,09323 | 0,10977 |
| 536,82779 | 0,06975 | 0,08236 | 0,09356 | 0,09175 | 0,1082 |
| 536,86497 | 0,06835 | 0,08066 | 0,09162 | 0,09033 | 0,10657 |
| 536,90215 | 0,06699 | 0,0791 | 0,08961 | 0,08898 | 0,10487 |
| 536,93933 | 0,06564 | 0,07766 | 0,08757 | 0,0877 | 0,1031 |
| 536,97652 | 0,06428 | 0,07635 | 0,08551 | 0,08647 | 0,10124 |
| 537,0137 | 0,06291 | 0,07513 | 0,08348 | 0,08529 | 0,09932 |
| 537,05088 | 0,06152 | 0,07399 | 0,0815 | 0,08413 | 0,09735 |
| 537,08806 | 0,06011 | 0,07293 | 0,0796 | 0,08297 | 0,09536 |
| 537,12524 | 0,05868 | 0,07192 | 0,07782 | 0,08181 | 0,09338 |
| 537,16243 | 0,05723 | 0,07094 | 0,07616 | 0,08062 | 0,09145 |
| 537,19961 | 0,05579 | 0,06999 | 0,07464 | 0,07938 | 0,08961 |
| 537,23679 | 0,05435 | 0,06905 | 0,07325 | 0,07809 | 0,08787 |
| 537,27397 | 0,0529 | 0,0681 | 0,072 | 0,07673 | 0,08625 |
| 537,31115 | 0,05145 | 0,06712 | 0,07087 | 0,0753 | 0,08478 |
| 537,34834 | 0,04999 | 0,06612 | 0,06983 | 0,07382 | 0,08345 |
| 537,38552 | 0,04852 | 0,06506 | 0,06886 | 0,07227 | 0,08226 |
| 537,4227 | 0,04704 | 0,06394 | 0,06792 | 0,07069 | 0,08119 |
| 537,45988 | 0,04556 | 0,06276 | 0,06699 | 0,06909 | 0,08022 |
| 537,49706 | 0,0441 | 0,06152 | 0,06606 | 0,06747 | 0,07932 |
| 537,53425 | 0,04268 | 0,06021 | 0,0651 | 0,06587 | 0,07847 |
| 537,57143 | 0,04131 | 0,05885 | 0,0641 | 0,06429 | 0,07762 |
| 537,60861 | 0,04 | 0,05746 | 0,06307 | 0,06274 | 0,07675 |
| 537,64579 | 0,03878 | 0,05606 | 0,06201 | 0,06125 | 0,07584 |
| 537,68297 | 0,03763 | 0,05467 | 0,06091 | 0,05982 | 0,07486 |
| 537,72016 | 0,03656 | 0,05331 | 0,05979 | 0,05846 | 0,0738 |
| 537,75734 | 0,03554 | 0,05199 | 0,05866 | 0,05717 | 0,07265 |
| 537,79452 | 0,03455 | 0,05072 | 0,05754 | 0,05596 | 0,07141 |
| 537,8317 | 0,03358 | 0,04951 | 0,05641 | 0,05483 | 0,07006 |
| 537,86888 | 0,03262 | 0,04834 | 0,05529 | 0,05377 | 0,06862 |
| 537,90607 | 0,03164 | 0,04722 | 0,05417 | 0,05277 | 0,0671 |
| 537,94325 | 0,03065 | 0,04613 | 0,05304 | 0,05183 | 0,06552 |
| 537,98043 | 0,02965 | 0,04505 | 0,0519 | 0,05093 | 0,06389 |
| 538,01761 | 0,02864 | 0,04398 | 0,05073 | 0,05007 | 0,06224 |
| 538,05479 | 0,02763 | 0,04291 | 0,04953 | 0,04924 | 0,06059 |
| 538,09198 | 0,02664 | 0,04183 | 0,04829 | 0,0484 | 0,05894 |
| 538,12916 | 0,02568 | 0,04075 | 0,04702 | 0,04756 | 0,05733 |
| 538,16634 | 0,02475 | 0,03968 | 0,04573 | 0,04668 | 0,05576 |
| 538,20352 | 0,02387 | 0,03862 | 0,04442 | 0,04576 | 0,05424 |
| 538,2407 | 0,02303 | 0,03759 | 0,04313 | 0,04478 | 0,05279 |
| 538,27789 | 0,02224 | 0,0366 | 0,04187 | 0,04373 | 0,05141 |
| 538,31507 | 0,02149 | 0,03567 | 0,04066 | 0,04261 | 0,05011 |
| 538,35225 | 0,02078 | 0,03479 | 0,03953 | 0,04145 | 0,04887 |
| 538,38943 | 0,02011 | 0,03396 | 0,03848 | 0,04026 | 0,0477 |
| 538,42661 | 0,01948 | 0,0332 | 0,03753 | 0,03906 | 0,04658 |
| 538,4638 | 0,0189 | 0,03247 | 0,03667 | 0,03789 | 0,04553 |
| 538,50098 | 0,01836 | 0,03176 | 0,03591 | 0,03676 | 0,04451 |
| 538,53816 | 0,01787 | 0,03106 | 0,03523 | 0,03571 | 0,04353 |
| 538,57534 | 0,01741 | 0,03035 | 0,03462 | 0,03474 | 0,04258 |
| 538,61252 | 0,017 | 0,0296 | 0,03406 | 0,03386 | 0,04163 |
| 538,64971 | 0,0166 | 0,02881 | 0,03352 | 0,03308 | 0,04069 |
| 538,68689 | 0,01623 | 0,02797 | 0,033 | 0,03236 | 0,03972 |
| 538,72407 | 0,01586 | 0,0271 | 0,03246 | 0,03168 | 0,03872 |
| 538,76125 | 0,01548 | 0,02618 | 0,0319 | 0,03101 | 0,03768 |
| 538,79843 | 0,01508 | 0,02525 | 0,03131 | 0,03031 | 0,0366 |
| 538,83562 | 0,01466 | 0,0243 | 0,03067 | 0,02956 | 0,03546 |
| 538,8728 | 0,01421 | 0,02334 | 0,02999 | 0,02875 | 0,03428 |
| 538,90998 | 0,01372 | 0,02239 | 0,02926 | 0,02786 | 0,03304 |
| 538,94716 | 0,01321 | 0,02145 | 0,02849 | 0,0269 | 0,03177 |
| 538,98434 | 0,01266 | 0,02051 | 0,02767 | 0,02586 | 0,03048 |
| 539,02153 | 0,01208 | 0,01957 | 0,02682 | 0,02478 | 0,02917 |
| 539,05871 | 0,01149 | 0,01863 | 0,02595 | 0,02367 | 0,02787 |
| 539,09589 | 0,01088 | 0,01769 | 0,02505 | 0,02256 | 0,02659 |
| 539,13307 | 0,01027 | 0,01673 | 0,02414 | 0,02148 | 0,02536 |
| 539,17025 | 0,00967 | 0,01577 | 0,02323 | 0,02046 | 0,02418 |
| 539,20744 | 0,00908 | 0,01481 | 0,02232 | 0,01952 | 0,02308 |
| 539,24462 | 0,00852 | 0,01387 | 0,02142 | 0,01866 | 0,02206 |
| 539,2818 | 0,00799 | 0,01296 | 0,02054 | 0,0179 | 0,02113 |
| 539,31898 | 0,00749 | 0,0121 | 0,01967 | 0,01723 | 0,02029 |
| 539,35616 | 0,00703 | 0,01131 | 0,01883 | 0,01667 | 0,01956 |
| 539,39335 | 0,00661 | 0,01059 | 0,018 | 0,01619 | 0,01892 |
| 539,43053 | 0,00624 | 0,00996 | 0,0172 | 0,01579 | 0,01838 |
| 539,46771 | 0,00591 | 0,00943 | 0,01643 | 0,01545 | 0,01792 |
| 539,50489 | 0,00563 | 0,00899 | 0,01567 | 0,01517 | 0,01754 |
| 539,54207 | 0,00539 | 0,00862 | 0,01493 | 0,01493 | 0,0172 |
| 539,57926 | 0,0052 | 0,00833 | 0,01421 | 0,0147 | 0,0169 |
| 539,61644 | 0,00505 | 0,00809 | 0,01351 | 0,01447 | 0,01662 |
| 539,65362 | 0,00493 | 0,0079 | 0,01282 | 0,01423 | 0,01635 |
| 539,6908 | 0,00485 | 0,00774 | 0,01214 | 0,01396 | 0,01605 |
| 539,72798 | 0,0048 | 0,0076 | 0,01148 | 0,01366 | 0,01573 |
| 539,76517 | 0,00476 | 0,00746 | 0,01083 | 0,01331 | 0,01537 |
| 539,80235 | 0,00473 | 0,00733 | 0,0102 | 0,01292 | 0,01496 |
| 539,83953 | 0,00469 | 0,0072 | 0,00959 | 0,01248 | 0,0145 |
| 539,87671 | 0,00464 | 0,00706 | 0,00901 | 0,01199 | 0,01398 |
| 539,91389 | 0,00456 | 0,0069 | 0,00845 | 0,01146 | 0,01342 |
| 539,95108 | 0,00446 | 0,00673 | 0,00793 | 0,0109 | 0,01281 |
| 539,98826 | 0,00431 | 0,00655 | 0,00745 | 0,01031 | 0,01218 |
| 540,02544 | 0,00414 | 0,00635 | 0,00701 | 0,00972 | 0,01153 |
| 540,06262 | 0,00393 | 0,00613 | 0,00662 | 0,00913 | 0,01087 |
| 540,0998 | 0,00369 | 0,00588 | 0,00627 | 0,00855 | 0,01021 |
| 540,13699 | 0,00343 | 0,00561 | 0,00597 | 0,00799 | 0,00958 |
| 540,17417 | 0,00315 | 0,00532 | 0,00571 | 0,00746 | 0,00897 |
| 540,21135 | 0,00287 | 0,005 | 0,00547 | 0,00696 | 0,0084 |
| 540,24853 | 0,00259 | 0,00466 | 0,00527 | 0,00649 | 0,00789 |
| 540,28571 | 0,00232 | 0,0043 | 0,00508 | 0,00607 | 0,00743 |
| 540,3229 | 0,00205 | 0,00394 | 0,00489 | 0,00569 | 0,00703 |
| 540,36008 | 0,00181 | 0,00357 | 0,0047 | 0,00536 | 0,00668 |
| 540,39726 | 0,0016 | 0,00321 | 0,00451 | 0,00507 | 0,00639 |
| 540,43444 | 0,00141 | 0,00287 | 0,00431 | 0,00482 | 0,00615 |
| 540,47162 | 0,00125 | 0,00256 | 0,0041 | 0,00461 | 0,00595 |
| 540,50881 | 0,00113 | 0,00228 | 0,00388 | 0,00442 | 0,00579 |
| 540,54599 | 0,00105 | 0,00204 | 0,00366 | 0,00426 | 0,00567 |
| 540,58317 | 0,001 | 0,00184 | 0,00345 | 0,00411 | 0,00556 |
| 540,62035 | 0,00099 | 0,00168 | 0,00324 | 0,00398 | 0,00546 |
| 540,65753 | 0,00101 | 0,00155 | 0,00305 | 0,00384 | 0,00537 |
| 540,69472 | 0,00106 | 0,00144 | 0,00288 | 0,0037 | 0,00527 |
| 540,7319 | 0,00112 | 0,00136 | 0,00273 | 0,00356 | 0,00516 |
| 540,76908 | 0,00119 | 0,0013 | 0,0026 | 0,0034 | 0,00503 |
| 540,80626 | 0,00126 | 0,00125 | 0,0025 | 0,00322 | 0,00489 |
| 540,84344 | 0,00131 | 0,0012 | 0,00241 | 0,00304 | 0,00473 |
| 540,88063 | 0,00135 | 0,00115 | 0,00234 | 0,00284 | 0,00456 |
| 540,91781 | 0,00138 | 0,0011 | 0,00229 | 0,00263 | 0,00438 |
| 540,95499 | 0,00138 | 0,00105 | 0,00224 | 0,00242 | 0,00419 |
| 540,99217 | 0,00137 | 0,001 | 0,00219 | 0,0022 | 0,004 |
| 541,02935 | 0,00135 | 0,00095 | 0,00215 | 0,00199 | 0,00381 |
| 541,06654 | 0,00132 | 9e-04 | 0,00211 | 0,00178 | 0,00363 |
| 541,10372 | 0,00129 | 0,00086 | 0,00206 | 0,00159 | 0,00345 |
| 541,1409 | 0,00126 | 0,00082 | 0,002 | 0,0014 | 0,00328 |
| 541,17808 | 0,00123 | 0,00078 | 0,00193 | 0,00124 | 0,00311 |
| 541,21526 | 0,0012 | 0,00074 | 0,00185 | 0,0011 | 0,00295 |
| 541,25245 | 0,00117 | 0,00071 | 0,00175 | 0,00098 | 0,00279 |
| 541,28963 | 0,00113 | 0,00069 | 0,00165 | 0,00088 | 0,00262 |
| 541,32681 | 0,00108 | 0,00066 | 0,00154 | 0,00081 | 0,00246 |
| 541,36399 | 0,00102 | 0,00064 | 0,00142 | 0,00075 | 0,00229 |
| 541,40117 | 0,00095 | 0,00061 | 0,00129 | 7e-04 | 0,00212 |
| 541,43836 | 0,00086 | 0,00058 | 0,00117 | 0,00068 | 0,00194 |
| 541,47554 | 0,00077 | 0,00055 | 0,00105 | 0,00065 | 0,00177 |
| 541,51272 | 0,00068 | 0,00052 | 0,00093 | 0,00064 | 0,00159 |
| 541,5499 | 0,00059 | 0,00048 | 0,00082 | 0,00062 | 0,00142 |
| 541,58708 | 5e-04 | 0,00044 | 0,00073 | 0,00061 | 0,00126 |
| 541,62427 | 0,00043 | 0,00039 | 0,00064 | 0,00059 | 0,0011 |
| 541,66145 | 0,00036 | 0,00035 | 0,00057 | 0,00056 | 0,00096 |
| 541,69863 | 0,00031 | 0,00031 | 0,00052 | 0,00053 | 0,00083 |
| 541,73581 | 0,00027 | 0,00026 | 0,00047 | 5e-04 | 0,00072 |
| 541,77299 | 0,00023 | 0,00022 | 0,00043 | 0,00046 | 0,00062 |
| 541,81018 | 0,00021 | 0,00019 | 4e-04 | 0,00043 | 0,00053 |
| 541,84736 | 0,00019 | 0,00016 | 0,00038 | 0,00039 | 0,00046 |
| 541,88454 | 0,00017 | 0,00013 | 0,00036 | 0,00036 | 4e-04 |
| 541,92172 | 0,00015 | 1e-04 | 0,00034 | 0,00034 | 0,00034 |
| 541,9589 | 0,00014 | 8e-05 | 0,00032 | 0,00031 | 3e-04 |
| 541,99609 | 0,00012 | 6e-05 | 3e-04 | 3e-04 | 0,00026 |
| 542,03327 | 0,00011 | 5e-05 | 0,00028 | 0,00029 | 0,00022 |
| 542,07045 | 9e-05 | 3e-05 | 0,00026 | 0,00028 | 2e-04 |
| 542,10763 | 8e-05 | 2e-05 | 0,00024 | 0,00028 | 0,00017 |
| 542,14481 | 6e-05 | 2e-05 | 0,00022 | 0,00028 | 0,00016 |
| 542,182 | 5e-05 | 1e-05 | 0,00019 | 0,00028 | 0,00014 |
| 542,21918 | 4e-05 | 1e-05 | 0,00017 | 0,00028 | 0,00013 |
| 542,25636 | 3e-05 | 0 | 0,00015 | 0,00028 | 0,00013 |
| 542,29354 | 2e-05 | 0 | 0,00013 | 0,00027 | 0,00012 |
| 542,33072 | 1e-05 | 0 | 0,00011 | 0,00026 | 0,00012 |
| 542,36791 | 1e-05 | 0 | 9e-05 | 0,00025 | 0,00012 |
| 542,40509 | 0 | 0 | 7e-05 | 0,00023 | 0,00012 |
| 542,44227 | 0 | 0 | 6e-05 | 0,00021 | 0,00011 |
| 542,47945 | 0 | 0 | 4e-05 | 0,00018 | 0,00011 |
| 542,51663 | 0 | 0 | 3e-05 | 0,00016 | 0,00011 |
| 542,55382 | 0 | 0 | 3e-05 | 0,00013 | 1e-04 |
| 542,591 | 0 | 0 | 2e-05 | 0,00011 | 9e-05 |
| 542,62818 | 0 | 0 | 1e-05 | 9e-05 | 9e-05 |
| 542,66536 | 0 | 0 | 1e-05 | 7e-05 | 8e-05 |
| 542,70254 | 0 | 0 | 1e-05 | 5e-05 | 7e-05 |
| 542,73973 | 0 | 0 | 0 | 4e-05 | 6e-05 |
| 542,77691 | 0 | 0 | 0 | 3e-05 | 5e-05 |
| 542,81409 | 0 | 0 | 0 | 2e-05 | 4e-05 |
| 542,85127 | 0 | 0 | 0 | 1e-05 | 3e-05 |
| 542,88845 | 0 | 0 | 0 | 1e-05 | 3e-05 |
| 542,92564 | 0 | 0 | 0 | 1e-05 | 2e-05 |
| 542,96282 | 0 | 0 | 0 | 0 | 1e-05 |
| 543 | 0 | 0 | 0 | 0 | 1e-05 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00109 | 0,00098 | 0,00072 | 0,00021 | 2e-04 |
| 524,03718 | 0,00116 | 0,00097 | 0,00072 | 0,00024 | 0,00022 |
| 524,07436 | 0,00122 | 0,00096 | 0,00071 | 0,00027 | 0,00025 |
| 524,11155 | 0,00127 | 0,00094 | 7e-04 | 0,00031 | 0,00027 |
| 524,14873 | 0,00132 | 0,00092 | 0,00069 | 0,00034 | 0,00029 |
| 524,18591 | 0,00135 | 9e-04 | 0,00067 | 0,00037 | 3e-04 |
| 524,22309 | 0,00138 | 0,00088 | 0,00066 | 4e-04 | 0,00031 |
| 524,26027 | 0,00139 | 0,00086 | 0,00065 | 0,00043 | 0,00031 |
| 524,29746 | 0,0014 | 0,00084 | 0,00063 | 0,00046 | 0,00031 |
| 524,33464 | 0,00139 | 0,00083 | 0,00062 | 0,00048 | 0,00031 |
| 524,37182 | 0,00138 | 0,00083 | 0,00062 | 5e-04 | 3e-04 |
| 524,409 | 0,00137 | 0,00084 | 0,00062 | 0,00051 | 0,00029 |
| 524,44618 | 0,00135 | 0,00085 | 0,00063 | 0,00053 | 0,00027 |
| 524,48337 | 0,00134 | 0,00088 | 0,00065 | 0,00054 | 0,00026 |
| 524,52055 | 0,00133 | 0,00093 | 0,00067 | 0,00055 | 0,00025 |
| 524,55773 | 0,00133 | 0,00098 | 0,00071 | 0,00057 | 0,00025 |
| 524,59491 | 0,00133 | 0,00104 | 0,00075 | 0,00059 | 0,00024 |
| 524,63209 | 0,00134 | 0,00111 | 0,00079 | 0,00061 | 0,00025 |
| 524,66928 | 0,00137 | 0,00119 | 0,00085 | 0,00064 | 0,00026 |
| 524,70646 | 0,0014 | 0,00127 | 9e-04 | 0,00067 | 0,00028 |
| 524,74364 | 0,00144 | 0,00135 | 0,00096 | 7e-04 | 0,00031 |
| 524,78082 | 0,00148 | 0,00144 | 0,00103 | 0,00074 | 0,00034 |
| 524,818 | 0,00154 | 0,00153 | 0,00109 | 0,00077 | 0,00038 |
| 524,85519 | 0,0016 | 0,00162 | 0,00115 | 0,00081 | 0,00041 |
| 524,89237 | 0,00167 | 0,0017 | 0,00121 | 0,00083 | 0,00045 |
| 524,92955 | 0,00174 | 0,00178 | 0,00127 | 0,00085 | 0,00048 |
| 524,96673 | 0,00181 | 0,00186 | 0,00133 | 0,00085 | 5e-04 |
| 525,00391 | 0,00189 | 0,00194 | 0,00139 | 0,00084 | 0,00052 |
| 525,0411 | 0,00196 | 0,00201 | 0,00144 | 0,00082 | 0,00053 |
| 525,07828 | 0,00203 | 0,00208 | 0,0015 | 0,00079 | 0,00052 |
| 525,11546 | 0,00211 | 0,00215 | 0,00155 | 0,00076 | 0,00051 |
| 525,15264 | 0,00218 | 0,00221 | 0,00161 | 0,00071 | 0,00049 |
| 525,18982 | 0,00226 | 0,00227 | 0,00166 | 0,00067 | 0,00047 |
| 525,22701 | 0,00235 | 0,00233 | 0,00172 | 0,00063 | 0,00044 |
| 525,26419 | 0,00246 | 0,00239 | 0,00179 | 0,00059 | 0,00041 |
| 525,30137 | 0,00259 | 0,00247 | 0,00186 | 0,00057 | 0,00039 |
| 525,33855 | 0,00275 | 0,00255 | 0,00196 | 0,00057 | 0,00038 |
| 525,37573 | 0,00297 | 0,00266 | 0,00209 | 0,00058 | 0,00038 |
| 525,41292 | 0,00324 | 0,0028 | 0,00225 | 0,00063 | 4e-04 |
| 525,4501 | 0,00359 | 0,00298 | 0,00246 | 0,00071 | 0,00045 |
| 525,48728 | 0,00404 | 0,00322 | 0,00274 | 0,00083 | 0,00054 |
| 525,52446 | 0,00461 | 0,00353 | 0,00308 | 0,00101 | 0,00067 |
| 525,56164 | 0,00532 | 0,00393 | 0,00353 | 0,00125 | 0,00088 |
| 525,59883 | 0,00616 | 0,00443 | 0,00408 | 0,00158 | 0,00116 |
| 525,63601 | 0,00716 | 0,00505 | 0,00476 | 0,002 | 0,00155 |
| 525,67319 | 0,00831 | 0,00578 | 0,00556 | 0,00255 | 0,00206 |
| 525,71037 | 0,0096 | 0,00662 | 0,00648 | 0,00324 | 0,00272 |
| 525,74755 | 0,01103 | 0,00759 | 0,00754 | 0,00408 | 0,00354 |
| 525,78474 | 0,01258 | 0,00867 | 0,00871 | 0,00511 | 0,00456 |
| 525,82192 | 0,01421 | 0,00985 | 0,00999 | 0,00633 | 0,00578 |
| 525,8591 | 0,0159 | 0,01111 | 0,01135 | 0,00775 | 0,00723 |
| 525,89628 | 0,0176 | 0,01243 | 0,01277 | 0,00933 | 0,00887 |
| 525,93346 | 0,01927 | 0,01379 | 0,01422 | 0,01104 | 0,01067 |
| 525,97065 | 0,02086 | 0,01515 | 0,01567 | 0,01284 | 0,0126 |
| 526,00783 | 0,02234 | 0,01648 | 0,01707 | 0,01467 | 0,0146 |
| 526,04501 | 0,02369 | 0,01776 | 0,01839 | 0,01646 | 0,01659 |
| 526,08219 | 0,02489 | 0,01897 | 0,01962 | 0,01813 | 0,01852 |
| 526,11937 | 0,02591 | 0,0201 | 0,02073 | 0,01963 | 0,0203 |
| 526,15656 | 0,02677 | 0,02113 | 0,0217 | 0,02087 | 0,02185 |
| 526,19374 | 0,02747 | 0,02207 | 0,02254 | 0,02182 | 0,02313 |
| 526,23092 | 0,02803 | 0,02291 | 0,02323 | 0,02241 | 0,02407 |
| 526,2681 | 0,02847 | 0,02366 | 0,02381 | 0,02264 | 0,02462 |
| 526,30528 | 0,02883 | 0,02433 | 0,02426 | 0,02254 | 0,02481 |
| 526,34247 | 0,02914 | 0,02494 | 0,02462 | 0,02216 | 0,02469 |
| 526,37965 | 0,02943 | 0,02551 | 0,02491 | 0,02155 | 0,0243 |
| 526,41683 | 0,02972 | 0,02605 | 0,02517 | 0,02077 | 0,0237 |
| 526,45401 | 0,03003 | 0,02657 | 0,02539 | 0,0199 | 0,02298 |
| 526,49119 | 0,03036 | 0,02708 | 0,02561 | 0,01903 | 0,02222 |
| 526,52838 | 0,03071 | 0,02759 | 0,02583 | 0,01822 | 0,02149 |
| 526,56556 | 0,03109 | 0,0281 | 0,02606 | 0,01755 | 0,02087 |
| 526,60274 | 0,0315 | 0,02863 | 0,02632 | 0,01707 | 0,02042 |
| 526,63992 | 0,03193 | 0,02919 | 0,0266 | 0,01684 | 0,02019 |
| 526,6771 | 0,03239 | 0,02979 | 0,02692 | 0,01687 | 0,02021 |
| 526,71429 | 0,03289 | 0,03045 | 0,02728 | 0,01715 | 0,02046 |
| 526,75147 | 0,03343 | 0,03119 | 0,0277 | 0,01767 | 0,02092 |
| 526,78865 | 0,03404 | 0,03203 | 0,02819 | 0,01839 | 0,02154 |
| 526,82583 | 0,03475 | 0,03299 | 0,02877 | 0,01927 | 0,02228 |
| 526,86301 | 0,03558 | 0,0341 | 0,02946 | 0,02025 | 0,02309 |
| 526,9002 | 0,03657 | 0,03537 | 0,03028 | 0,02128 | 0,02389 |
| 526,93738 | 0,03773 | 0,0368 | 0,03124 | 0,02229 | 0,02465 |
| 526,97456 | 0,03911 | 0,03841 | 0,03237 | 0,02324 | 0,02531 |
| 527,01174 | 0,0407 | 0,04021 | 0,03368 | 0,02409 | 0,02584 |
| 527,04892 | 0,0425 | 0,04215 | 0,03519 | 0,02478 | 0,02621 |
| 527,08611 | 0,04448 | 0,04421 | 0,03686 | 0,02534 | 0,02642 |
| 527,12329 | 0,04663 | 0,04636 | 0,0387 | 0,02578 | 0,02649 |
| 527,16047 | 0,0489 | 0,04856 | 0,04067 | 0,02613 | 0,02647 |
| 527,19765 | 0,05125 | 0,05077 | 0,04276 | 0,02646 | 0,02642 |
| 527,23483 | 0,05364 | 0,05295 | 0,04495 | 0,02682 | 0,02641 |
| 527,27202 | 0,05604 | 0,05508 | 0,0472 | 0,02729 | 0,0265 |
| 527,3092 | 0,05839 | 0,05712 | 0,0495 | 0,02795 | 0,02679 |
| 527,34638 | 0,06066 | 0,05907 | 0,05182 | 0,02886 | 0,02733 |
| 527,38356 | 0,06283 | 0,06091 | 0,05414 | 0,03008 | 0,0282 |
| 527,42074 | 0,06488 | 0,06263 | 0,05645 | 0,03166 | 0,02944 |
| 527,45793 | 0,06681 | 0,06426 | 0,05873 | 0,03363 | 0,03109 |
| 527,49511 | 0,0686 | 0,06581 | 0,06096 | 0,03593 | 0,03314 |
| 527,53229 | 0,07025 | 0,06726 | 0,06313 | 0,03852 | 0,03555 |
| 527,56947 | 0,07176 | 0,06864 | 0,06523 | 0,04132 | 0,03824 |
| 527,60665 | 0,07312 | 0,06994 | 0,06722 | 0,04426 | 0,04114 |
| 527,64384 | 0,07432 | 0,07115 | 0,0691 | 0,04725 | 0,04419 |
| 527,68102 | 0,07536 | 0,07227 | 0,07083 | 0,05022 | 0,04729 |
| 527,7182 | 0,07622 | 0,07328 | 0,07239 | 0,05311 | 0,05039 |
| 527,75538 | 0,0769 | 0,07414 | 0,07374 | 0,05586 | 0,05342 |
| 527,79256 | 0,07741 | 0,07487 | 0,07489 | 0,05848 | 0,05636 |
| 527,82975 | 0,07776 | 0,07545 | 0,07583 | 0,06098 | 0,05921 |
| 527,86693 | 0,07799 | 0,07589 | 0,07657 | 0,0634 | 0,06198 |
| 527,90411 | 0,07811 | 0,0762 | 0,07715 | 0,06584 | 0,06474 |
| 527,94129 | 0,07818 | 0,07641 | 0,0776 | 0,06841 | 0,06758 |
| 527,97847 | 0,07824 | 0,07655 | 0,07796 | 0,0712 | 0,07059 |
| 528,01566 | 0,07836 | 0,07668 | 0,07831 | 0,07432 | 0,07385 |
| 528,05284 | 0,0786 | 0,07683 | 0,07869 | 0,07784 | 0,07746 |
| 528,09002 | 0,07904 | 0,07708 | 0,07917 | 0,08182 | 0,08146 |
| 528,1272 | 0,07972 | 0,07749 | 0,07985 | 0,08628 | 0,0859 |
| 528,16438 | 0,08067 | 0,07811 | 0,08075 | 0,09118 | 0,09076 |
| 528,20157 | 0,08194 | 0,07897 | 0,08192 | 0,09644 | 0,09597 |
| 528,23875 | 0,08353 | 0,08011 | 0,08337 | 0,10192 | 0,10143 |
| 528,27593 | 0,08544 | 0,08155 | 0,08512 | 0,10739 | 0,10694 |
| 528,31311 | 0,08766 | 0,0833 | 0,08717 | 0,11261 | 0,11227 |
| 528,35029 | 0,09019 | 0,08535 | 0,0895 | 0,1173 | 0,11717 |
| 528,38748 | 0,09299 | 0,08771 | 0,09212 | 0,12123 | 0,12141 |
| 528,42466 | 0,09606 | 0,09036 | 0,095 | 0,12419 | 0,12479 |
| 528,46184 | 0,09936 | 0,09333 | 0,09814 | 0,12604 | 0,12716 |
| 528,49902 | 0,10288 | 0,09657 | 0,10155 | 0,12671 | 0,12847 |
| 528,5362 | 0,1066 | 0,10009 | 0,1052 | 0,12625 | 0,12873 |
| 528,57339 | 0,11052 | 0,10388 | 0,10912 | 0,12479 | 0,1281 |
| 528,61057 | 0,11465 | 0,10795 | 0,1133 | 0,12259 | 0,1268 |
| 528,64775 | 0,11899 | 0,11228 | 0,11777 | 0,11998 | 0,12518 |
| 528,68493 | 0,12355 | 0,11689 | 0,12252 | 0,11745 | 0,12372 |
| 528,72211 | 0,12832 | 0,12176 | 0,12757 | 0,11549 | 0,1229 |
| 528,7593 | 0,13328 | 0,12686 | 0,13288 | 0,11453 | 0,12317 |
| 528,79648 | 0,1384 | 0,13216 | 0,13841 | 0,11491 | 0,12489 |
| 528,83366 | 0,14359 | 0,13759 | 0,14409 | 0,11691 | 0,12832 |
| 528,87084 | 0,14875 | 0,14303 | 0,14981 | 0,12064 | 0,13357 |
| 528,90802 | 0,15376 | 0,14836 | 0,15541 | 0,1261 | 0,14061 |
| 528,94521 | 0,15848 | 0,15345 | 0,16075 | 0,13309 | 0,14922 |
| 528,98239 | 0,16277 | 0,15816 | 0,16565 | 0,14129 | 0,15903 |
| 529,01957 | 0,16648 | 0,16234 | 0,16997 | 0,15024 | 0,16952 |
| 529,05675 | 0,16947 | 0,16585 | 0,17354 | 0,15937 | 0,18007 |
| 529,09393 | 0,17161 | 0,16856 | 0,17622 | 0,16795 | 0,18982 |
| 529,13112 | 0,17282 | 0,17038 | 0,17791 | 0,1754 | 0,19813 |
| 529,1683 | 0,17292 | 0,17121 | 0,17852 | 0,18123 | 0,20444 |
| 529,20548 | 0,17201 | 0,17096 | 0,17793 | 0,18509 | 0,20834 |
| 529,24266 | 0,17018 | 0,16978 | 0,17632 | 0,18677 | 0,20959 |
| 529,27984 | 0,16754 | 0,16775 | 0,1738 | 0,18625 | 0,20816 |
| 529,31703 | 0,16424 | 0,16501 | 0,17055 | 0,18364 | 0,20418 |
| 529,35421 | 0,16049 | 0,16171 | 0,16676 | 0,17922 | 0,19799 |
| 529,39139 | 0,15651 | 0,15807 | 0,16268 | 0,17338 | 0,19003 |
| 529,42857 | 0,15255 | 0,15431 | 0,15858 | 0,16659 | 0,18085 |
| 529,46575 | 0,14889 | 0,15066 | 0,15473 | 0,15934 | 0,17104 |
| 529,50294 | 0,1458 | 0,14738 | 0,15142 | 0,15221 | 0,16129 |
| 529,54012 | 0,14365 | 0,14477 | 0,14898 | 0,14565 | 0,15215 |
| 529,5773 | 0,14261 | 0,1431 | 0,14774 | 0,14 | 0,14407 |
| 529,61448 | 0,14288 | 0,14255 | 0,14785 | 0,13555 | 0,1374 |
| 529,65166 | 0,14459 | 0,1433 | 0,14947 | 0,13251 | 0,13237 |
| 529,68885 | 0,14787 | 0,1455 | 0,15273 | 0,13102 | 0,12919 |
| 529,72603 | 0,15277 | 0,14925 | 0,15772 | 0,13122 | 0,12799 |
| 529,76321 | 0,1593 | 0,15464 | 0,16444 | 0,13318 | 0,12885 |
| 529,80039 | 0,16742 | 0,16168 | 0,17286 | 0,13702 | 0,13187 |
| 529,83757 | 0,17703 | 0,17033 | 0,1829 | 0,14282 | 0,13713 |
| 529,87476 | 0,18803 | 0,1805 | 0,19441 | 0,15083 | 0,1448 |
| 529,91194 | 0,20021 | 0,19217 | 0,20725 | 0,16115 | 0,1551 |
| 529,94912 | 0,21316 | 0,20495 | 0,22105 | 0,17373 | 0,16793 |
| 529,9863 | 0,22659 | 0,2185 | 0,23542 | 0,18862 | 0,1833 |
| 530,02348 | 0,24015 | 0,2325 | 0,24998 | 0,20574 | 0,20118 |
| 530,06067 | 0,25347 | 0,24655 | 0,26434 | 0,2249 | 0,22137 |
| 530,09785 | 0,26619 | 0,26027 | 0,27808 | 0,24579 | 0,24357 |
| 530,13503 | 0,27795 | 0,27324 | 0,29083 | 0,26791 | 0,26728 |
| 530,17221 | 0,28841 | 0,28507 | 0,30219 | 0,29062 | 0,29184 |
| 530,20939 | 0,29727 | 0,2954 | 0,31182 | 0,31316 | 0,31644 |
| 530,24658 | 0,30414 | 0,30389 | 0,31945 | 0,33463 | 0,3401 |
| 530,28376 | 0,30885 | 0,31004 | 0,32457 | 0,35386 | 0,36164 |
| 530,32094 | 0,31144 | 0,31394 | 0,32729 | 0,36989 | 0,37981 |
| 530,35812 | 0,31191 | 0,31554 | 0,32764 | 0,38203 | 0,39385 |
| 530,3953 | 0,31033 | 0,31488 | 0,32567 | 0,38974 | 0,40305 |
| 530,43249 | 0,30686 | 0,31207 | 0,32154 | 0,39269 | 0,40699 |
| 530,46967 | 0,30167 | 0,30731 | 0,31545 | 0,39084 | 0,40555 |
| 530,50685 | 0,29501 | 0,30083 | 0,30766 | 0,38443 | 0,3989 |
| 530,54403 | 0,28715 | 0,2929 | 0,29845 | 0,37393 | 0,38751 |
| 530,58121 | 0,27835 | 0,28382 | 0,28813 | 0,36003 | 0,37209 |
| 530,6184 | 0,26885 | 0,27387 | 0,277 | 0,34354 | 0,35355 |
| 530,65558 | 0,25899 | 0,26336 | 0,26536 | 0,32538 | 0,33289 |
| 530,69276 | 0,24898 | 0,25262 | 0,25354 | 0,30643 | 0,31115 |
| 530,72994 | 0,239 | 0,24185 | 0,24175 | 0,28766 | 0,28947 |
| 530,76712 | 0,22919 | 0,23123 | 0,23018 | 0,26971 | 0,26869 |
| 530,80431 | 0,21964 | 0,22087 | 0,21894 | 0,25306 | 0,24942 |
| 530,84149 | 0,21041 | 0,21088 | 0,20813 | 0,23802 | 0,23211 |
| 530,87867 | 0,20157 | 0,20132 | 0,19784 | 0,22478 | 0,21703 |
| 530,91585 | 0,19313 | 0,19224 | 0,18809 | 0,21341 | 0,20431 |
| 530,95303 | 0,18511 | 0,18366 | 0,17894 | 0,2039 | 0,19395 |
| 530,99022 | 0,1776 | 0,17566 | 0,17044 | 0,19618 | 0,18589 |
| 531,0274 | 0,17055 | 0,16825 | 0,16263 | 0,19019 | 0,18 |
| 531,06458 | 0,16401 | 0,16144 | 0,15551 | 0,18582 | 0,17612 |
| 531,10176 | 0,15801 | 0,15529 | 0,14912 | 0,18312 | 0,17422 |
| 531,13894 | 0,15261 | 0,14984 | 0,14351 | 0,18186 | 0,17397 |
| 531,17613 | 0,14786 | 0,14517 | 0,13873 | 0,18187 | 0,17509 |
| 531,21331 | 0,14383 | 0,14134 | 0,13484 | 0,18298 | 0,17732 |
| 531,25049 | 0,14056 | 0,13842 | 0,13189 | 0,18495 | 0,18034 |
| 531,28767 | 0,13812 | 0,13646 | 0,12993 | 0,18747 | 0,1838 |
| 531,32485 | 0,13655 | 0,13552 | 0,12897 | 0,19018 | 0,18728 |
| 531,36204 | 0,13592 | 0,1357 | 0,12911 | 0,19267 | 0,19037 |
| 531,39922 | 0,13612 | 0,13688 | 0,13024 | 0,19451 | 0,19262 |
| 531,4364 | 0,13709 | 0,13896 | 0,13224 | 0,19528 | 0,19364 |
| 531,47358 | 0,13872 | 0,14184 | 0,135 | 0,19463 | 0,19308 |
| 531,51076 | 0,14088 | 0,14535 | 0,13837 | 0,19208 | 0,19051 |
| 531,54795 | 0,14341 | 0,1493 | 0,14215 | 0,18768 | 0,18596 |
| 531,58513 | 0,14611 | 0,15348 | 0,14614 | 0,18147 | 0,17953 |
| 531,62231 | 0,14879 | 0,15763 | 0,15012 | 0,17363 | 0,17141 |
| 531,65949 | 0,15123 | 0,16152 | 0,15382 | 0,16443 | 0,1619 |
| 531,69667 | 0,15317 | 0,16486 | 0,15703 | 0,15424 | 0,15138 |
| 531,73386 | 0,15439 | 0,16731 | 0,15938 | 0,14347 | 0,14026 |
| 531,77104 | 0,15475 | 0,16875 | 0,16077 | 0,13251 | 0,12895 |
| 531,80822 | 0,15414 | 0,16901 | 0,16105 | 0,12176 | 0,11786 |
| 531,8454 | 0,1525 | 0,16802 | 0,16013 | 0,11155 | 0,10731 |
| 531,88258 | 0,1498 | 0,16573 | 0,15798 | 0,10214 | 0,09756 |
| 531,91977 | 0,14608 | 0,16216 | 0,1546 | 0,09381 | 0,0889 |
| 531,95695 | 0,14142 | 0,15739 | 0,15007 | 0,08654 | 0,08132 |
| 531,99413 | 0,13591 | 0,15154 | 0,1445 | 0,08031 | 0,0748 |
| 532,03131 | 0,12973 | 0,14477 | 0,13804 | 0,07509 | 0,0693 |
| 532,06849 | 0,123 | 0,13726 | 0,13086 | 0,07076 | 0,06473 |
| 532,10568 | 0,11599 | 0,12926 | 0,12318 | 0,06724 | 0,061 |
| 532,14286 | 0,10888 | 0,12103 | 0,11527 | 0,06441 | 0,058 |
| 532,18004 | 0,10185 | 0,11278 | 0,10733 | 0,06217 | 0,05564 |
| 532,21722 | 0,09505 | 0,10472 | 0,09953 | 0,06043 | 0,05383 |
| 532,2544 | 0,08862 | 0,09698 | 0,09204 | 0,05912 | 0,05251 |
| 532,29159 | 0,08265 | 0,08973 | 0,08499 | 0,0582 | 0,05162 |
| 532,32877 | 0,07724 | 0,08306 | 0,07847 | 0,05767 | 0,05117 |
| 532,36595 | 0,07244 | 0,07706 | 0,07258 | 0,0575 | 0,05109 |
| 532,40313 | 0,06829 | 0,07178 | 0,06737 | 0,05769 | 0,05136 |
| 532,44031 | 0,06489 | 0,06734 | 0,06294 | 0,05825 | 0,05199 |
| 532,4775 | 0,0622 | 0,06372 | 0,05929 | 0,05921 | 0,05296 |
| 532,51468 | 0,06019 | 0,06091 | 0,0564 | 0,06057 | 0,05427 |
| 532,55186 | 0,05887 | 0,0589 | 0,05428 | 0,06234 | 0,05591 |
| 532,58904 | 0,05825 | 0,0577 | 0,05294 | 0,06448 | 0,05786 |
| 532,62622 | 0,0583 | 0,0573 | 0,05238 | 0,06699 | 0,06011 |
| 532,66341 | 0,05904 | 0,05772 | 0,05261 | 0,0698 | 0,06262 |
| 532,70059 | 0,06046 | 0,05895 | 0,05363 | 0,07287 | 0,06537 |
| 532,73777 | 0,06253 | 0,06096 | 0,05543 | 0,07614 | 0,06833 |
| 532,77495 | 0,06525 | 0,06374 | 0,058 | 0,07951 | 0,07144 |
| 532,81213 | 0,06862 | 0,06732 | 0,06139 | 0,08295 | 0,07469 |
| 532,84932 | 0,07252 | 0,07156 | 0,06545 | 0,08642 | 0,07807 |
| 532,8865 | 0,07686 | 0,07635 | 0,07009 | 0,08989 | 0,08156 |
| 532,92368 | 0,08153 | 0,08157 | 0,07521 | 0,09336 | 0,08517 |
| 532,96086 | 0,08641 | 0,08709 | 0,08067 | 0,09682 | 0,08889 |
| 532,99804 | 0,09136 | 0,09273 | 0,08632 | 0,10026 | 0,09269 |
| 533,03523 | 0,0962 | 0,09832 | 0,09197 | 0,10366 | 0,09655 |
| 533,07241 | 0,10077 | 0,10367 | 0,09744 | 0,10696 | 0,10037 |
| 533,10959 | 0,1049 | 0,10856 | 0,10253 | 0,11005 | 0,10404 |
| 533,14677 | 0,10839 | 0,11277 | 0,10702 | 0,11275 | 0,10734 |
| 533,18395 | 0,11101 | 0,11605 | 0,11064 | 0,11491 | 0,11009 |
| 533,22114 | 0,1127 | 0,1183 | 0,11329 | 0,11633 | 0,11208 |
| 533,25832 | 0,11339 | 0,11943 | 0,11486 | 0,11682 | 0,11309 |
| 533,2955 | 0,11302 | 0,11937 | 0,11527 | 0,11622 | 0,11297 |
| 533,33268 | 0,1116 | 0,1181 | 0,1145 | 0,11441 | 0,11159 |
| 533,36986 | 0,10915 | 0,11565 | 0,11255 | 0,11136 | 0,10891 |
| 533,40705 | 0,10575 | 0,1121 | 0,1095 | 0,10709 | 0,10495 |
| 533,44423 | 0,10152 | 0,10757 | 0,10544 | 0,10172 | 0,09983 |
| 533,48141 | 0,09658 | 0,10221 | 0,10051 | 0,09542 | 0,09373 |
| 533,51859 | 0,09108 | 0,09615 | 0,09484 | 0,08843 | 0,08688 |
| 533,55577 | 0,08521 | 0,08966 | 0,08868 | 0,08107 | 0,07962 |
| 533,59295 | 0,07918 | 0,08296 | 0,08225 | 0,0737 | 0,07229 |
| 533,63014 | 0,07314 | 0,07624 | 0,07574 | 0,06657 | 0,06517 |
| 533,66732 | 0,06724 | 0,06967 | 0,06933 | 0,05993 | 0,05849 |
| 533,7045 | 0,06159 | 0,06341 | 0,06316 | 0,05398 | 0,05245 |
| 533,74168 | 0,05629 | 0,05757 | 0,05736 | 0,04883 | 0,04718 |
| 533,77886 | 0,05143 | 0,05225 | 0,05203 | 0,04457 | 0,04275 |
| 533,81605 | 0,04705 | 0,04751 | 0,04724 | 0,04121 | 0,03917 |
| 533,85323 | 0,04319 | 0,04339 | 0,04303 | 0,03871 | 0,03642 |
| 533,89041 | 0,03991 | 0,03995 | 0,03949 | 0,037 | 0,03441 |
| 533,92759 | 0,03716 | 0,03713 | 0,03655 | 0,03599 | 0,03309 |
| 533,96477 | 0,03491 | 0,03487 | 0,03417 | 0,0355 | 0,03227 |
| 534,00196 | 0,03312 | 0,03311 | 0,03229 | 0,03536 | 0,0318 |
| 534,03914 | 0,03173 | 0,03179 | 0,03085 | 0,0354 | 0,03153 |
| 534,07632 | 0,0307 | 0,03084 | 0,0298 | 0,0355 | 0,03134 |
| 534,1135 | 0,02998 | 0,0302 | 0,02906 | 0,03554 | 0,03111 |
| 534,15068 | 0,0295 | 0,02978 | 0,02856 | 0,0354 | 0,03076 |
| 534,18787 | 0,02922 | 0,02953 | 0,02824 | 0,03502 | 0,03023 |
| 534,22505 | 0,02906 | 0,02939 | 0,02802 | 0,03437 | 0,02946 |
| 534,26223 | 0,02898 | 0,02929 | 0,02785 | 0,03342 | 0,02845 |
| 534,29941 | 0,02891 | 0,02918 | 0,02767 | 0,03219 | 0,02721 |
| 534,33659 | 0,02882 | 0,02902 | 0,02744 | 0,0307 | 0,02577 |
| 534,37378 | 0,02867 | 0,0288 | 0,02713 | 0,02904 | 0,0242 |
| 534,41096 | 0,02844 | 0,02848 | 0,02672 | 0,02729 | 0,02256 |
| 534,44814 | 0,0281 | 0,02807 | 0,0262 | 0,02551 | 0,02092 |
| 534,48532 | 0,02765 | 0,02756 | 0,02557 | 0,02376 | 0,01934 |
| 534,5225 | 0,02709 | 0,02695 | 0,02483 | 0,02211 | 0,01786 |
| 534,55969 | 0,02641 | 0,02624 | 0,02399 | 0,02059 | 0,01653 |
| 534,59687 | 0,02562 | 0,02545 | 0,02306 | 0,01923 | 0,01535 |
| 534,63405 | 0,02473 | 0,02458 | 0,02207 | 0,01804 | 0,01436 |
| 534,67123 | 0,02377 | 0,02366 | 0,02104 | 0,01703 | 0,01353 |
| 534,70841 | 0,02275 | 0,02271 | 0,01998 | 0,01617 | 0,01286 |
| 534,7456 | 0,0217 | 0,02172 | 0,01891 | 0,01548 | 0,01234 |
| 534,78278 | 0,02063 | 0,02073 | 0,01785 | 0,0149 | 0,01193 |
| 534,81996 | 0,01955 | 0,01973 | 0,01681 | 0,01442 | 0,01159 |
| 534,85714 | 0,0185 | 0,01874 | 0,01581 | 0,014 | 0,01132 |
| 534,89432 | 0,01747 | 0,01778 | 0,01486 | 0,01365 | 0,01108 |
| 534,93151 | 0,01649 | 0,01684 | 0,01395 | 0,01333 | 0,01086 |
| 534,96869 | 0,01556 | 0,01594 | 0,01311 | 0,01303 | 0,01064 |
| 535,00587 | 0,01471 | 0,01509 | 0,01234 | 0,01275 | 0,01042 |
| 535,04305 | 0,01392 | 0,01429 | 0,01163 | 0,01247 | 0,01019 |
| 535,08023 | 0,0132 | 0,01353 | 0,01099 | 0,01219 | 0,00996 |
| 535,11742 | 0,01255 | 0,01283 | 0,01042 | 0,01191 | 0,00971 |
| 535,1546 | 0,01197 | 0,01218 | 0,0099 | 0,01161 | 0,00946 |
| 535,19178 | 0,01146 | 0,01158 | 0,00945 | 0,0113 | 0,00921 |
| 535,22896 | 0,011 | 0,01103 | 0,00906 | 0,01098 | 0,00895 |
| 535,26614 | 0,01061 | 0,01053 | 0,00872 | 0,01065 | 0,00871 |
| 535,30333 | 0,01026 | 0,01008 | 0,00843 | 0,01031 | 0,00847 |
| 535,34051 | 0,00997 | 0,00967 | 0,0082 | 0,00997 | 0,00825 |
| 535,37769 | 0,00972 | 0,00931 | 0,00802 | 0,00962 | 0,00804 |
| 535,41487 | 0,00951 | 0,009 | 0,00787 | 0,00928 | 0,00786 |
| 535,45205 | 0,00933 | 0,00871 | 0,00777 | 0,00894 | 0,0077 |
| 535,48924 | 0,00918 | 0,00847 | 0,00771 | 0,00862 | 0,00757 |
| 535,52642 | 0,00906 | 0,00826 | 0,00768 | 0,00831 | 0,00746 |
| 535,5636 | 0,00896 | 0,00809 | 0,00768 | 0,00801 | 0,00739 |
| 535,60078 | 0,00888 | 0,00795 | 0,00771 | 0,00774 | 0,00734 |
| 535,63796 | 0,00882 | 0,00784 | 0,00777 | 0,00748 | 0,00733 |
| 535,67515 | 0,00878 | 0,00775 | 0,00786 | 0,00726 | 0,00735 |
| 535,71233 | 0,00874 | 0,0077 | 0,00797 | 0,00706 | 0,00739 |
| 535,74951 | 0,00871 | 0,00766 | 0,00809 | 0,00689 | 0,00746 |
| 535,78669 | 0,00867 | 0,00763 | 0,00824 | 0,00676 | 0,00755 |
| 535,82387 | 0,00863 | 0,00762 | 0,00839 | 0,00666 | 0,00766 |
| 535,86106 | 0,00857 | 0,0076 | 0,00855 | 0,00661 | 0,00778 |
| 535,89824 | 0,0085 | 0,00759 | 0,00872 | 0,0066 | 0,0079 |
| 535,93542 | 0,0084 | 0,00756 | 0,00888 | 0,00664 | 0,00803 |
| 535,9726 | 0,00827 | 0,00753 | 0,00905 | 0,00671 | 0,00814 |
| 536,00978 | 0,00811 | 0,00747 | 0,0092 | 0,00683 | 0,00823 |
| 536,04697 | 0,00792 | 0,0074 | 0,00935 | 0,00697 | 0,0083 |
| 536,08415 | 0,00769 | 0,00731 | 0,00947 | 0,00713 | 0,00833 |
| 536,12133 | 0,00743 | 0,00719 | 0,00957 | 0,0073 | 0,00832 |
| 536,15851 | 0,00714 | 0,00706 | 0,00963 | 0,00746 | 0,00827 |
| 536,19569 | 0,00682 | 0,0069 | 0,00967 | 0,0076 | 0,00818 |
| 536,23288 | 0,00648 | 0,00673 | 0,00966 | 0,0077 | 0,00804 |
| 536,27006 | 0,00613 | 0,00655 | 0,00962 | 0,00776 | 0,00786 |
| 536,30724 | 0,00576 | 0,00635 | 0,00952 | 0,00777 | 0,00764 |
| 536,34442 | 0,0054 | 0,00615 | 0,00939 | 0,0077 | 0,00739 |
| 536,3816 | 0,00505 | 0,00594 | 0,0092 | 0,00757 | 0,00713 |
| 536,41879 | 0,0047 | 0,00573 | 0,00897 | 0,00736 | 0,00685 |
| 536,45597 | 0,00438 | 0,00552 | 0,00869 | 0,0071 | 0,00657 |
| 536,49315 | 0,00408 | 0,00532 | 0,00838 | 0,00678 | 0,00629 |
| 536,53033 | 0,0038 | 0,00511 | 0,00805 | 0,00642 | 0,00603 |
| 536,56751 | 0,00356 | 0,00491 | 0,00769 | 0,00603 | 0,00579 |
| 536,6047 | 0,00335 | 0,00472 | 0,00731 | 0,00562 | 0,00556 |
| 536,64188 | 0,00317 | 0,00453 | 0,00692 | 0,0052 | 0,00536 |
| 536,67906 | 0,00302 | 0,00435 | 0,00653 | 0,00479 | 0,00517 |
| 536,71624 | 0,0029 | 0,00417 | 0,00615 | 0,0044 | 0,00499 |
| 536,75342 | 0,00281 | 0,004 | 0,00577 | 0,00403 | 0,00483 |
| 536,79061 | 0,00274 | 0,00384 | 0,00542 | 0,0037 | 0,00468 |
| 536,82779 | 0,00271 | 0,0037 | 0,00508 | 0,00342 | 0,00453 |
| 536,86497 | 0,00269 | 0,00356 | 0,00478 | 0,00317 | 0,00439 |
| 536,90215 | 0,00269 | 0,00344 | 0,0045 | 0,00296 | 0,00425 |
| 536,93933 | 0,0027 | 0,00334 | 0,00425 | 0,00279 | 0,00411 |
| 536,97652 | 0,00273 | 0,00325 | 0,00405 | 0,00265 | 0,00397 |
| 537,0137 | 0,00277 | 0,00319 | 0,00388 | 0,00254 | 0,00384 |
| 537,05088 | 0,00282 | 0,00315 | 0,00375 | 0,00246 | 0,00371 |
| 537,08806 | 0,00288 | 0,00314 | 0,00365 | 0,00241 | 0,0036 |
| 537,12524 | 0,00295 | 0,00314 | 0,0036 | 0,00237 | 0,0035 |
| 537,16243 | 0,00303 | 0,00318 | 0,00359 | 0,00235 | 0,00342 |
| 537,19961 | 0,00312 | 0,00323 | 0,0036 | 0,00235 | 0,00335 |
| 537,23679 | 0,00322 | 0,00329 | 0,00365 | 0,00236 | 0,00329 |
| 537,27397 | 0,00333 | 0,00337 | 0,00372 | 0,00238 | 0,00323 |
| 537,31115 | 0,00344 | 0,00346 | 0,0038 | 0,0024 | 0,00318 |
| 537,34834 | 0,00356 | 0,00356 | 0,0039 | 0,00244 | 0,00312 |
| 537,38552 | 0,00367 | 0,00365 | 0,004 | 0,00247 | 0,00306 |
| 537,4227 | 0,00378 | 0,00374 | 0,00411 | 0,00251 | 0,00299 |
| 537,45988 | 0,00388 | 0,00383 | 0,00421 | 0,00256 | 0,00292 |
| 537,49706 | 0,00397 | 0,0039 | 0,0043 | 0,00259 | 0,00284 |
| 537,53425 | 0,00404 | 0,00397 | 0,00437 | 0,00263 | 0,00276 |
| 537,57143 | 0,00408 | 0,00401 | 0,00443 | 0,00266 | 0,00269 |
| 537,60861 | 0,0041 | 0,00405 | 0,00447 | 0,00268 | 0,00262 |
| 537,64579 | 0,00409 | 0,00406 | 0,0045 | 0,0027 | 0,00258 |
| 537,68297 | 0,00406 | 0,00405 | 0,0045 | 0,00271 | 0,00256 |
| 537,72016 | 0,00399 | 0,00403 | 0,00449 | 0,00272 | 0,00257 |
| 537,75734 | 0,00389 | 0,00399 | 0,00445 | 0,00273 | 0,00261 |
| 537,79452 | 0,00377 | 0,00392 | 0,0044 | 0,00274 | 0,00267 |
| 537,8317 | 0,00362 | 0,00384 | 0,00433 | 0,00275 | 0,00275 |
| 537,86888 | 0,00346 | 0,00374 | 0,00424 | 0,00278 | 0,00285 |
| 537,90607 | 0,00328 | 0,00363 | 0,00413 | 0,00282 | 0,00296 |
| 537,94325 | 0,00309 | 0,0035 | 0,004 | 0,00288 | 0,00307 |
| 537,98043 | 0,0029 | 0,00337 | 0,00386 | 0,00296 | 0,00318 |
| 538,01761 | 0,00272 | 0,00322 | 0,00372 | 0,00306 | 0,00327 |
| 538,05479 | 0,00254 | 0,00308 | 0,00356 | 0,00317 | 0,00336 |
| 538,09198 | 0,00237 | 0,00294 | 0,00341 | 0,0033 | 0,00343 |
| 538,12916 | 0,00223 | 0,00281 | 0,00325 | 0,00342 | 0,00348 |
| 538,16634 | 0,0021 | 0,00268 | 0,00311 | 0,00355 | 0,00353 |
| 538,20352 | 0,002 | 0,00257 | 0,00298 | 0,00367 | 0,00356 |
| 538,2407 | 0,00192 | 0,00248 | 0,00287 | 0,00378 | 0,00359 |
| 538,27789 | 0,00187 | 0,0024 | 0,00279 | 0,00386 | 0,00362 |
| 538,31507 | 0,00185 | 0,00235 | 0,00274 | 0,00392 | 0,00364 |
| 538,35225 | 0,00185 | 0,00231 | 0,00272 | 0,00396 | 0,00367 |
| 538,38943 | 0,00188 | 0,00229 | 0,00273 | 0,00397 | 0,00369 |
| 538,42661 | 0,00194 | 0,00229 | 0,00278 | 0,00396 | 0,00372 |
| 538,4638 | 0,00201 | 0,0023 | 0,00286 | 0,00393 | 0,00375 |
| 538,50098 | 0,0021 | 0,00233 | 0,00296 | 0,00388 | 0,00378 |
| 538,53816 | 0,00221 | 0,00237 | 0,00309 | 0,00383 | 0,00381 |
| 538,57534 | 0,00233 | 0,00241 | 0,00322 | 0,00377 | 0,00384 |
| 538,61252 | 0,00244 | 0,00246 | 0,00336 | 0,00371 | 0,00386 |
| 538,64971 | 0,00255 | 0,00251 | 0,0035 | 0,00364 | 0,00387 |
| 538,68689 | 0,00266 | 0,00255 | 0,00361 | 0,00357 | 0,00387 |
| 538,72407 | 0,00274 | 0,00259 | 0,00371 | 0,0035 | 0,00386 |
| 538,76125 | 0,00281 | 0,00262 | 0,00377 | 0,00342 | 0,00383 |
| 538,79843 | 0,00285 | 0,00264 | 0,00379 | 0,00334 | 0,00378 |
| 538,83562 | 0,00287 | 0,00264 | 0,00378 | 0,00324 | 0,00371 |
| 538,8728 | 0,00286 | 0,00264 | 0,00372 | 0,00312 | 0,00361 |
| 538,90998 | 0,00281 | 0,00262 | 0,00362 | 0,00299 | 0,00351 |
| 538,94716 | 0,00274 | 0,00259 | 0,00348 | 0,00285 | 0,00338 |
| 538,98434 | 0,00265 | 0,00254 | 0,00331 | 0,0027 | 0,00325 |
| 539,02153 | 0,00253 | 0,00248 | 0,00311 | 0,00254 | 0,00311 |
| 539,05871 | 0,00239 | 0,00241 | 0,00289 | 0,00237 | 0,00296 |
| 539,09589 | 0,00225 | 0,00233 | 0,00266 | 0,0022 | 0,00282 |
| 539,13307 | 0,00209 | 0,00224 | 0,00243 | 0,00203 | 0,00268 |
| 539,17025 | 0,00194 | 0,00214 | 0,0022 | 0,00187 | 0,00255 |
| 539,20744 | 0,00179 | 0,00203 | 0,00199 | 0,00173 | 0,00243 |
| 539,24462 | 0,00165 | 0,00192 | 0,00179 | 0,0016 | 0,00232 |
| 539,2818 | 0,00152 | 0,00181 | 0,00162 | 0,0015 | 0,00223 |
| 539,31898 | 0,0014 | 0,0017 | 0,00148 | 0,00141 | 0,00214 |
| 539,35616 | 0,00131 | 0,00158 | 0,00138 | 0,00136 | 0,00207 |
| 539,39335 | 0,00123 | 0,00148 | 0,0013 | 0,00132 | 0,002 |
| 539,43053 | 0,00118 | 0,00137 | 0,00126 | 0,00131 | 0,00195 |
| 539,46771 | 0,00114 | 0,00128 | 0,00125 | 0,00132 | 0,0019 |
| 539,50489 | 0,00112 | 0,0012 | 0,00126 | 0,00133 | 0,00185 |
| 539,54207 | 0,00112 | 0,00113 | 0,0013 | 0,00136 | 0,0018 |
| 539,57926 | 0,00113 | 0,00107 | 0,00136 | 0,00139 | 0,00175 |
| 539,61644 | 0,00115 | 0,00102 | 0,00143 | 0,00141 | 0,0017 |
| 539,65362 | 0,00118 | 0,00098 | 0,00152 | 0,00143 | 0,00164 |
| 539,6908 | 0,00121 | 0,00096 | 0,00161 | 0,00143 | 0,00158 |
| 539,72798 | 0,00124 | 0,00095 | 0,00171 | 0,00141 | 0,00152 |
| 539,76517 | 0,00127 | 0,00095 | 0,00181 | 0,00138 | 0,00145 |
| 539,80235 | 0,0013 | 0,00095 | 0,0019 | 0,00132 | 0,00137 |
| 539,83953 | 0,00132 | 0,00097 | 0,00198 | 0,00125 | 0,00129 |
| 539,87671 | 0,00133 | 0,00098 | 0,00205 | 0,00117 | 0,00121 |
| 539,91389 | 0,00133 | 0,001 | 0,0021 | 0,00107 | 0,00112 |
| 539,95108 | 0,00132 | 0,00101 | 0,00214 | 0,00096 | 0,00104 |
| 539,98826 | 0,0013 | 0,00102 | 0,00216 | 0,00085 | 0,00095 |
| 540,02544 | 0,00127 | 0,00102 | 0,00216 | 0,00075 | 0,00086 |
| 540,06262 | 0,00122 | 0,00101 | 0,00214 | 0,00065 | 0,00078 |
| 540,0998 | 0,00117 | 0,00099 | 0,0021 | 0,00056 | 7e-04 |
| 540,13699 | 0,0011 | 0,00096 | 0,00204 | 0,00048 | 0,00063 |
| 540,17417 | 0,00103 | 0,00092 | 0,00197 | 0,00042 | 0,00057 |
| 540,21135 | 0,00096 | 0,00087 | 0,00188 | 0,00038 | 0,00051 |
| 540,24853 | 0,00088 | 0,00082 | 0,00177 | 0,00035 | 0,00047 |
| 540,28571 | 8e-04 | 0,00075 | 0,00166 | 0,00034 | 0,00045 |
| 540,3229 | 0,00073 | 0,00068 | 0,00154 | 0,00035 | 0,00043 |
| 540,36008 | 0,00065 | 0,00061 | 0,00142 | 0,00036 | 0,00043 |
| 540,39726 | 0,00058 | 0,00054 | 0,0013 | 0,00038 | 0,00045 |
| 540,43444 | 0,00052 | 0,00048 | 0,00118 | 0,00041 | 0,00048 |
| 540,47162 | 0,00046 | 0,00042 | 0,00107 | 0,00044 | 0,00052 |
| 540,50881 | 4e-04 | 0,00037 | 0,00096 | 0,00047 | 0,00056 |
| 540,54599 | 0,00035 | 0,00032 | 0,00086 | 5e-04 | 0,00062 |
| 540,58317 | 0,00031 | 0,00028 | 0,00077 | 0,00051 | 0,00067 |
| 540,62035 | 0,00027 | 0,00026 | 7e-04 | 0,00052 | 0,00072 |
| 540,65753 | 0,00023 | 0,00024 | 0,00063 | 0,00051 | 0,00077 |
| 540,69472 | 2e-04 | 0,00022 | 0,00057 | 5e-04 | 8e-04 |
| 540,7319 | 0,00017 | 0,00022 | 0,00051 | 0,00047 | 0,00083 |
| 540,76908 | 0,00014 | 0,00022 | 0,00047 | 0,00044 | 0,00084 |
| 540,80626 | 0,00012 | 0,00022 | 0,00043 | 4e-04 | 0,00084 |
| 540,84344 | 1e-04 | 0,00023 | 0,00039 | 0,00035 | 0,00083 |
| 540,88063 | 8e-05 | 0,00024 | 0,00035 | 3e-04 | 8e-04 |
| 540,91781 | 6e-05 | 0,00025 | 0,00032 | 0,00026 | 0,00076 |
| 540,95499 | 5e-05 | 0,00025 | 0,00029 | 0,00021 | 0,00072 |
| 540,99217 | 4e-05 | 0,00026 | 0,00026 | 0,00017 | 0,00068 |
| 541,02935 | 3e-05 | 0,00026 | 0,00023 | 0,00014 | 0,00063 |
| 541,06654 | 2e-05 | 0,00026 | 2e-04 | 0,00011 | 0,00059 |
| 541,10372 | 2e-05 | 0,00025 | 0,00017 | 8e-05 | 0,00055 |
| 541,1409 | 1e-05 | 0,00025 | 0,00015 | 6e-05 | 0,00052 |
| 541,17808 | 1e-05 | 0,00024 | 0,00012 | 4e-05 | 5e-04 |
| 541,21526 | 1e-05 | 0,00022 | 1e-04 | 3e-05 | 0,00047 |
| 541,25245 | 0 | 0,00021 | 8e-05 | 2e-05 | 0,00045 |
| 541,28963 | 0 | 0,00019 | 7e-05 | 1e-05 | 0,00044 |
| 541,32681 | 0 | 0,00017 | 5e-05 | 1e-05 | 0,00042 |
| 541,36399 | 0 | 0,00015 | 4e-05 | 1e-05 | 4e-04 |
| 541,40117 | 0 | 0,00013 | 3e-05 | 0 | 0,00037 |
| 541,43836 | 0 | 0,00011 | 2e-05 | 0 | 0,00034 |
| 541,47554 | 0 | 9e-05 | 2e-05 | 0 | 0,00031 |
| 541,51272 | 0 | 8e-05 | 1e-05 | 0 | 0,00028 |
| 541,5499 | 0 | 6e-05 | 1e-05 | 0 | 0,00025 |
| 541,58708 | 0 | 5e-05 | 1e-05 | 0 | 0,00021 |
| 541,62427 | 0 | 4e-05 | 0 | 0 | 0,00018 |
| 541,66145 | 0 | 3e-05 | 0 | 0 | 0,00015 |
| 541,69863 | 0 | 2e-05 | 0 | 0 | 0,00012 |
| 541,73581 | 0 | 2e-05 | 0 | 0 | 9e-05 |
| 541,77299 | 0 | 1e-05 | 0 | 0 | 7e-05 |
| 541,81018 | 0 | 1e-05 | 0 | 0 | 5e-05 |
| 541,84736 | 0 | 1e-05 | 0 | 0 | 4e-05 |
| 541,88454 | 0 | 0 | 0 | 0 | 3e-05 |
| 541,92172 | 0 | 0 | 0 | 0 | 2e-05 |
| 541,9589 | 0 | 0 | 0 | 0 | 1e-05 |
| 541,99609 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,03327 | 0 | 0 | 0 | 0 | 1e-05 |
| 542,07045 | 0 | 0 | 0 | 0 | 0 |
| 542,10763 | 0 | 0 | 0 | 0 | 0 |
| 542,14481 | 0 | 0 | 0 | 0 | 0 |
| 542,182 | 0 | 0 | 0 | 0 | 0 |
| 542,21918 | 0 | 0 | 0 | 0 | 0 |
| 542,25636 | 0 | 0 | 0 | 0 | 0 |
| 542,29354 | 0 | 0 | 0 | 0 | 0 |
| 542,33072 | 0 | 0 | 0 | 0 | 0 |
| 542,36791 | 0 | 0 | 0 | 0 | 0 |
| 542,40509 | 0 | 0 | 0 | 0 | 0 |
| 542,44227 | 0 | 0 | 0 | 0 | 0 |
| 542,47945 | 0 | 0 | 0 | 0 | 0 |
| 542,51663 | 0 | 0 | 0 | 0 | 0 |
| 542,55382 | 0 | 0 | 0 | 0 | 0 |
| 542,591 | 0 | 0 | 0 | 0 | 0 |
| 542,62818 | 0 | 0 | 0 | 0 | 0 |
| 542,66536 | 0 | 0 | 0 | 0 | 0 |
| 542,70254 | 0 | 0 | 0 | 0 | 0 |
| 542,73973 | 0 | 0 | 0 | 0 | 0 |
| 542,77691 | 0 | 0 | 0 | 0 | 0 |
| 542,81409 | 0 | 0 | 0 | 0 | 0 |
| 542,85127 | 0 | 0 | 0 | 0 | 0 |
| 542,88845 | 0 | 0 | 0 | 0 | 0 |
| 542,92564 | 0 | 0 | 0 | 0 | 0 |
| 542,96282 | 0 | 0 | 0 | 0 | 0 |
| 543 | 0 | 0 | 0 | 0 | 0 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0 | 0 | 0 | 0 | 0 |
| 524,03718 | 1e-05 | 0 | 0 | 0 | 0 |
| 524,07436 | 1e-05 | 0 | 0 | 0 | 0 |
| 524,11155 | 1e-05 | 0 | 1e-05 | 0 | 0 |
| 524,14873 | 1e-05 | 0 | 1e-05 | 0 | 0 |
| 524,18591 | 1e-05 | 0 | 1e-05 | 0 | 0 |
| 524,22309 | 2e-05 | 0 | 1e-05 | 0 | 0 |
| 524,26027 | 2e-05 | 0 | 1e-05 | 0 | 0 |
| 524,29746 | 2e-05 | 0 | 2e-05 | 0 | 0 |
| 524,33464 | 3e-05 | 0 | 2e-05 | 1e-05 | 0 |
| 524,37182 | 3e-05 | 0 | 2e-05 | 1e-05 | 0 |
| 524,409 | 4e-05 | 0 | 2e-05 | 1e-05 | 1e-05 |
| 524,44618 | 4e-05 | 0 | 3e-05 | 1e-05 | 1e-05 |
| 524,48337 | 5e-05 | 0 | 3e-05 | 1e-05 | 1e-05 |
| 524,52055 | 5e-05 | 0 | 3e-05 | 2e-05 | 1e-05 |
| 524,55773 | 6e-05 | 0 | 4e-05 | 2e-05 | 1e-05 |
| 524,59491 | 6e-05 | 0 | 4e-05 | 2e-05 | 2e-05 |
| 524,63209 | 7e-05 | 0 | 5e-05 | 2e-05 | 2e-05 |
| 524,66928 | 7e-05 | 0 | 5e-05 | 3e-05 | 2e-05 |
| 524,70646 | 8e-05 | 0 | 5e-05 | 3e-05 | 2e-05 |
| 524,74364 | 8e-05 | 0 | 6e-05 | 4e-05 | 3e-05 |
| 524,78082 | 8e-05 | 1e-05 | 6e-05 | 4e-05 | 3e-05 |
| 524,818 | 9e-05 | 1e-05 | 7e-05 | 5e-05 | 4e-05 |
| 524,85519 | 9e-05 | 1e-05 | 7e-05 | 5e-05 | 4e-05 |
| 524,89237 | 9e-05 | 1e-05 | 7e-05 | 5e-05 | 4e-05 |
| 524,92955 | 9e-05 | 1e-05 | 7e-05 | 6e-05 | 5e-05 |
| 524,96673 | 9e-05 | 2e-05 | 7e-05 | 6e-05 | 5e-05 |
| 525,00391 | 9e-05 | 2e-05 | 8e-05 | 7e-05 | 6e-05 |
| 525,0411 | 9e-05 | 2e-05 | 8e-05 | 7e-05 | 6e-05 |
| 525,07828 | 9e-05 | 3e-05 | 8e-05 | 7e-05 | 6e-05 |
| 525,11546 | 9e-05 | 3e-05 | 8e-05 | 7e-05 | 7e-05 |
| 525,15264 | 9e-05 | 4e-05 | 8e-05 | 8e-05 | 7e-05 |
| 525,18982 | 9e-05 | 4e-05 | 8e-05 | 8e-05 | 7e-05 |
| 525,22701 | 8e-05 | 5e-05 | 8e-05 | 8e-05 | 7e-05 |
| 525,26419 | 8e-05 | 5e-05 | 9e-05 | 8e-05 | 7e-05 |
| 525,30137 | 8e-05 | 6e-05 | 9e-05 | 8e-05 | 7e-05 |
| 525,33855 | 7e-05 | 6e-05 | 9e-05 | 8e-05 | 8e-05 |
| 525,37573 | 7e-05 | 7e-05 | 9e-05 | 8e-05 | 8e-05 |
| 525,41292 | 7e-05 | 7e-05 | 1e-04 | 9e-05 | 8e-05 |
| 525,4501 | 6e-05 | 8e-05 | 1e-04 | 9e-05 | 8e-05 |
| 525,48728 | 6e-05 | 8e-05 | 1e-04 | 9e-05 | 8e-05 |
| 525,52446 | 6e-05 | 9e-05 | 0,00011 | 9e-05 | 8e-05 |
| 525,56164 | 6e-05 | 1e-04 | 0,00011 | 9e-05 | 9e-05 |
| 525,59883 | 6e-05 | 1e-04 | 0,00011 | 9e-05 | 9e-05 |
| 525,63601 | 6e-05 | 0,00011 | 0,00012 | 9e-05 | 1e-04 |
| 525,67319 | 7e-05 | 0,00011 | 0,00013 | 9e-05 | 1e-04 |
| 525,71037 | 7e-05 | 0,00012 | 0,00013 | 1e-04 | 0,00011 |
| 525,74755 | 8e-05 | 0,00013 | 0,00014 | 1e-04 | 0,00012 |
| 525,78474 | 8e-05 | 0,00014 | 0,00015 | 0,00011 | 0,00013 |
| 525,82192 | 9e-05 | 0,00015 | 0,00016 | 0,00011 | 0,00014 |
| 525,8591 | 1e-04 | 0,00016 | 0,00017 | 0,00012 | 0,00015 |
| 525,89628 | 0,00011 | 0,00017 | 0,00018 | 0,00013 | 0,00017 |
| 525,93346 | 0,00013 | 0,00019 | 0,00019 | 0,00014 | 0,00019 |
| 525,97065 | 0,00015 | 0,00021 | 0,00021 | 0,00015 | 2e-04 |
| 526,00783 | 0,00016 | 0,00024 | 0,00023 | 0,00016 | 0,00023 |
| 526,04501 | 0,00019 | 0,00027 | 0,00025 | 0,00018 | 0,00025 |
| 526,08219 | 0,00021 | 3e-04 | 0,00027 | 0,00021 | 0,00027 |
| 526,11937 | 0,00024 | 0,00034 | 3e-04 | 0,00023 | 3e-04 |
| 526,15656 | 0,00027 | 0,00039 | 0,00033 | 0,00026 | 0,00032 |
| 526,19374 | 0,00031 | 0,00045 | 0,00036 | 3e-04 | 0,00035 |
| 526,23092 | 0,00035 | 0,00051 | 4e-04 | 0,00034 | 0,00039 |
| 526,2681 | 0,00039 | 0,00059 | 0,00044 | 0,00039 | 0,00042 |
| 526,30528 | 0,00045 | 0,00067 | 0,00049 | 0,00044 | 0,00046 |
| 526,34247 | 0,00051 | 0,00077 | 0,00054 | 5e-04 | 0,00051 |
| 526,37965 | 0,00057 | 0,00087 | 0,00059 | 0,00057 | 0,00055 |
| 526,41683 | 0,00065 | 0,00099 | 0,00065 | 0,00065 | 0,00061 |
| 526,45401 | 0,00073 | 0,00112 | 0,00072 | 0,00073 | 0,00067 |
| 526,49119 | 0,00083 | 0,00125 | 0,00079 | 0,00082 | 0,00073 |
| 526,52838 | 0,00093 | 0,00141 | 0,00087 | 0,00093 | 0,00081 |
| 526,56556 | 0,00105 | 0,00157 | 0,00096 | 0,00103 | 0,00089 |
| 526,60274 | 0,00118 | 0,00174 | 0,00105 | 0,00115 | 0,00098 |
| 526,63992 | 0,00132 | 0,00191 | 0,00115 | 0,00128 | 0,00108 |
| 526,6771 | 0,00147 | 0,0021 | 0,00125 | 0,00141 | 0,00119 |
| 526,71429 | 0,00164 | 0,00229 | 0,00137 | 0,00155 | 0,00131 |
| 526,75147 | 0,00182 | 0,00249 | 0,00149 | 0,00169 | 0,00144 |
| 526,78865 | 0,00201 | 0,00269 | 0,00162 | 0,00185 | 0,00158 |
| 526,82583 | 0,00222 | 0,0029 | 0,00175 | 0,00201 | 0,00172 |
| 526,86301 | 0,00244 | 0,0031 | 0,0019 | 0,00217 | 0,00188 |
| 526,9002 | 0,00267 | 0,00331 | 0,00205 | 0,00234 | 0,00205 |
| 526,93738 | 0,00292 | 0,00351 | 0,00221 | 0,00251 | 0,00222 |
| 526,97456 | 0,00317 | 0,00371 | 0,00238 | 0,00268 | 0,0024 |
| 527,01174 | 0,00344 | 0,00391 | 0,00256 | 0,00286 | 0,00258 |
| 527,04892 | 0,00371 | 0,0041 | 0,00275 | 0,00303 | 0,00277 |
| 527,08611 | 0,00399 | 0,00429 | 0,00294 | 0,00321 | 0,00296 |
| 527,12329 | 0,00428 | 0,00447 | 0,00314 | 0,00338 | 0,00316 |
| 527,16047 | 0,00457 | 0,00465 | 0,00335 | 0,00355 | 0,00335 |
| 527,19765 | 0,00487 | 0,00482 | 0,00357 | 0,00371 | 0,00355 |
| 527,23483 | 0,00517 | 0,00499 | 0,0038 | 0,00387 | 0,00375 |
| 527,27202 | 0,00547 | 0,00515 | 0,00403 | 0,00403 | 0,00395 |
| 527,3092 | 0,00577 | 0,00532 | 0,00428 | 0,00418 | 0,00414 |
| 527,34638 | 0,00607 | 0,00548 | 0,00453 | 0,00432 | 0,00434 |
| 527,38356 | 0,00637 | 0,00565 | 0,00478 | 0,00446 | 0,00454 |
| 527,42074 | 0,00666 | 0,00582 | 0,00505 | 0,00459 | 0,00474 |
| 527,45793 | 0,00696 | 0,00599 | 0,00532 | 0,00471 | 0,00495 |
| 527,49511 | 0,00726 | 0,00617 | 0,0056 | 0,00483 | 0,00516 |
| 527,53229 | 0,00755 | 0,00636 | 0,00588 | 0,00495 | 0,00537 |
| 527,56947 | 0,00785 | 0,00655 | 0,00618 | 0,00506 | 0,00559 |
| 527,60665 | 0,00814 | 0,00676 | 0,00648 | 0,00517 | 0,00582 |
| 527,64384 | 0,00844 | 0,00698 | 0,00678 | 0,00527 | 0,00605 |
| 527,68102 | 0,00873 | 0,00721 | 0,00709 | 0,00538 | 0,00629 |
| 527,7182 | 0,00903 | 0,00746 | 0,0074 | 0,00548 | 0,00655 |
| 527,75538 | 0,00934 | 0,00772 | 0,00772 | 0,00559 | 0,00681 |
| 527,79256 | 0,00964 | 0,00799 | 0,00804 | 0,0057 | 0,00708 |
| 527,82975 | 0,00995 | 0,00827 | 0,00836 | 0,00582 | 0,00737 |
| 527,86693 | 0,01027 | 0,00856 | 0,00868 | 0,00595 | 0,00766 |
| 527,90411 | 0,01059 | 0,00887 | 0,00899 | 0,00609 | 0,00796 |
| 527,94129 | 0,01091 | 0,00917 | 0,00931 | 0,00623 | 0,00827 |
| 527,97847 | 0,01124 | 0,00949 | 0,00962 | 0,0064 | 0,00858 |
| 528,01566 | 0,01157 | 0,0098 | 0,00992 | 0,00657 | 0,0089 |
| 528,05284 | 0,01191 | 0,01011 | 0,01022 | 0,00676 | 0,00921 |
| 528,09002 | 0,01224 | 0,01043 | 0,0105 | 0,00696 | 0,00953 |
| 528,1272 | 0,01257 | 0,01073 | 0,01078 | 0,00718 | 0,00985 |
| 528,16438 | 0,01291 | 0,01103 | 0,01104 | 0,00742 | 0,01016 |
| 528,20157 | 0,01323 | 0,01131 | 0,0113 | 0,00767 | 0,01047 |
| 528,23875 | 0,01356 | 0,01159 | 0,01154 | 0,00793 | 0,01077 |
| 528,27593 | 0,01387 | 0,01185 | 0,01178 | 0,00821 | 0,01106 |
| 528,31311 | 0,01418 | 0,01209 | 0,012 | 0,0085 | 0,01135 |
| 528,35029 | 0,01447 | 0,01233 | 0,01221 | 0,00879 | 0,01162 |
| 528,38748 | 0,01476 | 0,01255 | 0,01241 | 0,0091 | 0,01188 |
| 528,42466 | 0,01503 | 0,01275 | 0,01261 | 0,00941 | 0,01213 |
| 528,46184 | 0,01528 | 0,01294 | 0,0128 | 0,00972 | 0,01237 |
| 528,49902 | 0,01552 | 0,01312 | 0,01299 | 0,01004 | 0,01261 |
| 528,5362 | 0,01575 | 0,01328 | 0,01317 | 0,01035 | 0,01283 |
| 528,57339 | 0,01596 | 0,01344 | 0,01336 | 0,01067 | 0,01305 |
| 528,61057 | 0,01615 | 0,01359 | 0,01355 | 0,01099 | 0,01327 |
| 528,64775 | 0,01633 | 0,01374 | 0,01374 | 0,0113 | 0,01348 |
| 528,68493 | 0,0165 | 0,01388 | 0,01394 | 0,01161 | 0,01369 |
| 528,72211 | 0,01666 | 0,01402 | 0,01414 | 0,01193 | 0,0139 |
| 528,7593 | 0,01681 | 0,01417 | 0,01436 | 0,01224 | 0,01412 |
| 528,79648 | 0,01695 | 0,01432 | 0,01458 | 0,01255 | 0,01434 |
| 528,83366 | 0,01709 | 0,01447 | 0,01481 | 0,01285 | 0,01457 |
| 528,87084 | 0,01723 | 0,01463 | 0,01506 | 0,01317 | 0,01481 |
| 528,90802 | 0,01737 | 0,0148 | 0,01532 | 0,01348 | 0,01506 |
| 528,94521 | 0,01752 | 0,01499 | 0,01558 | 0,01379 | 0,01532 |
| 528,98239 | 0,01768 | 0,01518 | 0,01586 | 0,01411 | 0,0156 |
| 529,01957 | 0,01784 | 0,01539 | 0,01614 | 0,01443 | 0,0159 |
| 529,05675 | 0,01801 | 0,01562 | 0,01643 | 0,01476 | 0,01621 |
| 529,09393 | 0,0182 | 0,01587 | 0,01674 | 0,01509 | 0,01655 |
| 529,13112 | 0,0184 | 0,01614 | 0,01705 | 0,01543 | 0,0169 |
| 529,1683 | 0,01861 | 0,01643 | 0,01737 | 0,01577 | 0,01728 |
| 529,20548 | 0,01884 | 0,01673 | 0,0177 | 0,01612 | 0,01768 |
| 529,24266 | 0,01909 | 0,01706 | 0,01804 | 0,01648 | 0,0181 |
| 529,27984 | 0,01936 | 0,01741 | 0,01839 | 0,01685 | 0,01855 |
| 529,31703 | 0,01965 | 0,01779 | 0,01876 | 0,01722 | 0,01902 |
| 529,35421 | 0,01996 | 0,01818 | 0,01913 | 0,0176 | 0,01951 |
| 529,39139 | 0,02029 | 0,0186 | 0,01953 | 0,01799 | 0,02003 |
| 529,42857 | 0,02065 | 0,01905 | 0,01994 | 0,0184 | 0,02057 |
| 529,46575 | 0,02103 | 0,01951 | 0,02038 | 0,01882 | 0,02114 |
| 529,50294 | 0,02144 | 0,02 | 0,02084 | 0,01925 | 0,02173 |
| 529,54012 | 0,02188 | 0,02051 | 0,02133 | 0,0197 | 0,02235 |
| 529,5773 | 0,02235 | 0,02105 | 0,02185 | 0,02017 | 0,02299 |
| 529,61448 | 0,02286 | 0,02161 | 0,02239 | 0,02066 | 0,02365 |
| 529,65166 | 0,02341 | 0,0222 | 0,02297 | 0,02118 | 0,02433 |
| 529,68885 | 0,024 | 0,02281 | 0,0236 | 0,02172 | 0,02504 |
| 529,72603 | 0,02463 | 0,02344 | 0,02426 | 0,0223 | 0,02577 |
| 529,76321 | 0,02532 | 0,0241 | 0,02496 | 0,0229 | 0,02652 |
| 529,80039 | 0,02606 | 0,02478 | 0,0257 | 0,02354 | 0,02729 |
| 529,83757 | 0,02685 | 0,02548 | 0,02649 | 0,02421 | 0,02808 |
| 529,87476 | 0,02769 | 0,0262 | 0,02731 | 0,02492 | 0,02889 |
| 529,91194 | 0,02859 | 0,02695 | 0,02817 | 0,02567 | 0,02971 |
| 529,94912 | 0,02954 | 0,02772 | 0,02908 | 0,02646 | 0,03055 |
| 529,9863 | 0,03055 | 0,0285 | 0,03004 | 0,02728 | 0,03141 |
| 530,02348 | 0,0316 | 0,02931 | 0,03103 | 0,02815 | 0,03228 |
| 530,06067 | 0,03272 | 0,03014 | 0,03205 | 0,02904 | 0,03316 |
| 530,09785 | 0,03388 | 0,03099 | 0,03311 | 0,02998 | 0,03406 |
| 530,13503 | 0,03509 | 0,03187 | 0,03421 | 0,03095 | 0,03497 |
| 530,17221 | 0,03633 | 0,03277 | 0,03533 | 0,03195 | 0,03589 |
| 530,20939 | 0,03761 | 0,03369 | 0,03648 | 0,03299 | 0,03681 |
| 530,24658 | 0,03892 | 0,03464 | 0,03766 | 0,03406 | 0,03775 |
| 530,28376 | 0,04024 | 0,03562 | 0,03885 | 0,03516 | 0,03868 |
| 530,32094 | 0,04158 | 0,03663 | 0,04006 | 0,03629 | 0,03963 |
| 530,35812 | 0,04293 | 0,03767 | 0,04128 | 0,03744 | 0,04057 |
| 530,3953 | 0,04428 | 0,03874 | 0,04252 | 0,03861 | 0,04151 |
| 530,43249 | 0,04561 | 0,03985 | 0,04375 | 0,03981 | 0,04245 |
| 530,46967 | 0,04694 | 0,04099 | 0,04498 | 0,04103 | 0,04338 |
| 530,50685 | 0,04823 | 0,04217 | 0,04621 | 0,04226 | 0,04431 |
| 530,54403 | 0,04951 | 0,04337 | 0,04743 | 0,0435 | 0,04523 |
| 530,58121 | 0,05074 | 0,0446 | 0,04863 | 0,04475 | 0,04614 |
| 530,6184 | 0,05193 | 0,04585 | 0,04982 | 0,046 | 0,04703 |
| 530,65558 | 0,05307 | 0,04712 | 0,05098 | 0,04724 | 0,04792 |
| 530,69276 | 0,05415 | 0,04842 | 0,05212 | 0,04848 | 0,04879 |
| 530,72994 | 0,05518 | 0,04972 | 0,05322 | 0,0497 | 0,04964 |
| 530,76712 | 0,05614 | 0,05102 | 0,0543 | 0,05089 | 0,05048 |
| 530,80431 | 0,05704 | 0,05232 | 0,05533 | 0,05206 | 0,0513 |
| 530,84149 | 0,05788 | 0,05362 | 0,05632 | 0,05319 | 0,0521 |
| 530,87867 | 0,05866 | 0,0549 | 0,05728 | 0,05429 | 0,05288 |
| 530,91585 | 0,05937 | 0,05616 | 0,05819 | 0,05534 | 0,05364 |
| 530,95303 | 0,06002 | 0,0574 | 0,05906 | 0,05634 | 0,05438 |
| 530,99022 | 0,06061 | 0,05861 | 0,05989 | 0,05728 | 0,0551 |
| 531,0274 | 0,06116 | 0,05978 | 0,06068 | 0,05817 | 0,05579 |
| 531,06458 | 0,06166 | 0,06092 | 0,06143 | 0,05901 | 0,05647 |
| 531,10176 | 0,06214 | 0,06202 | 0,06213 | 0,0598 | 0,05712 |
| 531,13894 | 0,06259 | 0,06308 | 0,0628 | 0,06054 | 0,05776 |
| 531,17613 | 0,06302 | 0,06411 | 0,06344 | 0,06124 | 0,05838 |
| 531,21331 | 0,06345 | 0,0651 | 0,06405 | 0,0619 | 0,05898 |
| 531,25049 | 0,06389 | 0,06605 | 0,06464 | 0,06253 | 0,05958 |
| 531,28767 | 0,06434 | 0,06697 | 0,06522 | 0,06313 | 0,06017 |
| 531,32485 | 0,06482 | 0,06787 | 0,06578 | 0,06372 | 0,06076 |
| 531,36204 | 0,06533 | 0,06875 | 0,06634 | 0,0643 | 0,06136 |
| 531,39922 | 0,06589 | 0,06961 | 0,0669 | 0,06488 | 0,06196 |
| 531,4364 | 0,06649 | 0,07046 | 0,06746 | 0,06547 | 0,06259 |
| 531,47358 | 0,06715 | 0,07131 | 0,06805 | 0,06609 | 0,06323 |
| 531,51076 | 0,06789 | 0,07216 | 0,06865 | 0,06673 | 0,0639 |
| 531,54795 | 0,06869 | 0,07302 | 0,06928 | 0,06741 | 0,0646 |
| 531,58513 | 0,06957 | 0,07389 | 0,06994 | 0,06814 | 0,06534 |
| 531,62231 | 0,07052 | 0,07477 | 0,07064 | 0,06891 | 0,06613 |
| 531,65949 | 0,07154 | 0,07567 | 0,07138 | 0,06975 | 0,06696 |
| 531,69667 | 0,07264 | 0,0766 | 0,07217 | 0,07065 | 0,06784 |
| 531,73386 | 0,07381 | 0,07754 | 0,07301 | 0,07161 | 0,06876 |
| 531,77104 | 0,07505 | 0,0785 | 0,07389 | 0,07263 | 0,06973 |
| 531,80822 | 0,07637 | 0,07948 | 0,07483 | 0,07373 | 0,07075 |
| 531,8454 | 0,07774 | 0,08048 | 0,07581 | 0,07491 | 0,07181 |
| 531,88258 | 0,07915 | 0,08149 | 0,07685 | 0,07615 | 0,07291 |
| 531,91977 | 0,08061 | 0,0825 | 0,07794 | 0,07745 | 0,07405 |
| 531,95695 | 0,08209 | 0,08352 | 0,07907 | 0,07881 | 0,07523 |
| 531,99413 | 0,08358 | 0,08454 | 0,08024 | 0,08023 | 0,07642 |
| 532,03131 | 0,08508 | 0,08555 | 0,08145 | 0,08168 | 0,07763 |
| 532,06849 | 0,08656 | 0,08654 | 0,08268 | 0,08318 | 0,07885 |
| 532,10568 | 0,08801 | 0,08751 | 0,08393 | 0,08469 | 0,08008 |
| 532,14286 | 0,08942 | 0,08845 | 0,08519 | 0,08622 | 0,0813 |
| 532,18004 | 0,09076 | 0,08935 | 0,08646 | 0,08775 | 0,08251 |
| 532,21722 | 0,09203 | 0,09021 | 0,08772 | 0,08926 | 0,08371 |
| 532,2544 | 0,09322 | 0,09102 | 0,08895 | 0,09074 | 0,08488 |
| 532,29159 | 0,09431 | 0,09177 | 0,09016 | 0,09218 | 0,08602 |
| 532,32877 | 0,0953 | 0,09245 | 0,09133 | 0,09358 | 0,08714 |
| 532,36595 | 0,09616 | 0,09307 | 0,09245 | 0,09491 | 0,08822 |
| 532,40313 | 0,0969 | 0,0936 | 0,0935 | 0,09616 | 0,08926 |
| 532,44031 | 0,09752 | 0,09405 | 0,09448 | 0,09732 | 0,09025 |
| 532,4775 | 0,09802 | 0,09442 | 0,09537 | 0,09839 | 0,0912 |
| 532,51468 | 0,0984 | 0,0947 | 0,09617 | 0,09938 | 0,09211 |
| 532,55186 | 0,09866 | 0,09489 | 0,09687 | 0,10027 | 0,09298 |
| 532,58904 | 0,09882 | 0,095 | 0,09748 | 0,10106 | 0,0938 |
| 532,62622 | 0,09887 | 0,09502 | 0,09798 | 0,10177 | 0,09459 |
| 532,66341 | 0,09882 | 0,09496 | 0,09837 | 0,10237 | 0,09534 |
| 532,70059 | 0,09869 | 0,09482 | 0,09863 | 0,10288 | 0,09605 |
| 532,73777 | 0,09848 | 0,09462 | 0,09879 | 0,10331 | 0,09673 |
| 532,77495 | 0,09822 | 0,09436 | 0,09883 | 0,10367 | 0,09739 |
| 532,81213 | 0,09791 | 0,09406 | 0,09878 | 0,10397 | 0,09804 |
| 532,84932 | 0,09756 | 0,09372 | 0,09862 | 0,10421 | 0,09867 |
| 532,8865 | 0,09719 | 0,09335 | 0,09838 | 0,10441 | 0,0993 |
| 532,92368 | 0,09681 | 0,09297 | 0,09804 | 0,10458 | 0,09994 |
| 532,96086 | 0,09642 | 0,09259 | 0,09763 | 0,10473 | 0,10058 |
| 532,99804 | 0,09604 | 0,09221 | 0,09715 | 0,10487 | 0,10126 |
| 533,03523 | 0,09567 | 0,09185 | 0,09661 | 0,10501 | 0,10196 |
| 533,07241 | 0,09533 | 0,09151 | 0,09602 | 0,10517 | 0,10269 |
| 533,10959 | 0,09502 | 0,09121 | 0,0954 | 0,10535 | 0,10347 |
| 533,14677 | 0,09474 | 0,09094 | 0,09476 | 0,10556 | 0,10429 |
| 533,18395 | 0,09451 | 0,09072 | 0,09411 | 0,1058 | 0,10516 |
| 533,22114 | 0,09432 | 0,09054 | 0,09346 | 0,10609 | 0,10609 |
| 533,25832 | 0,09418 | 0,09043 | 0,09282 | 0,10644 | 0,10706 |
| 533,2955 | 0,0941 | 0,09036 | 0,09221 | 0,10683 | 0,10809 |
| 533,33268 | 0,09407 | 0,09035 | 0,09164 | 0,10727 | 0,10916 |
| 533,36986 | 0,09409 | 0,0904 | 0,09111 | 0,10776 | 0,11026 |
| 533,40705 | 0,09417 | 0,0905 | 0,09064 | 0,10829 | 0,1114 |
| 533,44423 | 0,0943 | 0,09066 | 0,09023 | 0,10887 | 0,11254 |
| 533,48141 | 0,0945 | 0,09088 | 0,08989 | 0,10947 | 0,1137 |
| 533,51859 | 0,09475 | 0,09116 | 0,08964 | 0,11011 | 0,11485 |
| 533,55577 | 0,09506 | 0,09151 | 0,08949 | 0,11076 | 0,11597 |
| 533,59295 | 0,09543 | 0,09191 | 0,08942 | 0,11142 | 0,11705 |
| 533,63014 | 0,09586 | 0,09238 | 0,08945 | 0,11207 | 0,11809 |
| 533,66732 | 0,09634 | 0,0929 | 0,08957 | 0,11271 | 0,11907 |
| 533,7045 | 0,09687 | 0,09348 | 0,0898 | 0,11333 | 0,11997 |
| 533,74168 | 0,09745 | 0,09411 | 0,09011 | 0,11391 | 0,12079 |
| 533,77886 | 0,09808 | 0,0948 | 0,09053 | 0,11445 | 0,12151 |
| 533,81605 | 0,09875 | 0,09554 | 0,09105 | 0,11494 | 0,12211 |
| 533,85323 | 0,09946 | 0,09632 | 0,09165 | 0,11536 | 0,1226 |
| 533,89041 | 0,1002 | 0,09714 | 0,09233 | 0,11572 | 0,12298 |
| 533,92759 | 0,10097 | 0,098 | 0,09308 | 0,116 | 0,12325 |
| 533,96477 | 0,10175 | 0,09887 | 0,09389 | 0,11621 | 0,12339 |
| 534,00196 | 0,10254 | 0,09976 | 0,09474 | 0,11634 | 0,12342 |
| 534,03914 | 0,10332 | 0,10066 | 0,09564 | 0,11639 | 0,12333 |
| 534,07632 | 0,1041 | 0,10155 | 0,09657 | 0,11636 | 0,12311 |
| 534,1135 | 0,10486 | 0,10243 | 0,0975 | 0,11622 | 0,12277 |
| 534,15068 | 0,10558 | 0,10327 | 0,09843 | 0,11601 | 0,12233 |
| 534,18787 | 0,10626 | 0,10408 | 0,09934 | 0,11572 | 0,12179 |
| 534,22505 | 0,10688 | 0,10485 | 0,10022 | 0,11534 | 0,12116 |
| 534,26223 | 0,10745 | 0,10556 | 0,10105 | 0,11489 | 0,12044 |
| 534,29941 | 0,10795 | 0,1062 | 0,10183 | 0,11437 | 0,11963 |
| 534,33659 | 0,10837 | 0,10677 | 0,10253 | 0,11377 | 0,11875 |
| 534,37378 | 0,10872 | 0,10726 | 0,10315 | 0,1131 | 0,11779 |
| 534,41096 | 0,10896 | 0,10765 | 0,10368 | 0,11237 | 0,11678 |
| 534,44814 | 0,10912 | 0,10795 | 0,10411 | 0,11157 | 0,11572 |
| 534,48532 | 0,10919 | 0,10816 | 0,10445 | 0,11073 | 0,11462 |
| 534,5225 | 0,10918 | 0,10828 | 0,10469 | 0,10984 | 0,11348 |
| 534,55969 | 0,10909 | 0,10831 | 0,10483 | 0,10891 | 0,11232 |
| 534,59687 | 0,10892 | 0,10825 | 0,10488 | 0,10796 | 0,11114 |
| 534,63405 | 0,10869 | 0,10812 | 0,10482 | 0,10697 | 0,10996 |
| 534,67123 | 0,1084 | 0,10789 | 0,10467 | 0,10597 | 0,10877 |
| 534,70841 | 0,10806 | 0,1076 | 0,10445 | 0,10498 | 0,10759 |
| 534,7456 | 0,1077 | 0,10727 | 0,10416 | 0,10399 | 0,10643 |
| 534,78278 | 0,10731 | 0,10688 | 0,10382 | 0,10302 | 0,10529 |
| 534,81996 | 0,10694 | 0,10648 | 0,10343 | 0,10208 | 0,10418 |
| 534,85714 | 0,10657 | 0,10605 | 0,10302 | 0,10119 | 0,10311 |
| 534,89432 | 0,10624 | 0,10562 | 0,10258 | 0,10035 | 0,1021 |
| 534,93151 | 0,10596 | 0,10521 | 0,10214 | 0,09959 | 0,10115 |
| 534,96869 | 0,10576 | 0,10484 | 0,10171 | 0,09892 | 0,10026 |
| 535,00587 | 0,10565 | 0,10451 | 0,10131 | 0,09834 | 0,09944 |
| 535,04305 | 0,10564 | 0,10425 | 0,10095 | 0,09787 | 0,0987 |
| 535,08023 | 0,10576 | 0,10406 | 0,10064 | 0,09751 | 0,09804 |
| 535,11742 | 0,10601 | 0,10397 | 0,10039 | 0,09727 | 0,09748 |
| 535,1546 | 0,10641 | 0,10399 | 0,10021 | 0,09716 | 0,09702 |
| 535,19178 | 0,10697 | 0,10412 | 0,10014 | 0,09719 | 0,09667 |
| 535,22896 | 0,1077 | 0,10442 | 0,10015 | 0,09738 | 0,09643 |
| 535,26614 | 0,10863 | 0,10485 | 0,10028 | 0,09772 | 0,09631 |
| 535,30333 | 0,10974 | 0,10545 | 0,10051 | 0,09819 | 0,0963 |
| 535,34051 | 0,11104 | 0,1062 | 0,10086 | 0,09881 | 0,09641 |
| 535,37769 | 0,11252 | 0,10711 | 0,10134 | 0,09957 | 0,09664 |
| 535,41487 | 0,11417 | 0,1082 | 0,10194 | 0,10046 | 0,09698 |
| 535,45205 | 0,11599 | 0,10945 | 0,1027 | 0,10149 | 0,09747 |
| 535,48924 | 0,11797 | 0,11088 | 0,10359 | 0,10265 | 0,09807 |
| 535,52642 | 0,1201 | 0,11249 | 0,10462 | 0,10394 | 0,09879 |
| 535,5636 | 0,12238 | 0,11425 | 0,10578 | 0,10534 | 0,09961 |
| 535,60078 | 0,12477 | 0,11615 | 0,10707 | 0,10684 | 0,10054 |
| 535,63796 | 0,12725 | 0,11818 | 0,10848 | 0,10844 | 0,10156 |
| 535,67515 | 0,12981 | 0,12033 | 0,11002 | 0,11011 | 0,10267 |
| 535,71233 | 0,13243 | 0,12258 | 0,11167 | 0,11185 | 0,10387 |
| 535,74951 | 0,13508 | 0,12492 | 0,11344 | 0,11366 | 0,10513 |
| 535,78669 | 0,13774 | 0,12732 | 0,1153 | 0,11551 | 0,10646 |
| 535,82387 | 0,14039 | 0,12976 | 0,11724 | 0,11741 | 0,10782 |
| 535,86106 | 0,143 | 0,13221 | 0,11925 | 0,11933 | 0,10923 |
| 535,89824 | 0,14556 | 0,13466 | 0,12131 | 0,12126 | 0,11065 |
| 535,93542 | 0,14804 | 0,13707 | 0,12342 | 0,12319 | 0,11209 |
| 535,9726 | 0,15043 | 0,13944 | 0,12555 | 0,12511 | 0,11353 |
| 536,00978 | 0,15271 | 0,14173 | 0,12769 | 0,127 | 0,11496 |
| 536,04697 | 0,15487 | 0,14393 | 0,12983 | 0,12887 | 0,11636 |
| 536,08415 | 0,15688 | 0,146 | 0,13194 | 0,13068 | 0,11774 |
| 536,12133 | 0,15872 | 0,14794 | 0,13402 | 0,13244 | 0,11909 |
| 536,15851 | 0,16038 | 0,14973 | 0,13605 | 0,13414 | 0,12039 |
| 536,19569 | 0,16185 | 0,15136 | 0,13803 | 0,13576 | 0,12165 |
| 536,23288 | 0,16312 | 0,15283 | 0,13992 | 0,13731 | 0,12285 |
| 536,27006 | 0,1642 | 0,15413 | 0,14173 | 0,13877 | 0,12399 |
| 536,30724 | 0,16506 | 0,15524 | 0,14342 | 0,14014 | 0,12507 |
| 536,34442 | 0,16571 | 0,15615 | 0,14501 | 0,14141 | 0,1261 |
| 536,3816 | 0,16612 | 0,15687 | 0,14648 | 0,14257 | 0,12706 |
| 536,41879 | 0,16629 | 0,1574 | 0,14783 | 0,14362 | 0,12795 |
| 536,45597 | 0,1662 | 0,15774 | 0,14904 | 0,14456 | 0,12879 |
| 536,49315 | 0,16589 | 0,15791 | 0,15012 | 0,14539 | 0,12956 |
| 536,53033 | 0,16534 | 0,1579 | 0,15105 | 0,1461 | 0,13026 |
| 536,56751 | 0,16457 | 0,15773 | 0,15181 | 0,1467 | 0,13089 |
| 536,6047 | 0,16357 | 0,15739 | 0,15242 | 0,14717 | 0,13146 |
| 536,64188 | 0,16236 | 0,15686 | 0,15287 | 0,1475 | 0,13195 |
| 536,67906 | 0,16094 | 0,15619 | 0,15317 | 0,1477 | 0,13238 |
| 536,71624 | 0,1593 | 0,15538 | 0,15332 | 0,14777 | 0,13273 |
| 536,75342 | 0,15748 | 0,15443 | 0,15331 | 0,14771 | 0,13302 |
| 536,79061 | 0,15551 | 0,15336 | 0,15315 | 0,14751 | 0,13322 |
| 536,82779 | 0,15339 | 0,15216 | 0,1528 | 0,14718 | 0,13334 |
| 536,86497 | 0,15115 | 0,15086 | 0,15231 | 0,14671 | 0,13338 |
| 536,90215 | 0,14881 | 0,14945 | 0,15168 | 0,14609 | 0,13335 |
| 536,93933 | 0,14637 | 0,14794 | 0,15091 | 0,14532 | 0,13323 |
| 536,97652 | 0,14387 | 0,14635 | 0,15 | 0,14441 | 0,13303 |
| 537,0137 | 0,14132 | 0,14469 | 0,14897 | 0,14338 | 0,13275 |
| 537,05088 | 0,13874 | 0,14297 | 0,14781 | 0,14222 | 0,13239 |
| 537,08806 | 0,13616 | 0,14119 | 0,14653 | 0,14094 | 0,13193 |
| 537,12524 | 0,13358 | 0,13936 | 0,14513 | 0,13954 | 0,1314 |
| 537,16243 | 0,13103 | 0,1375 | 0,14363 | 0,13804 | 0,13079 |
| 537,19961 | 0,12851 | 0,13561 | 0,14204 | 0,13643 | 0,13011 |
| 537,23679 | 0,12604 | 0,13371 | 0,14036 | 0,13474 | 0,12937 |
| 537,27397 | 0,12362 | 0,1318 | 0,13861 | 0,13299 | 0,12856 |
| 537,31115 | 0,12129 | 0,12989 | 0,13678 | 0,13117 | 0,12769 |
| 537,34834 | 0,11903 | 0,12798 | 0,13488 | 0,12931 | 0,12677 |
| 537,38552 | 0,11686 | 0,1261 | 0,13292 | 0,12743 | 0,1258 |
| 537,4227 | 0,11477 | 0,12423 | 0,13092 | 0,12552 | 0,1248 |
| 537,45988 | 0,11278 | 0,12238 | 0,12888 | 0,12361 | 0,12377 |
| 537,49706 | 0,11088 | 0,12057 | 0,12682 | 0,12171 | 0,12272 |
| 537,53425 | 0,10909 | 0,1188 | 0,12473 | 0,11983 | 0,12166 |
| 537,57143 | 0,1074 | 0,11706 | 0,12264 | 0,11798 | 0,12059 |
| 537,60861 | 0,10582 | 0,11535 | 0,12056 | 0,11618 | 0,11953 |
| 537,64579 | 0,10434 | 0,11369 | 0,11849 | 0,11442 | 0,11847 |
| 537,68297 | 0,10297 | 0,11207 | 0,11645 | 0,11271 | 0,11743 |
| 537,72016 | 0,10168 | 0,11048 | 0,11445 | 0,11106 | 0,11641 |
| 537,75734 | 0,10049 | 0,10894 | 0,1125 | 0,10948 | 0,11541 |
| 537,79452 | 0,09939 | 0,10744 | 0,11061 | 0,10797 | 0,11443 |
| 537,8317 | 0,09837 | 0,10598 | 0,10878 | 0,10653 | 0,11348 |
| 537,86888 | 0,09743 | 0,10455 | 0,10704 | 0,10516 | 0,11256 |
| 537,90607 | 0,09656 | 0,10316 | 0,10539 | 0,10385 | 0,11166 |
| 537,94325 | 0,09574 | 0,10181 | 0,10383 | 0,10261 | 0,11078 |
| 537,98043 | 0,09496 | 0,10049 | 0,10237 | 0,10143 | 0,10991 |
| 538,01761 | 0,09421 | 0,09919 | 0,101 | 0,1003 | 0,10906 |
| 538,05479 | 0,09349 | 0,09793 | 0,09973 | 0,09923 | 0,10821 |
| 538,09198 | 0,09277 | 0,0967 | 0,09855 | 0,0982 | 0,10736 |
| 538,12916 | 0,09204 | 0,09549 | 0,09745 | 0,09722 | 0,10651 |
| 538,16634 | 0,09129 | 0,0943 | 0,09644 | 0,09626 | 0,10564 |
| 538,20352 | 0,09051 | 0,09312 | 0,09551 | 0,09532 | 0,10475 |
| 538,2407 | 0,08969 | 0,09196 | 0,09464 | 0,0944 | 0,10382 |
| 538,27789 | 0,08881 | 0,09081 | 0,09383 | 0,09349 | 0,10286 |
| 538,31507 | 0,08788 | 0,08966 | 0,09305 | 0,09257 | 0,10186 |
| 538,35225 | 0,08687 | 0,08852 | 0,0923 | 0,09165 | 0,10081 |
| 538,38943 | 0,0858 | 0,08736 | 0,09156 | 0,09071 | 0,09971 |
| 538,42661 | 0,08464 | 0,0862 | 0,09083 | 0,08974 | 0,09855 |
| 538,4638 | 0,08339 | 0,08502 | 0,09008 | 0,08875 | 0,09733 |
| 538,50098 | 0,08206 | 0,08382 | 0,08931 | 0,08772 | 0,09605 |
| 538,53816 | 0,08065 | 0,08259 | 0,08851 | 0,08666 | 0,0947 |
| 538,57534 | 0,07916 | 0,08134 | 0,08766 | 0,08555 | 0,0933 |
| 538,61252 | 0,0776 | 0,08005 | 0,08676 | 0,08439 | 0,09184 |
| 538,64971 | 0,07597 | 0,07872 | 0,0858 | 0,08317 | 0,09032 |
| 538,68689 | 0,07427 | 0,07736 | 0,08478 | 0,08191 | 0,08876 |
| 538,72407 | 0,0725 | 0,07595 | 0,08368 | 0,08059 | 0,08714 |
| 538,76125 | 0,07068 | 0,07451 | 0,08251 | 0,07923 | 0,08548 |
| 538,79843 | 0,06882 | 0,07304 | 0,08125 | 0,07781 | 0,08378 |
| 538,83562 | 0,06692 | 0,07153 | 0,07993 | 0,07634 | 0,08206 |
| 538,8728 | 0,06499 | 0,06999 | 0,07852 | 0,07483 | 0,08031 |
| 538,90998 | 0,06305 | 0,06842 | 0,07705 | 0,07326 | 0,07855 |
| 538,94716 | 0,06109 | 0,06683 | 0,07551 | 0,07166 | 0,07677 |
| 538,98434 | 0,05912 | 0,06522 | 0,07391 | 0,07003 | 0,07498 |
| 539,02153 | 0,05716 | 0,0636 | 0,07223 | 0,06837 | 0,0732 |
| 539,05871 | 0,05522 | 0,06198 | 0,0705 | 0,06669 | 0,07142 |
| 539,09589 | 0,05329 | 0,06035 | 0,06873 | 0,06499 | 0,06965 |
| 539,13307 | 0,0514 | 0,05874 | 0,06692 | 0,06329 | 0,06789 |
| 539,17025 | 0,04954 | 0,05714 | 0,06508 | 0,0616 | 0,06615 |
| 539,20744 | 0,04773 | 0,05555 | 0,06321 | 0,05991 | 0,06444 |
| 539,24462 | 0,04597 | 0,05399 | 0,06133 | 0,05824 | 0,06275 |
| 539,2818 | 0,04427 | 0,05246 | 0,05944 | 0,05661 | 0,06109 |
| 539,31898 | 0,04264 | 0,05096 | 0,05756 | 0,055 | 0,05947 |
| 539,35616 | 0,04109 | 0,04949 | 0,05568 | 0,05344 | 0,05789 |
| 539,39335 | 0,03961 | 0,04805 | 0,05383 | 0,05192 | 0,05635 |
| 539,43053 | 0,0382 | 0,04666 | 0,05201 | 0,05045 | 0,05486 |
| 539,46771 | 0,03688 | 0,04531 | 0,05022 | 0,04906 | 0,05342 |
| 539,50489 | 0,03563 | 0,044 | 0,04848 | 0,04773 | 0,05202 |
| 539,54207 | 0,03447 | 0,04274 | 0,04679 | 0,04646 | 0,05069 |
| 539,57926 | 0,03339 | 0,04152 | 0,04518 | 0,04527 | 0,04942 |
| 539,61644 | 0,0324 | 0,04035 | 0,04362 | 0,04415 | 0,04821 |
| 539,65362 | 0,03149 | 0,03923 | 0,04215 | 0,04311 | 0,04706 |
| 539,6908 | 0,03064 | 0,03815 | 0,04074 | 0,04214 | 0,04597 |
| 539,72798 | 0,02987 | 0,03713 | 0,03942 | 0,04126 | 0,04495 |
| 539,76517 | 0,02916 | 0,03617 | 0,03819 | 0,04045 | 0,04398 |
| 539,80235 | 0,02851 | 0,03526 | 0,03704 | 0,03972 | 0,04308 |
| 539,83953 | 0,02791 | 0,0344 | 0,036 | 0,03905 | 0,04223 |
| 539,87671 | 0,02737 | 0,0336 | 0,03505 | 0,03844 | 0,04144 |
| 539,91389 | 0,02687 | 0,03286 | 0,03419 | 0,03789 | 0,04069 |
| 539,95108 | 0,02642 | 0,03217 | 0,03342 | 0,03739 | 0,03998 |
| 539,98826 | 0,02599 | 0,03154 | 0,03273 | 0,03692 | 0,0393 |
| 540,02544 | 0,0256 | 0,03098 | 0,03213 | 0,03649 | 0,03865 |
| 540,06262 | 0,02522 | 0,03048 | 0,03161 | 0,03607 | 0,03802 |
| 540,0998 | 0,02487 | 0,03003 | 0,03116 | 0,03565 | 0,03739 |
| 540,13699 | 0,02453 | 0,02964 | 0,03079 | 0,03523 | 0,03676 |
| 540,17417 | 0,0242 | 0,02929 | 0,03047 | 0,03478 | 0,03611 |
| 540,21135 | 0,02388 | 0,02899 | 0,03021 | 0,0343 | 0,03545 |
| 540,24853 | 0,02356 | 0,02872 | 0,02998 | 0,03378 | 0,03475 |
| 540,28571 | 0,02324 | 0,02849 | 0,02978 | 0,0332 | 0,03402 |
| 540,3229 | 0,02291 | 0,02829 | 0,0296 | 0,03255 | 0,03325 |
| 540,36008 | 0,02257 | 0,02811 | 0,02943 | 0,03183 | 0,03243 |
| 540,39726 | 0,02222 | 0,02793 | 0,02926 | 0,03103 | 0,03155 |
| 540,43444 | 0,02186 | 0,02775 | 0,02908 | 0,03016 | 0,03061 |
| 540,47162 | 0,02147 | 0,02756 | 0,02887 | 0,02921 | 0,02963 |
| 540,50881 | 0,02106 | 0,02735 | 0,02864 | 0,02819 | 0,02859 |
| 540,54599 | 0,02062 | 0,02712 | 0,02837 | 0,0271 | 0,0275 |
| 540,58317 | 0,02016 | 0,02683 | 0,02806 | 0,02594 | 0,02637 |
| 540,62035 | 0,01967 | 0,0265 | 0,02769 | 0,02472 | 0,02519 |
| 540,65753 | 0,01914 | 0,02612 | 0,02727 | 0,02346 | 0,02398 |
| 540,69472 | 0,01859 | 0,02567 | 0,02679 | 0,02217 | 0,02275 |
| 540,7319 | 0,01801 | 0,02516 | 0,02624 | 0,02086 | 0,0215 |
| 540,76908 | 0,01739 | 0,02458 | 0,02564 | 0,01954 | 0,02025 |
| 540,80626 | 0,01674 | 0,02393 | 0,02498 | 0,01823 | 0,01901 |
| 540,84344 | 0,01606 | 0,02321 | 0,02425 | 0,01694 | 0,01777 |
| 540,88063 | 0,01535 | 0,02241 | 0,02348 | 0,01569 | 0,01656 |
| 540,91781 | 0,01463 | 0,02155 | 0,02264 | 0,01447 | 0,01539 |
| 540,95499 | 0,01388 | 0,02063 | 0,02176 | 0,01331 | 0,01426 |
| 540,99217 | 0,01313 | 0,01966 | 0,02084 | 0,01221 | 0,01318 |
| 541,02935 | 0,01236 | 0,01865 | 0,01988 | 0,01117 | 0,01215 |
| 541,06654 | 0,01159 | 0,01761 | 0,01889 | 0,0102 | 0,01117 |
| 541,10372 | 0,01081 | 0,01653 | 0,01789 | 0,00929 | 0,01026 |
| 541,1409 | 0,01005 | 0,01544 | 0,01687 | 0,00847 | 0,00941 |
| 541,17808 | 0,0093 | 0,01435 | 0,01585 | 0,00772 | 0,00863 |
| 541,21526 | 0,00857 | 0,01327 | 0,01483 | 0,00704 | 0,00791 |
| 541,25245 | 0,00786 | 0,0122 | 0,01383 | 0,00642 | 0,00726 |
| 541,28963 | 0,00718 | 0,01116 | 0,01284 | 0,00587 | 0,00667 |
| 541,32681 | 0,00653 | 0,01016 | 0,01189 | 0,00537 | 0,00613 |
| 541,36399 | 0,00593 | 0,00919 | 0,01097 | 0,00493 | 0,00564 |
| 541,40117 | 0,00536 | 0,00828 | 0,01008 | 0,00454 | 0,00521 |
| 541,43836 | 0,00483 | 0,00743 | 0,00924 | 0,0042 | 0,00482 |
| 541,47554 | 0,00434 | 0,00663 | 0,00845 | 0,0039 | 0,00448 |
| 541,51272 | 0,00389 | 0,0059 | 0,00772 | 0,00364 | 0,00418 |
| 541,5499 | 0,00349 | 0,00524 | 0,00703 | 0,0034 | 0,00391 |
| 541,58708 | 0,00312 | 0,00463 | 0,0064 | 0,0032 | 0,00367 |
| 541,62427 | 0,0028 | 0,00409 | 0,00583 | 0,00302 | 0,00346 |
| 541,66145 | 0,00252 | 0,00361 | 0,0053 | 0,00286 | 0,00326 |
| 541,69863 | 0,00228 | 0,00318 | 0,00482 | 0,00272 | 0,00309 |
| 541,73581 | 0,00207 | 0,00282 | 0,0044 | 0,00259 | 0,00294 |
| 541,77299 | 0,00189 | 0,00251 | 0,00402 | 0,00249 | 0,0028 |
| 541,81018 | 0,00173 | 0,00225 | 0,00369 | 0,00239 | 0,00267 |
| 541,84736 | 0,0016 | 0,00202 | 0,00339 | 0,0023 | 0,00255 |
| 541,88454 | 0,00149 | 0,00184 | 0,00313 | 0,00221 | 0,00244 |
| 541,92172 | 0,0014 | 0,00169 | 0,00289 | 0,00213 | 0,00233 |
| 541,9589 | 0,00133 | 0,00156 | 0,00269 | 0,00206 | 0,00223 |
| 541,99609 | 0,00126 | 0,00146 | 0,00251 | 0,00198 | 0,00213 |
| 542,03327 | 0,00121 | 0,00139 | 0,00235 | 0,00191 | 0,00203 |
| 542,07045 | 0,00117 | 0,00133 | 0,00221 | 0,00184 | 0,00194 |
| 542,10763 | 0,00113 | 0,00128 | 0,00208 | 0,00176 | 0,00184 |
| 542,14481 | 0,00109 | 0,00124 | 0,00197 | 0,00169 | 0,00175 |
| 542,182 | 0,00106 | 0,00121 | 0,00186 | 0,00161 | 0,00165 |
| 542,21918 | 0,00102 | 0,00118 | 0,00177 | 0,00153 | 0,00156 |
| 542,25636 | 0,00099 | 0,00115 | 0,00168 | 0,00144 | 0,00147 |
| 542,29354 | 0,00096 | 0,00113 | 0,0016 | 0,00136 | 0,00138 |
| 542,33072 | 0,00092 | 0,00111 | 0,00152 | 0,00127 | 0,00129 |
| 542,36791 | 0,00089 | 0,00108 | 0,00145 | 0,00118 | 0,0012 |
| 542,40509 | 0,00085 | 0,00105 | 0,00138 | 0,0011 | 0,00111 |
| 542,44227 | 0,00081 | 0,00102 | 0,00131 | 0,00101 | 0,00102 |
| 542,47945 | 0,00077 | 0,00099 | 0,00124 | 0,00092 | 0,00094 |
| 542,51663 | 0,00072 | 0,00095 | 0,00118 | 0,00084 | 0,00086 |
| 542,55382 | 0,00068 | 0,00091 | 0,00111 | 0,00076 | 0,00078 |
| 542,591 | 0,00063 | 0,00087 | 0,00105 | 0,00068 | 0,00071 |
| 542,62818 | 0,00059 | 0,00082 | 0,00099 | 0,00061 | 0,00064 |
| 542,66536 | 0,00054 | 0,00078 | 0,00093 | 0,00054 | 0,00058 |
| 542,70254 | 5e-04 | 0,00073 | 0,00087 | 0,00048 | 0,00052 |
| 542,73973 | 0,00046 | 0,00068 | 0,00081 | 0,00042 | 0,00046 |
| 542,77691 | 0,00042 | 0,00063 | 0,00075 | 0,00037 | 0,00041 |
| 542,81409 | 0,00038 | 0,00058 | 7e-04 | 0,00032 | 0,00036 |
| 542,85127 | 0,00034 | 0,00053 | 0,00064 | 0,00028 | 0,00031 |
| 542,88845 | 3e-04 | 0,00048 | 0,00059 | 0,00024 | 0,00027 |
| 542,92564 | 0,00027 | 0,00043 | 0,00054 | 2e-04 | 0,00024 |
| 542,96282 | 0,00024 | 0,00038 | 0,00049 | 0,00017 | 2e-04 |
| 543 | 0,00021 | 0,00034 | 0,00044 | 0,00015 | 0,00018 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00018 | 0,00018 | 8e-05 | 3e-05 | 2e-05 |
| 524,03718 | 0,00019 | 0,00018 | 8e-05 | 3e-05 | 3e-05 |
| 524,07436 | 2e-04 | 0,00019 | 8e-05 | 3e-05 | 3e-05 |
| 524,11155 | 0,00021 | 0,00019 | 9e-05 | 4e-05 | 3e-05 |
| 524,14873 | 0,00021 | 0,00019 | 9e-05 | 4e-05 | 3e-05 |
| 524,18591 | 0,00022 | 0,00019 | 9e-05 | 4e-05 | 4e-05 |
| 524,22309 | 0,00022 | 2e-04 | 1e-04 | 5e-05 | 4e-05 |
| 524,26027 | 0,00023 | 2e-04 | 1e-04 | 5e-05 | 4e-05 |
| 524,29746 | 0,00023 | 0,00019 | 0,00011 | 5e-05 | 4e-05 |
| 524,33464 | 0,00023 | 0,00019 | 0,00011 | 6e-05 | 5e-05 |
| 524,37182 | 0,00023 | 0,00019 | 0,00011 | 6e-05 | 5e-05 |
| 524,409 | 0,00023 | 0,00019 | 0,00012 | 6e-05 | 5e-05 |
| 524,44618 | 0,00024 | 0,00019 | 0,00012 | 7e-05 | 5e-05 |
| 524,48337 | 0,00024 | 0,00019 | 0,00013 | 7e-05 | 5e-05 |
| 524,52055 | 0,00024 | 0,00019 | 0,00014 | 7e-05 | 6e-05 |
| 524,55773 | 0,00024 | 0,00019 | 0,00014 | 8e-05 | 6e-05 |
| 524,59491 | 0,00025 | 0,00019 | 0,00015 | 8e-05 | 6e-05 |
| 524,63209 | 0,00025 | 0,00019 | 0,00015 | 8e-05 | 6e-05 |
| 524,66928 | 0,00025 | 0,00019 | 0,00016 | 9e-05 | 6e-05 |
| 524,70646 | 0,00026 | 2e-04 | 0,00017 | 9e-05 | 6e-05 |
| 524,74364 | 0,00027 | 2e-04 | 0,00017 | 1e-04 | 7e-05 |
| 524,78082 | 0,00027 | 0,00021 | 0,00018 | 1e-04 | 7e-05 |
| 524,818 | 0,00028 | 0,00022 | 0,00019 | 0,00011 | 7e-05 |
| 524,85519 | 0,00029 | 0,00023 | 2e-04 | 0,00011 | 7e-05 |
| 524,89237 | 3e-04 | 0,00024 | 2e-04 | 0,00011 | 7e-05 |
| 524,92955 | 0,00031 | 0,00025 | 0,00021 | 0,00012 | 8e-05 |
| 524,96673 | 0,00032 | 0,00026 | 0,00022 | 0,00012 | 8e-05 |
| 525,00391 | 0,00034 | 0,00028 | 0,00023 | 0,00013 | 8e-05 |
| 525,0411 | 0,00035 | 3e-04 | 0,00024 | 0,00013 | 8e-05 |
| 525,07828 | 0,00037 | 0,00031 | 0,00025 | 0,00013 | 8e-05 |
| 525,11546 | 0,00039 | 0,00033 | 0,00026 | 0,00014 | 9e-05 |
| 525,15264 | 0,00042 | 0,00035 | 0,00028 | 0,00015 | 9e-05 |
| 525,18982 | 0,00044 | 0,00037 | 0,00029 | 0,00015 | 1e-04 |
| 525,22701 | 0,00047 | 0,00039 | 0,00031 | 0,00016 | 1e-04 |
| 525,26419 | 0,00051 | 0,00042 | 0,00033 | 0,00017 | 0,00011 |
| 525,30137 | 0,00055 | 0,00045 | 0,00036 | 0,00018 | 0,00012 |
| 525,33855 | 6e-04 | 0,00048 | 0,00038 | 2e-04 | 0,00013 |
| 525,37573 | 0,00066 | 0,00051 | 0,00042 | 0,00022 | 0,00015 |
| 525,41292 | 0,00072 | 0,00055 | 0,00046 | 0,00024 | 0,00017 |
| 525,4501 | 0,00079 | 0,00059 | 5e-04 | 0,00027 | 0,00019 |
| 525,48728 | 0,00087 | 0,00064 | 0,00055 | 0,00031 | 0,00022 |
| 525,52446 | 0,00096 | 7e-04 | 0,00061 | 0,00035 | 0,00026 |
| 525,56164 | 0,00107 | 0,00076 | 0,00068 | 0,00041 | 0,00031 |
| 525,59883 | 0,00118 | 0,00083 | 0,00075 | 0,00047 | 0,00036 |
| 525,63601 | 0,0013 | 0,00091 | 0,00083 | 0,00055 | 0,00043 |
| 525,67319 | 0,00143 | 0,00099 | 0,00092 | 0,00063 | 0,00051 |
| 525,71037 | 0,00158 | 0,00109 | 0,00102 | 0,00074 | 6e-04 |
| 525,74755 | 0,00173 | 0,00119 | 0,00112 | 0,00086 | 0,00071 |
| 525,78474 | 0,00189 | 0,00131 | 0,00123 | 0,001 | 0,00083 |
| 525,82192 | 0,00206 | 0,00143 | 0,00135 | 0,00115 | 0,00097 |
| 525,8591 | 0,00224 | 0,00156 | 0,00147 | 0,00132 | 0,00112 |
| 525,89628 | 0,00243 | 0,0017 | 0,0016 | 0,00151 | 0,0013 |
| 525,93346 | 0,00262 | 0,00185 | 0,00174 | 0,00172 | 0,00148 |
| 525,97065 | 0,00283 | 0,00201 | 0,00188 | 0,00194 | 0,00169 |
| 526,00783 | 0,00304 | 0,00217 | 0,00203 | 0,00218 | 0,00191 |
| 526,04501 | 0,00326 | 0,00235 | 0,00218 | 0,00244 | 0,00214 |
| 526,08219 | 0,00349 | 0,00254 | 0,00234 | 0,00271 | 0,00238 |
| 526,11937 | 0,00372 | 0,00273 | 0,00251 | 0,003 | 0,00264 |
| 526,15656 | 0,00397 | 0,00294 | 0,00268 | 0,00329 | 0,0029 |
| 526,19374 | 0,00423 | 0,00315 | 0,00286 | 0,00358 | 0,00316 |
| 526,23092 | 0,00449 | 0,00338 | 0,00305 | 0,00388 | 0,00342 |
| 526,2681 | 0,00477 | 0,00361 | 0,00326 | 0,00418 | 0,00368 |
| 526,30528 | 0,00505 | 0,00386 | 0,00347 | 0,00446 | 0,00392 |
| 526,34247 | 0,00535 | 0,00412 | 0,00369 | 0,00474 | 0,00416 |
| 526,37965 | 0,00565 | 0,00439 | 0,00392 | 0,00499 | 0,00438 |
| 526,41683 | 0,00596 | 0,00466 | 0,00415 | 0,00523 | 0,00458 |
| 526,45401 | 0,00628 | 0,00494 | 0,0044 | 0,00544 | 0,00475 |
| 526,49119 | 0,00659 | 0,00522 | 0,00465 | 0,00562 | 0,0049 |
| 526,52838 | 0,00691 | 0,00551 | 0,00491 | 0,00578 | 0,00502 |
| 526,56556 | 0,00722 | 0,0058 | 0,00517 | 0,0059 | 0,00512 |
| 526,60274 | 0,00754 | 0,00609 | 0,00543 | 0,00598 | 0,00518 |
| 526,63992 | 0,00784 | 0,00637 | 0,00569 | 0,00604 | 0,00522 |
| 526,6771 | 0,00814 | 0,00665 | 0,00594 | 0,00607 | 0,00524 |
| 526,71429 | 0,00842 | 0,00692 | 0,00618 | 0,00607 | 0,00523 |
| 526,75147 | 0,0087 | 0,00718 | 0,00642 | 0,00604 | 0,00521 |
| 526,78865 | 0,00896 | 0,00744 | 0,00665 | 0,006 | 0,00517 |
| 526,82583 | 0,00921 | 0,00768 | 0,00686 | 0,00595 | 0,00512 |
| 526,86301 | 0,00946 | 0,00792 | 0,00707 | 0,00589 | 0,00506 |
| 526,9002 | 0,0097 | 0,00816 | 0,00727 | 0,00582 | 0,005 |
| 526,93738 | 0,00993 | 0,00839 | 0,00746 | 0,00576 | 0,00495 |
| 526,97456 | 0,01016 | 0,00862 | 0,00765 | 0,00571 | 0,0049 |
| 527,01174 | 0,01039 | 0,00885 | 0,00784 | 0,00567 | 0,00487 |
| 527,04892 | 0,01063 | 0,00908 | 0,00803 | 0,00565 | 0,00485 |
| 527,08611 | 0,01088 | 0,00932 | 0,00823 | 0,00565 | 0,00484 |
| 527,12329 | 0,01114 | 0,00957 | 0,00844 | 0,00568 | 0,00486 |
| 527,16047 | 0,01143 | 0,00984 | 0,00868 | 0,00573 | 0,0049 |
| 527,19765 | 0,01173 | 0,01013 | 0,00893 | 0,00581 | 0,00496 |
| 527,23483 | 0,01205 | 0,01044 | 0,00921 | 0,00593 | 0,00505 |
| 527,27202 | 0,01241 | 0,01077 | 0,00952 | 0,00608 | 0,00517 |
| 527,3092 | 0,01279 | 0,01113 | 0,00986 | 0,00627 | 0,00531 |
| 527,34638 | 0,01322 | 0,01152 | 0,01024 | 0,00649 | 0,00549 |
| 527,38356 | 0,01368 | 0,01195 | 0,01066 | 0,00676 | 0,00571 |
| 527,42074 | 0,01418 | 0,01241 | 0,01113 | 0,00707 | 0,00596 |
| 527,45793 | 0,01471 | 0,01291 | 0,01165 | 0,00742 | 0,00625 |
| 527,49511 | 0,01528 | 0,01344 | 0,01221 | 0,00783 | 0,00659 |
| 527,53229 | 0,01589 | 0,01402 | 0,01281 | 0,00829 | 0,00697 |
| 527,56947 | 0,01653 | 0,01462 | 0,01345 | 0,0088 | 0,0074 |
| 527,60665 | 0,01721 | 0,01526 | 0,01414 | 0,00937 | 0,00788 |
| 527,64384 | 0,01792 | 0,01593 | 0,01485 | 0,01 | 0,00842 |
| 527,68102 | 0,01864 | 0,01662 | 0,0156 | 0,01068 | 0,00901 |
| 527,7182 | 0,01938 | 0,01733 | 0,01638 | 0,01142 | 0,00967 |
| 527,75538 | 0,02013 | 0,01805 | 0,01716 | 0,01223 | 0,01039 |
| 527,79256 | 0,02088 | 0,01877 | 0,01796 | 0,01309 | 0,01117 |
| 527,82975 | 0,02163 | 0,0195 | 0,01875 | 0,01402 | 0,01201 |
| 527,86693 | 0,02237 | 0,02021 | 0,01953 | 0,01499 | 0,01289 |
| 527,90411 | 0,02308 | 0,0209 | 0,02029 | 0,01601 | 0,01383 |
| 527,94129 | 0,02377 | 0,02158 | 0,02103 | 0,01706 | 0,01481 |
| 527,97847 | 0,02443 | 0,02222 | 0,02172 | 0,01813 | 0,01582 |
| 528,01566 | 0,02505 | 0,02284 | 0,02238 | 0,01922 | 0,01687 |
| 528,05284 | 0,02564 | 0,02341 | 0,02299 | 0,02032 | 0,01792 |
| 528,09002 | 0,02619 | 0,02394 | 0,02356 | 0,0214 | 0,01896 |
| 528,1272 | 0,0267 | 0,02444 | 0,02408 | 0,02245 | 0,01999 |
| 528,16438 | 0,02717 | 0,02489 | 0,02455 | 0,02346 | 0,021 |
| 528,20157 | 0,0276 | 0,02531 | 0,02497 | 0,02441 | 0,02195 |
| 528,23875 | 0,028 | 0,0257 | 0,02535 | 0,0253 | 0,02285 |
| 528,27593 | 0,02836 | 0,02606 | 0,02568 | 0,02611 | 0,02369 |
| 528,31311 | 0,0287 | 0,02638 | 0,02598 | 0,02682 | 0,02444 |
| 528,35029 | 0,02901 | 0,02669 | 0,02625 | 0,02745 | 0,02509 |
| 528,38748 | 0,02931 | 0,02697 | 0,02649 | 0,02798 | 0,02566 |
| 528,42466 | 0,02959 | 0,02724 | 0,02671 | 0,0284 | 0,02613 |
| 528,46184 | 0,02986 | 0,0275 | 0,02692 | 0,02873 | 0,02652 |
| 528,49902 | 0,03012 | 0,02776 | 0,02712 | 0,02897 | 0,02683 |
| 528,5362 | 0,03038 | 0,02801 | 0,02732 | 0,02915 | 0,02707 |
| 528,57339 | 0,03064 | 0,02826 | 0,02751 | 0,02926 | 0,02724 |
| 528,61057 | 0,03091 | 0,02851 | 0,02771 | 0,02933 | 0,02736 |
| 528,64775 | 0,03119 | 0,02877 | 0,02792 | 0,02936 | 0,02746 |
| 528,68493 | 0,03147 | 0,02903 | 0,02813 | 0,02938 | 0,02753 |
| 528,72211 | 0,03177 | 0,0293 | 0,02836 | 0,02939 | 0,02761 |
| 528,7593 | 0,03208 | 0,02957 | 0,02859 | 0,02941 | 0,0277 |
| 528,79648 | 0,03239 | 0,02985 | 0,02883 | 0,02945 | 0,02781 |
| 528,83366 | 0,03272 | 0,03013 | 0,02908 | 0,02951 | 0,02794 |
| 528,87084 | 0,03305 | 0,0304 | 0,02934 | 0,02959 | 0,02811 |
| 528,90802 | 0,03338 | 0,03067 | 0,02959 | 0,02971 | 0,0283 |
| 528,94521 | 0,03371 | 0,03094 | 0,02984 | 0,02984 | 0,02852 |
| 528,98239 | 0,03403 | 0,03119 | 0,03009 | 0,02999 | 0,02876 |
| 529,01957 | 0,03435 | 0,03142 | 0,03031 | 0,03015 | 0,029 |
| 529,05675 | 0,03465 | 0,03163 | 0,03053 | 0,03031 | 0,02925 |
| 529,09393 | 0,03494 | 0,03182 | 0,03072 | 0,03046 | 0,02947 |
| 529,13112 | 0,0352 | 0,03199 | 0,03089 | 0,03058 | 0,02968 |
| 529,1683 | 0,03545 | 0,03213 | 0,03103 | 0,03069 | 0,02985 |
| 529,20548 | 0,03568 | 0,03225 | 0,03115 | 0,03076 | 0,02999 |
| 529,24266 | 0,03589 | 0,03234 | 0,03125 | 0,0308 | 0,03008 |
| 529,27984 | 0,03608 | 0,03241 | 0,03133 | 0,0308 | 0,03013 |
| 529,31703 | 0,03626 | 0,03247 | 0,0314 | 0,03077 | 0,03013 |
| 529,35421 | 0,03643 | 0,03253 | 0,03147 | 0,03072 | 0,03011 |
| 529,39139 | 0,03659 | 0,03258 | 0,03153 | 0,03065 | 0,03006 |
| 529,42857 | 0,03677 | 0,03265 | 0,03161 | 0,03057 | 0,03 |
| 529,46575 | 0,03695 | 0,03274 | 0,03172 | 0,03049 | 0,02993 |
| 529,50294 | 0,03715 | 0,03286 | 0,03186 | 0,03042 | 0,02987 |
| 529,54012 | 0,03737 | 0,03303 | 0,03204 | 0,03037 | 0,02984 |
| 529,5773 | 0,03764 | 0,03325 | 0,03226 | 0,03036 | 0,02984 |
| 529,61448 | 0,03794 | 0,03353 | 0,03255 | 0,03039 | 0,02988 |
| 529,65166 | 0,03829 | 0,03387 | 0,0329 | 0,03048 | 0,02999 |
| 529,68885 | 0,03869 | 0,03428 | 0,03332 | 0,03064 | 0,03016 |
| 529,72603 | 0,03914 | 0,03477 | 0,03382 | 0,03086 | 0,0304 |
| 529,76321 | 0,03964 | 0,03534 | 0,03439 | 0,03116 | 0,03072 |
| 529,80039 | 0,04019 | 0,03599 | 0,03504 | 0,03155 | 0,03113 |
| 529,83757 | 0,04079 | 0,03671 | 0,03575 | 0,03202 | 0,03164 |
| 529,87476 | 0,04144 | 0,0375 | 0,03652 | 0,03258 | 0,03225 |
| 529,91194 | 0,04213 | 0,03834 | 0,03734 | 0,03326 | 0,03296 |
| 529,94912 | 0,04284 | 0,03924 | 0,03821 | 0,03403 | 0,03378 |
| 529,9863 | 0,04358 | 0,04017 | 0,03912 | 0,03491 | 0,03469 |
| 530,02348 | 0,04432 | 0,04113 | 0,04005 | 0,03588 | 0,03571 |
| 530,06067 | 0,04505 | 0,0421 | 0,04099 | 0,03694 | 0,03682 |
| 530,09785 | 0,04578 | 0,04306 | 0,04192 | 0,03809 | 0,03802 |
| 530,13503 | 0,04647 | 0,04399 | 0,04283 | 0,03931 | 0,03931 |
| 530,17221 | 0,04713 | 0,04489 | 0,04371 | 0,04059 | 0,04066 |
| 530,20939 | 0,04772 | 0,04574 | 0,04453 | 0,04193 | 0,04206 |
| 530,24658 | 0,04825 | 0,04652 | 0,0453 | 0,04328 | 0,04349 |
| 530,28376 | 0,04871 | 0,04722 | 0,04599 | 0,04463 | 0,04491 |
| 530,32094 | 0,04908 | 0,04782 | 0,04658 | 0,04595 | 0,0463 |
| 530,35812 | 0,04936 | 0,0483 | 0,04707 | 0,04721 | 0,04762 |
| 530,3953 | 0,04954 | 0,04866 | 0,04745 | 0,04839 | 0,04886 |
| 530,43249 | 0,04959 | 0,04889 | 0,04771 | 0,04945 | 0,04998 |
| 530,46967 | 0,04954 | 0,049 | 0,04785 | 0,05038 | 0,05093 |
| 530,50685 | 0,04938 | 0,04897 | 0,04787 | 0,05113 | 0,05169 |
| 530,54403 | 0,04911 | 0,04881 | 0,04776 | 0,05169 | 0,05225 |
| 530,58121 | 0,04875 | 0,04853 | 0,04752 | 0,05204 | 0,0526 |
| 530,6184 | 0,04829 | 0,04812 | 0,04716 | 0,0522 | 0,05273 |
| 530,65558 | 0,04775 | 0,04759 | 0,04669 | 0,05216 | 0,05265 |
| 530,69276 | 0,04713 | 0,04697 | 0,04612 | 0,05193 | 0,05235 |
| 530,72994 | 0,04646 | 0,04628 | 0,04549 | 0,05151 | 0,05187 |
| 530,76712 | 0,04576 | 0,04553 | 0,04479 | 0,05094 | 0,05119 |
| 530,80431 | 0,04505 | 0,04475 | 0,04407 | 0,05023 | 0,05038 |
| 530,84149 | 0,04435 | 0,04396 | 0,04333 | 0,04942 | 0,04948 |
| 530,87867 | 0,04369 | 0,0432 | 0,04262 | 0,04856 | 0,04854 |
| 530,91585 | 0,04309 | 0,04249 | 0,04197 | 0,04769 | 0,04758 |
| 530,95303 | 0,04258 | 0,04187 | 0,04141 | 0,04684 | 0,04666 |
| 530,99022 | 0,0422 | 0,04138 | 0,04097 | 0,04606 | 0,04583 |
| 531,0274 | 0,04196 | 0,04103 | 0,04068 | 0,04538 | 0,04512 |
| 531,06458 | 0,04188 | 0,04085 | 0,04057 | 0,04485 | 0,0446 |
| 531,10176 | 0,04199 | 0,04086 | 0,04066 | 0,0445 | 0,0443 |
| 531,13894 | 0,04228 | 0,04109 | 0,04098 | 0,04439 | 0,04424 |
| 531,17613 | 0,04276 | 0,04155 | 0,04155 | 0,04451 | 0,04445 |
| 531,21331 | 0,04345 | 0,04227 | 0,0424 | 0,04487 | 0,04493 |
| 531,25049 | 0,04435 | 0,04324 | 0,0435 | 0,04548 | 0,04569 |
| 531,28767 | 0,04546 | 0,04444 | 0,04484 | 0,04634 | 0,04674 |
| 531,32485 | 0,04674 | 0,04585 | 0,04641 | 0,04745 | 0,04807 |
| 531,36204 | 0,04818 | 0,04745 | 0,04818 | 0,04878 | 0,04967 |
| 531,39922 | 0,04973 | 0,04921 | 0,05013 | 0,05034 | 0,05153 |
| 531,4364 | 0,05137 | 0,0511 | 0,05221 | 0,05208 | 0,05359 |
| 531,47358 | 0,05306 | 0,05307 | 0,05438 | 0,05397 | 0,0558 |
| 531,51076 | 0,05477 | 0,05508 | 0,05659 | 0,05594 | 0,05812 |
| 531,54795 | 0,05645 | 0,05706 | 0,05877 | 0,05795 | 0,06049 |
| 531,58513 | 0,05804 | 0,05896 | 0,06087 | 0,05996 | 0,06286 |
| 531,62231 | 0,05951 | 0,06074 | 0,06283 | 0,06192 | 0,06517 |
| 531,65949 | 0,06083 | 0,06234 | 0,06461 | 0,06376 | 0,06736 |
| 531,69667 | 0,06196 | 0,06373 | 0,06616 | 0,06544 | 0,06931 |
| 531,73386 | 0,06287 | 0,06487 | 0,06744 | 0,06687 | 0,07101 |
| 531,77104 | 0,06354 | 0,06572 | 0,06838 | 0,06803 | 0,07239 |
| 531,80822 | 0,06396 | 0,06622 | 0,06896 | 0,06889 | 0,07341 |
| 531,8454 | 0,06406 | 0,0664 | 0,0692 | 0,06941 | 0,07405 |
| 531,88258 | 0,06389 | 0,06626 | 0,06909 | 0,0696 | 0,07427 |
| 531,91977 | 0,06347 | 0,06581 | 0,06865 | 0,06943 | 0,07408 |
| 531,95695 | 0,06281 | 0,06506 | 0,06788 | 0,06892 | 0,07347 |
| 531,99413 | 0,06192 | 0,06405 | 0,0668 | 0,06808 | 0,07242 |
| 532,03131 | 0,06083 | 0,06279 | 0,06546 | 0,0669 | 0,07101 |
| 532,06849 | 0,05958 | 0,06132 | 0,06386 | 0,06548 | 0,0693 |
| 532,10568 | 0,05818 | 0,05968 | 0,06209 | 0,06386 | 0,06736 |
| 532,14286 | 0,05668 | 0,05793 | 0,06019 | 0,0621 | 0,06525 |
| 532,18004 | 0,05513 | 0,05613 | 0,05821 | 0,06027 | 0,06304 |
| 532,21722 | 0,05358 | 0,05432 | 0,05622 | 0,05843 | 0,06082 |
| 532,2544 | 0,05206 | 0,05254 | 0,05424 | 0,05663 | 0,05865 |
| 532,29159 | 0,05061 | 0,05084 | 0,05234 | 0,05496 | 0,05663 |
| 532,32877 | 0,04927 | 0,04926 | 0,05057 | 0,05348 | 0,05485 |
| 532,36595 | 0,04806 | 0,04787 | 0,04899 | 0,05225 | 0,05334 |
| 532,40313 | 0,04707 | 0,0467 | 0,04764 | 0,05131 | 0,05216 |
| 532,44031 | 0,04629 | 0,04578 | 0,04655 | 0,05067 | 0,05133 |
| 532,4775 | 0,04575 | 0,04513 | 0,04575 | 0,05035 | 0,05088 |
| 532,51468 | 0,04546 | 0,04477 | 0,04526 | 0,05038 | 0,05082 |
| 532,55186 | 0,04545 | 0,04473 | 0,04512 | 0,05075 | 0,05116 |
| 532,58904 | 0,04572 | 0,045 | 0,04533 | 0,05145 | 0,05188 |
| 532,62622 | 0,04628 | 0,04561 | 0,04591 | 0,0525 | 0,053 |
| 532,66341 | 0,04714 | 0,0466 | 0,04692 | 0,05383 | 0,05443 |
| 532,70059 | 0,04831 | 0,04792 | 0,04828 | 0,0554 | 0,05612 |
| 532,73777 | 0,04973 | 0,04953 | 0,04998 | 0,05716 | 0,05803 |
| 532,77495 | 0,05138 | 0,05141 | 0,05199 | 0,05907 | 0,06011 |
| 532,81213 | 0,05323 | 0,05353 | 0,05427 | 0,06108 | 0,06229 |
| 532,84932 | 0,05524 | 0,05583 | 0,05678 | 0,06314 | 0,06453 |
| 532,8865 | 0,05737 | 0,05829 | 0,05947 | 0,06521 | 0,06677 |
| 532,92368 | 0,05957 | 0,06083 | 0,06227 | 0,06721 | 0,06893 |
| 532,96086 | 0,06178 | 0,06339 | 0,06511 | 0,06911 | 0,07097 |
| 532,99804 | 0,06392 | 0,06588 | 0,06791 | 0,07085 | 0,07284 |
| 533,03523 | 0,06595 | 0,06825 | 0,07057 | 0,0724 | 0,0745 |
| 533,07241 | 0,06781 | 0,07042 | 0,07304 | 0,07374 | 0,0759 |
| 533,10959 | 0,06945 | 0,07234 | 0,07525 | 0,07481 | 0,07703 |
| 533,14677 | 0,07082 | 0,07396 | 0,07713 | 0,07562 | 0,07784 |
| 533,18395 | 0,07189 | 0,07522 | 0,07863 | 0,07612 | 0,07833 |
| 533,22114 | 0,07262 | 0,07607 | 0,07968 | 0,07629 | 0,07842 |
| 533,25832 | 0,07292 | 0,07644 | 0,08021 | 0,07612 | 0,07816 |
| 533,2955 | 0,07285 | 0,07637 | 0,08026 | 0,07565 | 0,07756 |
| 533,33268 | 0,07241 | 0,07588 | 0,07984 | 0,07488 | 0,07663 |
| 533,36986 | 0,07162 | 0,07497 | 0,07895 | 0,07385 | 0,07541 |
| 533,40705 | 0,07049 | 0,07366 | 0,07762 | 0,07258 | 0,07393 |
| 533,44423 | 0,06905 | 0,072 | 0,07589 | 0,0711 | 0,07223 |
| 533,48141 | 0,06735 | 0,07003 | 0,07382 | 0,06947 | 0,07036 |
| 533,51859 | 0,06541 | 0,06778 | 0,07142 | 0,06774 | 0,06838 |
| 533,55577 | 0,0633 | 0,06533 | 0,0688 | 0,06596 | 0,06636 |
| 533,59295 | 0,06108 | 0,06276 | 0,06604 | 0,06422 | 0,06439 |
| 533,63014 | 0,05882 | 0,06014 | 0,06321 | 0,06257 | 0,06253 |
| 533,66732 | 0,05657 | 0,05752 | 0,06037 | 0,06106 | 0,06084 |
| 533,7045 | 0,05438 | 0,05497 | 0,0576 | 0,05974 | 0,05937 |
| 533,74168 | 0,0523 | 0,05254 | 0,05494 | 0,05867 | 0,05819 |
| 533,77886 | 0,05038 | 0,05029 | 0,05246 | 0,05789 | 0,05733 |
| 533,81605 | 0,0487 | 0,04829 | 0,05024 | 0,05744 | 0,05685 |
| 533,85323 | 0,04729 | 0,04659 | 0,04833 | 0,05737 | 0,0568 |
| 533,89041 | 0,04616 | 0,04521 | 0,04674 | 0,05764 | 0,05716 |
| 533,92759 | 0,04535 | 0,04417 | 0,04552 | 0,05827 | 0,05791 |
| 533,96477 | 0,04488 | 0,04351 | 0,04468 | 0,05923 | 0,05904 |
| 534,00196 | 0,04476 | 0,04324 | 0,04425 | 0,0605 | 0,06053 |
| 534,03914 | 0,04502 | 0,04338 | 0,04425 | 0,06205 | 0,06234 |
| 534,07632 | 0,04567 | 0,04394 | 0,04467 | 0,06384 | 0,06442 |
| 534,1135 | 0,04673 | 0,04498 | 0,04559 | 0,06581 | 0,06672 |
| 534,15068 | 0,04815 | 0,04643 | 0,04695 | 0,06792 | 0,06917 |
| 534,18787 | 0,04991 | 0,04826 | 0,04872 | 0,07006 | 0,07169 |
| 534,22505 | 0,05197 | 0,05046 | 0,05087 | 0,07218 | 0,07418 |
| 534,26223 | 0,05431 | 0,05298 | 0,05337 | 0,0742 | 0,07657 |
| 534,29941 | 0,05688 | 0,05579 | 0,05616 | 0,07606 | 0,07878 |
| 534,33659 | 0,05962 | 0,05883 | 0,05921 | 0,0777 | 0,08074 |
| 534,37378 | 0,06249 | 0,06203 | 0,06244 | 0,07904 | 0,08237 |
| 534,41096 | 0,06539 | 0,06534 | 0,06579 | 0,08003 | 0,08363 |
| 534,44814 | 0,06825 | 0,06863 | 0,06914 | 0,08059 | 0,0844 |
| 534,48532 | 0,071 | 0,07183 | 0,0724 | 0,08071 | 0,08466 |
| 534,5225 | 0,07356 | 0,07487 | 0,07549 | 0,0804 | 0,08443 |
| 534,55969 | 0,07586 | 0,07765 | 0,07833 | 0,07965 | 0,0837 |
| 534,59687 | 0,07784 | 0,0801 | 0,08083 | 0,07846 | 0,08247 |
| 534,63405 | 0,07942 | 0,08215 | 0,08292 | 0,07687 | 0,08078 |
| 534,67123 | 0,0805 | 0,0837 | 0,08452 | 0,0749 | 0,07866 |
| 534,70841 | 0,0811 | 0,08467 | 0,0855 | 0,07259 | 0,07617 |
| 534,7456 | 0,0812 | 0,08509 | 0,0859 | 0,06996 | 0,07333 |
| 534,78278 | 0,0808 | 0,08494 | 0,08571 | 0,06714 | 0,07024 |
| 534,81996 | 0,07991 | 0,08423 | 0,08493 | 0,06419 | 0,067 |
| 534,85714 | 0,07854 | 0,08297 | 0,08359 | 0,06117 | 0,06369 |
| 534,89432 | 0,07674 | 0,0812 | 0,08172 | 0,05815 | 0,06038 |
| 534,93151 | 0,07453 | 0,07898 | 0,07938 | 0,0552 | 0,05715 |
| 534,96869 | 0,07199 | 0,07632 | 0,07662 | 0,05238 | 0,05406 |
| 535,00587 | 0,06922 | 0,07337 | 0,07352 | 0,04975 | 0,05118 |
| 535,04305 | 0,06631 | 0,07021 | 0,07022 | 0,04741 | 0,04859 |
| 535,08023 | 0,06334 | 0,06696 | 0,06682 | 0,04538 | 0,04637 |
| 535,11742 | 0,06039 | 0,0637 | 0,06341 | 0,04369 | 0,04453 |
| 535,1546 | 0,05754 | 0,06052 | 0,0601 | 0,04237 | 0,04309 |
| 535,19178 | 0,05486 | 0,05751 | 0,05697 | 0,04145 | 0,04209 |
| 535,22896 | 0,0525 | 0,05476 | 0,0541 | 0,04093 | 0,04153 |
| 535,26614 | 0,05047 | 0,0524 | 0,05161 | 0,04084 | 0,04142 |
| 535,30333 | 0,04882 | 0,05047 | 0,0496 | 0,04116 | 0,04177 |
| 535,34051 | 0,0476 | 0,049 | 0,04807 | 0,04196 | 0,04256 |
| 535,37769 | 0,04683 | 0,04803 | 0,04706 | 0,04317 | 0,04385 |
| 535,41487 | 0,04653 | 0,04759 | 0,0466 | 0,04475 | 0,04555 |
| 535,45205 | 0,04671 | 0,04768 | 0,04668 | 0,04669 | 0,04762 |
| 535,48924 | 0,04738 | 0,04829 | 0,04731 | 0,04896 | 0,05003 |
| 535,52642 | 0,04855 | 0,04942 | 0,04846 | 0,05151 | 0,05275 |
| 535,5636 | 0,05014 | 0,0511 | 0,05016 | 0,05431 | 0,05573 |
| 535,60078 | 0,05209 | 0,05321 | 0,05234 | 0,05732 | 0,05893 |
| 535,63796 | 0,05437 | 0,05568 | 0,0549 | 0,06049 | 0,06228 |
| 535,67515 | 0,05691 | 0,05846 | 0,05779 | 0,06376 | 0,06575 |
| 535,71233 | 0,05966 | 0,06147 | 0,06092 | 0,06707 | 0,06924 |
| 535,74951 | 0,06255 | 0,06465 | 0,06423 | 0,07036 | 0,07271 |
| 535,78669 | 0,06551 | 0,06792 | 0,06764 | 0,07358 | 0,07609 |
| 535,82387 | 0,06845 | 0,07118 | 0,07105 | 0,07668 | 0,07933 |
| 535,86106 | 0,07129 | 0,07435 | 0,07438 | 0,07961 | 0,08238 |
| 535,89824 | 0,07398 | 0,07733 | 0,07753 | 0,08232 | 0,08518 |
| 535,93542 | 0,07644 | 0,08006 | 0,08042 | 0,08473 | 0,08769 |
| 535,9726 | 0,07863 | 0,08248 | 0,08298 | 0,08683 | 0,08984 |
| 536,00978 | 0,08049 | 0,08452 | 0,08517 | 0,08858 | 0,0916 |
| 536,04697 | 0,08196 | 0,08615 | 0,08692 | 0,08998 | 0,09296 |
| 536,08415 | 0,08296 | 0,08732 | 0,0882 | 0,09101 | 0,09393 |
| 536,12133 | 0,08353 | 0,08795 | 0,08897 | 0,09168 | 0,0945 |
| 536,15851 | 0,08366 | 0,08804 | 0,08916 | 0,09198 | 0,09468 |
| 536,19569 | 0,08335 | 0,08764 | 0,08881 | 0,09194 | 0,0945 |
| 536,23288 | 0,08262 | 0,08675 | 0,08796 | 0,09155 | 0,09399 |
| 536,27006 | 0,08149 | 0,08541 | 0,08663 | 0,09089 | 0,09318 |
| 536,30724 | 0,07999 | 0,08366 | 0,08487 | 0,09002 | 0,09214 |
| 536,34442 | 0,07813 | 0,08153 | 0,08272 | 0,08899 | 0,09096 |
| 536,3816 | 0,076 | 0,0791 | 0,08025 | 0,08789 | 0,08971 |
| 536,41879 | 0,07367 | 0,07639 | 0,07752 | 0,08675 | 0,08846 |
| 536,45597 | 0,07121 | 0,07352 | 0,07458 | 0,08565 | 0,08729 |
| 536,49315 | 0,06869 | 0,07057 | 0,07156 | 0,08465 | 0,08626 |
| 536,53033 | 0,06616 | 0,06762 | 0,06853 | 0,0838 | 0,08543 |
| 536,56751 | 0,06369 | 0,06474 | 0,06556 | 0,08316 | 0,08482 |
| 536,6047 | 0,06136 | 0,06199 | 0,06274 | 0,08271 | 0,08452 |
| 536,64188 | 0,05925 | 0,05945 | 0,06012 | 0,08246 | 0,08446 |
| 536,67906 | 0,05741 | 0,05717 | 0,05777 | 0,08239 | 0,08463 |
| 536,71624 | 0,05586 | 0,05527 | 0,05574 | 0,08245 | 0,08497 |
| 536,75342 | 0,05466 | 0,05374 | 0,05415 | 0,0826 | 0,08542 |
| 536,79061 | 0,05381 | 0,05261 | 0,05297 | 0,08278 | 0,08589 |
| 536,82779 | 0,05334 | 0,05191 | 0,05222 | 0,0829 | 0,08631 |
| 536,86497 | 0,05324 | 0,05163 | 0,05191 | 0,08285 | 0,08656 |
| 536,90215 | 0,05355 | 0,05177 | 0,05203 | 0,08257 | 0,08653 |
| 536,93933 | 0,05425 | 0,05232 | 0,05256 | 0,082 | 0,08612 |
| 536,97652 | 0,05526 | 0,05327 | 0,05348 | 0,08107 | 0,08529 |
| 537,0137 | 0,05655 | 0,05459 | 0,05475 | 0,07975 | 0,08399 |
| 537,05088 | 0,05807 | 0,0562 | 0,05636 | 0,07802 | 0,0822 |
| 537,08806 | 0,05977 | 0,05801 | 0,05819 | 0,07588 | 0,07992 |
| 537,12524 | 0,06159 | 0,05999 | 0,06017 | 0,07332 | 0,07718 |
| 537,16243 | 0,06346 | 0,06205 | 0,06224 | 0,0704 | 0,07402 |
| 537,19961 | 0,06533 | 0,06414 | 0,06432 | 0,06721 | 0,07051 |
| 537,23679 | 0,06711 | 0,06618 | 0,06635 | 0,06384 | 0,06676 |
| 537,27397 | 0,06875 | 0,0681 | 0,06826 | 0,06038 | 0,06289 |
| 537,31115 | 0,07021 | 0,06981 | 0,06997 | 0,05691 | 0,05902 |
| 537,34834 | 0,07144 | 0,07128 | 0,0714 | 0,05354 | 0,05526 |
| 537,38552 | 0,0724 | 0,07247 | 0,07253 | 0,05035 | 0,0517 |
| 537,4227 | 0,07309 | 0,07334 | 0,07332 | 0,04746 | 0,04845 |
| 537,45988 | 0,07346 | 0,07389 | 0,07377 | 0,04497 | 0,04559 |
| 537,49706 | 0,07348 | 0,0741 | 0,07386 | 0,04292 | 0,0432 |
| 537,53425 | 0,07322 | 0,07398 | 0,07361 | 0,04134 | 0,0414 |
| 537,57143 | 0,07269 | 0,07351 | 0,07302 | 0,04028 | 0,04015 |
| 537,60861 | 0,07193 | 0,07275 | 0,0721 | 0,03975 | 0,03947 |
| 537,64579 | 0,07096 | 0,07175 | 0,07091 | 0,03977 | 0,03936 |
| 537,68297 | 0,06985 | 0,07057 | 0,06953 | 0,04031 | 0,03981 |
| 537,72016 | 0,06865 | 0,06927 | 0,06802 | 0,0414 | 0,0408 |
| 537,75734 | 0,06741 | 0,06791 | 0,06644 | 0,04306 | 0,04231 |
| 537,79452 | 0,06623 | 0,06655 | 0,06487 | 0,0452 | 0,0443 |
| 537,8317 | 0,06517 | 0,06527 | 0,06338 | 0,0478 | 0,04682 |
| 537,86888 | 0,0643 | 0,06418 | 0,06204 | 0,05082 | 0,04975 |
| 537,90607 | 0,06371 | 0,06335 | 0,06098 | 0,05425 | 0,05307 |
| 537,94325 | 0,06345 | 0,06287 | 0,06027 | 0,05808 | 0,05676 |
| 537,98043 | 0,0636 | 0,0628 | 0,05999 | 0,06228 | 0,0608 |
| 538,01761 | 0,06423 | 0,06322 | 0,06021 | 0,06686 | 0,06519 |
| 538,05479 | 0,06551 | 0,06419 | 0,06099 | 0,07186 | 0,06993 |
| 538,09198 | 0,0674 | 0,06578 | 0,06241 | 0,07723 | 0,07501 |
| 538,12916 | 0,06995 | 0,06806 | 0,06452 | 0,08297 | 0,08051 |
| 538,16634 | 0,07319 | 0,07118 | 0,06736 | 0,08907 | 0,08639 |
| 538,20352 | 0,07713 | 0,07505 | 0,07107 | 0,09555 | 0,09266 |
| 538,2407 | 0,08177 | 0,0797 | 0,07561 | 0,10238 | 0,0993 |
| 538,27789 | 0,08711 | 0,0851 | 0,08093 | 0,10955 | 0,10631 |
| 538,31507 | 0,09316 | 0,09123 | 0,08701 | 0,11701 | 0,11365 |
| 538,35225 | 0,09984 | 0,09803 | 0,0938 | 0,12475 | 0,12129 |
| 538,38943 | 0,10701 | 0,10543 | 0,10122 | 0,13262 | 0,12914 |
| 538,42661 | 0,11457 | 0,11336 | 0,10917 | 0,14052 | 0,13711 |
| 538,4638 | 0,12237 | 0,12168 | 0,11754 | 0,14833 | 0,14505 |
| 538,50098 | 0,13029 | 0,13017 | 0,12619 | 0,1559 | 0,15279 |
| 538,53816 | 0,13818 | 0,13867 | 0,13489 | 0,16307 | 0,16016 |
| 538,57534 | 0,14587 | 0,14701 | 0,14344 | 0,16969 | 0,16698 |
| 538,61252 | 0,1531 | 0,15499 | 0,15166 | 0,17558 | 0,17307 |
| 538,64971 | 0,15971 | 0,16243 | 0,15936 | 0,18043 | 0,17825 |
| 538,68689 | 0,16558 | 0,16916 | 0,16635 | 0,18419 | 0,18237 |
| 538,72407 | 0,17056 | 0,1749 | 0,17245 | 0,18677 | 0,18523 |
| 538,76125 | 0,17453 | 0,17948 | 0,1775 | 0,1881 | 0,18663 |
| 538,79843 | 0,17741 | 0,18286 | 0,18117 | 0,18817 | 0,18668 |
| 538,83562 | 0,17913 | 0,18498 | 0,18352 | 0,18699 | 0,1854 |
| 538,8728 | 0,17961 | 0,18579 | 0,18454 | 0,18463 | 0,18287 |
| 538,90998 | 0,17875 | 0,18529 | 0,18421 | 0,18121 | 0,17923 |
| 538,94716 | 0,17679 | 0,18352 | 0,18258 | 0,1768 | 0,17464 |
| 538,98434 | 0,17382 | 0,18055 | 0,17972 | 0,17174 | 0,16932 |
| 539,02153 | 0,16995 | 0,17639 | 0,17575 | 0,1663 | 0,16352 |
| 539,05871 | 0,16533 | 0,17132 | 0,17081 | 0,16074 | 0,15753 |
| 539,09589 | 0,16014 | 0,16559 | 0,16502 | 0,1553 | 0,1517 |
| 539,13307 | 0,15455 | 0,1594 | 0,15875 | 0,15021 | 0,14629 |
| 539,17025 | 0,14877 | 0,15297 | 0,15222 | 0,14569 | 0,14152 |
| 539,20744 | 0,14306 | 0,14651 | 0,14567 | 0,14193 | 0,13759 |
| 539,24462 | 0,13761 | 0,14024 | 0,13931 | 0,13919 | 0,13464 |
| 539,2818 | 0,13259 | 0,13436 | 0,13336 | 0,1375 | 0,13276 |
| 539,31898 | 0,12815 | 0,12921 | 0,12801 | 0,13683 | 0,13199 |
| 539,35616 | 0,12441 | 0,12485 | 0,12347 | 0,13714 | 0,13244 |
| 539,39335 | 0,12147 | 0,12138 | 0,11996 | 0,13833 | 0,13389 |
| 539,43053 | 0,1194 | 0,11889 | 0,11748 | 0,14026 | 0,13615 |
| 539,46771 | 0,11837 | 0,11741 | 0,11605 | 0,14278 | 0,13902 |
| 539,50489 | 0,11821 | 0,11693 | 0,11567 | 0,14568 | 0,14228 |
| 539,54207 | 0,11886 | 0,11741 | 0,11629 | 0,14871 | 0,14569 |
| 539,57926 | 0,12023 | 0,11881 | 0,11783 | 0,1516 | 0,14901 |
| 539,61644 | 0,1222 | 0,12104 | 0,12018 | 0,1541 | 0,15199 |
| 539,65362 | 0,12465 | 0,12385 | 0,12323 | 0,15603 | 0,15435 |
| 539,6908 | 0,12743 | 0,12706 | 0,12677 | 0,15721 | 0,15583 |
| 539,72798 | 0,13038 | 0,13049 | 0,13053 | 0,15753 | 0,15636 |
| 539,76517 | 0,13327 | 0,13395 | 0,13433 | 0,15688 | 0,15585 |
| 539,80235 | 0,13593 | 0,13725 | 0,13795 | 0,15524 | 0,15427 |
| 539,83953 | 0,13821 | 0,14023 | 0,14123 | 0,15253 | 0,15162 |
| 539,87671 | 0,13999 | 0,14266 | 0,14399 | 0,14883 | 0,14798 |
| 539,91389 | 0,14116 | 0,14436 | 0,14608 | 0,14437 | 0,14347 |
| 539,95108 | 0,14163 | 0,14528 | 0,14729 | 0,13931 | 0,13822 |
| 539,98826 | 0,14135 | 0,14535 | 0,14752 | 0,13383 | 0,13244 |
| 540,02544 | 0,14015 | 0,14453 | 0,14681 | 0,12814 | 0,12646 |
| 540,06262 | 0,13816 | 0,14284 | 0,14515 | 0,12246 | 0,12051 |
| 540,0998 | 0,13546 | 0,14029 | 0,14259 | 0,11701 | 0,11482 |
| 540,13699 | 0,1321 | 0,13695 | 0,13918 | 0,11203 | 0,10962 |
| 540,17417 | 0,1282 | 0,13284 | 0,13503 | 0,1078 | 0,1051 |
| 540,21135 | 0,12386 | 0,12818 | 0,13027 | 0,10438 | 0,10143 |
| 540,24853 | 0,11921 | 0,12314 | 0,12499 | 0,10188 | 0,09873 |
| 540,28571 | 0,11439 | 0,11788 | 0,11946 | 0,10036 | 0,09724 |
| 540,3229 | 0,10959 | 0,11256 | 0,11385 | 0,0998 | 0,09682 |
| 540,36008 | 0,10497 | 0,10735 | 0,10836 | 0,10018 | 0,09739 |
| 540,39726 | 0,10066 | 0,10238 | 0,10312 | 0,1014 | 0,09885 |
| 540,43444 | 0,09676 | 0,09782 | 0,09831 | 0,10336 | 0,10106 |
| 540,47162 | 0,09339 | 0,09389 | 0,09405 | 0,10588 | 0,10383 |
| 540,50881 | 0,09063 | 0,09063 | 0,09045 | 0,10867 | 0,10695 |
| 540,54599 | 0,08852 | 0,08808 | 0,08772 | 0,11151 | 0,11019 |
| 540,58317 | 0,0872 | 0,0863 | 0,08583 | 0,1142 | 0,11325 |
| 540,62035 | 0,08661 | 0,08529 | 0,08476 | 0,11651 | 0,11587 |
| 540,65753 | 0,08668 | 0,08502 | 0,08449 | 0,11825 | 0,11784 |
| 540,69472 | 0,08735 | 0,08546 | 0,08497 | 0,11926 | 0,119 |
| 540,7319 | 0,08855 | 0,08654 | 0,08614 | 0,11936 | 0,1192 |
| 540,76908 | 0,09018 | 0,08821 | 0,08787 | 0,11836 | 0,11837 |
| 540,80626 | 0,09214 | 0,09026 | 0,09007 | 0,11632 | 0,11644 |
| 540,84344 | 0,0943 | 0,09254 | 0,09261 | 0,11328 | 0,11342 |
| 540,88063 | 0,09652 | 0,09492 | 0,09527 | 0,10927 | 0,10928 |
| 540,91781 | 0,09864 | 0,09726 | 0,09789 | 0,10439 | 0,10415 |
| 540,95499 | 0,10053 | 0,09942 | 0,10032 | 0,09875 | 0,09824 |
| 540,99217 | 0,10207 | 0,10127 | 0,10242 | 0,09248 | 0,09172 |
| 541,02935 | 0,10317 | 0,10264 | 0,10407 | 0,08574 | 0,08476 |
| 541,06654 | 0,10374 | 0,1034 | 0,10516 | 0,07868 | 0,07752 |
| 541,10372 | 0,1037 | 0,1035 | 0,10557 | 0,07154 | 0,07019 |
| 541,1409 | 0,10294 | 0,1029 | 0,10514 | 0,06444 | 0,06291 |
| 541,17808 | 0,10143 | 0,10158 | 0,10392 | 0,05754 | 0,05586 |
| 541,21526 | 0,09923 | 0,09952 | 0,10192 | 0,05092 | 0,04919 |
| 541,25245 | 0,09638 | 0,09674 | 0,09916 | 0,04469 | 0,04296 |
| 541,28963 | 0,0929 | 0,09329 | 0,09568 | 0,03891 | 0,03723 |
| 541,32681 | 0,08885 | 0,08915 | 0,09154 | 0,03363 | 0,03204 |
| 541,36399 | 0,08431 | 0,08446 | 0,08683 | 0,02896 | 0,02741 |
| 541,40117 | 0,07935 | 0,07935 | 0,08161 | 0,02481 | 0,02331 |
| 541,43836 | 0,07404 | 0,07392 | 0,076 | 0,02116 | 0,01975 |
| 541,47554 | 0,06853 | 0,06827 | 0,07016 | 0,018 | 0,01668 |
| 541,51272 | 0,06292 | 0,0625 | 0,06421 | 0,01527 | 0,01413 |
| 541,5499 | 0,05731 | 0,05672 | 0,05825 | 0,01296 | 0,01197 |
| 541,58708 | 0,05178 | 0,05102 | 0,05237 | 0,01101 | 0,01017 |
| 541,62427 | 0,04639 | 0,04551 | 0,04666 | 0,00938 | 0,00868 |
| 541,66145 | 0,04123 | 0,04027 | 0,04121 | 0,00808 | 0,00746 |
| 541,69863 | 0,03636 | 0,03534 | 0,03609 | 0,00701 | 0,00647 |
| 541,73581 | 0,03185 | 0,03076 | 0,03138 | 0,00615 | 0,00568 |
| 541,77299 | 0,0277 | 0,02656 | 0,02707 | 0,00547 | 0,00505 |
| 541,81018 | 0,02392 | 0,02276 | 0,02319 | 0,00493 | 0,00459 |
| 541,84736 | 0,02053 | 0,01937 | 0,01972 | 0,00452 | 0,00425 |
| 541,88454 | 0,01751 | 0,01638 | 0,01667 | 0,00422 | 0,00401 |
| 541,92172 | 0,01485 | 0,01384 | 0,01401 | 0,00401 | 0,00384 |
| 541,9589 | 0,01255 | 0,01166 | 0,01174 | 0,00388 | 0,00375 |
| 541,99609 | 0,01062 | 0,00981 | 0,00985 | 0,00381 | 0,00371 |
| 542,03327 | 0,009 | 0,00826 | 0,00829 | 0,00378 | 0,00371 |
| 542,07045 | 0,00764 | 0,007 | 0,00702 | 0,00377 | 0,00373 |
| 542,10763 | 0,00653 | 0,00597 | 0,00599 | 0,00379 | 0,00378 |
| 542,14481 | 0,00562 | 0,00516 | 0,00518 | 0,00381 | 0,00383 |
| 542,182 | 0,0049 | 0,00454 | 0,00455 | 0,00383 | 0,00387 |
| 542,21918 | 0,00433 | 0,0041 | 0,00408 | 0,00384 | 0,0039 |
| 542,25636 | 0,00391 | 0,00377 | 0,00374 | 0,00383 | 0,0039 |
| 542,29354 | 0,0036 | 0,00354 | 0,00351 | 0,0038 | 0,00388 |
| 542,33072 | 0,00337 | 0,00339 | 0,00337 | 0,00374 | 0,00382 |
| 542,36791 | 0,00321 | 0,00331 | 0,00328 | 0,00365 | 0,00374 |
| 542,40509 | 0,0031 | 0,00326 | 0,00324 | 0,00353 | 0,00362 |
| 542,44227 | 0,00303 | 0,00325 | 0,00323 | 0,00338 | 0,00346 |
| 542,47945 | 0,00298 | 0,00325 | 0,00323 | 0,00321 | 0,00328 |
| 542,51663 | 0,00295 | 0,00327 | 0,00324 | 0,00301 | 0,00307 |
| 542,55382 | 0,00292 | 0,00327 | 0,00325 | 0,0028 | 0,00285 |
| 542,591 | 0,00288 | 0,00327 | 0,00324 | 0,00257 | 0,00261 |
| 542,62818 | 0,00284 | 0,00325 | 0,00322 | 0,00234 | 0,00236 |
| 542,66536 | 0,00279 | 0,00322 | 0,00318 | 0,0021 | 0,00212 |
| 542,70254 | 0,00273 | 0,00316 | 0,00312 | 0,00187 | 0,00187 |
| 542,73973 | 0,00265 | 0,00309 | 0,00304 | 0,00165 | 0,00164 |
| 542,77691 | 0,00255 | 0,00298 | 0,00294 | 0,00144 | 0,00142 |
| 542,81409 | 0,00244 | 0,00286 | 0,00282 | 0,00124 | 0,00121 |
| 542,85127 | 0,00232 | 0,00272 | 0,00268 | 0,00106 | 0,00103 |
| 542,88845 | 0,00218 | 0,00256 | 0,00252 | 9e-04 | 0,00086 |
| 542,92564 | 0,00204 | 0,0024 | 0,00234 | 0,00076 | 0,00071 |
| 542,96282 | 0,00189 | 0,00222 | 0,00217 | 0,00064 | 0,00058 |
| 543 | 0,00174 | 0,00203 | 0,00198 | 0,00053 | 0,00047 |
In de figuren 3.3.1 tot en met 3.3.4 valt duidelijk te zien dat voor kinderen waarvan het hoogste opleidingsniveau van beide ouders bekend is, de frequentiedichtheid behoorlijk scheef naar rechts is verdeeld. De verdeling van de frequentiedichtheid voor kinderen waarvan het hoogste opleidingsniveau van alleen de vader bekend is, vertoont een ander patroon dan de verdeling voor de kinderen waarvan het hoogste opleidingsniveau van alleen de moeder bekend is. De reden hierachter is dat de variabelen die worden gebruikt om de het opleidingsniveau te schatten, verschillen tussen de vaders en de moeders. Denk hierbij bijvoorbeeld aan inkomen en inkomstenbron.
Daarnaast valt op dat voor de kinderen waarvan voor beide ouders het opleidingsniveau onbekend is, de verdeling van de onderwijsscore geconcentreerd is rondom het midden. Dit is een gevolg van het feit dat er relatief weinig bekend is over deze groep. De verdeling van onderwijsscores voor de overige deelpopulaties is wel stabiel over de jaren.
Imputatie van de onderwijsscore
De figuren 3.3.5 tot en met 3.3.9 tonen de verdeling van de frequentiedichtheid van de onderwijsscore naar de methode van directe imputatie van de onderwijsscore. Voor iedere groep maken we ook onderscheid tussen de schooljaren. De groepen zijn echter niet even groot. Het aandeel van de groep kinderen waarvan de onderwijsscore direct is berekend – en dus niet is geïmputeerd – is rond de 92 en 93 procent voor alle vier de schooljaren. Na de groep kinderen waarvan de onderwijsscore direct is berekend, is de groep kinderen waarbij de onderwijsscore is geïmputeerd omdat de vader onbekend is het grootst met een percentage tussen de drie en vier procent. Asielkinderen (niet meegenomen in dit onderzoek) zijn ongeveer twee procent van de populatie leerlingen afhankelijk van het jaar, en daarmee de derde grootste groep waarvan de onderwijsscores worden geïmputeerd. De andere groepen bevatten samen iets meer dan 0,4 procent van de populatie.
Uit de figuren 3.3.5 tot en met 3.3.9 valt af te lezen dat de geïmputeerde onderwijsscores relatief lager zijn dan de onderwijsscores die niet geïmputeerd zijn, conform verwachting. Bij de twee grootste groepen lijkt de verdeling redelijk stabiel te zijn over de schooljaren. De andere groepen zijn te klein om de verschillen tussen de schooljaren inhoudelijk goed te kunnen interpreteren. De grafiek voor de NOAT-kinderen (Nederlands Onderwijs Anders Taligen) hebben we deze publicatie gemaakt door de twee NOAT-categorieën (NOAT-1 en NOAT-2) samen te voegen.
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00011 | 0,00011 | 5e-05 | 1e-05 | 1e-05 |
| 524,03718 | 0,00012 | 0,00012 | 5e-05 | 2e-05 | 2e-05 |
| 524,07436 | 0,00012 | 0,00012 | 5e-05 | 2e-05 | 2e-05 |
| 524,11155 | 0,00013 | 0,00012 | 5e-05 | 2e-05 | 2e-05 |
| 524,14873 | 0,00013 | 0,00013 | 6e-05 | 2e-05 | 2e-05 |
| 524,18591 | 0,00013 | 0,00013 | 6e-05 | 3e-05 | 2e-05 |
| 524,22309 | 0,00014 | 0,00013 | 6e-05 | 3e-05 | 3e-05 |
| 524,26027 | 0,00014 | 0,00013 | 6e-05 | 3e-05 | 3e-05 |
| 524,29746 | 0,00014 | 0,00013 | 6e-05 | 3e-05 | 3e-05 |
| 524,33464 | 0,00014 | 0,00012 | 7e-05 | 4e-05 | 3e-05 |
| 524,37182 | 0,00014 | 0,00012 | 7e-05 | 4e-05 | 3e-05 |
| 524,409 | 0,00014 | 0,00012 | 8e-05 | 4e-05 | 3e-05 |
| 524,44618 | 0,00014 | 0,00012 | 8e-05 | 4e-05 | 3e-05 |
| 524,48337 | 0,00014 | 0,00011 | 9e-05 | 5e-05 | 4e-05 |
| 524,52055 | 0,00014 | 0,00011 | 9e-05 | 5e-05 | 4e-05 |
| 524,55773 | 0,00014 | 0,00011 | 1e-04 | 5e-05 | 4e-05 |
| 524,59491 | 0,00014 | 0,00011 | 0,00011 | 6e-05 | 4e-05 |
| 524,63209 | 0,00014 | 0,00011 | 0,00011 | 6e-05 | 4e-05 |
| 524,66928 | 0,00015 | 0,00011 | 0,00012 | 6e-05 | 4e-05 |
| 524,70646 | 0,00015 | 0,00012 | 0,00013 | 7e-05 | 4e-05 |
| 524,74364 | 0,00016 | 0,00012 | 0,00014 | 7e-05 | 4e-05 |
| 524,78082 | 0,00017 | 0,00012 | 0,00014 | 8e-05 | 5e-05 |
| 524,818 | 0,00017 | 0,00013 | 0,00015 | 8e-05 | 5e-05 |
| 524,85519 | 0,00018 | 0,00014 | 0,00016 | 9e-05 | 5e-05 |
| 524,89237 | 0,00019 | 0,00015 | 0,00016 | 9e-05 | 5e-05 |
| 524,92955 | 2e-04 | 0,00015 | 0,00017 | 1e-04 | 5e-05 |
| 524,96673 | 0,00021 | 0,00016 | 0,00017 | 1e-04 | 6e-05 |
| 525,00391 | 0,00021 | 0,00017 | 0,00018 | 1e-04 | 6e-05 |
| 525,0411 | 0,00022 | 0,00018 | 0,00019 | 0,00011 | 6e-05 |
| 525,07828 | 0,00023 | 0,00019 | 0,00019 | 0,00011 | 6e-05 |
| 525,11546 | 0,00024 | 0,00021 | 2e-04 | 0,00011 | 6e-05 |
| 525,15264 | 0,00025 | 0,00022 | 2e-04 | 0,00011 | 7e-05 |
| 525,18982 | 0,00026 | 0,00023 | 0,00021 | 0,00011 | 7e-05 |
| 525,22701 | 0,00027 | 0,00024 | 0,00021 | 0,00011 | 7e-05 |
| 525,26419 | 0,00028 | 0,00025 | 0,00022 | 0,00011 | 8e-05 |
| 525,30137 | 3e-04 | 0,00026 | 0,00023 | 0,00011 | 8e-05 |
| 525,33855 | 0,00032 | 0,00027 | 0,00024 | 0,00012 | 8e-05 |
| 525,37573 | 0,00034 | 0,00029 | 0,00025 | 0,00012 | 9e-05 |
| 525,41292 | 0,00036 | 3e-04 | 0,00027 | 0,00013 | 1e-04 |
| 525,4501 | 0,00039 | 0,00032 | 0,00029 | 0,00014 | 0,00011 |
| 525,48728 | 0,00043 | 0,00034 | 0,00031 | 0,00015 | 0,00012 |
| 525,52446 | 0,00048 | 0,00037 | 0,00034 | 0,00017 | 0,00014 |
| 525,56164 | 0,00053 | 0,00039 | 0,00038 | 0,00019 | 0,00016 |
| 525,59883 | 0,00059 | 0,00043 | 0,00042 | 0,00022 | 0,00018 |
| 525,63601 | 0,00066 | 0,00047 | 0,00047 | 0,00026 | 0,00022 |
| 525,67319 | 0,00074 | 0,00052 | 0,00052 | 3e-04 | 0,00026 |
| 525,71037 | 0,00083 | 0,00057 | 0,00059 | 0,00035 | 3e-04 |
| 525,74755 | 0,00093 | 0,00064 | 0,00066 | 0,00042 | 0,00036 |
| 525,78474 | 0,00103 | 0,00071 | 0,00074 | 5e-04 | 0,00044 |
| 525,82192 | 0,00114 | 0,00078 | 0,00082 | 0,00059 | 0,00052 |
| 525,8591 | 0,00125 | 0,00087 | 0,00091 | 0,00069 | 0,00062 |
| 525,89628 | 0,00136 | 0,00095 | 0,001 | 8e-04 | 0,00073 |
| 525,93346 | 0,00148 | 0,00105 | 0,00109 | 0,00093 | 0,00085 |
| 525,97065 | 0,0016 | 0,00115 | 0,00118 | 0,00108 | 0,00099 |
| 526,00783 | 0,00171 | 0,00125 | 0,00128 | 0,00124 | 0,00114 |
| 526,04501 | 0,00183 | 0,00135 | 0,00138 | 0,00141 | 0,0013 |
| 526,08219 | 0,00194 | 0,00146 | 0,00147 | 0,0016 | 0,00148 |
| 526,11937 | 0,00206 | 0,00157 | 0,00157 | 0,0018 | 0,00167 |
| 526,15656 | 0,00218 | 0,00169 | 0,00167 | 0,00201 | 0,00186 |
| 526,19374 | 0,00231 | 0,00181 | 0,00178 | 0,00223 | 0,00206 |
| 526,23092 | 0,00245 | 0,00194 | 0,00189 | 0,00245 | 0,00226 |
| 526,2681 | 0,0026 | 0,00208 | 0,00201 | 0,00268 | 0,00246 |
| 526,30528 | 0,00276 | 0,00224 | 0,00214 | 0,00291 | 0,00266 |
| 526,34247 | 0,00294 | 0,0024 | 0,00228 | 0,00313 | 0,00285 |
| 526,37965 | 0,00313 | 0,00258 | 0,00244 | 0,00335 | 0,00303 |
| 526,41683 | 0,00334 | 0,00278 | 0,0026 | 0,00354 | 0,00319 |
| 526,45401 | 0,00356 | 0,00298 | 0,00278 | 0,00372 | 0,00334 |
| 526,49119 | 0,0038 | 0,0032 | 0,00298 | 0,00387 | 0,00346 |
| 526,52838 | 0,00404 | 0,00343 | 0,00318 | 0,004 | 0,00355 |
| 526,56556 | 0,00428 | 0,00366 | 0,00338 | 0,0041 | 0,00363 |
| 526,60274 | 0,00453 | 0,00389 | 0,00359 | 0,00417 | 0,00367 |
| 526,63992 | 0,00477 | 0,00413 | 0,0038 | 0,00421 | 0,00369 |
| 526,6771 | 0,005 | 0,00435 | 0,004 | 0,00422 | 0,0037 |
| 526,71429 | 0,00522 | 0,00457 | 0,00419 | 0,0042 | 0,00368 |
| 526,75147 | 0,00543 | 0,00478 | 0,00437 | 0,00417 | 0,00364 |
| 526,78865 | 0,00562 | 0,00498 | 0,00454 | 0,00413 | 0,0036 |
| 526,82583 | 0,0058 | 0,00516 | 0,00469 | 0,00407 | 0,00355 |
| 526,86301 | 0,00597 | 0,00534 | 0,00483 | 0,00402 | 0,0035 |
| 526,9002 | 0,00614 | 0,0055 | 0,00496 | 0,00397 | 0,00346 |
| 526,93738 | 0,0063 | 0,00566 | 0,00508 | 0,00393 | 0,00342 |
| 526,97456 | 0,00646 | 0,00582 | 0,00519 | 0,00391 | 0,0034 |
| 527,01174 | 0,00664 | 0,00598 | 0,0053 | 0,0039 | 0,0034 |
| 527,04892 | 0,00682 | 0,00614 | 0,00542 | 0,00391 | 0,00341 |
| 527,08611 | 0,00701 | 0,0063 | 0,00554 | 0,00395 | 0,00343 |
| 527,12329 | 0,00723 | 0,00648 | 0,00567 | 0,004 | 0,00348 |
| 527,16047 | 0,00746 | 0,00666 | 0,00582 | 0,00408 | 0,00354 |
| 527,19765 | 0,0077 | 0,00685 | 0,00599 | 0,00417 | 0,00362 |
| 527,23483 | 0,00797 | 0,00706 | 0,00618 | 0,00429 | 0,00372 |
| 527,27202 | 0,00825 | 0,00728 | 0,0064 | 0,00443 | 0,00384 |
| 527,3092 | 0,00856 | 0,00752 | 0,00664 | 0,00459 | 0,00397 |
| 527,34638 | 0,00889 | 0,00778 | 0,00692 | 0,00477 | 0,00412 |
| 527,38356 | 0,00923 | 0,00806 | 0,00723 | 0,00497 | 0,0043 |
| 527,42074 | 0,00961 | 0,00837 | 0,00757 | 0,0052 | 0,00449 |
| 527,45793 | 0,01 | 0,0087 | 0,00796 | 0,00545 | 0,00471 |
| 527,49511 | 0,01043 | 0,00907 | 0,00838 | 0,00573 | 0,00496 |
| 527,53229 | 0,01089 | 0,00947 | 0,00884 | 0,00604 | 0,00525 |
| 527,56947 | 0,01138 | 0,00991 | 0,00934 | 0,00639 | 0,00556 |
| 527,60665 | 0,0119 | 0,01039 | 0,00989 | 0,00678 | 0,00592 |
| 527,64384 | 0,01245 | 0,01092 | 0,01047 | 0,0072 | 0,00632 |
| 527,68102 | 0,01303 | 0,01148 | 0,01109 | 0,00767 | 0,00676 |
| 527,7182 | 0,01362 | 0,01207 | 0,01174 | 0,00818 | 0,00725 |
| 527,75538 | 0,01423 | 0,01268 | 0,01241 | 0,00873 | 0,00779 |
| 527,79256 | 0,01485 | 0,01331 | 0,0131 | 0,00934 | 0,00838 |
| 527,82975 | 0,01546 | 0,01395 | 0,01378 | 0,00999 | 0,00903 |
| 527,86693 | 0,01606 | 0,01458 | 0,01446 | 0,0107 | 0,00973 |
| 527,90411 | 0,01664 | 0,0152 | 0,01512 | 0,01146 | 0,01049 |
| 527,94129 | 0,01719 | 0,0158 | 0,01576 | 0,01226 | 0,01129 |
| 527,97847 | 0,01771 | 0,01636 | 0,01636 | 0,0131 | 0,01213 |
| 528,01566 | 0,01819 | 0,01688 | 0,01692 | 0,01397 | 0,013 |
| 528,05284 | 0,01864 | 0,01737 | 0,01743 | 0,01486 | 0,0139 |
| 528,09002 | 0,01905 | 0,01781 | 0,0179 | 0,01577 | 0,01481 |
| 528,1272 | 0,01943 | 0,01821 | 0,01832 | 0,01666 | 0,01573 |
| 528,16438 | 0,01978 | 0,01858 | 0,0187 | 0,01755 | 0,01662 |
| 528,20157 | 0,02011 | 0,01891 | 0,01905 | 0,01839 | 0,01749 |
| 528,23875 | 0,02042 | 0,01921 | 0,01936 | 0,01918 | 0,01831 |
| 528,27593 | 0,02072 | 0,01949 | 0,01964 | 0,01991 | 0,01907 |
| 528,31311 | 0,021 | 0,01975 | 0,0199 | 0,02056 | 0,01975 |
| 528,35029 | 0,02128 | 0,02 | 0,02014 | 0,02112 | 0,02035 |
| 528,38748 | 0,02155 | 0,02024 | 0,02038 | 0,02158 | 0,02085 |
| 528,42466 | 0,02182 | 0,02048 | 0,0206 | 0,02195 | 0,02126 |
| 528,46184 | 0,02209 | 0,02072 | 0,02083 | 0,02222 | 0,02158 |
| 528,49902 | 0,02236 | 0,02095 | 0,02105 | 0,0224 | 0,0218 |
| 528,5362 | 0,02262 | 0,02119 | 0,02128 | 0,0225 | 0,02194 |
| 528,57339 | 0,02289 | 0,02143 | 0,02152 | 0,02253 | 0,02201 |
| 528,61057 | 0,02316 | 0,02168 | 0,02177 | 0,02252 | 0,02204 |
| 528,64775 | 0,02345 | 0,02194 | 0,02202 | 0,02249 | 0,02204 |
| 528,68493 | 0,02374 | 0,02221 | 0,0223 | 0,02246 | 0,02204 |
| 528,72211 | 0,02405 | 0,0225 | 0,02258 | 0,02244 | 0,02206 |
| 528,7593 | 0,02438 | 0,0228 | 0,02289 | 0,02246 | 0,02211 |
| 528,79648 | 0,02472 | 0,02311 | 0,0232 | 0,02252 | 0,02221 |
| 528,83366 | 0,02509 | 0,02344 | 0,02354 | 0,02264 | 0,02237 |
| 528,87084 | 0,02547 | 0,02378 | 0,02388 | 0,02282 | 0,02259 |
| 528,90802 | 0,02587 | 0,02414 | 0,02423 | 0,02306 | 0,02287 |
| 528,94521 | 0,02627 | 0,0245 | 0,02458 | 0,02336 | 0,02321 |
| 528,98239 | 0,02669 | 0,02485 | 0,02493 | 0,02369 | 0,02359 |
| 529,01957 | 0,0271 | 0,02521 | 0,02526 | 0,02404 | 0,024 |
| 529,05675 | 0,0275 | 0,02555 | 0,02558 | 0,02439 | 0,02441 |
| 529,09393 | 0,02789 | 0,02587 | 0,02588 | 0,02474 | 0,02481 |
| 529,13112 | 0,02825 | 0,02617 | 0,02614 | 0,02507 | 0,02518 |
| 529,1683 | 0,02859 | 0,02644 | 0,02638 | 0,02536 | 0,02552 |
| 529,20548 | 0,02891 | 0,02668 | 0,02658 | 0,02561 | 0,02581 |
| 529,24266 | 0,02919 | 0,0269 | 0,02676 | 0,02583 | 0,02605 |
| 529,27984 | 0,02945 | 0,0271 | 0,02691 | 0,026 | 0,02623 |
| 529,31703 | 0,02969 | 0,02727 | 0,02704 | 0,02613 | 0,02637 |
| 529,35421 | 0,02992 | 0,02744 | 0,02716 | 0,02625 | 0,02647 |
| 529,39139 | 0,03014 | 0,02761 | 0,02729 | 0,02636 | 0,02655 |
| 529,42857 | 0,03037 | 0,0278 | 0,02744 | 0,02648 | 0,02663 |
| 529,46575 | 0,03061 | 0,028 | 0,02761 | 0,02661 | 0,02672 |
| 529,50294 | 0,03088 | 0,02825 | 0,02782 | 0,02677 | 0,02683 |
| 529,54012 | 0,03119 | 0,02853 | 0,02809 | 0,02697 | 0,02698 |
| 529,5773 | 0,03154 | 0,02888 | 0,02842 | 0,02723 | 0,02717 |
| 529,61448 | 0,03194 | 0,02929 | 0,02882 | 0,02753 | 0,02743 |
| 529,65166 | 0,0324 | 0,02976 | 0,0293 | 0,0279 | 0,02775 |
| 529,68885 | 0,03292 | 0,03032 | 0,02986 | 0,02834 | 0,02814 |
| 529,72603 | 0,03352 | 0,03097 | 0,03051 | 0,02883 | 0,0286 |
| 529,76321 | 0,03418 | 0,03169 | 0,03124 | 0,02938 | 0,02913 |
| 529,80039 | 0,03491 | 0,03249 | 0,03205 | 0,03 | 0,02973 |
| 529,83757 | 0,03571 | 0,03337 | 0,03293 | 0,03067 | 0,0304 |
| 529,87476 | 0,03656 | 0,03432 | 0,03388 | 0,03141 | 0,03114 |
| 529,91194 | 0,03747 | 0,03532 | 0,03488 | 0,03221 | 0,03195 |
| 529,94912 | 0,03842 | 0,03638 | 0,03593 | 0,03308 | 0,03284 |
| 529,9863 | 0,0394 | 0,03748 | 0,03702 | 0,03402 | 0,03382 |
| 530,02348 | 0,04041 | 0,03861 | 0,03813 | 0,03505 | 0,03488 |
| 530,06067 | 0,04143 | 0,03975 | 0,03924 | 0,03615 | 0,03603 |
| 530,09785 | 0,04245 | 0,04089 | 0,04035 | 0,03732 | 0,03726 |
| 530,13503 | 0,04345 | 0,042 | 0,04144 | 0,03856 | 0,03857 |
| 530,17221 | 0,04442 | 0,04308 | 0,0425 | 0,03987 | 0,03995 |
| 530,20939 | 0,04535 | 0,04412 | 0,04351 | 0,04123 | 0,04139 |
| 530,24658 | 0,04623 | 0,04509 | 0,04446 | 0,04263 | 0,04288 |
| 530,28376 | 0,04704 | 0,04598 | 0,04535 | 0,04404 | 0,04438 |
| 530,32094 | 0,04777 | 0,04679 | 0,04615 | 0,04544 | 0,04587 |
| 530,35812 | 0,04842 | 0,04749 | 0,04686 | 0,04679 | 0,04731 |
| 530,3953 | 0,04897 | 0,04808 | 0,04746 | 0,04806 | 0,04866 |
| 530,43249 | 0,04941 | 0,04854 | 0,04795 | 0,04922 | 0,04989 |
| 530,46967 | 0,04974 | 0,04888 | 0,04832 | 0,05024 | 0,05095 |
| 530,50685 | 0,04996 | 0,04909 | 0,04856 | 0,05109 | 0,05183 |
| 530,54403 | 0,05006 | 0,04917 | 0,04868 | 0,05176 | 0,05249 |
| 530,58121 | 0,05005 | 0,04913 | 0,04868 | 0,05222 | 0,05291 |
| 530,6184 | 0,04993 | 0,04897 | 0,04855 | 0,05246 | 0,0531 |
| 530,65558 | 0,0497 | 0,04869 | 0,0483 | 0,05249 | 0,05303 |
| 530,69276 | 0,04936 | 0,0483 | 0,04794 | 0,05227 | 0,0527 |
| 530,72994 | 0,04894 | 0,04781 | 0,04747 | 0,05186 | 0,05216 |
| 530,76712 | 0,04843 | 0,04723 | 0,04691 | 0,05127 | 0,05144 |
| 530,80431 | 0,04786 | 0,0466 | 0,04628 | 0,05054 | 0,05057 |
| 530,84149 | 0,04726 | 0,04594 | 0,04561 | 0,04969 | 0,0496 |
| 530,87867 | 0,04664 | 0,04526 | 0,04492 | 0,04878 | 0,04857 |
| 530,91585 | 0,04603 | 0,0446 | 0,04424 | 0,04784 | 0,04753 |
| 530,95303 | 0,04545 | 0,04399 | 0,04361 | 0,04691 | 0,04653 |
| 530,99022 | 0,04494 | 0,04345 | 0,04305 | 0,04604 | 0,04562 |
| 531,0274 | 0,04452 | 0,04302 | 0,04261 | 0,04527 | 0,04484 |
| 531,06458 | 0,04422 | 0,04273 | 0,04231 | 0,04466 | 0,04426 |
| 531,10176 | 0,04408 | 0,04263 | 0,0422 | 0,04423 | 0,04389 |
| 531,13894 | 0,04413 | 0,04274 | 0,04232 | 0,04402 | 0,04375 |
| 531,17613 | 0,04439 | 0,04307 | 0,04269 | 0,04403 | 0,04387 |
| 531,21331 | 0,04486 | 0,04365 | 0,04332 | 0,0443 | 0,04427 |
| 531,25049 | 0,04555 | 0,04448 | 0,04423 | 0,04482 | 0,04495 |
| 531,28767 | 0,04648 | 0,04558 | 0,04541 | 0,04562 | 0,04591 |
| 531,32485 | 0,04763 | 0,04693 | 0,04688 | 0,04668 | 0,04715 |
| 531,36204 | 0,04901 | 0,04854 | 0,0486 | 0,048 | 0,04866 |
| 531,39922 | 0,05058 | 0,05037 | 0,05057 | 0,0496 | 0,05046 |
| 531,4364 | 0,05234 | 0,05241 | 0,05274 | 0,05143 | 0,05251 |
| 531,47358 | 0,05425 | 0,05462 | 0,05509 | 0,05346 | 0,05477 |
| 531,51076 | 0,05624 | 0,05693 | 0,05754 | 0,05566 | 0,0572 |
| 531,54795 | 0,05829 | 0,05929 | 0,06003 | 0,05798 | 0,05977 |
| 531,58513 | 0,06033 | 0,06164 | 0,06249 | 0,06039 | 0,06242 |
| 531,62231 | 0,06232 | 0,06393 | 0,06488 | 0,06284 | 0,0651 |
| 531,65949 | 0,06423 | 0,0661 | 0,06712 | 0,06527 | 0,06775 |
| 531,69667 | 0,066 | 0,0681 | 0,06918 | 0,06762 | 0,0703 |
| 531,73386 | 0,06761 | 0,06988 | 0,071 | 0,06982 | 0,07266 |
| 531,77104 | 0,06902 | 0,07141 | 0,07253 | 0,0718 | 0,07476 |
| 531,80822 | 0,07019 | 0,07262 | 0,07373 | 0,07352 | 0,07653 |
| 531,8454 | 0,07112 | 0,07353 | 0,07459 | 0,07494 | 0,07792 |
| 531,88258 | 0,07184 | 0,07413 | 0,07512 | 0,07601 | 0,07891 |
| 531,91977 | 0,07233 | 0,07445 | 0,07534 | 0,07673 | 0,07947 |
| 531,95695 | 0,07263 | 0,0745 | 0,07526 | 0,07709 | 0,07958 |
| 531,99413 | 0,07275 | 0,0743 | 0,07491 | 0,07709 | 0,07927 |
| 532,03131 | 0,07271 | 0,07389 | 0,07433 | 0,07676 | 0,07855 |
| 532,06849 | 0,07254 | 0,07331 | 0,07354 | 0,07614 | 0,07749 |
| 532,10568 | 0,07228 | 0,07259 | 0,0726 | 0,07525 | 0,07612 |
| 532,14286 | 0,07194 | 0,07177 | 0,07153 | 0,07418 | 0,07453 |
| 532,18004 | 0,07157 | 0,0709 | 0,07039 | 0,073 | 0,07282 |
| 532,21722 | 0,0712 | 0,07002 | 0,06923 | 0,07177 | 0,07108 |
| 532,2544 | 0,07083 | 0,06916 | 0,06807 | 0,07057 | 0,06937 |
| 532,29159 | 0,07051 | 0,06835 | 0,06696 | 0,06945 | 0,06777 |
| 532,32877 | 0,07023 | 0,06762 | 0,06591 | 0,06847 | 0,06636 |
| 532,36595 | 0,07003 | 0,06698 | 0,06497 | 0,06768 | 0,06518 |
| 532,40313 | 0,06992 | 0,06645 | 0,06416 | 0,06712 | 0,06429 |
| 532,44031 | 0,06991 | 0,06606 | 0,0635 | 0,06682 | 0,06372 |
| 532,4775 | 0,07003 | 0,06583 | 0,06303 | 0,06686 | 0,06354 |
| 532,51468 | 0,07031 | 0,06579 | 0,06279 | 0,06719 | 0,06372 |
| 532,55186 | 0,07076 | 0,06595 | 0,06279 | 0,06782 | 0,06424 |
| 532,58904 | 0,07139 | 0,06632 | 0,06304 | 0,06873 | 0,0651 |
| 532,62622 | 0,07223 | 0,06693 | 0,06358 | 0,06992 | 0,06627 |
| 532,66341 | 0,07329 | 0,06778 | 0,06442 | 0,07134 | 0,06771 |
| 532,70059 | 0,07458 | 0,0689 | 0,06557 | 0,07297 | 0,06939 |
| 532,73777 | 0,07612 | 0,0703 | 0,06704 | 0,07476 | 0,07126 |
| 532,77495 | 0,0779 | 0,07197 | 0,06882 | 0,07669 | 0,07329 |
| 532,81213 | 0,07992 | 0,07391 | 0,07092 | 0,07871 | 0,07541 |
| 532,84932 | 0,08219 | 0,07613 | 0,07334 | 0,08077 | 0,07759 |
| 532,8865 | 0,08464 | 0,07856 | 0,07599 | 0,08284 | 0,07978 |
| 532,92368 | 0,08723 | 0,08116 | 0,07883 | 0,08488 | 0,08193 |
| 532,96086 | 0,08991 | 0,08388 | 0,08179 | 0,08686 | 0,08403 |
| 532,99804 | 0,09263 | 0,08665 | 0,0848 | 0,08877 | 0,08604 |
| 533,03523 | 0,09533 | 0,08941 | 0,08779 | 0,09058 | 0,08793 |
| 533,07241 | 0,09793 | 0,09208 | 0,09066 | 0,09227 | 0,08969 |
| 533,10959 | 0,10037 | 0,0946 | 0,09333 | 0,09383 | 0,0913 |
| 533,14677 | 0,10259 | 0,09688 | 0,09574 | 0,09523 | 0,09272 |
| 533,18395 | 0,10449 | 0,09884 | 0,09776 | 0,09643 | 0,09391 |
| 533,22114 | 0,10605 | 0,10044 | 0,09935 | 0,09743 | 0,09488 |
| 533,25832 | 0,10725 | 0,10165 | 0,10049 | 0,0982 | 0,0956 |
| 533,2955 | 0,10808 | 0,10246 | 0,10117 | 0,09875 | 0,09606 |
| 533,33268 | 0,10853 | 0,10287 | 0,10138 | 0,09906 | 0,09626 |
| 533,36986 | 0,10863 | 0,10289 | 0,10115 | 0,09914 | 0,09621 |
| 533,40705 | 0,10839 | 0,10256 | 0,10051 | 0,099 | 0,09591 |
| 533,44423 | 0,10786 | 0,10191 | 0,09952 | 0,09865 | 0,09539 |
| 533,48141 | 0,10709 | 0,10099 | 0,09823 | 0,09814 | 0,0947 |
| 533,51859 | 0,10611 | 0,09985 | 0,09671 | 0,0975 | 0,09386 |
| 533,55577 | 0,10499 | 0,09857 | 0,09503 | 0,09678 | 0,09294 |
| 533,59295 | 0,10379 | 0,0972 | 0,09329 | 0,09606 | 0,09202 |
| 533,63014 | 0,10256 | 0,09582 | 0,09155 | 0,09537 | 0,09114 |
| 533,66732 | 0,10133 | 0,09445 | 0,08986 | 0,09476 | 0,09035 |
| 533,7045 | 0,10015 | 0,09314 | 0,08827 | 0,09428 | 0,08971 |
| 533,74168 | 0,09904 | 0,09193 | 0,08681 | 0,09395 | 0,08926 |
| 533,77886 | 0,09802 | 0,09083 | 0,08551 | 0,09381 | 0,08901 |
| 533,81605 | 0,0971 | 0,08987 | 0,08439 | 0,09387 | 0,08899 |
| 533,85323 | 0,09632 | 0,08907 | 0,08347 | 0,09413 | 0,08923 |
| 533,89041 | 0,09568 | 0,08845 | 0,08277 | 0,09462 | 0,08975 |
| 533,92759 | 0,09519 | 0,08799 | 0,08228 | 0,09531 | 0,09051 |
| 533,96477 | 0,09486 | 0,08772 | 0,082 | 0,09619 | 0,09152 |
| 534,00196 | 0,0947 | 0,08764 | 0,08194 | 0,09724 | 0,09275 |
| 534,03914 | 0,09471 | 0,08775 | 0,0821 | 0,09843 | 0,09418 |
| 534,07632 | 0,09492 | 0,08807 | 0,08249 | 0,09974 | 0,09578 |
| 534,1135 | 0,09534 | 0,08861 | 0,08312 | 0,10113 | 0,09751 |
| 534,15068 | 0,09597 | 0,08937 | 0,08401 | 0,10257 | 0,09933 |
| 534,18787 | 0,09682 | 0,09036 | 0,08515 | 0,104 | 0,10118 |
| 534,22505 | 0,09792 | 0,09162 | 0,08659 | 0,10538 | 0,10299 |
| 534,26223 | 0,09923 | 0,09311 | 0,08829 | 0,10662 | 0,10468 |
| 534,29941 | 0,10074 | 0,09481 | 0,09022 | 0,10767 | 0,10618 |
| 534,33659 | 0,1024 | 0,0967 | 0,09236 | 0,10848 | 0,10743 |
| 534,37378 | 0,10419 | 0,09873 | 0,09467 | 0,10899 | 0,10834 |
| 534,41096 | 0,10604 | 0,10086 | 0,09709 | 0,10915 | 0,10887 |
| 534,44814 | 0,10789 | 0,10302 | 0,09955 | 0,10892 | 0,10898 |
| 534,48532 | 0,10968 | 0,10514 | 0,10198 | 0,10829 | 0,10861 |
| 534,5225 | 0,11131 | 0,10715 | 0,10429 | 0,10722 | 0,10777 |
| 534,55969 | 0,1127 | 0,10894 | 0,10637 | 0,10573 | 0,10644 |
| 534,59687 | 0,11374 | 0,11039 | 0,10811 | 0,10378 | 0,10459 |
| 534,63405 | 0,11437 | 0,11146 | 0,10944 | 0,10145 | 0,1023 |
| 534,67123 | 0,11454 | 0,11206 | 0,11029 | 0,09879 | 0,09964 |
| 534,70841 | 0,11421 | 0,11216 | 0,1106 | 0,09585 | 0,09666 |
| 534,7456 | 0,11335 | 0,1117 | 0,11033 | 0,0927 | 0,09343 |
| 534,78278 | 0,11196 | 0,11068 | 0,10945 | 0,0894 | 0,09002 |
| 534,81996 | 0,11004 | 0,10909 | 0,10798 | 0,08602 | 0,0865 |
| 534,85714 | 0,10762 | 0,10696 | 0,10594 | 0,08263 | 0,08296 |
| 534,89432 | 0,10477 | 0,10434 | 0,10334 | 0,07929 | 0,07946 |
| 534,93151 | 0,10151 | 0,10124 | 0,10026 | 0,07608 | 0,07607 |
| 534,96869 | 0,098 | 0,09783 | 0,09683 | 0,07307 | 0,07288 |
| 535,00587 | 0,09432 | 0,09419 | 0,09314 | 0,0703 | 0,06993 |
| 535,04305 | 0,09057 | 0,09042 | 0,0893 | 0,0678 | 0,06726 |
| 535,08023 | 0,08684 | 0,08663 | 0,08541 | 0,06561 | 0,06491 |
| 535,11742 | 0,08323 | 0,08291 | 0,08156 | 0,06375 | 0,06289 |
| 535,1546 | 0,07981 | 0,07936 | 0,07786 | 0,06224 | 0,06124 |
| 535,19178 | 0,07666 | 0,07605 | 0,07439 | 0,06108 | 0,05996 |
| 535,22896 | 0,07384 | 0,07307 | 0,07124 | 0,06029 | 0,05906 |
| 535,26614 | 0,07145 | 0,07052 | 0,06852 | 0,05986 | 0,05855 |
| 535,30333 | 0,06951 | 0,06844 | 0,06625 | 0,05984 | 0,05846 |
| 535,34051 | 0,06803 | 0,06685 | 0,06446 | 0,06017 | 0,05876 |
| 535,37769 | 0,06702 | 0,06575 | 0,06317 | 0,06086 | 0,05943 |
| 535,41487 | 0,06648 | 0,06518 | 0,06241 | 0,06188 | 0,06047 |
| 535,45205 | 0,06641 | 0,06512 | 0,06218 | 0,06323 | 0,06185 |
| 535,48924 | 0,06681 | 0,06556 | 0,06247 | 0,06488 | 0,06357 |
| 535,52642 | 0,06763 | 0,06649 | 0,06326 | 0,06681 | 0,06559 |
| 535,5636 | 0,06887 | 0,06788 | 0,06452 | 0,06899 | 0,06789 |
| 535,60078 | 0,07051 | 0,06971 | 0,06629 | 0,0714 | 0,07042 |
| 535,63796 | 0,0725 | 0,07194 | 0,06844 | 0,074 | 0,07317 |
| 535,67515 | 0,07475 | 0,07448 | 0,07093 | 0,07674 | 0,07607 |
| 535,71233 | 0,07723 | 0,07727 | 0,07369 | 0,07956 | 0,07905 |
| 535,74951 | 0,07986 | 0,08024 | 0,07666 | 0,08241 | 0,08207 |
| 535,78669 | 0,0826 | 0,08333 | 0,07976 | 0,08526 | 0,08507 |
| 535,82387 | 0,08537 | 0,08645 | 0,08292 | 0,08805 | 0,08799 |
| 535,86106 | 0,08812 | 0,08954 | 0,08606 | 0,09075 | 0,09079 |
| 535,89824 | 0,09077 | 0,09252 | 0,08911 | 0,09331 | 0,09343 |
| 535,93542 | 0,09326 | 0,09531 | 0,09197 | 0,0957 | 0,09587 |
| 535,9726 | 0,0955 | 0,09782 | 0,09457 | 0,09789 | 0,09807 |
| 536,00978 | 0,09746 | 0,09999 | 0,09684 | 0,09982 | 0,09997 |
| 536,04697 | 0,09909 | 0,10179 | 0,09873 | 0,10148 | 0,10156 |
| 536,08415 | 0,10035 | 0,10316 | 0,10022 | 0,10284 | 0,10283 |
| 536,12133 | 0,10123 | 0,1041 | 0,10126 | 0,1039 | 0,10376 |
| 536,15851 | 0,10171 | 0,10457 | 0,10184 | 0,10464 | 0,10436 |
| 536,19569 | 0,10179 | 0,10458 | 0,10197 | 0,10505 | 0,10462 |
| 536,23288 | 0,10146 | 0,10414 | 0,10164 | 0,10514 | 0,10457 |
| 536,27006 | 0,10076 | 0,10328 | 0,10087 | 0,10493 | 0,10422 |
| 536,30724 | 0,09968 | 0,10198 | 0,09969 | 0,10445 | 0,10361 |
| 536,34442 | 0,09829 | 0,10035 | 0,09818 | 0,10375 | 0,10281 |
| 536,3816 | 0,09665 | 0,09844 | 0,09641 | 0,10289 | 0,10188 |
| 536,41879 | 0,09482 | 0,09632 | 0,09443 | 0,10198 | 0,10094 |
| 536,45597 | 0,09285 | 0,09406 | 0,09231 | 0,1011 | 0,10007 |
| 536,49315 | 0,0908 | 0,09172 | 0,09012 | 0,10034 | 0,09935 |
| 536,53033 | 0,08873 | 0,08937 | 0,08792 | 0,09977 | 0,09888 |
| 536,56751 | 0,08671 | 0,08707 | 0,08578 | 0,09947 | 0,09871 |
| 536,6047 | 0,08477 | 0,08489 | 0,08375 | 0,09948 | 0,09888 |
| 536,64188 | 0,08301 | 0,08289 | 0,08192 | 0,09981 | 0,09941 |
| 536,67906 | 0,08146 | 0,08115 | 0,08033 | 0,10046 | 0,10029 |
| 536,71624 | 0,08016 | 0,07968 | 0,079 | 0,10142 | 0,1015 |
| 536,75342 | 0,07915 | 0,07853 | 0,07797 | 0,10258 | 0,10291 |
| 536,79061 | 0,07843 | 0,07772 | 0,07726 | 0,10382 | 0,1044 |
| 536,82779 | 0,07804 | 0,07727 | 0,07689 | 0,10502 | 0,10584 |
| 536,86497 | 0,07798 | 0,07719 | 0,07687 | 0,10606 | 0,10709 |
| 536,90215 | 0,07824 | 0,07747 | 0,07719 | 0,10682 | 0,10803 |
| 536,93933 | 0,07882 | 0,07811 | 0,07785 | 0,10718 | 0,10852 |
| 536,97652 | 0,07969 | 0,07909 | 0,07886 | 0,10704 | 0,10847 |
| 537,0137 | 0,08083 | 0,0804 | 0,08015 | 0,10634 | 0,1078 |
| 537,05088 | 0,08217 | 0,08196 | 0,08167 | 0,10503 | 0,10648 |
| 537,08806 | 0,08364 | 0,08369 | 0,08337 | 0,10305 | 0,10443 |
| 537,12524 | 0,08518 | 0,08555 | 0,08518 | 0,10051 | 0,1018 |
| 537,16243 | 0,08673 | 0,08745 | 0,08705 | 0,0975 | 0,09867 |
| 537,19961 | 0,08822 | 0,08932 | 0,08889 | 0,09411 | 0,09514 |
| 537,23679 | 0,08957 | 0,09108 | 0,09064 | 0,09046 | 0,09134 |
| 537,27397 | 0,09073 | 0,09267 | 0,09222 | 0,08667 | 0,08742 |
| 537,31115 | 0,09164 | 0,09401 | 0,09354 | 0,08286 | 0,08349 |
| 537,34834 | 0,09221 | 0,09501 | 0,09453 | 0,07914 | 0,07968 |
| 537,38552 | 0,09243 | 0,09564 | 0,09518 | 0,07563 | 0,07611 |
| 537,4227 | 0,09231 | 0,09588 | 0,09544 | 0,07245 | 0,07291 |
| 537,45988 | 0,09183 | 0,09574 | 0,09531 | 0,06967 | 0,07014 |
| 537,49706 | 0,09101 | 0,0952 | 0,09478 | 0,06732 | 0,06785 |
| 537,53425 | 0,08987 | 0,09429 | 0,09388 | 0,06543 | 0,06604 |
| 537,57143 | 0,08846 | 0,09304 | 0,09263 | 0,064 | 0,06472 |
| 537,60861 | 0,08681 | 0,0915 | 0,09108 | 0,06304 | 0,06389 |
| 537,64579 | 0,08497 | 0,0897 | 0,08926 | 0,06253 | 0,06351 |
| 537,68297 | 0,08299 | 0,0877 | 0,08723 | 0,06244 | 0,06357 |
| 537,72016 | 0,08092 | 0,08556 | 0,08507 | 0,06274 | 0,06401 |
| 537,75734 | 0,07884 | 0,08335 | 0,08285 | 0,06341 | 0,0648 |
| 537,79452 | 0,07678 | 0,08112 | 0,08063 | 0,06443 | 0,06593 |
| 537,8317 | 0,07479 | 0,07894 | 0,07845 | 0,06574 | 0,06732 |
| 537,86888 | 0,07291 | 0,07684 | 0,07638 | 0,06729 | 0,06892 |
| 537,90607 | 0,07119 | 0,07488 | 0,07447 | 0,06906 | 0,0707 |
| 537,94325 | 0,06966 | 0,07311 | 0,07276 | 0,07101 | 0,07264 |
| 537,98043 | 0,06838 | 0,07158 | 0,07131 | 0,07314 | 0,07472 |
| 538,01761 | 0,06739 | 0,07034 | 0,07021 | 0,07542 | 0,07692 |
| 538,05479 | 0,06678 | 0,0695 | 0,0695 | 0,07785 | 0,07926 |
| 538,09198 | 0,06657 | 0,06909 | 0,06923 | 0,08044 | 0,08174 |
| 538,12916 | 0,06682 | 0,06915 | 0,06944 | 0,08322 | 0,08439 |
| 538,16634 | 0,06758 | 0,06976 | 0,0702 | 0,08621 | 0,08727 |
| 538,20352 | 0,0689 | 0,07096 | 0,07157 | 0,08943 | 0,09041 |
| 538,2407 | 0,07082 | 0,0728 | 0,07358 | 0,09294 | 0,09385 |
| 538,27789 | 0,07337 | 0,07533 | 0,07628 | 0,09677 | 0,09764 |
| 538,31507 | 0,07658 | 0,07856 | 0,0797 | 0,10094 | 0,10181 |
| 538,35225 | 0,08043 | 0,08251 | 0,0839 | 0,10547 | 0,1064 |
| 538,38943 | 0,08499 | 0,0872 | 0,08882 | 0,11037 | 0,11138 |
| 538,42661 | 0,0901 | 0,09254 | 0,09437 | 0,11559 | 0,11673 |
| 538,4638 | 0,09566 | 0,09842 | 0,10045 | 0,12108 | 0,12238 |
| 538,50098 | 0,10156 | 0,1047 | 0,10696 | 0,12671 | 0,12821 |
| 538,53816 | 0,10763 | 0,11122 | 0,11373 | 0,1323 | 0,13401 |
| 538,57534 | 0,11371 | 0,11782 | 0,1206 | 0,13764 | 0,13956 |
| 538,61252 | 0,11961 | 0,12428 | 0,12736 | 0,14251 | 0,14465 |
| 538,64971 | 0,12511 | 0,13041 | 0,1338 | 0,1467 | 0,14903 |
| 538,68689 | 0,13003 | 0,13597 | 0,13965 | 0,14996 | 0,15247 |
| 538,72407 | 0,13409 | 0,14072 | 0,14464 | 0,15211 | 0,15475 |
| 538,76125 | 0,1371 | 0,14437 | 0,14862 | 0,15298 | 0,15572 |
| 538,79843 | 0,13896 | 0,14684 | 0,15143 | 0,15246 | 0,15525 |
| 538,83562 | 0,1396 | 0,14802 | 0,15295 | 0,15044 | 0,15326 |
| 538,8728 | 0,13898 | 0,14786 | 0,15311 | 0,14694 | 0,14972 |
| 538,90998 | 0,13708 | 0,14633 | 0,15188 | 0,14223 | 0,14492 |
| 538,94716 | 0,13399 | 0,14349 | 0,1493 | 0,13651 | 0,13908 |
| 538,98434 | 0,12978 | 0,13941 | 0,14543 | 0,13006 | 0,13248 |
| 539,02153 | 0,12461 | 0,13425 | 0,14041 | 0,12317 | 0,12543 |
| 539,05871 | 0,11865 | 0,12818 | 0,13434 | 0,11619 | 0,11827 |
| 539,09589 | 0,1121 | 0,12136 | 0,12758 | 0,10942 | 0,11133 |
| 539,13307 | 0,10529 | 0,11416 | 0,12039 | 0,1032 | 0,10493 |
| 539,17025 | 0,09845 | 0,10685 | 0,11302 | 0,09779 | 0,09937 |
| 539,20744 | 0,09181 | 0,09966 | 0,10571 | 0,09356 | 0,095 |
| 539,24462 | 0,08559 | 0,09284 | 0,09873 | 0,0906 | 0,09195 |
| 539,2818 | 0,07999 | 0,0866 | 0,09229 | 0,08896 | 0,09024 |
| 539,31898 | 0,07518 | 0,08115 | 0,0866 | 0,08862 | 0,08988 |
| 539,35616 | 0,07128 | 0,07662 | 0,08182 | 0,08953 | 0,0908 |
| 539,39335 | 0,06841 | 0,07315 | 0,07824 | 0,09155 | 0,09288 |
| 539,43053 | 0,06675 | 0,0709 | 0,07584 | 0,09451 | 0,09593 |
| 539,46771 | 0,06619 | 0,06989 | 0,07461 | 0,09817 | 0,09972 |
| 539,50489 | 0,06668 | 0,07 | 0,07455 | 0,10228 | 0,10398 |
| 539,54207 | 0,06813 | 0,07118 | 0,07558 | 0,10655 | 0,10843 |
| 539,57926 | 0,07044 | 0,07332 | 0,07761 | 0,11063 | 0,11272 |
| 539,61644 | 0,07345 | 0,07627 | 0,08051 | 0,11424 | 0,11653 |
| 539,65362 | 0,077 | 0,07987 | 0,0841 | 0,11712 | 0,11962 |
| 539,6908 | 0,0809 | 0,08392 | 0,08819 | 0,11909 | 0,12178 |
| 539,72798 | 0,08495 | 0,08822 | 0,09257 | 0,11998 | 0,12283 |
| 539,76517 | 0,08891 | 0,09253 | 0,09696 | 0,11969 | 0,12268 |
| 539,80235 | 0,09255 | 0,09659 | 0,10113 | 0,11819 | 0,12127 |
| 539,83953 | 0,09568 | 0,10019 | 0,10486 | 0,11549 | 0,11862 |
| 539,87671 | 0,09815 | 0,10316 | 0,10799 | 0,11167 | 0,11481 |
| 539,91389 | 0,09983 | 0,10534 | 0,11033 | 0,10681 | 0,10992 |
| 539,95108 | 0,10063 | 0,10663 | 0,11177 | 0,1012 | 0,10421 |
| 539,98826 | 0,10049 | 0,10694 | 0,11222 | 0,09512 | 0,09799 |
| 540,02544 | 0,09941 | 0,10625 | 0,11163 | 0,08883 | 0,09153 |
| 540,06262 | 0,0974 | 0,10455 | 0,10996 | 0,08259 | 0,0851 |
| 540,0998 | 0,0945 | 0,10189 | 0,10721 | 0,07666 | 0,07898 |
| 540,13699 | 0,09078 | 0,09828 | 0,10357 | 0,07129 | 0,07342 |
| 540,17417 | 0,08646 | 0,09395 | 0,09918 | 0,0667 | 0,06864 |
| 540,21135 | 0,0817 | 0,08908 | 0,0942 | 0,06306 | 0,06485 |
| 540,24853 | 0,07667 | 0,08385 | 0,08879 | 0,06054 | 0,06219 |
| 540,28571 | 0,07155 | 0,07842 | 0,08315 | 0,05932 | 0,06088 |
| 540,3229 | 0,06649 | 0,07299 | 0,07746 | 0,05926 | 0,0608 |
| 540,36008 | 0,06168 | 0,06774 | 0,07192 | 0,06032 | 0,06187 |
| 540,39726 | 0,05725 | 0,06284 | 0,06671 | 0,06237 | 0,06399 |
| 540,43444 | 0,05334 | 0,05843 | 0,06207 | 0,06525 | 0,06697 |
| 540,47162 | 0,05015 | 0,05471 | 0,05808 | 0,06876 | 0,0706 |
| 540,50881 | 0,04771 | 0,05177 | 0,05486 | 0,07263 | 0,07463 |
| 540,54599 | 0,04603 | 0,04964 | 0,05246 | 0,07662 | 0,07878 |
| 540,58317 | 0,04515 | 0,04834 | 0,05093 | 0,08044 | 0,08276 |
| 540,62035 | 0,04504 | 0,04786 | 0,05026 | 0,08376 | 0,08625 |
| 540,65753 | 0,04567 | 0,04818 | 0,05043 | 0,08631 | 0,08892 |
| 540,69472 | 0,04696 | 0,04922 | 0,0514 | 0,08791 | 0,09062 |
| 540,7319 | 0,04884 | 0,05091 | 0,05306 | 0,08844 | 0,0912 |
| 540,76908 | 0,05118 | 0,05313 | 0,05537 | 0,08781 | 0,09057 |
| 540,80626 | 0,05389 | 0,05577 | 0,05811 | 0,08599 | 0,08871 |
| 540,84344 | 0,05678 | 0,05866 | 0,06112 | 0,08305 | 0,08568 |
| 540,88063 | 0,05969 | 0,06162 | 0,06425 | 0,07907 | 0,08157 |
| 540,91781 | 0,06247 | 0,06449 | 0,06732 | 0,07421 | 0,07654 |
| 540,95499 | 0,06499 | 0,06712 | 0,07018 | 0,06864 | 0,07078 |
| 540,99217 | 0,06711 | 0,06938 | 0,07268 | 0,06256 | 0,06448 |
| 541,02935 | 0,06873 | 0,07113 | 0,07468 | 0,05627 | 0,05796 |
| 541,06654 | 0,06975 | 0,07228 | 0,07607 | 0,04997 | 0,05143 |
| 541,10372 | 0,07009 | 0,07275 | 0,0767 | 0,04383 | 0,04508 |
| 541,1409 | 0,06969 | 0,07247 | 0,07649 | 0,03802 | 0,03905 |
| 541,17808 | 0,06848 | 0,07133 | 0,07548 | 0,03263 | 0,03348 |
| 541,21526 | 0,06656 | 0,06944 | 0,07367 | 0,02774 | 0,02843 |
| 541,25245 | 0,06398 | 0,06683 | 0,07111 | 0,02341 | 0,02396 |
| 541,28963 | 0,06079 | 0,06359 | 0,06786 | 0,01964 | 0,02006 |
| 541,32681 | 0,05711 | 0,05981 | 0,06401 | 0,01645 | 0,01677 |
| 541,36399 | 0,05302 | 0,05558 | 0,05967 | 0,01378 | 0,01403 |
| 541,40117 | 0,04865 | 0,05104 | 0,05495 | 0,01156 | 0,01176 |
| 541,43836 | 0,0441 | 0,0463 | 0,05 | 0,00972 | 0,00988 |
| 541,47554 | 0,03949 | 0,04148 | 0,04494 | 0,00821 | 0,00834 |
| 541,51272 | 0,03495 | 0,0367 | 0,03993 | 0,00698 | 0,00708 |
| 541,5499 | 0,03058 | 0,03211 | 0,03507 | 0,00597 | 0,00606 |
| 541,58708 | 0,02646 | 0,02776 | 0,03044 | 0,00514 | 0,00523 |
| 541,62427 | 0,02263 | 0,02372 | 0,02613 | 0,00447 | 0,00455 |
| 541,66145 | 0,01915 | 0,02005 | 0,02217 | 0,00392 | 0,00399 |
| 541,69863 | 0,01603 | 0,01675 | 0,01861 | 0,00348 | 0,00355 |
| 541,73581 | 0,01329 | 0,01386 | 0,01547 | 0,00313 | 0,0032 |
| 541,77299 | 0,01091 | 0,01135 | 0,01273 | 0,00285 | 0,00292 |
| 541,81018 | 0,00889 | 0,00922 | 0,01044 | 0,00264 | 0,00271 |
| 541,84736 | 0,00722 | 0,00745 | 0,00851 | 0,0025 | 0,00257 |
| 541,88454 | 0,00586 | 0,00603 | 0,00692 | 0,00241 | 0,00248 |
| 541,92172 | 0,00475 | 0,00489 | 0,00562 | 0,00236 | 0,00244 |
| 541,9589 | 0,00386 | 0,00398 | 0,00458 | 0,00237 | 0,00245 |
| 541,99609 | 0,00317 | 0,00328 | 0,00376 | 0,00241 | 0,0025 |
| 542,03327 | 0,00264 | 0,00275 | 0,00314 | 0,00247 | 0,00257 |
| 542,07045 | 0,00224 | 0,00236 | 0,00267 | 0,00256 | 0,00267 |
| 542,10763 | 0,00196 | 0,00209 | 0,00234 | 0,00265 | 0,00277 |
| 542,14481 | 0,00176 | 0,00191 | 0,00212 | 0,00274 | 0,00286 |
| 542,182 | 0,00164 | 0,00181 | 0,00199 | 0,00282 | 0,00295 |
| 542,21918 | 0,00158 | 0,00178 | 0,00193 | 0,00287 | 0,00301 |
| 542,25636 | 0,00157 | 0,00179 | 0,00191 | 0,0029 | 0,00304 |
| 542,29354 | 0,00158 | 0,00183 | 0,00194 | 0,00289 | 0,00304 |
| 542,33072 | 0,00162 | 0,00189 | 0,00199 | 0,00285 | 0,003 |
| 542,36791 | 0,00167 | 0,00197 | 0,00205 | 0,00277 | 0,00292 |
| 542,40509 | 0,00173 | 0,00205 | 0,00213 | 0,00265 | 0,0028 |
| 542,44227 | 0,00179 | 0,00213 | 0,00221 | 0,0025 | 0,00265 |
| 542,47945 | 0,00185 | 0,00221 | 0,00229 | 0,00232 | 0,00247 |
| 542,51663 | 0,00189 | 0,00228 | 0,00235 | 0,00213 | 0,00226 |
| 542,55382 | 0,00192 | 0,00232 | 0,0024 | 0,00192 | 0,00204 |
| 542,591 | 0,00194 | 0,00235 | 0,00242 | 0,0017 | 0,00182 |
| 542,62818 | 0,00193 | 0,00235 | 0,00242 | 0,00149 | 0,00159 |
| 542,66536 | 0,0019 | 0,00233 | 0,00239 | 0,00128 | 0,00137 |
| 542,70254 | 0,00186 | 0,00229 | 0,00234 | 0,00109 | 0,00116 |
| 542,73973 | 0,00179 | 0,00221 | 0,00227 | 0,00091 | 0,00097 |
| 542,77691 | 0,00171 | 0,00212 | 0,00217 | 0,00075 | 8e-04 |
| 542,81409 | 0,00161 | 0,002 | 0,00205 | 0,00062 | 0,00066 |
| 542,85127 | 0,00149 | 0,00187 | 0,00191 | 5e-04 | 0,00053 |
| 542,88845 | 0,00137 | 0,00172 | 0,00176 | 4e-04 | 0,00042 |
| 542,92564 | 0,00124 | 0,00156 | 0,0016 | 0,00032 | 0,00033 |
| 542,96282 | 0,00111 | 0,0014 | 0,00143 | 0,00025 | 0,00026 |
| 543 | 0,00098 | 0,00124 | 0,00127 | 2e-04 | 2e-04 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00053 | 3e-05 | 0,00022 | 4e-05 | 1e-05 |
| 524,03718 | 0,00058 | 4e-05 | 0,00024 | 5e-05 | 1e-05 |
| 524,07436 | 0,00065 | 4e-05 | 0,00026 | 5e-05 | 2e-05 |
| 524,11155 | 0,00072 | 5e-05 | 0,00029 | 6e-05 | 2e-05 |
| 524,14873 | 0,00079 | 5e-05 | 0,00031 | 6e-05 | 2e-05 |
| 524,18591 | 0,00087 | 6e-05 | 0,00034 | 7e-05 | 2e-05 |
| 524,22309 | 0,00096 | 7e-05 | 0,00038 | 8e-05 | 3e-05 |
| 524,26027 | 0,00105 | 8e-05 | 0,00041 | 9e-05 | 3e-05 |
| 524,29746 | 0,00116 | 9e-05 | 0,00045 | 1e-04 | 4e-05 |
| 524,33464 | 0,00127 | 1e-04 | 0,00049 | 0,00011 | 4e-05 |
| 524,37182 | 0,00138 | 0,00011 | 0,00053 | 0,00012 | 5e-05 |
| 524,409 | 0,00151 | 0,00013 | 0,00058 | 0,00013 | 5e-05 |
| 524,44618 | 0,00165 | 0,00014 | 0,00063 | 0,00015 | 6e-05 |
| 524,48337 | 0,0018 | 0,00016 | 0,00068 | 0,00016 | 7e-05 |
| 524,52055 | 0,00195 | 0,00018 | 0,00073 | 0,00018 | 8e-05 |
| 524,55773 | 0,00212 | 2e-04 | 0,00079 | 2e-04 | 9e-05 |
| 524,59491 | 0,0023 | 0,00023 | 0,00086 | 0,00022 | 1e-04 |
| 524,63209 | 0,00249 | 0,00026 | 0,00093 | 0,00024 | 0,00011 |
| 524,66928 | 0,00269 | 0,00029 | 0,001 | 0,00026 | 0,00012 |
| 524,70646 | 0,00291 | 0,00032 | 0,00107 | 0,00028 | 0,00014 |
| 524,74364 | 0,00313 | 0,00035 | 0,00116 | 0,00031 | 0,00016 |
| 524,78082 | 0,00337 | 0,00039 | 0,00124 | 0,00034 | 0,00018 |
| 524,818 | 0,00363 | 0,00044 | 0,00133 | 0,00037 | 2e-04 |
| 524,85519 | 0,00389 | 0,00049 | 0,00143 | 4e-04 | 0,00022 |
| 524,89237 | 0,00417 | 0,00054 | 0,00153 | 0,00043 | 0,00025 |
| 524,92955 | 0,00446 | 0,00059 | 0,00164 | 0,00047 | 0,00028 |
| 524,96673 | 0,00477 | 0,00066 | 0,00176 | 0,00051 | 0,00031 |
| 525,00391 | 0,00509 | 0,00072 | 0,00188 | 0,00055 | 0,00034 |
| 525,0411 | 0,00543 | 8e-04 | 0,002 | 0,00059 | 0,00038 |
| 525,07828 | 0,00578 | 0,00088 | 0,00214 | 0,00064 | 0,00043 |
| 525,11546 | 0,00615 | 0,00096 | 0,00228 | 0,00068 | 0,00047 |
| 525,15264 | 0,00653 | 0,00106 | 0,00242 | 0,00073 | 0,00052 |
| 525,18982 | 0,00692 | 0,00116 | 0,00258 | 0,00079 | 0,00058 |
| 525,22701 | 0,00734 | 0,00126 | 0,00274 | 0,00085 | 0,00064 |
| 525,26419 | 0,00776 | 0,00138 | 0,00291 | 0,00091 | 0,00071 |
| 525,30137 | 0,0082 | 0,00151 | 0,00309 | 0,00097 | 0,00078 |
| 525,33855 | 0,00866 | 0,00164 | 0,00328 | 0,00104 | 0,00086 |
| 525,37573 | 0,00913 | 0,00179 | 0,00348 | 0,00111 | 0,00094 |
| 525,41292 | 0,00961 | 0,00194 | 0,00368 | 0,00118 | 0,00103 |
| 525,4501 | 0,01011 | 0,0021 | 0,0039 | 0,00126 | 0,00113 |
| 525,48728 | 0,01063 | 0,00228 | 0,00413 | 0,00134 | 0,00124 |
| 525,52446 | 0,01116 | 0,00247 | 0,00437 | 0,00143 | 0,00135 |
| 525,56164 | 0,0117 | 0,00267 | 0,00461 | 0,00152 | 0,00148 |
| 525,59883 | 0,01226 | 0,00288 | 0,00487 | 0,00162 | 0,00161 |
| 525,63601 | 0,01284 | 0,0031 | 0,00514 | 0,00172 | 0,00176 |
| 525,67319 | 0,01343 | 0,00334 | 0,00542 | 0,00183 | 0,00191 |
| 525,71037 | 0,01403 | 0,00359 | 0,00572 | 0,00194 | 0,00208 |
| 525,74755 | 0,01464 | 0,00386 | 0,00603 | 0,00206 | 0,00225 |
| 525,78474 | 0,01528 | 0,00414 | 0,00635 | 0,00219 | 0,00244 |
| 525,82192 | 0,01592 | 0,00444 | 0,00669 | 0,00232 | 0,00264 |
| 525,8591 | 0,01658 | 0,00475 | 0,00704 | 0,00246 | 0,00286 |
| 525,89628 | 0,01725 | 0,00508 | 0,00741 | 0,00261 | 0,00308 |
| 525,93346 | 0,01794 | 0,00542 | 0,00779 | 0,00277 | 0,00332 |
| 525,97065 | 0,01864 | 0,00579 | 0,00818 | 0,00293 | 0,00358 |
| 526,00783 | 0,01936 | 0,00616 | 0,0086 | 0,00311 | 0,00385 |
| 526,04501 | 0,0201 | 0,00656 | 0,00903 | 0,0033 | 0,00414 |
| 526,08219 | 0,02084 | 0,00698 | 0,00948 | 0,0035 | 0,00444 |
| 526,11937 | 0,0216 | 0,00741 | 0,00995 | 0,00371 | 0,00477 |
| 526,15656 | 0,02238 | 0,00786 | 0,01044 | 0,00393 | 0,00511 |
| 526,19374 | 0,02318 | 0,00834 | 0,01094 | 0,00417 | 0,00546 |
| 526,23092 | 0,02399 | 0,00883 | 0,01148 | 0,00442 | 0,00584 |
| 526,2681 | 0,02481 | 0,00934 | 0,01203 | 0,00468 | 0,00623 |
| 526,30528 | 0,02566 | 0,00987 | 0,01259 | 0,00497 | 0,00664 |
| 526,34247 | 0,02653 | 0,01043 | 0,01319 | 0,00527 | 0,00708 |
| 526,37965 | 0,02741 | 0,011 | 0,01381 | 0,00559 | 0,00753 |
| 526,41683 | 0,02831 | 0,01159 | 0,01444 | 0,00593 | 0,00801 |
| 526,45401 | 0,02923 | 0,01221 | 0,0151 | 0,00629 | 0,0085 |
| 526,49119 | 0,03017 | 0,01285 | 0,01579 | 0,00666 | 0,00902 |
| 526,52838 | 0,03112 | 0,0135 | 0,01651 | 0,00707 | 0,00956 |
| 526,56556 | 0,03211 | 0,01418 | 0,01724 | 0,0075 | 0,01012 |
| 526,60274 | 0,03311 | 0,01489 | 0,018 | 0,00795 | 0,0107 |
| 526,63992 | 0,03413 | 0,01561 | 0,0188 | 0,00843 | 0,01131 |
| 526,6771 | 0,03518 | 0,01636 | 0,01961 | 0,00894 | 0,01194 |
| 526,71429 | 0,03625 | 0,01713 | 0,02045 | 0,00948 | 0,01258 |
| 526,75147 | 0,03734 | 0,01792 | 0,02132 | 0,01004 | 0,01326 |
| 526,78865 | 0,03845 | 0,01874 | 0,02221 | 0,01064 | 0,01396 |
| 526,82583 | 0,03959 | 0,01957 | 0,02313 | 0,01127 | 0,01468 |
| 526,86301 | 0,04076 | 0,02043 | 0,02408 | 0,01193 | 0,01542 |
| 526,9002 | 0,04195 | 0,02132 | 0,02506 | 0,01262 | 0,01618 |
| 526,93738 | 0,04315 | 0,02223 | 0,02606 | 0,01335 | 0,01697 |
| 526,97456 | 0,04439 | 0,02315 | 0,02708 | 0,01412 | 0,01778 |
| 527,01174 | 0,04565 | 0,02411 | 0,02814 | 0,01492 | 0,01861 |
| 527,04892 | 0,04694 | 0,02509 | 0,02922 | 0,01575 | 0,01947 |
| 527,08611 | 0,04824 | 0,02609 | 0,03032 | 0,01663 | 0,02034 |
| 527,12329 | 0,04957 | 0,02711 | 0,03145 | 0,01755 | 0,02124 |
| 527,16047 | 0,05093 | 0,02816 | 0,0326 | 0,01849 | 0,02216 |
| 527,19765 | 0,0523 | 0,02923 | 0,03377 | 0,01948 | 0,0231 |
| 527,23483 | 0,05369 | 0,03032 | 0,03497 | 0,02051 | 0,02406 |
| 527,27202 | 0,05511 | 0,03144 | 0,03619 | 0,02157 | 0,02503 |
| 527,3092 | 0,05655 | 0,03258 | 0,03743 | 0,02267 | 0,02603 |
| 527,34638 | 0,058 | 0,03374 | 0,03868 | 0,02381 | 0,02705 |
| 527,38356 | 0,05947 | 0,03493 | 0,03996 | 0,02498 | 0,02808 |
| 527,42074 | 0,06096 | 0,03614 | 0,04126 | 0,02619 | 0,02913 |
| 527,45793 | 0,06246 | 0,03737 | 0,04256 | 0,02743 | 0,0302 |
| 527,49511 | 0,06397 | 0,03862 | 0,04389 | 0,02871 | 0,03129 |
| 527,53229 | 0,0655 | 0,03989 | 0,04523 | 0,03003 | 0,03238 |
| 527,56947 | 0,06704 | 0,04119 | 0,04658 | 0,03137 | 0,0335 |
| 527,60665 | 0,06858 | 0,04251 | 0,04793 | 0,03274 | 0,03463 |
| 527,64384 | 0,07013 | 0,04384 | 0,0493 | 0,03415 | 0,03576 |
| 527,68102 | 0,07169 | 0,04521 | 0,05068 | 0,03558 | 0,03692 |
| 527,7182 | 0,07325 | 0,04658 | 0,05206 | 0,03703 | 0,03808 |
| 527,75538 | 0,07481 | 0,04798 | 0,05345 | 0,03851 | 0,03925 |
| 527,79256 | 0,07637 | 0,04939 | 0,05484 | 0,04002 | 0,04043 |
| 527,82975 | 0,07793 | 0,05083 | 0,05623 | 0,04154 | 0,04163 |
| 527,86693 | 0,07948 | 0,05228 | 0,05762 | 0,04308 | 0,04283 |
| 527,90411 | 0,08103 | 0,05374 | 0,05901 | 0,04464 | 0,04403 |
| 527,94129 | 0,08256 | 0,05523 | 0,0604 | 0,04621 | 0,04525 |
| 527,97847 | 0,08409 | 0,05672 | 0,06179 | 0,04779 | 0,04647 |
| 528,01566 | 0,0856 | 0,05823 | 0,06316 | 0,04938 | 0,04769 |
| 528,05284 | 0,0871 | 0,05976 | 0,06453 | 0,05098 | 0,04892 |
| 528,09002 | 0,08858 | 0,06129 | 0,0659 | 0,05258 | 0,05015 |
| 528,1272 | 0,09004 | 0,06284 | 0,06725 | 0,05419 | 0,05139 |
| 528,16438 | 0,09149 | 0,06439 | 0,06859 | 0,05579 | 0,05263 |
| 528,20157 | 0,09291 | 0,06596 | 0,06992 | 0,0574 | 0,05387 |
| 528,23875 | 0,09431 | 0,06753 | 0,07124 | 0,05899 | 0,05511 |
| 528,27593 | 0,09569 | 0,06911 | 0,07254 | 0,06059 | 0,05635 |
| 528,31311 | 0,09704 | 0,07069 | 0,07383 | 0,06217 | 0,05759 |
| 528,35029 | 0,09836 | 0,07227 | 0,07511 | 0,06374 | 0,05883 |
| 528,38748 | 0,09965 | 0,07386 | 0,07637 | 0,0653 | 0,06008 |
| 528,42466 | 0,10091 | 0,07545 | 0,0776 | 0,06685 | 0,06132 |
| 528,46184 | 0,10215 | 0,07703 | 0,07883 | 0,06838 | 0,06256 |
| 528,49902 | 0,10334 | 0,07862 | 0,08003 | 0,06989 | 0,06379 |
| 528,5362 | 0,1045 | 0,0802 | 0,08122 | 0,07138 | 0,06503 |
| 528,57339 | 0,10564 | 0,08178 | 0,08239 | 0,07285 | 0,06626 |
| 528,61057 | 0,10674 | 0,08335 | 0,08354 | 0,07429 | 0,0675 |
| 528,64775 | 0,10779 | 0,08491 | 0,08467 | 0,07572 | 0,06873 |
| 528,68493 | 0,10882 | 0,08646 | 0,08577 | 0,07712 | 0,06995 |
| 528,72211 | 0,10981 | 0,088 | 0,08686 | 0,07849 | 0,07118 |
| 528,7593 | 0,11076 | 0,08952 | 0,08794 | 0,07983 | 0,0724 |
| 528,79648 | 0,11167 | 0,09103 | 0,08898 | 0,08115 | 0,07362 |
| 528,83366 | 0,11255 | 0,09253 | 0,09001 | 0,08245 | 0,07484 |
| 528,87084 | 0,11339 | 0,09401 | 0,09102 | 0,0837 | 0,07605 |
| 528,90802 | 0,11419 | 0,09546 | 0,09201 | 0,08493 | 0,07727 |
| 528,94521 | 0,11495 | 0,0969 | 0,09298 | 0,08614 | 0,07847 |
| 528,98239 | 0,11568 | 0,09832 | 0,09393 | 0,08731 | 0,07968 |
| 529,01957 | 0,11636 | 0,09971 | 0,09486 | 0,08845 | 0,08088 |
| 529,05675 | 0,117 | 0,10107 | 0,09577 | 0,08956 | 0,08208 |
| 529,09393 | 0,11761 | 0,10241 | 0,09665 | 0,09065 | 0,08328 |
| 529,13112 | 0,11819 | 0,10372 | 0,09753 | 0,0917 | 0,08448 |
| 529,1683 | 0,11872 | 0,105 | 0,09837 | 0,09273 | 0,08567 |
| 529,20548 | 0,11921 | 0,10625 | 0,0992 | 0,09373 | 0,08685 |
| 529,24266 | 0,11967 | 0,10747 | 0,10001 | 0,0947 | 0,08803 |
| 529,27984 | 0,12009 | 0,10866 | 0,1008 | 0,09564 | 0,08921 |
| 529,31703 | 0,12047 | 0,1098 | 0,10157 | 0,09656 | 0,09039 |
| 529,35421 | 0,12081 | 0,11091 | 0,10232 | 0,09745 | 0,09155 |
| 529,39139 | 0,12112 | 0,11199 | 0,10305 | 0,09832 | 0,09272 |
| 529,42857 | 0,12139 | 0,11303 | 0,10375 | 0,09916 | 0,09387 |
| 529,46575 | 0,12163 | 0,11403 | 0,10444 | 0,09998 | 0,09502 |
| 529,50294 | 0,12183 | 0,11499 | 0,1051 | 0,10078 | 0,09616 |
| 529,54012 | 0,122 | 0,11592 | 0,10575 | 0,10155 | 0,09729 |
| 529,5773 | 0,12212 | 0,1168 | 0,10636 | 0,1023 | 0,09841 |
| 529,61448 | 0,12221 | 0,11763 | 0,10696 | 0,10304 | 0,09953 |
| 529,65166 | 0,12227 | 0,11843 | 0,10753 | 0,10376 | 0,10063 |
| 529,68885 | 0,1223 | 0,1192 | 0,10808 | 0,10446 | 0,10171 |
| 529,72603 | 0,12229 | 0,1199 | 0,1086 | 0,10514 | 0,10278 |
| 529,76321 | 0,12225 | 0,12057 | 0,1091 | 0,10581 | 0,10384 |
| 529,80039 | 0,12218 | 0,12121 | 0,10958 | 0,10647 | 0,10489 |
| 529,83757 | 0,12207 | 0,1218 | 0,11002 | 0,1071 | 0,10591 |
| 529,87476 | 0,12194 | 0,12233 | 0,11044 | 0,10773 | 0,10691 |
| 529,91194 | 0,12177 | 0,12284 | 0,11083 | 0,10834 | 0,1079 |
| 529,94912 | 0,12158 | 0,1233 | 0,11119 | 0,10894 | 0,10885 |
| 529,9863 | 0,12135 | 0,12372 | 0,11152 | 0,10953 | 0,10978 |
| 530,02348 | 0,1211 | 0,12409 | 0,11183 | 0,11011 | 0,11069 |
| 530,06067 | 0,12083 | 0,12443 | 0,1121 | 0,11068 | 0,11157 |
| 530,09785 | 0,12053 | 0,12473 | 0,11234 | 0,11124 | 0,11242 |
| 530,13503 | 0,1202 | 0,12498 | 0,11254 | 0,11178 | 0,11324 |
| 530,17221 | 0,11985 | 0,12519 | 0,11273 | 0,11232 | 0,11403 |
| 530,20939 | 0,11948 | 0,12537 | 0,11286 | 0,11285 | 0,11478 |
| 530,24658 | 0,11908 | 0,12552 | 0,11297 | 0,11337 | 0,11549 |
| 530,28376 | 0,11867 | 0,12561 | 0,11305 | 0,11388 | 0,11617 |
| 530,32094 | 0,11824 | 0,12568 | 0,11309 | 0,11438 | 0,1168 |
| 530,35812 | 0,11779 | 0,12571 | 0,1131 | 0,11487 | 0,11739 |
| 530,3953 | 0,11732 | 0,12571 | 0,11307 | 0,11534 | 0,11794 |
| 530,43249 | 0,11684 | 0,12567 | 0,11301 | 0,11581 | 0,11846 |
| 530,46967 | 0,11634 | 0,1256 | 0,11291 | 0,11627 | 0,11891 |
| 530,50685 | 0,11584 | 0,1255 | 0,11278 | 0,11671 | 0,11932 |
| 530,54403 | 0,11532 | 0,12536 | 0,11262 | 0,11714 | 0,11969 |
| 530,58121 | 0,11479 | 0,12519 | 0,11242 | 0,11755 | 0,12001 |
| 530,6184 | 0,11426 | 0,125 | 0,11219 | 0,11795 | 0,12027 |
| 530,65558 | 0,11371 | 0,12478 | 0,11193 | 0,11833 | 0,12049 |
| 530,69276 | 0,11316 | 0,12453 | 0,11164 | 0,1187 | 0,12066 |
| 530,72994 | 0,11261 | 0,12425 | 0,11131 | 0,11905 | 0,12077 |
| 530,76712 | 0,11205 | 0,12395 | 0,11095 | 0,11938 | 0,12083 |
| 530,80431 | 0,11149 | 0,12362 | 0,11057 | 0,11969 | 0,12084 |
| 530,84149 | 0,11092 | 0,12326 | 0,11016 | 0,11998 | 0,12081 |
| 530,87867 | 0,11036 | 0,12288 | 0,10971 | 0,12025 | 0,1207 |
| 530,91585 | 0,1098 | 0,12249 | 0,10925 | 0,12049 | 0,12056 |
| 530,95303 | 0,10924 | 0,12206 | 0,10876 | 0,12071 | 0,12037 |
| 530,99022 | 0,10868 | 0,12161 | 0,10824 | 0,1209 | 0,12013 |
| 531,0274 | 0,10812 | 0,12115 | 0,10771 | 0,12107 | 0,11983 |
| 531,06458 | 0,10756 | 0,12067 | 0,10716 | 0,12121 | 0,11949 |
| 531,10176 | 0,10701 | 0,12016 | 0,10658 | 0,12131 | 0,11911 |
| 531,13894 | 0,10647 | 0,11964 | 0,10599 | 0,1214 | 0,11867 |
| 531,17613 | 0,10593 | 0,1191 | 0,10539 | 0,12145 | 0,11819 |
| 531,21331 | 0,10539 | 0,11854 | 0,10477 | 0,12146 | 0,11768 |
| 531,25049 | 0,10487 | 0,11796 | 0,10413 | 0,12145 | 0,11713 |
| 531,28767 | 0,10434 | 0,11737 | 0,10349 | 0,12141 | 0,11653 |
| 531,32485 | 0,10383 | 0,11677 | 0,10284 | 0,12133 | 0,1159 |
| 531,36204 | 0,10332 | 0,11614 | 0,10219 | 0,12121 | 0,11524 |
| 531,39922 | 0,10282 | 0,11551 | 0,10152 | 0,12106 | 0,11454 |
| 531,4364 | 0,10233 | 0,11486 | 0,10086 | 0,12089 | 0,11382 |
| 531,47358 | 0,10184 | 0,1142 | 0,10019 | 0,12066 | 0,11307 |
| 531,51076 | 0,10136 | 0,11353 | 0,09953 | 0,12041 | 0,1123 |
| 531,54795 | 0,10089 | 0,11284 | 0,09886 | 0,12013 | 0,1115 |
| 531,58513 | 0,10043 | 0,11215 | 0,0982 | 0,11981 | 0,11068 |
| 531,62231 | 0,09997 | 0,11145 | 0,09754 | 0,11946 | 0,10985 |
| 531,65949 | 0,09953 | 0,11074 | 0,09689 | 0,11907 | 0,10901 |
| 531,69667 | 0,09909 | 0,11002 | 0,09625 | 0,11865 | 0,10815 |
| 531,73386 | 0,09866 | 0,1093 | 0,09561 | 0,1182 | 0,10728 |
| 531,77104 | 0,09824 | 0,10856 | 0,09499 | 0,11772 | 0,10641 |
| 531,80822 | 0,09782 | 0,10783 | 0,09437 | 0,11721 | 0,10553 |
| 531,8454 | 0,09742 | 0,10709 | 0,09376 | 0,11667 | 0,10465 |
| 531,88258 | 0,09702 | 0,10635 | 0,09317 | 0,11609 | 0,10377 |
| 531,91977 | 0,09663 | 0,1056 | 0,09259 | 0,1155 | 0,10289 |
| 531,95695 | 0,09625 | 0,10486 | 0,09202 | 0,11488 | 0,10201 |
| 531,99413 | 0,09588 | 0,10412 | 0,09147 | 0,11423 | 0,10115 |
| 532,03131 | 0,09552 | 0,10337 | 0,09093 | 0,11356 | 0,10029 |
| 532,06849 | 0,09517 | 0,10263 | 0,09041 | 0,11287 | 0,09944 |
| 532,10568 | 0,09482 | 0,1019 | 0,0899 | 0,11216 | 0,0986 |
| 532,14286 | 0,09449 | 0,10116 | 0,08941 | 0,11143 | 0,09777 |
| 532,18004 | 0,09416 | 0,10044 | 0,08893 | 0,11068 | 0,09696 |
| 532,21722 | 0,09385 | 0,09972 | 0,08846 | 0,10993 | 0,09616 |
| 532,2544 | 0,09354 | 0,09901 | 0,08801 | 0,10916 | 0,09539 |
| 532,29159 | 0,09324 | 0,0983 | 0,08758 | 0,10837 | 0,09462 |
| 532,32877 | 0,09295 | 0,09761 | 0,08715 | 0,10758 | 0,09388 |
| 532,36595 | 0,09267 | 0,09692 | 0,08675 | 0,10678 | 0,09316 |
| 532,40313 | 0,0924 | 0,09625 | 0,08635 | 0,10597 | 0,09246 |
| 532,44031 | 0,09214 | 0,09559 | 0,08597 | 0,10516 | 0,09177 |
| 532,4775 | 0,09189 | 0,09494 | 0,08559 | 0,10435 | 0,09111 |
| 532,51468 | 0,09165 | 0,09431 | 0,08523 | 0,10354 | 0,09048 |
| 532,55186 | 0,09141 | 0,09369 | 0,08488 | 0,10273 | 0,08986 |
| 532,58904 | 0,09118 | 0,09309 | 0,08453 | 0,10192 | 0,08926 |
| 532,62622 | 0,09096 | 0,0925 | 0,08419 | 0,10111 | 0,08869 |
| 532,66341 | 0,09075 | 0,09193 | 0,08386 | 0,10031 | 0,08814 |
| 532,70059 | 0,09054 | 0,09137 | 0,08354 | 0,09951 | 0,0876 |
| 532,73777 | 0,09034 | 0,09083 | 0,08322 | 0,09872 | 0,0871 |
| 532,77495 | 0,09014 | 0,09031 | 0,0829 | 0,09794 | 0,08661 |
| 532,81213 | 0,08995 | 0,08981 | 0,08259 | 0,09716 | 0,08614 |
| 532,84932 | 0,08976 | 0,08932 | 0,08228 | 0,0964 | 0,08569 |
| 532,8865 | 0,08957 | 0,08886 | 0,08197 | 0,09565 | 0,08527 |
| 532,92368 | 0,08939 | 0,08841 | 0,08166 | 0,0949 | 0,08486 |
| 532,96086 | 0,0892 | 0,08797 | 0,08134 | 0,09417 | 0,08446 |
| 532,99804 | 0,08902 | 0,08756 | 0,08103 | 0,09345 | 0,08409 |
| 533,03523 | 0,08883 | 0,08717 | 0,08071 | 0,09274 | 0,08373 |
| 533,07241 | 0,08864 | 0,08679 | 0,08038 | 0,09204 | 0,08338 |
| 533,10959 | 0,08845 | 0,08643 | 0,08006 | 0,09135 | 0,08305 |
| 533,14677 | 0,08825 | 0,08609 | 0,07972 | 0,09068 | 0,08274 |
| 533,18395 | 0,08804 | 0,08576 | 0,07938 | 0,09002 | 0,08244 |
| 533,22114 | 0,08783 | 0,08544 | 0,07903 | 0,08936 | 0,08214 |
| 533,25832 | 0,08761 | 0,08515 | 0,07868 | 0,08872 | 0,08186 |
| 533,2955 | 0,08738 | 0,08487 | 0,07831 | 0,08809 | 0,08159 |
| 533,33268 | 0,08714 | 0,08461 | 0,07794 | 0,08746 | 0,08132 |
| 533,36986 | 0,08689 | 0,08435 | 0,07755 | 0,08685 | 0,08106 |
| 533,40705 | 0,08662 | 0,08412 | 0,07716 | 0,08624 | 0,08081 |
| 533,44423 | 0,08634 | 0,08389 | 0,07675 | 0,08565 | 0,08056 |
| 533,48141 | 0,08605 | 0,08368 | 0,07634 | 0,08505 | 0,08032 |
| 533,51859 | 0,08573 | 0,08348 | 0,07592 | 0,08447 | 0,08008 |
| 533,55577 | 0,0854 | 0,08329 | 0,07548 | 0,08389 | 0,07984 |
| 533,59295 | 0,08506 | 0,08311 | 0,07504 | 0,08332 | 0,0796 |
| 533,63014 | 0,0847 | 0,08294 | 0,07458 | 0,08274 | 0,07936 |
| 533,66732 | 0,08431 | 0,08278 | 0,07411 | 0,08218 | 0,07911 |
| 533,7045 | 0,08391 | 0,08262 | 0,07364 | 0,08162 | 0,07887 |
| 533,74168 | 0,08349 | 0,08247 | 0,07315 | 0,08106 | 0,07862 |
| 533,77886 | 0,08305 | 0,08233 | 0,07266 | 0,0805 | 0,07837 |
| 533,81605 | 0,08258 | 0,0822 | 0,07216 | 0,07994 | 0,07811 |
| 533,85323 | 0,0821 | 0,08207 | 0,07165 | 0,07939 | 0,07785 |
| 533,89041 | 0,0816 | 0,08194 | 0,07113 | 0,07884 | 0,07758 |
| 533,92759 | 0,08107 | 0,08182 | 0,07061 | 0,07829 | 0,0773 |
| 533,96477 | 0,08053 | 0,0817 | 0,07008 | 0,07775 | 0,07702 |
| 534,00196 | 0,07996 | 0,08158 | 0,06955 | 0,0772 | 0,07673 |
| 534,03914 | 0,07938 | 0,08147 | 0,06901 | 0,07666 | 0,07643 |
| 534,07632 | 0,07878 | 0,08135 | 0,06847 | 0,07612 | 0,07612 |
| 534,1135 | 0,07815 | 0,08123 | 0,06793 | 0,07558 | 0,0758 |
| 534,15068 | 0,07752 | 0,08112 | 0,06738 | 0,07504 | 0,07548 |
| 534,18787 | 0,07686 | 0,081 | 0,06684 | 0,07451 | 0,07515 |
| 534,22505 | 0,07619 | 0,08088 | 0,0663 | 0,07399 | 0,0748 |
| 534,26223 | 0,0755 | 0,08075 | 0,06576 | 0,07347 | 0,07445 |
| 534,29941 | 0,07479 | 0,08062 | 0,06523 | 0,07296 | 0,07409 |
| 534,33659 | 0,07408 | 0,08049 | 0,0647 | 0,07245 | 0,07373 |
| 534,37378 | 0,07334 | 0,08035 | 0,06417 | 0,07195 | 0,07335 |
| 534,41096 | 0,0726 | 0,08021 | 0,06366 | 0,07146 | 0,07297 |
| 534,44814 | 0,07185 | 0,08006 | 0,06315 | 0,07098 | 0,07259 |
| 534,48532 | 0,07109 | 0,0799 | 0,06265 | 0,07051 | 0,0722 |
| 534,5225 | 0,07031 | 0,07973 | 0,06216 | 0,07005 | 0,0718 |
| 534,55969 | 0,06954 | 0,07956 | 0,06169 | 0,06961 | 0,0714 |
| 534,59687 | 0,06875 | 0,07938 | 0,06123 | 0,06917 | 0,071 |
| 534,63405 | 0,06796 | 0,07918 | 0,06078 | 0,06876 | 0,0706 |
| 534,67123 | 0,06716 | 0,07898 | 0,06035 | 0,06836 | 0,0702 |
| 534,70841 | 0,06637 | 0,07877 | 0,05993 | 0,06797 | 0,0698 |
| 534,7456 | 0,06557 | 0,07854 | 0,05953 | 0,0676 | 0,0694 |
| 534,78278 | 0,06477 | 0,07831 | 0,05915 | 0,06726 | 0,069 |
| 534,81996 | 0,06397 | 0,07806 | 0,05879 | 0,06693 | 0,06861 |
| 534,85714 | 0,06318 | 0,0778 | 0,05844 | 0,06661 | 0,06822 |
| 534,89432 | 0,06238 | 0,07753 | 0,05812 | 0,06632 | 0,06784 |
| 534,93151 | 0,0616 | 0,07725 | 0,05782 | 0,06605 | 0,06747 |
| 534,96869 | 0,06081 | 0,07695 | 0,05754 | 0,0658 | 0,0671 |
| 535,00587 | 0,06004 | 0,07664 | 0,05728 | 0,06557 | 0,06675 |
| 535,04305 | 0,05927 | 0,07631 | 0,05704 | 0,06536 | 0,06641 |
| 535,08023 | 0,05851 | 0,07597 | 0,05683 | 0,06517 | 0,06607 |
| 535,11742 | 0,05776 | 0,07562 | 0,05664 | 0,065 | 0,06576 |
| 535,1546 | 0,05702 | 0,07525 | 0,05647 | 0,06485 | 0,06545 |
| 535,19178 | 0,0563 | 0,07487 | 0,05632 | 0,06473 | 0,06516 |
| 535,22896 | 0,05559 | 0,07447 | 0,05621 | 0,06462 | 0,06488 |
| 535,26614 | 0,05489 | 0,07407 | 0,05611 | 0,06453 | 0,06463 |
| 535,30333 | 0,05421 | 0,07364 | 0,05603 | 0,06446 | 0,06438 |
| 535,34051 | 0,05354 | 0,0732 | 0,05598 | 0,06441 | 0,06415 |
| 535,37769 | 0,05289 | 0,07275 | 0,05595 | 0,06437 | 0,06394 |
| 535,41487 | 0,05225 | 0,07228 | 0,05594 | 0,06434 | 0,06375 |
| 535,45205 | 0,05164 | 0,0718 | 0,05596 | 0,06434 | 0,06356 |
| 535,48924 | 0,05104 | 0,07131 | 0,05599 | 0,06435 | 0,0634 |
| 535,52642 | 0,05047 | 0,0708 | 0,05604 | 0,06436 | 0,06325 |
| 535,5636 | 0,04991 | 0,07029 | 0,05611 | 0,06439 | 0,06312 |
| 535,60078 | 0,04938 | 0,06975 | 0,05621 | 0,06443 | 0,063 |
| 535,63796 | 0,04886 | 0,06921 | 0,05632 | 0,06448 | 0,0629 |
| 535,67515 | 0,04836 | 0,06866 | 0,05644 | 0,06453 | 0,06281 |
| 535,71233 | 0,0479 | 0,06809 | 0,05658 | 0,06459 | 0,06274 |
| 535,74951 | 0,04745 | 0,06751 | 0,05674 | 0,06466 | 0,06267 |
| 535,78669 | 0,04702 | 0,06692 | 0,05691 | 0,06473 | 0,06262 |
| 535,82387 | 0,04662 | 0,06633 | 0,05709 | 0,06479 | 0,06258 |
| 535,86106 | 0,04624 | 0,06572 | 0,05728 | 0,06486 | 0,06255 |
| 535,89824 | 0,04588 | 0,06511 | 0,05748 | 0,06493 | 0,06253 |
| 535,93542 | 0,04555 | 0,06449 | 0,05769 | 0,06499 | 0,06251 |
| 535,9726 | 0,04523 | 0,06386 | 0,05791 | 0,06505 | 0,0625 |
| 536,00978 | 0,04495 | 0,06323 | 0,05813 | 0,06511 | 0,0625 |
| 536,04697 | 0,04468 | 0,06259 | 0,05836 | 0,06515 | 0,0625 |
| 536,08415 | 0,04443 | 0,06195 | 0,05859 | 0,0652 | 0,0625 |
| 536,12133 | 0,04421 | 0,06131 | 0,05882 | 0,06523 | 0,0625 |
| 536,15851 | 0,04401 | 0,06066 | 0,05906 | 0,06525 | 0,06251 |
| 536,19569 | 0,04382 | 0,06001 | 0,05929 | 0,06526 | 0,06251 |
| 536,23288 | 0,04366 | 0,05936 | 0,05953 | 0,06526 | 0,06252 |
| 536,27006 | 0,04352 | 0,05871 | 0,05976 | 0,06525 | 0,06252 |
| 536,30724 | 0,04339 | 0,05806 | 0,05998 | 0,06523 | 0,06252 |
| 536,34442 | 0,04328 | 0,05742 | 0,0602 | 0,06519 | 0,06252 |
| 536,3816 | 0,04319 | 0,05678 | 0,06042 | 0,06515 | 0,06251 |
| 536,41879 | 0,04311 | 0,05614 | 0,06063 | 0,06508 | 0,0625 |
| 536,45597 | 0,04305 | 0,05551 | 0,06083 | 0,065 | 0,06248 |
| 536,49315 | 0,04299 | 0,05488 | 0,06103 | 0,06491 | 0,06246 |
| 536,53033 | 0,04295 | 0,05426 | 0,06121 | 0,06481 | 0,06244 |
| 536,56751 | 0,04292 | 0,05366 | 0,06139 | 0,06469 | 0,06241 |
| 536,6047 | 0,0429 | 0,05306 | 0,06156 | 0,06456 | 0,06237 |
| 536,64188 | 0,04288 | 0,05246 | 0,06171 | 0,06441 | 0,06233 |
| 536,67906 | 0,04287 | 0,05189 | 0,06186 | 0,06425 | 0,06228 |
| 536,71624 | 0,04286 | 0,05132 | 0,06199 | 0,06408 | 0,06223 |
| 536,75342 | 0,04285 | 0,05076 | 0,06211 | 0,06389 | 0,06217 |
| 536,79061 | 0,04285 | 0,05022 | 0,06223 | 0,0637 | 0,06211 |
| 536,82779 | 0,04284 | 0,0497 | 0,06233 | 0,06349 | 0,06205 |
| 536,86497 | 0,04283 | 0,04918 | 0,06241 | 0,06327 | 0,06198 |
| 536,90215 | 0,04282 | 0,04868 | 0,06249 | 0,06304 | 0,06191 |
| 536,93933 | 0,0428 | 0,04821 | 0,06255 | 0,0628 | 0,06184 |
| 536,97652 | 0,04277 | 0,04774 | 0,0626 | 0,06255 | 0,06177 |
| 537,0137 | 0,04273 | 0,04729 | 0,06264 | 0,06229 | 0,0617 |
| 537,05088 | 0,04268 | 0,04685 | 0,06267 | 0,06202 | 0,06162 |
| 537,08806 | 0,04262 | 0,04644 | 0,06269 | 0,06175 | 0,06155 |
| 537,12524 | 0,04254 | 0,04604 | 0,0627 | 0,06147 | 0,06148 |
| 537,16243 | 0,04246 | 0,04565 | 0,06269 | 0,06119 | 0,06141 |
| 537,19961 | 0,04235 | 0,04529 | 0,06268 | 0,0609 | 0,06135 |
| 537,23679 | 0,04223 | 0,04494 | 0,06266 | 0,06061 | 0,06129 |
| 537,27397 | 0,04209 | 0,0446 | 0,06263 | 0,06031 | 0,06123 |
| 537,31115 | 0,04193 | 0,04428 | 0,06259 | 0,06001 | 0,06117 |
| 537,34834 | 0,04175 | 0,04398 | 0,06254 | 0,05971 | 0,06112 |
| 537,38552 | 0,04154 | 0,04369 | 0,06248 | 0,0594 | 0,06108 |
| 537,4227 | 0,04132 | 0,04341 | 0,06242 | 0,0591 | 0,06104 |
| 537,45988 | 0,04108 | 0,04315 | 0,06235 | 0,0588 | 0,06101 |
| 537,49706 | 0,04081 | 0,0429 | 0,06227 | 0,05849 | 0,06098 |
| 537,53425 | 0,04053 | 0,04266 | 0,06219 | 0,05819 | 0,06095 |
| 537,57143 | 0,04022 | 0,04243 | 0,0621 | 0,05789 | 0,06094 |
| 537,60861 | 0,03989 | 0,04222 | 0,06201 | 0,05758 | 0,06092 |
| 537,64579 | 0,03954 | 0,04201 | 0,06191 | 0,05728 | 0,06091 |
| 537,68297 | 0,03916 | 0,04181 | 0,06181 | 0,05699 | 0,06091 |
| 537,72016 | 0,03877 | 0,04162 | 0,0617 | 0,05669 | 0,06091 |
| 537,75734 | 0,03836 | 0,04144 | 0,06159 | 0,05639 | 0,06091 |
| 537,79452 | 0,03792 | 0,04126 | 0,06147 | 0,0561 | 0,06091 |
| 537,8317 | 0,03747 | 0,04108 | 0,06135 | 0,05581 | 0,06091 |
| 537,86888 | 0,03701 | 0,04091 | 0,06122 | 0,05552 | 0,06091 |
| 537,90607 | 0,03652 | 0,04074 | 0,06109 | 0,05523 | 0,06091 |
| 537,94325 | 0,03602 | 0,04058 | 0,06096 | 0,05495 | 0,06091 |
| 537,98043 | 0,03551 | 0,04041 | 0,06083 | 0,05466 | 0,0609 |
| 538,01761 | 0,03499 | 0,04025 | 0,06068 | 0,05438 | 0,06089 |
| 538,05479 | 0,03445 | 0,04008 | 0,06054 | 0,05409 | 0,06087 |
| 538,09198 | 0,03391 | 0,03991 | 0,06039 | 0,05381 | 0,06085 |
| 538,12916 | 0,03336 | 0,03974 | 0,06023 | 0,05352 | 0,06081 |
| 538,16634 | 0,0328 | 0,03957 | 0,06007 | 0,05324 | 0,06076 |
| 538,20352 | 0,03224 | 0,03939 | 0,0599 | 0,05295 | 0,0607 |
| 538,2407 | 0,03167 | 0,03921 | 0,05973 | 0,05266 | 0,06063 |
| 538,27789 | 0,0311 | 0,03902 | 0,05954 | 0,05236 | 0,06054 |
| 538,31507 | 0,03053 | 0,03882 | 0,05936 | 0,05207 | 0,06043 |
| 538,35225 | 0,02997 | 0,03862 | 0,05916 | 0,05176 | 0,0603 |
| 538,38943 | 0,0294 | 0,03841 | 0,05895 | 0,05145 | 0,06015 |
| 538,42661 | 0,02884 | 0,03819 | 0,05874 | 0,05114 | 0,05998 |
| 538,4638 | 0,02828 | 0,03796 | 0,05851 | 0,05082 | 0,05979 |
| 538,50098 | 0,02773 | 0,03773 | 0,05828 | 0,05048 | 0,05957 |
| 538,53816 | 0,02719 | 0,03749 | 0,05803 | 0,05014 | 0,05933 |
| 538,57534 | 0,02666 | 0,03724 | 0,05777 | 0,0498 | 0,05906 |
| 538,61252 | 0,02613 | 0,03697 | 0,0575 | 0,04943 | 0,05876 |
| 538,64971 | 0,02562 | 0,0367 | 0,05722 | 0,04906 | 0,05844 |
| 538,68689 | 0,02511 | 0,03642 | 0,05691 | 0,04868 | 0,05809 |
| 538,72407 | 0,02462 | 0,03613 | 0,0566 | 0,04828 | 0,05771 |
| 538,76125 | 0,02415 | 0,03583 | 0,05627 | 0,04787 | 0,0573 |
| 538,79843 | 0,02368 | 0,03552 | 0,05592 | 0,04745 | 0,05686 |
| 538,83562 | 0,02323 | 0,0352 | 0,05556 | 0,04701 | 0,05639 |
| 538,8728 | 0,02279 | 0,03487 | 0,05518 | 0,04656 | 0,05589 |
| 538,90998 | 0,02237 | 0,03453 | 0,05478 | 0,04608 | 0,05536 |
| 538,94716 | 0,02195 | 0,03418 | 0,05436 | 0,0456 | 0,05481 |
| 538,98434 | 0,02156 | 0,03382 | 0,05392 | 0,0451 | 0,05421 |
| 539,02153 | 0,02118 | 0,03345 | 0,05346 | 0,04458 | 0,0536 |
| 539,05871 | 0,02081 | 0,03307 | 0,05298 | 0,04404 | 0,05296 |
| 539,09589 | 0,02045 | 0,03268 | 0,05249 | 0,04349 | 0,05229 |
| 539,13307 | 0,02011 | 0,03228 | 0,05197 | 0,04292 | 0,05159 |
| 539,17025 | 0,01979 | 0,03188 | 0,05143 | 0,04233 | 0,05087 |
| 539,20744 | 0,01947 | 0,03146 | 0,05087 | 0,04173 | 0,05013 |
| 539,24462 | 0,01917 | 0,03104 | 0,0503 | 0,04112 | 0,04936 |
| 539,2818 | 0,01888 | 0,03061 | 0,0497 | 0,04048 | 0,04858 |
| 539,31898 | 0,0186 | 0,03017 | 0,04908 | 0,03983 | 0,04777 |
| 539,35616 | 0,01833 | 0,02972 | 0,04844 | 0,03916 | 0,04695 |
| 539,39335 | 0,01807 | 0,02927 | 0,04778 | 0,03849 | 0,04611 |
| 539,43053 | 0,01782 | 0,02881 | 0,0471 | 0,03779 | 0,04526 |
| 539,46771 | 0,01758 | 0,02834 | 0,0464 | 0,03709 | 0,0444 |
| 539,50489 | 0,01735 | 0,02787 | 0,04569 | 0,03637 | 0,04352 |
| 539,54207 | 0,01713 | 0,02739 | 0,04496 | 0,03564 | 0,04264 |
| 539,57926 | 0,01691 | 0,0269 | 0,0442 | 0,0349 | 0,04175 |
| 539,61644 | 0,0167 | 0,02641 | 0,04344 | 0,03415 | 0,04085 |
| 539,65362 | 0,01649 | 0,02592 | 0,04266 | 0,0334 | 0,03995 |
| 539,6908 | 0,01629 | 0,02542 | 0,04186 | 0,03263 | 0,03905 |
| 539,72798 | 0,0161 | 0,02491 | 0,04105 | 0,03186 | 0,03815 |
| 539,76517 | 0,01591 | 0,02441 | 0,04024 | 0,03109 | 0,03724 |
| 539,80235 | 0,01572 | 0,0239 | 0,0394 | 0,03031 | 0,03635 |
| 539,83953 | 0,01554 | 0,02339 | 0,03856 | 0,02953 | 0,03545 |
| 539,87671 | 0,01535 | 0,02287 | 0,03771 | 0,02875 | 0,03457 |
| 539,91389 | 0,01517 | 0,02236 | 0,03685 | 0,02797 | 0,03369 |
| 539,95108 | 0,015 | 0,02184 | 0,03598 | 0,02719 | 0,03282 |
| 539,98826 | 0,01482 | 0,02133 | 0,03511 | 0,02641 | 0,03196 |
| 540,02544 | 0,01464 | 0,02081 | 0,03423 | 0,02564 | 0,03111 |
| 540,06262 | 0,01447 | 0,0203 | 0,03335 | 0,02487 | 0,03028 |
| 540,0998 | 0,01429 | 0,01978 | 0,03247 | 0,02411 | 0,02945 |
| 540,13699 | 0,01412 | 0,01927 | 0,03159 | 0,02335 | 0,02864 |
| 540,17417 | 0,01394 | 0,01876 | 0,03071 | 0,0226 | 0,02785 |
| 540,21135 | 0,01377 | 0,01826 | 0,02983 | 0,02186 | 0,02707 |
| 540,24853 | 0,01359 | 0,01775 | 0,02895 | 0,02113 | 0,02631 |
| 540,28571 | 0,01341 | 0,01725 | 0,02807 | 0,02041 | 0,02557 |
| 540,3229 | 0,01324 | 0,01676 | 0,02721 | 0,0197 | 0,02484 |
| 540,36008 | 0,01306 | 0,01627 | 0,02635 | 0,019 | 0,02413 |
| 540,39726 | 0,01288 | 0,01579 | 0,02549 | 0,01832 | 0,02344 |
| 540,43444 | 0,0127 | 0,01531 | 0,02464 | 0,01765 | 0,02277 |
| 540,47162 | 0,01252 | 0,01484 | 0,02381 | 0,01699 | 0,02211 |
| 540,50881 | 0,01234 | 0,01437 | 0,02298 | 0,01635 | 0,02147 |
| 540,54599 | 0,01216 | 0,01392 | 0,02216 | 0,01572 | 0,02085 |
| 540,58317 | 0,01197 | 0,01347 | 0,02136 | 0,01511 | 0,02025 |
| 540,62035 | 0,01179 | 0,01303 | 0,02057 | 0,01451 | 0,01966 |
| 540,65753 | 0,0116 | 0,01259 | 0,01979 | 0,01393 | 0,01909 |
| 540,69472 | 0,01142 | 0,01217 | 0,01903 | 0,01337 | 0,01854 |
| 540,7319 | 0,01123 | 0,01175 | 0,01829 | 0,01282 | 0,01801 |
| 540,76908 | 0,01105 | 0,01135 | 0,01755 | 0,01228 | 0,01748 |
| 540,80626 | 0,01086 | 0,01095 | 0,01683 | 0,01177 | 0,01698 |
| 540,84344 | 0,01067 | 0,01056 | 0,01614 | 0,01127 | 0,01649 |
| 540,88063 | 0,01048 | 0,01018 | 0,01545 | 0,01078 | 0,01601 |
| 540,91781 | 0,01029 | 0,00982 | 0,01478 | 0,01031 | 0,01554 |
| 540,95499 | 0,0101 | 0,00946 | 0,01414 | 0,00986 | 0,01509 |
| 540,99217 | 0,00991 | 0,00911 | 0,01351 | 0,00943 | 0,01465 |
| 541,02935 | 0,00972 | 0,00877 | 0,01289 | 0,009 | 0,01423 |
| 541,06654 | 0,00953 | 0,00844 | 0,01229 | 0,00859 | 0,01381 |
| 541,10372 | 0,00934 | 0,00812 | 0,01172 | 0,0082 | 0,0134 |
| 541,1409 | 0,00915 | 0,00781 | 0,01116 | 0,00783 | 0,01301 |
| 541,17808 | 0,00896 | 0,00752 | 0,01062 | 0,00746 | 0,01262 |
| 541,21526 | 0,00877 | 0,00723 | 0,01009 | 0,00711 | 0,01224 |
| 541,25245 | 0,00858 | 0,00694 | 0,00959 | 0,00678 | 0,01187 |
| 541,28963 | 0,00839 | 0,00667 | 0,0091 | 0,00645 | 0,01151 |
| 541,32681 | 0,0082 | 0,00641 | 0,00863 | 0,00614 | 0,01115 |
| 541,36399 | 0,00801 | 0,00616 | 0,00818 | 0,00584 | 0,0108 |
| 541,40117 | 0,00781 | 0,00591 | 0,00775 | 0,00556 | 0,01046 |
| 541,43836 | 0,00762 | 0,00567 | 0,00733 | 0,00528 | 0,01013 |
| 541,47554 | 0,00743 | 0,00544 | 0,00693 | 0,00502 | 0,0098 |
| 541,51272 | 0,00724 | 0,00522 | 0,00654 | 0,00477 | 0,00948 |
| 541,5499 | 0,00705 | 0,00501 | 0,00617 | 0,00453 | 0,00916 |
| 541,58708 | 0,00686 | 0,0048 | 0,00582 | 0,00429 | 0,00885 |
| 541,62427 | 0,00667 | 0,0046 | 0,00549 | 0,00407 | 0,00854 |
| 541,66145 | 0,00649 | 0,00441 | 0,00517 | 0,00386 | 0,00824 |
| 541,69863 | 0,0063 | 0,00422 | 0,00486 | 0,00366 | 0,00794 |
| 541,73581 | 0,00611 | 0,00404 | 0,00457 | 0,00346 | 0,00765 |
| 541,77299 | 0,00593 | 0,00387 | 0,00429 | 0,00328 | 0,00736 |
| 541,81018 | 0,00574 | 0,0037 | 0,00402 | 0,0031 | 0,00708 |
| 541,84736 | 0,00556 | 0,00354 | 0,00377 | 0,00293 | 0,0068 |
| 541,88454 | 0,00537 | 0,00338 | 0,00353 | 0,00277 | 0,00653 |
| 541,92172 | 0,00519 | 0,00323 | 0,0033 | 0,00261 | 0,00626 |
| 541,9589 | 0,00501 | 0,00308 | 0,00309 | 0,00246 | 0,006 |
| 541,99609 | 0,00484 | 0,00294 | 0,00289 | 0,00232 | 0,00574 |
| 542,03327 | 0,00466 | 0,0028 | 0,00269 | 0,00219 | 0,00549 |
| 542,07045 | 0,00449 | 0,00267 | 0,00251 | 0,00206 | 0,00525 |
| 542,10763 | 0,00431 | 0,00254 | 0,00234 | 0,00194 | 0,00501 |
| 542,14481 | 0,00415 | 0,00242 | 0,00218 | 0,00182 | 0,00477 |
| 542,182 | 0,00398 | 0,0023 | 0,00202 | 0,00171 | 0,00455 |
| 542,21918 | 0,00381 | 0,00218 | 0,00188 | 0,0016 | 0,00433 |
| 542,25636 | 0,00365 | 0,00207 | 0,00175 | 0,0015 | 0,00411 |
| 542,29354 | 0,0035 | 0,00197 | 0,00162 | 0,00141 | 0,0039 |
| 542,33072 | 0,00334 | 0,00186 | 0,0015 | 0,00132 | 0,0037 |
| 542,36791 | 0,00319 | 0,00176 | 0,00139 | 0,00123 | 0,0035 |
| 542,40509 | 0,00304 | 0,00167 | 0,00128 | 0,00115 | 0,00331 |
| 542,44227 | 0,0029 | 0,00158 | 0,00119 | 0,00107 | 0,00312 |
| 542,47945 | 0,00276 | 0,00149 | 0,00109 | 0,001 | 0,00295 |
| 542,51663 | 0,00262 | 0,0014 | 0,00101 | 0,00093 | 0,00277 |
| 542,55382 | 0,00248 | 0,00132 | 0,00093 | 0,00086 | 0,00261 |
| 542,591 | 0,00236 | 0,00124 | 0,00086 | 8e-04 | 0,00245 |
| 542,62818 | 0,00223 | 0,00117 | 0,00079 | 0,00075 | 0,0023 |
| 542,66536 | 0,00211 | 0,0011 | 0,00072 | 0,00069 | 0,00215 |
| 542,70254 | 0,00199 | 0,00103 | 0,00066 | 0,00064 | 0,00202 |
| 542,73973 | 0,00188 | 0,00096 | 0,00061 | 0,00059 | 0,00188 |
| 542,77691 | 0,00177 | 9e-04 | 0,00056 | 0,00055 | 0,00176 |
| 542,81409 | 0,00166 | 0,00084 | 0,00051 | 5e-04 | 0,00164 |
| 542,85127 | 0,00156 | 0,00078 | 0,00046 | 0,00046 | 0,00152 |
| 542,88845 | 0,00147 | 0,00073 | 0,00042 | 0,00043 | 0,00142 |
| 542,92564 | 0,00137 | 0,00068 | 0,00039 | 0,00039 | 0,00131 |
| 542,96282 | 0,00129 | 0,00063 | 0,00035 | 0,00036 | 0,00122 |
| 543 | 0,0012 | 0,00058 | 0,00032 | 0,00033 | 0,00113 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00014 | 0,00041 | 0,00041 | 0,00029 | 2e-04 |
| 524,03718 | 0,00016 | 0,00045 | 0,00045 | 0,00031 | 0,00022 |
| 524,07436 | 0,00017 | 0,00049 | 0,00048 | 0,00034 | 0,00024 |
| 524,11155 | 0,00019 | 0,00054 | 0,00053 | 0,00037 | 0,00026 |
| 524,14873 | 0,00021 | 0,00059 | 0,00057 | 4e-04 | 0,00029 |
| 524,18591 | 0,00023 | 0,00064 | 0,00062 | 0,00043 | 0,00031 |
| 524,22309 | 0,00025 | 7e-04 | 0,00067 | 0,00047 | 0,00034 |
| 524,26027 | 0,00028 | 0,00076 | 0,00072 | 0,00051 | 0,00037 |
| 524,29746 | 3e-04 | 0,00083 | 0,00078 | 0,00055 | 0,00041 |
| 524,33464 | 0,00033 | 9e-04 | 0,00084 | 0,00059 | 0,00044 |
| 524,37182 | 0,00036 | 0,00098 | 9e-04 | 0,00064 | 0,00048 |
| 524,409 | 4e-04 | 0,00107 | 0,00097 | 0,00069 | 0,00052 |
| 524,44618 | 0,00043 | 0,00116 | 0,00104 | 0,00074 | 0,00057 |
| 524,48337 | 0,00047 | 0,00126 | 0,00112 | 0,00079 | 0,00062 |
| 524,52055 | 0,00051 | 0,00136 | 0,00121 | 0,00085 | 0,00067 |
| 524,55773 | 0,00056 | 0,00147 | 0,00129 | 0,00091 | 0,00072 |
| 524,59491 | 0,00061 | 0,00159 | 0,00139 | 0,00098 | 0,00078 |
| 524,63209 | 0,00066 | 0,00172 | 0,00149 | 0,00104 | 0,00084 |
| 524,66928 | 0,00072 | 0,00185 | 0,00159 | 0,00111 | 0,00091 |
| 524,70646 | 0,00078 | 0,00199 | 0,0017 | 0,00119 | 0,00098 |
| 524,74364 | 0,00084 | 0,00215 | 0,00182 | 0,00127 | 0,00106 |
| 524,78082 | 0,00091 | 0,00231 | 0,00194 | 0,00135 | 0,00114 |
| 524,818 | 0,00098 | 0,00248 | 0,00207 | 0,00144 | 0,00122 |
| 524,85519 | 0,00106 | 0,00267 | 0,00221 | 0,00153 | 0,00131 |
| 524,89237 | 0,00115 | 0,00286 | 0,00236 | 0,00162 | 0,00141 |
| 524,92955 | 0,00124 | 0,00307 | 0,00251 | 0,00172 | 0,00151 |
| 524,96673 | 0,00133 | 0,00329 | 0,00267 | 0,00182 | 0,00162 |
| 525,00391 | 0,00143 | 0,00352 | 0,00284 | 0,00193 | 0,00173 |
| 525,0411 | 0,00154 | 0,00376 | 0,00302 | 0,00204 | 0,00185 |
| 525,07828 | 0,00165 | 0,00402 | 0,0032 | 0,00215 | 0,00198 |
| 525,11546 | 0,00178 | 0,0043 | 0,0034 | 0,00227 | 0,00211 |
| 525,15264 | 0,0019 | 0,00458 | 0,0036 | 0,0024 | 0,00225 |
| 525,18982 | 0,00204 | 0,00488 | 0,00382 | 0,00253 | 0,0024 |
| 525,22701 | 0,00218 | 0,0052 | 0,00404 | 0,00266 | 0,00255 |
| 525,26419 | 0,00233 | 0,00553 | 0,00427 | 0,0028 | 0,00272 |
| 525,30137 | 0,00249 | 0,00588 | 0,00452 | 0,00294 | 0,00289 |
| 525,33855 | 0,00266 | 0,00625 | 0,00477 | 0,00309 | 0,00307 |
| 525,37573 | 0,00284 | 0,00663 | 0,00504 | 0,00324 | 0,00326 |
| 525,41292 | 0,00303 | 0,00703 | 0,00531 | 0,0034 | 0,00345 |
| 525,4501 | 0,00322 | 0,00745 | 0,00561 | 0,00356 | 0,00366 |
| 525,48728 | 0,00343 | 0,00789 | 0,00591 | 0,00373 | 0,00387 |
| 525,52446 | 0,00364 | 0,00835 | 0,00622 | 0,0039 | 0,0041 |
| 525,56164 | 0,00387 | 0,00883 | 0,00654 | 0,00408 | 0,00433 |
| 525,59883 | 0,00411 | 0,00932 | 0,00688 | 0,00426 | 0,00458 |
| 525,63601 | 0,00436 | 0,00984 | 0,00723 | 0,00445 | 0,00483 |
| 525,67319 | 0,00462 | 0,01038 | 0,0076 | 0,00465 | 0,0051 |
| 525,71037 | 0,00489 | 0,01093 | 0,00798 | 0,00485 | 0,00538 |
| 525,74755 | 0,00518 | 0,01151 | 0,00836 | 0,00506 | 0,00566 |
| 525,78474 | 0,00548 | 0,01211 | 0,00877 | 0,00527 | 0,00596 |
| 525,82192 | 0,00579 | 0,01274 | 0,00919 | 0,00549 | 0,00628 |
| 525,8591 | 0,00611 | 0,01338 | 0,00962 | 0,00571 | 0,0066 |
| 525,89628 | 0,00645 | 0,01405 | 0,01007 | 0,00594 | 0,00693 |
| 525,93346 | 0,0068 | 0,01474 | 0,01053 | 0,00618 | 0,00728 |
| 525,97065 | 0,00717 | 0,01544 | 0,01101 | 0,00643 | 0,00764 |
| 526,00783 | 0,00755 | 0,01618 | 0,0115 | 0,00668 | 0,00802 |
| 526,04501 | 0,00795 | 0,01693 | 0,01201 | 0,00694 | 0,00841 |
| 526,08219 | 0,00836 | 0,0177 | 0,01253 | 0,00721 | 0,00881 |
| 526,11937 | 0,00879 | 0,0185 | 0,01307 | 0,00748 | 0,00922 |
| 526,15656 | 0,00923 | 0,01933 | 0,01362 | 0,00777 | 0,00965 |
| 526,19374 | 0,00969 | 0,02017 | 0,01419 | 0,00806 | 0,0101 |
| 526,23092 | 0,01017 | 0,02103 | 0,01477 | 0,00836 | 0,01055 |
| 526,2681 | 0,01066 | 0,02191 | 0,01537 | 0,00868 | 0,01102 |
| 526,30528 | 0,01117 | 0,02282 | 0,01599 | 0,009 | 0,01152 |
| 526,34247 | 0,0117 | 0,02374 | 0,01662 | 0,00933 | 0,01202 |
| 526,37965 | 0,01225 | 0,02469 | 0,01726 | 0,00967 | 0,01254 |
| 526,41683 | 0,01281 | 0,02566 | 0,01792 | 0,01003 | 0,01307 |
| 526,45401 | 0,0134 | 0,02664 | 0,0186 | 0,01039 | 0,01363 |
| 526,49119 | 0,014 | 0,02764 | 0,01929 | 0,01077 | 0,01419 |
| 526,52838 | 0,01462 | 0,02867 | 0,02 | 0,01115 | 0,01478 |
| 526,56556 | 0,01527 | 0,0297 | 0,02072 | 0,01155 | 0,01538 |
| 526,60274 | 0,01593 | 0,03076 | 0,02145 | 0,01197 | 0,016 |
| 526,63992 | 0,01661 | 0,03183 | 0,0222 | 0,0124 | 0,01663 |
| 526,6771 | 0,01731 | 0,03291 | 0,02296 | 0,01284 | 0,01728 |
| 526,71429 | 0,01803 | 0,03402 | 0,02374 | 0,01329 | 0,01795 |
| 526,75147 | 0,01878 | 0,03513 | 0,02453 | 0,01376 | 0,01864 |
| 526,78865 | 0,01954 | 0,03626 | 0,02533 | 0,01425 | 0,01934 |
| 526,82583 | 0,02032 | 0,0374 | 0,02615 | 0,01475 | 0,02007 |
| 526,86301 | 0,02113 | 0,03855 | 0,02698 | 0,01527 | 0,0208 |
| 526,9002 | 0,02195 | 0,0397 | 0,02782 | 0,0158 | 0,02156 |
| 526,93738 | 0,0228 | 0,04087 | 0,02867 | 0,01635 | 0,02233 |
| 526,97456 | 0,02367 | 0,04205 | 0,02953 | 0,01691 | 0,02312 |
| 527,01174 | 0,02456 | 0,04323 | 0,03041 | 0,0175 | 0,02393 |
| 527,04892 | 0,02547 | 0,04442 | 0,03129 | 0,01809 | 0,02475 |
| 527,08611 | 0,0264 | 0,04561 | 0,03218 | 0,01871 | 0,0256 |
| 527,12329 | 0,02736 | 0,0468 | 0,03308 | 0,01935 | 0,02645 |
| 527,16047 | 0,02833 | 0,048 | 0,034 | 0,02 | 0,02733 |
| 527,19765 | 0,02933 | 0,0492 | 0,03491 | 0,02067 | 0,02822 |
| 527,23483 | 0,03035 | 0,0504 | 0,03584 | 0,02136 | 0,02913 |
| 527,27202 | 0,03138 | 0,05159 | 0,03677 | 0,02206 | 0,03004 |
| 527,3092 | 0,03245 | 0,05278 | 0,03771 | 0,02278 | 0,03098 |
| 527,34638 | 0,03353 | 0,05397 | 0,03866 | 0,02352 | 0,03193 |
| 527,38356 | 0,03463 | 0,05516 | 0,03961 | 0,02428 | 0,0329 |
| 527,42074 | 0,03576 | 0,05634 | 0,04056 | 0,02506 | 0,03388 |
| 527,45793 | 0,0369 | 0,05751 | 0,04152 | 0,02585 | 0,03487 |
| 527,49511 | 0,03806 | 0,05867 | 0,04248 | 0,02666 | 0,03587 |
| 527,53229 | 0,03924 | 0,05983 | 0,04344 | 0,02749 | 0,03688 |
| 527,56947 | 0,04045 | 0,06097 | 0,0444 | 0,02833 | 0,03791 |
| 527,60665 | 0,04167 | 0,06211 | 0,04537 | 0,02919 | 0,03895 |
| 527,64384 | 0,04291 | 0,06323 | 0,04633 | 0,03007 | 0,03999 |
| 527,68102 | 0,04417 | 0,06433 | 0,0473 | 0,03095 | 0,04104 |
| 527,7182 | 0,04544 | 0,06543 | 0,04826 | 0,03186 | 0,04211 |
| 527,75538 | 0,04673 | 0,06651 | 0,04922 | 0,03278 | 0,04317 |
| 527,79256 | 0,04804 | 0,06757 | 0,05018 | 0,03371 | 0,04425 |
| 527,82975 | 0,04937 | 0,06862 | 0,05114 | 0,03466 | 0,04533 |
| 527,86693 | 0,05071 | 0,06965 | 0,05209 | 0,03562 | 0,04641 |
| 527,90411 | 0,05206 | 0,07066 | 0,05304 | 0,03659 | 0,0475 |
| 527,94129 | 0,05343 | 0,07166 | 0,05398 | 0,03757 | 0,04859 |
| 527,97847 | 0,05481 | 0,07264 | 0,05491 | 0,03856 | 0,04968 |
| 528,01566 | 0,05621 | 0,07359 | 0,05584 | 0,03956 | 0,05077 |
| 528,05284 | 0,05761 | 0,07452 | 0,05677 | 0,04057 | 0,05186 |
| 528,09002 | 0,05903 | 0,07544 | 0,05768 | 0,04159 | 0,05295 |
| 528,1272 | 0,06046 | 0,07634 | 0,05859 | 0,04262 | 0,05404 |
| 528,16438 | 0,06189 | 0,07721 | 0,05949 | 0,04366 | 0,05512 |
| 528,20157 | 0,06334 | 0,07807 | 0,06038 | 0,0447 | 0,05621 |
| 528,23875 | 0,06479 | 0,0789 | 0,06126 | 0,04575 | 0,05728 |
| 528,27593 | 0,06624 | 0,07971 | 0,06213 | 0,0468 | 0,05836 |
| 528,31311 | 0,06771 | 0,0805 | 0,06299 | 0,04785 | 0,05942 |
| 528,35029 | 0,06917 | 0,08127 | 0,06384 | 0,04892 | 0,06048 |
| 528,38748 | 0,07064 | 0,08202 | 0,06467 | 0,04998 | 0,06153 |
| 528,42466 | 0,07211 | 0,08274 | 0,0655 | 0,05104 | 0,06258 |
| 528,46184 | 0,07358 | 0,08345 | 0,06631 | 0,05211 | 0,06361 |
| 528,49902 | 0,07506 | 0,08413 | 0,06711 | 0,05318 | 0,06464 |
| 528,5362 | 0,07652 | 0,08479 | 0,06789 | 0,05425 | 0,06566 |
| 528,57339 | 0,07799 | 0,08544 | 0,06866 | 0,05532 | 0,06666 |
| 528,61057 | 0,07945 | 0,08606 | 0,06942 | 0,05638 | 0,06766 |
| 528,64775 | 0,08091 | 0,08666 | 0,07016 | 0,05745 | 0,06865 |
| 528,68493 | 0,08236 | 0,08725 | 0,07089 | 0,05851 | 0,06962 |
| 528,72211 | 0,0838 | 0,0878 | 0,0716 | 0,05957 | 0,07059 |
| 528,7593 | 0,08523 | 0,08835 | 0,07229 | 0,06063 | 0,07154 |
| 528,79648 | 0,08665 | 0,08887 | 0,07298 | 0,06168 | 0,07248 |
| 528,83366 | 0,08806 | 0,08937 | 0,07364 | 0,06273 | 0,0734 |
| 528,87084 | 0,08946 | 0,08986 | 0,07429 | 0,06378 | 0,07432 |
| 528,90802 | 0,09084 | 0,09033 | 0,07492 | 0,06482 | 0,07522 |
| 528,94521 | 0,09221 | 0,09078 | 0,07554 | 0,06586 | 0,07611 |
| 528,98239 | 0,09356 | 0,09122 | 0,07614 | 0,06688 | 0,07699 |
| 529,01957 | 0,09488 | 0,09164 | 0,07672 | 0,06791 | 0,07785 |
| 529,05675 | 0,09619 | 0,09204 | 0,07729 | 0,06892 | 0,0787 |
| 529,09393 | 0,09748 | 0,09243 | 0,07784 | 0,06993 | 0,07954 |
| 529,13112 | 0,09874 | 0,0928 | 0,07838 | 0,07093 | 0,08037 |
| 529,1683 | 0,09998 | 0,09315 | 0,0789 | 0,07193 | 0,08118 |
| 529,20548 | 0,10119 | 0,09349 | 0,0794 | 0,07291 | 0,08198 |
| 529,24266 | 0,10238 | 0,09382 | 0,07989 | 0,07389 | 0,08277 |
| 529,27984 | 0,10354 | 0,09414 | 0,08036 | 0,07486 | 0,08355 |
| 529,31703 | 0,10467 | 0,09443 | 0,08081 | 0,07582 | 0,08431 |
| 529,35421 | 0,10578 | 0,09472 | 0,08126 | 0,07677 | 0,08506 |
| 529,39139 | 0,10684 | 0,095 | 0,08169 | 0,07771 | 0,08579 |
| 529,42857 | 0,10788 | 0,09525 | 0,0821 | 0,07865 | 0,08651 |
| 529,46575 | 0,10889 | 0,0955 | 0,0825 | 0,07957 | 0,08722 |
| 529,50294 | 0,10985 | 0,09574 | 0,08288 | 0,08048 | 0,08792 |
| 529,54012 | 0,11079 | 0,09596 | 0,08326 | 0,08138 | 0,0886 |
| 529,5773 | 0,11169 | 0,09618 | 0,08362 | 0,08227 | 0,08927 |
| 529,61448 | 0,11256 | 0,09638 | 0,08397 | 0,08315 | 0,08993 |
| 529,65166 | 0,11338 | 0,09657 | 0,08431 | 0,08402 | 0,09058 |
| 529,68885 | 0,11417 | 0,09674 | 0,08463 | 0,08488 | 0,09121 |
| 529,72603 | 0,11493 | 0,09691 | 0,08495 | 0,08573 | 0,09182 |
| 529,76321 | 0,11564 | 0,09707 | 0,08527 | 0,08656 | 0,09243 |
| 529,80039 | 0,11631 | 0,09721 | 0,08557 | 0,08739 | 0,09301 |
| 529,83757 | 0,11696 | 0,09735 | 0,08586 | 0,0882 | 0,09359 |
| 529,87476 | 0,11755 | 0,09747 | 0,08615 | 0,089 | 0,09415 |
| 529,91194 | 0,1181 | 0,09758 | 0,08643 | 0,0898 | 0,0947 |
| 529,94912 | 0,11863 | 0,09768 | 0,08671 | 0,09057 | 0,09523 |
| 529,9863 | 0,11911 | 0,09777 | 0,08698 | 0,09134 | 0,09575 |
| 530,02348 | 0,11955 | 0,09785 | 0,08725 | 0,09209 | 0,09626 |
| 530,06067 | 0,11995 | 0,09792 | 0,08752 | 0,09284 | 0,09675 |
| 530,09785 | 0,12032 | 0,09798 | 0,08779 | 0,09356 | 0,09722 |
| 530,13503 | 0,12064 | 0,09803 | 0,08805 | 0,09428 | 0,09769 |
| 530,17221 | 0,12094 | 0,09807 | 0,08832 | 0,09499 | 0,09814 |
| 530,20939 | 0,1212 | 0,0981 | 0,08858 | 0,09568 | 0,09857 |
| 530,24658 | 0,12141 | 0,09811 | 0,08885 | 0,09636 | 0,09899 |
| 530,28376 | 0,1216 | 0,09811 | 0,08911 | 0,09704 | 0,0994 |
| 530,32094 | 0,12175 | 0,09811 | 0,08938 | 0,09769 | 0,09979 |
| 530,35812 | 0,12186 | 0,09809 | 0,08965 | 0,09834 | 0,10018 |
| 530,3953 | 0,12195 | 0,09806 | 0,08993 | 0,09897 | 0,10054 |
| 530,43249 | 0,122 | 0,09802 | 0,09021 | 0,09959 | 0,1009 |
| 530,46967 | 0,12203 | 0,09797 | 0,09049 | 0,1002 | 0,10124 |
| 530,50685 | 0,12202 | 0,09791 | 0,09078 | 0,10079 | 0,10158 |
| 530,54403 | 0,12198 | 0,09783 | 0,09108 | 0,10138 | 0,1019 |
| 530,58121 | 0,12192 | 0,09775 | 0,09137 | 0,10195 | 0,10221 |
| 530,6184 | 0,12183 | 0,09765 | 0,09168 | 0,10251 | 0,10251 |
| 530,65558 | 0,12172 | 0,09754 | 0,09198 | 0,10306 | 0,10281 |
| 530,69276 | 0,12158 | 0,09742 | 0,0923 | 0,10359 | 0,10309 |
| 530,72994 | 0,12142 | 0,09729 | 0,09261 | 0,10412 | 0,10337 |
| 530,76712 | 0,12124 | 0,09714 | 0,09294 | 0,10463 | 0,10364 |
| 530,80431 | 0,12104 | 0,09699 | 0,09326 | 0,10513 | 0,1039 |
| 530,84149 | 0,12082 | 0,09682 | 0,09359 | 0,10562 | 0,10416 |
| 530,87867 | 0,12058 | 0,09664 | 0,09392 | 0,10609 | 0,10441 |
| 530,91585 | 0,12032 | 0,09645 | 0,09426 | 0,10656 | 0,10466 |
| 530,95303 | 0,12005 | 0,09625 | 0,0946 | 0,10701 | 0,10491 |
| 530,99022 | 0,11976 | 0,09603 | 0,09494 | 0,10744 | 0,10515 |
| 531,0274 | 0,11946 | 0,09581 | 0,09528 | 0,10787 | 0,10539 |
| 531,06458 | 0,11915 | 0,09557 | 0,09562 | 0,10828 | 0,10563 |
| 531,10176 | 0,11882 | 0,09533 | 0,09596 | 0,10868 | 0,10587 |
| 531,13894 | 0,11848 | 0,09507 | 0,09629 | 0,10907 | 0,10611 |
| 531,17613 | 0,11814 | 0,0948 | 0,09662 | 0,10944 | 0,10636 |
| 531,21331 | 0,11778 | 0,09453 | 0,09695 | 0,1098 | 0,1066 |
| 531,25049 | 0,11741 | 0,09424 | 0,09727 | 0,11015 | 0,10685 |
| 531,28767 | 0,11704 | 0,09394 | 0,09759 | 0,11048 | 0,1071 |
| 531,32485 | 0,11666 | 0,09363 | 0,0979 | 0,11079 | 0,10735 |
| 531,36204 | 0,11627 | 0,09332 | 0,0982 | 0,1111 | 0,1076 |
| 531,39922 | 0,11588 | 0,093 | 0,09848 | 0,11139 | 0,10786 |
| 531,4364 | 0,11548 | 0,09266 | 0,09876 | 0,11166 | 0,10813 |
| 531,47358 | 0,11507 | 0,09232 | 0,09902 | 0,11192 | 0,1084 |
| 531,51076 | 0,11466 | 0,09198 | 0,09927 | 0,11216 | 0,10867 |
| 531,54795 | 0,11425 | 0,09162 | 0,0995 | 0,11239 | 0,10895 |
| 531,58513 | 0,11383 | 0,09126 | 0,09972 | 0,11259 | 0,10923 |
| 531,62231 | 0,11341 | 0,0909 | 0,09991 | 0,11279 | 0,10952 |
| 531,65949 | 0,11298 | 0,09053 | 0,10009 | 0,11297 | 0,10981 |
| 531,69667 | 0,11255 | 0,09015 | 0,10025 | 0,11312 | 0,1101 |
| 531,73386 | 0,11212 | 0,08977 | 0,10038 | 0,11327 | 0,1104 |
| 531,77104 | 0,11168 | 0,08939 | 0,1005 | 0,1134 | 0,11071 |
| 531,80822 | 0,11124 | 0,089 | 0,10059 | 0,1135 | 0,11101 |
| 531,8454 | 0,1108 | 0,08861 | 0,10065 | 0,11359 | 0,11132 |
| 531,88258 | 0,11035 | 0,08823 | 0,10069 | 0,11366 | 0,11163 |
| 531,91977 | 0,10991 | 0,08783 | 0,10071 | 0,11371 | 0,11193 |
| 531,95695 | 0,10945 | 0,08744 | 0,1007 | 0,11375 | 0,11224 |
| 531,99413 | 0,109 | 0,08705 | 0,10066 | 0,11376 | 0,11255 |
| 532,03131 | 0,10854 | 0,08667 | 0,1006 | 0,11376 | 0,11286 |
| 532,06849 | 0,10808 | 0,08628 | 0,10051 | 0,11374 | 0,11316 |
| 532,10568 | 0,10761 | 0,08589 | 0,10038 | 0,1137 | 0,11346 |
| 532,14286 | 0,10715 | 0,08551 | 0,10024 | 0,11365 | 0,11376 |
| 532,18004 | 0,10668 | 0,08513 | 0,10007 | 0,11357 | 0,11404 |
| 532,21722 | 0,1062 | 0,08476 | 0,09986 | 0,11347 | 0,11433 |
| 532,2544 | 0,10573 | 0,08439 | 0,09963 | 0,11336 | 0,1146 |
| 532,29159 | 0,10525 | 0,08403 | 0,09938 | 0,11323 | 0,11486 |
| 532,32877 | 0,10476 | 0,08367 | 0,09909 | 0,11308 | 0,11512 |
| 532,36595 | 0,10428 | 0,08332 | 0,09878 | 0,11291 | 0,11536 |
| 532,40313 | 0,10379 | 0,08298 | 0,09846 | 0,11273 | 0,11559 |
| 532,44031 | 0,10329 | 0,08265 | 0,09809 | 0,11252 | 0,1158 |
| 532,4775 | 0,1028 | 0,08232 | 0,09771 | 0,11231 | 0,116 |
| 532,51468 | 0,1023 | 0,082 | 0,09731 | 0,11208 | 0,11619 |
| 532,55186 | 0,1018 | 0,08169 | 0,09688 | 0,11182 | 0,11635 |
| 532,58904 | 0,10129 | 0,0814 | 0,09643 | 0,11156 | 0,1165 |
| 532,62622 | 0,10078 | 0,08111 | 0,09597 | 0,11128 | 0,11663 |
| 532,66341 | 0,10027 | 0,08083 | 0,09549 | 0,11098 | 0,11673 |
| 532,70059 | 0,09976 | 0,08056 | 0,09498 | 0,11067 | 0,11681 |
| 532,73777 | 0,09924 | 0,0803 | 0,09446 | 0,11035 | 0,11687 |
| 532,77495 | 0,09872 | 0,08006 | 0,09393 | 0,11002 | 0,1169 |
| 532,81213 | 0,0982 | 0,07982 | 0,09338 | 0,10967 | 0,11691 |
| 532,84932 | 0,09768 | 0,0796 | 0,09283 | 0,10931 | 0,1169 |
| 532,8865 | 0,09715 | 0,07938 | 0,09226 | 0,10894 | 0,11686 |
| 532,92368 | 0,09662 | 0,07918 | 0,09168 | 0,10856 | 0,11678 |
| 532,96086 | 0,09609 | 0,07899 | 0,09109 | 0,10816 | 0,11668 |
| 532,99804 | 0,09555 | 0,07881 | 0,0905 | 0,10776 | 0,11655 |
| 533,03523 | 0,09501 | 0,07863 | 0,0899 | 0,10735 | 0,11639 |
| 533,07241 | 0,09447 | 0,07848 | 0,0893 | 0,10693 | 0,1162 |
| 533,10959 | 0,09393 | 0,07833 | 0,0887 | 0,10651 | 0,11598 |
| 533,14677 | 0,09339 | 0,07819 | 0,08809 | 0,10607 | 0,11572 |
| 533,18395 | 0,09284 | 0,07806 | 0,08748 | 0,10563 | 0,11543 |
| 533,22114 | 0,09229 | 0,07794 | 0,08688 | 0,10518 | 0,11512 |
| 533,25832 | 0,09174 | 0,07783 | 0,08628 | 0,10472 | 0,11477 |
| 533,2955 | 0,09119 | 0,07773 | 0,08568 | 0,10426 | 0,11438 |
| 533,33268 | 0,09063 | 0,07763 | 0,08508 | 0,1038 | 0,11396 |
| 533,36986 | 0,09008 | 0,07754 | 0,08449 | 0,10333 | 0,11352 |
| 533,40705 | 0,08952 | 0,07746 | 0,0839 | 0,10285 | 0,11303 |
| 533,44423 | 0,08895 | 0,07739 | 0,08332 | 0,10237 | 0,11251 |
| 533,48141 | 0,08839 | 0,07732 | 0,08275 | 0,10188 | 0,11197 |
| 533,51859 | 0,08782 | 0,07725 | 0,08219 | 0,1014 | 0,11138 |
| 533,55577 | 0,08725 | 0,07719 | 0,08164 | 0,1009 | 0,11077 |
| 533,59295 | 0,08668 | 0,07713 | 0,08109 | 0,10041 | 0,11012 |
| 533,63014 | 0,0861 | 0,07708 | 0,08056 | 0,09991 | 0,10945 |
| 533,66732 | 0,08553 | 0,07703 | 0,08003 | 0,09941 | 0,10874 |
| 533,7045 | 0,08495 | 0,07697 | 0,07952 | 0,0989 | 0,108 |
| 533,74168 | 0,08437 | 0,07692 | 0,07901 | 0,09839 | 0,10724 |
| 533,77886 | 0,08378 | 0,07687 | 0,07853 | 0,09788 | 0,10645 |
| 533,81605 | 0,0832 | 0,07682 | 0,07805 | 0,09737 | 0,10562 |
| 533,85323 | 0,08261 | 0,07676 | 0,07758 | 0,09685 | 0,10478 |
| 533,89041 | 0,08202 | 0,0767 | 0,07712 | 0,09633 | 0,10391 |
| 533,92759 | 0,08142 | 0,07664 | 0,07668 | 0,09581 | 0,10301 |
| 533,96477 | 0,08083 | 0,07657 | 0,07625 | 0,09528 | 0,1021 |
| 534,00196 | 0,08023 | 0,07649 | 0,07583 | 0,09475 | 0,10116 |
| 534,03914 | 0,07964 | 0,07641 | 0,07543 | 0,09422 | 0,1002 |
| 534,07632 | 0,07904 | 0,07633 | 0,07503 | 0,09368 | 0,09923 |
| 534,1135 | 0,07844 | 0,07623 | 0,07465 | 0,09314 | 0,09824 |
| 534,15068 | 0,07783 | 0,07613 | 0,07429 | 0,09259 | 0,09723 |
| 534,18787 | 0,07723 | 0,07602 | 0,07393 | 0,09205 | 0,09621 |
| 534,22505 | 0,07663 | 0,07589 | 0,07358 | 0,0915 | 0,09517 |
| 534,26223 | 0,07603 | 0,07576 | 0,07325 | 0,09094 | 0,09413 |
| 534,29941 | 0,07543 | 0,07562 | 0,07293 | 0,09038 | 0,09308 |
| 534,33659 | 0,07483 | 0,07547 | 0,07262 | 0,08982 | 0,09202 |
| 534,37378 | 0,07423 | 0,0753 | 0,07233 | 0,08925 | 0,09096 |
| 534,41096 | 0,07363 | 0,07512 | 0,07205 | 0,08867 | 0,08989 |
| 534,44814 | 0,07303 | 0,07493 | 0,07177 | 0,08809 | 0,08883 |
| 534,48532 | 0,07243 | 0,07472 | 0,07151 | 0,08751 | 0,08776 |
| 534,5225 | 0,07184 | 0,07451 | 0,07126 | 0,08692 | 0,08669 |
| 534,55969 | 0,07125 | 0,07428 | 0,07102 | 0,08633 | 0,08563 |
| 534,59687 | 0,07066 | 0,07403 | 0,0708 | 0,08573 | 0,08458 |
| 534,63405 | 0,07008 | 0,07377 | 0,07058 | 0,08513 | 0,08353 |
| 534,67123 | 0,0695 | 0,07351 | 0,07038 | 0,08452 | 0,08249 |
| 534,70841 | 0,06893 | 0,07322 | 0,07018 | 0,08391 | 0,08146 |
| 534,7456 | 0,06836 | 0,07292 | 0,07001 | 0,08329 | 0,08044 |
| 534,78278 | 0,06779 | 0,07261 | 0,06984 | 0,08267 | 0,07944 |
| 534,81996 | 0,06723 | 0,07229 | 0,06967 | 0,08204 | 0,07846 |
| 534,85714 | 0,06668 | 0,07195 | 0,06953 | 0,08141 | 0,07748 |
| 534,89432 | 0,06613 | 0,07161 | 0,06939 | 0,08078 | 0,07653 |
| 534,93151 | 0,06559 | 0,07125 | 0,06926 | 0,08013 | 0,07559 |
| 534,96869 | 0,06506 | 0,07087 | 0,06915 | 0,07949 | 0,07467 |
| 535,00587 | 0,06453 | 0,07049 | 0,06905 | 0,07884 | 0,07377 |
| 535,04305 | 0,06401 | 0,0701 | 0,06895 | 0,07819 | 0,0729 |
| 535,08023 | 0,0635 | 0,0697 | 0,06887 | 0,07753 | 0,07204 |
| 535,11742 | 0,06299 | 0,06929 | 0,0688 | 0,07687 | 0,07121 |
| 535,1546 | 0,06249 | 0,06887 | 0,06874 | 0,0762 | 0,0704 |
| 535,19178 | 0,062 | 0,06844 | 0,06869 | 0,07554 | 0,06962 |
| 535,22896 | 0,06152 | 0,068 | 0,06865 | 0,07487 | 0,06885 |
| 535,26614 | 0,06105 | 0,06756 | 0,06862 | 0,07419 | 0,06811 |
| 535,30333 | 0,06058 | 0,06711 | 0,0686 | 0,07352 | 0,0674 |
| 535,34051 | 0,06012 | 0,06666 | 0,06859 | 0,07284 | 0,0667 |
| 535,37769 | 0,05967 | 0,06621 | 0,06859 | 0,07216 | 0,06603 |
| 535,41487 | 0,05922 | 0,06575 | 0,0686 | 0,07148 | 0,06539 |
| 535,45205 | 0,05878 | 0,06529 | 0,06862 | 0,0708 | 0,06476 |
| 535,48924 | 0,05835 | 0,06483 | 0,06864 | 0,07012 | 0,06416 |
| 535,52642 | 0,05793 | 0,06437 | 0,06868 | 0,06944 | 0,06358 |
| 535,5636 | 0,05751 | 0,0639 | 0,06872 | 0,06875 | 0,06302 |
| 535,60078 | 0,0571 | 0,06344 | 0,06877 | 0,06807 | 0,06248 |
| 535,63796 | 0,0567 | 0,06298 | 0,06883 | 0,06739 | 0,06196 |
| 535,67515 | 0,0563 | 0,06253 | 0,06889 | 0,06671 | 0,06147 |
| 535,71233 | 0,05591 | 0,06207 | 0,06896 | 0,06604 | 0,06098 |
| 535,74951 | 0,05552 | 0,06163 | 0,06904 | 0,06536 | 0,06051 |
| 535,78669 | 0,05514 | 0,06118 | 0,06912 | 0,06469 | 0,06006 |
| 535,82387 | 0,05476 | 0,06075 | 0,06921 | 0,06402 | 0,05963 |
| 535,86106 | 0,05439 | 0,06031 | 0,0693 | 0,06335 | 0,0592 |
| 535,89824 | 0,05402 | 0,05989 | 0,06939 | 0,06269 | 0,05879 |
| 535,93542 | 0,05366 | 0,05948 | 0,06948 | 0,06203 | 0,05839 |
| 535,9726 | 0,0533 | 0,05907 | 0,06958 | 0,06138 | 0,058 |
| 536,00978 | 0,05294 | 0,05867 | 0,06968 | 0,06073 | 0,05762 |
| 536,04697 | 0,05258 | 0,05829 | 0,06978 | 0,06009 | 0,05725 |
| 536,08415 | 0,05223 | 0,05791 | 0,06988 | 0,05945 | 0,05688 |
| 536,12133 | 0,05188 | 0,05754 | 0,06998 | 0,05883 | 0,05652 |
| 536,15851 | 0,05154 | 0,05719 | 0,07007 | 0,05821 | 0,05617 |
| 536,19569 | 0,05119 | 0,05684 | 0,07017 | 0,05759 | 0,05581 |
| 536,23288 | 0,05085 | 0,05651 | 0,07026 | 0,05699 | 0,05546 |
| 536,27006 | 0,05051 | 0,0562 | 0,07035 | 0,0564 | 0,05511 |
| 536,30724 | 0,05017 | 0,05589 | 0,07043 | 0,05581 | 0,05476 |
| 536,34442 | 0,04984 | 0,0556 | 0,07051 | 0,05524 | 0,05442 |
| 536,3816 | 0,0495 | 0,05532 | 0,07058 | 0,05467 | 0,05407 |
| 536,41879 | 0,04917 | 0,05505 | 0,07065 | 0,05412 | 0,05371 |
| 536,45597 | 0,04884 | 0,0548 | 0,07071 | 0,05358 | 0,05336 |
| 536,49315 | 0,04851 | 0,05456 | 0,07076 | 0,05305 | 0,05301 |
| 536,53033 | 0,04818 | 0,05433 | 0,07081 | 0,05254 | 0,05265 |
| 536,56751 | 0,04785 | 0,05412 | 0,07084 | 0,05204 | 0,05228 |
| 536,6047 | 0,04752 | 0,05393 | 0,07087 | 0,05155 | 0,05192 |
| 536,64188 | 0,0472 | 0,05374 | 0,07089 | 0,05109 | 0,05155 |
| 536,67906 | 0,04687 | 0,05357 | 0,0709 | 0,05063 | 0,05117 |
| 536,71624 | 0,04655 | 0,05342 | 0,07089 | 0,05019 | 0,0508 |
| 536,75342 | 0,04623 | 0,05328 | 0,07088 | 0,04977 | 0,05041 |
| 536,79061 | 0,04591 | 0,05315 | 0,07086 | 0,04936 | 0,05003 |
| 536,82779 | 0,0456 | 0,05303 | 0,07082 | 0,04897 | 0,04964 |
| 536,86497 | 0,04528 | 0,05293 | 0,07078 | 0,0486 | 0,04924 |
| 536,90215 | 0,04497 | 0,05284 | 0,07072 | 0,04824 | 0,04885 |
| 536,93933 | 0,04466 | 0,05277 | 0,07064 | 0,04791 | 0,04845 |
| 536,97652 | 0,04435 | 0,0527 | 0,07056 | 0,04759 | 0,04805 |
| 537,0137 | 0,04405 | 0,05265 | 0,07046 | 0,04729 | 0,04764 |
| 537,05088 | 0,04374 | 0,05261 | 0,07035 | 0,04701 | 0,04724 |
| 537,08806 | 0,04344 | 0,05258 | 0,07023 | 0,04674 | 0,04683 |
| 537,12524 | 0,04315 | 0,05256 | 0,0701 | 0,0465 | 0,04643 |
| 537,16243 | 0,04285 | 0,05255 | 0,06995 | 0,04628 | 0,04602 |
| 537,19961 | 0,04256 | 0,05255 | 0,06978 | 0,04607 | 0,04562 |
| 537,23679 | 0,04227 | 0,05256 | 0,06961 | 0,04588 | 0,04522 |
| 537,27397 | 0,04199 | 0,05258 | 0,06942 | 0,04571 | 0,04482 |
| 537,31115 | 0,04171 | 0,0526 | 0,06922 | 0,04556 | 0,04443 |
| 537,34834 | 0,04143 | 0,05263 | 0,069 | 0,04542 | 0,04404 |
| 537,38552 | 0,04116 | 0,05267 | 0,06878 | 0,04531 | 0,04366 |
| 537,4227 | 0,04089 | 0,05272 | 0,06853 | 0,04521 | 0,04328 |
| 537,45988 | 0,04063 | 0,05277 | 0,06828 | 0,04512 | 0,04291 |
| 537,49706 | 0,04037 | 0,05282 | 0,06802 | 0,04505 | 0,04255 |
| 537,53425 | 0,04011 | 0,05288 | 0,06774 | 0,045 | 0,0422 |
| 537,57143 | 0,03986 | 0,05294 | 0,06744 | 0,04495 | 0,04186 |
| 537,60861 | 0,03961 | 0,053 | 0,06714 | 0,04493 | 0,04152 |
| 537,64579 | 0,03936 | 0,05306 | 0,06682 | 0,04491 | 0,04121 |
| 537,68297 | 0,03913 | 0,05313 | 0,06649 | 0,04491 | 0,0409 |
| 537,72016 | 0,03889 | 0,05319 | 0,06616 | 0,04491 | 0,0406 |
| 537,75734 | 0,03866 | 0,05325 | 0,0658 | 0,04493 | 0,04032 |
| 537,79452 | 0,03843 | 0,0533 | 0,06544 | 0,04495 | 0,04005 |
| 537,8317 | 0,03821 | 0,05336 | 0,06506 | 0,04499 | 0,0398 |
| 537,86888 | 0,03799 | 0,05341 | 0,06467 | 0,04503 | 0,03956 |
| 537,90607 | 0,03778 | 0,05345 | 0,06427 | 0,04507 | 0,03934 |
| 537,94325 | 0,03757 | 0,05348 | 0,06386 | 0,04512 | 0,03913 |
| 537,98043 | 0,03737 | 0,05351 | 0,06345 | 0,04517 | 0,03893 |
| 538,01761 | 0,03717 | 0,05353 | 0,06301 | 0,04523 | 0,03876 |
| 538,05479 | 0,03697 | 0,05354 | 0,06257 | 0,04529 | 0,03859 |
| 538,09198 | 0,03678 | 0,05354 | 0,06212 | 0,04534 | 0,03845 |
| 538,12916 | 0,03659 | 0,05353 | 0,06165 | 0,0454 | 0,03831 |
| 538,16634 | 0,03641 | 0,0535 | 0,06118 | 0,04545 | 0,0382 |
| 538,20352 | 0,03623 | 0,05347 | 0,0607 | 0,04551 | 0,0381 |
| 538,2407 | 0,03606 | 0,05341 | 0,0602 | 0,04555 | 0,03801 |
| 538,27789 | 0,03589 | 0,05334 | 0,0597 | 0,0456 | 0,03794 |
| 538,31507 | 0,03572 | 0,05326 | 0,05919 | 0,04564 | 0,03789 |
| 538,35225 | 0,03556 | 0,05316 | 0,05867 | 0,04567 | 0,03784 |
| 538,38943 | 0,0354 | 0,05305 | 0,05813 | 0,04569 | 0,03781 |
| 538,42661 | 0,03525 | 0,05291 | 0,05759 | 0,04571 | 0,03779 |
| 538,4638 | 0,0351 | 0,05276 | 0,05705 | 0,04571 | 0,03778 |
| 538,50098 | 0,03495 | 0,05259 | 0,05649 | 0,04571 | 0,03777 |
| 538,53816 | 0,03481 | 0,0524 | 0,05592 | 0,0457 | 0,03778 |
| 538,57534 | 0,03467 | 0,05219 | 0,05535 | 0,04568 | 0,0378 |
| 538,61252 | 0,03453 | 0,05195 | 0,05476 | 0,04564 | 0,03782 |
| 538,64971 | 0,0344 | 0,05171 | 0,05417 | 0,04559 | 0,03785 |
| 538,68689 | 0,03427 | 0,05143 | 0,05357 | 0,04554 | 0,03788 |
| 538,72407 | 0,03414 | 0,05114 | 0,05297 | 0,04547 | 0,03792 |
| 538,76125 | 0,03401 | 0,05083 | 0,05235 | 0,04538 | 0,03796 |
| 538,79843 | 0,03389 | 0,05049 | 0,05173 | 0,04529 | 0,038 |
| 538,83562 | 0,03377 | 0,05013 | 0,05111 | 0,04518 | 0,03803 |
| 538,8728 | 0,03365 | 0,04976 | 0,05047 | 0,04506 | 0,03807 |
| 538,90998 | 0,03354 | 0,04936 | 0,04983 | 0,04492 | 0,0381 |
| 538,94716 | 0,03342 | 0,04894 | 0,04919 | 0,04478 | 0,03812 |
| 538,98434 | 0,03331 | 0,0485 | 0,04854 | 0,04461 | 0,03815 |
| 539,02153 | 0,0332 | 0,04805 | 0,04788 | 0,04444 | 0,03816 |
| 539,05871 | 0,03309 | 0,04757 | 0,04722 | 0,04426 | 0,03816 |
| 539,09589 | 0,03298 | 0,04708 | 0,04655 | 0,04406 | 0,03815 |
| 539,13307 | 0,03287 | 0,04657 | 0,04588 | 0,04384 | 0,03813 |
| 539,17025 | 0,03276 | 0,04603 | 0,04521 | 0,04362 | 0,0381 |
| 539,20744 | 0,03265 | 0,04548 | 0,04453 | 0,04339 | 0,03805 |
| 539,24462 | 0,03254 | 0,04492 | 0,04385 | 0,04314 | 0,03799 |
| 539,2818 | 0,03243 | 0,04434 | 0,04317 | 0,04288 | 0,03791 |
| 539,31898 | 0,03231 | 0,04374 | 0,04249 | 0,04261 | 0,03781 |
| 539,35616 | 0,0322 | 0,04314 | 0,0418 | 0,04233 | 0,0377 |
| 539,39335 | 0,03208 | 0,04252 | 0,04111 | 0,04204 | 0,03757 |
| 539,43053 | 0,03196 | 0,04188 | 0,04042 | 0,04174 | 0,03741 |
| 539,46771 | 0,03184 | 0,04124 | 0,03973 | 0,04143 | 0,03724 |
| 539,50489 | 0,03172 | 0,04059 | 0,03905 | 0,04111 | 0,03704 |
| 539,54207 | 0,03159 | 0,03992 | 0,03836 | 0,04078 | 0,03682 |
| 539,57926 | 0,03146 | 0,03925 | 0,03767 | 0,04044 | 0,03659 |
| 539,61644 | 0,03133 | 0,03857 | 0,03699 | 0,04009 | 0,03633 |
| 539,65362 | 0,03119 | 0,03789 | 0,0363 | 0,03974 | 0,03604 |
| 539,6908 | 0,03104 | 0,0372 | 0,03562 | 0,03938 | 0,03573 |
| 539,72798 | 0,03089 | 0,0365 | 0,03494 | 0,03901 | 0,0354 |
| 539,76517 | 0,03073 | 0,0358 | 0,03427 | 0,03863 | 0,03505 |
| 539,80235 | 0,03057 | 0,0351 | 0,0336 | 0,03825 | 0,03467 |
| 539,83953 | 0,0304 | 0,0344 | 0,03293 | 0,03786 | 0,03427 |
| 539,87671 | 0,03023 | 0,0337 | 0,03227 | 0,03747 | 0,03385 |
| 539,91389 | 0,03005 | 0,033 | 0,03161 | 0,03707 | 0,0334 |
| 539,95108 | 0,02986 | 0,03229 | 0,03096 | 0,03666 | 0,03294 |
| 539,98826 | 0,02966 | 0,03159 | 0,03032 | 0,03624 | 0,03246 |
| 540,02544 | 0,02945 | 0,0309 | 0,02967 | 0,03582 | 0,03195 |
| 540,06262 | 0,02924 | 0,0302 | 0,02904 | 0,0354 | 0,03143 |
| 540,0998 | 0,02902 | 0,02951 | 0,02842 | 0,03497 | 0,03089 |
| 540,13699 | 0,02879 | 0,02883 | 0,0278 | 0,03454 | 0,03033 |
| 540,17417 | 0,02855 | 0,02815 | 0,02719 | 0,0341 | 0,02976 |
| 540,21135 | 0,0283 | 0,02748 | 0,02658 | 0,03366 | 0,02917 |
| 540,24853 | 0,02804 | 0,02681 | 0,02598 | 0,03321 | 0,02857 |
| 540,28571 | 0,02777 | 0,02615 | 0,0254 | 0,03276 | 0,02795 |
| 540,3229 | 0,0275 | 0,0255 | 0,02482 | 0,0323 | 0,02733 |
| 540,36008 | 0,02721 | 0,02485 | 0,02425 | 0,03184 | 0,02669 |
| 540,39726 | 0,02692 | 0,02421 | 0,02368 | 0,03138 | 0,02604 |
| 540,43444 | 0,02661 | 0,02358 | 0,02313 | 0,03091 | 0,02539 |
| 540,47162 | 0,0263 | 0,02297 | 0,02258 | 0,03044 | 0,02473 |
| 540,50881 | 0,02598 | 0,02236 | 0,02204 | 0,02996 | 0,02406 |
| 540,54599 | 0,02564 | 0,02175 | 0,02152 | 0,02948 | 0,02339 |
| 540,58317 | 0,0253 | 0,02116 | 0,021 | 0,029 | 0,02272 |
| 540,62035 | 0,02495 | 0,02058 | 0,02049 | 0,02852 | 0,02205 |
| 540,65753 | 0,02459 | 0,02001 | 0,01998 | 0,02803 | 0,02138 |
| 540,69472 | 0,02422 | 0,01945 | 0,01949 | 0,02754 | 0,0207 |
| 540,7319 | 0,02385 | 0,0189 | 0,01901 | 0,02705 | 0,02003 |
| 540,76908 | 0,02346 | 0,01835 | 0,01853 | 0,02656 | 0,01936 |
| 540,80626 | 0,02307 | 0,01782 | 0,01806 | 0,02606 | 0,0187 |
| 540,84344 | 0,02267 | 0,0173 | 0,0176 | 0,02557 | 0,01804 |
| 540,88063 | 0,02226 | 0,01679 | 0,01715 | 0,02507 | 0,01739 |
| 540,91781 | 0,02185 | 0,01629 | 0,01671 | 0,02457 | 0,01675 |
| 540,95499 | 0,02143 | 0,01579 | 0,01627 | 0,02407 | 0,01612 |
| 540,99217 | 0,021 | 0,01531 | 0,01584 | 0,02357 | 0,01549 |
| 541,02935 | 0,02057 | 0,01484 | 0,01542 | 0,02308 | 0,01488 |
| 541,06654 | 0,02013 | 0,01438 | 0,01501 | 0,02258 | 0,01427 |
| 541,10372 | 0,01969 | 0,01392 | 0,01461 | 0,02208 | 0,01367 |
| 541,1409 | 0,01925 | 0,01348 | 0,01421 | 0,02158 | 0,0131 |
| 541,17808 | 0,0188 | 0,01305 | 0,01382 | 0,02109 | 0,01253 |
| 541,21526 | 0,01835 | 0,01262 | 0,01343 | 0,0206 | 0,01197 |
| 541,25245 | 0,01789 | 0,0122 | 0,01305 | 0,02011 | 0,01143 |
| 541,28963 | 0,01744 | 0,0118 | 0,01268 | 0,01962 | 0,0109 |
| 541,32681 | 0,01698 | 0,0114 | 0,01232 | 0,01914 | 0,01039 |
| 541,36399 | 0,01652 | 0,01101 | 0,01196 | 0,01865 | 0,00989 |
| 541,40117 | 0,01606 | 0,01063 | 0,01161 | 0,01818 | 0,00941 |
| 541,43836 | 0,0156 | 0,01026 | 0,01126 | 0,0177 | 0,00894 |
| 541,47554 | 0,01515 | 0,00989 | 0,01092 | 0,01724 | 0,00848 |
| 541,51272 | 0,01469 | 0,00954 | 0,01058 | 0,01677 | 0,00805 |
| 541,5499 | 0,01424 | 0,00919 | 0,01025 | 0,01631 | 0,00763 |
| 541,58708 | 0,01379 | 0,00885 | 0,00993 | 0,01586 | 0,00722 |
| 541,62427 | 0,01334 | 0,00852 | 0,00961 | 0,01541 | 0,00683 |
| 541,66145 | 0,0129 | 0,0082 | 0,0093 | 0,01497 | 0,00645 |
| 541,69863 | 0,01246 | 0,00789 | 0,00899 | 0,01454 | 0,00609 |
| 541,73581 | 0,01202 | 0,00758 | 0,00869 | 0,01411 | 0,00574 |
| 541,77299 | 0,01159 | 0,00728 | 0,00839 | 0,01368 | 0,00541 |
| 541,81018 | 0,01117 | 0,00699 | 0,0081 | 0,01327 | 0,00509 |
| 541,84736 | 0,01075 | 0,00671 | 0,00782 | 0,01286 | 0,00479 |
| 541,88454 | 0,01034 | 0,00643 | 0,00754 | 0,01246 | 0,0045 |
| 541,92172 | 0,00993 | 0,00616 | 0,00726 | 0,01207 | 0,00422 |
| 541,9589 | 0,00953 | 0,0059 | 0,00699 | 0,01168 | 0,00396 |
| 541,99609 | 0,00914 | 0,00565 | 0,00673 | 0,0113 | 0,00371 |
| 542,03327 | 0,00876 | 0,0054 | 0,00647 | 0,01093 | 0,00347 |
| 542,07045 | 0,00839 | 0,00516 | 0,00622 | 0,01057 | 0,00325 |
| 542,10763 | 0,00802 | 0,00493 | 0,00597 | 0,01022 | 0,00303 |
| 542,14481 | 0,00766 | 0,00471 | 0,00573 | 0,00987 | 0,00283 |
| 542,182 | 0,00731 | 0,00449 | 0,00549 | 0,00954 | 0,00264 |
| 542,21918 | 0,00698 | 0,00428 | 0,00526 | 0,0092 | 0,00246 |
| 542,25636 | 0,00665 | 0,00408 | 0,00504 | 0,00888 | 0,00229 |
| 542,29354 | 0,00632 | 0,00388 | 0,00482 | 0,00857 | 0,00213 |
| 542,33072 | 0,00601 | 0,00369 | 0,0046 | 0,00826 | 0,00197 |
| 542,36791 | 0,00571 | 0,0035 | 0,00439 | 0,00796 | 0,00183 |
| 542,40509 | 0,00542 | 0,00333 | 0,00419 | 0,00767 | 0,0017 |
| 542,44227 | 0,00514 | 0,00315 | 0,004 | 0,00739 | 0,00157 |
| 542,47945 | 0,00487 | 0,00299 | 0,00381 | 0,00711 | 0,00145 |
| 542,51663 | 0,0046 | 0,00283 | 0,00362 | 0,00684 | 0,00134 |
| 542,55382 | 0,00435 | 0,00268 | 0,00344 | 0,00658 | 0,00124 |
| 542,591 | 0,00411 | 0,00253 | 0,00327 | 0,00633 | 0,00114 |
| 542,62818 | 0,00387 | 0,00239 | 0,0031 | 0,00608 | 0,00105 |
| 542,66536 | 0,00365 | 0,00226 | 0,00294 | 0,00584 | 0,00097 |
| 542,70254 | 0,00344 | 0,00213 | 0,00278 | 0,00561 | 0,00089 |
| 542,73973 | 0,00323 | 0,00201 | 0,00264 | 0,00539 | 0,00082 |
| 542,77691 | 0,00303 | 0,00189 | 0,00249 | 0,00517 | 0,00075 |
| 542,81409 | 0,00285 | 0,00178 | 0,00235 | 0,00496 | 0,00069 |
| 542,85127 | 0,00267 | 0,00167 | 0,00222 | 0,00475 | 0,00063 |
| 542,88845 | 0,0025 | 0,00157 | 0,00209 | 0,00455 | 0,00058 |
| 542,92564 | 0,00234 | 0,00147 | 0,00197 | 0,00436 | 0,00053 |
| 542,96282 | 0,00218 | 0,00138 | 0,00185 | 0,00417 | 0,00048 |
| 543 | 0,00204 | 0,00129 | 0,00174 | 0,00399 | 0,00044 |
| "Onderwijsscore" | "2019/'20" (Dichtheid) | "2020/'21" (Dichtheid) | "2021/'22, okt" (Dichtheid) | "2021/'22, feb" (Dichtheid) | "2022/'23" (Dichtheid) |
|---|---|---|---|---|---|
| 524 | 0,00015 | 0,00023 | 3e-04 | 0 | 0,00022 |
| 524,03718 | 0,00016 | 0,00024 | 0,00031 | 0 | 0,00024 |
| 524,07436 | 0,00017 | 0,00026 | 0,00032 | 0 | 0,00025 |
| 524,11155 | 0,00018 | 0,00027 | 0,00034 | 1e-05 | 0,00026 |
| 524,14873 | 0,00019 | 0,00029 | 0,00036 | 1e-05 | 0,00027 |
| 524,18591 | 2e-04 | 0,00031 | 0,00038 | 1e-05 | 0,00028 |
| 524,22309 | 0,00022 | 0,00033 | 4e-04 | 1e-05 | 0,00029 |
| 524,26027 | 0,00023 | 0,00035 | 0,00042 | 1e-05 | 0,00029 |
| 524,29746 | 0,00025 | 0,00037 | 0,00045 | 2e-05 | 3e-04 |
| 524,33464 | 0,00027 | 4e-04 | 0,00047 | 2e-05 | 0,00031 |
| 524,37182 | 0,00029 | 0,00043 | 5e-04 | 2e-05 | 0,00032 |
| 524,409 | 0,00032 | 0,00046 | 0,00053 | 3e-05 | 0,00032 |
| 524,44618 | 0,00035 | 0,00049 | 0,00056 | 3e-05 | 0,00033 |
| 524,48337 | 0,00038 | 0,00052 | 0,00059 | 4e-05 | 0,00033 |
| 524,52055 | 0,00041 | 0,00055 | 0,00063 | 5e-05 | 0,00034 |
| 524,55773 | 0,00044 | 0,00059 | 0,00066 | 6e-05 | 0,00034 |
| 524,59491 | 0,00048 | 0,00063 | 7e-04 | 7e-05 | 0,00034 |
| 524,63209 | 0,00053 | 0,00067 | 0,00074 | 8e-05 | 0,00035 |
| 524,66928 | 0,00057 | 0,00072 | 0,00079 | 1e-04 | 0,00035 |
| 524,70646 | 0,00062 | 0,00077 | 0,00084 | 0,00011 | 0,00036 |
| 524,74364 | 0,00068 | 0,00082 | 0,00088 | 0,00013 | 0,00036 |
| 524,78082 | 0,00074 | 0,00088 | 0,00094 | 0,00015 | 0,00037 |
| 524,818 | 8e-04 | 0,00093 | 0,00099 | 0,00018 | 0,00038 |
| 524,85519 | 0,00087 | 0,001 | 0,00105 | 0,00021 | 0,00039 |
| 524,89237 | 0,00095 | 0,00106 | 0,00111 | 0,00024 | 4e-04 |
| 524,92955 | 0,00103 | 0,00114 | 0,00118 | 0,00028 | 0,00042 |
| 524,96673 | 0,00112 | 0,00121 | 0,00125 | 0,00033 | 0,00043 |
| 525,00391 | 0,00122 | 0,00129 | 0,00132 | 0,00038 | 0,00046 |
| 525,0411 | 0,00133 | 0,00138 | 0,0014 | 0,00043 | 0,00048 |
| 525,07828 | 0,00144 | 0,00147 | 0,00148 | 5e-04 | 0,00051 |
| 525,11546 | 0,00156 | 0,00158 | 0,00157 | 0,00057 | 0,00055 |
| 525,15264 | 0,00169 | 0,00169 | 0,00166 | 0,00065 | 6e-04 |
| 525,18982 | 0,00184 | 0,0018 | 0,00176 | 0,00074 | 0,00065 |
| 525,22701 | 0,00199 | 0,00193 | 0,00186 | 0,00084 | 0,00071 |
| 525,26419 | 0,00216 | 0,00206 | 0,00198 | 0,00094 | 0,00078 |
| 525,30137 | 0,00233 | 0,00221 | 0,0021 | 0,00107 | 0,00086 |
| 525,33855 | 0,00252 | 0,00236 | 0,00223 | 0,0012 | 0,00094 |
| 525,37573 | 0,00272 | 0,00253 | 0,00236 | 0,00134 | 0,00104 |
| 525,41292 | 0,00294 | 0,00271 | 0,00251 | 0,0015 | 0,00116 |
| 525,4501 | 0,00317 | 0,0029 | 0,00267 | 0,00167 | 0,00128 |
| 525,48728 | 0,00341 | 0,00311 | 0,00284 | 0,00185 | 0,00142 |
| 525,52446 | 0,00367 | 0,00333 | 0,00302 | 0,00205 | 0,00157 |
| 525,56164 | 0,00394 | 0,00357 | 0,00321 | 0,00226 | 0,00174 |
| 525,59883 | 0,00423 | 0,00382 | 0,00341 | 0,00249 | 0,00192 |
| 525,63601 | 0,00454 | 0,00409 | 0,00363 | 0,00273 | 0,00212 |
| 525,67319 | 0,00486 | 0,00438 | 0,00386 | 0,00298 | 0,00233 |
| 525,71037 | 0,00519 | 0,00468 | 0,00411 | 0,00325 | 0,00256 |
| 525,74755 | 0,00554 | 0,005 | 0,00437 | 0,00353 | 0,0028 |
| 525,78474 | 0,00591 | 0,00535 | 0,00465 | 0,00382 | 0,00306 |
| 525,82192 | 0,0063 | 0,00571 | 0,00494 | 0,00412 | 0,00334 |
| 525,8591 | 0,0067 | 0,00608 | 0,00525 | 0,00443 | 0,00363 |
| 525,89628 | 0,00711 | 0,00648 | 0,00557 | 0,00476 | 0,00393 |
| 525,93346 | 0,00754 | 0,0069 | 0,00591 | 0,00509 | 0,00425 |
| 525,97065 | 0,00798 | 0,00734 | 0,00627 | 0,00542 | 0,00458 |
| 526,00783 | 0,00843 | 0,0078 | 0,00664 | 0,00577 | 0,00492 |
| 526,04501 | 0,0089 | 0,00827 | 0,00703 | 0,00611 | 0,00527 |
| 526,08219 | 0,00938 | 0,00876 | 0,00743 | 0,00646 | 0,00563 |
| 526,11937 | 0,00987 | 0,00928 | 0,00785 | 0,00682 | 0,006 |
| 526,15656 | 0,01037 | 0,00981 | 0,00828 | 0,00717 | 0,00638 |
| 526,19374 | 0,01088 | 0,01036 | 0,00873 | 0,00752 | 0,00676 |
| 526,23092 | 0,0114 | 0,01092 | 0,00919 | 0,00787 | 0,00715 |
| 526,2681 | 0,01193 | 0,0115 | 0,00967 | 0,00822 | 0,00754 |
| 526,30528 | 0,01246 | 0,0121 | 0,01015 | 0,00856 | 0,00793 |
| 526,34247 | 0,013 | 0,01272 | 0,01066 | 0,0089 | 0,00832 |
| 526,37965 | 0,01354 | 0,01335 | 0,01117 | 0,00924 | 0,00871 |
| 526,41683 | 0,0141 | 0,01399 | 0,0117 | 0,00957 | 0,0091 |
| 526,45401 | 0,01466 | 0,01465 | 0,01224 | 0,0099 | 0,00948 |
| 526,49119 | 0,01523 | 0,01532 | 0,01279 | 0,01023 | 0,00987 |
| 526,52838 | 0,0158 | 0,01601 | 0,01336 | 0,01055 | 0,01025 |
| 526,56556 | 0,01638 | 0,01671 | 0,01394 | 0,01087 | 0,01062 |
| 526,60274 | 0,01698 | 0,01742 | 0,01454 | 0,01119 | 0,011 |
| 526,63992 | 0,01759 | 0,01815 | 0,01516 | 0,01151 | 0,01136 |
| 526,6771 | 0,01821 | 0,01889 | 0,01579 | 0,01184 | 0,01173 |
| 526,71429 | 0,01885 | 0,01964 | 0,01645 | 0,01217 | 0,0121 |
| 526,75147 | 0,0195 | 0,02042 | 0,01712 | 0,01251 | 0,01247 |
| 526,78865 | 0,02018 | 0,02121 | 0,01782 | 0,01285 | 0,01284 |
| 526,82583 | 0,02089 | 0,02201 | 0,01855 | 0,01321 | 0,01321 |
| 526,86301 | 0,02162 | 0,02284 | 0,0193 | 0,01359 | 0,0136 |
| 526,9002 | 0,02239 | 0,02368 | 0,02009 | 0,01398 | 0,01399 |
| 526,93738 | 0,02319 | 0,02455 | 0,0209 | 0,01439 | 0,0144 |
| 526,97456 | 0,02402 | 0,02545 | 0,02175 | 0,01483 | 0,01482 |
| 527,01174 | 0,0249 | 0,02636 | 0,02263 | 0,0153 | 0,01526 |
| 527,04892 | 0,02583 | 0,02731 | 0,02356 | 0,0158 | 0,01573 |
| 527,08611 | 0,02681 | 0,02828 | 0,02453 | 0,01633 | 0,01623 |
| 527,12329 | 0,02783 | 0,02928 | 0,02553 | 0,0169 | 0,01677 |
| 527,16047 | 0,0289 | 0,03032 | 0,02658 | 0,01752 | 0,01733 |
| 527,19765 | 0,03002 | 0,03139 | 0,02767 | 0,01819 | 0,01794 |
| 527,23483 | 0,03121 | 0,0325 | 0,02881 | 0,0189 | 0,0186 |
| 527,27202 | 0,03245 | 0,03364 | 0,03 | 0,01966 | 0,01932 |
| 527,3092 | 0,03375 | 0,03482 | 0,03122 | 0,02047 | 0,02008 |
| 527,34638 | 0,0351 | 0,03603 | 0,03249 | 0,02135 | 0,0209 |
| 527,38356 | 0,0365 | 0,03729 | 0,0338 | 0,0223 | 0,02178 |
| 527,42074 | 0,03796 | 0,03857 | 0,03515 | 0,02331 | 0,02273 |
| 527,45793 | 0,03948 | 0,03989 | 0,03655 | 0,02438 | 0,02376 |
| 527,49511 | 0,04105 | 0,04125 | 0,03797 | 0,02552 | 0,02485 |
| 527,53229 | 0,04266 | 0,04265 | 0,03943 | 0,02672 | 0,02601 |
| 527,56947 | 0,04432 | 0,04407 | 0,04092 | 0,02801 | 0,02724 |
| 527,60665 | 0,04601 | 0,04552 | 0,04244 | 0,02936 | 0,02854 |
| 527,64384 | 0,04776 | 0,047 | 0,04399 | 0,03078 | 0,02993 |
| 527,68102 | 0,04953 | 0,04849 | 0,04555 | 0,03226 | 0,03139 |
| 527,7182 | 0,05134 | 0,05001 | 0,04712 | 0,03381 | 0,03292 |
| 527,75538 | 0,05317 | 0,05155 | 0,04871 | 0,03543 | 0,03451 |
| 527,79256 | 0,05503 | 0,0531 | 0,05031 | 0,03711 | 0,03616 |
| 527,82975 | 0,05691 | 0,05466 | 0,05191 | 0,03884 | 0,03788 |
| 527,86693 | 0,05881 | 0,05622 | 0,05352 | 0,04062 | 0,03966 |
| 527,90411 | 0,06071 | 0,05778 | 0,05512 | 0,04244 | 0,04148 |
| 527,94129 | 0,06263 | 0,05934 | 0,05672 | 0,0443 | 0,04334 |
| 527,97847 | 0,06455 | 0,0609 | 0,05831 | 0,0462 | 0,04524 |
| 528,01566 | 0,06647 | 0,06245 | 0,05989 | 0,04812 | 0,04717 |
| 528,05284 | 0,06839 | 0,06399 | 0,06145 | 0,05006 | 0,04913 |
| 528,09002 | 0,07031 | 0,06551 | 0,06301 | 0,05201 | 0,0511 |
| 528,1272 | 0,07221 | 0,06702 | 0,06455 | 0,05396 | 0,05307 |
| 528,16438 | 0,07411 | 0,06851 | 0,06607 | 0,05591 | 0,05505 |
| 528,20157 | 0,07599 | 0,06998 | 0,06757 | 0,05784 | 0,05701 |
| 528,23875 | 0,07785 | 0,07143 | 0,06906 | 0,05976 | 0,05896 |
| 528,27593 | 0,07969 | 0,07286 | 0,07053 | 0,06165 | 0,06089 |
| 528,31311 | 0,08151 | 0,07427 | 0,07199 | 0,06351 | 0,06278 |
| 528,35029 | 0,0833 | 0,07565 | 0,07343 | 0,06534 | 0,06465 |
| 528,38748 | 0,08506 | 0,07702 | 0,07485 | 0,06712 | 0,06647 |
| 528,42466 | 0,08679 | 0,07836 | 0,07626 | 0,06886 | 0,06826 |
| 528,46184 | 0,08848 | 0,07969 | 0,07765 | 0,07056 | 0,06998 |
| 528,49902 | 0,09013 | 0,08099 | 0,07903 | 0,07221 | 0,07166 |
| 528,5362 | 0,09174 | 0,08227 | 0,0804 | 0,07381 | 0,07328 |
| 528,57339 | 0,0933 | 0,08354 | 0,08176 | 0,07536 | 0,07486 |
| 528,61057 | 0,09482 | 0,08479 | 0,0831 | 0,07685 | 0,07638 |
| 528,64775 | 0,09627 | 0,08602 | 0,08443 | 0,07831 | 0,07784 |
| 528,68493 | 0,09767 | 0,08723 | 0,08576 | 0,07972 | 0,07924 |
| 528,72211 | 0,09901 | 0,08843 | 0,08707 | 0,08108 | 0,0806 |
| 528,7593 | 0,1003 | 0,08961 | 0,08837 | 0,08242 | 0,08191 |
| 528,79648 | 0,10152 | 0,09078 | 0,08965 | 0,0837 | 0,08317 |
| 528,83366 | 0,10267 | 0,09192 | 0,09092 | 0,08496 | 0,08438 |
| 528,87084 | 0,10375 | 0,09306 | 0,09218 | 0,08618 | 0,08555 |
| 528,90802 | 0,10475 | 0,09417 | 0,09342 | 0,08739 | 0,08669 |
| 528,94521 | 0,10569 | 0,09526 | 0,09465 | 0,08857 | 0,08779 |
| 528,98239 | 0,10656 | 0,09634 | 0,09586 | 0,08972 | 0,08886 |
| 529,01957 | 0,10736 | 0,0974 | 0,09704 | 0,09086 | 0,08991 |
| 529,05675 | 0,10808 | 0,09843 | 0,0982 | 0,09199 | 0,09093 |
| 529,09393 | 0,10872 | 0,09945 | 0,09934 | 0,0931 | 0,09193 |
| 529,13112 | 0,1093 | 0,10043 | 0,10046 | 0,0942 | 0,09291 |
| 529,1683 | 0,10982 | 0,1014 | 0,10155 | 0,09529 | 0,09388 |
| 529,20548 | 0,11027 | 0,10233 | 0,1026 | 0,09637 | 0,09485 |
| 529,24266 | 0,11067 | 0,10325 | 0,10363 | 0,09744 | 0,0958 |
| 529,27984 | 0,111 | 0,10414 | 0,10463 | 0,0985 | 0,09676 |
| 529,31703 | 0,11128 | 0,105 | 0,1056 | 0,09955 | 0,09771 |
| 529,35421 | 0,11152 | 0,10583 | 0,10654 | 0,1006 | 0,09866 |
| 529,39139 | 0,11172 | 0,10664 | 0,10744 | 0,10163 | 0,09962 |
| 529,42857 | 0,11189 | 0,10743 | 0,10831 | 0,10266 | 0,10059 |
| 529,46575 | 0,11203 | 0,10819 | 0,10914 | 0,10367 | 0,10156 |
| 529,50294 | 0,11215 | 0,10892 | 0,10995 | 0,10468 | 0,10254 |
| 529,54012 | 0,11225 | 0,10963 | 0,11072 | 0,10568 | 0,10353 |
| 529,5773 | 0,11235 | 0,11032 | 0,11146 | 0,10666 | 0,10452 |
| 529,61448 | 0,11244 | 0,11098 | 0,11217 | 0,10763 | 0,10553 |
| 529,65166 | 0,11254 | 0,11163 | 0,11285 | 0,10859 | 0,10655 |
| 529,68885 | 0,11264 | 0,11225 | 0,11351 | 0,10954 | 0,10758 |
| 529,72603 | 0,11276 | 0,11285 | 0,11413 | 0,11048 | 0,10862 |
| 529,76321 | 0,1129 | 0,11343 | 0,11473 | 0,1114 | 0,10966 |
| 529,80039 | 0,11306 | 0,114 | 0,1153 | 0,11232 | 0,11071 |
| 529,83757 | 0,11323 | 0,11454 | 0,11585 | 0,11321 | 0,11176 |
| 529,87476 | 0,11344 | 0,11507 | 0,11637 | 0,1141 | 0,11281 |
| 529,91194 | 0,11368 | 0,11557 | 0,11687 | 0,11497 | 0,11386 |
| 529,94912 | 0,11394 | 0,11605 | 0,11734 | 0,11582 | 0,1149 |
| 529,9863 | 0,11422 | 0,11651 | 0,11779 | 0,11666 | 0,11592 |
| 530,02348 | 0,11453 | 0,11695 | 0,11821 | 0,11747 | 0,11693 |
| 530,06067 | 0,11486 | 0,11736 | 0,1186 | 0,11826 | 0,11792 |
| 530,09785 | 0,11521 | 0,11775 | 0,11897 | 0,11902 | 0,11887 |
| 530,13503 | 0,11558 | 0,1181 | 0,11932 | 0,11976 | 0,11979 |
| 530,17221 | 0,11596 | 0,11842 | 0,11963 | 0,12047 | 0,12067 |
| 530,20939 | 0,11634 | 0,11871 | 0,11991 | 0,12114 | 0,12151 |
| 530,24658 | 0,11672 | 0,11897 | 0,12015 | 0,12176 | 0,1223 |
| 530,28376 | 0,11709 | 0,11919 | 0,12037 | 0,12233 | 0,12302 |
| 530,32094 | 0,11746 | 0,11938 | 0,12055 | 0,12286 | 0,12369 |
| 530,35812 | 0,1178 | 0,11952 | 0,12069 | 0,12334 | 0,12429 |
| 530,3953 | 0,11813 | 0,11963 | 0,12079 | 0,12376 | 0,12482 |
| 530,43249 | 0,11843 | 0,1197 | 0,12086 | 0,12412 | 0,12529 |
| 530,46967 | 0,11869 | 0,11974 | 0,12088 | 0,1244 | 0,12567 |
| 530,50685 | 0,11891 | 0,11973 | 0,12087 | 0,12462 | 0,12597 |
| 530,54403 | 0,1191 | 0,11969 | 0,12081 | 0,12478 | 0,12619 |
| 530,58121 | 0,11924 | 0,11962 | 0,12071 | 0,12486 | 0,12635 |
| 530,6184 | 0,11933 | 0,11953 | 0,12057 | 0,12489 | 0,12643 |
| 530,65558 | 0,11938 | 0,1194 | 0,1204 | 0,12483 | 0,12643 |
| 530,69276 | 0,11938 | 0,11926 | 0,12019 | 0,1247 | 0,12635 |
| 530,72994 | 0,11933 | 0,11909 | 0,11996 | 0,12453 | 0,12621 |
| 530,76712 | 0,11923 | 0,11891 | 0,11968 | 0,12429 | 0,12602 |
| 530,80431 | 0,1191 | 0,11872 | 0,11938 | 0,12401 | 0,12576 |
| 530,84149 | 0,11893 | 0,11852 | 0,11906 | 0,12369 | 0,12546 |
| 530,87867 | 0,11872 | 0,11832 | 0,11873 | 0,12332 | 0,12512 |
| 530,91585 | 0,11847 | 0,11813 | 0,11838 | 0,12294 | 0,12473 |
| 530,95303 | 0,11821 | 0,11794 | 0,11801 | 0,12253 | 0,12432 |
| 530,99022 | 0,11792 | 0,11777 | 0,11765 | 0,12212 | 0,1239 |
| 531,0274 | 0,11763 | 0,11761 | 0,11728 | 0,12171 | 0,12346 |
| 531,06458 | 0,11732 | 0,11746 | 0,11691 | 0,1213 | 0,12301 |
| 531,10176 | 0,11701 | 0,11734 | 0,11655 | 0,12092 | 0,12257 |
| 531,13894 | 0,11671 | 0,11724 | 0,1162 | 0,12056 | 0,12213 |
| 531,17613 | 0,11642 | 0,11716 | 0,11585 | 0,12023 | 0,12171 |
| 531,21331 | 0,11613 | 0,1171 | 0,11553 | 0,11994 | 0,12131 |
| 531,25049 | 0,11587 | 0,11706 | 0,11521 | 0,11969 | 0,12093 |
| 531,28767 | 0,11562 | 0,11704 | 0,1149 | 0,11949 | 0,12057 |
| 531,32485 | 0,11539 | 0,11703 | 0,11461 | 0,11933 | 0,12025 |
| 531,36204 | 0,11519 | 0,11704 | 0,11434 | 0,11921 | 0,11995 |
| 531,39922 | 0,115 | 0,11705 | 0,11407 | 0,11914 | 0,11968 |
| 531,4364 | 0,11484 | 0,11706 | 0,1138 | 0,1191 | 0,11943 |
| 531,47358 | 0,11469 | 0,11707 | 0,11355 | 0,11911 | 0,11921 |
| 531,51076 | 0,11456 | 0,11707 | 0,11329 | 0,11914 | 0,11902 |
| 531,54795 | 0,11443 | 0,11706 | 0,11302 | 0,11919 | 0,11885 |
| 531,58513 | 0,11432 | 0,11702 | 0,11275 | 0,11925 | 0,11868 |
| 531,62231 | 0,1142 | 0,11696 | 0,11247 | 0,11931 | 0,11853 |
| 531,65949 | 0,11408 | 0,11686 | 0,11217 | 0,11937 | 0,11839 |
| 531,69667 | 0,11395 | 0,11673 | 0,11185 | 0,11942 | 0,11824 |
| 531,73386 | 0,1138 | 0,11655 | 0,1115 | 0,11944 | 0,11809 |
| 531,77104 | 0,11363 | 0,11632 | 0,11112 | 0,11943 | 0,11793 |
| 531,80822 | 0,11344 | 0,11603 | 0,11072 | 0,11939 | 0,11776 |
| 531,8454 | 0,11322 | 0,1157 | 0,11028 | 0,1193 | 0,11756 |
| 531,88258 | 0,11296 | 0,11531 | 0,10981 | 0,11915 | 0,11735 |
| 531,91977 | 0,11266 | 0,11486 | 0,1093 | 0,11894 | 0,11711 |
| 531,95695 | 0,11232 | 0,11435 | 0,10875 | 0,11868 | 0,11684 |
| 531,99413 | 0,11194 | 0,11378 | 0,10818 | 0,11835 | 0,11654 |
| 532,03131 | 0,11152 | 0,11316 | 0,10757 | 0,11797 | 0,11621 |
| 532,06849 | 0,11106 | 0,11249 | 0,10693 | 0,11752 | 0,11585 |
| 532,10568 | 0,11055 | 0,11178 | 0,10627 | 0,11701 | 0,11546 |
| 532,14286 | 0,11 | 0,11101 | 0,10559 | 0,11644 | 0,11504 |
| 532,18004 | 0,10942 | 0,11021 | 0,10488 | 0,11582 | 0,1146 |
| 532,21722 | 0,10881 | 0,10939 | 0,10417 | 0,11516 | 0,11413 |
| 532,2544 | 0,10818 | 0,10854 | 0,10346 | 0,11446 | 0,11364 |
| 532,29159 | 0,10752 | 0,10768 | 0,10274 | 0,11373 | 0,11313 |
| 532,32877 | 0,10685 | 0,1068 | 0,10203 | 0,11297 | 0,1126 |
| 532,36595 | 0,10616 | 0,10592 | 0,10133 | 0,11219 | 0,11206 |
| 532,40313 | 0,10547 | 0,10505 | 0,10065 | 0,1114 | 0,11152 |
| 532,44031 | 0,10478 | 0,10419 | 0,09999 | 0,11061 | 0,11097 |
| 532,4775 | 0,1041 | 0,10335 | 0,09936 | 0,10981 | 0,11042 |
| 532,51468 | 0,10342 | 0,10253 | 0,09875 | 0,10903 | 0,10987 |
| 532,55186 | 0,10277 | 0,10175 | 0,09819 | 0,10826 | 0,10933 |
| 532,58904 | 0,10213 | 0,101 | 0,09766 | 0,10751 | 0,10879 |
| 532,62622 | 0,10151 | 0,10028 | 0,09717 | 0,10678 | 0,10826 |
| 532,66341 | 0,10092 | 0,09959 | 0,09672 | 0,10606 | 0,10774 |
| 532,70059 | 0,10035 | 0,09895 | 0,0963 | 0,10538 | 0,10723 |
| 532,73777 | 0,09981 | 0,09835 | 0,09593 | 0,10473 | 0,10673 |
| 532,77495 | 0,09929 | 0,09778 | 0,0956 | 0,10409 | 0,10624 |
| 532,81213 | 0,0988 | 0,09725 | 0,09529 | 0,10348 | 0,10575 |
| 532,84932 | 0,09833 | 0,09675 | 0,09502 | 0,1029 | 0,10527 |
| 532,8865 | 0,09788 | 0,09628 | 0,09478 | 0,10233 | 0,10479 |
| 532,92368 | 0,09744 | 0,09583 | 0,09455 | 0,10179 | 0,10432 |
| 532,96086 | 0,09702 | 0,0954 | 0,09435 | 0,10126 | 0,10384 |
| 532,99804 | 0,0966 | 0,09498 | 0,09415 | 0,10074 | 0,10336 |
| 533,03523 | 0,09618 | 0,09457 | 0,09396 | 0,10024 | 0,10288 |
| 533,07241 | 0,09576 | 0,09416 | 0,09376 | 0,09974 | 0,10238 |
| 533,10959 | 0,09533 | 0,09374 | 0,09356 | 0,09924 | 0,10187 |
| 533,14677 | 0,09488 | 0,09331 | 0,09334 | 0,09874 | 0,10135 |
| 533,18395 | 0,09442 | 0,09286 | 0,0931 | 0,09824 | 0,10081 |
| 533,22114 | 0,09393 | 0,09238 | 0,09284 | 0,09774 | 0,10025 |
| 533,25832 | 0,09343 | 0,09188 | 0,09255 | 0,09723 | 0,09967 |
| 533,2955 | 0,0929 | 0,09135 | 0,09222 | 0,09672 | 0,09907 |
| 533,33268 | 0,09233 | 0,09078 | 0,09185 | 0,0962 | 0,09845 |
| 533,36986 | 0,09173 | 0,09017 | 0,09144 | 0,09567 | 0,0978 |
| 533,40705 | 0,0911 | 0,08953 | 0,09099 | 0,09513 | 0,09713 |
| 533,44423 | 0,09045 | 0,08885 | 0,09049 | 0,09458 | 0,09643 |
| 533,48141 | 0,08977 | 0,08813 | 0,08995 | 0,09403 | 0,09572 |
| 533,51859 | 0,08907 | 0,08738 | 0,08936 | 0,09346 | 0,09498 |
| 533,55577 | 0,08834 | 0,0866 | 0,08872 | 0,0929 | 0,09422 |
| 533,59295 | 0,0876 | 0,08579 | 0,08805 | 0,09232 | 0,09344 |
| 533,63014 | 0,08685 | 0,08497 | 0,08734 | 0,09174 | 0,09264 |
| 533,66732 | 0,0861 | 0,08413 | 0,08659 | 0,09116 | 0,09183 |
| 533,7045 | 0,08534 | 0,08327 | 0,08581 | 0,09058 | 0,091 |
| 533,74168 | 0,0846 | 0,08242 | 0,085 | 0,08999 | 0,09015 |
| 533,77886 | 0,08387 | 0,08157 | 0,08417 | 0,0894 | 0,0893 |
| 533,81605 | 0,08316 | 0,08072 | 0,08333 | 0,08881 | 0,08843 |
| 533,85323 | 0,08247 | 0,0799 | 0,08247 | 0,08822 | 0,08756 |
| 533,89041 | 0,08181 | 0,0791 | 0,0816 | 0,08762 | 0,08667 |
| 533,92759 | 0,08119 | 0,07833 | 0,08074 | 0,08702 | 0,08578 |
| 533,96477 | 0,08061 | 0,0776 | 0,07988 | 0,08642 | 0,08488 |
| 534,00196 | 0,08007 | 0,07691 | 0,07902 | 0,08581 | 0,08398 |
| 534,03914 | 0,07956 | 0,07626 | 0,07818 | 0,08518 | 0,08307 |
| 534,07632 | 0,0791 | 0,07565 | 0,07735 | 0,08455 | 0,08216 |
| 534,1135 | 0,07868 | 0,0751 | 0,07655 | 0,08391 | 0,08124 |
| 534,15068 | 0,07831 | 0,0746 | 0,07576 | 0,08324 | 0,08031 |
| 534,18787 | 0,07798 | 0,07414 | 0,075 | 0,08256 | 0,07938 |
| 534,22505 | 0,07767 | 0,07373 | 0,07426 | 0,08186 | 0,07845 |
| 534,26223 | 0,07739 | 0,07337 | 0,07355 | 0,08114 | 0,07751 |
| 534,29941 | 0,07714 | 0,07304 | 0,07286 | 0,08039 | 0,07656 |
| 534,33659 | 0,0769 | 0,07276 | 0,0722 | 0,07962 | 0,07561 |
| 534,37378 | 0,07667 | 0,07251 | 0,07156 | 0,07882 | 0,07466 |
| 534,41096 | 0,07643 | 0,07229 | 0,07093 | 0,07799 | 0,07371 |
| 534,44814 | 0,07619 | 0,07208 | 0,07033 | 0,07713 | 0,07275 |
| 534,48532 | 0,07594 | 0,07188 | 0,06974 | 0,07625 | 0,0718 |
| 534,5225 | 0,07567 | 0,07169 | 0,06917 | 0,07535 | 0,07085 |
| 534,55969 | 0,07536 | 0,07149 | 0,0686 | 0,07442 | 0,0699 |
| 534,59687 | 0,07502 | 0,07129 | 0,06804 | 0,07347 | 0,06897 |
| 534,63405 | 0,07464 | 0,07107 | 0,06748 | 0,07251 | 0,06804 |
| 534,67123 | 0,07421 | 0,07083 | 0,06693 | 0,07153 | 0,06713 |
| 534,70841 | 0,07374 | 0,07057 | 0,06637 | 0,07055 | 0,06623 |
| 534,7456 | 0,0732 | 0,07027 | 0,06581 | 0,06956 | 0,06536 |
| 534,78278 | 0,07262 | 0,06993 | 0,06524 | 0,06858 | 0,06452 |
| 534,81996 | 0,07198 | 0,06956 | 0,06466 | 0,06761 | 0,0637 |
| 534,85714 | 0,07129 | 0,06915 | 0,06408 | 0,06665 | 0,06291 |
| 534,89432 | 0,07056 | 0,06871 | 0,0635 | 0,06571 | 0,06216 |
| 534,93151 | 0,06978 | 0,06822 | 0,0629 | 0,0648 | 0,06145 |
| 534,96869 | 0,06895 | 0,0677 | 0,0623 | 0,06392 | 0,06079 |
| 535,00587 | 0,0681 | 0,06715 | 0,0617 | 0,06309 | 0,06018 |
| 535,04305 | 0,06722 | 0,06657 | 0,0611 | 0,06229 | 0,05961 |
| 535,08023 | 0,06632 | 0,06596 | 0,0605 | 0,06154 | 0,05909 |
| 535,11742 | 0,06541 | 0,06534 | 0,05991 | 0,06085 | 0,05862 |
| 535,1546 | 0,06449 | 0,0647 | 0,05933 | 0,0602 | 0,05822 |
| 535,19178 | 0,06359 | 0,06406 | 0,05876 | 0,05963 | 0,05787 |
| 535,22896 | 0,0627 | 0,06342 | 0,05821 | 0,05911 | 0,05758 |
| 535,26614 | 0,06184 | 0,06279 | 0,05768 | 0,05866 | 0,05734 |
| 535,30333 | 0,061 | 0,06217 | 0,05718 | 0,05826 | 0,05715 |
| 535,34051 | 0,06021 | 0,06157 | 0,05671 | 0,05793 | 0,05702 |
| 535,37769 | 0,05946 | 0,061 | 0,05628 | 0,05766 | 0,05695 |
| 535,41487 | 0,05877 | 0,06046 | 0,05588 | 0,05746 | 0,05692 |
| 535,45205 | 0,05812 | 0,05995 | 0,05552 | 0,05731 | 0,05694 |
| 535,48924 | 0,05753 | 0,05948 | 0,0552 | 0,05722 | 0,057 |
| 535,52642 | 0,057 | 0,05906 | 0,05493 | 0,05717 | 0,0571 |
| 535,5636 | 0,05654 | 0,05868 | 0,0547 | 0,05717 | 0,05724 |
| 535,60078 | 0,05614 | 0,05835 | 0,05451 | 0,05722 | 0,05741 |
| 535,63796 | 0,0558 | 0,05805 | 0,05436 | 0,0573 | 0,05761 |
| 535,67515 | 0,05551 | 0,0578 | 0,05425 | 0,05742 | 0,05783 |
| 535,71233 | 0,05526 | 0,05758 | 0,05419 | 0,05756 | 0,05807 |
| 535,74951 | 0,05507 | 0,05741 | 0,05416 | 0,05772 | 0,05832 |
| 535,78669 | 0,05493 | 0,05727 | 0,05415 | 0,0579 | 0,05858 |
| 535,82387 | 0,05481 | 0,05715 | 0,05418 | 0,05809 | 0,05885 |
| 535,86106 | 0,05473 | 0,05706 | 0,05422 | 0,05828 | 0,05911 |
| 535,89824 | 0,05467 | 0,05698 | 0,05429 | 0,05847 | 0,05937 |
| 535,93542 | 0,05462 | 0,05692 | 0,05436 | 0,05866 | 0,05963 |
| 535,9726 | 0,05458 | 0,05686 | 0,05444 | 0,05884 | 0,05987 |
| 536,00978 | 0,05454 | 0,0568 | 0,05452 | 0,05901 | 0,06009 |
| 536,04697 | 0,05449 | 0,05674 | 0,05459 | 0,05915 | 0,06029 |
| 536,08415 | 0,05443 | 0,05667 | 0,05466 | 0,05927 | 0,06048 |
| 536,12133 | 0,05435 | 0,05658 | 0,05471 | 0,05937 | 0,06064 |
| 536,15851 | 0,05425 | 0,05646 | 0,05473 | 0,05945 | 0,06077 |
| 536,19569 | 0,05411 | 0,05633 | 0,05474 | 0,05949 | 0,06087 |
| 536,23288 | 0,05395 | 0,05617 | 0,05472 | 0,05949 | 0,06094 |
| 536,27006 | 0,05375 | 0,05597 | 0,05467 | 0,05946 | 0,06097 |
| 536,30724 | 0,05351 | 0,05575 | 0,05458 | 0,0594 | 0,06097 |
| 536,34442 | 0,05324 | 0,05549 | 0,05446 | 0,05931 | 0,06094 |
| 536,3816 | 0,05293 | 0,0552 | 0,05431 | 0,05919 | 0,06086 |
| 536,41879 | 0,05257 | 0,05488 | 0,05412 | 0,05902 | 0,06075 |
| 536,45597 | 0,05219 | 0,05454 | 0,05391 | 0,05881 | 0,06059 |
| 536,49315 | 0,05177 | 0,05416 | 0,05366 | 0,05858 | 0,0604 |
| 536,53033 | 0,05132 | 0,05375 | 0,05338 | 0,05832 | 0,06017 |
| 536,56751 | 0,05084 | 0,05333 | 0,05307 | 0,05802 | 0,05989 |
| 536,6047 | 0,05034 | 0,05288 | 0,05275 | 0,0577 | 0,05957 |
| 536,64188 | 0,04982 | 0,05242 | 0,0524 | 0,05734 | 0,05921 |
| 536,67906 | 0,04929 | 0,05195 | 0,05204 | 0,05696 | 0,05882 |
| 536,71624 | 0,04875 | 0,05147 | 0,05167 | 0,05656 | 0,05838 |
| 536,75342 | 0,0482 | 0,05098 | 0,0513 | 0,05614 | 0,05791 |
| 536,79061 | 0,04766 | 0,0505 | 0,05092 | 0,0557 | 0,0574 |
| 536,82779 | 0,04712 | 0,05002 | 0,05054 | 0,05524 | 0,05686 |
| 536,86497 | 0,0466 | 0,04955 | 0,05017 | 0,05478 | 0,05629 |
| 536,90215 | 0,04608 | 0,04908 | 0,04981 | 0,0543 | 0,05569 |
| 536,93933 | 0,04558 | 0,04863 | 0,04946 | 0,05382 | 0,05508 |
| 536,97652 | 0,0451 | 0,0482 | 0,04913 | 0,05333 | 0,05444 |
| 537,0137 | 0,04465 | 0,04778 | 0,04881 | 0,05285 | 0,05379 |
| 537,05088 | 0,04421 | 0,04737 | 0,04852 | 0,05237 | 0,05313 |
| 537,08806 | 0,0438 | 0,04698 | 0,04824 | 0,0519 | 0,05247 |
| 537,12524 | 0,04341 | 0,04661 | 0,04799 | 0,05144 | 0,05181 |
| 537,16243 | 0,04304 | 0,04626 | 0,04775 | 0,05099 | 0,05116 |
| 537,19961 | 0,0427 | 0,04593 | 0,04754 | 0,05056 | 0,05052 |
| 537,23679 | 0,04238 | 0,0456 | 0,04734 | 0,05015 | 0,04991 |
| 537,27397 | 0,04207 | 0,0453 | 0,04716 | 0,04977 | 0,04931 |
| 537,31115 | 0,04178 | 0,045 | 0,047 | 0,04942 | 0,04875 |
| 537,34834 | 0,0415 | 0,04472 | 0,04685 | 0,04909 | 0,04822 |
| 537,38552 | 0,04123 | 0,04444 | 0,04672 | 0,04879 | 0,04774 |
| 537,4227 | 0,04098 | 0,04417 | 0,04659 | 0,04853 | 0,0473 |
| 537,45988 | 0,04072 | 0,04391 | 0,04647 | 0,04831 | 0,04691 |
| 537,49706 | 0,04047 | 0,04365 | 0,04636 | 0,04812 | 0,04657 |
| 537,53425 | 0,04022 | 0,0434 | 0,04625 | 0,04796 | 0,04628 |
| 537,57143 | 0,03997 | 0,04315 | 0,04615 | 0,04785 | 0,04604 |
| 537,60861 | 0,03971 | 0,04291 | 0,04605 | 0,04776 | 0,04588 |
| 537,64579 | 0,03945 | 0,04267 | 0,04594 | 0,04772 | 0,04576 |
| 537,68297 | 0,03919 | 0,04243 | 0,04584 | 0,04772 | 0,0457 |
| 537,72016 | 0,03893 | 0,04219 | 0,04574 | 0,04774 | 0,0457 |
| 537,75734 | 0,03866 | 0,04197 | 0,04565 | 0,04779 | 0,04574 |
| 537,79452 | 0,0384 | 0,04175 | 0,04555 | 0,04786 | 0,04585 |
| 537,8317 | 0,03813 | 0,04154 | 0,04546 | 0,04796 | 0,046 |
| 537,86888 | 0,03787 | 0,04133 | 0,04537 | 0,04809 | 0,04619 |
| 537,90607 | 0,03762 | 0,04115 | 0,0453 | 0,04822 | 0,04643 |
| 537,94325 | 0,03737 | 0,04097 | 0,04523 | 0,04837 | 0,04669 |
| 537,98043 | 0,03714 | 0,04082 | 0,04517 | 0,04852 | 0,04699 |
| 538,01761 | 0,03692 | 0,04068 | 0,04512 | 0,04867 | 0,04731 |
| 538,05479 | 0,03672 | 0,04056 | 0,04508 | 0,04882 | 0,04764 |
| 538,09198 | 0,03654 | 0,04046 | 0,04507 | 0,04896 | 0,04799 |
| 538,12916 | 0,03638 | 0,04039 | 0,04506 | 0,04909 | 0,04834 |
| 538,16634 | 0,03624 | 0,04034 | 0,04508 | 0,0492 | 0,04868 |
| 538,20352 | 0,03613 | 0,04031 | 0,0451 | 0,04929 | 0,04902 |
| 538,2407 | 0,03604 | 0,04029 | 0,04515 | 0,04935 | 0,04934 |
| 538,27789 | 0,03598 | 0,0403 | 0,04521 | 0,04938 | 0,04963 |
| 538,31507 | 0,03593 | 0,04032 | 0,04528 | 0,04937 | 0,04989 |
| 538,35225 | 0,03591 | 0,04036 | 0,04536 | 0,04933 | 0,05013 |
| 538,38943 | 0,03591 | 0,04041 | 0,04544 | 0,04925 | 0,05032 |
| 538,42661 | 0,03592 | 0,04047 | 0,04553 | 0,04912 | 0,05045 |
| 538,4638 | 0,03595 | 0,04053 | 0,04562 | 0,04895 | 0,05053 |
| 538,50098 | 0,03598 | 0,04058 | 0,0457 | 0,04873 | 0,05056 |
| 538,53816 | 0,03601 | 0,04063 | 0,04577 | 0,04846 | 0,05053 |
| 538,57534 | 0,03604 | 0,04067 | 0,04583 | 0,04815 | 0,05044 |
| 538,61252 | 0,03607 | 0,04069 | 0,04587 | 0,04779 | 0,05028 |
| 538,64971 | 0,03607 | 0,04069 | 0,04589 | 0,04739 | 0,05005 |
| 538,68689 | 0,03607 | 0,04066 | 0,04587 | 0,04693 | 0,04975 |
| 538,72407 | 0,03603 | 0,0406 | 0,04582 | 0,04644 | 0,0494 |
| 538,76125 | 0,03598 | 0,0405 | 0,04574 | 0,04591 | 0,04898 |
| 538,79843 | 0,03589 | 0,04037 | 0,04563 | 0,04535 | 0,04849 |
| 538,83562 | 0,03576 | 0,04019 | 0,04547 | 0,04475 | 0,04794 |
| 538,8728 | 0,0356 | 0,03998 | 0,04526 | 0,04412 | 0,04733 |
| 538,90998 | 0,0354 | 0,03972 | 0,04502 | 0,04347 | 0,04667 |
| 538,94716 | 0,03516 | 0,0394 | 0,04473 | 0,04281 | 0,04597 |
| 538,98434 | 0,03489 | 0,03905 | 0,0444 | 0,04213 | 0,04523 |
| 539,02153 | 0,03457 | 0,03865 | 0,04403 | 0,04144 | 0,04444 |
| 539,05871 | 0,03421 | 0,03821 | 0,04361 | 0,04074 | 0,04363 |
| 539,09589 | 0,03382 | 0,03773 | 0,04316 | 0,04004 | 0,04279 |
| 539,13307 | 0,0334 | 0,03721 | 0,04268 | 0,03934 | 0,04193 |
| 539,17025 | 0,03295 | 0,03666 | 0,04218 | 0,03865 | 0,04106 |
| 539,20744 | 0,03248 | 0,03608 | 0,04164 | 0,03797 | 0,04017 |
| 539,24462 | 0,03198 | 0,03548 | 0,04109 | 0,03729 | 0,03928 |
| 539,2818 | 0,03147 | 0,03486 | 0,04052 | 0,03663 | 0,0384 |
| 539,31898 | 0,03094 | 0,03422 | 0,03993 | 0,03598 | 0,03751 |
| 539,35616 | 0,03041 | 0,03357 | 0,03934 | 0,03534 | 0,03664 |
| 539,39335 | 0,02987 | 0,03292 | 0,03874 | 0,03471 | 0,03577 |
| 539,43053 | 0,02934 | 0,03226 | 0,03814 | 0,0341 | 0,03491 |
| 539,46771 | 0,02881 | 0,0316 | 0,03754 | 0,03349 | 0,03407 |
| 539,50489 | 0,02828 | 0,03095 | 0,03694 | 0,03289 | 0,03324 |
| 539,54207 | 0,02776 | 0,0303 | 0,03635 | 0,03229 | 0,03242 |
| 539,57926 | 0,02725 | 0,02967 | 0,03576 | 0,0317 | 0,03161 |
| 539,61644 | 0,02675 | 0,02904 | 0,03518 | 0,03111 | 0,03082 |
| 539,65362 | 0,02626 | 0,02843 | 0,03461 | 0,03051 | 0,03005 |
| 539,6908 | 0,02578 | 0,02782 | 0,03403 | 0,02991 | 0,02929 |
| 539,72798 | 0,02531 | 0,02723 | 0,03347 | 0,0293 | 0,02853 |
| 539,76517 | 0,02485 | 0,02665 | 0,0329 | 0,02868 | 0,02779 |
| 539,80235 | 0,02439 | 0,02608 | 0,03233 | 0,02804 | 0,02706 |
| 539,83953 | 0,02394 | 0,02552 | 0,03176 | 0,0274 | 0,02634 |
| 539,87671 | 0,02349 | 0,02496 | 0,03119 | 0,02674 | 0,02562 |
| 539,91389 | 0,02305 | 0,02442 | 0,03061 | 0,02607 | 0,02492 |
| 539,95108 | 0,0226 | 0,02387 | 0,03002 | 0,02538 | 0,02423 |
| 539,98826 | 0,02215 | 0,02334 | 0,02942 | 0,02469 | 0,02354 |
| 540,02544 | 0,0217 | 0,0228 | 0,02881 | 0,02398 | 0,02287 |
| 540,06262 | 0,02124 | 0,02226 | 0,02818 | 0,02326 | 0,02221 |
| 540,0998 | 0,02077 | 0,02173 | 0,02754 | 0,02253 | 0,02156 |
| 540,13699 | 0,02029 | 0,02119 | 0,02689 | 0,0218 | 0,02092 |
| 540,17417 | 0,01981 | 0,02065 | 0,02622 | 0,02107 | 0,02029 |
| 540,21135 | 0,01932 | 0,02012 | 0,02555 | 0,02034 | 0,01968 |
| 540,24853 | 0,01883 | 0,01958 | 0,02485 | 0,01961 | 0,01909 |
| 540,28571 | 0,01833 | 0,01904 | 0,02415 | 0,01888 | 0,01851 |
| 540,3229 | 0,01782 | 0,01851 | 0,02344 | 0,01816 | 0,01794 |
| 540,36008 | 0,01732 | 0,01797 | 0,02273 | 0,01745 | 0,01739 |
| 540,39726 | 0,01681 | 0,01744 | 0,02201 | 0,01676 | 0,01686 |
| 540,43444 | 0,01631 | 0,01692 | 0,02129 | 0,01607 | 0,01634 |
| 540,47162 | 0,01581 | 0,0164 | 0,02057 | 0,0154 | 0,01584 |
| 540,50881 | 0,01531 | 0,01588 | 0,01986 | 0,01475 | 0,01536 |
| 540,54599 | 0,01483 | 0,01538 | 0,01915 | 0,01411 | 0,01488 |
| 540,58317 | 0,01435 | 0,01489 | 0,01846 | 0,01349 | 0,01442 |
| 540,62035 | 0,01388 | 0,01441 | 0,01778 | 0,01289 | 0,01397 |
| 540,65753 | 0,01343 | 0,01394 | 0,01711 | 0,0123 | 0,01353 |
| 540,69472 | 0,01299 | 0,01348 | 0,01646 | 0,01173 | 0,01309 |
| 540,7319 | 0,01257 | 0,01303 | 0,01583 | 0,01118 | 0,01266 |
| 540,76908 | 0,01216 | 0,0126 | 0,01521 | 0,01064 | 0,01224 |
| 540,80626 | 0,01176 | 0,01218 | 0,01462 | 0,01012 | 0,01182 |
| 540,84344 | 0,01138 | 0,01177 | 0,01405 | 0,00961 | 0,01141 |
| 540,88063 | 0,01101 | 0,01138 | 0,0135 | 0,00911 | 0,011 |
| 540,91781 | 0,01066 | 0,01099 | 0,01296 | 0,00863 | 0,01058 |
| 540,95499 | 0,01031 | 0,01062 | 0,01245 | 0,00816 | 0,01017 |
| 540,99217 | 0,00998 | 0,01025 | 0,01195 | 0,0077 | 0,00976 |
| 541,02935 | 0,00965 | 0,00989 | 0,01147 | 0,00725 | 0,00935 |
| 541,06654 | 0,00933 | 0,00954 | 0,01101 | 0,00682 | 0,00895 |
| 541,10372 | 0,00902 | 0,0092 | 0,01056 | 0,0064 | 0,00854 |
| 541,1409 | 0,00871 | 0,00886 | 0,01013 | 0,00599 | 0,00813 |
| 541,17808 | 0,00841 | 0,00852 | 0,00971 | 0,0056 | 0,00773 |
| 541,21526 | 0,0081 | 0,00819 | 0,00929 | 0,00522 | 0,00733 |
| 541,25245 | 0,0078 | 0,00786 | 0,00889 | 0,00485 | 0,00694 |
| 541,28963 | 0,0075 | 0,00753 | 0,0085 | 0,00449 | 0,00655 |
| 541,32681 | 0,00719 | 0,0072 | 0,00811 | 0,00415 | 0,00616 |
| 541,36399 | 0,00689 | 0,00687 | 0,00773 | 0,00383 | 0,00579 |
| 541,40117 | 0,00658 | 0,00655 | 0,00736 | 0,00352 | 0,00542 |
| 541,43836 | 0,00627 | 0,00623 | 0,00699 | 0,00323 | 0,00507 |
| 541,47554 | 0,00597 | 0,00591 | 0,00663 | 0,00296 | 0,00472 |
| 541,51272 | 0,00566 | 0,00559 | 0,00627 | 0,0027 | 0,00439 |
| 541,5499 | 0,00535 | 0,00528 | 0,00592 | 0,00245 | 0,00407 |
| 541,58708 | 0,00505 | 0,00497 | 0,00557 | 0,00223 | 0,00377 |
| 541,62427 | 0,00474 | 0,00467 | 0,00524 | 0,00202 | 0,00347 |
| 541,66145 | 0,00444 | 0,00437 | 0,00491 | 0,00182 | 0,00319 |
| 541,69863 | 0,00415 | 0,00408 | 0,00458 | 0,00164 | 0,00293 |
| 541,73581 | 0,00386 | 0,0038 | 0,00427 | 0,00147 | 0,00268 |
| 541,77299 | 0,00358 | 0,00353 | 0,00397 | 0,00133 | 0,00245 |
| 541,81018 | 0,00331 | 0,00327 | 0,00367 | 0,00119 | 0,00223 |
| 541,84736 | 0,00305 | 0,00302 | 0,00339 | 0,00107 | 0,00202 |
| 541,88454 | 0,00279 | 0,00278 | 0,00312 | 0,00095 | 0,00183 |
| 541,92172 | 0,00255 | 0,00255 | 0,00286 | 0,00085 | 0,00166 |
| 541,9589 | 0,00232 | 0,00233 | 0,00261 | 0,00076 | 0,00149 |
| 541,99609 | 0,00211 | 0,00213 | 0,00238 | 0,00068 | 0,00134 |
| 542,03327 | 0,0019 | 0,00194 | 0,00216 | 0,00061 | 0,0012 |
| 542,07045 | 0,00171 | 0,00176 | 0,00196 | 0,00055 | 0,00107 |
| 542,10763 | 0,00153 | 0,0016 | 0,00176 | 0,00049 | 0,00096 |
| 542,14481 | 0,00137 | 0,00144 | 0,00158 | 0,00044 | 0,00085 |
| 542,182 | 0,00121 | 0,0013 | 0,00142 | 4e-04 | 0,00075 |
| 542,21918 | 0,00107 | 0,00118 | 0,00126 | 0,00036 | 0,00066 |
| 542,25636 | 0,00095 | 0,00106 | 0,00112 | 0,00033 | 0,00058 |
| 542,29354 | 0,00083 | 0,00095 | 0,00099 | 3e-04 | 0,00051 |
| 542,33072 | 0,00073 | 0,00085 | 0,00088 | 0,00027 | 0,00045 |
| 542,36791 | 0,00063 | 0,00077 | 0,00077 | 0,00025 | 0,00039 |
| 542,40509 | 0,00055 | 0,00069 | 0,00067 | 0,00023 | 0,00034 |
| 542,44227 | 0,00047 | 0,00062 | 0,00059 | 0,00021 | 3e-04 |
| 542,47945 | 0,00041 | 0,00055 | 0,00051 | 0,00019 | 0,00026 |
| 542,51663 | 0,00035 | 5e-04 | 0,00044 | 0,00018 | 0,00022 |
| 542,55382 | 3e-04 | 0,00045 | 0,00038 | 0,00016 | 0,00019 |
| 542,591 | 0,00025 | 4e-04 | 0,00033 | 0,00015 | 0,00016 |
| 542,62818 | 0,00021 | 0,00037 | 0,00028 | 0,00014 | 0,00014 |
| 542,66536 | 0,00018 | 0,00033 | 0,00024 | 0,00013 | 0,00012 |
| 542,70254 | 0,00015 | 3e-04 | 0,00021 | 0,00012 | 1e-04 |
| 542,73973 | 0,00012 | 0,00027 | 0,00017 | 0,00011 | 9e-05 |
| 542,77691 | 1e-04 | 0,00025 | 0,00015 | 1e-04 | 7e-05 |
| 542,81409 | 9e-05 | 0,00023 | 0,00012 | 9e-05 | 6e-05 |
| 542,85127 | 7e-05 | 0,00021 | 1e-04 | 8e-05 | 5e-05 |
| 542,88845 | 6e-05 | 0,00019 | 9e-05 | 7e-05 | 4e-05 |
| 542,92564 | 5e-05 | 0,00018 | 7e-05 | 7e-05 | 4e-05 |
| 542,96282 | 4e-05 | 0,00016 | 6e-05 | 6e-05 | 3e-05 |
| 543 | 3e-05 | 0,00015 | 5e-05 | 6e-05 | 2e-05 |
| "Onderwijsscore" | "2019/'20" | "2021/'22, okt" | "2021/'22, feb" | "2022/'23" |
|---|---|---|---|---|
| 524 | 0,0037 | 0,00882 | 0,00568 | 0,00055 |
| 524,03718 | 0,00385 | 0,00914 | 0,00591 | 0,00059 |
| 524,07436 | 0,00401 | 0,00946 | 0,00614 | 0,00064 |
| 524,11155 | 0,00417 | 0,0098 | 0,00638 | 0,00069 |
| 524,14873 | 0,00433 | 0,01014 | 0,00663 | 0,00075 |
| 524,18591 | 0,00451 | 0,01048 | 0,00689 | 0,00081 |
| 524,22309 | 0,00468 | 0,01084 | 0,00715 | 0,00087 |
| 524,26027 | 0,00486 | 0,0112 | 0,00742 | 0,00094 |
| 524,29746 | 0,00505 | 0,01157 | 0,0077 | 0,00101 |
| 524,33464 | 0,00524 | 0,01195 | 0,00799 | 0,00109 |
| 524,37182 | 0,00543 | 0,01234 | 0,00828 | 0,00117 |
| 524,409 | 0,00563 | 0,01273 | 0,00858 | 0,00126 |
| 524,44618 | 0,00584 | 0,01313 | 0,00889 | 0,00135 |
| 524,48337 | 0,00605 | 0,01354 | 0,0092 | 0,00145 |
| 524,52055 | 0,00627 | 0,01396 | 0,00953 | 0,00155 |
| 524,55773 | 0,00649 | 0,01438 | 0,00986 | 0,00166 |
| 524,59491 | 0,00672 | 0,01482 | 0,0102 | 0,00178 |
| 524,63209 | 0,00695 | 0,01526 | 0,01054 | 0,00191 |
| 524,66928 | 0,00719 | 0,0157 | 0,0109 | 0,00204 |
| 524,70646 | 0,00743 | 0,01615 | 0,01126 | 0,00218 |
| 524,74364 | 0,00768 | 0,01662 | 0,01163 | 0,00233 |
| 524,78082 | 0,00793 | 0,01708 | 0,01201 | 0,00248 |
| 524,818 | 0,00819 | 0,01756 | 0,01239 | 0,00265 |
| 524,85519 | 0,00846 | 0,01804 | 0,01279 | 0,00282 |
| 524,89237 | 0,00872 | 0,01853 | 0,01319 | 0,003 |
| 524,92955 | 0,009 | 0,01903 | 0,0136 | 0,0032 |
| 524,96673 | 0,00928 | 0,01952 | 0,01402 | 0,0034 |
| 525,00391 | 0,00957 | 0,02003 | 0,01444 | 0,00361 |
| 525,0411 | 0,00986 | 0,02054 | 0,01487 | 0,00384 |
| 525,07828 | 0,01016 | 0,02106 | 0,01531 | 0,00407 |
| 525,11546 | 0,01046 | 0,02159 | 0,01576 | 0,00432 |
| 525,15264 | 0,01077 | 0,02212 | 0,01621 | 0,00458 |
| 525,18982 | 0,01108 | 0,02265 | 0,01667 | 0,00485 |
| 525,22701 | 0,0114 | 0,02319 | 0,01714 | 0,00513 |
| 525,26419 | 0,01172 | 0,02373 | 0,01762 | 0,00543 |
| 525,30137 | 0,01205 | 0,02428 | 0,0181 | 0,00574 |
| 525,33855 | 0,01239 | 0,02483 | 0,01859 | 0,00606 |
| 525,37573 | 0,01273 | 0,02539 | 0,01909 | 0,0064 |
| 525,41292 | 0,01307 | 0,02594 | 0,01959 | 0,00676 |
| 525,4501 | 0,01342 | 0,02651 | 0,0201 | 0,00712 |
| 525,48728 | 0,01378 | 0,02707 | 0,02062 | 0,00751 |
| 525,52446 | 0,01414 | 0,02764 | 0,02114 | 0,00791 |
| 525,56164 | 0,0145 | 0,02821 | 0,02167 | 0,00833 |
| 525,59883 | 0,01487 | 0,02878 | 0,0222 | 0,00876 |
| 525,63601 | 0,01525 | 0,02935 | 0,02274 | 0,00921 |
| 525,67319 | 0,01563 | 0,02993 | 0,02328 | 0,00968 |
| 525,71037 | 0,01601 | 0,0305 | 0,02383 | 0,01016 |
| 525,74755 | 0,0164 | 0,03108 | 0,02439 | 0,01066 |
| 525,78474 | 0,0168 | 0,03166 | 0,02495 | 0,01118 |
| 525,82192 | 0,0172 | 0,03224 | 0,02551 | 0,01172 |
| 525,8591 | 0,0176 | 0,03281 | 0,02608 | 0,01228 |
| 525,89628 | 0,018 | 0,03339 | 0,02665 | 0,01286 |
| 525,93346 | 0,01842 | 0,03397 | 0,02723 | 0,01345 |
| 525,97065 | 0,01883 | 0,03454 | 0,02781 | 0,01407 |
| 526,00783 | 0,01925 | 0,03512 | 0,0284 | 0,01471 |
| 526,04501 | 0,01968 | 0,03569 | 0,02898 | 0,01536 |
| 526,08219 | 0,0201 | 0,03626 | 0,02957 | 0,01603 |
| 526,11937 | 0,02054 | 0,03683 | 0,03017 | 0,01673 |
| 526,15656 | 0,02097 | 0,03739 | 0,03076 | 0,01745 |
| 526,19374 | 0,02141 | 0,03795 | 0,03136 | 0,01818 |
| 526,23092 | 0,02186 | 0,03851 | 0,03196 | 0,01895 |
| 526,2681 | 0,0223 | 0,03907 | 0,03256 | 0,01972 |
| 526,30528 | 0,02275 | 0,03962 | 0,03316 | 0,02052 |
| 526,34247 | 0,02321 | 0,04016 | 0,03376 | 0,02134 |
| 526,37965 | 0,02367 | 0,0407 | 0,03436 | 0,02218 |
| 526,41683 | 0,02413 | 0,04124 | 0,03497 | 0,02304 |
| 526,45401 | 0,02459 | 0,04177 | 0,03557 | 0,02393 |
| 526,49119 | 0,02506 | 0,0423 | 0,03617 | 0,02483 |
| 526,52838 | 0,02553 | 0,04282 | 0,03677 | 0,02575 |
| 526,56556 | 0,026 | 0,04334 | 0,03737 | 0,0267 |
| 526,60274 | 0,02648 | 0,04385 | 0,03797 | 0,02766 |
| 526,63992 | 0,02695 | 0,04435 | 0,03857 | 0,02864 |
| 526,6771 | 0,02744 | 0,04485 | 0,03917 | 0,02965 |
| 526,71429 | 0,02792 | 0,04534 | 0,03976 | 0,03067 |
| 526,75147 | 0,0284 | 0,04582 | 0,04036 | 0,03171 |
| 526,78865 | 0,02889 | 0,0463 | 0,04094 | 0,03277 |
| 526,82583 | 0,02938 | 0,04676 | 0,04153 | 0,03384 |
| 526,86301 | 0,02988 | 0,04722 | 0,04211 | 0,03494 |
| 526,9002 | 0,03037 | 0,04768 | 0,04269 | 0,03606 |
| 526,93738 | 0,03087 | 0,04812 | 0,04327 | 0,03718 |
| 526,97456 | 0,03136 | 0,04856 | 0,04384 | 0,03833 |
| 527,01174 | 0,03186 | 0,04899 | 0,0444 | 0,03949 |
| 527,04892 | 0,03236 | 0,04941 | 0,04496 | 0,04067 |
| 527,08611 | 0,03287 | 0,04982 | 0,04552 | 0,04186 |
| 527,12329 | 0,03337 | 0,05023 | 0,04607 | 0,04306 |
| 527,16047 | 0,03388 | 0,05062 | 0,04661 | 0,04428 |
| 527,19765 | 0,03438 | 0,05101 | 0,04715 | 0,04551 |
| 527,23483 | 0,03489 | 0,05139 | 0,04768 | 0,04675 |
| 527,27202 | 0,0354 | 0,05176 | 0,04821 | 0,048 |
| 527,3092 | 0,0359 | 0,05213 | 0,04873 | 0,04926 |
| 527,34638 | 0,03641 | 0,05248 | 0,04924 | 0,05053 |
| 527,38356 | 0,03692 | 0,05283 | 0,04975 | 0,05181 |
| 527,42074 | 0,03743 | 0,05316 | 0,05024 | 0,0531 |
| 527,45793 | 0,03794 | 0,05349 | 0,05073 | 0,05439 |
| 527,49511 | 0,03845 | 0,05381 | 0,05121 | 0,05568 |
| 527,53229 | 0,03895 | 0,05412 | 0,05168 | 0,05699 |
| 527,56947 | 0,03946 | 0,05443 | 0,05214 | 0,05829 |
| 527,60665 | 0,03997 | 0,05472 | 0,0526 | 0,0596 |
| 527,64384 | 0,04048 | 0,05501 | 0,05304 | 0,0609 |
| 527,68102 | 0,04098 | 0,05529 | 0,05348 | 0,06221 |
| 527,7182 | 0,04149 | 0,05557 | 0,05391 | 0,06351 |
| 527,75538 | 0,04199 | 0,05583 | 0,05432 | 0,06482 |
| 527,79256 | 0,04249 | 0,05609 | 0,05473 | 0,06612 |
| 527,82975 | 0,04299 | 0,05634 | 0,05513 | 0,06741 |
| 527,86693 | 0,04349 | 0,05658 | 0,05551 | 0,0687 |
| 527,90411 | 0,04398 | 0,05682 | 0,05589 | 0,06999 |
| 527,94129 | 0,04447 | 0,05705 | 0,05626 | 0,07126 |
| 527,97847 | 0,04497 | 0,05728 | 0,05662 | 0,07253 |
| 528,01566 | 0,04545 | 0,05749 | 0,05696 | 0,07379 |
| 528,05284 | 0,04594 | 0,0577 | 0,0573 | 0,07503 |
| 528,09002 | 0,04642 | 0,05791 | 0,05762 | 0,07627 |
| 528,1272 | 0,0469 | 0,05811 | 0,05793 | 0,07749 |
| 528,16438 | 0,04737 | 0,05831 | 0,05824 | 0,0787 |
| 528,20157 | 0,04785 | 0,0585 | 0,05853 | 0,07989 |
| 528,23875 | 0,04831 | 0,05868 | 0,05881 | 0,08107 |
| 528,27593 | 0,04878 | 0,05886 | 0,05908 | 0,08223 |
| 528,31311 | 0,04924 | 0,05904 | 0,05933 | 0,08337 |
| 528,35029 | 0,04969 | 0,05921 | 0,05958 | 0,0845 |
| 528,38748 | 0,05014 | 0,05938 | 0,05982 | 0,0856 |
| 528,42466 | 0,05059 | 0,05955 | 0,06004 | 0,08668 |
| 528,46184 | 0,05102 | 0,05971 | 0,06026 | 0,08775 |
| 528,49902 | 0,05146 | 0,05987 | 0,06046 | 0,08879 |
| 528,5362 | 0,05189 | 0,06002 | 0,06065 | 0,08981 |
| 528,57339 | 0,05231 | 0,06018 | 0,06082 | 0,0908 |
| 528,61057 | 0,05273 | 0,06033 | 0,06099 | 0,09178 |
| 528,64775 | 0,05314 | 0,06048 | 0,06115 | 0,09273 |
| 528,68493 | 0,05354 | 0,06063 | 0,0613 | 0,09365 |
| 528,72211 | 0,05394 | 0,06077 | 0,06143 | 0,09455 |
| 528,7593 | 0,05433 | 0,06092 | 0,06155 | 0,09543 |
| 528,79648 | 0,05472 | 0,06106 | 0,06167 | 0,09628 |
| 528,83366 | 0,05509 | 0,06121 | 0,06177 | 0,0971 |
| 528,87084 | 0,05547 | 0,06135 | 0,06186 | 0,0979 |
| 528,90802 | 0,05583 | 0,06149 | 0,06195 | 0,09867 |
| 528,94521 | 0,05618 | 0,06163 | 0,06202 | 0,09942 |
| 528,98239 | 0,05653 | 0,06178 | 0,06208 | 0,10015 |
| 529,01957 | 0,05687 | 0,06192 | 0,06213 | 0,10083 |
| 529,05675 | 0,05721 | 0,06206 | 0,06217 | 0,1015 |
| 529,09393 | 0,05753 | 0,06221 | 0,0622 | 0,10215 |
| 529,13112 | 0,05784 | 0,06235 | 0,06222 | 0,10276 |
| 529,1683 | 0,05815 | 0,0625 | 0,06224 | 0,10336 |
| 529,20548 | 0,05845 | 0,06265 | 0,06224 | 0,10393 |
| 529,24266 | 0,05874 | 0,06279 | 0,06224 | 0,10447 |
| 529,27984 | 0,05903 | 0,06295 | 0,06222 | 0,10499 |
| 529,31703 | 0,0593 | 0,0631 | 0,0622 | 0,10549 |
| 529,35421 | 0,05957 | 0,06325 | 0,06217 | 0,10596 |
| 529,39139 | 0,05982 | 0,0634 | 0,06213 | 0,10641 |
| 529,42857 | 0,06007 | 0,06356 | 0,06208 | 0,10684 |
| 529,46575 | 0,06031 | 0,06372 | 0,06203 | 0,10725 |
| 529,50294 | 0,06054 | 0,06388 | 0,06196 | 0,10764 |
| 529,54012 | 0,06077 | 0,06404 | 0,06189 | 0,108 |
| 529,5773 | 0,06098 | 0,06421 | 0,06182 | 0,10835 |
| 529,61448 | 0,06119 | 0,06437 | 0,06174 | 0,10868 |
| 529,65166 | 0,06138 | 0,06454 | 0,06165 | 0,10899 |
| 529,68885 | 0,06158 | 0,06471 | 0,06155 | 0,10928 |
| 529,72603 | 0,06175 | 0,06488 | 0,06145 | 0,10956 |
| 529,76321 | 0,06193 | 0,06506 | 0,06135 | 0,10981 |
| 529,80039 | 0,06209 | 0,06523 | 0,06124 | 0,11005 |
| 529,83757 | 0,06225 | 0,06541 | 0,06112 | 0,11029 |
| 529,87476 | 0,0624 | 0,06559 | 0,061 | 0,1105 |
| 529,91194 | 0,06254 | 0,06577 | 0,06088 | 0,1107 |
| 529,94912 | 0,06267 | 0,06596 | 0,06075 | 0,11089 |
| 529,9863 | 0,0628 | 0,06614 | 0,06062 | 0,11107 |
| 530,02348 | 0,06291 | 0,06633 | 0,06048 | 0,11123 |
| 530,06067 | 0,06303 | 0,06652 | 0,06034 | 0,11139 |
| 530,09785 | 0,06313 | 0,0667 | 0,0602 | 0,11153 |
| 530,13503 | 0,06323 | 0,06689 | 0,06006 | 0,11166 |
| 530,17221 | 0,06332 | 0,06708 | 0,05991 | 0,11179 |
| 530,20939 | 0,0634 | 0,06728 | 0,05977 | 0,11191 |
| 530,24658 | 0,06348 | 0,06747 | 0,05962 | 0,11202 |
| 530,28376 | 0,06355 | 0,06766 | 0,05947 | 0,11212 |
| 530,32094 | 0,06362 | 0,06785 | 0,05932 | 0,11221 |
| 530,35812 | 0,06368 | 0,06805 | 0,05917 | 0,1123 |
| 530,3953 | 0,06374 | 0,06824 | 0,05902 | 0,11238 |
| 530,43249 | 0,06379 | 0,06843 | 0,05887 | 0,11245 |
| 530,46967 | 0,06384 | 0,06862 | 0,05872 | 0,11252 |
| 530,50685 | 0,06388 | 0,06881 | 0,05857 | 0,11259 |
| 530,54403 | 0,06392 | 0,06901 | 0,05843 | 0,11264 |
| 530,58121 | 0,06395 | 0,06919 | 0,05828 | 0,1127 |
| 530,6184 | 0,06398 | 0,06938 | 0,05814 | 0,11274 |
| 530,65558 | 0,06401 | 0,06957 | 0,05799 | 0,11279 |
| 530,69276 | 0,06403 | 0,06975 | 0,05786 | 0,11282 |
| 530,72994 | 0,06406 | 0,06994 | 0,05772 | 0,11286 |
| 530,76712 | 0,06407 | 0,07012 | 0,05759 | 0,11289 |
| 530,80431 | 0,06409 | 0,0703 | 0,05746 | 0,11291 |
| 530,84149 | 0,06411 | 0,07047 | 0,05733 | 0,11293 |
| 530,87867 | 0,06412 | 0,07065 | 0,05721 | 0,11294 |
| 530,91585 | 0,06413 | 0,07082 | 0,05709 | 0,11295 |
| 530,95303 | 0,06414 | 0,07099 | 0,05698 | 0,11296 |
| 530,99022 | 0,06415 | 0,07115 | 0,05687 | 0,11296 |
| 531,0274 | 0,06416 | 0,07131 | 0,05677 | 0,11295 |
| 531,06458 | 0,06417 | 0,07147 | 0,05667 | 0,11294 |
| 531,10176 | 0,06417 | 0,07162 | 0,05658 | 0,11292 |
| 531,13894 | 0,06418 | 0,07178 | 0,05649 | 0,1129 |
| 531,17613 | 0,06419 | 0,07192 | 0,05641 | 0,11288 |
| 531,21331 | 0,0642 | 0,07206 | 0,05634 | 0,11284 |
| 531,25049 | 0,06421 | 0,0722 | 0,05627 | 0,1128 |
| 531,28767 | 0,06422 | 0,07233 | 0,05621 | 0,11276 |
| 531,32485 | 0,06423 | 0,07246 | 0,05616 | 0,11271 |
| 531,36204 | 0,06424 | 0,07258 | 0,05611 | 0,11265 |
| 531,39922 | 0,06426 | 0,0727 | 0,05607 | 0,11258 |
| 531,4364 | 0,06427 | 0,07281 | 0,05604 | 0,11251 |
| 531,47358 | 0,06429 | 0,07292 | 0,05601 | 0,11243 |
| 531,51076 | 0,06431 | 0,07302 | 0,056 | 0,11235 |
| 531,54795 | 0,06433 | 0,07312 | 0,05599 | 0,11225 |
| 531,58513 | 0,06435 | 0,07321 | 0,05599 | 0,11215 |
| 531,62231 | 0,06438 | 0,0733 | 0,05599 | 0,11204 |
| 531,65949 | 0,06441 | 0,07338 | 0,05601 | 0,11193 |
| 531,69667 | 0,06444 | 0,07345 | 0,05603 | 0,1118 |
| 531,73386 | 0,06447 | 0,07352 | 0,05606 | 0,11167 |
| 531,77104 | 0,0645 | 0,07359 | 0,0561 | 0,11153 |
| 531,80822 | 0,06454 | 0,07365 | 0,05615 | 0,11138 |
| 531,8454 | 0,06458 | 0,0737 | 0,05621 | 0,11122 |
| 531,88258 | 0,06463 | 0,07375 | 0,05627 | 0,11106 |
| 531,91977 | 0,06467 | 0,07379 | 0,05635 | 0,11089 |
| 531,95695 | 0,06472 | 0,07382 | 0,05643 | 0,1107 |
| 531,99413 | 0,06478 | 0,07385 | 0,05652 | 0,11052 |
| 532,03131 | 0,06483 | 0,07388 | 0,05662 | 0,11032 |
| 532,06849 | 0,06489 | 0,0739 | 0,05673 | 0,11011 |
| 532,10568 | 0,06495 | 0,07391 | 0,05685 | 0,1099 |
| 532,14286 | 0,06502 | 0,07392 | 0,05697 | 0,10968 |
| 532,18004 | 0,06508 | 0,07392 | 0,0571 | 0,10945 |
| 532,21722 | 0,06515 | 0,07392 | 0,05725 | 0,10921 |
| 532,2544 | 0,06523 | 0,07391 | 0,05739 | 0,10896 |
| 532,29159 | 0,0653 | 0,0739 | 0,05755 | 0,10871 |
| 532,32877 | 0,06538 | 0,07388 | 0,05772 | 0,10845 |
| 532,36595 | 0,06546 | 0,07386 | 0,05789 | 0,10818 |
| 532,40313 | 0,06555 | 0,07383 | 0,05808 | 0,1079 |
| 532,44031 | 0,06563 | 0,0738 | 0,05827 | 0,10762 |
| 532,4775 | 0,06572 | 0,07377 | 0,05847 | 0,10733 |
| 532,51468 | 0,06582 | 0,07373 | 0,05867 | 0,10703 |
| 532,55186 | 0,06591 | 0,07368 | 0,05888 | 0,10672 |
| 532,58904 | 0,06601 | 0,07364 | 0,0591 | 0,10641 |
| 532,62622 | 0,06611 | 0,07359 | 0,05933 | 0,10609 |
| 532,66341 | 0,06621 | 0,07353 | 0,05956 | 0,10576 |
| 532,70059 | 0,06632 | 0,07347 | 0,0598 | 0,10543 |
| 532,73777 | 0,06642 | 0,07341 | 0,06005 | 0,10509 |
| 532,77495 | 0,06653 | 0,07335 | 0,06031 | 0,10474 |
| 532,81213 | 0,06664 | 0,07328 | 0,06057 | 0,10439 |
| 532,84932 | 0,06675 | 0,07321 | 0,06083 | 0,10403 |
| 532,8865 | 0,06687 | 0,07314 | 0,0611 | 0,10366 |
| 532,92368 | 0,06699 | 0,07306 | 0,06138 | 0,10329 |
| 532,96086 | 0,0671 | 0,07299 | 0,06167 | 0,10291 |
| 532,99804 | 0,06723 | 0,07291 | 0,06196 | 0,10253 |
| 533,03523 | 0,06735 | 0,07283 | 0,06225 | 0,10214 |
| 533,07241 | 0,06747 | 0,07275 | 0,06255 | 0,10174 |
| 533,10959 | 0,0676 | 0,07266 | 0,06285 | 0,10133 |
| 533,14677 | 0,06773 | 0,07258 | 0,06316 | 0,10092 |
| 533,18395 | 0,06785 | 0,07249 | 0,06347 | 0,10051 |
| 533,22114 | 0,06799 | 0,07241 | 0,06379 | 0,10008 |
| 533,25832 | 0,06812 | 0,07232 | 0,06411 | 0,09965 |
| 533,2955 | 0,06825 | 0,07223 | 0,06444 | 0,09922 |
| 533,33268 | 0,06839 | 0,07215 | 0,06476 | 0,09877 |
| 533,36986 | 0,06853 | 0,07206 | 0,0651 | 0,09832 |
| 533,40705 | 0,06866 | 0,07197 | 0,06543 | 0,09787 |
| 533,44423 | 0,06881 | 0,07189 | 0,06577 | 0,09741 |
| 533,48141 | 0,06895 | 0,0718 | 0,06611 | 0,09694 |
| 533,51859 | 0,06909 | 0,07171 | 0,06645 | 0,09646 |
| 533,55577 | 0,06924 | 0,07163 | 0,0668 | 0,09598 |
| 533,59295 | 0,06939 | 0,07155 | 0,06715 | 0,09549 |
| 533,63014 | 0,06954 | 0,07146 | 0,0675 | 0,095 |
| 533,66732 | 0,06969 | 0,07138 | 0,06785 | 0,09449 |
| 533,7045 | 0,06984 | 0,0713 | 0,0682 | 0,09399 |
| 533,74168 | 0,07 | 0,07122 | 0,06856 | 0,09347 |
| 533,77886 | 0,07016 | 0,07115 | 0,06892 | 0,09294 |
| 533,81605 | 0,07032 | 0,07107 | 0,06928 | 0,09242 |
| 533,85323 | 0,07048 | 0,071 | 0,06964 | 0,09188 |
| 533,89041 | 0,07064 | 0,07093 | 0,07 | 0,09133 |
| 533,92759 | 0,07081 | 0,07086 | 0,07036 | 0,09078 |
| 533,96477 | 0,07098 | 0,07079 | 0,07072 | 0,09022 |
| 534,00196 | 0,07116 | 0,07073 | 0,07109 | 0,08966 |
| 534,03914 | 0,07133 | 0,07066 | 0,07145 | 0,08908 |
| 534,07632 | 0,07151 | 0,0706 | 0,07181 | 0,0885 |
| 534,1135 | 0,07169 | 0,07055 | 0,07218 | 0,08792 |
| 534,15068 | 0,07188 | 0,07049 | 0,07254 | 0,08732 |
| 534,18787 | 0,07207 | 0,07044 | 0,07291 | 0,08672 |
| 534,22505 | 0,07226 | 0,07039 | 0,07327 | 0,08611 |
| 534,26223 | 0,07245 | 0,07034 | 0,07364 | 0,0855 |
| 534,29941 | 0,07265 | 0,0703 | 0,074 | 0,08488 |
| 534,33659 | 0,07285 | 0,07026 | 0,07437 | 0,08425 |
| 534,37378 | 0,07306 | 0,07022 | 0,07473 | 0,08362 |
| 534,41096 | 0,07327 | 0,07018 | 0,07509 | 0,08298 |
| 534,44814 | 0,07349 | 0,07015 | 0,07545 | 0,08234 |
| 534,48532 | 0,07371 | 0,07012 | 0,07581 | 0,08169 |
| 534,5225 | 0,07393 | 0,07009 | 0,07617 | 0,08104 |
| 534,55969 | 0,07416 | 0,07006 | 0,07653 | 0,08038 |
| 534,59687 | 0,07439 | 0,07004 | 0,07689 | 0,07972 |
| 534,63405 | 0,07463 | 0,07002 | 0,07725 | 0,07905 |
| 534,67123 | 0,07487 | 0,07001 | 0,0776 | 0,07838 |
| 534,70841 | 0,07512 | 0,06999 | 0,07796 | 0,07771 |
| 534,7456 | 0,07537 | 0,06998 | 0,07831 | 0,07704 |
| 534,78278 | 0,07563 | 0,06997 | 0,07866 | 0,07636 |
| 534,81996 | 0,07589 | 0,06996 | 0,07901 | 0,07568 |
| 534,85714 | 0,07616 | 0,06996 | 0,07936 | 0,075 |
| 534,89432 | 0,07643 | 0,06995 | 0,0797 | 0,07432 |
| 534,93151 | 0,07671 | 0,06995 | 0,08004 | 0,07364 |
| 534,96869 | 0,077 | 0,06995 | 0,08038 | 0,07296 |
| 535,00587 | 0,07729 | 0,06996 | 0,08072 | 0,07228 |
| 535,04305 | 0,07758 | 0,06996 | 0,08106 | 0,0716 |
| 535,08023 | 0,07788 | 0,06997 | 0,08139 | 0,07093 |
| 535,11742 | 0,07818 | 0,06998 | 0,08172 | 0,07025 |
| 535,1546 | 0,07849 | 0,06999 | 0,08205 | 0,06958 |
| 535,19178 | 0,07881 | 0,07 | 0,08238 | 0,06892 |
| 535,22896 | 0,07913 | 0,07002 | 0,0827 | 0,06826 |
| 535,26614 | 0,07946 | 0,07003 | 0,08301 | 0,0676 |
| 535,30333 | 0,07978 | 0,07005 | 0,08333 | 0,06695 |
| 535,34051 | 0,08012 | 0,07006 | 0,08364 | 0,0663 |
| 535,37769 | 0,08046 | 0,07008 | 0,08395 | 0,06566 |
| 535,41487 | 0,0808 | 0,0701 | 0,08425 | 0,06503 |
| 535,45205 | 0,08115 | 0,07012 | 0,08455 | 0,06441 |
| 535,48924 | 0,08151 | 0,07014 | 0,08484 | 0,06379 |
| 535,52642 | 0,08186 | 0,07016 | 0,08513 | 0,06318 |
| 535,5636 | 0,08222 | 0,07018 | 0,08542 | 0,06258 |
| 535,60078 | 0,08259 | 0,0702 | 0,0857 | 0,062 |
| 535,63796 | 0,08296 | 0,07021 | 0,08598 | 0,06142 |
| 535,67515 | 0,08333 | 0,07023 | 0,08624 | 0,06085 |
| 535,71233 | 0,0837 | 0,07025 | 0,08651 | 0,06029 |
| 535,74951 | 0,08408 | 0,07027 | 0,08677 | 0,05974 |
| 535,78669 | 0,08445 | 0,07029 | 0,08702 | 0,05921 |
| 535,82387 | 0,08483 | 0,0703 | 0,08727 | 0,05868 |
| 535,86106 | 0,08522 | 0,07032 | 0,0875 | 0,05817 |
| 535,89824 | 0,0856 | 0,07033 | 0,08774 | 0,05767 |
| 535,93542 | 0,08598 | 0,07034 | 0,08796 | 0,05718 |
| 535,9726 | 0,08636 | 0,07035 | 0,08818 | 0,0567 |
| 536,00978 | 0,08675 | 0,07036 | 0,08839 | 0,05624 |
| 536,04697 | 0,08713 | 0,07037 | 0,08859 | 0,05579 |
| 536,08415 | 0,08751 | 0,07037 | 0,08879 | 0,05535 |
| 536,12133 | 0,08789 | 0,07037 | 0,08898 | 0,05492 |
| 536,15851 | 0,08826 | 0,07037 | 0,08916 | 0,0545 |
| 536,19569 | 0,08864 | 0,07037 | 0,08932 | 0,0541 |
| 536,23288 | 0,08901 | 0,07036 | 0,08948 | 0,05371 |
| 536,27006 | 0,08938 | 0,07036 | 0,08963 | 0,05332 |
| 536,30724 | 0,08974 | 0,07034 | 0,08977 | 0,05295 |
| 536,34442 | 0,0901 | 0,07033 | 0,0899 | 0,05259 |
| 536,3816 | 0,09045 | 0,07031 | 0,09002 | 0,05224 |
| 536,41879 | 0,0908 | 0,07029 | 0,09013 | 0,0519 |
| 536,45597 | 0,09114 | 0,07026 | 0,09023 | 0,05156 |
| 536,49315 | 0,09148 | 0,07023 | 0,09032 | 0,05124 |
| 536,53033 | 0,0918 | 0,0702 | 0,0904 | 0,05092 |
| 536,56751 | 0,09212 | 0,07016 | 0,09046 | 0,05061 |
| 536,6047 | 0,09243 | 0,07012 | 0,09051 | 0,05031 |
| 536,64188 | 0,09273 | 0,07007 | 0,09055 | 0,05002 |
| 536,67906 | 0,09302 | 0,07002 | 0,09058 | 0,04973 |
| 536,71624 | 0,0933 | 0,06997 | 0,0906 | 0,04944 |
| 536,75342 | 0,09357 | 0,06991 | 0,0906 | 0,04916 |
| 536,79061 | 0,09382 | 0,06984 | 0,09059 | 0,04888 |
| 536,82779 | 0,09407 | 0,06977 | 0,09056 | 0,0486 |
| 536,86497 | 0,0943 | 0,06969 | 0,09053 | 0,04833 |
| 536,90215 | 0,09451 | 0,06962 | 0,09047 | 0,04805 |
| 536,93933 | 0,09472 | 0,06953 | 0,09041 | 0,04778 |
| 536,97652 | 0,0949 | 0,06944 | 0,09033 | 0,04751 |
| 537,0137 | 0,09508 | 0,06934 | 0,09024 | 0,04723 |
| 537,05088 | 0,09523 | 0,06924 | 0,09013 | 0,04696 |
| 537,08806 | 0,09537 | 0,06913 | 0,09 | 0,04667 |
| 537,12524 | 0,0955 | 0,06901 | 0,08987 | 0,04639 |
| 537,16243 | 0,0956 | 0,06889 | 0,08971 | 0,0461 |
| 537,19961 | 0,09569 | 0,06876 | 0,08955 | 0,04581 |
| 537,23679 | 0,09575 | 0,06863 | 0,08936 | 0,04551 |
| 537,27397 | 0,0958 | 0,06849 | 0,08916 | 0,04521 |
| 537,31115 | 0,09583 | 0,06834 | 0,08895 | 0,04489 |
| 537,34834 | 0,09584 | 0,06819 | 0,08872 | 0,04457 |
| 537,38552 | 0,09583 | 0,06803 | 0,08847 | 0,04424 |
| 537,4227 | 0,09579 | 0,06787 | 0,08821 | 0,0439 |
| 537,45988 | 0,09574 | 0,06769 | 0,08793 | 0,04356 |
| 537,49706 | 0,09567 | 0,06751 | 0,08764 | 0,0432 |
| 537,53425 | 0,09556 | 0,06733 | 0,08733 | 0,04283 |
| 537,57143 | 0,09545 | 0,06713 | 0,08701 | 0,04246 |
| 537,60861 | 0,0953 | 0,06693 | 0,08666 | 0,04207 |
| 537,64579 | 0,09514 | 0,06673 | 0,08631 | 0,04167 |
| 537,68297 | 0,09495 | 0,06651 | 0,08594 | 0,04126 |
| 537,72016 | 0,09473 | 0,06629 | 0,08555 | 0,04083 |
| 537,75734 | 0,0945 | 0,06606 | 0,08515 | 0,0404 |
| 537,79452 | 0,09424 | 0,06583 | 0,08472 | 0,03995 |
| 537,8317 | 0,09395 | 0,06559 | 0,08429 | 0,03949 |
| 537,86888 | 0,09365 | 0,06534 | 0,08384 | 0,03902 |
| 537,90607 | 0,09331 | 0,06508 | 0,08337 | 0,03854 |
| 537,94325 | 0,09296 | 0,06482 | 0,08289 | 0,03805 |
| 537,98043 | 0,09257 | 0,06454 | 0,08239 | 0,03754 |
| 538,01761 | 0,09217 | 0,06426 | 0,08189 | 0,03702 |
| 538,05479 | 0,09174 | 0,06398 | 0,08136 | 0,03649 |
| 538,09198 | 0,09129 | 0,06368 | 0,08082 | 0,03595 |
| 538,12916 | 0,09082 | 0,06338 | 0,08026 | 0,0354 |
| 538,16634 | 0,09031 | 0,06307 | 0,07969 | 0,03484 |
| 538,20352 | 0,08979 | 0,06276 | 0,07911 | 0,03427 |
| 538,2407 | 0,08924 | 0,06243 | 0,07851 | 0,03369 |
| 538,27789 | 0,08867 | 0,0621 | 0,07791 | 0,0331 |
| 538,31507 | 0,08808 | 0,06177 | 0,07728 | 0,0325 |
| 538,35225 | 0,08746 | 0,06142 | 0,07665 | 0,0319 |
| 538,38943 | 0,08683 | 0,06107 | 0,076 | 0,03128 |
| 538,42661 | 0,08617 | 0,06071 | 0,07534 | 0,03066 |
| 538,4638 | 0,08549 | 0,06034 | 0,07467 | 0,03004 |
| 538,50098 | 0,08479 | 0,05997 | 0,07398 | 0,02941 |
| 538,53816 | 0,08406 | 0,05959 | 0,07328 | 0,02877 |
| 538,57534 | 0,08333 | 0,0592 | 0,07258 | 0,02813 |
| 538,61252 | 0,08256 | 0,0588 | 0,07186 | 0,02749 |
| 538,64971 | 0,08178 | 0,0584 | 0,07113 | 0,02684 |
| 538,68689 | 0,08098 | 0,05799 | 0,07039 | 0,02619 |
| 538,72407 | 0,08015 | 0,05758 | 0,06964 | 0,02554 |
| 538,76125 | 0,07932 | 0,05715 | 0,06888 | 0,02489 |
| 538,79843 | 0,07846 | 0,05672 | 0,06812 | 0,02425 |
| 538,83562 | 0,0776 | 0,05629 | 0,06734 | 0,0236 |
| 538,8728 | 0,07671 | 0,05584 | 0,06656 | 0,02295 |
| 538,90998 | 0,07581 | 0,05539 | 0,06577 | 0,02231 |
| 538,94716 | 0,0749 | 0,05494 | 0,06497 | 0,02166 |
| 538,98434 | 0,07396 | 0,05447 | 0,06417 | 0,02103 |
| 539,02153 | 0,07302 | 0,054 | 0,06336 | 0,02039 |
| 539,05871 | 0,07207 | 0,05353 | 0,06254 | 0,01977 |
| 539,09589 | 0,0711 | 0,05305 | 0,06172 | 0,01914 |
| 539,13307 | 0,07012 | 0,05256 | 0,06089 | 0,01853 |
| 539,17025 | 0,06913 | 0,05207 | 0,06006 | 0,01792 |
| 539,20744 | 0,06814 | 0,05157 | 0,05922 | 0,01732 |
| 539,24462 | 0,06713 | 0,05107 | 0,05838 | 0,01672 |
| 539,2818 | 0,06611 | 0,05056 | 0,05753 | 0,01614 |
| 539,31898 | 0,06509 | 0,05004 | 0,05669 | 0,01556 |
| 539,35616 | 0,06406 | 0,04952 | 0,05584 | 0,015 |
| 539,39335 | 0,06303 | 0,049 | 0,05498 | 0,01444 |
| 539,43053 | 0,06199 | 0,04847 | 0,05413 | 0,01389 |
| 539,46771 | 0,06094 | 0,04793 | 0,05327 | 0,01336 |
| 539,50489 | 0,0599 | 0,04739 | 0,05242 | 0,01283 |
| 539,54207 | 0,05884 | 0,04685 | 0,05156 | 0,01232 |
| 539,57926 | 0,05779 | 0,0463 | 0,0507 | 0,01182 |
| 539,61644 | 0,05674 | 0,04575 | 0,04984 | 0,01133 |
| 539,65362 | 0,05568 | 0,0452 | 0,04899 | 0,01085 |
| 539,6908 | 0,05463 | 0,04464 | 0,04813 | 0,01039 |
| 539,72798 | 0,05357 | 0,04407 | 0,04728 | 0,00993 |
| 539,76517 | 0,05252 | 0,04351 | 0,04643 | 0,00949 |
| 539,80235 | 0,05147 | 0,04294 | 0,04558 | 0,00906 |
| 539,83953 | 0,05042 | 0,04237 | 0,04473 | 0,00865 |
| 539,87671 | 0,04937 | 0,04179 | 0,04389 | 0,00824 |
| 539,91389 | 0,04833 | 0,04122 | 0,04305 | 0,00785 |
| 539,95108 | 0,0473 | 0,04064 | 0,04221 | 0,00747 |
| 539,98826 | 0,04627 | 0,04006 | 0,04138 | 0,00711 |
| 540,02544 | 0,04524 | 0,03947 | 0,04055 | 0,00676 |
| 540,06262 | 0,04422 | 0,03889 | 0,03973 | 0,00642 |
| 540,0998 | 0,04321 | 0,0383 | 0,03891 | 0,00609 |
| 540,13699 | 0,0422 | 0,03772 | 0,0381 | 0,00578 |
| 540,17417 | 0,04121 | 0,03713 | 0,0373 | 0,00547 |
| 540,21135 | 0,04022 | 0,03654 | 0,0365 | 0,00518 |
| 540,24853 | 0,03924 | 0,03595 | 0,0357 | 0,0049 |
| 540,28571 | 0,03827 | 0,03536 | 0,03492 | 0,00463 |
| 540,3229 | 0,03731 | 0,03477 | 0,03413 | 0,00437 |
| 540,36008 | 0,03637 | 0,03418 | 0,03336 | 0,00413 |
| 540,39726 | 0,03542 | 0,0336 | 0,0326 | 0,00389 |
| 540,43444 | 0,0345 | 0,03301 | 0,03184 | 0,00367 |
| 540,47162 | 0,03358 | 0,03242 | 0,03109 | 0,00345 |
| 540,50881 | 0,03268 | 0,03184 | 0,03035 | 0,00325 |
| 540,54599 | 0,03179 | 0,03125 | 0,02962 | 0,00305 |
| 540,58317 | 0,03091 | 0,03067 | 0,0289 | 0,00287 |
| 540,62035 | 0,03005 | 0,03009 | 0,02818 | 0,00269 |
| 540,65753 | 0,02919 | 0,02951 | 0,02748 | 0,00252 |
| 540,69472 | 0,02836 | 0,02894 | 0,02678 | 0,00236 |
| 540,7319 | 0,02753 | 0,02837 | 0,0261 | 0,00221 |
| 540,76908 | 0,02672 | 0,0278 | 0,02542 | 0,00207 |
| 540,80626 | 0,02593 | 0,02723 | 0,02475 | 0,00193 |
| 540,84344 | 0,02514 | 0,02667 | 0,02409 | 0,0018 |
| 540,88063 | 0,02437 | 0,02611 | 0,02345 | 0,00168 |
| 540,91781 | 0,02362 | 0,02555 | 0,02281 | 0,00157 |
| 540,95499 | 0,02288 | 0,025 | 0,02218 | 0,00146 |
| 540,99217 | 0,02216 | 0,02445 | 0,02157 | 0,00136 |
| 541,02935 | 0,02144 | 0,02391 | 0,02096 | 0,00126 |
| 541,06654 | 0,02075 | 0,02337 | 0,02037 | 0,00118 |
| 541,10372 | 0,02007 | 0,02283 | 0,01978 | 0,00109 |
| 541,1409 | 0,0194 | 0,02231 | 0,01921 | 0,00101 |
| 541,17808 | 0,01875 | 0,02178 | 0,01864 | 0,00094 |
| 541,21526 | 0,01811 | 0,02126 | 0,01809 | 0,00087 |
| 541,25245 | 0,0175 | 0,02075 | 0,01755 | 8e-04 |
| 541,28963 | 0,01688 | 0,02024 | 0,01701 | 0,00074 |
| 541,32681 | 0,0163 | 0,01974 | 0,01649 | 0,00069 |
| 541,36399 | 0,01572 | 0,01924 | 0,01598 | 0,00063 |
| 541,40117 | 0,01515 | 0,01875 | 0,01548 | 0,00059 |
| 541,43836 | 0,01461 | 0,01827 | 0,015 | 0,00054 |
| 541,47554 | 0,01407 | 0,01779 | 0,01451 | 5e-04 |
| 541,51272 | 0,01355 | 0,01732 | 0,01405 | 0,00046 |
| 541,5499 | 0,01305 | 0,01686 | 0,01359 | 0,00042 |
| 541,58708 | 0,01256 | 0,0164 | 0,01314 | 0,00039 |
| 541,62427 | 0,01208 | 0,01595 | 0,01271 | 0,00035 |
| 541,66145 | 0,01161 | 0,01551 | 0,01228 | 0,00032 |
| 541,69863 | 0,01116 | 0,01507 | 0,01187 | 3e-04 |
| 541,73581 | 0,01073 | 0,01464 | 0,01146 | 0,00027 |
| 541,77299 | 0,0103 | 0,01422 | 0,01106 | 0,00025 |
| 541,81018 | 0,00989 | 0,01381 | 0,01068 | 0,00023 |
| 541,84736 | 0,00949 | 0,0134 | 0,0103 | 0,00021 |
| 541,88454 | 0,00911 | 0,013 | 0,00994 | 0,00019 |
| 541,92172 | 0,00873 | 0,0126 | 0,00958 | 0,00017 |
| 541,9589 | 0,00837 | 0,01222 | 0,00924 | 0,00016 |
| 541,99609 | 0,00802 | 0,01184 | 0,0089 | 0,00014 |
| 542,03327 | 0,00768 | 0,01147 | 0,00857 | 0,00013 |
| 542,07045 | 0,00735 | 0,01111 | 0,00825 | 0,00012 |
| 542,10763 | 0,00703 | 0,01075 | 0,00794 | 0,00011 |
| 542,14481 | 0,00673 | 0,0104 | 0,00764 | 1e-04 |
| 542,182 | 0,00644 | 0,01006 | 0,00735 | 9e-05 |
| 542,21918 | 0,00615 | 0,00973 | 0,00707 | 8e-05 |
| 542,25636 | 0,00588 | 0,00941 | 0,00679 | 7e-05 |
| 542,29354 | 0,00561 | 0,00909 | 0,00652 | 7e-05 |
| 542,33072 | 0,00536 | 0,00878 | 0,00627 | 6e-05 |
| 542,36791 | 0,00511 | 0,00847 | 0,00602 | 5e-05 |
| 542,40509 | 0,00488 | 0,00818 | 0,00578 | 5e-05 |
| 542,44227 | 0,00465 | 0,00789 | 0,00554 | 4e-05 |
| 542,47945 | 0,00443 | 0,00761 | 0,00531 | 4e-05 |
| 542,51663 | 0,00423 | 0,00734 | 0,00509 | 3e-05 |
| 542,55382 | 0,00402 | 0,00707 | 0,00488 | 3e-05 |
| 542,591 | 0,00383 | 0,00681 | 0,00468 | 3e-05 |
| 542,62818 | 0,00365 | 0,00656 | 0,00448 | 3e-05 |
| 542,66536 | 0,00347 | 0,00631 | 0,00429 | 2e-05 |
| 542,70254 | 0,0033 | 0,00607 | 0,0041 | 2e-05 |
| 542,73973 | 0,00313 | 0,00584 | 0,00393 | 2e-05 |
| 542,77691 | 0,00298 | 0,00562 | 0,00376 | 2e-05 |
| 542,81409 | 0,00283 | 0,0054 | 0,00359 | 1e-05 |
| 542,85127 | 0,00268 | 0,00519 | 0,00343 | 1e-05 |
| 542,88845 | 0,00255 | 0,00498 | 0,00328 | 1e-05 |
| 542,92564 | 0,00241 | 0,00478 | 0,00313 | 1e-05 |
| 542,96282 | 0,00229 | 0,00459 | 0,00299 | 1e-05 |
| 543 | 0,00217 | 0,0044 | 0,00285 | 1e-05 |
4. Resultaten correlatie- en regressieanalyses
In dit hoofdstuk onderzoeken we het verband tussen de onderwijsscore en de eindtoetsscore. In de eerste sectie voeren we daartoe een correlatieanalyse uit om een eerste beeld te krijgen. In aanvulling daarop onderzoeken we in de tweede sectie met behulp van regressieanalyse welk deel van de variantie in de eindtoetsscore met de onderwijsscore kan worden verklaard.
4.1 Correlatieanalyse
In deze sectie bekijken we de correlatie tussen de onderwijsscore en de eindtoetsscore uitgesplitst naar de deelpopulatie voor wat betreft het imputeren van het hoogste opleidingsniveau van de ouders, de verschillende soorten eindtoets en de schooljaren. Bij een correlatie van 0 is er geen lineaire samenhang tussen de onderwijsscore en de eindtoetsscore. Bij een correlatie van 1 respectievelijk -1 is er sprake van een perfecte positieve respectievelijk perfecte negatieve lineaire samenhang tussen de onderwijsscore en de eindtoetsscore. Een correlatie van rond 0,1 is een zwakke correlatie, rond de 0,3 is een middelmatige correlatie, en rond 0,5 is een sterke correlatie.
Omdat het model voor de onderwijsachterstandenindicator ontwikkeld is met behulp van de CET, mag verwacht worden dat de correlatie tussen de onderwijsscores en de eindtoetsscores hoger is voor de CET dan voor eindtoetsen van andere aanbieders. Verder kunnen we verwachten dat de correlatie hoger is naarmate er minder gegevens zijn geïmputeerd bij de hoogste opleidingsniveau-variabelen.
Tabel 4.1.1 toont de correlatie tussen de onderwijsscore en de eindtoetsscore uitgesplitst naar eindtoetsaanbieder en schooljaar en tabel 4.1.2 toont de correlatie tussen de onderwijsscore en de eindtoetsscore uitgesplitst naar deelpopulatie, type eindtoetsaanbieder en schooljaar.
| Eindtoetsaanbieder | 2020/'21 | 2021/'22, okt | 2021/'22, feb | 2022/'23 |
|---|---|---|---|---|
| CET | 0.39 | 0,38 | 0,38 | 0,39 |
| IEP | 0.36 | 0,35 | 0,36 | 0,36 |
| ROUTE 8 | 0.37 | 0,37 | 0,37 | 0,38 |
| Eindtoetsaanbieder | Deelpopulatie | 2020/'21 | 2021/'22, okt | 2021/'22, feb | 2022/'23 |
|---|---|---|---|---|---|
| CET | A | 0.13 | 0,15 | 0,16 | 0,17 |
| B | 0.31 | 0,29 | 0,29 | 0,29 | |
| C | 0.31 | 0,3 | 0,3 | 0,29 | |
| D | 0.45 | 0,43 | 0,43 | 0,43 | |
| IEP | A | 0.13 | 0,12 | 0,13 | 0,15 |
| B | 0.27 | 0,27 | 0,27 | 0,26 | |
| C | 0.27 | 0,26 | 0,26 | 0,27 | |
| D | 0.41 | 0,4 | 0,4 | 0,4 | |
| ROUTE 8 | A | 0.13 | 0,14 | 0,15 | 0,16 |
| B | 0.27 | 0,25 | 0,24 | 0,25 | |
| C | 0.25 | 0,28 | 0,28 | 0,27 | |
| D | 0.42 | 0,43 | 0,43 | 0,43 | |
Op basis van tabel 4.1.1 kunnen we concluderen dat de correlatie tussen de onderwijsscores en de eindtoetsscores – conform verwachting – het hoogst is voor de kinderen die de CET hebben gemaakt. Voor de twee andere grote aanbieders – IEP en ROUTE 8 – levert de analyse een minder sterke, maar vergelijkbare correlatie op. Dit patroon is hetzelfde voor alle onderzochte schooljaren. Hoewel de correlaties voor de verschillende aanbieders vergelijkbaar zijn, is geen van de correlaties sterk te noemen. Deze correlaties liggen in lijn met wat verwacht mag worden op basis van de methodologische onderzoeken die ten grondslag liggen aan de onderwijsachterstandenindicator. Wel zien we dat de correlaties redelijk stabiel blijven in de tijd. De correlaties zijn voor oktober 2021 en februari 2022 nagenoeg gelijk, wat betekent dat de herijking van het model weinig invloed heeft gehad op de correlaties tussen onderwijs- en eindtoetsscore.
Kijken we naar de uitsplitsing naar deelpopulatie in tabel 4.1.2, dan zien we dat – conform verwachting – de correlaties voor de deelpopulatie D (het opleidingsniveau van beide ouders is bekend) het hoogst is, maar er is geen sprake van sterke correlatie. Er is met r ≈ 0,13-0,17 een zwakke correlatie tussen de onderwijsscore en de eindtoetsscore voor deelpopulatie A (het opleidingsniveau van beide ouders is onbekend). Voor deelpopulaties B (het opleidingsniveau van de vader is onbekend) en C (het opleidingsniveau van de moeder is onbekend) ligt de correlatie ongeveer twee keer zo hoog als voor deelpopulatie A: met een correlatie van r ≈ 0,25-0,31 is hier sprake van een middelmatige correlatie tussen onderwijsscores en eindtoetsscores in de onderzochte schooljaren.
4.2 Regressieanalyse (alleen CET)
In deze sectie onderzoeken we welk gedeelte van de variantie in de CET-eindtoetsscore door de onderwijsscore wordt verklaard met behulp van een regressieanalyse. Zoals in hoofdstuk 2 uiteengezet, maken we bij de regressieanalyse gebruik van een stapsgewijze aanpak. In deze sectie kijken we alleen naar het startmodel en het uiteindelijke – best passende– model.
Eenvoudig model
Het eenvoudige model is opgebouwd uit de CET-eindtoetsscore als afhankelijke variabele en onderwijsscore als voorspeller (lees: onafhankelijke variabele). Tabel 4.2.1 toont de resultaten van het eenvoudige regressiemodel. De verwachting is dat het model de meeste variantie verklaart voor het eerste cohort en de minste voor het laatste cohort, omdat het tijdsinterval tussen ontwikkeling van de onderwijsachterstandenindicator en het moment van berekenen van de onderwijsscore en de afname van de eindtoets steeds groter wordt (zie ook de derde alinea van de inleiding). Daarnaast is de verwachting dat R2 vanaf februari 2022 afwijkt van de rest, omdat de onderwijsscore voor deze peilmomenten op een andere manier zijn berekend.
| 2020/'21 | 2021/'22, okt | 2021/'22, feb | 2022/'23 | |
|---|---|---|---|---|
| (Intercept) | -22.99 (4.58)*** | -4.06 (4.67) | -23.66 (4.84)*** | -10.08 (4.76)* |
| score | 1.04 (0.01)*** | 1.01 (0.01)*** | 1.04 (0.01)*** | 1.02 (0.01)*** |
| R2 | 0.156 | 0.148 | 0.148 | 0.15 |
| AIC | 576433.6 | 551187 | 551172.5 | 530272.1 |
| *** p < 0,001, ** p < 0,05, * p < 0,1 | ||||
Uit de resultaten zoals weergeven in tabel 4.2.1. kunnen we opmaken dat het model ongeveer dezelfde verklarende kracht heeft voor de laatste drie schooljaren met R² ≈ 0,148-0,150 en het grootste verklarende kracht voor het schooljaar 2020/’21 met R² ≈ 0,156. In dit schooljaar is echter geen eindtoets geweest als gevolg van de coronapandemie. Dit vertekent het beeld. De R2 is hetzelfde voor zowel oktober 2021 als februari 2022. Dit is tegen de verwachting in, maar wel goed nieuws: Dit betekent dat de voorspellende kracht van het herijkte model hetzelfde is als het oude model en dat dit model dus evenveel variantie in eindtoetsscore verklaart. Daarnaast blijft de R2 vooralsnog dus stabiel, wat betekent dat de voorspellende kracht van het model over tijd niet minder lijkt te worden. De analyses voor de komende jaren zullen uitwijzen in hoeverre de verklaarde variantie zich ontwikkelt.
De uitkomsten van het eenvoudige model kunnen we vergelijken met de uitkomsten die zijn beschreven in het eerste methoderapport . Daarin zien we dat wanneer de modelvariabelen als voorspellers zijn opgenomen en de CET-eindtoetsscore als afhankelijke variabele, het model resulteert in een hogere verklaarde variantie (R² = 0,198). Hoewel de verklaarde variantie in het eerste methoderapport hoger is, is er ook een wezenlijk verschil in de gebruikte populaties. De populatie die we hebben gebruikt voor tabel 4.2.1 is inclusief leerlingen waarvoor de onderwijsscore is geïmputeerd. De populatie die is gebruikt voor de uitkomsten in het eerste methoderapport bevat geen kinderen waarvoor de onderwijsscore is geïmputeerd. Verder is de verklaarde variantie in het eerste methoderapport berekend op dezelfde steekproef van kinderen waarop het model voor de onderwijsscore is ontwikkeld. Het is dan geen verrassing dat de verklaarde variantie bij toepassing van de onderwijsscore op een andere populatie iets kleiner is.
Uitgebreid model
Het uiteindelijke – best passende – model heeft naast de CET-eindtoetsscore als afhankelijke variabele en onderwijsscore als onafhankelijke variabele deelpopulatie 3 als tweede onafhankelijke variabele. Daarnaast hebben we in dit model een interactie tussen deelpopulatie en de onderwijsscore opgenomen. In dit model is deelpopulatie D0 de referentiecategorie. De verwachting is dat het model beter aansluit op de data ten opzichte van het eenvoudige model, omdat we rekening houden met (lees: corrigeren voor) de twee verschillende wijzen van imputeren. Tabel 4.2.2 toont de resultaten van het uiteindelijke model.
| 2020/'21 | 2021/'22,okt | 2021/'22, feb | 2022/'23 | |
|---|---|---|---|---|
| (Intercept) | -36.94 (5.61)*** | -15.45 (5.67)** | -35.54 (5.87)*** | -25.18 (5.7)*** |
| deelpop_IMPUTATIEA0 | 195.68 (28.43)*** | 139.84 (29.65)*** | 119.96 (29.86)*** | 108.17 (31)*** |
| deelpop_IMPUTATIEA1 | 338.63 (51.51)*** | 328.33 (48.54)*** | 378.73 (51.5)*** | 412.73 (49.62)*** |
| deelpop_IMPUTATIEB0 | 80.8 (13.87)*** | 89.53 (14.37)*** | 99.12 (14.79)*** | 107.95 (14.67)*** |
| deelpop_IMPUTATIEB1 | 302.23 (27.45)*** | 298.6 (27.64)*** | 317.52 (29.08)*** | 338.06 (29.23)*** |
| deelpop_IMPUTATIEC0 | 56.68 (17.9)** | 56.59 (18.67)** | 51.68 (19.35)** | 77.26 (18.98)*** |
| deelpop_IMPUTATIEC1 | 246.93 (136.32) | 339 (128.65)** | 459.79 (140.4)** | 379.01 (140.45)** |
| score | 1.07 (0.01)*** | 1.03 (0.01)*** | 1.07 (0.01)*** | 1.05 (0.01)*** |
| deelpop_IMPUTATIEA0:score | -0.37 (0.05)*** | -0.26 (0.06)*** | -0.23 (0.06)*** | -0.2 (0.06)*** |
| deelpop_IMPUTATIEA1:score | -0.64 (0.1)*** | -0.62 (0.09)*** | -0.71 (0.1)*** | -0.78 (0.09)*** |
| deelpop_IMPUTATIEB0:score | -0.15 (0.03)*** | -0.17 (0.03)*** | -0.19 (0.03)*** | -0.2 (0.03)*** |
| deelpop_IMPUTATIEB1:score | -0.57 (0.05)*** | -0.57 (0.05)*** | -0.6 (0.05)*** | -0.64 (0.05)*** |
| deelpop_IMPUTATIEC0:score | -0.11 (0.03)** | -0.11 (0.03)** | -0.1 (0.04)** | -0.15 (0.04)*** |
| deelpop_IMPUTATIEC1:score | -0.47 (0.26) | -0.64 (0.24)** | -0.87 (0.26)*** | -0.71 (0.26)** |
| R2 | 0.161 | 0.154 | 0.155 | 0.157 |
| AIC | 575940.2 | 550654.1 | 550595.2 | 529667.9 |
| *** p < 0,001, ** p < 0,05, * p < 0,1 | ||||
Het uiteindelijke model verklaart met R² ≈ 0.157-0,161 in alle onderzochte schooljaren een groter deel van de variantie in de CET- ten opzichte van het eenvoudige model met R² ≈ 0.156-0,150. De verschillen zijn echter marginaal. Daarnaast is de AIC lager voor het complexe model ten opzichte van het eenvoudige model voor elk jaar. De AIC kan alleen tussen modellen binnen hetzelfde jaar worden vergeleken met elkaar, en zoals eerder gezegd betekent een lagere AIC dat het model beter bij de data past.
5. Samenvatting en conclusie
Voor het herziene onderwijsachterstandenbeleid maakt OCW gebruik van de onderwijsachterstandenindicator die het Centraal Bureau voor de Statistiek (CBS) eerder in opdracht van het ministerie heeft ontwikkeld (zie voetnoot 1). Met deze indicator wordt voor alle peuters van 2,5 tot 4 jaar en alle basisschoolleerlingen een onderwijsscore berekend. De hoogte van deze onderwijsscore wordt bepaald door een aantal omgevingskenmerken: het opleidingsniveau van de vader, opleidingsniveau van de moeder, verblijfsduur van de moeder in Nederland, land van herkomst van de ouders, of ouders in de Wet Schuldsanering Natuurlijke Personen (WSNP) zitten en het gemiddelde opleidingsniveau van moeders op school. Conform de Besluiten (zie voetnoot 2) worden deze onderwijsscores geaggregeerd tot achterstandsscores per school en per gemeente. Om deze indicator actueel te kunnen houden, wil OCW de indicator jaarlijks evalueren. Daartoe hebben we verschillende analyses uitgevoerd voor de schooljaren 2019/’20 tot met 2022/’23.9)
In hoofdstuk 3 hebben we gekeken naar de frequentiedichtheid. Daarbij hebben we uitsplitsingen gemaakt naar de modelvariabelen, typen imputatie en eindtoetsaanbieder. In deze verkennende analyse hebben wij geen onverwachte patronen ontdekt. De belangrijkste conclusie die we uit deze analyses kunnen trekken is dat de verdelingen van de frequentiedichtheid over het algemeen stabiel zijn over de schooljaren heen. Het is echter wel zo dat er voor een aantal categorieën een verschuiving in dichtheid voor onderwijsscores plaatsvindt over de jaren heen. Jaar op jaar zijn die verschillen klein, maar als we het eerste jaar met het laatste jaar vergelijken, zijn de verschillen groter. Daarnaast is het zo dat de herijking van de coëfficiënten en schaalwaarden van het model dat gebruikt wordt om de onderwijsscore te bepalen bij een aantal categorieën tot afwijkingen in dichtheid heeft geleid ten opzichte van het oude model. Dit is met name te zien aan de verschillen tussen de peilmoment in oktober 2021 en februari 2022. Omdat de data voor deze peilmomenten voor een belangrijk deel is gebaseerd op dezelfde groep, zijn verschillen tussen deze peilmomenten voor een groot deel te verklaren door verschillen in het onderliggende model.
Zoals verwacht zijn verschillen in bijdrage aan de onderwijsscore voor de betreffende categorieën binnen modelvariabelen (zie figuur 1.1.1) te herkennen in de patronen die de afzonderlijke frequentiedichtheid-verdelingen per modelvariabele in hoofdstuk 3 tonen.
Vervolgens hebben we met correlatie- en regressieanalyses het verband tussen de onderwijsscore en de eindtoetsscore onderzocht. De resultaten van de correlatieanalyse laten een zwakke correlatie tussen de onderwijsscores en de eindtoetsscores zien. Deze correlatie ligt in lijn met wat verwacht mag worden op basis van de methodologische onderzoeken die ten grondslag liggen aan de onderwijsachterstandenindicator. Uitgesplitst naar deelpopulatie zien we dat voor de deelpopulatie waarbij het hoogste opleidingsniveau van beide ouders bekend is, de correlatie het sterkst is. De resultaten van de regressieanalyse laten een lage, maar stabiele verklaarde variantie zien voor de verschillende schooljaren. De herijking van het model dat gebruikt wordt om onderwijsscores te berekenen lijkt hierop ook geen effect gehad te hebben.
Als eindconclusie kunnen we dan ook stellen dat – op basis van de onderzochte schooljaren – het model van de onderwijsachterstandenindicator ieder jaar tot vergelijkbare uitkomsten leidt. Het is weliswaar zo dat er over de jaren heen bij een aantal categorieën wat verschuift in de frequentiedichtheden van onderwijsscores, maar dit leidt vooralsnog niet tot verschillen in de correlaties of in de verklaarde variantie van de regressiemodellen.